A computational study of invariant I₅ in a nearly incompressible transversely isotropic model for white matter

Abstract

The aligned axonal fiber bundles in white matter make it suitable to be modeled as a transversely isotropic material. Recent experimental studies have shown that a minimal form, nearly incompressible transversely isotropic (MITI) material model, is capable of describing mechanical anisotropy of white matter. Here, we used a finite element (FE) computational approach to demonstrate the significance of the fifth invariant (I₅) when modeling the anisotropic behavior of white matter in the large-strain regime. We first implemented and validated the MITI model in an FE simulation framework for large deformations. Next, we applied the model to a plate-hole structural problem to highlight the significance of the invariant I₅ by comparing with the standard fiber reinforcement (SFR) model. We also compared the two models by fitting the experiment data of asymmetric indentation, shear test, and uniaxial stretch of white matter. Our results demonstrated the significance of I₅ in describing shear deformation/anisotropy, and illustrated the potential of the MITI model to characterize transversely isotropic white matter tissues in the large-strain regime.

1 Introduction

Transverse isotropy is one of the most common types of material anisotropy in soft biological tissues (Feng et al., 2013; Humphrey, 2002; Liu et al., 2014; Morrow et al., 2010; Ning et al., 2006; Taber, 2004; Weiss et al., 1996). The mechanical properties of the white matter are important to understand brain injuries such as diffuse axonal injury (Bayly et al., 2005; Iwata et al., 2004). As the white matter consists of distinctly oriented axonal fibers, it is suitable to be treated as a fiber-reinforced, transversely isotropic material (Feng et al., 2013; Ning et al., 2006). In injury-related scenarios (Crisco et al., 2011; Kulkarni et al., 2013), white matter is usually subjected to large deformations; hence, hyperelastic models are typically adopted (Chatelin et al., 2012; Cloots et al., 2008; Labus and Puttlitz, 2016; Ning et al., 2006; Prange and Margulies, 2002; Velardi et al., 2006).

Many strain energy functional (SEF) forms have been studied analytically in the hyperelasticity framework (Criscione et al., 2001; Destrade et al., 2014; Holzapfel and Ogden, 2009; Horgan and Murphy, 2014; Horgan and Saccomandi, 2005; Kulkarni et al., 2016; Lu and Zhang, 2005; Merodio and Ogden, 2005; Schröder et al., 2005; Taber, 2004). For the white matter, most of the SEF forms utilize only the fourth invariant (I₄) (Ning et al., 2006; Velardi et al., 2006). However, recent analytical and experimental studies (Destrade et al., 2013; Feng et al., 2013) have shown that at least two anisotropic invariants, I₄ and the fifth invariant, I₅, are needed to fully characterize the transverse isotropy. To understand the behavior of white matter for large deformations in injury-level loading conditions, finite element (FE) simulations are used (Bayly et al., 2005; Iwata et al., 2004; Ji et al., 2015; Miller et al., 2016; Zhang et al., 2004). However, most of the FE implementations of hyperelasticity are based on a single anisotropic invariant, I₄, which contains only the fiber stretch information (Holzapfel, 2000; Lu and Zhang, 2005; Swedberg et al., 2014), with the corresponding anisotropic component described in a quadratic form (Ning et al., 2006) or in an exponential form (Chatelin et al., 2012; Gasser et al., 2006). The quadratic form was usually referred to as standard fiber reinforcement model (SFR) (Qiu and Pence, 1997). Therefore, it is essential to integrate both I₄ and I₅ invariants into the transversely isotropic model for the white matter, especially in a large-deformation framework relevant to brain injury.

Previously, a minimal form of nearly incompressible transversely isotropic (MITI) model, containing invariants I₄ and I₅, was proposed in the small-strain regime (Feng et al., 2013). Here, we extend the MITI model to the large-strain regime by investigating the role of I₅ for modeling the white matter. Specifically, the MITI model was first implemented and validated by comparing the FE predictions with analytical solutions of typical canonical mechanical testing scenarios. Next, performance of the MITI model was compared with the SFR counterpart to demonstrate the significance of I₅ in biomechanical applications for large deformations.

2 Methods and Materials

2.1 Material model and FE implementation

For the invariant-based formulation of the strain energy function, a transversely isotropic material can be expressed in terms of the five invariants of the right Cauchy-Green deformation tensor C = F^TF (Holzapfel, 2000; Spencer, 1984):

$$\begin{array}{c}{I}_1=tr(\mathbf{C}),I_2=\frac{1}{2}\left[{(tr(\mathbf{C}))}^2-tr({\mathbf{C}}^2)\right],I_3=\det (\mathbf{C})=J^2,\\ I_4=\mathbf{A}·\mathbf{C}\mathbf{A},I_5=\mathbf{A}·{\mathbf{C}}^2\mathbf{A}.\end{array}$$ (1)

Here, J = det(F) and A is the unit vector of the fiber direction in the reference configuration. The SEF of the MITI material is described by (Feng et al., 2013):

$$\psi =\frac{\mu }{2}[(I_1-3)+\zeta {(I_4-1)}^2+\varphi I_5^{\ast }],$$ (2)

where $I_5^{\ast }=I_5-I_4^2$ is a modified invariant containing fiber shear information, and μ,ζ,ϕ are the model parameters. Note that when ϕ=0, the MITI model is reduced to the standard fiber-reinforced (SFR) model (Qiu and Pence, 1997). To implement the MITI model of Eq. (2), we adopted the decoupled form of the deformation gradient tensor, $\overline{\mathbf{F}}=J^{-1/3}\mathbf{F}$ (Simo and Hughes, 1998), which leads to the following decoupled SEF form:

$$\overline{\psi }=\frac{\mu }{2}[({\overline{I}}_1-3)+\zeta {({\overline{I}}_4-1)}^2+\varphi \overline{I_5^{\ast }}]+U(J)$$ (3)

where the corresponding decoupled invariants are ${\overline{I}}_1=J^{-\frac{2}{3}}{I}_1,{\overline{I}}_4=J^{-\frac{2}{3}}{I}_4,{\overline{I}}_5^{\ast }=J^{-\frac{4}{3}}{I}_5^{\ast },$ and u(J) is a penalty term to enforce material incompressibility (with к as the bulk modulus). The MITI model in Eq. (3) was implemented into a nonlinear FE simulation package ABAQUS/STANDARD™ (ABAQUS 6.12, SIMULIA, Providence, RI) using a customized user subroutine UMAT (Young et al., 2010). For simulations of biological tissues, we adopted U(J) = к[(J − 1)²/2 − InJ] (Young et al., 2010), and a large bulk modulus κ for modeling a nearly incompressible transversely isotropic material (Simo and Hughes, 1998)

2.2 Verification of the FE implementation

To verify the implementation, we simulated several canonical mechanical testing scenarios in the large-strain regime and compared the FE results with the analytical solutions (Feng et al., 2016). In these simulations, a single element (C3D8H) with uniaxial stretching (Jacquemoud et al., 2007), biaxial stretching (Sacks, 2000; Sacks, 1999), and shear deformation was considered. Specifically, we simulated the following stretch cases: (i) uniaxial stretching parallel to the fiber direction (Figure 1a), (ii) uniaxial stretching perpendicular to the fiber direction (Figure 1b), and (iii) equibiaxial stretching (Figure 1c). In each case, the fiber direction was set to be along the X₁ axis, and the stretch was applied up to a stretch ratio of 1.5. For shear deformation cases, we simulated (i) simple shear parallel to the fiber direction (Figure 1d), (ii) simple shear perpendicular to the fiber direction (Figure 1e), and (iii) simple shear 45° to the fiber direction (Figure 1f). In each case, a simple shear deformation was imposed by a displacement, d=1.5, along the shearing direction.

Figure 1.

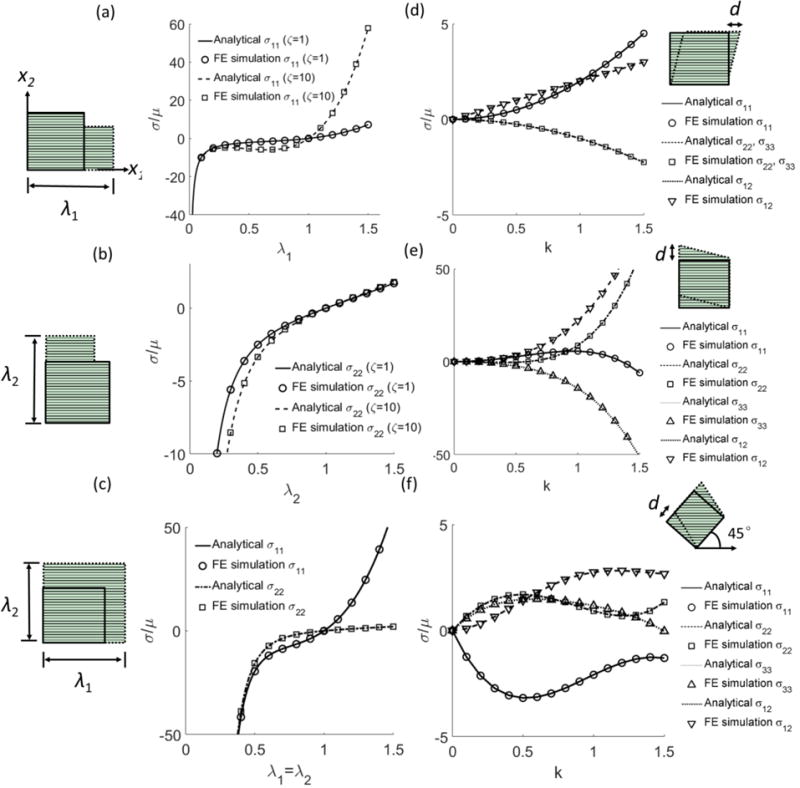
Comparison of the analytical solutions and FE simulation results of the MITI model for stretch and shear deformation. Uniaxial stretching (a) along and (b) perpendicular to the fiber direction with ζ=1, and 10. (c) Equibiaxial stretching with ζ=10. Simple shear with shear displacement (d) along, (e) perpendicular, and (f) 4 5° with respect to the fiber direction (ζ=10, and ϕ=1). Other model parameters are μ=2.5 kPa, к=10⁶ kPa. The fiber direction is along the x₁ axis in the reference configuration. The plane of symmetry is perpendicular to x₁.

2.3 Effect of I₅

To investigate the effect of I₅, we compared the SFR and MITI models by (i) simulating a plate-hole structure in simple shear, (ii) inverse modeling of white matter indentation in large strain, and (iii) fitting shear and stretch data of the white matter experiment.

2.3.1 Simulation of a plate-hole structure

A rectangular plate of 32×16 and a unit thickness with a circular hole (r = 3) at the center was considered. The dimensions of the plate were normalized with respect to the unit thickness of the plate and the geometry was meshed by 902 C3D8H elements. The material parameters for the following simulations of uniaxial stretching and simple shear deformation were μ=2.5 kPa, ζ=5.0, ϕ=0.5, which were close to the estimated parameters of the white matter (Feng et al., 2017; Feng et al., 2013). The SFR material model was simulated by setting ϕ=0. The fiber directions were set to 0°, 45°, and 90° with respect to the X₁-axis. A uniform displacement was applied on the top surface of the plate-hole structure with the bottom surface fixed. The shear displacement on the top surface was set to be 3.2, rendering an approximate shear angle of 11.3°. Simulations using the two material models were carried out for three configurations of the fiber direction (Figure 2).

Figure 2.

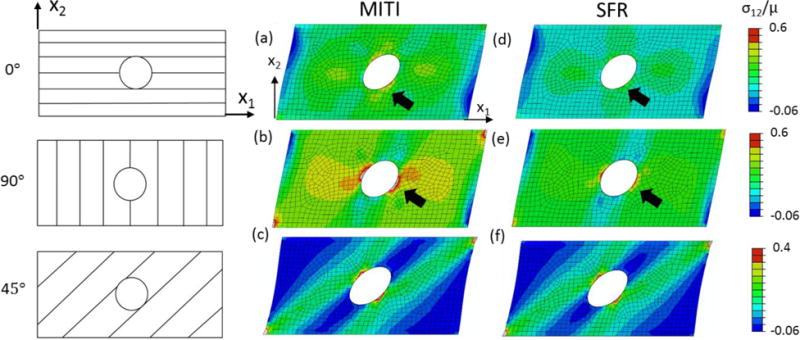
Predictions of the shear deformation of a plate-hole structure with fibers (a, d) 0°, (b, e) 90°, and (c, f) 45° with respect to the x1-axis (1st column on left). The material used: (a–c) MITI model, (d–f) SFR model. The shear stress (σ12) is normalized with respect to μ. Arrows indicate a large differences of stress distribution around the hole between the MITI and SFR models.

2.3.2 White matter indentation

The MITI material model has been used to interpret asymmetric indentation tests of white matter both in the small strain (Feng et al., 2013) and large strain (Feng et al., 2016) regime. To illustrate the effect of I₅, we applied the same genetic algorithm based inverse modeling method (Lee et al., 2014) to estimate the SFR model parameters as used for the MITI model (Feng et al., 2016). Parameter estimates of the SFR model from 10% indentation data of white matter were compared with those of MITI model.

2.3.3 Fitting experiment data of white matter

Previous studies have identified mechanical tests that have special utility for fitting of transversely isotropic constitutive models (Feng et al., 2016). Prange and Margulies (2002) carried out comprehensive shear tests of white matter and measured the parameters of the Ogden hyperelastic material model from a series of shear tests. Therefore, we simulated the shear tests in the plane of isotropy and along the fiber direction with the estimated model parameters using FEBio (Maas et al., 2012). Labus and Puttlitz (2016) measured the responses of the white matter using uniaxial and biaxial tensile tests. We fitted these data using both the MITI and SFR model using the following procedure (Feng et al., 2016): (i) estimation of parameter μ by fitting the shear response in the plane of isotropy; (ii) estimation of parameter ζ by fitting the uniaxial tensile response along the fiber direction; (iii) estimation of parameter ϕ by fitting the shear response along the fiber direction.

3 Results

The FE simulation results agreed well with the analytical solutions in all of the canonical deformation cases (Figure 1a–f). Shear deformation of the plate-hole structure showed the circular hole was deformed into an ellipse, with the major axis tilted toward the first quadrant for both material models (Figure 2). Compared with SFR model, the MITI model had a larger stress distribution when the shear displacement was along and perpendicular to the fiber direction, especially around the center hole when the fibers were in shear (Figure 2a, b). When the shear displacement was 45 degrees to the fiber direction, both models had similar stress responses for there was little shear deformation of the fibers (Figure 2c, f).

With regard to parameter estimates from the indentation test, compared with the MITI model estimate (μ=1.49 kPa, ζ=4.68, and ϕ=0.68) (Feng et al., 2016), the estimated parameters of the SFR model were μ=1.48 kPa, and ζ=7.07. The R² values for the 0-deg and 90-deg tests were 0.860 and 0.924 for the SFR model, and 0.998 and 0.994 for the MITI model, respectively (Figure 3). F-tests showed that the MITI model fitted both 0-deg and 90-deg indentation data better than the SFR model (p<0.05).

Figure 3.

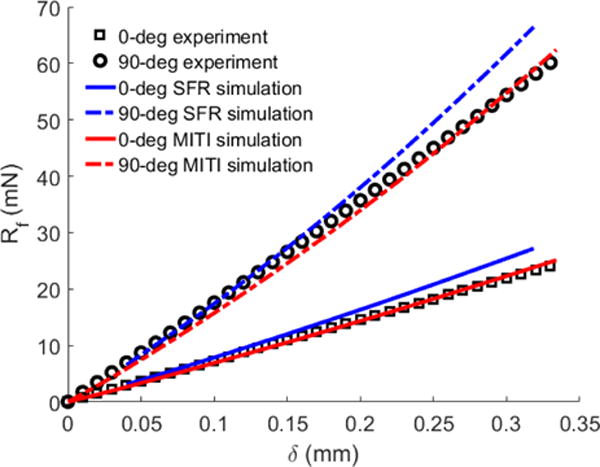
Comparisons of the simulation and experimental results of the asymmetric indentation test of the brain white matter with 10% indentation strain. R_f is the indentation force and δ is the indentation displacement. The FE simulation with the MITI model were adopted from Feng et al. (2016) (μ=1.49 kPa, ζ=4.68, ϕ=0.68). The R² value for the 0-deg and 90-deg tests were 0.9977 and 0.9940, respectively. The same indentation data set was used to estimate the SFR model (μ=1.48 kPa, ζ=7.07). The R² value for the 0-deg and 90-deg tests were 0.8595 and 0.924, respectively.

Moreover, although both MITI and SFR model can be used to fit testing data of the shear deformation in the plane of isotropy and uniaxial stretch along the fiber direction (Figure 4a, b), the SFR model could not simultaneously fit the data of simple shear along the fiber direction well (Figure 4c). The estimated parameters for the MITI model were μ=205.78 Pa, ζ=1.96, and ϕ=0.39, whereas only μ and ζ were obtained for the SFR model with the same values.

Figure 4.

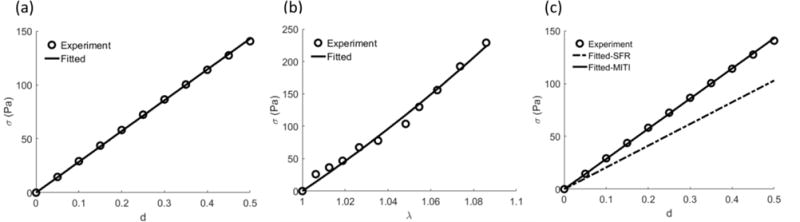
Experimental data from simple shear (Prange and Margulies, 2002) and uniaxial stretch (Labus and Puttlitz, 2016) of white matter and the corresponding fitted results. (a) Simple shear in the plane of isotropy (X₁∓X₃). (b) Uniaxial stretch along the fiber direction (X₁). The fitted curves were the same for both SFR and MITI models. (c) The SFR model could not fit the data of simple shear along the fiber direction at the same time.

4 Discussion

In a previous study (Feng et al., 2013), the necessity of including invariant I₅ was demonstrated by experiments in the small strain regime. In this paper we showed the effect of including I₅ in a computational framework in the large strain regime. By comparing with the SFR model, we selected experimental data from literature to illustrate the application of MITI model in modeling white matter for large deformations.

4.1 Effect of I₅

In the simple shear of the plate-hole structure, when the fiber was along the X₁-axis, the MITI model predicted a 51% higher concentrated stress than the SFR counterpart (Figure 2a, d). When the fiber was perpendicular to the X₁-axis, the MITI model predicted a concentrated stress around the hole ~90 times higher than that of SFR (Figure 2b, e). Both cases had a large shear deformation of the fibers. When the fiber was 45°, the difference of the predicted stress around the hole was within 5% (Figure 2c, f), since fiber stretch, rather than fiber shear, is dominant in this case. These results indicated that when shear deformation is large, the contribution of anisotropic invariant I₅ plays a critical role. These observations also suggested the importance of the fifth invariant and the potential of the MITI model to study fiber-reinforced soft biological tissues.

4.2 Applications to the white matter

In the previous experimental study, we have shown that the inclusion of I₅ is necessary to explain mechanical anisotropy in the small-strain regime (Feng et al., 2013). In the current study, we compared the parameter estimates from the inverse FE modeling between the MITI and SFR models. Results showed that, in the large-strain regime, inclusion of I₅ is necessary to characterize both the 0-deg and 90-deg indentation tests. Although the estimated shear modulus μ was similar for both the MITI and SFR models, the estimated ζ value of the SFR model was about 1.5 times of that MITI model, indicating that the estimated ζ has combined shear contributions of the indentation tests. However, the SFR model had a relatively lower R² value in experimental data fitting, indicating that it is less accurate in describing large shear deformation.

Finally, by fitting the shear and tensile tests data, we have shown that although the SFR model can describe the shear in the plane of isotropy and uniaxial stretch along the fiber direction, it cannot capture different shear modes and the stretch simultaneously. On the other hand, the MITI model was able to better represent the mechanical behaviors of both the shear and tensile tests. These results indicated that it is necessary to include invariant I₅ when modeling white matter with large shear deformation.

5 Conclusions

White matter with aligned axonal fibers can be modeled as a transversely isotropic material. In this study, we demonstrated the effect of I₅ on modeling the white matter tissue in a computational framework. By comparing the model performance to the SFR counterpart in a structure problem and in describing white matter experiments, we showed that the inclusion of I₅ is critical in large shear deformations. Applications of the MITI model to white matter showed that this model was capable of properly capturing tissue behaviors, especially for shear in the large-strain regime. Future studies include applications of the model to biaxial experiments of cardiovascular tissues (Sacks, 2000; Sacks, 1999) and indentation/compression tests (Namani et al., 2012; Rashid et al., 2013), and incorporating the white matter anisotropy to improve injury predictions in realistic human head FE models (Giordano and Kleiven, 2014; Miller et al., 2016; Zhang et al., 2004; Zhao et al., 2016).