Strategies for handling missing clinical data for automated surgical site infection detection from the electronic health record

Abstract

Proper handling of missing data is important for many secondary uses of electronic health record (EHR) data. Data imputation methods can be used to handle missing data, but their use for analyzing EHR data is limited and specific efficacy for postoperative complication detection is unclear. Several data imputation methods were used to develop data models for automated detection of three types (i.e., superficial, deep, and organ space) of surgical site infection (SSI) and overall SSI using American College of Surgeons National Surgical Quality Improvement Project (NSQIP) Registry 30-day SSI occurrence data as a reference standard. Overall, models with missing data imputation almost always outperformed reference models without imputation that included only cases with complete data for detection of SSI overall achieving very good average area under the curve values. Missing data imputation appears to be an effective means for improving postoperative SSI detection using EHR clinical data.

1. Introduction

With the widespread adoption of Electronic Health Record (EHR) systems, progressively greater amounts of electronic clinical data are being generated, making researchers, healthcare administrators, and clinicians alike increasingly interested in the secondary use of EHR data to improve clinical knowledge and our ability to deliver patient care. With respect to clinical research and quality improvement, the availability of EHR data offers new opportunities for knowledge advancement covering a wide range of categories including clinical and translational research, public health surveillance, and healthcare quality measurement and improvement^1,2. Among these, EHR-based detection of specific outcomes and adverse conditions (e.g., diabetes incidence³_, adverse drug interactions⁴, Clostridium difficile infection relapse⁵), related risk factors, or risk stratification of patient populations may add particular value to clinical stakeholders.

1.1 Significance and purpose of postoperative complication detection models

The American College of Surgeons (ACS) National Surgical Quality Improvement Project (NSQIP) is widely recognized as “the best in the nation” surgical quality improvement resource in the United States⁶. With the guidance of NSQIP, participating hospitals track outcomes around the process of surgical care by manually abstracting and collecting preoperative, intraoperative, and postoperative clinical data elements and morbidity/complication occurrences. The preoperative and intraoperative clinical data elements include patient demographics, co-morbidities and disease history, functional status, laboratory results, operation duration, and wound classification scores. Postoperative morbidity outcomes include 21 well-defined adverse events (i.e., complications) within the 30-day postoperative window and are labor intensive to accurately abstract and detect. These adverse event occurrences include surgical site infections (SSIs), urinary tract infections, and acute renal failure, etc. Because data collection for NSQIP is labor intensive, only a subset of surgical patients are selected annually at each hospital for inclusion into NSQIP (based on a cyclical schedule and a certain target number with stratified sampling to preferentially select major surgical cases). For each of these patient cases, all preoperative, intraoperative, and postoperative data are collected and included in NSQIP.

NSQIP uses the collected data from all member hospitals to calculate the hospital’s relative performance with respect to adjusted postoperative morbidity and mortality and compares each member hospital’s performance with a benchmark for each postoperative adverse event. Specifically, a ratio of observed to expected number of events is provided to each hospital for each event adjusted by patient morbidity, case complexity, and a number of other factors⁷. An O/E ratio of 1 means the performance is as expected for a particular outcome given the composite patient and case severity, whereas less or greater than one indicates better or worse performance, respectively⁸. With this feedback, NSQIP member hospitals are able to focus on areas of improvement and have achieved measurable improvement in surgical care quality and in many cases have saved money by reducing length of stay and preventable readmissions^7,8.

The success of NSQIP in improving surgical quality for member hospitals is ensured by the high quality collection of the preoperative and postoperative clinical data elements performed with manual abstraction as follows. To maintain the high reliability of this data collection, formally trained surgical clinical reviewers (SCR) are employed by hospitals to select surgery cases strictly following NSQIP inclusion and exclusion criteria, manually extract preoperative data characteristics, and then recognize and record postoperative morbidity events and mortality. The NSQIP data elements abstraction process based on manual clinical charts review is very time and labor intensive, which makes NSQIP expensive to implement, but overall it provides very high quality and trustworthy data to frontline clinical stakeholders. Unfortunately, mainly due to this costly manual manner of clinical data collection and other costs like its associated participation fee, less than 20% of hospitals in the United States currently are enrolled in NSQIP⁹. To make NSQIP more accessible, one proposed and promising solution is to accelerate the process of data extraction by automatically abstracting NSQIP elements from EHR systems. Accordingly, the ultimate goal of our study is to utilize automated techniques, specifically machine-learning, to classify surgical patients with or without particular postoperative adverse events.

In this manuscript, we focus on the detection of SSIs within 30 days after surgery; however, we expect this methodology to generalize to other postoperative adverse events, as well. An SSI is an infection occurring after surgery in the part of body where surgery took place. Nationally standardized definitions of SSIs used by NSQIP and the Centers for Disease Control and Prevention (CDC) through the National Healthcare Safety Network (NHSN) can be classified into superficial, deep, and organ space, based on the depth and severity of infection¹⁰. Although most surgical patients do not experience an SSI, SSIs are very costly and morbid, and certain areas of surgery, like colorectal surgery, have relatively high incidence of SSIs (i.e., between 7 to 20%)¹¹. SSIs are also associated with increased costs, length of hospital stay, readmission rates, and mortality¹². An SSI costs between 6,200 to 15,000 US dollars per patient, and up to 10 billion US dollars per year in the United States alone¹³ and has become a particular area of interest nationally under government performance-based programs such as value-based purchasing.

The overall aim of this research is to develop valid, robust, and practical EHR-derived models for detecting three kinds of postoperative SSI and overall SSI. Compared with administrative data or claims data upon which several previous studies relied^14,15, EHR data contains richer clinical information (e.g., vital signs, lab results, social history information), which might provide important additional significant indicators to aid in SSI detection. Our use of EHR data is more likely to allow the construction of more detailed and informative SSI detection models.

1.2 Capturing the context of “missing data”

Unfortunately, secondary use of EHR data can be challenging due to the inconsistent and incomplete nature of patient records within the EHR. The presence or absence of elements, the timing and sequence, and other characteristics of the collected data can vary greatly from patient to patient. Sometimes necessary or expected data elements might be missing in a patient’s record. Missing data rates in the EHR have been previously reported from 20% to 80%^{16, 17}. In this study, we were interested in clinical data between postoperative day 3 to 30 (which we refer to as the postoperative window henceforth) because the first two days after surgery often constitute a recovery period, where abnormal measurements are common and may simply be a result of healing from the trauma caused by surgery, rather than a sign of SSI. During the postoperative window, the problem of missingness commonly exists for many data elements. Researchers traditionally categorize missing data mechanisms into three types according to the characteristics of the missingness: missing completely at random (MCAR), missing at random (MAR), and missing not at random (MNAR)^18,19.

• MCAR - Causes of missingness are not related with any characteristics of the dataset (e.g., whether a data point is missing is not related with any values in the dataset). For example, the urine culture test is usually ordered to help make diagnosis of urinary tract infection. However, a urine sample might be randomly broken and the test result is missing completely at random.

• MAR - Data are not missing at random, but the probability that a data element is missing depends on values of other observed variables in the dataset. As an example, suppose men are more likely to drop out of a clinical trial, but the chance of dropping out is the same for all men. We can say that male subjects are just MAR. Both MCAR and MAR are viewed as ignorable missingness.

• MNAR - When the likelihood of missingness is related to missing variables, a third type of non-ignorable non-response missingness, MNAR, arises. For example, consider a study aiming to evaluate treatments to reduce cocaine use. In this hypothetical study, the outcome drug level is measured from a urine drug test every Monday morning. Participants who use cocaine over the weekend and do not show up for their urine test would be expected to have higher cocaine metabolites. Therefore, the likelihood of the data being missing is directly related to the unobserved cocaine level, which is viewed as MNAR.

The traditional three missing data categories are not sufficient to capture the complexity of missing data in EHR-derived applications. Missing data in EHR-derived datasets could be caused by a lack of collection or a lack of documentation²⁰. Lack of collection, for example, refers to orders or other items that are not placed or measured. In this instance, the missing data element is typically a negative value, i.e. a normal state patient. Alternatively, the.clinician may not be considering the measurement since the test or measure is thought to be low yield for the patient in question. Such missing values are MNAR. Lack of documentation refers to orders or other items that are placed or performed but the response values are not recorded or obtained during the process of data collection. In this instance, data was lost during the extraction, transformation, and loading (ETL) of clinical data²¹. Such missing values are MCAR or MAR. Furthermore, a good working knowledge of the specific research question is likely helpful for understanding missing data mechanisms and potentially for selecting the most suitable missing data imputation methods for a particular secondary use application of EHR data.

In our SSI detection use case with EHR data, possible missing data can potentially be caused by either lack of collection or lack of documentation and thus we are facing a mixture of MNAR and MCAR/MAR mechanisms. In the situation of lack of collection, for example, a white blood cell (WBC) count is usually measured repeatedly to monitor a patient’s status after surgery. However, WBC test is not necessarily ordered for all patients—patients doing well clinically are less likely to have the WBC test. Similarly, an image-guided order with interventional radiology related to SSI treatment or a microbiology culture test is less likely to be placed on patients for whom there is minimal to no suspicion of an SSI. There are also examples of lack of documentation. For instance, the microbiology gram stain specimen from a wound suspected of harboring an SSI may be sent to an outside laboratory and therefore not recorded in the system. It is difficult to tell to which category of data missingness a case of missingness belongs (e.g., lack of collection or lack of documentation). Additionally, performance of common missing value imputation methods in the context of MNAR is unknown. Therefore, we need to explore and compare different missing data imputation methods, and find the most suitable approach.

1.3 Related work

Though numerous missing data treatments have been developed, selecting the most appropriate one depends strongly on the problem at hand^22,23. Overall, most studies have not demonstrated one technique to be universally better than others. This section briefly summarizes traditional statistical and model-based methods. Our aim is to suggest ways that clinical research practitioners without extensive statistical backgrounds can handle missing data by exploring several of the most commonly used strategies to handle missing data for the real problem of postoperative SSI detection with EHR data.

The most common and easiest method is to exclude cases or single variables with missing data. Researchers either consciously or by default drop incomplete cases since many statistical and machine learning tools operate on complete cases and only rarely have built-in capabilities to handle missing data^24,25. However, discarding cases or variables with missing data not only decreases the number of available cases in a given dataset but may also result in significant bias^26,27. As an alternative to complete-case analysis, many researchers will impute missing values for variables with a small percentage of missing data^28,29, such as using the mean value of the observed cases on variables of interest. However, filling in the mean value usually causes standard errors to appear smaller than they actually are, since it ignores the uncertainty of missing data³⁰.

Compared with filling in the mean value, advanced methods, such as multivariate and maximum likelihood imputation, were developed several decades ago. In particular, multivariate imputation enables researchers to use existing data to generate or impute values approximating the “real” value and has been widely applied in clinical data analysis^31,32. In addition, multivariate imputation by chained equations (MICE) approach generates a regression model for each variable with missing data, with other variables as predictors, to impute the missing data. This method, being a regression model, can handle different types of variables (continuous or discrete). More recently, imputation methods based on more sophisticated models have been developed. Some well-known approaches, such as multilayer perceptron, self-organizing maps, and K-nearest neighbors (KNN), have been employed as the predictive models to estimate values for the missing data in specific applications such as breast cancer diagnosis, detection of cardiovascular patients and intensive care unit monitoring^33,34. However, for clinical researchers, most complicated methods typically are not easy to implement. Also, to date they have failed to show a convincing and significant improvement over univariate imputation (e.g., filling in the mean value or MICE).

At the present time, most algorithms apply to MCAR or MAR. Imputation for MNAR is generally not recommended, and hence few algorithms exist. Algorithms like selection method and pattern mixture models could jointly model data and missingness. The former assigns weights to observations based on their propensity for missingness³⁵, while the latter constructs imputation models for each pattern of missingness³⁶. Both methods have the potential to reduce bias in the results. However, due to their untestable assumptions, they may perform worse than imputation methods developed for MCAR or MAR. Several researchers have previously applied the combination of Fourier transformation³⁷ and lagged KNN to impute biomedical time series data in which up to 50% of data are missing³⁸.

In our work, the potential for non-random missing data exists. Discarding patients with missing values would be a conservative choice. However, if we discarded all observations (patients) that contain missing values, we would discard close to 80% of our study population. This alone could fatally bias the results and hence imputation is imperative. In this work, we seek to explore several commonly used missing data imputation methods in our SSI dataset to increase our sample size and to avoid discarding a large portion of patients with missing values. In particular, eight imputation methods were used to fill in absent values for lab tests and vital signs in the postoperative SSI dataset. To compare different imputation methods, the performance of multiple detection models based on different missing data treatments were evaluated by using the reference standard SSI outcome from NSQIP.

2. Materials and Methods

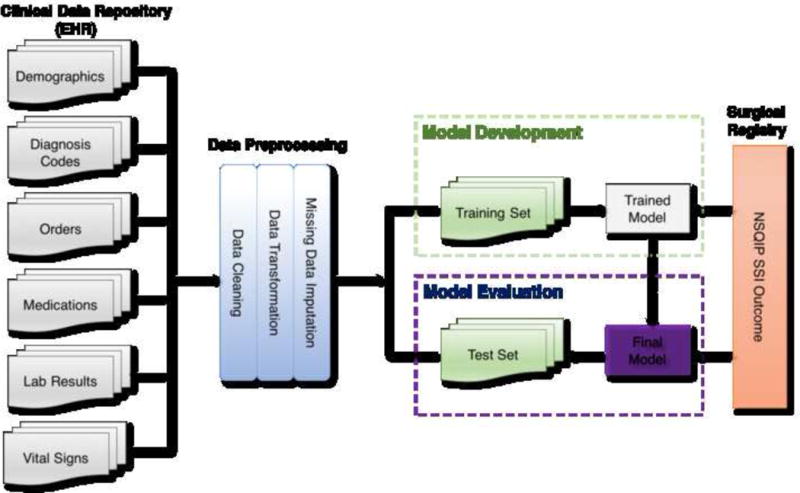
Our overall methodological approach for this study included five steps: (1) Identification of the surgical patients and associated EHR data from the University of Minnesota clinical data repository; (2) Data preprocessing; (3) Handling missing data by using different imputation methods; (4) Supervised learning model development using different imputed datasets seperately; (5) Evaluation of final models using reference standard SSI outcome data from the NSQIP registry. Institutional review board approval (IRB) was obtained and informed consent waived for this minimal risk study.

2.1 Data Collection

The clinical data repository (CDR) at the University of Minnesota Medical Center (UMMC) is a database that makes EHR data accumulated from a larger, tertiary care medical center available for researchers. We extracted clinical EHR data from CDR for surgical patients included in the NSQIP registry 2011 through 2013 and retrieved their NSQIP postoperative SSI outcome from the registry. The patient’s medical record number and date of surgery were used to link CDR data to the NSQIP registry. Though UMMC has been a member of NSQIP since 2007, the CDR only has consistent clinical data since 2011 when the institution implemented its current Enterprise EHR system (Epic systems). Patients without matching records in the CDR (22 total, from incorrectly entered medical record numbers) were removed. Our goal was to assess the models’ robustness in the face of changes that take place over time, since the purpose of our model will be to ultimately detect future SSIs. Thus, our dataset was divided into a training set of patients with surgery dates between 2011 to the end of 2012 and a test set of patients with surgery dates in 2013. The training dataset was used for model development, while the test set was used solely for evaluation of the models we developed.

The standard definition of SSI by CDC has been used by NSQIP reviewers³⁵ to determine if a patient experienced an SSI. However, some clinically important indicators mentioned in the standard definition, such as imaging orders and cultures, are not included in the NSQIP elements. We collected relevant data elements from six types of data: demographics, medications, orders, diagnosis codes, lab results and vital signs, based on the opinion of three content experts (all surgeons familiar with NSQIP definitions and the EHR). Demographics contained each patient’s basic information (e.g., gender, race, age). Among medications, we focused only on the use of antibiotics after surgery. Orders known to be associated with the diagnosis and treatment of an SSI were also gathered from CDR, including orders of imaging studies, infectious disease consultation, and interventional radiology drainage procedures for abscess drainage. Diagnosis codes consisted of relevant ICD-9 codes created during the encounter and hospital stay at the time of surgery from coding, as well as diagnoses from the past medical history and problem list. Lab values (e.g., WBC, hemoglobin, lactate, etc.) and vital signs (e.g., temperature, pain scale, etc.) before surgery and those generated during the postoperative window after surgery were extracted, as well, from the CDR. Microbiology cultures, such as wound culture, abscess culture, were collected. We also included surgical wound classification and American Society of Anesthesiologists (ASA) physical status classification that was recorded prior to surgery³⁹. The surgical wound classification is used to grade intra-operative wound contamination, which is highly correlated with the chance of developing a postoperative SSI, and is part of intra-operative case documentation. ASA classification reflects a patient’s overall status with respect to surgical risk from normal healthy patient to a brain-dead patient⁴⁰.

2.2 Data Preprocessing

Data preprocessing consisted of transforming the data (if necessary), and correcting any inappropriate formating in the data for further modeling (e.g., the erythrocyte sedimentation rate value could be entered as “56 H” in EHR system, however, to keep the value consistent in numerical format for further modeling, we needed to remove “H”.) Lab results and vital signs, viewed as continuous variables, are measured periodically. The resulting longitudinal data were summarized into three features: two extreme values (highest and lowest values) as well as average value during the postoperative window. To establish a baseline, the preoperative extreme and average values were also extracted. Binary features (taking the values of 0 and 1) are created for medications, orders and diagnosis codes, indicating the presence or absence of that data element during the postoperative window. For example, the value of 1 for a particular antibiotic (medication) signifies that the patient received the antibiotic during the postoperative window. Another two variables, ASA score and wound classification, are ordinal variables with multiple levels. A univariate logistic regression model was used to compare the effects of different levels, and levels regrouping might be necessary. In our dataset ASA classes I and II were grouped and classes III, IV, V and VI were grouped. For wound classification, classes I and II were grouped and classes of III and IV were grouped. We made age an ordinal variable—above the age of 65 and under 65. Other SSI risk factors, such as smoking, alcohol use, history of diabetes, anesthetic type, etc., however, were not selected as significant indicators to SSI by the detection model in our pilot study using the completed dataset, therefore, were not included in this study⁴¹.

All the data were transformed into a data matrix amenable to statistical modeling. The rows of this matrix correspond to patients and the columns to features (predictors). It is worth noting that a patient may have multiple visits during the postoperative window. All the EHR data generated during the postoperative window were collected for modeling.

2.3 Missing Data Imputation of the Incomplete Dataset

We define a missing value as a specific lab result or vital sign that is missing entirely during the postoperative window. For example, a patient’s WBC values could be completely missing during the postoperative window. In this instance, there is no way to summarize the WBC values. We need to impute the WBC related variables (i.e., maximum WBC, minimum WBC, and average of WBC). If a patient has several WBC measurements during the postoperative window, imputation is unnecessary. In this work, mean-imputation, 0-imputation, imputing normal values, and MICE methods were utilized. In the case of first three non-model-based methods, for each feature, a single value is imputed every time the value for that feature is missing. For example, in case of “mean” imputation, for each feature, the mean of the non-missing entries was calculated in the training dataset and imputed into both the training and test datasets every time the value was missing for that feature. In case of “0” imputation, we simply imputed the numeric value “0” for every missing entry; and in case of “normal” imputation, the average value of patients in the training set with no postoperative SSI was imputed into both the training and test datasets.

Non-model-based imputation ignores the concept that related features can be used to “predict” what the missing value could be. In MICE method, we utilized linear regression modeling to impute missing values based on the non-missing values of other features, essentially a multivariate imputation through chained equations⁴².

In the course of imputation, bias can be introduced when values are not missing at random. To reduce some of this bias, indicator variables were used. An indicator variable, implemented as a dummy variable, takes the values of 1 and 0; 1 indicates that the corresponding value is missing. For example, if a dummy variable for postoperative WBC is created and takes the value 1 for a patient (observation), then the patient in question does not have any postoperative WBC value during the postoperative window; the corresponding features (minimal, maximal postoperative WBC) contain imputed values. In total, for our dataset, this resulted in 15 original features, 33 transformed features and 22 dummy variables. Table 1 summarized the different imputed datasets by different methods.

Table 1.

Imputed datasets with eight imputation methods.

Imputed Datasets	Imputation Method
Mean	filling in the mean of all non-missing observations in training set; filling in the mean of all non-missing observations in test set, separately
Normal	filling in the mean of non-SSI patients in training set; filling in the mean of non-SSI patients in test set, separately
MICE	using multivariate regression model
0	filling in 0 for all missing values
Dummy+Mean	adding dummy variables to model “mean”
Dummy+Normal	adding dummy variables to model “normal”
Dummy+MICE	adding dummy variables to model “MICE”
Dummy+0	adding dummy variables to model “0”

2.4 Model Development

After missing data imputation, eight datasets (including both training and test sets) based on different imputation methods were prepared, and detection models for each kind of SSI and overall SSI were constructed on the eight training sets. Features were pre-selected based on expert opinion. Variables irrelevant to SSI were eliminated. Backwards elimination was utilized for data-driven feature selection. One logistic regression model for each SSI type (including overall SSI) was built for each training set, and no regularization terms were used. We also developed one SSI detection model for each SSI type without imputation, by discarding all records with missing values. This served as the reference model.

2.5 Model Evaluation

The performance of the SSI detection models was evaluated both on the training set and on the leave-out test set. In order to assess the detection performance of the model on the training set, 10-fold cross validation (CV) was employed and the values of area under the curve (AUC)⁴³, as well as the bias, were calculated. AUC is an accepted performance metric and quantifies the ability of a model to discriminate between positive and negative outcome. Bias is used to examine whether the estimation of outcome systematically differs from the true outcome¹⁸. The closer the absolute value of bias is to 0, the smaller the bias is for SSI detection. Positive or negative bias indicates the overestimate or underestimate of a model.

Evaluating the reference model raises important issues. We could evaluate its performance on the unimputed test dataset as a reference. However, the reference model would not be able to make predictions for the vast majority of patients, since many (around 50%) would be deleted due to missing values. For this reason, we applied the reference model (without imputation) to all imputed test sets and selected the one with best performance as the performance for the reference model. The reference model was evaluated on each imputed test dataset. Every model that was constructed on a specific imputed training set was evaluated by the imputed test set that used the same imputation method.

3. Results

We retrieved the clinical data from EHR for 4,491 patients in the NSQIP registry at UMMC between 2011 and 2013. Table 2 includes detailed demographic information. The training set covers years 2011 and 2012, and encompasses 2,840 patients with 132, 51, and 81 postoperative superficial SSI, deep SSI, and organ space SSI, respectively. The test data set covers the year 2013 and contains 1,651 patients with 41, 34, and 41 respective SSI types. Some patients may have multiple SSI types.

Table 2.

Training and Test Set Patient and Surgical Site Infection (SSI) Characteristics

Characteristic	Training set (2011–2012)					Test set (2013)
	ALL Procedure	Overall SSI	Superficial SSI	Deep SSI	Organ Space SSI	ALL Procedure	Overall SSI	Superficial SSI	Deep SSI	Organ Space SSI
Total	2840	252	132	51	81	1651	114	41	34	41
Encounter type
Inpatient	2429	242	129	47	78	1052	104	35	32	38
Outpatient	411	10	3	4	3	599	10	6	2	3
Age group
< 65	2259	210	109	41	67	1269	91	30	28	34
≧65	581	42	23	10	14	382	23	11	6	7
Gender
Male	1246	119	63	22	39	774	51	19	15	18
Female	1594	133	69	29	42	877	63	22	19	23
Race
White	2386	213	112	44	66	1481	99	34	30	38
African American	189	18	8	5	7	112	7	3	1	2
Other/unknown	265	21	12	2	8	58	8	4	3	1

Model performance in detecting superficial, deep, organ space and overall SSI are shown in Figure 1. AUC scores obtained through a 10-fold cross validation on the training set and the final AUC scores on the test set are also reported. Generally, imputed models performed substantially better (statistically significant difference, with at least a 2nd digit difference in AUC) than the reference model, except for superficial SSI detection, where the reference model offered comparable performance.

Figure 1.

Detection Performance for each category of SSI with different imputation methods. The AUC scores are calculated based on both the training set (using the 10-fold cross validation) and the test set. Generally, the results indicate that developed models have a better performance on the test sets.

The final AUC score and bias of each model are reported in Table 3. We observed that for superficial SSI, every model performed similarly except “Dummy+0” and the reference model, which had the largest bias. Among models of deep SSI, imputed models without dummy variables performed best and the reference model performed worst in terms of AUC. Also, “Dummy+MICE” had the smallest bias among the different models. For organ space SSI, models with dummy variables performed best except “Dummy+0”, and all models had similar bias except “Dummy+0”. For detecting any SSI, most imputed models had similar performance and were substantially better than the reference model. Biases were also similar except the reference model and “Dummy+0”, which were more biased than the other models. Selected important variables, the estimated coefficients of variables and the 95% confidence intervals for the coefficients, are included in the supplemental appendix.

Table 3.

Bias analysis for eight imputed models as well as the reference model when detecting postoperative SSI. The average AUC and bias across the three sub-types of SSI and overall SSI are calculated as well.

	Superficial SSI		Deep SSI		Organ Space SSI		Overall SSI
	AUC	Bias	AUC	Bias	AUC	Bias	AUC	Bias	Average AUC	Average Bias
Reference	0.855	0.0600	0.702	−0.0032	0.864	−0.0136	0.864	−0.0159	0.821	−0.0079
Mean	0.841	0.0131	0.864	−0.0085	0.867	−0.0086	0.863	−0.0055	0.858	−0.0024
Normal	0.845	0.0132	0.866	−0.0014	0.896	−0.0092	0.935	0.0038	0.884	0.0016
MICE	0.832	0.0191	0.865	−0.0010	0.894	−0.0087	0.927	0.0053	0.879	0.0037
0	0.852	0.0122	0.886	−0.0090	0.903	−0.0105	0.934	−0.0072	0.893	−0.0036
Dummy+Mean	0.851	0.0155	0.823	−0.0155	0.935	−0.0088	0.906	0.0052	0.878	−0.0009
Dummy+Normal	0.856	0.0155	0.844	−0.0009	0.934	−0.0082	0.926	0.0052	0.888	0.0029
Dummy+MICE	0.843	0.0195	0.826	0.0001	0.946	−0.0082	0.903	0.0089	0.879	0.0051
Dummy+0	0.724	0.1679	0.813	−0.0154	0.774	0.1349	0.655	0.0639	0.741	0.0879

Pairwise t-tests on the 1000 replications of the Bootstrap procedure were conducted to test for statistical difference in AUC scores between the methods for each SSI event. The majority of imputation methods in each category of SSI showed statistical difference, with p-values less than 0.01, except “0” vs. “Dummy+Mean” for superficial SSI (p-value=0.102), “MICE” vs. “Normal” for Deep SSI (p-value=0.129), “Dummy+Mean” vs. “Dummy+Normal” for organ space SSI (p-value=0.098), and “Reference” vs. “Mean” (p-value = 0.094) and “Normal” “vs. “0” (p-value=0.143) for overall SSI. The detailed results are included in the supplemental appendix.

4. Discussion

In this work, we explored the use of nine methods for treating missing data (one where records with missing values were completely discarded and eight methods using imputation for missing values) and evaluated the performance of the SSI-detection models constructed on nine training sets that utilized these imputation methods. Overall, we found imputation to be beneficial. Models built on imputed data outperformed the reference model for all SSI types except superficial SSI. In case of superficial SSI, essentially all models had very similar performance; only “Dummy+0”, the model built on the 0-imputed dataset utilizing bias-correcting dummy variables, had lower performance. We will explore the reasons for its lower performance later.

The most surprising finding from this study is that the models with bias-correcting dummy variables did not perform as well as we expected. We expected that missing values signal that the patient is at a lower risk of SSI (the lab test is not necessary), giving rise to a “healthiness” bias. We originally thought that models without the dummy variables would have no ability to correct for this “healthiness” bias; hence, the addition of the bias-correcting dummy variables would allow the model to correct the bias, improving its performance. Instead, the performance did not improve. There are two possible reasons for this. First, potentially the rates of missing values in the cases (SSI patients) and the controls (patients without SSI) are significantly different between the training and test set. In 2013, non-SSI patients appear to have more results (e.g. WBC and vital signs like body temperature) than in 2011–2012; thus, the “healthiness” bias in the training set is different from that on the test set. Second, there are some variables in the dataset that can take on the role of the dummy variables to some extent. For example, the variable “patient type”, which indicates whether the patient had an inpatient or outpatient surgery, captures the “healthiness” bias well: outpatient surgeries are traditionally less complicated and thus are less likely to have complications; or conversely, if a procedure is associated with higher risk and a higher complication rate, it is less likely to be performed in the outpatient setting. This is similar to dummy variables, which also indicate a lowered risk of complication when the corresponding lab tests are not ordered.

The “0” model, where the value 0 was imputed for missing elements, performed surprisingly well. It achieved AUC scores ranging from 0.852 to 0.934. In most cases, imputing 0 is not clinically meaningful. Typically, imputing 0 for temperature would be a disastrous choice, as it would create large biases. The model for superficial SSI is one example. Among its significant variables, two are related to temperature: the postoperative maximum temperature and the minimum temperature. Their coefficients have the opposite signs, with the maximal temperature having the positive coefficient and the minimum having the negative. This can be interpreted as the difference between the maximum and minimum postoperative temperatures, which automatically corrects for the bias.

MICE exploits the structure of the problem, namely the relationship between the variables with the missing value and other variables; compared with other non-model-based imputation methods that ignore such structure, MICE methods are expected to perform best. Surprisingly, we did not find that the performance of the MICE models is significantly better than that of other imputation models. This is a result of differences in the problem structure between unhealthy and healthy patients: variables of healthy non-SSI patients are different in range from unhealthy SSI patients, and are more likely to have higher rate of missingness than unhealthy SSI patients, which affects the models in two ways: (1) the observations of unhealthy SSI patients contributes more in modeling imputation models because only complete observations are used to build imputation models; and (2) as a result, biases were likely introduced when applying the model to impute missing values for healthy non-SSI subjects. In spite of this, it is worth pointing out that “Dummy+MICE” achieved the best AUC on Organ Space SSI and the lowest bias on Superficial SSI. Overall, the performance of MICE method is good, but other simpler imputation techniques appear to be able to match their performance for the use case of SSI detection.

Another interesting fact worth noting is that in some cases, the performance of the models on test set was actually better than that in the training set. There are two possible reasons for this observation. First, this may be related to the SSI rates in the year of 2013 (test dataset) and 2011–2 (training dataset). For example, the rate of superficial SSI in the two sets was most different, 2.5% and 4.6%, respectively; consequently, the performance of models for superficial SSI between the two datasets differed and was higher for the test dataset. As for other types of SSI, rates were close between the two datasets, specifically 2.5% vs. 2.8% for organ SSI and 2.1% vs 2.1% for deep SSI. While the EHR system was not changed from the 2011 to 2013, other possible unseen factors which may influence the distribution of patients in 2013. Second, it is possible the constructed models underestimate the risk of SSI on the training set; therefore, the performance on the training dataset is relatively lower than for the test dataset; yet, the biases remain small. We also hypothesize that the increased collection of lab results may have also biased the regression models we used to fill in missing values since they were constructed on the training set. This is an analogous effect to the inability of the dummy variables to “un-bias” the estimates.

Limitations

The NSQIP database can provide insight into the importance of adequately addressing the problem of missing data. Data in NSQIP is manually abstracted directly from the EHR by trained personnel. If WBC values are entirely missing in the NSQIP file, it is most likely that the cause of missingness is lack of collection (i.e. there was no need to measure it). However, in our experiment, we have not fully explored the characteristics of missingness in the NSQIP dataset. This will be addressed in future work.

The NSQIP population in this experiment had some patients with primary providers who utilized a different EHR from the one used for manual data extraction and entry into the NSQIP database. In general, the EHR for the institution enrolled in the NSQIP database includes all pre-, intra-, and post-operative data on included patients. However, there are examples where the surgeon’s outpatient EHR or the patient’s primary care provider’s EHR differs from the EHR of NSQIP-enrolled institution. This is relevant to our present study of missing data, since preoperative data as well as post-operative complication data may be recorded in a database to which the trained manual abstractors do not have access. In our study, the EHR for the surgeon remained the same as the NSQIP-enrolled institutional EHR. However, the EHR for the primary care provider often differed (approximately 50% of cases). Patients with primary care providers who utilize a different outpatient EHR (compared to the NSQIP-enrolled institution’s EHR) might have some relevant data within the postoperative window missing after discharge from the hospital. We did not exclude/censor these patients. In addition, a subset of SSIs in our study were noted in the ICU or acute care (i.e., inpatient) setting. Some SSIs, most notably superficial SSI, can occur as wound infections in the outpatient and ambulatory settings after the index stay. Others, namely, deep and organ space SSI can be typically discovered during the index inpatient stay. However, some occur after discharge. These SSIs often require readmission and further inpatient treatment. Therefore, missing data after discharge could be an important potential limitation to applying our approach more widely. Actually, 5% of SSI cases in our cohort are those patients with SSIs who have no data collected. Presumably, these patients were both seen and treated at clinics that utilized a different EHR from the NSQIP-enrolled institutional EHR.

As introduced in section 2.1, our dataset was divided into a training set and a test set by calendar year rather than randomly sampling, since we are interested in investigating how robust the models are in face of institutional changes at a relatively short time horizon. It is inevitable that due to institutional changes the model performance will drift. With every passing year the model’s performance can decrease. At some point in the future, the model will have to be recalibrated or outright reconstructed. It is undesirable to have to rebuild a model every year. Our method of dividing the data set by year allows us to assess how resilient the models are to such institutional changes.

The application of EHR data in surveillance continues to be an issue of importance in the informatics and quality literature. Though the main purpose of our work is to accelerate the manual process of NSQIP data collection, EHR data could be used to help surveillance as well. At this point, we do not believe that we can entirely rely on the EHR since a number of challenges remain. These include the real-time availability of EHR data, the heterogeneity of EHR systems utilized by different providers treating the patients enrolled in the NSQIP database, and the variability of signals for event detection.

The relative infrequent nature of these events is part of the challenge with event detection. When events (e.g., myocardial infarction) are relatively rare, the imbalanced nature of the data could be a large part of the challenge. Possible solutions to deal with this challenge when investigating more adverse (and thankfully rarer) events will be explored in future work.

Unstructured data refers to narrative clinical notes such as discharge summaries, progress notes, operative notes, microbiology reports, imaging reports, and outpatient visit notes. In the narrative notes, there are some keywords related to the diagnosis and treatment of SSI, such as abdominal abscess, anastomotic leak, and wound dehiscence, etc. Unfortunately, we did not include unstructured data in this experiment. By using natural language processing tools, we will extract those relevant keywords, include them as new features, and combine both current and new potential features. We hypothesize that the combination of structured and unstructured clinical data would include more significant indicators and signals of SSIs, and thus improve the performance of detection. The performance of the model solely with structured data and that of the model with both structured and unstructured data will be compared and evaluated in future work.

5. Conclusion

In summary, we found models with imputation perform almost always better than models that discarded patient records with missing values. However, the optimal choice of imputation method is not clear. Data characteristics and data collection variation all affect the performance of imputation methods. If the test and training datasets have similar characteristics in terms of missing values, the use of bias-correcting dummy variables can be advantageous; if the characteristics differ, the estimated bias will be incorrect and can be similar in magnitude to the bias caused by the missing value they try to correct for, which is what happened in the present study. Similarly, if variables present in the dataset, such as “patient type” can take on the role of correcting for the bias, then dummy variables may not be necessary.

If it is guaranteed that test datasets have the same missing value biases as training or evaluation datasets, then the use of bias-correcting dummy variables can be advantageous. Similarly, MICE is advantageous only if the structure of the training dataset is similar to the structure of the test dataset. In our example, increased lab result collection created significant differences between the training and test datasets, rendering MICE only marginally useful. In our experiments, we found that imputing the mean of the non-SSI cases was successful in reducing the bias introduced by the fact that missing labs and vitals were suggestive of the lack of SSI event.

Highlights.

• For each patient, many data elements in EHR are missing (e.g. tests that were not necessary to order) and these data elements are missing not-at-random. Other data elements might be missing at random. We compared a number of commonly-used imputation methods for a problem, where the exact nature of the missing value is unknown.

• Imputation offered superior predictive performance over complete-case-analysis, where patients with missing values are excluded.

• Some of the simplest methods (e.g. imputing the mean of the normal patients) offered excellent performance.