Abstract
Collective behavior emerges from interactions among group members who often vary in their behavior. The presence of just one or a few keystone individuals, such as leaders or tutors, may have a large effect on collective outcomes. These individuals can catalyze behavioral changes in other group members, thus altering group composition and collective behavior. The influence of keystone individuals on group function may lead to trade-offs between ecological situations, because the behavioral composition they facilitate may be suitable in one situation but not another. We use computer simulations to examine various mechanisms that allow keystone individuals to exert their influence on group members. We further discuss a trade-off between two potentially conflicting collective outcomes, cooperative prey attack and disease dynamics. Our simulations match empirical data from a social spider system and produce testable predictions for the causes and consequences of the influence of keystone individuals on group composition and collective outcomes. We find that a group’s behavioral composition can be impacted by the keystone individual through changes to interaction patterns or behavioral persistence over time. Group behavioral composition and the mechanisms that drive the distribution of phenotypes influence collective outcomes and lead to trade-offs between disease dynamics and cooperative prey attack.
Keywords: agent-based model, collective behavior, individual variation, keystone individual, trade-offs
Introduction
Collective actions emerge from local interactions among group members that follow certain behavioral rules. Traditional models of the emergence of collective behavior have regarded all group members as identical agents (Couzin et al. 2002; Sumpter 2006). However, consistent individual differences in behavior are prevalent in most social systems (Sih et al. 2004; Jandt et al. 2014), and the behavioral composition of a group is often fundamental for its success (Pruitt and Goodnight 2014). Furthermore, individuals’ endogenous behavioral tendencies and the frequency of various behavioral types within groups can influence interaction patterns (Sih et al. 2009; Krause et al. 2010; Pinter-Wollman 2015). The structure of these interaction patterns, or social networks, can greatly influence the outcome of collective actions (Watts and Strogatz 1998; Bansal et al. 2007; O’Donnell and Bulova 2007; Pinter-Wollman et al. 2011). Therefore, a complete understanding of the emergence of collective behavior requires examination of the interdependency between within-group behavioral variation and interaction patterns.
A diversity of phenotypes in a group is often considered beneficial, but little is known about how such variation emerges or is maintained. Group phenotypic composition may influence individual fitness, group success, and population dynamics (Farine et al. 2015). The disproportionate influence of one or a few key individuals, such as tutors or leaders, on collective outcomes demonstrates that even little phenotypic variation may have large impacts on group success (Robson and Traniello 1999; Conradt and Roper 2003; Modlmeier et al. 2014). Keystone individuals may catalyze long-lasting behavioral changes in other group members (Robson and Traniello 1999; Pruitt and Pinter-Wollman 2015) or change the social structure of the society, influencing who interacts with whom (Lloyd-Smith et al. 2005). These influential individuals can drive groups’ collective behavior, with far-reaching implications on group success (Keiser et al. 2014; Pruitt and Keiser 2014). For example, if keystone individuals anchor the collective behavior of groups across situations, they might generate superior collective performance in response to some challenges at the cost of success in others, generating trade-offs across situations (Pruitt et al. 2016). The impact of such keystone-imposed trade-offs on group success may vary across environments. Because the importance of keystone individuals’ impact on collective behavior has been emphasized only recently, a theory on how these keystone individuals emerge and are maintained and how they shape trade-offs among collective outcomes is still lacking.
Behavioral variation among individuals of a social group may arise from internal genetic and developmental differences or from external social influence and ecological conditions (Gordon 1996; Schradin 2013). We present a model that examines how these internal (behavioral persistence) and external (social interaction) factors mediate the influence of keystone individuals on a group’s behavioral composition and its collective behavior. Specifically, our model explores the process by which keystone individuals influence collective behavior by determining (1) whether and how keystone individuals catalyze and maintain variation in behavior within a social group and (2) how the effects of keystone individuals on the behavior of other group members influence trade-offs between collective outcomes (i.e., any collective behavior or a consequence of it).
We base our model on the biology of the social spider Stegodyphus dumicola (Araneae, Eresidae), which, like other social spiders, lives in cooperative multifemale societies (Aviles 1986, 1997; Frank 1987; Lubin and Bilde 2007) that exhibit interindividual variation in boldness. This individual variation in boldness determines a colony’s success in prey capture (Keiser and Pruitt 2014), to the extent that colonies with just one very bold individual exhibit heightened aggressiveness during prey capture and gain mass rapidly in laboratory conditions (Pruitt and Keiser 2014). These bold keystone individuals can catalyze lasting changes in the boldness of other group members, such that particularly bold keystone individuals beget bolder behavior in their normally shy colony mates (Pruitt and Keiser 2014; Pruitt and Pinter-Wollman 2015). Furthermore, keystone presence has been associated with cross-contextual performance tradeoffs at the group level: groups with very bold keystone individuals are more successful at rapidly subduing prey (Keiser and Pruitt 2014) but are slower to evacuate exposed portions of the web during staged predator attacks (Wright et al. 2015). Stegodyphus dumicola colonies often succumb to idiopathic colony collapse, hypothesized to result from fungal disease (Henschel 1998), and harmful cuticular microbes are readily transmitted from bold individuals to shier colony mates but are less likely to transfer from shy to bold individuals (Keiser et al. 2016). This suggests that a group’s behavioral composition and not only its mean behavior may have far-reaching implications for collective outcomes. Therefore, this species provides a good example for how keystone individuals influence the behavior of other group members and how their presence may limit plasticity in more than one collective outcome at the group level, generating cross-contextual performance trade-offs.
To examine how keystone individuals influence group composition and collective behavior, we ran simulations that result in the emergence of stable behavioral variation within a group, producing alternative hypotheses for how a keystone individual may shape a group’s behavioral distribution. We then formulated a model and developed further simulations to discuss how the model parameters and resulting behavioral distributions influence various collective outcomes.
Methods
Simulations of Behavioral Distribution
Behavioral dynamics were simulated using social interactions that led to behavioral changes and an intrinsic factor, behavioral persistence, which modulated the effect of these social interactions. To allow for a comparison with an empirical system, we used boldness as the focal behavior for the model (see the appendix, available online).
Boldness Dynamics
Simulated colonies contained 25 individuals, of which 24 were initiated with a boldness score of 0 (i.e., were extremely shy) and one individual was the keystone, whose boldness was set for the entire simulation (e.g., 10, 300, or the maximum of 600; see details on empirical values in the appendix). These parameters were selected based on our experimental work (Keiser and Pruitt 2014; Pruitt and Keiser 2014; Pruitt and Pinter-Wollman 2015) to produce a model that closely simulates the biological system. In each of 150 time steps, two to 10 social interactions occurred. This range was determined based on empirical observations of spiders interacting while capturing prey. The number of interactions in each time step (2 ≤ m ≤ 10) was randomly selected from a uniform distribution. Setting m to just one value between 2 and 10 did not qualitatively affect the simulation results. Which individuals interacted during each step was determined according to one of five interaction rules described below. We selected 2m individuals based on their probability to interact (see below) and then randomly paired the first m individuals with the other m individuals. Each individual could interact only once in each time step (i.e., the 2m individuals were sampled without replacement). During each interaction, the shier individual acquired a proportion A of the difference in boldness between the two interacting individuals. The boldness of the bolder individual did not change. At the end of each time step, all individuals (whether they interacted or not) kept a proportion P of their boldness, except for the keystone individual, whose boldness did not change throughout the duration of the simulation (Pkeystone = 1). The parameter P represents behavioral persistence, and 1 − P would be akin to forgetting or a decay of the focal behavioral trait (boldness). This model assumes that boldness can increase only through social interactions and decreases spontaneously. Based on a scan of the parameter space of A and P (see supplementary material, available online), we selected four parameter pairs that depict the effect of high or low boldness acquisition (A) and high or low behavioral persistence (P; table 1).
Table 1.
Values of four parameter pairs of boldness acquisition and persistence
| Acronym | Persistence | Acquisition | P | A |
|---|---|---|---|---|
| HPLA | High | Low | .95 | .2 |
| HPHA | High | High | .8 | .75 |
| LPLA | Low | Low | .5 | .5 |
| LPHA | Low | High | .5 | .85 |
Note: A = boldness acquisition; P = persistence.
Interaction Rules
The probability of individuals to interact at each time step followed one of the following five rules:
Rule 1: Uniform. All individuals were equally likely to interact, regardless of their boldness.
Rule 2: Keystone Uniform (KI Uniform). All individuals were equally likely to interact, except for the keystone, who was twice as likely as any other group member to be selected for an interaction.
Rule 3: Skewed. The probability of individuals to interact was skewed, following an exponential distribution with a mean probability equal to that of the uniform probability in the Uniform rule above. Thus, most individuals had a low probability of interacting, and few were highly likely to interact. The probability of each individual to interact was assigned at the beginning of the simulation regardless of boldness and did not change throughout the simulation.
Rule 4: Keystone Skewed (KI Skewed). The probability of individuals to interact was skewed, following an exponential distribution as in the Skewed rule, but the keystone individual was twice as likely as the mean of the distribution to interact, thus usually but not always setting it to be the most interactive individual.
-
Rule 5: Changing. The probability of an individual to interact was a function of its boldness in the previous time step. In contrast with the four previous rules that assigned a static interaction probability to each individual at the beginning of the simulation, the interaction probability of an individual in the Changing rule was dynamic and changed throughout the simulation. At each time step, the probability of an individual to interact was
(1) where t is time, punif is the probability to interact in the Uniform rule, and bt−1 is the boldness of the individual in the previous time step, which was normalized by the maximum possible boldness (bmax = 600). A very small constant, c, was added to allow individuals with zero boldness to interact, thus slightly increasing the stochastisity of this interaction rule. Relating interaction probability with the boldness of an individual most closely matches empirical findings from studies on Stegodyphus dumicola, which show that bolder individuals are more likely to interact during cooperative prey capture events (Keiser and Pruitt 2014; Wright et al. 2015) and are more likely to spread potentially harmful cuticular microbes to fellow colony members via body contact (Keiser et al. 2016).
Because the number of interactions in each time step was similar for all simulations (2 ≤ m ≤ 10, as explained above), mean contact rates were similar among all five models (fig. 1C).
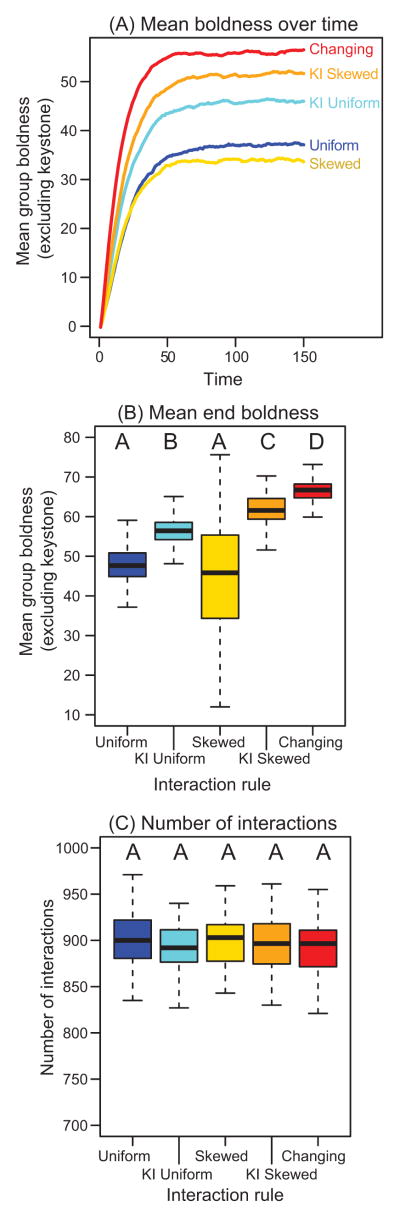
Figure 1.
Interaction rules differed in group boldness. A, Progression of mean group boldness throughout the simulation for high behavioral persistence and low acquisition values (table 1). B, C, Final mean boldness (B) and total number of interactions (C) in 100 simulations for each of the five interaction rules. Here and in all following boxplots, boxes indicate the lower and upper quartiles, horizontal lines within boxes indicate the median, whiskers extend to the 1.5 inter-quartile range from the box, and different letters indicate significant differences using a post hoc Tukey test (Pr < .05).
We ran 100 simulations for each interaction rule (Uniform, Skewed, etc.) and each P-A parameter pair (table 1) and compared among the various rules and parameters the final simulated boldness distributions (i.e., the boldness distribution at the end of the 150 time steps averaged across 100 simulation runs). These simulated boldness distributions were also compared with empirical distributions of boldness from wild S. dumicola colonies (N = 16). Graphical representations of examples of boldness dynamics throughout the progression of the simulation are presented in figure S1 (figs. S1–S24 are available online).
Collective Behaviors
To examine the success of the various simulated behavioral distributions in response to ecological challenges that may produce trade-offs, we used the simulated boldness distributions and interaction patterns to examine disease dynamics and collective prey attack, both of which are fundamental for the survival of the colony (Henschel 1998; Pruitt and Keiser 2014; Pruitt et al. 2016).
Disease Dynamics
To examine disease dynamics, we quantified pathogen transmission speed and disease prevalence. We simulated the propagation of an infectious disease across the interactions among agents during the first and last 20 time steps of each simulation. We used the Timeordered package in R (Blonder and Dornhaus 2011; Blonder et al. 2012) to simulate pathogen transmission whenever there was an interaction with an infected individual in a sequential manner—that is, in the order in which interactions occurred. Each individual had an opportunity to be the first individual infected, termed the “index case,” also known as “patient zero.” The probability of transmission was equal across all interactions. Furthermore, for simplicity, we assumed susceptible/infected (SI) epidemiological dynamics in which all individuals were initially susceptible to the disease and once infected, after interacting with an infected individual, remained infected (Anderson and May 1991; Barthelemy et al. 2004, 2005; Bai et al. 2007). To quantify the colony-wide incidence of infection, we examined the proportion of individuals infected by the end of the 20 time steps, referred to as “disease prevalence.” To quantify “transmission speed,” we used the inverse of the number of time steps it took 50% of the colony to become infected. We compared disease prevalence and transmission speed among interaction rules and between cases when generic individuals or the keystone individual were the index case. Detailed examination of disease dynamics required further simulations, in addition to those of boldness dynamics, because (1) in our simulations, disease can be transmitted from both bold and shy individuals, depending on the order of their interactions, whereas only the boldness of the shy individual increases in the boldness dynamics simulations; (2) pathogen transmission was a binary event (infected [1] or not [0]), whereas boldness acquisition depended on the difference in boldness between the two interacting individuals (parameter A); (3) the source of disease (i.e., the index case) could be any group member, however, the source of boldness could only be the keystone individual; and (4) infection status did not decay over time, yet boldness did (parameter P). Therefore, the disease dynamics simulations added to and did not replicate our boldness dynamics simulations.
The structure of the interaction network differed among the various interaction rules (figs. S6–S9), but only in the Changing rule was there a difference in the structure of the network created from interactions at the start of the simulation (time steps 1–20) and its end (time steps 131–150; figs. S10, S11). Therefore, comparison of disease dynamics between the start and the end of the simulation was conducted only for the Changing interaction rule. Furthermore, although boldness values changed from the beginning to the end of the simulation (figs. S6–S11), the relationship between each individual’s boldness and its number of interactions did not (fig. S12). Note that because the interaction patterns depended on boldness only in the Changing rule, we examined how various A and P parameter pairs (table 1) affected disease dynamics in the Changing rule but not in the other interaction rules (for which we used high persistence–low acquisition [HPLA]; table 1). We provide these results in the supplementary material.
Prey Attack
To compare the speed of collective prey attack as a function of the behavioral compositions that arise under different mechanisms of social influence by keystone individuals, we formulated a simple analytic model. Based on empirical observations, the probability of an individual to attack a prey item is linearly proportional to its boldness (Pruitt and Keiser 2014). Furthermore, there is a linear relationship between average colony boldness and collective prey attack success in this species (Keiser and Pruitt 2014; Keiser et al. 2014) and potentially in other social foragers (Kurvers et al. 2010; Aplin et al. 2014). To determine the effect of the parameters P and A on average boldness and therefore collective prey attack, we describe change in average group boldness, B, as
| (2) |
P and A are as described above, persistence and acquisition, and Bmax is the boldness of the keystone individual. For simplicity, this model assumes that because under most conditions Bmax ≫ B, one can neglect any boldness acquisition that occurs when neither of the two interacting individuals are the keystone individual. For further simplicity, this model collapses interaction probability into the parameter A. Thus, it does not allow us to distinguish between the various interaction rules—the effect of interaction rules on mean boldness is shown using the simulations of boldness dynamics. Further simulations of prey attack as both linearly and nonlinearly related to boldness and comparisons of the various interaction rules are presented in the supplementary material. All simulations were run in R, version 3.1.2 (R Core Team 2014), and the annotated code is available in the Dryad Digital Repository: http://dx.doi.org/10.5061/dryad.5mm01 (Pinter-Wollman et al. 2016).
Results
Behavioral Distribution
A group’s mean boldness depended on the interaction rule it followed. Interaction rules differed in the mean group boldness they reached (ANOVA: F4, 495 = 130.7, Pr < .0001; fig. 1A, 1B) even though the total number of interactions did not differ among the various rules (ANOVA: F4, 495 = 1.36, Pr = .25; fig. 1C). The progression of boldness throughout the simulation was similar across interaction rules and for various values of keystone boldness: a group’s mean boldness increased until approximately the 50th time step and then saturated (figs. 1A, S2). Groups with bolder keystones had higher mean boldness (fig. S3) and greater boldness variability (fig. S4). Because the overall progression of group boldness was similar across the various keystone boldness values that we tested (10, 300, and 600; figs. S3, S4), we focused our analysis of boldness distribution on just one keystone boldness (300).
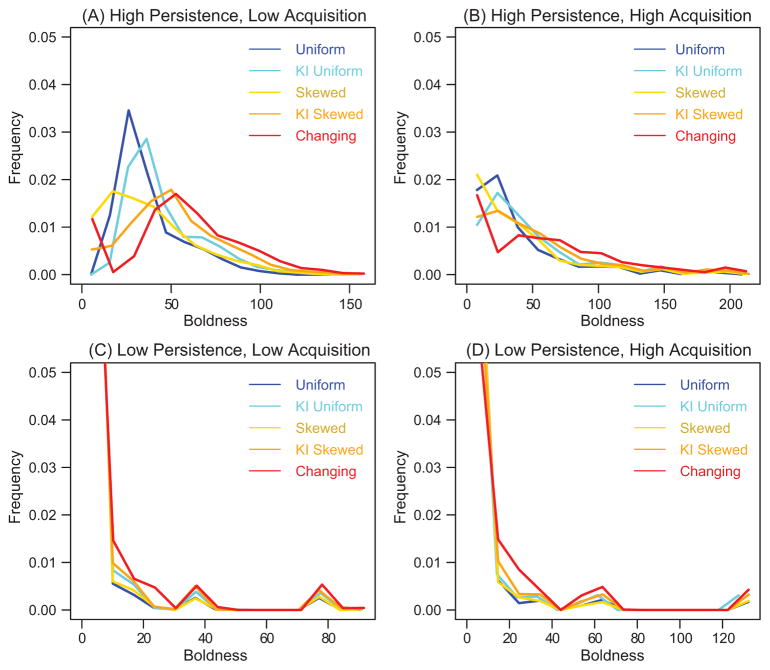
The shape of the boldness distribution at the end of the simulation depended on the interaction rule and the acquisition (A) and behavioral persistence (P) values. Boldness distribution varied among interaction rules only when behavioral persistence was high and boldness acquisition was low (HPLA; fig. 2A). The Uniform and Keystone Uniform interaction rules resulted in the least skewed boldness distributions, the Skewed and Keystone Skewed interaction rules resulted in right-skewed boldness distributions, and the Changing interaction rule resulted in a bimodal distribution (fig. 2A). For low persistence or high acquisition values, there was no difference in the shape of the boldness distribution among the various interaction rules (fig. 2B–2D). However, when persistence levels were low, the resulting boldness distributions were bimodal, with most individuals having close to zero boldness and only a few individuals with higher boldness levels (figs. 2C, 2D, 3). When persistence levels were high and boldness acquisition was high, the resulting boldness distributions were right skewed, in a similar manner to the skewness of the Skewed interaction rule when there was high persistence and low acquisition (fig. 3).
Figure 2.
Boldness distributions. Distributions of boldness at the end of the simulation (t = 150), excluding the keystone individual, averaged over the 100 simulation runs for each of the four persistence-acquisition parameter pairs from table 1 and for each of the interaction rules (see key in plots).
Figure 3.
Boldness distribution for the Skewed interaction rule. Distributions of boldness at the end of the simulation (t = 150) excluding the keystone individual, averaged over the 100 simulation runs for each of the four persistence-acquisition parameter pairs (see key in plot; table 1) for the Skewed interaction rule (see fig. S5 for the other interaction rules).
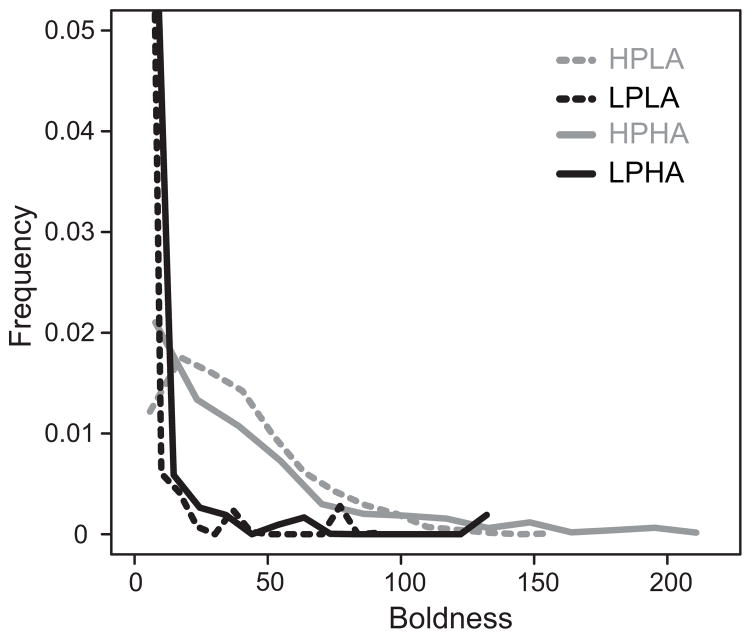
Comparison between simulation predictions and empirical observation allowed us to identify plausible mechanisms that underlie the effects of the keystone individual on collective outcomes. Empirical boldness distributions resembled the simulated right-skewed and simulated bimodal boldness distributions (fig. 4). Furthermore, empirical values of behavioral persistence that resulted in a reduction of boldness over time ranged from 0.03 to 1; however, most persistence values fell between 0.5 and 1 (see appendix for details). Our model thus predicts that the differences between the empirical right-skewed and the bimodal boldness distributions result from differences in behavioral persistence (fig. 3) or differences in interaction patterns in populations with high behavioral persistence (fig. 2A).
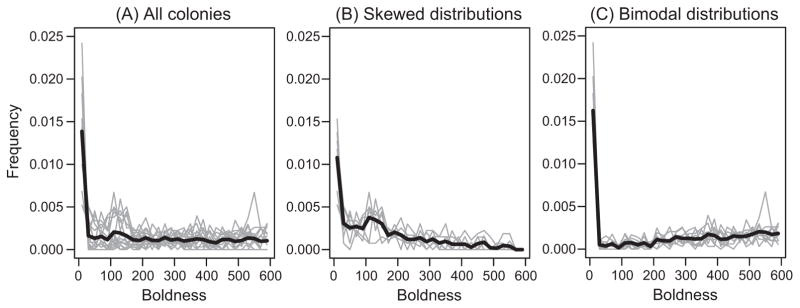
Figure 4.
Empirical boldness distributions. Each gray line represents the boldness distribution of one colony studied in 2014, and the black line represents the average distribution. A, All 16 colonies. B, Seven colonies in which more individuals had low boldness than high boldness (N 100 > N 600), resulting in a right-skewed distribution. C, Nine colonies in which more individuals had high boldness than low boldness (N 100 ≤ N 600), resulting in a bimodal distribution.
Collective Outcomes
Disease Dynamics
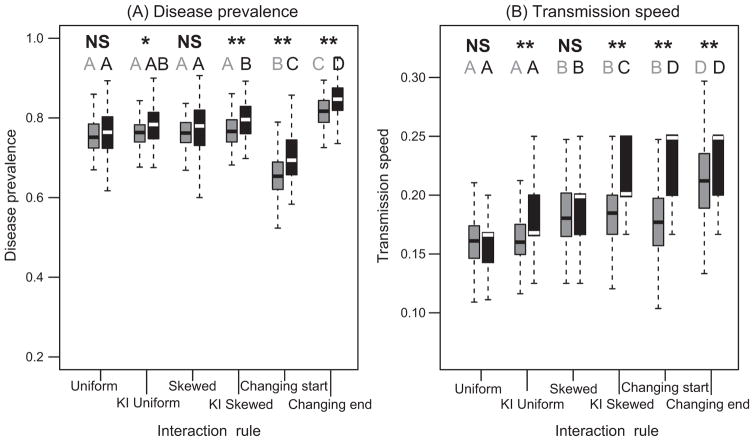
Disease dynamics changed according to the interaction rule and the identity of the index case. The Uniform and Keystone Uniform interaction rules resulted in the slowest transmission speeds (ANOVA, generic index case: F5, 594 = 50.87, Pr < .0001; keystone index case: F5, 592 = 91.41, Pr < .0001; fig. 5B). Furthermore, when the keystone individual was more likely to interact with others (interaction rules Keystone Uniform, Keystone Skewed, and Changing), infections were more prevalent, and transmission speed was faster when the keystone was the index case (first individual to become infected) compared to when generic individuals were the index case (t-test, disease prevalence, Uniform: t167.5 = −1.18, Pr = .24; Keystone Uniform: t186.8 = −2.52, Pr = .012; Skewed: t138.8 = −0.09, Pr = .92; Keystone Skewed: t192.7 = −4.86, Pr < .0001; Changing, start: t197.9 = −5.51, Pr < .0001; Changing, end: t197.9 = −4.81, Pr < .0001; transmission speed: Uniform: t192.7 = −1.34, Pr = .18; Keystone Uniform: t185.7 =−4.35, Pr < .0001; Skewed: t153.5 = −1.61, Pr = .11; Keystone Skewed: t186.6 = −7.62, Pr < .0001; Changing, start: t196.1= −13.31, Pr < .0001; Changing, end: t193.4 = −6.49, Pr < .0001; fig. 5).
Figure 5.
Disease dynamics. A, Disease prevalence. B, Transmission speed. Boxplots represent 100 simulation runs for the various interaction rules and high persistence and low acquisition parameters. Gray boxes represent simulations in which generic individuals were the index case, and black boxes are simulations in which the keystone individual was the index case. Significant differences between these two types of index cases are indicated in boldface in the top row. A single asterisk indicates Pr < .05, and a double asterisk indicates Pr < .001. The first five boxplot pairs in each panel represent the first 20 time steps of the simulation for the various interaction rules, and the last pair of boxplots is for the last 20 time steps of the Changing interaction rule. Boxes that share a letter of the same color on the second row are not significantly different, according to a post hoc Tukey test.
Disease dynamics differed between the start (first 20 time steps) and end (last 20 time steps) of the simulation for the Changing interaction rule. Transmission was faster later in the simulation compared with early networks when the Changing interaction rule was used (fig. 5B). Furthermore, when the Changing interaction rule was used, disease prevalence was lowest (i.e., the fewest individuals became infected) early on in a colony’s life, but later in the life of a colony, disease actually became most prevalent (ANOVA, generic index case: F5, 594 = 132.1, Pr < .0001; keystone index case: F5, 594 = 55.81, Pr < .0001; fig. 5A). No such differences between the start and the end of the simulation were observed for the other interaction rules, which did not change interaction patterns over the course of the simulation (figs. S13, S14).
Prey Attack
To examine the role of behavioral persistence and boldness acquisition (parameters P and A) on prey attack, which is linearly related to the colony’s mean boldness, we solved equation (2) to produce the steady state solution for mean colony boldness:
| (3) |
An analysis of the limits of P shows that when P = 1, then B = Bmax; that is, when behavioral persistence is absolute and there is no decay in boldness, the average boldness of the colony at the steady state will be the same as the boldness of the keystone individual, regardless of acquisition value. Thus, prey attack will be directly related to the boldness of the keystone individual. Furthermore, when P ≈ 0, then
such that when A ≪ 1, then B ~ 0; that is, when behavioral persistence is extremely low and very little boldness is acquired in each interaction, the average boldness of the colony will be close to 0 at the steady state, and only the keystone individual (whose boldness does not decay in our model) will contribute to the average boldness, thus again relating prey attack to the boldness of the keystone individual. These results recapitulate the parameter scan shown in figures S22–S24.
Further examination of the effects of the various interaction rules and the parameters A and P on collective prey attack using simulations can be found in the supplementary material.
Discussion
Our mathematical models and simulations produced testable predictions for the causes and consequences of various behavioral distributions within animal societies. We found that behavioral distributions within groups can vary based on the interactions among individuals and/or individuals’ behavioral persistence. Furthermore, a group’s behavioral distribution and the mechanisms that determine this distribution (i.e., social interaction patterns and behavioral persistence) influence collective outcomes, potentially leading to trade-offs between situations such as disease dynamics and cooperative prey attack.
Behavioral Distribution
Our model predicts that the effect of a keystone individual on the behavior of other group members can be mediated through the pattern of social interactions, the level to which interactions impact behavior (A), or through internal processes such as behavioral persistence (P). When behavioral persistence (P) was high, the pattern in which individuals interacted with one another determined the distribution of boldness in the group, especially when interactions resulted in little influence over boldness (HPLA; fig. 2A). This result emerged because when persistence was high, (1) boldness changed primarily through interactions because only little boldness was lost to forgetting or decay and (2) the effect of each interaction on boldness persisted. As the behavioral influence during an interaction (i.e., acquisition [A]) increased (HPHA), so did the effect of the keystone individual on colony boldness, skewing the boldness distributions to the right (fig. 2B). High behavioral acquisition caused each interaction with the keystone individual to have a high impact on the boldness of the individual it interacted with, and high behavioral persistence maintained this keystone effect. Thus, these highly influential interactions with the keystone individual skewed the underlying effect of the interaction rule to the right, as seen when comparing figure 2A and 2B. At the extreme, when behavioral persistence was absolute, interaction patterns became irrelevant, because the impact of each interaction never decayed and boldness only increased during interactions in our model. Thus, when the system reached steady state, all individuals interacted sufficiently with one another (and more importantly, with the keystone individual) without ever losing any of their boldness. Therefore, the mean boldness of the group converged on that of the keystone individual, as seen in the solution of the analytic model (eq. [3]).
When behavioral persistence (P) was low, behavioral influence (A) and interaction patterns had little impact on boldness distribution. These dynamics were observed because when there was little memory of boldness, the boldness distribution was determined by only a few time steps. Furthermore, because all individuals except the keystone individual began our simulations with no boldness, effectively, only the keystone individual increased colony boldness, because others did not accrue enough boldness to have a substantial impact during interactions due to their low behavioral persistence. These dynamics resulted in bimodal distributions in which most individuals had very low boldness and only the few individuals that recently interacted with the keystone individual exhibited some boldness (fig. 2C, 2D). Because the boldness of the keystone individual and behavioral acquisition (A) were identical for all interaction rules in each parameter pair, the boldness of those few individuals was similar across interaction rules. As behavioral acquisition (A) increased, the boldness of those few bold individuals increased (cf. fig. 2C, 2D), because the effect of interacting with the keystone on their boldness increased. The only difference observed among interaction rules when behavioral persistence was low was that when the keystone was more likely to interact (KI Uniform, KI Skewed, and Changing), there were more individuals with high boldness, but this effect was small (fig. 2C, 2D). At the extreme, our analytic solution (eq. [3]) shows that when persistence (P) and acquisition (A) were close to 0, mean colony boldness approached 0 and was impacted only by the boldness of the keystone individual.
We employed a “sink-source” dynamics to produce a steady state skewed behavioral distribution. When individuals influence the behavior of one another, a group can quickly converge on a single average behavior (Herbert-Read et al. 2013). However, empirical work in our system (fig. 4), many social insects (Oster and Wilson 1978; Julian and Fewell 2004; Dornhaus 2008; Pinter-Wollman et al. 2012), and vertebrate systems (Lott 1991; Schradin 2013; Aplin et al. 2014) show that groups exhibit variation in behavior and often highly skewed behavioral compositions. We simulated a skewed and stable behavioral distribution by designating the keystone individual as a “source” of a behavior (boldness) and the limits of behavioral persistence as a “sink” for the behavior. The keystone individual’s boldness never changed throughout the simulation, but the boldness of all other individuals spontaneously decreased (persistence < 1). These rules are consistent with empirical data showing that the persistence of boldness of keystone individuals is the highest in the colony (Pruitt and Keiser 2014). For simplicity, our model assumed that boldness can increase only through social interactions and decrease spontaneously. Other rules, such as spontaneous increases in boldness, variation in persistence among group members, and interactions that lead to a decrease in boldness, will likely generate similar results as long as they follow an overall sink-source pattern. Furthermore, other mechanisms can also result in stable skewed behavioral distributions—for example, consistent variability in gene expression (Whitfield et al. 2003; Ingram et al. 2005), events during development (Bengston and Jandt 2014), and variation in morphology (Oster and Wilson 1978; Wilson 1980). Our simulation shows that a simple behavioral phenomenon, persistence, can produce highly skewed and stable behavioral distributions in a society when just one individual is highly influential. Such anchor individuals are a relatively common phenomenon in animal societies (Modlmeier et al. 2014).
Whether behavioral persistence, acquisition, or interaction patterns impact the phenotypic composition of a group could determine the group’s success in particular environments. For example, interaction patterns are potentially flexible because they can be determined by walking patterns (Pinter-Wollman et al. 2014; Pinter-Wollman 2015), yet behavioral persistence can be rigid because it can be governed by gene expression (Whitfield et al. 2003; Ingram et al. 2005) and events during development (Bengston and Jandt 2014; Laskowski and Pruitt 2014). Therefore, we predict that dynamic environments will favor groups that can modify their behavioral composition through changes to interaction patterns, as in the high persistence–low acquisition scenario in our model. However, when environmental conditions are stable, our model predicts that group composition determination through behavioral persistence (fig. 3) may provide more robustness. These predictions can be examined empirically to uncover the mechanisms that influence behavioral distributions under different ecological conditions.
Collective Outcomes
Our simulations of disease dynamics and analysis of collective prey capture unveil potential trade-offs between these two collective outcomes. Interaction rules and persistence parameters that facilitated rapid prey attack also resulted in faster disease dynamics and vice versa.
Interaction rules that resulted in high mean boldness and therefore rapid prey attack also led to high disease prevalence and faster transmission when the keystone individual was the index case. The interaction rules in which the keystone individual was more likely to interact than others (KI Uniform, KI Skewed, and Changing) resulted in greater mean boldness (fig. 2B), a proxy for collective prey attack, and higher disease prevalence and transmission speed (fig. 5B), but only when the keystone individual was the index case. However, transmission was faster in the Skewed interaction rule compared with the Uniform rule, even though the mean boldness of these two scenarios was the same. This result suggests that although mean boldness underlies prey capture success, the distribution of boldness should also be considered when examining trade-offs with other collective outcomes. Individual variation in interaction rate, as in all interaction rules except for Uniform, often produces interaction hubs that facilitate rapid flow, as seen in transportation (Barabási 2002), information (Pinter-Wollman et al. 2011), and disease (Cross et al. 2004; Bansal et al. 2007; Fefferman and Ng 2007; Hock and Fefferman 2012) networks. When keystone individuals were highly interactive, they became interaction hubs and facilitated rapid flow of disease and boldness.
Although in our model both disease and boldness spread through the same interactions, disease and boldness dynamics were not identical. Most importantly for explaining the effects of interaction rules on these collective outcomes is that the source of disease (i.e., the index case) could have been any group member; however, the source of boldness was always the keystone individual. Furthermore, infection could have been transmitted from both bold and shy individuals, but only the boldness of the shy individual increased during interactions. Thus, only when the keystone individual was the index case did we see similarities in the effect of the interaction rule on both collective outcomes, not when generic individuals were the source of disease (fig. 5). These model outcomes are important if keystones are more likely than other group members to become exposed to infectious agents or if disease can increase the boldness of an infected individual. Similar detrimental effects of keystone presence on the spread of bad information within the colony have been recently shown (Pruitt et al. 2016), questioning the benefits of relying on a keystone individual. Our simulations suggest that the detrimental effects of the keystone individual on its society should be weighed against the potential benefits in other situations, such as prey capture, and be considered in the context of the environment in which the colony resides and has developed (Yang et al. 2004) and evolved (Pruitt and Goodnight 2014).
Behavioral persistence further highlights the trade-off between prey capture and disease dynamics. Our analysis of the steady state of mean colony boldness (eq. [3]) and our supplementary simulations show that regardless of interaction pattern and behavioral acquisition values, mean colony boldness increases with behavioral persistence. Because there was no relationship between interaction rate and boldness in four of the five interaction models, and because disease dynamics emerged only from interaction patterns, we could analyze the effect of behavioral persistence on disease dynamics only for the Changing model (see supplementary material). The effect of behavioral persistence on disease dynamics changed over time. Early in our simulations, akin to young colonies, behavioral persistence decreased disease prevalence (fig. S15A, S15C). However, over time, as colonies aged, behavioral persistence increased disease prevalence (fig. S15B, S15D) and transmission speed (fig. S16B). The opposite effects of behavioral persistence on young and old colonies likely emerged from the number of individuals that regularly interacted with one another at each life stage. Indeed, temporal changes in interaction patterns can change disease dynamics (Hock and Fefferman 2012). Early on, individuals formed weak ties with one another, creating a large connected network that included most of the individuals in the colony (figs. S10, S11). Because in the Changing interaction rule interactions are a function of boldness, a low level of behavioral persistence means that individuals change their boldness frequently, thus allowing them to change who they interact with and sample a large number of individuals, leading to an increase in disease prevalence. However, because of the positive feedback between boldness and interaction probability in the Changing interaction rule, the interactions among individuals become stronger and more selective with time, reducing the size of the connected component of the network (figs. S10, S11). Low persistence decreased the size of the connected component in old colonies, thus reducing the proportion of susceptible individuals to which pathogens may be spread by infected individuals. Such compartmentalization of interactions within a behavioral task (in this case, bold individuals who perform prey attacks) has been observed in social insects (Mersch et al. 2013) and has the potential to buffer other task groups from contracting a disease (Pie et al. 2004; Naug 2008).
Our model provides testable predictions for the influence of behavioral persistence and interaction patterns on the trade-off between collective prey attack and disease dynamics, which can be examined with empirical work in various environments. For example, we predict that where disease is prevalent and prey is abundant, uniform interactions or low behavioral persistence will be found, because they decrease pathogen transmission and disease prevalence despite prey attack being less efficient. Presumably, reduced prey capture success could be offset by prey abundance (Hedrick and Riechert 1989; Riechert and Hedrick 1990, 1993). Conversely, where disease and prey are rare, interaction rules in which the keystone is more likely to interact than others (KI Uniform, KI Skewed, and Changing) or high persistence would be expected, because they produce efficient prey attacks despite the increase in disease prevalence. Interestingly, Stegodyphus dumicola is often found in high-resource environments (Bilde et al. 2007; Majer et al. 2015) where infectious disease may be common (Henschel 1998). It remains to be determined whether the two types of behavioral distributions we observed empirically (fig. 4) appear in the environments they are most suited for. Our work provides a theoretical basis for further work on the exact parameter values that produce optimal solutions in other environments.
Conclusions
Despite the ubiquity of keystone individuals in various social systems (Modlmeier et al. 2014), theoretical work on the influence of keystone individuals on collective behavior is scant. Our theoretical study produces testable predictions for the mechanisms by which keystone individuals shape a group’s behavioral composition and the resulting collective outcomes. We show how the effect of keystone individuals on social organization can be mediated through both internal (behavioral persistence) and external (social interaction) factors. The influence of each mechanism carries over into collective outcomes and trade-offs among them. Due to the trade-offs among collective outcomes, there are potential benefits and costs to utilizing either internal or external mechanisms. It remains to be empirically determined under what conditions each mechanism is most likely to influence group composition and success.
Supplementary Material
Acknowledgments
We thank R. Berger-Tal, A. Carlson, M. Rebeiz, and J. Stamps for helpful discussion. We thank F. Armagost and A. DeMarco for their assistance with data collection. D. Farine, B. Wcislo, and an anonymous reviewer provided thoughtful suggestions on earlier versions of the manuscript. We are indebted to the Northern Cape of South Africa for issuing research and collection permits (FAUNA 1060/2012, FAUNA 1072, FAUNA 2013). Funding for this work was generously provided by National Science Foundation IOS grants 1352705 and 1455895 to J.N.P. and 1456010 to N.P.-W.
Footnotes
Online enhancements: appendix, supplementary material. Dryad data: http://dx.doi.org/10.5061/dryad.5mm01.
Literature Cited
- Anderson RM, May RM. Infectious diseases of humans: dynamics and control. Oxford University Press; Oxford: 1991. [Google Scholar]
- Aplin LM, Farine DR, Mann RP, Sheldon BC. Individual-level personality influences social foraging and collective behaviour in wild birds. Proceedings of the Royal Society B: Biological Sciences. 2014;281:20141016. doi: 10.1098/rspb.2014.1016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Avilés L. Sex-ratio bias and possible group selection in the social spider Anelosimus eximius. American Naturalist. 1986;128:1–12. doi: 10.1086/286178. [DOI] [PubMed] [Google Scholar]
- Avilés L. Causes and consequences of cooperation and permanent-sociality in spiders. In: Choe J, Crespi B, editors. The evolution of social behavior in insects and arachnids. Cambridge University Press; Cambridge: 1997. pp. 476–498. [Google Scholar]
- Bai WH, Zhou T, Wang BH. Immunization of susceptible-infected model on scale-free networks. Physica A: Statistical Mechanics and Its Applications. 2007;384:656–662. [Google Scholar]
- Bansal S, Grenfell BT, Meyers LA. When individual behaviour matters: homogeneous and network models in epidemiology. Journal of the Royal Society Interface. 2007;4:879–891. doi: 10.1098/rsif.2007.1100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barabási A-LS. Linked: the new science of networks. Perseus; Cambridge, MA: 2002. [Google Scholar]
- Barthelemy M, Barrat A, Pastor-Satorras R, Vespignani A. Velocity and hierarchical spread of epidemic outbreaks in scale-free networks. Physical Review Letters. 2004;92:17870. doi: 10.1103/PhysRevLett.92.178701. [DOI] [PubMed] [Google Scholar]
- Barthelemy M, Barrat A, Pastor-Satorras R, Vespignani A. Dynamical patterns of epidemic outbreaks in complex heterogeneous networks. Journal of Theoretical Biology. 2005;235:275–288. doi: 10.1016/j.jtbi.2005.01.011. [DOI] [PubMed] [Google Scholar]
- Bengston SE, Jandt JM. The development of collective personality: the ontogenetic drivers of behavioral variation across groups. Frontiers in Ecology and Evolution. 2014;2:81. [Google Scholar]
- Bilde T, Coates KS, Birkhofer K, Bird T, Maklakov AA, Lubin Y, Aviles L. Survival benefits select for group living in a social spider despite reproductive costs. Journal of Evolutionary Biology. 2007;20:2412–2426. doi: 10.1111/j.1420-9101.2007.01407.x. [DOI] [PubMed] [Google Scholar]
- Blonder B, Dornhaus A. Time-ordered networks reveal limitations to information flow in ant colonies. PLoS ONE. 2011;6:e20298. doi: 10.1371/journal.pone.0020298. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blonder B, Wey TW, Dornhaus A, James R, Sih A. Temporal dynamics and network analysis. Methods in Ecology and Evolution. 2012;3:958–972. [Google Scholar]
- Conradt L, Roper TJ. Group decision-making in animals. Nature. 2003;421:155–158. doi: 10.1038/nature01294. [DOI] [PubMed] [Google Scholar]
- Couzin ID, Krause J, James R, Ruxton GD, Franks NR. Collective memory and spatial sorting in animal groups. Journal of Theoretical Biology. 2002;218:1–11. doi: 10.1006/jtbi.2002.3065. [DOI] [PubMed] [Google Scholar]
- Cross PC, Lloyd-Smith JO, Bowers JA, Hay CT, Hofmeyr M, Getz WM. Integrating association data and disease dynamics in a social ungulate: bovine tuberculosis in African buffalo in the Kruger National Park. Annales Zoologici Fennici. 2004;41:879–892. [Google Scholar]
- Dornhaus A. Specialization does not predict individual efficiency in an ant. PLoS Biology. 2008;6:2368–2375. doi: 10.1371/journal.pbio.0060285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farine DR, Montiglio PO, Spiegel O. From individuals to groups and back: the evolutionary implications of group phenotypic composition. Trends in Ecology and Evolution. 2015;30:609–621. doi: 10.1016/j.tree.2015.07.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fefferman NH, Ng KL. How disease models in static networks can fail to approximate disease in dynamic networks. Physical Review E. 2007;76:031919. doi: 10.1103/PhysRevE.76.031919. [DOI] [PubMed] [Google Scholar]
- Frank SA. Demography and sex-ratio in social spiders. Evolution. 1987;41:1267–1281. doi: 10.1111/j.1558-5646.1987.tb02465.x. [DOI] [PubMed] [Google Scholar]
- Gordon DM. The organization of work in social insect colonies. Nature. 1996;380:121–124. [Google Scholar]
- Hedrick AV, Riechert SE. Genetically-based variation between two spider populations in foraging behavior. Oecologia. 1989;80:533–539. doi: 10.1007/BF00380078. [DOI] [PubMed] [Google Scholar]
- Henschel JR. Predation on social and solitary individuals of the spider Stegodyphus dumicola (Araneae, Eresidae) Journal of Arachnology. 1998;26:61–69. [Google Scholar]
- Herbert-Read JE, Krause S, Morrell LJ, Schaerf TM, Krause J, Ward AJW. The role of individuality in collective group movement. Proceedings of the Royal Society B: Biological Sciences. 2013;280:20122564. doi: 10.1098/rspb.2012.2564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hock K, Fefferman NH. Social organization patterns can lower disease risk without associated disease avoidance or immunity. Ecological Complexity. 2012;12:34–42. [Google Scholar]
- Ingram KK, Oefner P, Gordon DM. Task-specific expression of the foraging gene in harvester ants. Molecular Ecology. 2005;14:813–818. doi: 10.1111/j.1365-294X.2005.02450.x. [DOI] [PubMed] [Google Scholar]
- Jandt JM, Bengston S, Pinter-Wollman N, Pruitt JN, Raine NE, Dornhaus A, Sih A. Behavioral syndromes and social insects: multiple levels of personality. Biological Reviews. 2014;89:48–67. doi: 10.1111/brv.12042. [DOI] [PubMed] [Google Scholar]
- Julian GE, Fewell JH. Genetic variation and task specialization in the desert leaf-cutter ant, Acromyrmex versicolor. Animal Behaviour. 2004;68:1–8. doi: 10.1006/anbe.1999.1184. [DOI] [PubMed] [Google Scholar]
- Keiser CN, Jones DK, Modlmeier AP, Pruitt JN. Exploring the effects of individual traits and within-colony variation on task differentiation and collective behavior in a desert social spider. Behavioral Ecology and Sociobiology. 2014;68:839–850. [Google Scholar]
- Keiser CN, Pinter-Wollman N, Augustine DA, Ziemba MJ, Hao L, Lawrence JG, Pruitt JN. Individual differences in boldness influence patterns of social interactions and the transmission of cuticular bacteria among group-mates. Proceedings of the Royal Society B: Biological Sciences. 2016;283:20160457. doi: 10.1098/rspb.2016.0457. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Keiser CN, Pruitt JN. Personality composition is more important than group size in determining collective foraging behaviour in the wild. Proceedings of the Royal Society B: Biological Sciences. 2014;281:20141424. doi: 10.1098/rspb.2014.1424. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krause J, James R, Croft DP. Personality in the context of social networks. Philosophical Transactions of the Royal Society B: Biological Sciences. 2010;365:4099–4106. doi: 10.1098/rstb.2010.0216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kurvers R, Prins HHT, van Wieren SE, van Oers K, Nolet BA, Ydenberg RC. The effect of personality on social foraging: shy barnacle geese scrounge more. Proceedings of the Royal Society B: Biological Sciences. 2010;277:601–608. doi: 10.1098/rspb.2009.1474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laskowski KL, Pruitt JN. Evidence of social niche construction: persistent and repeated social interactions generate stronger personalities in a social spider. Proceedings of the Royal Society B: Biological Sciences. 2014;281:20133166. doi: 10.1098/rspb.2013.3166. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Lloyd-Smith JO, Schreiber SJ, Kopp PE, Getz WM. Superspreading and the effect of individual variation on disease emergence. Nature. 2005;438:355–359. doi: 10.1038/nature04153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lott DF. Intraspecific variation in the social systems of wild vertebrates. Cambridge University Press; Cambridge: 1991. [Google Scholar]
- Lubin Y, Bilde T. The evolution of sociality in spiders. Advances in the Study of Behavior. 2007;37:83–145. [Google Scholar]
- Majer M, Svenning JC, Bilde T. Habitat productivity predicts the global distribution of social spiders. Frontiers in Ecology and Evolution. 2015;3:101. doi: 10.1186/1742-9994-10-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mersch DP, Crespi A, Keller L. Tracking individuals shows spatial fidelity is a key regulator of ant social organization. Science. 2013;340:1090–1093. doi: 10.1126/science.1234316. [DOI] [PubMed] [Google Scholar]
- Modlmeier AP, Keiser CN, Watters JV, Sih A, Pruitt JN. The keystone individual concept: an ecological and evolutionary overview. Animal Behaviour. 2014;89:53–62. [Google Scholar]
- Naug D. Structure of the social network and its influence on transmission dynamics in a honeybee colony. Behavioral Ecology and Sociobiology. 2008;62:1719–1725. [Google Scholar]
- O’Donnell S, Bulova SJ. Worker connectivity: a simulation model of variation in worker communication and its effects on task performance. Insectes Sociaux. 2007;54:211–218. [Google Scholar]
- Oster GF, Wilson EO. Caste and ecology in the social insects: monographs in population biology. Princeton University Press; Princeton, NJ: 1978. [PubMed] [Google Scholar]
- Pie MR, Rosengaus RB, Traniello JFA. Nest architecture, activity pattern, worker density and the dynamics of disease transmission in social insects. Journal of Theoretical Biology. 2004;226:45–51. doi: 10.1016/j.jtbi.2003.08.002. [DOI] [PubMed] [Google Scholar]
- Pinter-Wollman N. Persistent variation in spatial behavior affects the structure and function of interaction networks. Current Zoology. 2015;61:98–106. [Google Scholar]
- Pinter-Wollman N, Hobson EA, Smith JE, Edelman AJ, Shizuka D, de Silva S, Waters JS, et al. The dynamics of animal social networks: analytical, conceptual, and theoretical advances. Behavioural Ecology. 2014;25:242–255. [Google Scholar]
- Pinter-Wollman N, Hubler J, Holley JA, Franks NR, Dornhaus A. How is activity distributed among and within tasks in Temnothorax ants? Behavioral Ecology and Sociobiology. 2012;66:1407–1420. [Google Scholar]
- Pinter-Wollman N, Keiser CN, Wollman R, Pruitt J. Data from: The effect of keystone individuals on collective outcomes can be mediated through interactions or behavioral persistence. American Naturalist, Dryad Digital Repository. 2016 doi: 10.1086/687235. http://dx.doi.org/10.5061/dryad.5mm01. [DOI] [PMC free article] [PubMed]
- Pinter-Wollman N, Wollman R, Guetz A, Holmes S, Gordon DM. The effect of individual variation on the structure and function of interaction networks in harvester ants. Journal of the Royal Society Interface. 2011;8:1562–1573. doi: 10.1098/rsif.2011.0059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt JN, Goodnight CJ. Site-specific group selection drives locally adapted colony compositions. Nature. 2014;514:359–362. doi: 10.1038/nature13811. [DOI] [PubMed] [Google Scholar]
- Pruitt JN, Keiser CN. The personality types of key catalytic individuals shape colonies’ collective behaviour and success. Animal Behaviour. 2014;93:87–95. doi: 10.1016/j.anbehav.2014.04.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt JN, Pinter-Wollman N. The legacy effects of keystone individuals on collective behaviour scale to how long they remain within a group. Proceedings of the Royal Society B: Biological Sciences. 2015;282:89–96. doi: 10.1098/rspb.2015.1766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pruitt JN, Wright CM, Keiser CN, DeMarco A, Grobis MM, Pinter-Wollman N. The Achilles’ heel hypothesis: misinformed keystone individuals impair collective learning and reduce group success. Proceedings of the Royal Society B: Biological Sciences. 2016;283:20152888. doi: 10.1098/rspb.2015.2888. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- R Core Team. R: a language and environment for statistical computing. R Foundation for Statistical Computing; Vienna: 2014. http://www.R-project.org. [Google Scholar]
- Riechert SE, Hedrick AV. Levels of predation and genetically based antipredator behavior in the spider, Agelenopsis aperta. Animal Behaviour. 1990;40:679–687. [Google Scholar]
- Riechert SE, Hedrick AV. A test for correlations among fitness-linked behavioral traits in the spider Agelenopsis aperta (Araneae, Agelenidae) Animal Behaviour. 1993;46:669–675. [Google Scholar]
- Robson SK, Traniello JFA. Key individuals and the organization of labor in ants. In: Detrain C, Deneubourg JL, Pasteels JM, editors. Information processing in social insects. Birkhäuser; Basel: 1999. pp. 239–260. [Google Scholar]
- Schradin C. Intraspecific variation in social organization by genetic variation, developmental plasticity, social flexibility or entirely extrinsic factors. Philosophical Transactions of the Royal Society B: Biological Sciences. 2013;368:20120346. doi: 10.1098/rstb.2012.0346. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sih A, Bell A, Johnson JC. Behavioral syndromes: an ecological and evolutionary overview. Trends in Ecology and Evolution. 2004;19:372–378. doi: 10.1016/j.tree.2004.04.009. [DOI] [PubMed] [Google Scholar]
- Sih A, Hanser SF, McHugh KA. Social network theory: new insights and issues for behavioral ecologists. Behavioral Ecology and Sociobiology. 2009;63:975–988. [Google Scholar]
- Sumpter DJT. The principles of collective animal behaviour. Philosophical Transactions of the Royal Society B: Biological Sciences. 2006;361:5–22. doi: 10.1098/rstb.2005.1733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Watts DJ, Strogatz SH. Collective dynamics of “small-world” networks. Nature. 1998;393:440–442. doi: 10.1038/30918. [DOI] [PubMed] [Google Scholar]
- Whitfield CW, Cziko AM, Robinson GE. Gene expression profiles in the brain predict behavior in individual honey bees. Science. 2003;302:296–299. doi: 10.1126/science.1086807. [DOI] [PubMed] [Google Scholar]
- Wilson EO. Caste and division of labor in leaf-cutter ants. I. The overall pattern in Atta sexdens. Behavioral Ecology and Socio-biology. 1980;7:143–156. [Google Scholar]
- Wright CM, Keiser CN, Pruitt JN. Personality and morphology shape task participation, collective foraging and escape behaviour in the social spider Stegodyphus dumicola. Animal Behaviour. 2015;105:47–54. [Google Scholar]
- Yang AS, Martin CH, Nijhout HF. Geographic variation of caste structure among ant populations. Current Biology. 2004;14:514–519. doi: 10.1016/j.cub.2004.03.005. [DOI] [PubMed] [Google Scholar]
References Cited Only in the Online Appendixes
- Grinsted L, Pruitt JN, Settepani V, Bilde T. Individual personalities drive task differentiation in a social spider. Proceedings of the Royal Society B: Biological Sciences. 2013;280:20131407. doi: 10.1098/rspb.2013.1407. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Jones TC, Akoury TS, Hauser CK, Moore D. Evidence of circadian rhythm in antipredator behaviour in the orb-weaving spider Larinioides cornutus. Animal Behaviour. 2011;82:549–555. [Google Scholar]
- Modlmeier AP, Laskowski KL, DeMarco AE, Coleman A, Zhao K, Brittingham HA, McDermott DR, et al. Persistent social interactions beget more pronounced personalities in a desert-dwelling social spider. Biology Letters. 2014;10:20140419. doi: 10.1098/rsbl.2014.0419. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- Pruitt JN, Grinsted L, Settepani V. Linking levels of personality: personalities of the “average” and “most extreme” group members predict colony-level personality. Animal Behaviour. 2013;86:391–399. [Google Scholar]
- Watts JC, Herrig A, Allen WD, Jones TC. Diel patterns of foraging aggression and antipredator behaviour in the trashline orb-weaving spider, Cyclosa turbinata. Animal Behaviour. 2014;94:79–86. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.