Daily Light Exposure Patterns Reveal Phase and Period of the Human Circadian Clock

Abstract

Light is the most potent time cue that synchronizes (entrains) the circadian pacemaker to the 24-h solar cycle. This entrainment process is an interplay between an individual’s daily light perception and intrinsic pacemaker period under free-running conditions. Establishing individual estimates of circadian phase and period can be time-consuming. We show that circadian phase can be accurately predicted (SD = 1.1 h for dim light melatonin onset, DLMO) using 9 days of ambulatory light and activity data as an input to Kronauer’s limit-cycle model for the human circadian system. This approach also yields an estimated circadian period of 24.2 h (SD = 0.2 h), with longer periods resulting in later DLMOs. A larger amount of daylight exposure resulted in an earlier DLMO. Individuals with a long circadian period also showed shorter intervals between DLMO and sleep timing. When a field-based estimation of tau can be validated under laboratory studies in a wide variety of individuals, the proposed methods may prove to be essential tools for individualized chronotherapy and light treatment for shift work and jetlag applications. These methods may improve our understanding of fundamental properties of human circadian rhythms under daily living conditions.

Humans possess a circadian pacemaker, located in the suprachiasmatic nucleus of the hypothalamus (SCN), which synchronizes many rhythmic processes such as hormone secretion, skin temperature, heart rate, and the sleep-wake cycle (Schmidt et al., 2007). Light can phase shift the circadian pacemaker, which allows for synchronization of behavioral and physiological rhythms with the 24-h solar cycle, a process called entrainment (Duffy and Wright, 2005). Humans are unique in their light-exposure patterns due to the fact that this pattern can be altered with self-employed electrical lighting patterns. The individual regulation of light exposure seems to broaden the distribution of phase of entrainment in humans (Wright et al., 2013) compared with other species. This exceptionally broad distribution of entrainment has been related to numerous health problems (Bonmati-Carrion et al., 2014), and understanding the complexity of human light entrainment is therefore important.

Assessment of circadian phase typically requires relatively expensive laboratory hormone assessments (dim light melatonin onset; DLMO). To make circadian phase assessment more accessible for researchers and clinicians, less expensive alternatives are needed. Modeling the effect of light on the human circadian system may provide such an alternative, as ambulatory (wrist-actigraph) light exposure data can be collected in a low-cost and noninvasive manner, without the need for subjects to change their daily living routines. Furthermore, such approaches may provide knowledge on human circadian organization in real-life settings. One mathematical model that has been particularly accurate in modeling the circadian response to light is the limit-cycle oscillator model developed by Kronauer and others (Kronauer, 1990; Kronauer et al., 1999) with revised versions presented by Jewett et al. (1999) and St. Hilaire et al. (2007b). This model describes a light-sensitive circadian pacemaker where the circadian phase of the pacemaker defines its sensitivity to light. Not only can this model be used to replicate phase-response curves reported in literature (e.g., Khalsa et al., 2003), it may also be a valuable tool to evaluate light exposure patterns in human entrainment.

Whether this model can reliably predict circadian phase in the field is unknown, as it was developed, refined, and validated using only controlled laboratory studies on amplitude-suppressing and phase-shifting effects of light on the circadian pacemaker (Jewett et al., 1991, 1994; Khalsa et al., 1997; St. Hilaire et al., 2007b). Here we will test whether Kronauer’s model can be used to estimate circadian phase under daily living conditions by entering individually collected ambulatory light data into the model. By letting Kronauer’s model entrain to the light data that were collected for each individual, the entrained phase of each individual (DLMO) can be directly compared with the entrained phase of the model. Because intrinsic circadian period length (τ) will not be determined for the participants described here, the default value of 24.2 h will initially be assumed for the model parameter describing τ. However, it is well known that humans differ considerably in intrinsic period length (Czeisler et al., 1999; Duffy et al., 2011; Hiddinga et al., 1997). This variation in intrinsic period may affect the phase angle of entrainment between the external light-dark cycle (sunlight and/or artificial light) and the entrained circadian rhythm in humans (Duffy et al., 2001; Wright et al., 2005; Gronfier et al., 2007; Eastman et al., 2015; Hasan et al., 2012), as has been observed in other species (e.g., Pittendrigh and Daan, 1976; Merrow et al., 2006). After determining the amount of variance in circadian phase attributable to ambulatory light exposure, we assumed that τ is the dominant factor in explaining individual differences in the timing of DLMO and that the remaining unexplained variance will be mainly attributable to individual differences in intrinsic period. Minimizing this unexplained variance through iterative tuning of individual τ, we present the possibility that Kronauer’s model can be used as a tool to predict not only circadian phase but also human intrinsic period.

Methods

Participants included 20 healthy male (n = 9) and female (n = 11) subjects, age 20 to 27 years (average ± SD, 23.2 ± 1.7 years). Chronotype was assessed via the Munich Chronotype Questionnaire (MCTQ; Roenneberg et al., 2003). A broad distribution of chronotypes was achieved by including only very early (MSF 2.75-3.79), intermediate (MSF 4.63-4.83), and very late chronotypes (MSF 7.04-7.75) (where MSF refers to “midsleep on free days”). The cut-off values used for classification of chronotype groups were determined by analyzing the distribution of chronotypes available in the MCTQ Dutch database (updated from Zavada et al., 2005), containing 4132 individuals within the age range of 20 to 30 years (very early, intermediate, and very late types fell within the lowest, middle, and highest 10% of this distribution, respectively). The dataset contained 8 very early (MSF mean ± SD, 3.5 ± 0.3), 9 intermediate (MSF 4.7 ± 0.1), and 3 very late (MSF 7.3 ± 0.4) chronotypes.

Exclusion criteria were the presence of considerable sleep disturbances assessed with the Pittsburgh Sleep Quality Index (PSQI; >9 [average ± SD, 3.52 ± 1.71; 2 individuals scored >5]) (Buysse et al., 1989); tendencies for anxiety and/or depression, determined via the Beck Depression Inventory (BDI; >7) (Beck et al., 1996) and Hospital Anxiety and Depression Scale (HADS; >7) (Zigmond and Snaith, 1983); and color-blindness, indicated by the inability to complete an Ishihara color blindness test (Clark, 1924) without errors. All participants completed an in-house-developed general health questionnaire, which was assessed in order to exclude participants who reported chronic medical conditions or the need for medication use, previous head injury, epilepsy, smoking, excessive use of alcohol or caffeine (>3 and >8 × ~60-mg consumptions per day, respectively), the use of recreational drugs during the last year, a body mass index outside the range of 18 to 27, a body weight of less than 36 kg, or a history of shift work and/or having travelled across more than one time zone in the last month prior to the experiment.

From a total of 23 participants enrolled into the study, 1 participant dropped out and 2 participants were excluded from analysis because of malfunctioning of the equipment, leaving a total of 20 participants for analysis.

The study procedures were approved by the Medical Ethical Research Committee of the University Medical Centre Groningen (NL48468.042.14), Netherlands, and are in accordance with the Declaration of Helsinki (2013). All participants gave written informed consent.

Study Procedures

The procedures described here are part of a 3-week field study protocol in which ambulatory data were collected for the assessment of human biological rhythms in the field. Only the first 9 days are relevant for the current study. All measurements were conducted in the Groningen area (the Netherlands), between November 2014 and January 2016.

Light-intensity and activity were continuously monitored from Friday evening (day 0) until Sunday afternoon (day 9) using actigraph devices (MotionWatch 8; CamNtech Ltd., Cambridge, UK), containing an accelerometer and a broadband light sensor. On day 8, a laboratory session was scheduled to assess circadian clock phase under dim light conditions (fluorescent ceiling illumination <10 lux in all possible directions of gaze, measured at start and finish of study; DLMO). Participants entered the laboratory 9 h before habitual sleep onset. For each participant, 8 hourly saliva samples were obtained with the last sample scheduled at the time of habitual sleep onset. Participants remained in a posture-controlled position for 15 min preceding saliva sampling. Participants needed to attend the laboratory for device changes twice during the week for less than 30 min each time, at a time of choice that was not restrictive to their sleep-wake schedule. No further interventions were applied during these 9 days of data collection.

Measurements

Data were collected throughout the year, but not within 1 week after daylight savings time transitions (end of March and end of October). For all data collected under daylight savings time, 1 h was subtracted from the time values, such that all time values were expressed as GMT+1 for the time zone of the Netherlands.

Actigraphy

Activity was measured using the MotionWatch 8, which returns activity counts per 1-min epoch as the cumulative sum of motion, as recorded by a triaxial accelerometer. The average activity acrophase was estimated by fitting a single sine wave harmonic with a period of 24 h to the available 9 days of actigraphy data (CircWave, version 1.4; Roelof A. Hut, University of Groningen, the Netherlands).

Light Intensity

Light intensity (in lux) was measured per second and recorded as 1-min averages. The light data that were used for all analyses were the per-minute averages as returned by the MotionWatch 8. The sensor accurately describes light intensity in the 0- to 64,000-lux range, which we validated using a photo spectrometer (SpecBos 1211 LAN UV; JETI Technische Instrumente GmbH, Jena, Germany). A distribution of light intensities measured for each participant over the course of the 9-day protocol is presented in Supplementary Figure S2. Furthermore, an estimation of the amount of daylight each participant was exposed to was calculated as the percentage of lux values greater than 615 for each individual separately. This threshold was chosen because 99% of all light intensities measured during solar darkness did not exceed 615 lux (Suppl. Fig. S3), which means that any values greater than 615 lux must have been collected during daytime. For 1 participant, the device measured 7 h of aberrant high light intensities. As no concomitant activity was measured during this time window, these deviating lux values were marked as an artifact and were set to 0 accordingly (analysis was performed with and without this artifact correction, and it was found not to affect the results).

Sleep Timing

Sleep timing parameters (onset and offset) were calculated from the activity and light data using Sleep analysis software (version 7, CamNtech Ltd.). Sleep offset was calculated as the time when activity and light intensity showed an increase compared with preceding values and maintained that increased level for at least 10 min. Sleep onset was calculated as the time when the reverse was true.

Core-body Temperature

Participants were asked to swallow a core body temperature (CBT) measuring pill (CorTemp; HQ Inc., Palmetto, FL) on the afternoon of day 1 (Saturday) and day 5 (Wednesday). A belt-worn receiver at the abdomen collected the data emitted by the pill until it was excreted from the body after 24 to 32 h. For each participant, CBT data were smoothed by locally weighted scatterplot smoothing (R function loess, after Cleveland et al., 1992), using a 10-h smoothing span. The smoothed data were used to determine CBT minimum (CBT_min) for each night.

DLMO Assessment

Salivary melatonin was collected using Salivette (Sarstedt Ltd., Nümbrecht, Germany). Samples were centrifuged and stored overnight at ~4 °C and then stored in a −80 °C freezer. To assess melatonin concentration, a double-antibody radioimmunoassay (RIA) (intra-assay variation coefficients of 13.97% and 9.11% for low and high concentration controls, respectively; interassay variation coefficients of 13.99% and 14.64% for low and high concentration controls, respectively) was performed (Bühlmann Direct Saliva Melatonin kit; Bühlmann Laboratories AG, Schönenbuch, Switzerland) after termination of the study. DLMO was marked as the first time when linear interpolated melatonin concentrations exceeded the 4 pg/mL threshold.

Modeling the Circadian Response to Ambulatory Light Data

For each participant, 9 days of light data were available (average lux value per minute from Friday evening until the next Sunday afternoon). Light data were cut to start at the time of the first estimated CBT_min (estimated as measured DLMO + 7 h; based on, e.g., Brown et al., 1997; Benloucif et al., 2005) and to end on Sunday afternoon. As the first estimated CBT_min always occurred during early Saturday morning, the final dataset that was processed by the model consisted of ~8 days of data (from Saturday morning until Sunday afternoon). As each individual light profile was cut to start at (DLMO – 7), the clock time associated with the onset of each light profile was different for each individual profile. Kronauer’s model was implemented in R (R Core Team, 2015; version 3.2.3), based on the most recent formulas and parameter values described by St. Hilaire et al. (2007b).

Kronauer’s Limit Cycle Oscillator for the Human Circadian Pacemaker

To model individual circadian responses to the ambulatory light data, the revised limit cycle oscillator model of the human circadian pacemaker was implemented, which is explained in detail by Jewett et al. (1999) with minor revisions proposed by St. Hilaire et al. (2007b). The model consists of a pacemaker that, in the absence of light, oscillates in a circular fashion (the limit cycle) with a period of 24.2 h and amplitude normalized to 1. Light has the potential to push the oscillator away from the limit cycle, effectively influencing both the amplitude of the cycle and the speed at which the pacemaker traverses through this cycle. The effect of light on speed and amplitude depends on the phase of the circadian pacemaker, such that light is most efficient in influencing these parameters when the pacemaker phase is close to CBT_min. When light is perceived before the critical phase (close to CBT_min), the speed of the pacemaker is reduced, resulting in a phase-delay. This phase-delay gradually changes into a phase-advance when light is perceived after the critical phase. Light and dark adaptation is incorporated in the model, such that the efficiency of light to affect the pacemaker gradually decreases during prolonged light exposure, whereas the opposite occurs during prolonged darkness. This adaptation mechanism is modeled by a pool of photosensitive elements in the light-sensitive module that can be in either the “used” (variable n) state or the “ready” (fraction 1 – n) state, which is analogous to the effect of light on retinal photo pigments: The photon-induced conformational change of a photo pigment molecule renders it insensitive to light until it is recycled. A graphic representation of the processes described above is presented in Figure 1. As an example, a simulated phase-delay is presented in Figure 2. A complete overview of the model parameters and formulas are presented in Supplementary Table S1. No modifications to the core model components were applied. Slight alterations to initial variable values (values that are required to describe the baseline state of the model when the first lux value in a light profile is evaluated) are described below when the ambulatory light data modeling are discussed.

Figure 1.

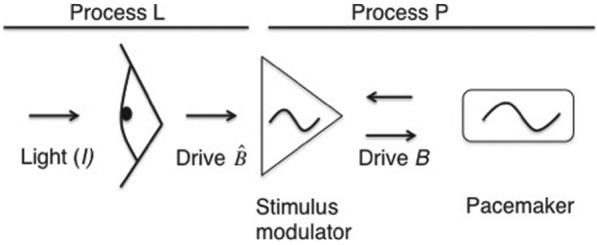
Graphic overview of information flow at each model iteration. On a per-minute basis, Kronauer’s model evaluates the effect of light (in lux) on the circadian pacemaker. When light is presented to the model, process L generates a drive $\widehat{B}$, which is influenced by both the current intensity of light and the state of adaptation. This drive $\widehat{B}$ is then altered by a stimulus modulator, based on the current phase and amplitude of the pacemaker, resulting in a modulated drive B. Drive B in turn affects the speed and amplitude with which the pacemaker oscillates.

Figure 2.

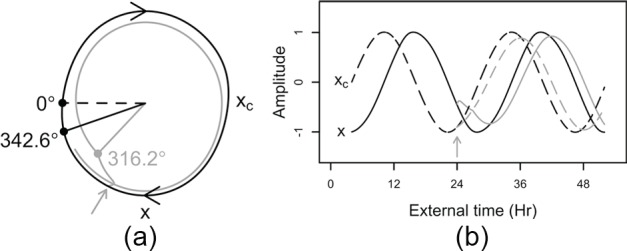
Example of a simulated phase-delay. The Kronauer model responds to a 3-h, 9500-lux light pulse (gray arrow) starting 5 h before CBT_min (midnight in this example). (A) At baseline, the pacemaker follows the limit-cycle oscillation (black curve). This oscillation is modeled by 2 coupled variables describing the state of the pacemaker, x and x_c. Variable x closely follows the core body temperature rhythm, whereas x_c is a complementary variable that is mathematically required to achieve this oscillation. When the light stimulus is presented, the system is pushed away from the limit cycle (gray curve), leading to a deceleration of the pacemaker. At the end of the light-pulse (0300 h; filled circles connected to solid lines), the pacemaker is delayed as only 316.2° of 1 oscillation was traversed versus 342.6° in the absence of a light stimulus (0° and dashed line mark x_min, which corresponds to predicted CBT_min – 0.97h). (B) Overview of the state variable responses (solid lines, x; dashed lines, x_c) to the same light pulse as in panel A. Compared with no light pulse (black lines), the rate of change in the 2 state variables (i.e., the speed of the pacemaker) is slowed down in response to light (gray curve), leading to a phase-delay.

Core-body Temperature Minimum as a Phase Marker

As a circadian phase marker, the time of CBT_min can be calculated from the relationship between state variables x_c and x (see Figure 2) (May et al., 2002; St. Hilaire et al., 2007b) such that CBT_min = [time when atan(x_c, x) = −2.98] + ${\mathrm{\varphi }}_{\mathrm{ref}}$, where ${\mathrm{\varphi }}_{\mathrm{ref}}$ = 0.97 h. Typically, CBT_min occurs approximately 1 h after the occurrence of x_min. Although St. Hilaire et al. (2007a) provide a method to use predicted melatonin synthesis onset as a phase marker of Kronauer’s model, we have decided to use the time of predicted CBT_min as the model output. As the time interval between CBT_min and DLMO has consistently been reported to approximate 7 h (e.g., Brown et al., 1997; Benloucif et al., 2005), the time of the model-predicted CBT_min is easily converted into a model-predicted DLMO by subtracting 7 h from predicted CBT_min.

Baseline Model Entrainment

With its phase-dependent sensitivity to light, Kronauer’s oscillator has the property to entrain to a given 24-h light-dark cycle. By letting the model entrain to the same light-dark cycle that each individual is entrained to, the phase of entrainment of Kronauer’s oscillator can be directly compared with the measured phase marker (DLMO or CBT_min) of each individual. This comparison requires stable entrainment to the same light-dark cycle for both the model and the individual. As only 1 week of light data were available before the DLMO was measured, it was assumed that this week of light data were representative for the typical light-dark cycle to which each individual was stably entrained. Unlike what was assumed for the participants, the model is not stably entrained to this 1 week of light data by default. In fact, the model requires time to stably entrain to any light-dark cycle it is presented with, analogous to recovering from jetlag. Kronauer’s model typically requires multiple baseline weeks to reach stable entrainment, which were here constructed from the light data that were obtained for each individual separately as follows: The first 7 days of the individual 8-day light profiles described earlier were repeated 4 times (i.e., 4 weeks of artificial baseline data) and used as an input for the model to entrain to. When constructing these artificial baseline weeks, day 8 was not included, as this was the semi-constant routine day at which DLMO was assessed and therefore not a representative day of light data. During the processing of each individual’s artificial baseline weeks, the model’s phase of entrainment gradually shifted toward an asymptote (a gradual day-to-day shift in predicted core-body temperature minimum) which, when reached, indicated that the requirement of stable entrainment was met. Although the time to reach stable entrainment varied between individual baseline profiles, the model was stably entrained after 4 weeks in all individuals. The entire 8 days of individual light data were then added to the end of this 4-week baseline period. This procedure allowed for a direct comparison between the model-predicted DLMO on the last Saturday (day 8 of “week 5”) evening (predicted CBT_min on the Sunday morning – 7 h) to the actual DLMO measured on that Saturday evening.

It is important to note that for each individual baseline profile, the model will eventually always reach the same phase angle of (stable) entrainment, regardless of the initial state of the model at the start of the baseline weeks. This is analogous to an SCN that will recover from jetlag, reaching stable entrainment to the new time zone, regardless of the initial time zone. Therefore, no a priori knowledge on the state of the oscillator is required at the start of the baseline procedure. Nevertheless, a value needs to be assigned to each of the variables describing the initial state of the model to start processing the data. For completeness, the initial state variable values (x and x_c) were set to −1.04 and 0.09, respectively, whereas variable n was set to 0.014. This is the state of the model that would occur at predicted CBT_min when simulating stable entrainment to days consisting of 16 h of wakefulness under 150 lux and 8 h of sleep under 0 lux (Jewett et al., 1999) at the beginning of the baseline weeks. At the start of week 5, the state of the model was unique for each individual, as it was uniquely entrained to each individual’s baseline 4-week light profile.

Statistical Analyses

Statistical analyses were performed in R (R Core Team, 2015; version 3.2.3), using the most recent shell of Rstudio (version 0.99.491). Linear regression models were fitted with the base lm function. To test whether individual terms significantly (α = 0.05) contributed to the model when multiple explanatory variables were included, the drop1 function from the lme4 library (Bates et al., 2012) was implemented. Model selection was based on the Akaike information criterion (AIC) using a backward step-wise multiple regression approach.

Results

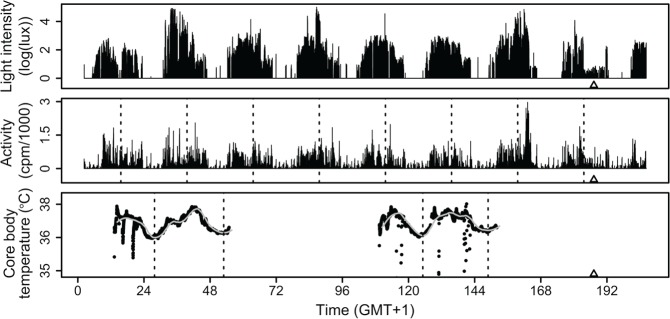
For each participant, the final dataset contained ~8 days of activity and light intensity data, at least (depending on metabolic rate) 2 days of CBT data (day 1 and day 5), one DLMO value (day 8), the cosine-fitted average activity acrophase, and the average CBT_min clock times of at least 2 nights. As an example, Figure 3 provides the compiled dataset of 1 participant. Table 1 contains demographic data for the sample.

Figure 3.

Compiled dataset of participant BCM15. Top panel: 9 days of ambulatory light intensity data, plotted as log(lux; >1 lux), although the actual modeling was performed on the untransformed lux values. Middle panel: Concomitant ambulatory activity data. Dashed lines mark the estimated time of maximum activity. Bottom panel: Core body temperature data collected by 2 separate CBT pills. The dashed vertical lines mark CBT_min times for days 1, 2, 5, and 6. The gray curve follows the smoothed fit of CBT. △ denotes measured DLMO in all panels.

Table 1.

Participant demographics.

Demographic
Gender, n	9 males, 11 females
Age, years	23.2 ± 1.7 (20.0-27.0)
MSF	4.6 ± 1.3 (2.8-7.8)
Average sleep onset	24.0 ± 1.2 (21.5-26.9)
Average sleep offset	8.0 ± 1.2 (6.3-12.5)
Average midpoint of sleep	4.0 ± 1.2 (1.9-7.7)
Activity acrophase	15.9 ± 1.5 (13.9-19.0)
Average CBTmin	3.6 ± 2.1 (1.2-9.9)
DLMO	20.5 ± 1.9 (17.0-26.3)
Average light intensity, log(lux); lux >0	1.3 ± 0.2 (0.7-1.6)

Values expressed as mean ± SD (minimum to maximum), except for gender.

Relationship between DLMO and Ambulatory CBT_min

First we assessed whether core-body temperature minimum (CBT_min) can be a reliable estimate of circadian phase in the field. Linear regression analysis revealed a significantly positive relationship between DLMO and CBT_min (Figure 4; F_1,18 = 19.2; p < 0.001). The average ± SD difference between DLMO and CBT_min was 7.1 ± 1.5 h. As the data points were nonequidistant due to the inclusion of 1 individual with a relatively late DLMO, the strength of the relationship between DLMO and CBT_min was tested by repeating the regression analysis without this individual (F_1,17 = 3.59; p = 0.07).

Figure 4.

Relationship DLMO and time of core-body temperature minimum. Each data point represents the average of all CBT_min times available for each participant.

Predicting DLMO with Ambulatory Light and Actigraphy Data

Next, we tested whether modeling ambulatory light data could generate accurate predictions of clock phase. For each participant, the individual 8-day light profile was processed by Kronauer’s model, resulting in 8 individual daily predictions of CBT_min. From these 8 predicted CBT_min values, only those days on which CBT_min data were available were used for further analysis, together with the predicted CBT_min following the day of DLMO assessment (Figure 5). Predicted DLMO (DLMO^p) was calculated from the predicted CBT_min following the DLMO assessment day. For this calculation, a phase difference of 7 h was assumed between DLMO and CBT_min, which is in line with the phase difference of 7.1 h reported here and the phase difference of ~7 h reported previously (e.g., Brown et al., 1997; Benloucif et al., 2005). Accordingly, DLMO^p was calculated as (Predicted CBT_min on Night 8) – 7. Finally, average predicted CBT_min (CBT_min^p) was calculated as the average of the predicted CBT_min values determined for the nights on which CBT data were available. For clarity, the model-predicted time of CBT_min should not be confused with the measured CBT_min values. Predicted CBT_min is a phase-marker of the limit-cycle oscillator (from which predicted DLMO was directly calculated by subtracting 7 h), whereas measured CBT_min and DLMO can be considered measured phase markers of the individuals.

Figure 5.

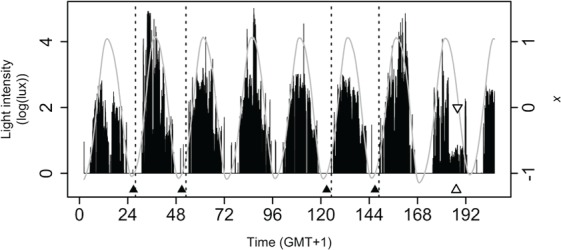
Model predictions for participant BCM15. Model-predicted CBT_min and DLMO (CBT_min^p▲, DLMO^p▽), DLMO△ and Kronauer’s model prediction (variable x; gray curve) are plotted together with the relevant light profile. For this individual, DLMO^p was at 1949 h, whereas measured DLMO was at 1915 h. Only intensities higher than 0 log(lux) were included for graphic display purposes. The actual modeling involved the raw lux values. The vertical dashed lines mark the measured CBT_min times during nights 1, 2, 5, and 6.

As Kronauer’s model returns the time of core body temperature minimum as a circadian phase marker, we first tested whether average CBT_min was related to CBT_min^p, and a significant positive relationship was found (Figure 6A; F_1,18 = 19.58; p < 0.001). Also in this analysis, the data points are nonequidistant, and when the regression was repeated without the late individual, a trend was observed (F_1,17 = 3.612; p = 0.07). Furthermore, DLMO^p values were positively related to the measured DLMO values (Figure 6C; F_1,18 = 19.44; p < 0.001). This significant relationship disappeared when the late individual was omitted from the analysis (F_1,17 = 2.876; p = 0.11). Although DLMO^p and CBT_min^p both significantly explained 52% of the variance in the measured DLMO and average CBT_min values, respectively, a considerable amount of residual variance was still observed (Figure 6, A and C; CBT_min^p and DLMO^p). As CBT measurements are especially sensitive to masking by activity, it was tested whether a combination of CBT_min^p and time of activity acrophase would explain more variance in average CBT_min than CBT_min^p alone. A simple regression analysis revealed that CBT_min^p together with activity acrophase (added as a covariate) explained 67% (an increase of 15%) of the variance in average CBT_min (Figure 6B; F_2,17 = 17.5, p < 0.001). Next, it was tested whether more variance in DLMO could be explained with a combination of DLMO^p and time of activity acrophase (covariate) than with DLMO^p alone. Together, DLMO^p and activity acrophase explained 71% (an increase of 19%) of the total variance in DLMO (Figure 6D; F_2,17 = 20.74, p < 0.001). When the late individual was omitted from the latter 2 analyses, Kronauer’s model prediction did not significantly contribute to either one of these regression models (CBT_min^p, p = 0.15; DLMO^p, p = 0.1).

Figure 6.

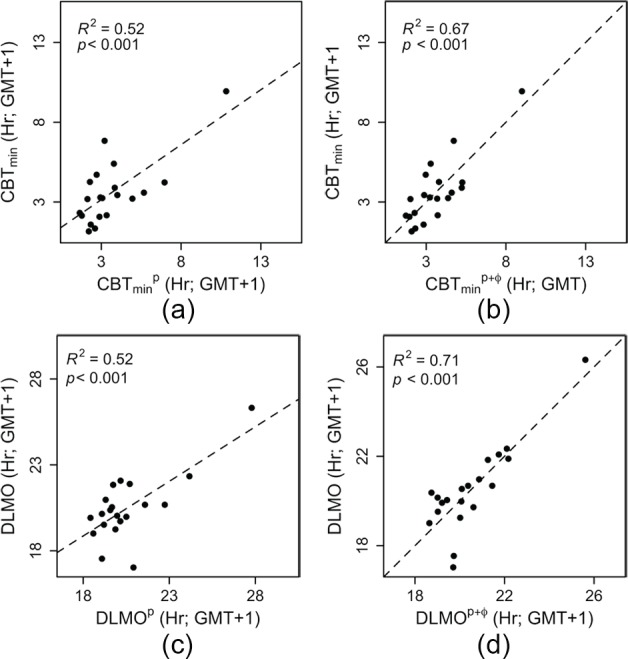
Model predictions for both CBT_min and DLMO. (A and C) The model-predicted CBT_min and DLMO times (CBT_min^p and DLMO^p) show a significant positive relationship with CBT_min and DLMO, respectively. (B and D) When correcting the model predictions of CBT_min and DLMO for activity acrophase (CBT_min^p+φ and DLMO^p+φ, respectively), 15% more variance in CBT_min and 19% more variance in DLMO were explained. The residual standard deviations corresponding to the regression analyses presented in panels A, B, C, and D were 1.46, 1.24, 1.4 and 1.1 h, respectively.

We finally tested how well the model would predict DLMO when the default light settings of the model were used, by assuming 150 lux during wake and 0 lux during sleep. The residual sum of squares between DLMO^p and DLMO was reduced (by 51%) from 90.83 h² when default light settings were used to 46.18 h² when individual light profiles were used. A consistent bias toward later DLMO predictions (+1.82 ± 1.14 h [SD]) was also observed when using the default settings but not when using the individualized light profiles (+0.07 ± 1.56 h [SD]). This suggests that assuming 150 lux during the wake period results in an overestimation of light exposure in the evening.

Estimating Intrinsic Circadian Period with Ambulatory Light Data and Measured DLMO

The results indicate that not all variance in circadian phase can be explained by modeling light data only, a finding that was assumed to originate mainly from individual variation in intrinsic circadian period. To obtain the set of estimated individual $\tau$ values ($\widehat{\tau }$_{i….n}) that could explain the remaining variance, the difference between DLMO^p and DLMO was minimized (<1 min) for each individual separately by manipulating the value of the $\tau$ parameter according to the schematic in Figure 7A (an example is presented in Figure 7B).

Figure 7.

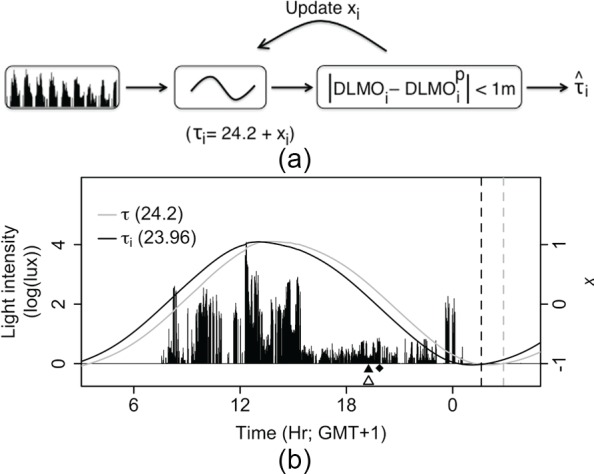
Intrinsic period estimation method. (A) The intrinsic $\tau$ of the model was iterated stepwise (from the initial $\tau$ of 24.2 h) for each participant until the time between DLMO_i and DLMO^p was <1 min. (B) Light intensity data of day 8 for participant BCM15, who showed a DLMO (△) earlier than predicted by the model with the default $\tau$ (◆). For this individual, a$\tau$ of 23.96 h resulted in a DLMO^p (▲) that was identical to the measured DLMO. Dashed lines show CBT_min^p using the default (gray) and individual (black) $\tau$. Solid lines show the value of state-variable x when the default (gray) or individual (black)$\tau$ was used.

Intrinsic Period Distribution

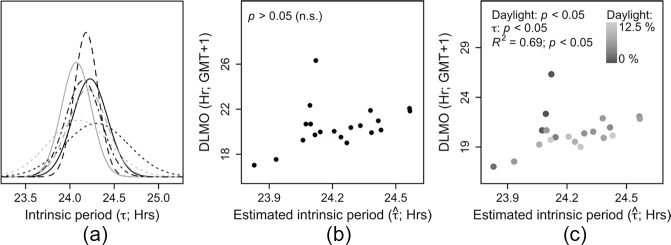
The intrinsic period estimates ranged from 2350 to 2434 h, with an average ± SD of 2414 ± 0012 h. We found our distribution to match previous literature well (Figure 8A), as average ± SD intrinsic periods from previous literature were 2418 ± 0022 h (Hiddinga et al., 1997), 2411 ± 0008 h (Czeisler et al., 1999), 2404 ± 0010 h (Wright et al., 2005), 2406 ± 0020 h (Gronfier et al., 2007), 2412 ± 0008 h (Burgess and Eastman, 2008), and 2409 ± 0012 h (Duffy et al., 2011). This similarity suggests that the discrepancy observed between DLMO and DLMO^p may be attributable to a distribution of intrinsic periods in our sample that is comparable to distributions reported previously. Acknowledging the possibility that there are other physiological parameters than $\tau$ that could explain the observed remaining variance in phase angle of entrainment (e.g., light sensitivity, differently shaped phase response curves [PRCs]), we tested whether the individual variation around a laboratory-constructed PRC (Khalsa et al., 2003) followed the distribution that would be expected based on a known distribution of $\tau$ (Czeisler et al., 1999). This was found to be the case (Suppl. Fig. S1), suggesting that $\tau$is indeed the dominant factor determining phase in human circadian entrainment. Next, we tested whether tuning other model variables (while leaving τ at the default value of 24.2 h) could minimize the discrepancy between DLMO and DLMO^p. For 6 participants, adjusting the saturating level of light intensity did not result in an optimal solution (DLMO = DLMO^p), by manually tuning I₀, leaving an unexplained variance of 14.32 h², which was 69% of the total variance in DLMO. Parameter values leading to a solution were often unrealistic (e.g., more than half of the required saturating light levels were <200 or >30,000 lux). Also, tuning B and $\widehat{B}$ variable values did not lead to an optimal solution in 4 participants, leaving an unexplained variance of 12.62 h² (72.7% of the total variance). These findings support our assumption that τ may be the dominant source of individual variation when using Kronauer’s model to predict clock phase.

Figure 8.

Distribution and relationships of $\widehat{\tau }$ (A) Distribution of estimated intrinsic period compared with a sample of intrinsic period distributions reported using forced desynchrony protocols. The separate intrinsic periods are distributed with means (±SD) of 24.23 (±0.20; $\widehat{\tau }$_{i….n}; field estimation; solid black line), 24.3 (±0.36; Hiddinga et al., 1997; dotted black line), 24.18 (±0.13; Czeisler et al., 1999; dashed black line), 24.07 (±0.17; Wright et al., 2005; solid gray line), 24.10 (±0.34; Gronfier et al., 2007; dotted gray line), 24.2 (±0.13; Burgess and Eastman, 2008; dashed gray line), and 24.15 (±0.20; Duffy et al., 2011; black dotted dashed line). (B) The relationship between DLMO and estimated intrinsic period was not significant. (C) The same relationship as in panel B. The color coding indicates the amount of daylight (% of minutes >615 lux, see Methods) to which each individual was exposed. Later DLMO values were related to longer intrinsic periods, apart from the individuals with the lowest amount of daylight exposure (dark points at $\tau$ ~ 24.1). DLMO was significantly (p < 0.001) explained by both estimated intrinsic period and the amount of daylight exposure, together contributing to a linear model that explained 69% of the variance in DLMO.

Relationship between Estimated Intrinsic Period and Measured Clock Phase

As intrinsic period was directly calculated from DLMO, we expected to find a correlation between these 2 measures. However, no relationship between estimated intrinsic period and clock phase was found (Figure 8B; p = 0.1). A significant relationship between the timing of CBT_min and intrinsic period has been reported by Duffy et al. (2001), which could not be replicated by Wright et al. (2005) when DLMO was taken as the circadian phase marker. To explain these conflicting results, we considered the origin of light to which our subjects were exposed. We hypothesized DLMO to be earlier in individuals when the majority of light exposure originated from daylight rather than artificial light for 2 reasons. First, the intensity of daylight is relatively high compared with artificial light, and higher light intensities have been related to an earlier sleep timing in humans (Roenneberg et al., 2003). Second, daylight typically precedes artificial light (which mostly occurs after sunset rather than before sunrise; Wright et al., 2013). A larger amount of daylight is therefore expected to be related to earlier DLMO values due to both its high intensity and relatively early timing. To test this hypothesis, the relationship between DLMO and estimated intrinsic period was controlled for the log-transformed estimated amount of daylight (minutes >615 lux; see Methods) to which each individual was exposed. After adding the log-transformed amount of daylight as a covariate to the regression equation, 69% of the variance in DLMO was significantly explained (F_2,17 = 18.53; p < 0.001) by both intrinsic period and the amount of daylight exposure. A later DLMO was related to a longer estimated intrinsic period, and more estimated daylight exposure was related to earlier DLMO values (Figure 8C). This improved fit was not only attributable to the late individual: Both log-transformed daylight and $\tau$ remained significant contributors to the regression model when this individual was omitted from the regression analysis (F_2,16 = 21.25; p < 0.001). This shows that the amount of daylight indeed influences the relationship between DLMO and $\tau$, in particular for individuals with very low amounts of daylight exposure (Figure 8C). These results suggest that individual differences in the amount of daylight exposure obscure the expected relationship between DLMO and intrinsic period. As a consequence, when by chance there is little variation between participants in the timing and intensity of the light schedule (indicated by the amount of daylight exposure), a relationship between DLMO and intrinsic period may be revealed, perhaps explaining conflicting results in literature.

Relationship between Estimated Intrinsic Period and the Phase Difference between DLMO and Sleep Timing

To correct for the timing of the light schedule, phase of entrainment can be expressed as the phase angle between DLMO and the light-dark cycle. For this reason, the interval between DLMO and sleep onset (which can be considered as the onset of the dark phase) has been shown to be more strongly related with intrinsic period and is conceptually a more reasonable measure of phase of entrainment (clock phase with respect to zeitgeber phase) than the clock time of DLMO without light timing information (Wright et al., 2005; Gronfier et al., 2007; Burgess and Eastman, 2008; Hasan et al., 2012; Eastman et al., 2015). Therefore, we tested whether a relationship between phase of entrainment and intrinsic period could be revealed in the current dataset. Phase of entrainment was calculated with respect to sleep onset (i.e., lights-off; DLMO – sleep onset) and sleep offset (i.e., lights-on; DLMO – sleep offset) separately. Estimated intrinsic period was significantly related to the phase difference between DLMO and sleep onset (Figure 9A; F_1,18 = 4.67; p < 0.05) and between DLMO and sleep offset (Figure 9B; F_1,18 = 12; p < 0.01). The analysis revealed that individuals with longer estimated intrinsic periods showed a shorter time interval between DLMO and sleep onset/offset and vice versa for individuals with shorter estimated intrinsic periods.

Figure 9.

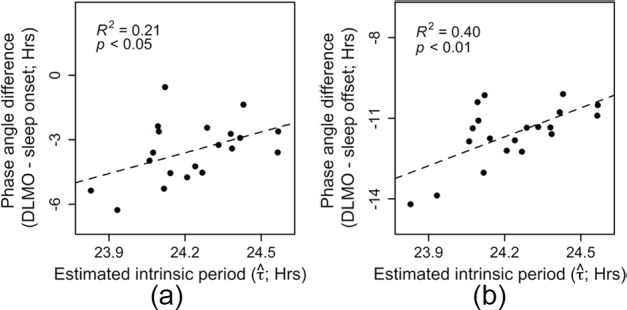
Relationships between sleep timing and estimated $\widehat{\tau }$ The phase angles between (A) sleep onset and DLMO and between (B) sleep offset and DLMO were both significantly and positively related to estimated intrinsic period such that individuals with longer estimated intrinsic periods scheduled their sleep window at a relatively early circadian phase (shorter duration between DLMO and sleep onset).

Relationship between Estimated Intrinsic Period and Phase of Entrainment, Corrected for Light Intensity

As stated previously, phase of entrainment is influenced not only by intrinsic period but also by light intensity. To test the assumption that higher light intensities are related to an earlier phase of entrainment (Roenneberg et al., 2003), we tested whether phase of entrainment could be significantly explained by both intrinsic period and average light intensity. Therefore, the average of the log-transformed lux values (only values >0 lux included) were calculated for each individual separately as a measure of average light intensity. Regression analysis revealed that the phase angles between DLMO and sleep onset (R² = 0.55; F_2,17 = 10.4; p < 0.01) and sleep offset (R² = 0.72; F_2,17 = 21.6; p < 0.001) were significantly related to both estimated intrinsic period (as above) and the average light intensity (now added as a covariate). As expected, later intrinsic period was related to later phase of entrainment, whereas higher light intensities were related to earlier phase of entrainment. For (DLMO – sleep offset), an increase of 1 h in intrinsic period was estimated to delay phase of entrainment by 4.6 ± 0.77 (±SE) h, whereas an increase in average light intensity by 1 log(lux) was estimated to advance phase of entrainment by 2.84 ± 0.65 (±SE) h. For (DLMO – sleep onset), a delay of 4.54 ± 1.21 (±SE) h and an advance of 3.71 ± 1.03 (±SE) h were estimated for these parameters, respectively.

Discussion

The results provide evidence that analyzing ambulatory light, activity, and core-body temperature (CBT) data provides reliable estimations of human clock phase (DLMO). Although CBT_min by itself correlated with DLMO, analyzing the combination of light and activity data provided more accurate estimations. The finding that CBT_min only is a less accurate predictor of DLMO than a combination of light and activity data is likely attributable to known masking effects on CBT (Klerman et al., 1999). By modeling the circadian impact of ambulatory collected light data, we show that Kronauer’s model predictions explain a significant amount of variance in DLMO. This shows that this model may be a useful tool for estimating clock phase in the field, especially when it is combined with activity measurements. The relationship between the DLMO and CBT_min values and Kronauer’s model predictions of these circadian phase markers was not strong, which is likely attributable to large interindividual variation in intrinsic period. Inclusion of individuals with DLMO values deviating from the normal range (shift workers, patients) will be interesting for future testing, as this may show that Kronauer’s model can give a rough estimation of DLMO, even for individuals who are entrained outside the normal range. The fact that the model predicts a late DLMO for the late individual in our dataset is promising, but further testing is required. Furthermore, to the authors’ knowledge, the current study is the first to highlight the possibility that intrinsic period may be estimated by modeling ambulatory light exposure data followed by one clock-phase assessment in the laboratory. Finally, the results presented here provide experimental and theoretical support for the notion that intrinsic period and zeitgeber strength of the light-dark cycle are the dominant factors in determining human phase of entrainment.

Both methods described rely on the integrity of ambulatory collected light data. It should be noted that light was measured at the level of the wrist, not the eye, which might have influenced the model predictions. Furthermore, the device returns light intensity in units of photopic illuminance (lux), which is not entirely representative for the human circadian system. Where Kronauer’s model should ideally be modified to take melanopic lux (Lucas et al., 2014) as an input, the impact of light on the clock can likely be more accurately described when actigraph devices return melanopic lux or photon flux corrected for the spectral sensitivity of melanopsin. It might be that individual differences in light sensitivity induced additional variance as well. Nevertheless, tuning of the light-sensitivity parameter in Kronauer’s model indicated that unlike differences in intrinsic period, differences in light sensitivity are an unlikely factor in explaining the majority of the mismatch between DLMO and predicted DLMO. Finally, the methods presented here will not be applicable to blind individuals, and models incorporating nonphotic entrainment (i.e. St. Hilaire et al., 2007b) could perhaps offer a suitable alternative.

Modeling ambulatory light data explained 52% of the total variance in measured DLMO and timing of CBT_min. Accounting for activity acrophase (added as a covariate) generated more accurate predictions of these parameters (67% and 71%, respectively). CBT_min is particularly sensitive to masking by activity (Klerman et al., 1999), and correcting for activity acrophase may have therefore resulted in the additional amount of explained variance (15%). As DLMO was assessed in a posture-controlled setting, it is unlikely that the additional amount of variance explained in DLMO (19%) originated by accounting for masking effects by activity. It is also unlikely that time of activity acrophase increased the accuracy of DLMO phase estimations through nonphotic effects, since the nonphotic circadian drive by activity is expected to be small in light-entrained individuals (St. Hilaire et al., 2007b). The most parsimonious explanation is that activity acrophase in itself is a reliable phase marker of the central clock (Lim et al., 2012), therefore adding to the predictive power of the light data. This may allow for other indirect measures of clock phase to increase the estimation accuracy of human circadian clock phase.

When entrainment is considered as a mathematical system with 3 unknown variables (light exposure, intrinsic period, and resulting clock phase), the value of one of these variables can be calculated when the remaining two are known. Our method to estimate intrinsic period builds on the assumption that these are the dominant factors determining human entrainment. This is likely a simplification of the human circadian system. Other factors such as measurement errors in DLMO and light intensity and individual differences in the shape of the PRC and sensitivity to light could have also contributed to the remaining variance, which we have herewith included in our intrinsic period estimations. Therefore, our method awaits validation using individual τ estimates in a laboratory study. However, we show that deviations from the PRC reported by Khalsa et al. (2003) could be explained by accounting only for individual differences in intrinsic period (see Suppl. Fig. S1) and that tuning the model parameter describing light sensitivity did not reliably result in a minimization of the discrepancy between DLMO and DLMO^p in our dataset. Together with the observed similarity between the distribution of estimated τ values and distributions of τ reported using forced-desynchrony protocols (e.g., Hiddinga et al., 1997; Czeisler et al., 1999; Wright et al., 2005; Gronfier et al., 2007; Burgess and Eastman, 2008; Duffy et al., 2011), our results indicate the validity of our τ estimates.

The data suggest that DLMO is related to intrinsic period, as long as the average amount of daylight exposure is accounted for (Fig. 8C). The weak relationship between DLMO and intrinsic period (Wright et al., 2005) may be due to individual differences in the timing and intensity of light exposure, which are both expected to be related to the amount of daylight exposure (Roenneberg et al., 2003; Wright et al., 2013). Our analyses predict a relationship between DLMO and intrinsic period to be observable when there is little interindividual variability in the timing and intensity of light exposure. Indeed, those individuals with the least amounts of daylight exposure showed DLMO values that were later than predicted by the corresponding $\tau$ estimations. Importantly, the low amount of daylight exposure also explains the DLMO of the latest individual in our dataset, suggesting that this DLMO was the result of deviating daylight exposure, rather than being of clinical nature. By correcting for individual differences in the timing of light exposure (sleep-wake cycle), it has previously been shown that the phase difference between DLMO and sleep onset (DLMO – sleep onset) is positively related with intrinsic period (Wright et al., 2005; Burgess and Eastman, 2008; Gronfier et al., 2007; Hasan et al., 2012; Eastman et al., 2015). Our intrinsic period estimates show the same positive relationship, suggesting that our estimations were valid. It is unlikely that this finding is caused by a “regression to the mean,” because DLMO and estimated intrinsic period did not correlate (Figure 8B) (R² = 0.144; p = 0.099). As a result, the probability of finding a significant relationship between (DLMO – sleep onset/offset) and intrinsic period purely by chance was only 5% (see the Supplementary Material).

The positive relationship between phase angle of entrainment (DLMO – sleep onset/offset) and estimated intrinsic period reported here is in line with the premise that humans obey the phase-period rule: Individuals with long intrinsic periods show a late phase of entrainment with regard to the light-dark cycle such that the majority of the light hits the advance zone of a typical PRC (i.e., sleep is scheduled at an early phase such that darkness coincides with the delay zone of that PRC). Additionally, as expected (Roenneberg et al., 2003), light intensity exerts an additional influence on phase angle of entrainment over estimated intrinsic period, where higher light intensities are related to an earlier phase of entrainment. Although sleep onset and offset both contain information on the timing of light exposure in humans, our analysis revealed a relationship with intrinsic period that was weaker for (DLMO – sleep onset) than for (DLMO – sleep offset). This suggests that most humans are stronger entrained to lights-on (morning light) than to lights-off (evening light), as expected when τ > 24 h.

In summary, the distribution of estimated intrinsic periods and their relationship with phase of entrainment suggest that we developed an accurate method to estimate circadian period from field data. Our results show that low-cost estimations of circadian phase, intrinsic period, and phase of entrainment may be possible by analyzing ambulatory collected light and activity data, while imposing no restrictions on the participants’ daily routines. Such advances not only are useful from a scientific point of view but may prove to be of crucial importance when optimizing individual light treatment for shift work and jetlag applications and designing individualized chronotherapy treatment schedules.