Abstract
A novel strategy for controlling the spread of arboviral diseases such as dengue, Zika and chikungunya is to transform mosquito populations with virus-suppressing Wolbachia. In general, Wolbachia transinfected into mosquitoes induce fitness costs through lower viability or fecundity. These maternally inherited bacteria also produce a frequency-dependent advantage for infected females by inducing cytoplasmic incompatibility (CI), which kills the embryos produced by uninfected females mated to infected males. These competing effects, a frequency-dependent advantage and frequency-independent costs, produce bistable Wolbachia frequency dynamics. Above a threshold frequency, denoted p̂, CI drives fitness-decreasing Wolbachia transinfections through local populations; but below p̂, infection frequencies tend to decline to zero. If p̂ is not too high, CI also drives spatial spread once infections become established over sufficiently large areas. We illustrate how simple models provide testable predictions concerning the spatial and temporal dynamics of Wolbachia introductions, focusing on rate of spatial spread, the shape of spreading waves, and the conditions for initiating spread from local introductions. First, we consider the robustness of diffusion-based predictions to incorporating two important features of wMel-Aedes aegypti biology that may be inconsistent with the diffusion approximations, namely fast local dynamics induced by complete CI (i.e., all embryos produced from incompatible crosses die) and long-tailed, non-Gaussian dispersal. With complete CI, our numerical analyses show that long-tailed dispersal changes wave-width predictions only slightly; but it can significantly reduce wave speed relative to the diffusion prediction; it also allows smaller local introductions to initiate spatial spread. Second, we use approximations for p̂ and dispersal distances to predict the outcome of 2013 releases of wMel-infected Aedes aegypti in Cairns, Australia, Third, we describe new data from Aedes aegypti populations near Cairns, Australia that demonstrate long-distance dispersal and provide an approximate lower bound on p̂ for wMel in northeastern Australia. Finally, we apply our analyses to produce operational guidelines for efficient transformation of vector populations over large areas. We demonstrate that even very slow spatial spread, on the order of 10-20 m/month (as predicted), can produce area-wide population transformation within a few years following initial releases covering about 20-30% of the target area.
Keywords: population transformation, population replacement, bistable wave dynamics, disease suppression, Zika, biocontrol
1. Introduction
Wolbachia are maternally inherited endosymbionts, pervasive among arthropods (Weinert et al. 2015) and best known for reproductive manipulation (Werren et al. 2008). Their most widely documented reproductive manipulation is cytoplasmic incompatibility (CI) (Hoffmann and Turelli 1997; Hamm et al. 2014), which kills embryos produced by Wolbachia-uninfected females mated to infected males. Wolbachia-infected females are compatible with both infected and uninfected males and generally produce only infected progeny. CI gives infected females a reproductive advantage that increases with the infection frequency. Consequently, CI-inducing Wolbachia can spread within and among populations, at least once they become sufficiently common that the CI-induced advantage overcomes any frequency-independent disadvantages (Caspari and Watson 1959; Turelli and Hoffmann 1991; Turelli 2010; Barton and Turelli 2011). Because Wolbachia are maternally transmitted, selection favors variants that increase the fitness of infected females (Turelli 1994; Haywood and Turelli 2009). Teixeira et al. (2008) and Hedges et al. (2008) discovered that Wolbachia-infected individuals are protected from some pathogens, including viruses. Pathogen protection is not universal (Osborne et al. 2009), and studies of both transient somatic Wolbachia transinfections (Dodson et al. 2014) and stable transinfections (Martinez et al. 2014) suggest that Wolbachia can occasionally enhance susceptibility to pathogens. However, virus protection seems to be a common property of both natural and introduced Wolbachia infections (Martinez et al. 2014).
This anti-pathogen effect has revitalized efforts to use Wolbachia for disease control, an idea first proposed in the 1960s (Laven 1967; McGraw & O'Neill 2013). The disease-vector mosquito Aedes aegypti has been transinfected with two Wolbachia strains from Drosophila melanogaster (wMelPop, McMeniman et al. 2009; and wMel, Walker et al. 2011). Two isolated natural Australian Ae. aegypti populations have been transformed with wMel to suppress dengue virus transmission (Hoffmann et al. 2011), and these populations have remained stably transformed for more than four years (Hoffmann et al. 2014; S. L. O'Neill, pers. comm.). The dengue-suppressing phenotype of wMel-transinfected Ae. aegypti, first demonstrated in laboratory colonies (Walker et al. 2011), has been maintained, and possibly enhanced, after two years in nature (Frentiu et al. 2014). Recently, wMel has also been shown to block the spread of the Zika virus by Ae. aegypti (Dutra et al. 2016). Anopheles stephensi was also transinfected with Wolbachia, making them less able to transmit the malaria-causing parasite (Bian et al. 2013). Wolbachia transinfections are now being deployed for disease control in at least five countries (Australia, Vietnam, Indonesia, Brazil and Colombia, see the “Eliminate Dengue” website: http://www.eliminatedengue.com/program), with many more releases planned. We present simple approximation-based predictions to understand and aid the deployment of these transinfections.
Our mathematical analyses rest on bistable frequency dynamics for Wolbachia transinfections. Namely, the frequency-independent costs associated with introduced infections cause frequencies to decline when the infections are rare; but the frequency-dependent advantage associated with CI overcomes these costs when the infections become sufficiently common. As explained in the Discussion, bistability now seems implausible for naturally occurring Wolbachia infections (cf. Fenton et al. 2011; Kriesner et al. 2013; Hamm et al. 2014). However, we present several lines of evidence, including new field data, indicating that wMel transinfections in Ae. aegypti experience bistable dynamics in nature.
Why does bistability matter? As reviewed in Barton and Turelli (2011), bistability constrains which variants can spread spatially, how fast they spread, how difficult it is to initiate spread, and how easily spread is stopped. Roughly speaking, spatial spread can occur only if the critical frequency, denoted p̂, above which local dynamics predict deterministic increase rather than decrease, is less than a threshold value near ½. As discussed in Turelli (2010), p̂ is determined by a balance between the frequency-dependent advantage provided by cytoplasmic incompatibility and frequency-dependent disadvantages associated with possible deleterious Wolbachia effects on fecundity, viability and development time. As p̂ increases, the rate of predicted spatial spread slows to zero (then reverses direction), the area in which the variant must be introduced to initiate spread approaches infinity, and smaller spatial heterogeneities suffice to halt spread. Spatial dynamics depend on details of local frequency dynamics and dispersal that are not well understood empirically. This motivates our exploration of quantitative predictions using relatively simple but robust models that focus on three key biological phenomena, dispersal, deleterious fitness effects and cytoplasmic incompatibility.
We seek conditions under which minimal releases of dengue-suppressing Wolbachia transinfections achieve area-wide disease control by transforming a significant fraction of the vector population in a relatively short period. We focus on simple models to provide quantitative predictions and guidelines, and test the robustness of the predictions to long-distance dispersal. Our simple approximations make testable predictions that may be improved as additional data become available. Many parameters in detailed models will be difficult to estimate and are likely to vary in time and space. Our idealization is motivated by the scarce information concerning the ecology of disease vectors such as Ae. aegypti. For instance, the dynamics of introductions must depend on ecological factors such as density regulation (Hancock et al. 2011a,b). However, the ecology of Ae. aegypti is so poorly understood that increases in embryo lethality associated with CI might lead to either decreasing or increasing adult numbers (cf Prout 1980; Walsh et al. 2013; but see Hancock et al. 2016). As in Barton and Turelli (2011), we ignore these ecological complications and emphasize quantitative conclusions that depend on only two key parameters: σ, a measure of average dispersal distance, and p̂, the unstable equilibrium frequency. We illustrate how these two parameters can be estimated from introduced-Wolbachia frequency data (producing predictions that can be cross-validated) and explore the robustness of the resulting predictions.
Our new analyses build on Barton and Turelli (2011), which used diffusion approximations to understand spatial and temporal dynamics. To determine the robustness of those diffusion-based predictions, which make mathematical assumptions that may not be consistent with the biology of Wolbachia-transinfected mosquitoes, we examine dispersal patterns that assign higher probabilities to long-distance (and very short-distance) dispersal. We ask how dispersal patterns affect wave speed, wave shape, and the conditions for initiating an expanding wave (Section 4). We use these new, more robust predictions to propose guidelines for field deployment of dengue-suppressing Wolbachia. This involves addressing new questions. For instance, Barton and Turelli (2011) determined the minimum area over which Wolbachia must be introduced to initiate spatial spread, but ignored the fact that near this critical size threshold, dynamics would be extremely slow. Effective field deployment requires initiating multiple waves to cover a broad area relatively quickly, given constraints on how many mosquitoes can be released. This requires understanding how transient dynamics depend on initial conditions. We synthesize data-based and model-based analyses of spatial spread to outline efficient strategies for area-wide transformation of vector populations (Section 7).
In addition to our theoretical results concerning predicted properties of spatial spread and near-optimal release strategies, we illustrate the theory with predictions concerning the outcome of wMel releases in Cairns, Australia in 2013 (Section 5). We also analyze some previously unpublished data from the 2011 releases reported in Hoffmann et al. (2011) to approximate a lower bound for p̂ relevant to the Cairns releases (Section 6).
2. Mathematical background, models and methods
Our initial numerical analyses focus on testing the robustness of predictions presented in Barton and Turelli (2011). We first describe the diffusion approximations and results from Barton and Turelli (2011) before describing the alternative approximations and analyses. Next we describe the model used to analyze the new data we present. Finally we describe our approaches to approximating optimal release strategies.
2.1. Diffusion approximations, alternative dynamics and predictions
The simplest spatial model relevant to understanding Wolbachia frequency dynamics in space and time is a one-dimensional diffusion approximation:
| (1) |
where f(p) describes local dynamics and p(x, t) denotes the infection frequency at point x and time t, and σ denotes the standard deviation of dispersal distances. If we approximate the local bistable dynamics by the cubic
| (2) |
where sh describes the intensity of CI, there is an explicit asymptotic traveling wave solution of (1), given as Eq. 13 of Barton and Turelli (2011). Eq. (1), extended to two dimensions as described by Eq. 22 of Barton and Turelli (2011), can be solved numerically to address transient dynamics associated with local releases. In two dimensions, we interpret σ2 as the variance in dispersal distance per generation along any axis. (This implies that the average Euclidean distance between the birthplaces of mothers and daughters is , assuming Gaussian dispersal.) The model defined by (1) and (2) provides analytical predictions for wave speed and wave shape and numerical conditions for establishing a spreading wave from a local introduction.
To more accurately approximate CI dynamics, Barton and Turelli (2011) replaced the cubic approximation (2) with the model of Schraiber et al. (2012)
| (3a) |
| (3b) |
(Eq. 3a assumes that the daily death rate for the infected individuals is dI = 1, so that time is measured in terms of the average lifetime of an infected individual.) As in Eq. (2), sh measures the intensity of CI; whereas sr measures the net reduction in fitness caused by the Wolbachia infection. As in the discrete-time model of Turelli (2010), fitness costs may involve reductions of both fecundity and mean life length (viability), as measured by sf and sv, respectively; however, sv enters the dynamics only through p̂. Numerical integration can be used to compare the cubic-based analytical predictions with those produced by this more biologically explicit approximation. For fixed p̂, the dynamics described by Eq. (3a) depend on whether fitness costs primarily involve viability or fecundity effects (because only sf appears in the denominator). The data of Hoffmann et al. (2014) suggest that fecundity effects may dominate.
In our discrete-time, discrete-space analyses, we approximate local dynamics with the Caspari-Watson model (1959) which incorporates CI and fecundity effects (cf Hoffmann and Turelli 1988; Weeks et al. 2007). Let H denote the relative hatch rate of embryos produced from an incompatible cross. Setting H = 1 – sh and F = 1 – sf, and letting p denote the frequency of infected adults, the local dynamics are described by
| (4a) |
| (4b) |
In this model, the condition for bistability (i.e., simultaneous local stability of p = 0 and p = 1) is sh > sf > 0, i.e., the (frequency dependent) benefit to the infection from CI must exceed its (frequency independent) cost, modeled as decreased fecundity. Both lab and field experiments indicate that wMel causes complete CI, i.e., sh ≈ 1 in Ae. aegypti (Hoffmann et al. 2014).
2.1.1. Wave speed
Measuring time in generations, the predicted wave speed from (1) with cubic dynamics (2) is
| (5) |
provided that p̂ > 0. This one-dimensional result also describes the asymptotic speed of a radially expanding wave in two dimensions (see Eqs. 23-25 of Barton and Turelli 2011). Barton and Turelli (2011) used numerical solutions of (1) to compare this speed prediction to the wave speed produced by (3), which explicitly models the fast local dynamics associated with strong CI. The more realistic dynamics (3) led to slightly faster wave propagation (as expected because the denominator of f(p) is less than one).
2.1.2. Wave width
The explicit traveling-wave solution of (1) for cubic f(p) provides a simple description for the asymptotic wave width, the spatial scale over which infection frequencies change. Defining wave width as the inverse of the maximum slope of infection frequencies (Endler 1977), the diffusion approximation with cubic dynamics implies that the traveling wave has width
| (6) |
which becomes 4σ with complete CI, as in Ae. aegypti. The explicit solution that produces (6) implies that with sh = 1, the scaled wave (with space measured in units of σ) has shape 1/[1 + Exp(−x)]. Thus, infection frequencies increase from about 0.18 to 0.82 over 3σ. If steady spread is observed in the field, we can use this wave-shape approximation to estimate σ from spatial infection-frequency data. These estimates can be compared to independent estimates from release-recapture experiments or genetic data. We show below that relation (6) is relatively robust to more realistic descriptions of local frequency dynamics and long-tailed dispersal.
2.1.3. Wave initiation
Finally, the diffusion approximation predicts the minimum area that must be actively transformed to initiate deterministic spatial spread. Barton and Turelli (2011) consider introductions over a circular area with initial infection frequency p0 in the circle. This initial state corresponds to rapid local establishment of a transinfection from intensive releases. Hoffmann et al. (2011) showed that releases in isolated suburbs near Cairns produced wMel frequencies over 80% within 12 weeks, about three Ae. aegypti generations. Fig. 3 of Barton and Turelli (2011) summarizes the diffusion predictions concerning the minimum radius of release areas, measured in units of dispersal distance σ, needed to initiate a spreading wave. In their analysis, the scaled critical radius, denoted Rcrit, depends only on p̂). As p̂ increases from 0 to 0.3, Rcrit increases from 0 to about 3.5σ, then rapidly increases towards infinity as p̂ approaches 0.5, the approximate upper bound on p̂ consistent with spatial spread. Releases over areas smaller than Rcrit are predicted to fail, with the infection locally eliminated by immigration from surrounding uninfected populations. Barton and Turelli (2011) used the Schraiber et al. (2012) model (3) to assess the robustness of these cubic-based predictions to more realistic local CI dynamics. Model (3) produced Rcrit predictions within a few percent of those derived from the cubic (see Fig. 3 of Barton and Turelli 2011), assuming that Wolbachia reduce fitness primarily through viability effects. Below, we contrast the diffusion predictions of Barton and Turelli (2011) with numerical results that account for fecundity effects, faster local dynamics and alternative forms of dispersal.
Fig. 3.
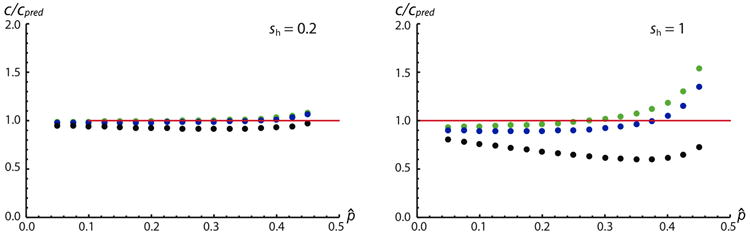
Wave speed. Speed calculated from DSDT analyses compared to the cubic-based diffusion prediction, , as a function of p̂, for sh = 0.2 (left) and sh = 1 (right). As in (2), σ denotes the standard deviation of dispersal distances; sh denotes the intensity of CI. The green dots were produced with Gaussian dispersal, blue with Laplace and black with Exponential Square root (ExpSqrt).
2.1.4. Time scale for asymptotic wave speed and width
Predictions (5) and (6) for wave speed and wave width are based on the asymptotic behavior of the traveling wave solutions to the diffusion model (1) assuming cubic dynamics. (As discussed in Barton and Turelli (2011), the asymptotic wave speed and width are the same in one dimension and two.) To apply these predictions to frequency data generated from field releases, it is important to know how quickly these asymptotic values are approached. Fig. 1 illustrates numerical solutions for the transient dynamics of the cubic-diffusion model in two dimensions with plausible parameter values for wMel in Aedes aegypti, sh = 1 and p̂ = 0.25 (discussed below). The calculations use two initial conditions. In the first, the infection is introduced with p0 near 0.8 over a circular region with diameter 3 (see Fig. 1 legend for details), which is about 14% larger than Rcrit = 2.64, the critical radius needed to initiate spatial spread. In the second, the infection frequency drops smoothly from 0.65 at the center of the introduction to 0.25 (the unstable point, p̂) at about R = 4.6. As shown in Fig. 1, for these parameters and initial conditions, the approach to the asymptotic wave speed and width is rapid, on the order of five-to-ten generations. Similar results hold for our discrete-time models and data from field releases of wMel in Aedes aegypti (data not shown).
Fig. 1.
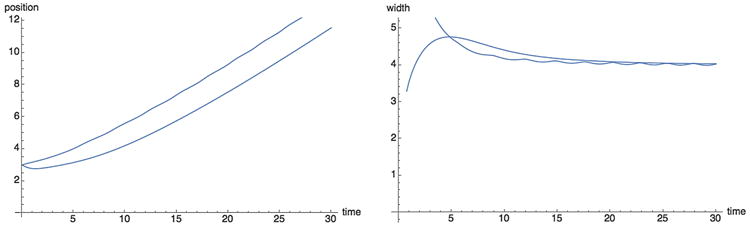
Transient dynamics of wave position and wave width from numerical solutions of the two-dimension version of diffusion model (1) with cubic dynamics (2), sh = 1 (i.e., complete CI) and p̂ = 0.25. The calculations assume circular introductions with radial symmetry and initial frequency p(R) = 0.8/{1 + exp[4(R – 3)/v]} for v = 0.8 and 8. (Note that v is a scale factor that determines the steepness with which infection frequency falls.) Setting v = 0.8 produces an abrupt drop in the initial frequency from 0.75 to 0.05 over roughly R = 2.5 to R = 3.5; with v = 8, the initial frequency drops from 0.65 at R = 0 to 0.25 at R = 4.6. The left panel shows wave position measured as the point of maximum slope, the right panel shows the width, measured as the inverse of the maximum slope (see Eq. (6)). The dotted curves correspond to v = 0.8, modeling a rapid introduction in a confined area. This produces a faster approach to the expected asymptotic speed of 0.25. Both initial conditions, one with narrower width than the asymptotic value of four, the other wider, approach the asymptotic width of four within 7-10 generations.
2.2. Numerical analyses of discrete-time, discrete-state (DTDS) models
To explore the robustness of the diffusion predictions, we consider the simultaneous effects of fast local dynamics, associated with complete CI, and long-tailed dispersal. To do this, we replace the PDE approximation (1) with discrete-time, discrete-space (DTDS) models that assume discrete generations and discrete patches in which the consequences of mating, fecundity effects and CI occur and between which adult migration occurs.
2.2.1. Model structure and dynamics
Let i denote a patch in one or two dimensions, let g(p) = p′ denote a function that describes how mating, fecundity differences and CI transform local infection frequencies between generations, and let m(i, j) denote the probability that an individual at location i after migration originated in location j. Assuming discrete generations in which migration of newly eclosed individuals precedes local CI dynamics, the infection frequencies among adults in each patch follow
| (7) |
Our choice of patch spacing for these discretizations is discussed below. We approximate local dynamics with the Caspari-Watson model (4).
2.2.2. Alternative dispersal kernels
Following Wang et al. (2002), we compare results obtained with three models of dispersal: a Gaussian, denoted G(x), versus two “long tailed” distributions, the Laplace (or reflected exponential), denoted L(x), and the exponential square root (ExpSqrt), denoted S(x). Letting σ denote the standard deviation of dispersal distances, our dispersal kernels in one dimension (proportional to the probability of moving distance x in one dimension) are
| (8a) |
| (8b) |
| (8c) |
These alternative dispersal models are illustrated in Fig. 2. Our DTDS calculations used patch spacing of 0.5σ We truncated the dispersal functions at ±10σ. We adjusted the variance parameter in our discrete calculations so that the actual standard deviation of the discrete distribution was σ. In two dimensions, (x, y), the dispersal models, generally denoted m(z), were implemented as .
Fig. 2.
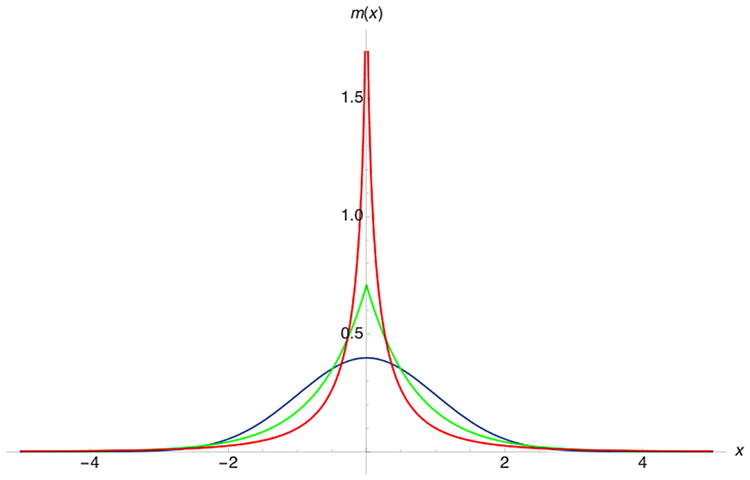
Alternative dispersal models with σ = 1. The three models are: Gaussian (blue), Laplace (green), and ExpSqrt (red) as described by (8). Each describes the probability, denoted m(x) in the figure, of moving distance x along any axis.
Taking logs of the densities, the tails of G(x) decline as −x2, whereas the tails of L(x) and S(x) decline as −|x| and , respectively, corresponding to successively higher probabilities of long-distance dispersal. Denoting the random variables corresponding to these densities as G, L and S, we have P(|G| > 3σ) = 0.003, P(|L| > 3σ) = 0.014 and P(|S| > 3σ) = 0.022. As Fig. 2 shows, higher probabilities of long-distance dispersal are accompanied by higher probabilities of short-distance dispersal (e.g., P(|G| < 0.5σ) = 0.383, P(|L| < 0.5σ) = 0.507 and P(|S| < 0.5σ) = 0.678), with corresponding medians for |G|, |L| and |S| of 0.67σ, 0.49σ and 0.28σ, respectively.
In two dimensions, we assume that dispersal is isotropic, with radial distribution given by the kernels defined by (8), and scaled such that the standard deviation along any one axis is σ. To approximate σ from experiments that estimate mean Euclidean dispersal distances, D, note that the Gaussian produces , whereas for the Laplace and ExpSqrt, we have E(DL) ≈ 1.15σ and E(DS) ≈ 0.94σ, respectively. Thus, empirical estimates of average Euclidean dispersal distance can imply values of σ that differ by over 30% depending on the shape of the dispersal function, with longer tails implying higher values of σ. (Note that statistical estimation of dispersal requires some assumption about the distribution of dispersal distance.) We compare the predictions resulting from alternative dispersal models by holding fixed the variance parameter σ2, which is natural measure of dispersal distance for diffusion approximations (see, for instance, the derivations in Haldane (1948), Slatkin (1973) or Nagylaki (1975)).
2.3 Model used for data analysis: an isolated deme subject to immigration
Barton and Turelli (2011) adapted the “island model” of Haldane (1930) to approximate the rate of immigration of Wolbachia-infected individuals required to “flip” an isolated population from uninfected to infected. In addition to approximating the critical migration rate, m, the analysis produces an analytical approximation for the equilibrium infection frequency when the immigration rate is too low to flip the recipient population to Wolbachia fixation. Assuming complete CI, 100% frequency of Wolbachia in the donor population and one-way immigration into the recipient population, Eq. (31) of Barton and Turelli (2011) predicts that Wolbachia should take over the recipient population if m, the fraction of individuals who were new migrants each generation, exceeds m* = p̂2/4. For m < m*, the predicted Wolbachia equilibrium frequency in the recipient population, using a cubic approximation for local dynamics, is
| (9) |
(this is a reparameterization of Eq. (31) of Barton and Turelli 2011). Hence, if we use the long-term average Wolbachia frequency, p̄, to approximate p*, the equilibrium described by (9), we can approximate a lower bound for the unstable equilibrium, p̂, as 2p̄.
2.4. Near-optimal release strategies
We analyze alternative release strategies using a combination of numerical solutions of diffusion models, DTDS models and even simpler models that assume constant rates of radial spread from release foci. Each analysis is described below along with the results it produces.
3. New data demonstrating bistability
We analyze a small subset of the Wolbachia infection frequency data collected subsequent to the first “Eliminate Dengue” field releases of wMel-infected Ae. aegypti, described in Hoffmann et al. (2011). The releases occurred in early 2011 in two isolated towns, Gordonvale (668 houses) and Yorkeys Knob (614 houses), near Cairns in northeast Australia. As described in Hoffmann et al. (2011), Pyramid Estate (PE) is an area of Gordonvale separated from the town center by a major highway, with roughly 100 m separating the nearest houses on either side. Highways seem to inhibit Ae. aegypti migration (Hemme et al. 2010). The 2011 wMel releases were restricted to the main part of Gordonvale; but as reported in Hoffmann et al. (2011), wMel-infected mosquitoes were found in PE within months of the initial releases. The PE capture sites were scattered over an area of houses on the order of 1 km2 with traps roughly 100-500 m from the nearest residences in the Gordonvale release area. As described in Hoffmann et al. (2011, 2014), infection frequencies were estimated using PCR of DNA from adults reared from eggs collected in oviposition traps. Between late March 2011 and January 2015, 2689 adults were assayed in PE. The data are archived in Dryad (http://XXX).
4. Results: Robustness of diffusion results to long-tailed dispersal and rapid CI dynamics
4.1. Wave speed
We initially calculated wave speed in a one-dimensional spatial array, then as in Barton and Turelli (2011), we checked the results with two-dimensional calculations. To disentangle the effects of non-Gaussian dispersal from the effects of fast local dynamics, we contrast results obtained assuming complete CI (sh = 1), as observed with wMel-infected Ae. aegypti, with results assuming weak CI (sh = 0.2). Fig. 3 compares the numerically approximated wave speeds to the analytical prediction, , from the diffusion approximation with cubic dynamics. The left panel shows that with relatively slow local dynamics (sh = 0.2), the cubic diffusion approximation is accurate and robust to the shape of the dispersal function. This is expected from the derivation of approximation (1) as a limit of discrete-time, discrete-space dynamics (Haldane 1948; Nagylaki 1975). The derivation explicitly invokes slow local dynamics and limited dispersal, retaining only the variance of dispersal distances in the quadratic approximation. The sh = 0.2 results have two other notable features. First, despite the overall accuracy of approximation (5), we see that ExpSqrt dispersal slightly slows propagation. This can be understood in terms of the lower median dispersal distance and the fact that with bistability, rare long-distance dispersal is not effective at pushing the wave forward, because long-distance migrants are swamped by the much more abundant natives. This distinguishes bistable spatial dynamics from those with zero as an unstable equilibrium. For such systems, long-tailed dispersal can produce accelerating waves (see Supporting Information Appendix A for references and comparison of bistable versus Fisherian wave speeds). Moreover, geographic spread associated with spatially non-contiguous, successful long-distance colonization events (cf Shigesada and Kawasaki 1997, Ch. 5), can greatly exceed predictions based on average dispersal distances. Second, note that as p̂ approaches 0.5, the analytical approximation starts to underestimate wave speed. As described by Barton and Turelli (2011), this reflects the fact that the cubic model produces the threshold p̂ ≤ 0.5 for spatial spread, whereas models more accurately describing CI and fitness costs, such as (3) and (4), predict spatial spread with p̂ slightly above 0.5.
The right panel of Fig. 3 (sh = 1) shows that faster local dynamics accentuate both phenomena seen with sh = 0.2: slower speed with more long-tailed dispersal and underestimation of observed speed as p̂ approaches 0.5. With complete CI and plausible p̂ (i.e., 0.2 ≤ p̂ ≤ 0.35), observed speed closely follows the cubic-based diffusion prediction with Gaussian dispersal, but is reduced by about 10% for Laplace dispersal and by much more (25-40%) for ExpSqrt dispersal. A simple interpretation is that long-tailed dispersal is associated with smaller median dispersal distances. Long-distance migrants are effectively “wasted” in that they cannot initiate local spread.
Appendix A provides a more complete description of the consequences of alternative dispersal models on wave speed under bistable versus monostable local dynamics, including the consequences of finite population size at the front on wave propagation.
4.2. Wave width
Under the diffusion model with cubic dynamics, the predicted wave width is (6). Fig. 4 compares this prediction with the results obtained from DTDS with Caspari-Watson dynamics and alternative dispersal models. With relatively slow local dynamics (sh = 0.2), Panel A shows that the cubic-diffusion prediction remains accurate for all three dispersal models, analogous to the results for wave speed illustrated in Fig. 3A. ExpSqrt dispersal slightly reduces wave width, presumably reflecting the lower median dispersal. As with wave speed, sh = 1 produces larger departures from the cubic-diffusion prediction and much greater effects of dispersal shape. However, for plausible values of p̂ (i.e., 0.2 ≤ p̂ < 0.35), the observed width remains within about 15% of prediction (6) for Gaussian and Laplace and very close to the prediction for ExpSqrt.
Fig. 4.
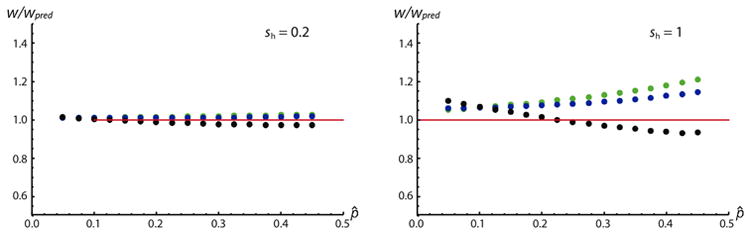
Wave width. Wave width as a function of p̂ calculated using discrete-time, discrete-space (DTDS) analyses with alternative dispersal models. The dots from the DTDS analyses are compared to the diffusion prediction ( , red line) for sh = 0.2 (left) and sh = 1 (right). As in Fig. 3, σ denotes the standard deviation of dispersal distances and sh denotes the intensity of CI. The green dots were produced with Gaussian dispersal, blue with Laplace and black with Exponential Square root (ExpSqrt).
4.3. Wave initiation: critical radius Rcrit
Fig. 3 of Barton and Turelli (2011) showed how Rcrit, the minimal radius of an introduction needed to initiate spread (measured in units of the dispersal parameter σ), depends on p̂ and p0 under the diffusion approximation. It contrasts the predictions for cubic dynamics versus Schraiber et al. (2012) Wolbachia dynamics (Eq. 3). Fig. 5 compares those predictions to DTDS results under Caspari-Watson Wolbachia dynamics (Eq. 4). The key result is that long-tailed dispersal produces smaller critical radii, and the effect of long-tailed dispersal increases as p̂ increases. This result is complementary to the wave-speed results. With longer-tailed dispersal, more individuals move very little so that the median dispersal falls, making it easier to establish a wave (but the resulting wave moves more slowly). The discrepancies between the diffusion results with Schraiber et al. (2012) dynamics and the DTDS results for Gaussian dispersal are mainly attributable to the fact that the Schraiber et al. (2012) results illustrated in Fig. 5 assume only viability costs, which produces slower dynamics (see Eq. 4a) and requires larger introductions, than if one assumes fecundity costs, as done in the DTDS Caspari-Watson model. The effect of fecundity vs. viability costs is illustrated in Table 1 in section 5.1. For p̂ = 0.35 and p0 = 0.8, numerical solution of the diffusion equation with Schraiber et al. (2012) dynamics produces Rcrit = 3.36 if sf = 0 (so that p̂ = sv), but this drops to Rcrit = 2.76 if sv = 0 (so that p̂ = sf). The corresponding values under the DTDS model with Caspari-Watson dynamics are Rcrit = 3.01, 2.91, 2.55, for Gaussian, Laplace and ExpSqrt dispersal, respectively.
Fig. 5.
Critical radius, Rcrit, assuming complete CI and alternative dynamics. The upper points reproduce the diffusion results from Barton and Turelli (2011) with cubic (red curve) and Schraiber et al. (2012) CI dynamics (assuming only viability fitness costs). The red curve shows the cubic-diffusion predictions with initial infection frequency p0 = 0.8, the large blue dots are the cubic with p0 = 0.6. The small red (blue) dots are produced by the diffusion analysis of Schraiber et al. (2012) CI dynamics with p0 = 0.8 (p0 = 0.6). The lower points and curves show our DTDS predictions as a function of p̂ and p0 with alternative dispersal models. The lower lines correspond to p0 = 0.8 with Gaussian (green), Laplace (blue) and ExpSqrt (black) dispersal. The points above and below these lines correspond to p0 = 0.6 and p0 = 1, respectively.
Table 1. Diffusion-based predictions for spatial spread.
| Unstable point | Speed (m/gen) | Width (m) | Minimum Release Area (km2) |
|---|---|---|---|
| p̂ = 0.2 | 30 | 400 | 0.13 |
| p̂ = 0.35 | 15 | 400 | 0.25-0.38a (0.5) |
These predictions assume σ ≈ 100 m, p0 = 0.8, and 0.2 ≤ p̂ ≤ 0.35. They are based on Eq. 5, Eq. 6 and Fig. 3 of Barton and Turelli (2011).
The smaller prediction (0.25) is derived with Schraiber et al. (2012) CI dynamics (3) assuming that wMel reduces only the fecundity of Ae. aegypti (i.e., sr = sf in 3b), the larger result (0.38) assumes that wMel reduces only viability. The cubic model produces the still larger value (0.5).
There are two striking results concerning the DTDS-derived values of Rcrit. First, like the wave-width results, the critical radii are relatively insensitive to the dispersal model. Second, however, unlike the wave-width results, the critical radii are significantly different and smaller than those produced by the diffusion approximation. Barton and Turelli (2011) showed that the Schraiber et al. (2012) dynamics produced smaller Rcrit values than the cubic model, even if fitness costs were purely based on reduced viability. Reduced fecundity, as assumed in the Caspari-Watson model, accelerates the local dynamics and hence allows much smaller introductions to initiate a traveling wave. Even with p̂ = 0.35, introductions with p0 = 0.8 will succeed as long as the initial radius of release, denoted RI, satisfies RI ≥ 2.5σ (or 3.0σ) with ExpSqrt (or Gaussian) dispersal.
5. Results: Predictions for 2013 Cairns releases
5.1. Diffusion-based predictions
One of our primary aims is to understand the robustness of the Barton and Turelli (2011) diffusion predictions. Rather than discuss generalities, we will focus on specific field releases. In early 2013, three localized releases were performed within the city of Cairns. Releases were made in three neighborhoods, Edgehill/Whitfield (EHW), Parramatta Park (PP), and Westcourt (WC). The release areas were roughly 0.97 km2 for EHW, 0.52 km2 for PP, and only 0.11 km2 for WC. Infection frequencies quickly rose above 0.8 within all three release areas, and each release area adjoined housing into which the wMel infection might plausibly spread. What predictions emerge from the diffusion approximations?
Numerical predictions require estimates of σ and p̂. Russell et al. (2005) performed a mark-release-recapture experiment with Ae. aegypti using a release site abutting the 2013 EHW release area. The mean absolute distance of recaptures from the release point was about 78 m. The diffusion approximation assumes that dispersal is measured as the standard deviation of dispersal distance along any axis. If we assume that dispersal distance is roughly Gaussian distributed with mean 0 and standard deviation σ along each axis, the mean absolute dispersal distance is or about 1.25σ. With this assumption, the estimate from Russell et al. (2005) implies σ ≈ 62 m/(generation)1/2. In general, however, release-recapture estimates tend to be systematically lower than those based on genetic data (see, for instance, Barton and Hewitt 1985, Fig. 3). Moreover, estimates of dispersal distance for Ae. aegypti are extremely variable in time and space. For instance, Harrington et al. (2005) found that repeated estimates of mean dispersal distance in the same village in Thailand ranged from about 40 m/(generation)1/2 to about 160 m/(generation)1/2. Our theoretical predictions concerning the consequences of dispersal are best interpreted as temporal averages, which are more likely to be accurately captured by indirect estimates of average dispersal such as wave width (or genetic data describing the decline of relatedness with distance). Given that direct estimates systematically underestimate average dispersal in nature, we use σ ≈ 100 m/(generation)1/2 as a plausible estimate for Cairns. We recognize, however, that dispersal is likely to vary significantly with local conditions.
Assuming σ ≈ 100 m/(generation)1/2, Eq. (6) implies that if spatial spread is observed, the wave width should be about 400 m. From Eq. (5), the corresponding wave speed is c = 100(½ – p̂) m per generation (m/gen). As argued in section 6.1 below, p̂ is probably above 0.2. Thus, the maximum predicted speed is about 30 m/gen. However, if p̂ is as high as 0.35, predicted speed falls to 15 m/gen. Assuming about 10 Ae. aegypti generations per year near Cairns, these crude estimates indicate that wMel spread in Ae. aegypti is likely to be on the order of 150-300 m/year – two or three orders of magnitude slower than the spread of wRi in California and eastern Australia D. simulans (100 km/year, Kriesner et al. 2013). Yet repeated estimates of dispersal distances for various Drosophila species suggest that natural dispersal distances are at most 5-10 times greater for D. simulans than for Ae. aegypti (e.g., Dobzhansky and Wright 1943; Powell et al. 1976; McInnis et al. 1982). The critical difference between the speeds associated with these exemplars of Wolbachia spread is unlikely to be dispersal, but more probably the bistability of wMel dynamics in Ae. aegypti versus the monostability of wRi dynamics (see Discussion section 8.3). Monostability allows relatively rare human-mediated, long-distance dispersal to greatly enhance spatial spread, as described, for instance, by “structured diffusion” models (Shigesada and Kawasaki 1997, Ch. 5).
Whether spatial spread occurs with bistability depends on the size of the release area, the initial frequency produced in the release area (p0), and p̂. From Fig. 3 of Barton and Turelli (2011) with p0 = 0.8, if p̂ were as large as 0.35, the minimum radius of a circular release needed to produce an expanding wave would be on the order of 4σ, implying a minimal release area of about 0.5 km2 (assuming σ ≈ 100 m/(generation)1/2). Replacing the cubic in (2) with the Schraiber et al. (2012) description of CI dynamics (3), Barton and Turelli (2011) showed that the minimal radius with p̂ = 0.35 falls from about 4σ to about 2.8-3.5σ, with the value depending on whether wMel-infected Ae. aegypti lose fitness primarily through fecundity (as the data of Hoffmann et al. 2014 suggest), which produces 2.8σ, or viability, which produces 3.5σ. The smaller values (from Schraiber et al. 2012) imply minimal release areas of about 0.25-0.38 km2 (the lower value assumes only fecundity effects). In contrast, if p̂ were as small as 0.2, the minimum radius falls to about 2σ for both the cubic model and Schraiber et al. (2012) dynamics (with either fecundity or viability effects), corresponding to a minimal area of about 0.13 km2.
Table 1 summarizes our diffusion-based predictions. Note that according to these analyses, the releases at EHW and PP should certainly lead to spatial spread, but the WC release is close to minimal release area even if p̂ is as small as 0.2. Next we address the robustness of these predictions to long-tailed dispersal and patchy spatial distributions.
5.2. DTDS-based predictions
Our robustness analyses of the wave-width predictions emerging from the cubic-diffusion model indicate that σ can be reliably estimated from observed widths of traveling waves of Wolbachia infections. In contrast, our wave-speed analyses suggest that given an estimate of σ, the predicted wave speed depends significantly on the shape of dispersal with plausible speeds that may be on the order of 20-30% below the cubic-diffusion prediction .
Our final prediction concerns spatial spread from individual localized releases. As shown in Fig. 5, the critical release radius for spread depends on: 1) p̂, the unstable point; 2) p0, the initial infection frequency produced within the release areas; 3) the shape of the dispersal function; and 4) σ, dispersal distance. As dispersal becomes more long-tailed (moving from Gaussian to ExpSqrt), the critical radius of the initial introduction decreases. If we assume that p̂ = 0.3 and p0 = 0.8, Rcrit is about 2.61σ if dispersal is Gaussian, but falls to about 2.51σ (or 2.16σ) if dispersal is Laplace (or ExpSqrt). Hence, for each of the three release areas in Cairns, we can ask what is the maximum σ consistent with our deterministic predictions for spatial spread. Given that spread occurs only if the release area exceeds , for each release area, we can approximate an upper bound on σ consistent with spatial spread by
| (10) |
Table 2 presents these upper bounds on σ associated with the three 2013 release areas in central Cairns for a plausible range of p̂.
Table 2. Predicted maximum σ(in meters) consistent with spatial spread.
| Location | p̂ | Gaussian | Laplace | ExpSqrt |
|---|---|---|---|---|
| Westcourt (0.11 km2) | 0.2 | 92 | 95 | 115 |
| 0.25 | 81 | 84 | 101 | |
| 0.3 | 72 | 74 | 87 | |
| 0.35 | 62 | 64 | 73 | |
| Parramatta Park (0.52 km2) | 0.35 | 135 | 140 | 160 |
| Edge Hill/Whitfield (0.97 km2) | 0.35 | 184 | 191 | 218 |
These prediction, based on inequality (10), assume that assuming that p0 = 0.8 and 0.2 ≤ p̂ ≤ 0.35.
Given that very few empirical estimates of σ for Aedes aegypti exceed 100 m, these results suggest that spatial spread should certainly be observed for the Edge Hill/Whitfield and Parramatta Park releases. The prediction for Westcourt is more ambiguous. Note that from Table 1, our diffusion predictions with 0.2 ≤ p̂ ≤ 0.35 indicated a minimum release area of 0.14 km2. This lower bound assumes σ = 100 m and p̂ = 0.2. Thus the diffusion analyses suggested probable failure of the Westcourt release. In contrast, as shown in Fig. 5, our DTDS analyses indicate that the Westcourt release area may be near the lower limit for spread, with the outcome depending critically on the exact values of σ and p̂.
Empirically testing these predictions concerning minimal release areas is confounded by the fact that dynamics very close to the critical values for spread are expected to be slow. Assuming that p̂ = 0.25, if the release area is 10% (5%) smaller than the critical value, the time for collapse is on the order of 15-20 (20-25) generations, roughly two years. Conversely, if the release area is only 10% (5%) larger that the critical area, the time scale for appreciable spatial spread is also on the order of 15-20 (20-25) generations. In contrast, release areas twice as large as necessary should produce appreciable spread in only 10-15 generations; whereas release areas only half as large as needed should essentially collapse in 10-15 generations. These calculations motivated our analyses presented below of “optimal” release sizes aimed at area-wide coverage within a few years.
6. Results: Data relevant to bistability and long-distance dispersal
6.1. Heuristic approximation for p̂ from Pyramid Estates data
Pyramid Estates (PE) was sampled for over two years after the releases stopped. The few capture sites were scattered over an area of houses that is on the order of 1 km2 with traps varying between about 100 m and 500 m from the nearest residences in our release area. For over two years, the wMel frequency in PE remained persistently low, but non-zero with p̄ ≈ 0.106 (N = 2689, averaged over space and time). (We found no evidence that infection frequency varied with distance from the release area). For instance, a sample of 43 Ae. aegypti from the week ending 9 January 2015 yielded an infection frequency of 0.07 [with 95% binomial confidence interval (0.01, 0.19)]. From Eq. (9), a long-term average of 0.105 implies p̂ ≥ 0.21. The persistence of a low infection frequency for over two years clearly demonstrates regular immigration of infected individuals that has been unable to push the local PE population past its unstable point. The fitness data from Hoffmann et al. (2014) suggest that p̂ for wMel near Cairns is likely to be at least 0.2. This is corroborated by the transient dynamics described in Hoffmann et al. (2011) which also suggest that p̂ is unlikely to be significantly above 0.3.
6.2. Long-tailed dispersal
Gordonvale and Yorkeys Knob are separated from other sizable populations of Ae. aegypti by kilometers. Yet, Hoffmann et al. (2014) found consistent low frequencies of uninfected individuals more than three years after wMel reached near-fixation, despite no evidence for imperfect maternal transmission. Yorkeys Knob is less isolated than Gordonvale and shows a significantly higher frequency of uninfected individuals, about 6% versus 3%. Long-distance dispersal is the most plausible explanation for uninfected individuals in Gordonvale and Yorkeys Knob – and the persistence of rare infected individuals at Pyramid Estate.
7. Results: Near-optimal release strategies
We seek conditions under which releases of disease-suppressing Wolbachia transinfections achieve area-wide control of a disease such as dengue (cf. Ferguson et al. 2015) by transforming a significant fraction of the vector population, say 80%, in a relatively rapid period, say two to four years (on the order of 20-40 generations), while releasing as few Wolbachia-infected vectors as possible. We consider several questions associated with the optimizing the timing, spacing and intensity of releases. First, we contrast pulsed releases, over a time scale of very few vector generations, with prolonged low-intensity releases. Second, we consider optimizing the spacing and intensity of releases, as quantified by three parameters: a) local initial infection frequencies after releases, b) areas of local releases, and c) the spacing of releases. Third, given that optimization requires knowing parameters that can only be approximated, we consider the consequences of non-optimal releases.
7.1. Timing of releases: pulse versus gradual introduction
With bistable dynamics, the frequency of an infection (or allele) must be raised above a critical threshold, p̂, over a sufficiently large area to initiate spread. What is the most efficient way to establish an infection? At one extreme, the frequency could be raised essentially instantaneously to some p0(x); if p0 > p̂ over a large enough region (cf. Fig. 5), the infection will spread. At the other extreme, there might be a gradual introduction, described by a local introduction rate m(x), sustained until deterministic spread is initiated. If this input is sufficiently high over a sufficiently large region, the infection will be locally established and spread. Between these extremes, releases might be sustained for a set period of many months or a few years. Supporting Information Appendix B investigates conditions for local establishment and wave initiation, providing analytical results for a single deme and for a point source of introduction in one dimension, and numerical results for two dimensions. We show that it is most efficient to raise infection frequency rapidly, in a brief pulse, rather than making gradual introductions. This accords with the intuition that it is most efficient to raise the frequency as quickly as possible above the threshold p̂: this maximizes the reproductive value of introduced individuals. The principle is simple; during gradual introductions, until local infection frequencies exceed p̂, the introduced infected individuals are systematically eliminated by deterministic selection that dominates the weaker (frequency-dependent) force of CI at low Wolbachia frequencies. Assuming that releases quickly drive the local infection frequency to a value p0 sufficient to initiate spatial spread, we ask how long it might take to cover a large area and what spatial patterns of release minimize the time to reach a desired coverage.
7.2. Spacing and intensity of releases
We start with idealized analyses, then discuss their relative robustness and the effects of environmental heterogeneity. Consider an area with a relatively uniform vector density. What is the optimal release strategy? The calculations in Appendix B show that for a given number of mosquitoes, the best strategy is to release a short pulse, i.e., to essentially instantly produce a local infection frequency sufficient to initiate a wave. Obviously there are practical constraints on numbers that can be released, as well as density-dependent effects, that limit the rate of local transformation. However, empirical results of Hoffmann et al. (2011) demonstrate that patches on the order of 1 km2 can be converted to relatively high Wolbachia-infection frequencies, on the order of 0.8, within two or three months. For simplicity, we focus on releasing Wolbachia-infected mosquitoes in circular areas of radius RI that will form expanding waves. Because the expansion rate approaches zero as the release radius approaches the critical size threshold needed to produce an expanding wave, RI must exceed this critical size. We assume that because of limitations associated with density regulation and constraints on numbers released, the highest initial frequency, p0, that can plausibly be achieved in each release area is pmax < 1. We consider laying out release areas in a uniform grid with spacing D between the centers of each release.
We envision expanding waves from each release. When the waves meet, the radius of each infected patch is D/2 and the fraction of the space occupied by Wolbachia-transformed mosquitoes is π/4 = 0.785 (i.e., π(D/2)2/D2), or roughly 80%. If the waves were instantly moving at the asymptotic speed c, they would meet in (D/2 – RI)/c time units. The actual time will be slower because the infection frequency must rise in the release area and the proper wave shape establish. Given that we can control p0 (≤ pmax), RI, and D, we can ask: what values of these three parameters produce waves that meet in a minimum time for a fixed number of mosquitoes released – and what is that time? Alternatively, we can ask what is the minimum number of mosquitoes that must be released to produce advancing waves that meet within a fixed time? Given practical constraints on achieving specific values for p0, RI, and D, we then consider how sensitive our results are to these parameters and to model assumptions concerning dynamics and dispersal.
7.3. Empirically based approximations for area-wide coverage
Before addressing these questions with detailed dynamic models, we provide informative approximations from empirical results. From the data reported in Hoffmann et al. (2011) and Hoffmann et al. (2014), we know that releases of wMel-infected Aedes aegypti can be used to stably transform areas with radius roughly RI = 400 m. A Wolbachia frequency of about 80% within such release areas can be achieved in about 10 weeks (under three generations) by releasing weekly a number of adults on the order of 50-100% of the resident adult population (Hoffmann et al. 2011; Ritchie et al. 2013). Our theoretical analyses above and in Barton and Turelli (2011) suggest that rates of spatial spread are likely to be habitat dependent. But in relatively uniform habitats, comparable our release areas near Cairns with σ ≈ 100 m/(generation)1/2 and p̂ ≈ 0.25-0.3, we expect wave speeds on the order of 10-20 m per month.
To understand the consequences of slow spatial spread, we initially consider dividing the target region into non-overlapping D × D squares. We will determine the value of D that achieves about 80% coverage over the desired period. Suppose that at the center of each square, we release Wolbachia-infected mosquitoes over a circle of radius RI. Assume that each release initiates a wave moving c meters per generation (roughly per month). If we want the expanding circles to hit the edges of the D × D squares within T generations, the wave front must move a distance D/2 – RI in T generations. Hence, the distance between adjacent centers must be
| (11) |
The fraction, F, of the target area that must be actively transformed to achieve π/4 coverage in T generations is F = πRI2/D2, where D is given by (11). Thus,
| (12) |
Table 3 shows how F depends on time (T, in generations), wave speed per generation (c), and the initial release radius (RI). The target times correspond roughly to one-to-four years. These approximations make sense only if the initial frequency in the release area is high enough that the asymptotic wave speed is reached within a few generations. They imply that for relatively homogeneous target areas consistent with steady spatial spread, roughly 80% can be covered in three or four years with initial releases of 0.5-1 km2 that cover about 10-30% of the target. Comparable results are obtained below from explicit dynamic models for wave initiation and spread.
Table 3. Fraction of the target area that must be actively transformed to produce about 80% (π/4) coverage in T generations.
| RI (area) | 40 generations | 30 generations | 20 generations | 10 generations |
|---|---|---|---|---|
| 400 m (0.5 km2) | 0.09-0.20 | 0.13-0.26 | 0.20-0.35 | 0.35-0.50 |
| 560 m (0.99 km2) | 0.13-0.27 | 0.18-0.33 | 0.27-0.43 | 0.43-0.57 |
These calculations assume wave speed c = 10-20 m/generation starting from initial releases in circles of radius RI that produce local infection frequencies p0 near 1.
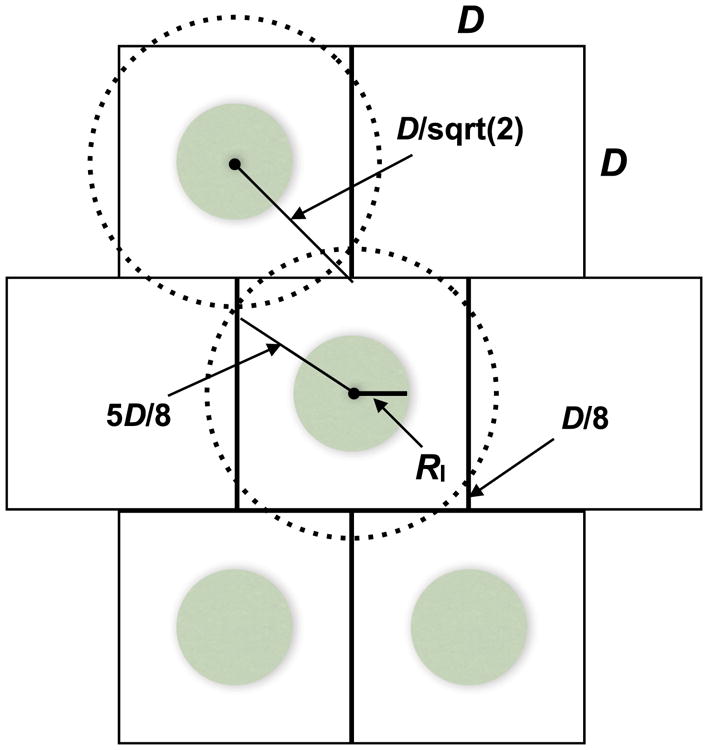
To completely cover a region as quickly as possible, a regular grid of releases is not optimal. Fig. 6 shows how rows of releases with the centers offset between adjacent rows reduces the distance each wave must travel by D/√2 – 5D/8 ≈ 0.08D. (Note that with the release configuration shown in Fig. 6, when the radii of the expanding waves reach 5D/8, the entire target area has been transformed.) The empirical relevance of such idealized release spacings is considered in the Discussion.
Fig. 6.
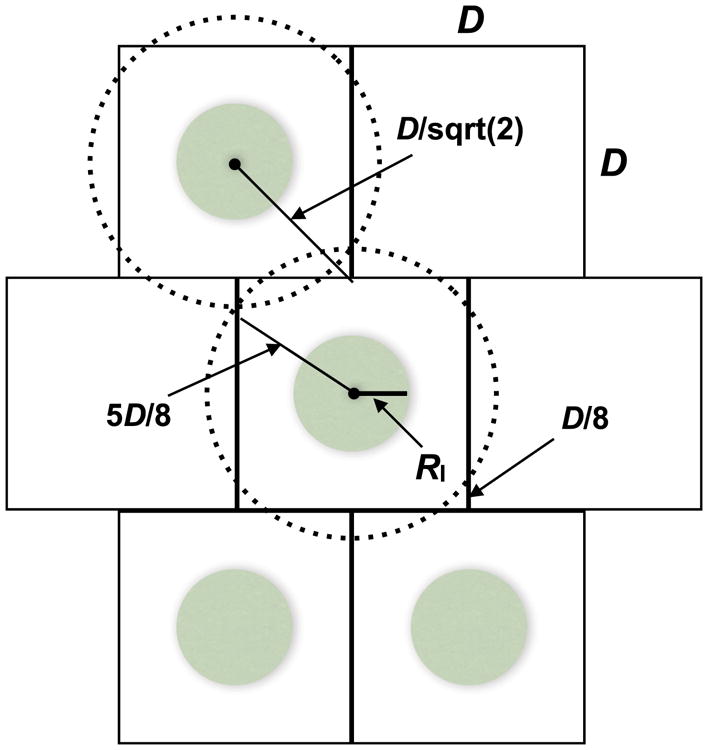
Optimal spacing. The green circles within the D × D squares represent release areas with radii RI. If the release areas were laid out on a regular grid, each expanding wave would have to travel to the corner of the enclosing square, a distance of (D/√2) – RI, to transform the entire target area. In contrast, by offsetting the release centers between adjacent rows, as illustrated, each wave must travel only (5D/8) – RI for area-wide transformation.
7.4. Model-based approximations
Next, we reconsider the times to achieve roughly 80% coverage using explicit models for temporal and spatial dynamics. With explicit dynamics we can address various questions involving, for instance, optimal size and spacing of release areas and optimal initial frequencies in the release areas. Release areas have a major impact on subsequent dynamics. For releases near the minimal sizes required to initiate spread (cf. Fig. 5), dynamics will be extremely slow. In contrast, our calculations above assume that asymptotic wave speed is reached essentially instantaneously. Assuming Caspari-Watson dynamics with alternative dispersal models, we use the DTDS approximations (7) to describe optimal release strategies under different constraints.
7.4.1. Optimal spacing and sizes of releases
For these calculations, we assume that releases occur in a fixed fraction, ρ, of the target area and that the initial Wolbachia frequency within the release areas is p0. To understand fully how mosquito releases translate into local infection frequencies, density regulation must be understood. Instead, we consider ρ and p0 as simple proxies for release effort. As above, we assume that release areas are circles of radius RI set at the centers of D × D squares that cover the target area. Given ρ, the spacing D dictates the radii, RI, of the releases, with . For fixed ρ, we seek the spacing D (or equivalently the release area) that minimizes the time until the waves meet (covering π/4 of the target area). The minimal time is denoted Tmin.
Assuming releases over 20% of the target area (ρ = 0.2) with initial infection frequencies, p0, of 0.6 or 0.8 in each release area, Table 4 presents optimal spacing for releases and the number of generations to reach 80% coverage for two plausible values of p̂. What seems most notable is that for these parameters, the optimal release radii are only about 30-45% larger than the minimum radii needed to initiate spatial spread. With “optimal” spacing, 80% coverage is predicted in about 1.25-3.5 years, assuming about 10 generations per year. The values of Tmin are considerably smaller than those reported in Table 3, and the critical difference is that the release areas are considerably smaller. Table 3 assumes σ = 100 m, so the release sizes are fixed at RI = 4 and 5.6. The shorter times in Table 4 are associated with the fact that in principle smaller releases will suffice to start waves that relatively quickly approach their asymptotic speed.
Table 4. Optimal spacing of releases.
| p0 = 0.6 | p̂ = 0.2 | p̂ = 0.3 | ||||||
|---|---|---|---|---|---|---|---|---|
|
| ||||||||
| Dispersal | D | RI | Rcrit | Tmin | D | RI | Rcrit | Tmin |
| Gaussian | 13.06 | 3.30 | 2.48 | 17.60 | 16.26 | 4.10 | 3.19 | 30.22 |
| Laplace | 12.21 | 3.08 | 2.35 | 17.95 | 16.22 | 4.09 | 3.06 | 31.13 |
| ExpSqrt | 11.30 | 2.85 | 1.99 | 19.54 | 15.11 | 3.81 | 2.64 | 34.87 |
|
| ||||||||
| p0 = 0.8 | p̂ = 0.2 | p̂ = 0.3 | ||||||
|
| ||||||||
| Dispersal | D | RI | Rcrit | Tmin | D | RI | Rcrit | Tmin |
|
| ||||||||
| Gaussian | 11.26 | 2.86 | 2.05 | 14.17 | 13.43 | 3.39 | 2.61 | 24.26 |
| Laplace | 10.25 | 2.60 | 1.97 | 14.57 | 13.39 | 3.38 | 2.52 | 25.09 |
| ExpSqrt | 9.34 | 2.36 | 1.62 | 16.25 | 12.18 | 3.07 | 2.16 | 28.59 |
All distances are measured in units of σ. Assuming releases over 20% of the target area (i.e., ρ = 0.2 and p0 = 0.6 or 0.8), we compare the spacing, D (distance between adjacent release centers), that produces the shortest time (in generations), Tmin, required to reach 80% coverage as a function of p0, initial infection frequency in release areas, p̂ and dispersal shape. The initial radius of these optimal releases, , is compared to the minimum radius, Rcrit, required to initiate an expanding wave for the specified p0 and p̂.
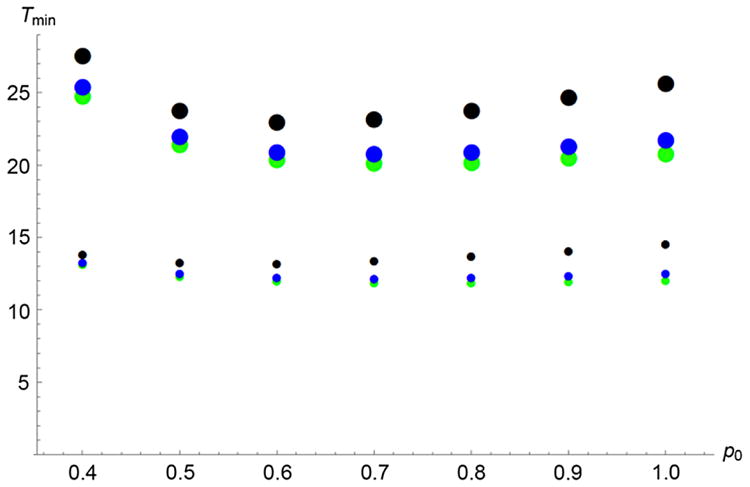
Table 4 shows that Tmin depends only weakly on the shape of dispersal. As expected from our speed calculations, long-tailed dispersal leads to longer wait times. Two factors contribute to this, the differences in wave speed demonstrated in Fig. 3 and the differences in the optimal spacing. With longer dispersal tails, wave speed slows down, but the optimal spacing is closer (because smaller release radii suffice to initiate spread), and these effects partially cancel. In contrast, as p̂ increases from 0.2 to 0.3, Tmin increases by 70-80%, whereas the analytical prediction and the numerical results in Fig. 3 indicate that wave speed should decrease by only about 50%, at most. The additional factor explaining the discrepancy is that larger releases are needed, producing larger spacing, D, so that the waves must travel farther to meet. Table 4 also predicts how Tmin varies with the number of infected mosquitoes released, as measured by p0. As expected, the critical spacing, D, and the minimal time, Tmin, fall as initial frequencies rise. For instance, with Gaussian dispersal and p̂ = 0.3, (D, Tmin) fall from (13.06, 17.60) with p0 = 0.6 to (10.74, 14.25) with p0 = 0.8 and to (9.36, 12.03) with p0 = 1.0. Overall, decreasing p0 from 0.8 to 0.6 leads to lengthening Tmin by a factor of 1.20-1.25.
7.4.2. Optimal distribution: release area, ρ, versus initial frequency, p0
Optimization depends on constraints. Above we assume that ρ and p0 have been chosen, then seek the optimal spacing (or equivalently the optimal sizes for the individual release areas), conditioned on ρ, the total area over which releases will occur. An alternative is to assume that available resources dictate the number of mosquitoes that can be released, then ask whether it is more efficient to produce a low initial frequency over a large area or a higher frequency over a smaller area. In general, we expect that achieving a frequency of 0.45 requires less than half the effort required to achieve 0.9 for at least two reasons. First, density-dependence is likely to produce diminishing returns from very intensive releases (Hancock et al. 2016); and second, very high frequencies can only be achieved with repeated releases, which are less efficient than more intense releases over shorter periods. Nevertheless, if we view that product ρ p0 as proportional to total release effort, it is instructive to ask for a fixed ρ p0 what p0 achieves 80% coverage as quickly as possible?
Using all three dispersal models and p̂ = 0.2 or 0.3, Fig. 7 plots the minimal time to achieve 80% cover as a function of p0 assuming ρ p0 = 0.2. The results indicate that releases producing initial frequencies between roughly 0.5 and 0.8 are essentially equivalent, with coverage times varying less than 10%. In contrast, the considerable additional effort required to produce p0 ≥ 0.9 yields slightly slower rather than faster coverage. Conversely, reaching only p0 = 0.04-0.5 requires significantly larger optimal release areas and yields slower coverage. For instance, with Laplace dispersal, p̂ = 0.3, and ρ p0 = 0.2, Tmin is achieved with RI = 4.10 for p0 = 0.7 but RI = 5.84 for p0 = 0.5, corresponding to roughly doubling the release areas. These results suggest that releases should aim for initial Wolbachia frequencies in the neighborhood of 60-80%.
Fig. 7.
Time to reach about 80% (∼π/4) coverage as a function of initial frequency in the release area, p0. The calculations assume ρ p0 = 0.2, where ρ is the fraction of the target area over which releases occur. The small dots are produced with p̂ = 0.2; the large dots with p̂ = 0.3. Green points are for Gaussian dispersal, blue points for Laplace, and black for ExpSqrt.
7.4.3. Robustness of coverage times to incomplete knowledge
Although one can propose optimal spacing and release areas for fixed ρ and p0, the optimal values are unlikely to be achieved in practice because they depend critically on two parameters, the local dispersal parameter σ and the value of the unstable equilibrium p̂, that will be known only approximately. Moreover, the geometry of field releases will be influenced by factors such as housing density and type, barriers to wave movement, and local community acceptance. Although the fraction of the target area in which releases are initially performed, ρ, is clearly under experimental control, as is the initial frequency in those release areas, p0, it is important to understand the robustness of the minimum times presented in Table 4 and Fig. 7 to alternative release areas, RI, which are measured in units of σ.
Fig. 8 summarizes the results for all three dispersal models, assuming that we initially release over 20% of the target area (ρ = 0.2) and produce an initial infection frequency p0 = 0.8 relatively rapidly. As RI departs from the optima given in Table 4, Fig. 8 shows how the time to achieve 80% coverage increases relative to opt, the minimal time achievable. As expected from Table 4, there is a fundamental asymmetry produced by the fact that the optimal RI is typically only about 25-30% larger than the minimal release size needed to produce an expanding wave. Hence, undershooting the optimal release size by as little as 25% can lead to releases that collapse rather than expand. In contrast, for a realistic range of unstable points and all three models of dispersal, overshooting the optimal release area by 50% increases Tπ/4 by less than 20%. Even releases twice as large as optimal increase Tπ/4 by at most 43%. The clear implication is that one should use conservatively large estimates of σ and p̂ to design releases that will produce near-optimal results with little possibility of collapse. The practical implications of Table 4 and Fig. 7 are discussed below.
Fig. 8.
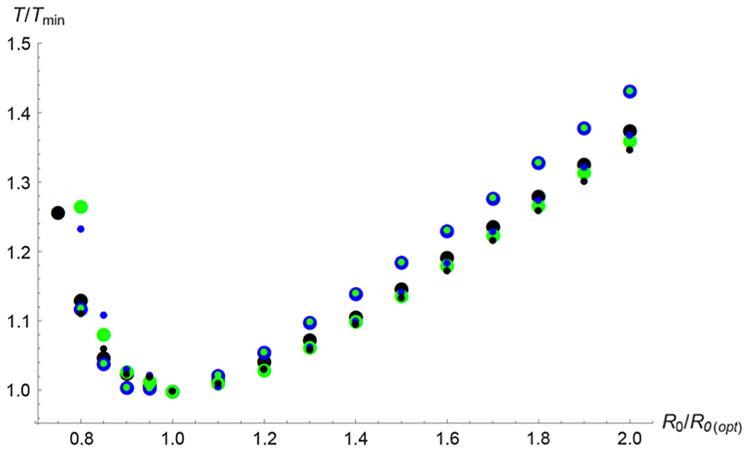
Time to reach about 80% (∼π/4) coverage, relative to the minimum time, as a function of release area. For each model, release areas are measured relative to the release area, RI(opt), that produces Tmin for that model. The DTDS calculations assume Caspari-Watson dynamics with ρ = 0.2 and p0 = 0.8 (i.e., releases produce an initial frequency of 0.8 over 20% of the target area). The small dots are produced with p̂ = 0.2; the large dots with p̂ = 0.3. Green points are for Gaussian dispersal, blue points for Laplace, and black for ExpSqrt.
8. Discussion
8.1 Robustness of the cubic-diffusion predictions for spatial spread
8.1.1. Wave width
The point of estimating wave width is that it provides an average estimate – under natural field conditions – of the dispersal parameter σ that is central to predicting wave speed (see Eqs. 2.5 and 2.6). Using discrete-time, discrete-space (DTDS) approximations with alternative models of dispersal, we have tested the robustness of diffusion-based approximations for wave speed, wave width and the size of releases needed to initiate spatial spread. The most robust prediction concerns wave width (see Eq. 6 and Fig. 4). For a wide range of dispersal models and parameters, wave width is observed to be within about 10% of the analytical prediction, Eq. (6), produced by the cubic-diffusion approximation for bistable dynamics. This implies that estimates of the dispersal parameter σ can be obtained from data on the spatial pattern of infection frequencies after local releases. Unlike dispersal estimates obtained from short-term release-recapture experiments, estimates based on infection-frequency wave width average over seasons and are largely free from behavioral artifacts associated with inflated population densities or the effects of lab rearing, marking or handling.
8.1.2. Wave speed
The cubic-diffusion model produces the wave-speed approximation Eq. (5): c = σ(½ – p̂) per generation, assuming complete cytoplasmic incompatibility (i.e., sh = 1 in Eq. 3a or 4a). Our DTDS calculations show that this approximation remains accurate even for the rapid local dynamics produced by complete CI if dispersal is near-Gaussian (i.e., Gaussian or Laplace in Eq. 2.8) and the unstable point is below 0.4 (Fig. 3B). However, for long-tailed dispersal as described by the ExpSqrt model (see Eq. 8c and Fig. 2), spatial spread is slowed by 30-40% relative to the analytical prediction for 0.2 ≤ p̂ ≤ 0.35. Hence, if σ is on the order of 100 m/(generation)1/2 and p̂ is near 0.25, the predicted wave speed can drop from about 25 m/generation to about 15 m/generation. The result is that with about 10 Ae. aegypti generations per year, wMel is expected to spread through natural populations of Ae. aegypti at a rate nearly three orders of magnitude slower than the 100 km/year rate at which wRi spread through D. simulans populations in California and eastern Australia.
8.1.3. Wave initiation
Finally, our DTDS calculations indicate that the cubic-diffusion approximations for the minimum radii of release areas from Barton and Turelli (2011) are likely to be significant overestimates, especially if fitness is reduced primarily through fecundity. Fig. 5 shows that the diffusion approximation may overestimate minimum release sizes by a factor of two for 0.2 ≤ p̂ ≤ 0.35 (as noted in Section 4.3, most of this discrepancy is attributable to using a model that explicitly models Wolbachia dynamics, assuming that the cost of transinfections is mainly associated with a fecundity reduction). In general, for fixed σ, smaller releases will initiate spatial spread when dispersal is more long-tailed. With σ ≈ 100 m/(generation)1/2, releases that produce initial frequencies of 0.8 over about 0.13 km2 should suffice to initiate spatial spread, assuming that p̂ ≤ 0.3. However, near this minimum, expansion (or collapse) is expected to be extremely slow, easily on the order of two years.
8.2. Predictions for 2013 Cairns releases
In 2013, the wMel releases in the Edgehill/Whitfield (EHW) and Parramatta Park (PP) regions of Cairns quickly produced infection frequencies about 0.8 within the release areas (S. L. O'Neill, pers. comm.). Given that these sites are roughly 0.97 km2 (EHW) and 0.52 km2 (PP), we expect spatial spread of the infection from both release areas. Assuming σ ≈ 100 m/(generation)1/2 (corresponding to wave width on the order of 400 m), our analyses predict spread on the order of 10-25 m/generation, assuming p̂ ≈ 0.25. In contrast, the Westcourt (WC) release encompassed only 0.11 km2, very close to the critical value that separates expected local establishment from collapse, assuming p̂ ≈ 0.25 and 100 m/(generation)1/2 (see Table 2 for additional details). Given the slow rate of change expected near this threshold, considerable replication of such small releases would be required to convert our ambiguous prediction into a rigorous test. In contrast to the difficulty of testing our predictions concerning the minimum sizes of releases, our wave-speed and wave-width predictions can be easily compared to empirical data from urban field releases. The “Eliminate Dengue” project is currently preparing the data from the 2013 Cairns releases for publication.
8.3 Bistability for Wolbachia transinfections but probably not for natural infections
8.3.1. Background
Early proposals by O'Neill and his collaborators (e.g., Sinkins et al. 1997) to transform natural populations with introduced Wolbachia were motivated at least in part by the belief that even fitness-decreasing infections might spread rapidly in nature, driven by the force of cytoplasmic incompatibility (Turelli and Hoffmann 1991, 1995). However, the rapid spatial spread of natural Wolbachia infections in Drosophila now seems dependent on net fitness advantages, previously unknown – and still not fully understood, that allow them to increase systematically in frequency even when they are so rare that cytoplasmic incompatibility provides no appreciable benefit (Fenton et al. 2011; Kriesner et al. 2013; Hamm et al. 2014). For Wolbachia infections that tend to increase when rare, occasional long-distance dispersal events can allow them to establish locally, spread and coalesce with other propagules, speeding their spatial spread far beyond what might be expected from more typical dispersal. Bistable dynamics, as produced by the appreciable fitness costs associated with wMel-infected Aedes aegypti in Australia, restrict spatial spread to speeds set by average dispersal. Moreover, bistability sets a fundamental constraint on which transinfections might ever spread. S. L. O'Neill's “Eliminate Dengue” project (http://www.eliminatedengue.com/program) initially proposed introducing the life-shortening Wolbachia, wMelPop, into Ae. aegypti to greatly reduce the frequency of females old enough to transmit dengue virus. However, the fitness costs associated with wMelPop in Ae. aegypti produced an unstable infection frequency far above 0.5, precluding spatial spread (Barton 1979; Turelli 2010; Walker et al. 2011; Barton and Turelli 2011).
Turelli and Hoffmann (1991) proposed bistable dynamics to describe the northward spread of Wolbachia variant wRi through California populations of D. simulans. The rationale for bistability was that the frequency-dependent advantage associated with CI seemed to be counteracted at low frequencies by two factors: imperfect maternal transmission, whereby a few percent of the ova produced by infected mothers were uninfected (Hoffmann et al. 1990; Turelli and Hoffmann 1995; Carrington et al. 2011); and reduced fecundity for infected females, with a 10-20% fecundity disadvantage observed in the lab (Hoffmann and Turelli 1988, Hoffmann et al. 1990; Nigro and Prout 1990) and a smaller, but statistically significant, fecundity disadvantage observed once in nature (Turelli and Hoffmann 1995).
The generality of bistable frequency dynamics for natural Wolbachia infections was brought into question by two infections found first in Australia that cause little (wMel in D. melanogaster, Hoffmann 1988; Hoffmann et al. 1998) or no (wAu in D. simulans, Hoffmann et al. 1996) CI or other reproductive manipulation (Hoffmann and Turelli 1997). It was subsequently discovered that these Wolbachia nevertheless spread in nature. First noted was a turnover of Wolbachia variants among global populations of D. melanogaster (Riegler et al. 2005; Richardson et al. 2012), even though none of these variants cause appreciable CI when males are more than a few days old (Reynolds and Hoffmann 2002; Harcombe and Hoffmann 2004). Similarly, Wolbachia variant wAu, which does not cause CI in D. simulans (Hoffmann et al. 1996), was found spreading to intermediate frequencies through D. simulans populations in eastern Australia, despite imperfect maternal transmission (Kriesner et al. 2013). The spread of wAu was followed by the spread of wRi through these same populations, beginning from three widely separated geographical locations (Kriesner et al. 2013). Although spread of bistable Wolbachia could in principle be initiated by chance fluctuations (Jansen et al. 2008), a net fitness advantage that counteracts imperfect transmission seems far more plausible (Hoffmann and Turelli 1997; Fenton et al. 2011; Hamm et al. 2014). The observed rate of spread for wRi, approximately 100 km/yr., in both California and eastern Australia, is easy to understand only if long-distance, human-mediated dispersal can establish local infections that spread and coalesce (see Shigesada and Kawasaki 1997, Ch. 5). Such rapid expansion is implausible if local introductions must be sufficiently extensive to exceed initial area and frequency thresholds imposed by bistability (Lewis and Kareiva 1993; Soboleva et al. 2003; Alrock et al. 2011; Barton and Turelli 2011). With bistability, spatial spread is likely to be limited by the relatively slow processes of active insect dispersal. As demonstrated below, this indicates that the spread of transinfections with bistable dynamics in Ae. aegypti will be orders of magnitude slower than the 100 km/year observed for wRi in California and Australia populations of D. simulans.
A net fitness benefit for natural Wolbachia infections helps explain the persistence and spread of Wolbachia variants, such as wAu and wMel, that do not cause appreciable CI in their native Drosophila hosts. A net fitness benefit, so that the relative fitness of infected females, F, and their maternal transmission rate, 1 – μ, satisfy F(1 – μ) > 1, would also help explain the extraordinarily rapid human-mediated spatial spread of wRi in both California and Australia. Mitochondrial data reported in Kriesner et al. (2013) suggest that wRi spread northward in California shortly after it was introduced to southern California, rather than being stalled by a transverse mountain range, as might be expected with bistability (cf. Turelli and Hoffmann 1995). Several fitness advantages have been proposed to counteract imperfect transmission and possible fecundity disadvantages, including nutritional effects (Brownlie et al. 2009; Gill et al. 2014) and microbe protection (Hedges et al. 2008; Teixeira et al. 2008).
These arguments against bistability for natural Wolbachia infections may suggest that intrinsic fitness advantages, together with CI, could lead to rapid spread of disease-suppressing Wolbachia transinfections in nature from minimal introductions. The data we discuss in Section 6 argue strongly against this.
8.3.2. New evidence for bistability of transinfections
Based on the theory in Barton and Turelli (2011) and the expectation that few mosquitoes would cross the highway, Hoffmann et al. (2011) predicted that “Unless fitness costs are essentially zero or there are unexpected fitness benefits, we do not expect the infection to spread further …” Four years later, wMel has not become established in PE despite repeated immigration. An adaptation of Haldane's (1930) island model, Eq. (9), indicates a lower bound on the unstable equilibrium, p̂, of about 0.21. This local frequency threshold for population transformation appreciably slows the predicted rate of spatial spread, as indicated by Eq. (5).
Our new data and analyses bolster previous evidence for bistability. In Hoffmann et al. (2011), an informal quantitative analysis of the rising frequency of wMel in response to several weekly releases indicated fitness costs on the order of 20%. However, the frequency data could not distinguish fitness costs associated with laboratory rearing from reduced fitness intrinsic to the Wolbachia transinfection. Two years later, Hoffmann et al. (2014) resampled these stably transformed populations and determined that the infected females produced about 20% fewer eggs under laboratory conditions, suggesting that p̂ ≥ 0.2. As a consequence of bistability, the rate of spatial spread is limited by natural dispersal ability, with a maximum speed bounded above by σ/2 per generation, where σ is the dispersal parameter discussed below. In particular, bistability precludes very rapid spatial spread based on long-distance, human-mediated dispersal. Even when large numbers are transported by accident, the area transformed would be unlikely to exceed the minimum size needed to initiate spatial spread (Fig. 4).
The unstable equilibrium frequency, p̂, is a useful abstraction that captures key features of the complex frequency dynamics of Wolbachia transinfections. The true dynamics are multidimensional (Turelli 2010; Zheng et al. 2014) and depend on age-specific effects as well as ecological factors, such as intraspecific density-dependence (Hancock et al. 2011a,b; Hancock et al. 2016) and interaction with other insects and microbes (Fenton et al. 2011). However, a full description of this biology would involve many parameters that would have to be estimated in each locale. We doubt that these parameters could be estimated accurately enough for more realistic models to produce better predictions that our simple two-parameter approximations. Our idealized models of frequency dynamics produce field-testable predictions and empirically useful guidance for field releases.
8.4. Consequences of patchy population structure with bistable dynamics
We have assumed throughout a uniform population density and dispersal rate. In reality, habitat heterogeneity may slow – or stop – the spread of a wave. If increase is expected from low frequencies, then a few long-range migrants can take the infection beyond a local barrier. We expect this has happened repeatedly with the observed spread of wAu and wRi in Drosophila simulans (cf Coyne et al. 1982; Coyne et al. 1987; Kriesner et al. 2013). Similarly, many episodes of successful long-distance dispersal and local establishment must underlie the global spread of Aedes aegypti out of Africa (Brown et al. 2011). However, bistability, as expected for the wMel infection in Ae. aegypti, implies that infection spread can be stopped indefinitely, as seems to be the case with Pyramid Estate/Gordonvale near Cairns. Barton and Turelli (2011, Eq. 20) gave a simple result that shows how a gradient in population density alters wave speed: regardless of the detailed dynamics, a gradient in log density will slow (or accelerate) a travelling wave by σ2d(log(ρ(x))/dx, where ρ(x) denotes the population density at x. However, such a gradient must be sustained over a sufficient distance. Local heterogeneities, such as those due to the spacing between discrete demes (e.g., individual households harboring Ae. aegypti), have a negligible effect if they are over a shorter scale than the width of the wave (Barton 1979, p. 357).
In contrast, when the wave encounters a significant barrier, such as the highway separating Pyramid Estate from Gordonvale, we can understand wave stopping either in terms of sharp breaks in density, as considered in Fig. 6 of Barton and Turelli (2011), or in terms of migration from an infected population into an uninfected population. The latter produces a lower bound on immigration rate needed to “flip” the uninfected population past the unstable point, as discussed above Eq. 1. Because large tropical cities that are the targets of control efforts for arboviruses such as dengue and Zika are filled with significant dispersal barriers, we have not considered release schemes more elaborate than regularly spaced, equal-sized release foci. Nevertheless, we hope these abstractions accurately indicate the potential for area-wide control with plausible effort over a span of a few years.
8.5. Practical guidelines for field releases
When the “Eliminate Dengue” program initially obtained Gates Foundation “Grand Challenges” funding in 2006, the extraordinarily rapid spread of wRi through California populations of D. simulans provided a plausible paradigm supporting the conjecture that natural Ae. aegypti populations could be rapidly transformed with disease-suppressing Wolbachia. The D. simulans paradigm also suggested that very few local introductions could lead to area-wide transformation within a few years for large metropolitan areas with relatively continuous Ae. aegypti habitat. Unfortunately, this rapid-spread paradigm, which remains demonstrably true for natural Wolbachia infections (Kriesner et al. 2013), now seems clearly inapplicable to Wolbachia transinfections that significantly reduce the fitness of their Ae. aegypti hosts. More plausible rates of spatial spread seem to be at most 0.25 km per year, and even those slow rates are expected only in near-continuous habitats. From our analysis of the Pyramid Estate data, it seems that barriers on the order of 100-200 m, such as highways, will suffice to halt spread. Hence, it is reasonable to ask whether spatial spread can play a significant role in achieving area-wide coverage over a time scale of a few years.
A central question is whether real urban/suburban landscapes provide enough nearly-continuous habitat to apply our optimal – or near-optimal – release designs, involving a series of releases set out in grids. We have showcased an empirical example in which wMel has apparently not been able to cross a highway. We do not yet know enough to characterize a priori the barriers that will halt wMel spread. What is clear is that area-wide control over just a few years will require many release areas. We can offer simple guidance based on our mathematical results and the population biology of vector-borne disease transmission. Given that spatial spread will preferentially occur from high-density areas to low-density areas, a guiding principle is that releases should initially occur in areas that support the highest Ae. aegypti densities. Because disease transmission is proportional to vector density, these areas are the natural targets for initial control efforts.
Our calculations provide more detailed guidance concerning the size of individual releases, their spacing, and the initial infection frequencies that should be achieved. Fig. 7 shows that for a wide range of parameters, releases need not produce initial frequencies above 0.6. Indeed, the effort to achieve much higher initial frequencies may produce slightly slower area-wide coverage, if a fixed fraction of the local mosquito population is initially replaced. As demonstrated by Fig. 7, overshooting optimal release areas even by a factor of two should increase the time to produce large-scale coverage by at most 50%. In contrast, Table 2 shows that “optimal” release areas are often only twice as large as the minimal release areas needed to initiate spread (corresponding to RI/Rcrit = √2 in Table 2). Thus, release areas should be based on conservatively large estimates of σ and p̂. Assuming σ ≤ 120 m/gen1/2 and p̂ ≤ 0.3, individual releases on the order of 1 km2, producing initial frequencies of 60-80%, should generally suffice to guarantee local spread, assuming that the surrounding habitat has population densities comparable to or lower than the release area. If the habitat is sufficiently homogeneous, covering only about a third of the target area with such releases should produce about 80% coverage in less than three years.
All of our guidelines are predicated on p̂ ≤ 0.35. The lower the unstable point the better. But if there is any significant cost of Wolbachia transinfections, so that p̂ ≥ 0.1, wave speed is likely to bounded above by σ/2. Although spatial spread of low-p̂ variants is unlikely to be significantly aided by occasional long-distance dispersal, the spread of such variants is far less likely to be stopped by minor barriers to dispersal. As shown in Fig. 6 of Barton and Turelli (2011), step-increases in population density of just over two-fold will stop the spatial spread of a transinfection that produces p̂ = 0.25; whereas an increase greater than five-fold is needed to stop a variant with p̂ = 0.1.
Given that only two Wolbachia transfections of Ae. aegypti have been released in nature in population transformation efforts, we don't know whether there are Wolbachia variants that can provide effective virus-blocking and produce low fitness costs. In preliminary analyses, high Wolbachia titer is associated with better virus blocking and also lower fitness of infected hosts (Walker et al. 2011; Martinez et al. 2015). Among Wolbachia found in Drosophila species and transferred into D. simulans, the relationships between titer and measures of fitness loss and virus protection are both highly significant; but they explain only about half of the variation observed in each trait. Hence, it seems likely that further exploration of Wolbachia variation in nature could uncover high-protection, low-fitness-cost variants.
Despite the fact that the wMel variant currently being released will spread very slowly and may be relatively easily stopped by barriers to dispersal, it still offers significant benefits over disease-control strategies like insecticide application and sterile-male release (or release of CI-causing males) that require continual applications to suppress local vector populations (McGraw and O'Neill 2013). As shown by Hoffmann et al. (2014), transformations of isolated populations with Wolbachia remain stable. Similarly, for sufficiently large local releases, we expect local Wolbachia introductions to at least persist and probably slowly expand as long as the surrounding areas do not harbor significantly higher Ae. aegypti densities. Even if half of a large area has to be actively transformed to achieve area-wide control, this will only have to be done once. We do not know how long-lasting dengue-blocking by wMel or other transinfections will be, but the comparative evidence from natural Wolbachia infections suggests that it should persist for at least a decade or more (Bull and Turelli 2013), a time-scale over which effective vaccines may well become available (Screaton et al. 2015).
8.6. Final comment: reversibility versus re-transformation
Population transformation carries a potential risk of unintended consequences (Bull and Turelli 2013). For instance, a Wolbachia strain that inhibits the transmission of one disease may in principle enhance the transmission of another (cf. Martinez et al. 2014). Hence, it is interesting to ask whether an introduced Wolbachia can be “recalled”, returning the population to its initial uninfected state. In principle, this could be done by swamping the population with uninfected individuals so that the infection frequency falls below p̂. However, given the tendency of variants with p̂ < 0.5 to spread spatially, this swamping strategy seems implausible outside of relatively small, isolated populations. It seems more plausible to re-transform populations with a more desirable Wolbachia variant that shows unidirectional incompatibility with the first. For example, when Wolbachia wMel is introduced from D. melanogaster into D. simulans, which is naturally infected by wRi, the wMel-infected females are incompatible with wRi infected males, whereas wRi females are protected from the incompatibility that wMel induces against uninfected females (Poinsot et al. 1998). Thus if a population has been transformed with wMel, it could in principle be transformed again by introducing wRi. The hit-and-miss process of identifying Wolbachia strains in nature with the desired properties is likely to be greatly accelerated as we begin to understand the loci within Wolbachia that cause CI (Beckmann and Fallon 2013; LePage et al. 2017; Beckmann et al. 2017) and virus inhibition.
Supplementary Material
S1 File. Appendix A. Effect of dispersal pattern and random fluctuations on travelling waves.
S2 File. Appendix B. Establishing a wave.
Acknowledgments
We thank Brandon S. Cooper, Ary A. Hoffmann, Scott L. O'Neill, two reviewers and the editor for constructive comments on earlier drafts. We thank S. L. O'Neill for allowing us to publish the Pyramid Estates Wolbachia data from his Eliminate Dengue Program (http://www.eliminatedengue.com/program). This work was supported by grants from the Foundation for the National Institutes of Health through the Grand Challenges in Global Health Initiative of the Bill and Melinda Gates Foundation, the Joel Keizer Endowment to UC Davis, and the National Institutes of Health [grant R01-GM-104325-01].
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Altrock PM, Traulsen A, Reed FA. Stability properties of underdominance in finite subdivided populations. PLoS Comput Biol. 2011;7:e1002260. doi: 10.1371/journal.pcbi.1002260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barton NH. Dynamics of hybrid zones. Heredity. 1979;43:341–359. [Google Scholar]
- Barton NH, Hewitt GM. Analysis of hybrid zones. Annu Rev Ecol Syst. 1985;16:113–148. [Google Scholar]
- Barton NH, Turelli M. Spatial waves of advance with bistable dynamics: cytoplasmic and genetic analogues of Allee effects. Am Nat. 2011;178:E48–E75. doi: 10.1086/661246. [DOI] [PubMed] [Google Scholar]
- Beckmann JF, Fallon AM. Detection of the Wolbachia protein WPIP0282 in mosquito spermathecae: Implications for cytoplasmic incompatibility. Insect Biochem Mol Biol. 2013;43:867–878. doi: 10.1016/j.ibmb.2013.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Beckmann JF, Ronau JA, Hochstrasser M. A Wolbachia deubiquitylating enzyme induces cytoplasmic incompatibility. Nature Micro. 2017;2:17007. doi: 10.1038/nmicrobiol.2017.7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bian G, Joshi D, Dong Y, Xie Y, Xi Z. Wolbachia invades Anopheles stephensi populations and induces refractoriness to Plasmodium infection. Science. 2013;340:748–751. doi: 10.1126/science.1236192. [DOI] [PubMed] [Google Scholar]
- Brown JE, McBride CS, Johnson P, Ritchie S, Paupy C, Bossin H, Lutomiah J, Fernandez-Salas I, Ponlawat A, Cornel AJ, Black WC, IV, Gorrochotegui-Escalante N, Urdaneta-Marquez L, Sylla M, Slotman M, Murray KO, Walker C, Powell JR. Worldwide patterns of genetic differentiation imply multiple domestications of Aedes aegypti, a major vector of human diseases. Proc R Soc Lond B Biol Sci. 2011;278:2446–2454. doi: 10.1098/rspb.2010.2469. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brownlie JC, Cass BN, Riegler M, Witsenburg JJ, Iturbe-Ormaetxe I, McGraw EA, O'Neill SL. Evidence for metabolic provisioning by a common endosymbiont, Wolbachia pipientis, during periods of nutritional stress. PLoS Pathog. 2009;5:e1000368. doi: 10.1371/journal.ppat.1000368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull JJ, Turelli M. Wolbachia versus dengue: evolutionary forecasts. Evol Med Public Health. 2013;2013:197–207. doi: 10.1093/emph/eot018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carrington LB, Lipkowitz JR, Hoffmann AA, Turelli M. A re-examination of Wolbachia-induced cytoplasmic incompatibility in California Drosophila simulans. PloS One. 2011;6:e22565. doi: 10.1371/journal.pone.0022565. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Caspari E, Watson GS. On the evolutionary importance of cytoplasmic sterility in mosquitoes. Evolution. 1959;13:568–570. [Google Scholar]
- Coyne JA, Boussy IA, Prout T, Bryant SH, Jones JS, Moore JA. Long-distance migration of Drosophila. Am Nat. 1982;119:589–595. [Google Scholar]
- Coyne JA, Bryant SH, Turelli M. Long-distance migration of Drosophila. 2. Presence in desolate sites and dispersal near a dessert oasis. Am Nat. 1987;126:847–861. [Google Scholar]
- Dobzhansky Th, Wright S. Genetics of natural populations. X. Dispersion rates in Drosophila pseudoobscura. Genetics. 1943;28:304–340. doi: 10.1093/genetics/28.4.304. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dodson BL, Hughes GL, Paul O, Matacchiero AC, Kramer LD, Rasgon JL. Wolbachia enhances West Nile virus (WNV) infection in the mosquito Culex tarsalis. PLoS Negl Trop Dis. 2014;8:e2965. doi: 10.1371/journal.pntd.0002965. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dutra HLC, Rocha MN, Dias FBS, Mansur SB, Caragata EP, Moreira LA. Wolbachia blocks currently circulating Zika virus isolates in Brazilian Aedes aegypti mosquitos. Cell Host & Microbe. 2016;19:1–4. doi: 10.1016/j.chom.2016.04.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Endler JA. Geographic variation, speciation, and clines. Princeton: Princeton University Press; 1977. [PubMed] [Google Scholar]
- Fenton A, Johnson KN, Brownlie JC, Hurst GDD. Solving the Wolbachia paradox: modeling the tripartite interaction between host, Wolbachia, and a natural enemy. Am Nat. 2011;178:333–342. doi: 10.1086/661247. [DOI] [PubMed] [Google Scholar]
- Ferguson NM, Kien DTH, Clapham H, Aguas R, Trung VT, Chau TNB, Popovici J, Ryan PA, O'Neill SL, McGraw EA, Long VT, Dui LT, Nguyen HL, Chau NVV, Wills B, Simmons CP. Modeling the impact on virus transmission of Wolbachia-mediated blocking of dengue virus infection of Aedes aegypti. Science Transl Med. 2015;7:279ra37. doi: 10.1126/scitranslmed.3010370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Frentiu FD, Zakir T, Walker T, Popovici J, Pyke AT, van den Hurk A, McGraw EA, O'Neill SL. Limited dengue virus replication in field-collected Aedes aegypti mosquitoes infected with Wolbachia. PLoS Negl Trop Dis. 2014;8:e2688. doi: 10.1371/journal.pntd.0002688. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gill AC, Darby AC, Makepeace BL. Iron necessity: The secret of Wolbachia's success? PLoS Negl Trop Dis. 2014;8:e3224. doi: 10.1371/journal.pntd.0003224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haldane JBS. A mathematical theory of natural and artificial selection. Part VI Isolation Proc Camb Phil Soc. 1930;26:220–230. [Google Scholar]
- Haldane JBS. The theory of a cline. J Genet. 1948;48:277–283. doi: 10.1007/BF02986626. [DOI] [PubMed] [Google Scholar]
- Hamm CA, Begun DJ, Vo A, Smith CCR, Saelao P, Shaver AO, Jaenike J, Turelli M. Wolbachia do not live by reproductive manipulation alone: infection polymorphism in Drosophila suzukii and D. subpulchrella. Mol Ecol. 2014;23:4871–4885. doi: 10.1111/mec.12901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock PA, Sinkins SP, Godfray HCJ. Population dynamic models of the spread of Wolbachia. Am Nat. 2011a;117:323–333. doi: 10.1086/658121. [DOI] [PubMed] [Google Scholar]
- Hancock PA, Sinkins SP, Godfray HCJ. Strategies for introducing Wolbachia to reduce transmission of mosquito-borne diseases. PLoS Negl Trop Dis. 2011b;5:e1024. doi: 10.1371/journal.pntd.0001024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hancock PA, Linley-White V, Callahan AG, Godfray HCJ, Hoffmann AA, Ritchie SA. Density-dependent population dynamics in Aedes aegypti slow the spread of wMel Wolbachia. J Appl Ecol. 2016;53:785–793. [Google Scholar]
- Harcombe W, Hoffmann AA. Wolbachia effects in Drosophila melanogaster: in search of fitness benefits. J Invert Path. 2004;87:45–50. doi: 10.1016/j.jip.2004.07.003. [DOI] [PubMed] [Google Scholar]
- Harrington LC, Scott TW, Lerdthusnee K, Coleman RC, Costero A, Clark GG, Jones JJ, Kitthawee P, Kittayapong P, Sithiprasasna R, Edman JD. Dispersal of the dengue vector Aedes aegypti within and between rural communities. Am J Trop Med Hyg. 2005;72:209–220. [PubMed] [Google Scholar]
- Haygood R, Turelli M. Evolution of incompatibility-inducing microbes in subdivided host populations. Evolution. 2009;63:432–447. doi: 10.1111/j.1558-5646.2008.00550.x. [DOI] [PubMed] [Google Scholar]
- Hedges LM, Brownlie JC, O'Neill SL, Johnson KN. Wolbachia and virus protection in insects. Science. 2008;322:702. doi: 10.1126/science.1162418. [DOI] [PubMed] [Google Scholar]
- Hemme RR, Thomas CL, Chadee DD, Severson DW. Influence of urban landscapes on population dynamics in a short-distance migrant mosquito: evidence for the dengue vector Aedes aegypti. PLoS Negl Trop Dis. 2010;4:e634. doi: 10.1371/journal.pntd.0000634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA. Partial incompatibility between two Australian populations of Drosophila melanogaster. Entomol Exp Appl. 1988;48:61–67. [Google Scholar]
- Hoffmann AA, Turelli M. Unidirectional incompatibility in Drosophila simulans: Inheritance, geographic variation and fitness effects. Genetics. 1988;119:435–444. doi: 10.1093/genetics/119.2.435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Turelli M. Cytoplasmic incompatibility in insects. In: O'Neill SL, Hoffmann AA, Werren JH, editors. Influential Passengers: Inherited Microorganisms and Arthropod Reproduction. New York: Oxford University Press; 1997. pp. 42–80. [Google Scholar]
- Hoffmann AA, Clancy D, Duncan J. Naturally-occurring Wolbachia infection in Drosophila simulans that does not cause cytoplasmic incompatibility. Heredity. 1996;76:1–8. doi: 10.1038/hdy.1996.1. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Hercus M, Daghar H. Population dynamics of the Wolbachia infection causing cytoplasmic incompatibility in Drosophila melanogaster. Genetics. 1998;148:221–231. doi: 10.1093/genetics/148.1.221. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Montgomery BL, Popovici J, Iturbe-Ormaetxe I, Johnson PH, Muzzi F, Greenfield M, Durkan M, Leong YS, Dong Y, Cook H, Axford J, Callahan AG, Kenny N, Omodei C, McGraw EA, Ryan PA, Ritchie SA, Turelli M, O'Neill SL. Successful establishment of Wolbachia in Aedes populations to suppress dengue transmission. Nature. 2011;476:454–457. doi: 10.1038/nature10356. [DOI] [PubMed] [Google Scholar]
- Hoffmann AA, Turelli M, Harshman LG. Factors affecting the distribution of cytoplasmic incompatibility in Drosophila simulans. Genetics. 1990;126:933–948. doi: 10.1093/genetics/126.4.933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hoffmann AA, Iturbe-Ormaetxe I, Callahan AG, Phillips BL, Billington K, Axford JK, Montgomery B, Turley AP, O'Neill SL. Stability of the wMel Wolbachia infection following invasion into Aedes aegypti populations. PLoS Negl Trop Dis. 2014;8:e3115. doi: 10.1371/journal.pntd.0003115. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jansen VAA, Turelli M, Godfray HCJ. Stochastic spread of Wolbachia. Proc R Soc Lond B Biol Sci. 2008;275:2769–2776. doi: 10.1098/rspb.2008.0914. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kriesner P, Hoffmann AA, Lee SF, Turelli M, Weeks AR. Rapid sequential spread of two Wolbachia variants in Drosophila simulans. PLoS Pathog. 2013;9:e1003607. doi: 10.1371/journal.ppat.1003607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laven H. Eradication of Culex pipiens fatigans through cytoplasmic incompatibility. Nature. 1967;216:383–384. doi: 10.1038/216383a0. [DOI] [PubMed] [Google Scholar]
- LePage DP, Metcalf JA, Bordenstein SR, On J, Perlmutter JI, Shropshire JD, Layton EM, Funkhouser-Jones LJ, Beckmann JF, Bordenstein SR. Prophage WO genes recapitulate and enhance Wolbachia-induced cytoplasmic incompatibility. Nature. 2017;543:243–247. doi: 10.1038/nature21391. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lewis MA, Kareiva P. Allee dynamics and the spread of invading organisms. Theor Popul Biol. 1993;43:141–158. [Google Scholar]
- Martinez J, Longdon B, Bauer S, Chan YS, Miller WJ, Bourtzis K, Teixeira L, Jiggins FM. Symbionts commonly provide broad spectrum resistance to viruses in insects: a comparative analysis of Wolbachia strains. PLoS Pathog. 2014;10:e1004369. doi: 10.1371/journal.ppat.1004369. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martinez J, Ok S, Smith S, Snoeck K, Day JP, Jiggins FM. Should symbionts be nice or selfish? Antiviral effects of Wolbachia are costly but reproductive parasitism is not. PLoS Pathog. 2015;10:e1005021. doi: 10.1371/journal.ppat.1005021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McGraw EA, O'Neill SL. Beyond insecticides: new thinking on an ancient problem. Nat Rev Microbiol. 2013;11:181–193. doi: 10.1038/nrmicro2968. [DOI] [PubMed] [Google Scholar]
- McInnis DO, Schaffer HE, Mettler LE. Field dispersal and population sizes of native Drosophila from North Carolina. Am Nat. 1982;119:319–330. [Google Scholar]
- McMeniman CJ, Lane RV, Cass BN, Fong AWC, Sidhu M, Wang YF, O'Neill SL. Stable introduction of a life-shortening Wolbachia infection into the mosquito Aedes aegypti. Science. 2009;323:141–144. doi: 10.1126/science.1165326. [DOI] [PubMed] [Google Scholar]
- Nagylaki T. Conditions for the existence of clines. Genetics. 1975;80:595–615. doi: 10.1093/genetics/80.3.595. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nigro L, Prout T. Is there selection on RFLP differences in mitochondrial DNA? Genetics. 1990;125:551–555. doi: 10.1093/genetics/125.3.551. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Osborne SE, Leong YS, O'Neill SL, Johnson KN. Variation in antiviral protection mediated by different Wolbachia strains in Drosophila simulans. PLoS Pathog. 2009;5:e1000656. doi: 10.1371/journal.ppat.1000656. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poinsot D, Bourtzis K, Markakis G, Savakis C, Mercot H. Wolbachia transfer from Drosophila melanogaster into D. simulans: host effect and cytoplasmic incompatibility relationships. Genetics. 1998;150:227–237. doi: 10.1093/genetics/150.1.227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Powell JR, Dobzhansky Th, Hook JE, Wistrand HE. Genetics of natural populations. XLIII. Further studies on rates of dispersal of Drosophila pseudoobscura and its relatives. Genetics. 1976;82:493–506. doi: 10.1093/genetics/82.3.493. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Prout T. Some relationships between density-independent selection and density-dependent population growth. Evol Biol. 1980;13:1–68. [Google Scholar]
- Reynolds KT, Hoffmann AA. Male age, host effects and the weak expression or non-expression of cytoplasmic incompatibility in Drosophila strains infected with maternally transmitted Wolbachia. Genet Res. 2002;80:79–87. doi: 10.1017/s0016672302005827. [DOI] [PubMed] [Google Scholar]
- Richardson MF, Weinert LA, Welch JJ, Linheiro RS, Magwire MM, Jiggins FM, Bergman CM. Population genomics of the Wolbachia endosymbiont in Drosophila melanogaster. PLoS Genet. 2012;8:e1003129. doi: 10.1371/journal.pgen.1003129. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Riegler M, Sidhu M, Miller MJ, O'Neill SL. Evidence for a global Wolbachia replacement in Drosophila melanogaster. Curr Biol. 2005;15:1428–1433. doi: 10.1016/j.cub.2005.06.069. [DOI] [PubMed] [Google Scholar]
- Ritchie SA, Montgomery BL, Hoffmann AA. Novel estimates of Aedes aegypti (Diptera: Culicidae) population size and adult survival based on Wolbachia releases. J Med Entomol. 2013;50:624–631. doi: 10.1603/me12201. [DOI] [PubMed] [Google Scholar]
- Russell RC, Webb CE, William CR, Ritchie SA. Mark-release-recapture study to measure dispersal of the mosquito Aedes aegypti in Cairns, Queensland, Australia. Med Vet Entomol. 2005;19:451–457. doi: 10.1111/j.1365-2915.2005.00589.x. [DOI] [PubMed] [Google Scholar]
- Schraiber J, Kaczmarczyk AN, Kwok R, Park M, Silverstein R, Rutaganira FU, Aggarwal T, Schwemmer MA, Hom CL, Grosberg RK, Schreiber SJ. Constraints on the use of lifespan-shortening Wolbachia to control dengue fever. J Theor Biol. 2012;297:26–32. doi: 10.1016/j.jtbi.2011.12.006. [DOI] [PubMed] [Google Scholar]
- Screaton G, Mongkolsapaya J, Yacoub S, Roberts C. New insights into the immunopathology and control of dengue virus infection. Nat Rev Immunol. 2015;15:745–759. doi: 10.1038/nri3916. [DOI] [PubMed] [Google Scholar]
- Shigesada N, Kawasaki K. Biological invasions: theory and practice. Oxford; Oxford University Press; 1997. [Google Scholar]
- Sinkins SP, Curtis CF, O'Neill SL. The potential application of inherited symbiont systems to pest control. In: O'Neill SL, Hoffmann AA, Werren JH, editors. Influential Passengers: Inherited Microorganisms and Arthropod Reproduction. New York: Oxford University Press; 1997. pp. 42–80. [Google Scholar]
- Slatkin M. Gene flow and selection in a cline. Genetics. 1973;75:733–756. doi: 10.1093/genetics/75.4.733. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soboleva TK, Shorten PR, Pleasants AB, Rae AL. Qualitative theory of the spread of a new gene into a resident population. Ecological Modelling. 2003;163:33–44. [Google Scholar]
- Teixeira L, Ferreira A, Ashburner M. The bacterial symbiont Wolbachia induces resistance to RNA viral infections in Drosophila melanogaster. Plos Biol. 2008;6:e1000002. doi: 10.1371/journal.pbio.1000002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turelli M. Evolution of incompatibility-inducing microbes and their hosts. Evolution. 1994;48:1500–1513. doi: 10.1111/j.1558-5646.1994.tb02192.x. [DOI] [PubMed] [Google Scholar]
- Turelli M. Cytoplasmic incompatibility in populations with overlapping generations. Evolution. 2010;64:232–241. doi: 10.1111/j.1558-5646.2009.00822.x. [DOI] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA. Rapid spread of an inherited incompatibility factor in California Drosophila. Nature. 1991;353:440–442. doi: 10.1038/353440a0. [DOI] [PubMed] [Google Scholar]
- Turelli M, Hoffmann AA. Cytoplasmic incompatibility in Drosophila simulans: dynamics and parameter estimates from natural populations. Genetics. 1995;140:1319–1338. doi: 10.1093/genetics/140.4.1319. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walker T, Johnson PH, Moreira LA, Iturbe-Ormaetxe I, Frentiu FD, McMeniman CJ, Leong YS, Dong Y, Axford J, Kriesner P, Lloyd AL, Ritchie SA, O'Neill SL, Hoffmann AA. The wMel Wolbachia strain blocks dengue and invades caged Aedes aegypti populations. Nature. 2011;476:450–453. doi: 10.1038/nature10355. [DOI] [PubMed] [Google Scholar]
- Walsh RK, Aguilar CL, Facchinelli L, Valerio L, Ramsey JM, Scott TW, Lloyd AL, Gould F. Regulation of Aedes aegypti population dynamics in field systems: quantifying direct and delayed density dependence. Am J Trop Med Hyg. 2013;89:68–77. doi: 10.4269/ajtmh.12-0378. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang MH, Kot M, Neubert MG. Integrodifference equations, Allee effects, and invasions. J Math Biol. 2002;44:150–168. doi: 10.1007/s002850100116. [DOI] [PubMed] [Google Scholar]
- Weeks AR, Turelli M, Harcombe WR, Reynolds KT, Hoffmann AA. From parasite to mutualist: rapid evolution of Wolbachia in natural populations of Drosophila. PLoS Biol. 2007;5:997–1005. doi: 10.1371/journal.pbio.0050114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinert LA, Araujo-Jnr EV, Ahmed MZ, Welch JJ. The incidence of bacterial endosymbionts in terrestrial arthropods. Proc R Soc Lond B Biol Sci. 2015;282:20150249. doi: 10.1098/rspb.2015.0249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Werren JH, Baldo L, Clark ME. Wolbachia: master manipulators of invertebrate biology. Nat Rev Microbiol. 2008;6:741–751. doi: 10.1038/nrmicro1969. [DOI] [PubMed] [Google Scholar]
- Zheng B, Tang M, Yu J. Modeling Wolbachia spread in mosquitoes through delay differential equations. SIAM J Appl Math. 2014;74:743–770. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
S1 File. Appendix A. Effect of dispersal pattern and random fluctuations on travelling waves.
S2 File. Appendix B. Establishing a wave.


