Improving Prediction of Helix-Helix Packing in Membrane Proteins Using Predicted Contact Numbers as Restraints

Abstract

One of the challenging problems in computational prediction of tertiary structure of helical membrane proteins (HMPs) is the determination of rotation of α-helices around the helix normal. Incorrect prediction of rotation of α-helices around the helix normal substantially disrupts native residue–residue contacts while inducing only a relatively small effect on the overall fold. To address this problem, we previously developed a predictor for residue contact numbers (CNs), which measure the local packing density of residues within the protein tertiary structure. In this study, we tested the idea of incorporating predicted CNs as restraints to guide the sampling of helix rotation. For a benchmark set of 15 HMPs with simple to rather complicated folds, the average contact recovery (CR) of best-sampled models was improved for all targets, the likelihood of sampling models with CR greater than 20% was increased for 13 targets, and the average RMSD100 of best-sampled models was improved for 12 targets. This study demonstrated that explicit incorporation of CNs as restraints improves the prediction of helix-helix packing.

Introduction

Helical membrane proteins (HMPs) are essential components of cells. They play crucial roles in orchestrating the interactions of the cell with its environment; for example, by mediating cell signaling upon binding of ligands, regulating ion gradients, and facilitating the transfer of molecules across the cell membrane. It was estimated that 20–30% of genes in most genomes encode HMPs.¹ In addition, about 50% of therapeutics on the market target HMPs.² The availability of a three-dimensional (3D) structure of a HMP not only improves our understanding of how the protein works at the atomic level³ but also facilitates the development of new therapeutics.^4–6 Despite great progress in experimental techniques for determining HMP structures, only ~2 % structures in the protein databank are HMPs,⁷ highlighting the fact that HMP structure characterization is still a challenge. Further, experimental data for HMP are often of limited resolution, requiring computational methods to elucidate atomic-level details. Similarly, not all biologically relevant conformations of HMPs – which tend to be very flexible – can be studied experimentally. Likewise, accurate computational methods for HMP structure prediction are a complement to existing experimental techniques to enable HMP structure determination from limited experimental data.^8–9

A commonly used computational approach for predicting protein tertiary structure is comparative modeling. However, a sequence identity of at least 25% between target and template proteins is recommended to give reliable models.¹⁰ Because the fold of most HMPs are unknown and it was estimated that comparative modeling covers at most 10% of HMPs,¹¹ a few de novo methods have been developed, such as Rosetta-Membrane¹² and BCL::MP-Fold.⁷ Rosetta-Membrane assembles models helix-by-helix starting from a helix near the middle of the protein.¹² For HMPs with ~150 residues or less, Rosetta-Membrane achieved RMSD100 (root-mean-square distance normalized to a sequence of 100 residues) values of < 4 Å to experimental structures. However, the prediction accuracy with respect to helix rotation around the main axis was either not evaluated or very poor.⁷ BCL::MP Fold uses secondary structure element (SSE) pools and inserts helices across the membrane to build complete models. It achieved RMSD100 values to the experimental structure in the range of 3 to 8 Å for most benchmark HMPs.⁷ For models assembled by BCL::MP-Fold, even though TMHs are predicted to span the membrane with the correct topology, ~40% were reported to contain helices with incorrect rotation.⁷ For example, contact-forming, buried residues are sometimes rotated toward the membrane. For HMP models to be useful in applications such as structure-based drug design, accurate modeling of helix rotation is essential.

One approach to improving the accuracy of de novo tertiary structure prediction is to incorporate restraints.¹³ These restraints may be experimental, such as NMR chemical shifts⁸ and electron-paramagnetic resonance (EPR) accessibilities,⁹ or computational, such as predicted residue residue contacts.^{11, 13–16} For example, Fischer et al. recently showed that using either experimental or simulated EPR accessibility increases the likelihood of sampling native-like HMP folds and improves the accuracy of predicting helix rotations.⁹ Residue residue contacts derived from experiments or accurate computational predictions also provide substantial guiding information for sampling. For instance, Evfold_membrane developed by Hopf et al. enables de novo prediction of tertiary structures of 25 HMPs by incorporating amino acid covariation extracted from the evolutionary sequence record.¹¹

Residue contact number (CN) is a real-valued quantity that measures the degree of local packing of a residue within the protein tertiary structure. The CN of a given residue was originally computed by applying a clear distance cutoff and considering indiscriminately residues within the cutoff.^17–18 Later improvements incorporated various distance-dependent weighting schemes to account for the distance-dependent nature of residue–residue interactions.^19–21 CNs have been used to derive protein dynamic properties such as B-factor profile.²⁰ Studies have also shown that CN is the main structural determinant of site-specific substitution rates of proteins.²² Although it has been suggested that CNs could help in tertiary structure prediction, to our knowledge, no studies on tertiary structure prediction have explicitly incorporated CNs.

The CNs of interfacial TMHs (peripheral TMHs of a helical bundle) follow a signature periodic trend. Importantly, the CN signature of a TMH is tightly coupled to its rotation: even a small perturbation of the helix rotation will disrupt the CN signature. Hence, the CN signature of a TMH should give a strong constraint over its rotation. However, experimental CNs are not available until the tertiary structure of the protein is determined. Very recently, we developed a dropout neural network-based method, BCL::TMH-Expo, specifically for predicting CNs for HMPs.²³ CNs predicted by BCL::TMH-Expo correlate well with CNs computed from experimental structures and mirror exposure patterns of TMHs.²³ In this study, CNs predicted by BCL::TMH-Expo were incorporated into the empirical scoring function of BCL::MP-Fold in the form of restraints to improve prediction of helix helix packing. We tested this method on a set of 15 benchmark HMPs that span a wide range of fold complexity.

Materials and Methods

Benchmark Set

A set of 15 multi-spanning HMP subunits were carefully selected to assess whether using CN restraints can improve the prediction of helix helix packing. This set consists of HMP subunits that are both structurally and functionally diverse (Table I). Pairwise sequence identity is 30% or less. Sequence length ranges from 156 to 467 residues. The number of TMHs ranges from 4 to 10. As a measure of the size of transmembrane domains, the number of TMH residues were also computed for each target. None of these HMPs was used in the training set of BCL::TMH-Expo or had a sequence identity of more than 30% to any of the HMPs in the training set of BCL::TMH-Expo. This benchmark set contains diverse folds ranging from simplistic four-helix bundles and 7-TM receptors, up to proteins with 10 TMHs or helices in reentrant regions. Six of these HMPs are homo-oligomers. Due to the complexity of folding oligomers, we limited the scope of the present investigation to consider only a single subunit of each oligomer.

Table I.

Summary of the benchmark set

PDB ID	Structure Method	Resolution	Length	TMH	TMH Residue	PCC	MAE	Oligomeric State
1OED	EM	4.0	227	4	104	0.35	2.23	Homopentamer
1OKC	X-ray	2.2	292	6	214	0.39	2.37	Monomer
1PV6	X-ray	3.5	189	6	163	0.62	1.66	Monomer
1PY6	X-ray	1.8	249	7	177	0.72	1.29	Monomer
1U19	X-ray	2.2	348	7	173	0.58	1.63	Monomer
2BL2	X-ray	2.1	156	4	119	0.65	2.42	Homo 10-mer
2K73	NMR	NA	164	4	99	0.45	1.78	Monomer
2O9G	X-ray	1.9	234	6	166	0.69	1.74	Homotetramer
2Y01	X-ray	2.6	315	7	185	0.76	1.45	Monomer
3M71	X-ray	1.2	314	10	242	0.85	1.33	Homotrimer
3QAP	X-ray	1.9	239	7	168	0.69	1.35	Monomer
3UG9	X-ray	2.3	333	7	194	0.45	1.75	Homodimer
3UON	X-ray	3.0	467	7	183	0.66	1.60	Monomer
4A2N	X-ray	3.4	194	5	123	0.58	1.67	Monomer
4O6Y	X-ray	1.7	230	6	156	0.58	1.55	Homodimer
Mean			265	6.6	164	0.60	1.72

PCC: Pearson correlation coefficient; MAE: mean absolute error; EM: electron microscopy; X-ray: x-ray diffraction; NMR: nuclear magnetic resonance; NA: not applicable

Computation of Experimental and Predicted Contact Numbers

The details of the algorithm for computing CNs from experimental strictures can be found in two previous studies.^{21, 23} Briefly, the experimental CN of residue i was computed as a weighted sum of contacts contributed by residues over the entire protein:

$${\text{CN}}_{\mathrm{i}}=\sum _{\mathrm{j}\in \mid \mathrm{j}-\mathrm{i}\mid >3}^{\mathrm{n}}{\mathrm{w}}_{\text{ij}}$$

where w_ij is the contribution made by residue j and is assigned in a distance-dependent manner such that short-range contacting residues have higher contribution than long-range contacting ones. Residues whose C_β atom is within 4.0 Å to the C_β atom of the residue of interest are assigned a contribution of 1.0; those with a distance longer than 11.4 Å are assigned a contribution of 0. Any residue 4–11.4 Å is assigned a contribution between 0.0 and 1.0 according to a smooth transition function.²¹ Only residues separated by more than three residues along the sequence were considered in the calculation to reduce the bias due to sequence proximity and local secondary structure. Experimental CNs were calculated based on structures retrieved from the OPM (Orientations of Proteins in Membranes) database.²⁴

Although a relatively low sequence identity (30%) was maintained while compiling a list of benchmark protein chains to reduce the homology between the modeling benchmark set and the training set for BCL::TMH-Expo, such level of sequence identity alone may not be sufficient to exclude homology among protein chains. In fact, substantial remote homology could still exist at this level placing HMPs in the same structural superfamily.²⁵ Such remote homology between proteins in the training set and proteins in the modeling benchmark set can lead to an optimistic estimate of the performance for new folds. As a way of preventing such optimism, the original training set for BCL::TMH-Expo was partitioned such that each SCOP superfamily²⁶ forms its own subset that contains all its members and no members from other SCOP superfamilies. Predicted CN of each residue of a modeling benchmark protein was then obtained through a specific variant of the neural network-based CN predictor BCL::TMH-Expo. This variant was trained using all the proteins obtained after excluding the subset of proteins that share the same SCOP superfamily as the modeling benchmark protein from the original training set of BCL::TMH-Expo. For example, for predicting the contact numbers for 3UON, all proteins that are in the same SCOP superfamily as 3UON were removed from the original training proteins of BCL::TMH-Expo and a neural network was trained using the remaining proteins. The contact numbers were then predicted using this retrained neural network. This strategy was applied to each protein in the modeling benchmark set. Note that BCL::TMH-Expo method is a dropout neural network-based algorithm that predicts CNs for HMPs. It uses the position-specific scoring matrix (PSSM)²⁷ derived from multiple sequence alignment (MSA) by PSI-BLAST²⁸ as predictive features and outputs residue-specific CN. The MSA for each protein chain in the benchmark set was obtained by searching the UniRef50²⁹ non-redundant sequence database with PSI-BLAST for five iterations.²⁸ The E-value inclusion threshold was set to 10⁻². Floating point-valued PSSM was generated from PSI-BLAST checkpoint files using the source code (chkparse.c) adapted from PSIPRED.³⁰ Predicted CN was obtained by feeding the floating point-valued PSSM to BCL::TMH-Expo.

Incorporating CNs as Restraints in Folding Simulations

The de novo membrane protein structure prediction algorithm BCL::MP-Fold⁷ developed by adapting the original algorithm BCL::Fold³¹ for membrane proteins was used to assemble 3D models. BCL::MP-Fold assembles 3D models by drawing TMHs from a pool of predicted TMHs. TMH pools were created from predictions made by the combined membrane association and secondary structure predictor BCL::MASP.³² A Monte Carlo minimizer with Metropolis criterion³³ was used for sampling models with low energy. To use CNs to guide sampling of helix-helix packing, a CN-based penalty score was added to the knowledge-based scoring function of BCL::MP-Fold:

$$\mathit{Score}=\sum _i{w}_i\times S_i+w_p\times \mathit{Penalty}$$

where S_i represents each of the individual knowledge-based potentials previously derived and w_i is the associated weight. These potentials have been detailed in prior studies.^{7, 34} The restraint scoring term was defined using the following formula:

$$\mathit{Penalty}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\delta }_i^2}$$

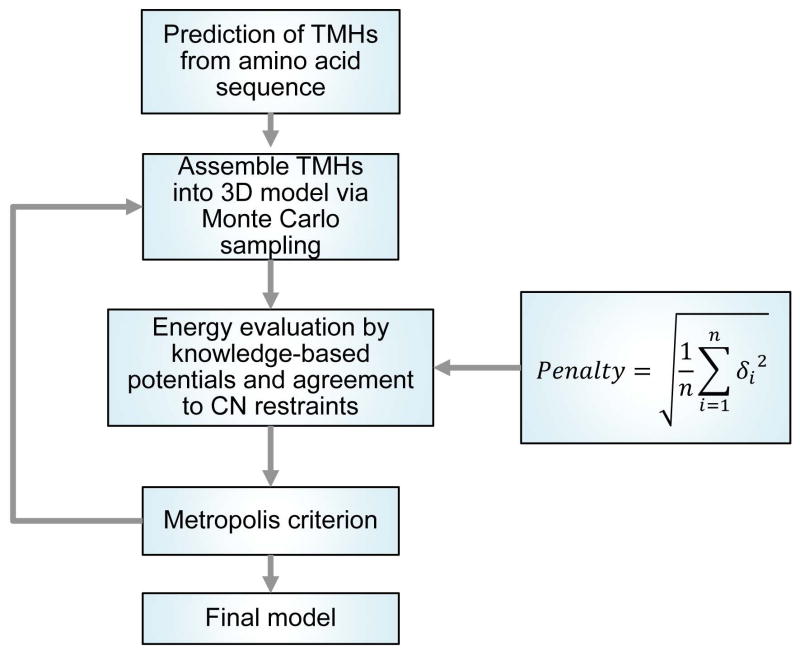
where n is the number of residues in the assembled structural model, δ is the difference between experimental CN or predicted CN and CN calculated from the assembled structural model. w_p is the corresponding weight of the penalty. An optimal balance between the knowledge-based potentials and the penalty score is critical for correcting helix rotation while sampling native-like folds. If the weight for the restraint penalty is too low, its capacity of correcting helix rotation is reduced, if the weight is too high, it dominants other scoring terms. An empirical approach, in which a range of w_p values were systematically tested in preliminary sampling, was used to determine a near-optimal weight. Finally, five thousand models were assembled for each target in the benchmark set. The procedure for generating 3D models is summarized in Figure 1.

Figure 1.

Protocol for assembling 3D models. BCL::MP-Fold predicts the tertiary structure of a HMP by assembling predicted TMHs in the 3D space. In the first step, the TMHs are predicted using the neural network-based membrane association and secondary structure prediction algorithm BCL::MASP. Predicted TMHs are assembled into a 3D model, and perturbed using a Monte Carlo sampling algorithm. The energy of the model after each perturbation is evaluated by knowledge-based potentials and agreement to CN restraints. The perturbation is subjected to the Metropolis criterion and is either accepted or rejected depending on the difference between the energies before and after the perturbation. This process is repeated for a specific number of iterations or until the maximum number of 2000 iterations without energy improvement is reached.

Metrics for Measuring of Model Quality

Root-mean-square distance (RMSD) gives a useful impression of the similarity between two structures if there is only a slight difference between their conformations. Unfortunately, a small perturbation in just one part of the protein (for instance, off position of a short loop) can lead to a large RMSD and it would seem that one structure substantially differs from the other. In order to address this issue, several quality measures have been introduced among which RMSD100 ³⁵ is commonly used. RMSD100 is a normalized, sequence length-independent version of RMSD calculated using:

$$\mathit{RMSD}100=\frac{\mathit{RMSD}}{1+ln\sqrt{\frac{n}{100}}}$$

where n is the number of residues superimposed. Using RMSD100 as an indicator of structural variability reduces the influence of the intuition that larger proteins are more likely to differ from one another.³⁵ In this study, RMSD100 was computed over the C_α atoms of all TMH residues.

A metric called contact recovery (CR), defined as the percentage of native contacts recovered in the assembled 3D model, was used to assess the quality of helix rotations in our previous study.⁷ However, the previous definition does not account for false positive contacts (FPC), which may be prevalent in 3D models assembled in a globular shape when the real shape of the protein is extended or rod-like and it has helices or strands that are somewhat “detached” from its main domain. In such cases, these “detached” secondary structure fragments could potentially be packed against the main domain of the protein by the folding algorithm, and thus, making a substantial fraction of FPCs. Thus, we redefined CR as the F1-score. Being the harmonic mean of precision and recall, the F1-score accounts for FPCs by weighting precision and recall equally:

$$\mathit{Contact}\mathit{Recovery}=\frac{2\times \mathit{Precision}\times \mathit{Recall}}{\mathit{Precision}+\mathit{Recall}}$$

where

$$\mathit{Precision}=\frac{\mathit{TPC}}{\mathit{TPC}+\mathit{FPC}}$$

and

$$\mathit{Recall}=\frac{\mathit{TPC}}{\mathit{TPC}+\mathit{FNC}}$$

TPC (true positive contacts) denotes the number of contacts observed in the experimental structure that are correctly predicted in the assembled model and FNC (false negative contacts) is the number of contacts in the experimental structure that are missed in the assembled model. Two residues are considered in contact if they are separated along the sequence by at least 12 residues and the distance between their C_β atoms is within 8 Å. CR reaches its best value at 100% and worst at 0%.

Computation of Enrichment

The enrichment was used to measure how capable a scoring function is to select the most accurate models from a pool of models. To calculate enrichment, models of a given set S are sorted by their CR values. The top 10% of the models with the highest CR values are put into the set T (true) and the rest of the models are put into the set F (false). The models in S are then sorted by their evaluated score. The top 10% of models with the lowest score are put into the set P (positive) and the rest are put into the set N (negative). The intersection of sets T and P are models that are correctly identified by the scoring function and referred to as TP (true positives). The intersection of sets F and P are models that are incorrectly identified by the scoring function and are referred to as FP (false positives). The enrichment value is then computed using the following formula:

$$\mathit{Enrichment}=\frac{TP}{TP+FP}/\frac{P}{P+N}$$

Intuitively, $\frac{P}{P+N}$ represents that probability of obtaining a native-like model when choosing a model from S at random, whereas $\frac{TP}{TP+FP}$ represents the probability of obtaining a native-like model when choosing from a set of models below an energy cutoff. By our experimental design, $\frac{P}{P+N}$ has a constant value of 0.1, and therefore, the maximum enrichment value that can be achieved is 10.

Results and Discussion

Predicting CNs for HMPs in the Benchmark Set

Table I shows the Pearson correlation coefficient (PCC) between experimental and predicted CNs as well as the mean absolute error (MAE) of predicted CNs for each target in the modeling benchmark set. The average PCC and the average MAE over the modeling benchmark set were 0.60 and 1.72 respectively. Notably, the CNs for three proteins, namely 1PY6, 2Y01, and 3M71, were predicted with a PCC > 0.70. Whereas, for 1OED, 1OKC, 3UG9, and 4A2N, the PCCs were below 0.50. Factors affecting the accuracy of CN prediction include oligomeric state, whether the protein chain is bitopic, and other factors that had been discussed previously in detail.²³ To illustrate the agreement between experimental and predicted CNs and visualize the predictions, the experimental and predicted CNs of 1PY6 were plotted and mapped onto its experimental structure. As shown in Figure 2a, the predicted CNs of 1PY6 are in close agreement with experimental CNs, particularly in transmembrane regions (vertical gray bars). As expected, predicted CNs generally distinguish between the exposed and buried faces of helices (Figures 2b and 2c). We, therefore, reasoned that the native rotation of helices can be confined by forcing them to satisfy predicted CN, thus improving the prediction of helix helix packing.

Figure 2.

Agreement between experimental and predicted CNs of 1PY6. a) Experimental and predicted CNs plotted against residues sequence positions, b) Experimental CNs mapped onto structure; c) Predicted CNs mapped onto structure. Color scheme in b) and c): as CN increases, color changes gradually from blue to red. Only TMHs are shown.

Incorporation of CNs Significantly Improved CR

Experimental CNs were tested as restraints to estimate an upper bound on the performance enhancements using CNs as restraints. The following three CR-based parameters were compared among the three simulation groups (E: with experimental CNs, P: with predicted CNs, N: without CNs):

• β_CR: the highest CR achieved,

• μ_CR: the average of the 10 highest CR values,

• π₂₀: the percentage of models with a CR greater than 20%,

β_CR and μ_CR measure how accurate the best-assembled models can be, whereas π₂₀ measures how often an accurate model can be sampled.

As summarized in Table II, model quality is generally improved using CNs as restraints. Specifically, μ_CR is improved for all targets when models were assembled using predicted CNs as restraints, and π₂₀ is improved for all but two targets (1OKC and 2O9G). β_CR is improved for all targets except 4O6Y and by an average amount of 8.07% and μ_CR is improved by an average amount of 8.04% compared to folding without CN restraints. A substantial increase in μ_CR (>5%) is seen for 10 of the 15 targets, with 4 of the targets (1PY6, 2K73, 3QAP, and 4A2N) showing over 10% of improvement. By using CN restraints, not only the best models are more accurate, but the probability that accurate models are sampled is also increased. For example, comparison of π₂₀ among groups shows that π₂₀ is increased by 6.75% on average when folded with predicted CNs compared to folded without CNs. It is worth noting that for 3 targets (2Y01, 3M71, and 3UON), models with CR greater than 20% were not sampled (π₂₀ = 0) without CN restraints but sampled with noticeable frequency with predicted CNs as restraints. Experimental CNs further improve CR results, for example, β_CR is improved by an average amount of 17.78% when using experimental CNs as restraints. Both experimental and predicted CNs enable strongly significant improvements in CR of folded protein models (p < 0.01, paired t-test).

Table II.

Summary of contact recovery

	βCR (%)			μCR (%)			Relative Improvement in μCR (%)	π20 (%)
Target	E	P	N	E	P	N	$\frac{{\mathrm{\mu }}_{CR(P)}-{\mathrm{\mu }}_{CR(N)}}{{\mathrm{\mu }}_{CR(N)}}\times 100$	E	P	N
1OED	73.10	38.02	28.93	70.59	32.88	23.47	40.09	51.77	5.17	0.33
1OKC	18.34	10.78	9.96	14.81	9.14	8.17	11.87	0.00	0.00	0.00
1PV6	31.55	30.02	21.90	26.93	23.09	17.06	35.35	1.37	0.35	0.03
1PY6	54.65	41.86	22.31	44.45	35.56	20.08	77.09	13.01	10.31	0.11
1U19	30.28	25.31	20.46	26.98	23.59	16.57	42.37	2.43	1.87	0.04
2BL2	68.40	59.29	54.50	66.78	55.22	49.63	11.26	76.26	50.98	29.80
2K73	59.49	49.33	30.70	57.04	44.13	27.82	58.63	72.04	33.58	1.45
2O9G	14.65	14.15	11.67	11.47	11.92	10.76	10.78	0.00	0.00	0.00
2Y01	36.15	21.97	19.42	30.60	20.70	17.30	19.65	1.94	0.19	0.00
3M71	23.46	23.58	17.14	21.77	20.35	14.42	41.12	0.54	0.20	0.00
3QAP	48.24	43.64	26.16	39.67	39.48	22.24	77.52	15.63	10.86	0.32
3UG9	38.38	35.90	24.16	35.98	30.08	20.66	45.60	14.71	6.77	0.14
3UON	32.37	21.81	19.16	25.93	20.02	16.01	25.05	1.11	0.09	0.00
4A2N	49.64	42.45	27.24	41.56	38.93	24.65	57.93	11.49	11.26	0.48
4O6Y	57.08	31.92	35.29	46.25	29.25	24.94	17.28	8.09	2.84	0.47
Mean	42.39	32.67	24.60	37.39	28.96	20.92	38.11	18.03	8.96	2.21

E: contact numbers computed using experimental structure; P: contact numbers predicted by neural network; N: no contact numbers; μ_CR improved by 5% or more (bold) and less than 5% (italic) when folded with predicted CNs.

Accurate Prediction of CNs is not Sufficient for Improving Prediction of TMH Rotations

Though a consistent improvement in CR is observed (Table II) when folded with predicted CNs as restraints, the improvement is not as substantial as with experimental CNs. In fact, the higher the PCC is of CN prediction, the closer the μ_CR obtained with predicted CNs (μ_CR(P)) is to that obtained with experimental CNs (μ_CR(E)). This relationship is illustrated by a scatter plot (Figure 3a) of the PCCs of CN prediction and the values of $\frac{{\mathrm{\mu }}_{CR(E)}-{\mathrm{\mu }}_{CR(P)}}{{\mathrm{\mu }}_{CR(E)}}$, which measures the relative difference between μ_CR(E) and μ_CR(P). And the correlation shows that there is still the need to improve the accuracy of CN prediction if one is to make the best of using contact number as restraints.

Figure 3.

a) Negative correlation (R = −0.57) between PCCs of CN prediction and relative differences between μ_CR(E) and μ_CR(P) μ_CR(P) values obtained with better CN predictions is closer to μ_CR(E) than those obtained with poorer CN predictions. b) μ_CR is negatively correlated with number of TMH residues. Orange dots indicate μ_CR(N) values and blue dots indicate μ_CR(E) values.

Intuitively, one might also expect that more accurate prediction of CNs leads to larger relative improvements in CR relative to folding without CNs. However, the correlation between PCCs and the values of $\frac{{\mathrm{\mu }}_{CR(P)}-{\mathrm{\mu }}_{CR(N)}}{{\mathrm{\mu }}_{CR(N)}}$, which measures the relative improvement in μ_CR(P) compared to μ_CR(N), is only very weak (0.28). For instance, μ_CR(P) is improved by 58.63% relative to μ_CR(N) for 2K73 although the accuracy of CN prediction for it is low (PCC: 0.45). Whereas for 2BL2 and 2O9G for which CN predictions are comparably accurate (PCCs are 0.65 and 0.69 respectively), μ_CR(P) is improved by only 11.26% and 10.78% relative to μ_CR(N) respectively. This suggests that other factors besides accurate CN prediction affect improvement in CR.

One intuitive factor is the size of proteins. In fact, as the size of transmembrane domain (measured by the number of TMH residues) increases it becomes more difficult to predict the correct rotation of helices. To illustrate this, the values of μ_CR(E) and μ_CR(N) are plotted against number of TMH residues. As shown in Figure 3b, μ_CR is negatively correlated with number of TMH residues (R = −0.78 for μ_CR(E) and −0.65 for μ_CR(N)). In addition to this negative correlation, improvement in μ_CR also becomes less substantial as transmembrane domain becomes larger. This is reflected on the fact that the gap between the two fitted lines shrinks as TMH residues increases. It is also worth noting that μ_CR(N) is below 20% for 7 out of 11 targets with more than 150 TMH residues, whereas μ_CR(E) is above 20% for all but two targets (1OKC and 2OG9).

Another factor is that some proteins might just represent easy cases whereas others difficult cases for the BCL::MP-Fold algorithm no matter whether CN restraints are incorporated or not. For easy cases, on the one hand, BCL::MP-Fold samples models with high CR even without CN restraints and for them it is difficult to improve substantially upon such a high CR with the current level of accuracy of CN prediction. For example, the membrane rotor of the V-type ATPase 2BL2 whose subunit adopts a four-helical bundle fold³⁶ can be considered an easy case for BCL::MP-Fold. As mentioned previously, its μ_CR(N) is as high as 49.63% even without CN restraints and the relative improvement in CR in terms of μ_CR is a comparably low value of 11.26%. For difficult cases on, the other hand, BCL::MP-Fold is not able to sample models with comparably high CR even experimental CN restraints partially due these proteins’ intrinsic topological complexity. In this modeling benchmark set, 1OKC and 2O9G represent such cases as all TMHs of 1OKC are kinked and 2O9G has two helices located in reentrant regions.^37–38

RMSD100 is Improved Using CN Restraints

While the primary motivation to introduce CNs as restraints was to improve prediction of helix rotation, an improvement in RMSD100 was also expected. To verify this, we compared the following parameters among the three simulation groups (E: with experimental CN, P: with predicted CN, N: without CN):

• β_RMSD100: the lowest RMSD100 achieved,

• μ_RMSD100: the average of the lowest ten RMSD100 values,

• π₅: the percentage of models with an RMSD100 value lower than 5 Å.

When using experimental CNs as restraints, β_RMSD100 was decreased for all targets and μ_RMSD100 was decreased for all but 2O9G. As discussed in the previous section, the subunit of the tetrameric aquaporin 2O9G is a special case in that it has two reentrant helices sitting on top of each other.³⁷ When using predicted CNs as restraints, a decrease in β_RMSD100 is seen for 13 targets and a decrease in μ_RMSD100 is seen for 12 cases. In terms of μ_RMSD100, a decrease of 0.5 Å or more is achieved for 4 targets and the most substantial improvement is a 0.79 Å decrease for 4A2N. Use of predicted CNs yields smaller, albeit still statistically significant (p < 0.05, paired t-test), improvements to μ_RMSD100. It is also interesting to note that models with RMSD100 within 5Å to experimental structures were assembled with noticeable frequencies for three targets (1PV6, 1U19, and 3UON) when using predicted CNs as restraints, whereas no such models were assembled without CNs as restraints.

Helix Rotation Accuracy is Improved by Predicted CN Restraints

To visualize the refinement of helix rotation using CN restraints in folding simulations, experimental CNs were mapped onto the experimental structure and 3D models with the lowest RMSD100 values was adopted. Helices with incorrect rotation would have buried residues exposed and exposed residues buried, thus by coloring buried and exposed residues differentially, incorrectly rotated helices in models can be readily identified. 1PY6 was selected, in part because its fold was generally predicted correctly even without the CN restraints. The CR values of the 1PY6 models with the lowest RMSD100 values are 44% and 7.3%, respectively when folded with predicted CNs and without CNs. As can be seen in Figure 4, without CN restraints, the buried face of TMH4 and that of TMH6 are rotated so as to be exposed by comparing the rotation of their buried face with that in the experimental structure in the best structure by RMSD100 (Figures 4a and 4c). This disrupted many native contacts between the buried residues of TMH4 and TMH6 (exemplified by red spheres), and likewise, leading to a significantly lower CR. With CN restraints, the rotations of TMH4 and TMH6 were consistent with the experimental structure (Figure 4b).

Figure 4.

Experimental CNs mapped onto experimental structures and folded models. a) experimental structure; b) model with lowest RMSD100 folded with predicted CNs as restraints; c) model with lowest RMSD100 folded without CN restraints. Color scheme: gradient from blue – fully exposed, red – fully buried. Only TMHs are shown for clarity. Spheres represent C_α atoms of buried residues of helices 4 and 6 in the experimental structure.

Increased Ability of the Scoring Function at Selecting Accurate Models

When folded without CN restraints, the average enrichment value over the benchmark set was 1.12. Using predicted CNs as restraints, enrichment was increased for 14 targets and the average enrichment was improved to 1.64 (Table IV). Paired t-test showed that enrichment is improved with statistical significance when folding with predicted CNs (p < 0.01). Indeed, enrichment exceeded 1.50 when folding with predicted CNs for 8 targets, vs. only 3 targets when folding without CN restraints. Enrichment was improved even further by using experimental CNs as restraints. For example, the average enrichment was increased to 1.92 and 13 targets had enrichment greater than or equal to 1.50. Due to the intrinsic inaccuracy of the scoring function in the approximation to the potential energy surface, it should be admitted that these enrichment values are indicative of a difficulty in selecting the most accurate models of the BCL::MP-Fold algorithm.³⁹ Nevertheless, the statistically significant improvement in enrichment indicates that CN restraints provide the scoring function with critical information about residue burial, often corresponding to mis-rotated helices.

Table IV.

Enrichment achieved with and without CN restraints

	Enrichment
Target	E	P	N
1OED	2.79	1.76	0.88
1OKC	0.51	0.97	0.71
1PV6	1.60	1.27	0.98
1PY6	1.95	1.97	1.16
1U19	1.61	1.29	1.05
2BL2	2.22	2.19	0.43
2K73	2.40	2.43	1.36
2O9G	2.22	1.05	1.08
2Y01	1.50	1.48	1.10
3M71	2.17	1.69	1.45
3QAP	2.20	1.75	1.60
3UG9	2.57	1.67	1.25
3UON	1.43	1.41	0.86
4A2N	1.61	1.89	0.80
4O6Y	1.97	1.80	2.14
Mean	1.92	1.64	1.12

E: contact numbers computed using experimental structure; P: contact numbers predicted by neural network; N: no contact numbers.

Limitations and Future Directions

Incorporating the burial status of residues has been shown to improve de novo structure prediction for soluble proteins.^{21, 31, 40} It is thought that the benefit of incorporating burial status in de novo structure prediction is even larger for HMPs ^41–42 because distinguishing buried from exposed residues in the apolar membrane environment is more challenging for non-specific scoring functions. Our results indicate that explicit incorporation of CN restraints into the BCL::MP-Fold algorithm significantly improves the prediction of TMH rotations and increases the accuracy of helix helix packing.

Our results indicate that using experimental CNs as restraints results in significantly more improvement in folding performance than using predicted CNs. This indicates that the performance of the CN predictor BCL::TMH-Expo is an important factor in the BCL::MP-Fold algorithm for HMPs, especially for simple folds such as 1OED. Although using predicted CNs improved folding outcomes for most targets, we found that accurate prediction of CNs does not guarantee a substantial improvement in CR or RMSD100 for every target. For example, only marginal improvement in CR was seen for 2O9G (Table II) even though its CNs were predicted with high PCC (Table I) and using predicted CNs did not improve RMSD100 for 1OKC or 2O9G (Table III).

Table III.

Summary of RMSD100

	βRMSD100 (Å)			μRMSD100 (Å)			π5 (%)
Target	E	P	N	E	P	N	E	P	N
1OED	1.88	3.69	3.70	2.08	3.85	3.89	13.47	3.80	4.28
1OKC	10.93	11.73	11.75	11.85	12.25	12.05	0	0	0
1PV6	4.34	4.14	5.09	4.92	4.72	5.49	0.16	0.16	0
1PY6	3.13	3.40	4.20	3.99	4.38	4.70	0.63	0.35	0.22
1U19	3.83	4.44	5.10	5.17	5.42	5.80	0.07	0.04	0
2BL2	2.14	2.36	2.77	2.25	2.84	2.86	11.99	8.14	13.67
2K73	3.01	3.59	3.82	3.06	3.72	4.03	32.44	10.76	7.07
2O9G	10.42	12.21	11.41	12.60	12.72	12.41	0	0	0
2Y01	4.94	5.06	5.26	5.21	5.46	5.76	0.04	0	0
3M71	5.63	5.75	5.94	6.05	6.26	6.36	0	0	0
3QAP	3.33	3.89	4.26	4.25	4.50	4.65	0.56	0.39	0.3
3UG9	3.36	3.24	4.57	3.76	4.19	4.83	1.54	0.77	0.28
3UON	3.70	4.94	5.30	5.17	5.30	5.81	0.13	0.02	0
4A2N	3.51	3.56	4.30	3.94	3.79	4.58	1.28	1.53	0.55
4O6Y	2.71	4.21	3.59	3.36	4.90	4.04	1.04	0.07	0.45
Mean	4.46	5.08	5.40	5.18	5.62	5.82	4.22	1.74	1.79

E: contact numbers computed using experimental structure; P: contact numbers predicted by neural network; N: no contact numbers; μ_RMSD100 improved by 0.5 Å or more (bold), 0.0–0.5 Å (italic), and no improvement (normal) when folded with predicted CNs.

1OKC and 2O9G represent intrinsically difficult targets for BCL::MP-Fold and probably for other methods too. The mitochondrial ADP/ATP carrier (1OKC) has its three odd-numbered TMHs kinked substantially by the presence of prolines,³⁸ whereas the aquaporin (2O9G) contains two reentrant regions.³⁷ Tertiary structure prediction for them was either not benchmarked by methods such as Rosetta-Membrane¹² or Evfold_membrane¹¹, or proved to be poor with BCL::MP-Fold. BCL::MP-Fold was not able to sample models remotely similar to their experimental structure. The best RMSD100 values for both are > 10 Å (Table III). BCL::MP-Fold does not typically accurately represent bent helices. It starts with an idealized, perfectly straight, pool of TMHs. While there are bending moves during the MC sampling that bend the TMHs, the current algorithm does not adequately capture the kinks and bends that are commonly seen in native TMHs. This limitation can be overcome with increased probabilities for the bending MC moves or more sophisticated bend moves that perturb several ϕ/ψ angles simultaneously by fitting to observed TMH fragments.

Conclusions

Contact number is a key property of amino acid residues of a protein structure that indicate their local packing density. We have demonstrated that explicitly incorporating contact numbers as restraints into the membrane protein structure prediction algorithm, BCL::MP-Fold, significantly improved prediction of helix helix packing. Specifically, contact number restraints helped sample more accurate helix rotation and fold, and improved the ability of the scoring function to select native-like models. The relative improvement from using CN restraints is often greatest for proteins with relatively simple folds, though improvements in contact recovery were observed across all proteins in the benchmark set when using predicted CNs. More accurate contact number predictors and structure sampling algorithms that can sample the correct fold of large proteins will be critical to future development of de novo tertiary structure prediction for HMPs.