Force generation by titin folding

Abstract

Titin is a giant protein that provides elasticity to muscle. As the sarcomere is stretched, titin extends hierarchically according to the mechanics of its segments. Whether titin's globular domains unfold during this process and how such unfolded domains might contribute to muscle contractility are strongly debated. To explore the force‐dependent folding mechanisms, here we manipulated skeletal‐muscle titin molecules with high‐resolution optical tweezers. In force‐clamp mode, after quenching the force (<10 pN), extension fluctuated without resolvable discrete events. In position‐clamp experiments, the time‐dependent force trace contained rapid fluctuations and a gradual increase of average force, indicating that titin can develop force via dynamic transitions between its structural states en route to the native conformation. In 4 M urea, which destabilizes H‐bonds hence the consolidated native domain structure, the net force increase disappeared but the fluctuations persisted. Thus, whereas net force generation is caused by the ensemble folding of the elastically‐coupled domains, force fluctuations arise due to a dynamic equilibrium between unfolded and molten‐globule states. Monte–Carlo simulations incorporating a compact molten‐globule intermediate in the folding landscape recovered all features of our nanomechanics results. The ensemble molten‐globule dynamics delivers significant added contractility that may assist sarcomere mechanics, and it may reduce the dissipative energy loss associated with titin unfolding/refolding during muscle contraction/relaxation cycles.

Introduction

Titin is a giant filamentous protein with multiple functions in the striated muscle: it is thought to be a template that sets the layout of sarcomeric organization1, 2, 3, 4; it is a sensor that gauges the sarcomere's mechanical status5, 6, 7, 8, 9; and most importantly it is a spring that defines the passive elastic properties of muscle.10, 11, 12, 13 Upon sarcomere stretch the I‐band section of titin is extended and force develops at the expense of reducing the protein chain's configurational entropy. Most of titin's physiological extension is attributed to the uncoiling of the PEVK domain (and the N2B unique sequence in cardiac muscle), and titin's globular domains are thought to remain folded.14, 15, 16 The ∼300 globular domains of titin are β‐barrel structures either of immunoglobulin (Ig) or fibronectin (FN) type.17, 18 In the I‐band, only Ig‐domains are found. Titin's globular domains can be unfolded by mechanical force in single‐molecule mechanics experiments.19, 20, 21 Given the stochastic nature of force‐driven biomolecular processes22, 23, 24 it has been a prevailing question whether titin's globular domains unfold under physiological conditions. Further, if domains unfold in situ, do they refold on the time scale of physiological muscle function? Recently we found, in single‐molecule mechanics experiments on full‐length titin molecules purified from skeletal muscle, that some domains in the proximal tandem‐Ig region of titin unfold at low, physiologically relevant forces.25 Furthermore, in situ domain unfolding has been detected in myofibrils, and it has been claimed, based on magnetic tweezers experiments on cloned titin fragments, that domain refolding may generate enough work to assist muscle contraction driven by myosin.26 This idea is debated, however, because the work done by titin‐domain folding may not be recruited fast enough.27

In the present work we manipulated skeletal‐muscle titin molecules with force‐ and position‐clamp optical tweezers to investigate the mechanisms of mechanically driven domain folding. At constant high forces (>100 pN) titin unfolded by stepwise extension. By contrast, at constant low forces (<10 pN) refolding was accompanied by large‐scale length fluctuations. Position‐clamp experiments directly demonstrated that the refolding of titin domains generates net force via rapid force fluctuations. Partial denaturation with urea revealed that net force generation is caused by ensemble folding of the elastically‐coupled domains, and the fluctuations arise because of a dynamic equilibrium between unfolded and molten‐globule states.28, 29, 30, 31, 32, 33 Monte–Carlo simulations indicate that molten‐globule dynamics within an ensemble of titin domains can generate a significant molecular contractility. Furthermore, the process may assist in minimizing the dissipative loss of mechanical energy during repetitive stretch and relaxation cycles.

Results

Individual molecules of skeletal‐muscle titin were manipulated with force‐clamp optical tweezers to reveal the molecule's folding mechanisms [Fig. 1(a)]. The N‐terminus of titin was held with a T12 anti‐titin antibody‐coated latex bead, whereas toward the other end the molecule was captured by using a bead coated with the photoreactive cross‐linker sulfo‐SANPAH. The T12‐bead was captured in the optical trap, while the photoreactive bead was manipulated with a movable glass micropipette by a feed‐back‐controlled piezo stage. Titin was mechanically unfolded and refolded in consecutive cycles of high and low constant‐force phases [Fig. 1(b)]. During the high‐force phase the extension of titin increased via distinctive steps [Fig. 1(b.i)], each of which corresponds to the discrete, all‐or‐none unfolding of a component globular domain.34 In the subsequent low‐force phase, contraction via distinctive steps could not be observed. Titin first contracted rapidly driven by an entropic collapse,30, 35 then large, up to 200 nm peak‐to‐peak extension fluctuations occurred [Fig. 1(b.ii)]. The extension fluctuation entails successive extension and contraction steps with no apparent pattern or frequency. In the subsequent high‐force phase titin again extended via discrete steps, and the steps began appearing at an extension essentially identical to that in the first high‐force phase. Thus, in this particular experiment essentially all the domains that unfolded in the first high‐force phase refolded during the low‐force period even though distinct contractile steps were absent.

Figure 1.

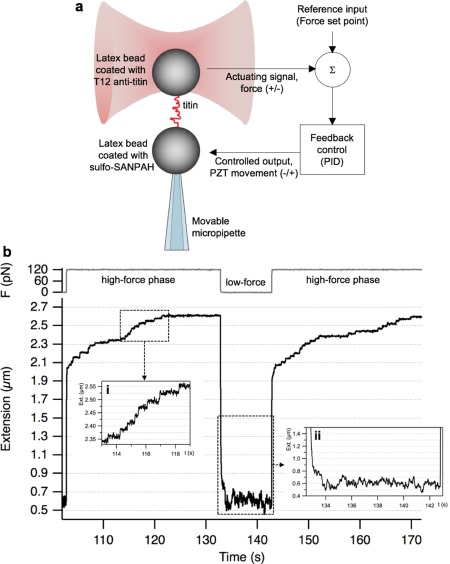
Manipulating individual titin molecules with force‐clamp optical tweezers. a. Experimental layout of titin manipulation and feedback control. b. Force and extension versus time trace of a single titin molecule recorded in a force‐clamp experiment. During the high‐force phase force was clamped at 120 pN, whereas during the low‐force phase it was 1 pN. Inset i, Extension steps corresponding to stepwise domain‐unfolding at high clamp force. Inset ii, Fluctuation of the molecular extension measured at low clamp force.

We quantitated the amount of refolded titin by measuring the extension (ΔZ) recovered during the low‐force phase [Fig. 2(a)]. At a given low clamp force (0.8 pN in this example) the recovered extension increased exponentially as a function of time [Fig. 2(a) inset], indicating that the mechanically‐driven refolding of titin domains follows first‐order kinetics. The amount of recovered extension also depended on the force at which titin was held during the low‐force phase [Fig. 2(b)]. Upon increasing the clamp force level to 10 pN no extension could be recovered, indicating that refolding was essentially completely inhibited. Notably, the extension‐contraction fluctuations were also dampened by the increased clamp force, suggesting that these fluctuations are manifestations of highly dynamic (i.e., nearly reversible) transitions along the folding pathway.

Figure 2.

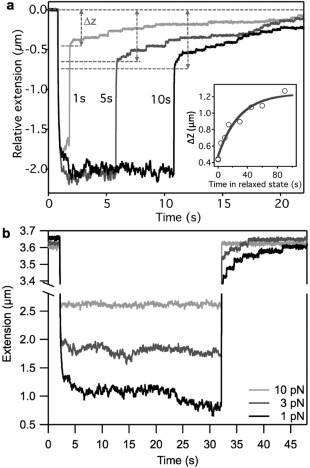
Titin refolding under mechanical load. a. Time dependence of titin refolding in force‐clamp experiments. Force was quenched (to 0.8 pN in this example) for varying amounts of time to allow for refolding to occur. Then the molecule was rapidly stretched to a high force level (115 pN) so as to assess the extent of refolding quantitated as the length of the refolded segment. Traces containing 1‐, 5‐ and 10‐second‐long refolding periods are shown. The extent of refolding was measured as the end‐to‐end length difference (ΔZ) of the manipulated molecular segment. ΔZ is the difference in extension just prior to force quench and the onset of the first unfolding step during re‐stretch (gray double arrows). Inset, Refolded titin length as a function of time in the quenched‐force state (1pN in this example). Data points were fitted with the equation ΔZ=ΔZ ₀ − Ae ^{− t/τ}, where ΔZ ₀ is maximal refolded length, the pre‐exponential factor A is the apparent refolded length at t ₀, and τ is the time constant of refolding. From the fit τ = 28.4 s was obtained. b. Extension versus time traces recorded at various refolding clamp forces. Traces recorded at clamp forces of 1, 3 and 10 pN are shown. Refolding of titin occurred only in the case of 1 and 3 pN clamp forces as indicated by the presence of unfolding steps in the successive high‐clamp‐force phase.

The details of the refolding process were investigated in position‐clamp experiments to circumvent the bandwidth limitations of the active force feedback (Fig. 3). Titin was first stretched with constant velocity to unfold its component globular domains then rapidly relaxed to allow refolding to occur. Finally, the molecule was restretched with constant velocity to assess the magnitude of domain refolding from the recovery of the force hysteresis [Fig. 3(a) and Supporting Information Fig. S1]. During the constant‐pipette‐position phase we monitored the force acting, via the refolding titin molecule, on the trapped bead. Force gradually increased on the time scale of a few seconds, indicating that the trapped bead was pulled in by the folding titin molecule. Forces up to 2 pN was generated in this experiment [Fig. 3(a)] at the expense of a mere 10 nm contraction (see Supporting Information Fig. S1). Fluctuations of force with peak‐to‐peak amplitude exceeding 0.5 pN, and easily discernible from thermal fluctuations (see Supporting Information Fig. S2), could be identified during this process [Fig. 3(a) inset], suggesting that titin domains fluctuate between contracted and extended conformational states. The force‐generation process could be followed in force versus extension graphs as well [Fig. 3(b)]. In titin which completely refolded during the waiting period of the position‐clamp experiment, the force‐generation process transferred the molecule from a long‐contour‐length state to a short‐contour‐length one [Fig. 3(b) inset]. We analyzed the kinetics of force generation as a function of initial force [Fig. 3(c)] by fitting the force versus time traces with a single‐exponential function (Supporting Information Fig. S3). Force generation was observed in the initial force range of 0–8 pN, and its rate decreased with the initial force [Fig. 3(c)]. The calculated force‐generation rate at an apparent zero force is 1.5 s⁻¹. The amplitude of force generation showed a weak positive correlation with the initial number of unfolded domains [Fig. 3(d)]. Our findings thus suggest that the magnitude of the force‐generation process scales with the number of domains involved and the process can be inhibited by raising the force titin is exposed to. Indeed, upon increasing the initial force during position clamp the refolded fraction, as judged from recovered force hysteresis, gradually decreased (Supporting Information Fig. S4). To explore the force‐generation process in greater detail, we performed position‐ramp measurements during which the titin molecule was allowed to shorten very slowly (Fig. 4). Force did not decrease continuously as expected for a purely elastic chain, but distinct force‐increment periods were observed. Furthermore, the locally averaged force fluctuated with rather large amplitudes. In the high‐force regime (∼6 pN) peak‐to‐peak amplitudes up to 0.5 pN were observed (Fig. 4 left inset). In the low‐force regime (∼2 pN) peak‐to‐peak amplitudes reaching 1 pN could be seen (Fig. 4 right inset). Notably, distinct states could be discerned in which the titin molecule spent time periods up to ∼100 ms. Force jumped back and forth between these states indicating that the underlying molecular process involves nearly reversible transitions between contracted and extended conformational states of titin's globular domains.

Figure 3.

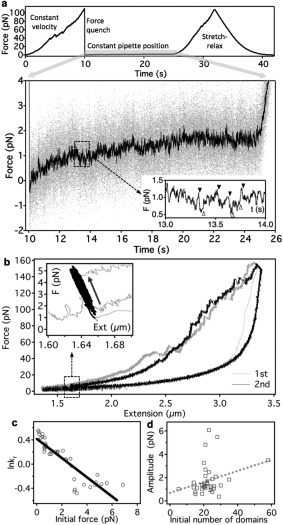
Force generation by titin folding. a. Position clamp experiment. Upper trace, Force versus time plot displaying the experimental protocol. Following a stretch period at constant velocity, force is rapidly quenched by quickly moving the pipette back to its initial position. Then the pipette is held in a constant position while the force on the trapped bead is monitored. The protocol ends with a complete stretch‐relaxation cycle to monitor refolding. Lower trace, Force versus time trace recorded during the position‐clamp phase. Grey and black traces correspond to raw and 100‐point median‐filtered data, respectively. Inset, Enlarged view of the framed area showing force fluctuations consisting of contraction (filled arrowheads) and relaxation steps (empty arrowheads) with sub‐pN amplitude. b. Force versus extension curves reconstituted from a position clamp experiment. Gray and black traces correspond to the first and second nanomechanical cycles, respectively. In between the two cycles the pipette position was clamped so that the initial force was 1.2 pN. Inset shows the gradual increase in force (∼4 pN, black arrow) during the 25 s waiting period in between the mechanical cycles. c. Rate of force generation (shown as lnk_r) as a function of initial force during the waiting time in position clamp experiments. Data obtained on 38 molecules are shown. Force generation rates were obtained from single‐exponential fits to the force versus time data (see Supporting Information Fig. S1). The rate data were locally averaged with a smoothing window (width 20 points). Black line is linear fit to the lnk_r versus force data. From the y‐intercept a zero‐force rate of 1.5 s⁻¹ was calculated. d. Force amplitude, corresponding to the maximum force generated during position clamp experiments, as a function of the initial number of unfolded domains. Raw data are shown. Dotted line is linear fit to the data.

Figure 4.

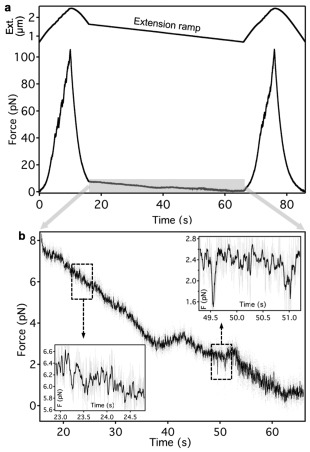
Position‐ramp nanomanipulation of titin. a. Experimental protocol. Titin was first stretched and relaxed with high velocity (pipette movement 200 nm/s), then the pipette was gradually moved toward the optical trap with a rate of 10 nm/s so as to allow titin to shorten slowly. Upper trace, extension as a function of time. Lower trace force as a function of time. The titin molecule refolded completely during the extension‐ramp experiment as evidenced by hysteresis recovery (Supporting Information Fig. S5). b. Enlarged view of the extension‐ramp regime. Raw force data (gray) with superimposed median‐filtered data (smoothing window100‐points, black) are shown. Insets correspond to enlarged views of the boxed data regions.

Within a two‐state model of domain folding20 the contracted and extended conformations would correspond to the folded and unfolded states, respectively. However, because spontaneous domain unfolding is highly unlikely at low forces, the contracted conformation is most likely different from the consolidated folded state and represents a compact yet compliant molten‐globule intermediate.28, 29, 30, 31, 32, 33 Titin domains thus dynamically fluctuate between the molten‐globule and unfolded states at the low force level. Eventually the native domain structure becomes consolidated by transition toward the folded state, as evidenced by the partially recovered force hysteresis in the subsequent mechanical cycle (Supporting Information Fig. S1). Net contraction and force generation are hence driven by a shift of the titin domain population from the molten‐globule toward the folded state, but the force fluctuations are caused by a dynamic equilibrium between the molten‐globule and unfolded states.

We tested the possibility of the three‐state folding model in titin by inducing a chemical bias toward the molten‐globule and unfolded states with urea, a denaturant that destabilizes H bonds and hence the native structure (Fig. 5 and Supporting Information Fig. S6).36, 37 In 0.5 M urea net contraction and extension fluctuations were observed in force‐clamp experiments in titin that completely refolded during the low‐force period [Fig. 5(a)]. In titin that refolded only partially, net contraction was smaller but the extension fluctuations persisted [Fig. 5(b)]. In the presence of 4 M urea net force generation [Fig. 5(c)] and contraction (Supporting Information Fig. S6) were alleviated but the force fluctuations persisted, indicating that even though the consolidation of the folded state was blocked, dynamic transitions between the molten‐globule and unfolded states were still possible. Thus, in the explored concentration range (0.5–4.0 M) urea progressively prevented the refolding of titin but conformational fluctuations were present, indicating that transitions between the unfolded and molten‐globule states were still possible.

Figure 5.

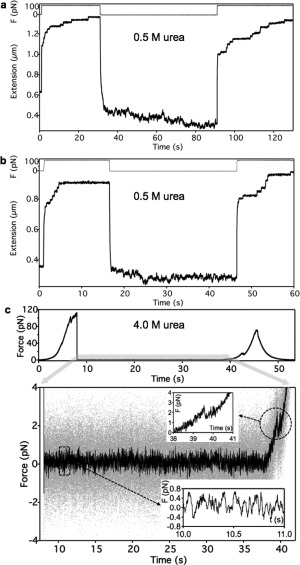
Nanomanipulation of titin in the presence of urea. a. Force‐clamp experiment in the presence of 0.5 M urea. Titin completely refolded during the low‐force rest phase. b. Force‐clamp experiment in the presence of 0.5 M urea. Titin partially refolded during the low‐force rest phase. c. Position‐clamp experiment in in 4M urea. Upper trace, Experimental protocol. Lower trace, Force versus time trace recorded during the position‐clamp phase. Grey and black traces correspond to raw and 100‐point median‐filtered data, respectively. Lower inset, enlarged view of the framed area showing force fluctuations. Upper inset, enlarged view of the encircled area showing a sawtooth‐shaped transition at ∼2 pN corresponding to the disruption of a low‐stability, transient structure.

The three‐state model may be represented with free‐energy minima, corresponding to the folded, molten‐globule and unfolded states, in the conformational space. A schematic section of this space, demarcated by the force vector that defines the reaction coordinate, is shown in Figure 6a. Conformational equilibrium is determined by the relative free energy levels of the states, and the rate of transition (k) between the states by the height of the barriers separating them. Mechanical force acting along the length (reaction) coordinate tilts the energy landscape,22 thereby altering the transition rates and the conformational equilibrium. At high forces, transition toward the unfolded state is strongly favored so that the molten‐globule state stays unpopulated and is passed unnoticed. By contrast, during refolding, at low (<10 pN) forces the energy landscape becomes less tilted, and even an equilibrium between the molten‐globule and unfolded states may occur. In this equilibrium titin domains dynamically repopulate the contracted molten‐globule and extended unfolded states, which results in large fluctuations of molecular extension and hence fluctuations of mechanical force measured at the ends of the molecule. Notably, force may even feed back on the equilibrium via its effect on the energy landscape, thereby further shifting and fine‐tuning the equilibrium. What makes the picture even more complex is the notion that the energy landscape, hence the force‐dependent rate constants (k), are very likely different for each of the ∼300 globular domains18 comprising the titin molecule. Consolidation of the folded structure occurs by a transition from the molten‐globule state toward the folded which, because of its apparent irreversibility at low forces, reduces the concentration of domains available for the dynamic shuffling between the molten‐globule and unfolded states. As a result, a net contraction and force generation will occur. In the end, within a single molecule of titin the ensemble folding/unfolding kinetics of the serially linked globular domains determine the nanomechanical properties including the net force generated and the magnitude of the force fluctuations.

Figure 6.

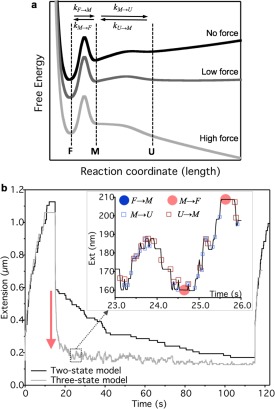
Model and simulation of molten‐globule dynamics during force‐dependent titin refolding. a. Schematics of the titin folding landscape based on the three‐state model. F, M and U correspond to the folded, molten‐globule and unfolded states, respectively. Arrows indicate reactions between the states with the force‐dependent rate k, the subscript of which refers to the direction of the transition (F→M, M→U, M→F and U→M for folded‐to‐molten globule, molten globule‐to‐unfolded, molten globule‐to‐folded and unfolded‐to‐molten globule, respectively). The length of the arrows, as shown in the figure, do not correspond to the actual rates. The landscape is tilted as force increases, and at low forces the free energies of the molten‐globule and unfolded states become similar. b. Monte–Carlo simulation of a force‐clamp experiment based on the classical two‐state (folded and unfolded) and the three‐state (folded, molten‐globule and unfolded) models, shown in black and gray traces, respectively. The time‐dependent protocol, similarly to that employed in the optical tweezers experiments (Figs 1‐3), is partitioned into an initial high‐force clamp (120 pN), followed by a low‐force‐clamp refolding phase (3.1 pN) and finally by high‐force‐clamp monitor phase (120 pN). Red arrow indicates the contraction gain in excess of the entropic collapse. Inset, Enlarged view of a section of the low‐force phase in the three‐state model. The transition steps are indicated with distinct markers to highlight the underlying processes. Notably, the M→U and U→M transitions are accompanied by lengthening (increasing extension) and contractile (decreasing extension), respectively, whereas the M→F transition does not result in significant change in extension due to the similar size of the molten‐globule and folded states. Because the actual extension change is determined not only by the intramolecular transitions but also by the simulated force feedback (see Supporting Information Fig. S7), variation is observed in the extension steps. At the low force F→M transitions are extremely rare.

We compared the two‐ and three‐state folding models adapted to titin by using Monte Carlo simulations [Fig. 6(b)]. While the two‐state model predicted stepwise contraction during refolding, the three‐state model recovered all the essential features of our experimental observations including the extension fluctuations and net contraction. Quite remarkably, the rapid shift of the domain population from the unfolded state toward the compact molten‐globule results in a contraction well in excess of the entropic collapse [Fig. 6(b) red arrow], indicating that titin is a true contractile protein of muscle.

Discussion

Full‐length titin molecules, purified from rabbit back muscle, were manipulated in the present work by using high‐resolution optical tweezers methods, to investigate the mechanisms of the force‐dependent refolding process. Our results indicate that a three‐state model that encompasses a compact molten‐globule intermediate more completely describes the folding of titin than a two‐state model. What might be the actual structural properties of the molten‐globule state of a titin domain? Immunoglobulin domains have been shown to display a molten‐globule conformational state under thermally partially denaturing conditions.33 To explore the partial denaturing effect of mechanical force, we carried our steered molecular dynamics simulations (SMD)38 using force‐clamp protocols on the I27 domain of titin (I91 in the new sequence nomenclature39), which has been shown to fold via a kinetic intermediate.40 Extension of I27 by 30 Å resulted in the separation of both the AB and A'G β‐strands. The latter is responsible for the appearance of a peak in the unfolding force spectrum of I27 in constant‐velocity pulling simulations (Supporting Information Movie S1).41 At this stage part of the N‐terminal is extended while the majority of the domain appears to largely preserve its tertiary structure [Fig. 7(a)]. Holding this partially extended I27 at a constant force with a coupled spring resulted in force‐dependent changes in end‐to‐end distance [Fig. 7(c)]. The exertion of small constant forces (0, 5, and 20 pN) leads to a reduction of the end‐to‐end distance which stabilized after 20–30 ns of simulation [Fig. 7(c)]. The stabilized end‐to‐end distance is similar to that of the native domain structure at zero force. Contraction is the result of the movement of the structured C‐terminus toward the fixed N‐terminus, which was observable in all simulations at 0, 5 and 20 pN constant forces. In the time period of the simulations the B and G β‐strands did not approach the extended A and A' β‐strands, and the broken H‐bonds between the strands were not re‐established (Supporting Information Movie S2). Comparing the residue contact maps of the native [Fig. 7(d) left] and the extended domain [Fig. 7(d) right] revealed that contacts are broken not only between the C‐ and N‐termini [Fig. 7(a,b)] but also in the middle of the sequence, indicating that the structured part of the extended I27 is less tightly packed than in the native I27. We suggest that the loosened β‐barrel configuration, in which one of the β‐strands is dissociated from the rest of the barrel, is the archetypical molten globule state of titin's globular domains. Because the effective contour length of this structure (∼8 nm) is significantly smaller than that of the unfolded domain (∼28 nm), the extension fluctuations observed during the low‐force phase of our nanomechanical experiments (Figs. 1 and 2) are well explained by a dynamic equilibrium between the unfolded and molten‐globule states. The conclusions of the above SMD simulation should be treated with caution, however, for a number of reasons: (1) I27 is one of the most stable domains in titin42 that requires large (150–250 pN) forces to unfold, therefore it might not be truly representative of all titin domains; (2) additional mechanisms, such as disulphide bridges,43 may stabilize the domain structure; (3) there is a gradient of mechanical stability among the globular domains in titin,25, 34 therefore the different domains are likely to display different structure and dynamics, and (4) the spatial map of mechanical stabilities along titin, although thought to be random,34 is not precisely known, therefore the contribution of the molten‐globule dynamics to sarcomeric behavior is yet to be understood.

Figure 7.

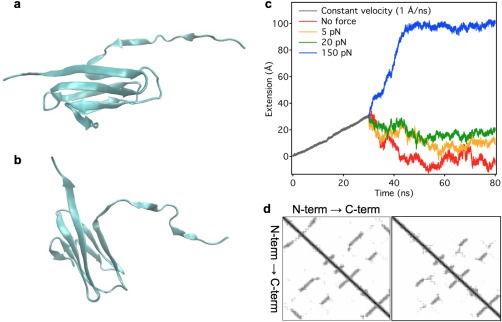
Steered molecular dynamics simulations of the titin I27 (I91 in the new nomenclature39) domain. a. Structure obtained after constant‐velocity pulling to 30 Å extension. b. Structure of I27 obtained after further stretch of the domain for 50 ns with a constant 5 pN force. c. Extension versus simulation time function of I27 obtained in a two‐phase experiment: constant‐velocity stretch followed by a constant‐force phase. In the initial, 30‐ns‐long phase (dark gray) the domain was extended with a rate of 1 Å/ns. In the constant‐force phase the domain was held at either 0 (red), 5 (orange), 20 (green) or 150 pN (blue) of force, respectively. d. Residue contact map of the native (left) and extended structures (right) of I27. The latter map corresponds to the structure with 30 Å extension and the map does not change during the 50 ns simulations applying 0, 5 and 20 pN constant force.

What might be the physiological function of titin dynamics back and forth along the folding pathway? It has been suggested that the folding of titin can produce mechanical work that assists active muscle contraction26. However, the occurrence and putative function of titin folding/unfolding in situ under physiological conditions has been strongly debated,13, 16, 26, 44, 45 for two main reasons. First, immunoelectron microscopic analyses using sequence‐specific antibodies that demarcate the boundaries between canonical structured (e.g., tandem‐Ig) and unstructured (e.g., PEVK) regions in titin16 were unable to demonstrate an increase in the contour length of the structured regions, expected to be caused by domain unfolding, even under extensive stretch procedures. However, as we show here [Fig. 6(b)], a shift of the domain population from the unfolded state to molten globule provides added contractility so that titin shortens to a length nearly indistinguishable from that of the folded structure. Accordingly, the measured length of a titin section may not fully reveal its structural status. Even if the length of a canonical structured titin segment appears to reflect a folded state, the component domains may have been unfolded and then collapsed into the compact molten globule state. Thus, our results strongly favor the idea that folding/unfolding dynamics of titin, via the molten‐globule state, are present in situ in the sarcomere. Second, the work‐producing function of titin folding is debated on grounds of its power (rate of work delivery) in comparison with that of the motor protein myosin.27 Indeed, there are uncertain issues related to the overall energy balance of titin folding/unfolding. After all, titin folding, during sarcomere contraction, can recover only part of the work invested into its unfolding during sarcomere stretch. Repetitive stretch‐relaxation cycles on single full‐length titin molecules are accompanied by a large force hysteresis, indicating that much of the mechanical energy invested into titin unfolding is lost as heat, and only a very small amount of the energy is recovered during refolding.19 Accordingly, dragging titin domains through repetitive unfolding‐refolding cycles is a very inefficient process, even if the transition from the unfolded to the folded state can indeed generate some work. The dissipative energy loss can be minimized, however, if some of titin's domains are kept in the molten‐globule state. An ensemble titin domain transition from the unfolded to molten‐globule state generates a contraction beyond entropic collapse and an associated force (hence mechanical work) [Fig. 6(b)], yet at the same time the molecule can be easily stretched, due to the compliance of the molten globule, to the unfolded state in the subsequent mechanical cycle. Such a dynamic transition between the molten‐globule and unfolded states may be particularly relevant and important in cyclically contracting tissues such as the cardiac muscle.

In conclusion, the ensemble folding/unfolding dynamics, via a compact molten‐globule state, play an important role in setting the nanomechanical behavior of the titin molecule. Besides generating force by added molecular contractility, molten‐globule dynamics may assist in minimizing the dissipative loss of mechanical energy during cyclic contractions of striated muscle.

Materials and Methods

Protein purification

Skeletal muscle titin was prepared from rabbit m. longissimus dorsi by using previously published protocols.19, 46 Use of rabbit as the source of specimen was approved by the Regional Ethics Committee (approval number: XIV‐I‐001/29‐7/2012). Purified titin samples were flash frozen in liquid nitrogen and stored at −80°C until further use. Except where noted otherwise, all chemicals were obtained from Sigma‐Aldrich.

Nanomanipulation of titin with optical tweezers

For nanomanipulation of titin we used procedures published previously.19, 25 Briefly, the Z‐line end of titin was captured with a 3.0 μm carboxylated latex bead (Kisker Biotech GmbH, Steinfurt, Germany) coated with the T12 antititin antibody. The other bead used was a 2.5 μm amino‐modified latex bead (Kisker Biotech GmbH, Steinfurt, Germany) coated with the photoreactive cross‐linker sulfo‐SANPAH (Thermo Scientific, Kvalitex, Hungary), providing a non‐sequence‐specific covalent linkage. One of the beads was captured in the optical trap, whereas the other one was held with a micropipette embedded in a custom‐built flow chamber mounted on a close‐loop piezoelectric stage (Nano‐PDQ375, Mad City Labs, Madison, WI, USA). Nanomechanical manipulation of titin was carried out with a custom‐built dual‐beam counter‐propagating photonic‐force optical tweezers apparatus19. Trap stiffness was ∼0.2 pN/nm. Instrument control was managed by using custom written LabView routines. Force was measured by calculating the change in photonic momentum with a resolution of ∼0.2 pN. Buffer condition was 25 mM imidazole‐HCl (pH 7.4), 200 mM KCl, 4 mM MgCl₂, 1 mM EGTA, 1 mM DTT, 20 μg/ml leupeptin, 10 μM E‐64, 0.1% NaN₃.

Force‐clamp experiments

In force‐clamp mode the force was held at a setpoint by stretching or extending titin via rapid movement (typically 20 μm/s) of the piezoelectric stage with custom written proportional, integrating, differential routines (bandwidth limited to 2.5 kHz by the resonance frequency of the stage). In a typical force‐clamp protocol a titin molecule was first rapidly stretched from its relaxed state (0 pN) to a length where the target force (∼120 pN) was reached; in a second phase the molecule was relaxed by quenching the force (1–10 pN) and allowed to refold for a pre‐adjusted time (1–10 s); finally, titin was re‐stretched to high force (∼120 pN) to monitor its folding status.

Position‐clamp experiments

In these experiments titin was stretch with constant velocity (250 nm/s) to reach a force above 100 pN to trigger domain unfolding. After this initial stretch phase, force was instantaneously quenched to 0 pN by the rapid movement of the micropipette (50 μm/s) and held at a constant position for 20–40 s. During the constant‐pipette‐position phase force was measured on the trapped bead with a sampling rate of 5 kHz. The position‐clamp was followed by a second constant‐velocity probe stretch to test for domain refolding measured as the recovered force hysteresis (see Supporting Information). Experiments were also carried out in buffer containing 0.5–4.0 M urea to chemically inhibit the refolding of titin domains and shift the conformational population toward the unfolded state. In some experiments, an position ramp was implemented instead of position clamp. In a position ramp, the pipette bead holding the end of titin was gradually moved as a function of time with a typical rate of 10 nm/s.

Monte–Carlo simulation

The global nanomechanical behavior of titin under constant force was modeled with Monte–Carlo simulations based on previously used algorithms.19, 25 A comparison was carried out between the two‐state and three‐state protein folding models. The two‐state model contained the folded and unfolded states, whereas the three‐state model contained, in addition, a molten‐globule state along the folding/unfolding pathway [see Fig. 4(a)]. The typical model titin molecule contained 40 globular domains serially linked with a 100‐nm‐long PEVK‐like domain with the properties of an unfolded protein chain. The simulation protocol contained three consecutive phases during which the extension of the protein chain was calculated as a function of time: (1) high‐force‐clamp phase (typically 120 pN), (2) low‐force‐clamp phase (typically 3.0–3.5 pN), and (3) high‐force‐clamp phase (typically 120 pN). Extension (Z) at the given force (F) was calculated based on the wormlike‐chain model of entropic elasticity47

$$\frac{{\text{FL}}_{\mathrm{P}}}{k_{\mathrm{B}}T}=\frac{Z}{L_{\mathrm{C}}}+\frac{1}{4{\left(1‐\mathrm{Z}/L_{\mathrm{C}}\right)}^2}-\frac{1}{4},$$ (1)

where L _P is persistence length (1548 and 1.549 nm for the folded and unfolded chains, respectively), L _C is contour length, k _B is Boltzmann's constant and T is absolute temperature (300 K). At each time point of the simulation the number of domains (dN) passing from one state to the next (e.g., from unfolded to molten‐globule) along the reaction coordinate was calculated. Calculations were thus made for four transitions in the three‐state model: folded to molten globule (F→M), molten globule to unfolded (M→U), unfolded to molten globule (U→M) and molten globule to folded (M→F). The transitions in the two‐state model were folded to unfolded (F→U) and unfolded to folded (U→F). dN was calculated according to

$$\mathrm{d}\mathrm{N}=N{\omega }_0\mathrm{d}t{e}^{-\left(E_{\mathrm{a}}-F\Delta x\right)/k_{\mathrm{B}}T,}$$ (2)

where N is the number of available domains in the starting state of the transition, ω ₀ is the attempt frequency set by Brownian dynamics (10⁸ Hz), dt is the time base of the simulation (8 ms), E _a is the activation barrier of the transition, and Δx is the distance, along the reaction coordinate, from the starting state to the transition state. In case of fractional dN, the transition was permitted or prohibited depending on a comparison with a number generated randomly between 0 and 1. The contribution of a titin domain to the overall contour length of the molecule was 4, 8, or 28 nm for its folded, molten‐globule or unfolded states, respectively. The contour length of the simulated molecule thus varied according to the rate of transition between its structural states. The extension was adjusted (incremented or decremented) so as to maintain the constant experimental force level. E _a and Δx values used in the simulation are listed in Table 1.

Table 1.

Parameters used in the Monte Carlo simulation

Transition	Ea (×10−21 J/molecule)	Δx (nm)
F→M	128	0.3
M→U	75	8
U→M	115	8
M→F	75	8
F→U	128	0.3
U→F	75	8

Molecular dynamics simulations

The titin I27 domain (PDB code 1WAA) was immersed in a TIP350 water box with 35 × 35 × 150 Å size using VMD.51 Simulations were carried out with the CHARMM36 force field52 using the NAMD 2.10 program.53 Equilibration started with 10,000 steps of minimization of water molecules with fixed protein atoms followed by 10,000 steps of minimization without any constraint. The system was heated to 300 K by a stepwise increment of temperature in 30 ps. 500‐ps volume equilibration completed the preparation of the system. Constant temperature was enforced using Langevin dynamics with a damping coefficient of 5 ps⁻¹. Constant pressure was enforced with Nosé‐Hoover‐Langevin piston with a period of 100 fs and a damping time scale of 50 fs. The van der Waals interaction cutoff was set to 12 Å and long‐range electrostatics was calculated using particle‐mesh Ewald summation with a grid size of <1 Å. Steered molecular dynamics (SMD) simulations were performed by fixing the Cα atom of the N‐terminal residue and exerting force on the Cα atom of the C‐terminal residue. First, a 1 Å/ns constant speed pulling was applied for 30 ns that resulted in an extension of ∼30 Å of the protein end‐to‐end distance. This structure was used in subsequent SMD simulation in which the C‐terminal was held with a constant force for 50 ps. The magnitude of the applied force was 0, 5, 20, and 150 pN. The apparent spring constant was 7 kcal/mol/Ų  51 in all SMD simulations.

Data processing and statistics

Data obtained in 228 nanomechanical cycles on 79 titin molecules were processed and analyzed in this paper. Data acquisition and initial data processing (corrections for zero extension, zero force and baseline) were performed by using custom LabView routines. For subsequent data analysis, such as smoothing, curve fitting and graph plotting we used IgorPro (Wavemetrics, Lake Oswego, OR, USA).

Conflict of Interest Statement

The authors declare no conflict of interest.

Supporting information

Supporting Information Movie 1.

Supporting Information Movie 2.

Supporting Information