AN AUTOMATIC 3D CT/PET SEGMENTATION FRAMEWORK FOR BONE MARROW PROLIFERATION ASSESSMENT

Abstract

Clinical assessment of bone marrow is limited by an inability to evaluate the marrow space comprehensively and dynamically and there is no current method for automatically assessing hematopoietic activity within the medullary space. Evaluating the hematopoietic space in its entirety could be applicable in blood disorders, malignancies, infections, and medication toxicity. In this paper, we introduce a CT/PET 3D automatic framework for measurement of the hematopoietic compartment proliferation within osseous sites. We first perform a full-body bone structure segmentation using 3D graph-cut on the CT volume. The vertebrae are segmented by detecting the discs between adjacent vertebrae. Finally, we register the bone marrow CT volume with its corresponding PET volume and capture the spinal bone marrow volume. The proposed framework was tested on 17 patients, achieving an average accuracy of 86.37% and a worst case accuracy of 82.3% in automatically extracting the aggregate volume of the spinal marrow cavities.

1. INTRODUCTION

The marrow space is the site of hematopoiesis in animal and human. It produces all the critical blood cells including red blood cells which disperse oxygen, white blood cells which are critical for the immune system, and platelets which are necessary for coagulation and hemostasis. Diseases of hematopoiesis are often life threatening and can include malignancies, medication or exposure toxicities, infection and autoimmune diseases. Currently there is no comprehensive way to evaluate the proliferation of hematopoetic cells within this compartment. Using current imaging modalities and techniques, the marrow space can be visualized by MRI or CT or proliferation can be assessed by PET, albeit with poor specificity and sensitivity. However, neither has been shown to aid in hematopoetic evaluation. This may be in part due the challenges of evaluating the marrow space, including the irregularity of the medullary border and trabecular surface from the internal blood vasculature within osseous structures.

Recent studies [1–5] showed that joint CT/PET imaging can enable physicians to noninvasively monitor and evaluate recovery progress in patients who have undergone bone marrow transplant. With CT/PET imaging technology, anatomic details such as bone structures, kidney, and water are best captured by CT while the PET modality is capable of measuring biochemical changes inside organs. When used in tandem, these two modalities can improve the accuracy of segmentations that are restricted to specific organs or ROIs. The biochemical properties captured by PET allow physicians to efficiently quantify the bone marrow cell proliferation. However, in previous CT/PET studies [1–5], the ROIs were generally designated manually by physicans, making the the process of evaluating the marrow space time consuming, labor intensive, and prone to error. In addition, the evaluation obtained from a set of selected ROIs may not generalize to the whole bone marrow volume of the patient. While 3D semi-automatic or automatic bone segmentation algorithms have been reported in the literature, most do not include extraction of the medullary cavities and most were not designed for measuring bone marrow proliferation. The combination of CT and PET for the bone marrow segmentation makes our approach unique.

Recent bone segmentation research can be categorized into two main approaches: estimation-free methods and machine learning methods. The estimation-free methods usually do not require an explicit model for the segmented objects. This category of algorithms includes classical region growing, watershed segmentation, active contours, and graph-cut methods [6]. Hybrid approaches such as the hierarchical approach also produce promising results. For example, Kang et al. [7] combined adaptive thresholding and region growing to perform 3D bone segmentation. Mastmeyer et al. [8] used a hierarchical scheme where region growing was followed by segmentation of the vertebrae via detection of the disks between them. In addition, auxiliary detection techniques are augmented to the segmentation workflow to take advantage of the prior topological knowledge of the human body. Yao et al. [9] and Klinder et al. [10] proposed algorithms to locate the spinal column by detecting the spinal cord. Recent advances in segmentation techniques employ machine learning techniques. In particular, the statistical learning methods are used to build trainable models for the objects to be segmented. Huang et al. [11] used training with Adaboost to construct vertebrae detectors. Ma and Liu [12] learned low-level edge descriptors to detect vertebrae. Glocker et al. [13] used a supervised classification forest to train a model to detect vertebrae shapes and label them.

In this paper we propose a new, fully automatic framework for segmenting the marrow compartments of the human spinal column from CT data and for measuring biochemical activity from joint PET data. We use a graph-cut segmentation [14] to obtain an initial 3D map of the full-body bone volume. We then refine this segmented volume to extract the vertebral bodies. The vertebrae are isolated by detecting the vertebral discs. To overcome false detections, we formulate the vertebrae detection task as a tracking problem and use a Kalman filter to reject false disc locations. The detected disc locations enable us to segment all the vertebral bodies in the spine. Once the medullary cavities inside the vertebral bodies are isolated, measurement of biochemical activity from joint PET images is achieved by registering the PET and CT voxels. While bone segmentation is a classical research problem, to the best of our knowledge, the proposed approach is the first automatic 3D bone marrow segmentation method to be specifically targeted for bone marrow cellularity analysis. We note that Sambucetti et al. [15] proposed an active contour approach to measure bone marrow volume. However, they used 2D active contour segmentation on a per-slice basis to construct the 3D bone volume and their method requires expert human intervention.

2. SEGMENTATION FRAMEWORK OVERVIEW

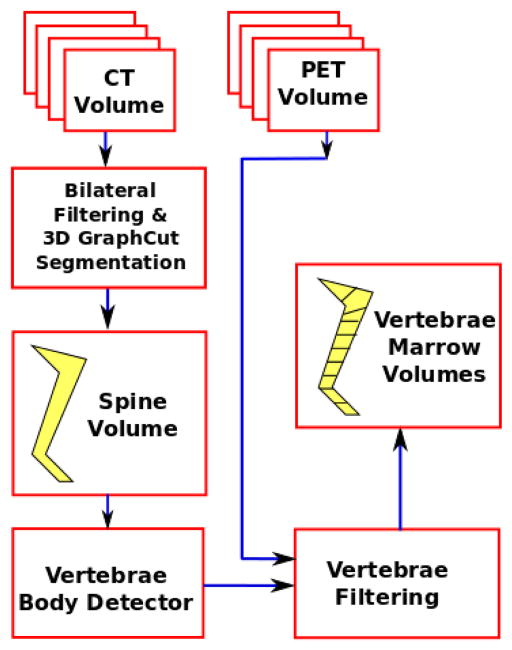
An overview of the proposed approach is given in Fig. 1. We use a 3D bilateral filter to smooth away certain artifacts that may be present in the original input CT volume (Sec. 2.1). We then perform 3D graph cut segmentation [14] to obtain the full-body bone structure. We isolate the spinal column and detect the discs between adjacent vertebral bodies. Bone cortex regions are rejected to obtain bone marrow spaces.

Fig. 1.

Block diagram of the proposed spinal column segmentation framework.

2.1. Volume Smoothing

We are specifically concerned with joint PET/CT scans of patients who have undergone marrow ablation with total body irradiation and chemotherapy prior to transplantation, which can lead to undesirable non-smooth artifacts in the CT data occurring at the interior of the hard bone regions. Prior to segmentation, we apply 3D bilateral filtering [16, 17] to remove these artifacts. The bilateral filter is a smoother that performs neighborhood averaging using weights given by the product of a spatial kernel and an intensity (range) kernel that are normally both Gaussian. It can smooth spurious artifacts while retaining the strong edges of the cortical bone tissue. For parameter tuning, we set the spatial bandwidth σ_s = 2, the range bandwidth σ_R = 5, the spatial sampling factor S_S = 5, and the range sampling factor S_R = 15.

2.2. Graph-cut Segmentation

In general, bone tissue tends to exhibit higher CT Hounsfield units (intensities) relative to non-bone material such as water, air, and muscle. Closely following the implementation described in [18], we use the graph-cut segmentation algorithm [6, 14] which optimizes a global energy functional consisting of a per-pixel component that penalizes misclassified voxels and a boundary component that enforces spatial coherence of the segmented objects.

Let 𝒩 be a system of symmetric 7-voxel 3D cross-shaped neighborhoods on the 3D CT volume and let I_p be the intensity of bilateral filtered CT voxel π in Hounsfield units (intensity). Each voxel is assigned a label B_p according to

$$B_p=\{\begin{array}{ll}1,\hfill & \text{if}\text{voxel}p\text{classified}\text{as}“\text{bone},”\hfill \\ 0,\hfill & \text{if}\text{voxel}p\text{classified}\text{as}“\text{not}\text{bone.}”\hfill \end{array}$$ (1)

As in [6], the labels B_p are assigned by minimizing the energy

$$\mathcal{E}=\sum _p{R}_p(B_p)+\lambda \sum _{p,q\in \mathcal{N}}{\mathbf{1}}_{p,q}S(p,q),$$ (2)

where λ = 0.03, 1_p,q = 1 if B_p and B_q assigned to different labels, and

$$R_p=\{\begin{array}{ll}1,\hfill & B_p=1\text{and}{I}_p<T_l,\hfill \\ 1,\hfill & B_p=0\text{and}{I}_p>T_h,\hfill \\ 0,\hfill & \text{otherwise.}\hfill \end{array}$$ (3)

The high and low thresholds T_h and T_l are set to -50 and 200 Hounsfield units, respectively, and were determined through empirical analysis of the bilateral filtered CT volume data. Unlike [6], we use a simplified boundary penalty given by S(p, q) = exp(−|I_p − I_q|/σ) with σ = 10.

3. VERTEBRAE FILTERING

From the segmented full-body bone structure described in Sec. 2.2, we isolate the vertebral bodies from each other by detecting the disc region between two adjacent vertebrae. We then track these detected disc locations with a Kalman filter. From these filtered positions, we obtain the segmented vertebral bodies for the whole spinal column by simple 3D morphological filtering.

3.1. Vertebral Disc Detection

In order to isolate the vertebrae, we detect the locations of the discs between vertebral bodies. We observe that the voxels in the neighborhood of the disc locations tend to have lower Hounsfield value in the CT component. Therefore, on a slice by slice basis in the transverse plane, we compute the average slice intensity by intersecting the bone voxels with straight lines of varying slopes. Let 𝒮 be the vertebral slice in the sagittal plane as shown in Fig. 3(a). Let ℒ_θi be a collection of lines with origins at slice i and slopes tan(θ). We compute the average distance for the slice i as

Fig. 3.

Vertebrae filtering and segmentation: (a) Sagittal plane view of spinal column segmented from CT data. (b) Vertebral discs detected by finding local minima. Red circles denote disc positions detected from the CT component while blue crosses denote disc positions detected from the PET component. (c) Final disc positions obtained by Kalman filtering. The tracked locations are marked with yellow circles. (d) Segmented vertebral volumes (prior to isolation of the marrow cavities by erosion).

$$H(i,\theta )=\text{avg}({\mathcal{L}}_{i,\theta }\cap \mathcal{S}).$$ (4)

We find the slope of the line ℒ_i by minimizing the average Hounsfield unit H(i,θ) as

$${\theta }^{\ast }=\underset{\theta }{\text{argmin}}H(i,\theta ).$$ (5)

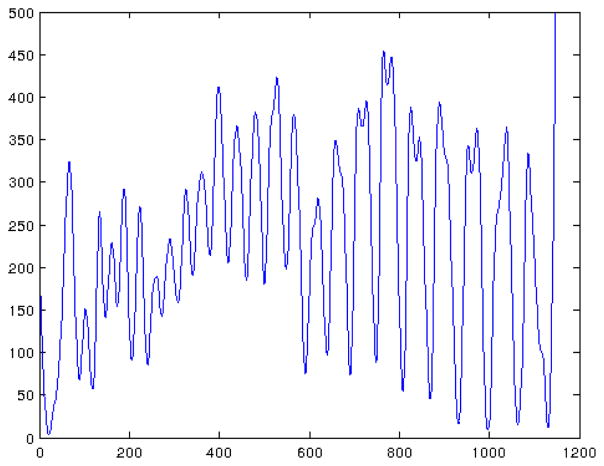
An instance of distance H(i, θ^*) is illustrated in Fig. 2. Here we are interested in the local minima of the distance H(i, θ^*) because they represent the detected disc positions between vertebral bodies. The local maxima are also useful to suppress false disc locations because they indicate the cortical bone region next to the vertebral discs. In our implementation, we sweep θ from −π/4 to π/4 in increments of π/32. The optimal θ^* is obtained by brute-force search. We also compute the distance H for the PET component. The combination of CT distance and PET distance gives us additional measurements to reduce false detections.

Fig. 2.

Average Hounsfield unit of each transverse slice of the segmented vertebrae mask shown in Fig. 3(a).

3.2. Disc Tracking by Kalman Filter

The disc detection process described in Sec. 3.1 is able to detect most disc locations. However, it often fails at a few locations due to noise, artifacts, and inherently non-visible vertebral discs. For example, in Fig. 3(b), the CT component gives false alarms at the 6^th and 8^th positions starting from the bottom of the image, while the PET component misdetects the 7^th disc. To address this issue, we model the disc filtering process with a constant velocity dynamic model and track the disc locations with a Kalman filter. The state space representation of the dynamic model is given by

$${\mathbf{x}}_{\mathbf{k}+\mathbf{1}}=\left[\begin{array}{cc}1& 1\\ 1& 0.95\end{array}\right]{\mathbf{x}}_{\mathbf{k}}+{\mathbf{u}}_{\mathbf{k}},$$ (6)

$${\mathbf{z}}_{\mathbf{k}}=\left[\begin{array}{cc}1& 0\end{array}\right]{\mathbf{x}}_{\mathbf{k}}+{\mathbf{v}}_{\mathbf{k}},$$ (7)

where ${\mathbf{x}}_{\mathbf{k}}={\left[\begin{array}{cc}{x}_k& {\stackrel{.}{x}}_k\end{array}\right]}^T$ and where u_k ~ 𝒩 (0, U_k) and v_k ~ 𝒩 (0, V_k) are zero-mean white Gaussian noises with covariance U_k and V_k. The state variable x_k models the position of the k^th detected disc, while ẋ_k measures the height of k^th vertebra in the sagittal plane. The gain of 0.95 in Eq. 6 implies that the height of vertebra decreases from the lumbar to the cervical region. In the experiments, we set the process noise variance and the observation noise variance to be 0.5 and 0.2. An example of tracking the disc locations is shown in Fig. 3. The Kalman filter is able to recover the missing disc positions while effectively rejecting the false detections.

From the tracked disc positions, we segment each vertebra by constructing a 3D boundary volume from these points. The segmented vertebral bodies include both cortical and cancellous bone tissue. The cancellous bone is located inside the cortical tissue and can therefore be extracted by applying a 3D morphological erosion filter having a ball structuring element of radius 3. Finally, we register the CT and PET voxels to measure biochemical activity within the bone marrow from the PET component. We select the simple rigid deformation model for the registration process and the cost function measures the mutual information between the CT and PET modalities. It is then straightforward to compute a statistical characterization of biochemical activity within the marrow volume.

4. EXPERIMENT AND DISCUSSION

We tested the proposed framework on 17 patients who underwent complete bone marrow transplant. Patients were prospectively enrolled on an IRB approved protocol and underwent imaging for marrow and organ evaluation. Patients were evaluated at multiple points, some of which included chemotherapy and/or radiation therapy with depletion of the marrow compartment. As this study uses a novel contrast agent, the size of our dataset is currently limited.

Using the segmentation volume 𝒢 obtained manually by expert physicians as a baseline, we evaluated the segmented volume ℳ delivered by the proposed automatic framework by computing the percent agreement D defined as

$$D=100\times \frac{\mid \mathcal{M}\cap \mathcal{G}\mid }{\mid \mathcal{G}\mid },$$ (8)

where |.| denotes bone volume summed across voxels. Intuitively, D measures the percentage overlap between the segmented volume and the manually labeled ground truth volume. A perfect segmentation result is 100%.

Results are shown in Table 1. Patient number is given in column 1 while column 2 shows the correct segmentation rate D. Across all 17 tested patients, the worst case performance is D = 82.3570% while the best result is D = 89.8072%. The mean and median are D = 86.3728% and 86.9578% respectively. Currently, we model the vertebral body with an ellipse. However, most of the detection error occurs in regions where the shape of the vertebral body deviates from circles or ellipses. Thus, these results can be improved by developing a more sophisticated shape model for the vertebral body. In column 3 of Table 1, we also show root mean square error (RMSE) results for the vertebral disc tracker computed between the tracked and ground truth disc positions. The tracker performed well on 14 out of the 17 patients. However, higher errors occurred on patients 7, 8, and 14 where significant noise and artifacts in the CT data degraded disc detection performance.

Table 1.

Segmentation results for proposed framework.

Patient	D (%)	ERMSE(voxel)
1	87.394	0.860464
2	85.002	0.942403
3	89.110	1.025827
4	87.289	1.026326
5	89.807	1.147532
6	84.976	0.884444
7	82.855	4.543005
8	88.439	5.821971
9	86.958	1.133246
10	84.273	0.860464
11	87.907	1.145727
12	88.523	2.000408
13	85.348	1.004205
14	82.357	5.006391
15	87.985	0.805521
16	84.626	0.805521
17	85.489	1.633903

5. CONCLUSION

We introduced a fully automatic CT/PET 3D bone marrow segmentation framework to measure proliferation within the cortico-medullary junction and medulla of the marrow space. The framework consists of three main components including full-body 3D graph-cut segmentation, spinal column segmentation, and cancellous region extraction. We isolated the vertebral bodies by detecting the discs between adjacent vertebrae. The disc detection process was guided by a Kalman tracker. Our novel method was able to capture the proliferation of the hematopoetic space with a high degree of reproducibility. This technique could be valuable in evaluation of marrow changes due to malignancy, toxins, infections and autoimmunity.