A combined treatment of hydration and dynamical effects for the modeling of host–guest binding thermodynamics: the SAMPL5 blinded challenge

Abstract

As part of the SAMPL5 blinded experiment, we computed the absolute binding free energies of 22 host–guest complexes employing a novel approach based on the BEDAM single-decoupling alchemical free energy protocol with parallel replica exchange conformational sampling and the AGBNP2 implicit solvation model specifically customized to treat the effect of water displacement as modeled by the Hydration Site Analysis method with explicit solvation. Initial predictions were affected by the lack of treatment of ionic charge screening, which is very significant for these highly charged hosts, and resulted in poor relative ranking of negatively versus positively charged guests. Binding free energies obtained with Debye–Hückel treatment of salt effects were in good agreement with experimental measurements. Water displacement effects contributed favorably and very significantly to the observed binding affinities; without it, the modeling predictions would have grossly underestimated binding. The work validates the implicit/explicit solvation approach employed here and it shows that comprehensive physical models can be effective at predicting binding affinities of molecular complexes requiring accurate treatment of conformational dynamics and hydration.

Introduction

Accurate modeling of hydration is important for understanding the thermodynamics of binding and molecular recognition [1–9]. Binding free energy models with explicit solvation are considered as the “gold standard” for modeling receptor-ligand complexation because of the critical role of desolvation, the hydrophobic effect, and bridging waters. In recent years, there has been significant progress in the development of computational tools to quantify the structure and thermodynamics of water molecules on host and protein surfaces [10–15]. Many of these approaches have highlighted the importance of displacing water molecules from enclosed regions of protein active sites in boosting the binding affinity [16–20].

In this work, we employ Hydration Site Analysis (HSA) [10, 18, 20], a methodology based on Inhomogeneous Solvation Theory (IST) [21] to map out solvation structural and thermodynamic features in protein binding sites. High density regions of water, termed hydration sites, are classified based on a number of energetic and structural measures such as the water-protein interaction energy, water entropy and the strength of local water-water and water-protein hydrogen bonding. These measures are used to identify regions from which the displacement of water leads to either significant gains or significant penalties to the predicted binding affinity. Ligands that displace high free energy water molecules are more likely to bind strongly.

Molecules are inherently flexible. Hence, computational models of molecular recognition can not ignore dynamical aspects of binding. In this work, we employ the Binding Energy Distribution Analysis Method (BEDAM) [22–24], a well established alchemical protocol for the quantitative prediction of absolute binding free energies. BEDAM has been specifically designed to capture conformational reorganization and entropic contributions to the binding free energies. To overcome the slow time-scales of conformational reorganization, the method employs parallel multidimensional replica exchange conformational sampling algorithms [25, 26] coupled with an implicit representation of the solvent [27–29].

The implicit solvent representation enables the formulation of binding in terms of the direct transfer of the ligand from the implicit solvent continuum to the receptor site [22]. This single-decoupling feature circumvents some of the convergence difficulties encountered with double-decoupling approaches with explicit solvation [30, 31]. Key to the method is the sampling of the effective binding energy function u(x), which represents the ligand-receptor interaction energy of a specific conformation x of the complex averaged over the conformations of the solvent. The benefits of the single-decoupling approach is particularly significant for large and charged ligands, as in the present application. The same approach is simply not feasible with explicit solvation since it would entail a lengthy potential of mean force calculation for each evaluation of the effective binding energy function [30].

The advantages of implicit solvation modeling in terms of conformational sampling and the single decoupling pathway are, however, counterbalanced by the lack of a detailed representation of hydration effects. A way around these conflicting requirements is to train the implicit solvent energy function based on explicit solvation data as we set out to do in this work. BEDAM employs the Analytic Generalized Born plus Non-Polar (AGBNP) model which has been specifically tailored for protein-drug binding applications [29]. One important aspect of the model is the treatment of short ranged water-solute interactions by means of hydration site spheres [24].

In this work, structural and thermodynamic data obtained from explicit solvent Hydration Site Analysis are used to inform the placement and energetic strength of AGBNP hydration site spheres to mimic the thermodynamics of enclosed water molecules [24, 32]. The resulting hybrid explicit/implicit model was then employed to predict the binding affinities of the SAMPL5 datasets. The SAMPL5 blinded experiment, based on the octa-acid, [33] tetra-endomethyl octa-acid [34] and CB-clip host–guest systems [35], offers a unique opportunity to validate the approach outlined here. The tetra-endomethyl octa-acid is referred to as methyl octa-acid throughout the article. We have studied the octa-acid system before as part of the previous SAMPL challenge [36], where we trained the AGBNP water sites empirically to reproduce available experimental data. Here instead, we intend to train the model systematically using data from the HSA method, grounded in well established hydration theories. Furthermore, the SAMPL5 datasets give us the opportunity to validate our approach in an unbiased manner on hosts for which experimental data is not available.

Methods

Hydration Site Analysis of the host binding cavity

We investigated the hydration properties of the three host molecules using Hydration Site Analysis (HSA) approach [10, 18]. HSA utilizes an explicit solvent MD simulation of the solute molecule to identify spherical sites where water is present at high density. The thermodynamic quantities for these sites, such as enthalpy, first-order entropy and free energy are calculated using inhomogeneous solvation theory (IST) [21]. A detailed description of the simulation setup used for HSA is given in the Computational Details section. In summary, the explicit solvent simulation for each of the host system in a restrained configuration is processed to obtain hydration site locations where water molecules are present with at least twice the bulk density. The clustering procedure to obtain hydration site locations is described in detail elsewhere [20]. Briefly, for each hydration site, the total energy of the water, E_total, is calculated as the sum of its mean water-water E_ww, and solute-water interaction energies E_sw, where E_ww is one half the mean interaction energy of the water in the site with all other waters, and E_sw is one half the mean interaction energy of the water in the site with the solute. The factors of one half follow the convention that half of the interaction energy in a pairwise interaction is assigned to each molecule of the pair. The locations and average solvation energies of the hydration sites obtained for each host molecule are shown in Fig. 1 and Table 1. The solvation energies were compared to TIP3P neat liquid simulations to determine which hydration sites contained favorable and unfavorable water molecules relative to bulk solvent. The relative solvation energies and positions of the explicit hydration sites were used to position and parameterize the strength of the AGBNP2 hydration site adjustments which account for enclosed hydration effects. We chose to only use HSA energies to parameterize the strength of hydrogen bond correction parameters because HSA entropies were previously shown to be non-predictive in a scoring function used to predict relative binding affinities of ligands binding to Factor Xa [20]. For each system, we derive scores for hydration sites and apply them as corrections to AGBNP2 sites for the corresponding system (Fig. 2a) as described below. The HSA scores (listed in Table 1) are given by the expression [E_total(i) − E_bulk]p(i) where i is the index of the HSA hydration sites, p(i) is the water occupancy of the site, E_total(i) is the total energy of the site and E_bulk is the corresponding reference value obtained from TIP3P neat water. Two water molecules are considered to be first-shell neighbors in a given MD frame if their oxygen atoms are separated by less than 3.5 Å This distance criterion is based on the location of the minima of the oxygen-oxygen radial distribution function for bulk water [37]. The mean number of these first shell neighbors for water in each hydration site is termed N^nbrs, and this first-shell neighbor count is used to define the fractional enclosure of a hydration site, by referencing the number of its first-shell neighbors to the mean number of first-shell neighbors of a TIP3P water molecule in bulk, $N_{\text{bulk}}^{\text{nbrs}}$:

$$f_{\text{enc}}=1-\frac{N^{\text{nbrs}}}{N_{\text{bulk}}^{\text{nbrs}}}$$ (1)

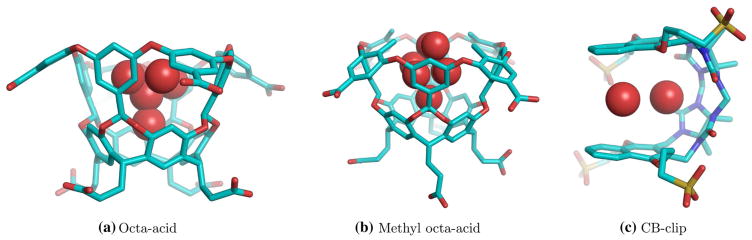
Fig. 1.

Location of hydration sites within the binding cavity of the hosts as identified from hydration site analysis. a Octa-acid, b methyl octa-acid, c CB-clip

Table 1.

Summary of Hydration Site Analysis(HSA) results for three host systems investigated in this study

	Site id	Location	Occupancy (p)	Esw	Eww	Etotal	[Etotal − Ebulk]p	Nnbrs	fenc
A.	Octa-acid
	0	Bottom	0.62	−4.57	−2.42	−6.99	1.58	1.27	0.76
	1	Top	0.40	−0.64	−7.59	−8.23	0.52	3.06	0.42
	2	Top	0.41	−0.61	−7.41	−8.02	0.62	2.89	0.45
	3	Top	0.40	−0.58	−7.62	−8.19	0.53	3.12	0.41
	4	Top	0.40	−0.58	−7.55	−8.13	0.56	2.96	0.44
	5	Middle	0.29	−1.48	−7.50	−8.98	0.16	2.89	0.45
B.	Methyl octa-acid
	0	Bottom	0.60	−4.52	−2.14	−6.66	1.72	1.32	0.75
	1	Top	0.36	−0.48	−7.00	−7.48	0.74	2.27	0.57
	2	Top	0.31	−0.73	−6.84	−7.57	0.61	2.54	0.52
	3	Rim	0.31	−0.02	−8.49	−8.51	0.31	3.19	0.39
	4	Top	0.32	−0.85	−6.83	−7.68	0.60	2.50	0.52
	5	Top	0.30	−0.62	−6.68	−7.30	0.66	2.24	0.57
	6	Rim	0.27	0.60	−9.67	−9.06	0.66	3.64	0.31
C.	CB-clip
	0	Center	0.92	−5.76	−2.27	−8.03	1.38	1.75	0.67
	3	Naphthalene rings	0.42	−1.55	−6.97	−8.52	0.42	3.43	0.35

All energetic quantities are expressed in kcal/mol. For CB-clip, a total of nine hydration site were obtained in the cavity, the two site used for AGBNP2 parametrization are reported here. E_bulk = −9.53 kcal/mol

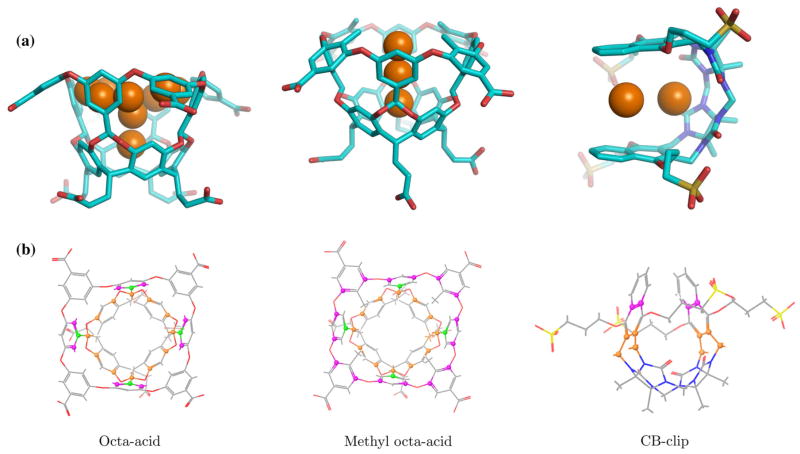
Fig. 2.

a Position of the hydration spheres added to AGBNP2 parameters for each hosts, b the carbon atoms used to position the hydration sphere in all three hosts; the carbon atoms marked in magenta are used for positioning the water sites on the top cavity of octa-acids; in CB-clip, those carbons are used to position water site in between two naphthalene rings; the center of masses of carbons marked in green were used to position water-sites in the middle cavity of the octa-acids; carbons marked in orange were used to model a water site at the bottom cavity of the octa-acids; in CB-clip, a water site is positioned at the center of mass of those four carbons

This quantity indicates the degree to which the water in a hydration site is blocked from contact with other water molecules. The value of $N_{\text{bulk}}^{\text{nbrs}}$ is 5.25 as calculated from TIP3P pure water.

The AGBNP2 implicit solvation model

Here we employed the OPLS-AA/AGBNP2 effective potential, where OPLS-AA [38, 39] represents the covalent and non-bonded inter-atomic interactions and solvation is modeled implicitly by the Analytic Generalized Born plus non-polar (AGBNP2) model [29]. The hydration free energy ΔG_h is computed as the sum of electrostatic ΔG_elec, non-polar ΔG_np, and short-range solute-water hydrogen bonding interaction ΔG_hs:

$$\mathrm{\Delta }{G}_{\mathrm{h}}=\mathrm{\Delta }{G}_{\text{elec}}+\mathrm{\Delta }{G}_{\text{np}}+\mathrm{\Delta }{G}_{\text{hs}}$$ (2)

The electrostatic component of the hydration free energy is represented by a pair-wise descreening implementation of the Generalized Born model [28, 40, 41]. The non-polar component of the hydration free energy is modeled as the sum of cavity and solute-solvent dispersions interactions [28]. AGBNP2 includes algorithms to place and score hydration spheres on the surface of the solute to describe short-range solute-solvent interactions such as hydrogen bonding [29]. The functional form of the short-ranged hydrogen bonding component of the solvation free energy in Eq. (2) above is

$$\mathrm{\Delta }{G}_{\text{hs}}=\sum _s{h}_{s}S(w_s)$$ (3)

where w_s is the water occupancy factor of the site measured as the fraction of the volume of the hydration site sphere actually accessible to water defined as

$$w_s=\frac{V_s^{\text{free}}}{V_s}$$ (4)

where V_s is the volume of the water sphere and $V_s^{\text{free}}$ is the free volume of the water site, that is the volume not occluded by solute atoms, obtained by summing all the two body, three body, etc. overlap volumes of the water sphere with the solute atoms i, j, k, etc. as [29]

$$V_s^{\text{free}}=V_s-\sum _i{V}_{si}+\sum _{i<j}{V}_{\mathit{sij}}-\sum _{i<j<k}{V}_{\mathit{sijk}}$$ (5)

In Eq. (3), S is a switching function, and the h_s are adjustable parameters which measure the strength of the hydrogen bonding energy (more precisely the portion of it not captured by the Generalized Born model) [29]. The specification of the solute atoms carrying such hydration spheres is accomplished by means of SMARTS patterns. A parameter database is used to map SMARTS patterns to the energetic parameters and placement geometry of hydration spheres [29]. The h_s parameters are normally negative and adjusted to describe favorable solute-solvent hydrogen bonding interactions. In this context, the ΔG_hs term disfavors binding by increasing the ligand and receptor desolvation penalties. In addition, in this work, we use the same functional form to model enclosed water molecules, which contribute favorably to binding, when displaced by the ligand. The key distinction between hydrogen bonding sites and enclosed hydration sites is the sign of the h_s parameter, which is positive for the latter and negative for the former. The specific values of h_s assigned to enclosed hydration sites are derived from explicit solvent HSA analysis and are given in the Results section below.

Incorporation of Debye–Hückel parameters in the implicit solvation model

In this work the Generalized Born components of the AGBNP2 model included modifications based on the Debye–Hückel screening aimed at modeling the effects of electrolytes present in the aqueous solution. Specifically, we adopted the following functional form for the GB pair potential [42]

$$u_{\text{GB}}(i,j)=-\left(\frac{1}{{\epsilon }_{\text{out}}}-\frac{e^{-\kappa r_{ij}}}{{\epsilon }_{\text{in}}}\right)\frac{q_i{q}_j}{\sqrt{\left[r_{ij}^2+B_i{B}_j{e}^{-(r_{ij}^2/4B_i{B}_j)}\right]}}$$ (6)

where r_ij is the distance between atoms i and j, ε_out = 80 and ε_in = 1 are the dielectric constants of the solvent and the interior of the solute respectively; q_i and q_j are the partial charges of atoms i and j. The terms B_i and B_j are the Born radii of atoms i and j. The Debye–Hückel screening parameter is defined as $\kappa =\sqrt{8\pi {\lambda }_{B}I}$ where I is the ionic strength of the solution and λ_B is the Bjerrum length [40, 42]. For water at room temperature, λ_B =7.0 Å. An ionic strength of 0.12 M, corresponding to the 20 mM sodium phosphate solution used for the measurements of CB-clip guest binding, was used throughout.

Binding free energy protocol

Binding free energies were computed using the Binding Energy Distribution Analysis Method (BEDAM) [22]. The method uses a single-decoupling alchemical approach with implicit solvation. An alchemical progress parameter λ is introduced ranging from 0, corresponding to the uncoupled state of the complex, to 1, corresponding to the coupled state of the complex. The λ-dependent effective soft-core hybrid potential energy function is:

$$U_{\lambda }(r)=U_0(r)+\lambda u(r)$$ (7)

where r = (r_A, r_B) are the atomic coordinates of the receptor-ligand complex and r_A and r_B denote the coordinates of the receptor and ligand, respectively. U₀(r) = U(r_A) + U(r_B) is the potential energy of the complex when the receptor and ligand are uncoupled, i.e. as if they are separated at infinite distance from each other. The quantity u(r) is the binding energy and is defined as the change in the effective potential energy of the complex for bringing the receptor and ligand from infinite separation to the conformation r of the complex:

$$u(r)=U(r_{\mathrm{A}},r_{\mathrm{B}})-(U(r_{\mathrm{A}})+U(r_{\mathrm{B}}))$$ (8)

In this work we adopted a soft-core form of the binding energy mentioned above and as described [23, 43]. UWHAM analysis of the binding energy samples was carried as described [43] to obtain binding free-energy estimates and their corresponding statistical uncertainties. Average interaction energies, ΔE_b were obtained by averaging the binding energy values collected at λ=1 (the bound state). The uncertainty on interaction energies were measured as the standard error of the mean. The entropic contribution to the free energy, the effect of reorganization energy and reorganization free energy to binding were derived [26, 44] from binding energies and other thermodynamic parameters as described in the computational details section. The uncertainties of all these quantities were computed by error propagation.

In this work, BEDAM conformational sampling is accelerated by means of two-dimensional replica exchange along alchemical and temperature parameters [26, 45]. λ exchanges facilitate the mixing of intermolecular degrees of freedom, while temperature exchanges activate intramolecular degrees of freedom thus allowing conformational transitions to explore the conformational space more efficiently [46].

Computational details

Explicit solvent calculations and Hydration Site Analysis (HSA)

For each host molecule, a molecular dynamics simulation was performed using the OPLS 2005 force field (Schrodinger Inc.) in a TIP3P [47] cubic water box, using the DESMOND package [48]. The initial starting structure for each simulation was a representative holo structure without the ligand. These representative structures were obtained from BEDAM simulations of the octa-acid and methyl octa-acid hosts with guest 4 and the CB-Clip host with guest 1. Each water box was built with a minimum distance of 10 Šbetween the solute and the edge of the box. The default Desmond equilibration protocol was used to minimize and thermalize the systems for the production run. The system was further relaxed for 25 ns under NPT conditions at 1 atm and 300 K. An NVT production run was started from a configuration in which the box volume was close to the average of the previous NPT simulation. The production MD simulations were run for 100 ns and snapshots were collected every 0.5 ps. The first 1 ns of the production run was discarded. In the octa-acid and methyl octa-acid simulations, positional restraints were used on all of the heavy atoms with a force constant of 5.0 kcal/mol/Ų which allowed for free rotation of hydrogens. In the CB-clip simulations, position restraints were used on all of the heavy atoms of the host with a force constant of 5.0 kcal/mol/Ų, excluding the sulfonate groups. The use of one rigid receptor should not have a significant effect on determining the hydration sites and the following free energy calculations due to the nature of the scaling function used to calculate enclosure energies and the rigidity of the SAMPL5 hosts. If the host structures are unrestrained during HSA analysis, the occupancies of the hydration sites are expected to decrease due to the effect of the conformational fluctuations of the host on the solvent. In contrast, the energies of these hydration sites may become more favorable due to the ability of the solvent to optimize its interactions with either the neighboring water molecules or nearby solute atoms. These changes to the HSA energies and occupancies will have an impact on the global parameter c and should not impact the enclosure energies used in the free energy calculations. On the other hand, this treatment is inappropriate for more flexible hosts that adopt multiple bound states because the hydration site locations will vary for each bound representative structure. SHAKE was used to constrain any bonds involving hydrogen atoms.

Hydration Site Analysis involved two steps: (1) identifying regions of high water density around each host surface and (2) calculating the average solvation energies of the water molecules in those locations. For each host, 190, 000 frames of the trajectory were processed with HSA analysis. Hydration site locations were identified using a subset of 10,000 frames which were evenly spaced in time. High density spherical regions (hydration sites) of 1 Å radius were identified using a clustering procedure [10] on the water molecules that were found within 5 Å of the host molecule. The resulting hydration sites were each populated by retrieving all water molecules, which had oxygen atoms within 1.0 Å from the corresponding hydration site center. The hydration sites were then enumerated according to their occupancies, with the highest populated site given the index 0. The average solvation energies were calculated based on energies of the water molecules that were within 1.0 Å from the coordinates of each hydration site center in the original 190,000 frames.

System preparation for the binding free energy calculations

The structures of the octa-acid and CB-clip hosts and their guests were prepared using Maestro (Schrodinger Inc.) starting from structure files provided by the SAMPL5 organizers. Bond orders and formal charges were adjusted as appropriate. All the eight carboxylate groups of the octa-acids were modeled as deprotonated resulting in a net negative charge of −8. Similarly, the four sulfonate groups CB-clip host were modeled as all ionized, resulting in a net overall charge of −4. Alternate protonation and tautomerization states of the CB-clip guests were generated using the LigPrep facility (Schrodinger Inc.) using Epik [49] with a pH range of 7±2. Ionization and tautomerization free energy penalties were recorded and added to the BEDAM binding free energy estimates to compute the predicted binding free energies. LigPrep predicted multiple protonation and tautomerization states for the CB-clip guests. Multiple protonation states of guests 1, 4, 5, 6, 8 and 9 were tested individually. Guests 3 and 5 which contain alkylammonium groups were modeled as positively charged and the guests containing carboxyl groups, guests 1, 2, and 4 were modeled as deprotonated each having a single negative charge. Guest 6, which is nitrobenzoic acid, holds an overall single negative charge contributed by the carboxyl moiety. To match the experimental pH, the acidic guests of the octa-acid set were modeled as deprotonated and ionization penalties were not applied.

All individual guests were manually docked to the binding cavity of the hosts in two of the octa-acids and the in-between space of the two naphthalene rings on CB-clip. Joint Hamiltonian and temperature 2-D Asynchronous Replica-exchange Molecular dynamics simulations [26] employed 18 intermediate λ steps as follows: λ = 0, 0.002, 0.004, 0.008, 0.01, 0.02, 0.04, 0.07, 0.1, 0.17, 0.25, 0.35, 0.5, 0.6, 0.7, 0.8, 0.9, and 1.0 and 8 temperatures were distributed between 300 K and 534 K (T = 300, 328, 358,390,424, 458, 494, 534). A total of 144 replicas were used corresponding to all possible pairing of temperature and λ values. The replica-exchange (AsyncRE) simulations were started from energy-minimized and thermalized structures from the manually docked models. A flat-bottom harmonic restraint with a tolerance of 5 Å between the centers of mass of the host and the guest was applied. Each cycle of a replica lasted for 100 picoseconds with 1 fs time-step. The average sampling time for a replica was approximately 10 ns. Calculations were performed on the campus computational grids at Brooklyn College and at Temple University and on the XSEDE SuperMIC cluster, the latter using 3 compute nodes utilizing all CPU’s and both MIC devices. The binding energies obtained from all replicas were analyzed using UWHAM [43] method and the R-statistical package to compute the binding free energy $\mathrm{\Delta }{G}_{\mathrm{b}}^{\circ }$ and average interaction energies ΔE_b of individual complexes. Energy values from the first 1 ns of each replica were excluded from the free energy calculation. Calculation at multiple temperature allows estimation of the conformational entropy of binding $\mathrm{\Delta }{S}_{\text{conf}}^{\circ }$ from the temperature derivative of the binding free energy (here we used a simple finite difference estimator using adjacent binding free energy values). Reorganization free energies $\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$ were measured as the difference between the binding free energy and the average interaction energy at the bound state as

$$\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }=\mathrm{\Delta }{G}_{\mathrm{b}}^{\circ }-\mathrm{\Delta }{E}_{\mathrm{b}}$$ (9)

Finally, the reorganization energy for each complex was measured by subtracting the entropic component from the reorganization free energy:

$$\mathrm{\Delta }{E}_{\text{reorg}}^{\circ }=\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }+T\mathrm{\Delta }{S}_{\text{conf}}^{\circ }$$ (10)

Statistical uncertainties for the reorganization free energy, conformational entropy and reorganization energy were obtained from error propagation of the uncertainties of the binding free energy and the average binding energy. The data submitted to SAMPL5 challenge were obtained from the 2D replica exchange binding free energy calculations without inclusion of salt effects. Uncertainties were reported as twice the standard error. The binding free energy predictions were submitted to the SAMPL5 host–guest challenge on January 29, 2016. For our submissions, the octa-acid, methyl octa-acid and CB-clip were assigned prediction IDs # 18, 20 and 10 respectively.

Results

The locations of hydration sites obtained for each host molecule are shown in Fig. 1. For the octa-acid host, a total of six hydration sites are identified, one in the bottom cavity, one in the middle cavity and four in the upper cavity (Fig. 1, left). For the methyl octa-acid host, a total of seven hydration sites are identified, one in the bottom cavity, four in the upper cavity and two at the level of the rim of the host (Fig. 1, middle). The introduction of the methyl substituents mainly causes partial ordering of water molecules near the rim of the octa-ocid host, which are otherwise bulk-like. In the particular conformation examined, two partially ordered sites are found at the center of the mouth of the cavity (Fig. 1, middle). For the CB-clip host, a total of nine hydration sites were identified, one of which is located at the center of the host and the remaining eight were symmetrically distributed, spanning the region from naphthalene rings to the outer edges of the cavity. In the binding free energy calculations (see below) we considered the central site plus the site sandwiched in between the two naphthalene rings (Fig. 1, right).

In this work, as in the previous SAMPL4 host–guest edition [36], we used custom AGBNP2 hydration spheres to model the effect of enclosed water molecules displaced upon ligand binding (see Methods). The idea is that these sites have large water occupancy (w_s ≃ 1) in the unbound state and small water occupancy (w_s ≃ 0) in the presence of the bound ligand. Hence positive values of the water site energy parameter (h_s) can mimic the favorable effect of water expulsion towards binding. The approach we followed here for SAMPL5 is to place and score enclosed hydration sites which are distinct from the empirical approach adopted for the octa-acid host in SAMPL4. In SAMPL4 hydration site parameterization was conducted essentially by trial and error in an attempt to reproduce known experimental data. In this work instead the placement and scoring of AGBNP2 hydration sites is based on HSA analysis of explicit solvent data. Furthermore, because of limitations of the AGBNP2 hydration site placement algorithm, in SAMPL4 some of the effects of water expulsion were captured by empirical modifications of surface tension and solute-solvent van der Waals parameters. For this work, we developed novel geometrical algorithms to place hydration sites based on geometrical centers of arbitrary groups of atoms and more significantly, thanks to HSA analysis, we were able to reduce substantially, the number of empirically-derived parameters as described next.

The locations of enclosed hydration sites identified by HSA analysis were reproduced as best as possible using AGBNP2 water spheres and the anchoring methods available in AGBNP2 [29] and those developed for this work. Solute anchoring points correspond to hydrogen bonding sites such as along polar hydrogen bonds and lone pairs in various geometries [29], in addition to anchoring points based on geometrical centers of groups of atoms. Water sphere locations defined in this way naturally follow solute movements. The four top sites of the octa-acid host, sites (1, 2, 3, and 4) in Table 1, were modeled with eight AGBNP2 hydration spheres placed perpendicularly to inner phenyl rings of the cavity (Fig. 2b, left). The middle hydration site of the octa-acid host (site 5, Table 1A) was modeled by an AGBNP2 site placed at the geometrical center of a set of aromatic carbons as shown in Fig. 2b, left. The bottom water site (site 0 in Table 1A) was placed similarly. The six hydration sites identified for the methyl-octa-acid host (Table 1B), were modeled using three AGBNP2 hydration spheres as indicated in Fig 2a, middle. The one at the rim of the cavity corresponds to sites 3 and 6, the second in the top region of the cavity corresponds to sites 1, 2, 4 and 5, and finally the bottom site. All these individual water sites were placed at the center of mass of specific set of carbons surrounding the three regions in the pocket (Fig. 2b, middle). For the CB-clip host, one water site was placed at the center of mass of 4 aromatic carbons and 4 alkyl carbons in the center of the cavity as shown in (Fig. 2b, right). The second water site was placed in between the two naphthalene rings at the center of mass of 4 aromatic carbon atoms indicated (Fig. 2b, right). We have not attempted to model hydration sites located above and below the CB-clip host cavity partly because of their polar character already captured by AGBNP2 hydrogen-bonding sites [29].

The solvation parameters h_s associated with each AGBNP2 water site of the octa-acid host were derived from HSA analysis using the water enclosure energies as

$$E_{\text{enclosure}}(i)=c[E_{\text{total}}(i)-E_{\text{bulk}}]p(i)$$ (11)

where p(i) is the water occupancy of the site and [E_total(i) − E_bulk] is the average energy of the site relative to the energy of bulk water (Table 1). Enclosure energies were rescaled by a global parameter, c, to obtain AGBNP2 hydration parameters for enclosed water spheres. The global scaling parameter was adjusted so as to reproduce the experimental binding free energies of the SAMPL4 octa-acid set as described below. Scaled enclosure energies of hydration sites corresponding to a single AGBNP2 hydration sphere were aggregated into the h_s parameter of that sphere. Conversely, the h_s parameters for AGBNP2 sites corresponding to more than one hydration sites were obtained by distributing enclosure energies equally.

Using the scheme above, we were unable to reproduce accurately the experimental affinities for the SAMPL4 octa-acid set [36]. Deviations from the experiments suggested that the HSA analysis over-emphasized the benefit of displacing water from the bottom site. To correct this deficiency we decided to assign h_s parameters by distributing the total enclosure energy equally over the six sites. This led to results in reasonable agreement with experimental affinities with a scaling factor of c = 2.88 without ionic screening and c = 1.85 with ionic screening. The predictions for the octa-acid and methyl octa-acid hosts were produced using this scheme. For the CB-clip host, lacking experimental evidence supporting one strategy over another, we employed the more physically reasonable approach of deriving h_s parameters from individual enclosure energies as described above. The same scaling factors derived for the octa-acid system were used for the CB-clip system.

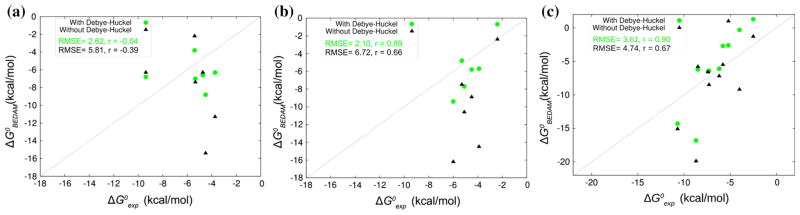
The blinded binding free energy predictions $\mathrm{\Delta }{G}_{\text{calc}}^{\circ }$ submitted to the SAMPL5 challenge, obtained without the inclusion of salt effects, are shown in Tables 2, 3 and 4 for the octa-acid, methyl octa-acid and CB-clip sets, respectively and Fig. 3, together with the corresponding experimental values. These predictions did not reproduce well the experimental measurements, with the most noticeable shortcoming being the significant overestimation of the affinities of positively charged guests (guests 3 and 5 of the octa-acid guests, and guests 6 and 10 of the CB-clip host). The results with the inclusion of ionic charge screening are in much better agreement with the experiments. Root mean square errors (RMSE) relative to experiments (Tables 2, 3; Fig. 3a, b) are reduced by more than a factor of 2 for the octa-acid host and by more than a factor of 3 for the methyl octa-acid host. The RMSE for the CB-clip set (Table 4; Fig. 3c) is reduced from 4.7 to 3.6 kcal/mol. Introduction of salt effects also improved the correlation between computational predictions and the experiments. Pearson correlation coefficients (r) improved from 0.66 to 0.89 and from 0.67 to 0.90 for the methyl octa-acid and CB-clip sets, respectively.

Table 2.

Calculated and experimental binding free energies with and without salt effects for octa-acid set and thermodynamic decomposition of binding free energies with the inclusion of salt effects

Guests	Structure	$\mathrm{\Delta }{G}_{exp}^{\circ }$ a	Without salt effects	With salt effects
			$\mathrm{\Delta }{G}_{\text{calc}}^{\circ }$ b	$\mathrm{\Delta }{G}_{\text{calcDH}}^{\circ }$ c	ΔEbd	$\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$ e	ΔEreorgf	$-T\mathrm{\Delta }{S}_{\text{conf}}^{\circ }$ g
G1		−5.4	−2.2 ± 0.06	−3.8 ± 0.08	−15.5 ± 0.01	11.7 ± 0.09	1.0 ± 1.4	10.7 ± 1.4
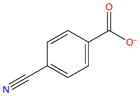
G2		−4.7	−6.3 ± 0.06	−6.6 ± 0.09	−15.9 ± 0.01	9.2 ± 0.09	0.9 ± 1.6	8.4 ± 1.5
G3		−4.5	−15.4 ± 0.06	−8.8 ± 0.09	−20.4 ± 0.01	11.6 ± 0.09	−0.9 ± 1.5	12.5 ± 1.5
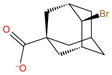
G4		−9.4	−6.3 ± 0.08	−6.8 ± 0.2	−20.0 ± 0.02	13.2 ± 0.1	1.3 ± 2.6	11.9 ± 2.6
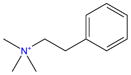
G5		−3.7	−11.3 ± 0.06	−6.3 ± 0.1	−16.6 ± 0.02	10.3 ± 0.1	1.7 ± 1.7	8.6 ± 1.7
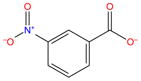
G6		−5.3	−7.4 ± 0.06	−7.0 ± 0.09	−18.8 ± 0.02	11.8 ± 0.1	0.2 ± 1.6	11.6 ± 1.6
RMSE			5.8	2.6
Correlation coefficient (r)			−0.39	−0.04

All values in kcal/mol.

^aExperimental ITC binding free energy [35].

^bPredicted binding free energy without addition of ionic effects.

^cBinding free energy prediction with the addition of salt effects.

^dAverage interaction energy of the bound complex at =1. The uncertainty is estimated as the standard error of the mean.

^eReorganization free energy as calculated using Eq. 9,

^fReorganization energy or intra-molecular strain as calculated using Eq. 10,

^gBinding entropy computed by finite difference method and evaluated at 300K; the uncertainty is computed by error propagation for all the decompositions

Table 3.

Experimental and computed binding free energies with and without salt effects for methyl octa-acid hosts and thermodynamic decompositions of binding free energies calculated with inclusion of salt effects

Guests	Structure	$\mathrm{\Delta }{G}_{exp}^{\circ }$ a	Without salt effects	With salt effects
			$\mathrm{\Delta }{G}_{\text{calc}}^{\circ }$ b	$\mathrm{\Delta }{G}_{\text{calcDH}}^{\circ }$ c	ΔEbd	$\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$ e	ΔEreorgf	$-T\mathrm{\Delta }{S}_{\text{conf}}^{\circ }$ g
G1		−5.3	−7.5 ± 0.06	−4.8 ± 0.08	−17.2 ± 0.01	12.4 ± 0.08	0.8 ± 1.4	11.5 ± 1.4
G2		−5.1	−10.6 ± 0.07	−7.7 ± 0.09	−17.6 ± 0.01	9.9 ± 0.1	1.4 ± 1.7	8.5 ± 1.6
G3		−6	−16.2 ± 0.07	−9.4 ± 0.1	−21.4 ± 0.01	12 ± 0.1	0.7 ± 1.7	11.3 ± 1.7
G4		−2.4	−2.4 ± 0.1	−0.7 ± 0.2	−21.1 ± 0.02	20.4 ± 0.2	6.7 ± 2.7	13.7 ± 2.7
G5		−3.9	−14.5 ± 0.07	−5.7 ± 0.1	−16.5 ± 0.02	10.8 ± 0.1	1.2 ± 1.8	9.6 ± 1.8
G6		−4.5	−8.9 ± 0.06	−5.8 ± 0.09	−18.0 ± 0.02	12.2 ± 0.1	1.4 ± 1.6	10.8 ± 1.6
RMSE			6.7	2.1
Correlation coefficient (r)			0.66	0.89

All values in kcal/mol.

^aExperimental ITC binding free energy, except for G4 and G5 for which only NMR measurements are available [35].

^bPredicted binding free energy without addition of ionic effects.

^cBinding free energy prediction with the addition of salt effects.

^dAverage interaction energy of the bound complex at =1. The uncertainty is estimated as the standard error of the mean.

^eReorganization free energy as calculated using Eq. 9,

^fReorganization energy or intra-molecular strain as calculated using Eq. 10,

^gBinding entropy computed by finite difference method and evaluated at 300K; the uncertainty is computed by error propagation for all the decompositions

Table 4.

Experimental and computed binding free energies with and without salt effects for CB-clip host–guest complexes and thermodynamic decompositions of binding free energies calculated with inclusion of salt effects

Guests	Structure	$\mathrm{\Delta }{G}_{exp}^{\circ }$ a	Without salt effects	With salt effects
			$\mathrm{\Delta }{G}_{\text{calc}}^{\circ }$ b	$\mathrm{\Delta }{G}_{\text{calcDH}}^{\circ }$ c	ΔEbd	$\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$ e	ΔEreorgf	$-T\mathrm{\Delta }{S}_{\text{conf}}^{\circ }$ g
G1		−5.8	−5.5 ± 0.07	−2.7 ± 0.1	−30.1 ± 0.03	27.4 ± 0.1	9.6 ± 1.7	17.8 ± 0.1
G2		−2.5	−1.3 ± 0.06	1.3 ± 0.08	−20.2 ± 0.03	21.5 ± 0.1	6.5 ± 1.3	15.0 ± 0.1
G3		−4.0	−9.2 ± 0.07	−0.3 ± 0.1	−47.2 ± 0.05	46.9 ± 0.1	14.4 ± 1.9	32.5 ± 0.1
G4		−7.3	−8.5 ± 0.08	−6.4 ± 0.1	−35.2 ± 0.02	28.8 ± 0.1	11.1 ± 2.1	17.7 ± 0.1
G5		−8.5	−5.8 ± 0.08	−6.2 ± 0.1	−26.2 ± 0.02	20.0 ± 0.1	5.0 ± 2.0	15.0 ± 0.1
G6		−8.7	−19.9 ± 0.1	−16.8 ± 0.1	−44.8 ± 0.03	28.0 ± 0.1	10.3 ± 2.5	17.7 ± 0.1
G7		−5.2	1.0 ± 0.07	−2.6 ± 0.2	−26.1 ± 0.03	23.5 ± 0.2	9.2 ± 2.9	14.2 ± 0.1
G8		−6.2	−7.2 ± 0.08	−6.1 ± 0.1	−32.3 ± 0.03	26.3 ± 0.2	6.8 ± 2.0	19.5 ± 0.1
G9		−7.4	−6.6 ± 0.08	−6.5 ± 0.1	−28.6 ± 0.03	22.1 ± 0.1	6.6 ± 2.1	15.5 ± 0.1
G10		−10.7	−15.1 ± 0.09	−14.3 ± 0.1	−36.6 ± 0.02	22.3 ± 0.1	5.6 ± 2.1	16.7 ± 0.1
RMSE			4.7	3.6
Correlation coefficient(r)			0.67	0.90

All values in kcal/mol.

^aExperimental binding free energy.[35].

^bPredicted binding free energy without addition of ionic effects.

^cBinding free energy prediction with the addition of salt effects.

^bAverage interaction energy of the bound complex at =1. The uncertainty is estimated as the standard error of the mean.

^eReorganization free energy as calculated using Eq. 9,

^fReorganization energy or intra-molecular strain as calculated using Eq. 10,

^gBinding entropy computed by finite difference method and evaluated at 300K; the uncertainty is computed by error propagation for all the decompositions

Fig. 3.

Calculated standard binding free energies from the SAMPL5 octa-acid (a), methyl octa-acid (b) and CB-clip (c) complexes against the corresponding experimental values. The points in green filled circles are the binding free energies obtained with the incorporation of salt effects. Filled black triangles are the free energies obtained without salt effects. RMSE = Root Mean-Squared Error, r = Pearson correlation coefficient

The correlation coefficient for the octa-acid set improved significantly with the inclusion of salt effects but remained low. This can be considered an acceptable result given that, with the exception of guest 4, the range of experimental affinities of the octa-acid set is small (less than 1.8 kcal/mol). The strongest binder in this set is guest 4. The calculations do not reproduce this feature well. Instead, guest 3, a positively charged ligand, is predicted to bind the strongest with −8.8 kcal/mol with ionic screening. The trend of overprediction of the affinity of positively charged ligands, while significantly reduced, remain even after inclusion of ionic screening. The origin of the relatively large deviation between experimental and calculated affinities for guest 4 is not clearly evident. This complex has the largest reorganization penalty in the set, which is surprising, given the rigidity of the guest. We ascribe this effect to the side-ways orientation of the bromine atom relative to the carboxylate substituent. This causes conformational strain in the host and tilting of the carboxylate to accomodate the bromine atom. We speculate that our model may be over-estimating the steric hindrance experienced by the bromine substituent.

Binding trends in the methyl octa-acid are better reproduced, partly thanks to larger variations in affinities in this set. Focusing on the more accurate results with ionic screening, guest 4, the strongest binding for the octa-acid host, is here the weakest binder both experimentally and computationally. The calculations reproduce the large loss of affinity of guest 4 upon methylation of the host reasonably well. Furthermore, in agreement with the experiments, the calculations predict that the strongest binder is guest 3.

The two strongest binders of the CB-clip host, guests 6 and 10, are correctly ranked the best by the computational model, although their relative rankings are reversed. The complex with guest 6 is predicted to have an unreasonably favorable binding free energy (−16.8 kcal/mol). Its negatively-charged counterpart, guest 7, is correctly predicted to be a relatively weak binder. Guest 2 is correctly predicted as the weakest binder of the set. The binding free energies of the guests in the middle of the pack are reproduced reasonably well and within the expected accuracy limits of the model. The inclusion of ionic screening has the general effect of weakening binding and shifting the predictions closer to the experimental values. For some guests the shift is very substantial (as much as 9 kcal/mol for guest 3), while the affinities of other guests (5, 8 and 9 for example) are barely affected by ionic screening. These differences appear to be related to the number of charged groups and the degree of solvent screening afforded by alkyl substituents.

In Tables 2, 3 and 4, we also report the results of free energy decomposition analyses [44] (values without ionic screening are not shown). Average binding energies (ΔE_b), obtained from the average of the binding energy values, u, in the bound state (λ = 1), reflect the strength of ligand-host interactions, including desolvation. Subtracting these from the binding free energies yields reorganization binding free energies ( $\mathrm{\Delta }{G}_{\text{reorg}}^{\circ }$). Using data from higher simulated temperatures, the latter is further decomposed into conformational entropy ( $-T\mathrm{\Delta }{S}_{\text{conf}}^{\circ }$) and reorganization energy (ΔE_reorg ) components. The conformational entropy component measures the entropy loss for the formation of the complex. The reorganization energy measures the intramolecular energy change of the guest and the host as they change conformations to bind to each other. The latter is commonly referred as intramolecular energy strain because it often (but not always) opposes binding. As further discussed below, decompositions of binding free energies provide useful physical interpretations of observed binding affinity trends. As often observed [32], the binding free energy is the result of a large compensation between the average binding energy and reorganization free energy. For example, the poor affinity of guest 4 to the methyl octa-acid host can be ascribed primarily to a large and unfavorable reorganization energy (20.4 kcal/mol) rather than the strength of the host–guest interaction energy (−21.1 kcal/mol), which is among the most favorable in the set. The average binding energies for the CB-clip complexes have a particular wide range, from −20.2 kcal/mol to −47.2 kcal/mol. Interestingly, these are imperfect predictors of affinity. For example, guest 3, which is the second weakest binder in the set, is predicted to have the strongest interactions with the host (−47.2 kcal/mol). Conversely, guest 5, which is one of the top binders, has relatively weak interactions with the host (−26.2 kcal/mol). Clearly, as observed previously [32, 36], reorganization (entropic loss and intramolecular energy strain) is an important determinant of binding.

Discussion

Water molecules solvating hydrophobic enclosures exhibit unique thermodynamic and structural signatures. Because they are in concave regions, they have fewer proximal water neighbors with which they can form favorable hydrogen bonding interactions. Simultaneously, due to the hydrophobicity of the solute, they are unable to compensate for these lost interactions by forming favorable hydrogen bond contacts with the solute surface. As a result, these water molecules are energetically unfavorable with respect to bulk and their displacement from the surface into the bulk upon ligand recognition can lead to a significant boost in binding affinity. In this work, we observe that all of the explicit water hydration sites inside the host cavities are in such hydrophobically enclosed regions and are energetically unfavorable (Table 1). For example, hydration sites in the bottom of the host cavities have high energies that can be attributed to the high degree of enclosure, while there are better interactions with the solute surface, there is a significant loss in neighbors relative to bulk (Table 1). The other hydration sites are relatively more exposed but interactions with the surface are weaker and therefore, they are also energetically unfavorable but to a lesser extent. These characteristics are similar to the high energy sites in proteins where enclosure and/or weak interactions with the surface cause a loss in enthalpy of water molecules relative to bulk [18, 20]. We should note, though that the hydrophobic enclosure observed in these hosts is more extreme than typically observed in protein binding sites. For example for 56 hydrophobic hydration sites found in 6 diverse proteins, the lowest energy was −8.22 kcal/mol [18], whereas many of the sites in these hosts were well below this value.

One key outcome of this work has been the realization of the significance of water displacement effects in these host–guest systems. Based on the comparison between AGBNP2 binding energies with and without the inclusion of the explicit solvent data derived from HSA analysis, we estimated that water displacement effects account for approximately 7 kcal/mol of the binding strength for the octa-acid host, 8 kcal/mol for the methyl octa-acid host and 4 kcal/mol for the CB-clip host. These values are very significant when compared to binding free energies values which range from −2 to −9 kcal/mol. Clearly, binding affinities would be grossly underestimated without accounting for water expulsion effects. Conversely, the accurate modeling of the thermodynamics of water enclosure is necessary to make accurate binding affinity predictions. Continuum solvent representations, which consider the solvent as a uniform medium with bulk properties everywhere including the interior of the host cavity, are, by definition unsuitable to represent the unique properties of discrete water molecules in these confined spaces.

Explicit solvent absolute alchemical binding free energy calculations are notoriously challenging because of slow conformational sampling and the need to compute the binding free energy as the difference of two decoupling free energies. We have shown that an implicit representation of the solvent can address some of these problems, albeit at the expense of a detailed description of hydration features, especially those related to enclosed water molecules. A way around these conflicting requirements is, as we have done here, to construct the implicit solvent energy function so as to incorporate explicit solvation characteristics. Specifically, we have integrated detailed information from HSA explicit solvent analysis about the number, location, and energetics of water molecules in the binding cavities of the hosts into the short-range hydration site component of the AGBNP2 implicit solvent model. We then employed this hybrid implicit solvation model in the binding free energy protocol.

Our submitted predictions to SAMPL5 were negatively affected by the overestimation of the affinity of positively charged guests relatively to negatively charged ones. Given that the hosts have a high negative charge, this trend pointed towards a lack of sufficient charge screening in our model, which did not take into account, screening from electrolytes in the solution. The need to model salt effects was not felt in our validation work on the SAMPL4 set [36], which included only negatively charged guests. These are affected by unfavorable charge-charge interactions by a similar constant factor, which was empirically included into the parameterization of the implicit solvation model. On the other hand, in the protein-ligand systems we have studied [22, 23, 50, 51], charge densities were too small to produce significant effects from ionic screening. Hence, the limitation of our Generalized Born-based electrostatic model became apparent only when challenged in this work with guests of varying charges binding to highly charged hosts. We have addressed the deficiency of the model by implementing Debye–Hückel ionic screening within the framework of the Generalized Born model following the work of David Case and collaborators [42]. This model requires an estimate of the Debye–Hückel screening length which was set according to the ionic strength of the solution used in the experiments (see Methods).

Re-evaluation of the SAMPL4 set with the Debye–Hückel model confirmed that the original model, lacking ionic screening, had required an additional correction of about 4 kcal/mol in favor of binding to counterbalance the charge-charge repulsion between the host and the negatively charged guests in the training set. This correction, had been absorbed by the HSA scaling parameter when empirically adjusted to reproduce experimental affinities. Hence the binding affinities of positively charged guests, which did not require such a correction, where further overestimated as a result. Adoption of the improved model with ionic screening had therefore the dual benefit of reducing the effect of charge-charge interactions and of removing the need of empirical corrections to boost the binding of negatively charged guests. Significantly, because corrections were incorrectly assigned to water expulsion effects, the model with ionic screening has also led to a more reliable description of the contribution of water expulsion towards binding as reported above.

With the adoption of Debye–Hückel charge screening and removal of the empirical boost to favor binding, the systematic bias in favor of positively charged guests is significantly reduced, as seen for examples in the case of guests 3 and 5 of the octa-acid hosts, whose revised binding affinities move substantially closer to the experimental values (Tables 2 and 3). The effect of ionic screening on negatively charged guests is smaller, particularly for the octa-acid host. This charge asymmetry is due to a conformational reorganization process that occurs for positively charged guests. Without ionic screening we observed that in approximately 70% of the bound conformations one of the benzoate groups of the host is flipped up so as to make a favorable short ranged ionic interaction with the alkylammonium group of the guest (Fig. 4b). With ionic screening, this interaction is disrupted (it is seen in less than 5% of the bound conformations) and binding is weakened. In complexes with negatively charge guests, instead, charge repulsion keeps like-charged groups away from each other and the effect of ionic screening is less important.

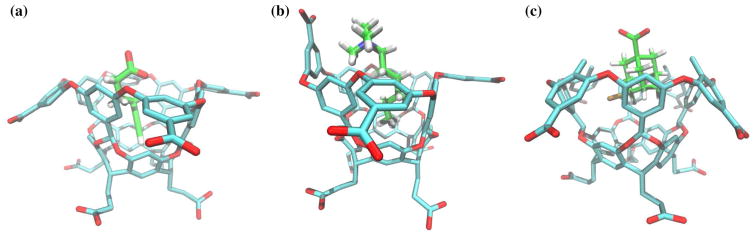
Fig. 4.

Representative structures from the simulations of the complexes with the octa-acid with a the negatively charged guest 1 (without flipping of the benzoate ring), and b with the positively charged guest 3 showing the flipping of the benzoate ring to form a short-ranged ionic interaction with the alkylammonium head group of the ligand. c Representative structure of the complex of the methyl octa-acid host with guest 4 showing the methyl benzoate rings forced upwards to accommodate the bulky ligand

The computational predictions correctly reproduce the large loss of affinity of guest 4 when going from the unmethylated and methylated forms of the octa-acid host. The main difference between octa-acid and methyl octa-acid is the presence of methyl group in para-position of the benzoate groups. The methyl groups protrude into the opening, partially occluding the mouth of the host cavity. Thermodynamic decomposition (see Tables 2 and 3) reveals that the loss of affinity is not due to weaker interaction between guest 4 and the host (average binding energies are −20.0 kcal/mol and −21.1 kcal/mol for the unmethylated and methylated hosts, respectively). Rather, the affinity loss is due to the more unfavorable reorganization free energy, and in particular to intramolecular strain energy which is 5 times greater for the methyl octa-acid than the octa-acid (Tables 2 and 3, Col. 8). Indeed, as shown in Fig. 4c, in order to accommodate guest 4, which is a bulky molecule with a bulky bromine lateral substituent, the methyl groups of the benzoate rings are forced upward, caused intramolecular strain in the host. This is not observed in the other guests of the set due to their slimmer profiles that can be accommodated in the interior of the host and through the narrow opening.

There is a wider variety of binding trends in the more complex CB-clip set (Table 4). Here, the effect of ionic screening is generally less striking than in the octa-acid host, partly because almost all of the hosts are positively charged. However, interesting exceptions exist which have been key to improved predictions. Consistent with its large charge density, ionic screening, for example, disfavors the binding of guest 3 by 9 kcal/mol. A similar effect, of smaller magnitude, is observed for guests 6 and 4. Conversely, the binding of the negatively charged guest (guest 7) is strengthened by ionic screening. In all of these cases ionic screening shifts the predictions closer to the experimental affinities, confirming the soundness of our model for this system.

Smaller guests, such as guests 2, are correctly predicted to be relatively poor binders of the CB-clip host due to their inability to form simultaneous strong ionic interactions with the sulfonate groups at both ends of the host. Guests with an aromatic core tend to to bind better due to effective stacking interactions with the naphthalene hydrophobic “claws” of the host. Guests 6 and 10, which optimally incorporate both of these features, are correctly predicted to be the best binders. Guests with negatively charged groups (guest 7) are correctly predicted to bind less well due to electrostatic repulsion with the sulfonate groups. Trends of this kind generally track host–guest interaction energies as measured by the average binding energy (Table 4, Col. 6). The most noticeable exception is guest 3, which is one of the worst binders (both computationally and experimentally) even though it is predicted to form the most favorable interactions with the host (−47 kcal/mol). These strong interactions originate by the ability of this guest to engage all four sulfonate groups of the host. However this is apparently achieved only at a great entropic loss (−32.5 kcal/mol, nearly double those of other guests in the set), reflecting the loss of flexibility of the guest (and the host) upon binding. The example of guest 3 underscores the complexity of molecular association equilibria and the often seemingly contradictory structure-activity relationships emerging from drug screening and optimization studies.

Conclusion

The present edition of the SAMPL blinded experiment offered unique challenges as well as invaluable opportunities for the validation and refinement of models and computational protocols. Displacement of water molecules by the ligand plays a crucial role in binding in these systems, especially for the octa-acid host. The high charge densities of the hosts make it challenging to correctly rank the affinities of negatively charged and positively charged guests unless charge-charge screening exercised by the ionic atmosphere is taken into account. Finally, in these systems binding is significantly affected by not only direct host–guest interactions but also dynamical conformational reorganization processes which must be fully modeled by free energy-based approaches.

To meet these challenges, we have employed a well established single-decoupling absolute binding free energy model (BEDAM) with implicit solvation (AGBNP2) and multi-dimensional replica exchange parallel conformational sampling along alchemical and temperature directions. The single-decoupling method is particularly suitable for the binding of charged ligands as it does not require separate estimation of the large free energies of transfer to vacuum as in the standard double-decoupling approach [52, 53]. To model the effects of water displacement within this framework, we have developed customized corrections to the implicit solvent models based on the thermodynamics of enclosed water molecules obtained from explicit solvent Hydration Site Analysis (HSA) studies. Our initial modeling predictions, which did not take into account salt effects, failed to correctly rank negatively charged guests versus positively charged guests. Modeling of ionic screening by means of the Debye–Hückel Generalized Born approach [42] yielded binding free energies in agreement with experimental data both in terms of accuracy of the absolute binding free energies and statistical correlation, thereby validating the physical basis of our approach.

This work underscores the need to accurately model the molecular nature of water enclosure in binding. Continuum implicit solvent models, while useful in other respects, do not capture these effects. The magnitude of water enclosure corrections, obtained by HSA and strictly validated in the present blinded fashion, cannot be ignored as they can be as large as the magnitude of binding free energies.

This SAMPL5 experience importantly also reminds us of the potential pitfalls of empirical parameterizations based on insufficiently diverse training sets. The extensive prior work on protein-ligand binding, because of the small charge densities involved, and the empirical training on the SAMPL4 dataset, which included only negatively charged guests, failed to provide crucial evidence about the role of ionic screening. The SAMPL5 blinded experiment allowed us to learn useful lessons to continue to improve the reliability of our binding free energy model.

Motivated by the promising results obtained in this study, we intend to extend the explicit/implicit solvent approach we followed here to protein receptors. The idea is to develop customized implicit solvation models of protein receptors incorporating the free energies of water displacement of specific hydration sites as measured by HSA. The combination of the accuracy of HSA with the full free energy treatment and conformational sampling capabilities of the BEDAM method is, we think a viable approach for the treatment of difficult protein-ligand binding equilibria.