CONTROL FUNCTION ASSISTED IPW ESTIMATION WITH A SECONDARY OUTCOME IN CASE-CONTROL STUDIES

Abstract

Case-control studies are designed towards studying associations between risk factors and a single, primary outcome. Information about additional, secondary outcomes is also collected, but association studies targeting such secondary outcomes should account for the case-control sampling scheme, or otherwise results may be biased. Often, one uses inverse probability weighted (IPW) estimators to estimate population effects in such studies. IPW estimators are robust, as they only require correct specification of the mean regression model of the secondary outcome on covariates, and knowledge of the disease prevalence. However, IPW estimators are inefficient relative to estimators that make additional assumptions about the data generating mechanism. We propose a class of estimators for the effect of risk factors on a secondary outcome in case-control studies that combine IPW with an additional modeling assumption: specification of the disease outcome probability model. We incorporate this model via a mean zero control function. We derive the class of all regular and asymptotically linear estimators corresponding to our modeling assumption, when the secondary outcome mean is modeled using either the identity or the log link. We find the efficient estimator in our class of estimators and show that it reduces to standard IPW when the model for the primary disease outcome is unrestricted, and is more efficient than standard IPW when the model is either parametric or semiparametric.

1. Introduction

Case-control studies are designed to study associations between exposures and, traditionally, a rare, primary outcome. Recently, genome-wide association studies (GWAS) are routinely conducted using a case-control study design, even when the primary disease outcome is relatively common, to increase power while maintaining relatively low cost. For instance, type 2 diabetes (T2D) is studied in a case-control GWAS study nested within the Nurses Health Study (NHS), and its prevalence in the cohort is estimated to be 8.4% (Cornelis et al., 2012). Such case-control studies typically collect information about additional, secondary outcomes, potentially associated with the primary disease. Specifically, body mass index (BMI) measurements, which are well known to be associated with T2D, were collected in the T2D case-control study. We are interested in re-purposing the T2D GWAS data to study associations of single nucleotide polymorphisms (SNPs) from the FTO gene, coding the Fat Mass and Obesity Protein, with BMI. As Nagelkerke et al. (1995) pointed out, and others later demonstrated (Jiang et al., 2006; Richardson et al., 2007; Wang and Shete, 2011, for instance), applying standard regression methods to case-control data for analysis of a secondary outcome can yield biased estimates, and therefore analysts need to adapt analysis schemes.

Several approaches have been proposed for the analysis of secondary outcomes from case-control studies. Nagelkerke et al. (1995) suggested that using solely the control group will be valid if it is fairly representative of the general population. This happens when the disease is rare, but may not hold otherwise. Richardson et al. (2007) and Monsees et al. (2009) discussed using inverse probability weighting (IPW), in which the contribution of each subject for the estimating equation is weighted by the inverse of its selection probability into the sample. IPW is robust to sampling bias, and is unbiased as long as the mean outcome model is correctly specified. However, IPW is less efficient than estimators that make additional modeling assumptions. Lin and Zeng (2009) proposed to estimate model parameters by maximizing the retrospective likelihood, taking into account case-control ascertainment by conditioning on disease status. Li and Gail (2012) generalized Lin and Zeng (2009)’s approach and suggested an adaptively weighted estimate of the association between the exposure and a binary secondary outcome, via a weighted sum of two retrospective likelihood-based estimators that differ in their assumed disease model. Chen et al. (2013) proposed a bias correction formula for an estimated odds ratio parameter, so that one can fit a regression model for the marginal or conditional analysis of the secondary outcome, and correct the estimate using the result from regressing the primary outcome on the secondary outcome and the exposure. Fewer methods are available for continuous secondary outcomes. Ghosh et al. (2013) elaborated on the retrospective likelihood approach, mainly to incorporate auxiliary covariates. These likelihood-based estimators rely heavily on distributional assumptions. Wei et al. (2013) modeled a continuous secondary outcome semi-parametrically and relaxed the distributional assumptions, but assumed that the primary disease is rare, which does not apply in many situations, including the T2D case-control study introduced earlier. Tchetgen Tchetgen (2014) proposed a general model based on a nonparametric parameterization for the secondary outcome conditional on disease status and covariates, for the identity, log, and logit link functions. Under the proposed parameterization, the mean model of the outcome conditional on disease status and covariates is factored into three functions: the mean model of the outcome conditional on covariates, the disease probability model, and a so-called selection bias function. This model requires correct specification of these functions, while it is robust to misspecification of the error distribution for the outcome. As this model requires maximization of factorized likelihood, it suffers from computational instability when incorporating auxiliary covariates, like most of the retrospective likelihood methods.

Current methodology (1) relies on distributional assumptions or (2) in the cases where fewer assumptions are made, proposed estimators are not necessarily efficient. Here, we use semiparametric theory to propose estimators for the population regression of the secondary outcome on covariates that are both robust and locally semiparametric efficient. We take the IPW estimator, which is the most robust of the existing estimators, and pose an additional modeling assumption by placing a model on the primary disease risk conditional on covariates. We construct a control function (Wooldridge, 2002; Petrin and Train, 2010) in terms of this model, and add it to the usual IPW estimating equation. We get a new estimating equation, which reduces to the usual IPW in the absence of any restriction on the model of disease risk given covariates. When this model is (semi)parametric, our proposed estimator is more efficient than IPW. Interestingly, we show that the new set of estimating equations uses the parameterization proposed by Tchetgen Tchetgen (2014). However, focusing on the identity and log links, our approach is more robust to certain forms of misspecification than the estimator of Tchetgen Tchetgen (2014). Our approach is reminiscent of Augmented IPW (AIPW) estimators in that a term is added to the IPW to reflect additional modeling assumptions. However, our estimators are crucially different than AIPW, which uses data external to the case-control sample. Specifically, AIPW augments IPW complete-cases with a score for the missingness/selection process which by analogy here would require both persons sampled and not sampled into the nested case-control study to contribute. However, in our setting only data available in the case-control sample contribute information, so that our estimators retain an IPW form. Furthermore, in a nested case-control study, one could in principle augment the estimating equations developed in this paper for additional efficiency gains using AIPW theory.

This paper is organized as follows. In Section 2 we describe the proposed class of estimators. In Section 3 we develop the semiparametric locally efficient estimator in the class of estimators, and its asymptotic properties. Throughout, we focus on the identity link (continuous outcome) and the log link (count, or positive outcome) for modeling the outcome mean. In Section 4 we present simulation results, empirically demonstrating the balance that our proposed estimators strike between robustness and efficiency, by comparing them to prevailing estimators in the literature. We use our proposed estimator in Section 5 in associating SNPs from the FTO gene with BMI, using the case-control, GWAS, T2D data set. Finally, in Section 6 we discuss our results.

2. Model

Suppose the case-control study has i = 1, …, n independent participants, with an indicator for the primary disease D_i, so that D_i = 1 if the ith participant is a case and D_i = 0 otherwise. Let Y_i denote the secondary outcome of interest, and X_i the q × 1 vector of covariates of subject i. Let S_i be an indicator of inclusion in the case-control study. The observed data are given by {(S_iY_i, S_iX_i, S_iD_i), i = 1 …, n}.

We assume that the probability of selection into the study depends solely on the disease status, D_i, and is denoted by Pr(S_i = 1|D_i, Y_i, X_i) = π(D_i). Further, we assume that π(D_i) is known by design. Equivalently, we assume that Pr(D_i = 1) in the population is known. Denote by p(X_i) = Pr(D_i = 1|X_i) the conditional probability of disease given covariates in the target population, and let

$$\mu \left({\mathbf{X}}_i;\mathit{\beta }\right)=g\left\{\mathbb{E}\left(Y_i|{\mathbf{X}}_i\right)\right\}$$ (2.1)

be the model for the mean after transformation using the link function g(·). In the case of a continuous outcome with the identity link, for instance, $\mu \left({\mathbf{X}}_i;\mathit{\beta }\right)=\mathbb{E}\left(Y_i|{\mathbf{X}}_i\right)$, and when the log link is used, $\exp \left\{\mu \left({\mathbf{X}}_i;\mathit{\beta }\right)\right\}=\mathbb{E}\left(Y_i|{\mathbf{X}}_i\right)$, where expectations are taken over the entire population (rather than the case-control study population). Note that β is the q × 1 vector of population regression coefficients that we wish to estimate. Let $ℳ$ denote the semiparametric model defined by the mean model specification (2.1) and the assumed model for p(X).

Hereafter, unless otherwise stated, all expectations are taken with respect to the case-control study population. For the target of inference in the general population, we use the notation μ(X; β), i.e. without explicitly writing it in term of expectations. Taking an estimating equations approach, parameter estimates are obtained by solving an equation of the form

$${\displaystyle \sum _{i=1}^n{\mathbf{U}}_i(\mathit{\beta })=0}$$ (2.2)

for β, where U_i(β) are q × 1 functions, with $\mathbb{E}\left\{{\mathbf{U}}_i\left(\mathit{\beta }\right)\right\}=0$, i.e. the estimating equation should be unbiased. A traditional approach for estimation in case-control studies, originating in the sample survey literature, is inverse probability weighting (IPW) of each equation according to its probability of selection into the study. IPW to estimate the population mean model entails solving equation (2.2) for β using

$${\mathbf{U}}_{\mathit{ipw},i}\left(\mathit{\beta }\right)=\frac{h\left({\mathbf{X}}_i\right)S_i}{\pi \left(D_i\right)}[Y_i-g^{-1}\{\mu ({\mathbf{X}}_i;\mathit{\beta })\}],$$ (2.3)

where h(X_i) is a user specified q×1 function, such that $\mathbb{E}(\partial {\mathbf{U}}_{\mathit{ipw}}/\partial \mathit{\beta })$ invertible. To see that this equation is unbiased, consider its expectation over the super-population of N individuals, and using the sampling indicator S_i, to obtain:

$${\displaystyle \sum _{i=1}^N\frac{S_{i}h\left({\mathbf{X}}_i\right)}{\pi \left(D_i\right)}[Y_i-g^{-1}\{\mu ({\mathbf{X}}_i;\mathit{\beta })\}]Pr(S_i=1|{\mathbf{X}}_i,D_i)}.$$

Since Pr(S_i = 1|X_i, D) = π(D_i), and $\mathbb{E}[Y|\mathbf{X}]=g^{-1}\{\mu (\mathbf{X};\beta )\}$ in the target population, consistency follows under fairly standard conditions. From now we suppress the sampling indicator S_i in the notation since we always use the case-control study sample in which S_i = 1 for all i = 1, …, n.

Consider an extension of the IPW estimating equation, constructed by an additive term of a general control function given below.

A set of estimating equations for β

Let $ℳ$ be the semiparametric model with known sampling probabilities into the case-control sample π(D) and assumed models g⁻¹{μ(X, β)} and p(X). Define the set of control-function assisted IPW estimating equations of the form

$${\mathbf{U}}_{\mathit{cont}}(\mathit{\beta })={\displaystyle \sum _{i=1}^n\frac{1}{\pi (D_i)}\left(h_1({\mathbf{X}}_i)[Y_i-g^{-1}\{\mu ({\mathbf{X}}_i;\mathit{\beta })\}]-h_2({\mathbf{X}}_i,D_i)\right)=0,}$$ (2.4)

where h₂(X, D) is a q × 1 vector control function that depends on the disease model and satisfies $\mathbb{E}\{h_2(\mathbf{X},D)/\pi (D)|\mathbf{X},S=1\}=0$. Control functions have been used in econometrics to control for bias due to specific forms of selection (see Wooldridge (2002); Petrin and Train (2010)). In the present setting, we adopt this framework for efficiency improvement.

Note that the control function h₂(X, D)/π(D) is inverse probability weighted, and has mean zero for all h₂, so that U_cont(β) is unbiased. The choice h₂(X, D) = 0 gives standard IPW. We aim to find h₂(X, D) ≠ 0 such that the resulting estimator is asymptotically at least as efficient as IPW for a fixed h₁(X). We subsequently characterize the optimal choice of h₁(X).

In Lemma 1 in the supplementary material, we show that the set of functions h₂(X, D) satisfying the mean zero restriction $\mathbb{E}\{h_2(\mathbf{X},D)/\pi (D)|\mathbf{X},S=1\}=0$ is equivalent to the set of functions ${\stackrel{\sim }{h}}_2(\mathbf{X})\{D-p(\mathbf{X})\}$, so that for any function h₂(X, D) from this set, there exists a function ${\stackrel{\sim }{h}}_2(\mathbf{X})$ such that $h_2(\mathbf{X},D)={\stackrel{\sim }{h}}_2(\mathbf{X})\{D-p(\mathbf{X})\}$. The mean zero restriction is thus satisfied when p(X) is correctly specified. Here, we use semiparametric theory to study in a unified framework the semiparametric efficiency implications of positing a nonparametric, semiparametric or parametric model for p(X), which is always assumed to be correctly specified.

3. Semiparametric theory

In this section, we develop the semiparametric framework that serves as a basis for our methods. We characterize the Regular Asymptotic Linear (RAL) estimators corresponding to a given disease model p(X) and subsequently discuss inference.

3.1. The RAL estimators for β

Denote the tangent space of a parametric, semiparametric, or nonparametric submodel for p(X) by Λ_D,sub. In the supplementary material, we provide examples for such tangent spaces. Let Π(v|Λ) denote the orthogonal projection of the vector v on the subspace Λ of ${ℒ}_2^0$.

Theorem 1

The set of influence functions of β is given by

$$\mathrm{\Gamma }=\left\{\frac{1}{\pi (D)}{h}_1(\mathbf{X})[Y-g^{-1}\{\mu (\mathbf{X},\mathit{\beta })\}]-\frac{h_2(\mathbf{X},D)}{\pi (D)}+\mathrm{\Pi }\left(\frac{h_2(\mathbf{X},D)}{\pi (D)}|{\mathrm{\Lambda }}_{D,\mathit{sub}}\right):\mathbb{E}\{\frac{1}{\pi (D)}{h}_2(\mathbf{X},D)|\mathbf{X}\}=0\right\}\cap {ℒ}_2^0$$

up to a multiplicative constant.

Theorem 1 characterizes all RAL estimators of β in a semiparametric model $ℳ$ defined by μ(X, β) and a choice of model for p(X). The proof (in the supplementary material) states that if

$$\frac{h_2(\mathbf{X},D)}{\pi (D)}=\mathrm{\Pi }\left(\frac{h_2(\mathbf{X},D)}{\pi (D)}|{\mathrm{\Lambda }}_{D,\mathit{sub}}\right),$$

then all influence functions for β are IPW influence functions. This equality holds, for instance, in the special case where the model p(X) is saturated, or nonparametric. In other words, even if one uses the estimator (2.4), for any choice of h₂(X, D) the asymptotic distribution of the estimator will mimic the IPW estimator, and the estimator could not be made more efficient. The following Corollary 1 summarizes this observation.

Corollary 1

Consider the model $ℳ$ with p(X) unrestricted. For a fixed choice of h₁(X) in (2.4), the optimal choice of function h₂(X, D) is $h_2^{\mathit{opt}}(\mathbf{X},D)=0$, and the most efficient estimator for β is the IPW estimator that solves the estimating equation

$${\mathbf{U}}_{\mathit{ipw}}(\mathit{\beta })={\displaystyle \sum _{i=1}^n\frac{1}{\pi (D_i)}\left(h_1({\mathbf{X}}_i)[Y_i-g^{-1}\{\mu ({\mathbf{X}}_i;\mathit{\beta })\}]\right)=0}.$$

In the following section we restrict p(X) by imposing modeling assumptions. We find the most efficient estimating equation for β in Γ, by deriving the optimal functions h₁(X) and h₂(X), and provide the locally efficient estimator of β.

3.2 Inference for a restricted model p(X)

Theorem 2

Let $ℳ$ be the model defined by the sampling probability π(D), the population mean function g⁻¹(μ(X; β)) and the disease model p(X). The following hold for the estimator for β in model $ℳ$:

1. Suppose that h₁(X) is fixed. The function $h_2^{\mathit{opt}}(\mathbf{X},D)$ that minimizes the variance of $\widehat{\mathit{\beta }}$ is given by

   $$h_2^{\mathit{opt}}(\mathbf{X},D)=h_1(\mathbf{X})[\mathbb{E}(Y|\mathbf{X},D;\mathit{\beta })-g^{-1}\{\mu (\mathbf{X};\mathit{\beta })\}].$$
   Denote $\stackrel{\sim }{\mu }(\mathbf{X},D;\mathit{\beta })=g\{\mathbb{E}(Y|\mathbf{X},D;\mathit{\beta })\}$ which satisfies $\mathbb{E}\left\{\mathbb{E}(Y|\mathbf{X},D;\beta )|\mathbf{X}\right\}=g^{-1}\{\mu (\mathbf{X};\mathit{\beta })\}$. Then the influence function corresponding to $h_2^{\mathit{opt}}(\mathbf{X},D)$, up to a multiplicative constant, is

   $$\frac{h_1(\mathbf{X})}{\pi (D)}[Y-g^{-1}\{\stackrel{\sim }{\mu }(\mathbf{X},D_i;\mathit{\beta })\}].$$
2. The semiparametric efficient influence function further has $h_1(\mathbf{X})=h_1^{\mathit{opt}}(\mathbf{X})$, with

   $$h_2^{\mathit{opt}}(\mathbf{X})=\mathbb{E}{\left\{\frac{1}{\pi (D)}\mathit{var}(Y|D,\mathbf{X})|\mathbf{X}\right\}}^{-1}\frac{\partial }{\partial \mathit{\beta }}[g^{-1}\{\stackrel{\sim }{\mu }(\mathbf{X},D;\mathit{\beta })\}].$$

The corresponding estimator $\widehat{\mathit{\beta }}$ is locally efficient in the submodel of $ℳ$ in which h₁(X) and h₂(X, D) are correctly modeled. If these functions are misspecified, $\widehat{\mathit{\beta }}$ will still be CAN, but less efficient. The proof is provided in the supplementary material.

Tchetgen Tchetgen (2014) provided parameterizations of $\stackrel{\sim }{\mu }(\mathbf{X},D;\mathit{\beta })$ in terms of μ(X; β) for the identity, log, and logit links. We use these parameterizations to construct feasible estimating equations ${\mathbf{U}}_{\mathit{ident}}^{\mathit{opt}}$ and ${\mathbf{U}}_{\log }^{\mathit{opt}}$ based on Theorem 2. Consider first the identity link function. As was shown in Tchetgen Tchetgen (2014), $\mathbb{E}(Y|\mathbf{X},D;\mathit{\beta })$ can be parameterized as $\mathbb{E}(Y|\mathbf{X},D;\mathit{\beta })=\mu (\mathbf{X};\mathit{\beta })+\gamma (\mathbf{X})\{D-p(\mathbf{X})\}$, where $\gamma (\mathbf{X})=\mathbb{E}(Y|D=1,\mathbf{X})-\mathbb{E}(Y|D=0,\mathbf{X})$ is the “selection bias function”, resulting from sampling according to disease status. We have that

$${\mathbf{U}}_{\mathit{ident}}^{\mathit{opt}}(\mathit{\beta })={\displaystyle \sum _{i=1}^n\frac{h_1^{\mathit{opt}}({\mathbf{X}}_i)}{\pi (D_i)}\left[Y_i-\mu ({\mathbf{X}}_i;\mathit{\beta })-\gamma ({\mathbf{X}}_i)\{D_i-p({\mathbf{X}}_i)\}\right]}.$$

For the log link, it was shown in Tchetgen Tchetgen (2014) that

$$\stackrel{\sim }{\mu }(\mathbf{X},D;\mathit{\beta })=\mathbb{E}(Y|\mathbf{X},D;\mathit{\beta })=\exp (\mu (\mathbf{X};\mathit{\beta })+\nu (\mathbf{X},D)-\log \mathbb{E}[\exp \{\nu (\mathbf{X},D)\left\}\right|\mathbf{X}]),$$

where the selection bias function ν(X, D) is defined as

$$\nu (\mathbf{X},D)=\log \left\{\frac{\mathbb{E}(Y|\mathbf{X},D)}{\mathbb{E}(Y|\mathbf{X},D=0)}\right\}$$

and reflects the log multiplicative association between D and Y given X. Note that the expectation in $\mathbb{E}[\exp \{\nu (\mathbf{X},D)\left\}\right|\mathbf{X}]$ is taken over the population. Therefore, we have that

$${\mathbf{U}}_{\log }^{\mathit{opt}}(\mathit{\beta })={\displaystyle \sum _{i=1}^n\frac{h_1^{\mathit{opt}}({\mathbf{X}}_i)}{\pi (D_i)}\left\{Y_i-\exp (\mu ({\mathbf{X}}_i;\mathit{\beta })+\nu ({\mathbf{X}}_i,D_i)-\log \mathbb{E}[\exp \{\nu ({\mathbf{X}}_i,D_i)\}|{\mathbf{X}}_i])\right\}}.$$

Note that these estimating equations are robust, in the sense that even if the selection bias functions γ and ν are misspecified, the estimating equations would remain unbiased as long as μ(X; β) and p(X) are correctly modeled.

Below we use the efficient influence function to define an estimating equation by substituting empirical estimates of all unknown nuisance parameters. The asymptotic distribution of the resulting estimator allowing for model misspecification is given in Section 3.3.

3.3. Asymptotic properties

We saw that $\widehat{\mathit{\beta }}$ is a RAL estimator in model $ℳ$ in which p(X) is correctly specified. We compute $\widehat{\mathit{\beta }}$ by solving the estimating equation ${\widehat{\mathbf{U}}}_{\mathit{cont}}^{\mathit{opt}}(\mathit{\beta })=0$, defined as ${\mathbf{U}}_{\mathit{cont}}^{\mathit{opt}}(\mathit{\beta })$ with ${\widehat{h}}_1(\mathbf{X})$, ${\widehat{h}}_2(\mathbf{X},D)$, and $\widehat{p}(\mathbf{X})$.

Let δ denote the parameters for the selection bias function, i.e. either ν(X, D; δ) (log link) or γ(X; δ) (identity link). Let θ = (β^T, δ^T)^T. It is convenient to estimate θ jointly, by modifying the estimating equation ${\mathbf{U}}_{\mathit{cont}}^{\mathit{opt}}(\mathit{\beta })$ to define ${\mathbf{U}}_{\mathit{cont}}^{\mathit{opt}}(\mathit{\theta })$ by taking

$$h_1^{\mathit{opt}}(\mathbf{X})=\mathbb{E}{\left\{\frac{1}{\pi (D)}\mathrm{var}(Y|D,\mathbf{X})|\mathbf{X}\right\}}^{-1}\frac{\partial }{\partial \mathit{\theta }}[g^{-1}\{\mu (\mathbf{X},D;\mathit{\theta })\}].$$

In the supplementary material, we describe how to compute the estimator $\widehat{\mathit{\theta }}$, and derive its asymptotic distribution. To this end, we need to know its influence function, which is found from the first order Taylor expansion of the estimating equation around the limiting value of $\widehat{\mathit{\theta }}={({\widehat{\mathit{\beta }}}^T,{\widehat{\mathit{\delta }}}^T)}^T$. Let V(α) be the estimating equation for α. The influence function for θ is given by

$$\begin{array}{l}\psi (\mathit{\theta };\mathit{\alpha })=-{\left[\mathbb{E}\frac{\partial }{\partial \mathit{\theta }}\left\{{\mathbf{U}}_{\mathit{cont}}(\mathit{\theta };\mathit{\alpha })\right\}\right]}^{-1}\times \\ \left[{\mathbf{U}}_{\mathit{cont}}(\mathit{\theta };\mathit{\alpha })-\mathbb{E}\left\{\frac{\partial }{\partial \mathit{\alpha }}{\mathbf{U}}_{\mathit{cont}}(\mathit{\theta };\mathit{\alpha })\right\}\mathbb{E}{\left\{\frac{\partial }{\partial \alpha }\mathbf{V}(\mathit{\alpha })\right\}}^{-1}\mathbf{V}(\mathit{\alpha })\right].\end{array}$$

A consistent estimator of the covariance matrix of the estimator $\widehat{\mathit{\theta }}$ is given by

$$\widehat{\sum }(\mathit{\theta })=\frac{1}{n}{\displaystyle \sum _{i=1}^n{\widehat{\psi }}_i\left(\widehat{\mathit{\theta }};\widehat{\mathit{\alpha }}\right){\widehat{\psi }}_i^T\left(\widehat{\mathit{\theta }};\widehat{\mathit{\alpha }}\right)},$$

where ${\widehat{\psi }}_i$ is the influence function evaluated at the ith subject, with all expectations in the expression ψ(θ; α) estimated by the corresponding sample means.

Corollary 2

The estimator $\widehat{\mathit{\theta }}$ that solves ${\mathbf{U}}_{\mathit{cont}}\left(\mathit{\beta },\mathit{\delta };\widehat{\mathit{\alpha }}\right)$ under $ℳ$ in which μ(X, β) and p(X) are correctly specified, is asymptotically normally distributed with asymptotic mean θ and covariance

$$\sum (\mathit{\theta })=\mathbb{E}\{\psi (\mathit{\theta };\mathit{\alpha })\psi {(\mathit{\theta };\mathit{\alpha })}^T\}.$$

Furthermore, in the submodel where ${\widehat{h}}_1^{\mathit{opt}}(\mathbf{X})\to p{\lim }_{n\to \infty }{h}_1^{\mathit{opt}}(\mathbf{X})$, and ${\widehat{h}}_2^{\mathit{opt}}(\mathbf{X},D)\to p{\lim }_{n\to \infty }{h}_2^{\mathit{opt}}(\mathbf{X},D)$, $\widehat{\mathit{\beta }}$is locally efficient.

Note that $\widehat{\mathit{\theta }}$ will be asymptotically normal with covariance matrix $\mathbb{E}\{\psi \left({\mathit{\theta }}^{\ast };\widehat{\mathit{\alpha }}\right)\psi {\left({\mathit{\theta }}^{\ast };\widehat{\mathit{\alpha }}\right)}^T\}$, where θ^∗ is $p{\lim }_{n\to \infty }\widehat{\mathit{\theta }}$, even if one of p(X), μ(X; β), or both, are misspecified. In the case of misspecification, θ^∗ is likely a biased estimate of the true θ.

4. Simulations

In this section, we demonstrate the robustness and efficiency of our proposed estimators, compared to the prevailing estimators, when modeling the mean via the identity link. We simulate case-control studies with continuous secondary outcomes in two sets of simulations. The goal of the first set was to investigate the robustness and efficiency of the proposed control function estimator (‘cont’) compared to multiple other prevailing estimators: the estimator that conditions on disease status, using disease indicator in the regression of the secondary outcome on covariates ‘Dind’, the estimator that treats all observations equally, ignoring disease status ‘pooled’, the usual IPW estimator (‘IPW’), and the estimator of Tchetgen Tchetgen (2014) (‘TT’), implemented via an approximate algorithm. The goal of the second set was to compare the performance of cont to the estimators proposed by Ghosh et al. (2013) and Lin and Zeng (2009). In each section below, we describe the simulations and provide results, where for cont, we provide two sets of results: when the model for $\mathbb{E}(Y|\mathbf{X},D)$ is correctly specified, and when it is misspecified. For each scenario, we calculated the mean bias of the estimates $\frac{1}{n.\mathit{sim}}{\displaystyle {\sum }_{k=1}^{n.\mathit{sim}}({\widehat{\beta }}_k-\beta )}$, the mean squared error (MSE) $\frac{1}{n.\mathit{sim}}{\displaystyle {\sum }_{k=1}^{n.\mathit{sim}}{({\widehat{\beta }}_k-\beta )}^2}$, the sample standard deviation of the estimator ${\{\frac{1}{n.\mathit{sim}}{\displaystyle {\sum }_{k=1}^{n.\mathit{sim}}{({\widehat{\beta }}_k-\widehat{\beta })}^2}\}}^{1/2}$, the mean of the estimated standard deviations in the simulations $\frac{1}{n.\mathit{sim}}{\displaystyle {\sum }_{k=1}^{n.\mathit{sim}}\widehat{\text{sd}\left({\beta }_k\right)}}$, and the Wald coverage probability. Due to limited space, only some of the simulation results are presented in the main manuscript. Additional extensive simulation results are relegated to the supplementary material, including all summaries pertaining to the performance of the estimators Dind and pooled.

The proposed cont estimators and the estimated standard deviations were calculated as described in the supplementary material. The IPW estimator and the estimated standard deviations were calculated using Newton-Raphson iterations of the estimating function U_ipw, with h₁(X_i) = X_i, with the robust (sandwich) covariance matrix. The naïve estimators Dind and pooled were calculated from linear regression.

All simulation scenarios included 500 cases and 500 controls, and were run 1000 times. The prevalence of the disease D in the population (the primary case-control outcome) was fixed at 0.12, i.e. the disease is relatively common.

We conducted other simulation studies under a variety of plausible scenarios. First, we performed a simulation study for the identity link with a single exposure variable, in which we also considered the maximum likelihood estimator proposed by Tchetgen Tchetgen (2014). Second, we performed simulations for the log link, and lastly, we carried out another identity link simulation study closely mimicking the observed data distribution in the T2D sample. Results for these additional scenarios are provided in the supplementary material. In general, they support the conclusions of the simulations presented here.

4.1. Simulation set 1 - studying robustness and efficiency

To design the simulations, we first note that we need to sample data from the distribution f(Y, D|X) in such a way that the parameter of interest $\mathbb{E}[Y|\mathbf{X}]$ can a priori be defined explicitly. We consider the decomposition f(Y, D|X) = f(Y|D, X)Pr(D|X), and we generate the data according to the two parts of the likelihood, Pr(D|X) and f(Y|D, X). Note that this decomposition always holds and makes no assumption on the underlying model. We use the the general reparameterization of $\mathbb{E}[Y|\mathbf{X},D]$ (proposed by Tchetgen Tchetgen (2014)) as an explicit function of $\mathbb{E}[Y|\mathbf{X}]$, which allows us to specify the two parts of the likelihood using variation independent parameters (Pr(D = 1|X), γ(X), and E(Y|X)). First, exposure/covariate variables X were sampled. Then, disease probabilities were calculated for each subject, based on exposure values. The intercept for the disease model p(X) was set so that disease prevalence was 0.12. Disease statuses were obtained from disease probabilities, and the secondary outcomes Y were generated based on exposure values and disease status.

In more detail, we simulated two covariates, X₁ and X₂ where $X_1~\mathcal{N}(2,4)$, and X₂ ~ Binary(0.1). The primary disease probability was calculated by

$$\mathrm{logit}\{Pr(D=1|\mathbf{X})\}=-3.2+0.3X_1+X_2,$$

and disease status was sampled. The conditional mean of the secondary outcome was:

$$\mathbb{E}(Y|\mathbf{X},D)=50+4X_1+3X_2+3X_1{X}_2+\{D-p(\mathbf{X})\}(3+2X_1+2X_2+2X_1{X}_2),$$

so that μ(X, β) = X^T β with X = (1, X₁, X₂, X₁X₂)^T and β = (50, 4, 3, 3)^T, and γ(X) = X^T α with α = (3, 2, 2, 2)^T. The residuals were sampled by $\epsilon ~\mathcal{N}(0,4)$. The design matrix for γ(X) was X = (1, X₁, X₂, X₁X₂)^T when the model was correctly specified. We studied the following forms of misspecification of the design matrix of γ(X). The estimator ‘cont-mis1’ had the design matrix X = (1, X₁, X₂)^T (no interaction term), ‘cont-mis2’ had X = (1, X₁)^T, ‘cont-mis3’ had X = (1, X₂)^T, and ‘cont-mis4’ accounted only for an intercept, i.e. design matrix X = 1. ‘cont-cor’ used the correct design matrix.

Table 1 compares the results of cont-cor, cont-mis1, IPW, and the TT estimator under correct specification, and misspecification (the same design matrix used by cont-mis1). Results for other estimators are in the supplementary material. One can see that all of cont-cor, cont-mis1 and IPW and TT-cor are approximately unbiased. Both the MSE and the empirical standard deviation of the cont estimator were higher when the model for γ(X) was misspecified, yet the MSE of cont-cor was always smaller than that of the IPW. In fact, the relative efficiency of cont-cor was from 17% (β₂) to 71% (β₃) lower than that of the IPW. TT-mis performed poorly under misspecification of γ(X), as expected. In the supplementary material, one can see that the estimator Dind and pooled perform poorly as well, as expected.

Table 1.

Simulation set 1 results. Results are reported for the cont-cor, cont-mis1 (the cont estimator under correct specification, and misspecification, of the selection bias function γ(X)), the IPW estimator, and the TT estimator (TT-cor, TT-mis) of Tchetgen Tchetgen (2014) under the same correct specification and misspecification of γ(X) used by cont. For each estimator and each estimated parameter the table reports the estimator’s mean bias, MSE, empirical standard deviation over all simulations, mean estimated standard deviation using the appropriate formula, and coverage probability.

estimator/value	bias	MSE	emp sd	est sd	coverage
	Intercept, β0 = 50
cont-cor	0.007	0.019	0.138	0.139	0.958
cont-mis1	0.007	0.019	0.138	0.139	0.959
IPW	0.006	0.019	0.139	0.141	0.964
TT-cor	0.006	0.033	0.183	0.172	0.929
TT-mis	−3.653	14.141	0.894	0.355	0.000
	X1, β1 = 4
cont-cor	−0.001	0.001	0.038	0.042	0.967
cont-mis1	−0.001	0.001	0.038	0.044	0.971
IPW	0.000	0.002	0.045	0.047	0.964
TT-cor	−0.001	0.001	0.036	0.032	0.922
TT-mis	−0.289	0.104	0.144	0.084	0.179
	X2, β2 = 3
cont-cor	0.028	0.228	0.477	0.491	0.960
cont-mis1	0.024	0.236	0.485	0.526	0.970
IPW	0.024	0.272	0.521	0.521	0.950
TT-cor	0.027	0.274	0.523	0.496	0.941
TT-mis	0.223	2.711	1.632	0.792	0.669
	X1 X2, β3 = 3
cont-cor	0.005	0.022	0.148	0.207	0.998
cont-mis1	0.011	0.025	0.159	0.164	0.955
IPW	0.018	0.076	0.275	0.247	0.909
TT-cor	0.003	0.020	0.143	0.099	0.821
TT-mis	1.015	1.121	0.301	0.145	0.006

4.2. Simulation set 2 - comparison to other recently proposed methods

Here we compare our estimator ‘cont’, and the IPW, to the pseudo-likelihood estimator proposed by Ghosh et al. (2013) and the retrospective likelihood estimator proposed by Lin and Zeng (2009). We followed the simulation scenario performed in Ghosh et al. (2013), using code shared by the authors. We also adapted our simulations from Section 4.1 to their assumed data structure, and compared the effects of the associations of the SNP with the disease (via p(X) and with the outcome in the cases versus controls (via γ(X)) on the performance of the IPW, cont and retrospective likelihood estimators.

First, we ran 1000 simulations in Ghosh et al. (2013) settings and compared the estimators. In their simulations, they focused on a single coefficient, namely the effect of a single nucleotide polymorphism (SNP) G on the outcome Y. G had a minor allele frequency (MAF) of 0.25 and effect size 0.1. In addition, there were two covariates Z, a continuous variable, and a binary one, the later with probability 0.45 of having the values 1. The disease and the secondary outcome were modeled by a bivariate normal distribution and thresholding, so that the disease model is dependent on G and Z via a logistic model. However, it is unclear how to correctly specify γ(X). We use a linear model of the form γ(X) = Xδ, though this is likely incorrect. The outcome Y had variance 1, and disease prevalence was 0.05. We used 500 cases and 500 controls. More details can be found in Ghosh et al. (2013). The results of these simulations are presented at the top part of Table 2.

Table 2.

Simulation set 2 results. We compare results for the usual IPW estimator, cont, the pseudo-likelihood estimator of Ghosh et al. (2013) (‘Ghosh 2013’), and the retrospective likelihood estimator of Lin and Zeng (2009) (‘Lin2009’). The top part of the table provides results of simulations in the settings in Ghosh et al. (2013), and the lower parts summarize simulations designed according to the conditional mean model $\mathbb{E}(Y|\mathbf{X},D)$. In all scenarios, the SNP effect was β = 0.1. The SNP effects on the disease model and the selection bias functions are provided in the section headers, with α_g being the SNP effect on the selection bias function, and δ_g the SNP effect of disease probability. For each estimator and each estimated parameter the table reports the estimator’s mean bias, MSE, empirical standard deviation over all simulations, mean estimated standard deviation using the appropriate formula, and coverage probability.

estimator/value	bias	MSE	emp sd	est sd	coverage
	Settings 1 (Ghosh, 2013)
Ghosh2013	0.000	0.003	0.056	0.057	0.961
cont	0.000	0.004	0.067	0.067	0.952
IPW	0.000	0.004	0.067	0.067	0.953
Lin2009	−0.765	0.588	0.049	0.055	0.000
	Settings 2a: δg = 0, αg = 0
Ghosh2013	−0.002	0.066	0.258	0.261	0.952
cont	−0.002	0.068	0.261	0.262	0.949
IPW	−0.002	0.069	0.262	0.263	0.946
Lin2009	0.006	0.039	0.197	0.200	0.949
	Settings 2b: δg = 0, αg = 0.6
Ghosh2013	0.027	0.067	0.257	0.260	0.950
cont	−0.002	0.068	0.262	0.262	0.951
IPW	−0.002	0.069	0.263	0.263	0.946
Lin2009	0.250	0.102	0.200	0.200	0.749
	Settings 2c: δg = 0.3, αg = 0
Ghosh2013	0.018	0.068	0.260	0.256	0.943
cont	0.008	0.072	0.269	0.259	0.940
IPW	0.008	0.072	0.269	0.260	0.946
Lin2009	−0.030	0.040	0.197	0.196	0.942
	Settings 2d: δg = 0. 3, αg = 0.6
Ghosh2013	0.049	0.069	0.259	0.255	0.934
cont	0.008	0.072	0.269	0.260	0.940
IPW	0.009	0.073	0.270	0.261	0.946
Lin2009	0.216	0.086	0.198	0.197	0.798

Then, we ran 1000 simulations in settings adapted from our simulations from Section 4.1. Here, we had the same G and Z variables, with Z₁ continuous and Z₂ binary. $Z_1~\mathcal{N}(0,4)$, and Z₂ ~ Binary(0.2). The primary disease probability was calculated by

$$\mathrm{logit}\{Pr(D=1|\mathbf{X})\}=-3.8+0.3Z_1+Z_2+{\delta }_{g}G,$$

with δ_g ∈ {0, 0.3} and disease status was sampled. Note that the intercept value was selected so that disease prevalence was roughly 0.05, as in Ghosh et al. (2013). The SNP G had MAF 0.3. The conditional mean model was:

$$\mathbb{E}(Y|\mathbf{X},D)=3+0.7Z_1+0.5Z_2+0.1G+\{D-p(\mathbf{X})\}(1+0.5Z_1+0.3Z_2+{\alpha }_{g}G),$$

with α_g ∈ {0, 0.6}. 500 cases and 500 controls were sampled from the simulated population. We compared the estimation of the effect of G on Y. The results of these simulations are presented at the bottom part of Table 2.

In the first simulation setting, the estimators Ghosh2013, IPW and cont were unbiased and achieved the nominal coverage level, while Lin2009 was heavily biased. Note that cont likely misspecified the model γ(X). The estimator of Ghosh et al. (2013) had slightly lower MSE than the IPW and control function estimators, as expected, since this estimator is based on the same model used to produce the simulated data. In the later simulation settings, in which the data were sampled by specifying models for p(X), γ(X), and μ(X; β), cont and IPW were nearly unbiased for all specifications of α_g and δ_g. Ghosh2013 had comparable, and slightly lower, MSE than IPW and cont in all settings, but was more biased when α_g = 0.6. Lin2009 had the lowest MSE when α_g = δ_g = 0, i.e. when there is no selection bias due to the SNP effect. However, when the SNP was associated with the probability of disease, it became biased and had low coverage of 75%–80%. This bias in Lin2009 is likely due to the parametric assumption on the disease model, which are different than the assumptions made by Ghosh2013, that was less affected by SNP effects on the disease or selection bias functions.

5. Analysis of Type 2 diabetes GWAS

We analyzed the case-control GWAS study of T2D, with the goal of identifying SNPs in the FTO gene region, associated with BMI. There were 3080 female participants in this data, genotyped on the affymetrix 6.0 array, with 1326 cases and 1754 controls (Cornelis et al., 2012). There were 152 genotyped SNPs from the region on chromosome 16 spanning the FTO variants. There are a few SNPs from the FTO gene associated with BMI (Speliotes et al., 2010), and validated on large cohorts. In particular, the SNP rs1558902 has the strongest association with log-BMI. This SNP is not in the data, but other SNPs in high Linkage Disequilabrium (LD) with it are. The population prevalence of T2D was 8.4% (Cornelis et al., 2012). We compared the usual IPW, the control function estimator cont, the pooled estimator ignoring disease status, the estimator Dind with disease indicator in the design matrix, and the estimator of Lin and Zeng (2009) dubbed Lin2009. We did not compare to the estimator proposed by Ghosh et al. (2013), since their code was not applicable to the specific setting of variables. Also, we could not compare to Tchetgen Tchetgen (2014) because the MLE he proposed suffered from (non)convergence problems in the data application mainly due to the presence of multiple covariates.

All analyses were adjusted to age, binary smoking status (current versus past or never), binary alcohol intake measure according to less or more than 10 grams a day, physical activity (above or under the median) and to the first four principal components of the genetic data. The outcome, BMI, was log transformed, as is usually done with BMI. For the analysis using the estimator cont, all models, i.e. the mean model of BMI, the model for disease probability Pr(D = 1|X), and the selection bias model γ(X) used the same covariates. All SNPs were analyzed in the additive mode of inheritance.

Figure 1 compares between the estimated effect sizes and their respective standard errors (SEs), of all 152 SNPs in the FTO gene, between cont, and the other estimators under consideration. The cont estimator yielded roughly identical results to that of the IPW. This is in agreement with the simulation study imitating the effect sizes in the T2D data set (see Supplementary Material), and is expected since both T2D and BMI are complex traits, and no single SNP highly affects them. Thus, incorporating the disease and selection bias models in the estimation cannot improve it much. As seen in Table 3, the p-values and adjusted p-values of the cont estimates are smaller than those of the IPW. Effect estimates of other estimators that make more assumptions on the data distribution, are quite different than those of cont, while their SEs are usually smaller.

Figure 1.

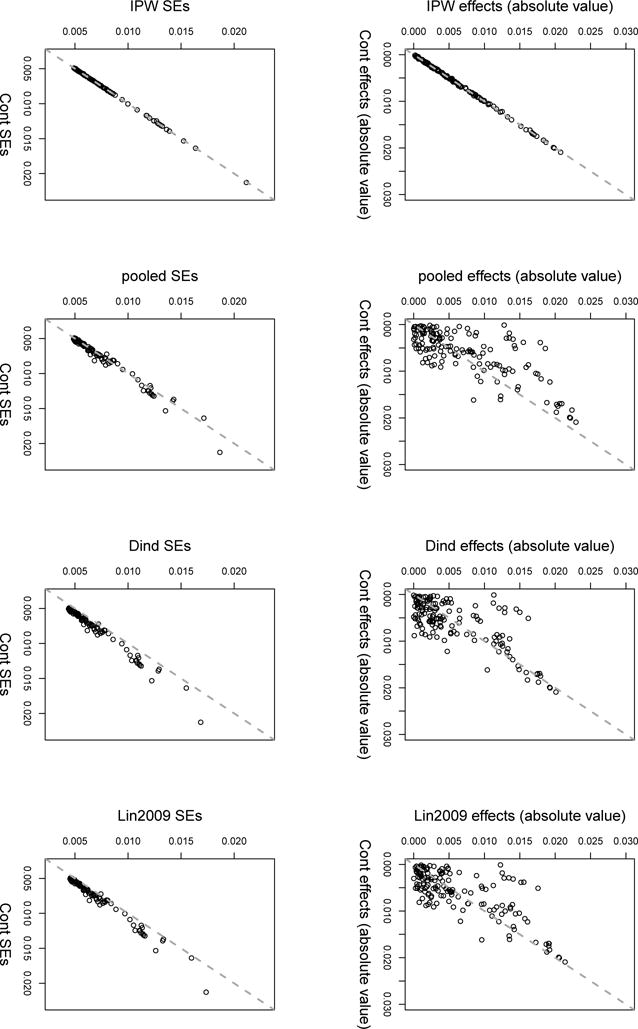
Comparison of effect estimates for the SNPs in the FTO gene on log-BMI, and their standard errors. Estimates of the control function estimator (‘cont’) and their SE were compared to the usual IPW, the estimator ignoring disease status (pooled), the estimator using disease indicator in its design matrix (‘Dind’) and the estimator of Lin and Zeng (2009) (‘Lin2009’). Every point in the plot represent a SNP. If a point falls on the diagonal - its associated effect (SE) estimate is equal in cont and the compared estimator. If it falls below the diagonal, its estimated effect (SE) is smaller in cont compared to the other estimator.

Table 3.

Effect estimates, and their respective SEs and p-values for the SNP rs1421085 from the FTO gene. The values were obtained by the control function estimator ‘cont’, the usual IPW, the ‘pooled’ estimator ignoring disease status, and the estimator with disease indicator in the design matrix ‘Dind’, and the estimator of Lin and Zeng (2009) (‘Lin2009’).

Estimator	effect	SE	p-value (raw)	p-value (adj)
Cont	−0.017	0.0054	1.7e-3	0.247
IPW	−0.017	0.0054	1.9e-3	0.273
pooled	−0.021	0.0050	4.2e-5	0.006
Dind	−0.018	0.0046	9.3e-5	0.014
Lin2009	−0.019	0.0047	4.7e-5	0.007

There were ten SNPs with Holm’s adjusted p-value ≤0.05 by the pooled estimator, which yielded the lowest p-values. As they were all in high LD, we selected the SNP that is in highest LD with rs1558902, namely rs1421085 (Johnson et al., 2008). Table 3 compares between the various analyses results on this SNP. As the effects are relatively low (~ −0.02), all estimates are within a range of 0.04 of each other. The absolute effect estimate is largest in the pooled estimator. Since pooled and Dind are likely biased estimators (as supported by the simulations mimicking the T2D diabetes data set, in the Supplementary Material), we now consider Lin2009. This estimator accounts for case-control sampling, but assumes that the outcome is normally distributed around the population mean. Figure 2 compares the density of the residuals of log-BMI after removing the population mean estimated by IPW to the normal density, suggesting that normality does not hold and that the estimator is potentially biased.

Figure 2.

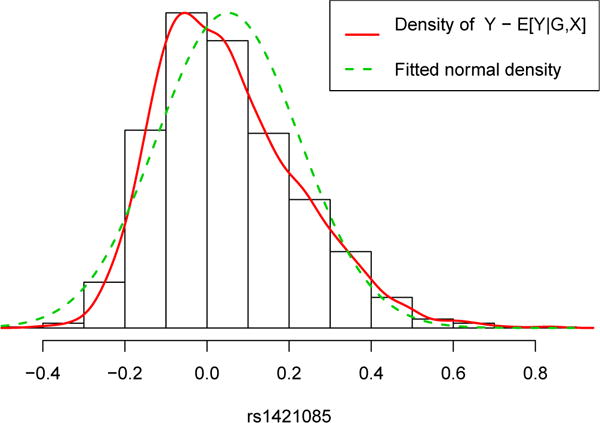
Histogram, and overlaid empirical and fitted normal densities to the residuals of log-BMI after removing estimated population mean.

Consistent with the plot, cont and IPW gave identical effect estimates (after rounding), and the efficiency gain in using the cont estimator is small. In the supplementary material, we describe an extensive simulation study guided by the diabetes data set. From this study we learn that for realistic effect sizes, the improvement in efficiency in cont compared to IPW is high when the SNP’s MAF is low and the SNP’s effect on γ(X) is relatively high. However, rs1421085 has MAF 0.22 (quite high), and we expect that its effect on γ(X) is small.

6. Discussion

In this work we propose and investigate the properties of estimators that extend the IPW for the population mean effects of covariates on secondary outcomes in case-control studies. The IPW estimator only requires a correct specification of the population mean model, and known sampling fractions for the case-control study. We extend the IPW estimator by incorporating a model for the disease, via an inverse probability weighted control function. Thus, the proposed cont estimator is more efficient than the IPW, as it uses more information, yet it is still robust for some parts of the statistical model being misspecified, namely the outcome distribution and the ‘selection bias function’. We propose estimators that may be used with identity and log links. This approach could potentially extend to the logit link, a challenge for future research.

The control function estimator is unbiased under correct specification of the disease model given covariates, even if the model for the selection bias function is misspecified. We recommend evaluating the disease model fit with respect to the model predictions (estimated disease probabilities). One can use Area Under the operating Curve (AUC) and cross validation as measures that give indications of fit due to good or poor prediction. For a comprehensive review of such methods see Harrell et al. (1996). It is also useful to compare the control function effect estimate to the IPW, as the IPW is robust to misspecification of the disease model. Under correct specification of the disease model we expect to see similar effect estimates for both IPW and control function estimators, with smaller standard errors for the later.

In recent work, especially that relying on the retrospective likelihood (Lin and Zeng, 2009; Li and Gail, 2012; Chen et al., 2013; Ghosh et al., 2013), the primary disease probability is modeled in a logistic regression, with both the exposure and the secondary outcome, and sometimes their interaction, as predictors. This model is limited because the secondary outcome will often occur on the causal pathway between the exposure and the primary outcome (e.g. mammographic density and breast cancer, or smoking and lung cancer) in which case the model for the D adjusting for X and Y is difficult to interpret. In contrast, our formulation does not explicitly use the secondary outcome in the disease model. However, the efficient control function estimator incorporates a selection bias function, namely γ(X), which encodes the association between the secondary outcome and the case control status conditional on covariates. Hence, as in any likelihood-based approach, this association is accounted for, while more general specifications of this association are readily applied. Thus, the control function estimator is both more general and relies on fewer assumptions, and it is guaranteed to be most efficient if all models are correctly specified.

IPW estimators, and as such, the control function estimator, require known sampling probabilities, or equivalently, known disease prevalence. In nested case-control studies, disease prevalence could be estimated from the underlying cohort. Alternatively, one can use registries. Still, disease prevalence may not be accurately estimated in the specific target population, for instance, minorities are less studies, and disease prevalence may differ between populations of the same ancestry due to environmental interactions. If the disease prevalence is over-estimated, and therefore the probability of selecting cases (controls) is assumed lower (higher) than it is, cases (controls) are assigned higher (lower) weight, and the IPW and cont estimators become biased towards the estimator that ignores the biased sampling. On the other hand, if the disease prevalence is under-estimated, the IPW and cont estimators become biased towards the “control-only” estimator, that discards cases. In the supplementary material, we provide results from a simulation study of the effect of assuming the wrong disease prevalence, either too high or too low, on the effect estimates, and indeed the estimators become somewhat biased. Therefore, it is important to consider the evidence towards a given disease prevalence when using IPW methods for secondary outcomes analysis. As suggested by a reviewer, finding semiparametric efficient estimators for secondary outcomes with unknown disease prevalence or sampling probabilities is an important research question. A recent paper by Ma and Carroll (2016) published after this paper was submitted, considers this problem. It is of interest for future interest to combine their approach with ours.