Motion Compensation in Extremity Cone-Beam CT Using a Penalized Image Sharpness Criterion

Abstract

Cone-beam CT (CBCT) for musculoskeletal imaging would benefit from a method to reduce the effects of involuntary patient motion. In particular, the continuing improvement in spatial resolution of CBCT may enable tasks such as quantitative assessment of bone microarchitecture (0.1 mm – 0.2 mm detail size), where even subtle, sub-mm motion blur might be detrimental. We propose a purely image based motion compensation method that requires no fiducials, tracking hardware or prior images. A statistical optimization algorithm (CMA-ES) is used to estimate a motion trajectory that optimizes an objective function consisting of an image sharpness criterion augmented by a regularization term that encourages smooth motion trajectories. The objective function is evaluated using a volume of interest (VOI, e.g. a single bone and surrounding area) where the motion can be assumed to be rigid. More complex motions can be addressed by using multiple VOIs. Gradient variance was found to be a suitable sharpness metric for this application. The performance of the compensation algorithm was evaluated in simulated and experimental CBCT data, and in a clinical dataset. Motion-induced artifacts and blurring were significantly reduced across a broad range of motion amplitudes, from 0.5 mm to 10 mm. Structure Similarity Index (SSIM) against a static volume was used in the simulation studies to quantify the performance of the motion compensation. In studies with translational motion, the SSIM improved from 0.86 before compensation to 0.97 after compensation for 0.5 mm motion, from 0.8 to 0.94 for 2 mm motion and from 0.52 to 0.87 for 10 mm motion (~70% increase). Similar reduction of artifacts was observed in a benchtop experiment with controlled translational motion of an anthropomorphic hand phantom, where SSIM (against a reconstruction of a static phantom) improved from 0.3 to 0.8 for 10 mm motion. Application to a clinical dataset of a lower extremity showed dramatic reduction of streaks and improvement in delineation of tissue boundaries and trabecular structures throughout the whole volume. The proposed method will support new applications of extremity CBCT in areas where patient motion may not be sufficiently managed by immobilization, such as imaging under load and quantitative assessment of subchondral bone architecture.

1. Introduction

Flat-panel detector (FPD) cone beam CT (CBCT) is finding increasing use in musculoskeletal radiology. In imaging of the extremities, applications of CBCT have been reported using both the general purpose C-arm scanners (Ellis et al 2010, Choi et al 2013) and using recently developed dedicated extremity CBCT (Zbijewski et al 2011, Koskinen et al 2013, Richter et al 2014), such as the device undergoing clinical studies at our institution, shown in Fig. 1A (Carrino et al 2014). Compared to conventional orthopaedic modalities (radiography, MRI, multidetector CT), extremity CBCT is potentially better suited for an in-office setting, provides a novel capability for weight-bearing volumetric imaging (Cao et al 2015, Tuominen et al 2013, Hirschmann et al 2014, Segal et al 2015) and offers high spatial resolution owing to the FPD technology (Demehri et al 2015, Huang et al 2015).

Figure 1.

(A) Extremities CBCT and (B) CMOS-based CBCT benchtop with a linear stage to simulate object motion.

The current generation of extremity CBCT is characterized by relatively long scan times (~30 sec) and is thus susceptible to involuntary patient motion during acquisition. In clinical experience with the system of Fig. 1A, gross motion artifacts are however rare, even in weight-bearing imaging. This indicates that immobilization, achieved by placing foam cuffs around the extremity, is often sufficient to manage patient motion. However, certain applications either do not permit the use of immobilization (e.g. weight-bearing imaging under flexion (Choi et al 2014)), or require very high spatial resolution, which might be challenged by slight motions that cannot be adequately controlled with immobilization. Quantitative in-vivo assessment of bone microarchitecture in humans is an example of an emerging application of extremity CBCT (Zbijewski et al 2015) that requires high spatial resolution (0.05 mm – 0. 2 mm, consistent with the size of trabeculae (Griffith and Genant 2011)). Sub-mm patient motion can bias measurements of trabecular architecture, even though such motion is unlikely to cause any gross artifacts in the reconstructed image. Development of robust motion compensation is thus crucial to new applications of extremity CBCT in areas such as functional evaluation of the joints (imaging under load) and in quantitative assessment of bone quality.

Motion compensation algorithms in CT and CBCT typically involve three components: (i) a model of the deformation imparted by the motion, e.g. rigid transformation of the volume or deformable organ motion; (ii) an estimate of the motion pattern; and (iii) a method to incorporate the deformation model (together with the motion estimate) into image reconstruction, e.g. by appropriately transforming the reconstructed volume during the backprojection step in Filtered Backprojection (FBP)-type methods. In conventional CT, the acquisition times are much faster (e.g., ~0.2–0.3 sec per rotation) than in extremity CBCT, and involuntary motion is less of a concern – the cardiac motion being a notable exception, often addressed via gating of cardiac phase according to ECG gating (Hsieh et al 2006). Alternatively, the estimation of the motion pattern from image data is aided by the assumed periodicity of such motions (Tang et al 2012). This is in contrast to extremity CBCT, where standard imaging protocols do not include tracking of the extremity and the motion trajectories are irregular. However, the motions of the extremities are typically slower and involve less complex deformations compared to the multi-organ motion occurring in the torso.

One possible approach to motion compensation in extremity CBCT involves estimation of the motion trajectory using a combination of skin-based fiducials and 2D/3D registration. While successful compensation has been achieved with fiducial-based methods in head CBCT (Jacobson and Stayman 2008, Kim et al 2015) and extremity CBCT (Choi et al 2014), the possible disadvantages of this technique include disruption of the imaging workflow and inaccuracies stemming from the assumption that the motion of the surface fiducials reflects the deformation of the internal structures. Fiducial-free motion compensation using 2D/3D registration that relied only on the data available in the motion-contaminated scan has been investigated, showing degraded performance compared to the fiducial-based approach (Unberath et al 2015). Better results, approaching or even surpassing the fiducial-based algorithm, were obtained using a 2D/3D registration with a motion-free prior CT or CBCT (Berger et al 2016, Ouadah et al 2016a). However, such prior information is not always available.

In contrast to the previously reported motion compensation algorithms for extremity CBCT, we propose a purely image based approach that does not require fiducials or prior images and does not rely on 2D/3D registration. We exploit the “autofocus” concept known from optical imaging (Bueno-Ibarra et al 2005, Mateos-Pérez et al 2012), where an iterative algorithm is used to estimate a motion trajectory that maximizes a sharpness metric computed on the reconstructed image (e.g. image entropy, total variation or a gradient-based metric). Autofocus techniques have been previously employed in CT and CBCT for correction of geometric misalignment (Wicklein et al 2013, Kyriakou et al 2008, Kingston et al 2011) and for motion compensation in cardiac (Brehm et al 2015, Wicklein et al 2015, Katsevich et al 2011, Hahn et al 2016) and head imaging (Wicklein et al 2013). Early application to extremities CBCT was reported in (Sisniega et al 2016).

Motion compensation using autofocus techniques can be restricted to a specific volume of interest (VOI) in a manner that only requires a reconstruction of the VOI. In contrast, the methods based on 2D/3D registration often involve reconstruction of a volume that is much larger than the VOI, either to capture the surface markers in fiducial-based algorithms, or to provide a complete support of the measured projections in prior-image-based methods. Because the autofocus techniques rely only on local image data, they do not require an estimate of the global motion of the extremity, potentially simplifying the motion model in applications where the compensation is sought only in a VOI. The method proposed here assumes that the entire VOI follows the same rigid motion. This assumption is not excessively restrictive in the extremities, where individual bones and their adjacent soft tissues undergo predominantly rigid motions. In applications such as imaging of the trabecular microarchitecture, the algorithm can be used to provide separate motion-compensated reconstructions for each bone. In other applications, future work will develop methods to combine motion estimates from multiple VOI to derive the deformation field of the entire joint.

The motion compensation algorithm developed in this work augments the image sharpness criterion with a regularization term that encourages smooth motion trajectories. The resulting non-convex objective function is solved using statistical optimization instead of the more common choice of simplex-like algorithms. We investigate various image sharpness metrics and assess the performance of the method in simulated and experimental data. The experiments are performed on a CMOS detector-based benchtop (Fig. 1B) developed to evaluate a novel high-resolution imaging chain for extremity CBCT. We conclude by demonstrating an application of the algorithm to motion contaminated patient data from current generation extremity CBCT.

2. Materials and Methods

2.1. Motion compensation framework

The processing begins with selection of a VOI where motion compensation is sought. It is assumed that the VOI undergoes a motion that only consists of rigid transformations. As mentioned earlier, this assumption is typically true for VOIs consisting of a single bone and the adjacent soft tissue, even if the motion of the whole extremity is more complex, involving different motion trajectories for different bones and deformations of the soft tissues. The VOI is typically selected in the original, motion-contaminated (uncompensated) image. Note that the VOI should be slightly larger than the anatomical region that the user intends to analyze. This is because the position and orientation of the motion compensated volume (with respect to the position of the object in the gantry coordinate system) are different than those of the initial volume due to the application of a motion trajectory during the reconstruction. As explained below, the overall amplitude of this displacement is no larger than the amplitude of object motion.

The motion trajectory T consists of a sequence of rigid transformations, one per angular projection. Note that the angular positions are used only as an index variable to discretize the continuous object motion at time points corresponding to the acquired frames. Such labeling by angle (c.f., time) is valid, since the scan involves a rapid, constant frame rate (~30 frame/s) yielding ~600 projections in ~20 s scan time.

The rigid transformations are applied to the object volume independently of the rotation of the source-detector pair (or equivalently, the rotation of the volume) associated with the CBCT scanning orbit. The 6 degrees of freedom (DoF) of the rigid transformations (3 translations and 3 rotations) are defined with respect to a fixed coordinate system defined by the position of the CBCT gantry at the first projection angle. A motion-compensated reconstruction is obtained using the Feldkamp (FDK) algorithm. The trajectory T is applied during the backprojection by appropriately changing the position of the reconstructed volume with respect to the source and detector. Only the coordinates of the voxels are changed according to the motion trajectory and thus no interpolation is applied in the reconstructed volume to accommodate motion. The backprojector is voxel-driven with bi-linear interpolation of the projection data (GPU texture fetch).

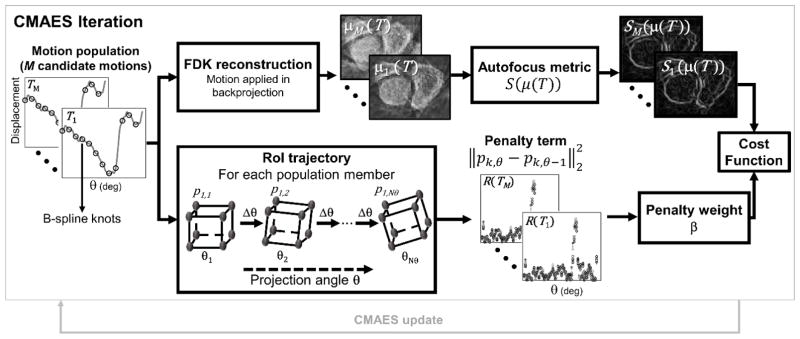
The algorithm estimates the trajectory T by minimizing a cost function consisting of: i) a sharpness term that applies an autofocus metric to the VOI; and, ii) a regularization term that encourages smooth motion trajectories. The cost function is given by:

$$C(T)=S(\mu (T))+\beta ·R(T),$$ (1)

where μ(T) is the reconstruction of the VOI compensated for motion using trajectory T, S(μ(T)) is an autofocus term, and R(T) is the penalty (regularization) term; the relative contribution of R(T) is controlled by the scalar weight β. The optimal trajectory T̂ is then computed as:

$$\widehat{T}=arg{min}_{T}C(T).$$ (2)

To reduce the dimensionality of the problem, each of the DoFs is modelled as a superposition of N cubic b-spline kernels, each centered at one of N knots located at angular positions θ_i. The spline model is consistent with the assumption of smooth motion trajectory implicit in the regularization term of Eq. 1 and justified by the relatively fast frame rate of the CBCT system. The knots were selected to be equally distributed across the total angular span of the acquisition. The number of knots is a free parameter that determines the number of unknowns in the optimization and can be adjusted to reflect the expected complexity of the motion pattern, as investigated in Sec. 3.2. In this spline representation, the value of a DoF at an angular frame index θ is obtained as:

$$T(\theta ,j)={\sum }_{i=0}^N{c}_{ij}B(\theta -{\theta }_i)-\left({\sum }_{k=0}^{N_{\theta }}{\sum }_{i=0}^N{c}_{ij}B({\theta }_k-{\theta }_i)\right)/N_{\theta },$$ (3)

where B is a cubic b-spline, N is the total number of cubic b-splines (knots), j denotes the DoF (j = 1,…,6), N_θ is the total number of projections, and k and j enumerate angular positions. With this parameterization, the coefficients c_ij are the unknowns to be estimated using Eq. 1. The second term in Eq. 3 detrends each DoF by its mean value across all angular frames, thus ensuring that the resulting transformation does not significantly displace the reconstructed VOI from its position and orientation in the original, uncompensated volume. Note that the pose of the uncompensated reconstruction is determined by the average transformation experienced by the volume as a result of patient motion. Even though the detrending implemented in Eq. 3 is not exactly equivalent to subtracting the mean transformation, it was nevertheless sufficient to precondition the statistical optimization algorithm so that the resulting motion trajectories remained essentially centered on the position and orientation of the initial, uncorrected volume. The magnitude of each DoF of the rigid transformation between the position of the VOI after motion-compensation and its initial position is no larger than the amplitude of patient motion for this DoF.

Several candidate sharpness metrics were evaluated for the autofocus term in Eq. 1 (see Sec. 3.1). The metrics are defined in Table 1. The directional gradient operators (∇_x, ∇_y, and ∇_z) were implemented as a convolution with the first derivatives (in the x, y, and z directions, respectively) of a three-dimensional Gaussian kernel, as described in (Otake et al 2012a). The convolution approach provided improved robustness against noise compared to a conventional implementation using first-order differences.

Table 1.

The autofocus metrics evaluated for motion estimation in extremity CBCT. Gradient variance was found best suited for this application and used in the majority of experimental studies.

Metric	Formula	References
Entropy	$S(\mu )=-{\displaystyle \sum _{l=1}^L}{h}_l(\mu )·log{h}_l(\mu )$	(Wicklein et al 2012).
Negative Variance	$S(\mu )=-{\sum }_k{({\mu }_k-\overline{\mu })}^2$	(Groen et al 1985, Mateos-Pérez et al 2012)
Total Variations	$S(\mu )=-{\sum }_k\sqrt{{\mathit{\nabla }}_x{({\mu }_k)}^2+{\mathit{\nabla }}_y{({\mu }_k)}^2+{\mathit{\nabla }}_z{({\mu }_k)}^2}$	(Wicklein et al 2012)
Gradient Norm	$S(\mu )=-{\sum }_k{\mathit{\nabla }}_x{({\mu }_k)}^2+{\mathit{\nabla }}_y{({\mu }_k)}^2+{\mathit{\nabla }}_z{({\mu }_k)}^2$	(Kingston et al 2011)
Gradient Variance	$S(\mu )=-{\sum }_k{\left(\sqrt{{\mathit{\nabla }}_x{({\mu }_k)}^2+{\mathit{\nabla }}_y{({\mu }_k)}^2+{\mathit{\nabla }}_z{({\mu }_k)}^2}-\frac{1}{N_v}{\sum }_k\left(\sqrt{{\mathit{\nabla }}_x{({\mu }_k)}^2+{\mathit{\nabla }}_y{({\mu }_k)}^2+{\mathit{\nabla }}_z{({\mu }_k)}^2}\right)\right)}^2$	(Bueno-Ibarra et al 2005)

Definition of symbols:

k enumerates the voxels in volume μ

N_v is the total number of voxels in the volume

h_l(μ) is the lth bin of a normalized intensity histogram of μ

L is the number of bins (set to 256)

∇_x, ∇_y, and ∇_z are 1D gradients along the three principal directions

The regularization term in Eq. 1 penalizes the squared 2-norm of the displacement of a set of reference points (computed between subsequent angular projections). To compute the penalty, a set of Q = 8 reference points was selected, where each point corresponded to a vertex of the motion compensation VOI and was thus independent of the anatomy. A schematic illustration is shown in the flowchart in Fig. 2. The 3-dimensional coordinate of the q^th reference point in angular projection θ is denoted as p_{q, θ}. To compute p_{q, θ}, the rigid transformation provided by the current guess of the motion trajectory of the VOI (T(θ)) was analytically applied to the position of the reference point during the acquisition of the first projection (p_q,1). The resulting penalty term is given by:

$$R(T)=\sum _{q=1}^Q\sum _{\theta =2}^{N_{\theta }}{\Vert p_{q,\theta }-p_{q,\theta -1}\Vert }_2^2,$$ (4)

where N_θ is the total number of projections, as defined previously. This regularization term discourages motions involving abrupt movements that are unlikely to occur in practice, particularly when immobilization is used. The penalty is computationally efficient, since it requires only analytical application of the rigid motion transform to the 3-dimensional coordinates of the 8 vertices of the VOI.

Figure 2.

Flowchart illustrating the CMA-ES optimization of the motion estimation cost function. In each iteration, M candidate motion trajectories are sampled from a random distribution. For each candidate solution, the autofocus metric and the penalty term are computed (top and bottom branches of the flowchart) and added to yield a cost function value for that trajectory.

The optimization problem in Eq. 1 is non-convex and thus challenging to solve with conventional gradient-based methods. We apply the Covariance Matrix Adaptation Evolution Strategy (CMA-ES) (Hansen and Kern 2004) to find a global optimum in a non-convex space. The CMA-ES algorithm was chosen as well suited to non-convex optimization as previously demonstrated in applications closely related to the motion compensation problem, such as estimation of object pose in 3D–2D registration (Uneri et al 2015, Otake et al 2012b) and estimation of system geometry (Ouadah et al 2016b).

One iteration of the CMA-ES optimization is illustrated in Fig. 2. For each iteration, a set of M candidate solutions (motion trajectories) is obtained by generating M random samples from a 6· N-dimensional normal distribution of the c_ij parameters to be estimated (where N is the number of spline knots for each DoF, as described in Eq. 3). Initially, the c_ij parameters are considered to be independent random variables, with a mean of zero, and the associated 6·N vector of standard deviations denoted as σ. During the CMA-ES iterations, the mean and covariance matrix of the joint probability distribution of the motion parameters evolve to favor solutions that minimize the cost function, as described in (Hansen and Kern 2004). The autofocus and penalty terms are computed in parallel for all candidate motions and then added to yield the cost function value for each candidate motion. Evaluation of the autofocus term (top branch in Fig. 2) consists of parallel FDK reconstructions of M motion-compensated VOI volumes, followed by the computation of the sharpness metric for each volume. The bottom branch in Fig. 2 illustrates the calculation of the penalty term, where Euclidean distance traveled by the control points between subsequent projections is computed. Both the FDK image reconstruction and the computation of the sharpness metric are parallelized on a graphic processing unit (GPU).

Failure to converge or residual motion after a fixed number of iterations was handled by restart of the CMA-ES iterations with increased σ (Hansen and Kern 2004).

2.2. Experimental Studies

2.2.1. CMOS-based CBCT benchtop with motion simulation

Fig. 1B illustrates a CBCT benchtop that was used in studies of the motion compensation algorithm. The bench was equipped with a Xineos 3030 CMOS x-ray detector (Teledyne DALSA, Eindhoven, NL) with native pixel size of 0.1 mm. A compact rotating anode IMD RTM 37 x-ray source (IMD, Grassobbio, IT) was used, providing 3 kW power and nominal focal spot size (as defined by the IEC336 standard) of 0.3 mm. The source was operated at 90 kV (+0.2 mm Cu added filtration), and 0.12 mAs per projection. The acquisitions involved 720 projections over 360° rotation. The benchtop system serves as a platform to test a new high resolution imaging chain for the next generation of the extremity CBCT scanner incorporating the higher resolution CMOS detector, which is currently under development for applications in imaging of bone microarchitecture in patients (Marinetto et al 2016).

The geometry of the benchtop was set to emulate the geometry of the clinical extremities scanner in Fig. 1A, with source-axis distance (SAD) of 430 mm and source-detector distance (SDD) of 540 mm. CBCT acquisitions were achieved using a rotation stage (B4800, Velmex, Bloomfield, NY) that performed a step-and-shoot motion synchronized with x-ray source pulsing. Patient motion was simulated by means of a linear translation stage (XSlide, Velmex, Bloomfield, NY) mounted on the rotation stage and synchronized with object rotation. The motion stages where actuated and synchronized through VXM-3 motion controllers (Velmex, Bloomfield, NY).

2.2.2. Simulation study

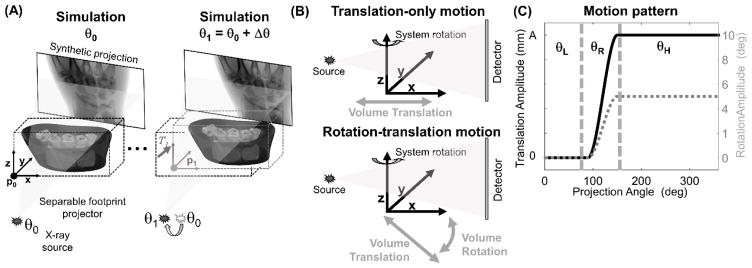
Synthetic motion-contaminated projections were generated from a static high-resolution x-ray reconstruction of a cadaveric hand acquired on the CBCT benchtop (voxel size 0.075 mm). The simulated CBCT geometry was identical with that of the benchtop and 720 projections over 360° rotation were computed. Motion trajectories were modelled as a sequence of rigid transformations (6 DoF) of the object volume, one per angular gantry position. For each gantry angle, the static volume was first displaced according to the motion trajectory and the forward projection was performed using a separable footprint projector (Long et al 2010). The simulation algorithm is illustrated in Fig. 3A. The coordinate system used to define the motion patterns is affixed to the object volume, as depicted in Fig. 3A and B. In the first frame of the scan, the z axis is parallel to the axis of rotation, and the x axis coincides with the source-detector axis. The origin and orientation of this coordinate system changes according to the motion pattern, but is independent of the rotation of the gantry during CBCT acquisition.

Figure 3.

Simulation of motion-contaminated projections. (A) A rigid transformation T₁ is applied to the simulated volume between the computation of two neighboring projections at gantry angles θ₀ and θ_1. This process is repeated for all projection frames. (B) Two types of motion were simulated: one consisting only of a translation of the volume along an axis perpendicular to the axis of rotation, and one combining a rotation of the volume (around axis y) with a translation along the rotating axis x. The motion trajectories were modelled as a step function both for the translational and for the rotational degrees of freedom (C). The trajectories were parameterized by the step size A (fixed to 5° in the case of rotations), the starting projection angle θ_L, and the motion interval θ_R. For the combined motion, the rotation and translation occurred simultaneously.

Two types of motion trajectories were studied as shown in Fig. 3B. The first experiment involved a step-like translation in the transaxial plane (x–y). The translation was applied along a vector perpendicular to the rotation axis of the scanner and parallel to the source-detector axis at the 0° gantry angle. We refer to this trajectory as “translation-only.” The second experiment implemented a motion trajectory combining rotations and translations (referred to as a “rotation-translation” trajectory). A step-like rotation of the volume around the y axis (out of the scan plane) was performed. Concurrently with the rotation, a translation along the rotating x axis of the volume was applied.

Smooth trajectories were obtained by spline interpolation of a discrete ramp function with 360 control points at 1° steps. Note that a large number of knots was used to avoid generating an unrealistically smooth motion trajectory. For both trajectories, the step-like motions were prescribed using the starting projection angle θ_L and the angular interval of the step θ_R (Fig. 3C). The volume remained static after the motion was completed for an interval of θ_H = 360° − (θ_L + θ_R). In the experiments, the translation step size A was varied between 0.25 mm and 10.0 mm both for the translation-only and for the rotation-translation trajectories. The amplitude of object rotation in the latter case was fixed at 5°; the rotation and translation occurred concurrently starting at the same θ_L. The θ_L was varied 0°– 300° (nominal value 90°), and θ_R was fixed at 60°.

Motion estimation involved a population of M = 20 volumes. Performance of the motion compensation algorithm was evaluated for regularization strengths β ranging from 10⁻¹ to 10⁴. The number of knots in the motion model N (see Eq. 3) was varied from 8 to 80 to investigate the effect of changing the number of unknowns in the autofocus objective function. The standard deviation of the population of candidate solutions was σ=0.1 mm for the translational DoFs and σ=0.01° for the rotational DoFs.

The CMA-ES was assumed to be converged and the iterations were terminated when changes in the cost function became smaller than 10⁻⁴. If convergence had not been achieved in 4000 iterations, a restart with a 4-fold increase in σ was performed. Only one restart was allowed. The restart strategy addresses the (rare) case in which the initial value of σ (selected based on preliminary studies with a small set of test motions) may not be large enough to capture the full extent of motion to achieve convergence.

The motion estimation was performed in a rectangular box VOI, located in the distal carpals, and measuring 37.5 × 50 × 10 mm³ for trajectories involving only translational motion and 37.5× 50× 20 mm³ for those including translations and rotations. Intermediate reconstructions of the VOI during CMA-ES were executed at 0.5 mm isotropic voxel size. This size was larger than that employed to obtain the final motion compensated reconstructions, which was set at 0.075 mm. The use of a coarser grid was found to reduce the computational burden of the evaluation of the autofocus metric without significant impact on the outcome of motion compensation, consistent with results reported for correction of geometric misalignment using autofocus methods (Kyriakou et al 2008, Kingston et al 2011).

The performance of the compensation algorithm was assessed using Structural Similarity Index (SSIM) (Wang et al 2004) between the motion compensated volume and the static volume (the input to the motion simulation):

$$\mathit{SSIM}(\mathit{ref},MC)=\frac{(2{\overline{\mu }}_{\mathit{ref}}{\overline{\mu }}_{MC}+c_1)(2{\sigma }_{\mathit{ref}-MC}+c_2)}{({\overline{\mu }}_{\mathit{ref}}^2+{\overline{\mu }}_{MC}^2+c_1)({\sigma }_{\mathit{ref}}^2+{\sigma }_{MC}^2+c_2)}$$ (5)

where μ̄_i is the average attenuation and σ_i is the variance of the attenuation values in image i. The index i takes the value ref for the reference static image, and MC for the motion compensated image, and σ_ref-MC is the covariance between the two images. The regularization terms c₁ (= 10⁻⁴) and c₂ (= 3×10⁻⁴) stabilize the metric in regions of very low attenuation.

As explained in Sec. 2.1, the position and orientation of the motion compensated volume with respect to the CBCT gantry coordinate system and the patient anatomy generally depend on the motion trajectory. While this displacement is kept small owing to the detrending applied in the model of the motion trajectory (Eq. 3), it needs to be accounted for in the computation of SSIM. Rigid registration of the motion compensated volumes (and of the uncompensated motion-contaminated image) to the reference static image was thus performed. This registration yielded the parameters of the relative displacement between the motion compensated and static volume that were then applied to rigidly transform the static image prior to the computation of the SSIM. The registration was implemented using a squared intensity difference metric and solved using a CMA-ES optimizer with a population of 10 candidate solutions and 10⁴ iterations.

2.2.3. Benchtop imaging study

The CMOS-based CBCT benchtop of Sec. 2.2.1 provided experimental validation of the findings of the simulation study. A phantom consisting of a hand skeleton embedded in soft-tissue equivalent plastic (The Phantom Laboratory, Salem, NY) was used. The object linear stage (Fig. 1B and Sec. 2.2.1) was used to generate step-like translations similar to those studied in the simulation study of the translation-only motion. The speed of the translational motion was fixed at 0.1 mm per degree of object rotation. Scans with three motion trajectories were obtained: (i) A = 0.5 mm, θ_R = 5°, (ii) A = 1.0 mm, θ_R = 10°, and A = 10.0 mm, θ_R = 100° (parameters defined as in Fig. 3B). A reference static volume was also acquired to facilitate assessment of the performance of motion compensation using SSIM, performed in a manner analogous to Sec. 2.2.2.

Motion estimation was performed in a 37.5 × 50 × 10 mm³ cubic volume located in the distal ulna and radius. All other parameters of image reconstruction and motion compensation were the same as in the simulation studies of Sec. 2.2.2.

2.2.4. Clinical data

CBCT scans of a patient’s knee were acquired on the dedicated extremity scanner in Fig. 1A (Carrino et al 2014) as part of a separate, IRB approved study. Two scans were performed in sequence – both with the subject in a standing position with weight evenly distributed between two legs: one scan with no additional load (“non-load bearing scan”, NLB), and one scan with the subject bearing an additional 20 kg shoulder-borne load (“load bearing scan”, LB). The subject did not leave the gantry between the scans.

Image acquisition was performed at 90 kV and 0.12 mAs/projection; 600 projections were collected over a 240° angular span. The detector (Varian2530CB, Varian, CA) was read out in a 2×2 binning mode with 0.274 mm pixel size. Total scan time was 20 sec.

Motion compensation was applied to the LB scan, which showed evidence of motion artifacts. The compensation was performed using 0.8 mm voxels in a 100×100×40 voxels VOI centered on the proximal tibia. Other parameters of the compensation algorithm were as follows: M=20, N=56, β=50, σ=0.1 mm for the translational DoFs and σ=0.01° for the rotational DoFs. The final images were reconstructed using 0.3 mm voxels.

Subtraction images were computed between the motion-contaminated LB volume after motion correction and the motion-free NLB volume of the same subject. It was assumed that after motion correction there would be almost no difference in the shape and trabecular structure of the tibia between the motion-compensated LB reconstruction and the NLB volume. To correct for a potential global misalignment of the tibial VOI (independent of subject motion), image registration between the two volumes was performed using the method described in Sec. 2.2.2. Since load bearing induces changes in the tissues outside of the tibial VOI (e.g. displacement of the patella and the patellar tendon), the registration transform was obtained using only the tibial surfaces (which were manually segmented based on intensity threshold and manual fine delineation of the segmented image), instead of the complete volumes.

3. Results

3.1. Performance of autofocus metrics

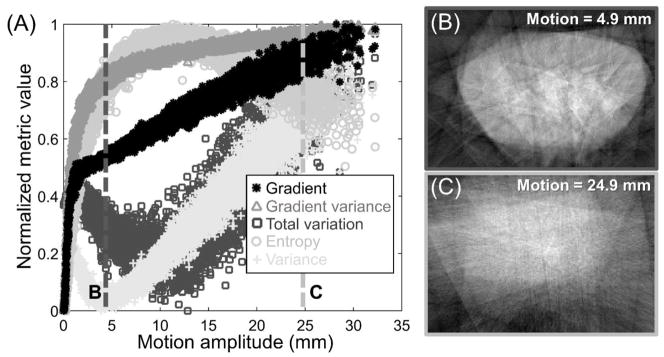
The five autofocus metrics in Table 1 were investigated for use in motion correction in extremity CBCT. A population of motion-contaminated hand images was obtained by simulating projection data for a population of 3000 random motion trajectories using the simulation setup in Sec. 2.2.2. The trajectories were generated by randomly sampling the values of each DoF for each projection angle under the constraint that the mean displacement of the volume across all projections (denoted as motion amplitude) is within a 0–50 mm range. Fig. 4A shows the normalized value of the autofocus metrics as a function of motion amplitude in motion-contaminated. The metric was computed in a 37.5 × 50 × 10 mm³ VOI located in distal carpals. Normalization was performed by subtracting the minimum and dividing by the maximum value in the population of motion trajectories, so that the static image should yield a metric value of 0. Note that this static image is equivalent to a reconstruction of motion-contaminated projections obtained using a perfect motion estimate. The action of the CMA-ES optimizer for a given autofocus metric can be visualized as a search that begins with some population of motions and then progressively moves along the distribution shown in Fig. 4A towards a motion that minimizes the metric, either globally or locally.

Figure 4.

(A) Normalized value of the autofocus metrics as a function of motion amplitude for a population of simulated random motions of a wrist phantom. Gradient-based metrics, except for total variation, exhibit monotonic decrease toward a unique global minimum corresponding to a static image and are thus preferable for motion correction. Images in (B) and (C) explain the decline in the entropy values for very large motion amplitudes. The 24.9 mm motion (C) results in large blur that homogenizes the intensity histogram, yielding a similar value of the entropy (~0.8) as for the image with much smaller, 4.9 mm motion (B).

An appropriate choice of autofocus metric for motion estimation should possess a global minimum at the static (or, equivalently, perfectly motion compensated) image, with no local minima and a steep slope around the global minimum to facilitate fast convergence of the optimization algorithm. Among the metrics investigated in Fig. 4A, the negative variance (denoted with gray cross markers) attained a clear local minimum at ~5 mm motion, in addition to the global minimum at 0 mm motion. For objects and motion patterns encountered in extremity CBCT, variance is thus a poor choice of the autofocus metric. Similar local minimum was observed for the total variation, in agreement with previous findings that showed limited utility of total variation in the compensation of geometric misalignment in CBCT (Wicklein et al 2012).

Alternatively, entropy is a common choice in correction of geometric misalignment in CBCT (Wicklein et al 2012, Kyriakou et al 2008). As shown in Fig. 4A, entropy (marked with gray circles) exhibited a strong global minimum for a static image, where the histogram of gray values is characterized by a reduced number of peaks (one per material and density in the image) compared to a more blurry, motion contaminated image, such as the one shown in Fig. 4B. However, for large motions (amplitudes greater than ~10 mm), entropy was found to decrease. As shown in Fig. 4C, the gray values in images with significant motion become homogenized, reducing the spread of the histogram and, in turn, the entropy value.

A subset of the candidate trajectories in CMA-ES might lie in this regime of the distribution in Fig. 4A, especially when the algorithm is started with relatively broad distribution of motions (σ) to account for large patient displacement. In such a case, the algorithm may trend toward a solution with very large motion amplitude and an almost uniform appearance of the motion-compensated image.

In contrast to entropy, negative variance, and total variation, the gradient-based autofocus metrics showed a monotonic increase for increasing motion amplitude with no evidence of local minima or maxima. A lower spread of metric values is observed for gradient variance (gray triangles in Fig. 4A) than for gradient norm (black star markers), indicating better robustness against local minima when a stochastic optimizer is used. Gradient variance was therefore employed in the subsequent experimental studies.

3.2. Simulation studies: motion compensation parameter selection

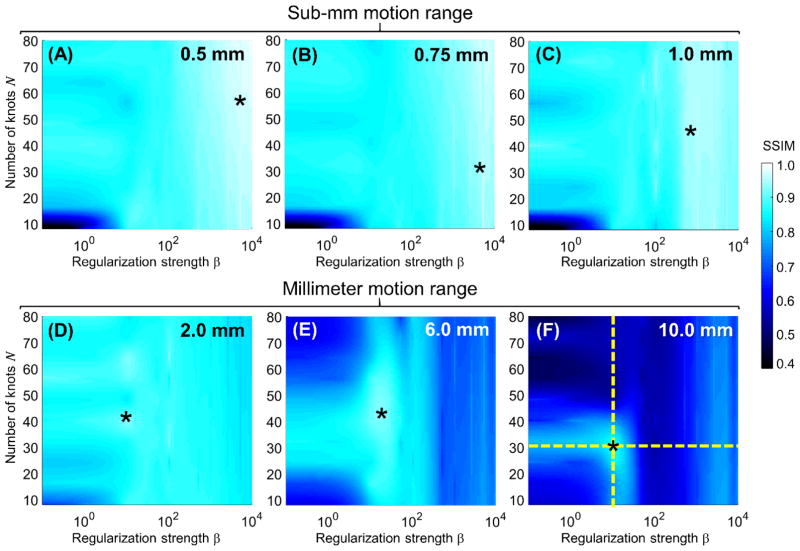
Fig. 5 shows the SSIM of motion compensated reconstructions of the translation-only simulated data of Sec. 2.2.2 as a function of the regularization strength β and the number of b-spline knots N. The motion amplitudes range from sub-mm to 10 mm. The starting angle θ_L of the step motion was fixed at the nominal value of 90°. CMA-ES required no restart for motions <= 2 mm; one restart was necessary for the 6 mm and 10 mm motions.

Figure 5.

SSIM as a function of the number of knots in the spline motion model N, and regularization strength β for translational motions ranging from 0.5 mm (A) to 10 mm (F). The star markers indicate the value of N and β that maximized SSIM.

The initial SSIM values in uncompensated images varied from 0.86 for the 0.5 mm motion to 0.52 for the 10 mm motion. For sub-mm motion, the compensation algorithm achieved almost perfect fidelity with the static image (SSIM > 0.9) throughout an extensive region of the parameter space. For 0.5 mm translation amplitude, the best SSIM achieved after compensation was as high as 0.97. Maximal SSIM (marked with a star) was attained using a strong regularization (large β). Beyond 1.0 mm motion amplitude, the optimal β shifted toward lower values (β = 50 for 6 mm compared to ~10³ for 1 mm motion and ~10⁴ for 0.5 mm motion). This trend is attributed to the smoothing of large amplitude motions when strong regularization is applied. While the maximal SSIM achieved after motion compensation for the 10 mm motion is lower than that obtained in the sub-mm range, the relative improvement in SSIM is the largest, equal to 67% (from 0.52 to 0.87).

The number of knots N corresponds to the number of unknowns and thus the conditioning of the objective function of the motion estimation algorithm. For sub-mm motion, the choice of N had an effect only for low β, where the regularization cannot control oscillations that emerge in the spline-based motion estimate for small number of control points. For larger motions, additional decline in SSIM was noticeable for a large number of control points and low β, where the increased number of unknowns becomes challenging for the optimization in the absence of sufficient prior information due to weak regularization.

Note that for large motion amplitudes, some of the cases with very low β or very large N were unable to converge (according to the criterion in Sec. 2.2.2) even after a single restart of CMA-ES. While more restarts might have yielded adequate compensation in such cases, it would come at a cost of increased computation time that may become impractical. Regardless of whether convergence was achieved, the primary observation from Fig. 5 is that the use of weak regularization or a very finely sampled motion curve leads to objective functions that are poorly conditioned and unlikely to provide accurate estimates of object trajectories for large motion amplitudes.

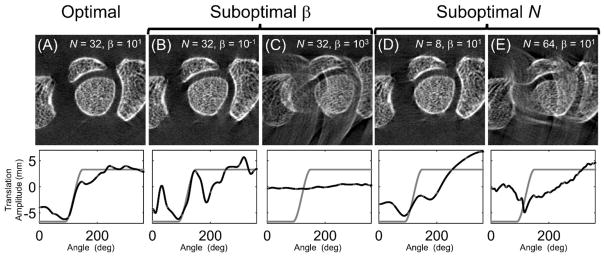
The effects of varying β and N are further evaluated in in Fig. 6 using magnified details of motion compensated reconstructions, along with the estimated and true (simulated) motion trajectories. Results for the 10 mm motion are used because SSIM exhibits strongest dependence on β and N for large motions. In Fig. 6A, the motion compensated reconstruction yielding the highest SSIM is shown. The estimated motion trajectory (black line) captures the principal features of the simulated motion pattern (gray line). The graphs in Fig. 6 plot the translation component of the motion along the axis of the simulated motion. Note that perfect agreement between the estimated and the true motion is not expected, as there are likely many motion patterns that yield equivalent images in terms of the autofocus metric.

Figure 6.

The reconstructed images (top) and translation component, along the axis of the simulated motion, of the motion trajectories (bottom) for the optimal (A) and suboptimal selections (B–E) of N and β. The amplitude of the true motion trajectory is shown as a gray line, the estimated trajectory is shown as a black line.

Fig. 6B and 6C investigate two cases of suboptimal regularization, but the same N as the optimal image [corresponding to the horizontal dashed line in Fig. 5F]. For β that is lower than the optimal value, residual streaks are present in the compensated reconstruction, likely because weak regularization admitted spurious high frequency motion components. When β is too high, the regularization suppresses large variations in the motion estimate, yielding a solution that is unable to capture the full extent of the step motion and an image with significant residual artifacts.

The results for varying N [at optimal β, corresponding to the vertical dashed line in Fig. 5F] are shown in Fig. 6D and 6E. When the number of b-spline knots is too low (Fig. 6D), the resulting model of the motion trajectory could not capture the sharp transitions corresponding to the beginning and end of the step, resulting in streak artifacts and distorted bone structures. In Fig. 6E, where N is larger than the optimum, the optimization algorithm was unable to converge due to the large number of unknowns.

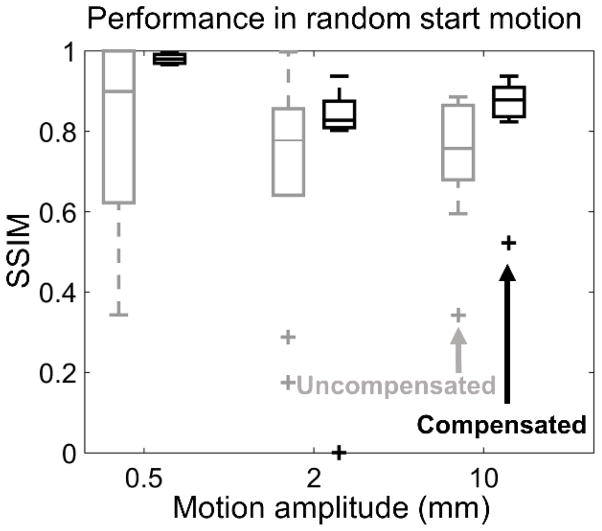
Robustness to phase shifts in the motion trajectory was investigated by generating a population of motions where the start angle of the translation step θ_L was randomly varied in the 0°– 300° range. Fifty cases each were generated for motion amplitudes of 0.5 mm, 2.0 mm, and 10.0 mm. SSIMs of uncompensated and motion-compensated reconstructions are explored in Fig. 7 using Tukey boxplots. Across the investigated range of amplitudes, motion compensation resulted in consistent increase in median SSIM and reduction of interquartile range compared to uncompensated reconstruction. Only two outliers (where the compensation algorithm failed) were found in the studied population of motions, indicating the robustness of the proposed method to variations in the motion pattern.

Figure 7.

Tukey boxplots are used to illustrate the distribution of SSIM values, before and after motion compensation, attained for a population of simulated motions (50 for each motion amplitude) where the starting point of the translation step was randomly selected for a range of translational motion amplitudes. SSIM was measured with respect to a static hand volume that was used to simulate the motion contaminated projections. Uncompensated reconstructions plotted in gray, compensated reconstructions in black.

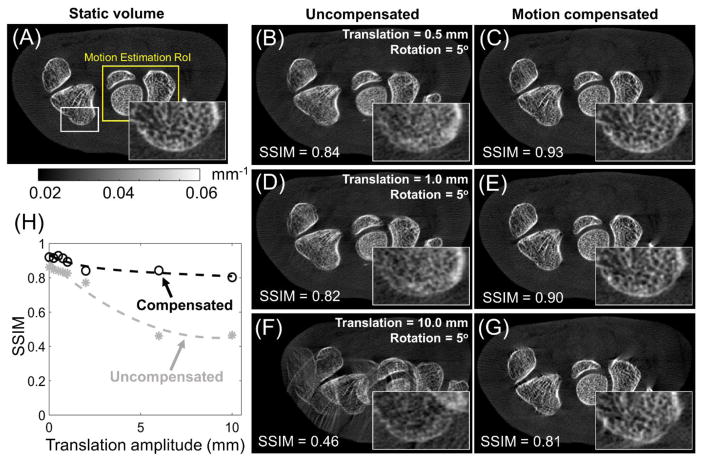
The results of motion compensation applied to the more complex rotation-translation trajectories are shown in Fig. 8. Analogously to the translation-only case, the translation amplitudes ranged from sub-mm to 10 mm, while the rotation amplitude was fixed at 5°. The starting angle θ_L of the combined rotation-translation was fixed at the nominal value of 90°. The parameters of the compensation algorithm were set to the optimal values (for each translation amplitude) established in the study of translation-only motion in Fig. 5. Even for the 0.5 mm translation + 5° rotation motion (Fig. 8B), distortions and blurring of the trabeculae are evident. Motion compensation restored (Fig. 8C) the image to appearance very similar to that of the static volume, as evidenced by the improvement in SSIM from 0.84 before compensation to 0.93. Increased amplitudes of the translational motion (1.0 mm in Fig. 8D and 10.0 mm in Fig. 8F) resulted in further degradation of image quality and SSIM. In both cases, the compensation algorithm achieved significant reduction of motion-induced blur, double contours and streaks. For the 1.0 mm translation + 5° rotation motion, the motion-compensated volume is very similar to the static gold standard (SSIM of 0.90). For the rotation-translation motion with 10 mm translation amplitude, motion artifacts were very severe, resulting in SSIM=0.46 in the uncompensated image. The compensation improved the SSIM to 0.81, which is slightly less that the SSIM achieved for the two smaller motions analyzed in Fig. 8, but represents the largest relative increase in SSIM, equal to 74%. The SSIM with and without motion compensation as a function of motion amplitude (at optimal values of β and N) is further investigated in Fig 8H. The plot shows consistent SSIM improvement across the explored range of motion amplitudes. Consistent with the earlier observations, the SSIM in the motion-compensated reconstruction is slightly degraded for large displacements compared to the sub-mm regime. However, the relative improvement in SSIM is most pronounced for large motions. The SSIM values achieved after compensation for the rotation-translation trajectory are slightly worse than the compensated SSIM for translation-only motion of the same translation amplitude. This is to be expected, as the cumulative displacement of the sample is larger for the rotation-translation trajectories (when compared at the same translation amplitude), and thus the initial distortion of the image is worse than for the translation-only motion.

Figure 8.

Comparison between the static volume (A) and reconstructions of projections contaminated by rotation-translation motion for motion amplitudes of 0.5 mm (uncompensated reconstruction in B, motion-compensated reconstruction in C), 1.0 mm (D and E), and 10.0 mm (F and G). Motion compensation was performed using optimal parameters found for the translation motion, shown in Fig. 5. (H) Comparison of SSIM of uncompensated (gray dashed line) and motion-compensated (black dotted line) reconstructions for a range of motion amplitudes. SSIM was measured with respect to a static hand volume that was used to simulate the motion contaminated projections.

3.3. Benchtop studies using an anthropomorphic hand phantom

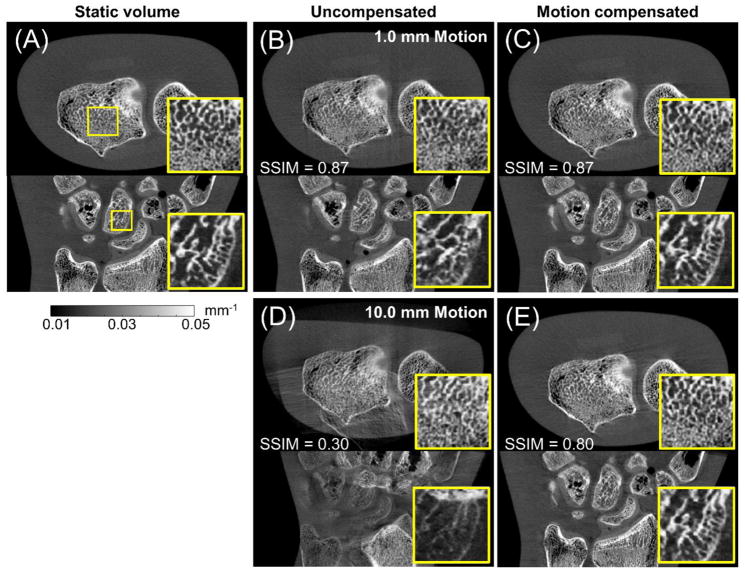
Fig. 9 compares the reconstructed volume with and without motion compensation for the hand phantom acquired on the imaging bench using a linear translation stage to generate object motion (Sec. 2.2.3). Reconstruction of a static phantom is also shown (Fig. 9A).

Figure 9.

Application of motion compensation to data acquired on a CMOS CBCT benchtop. Axial (top row) and sagittal (bottom row) views of the hand phantom are shown in (A) for a static acquisition. Reconstruction of motion contaminated projections without and with motion compensation are shown in (B) and (C) for 1.0 mm motion, and in (D) and (E) for 10.0 mm motion.

Motion compensation parameters were selected according to SSIM optima found in Sec. 3.2: β = 5×10³ and N = 40 for 1 mm motion and β = 10¹ and N = 32 for 10 mm motion.

Motion artifacts in the uncompensated image for 1.0 mm motion (Fig. 9B) are subtle, but close examination of the cancellous structures (particularly in the sagittal view) reveals blurring and a loss of trabecular detail. Motion compensation recovered the trabecular matrix, yielding a reconstruction closely resembling the static volume. Note that since the deformation was relatively minor, the SSIM remained unchanged at 0.87, likely because the metric was dominated by other differences between the static and motion compensated volume inherent to experimental data (compared to simulated data in Sec. 3.2) such as noise, image non-uniformity due to scatter etc. Similar results were obtained for 0.5 mm motion (not shown in Fig. 9) where an increase in SSIM from 0.90 to 0.92 was found after motion compensation.

For 10.0 mm motion (Fig. 9D), noticeable motion artifacts were found, including doubling of image structures. The motion compensated reconstruction in Fig. 9E shows significant reduction of artifacts and restoration of bone structures and phantom boundaries. SSIM increased from 0.30 for the motion-contaminated image to 0.80 after motion compensation. Consistent with the results of the simulation studies for large motions, some residual streak artifacts remain in the compensated image.

3.4. Application to clinical CBCT data

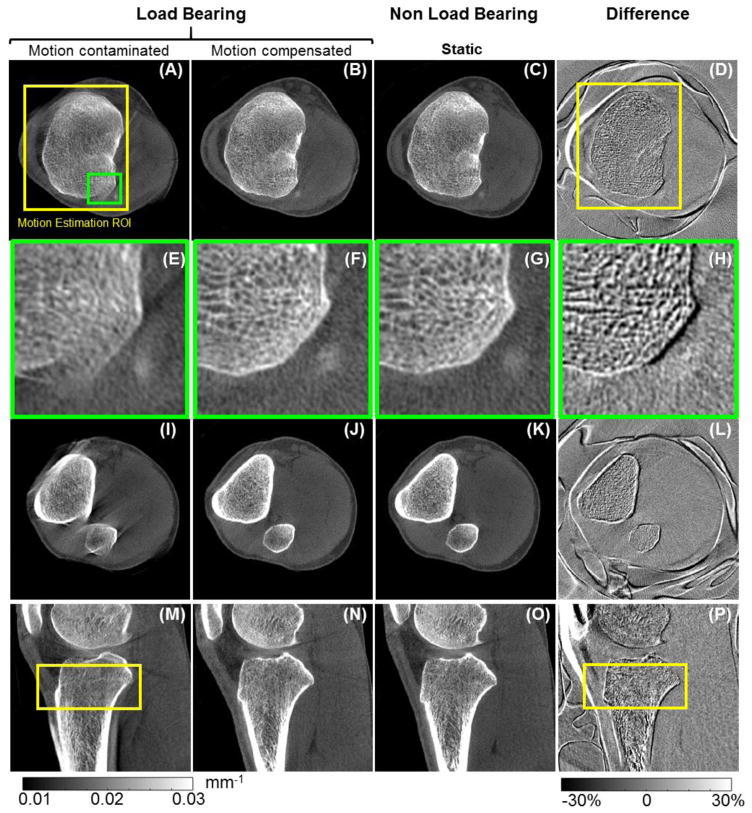
Application of the motion compensation method to clinical data is illustrated in Fig. 10. Motion artifacts are evident in the uncompensated LB reconstruction in Fig. 10A, E, I, and M.

Figure 10.

Motion compensation in clinical extremity CBCT. A motion contaminated load bearing scan before (A, E, I, and M) and after motion compensation (B, F, J, and N) is compared to a motion-free non-load-bearing scan of the same patient, shown in (C, G, K, and O). The difference images between the motion-compensated and motion-free volumes are provided in (D), (H), (L), and (P). Images E–H show a magnified view of the area marked with the green box in (A). The differences around the skin line, patella and patellar tendon are a result of load bearing and are independent of subject’s motion. Cross-sections of the motion estimation VOI are marked as yellow boxes in (A), (D), (M) and (P).

The VOI used for motion compensation is indicated as a yellow square in Fig 10A and M. Motion compensation (Fig. 10B, F, J, and N) achieved significant reduction of streak artifacts, improved delineation of high contrast boundaries and improved visualization of the trabeculae, especially inside the optimization VOI. The recovery of fine trabecular detail is further illustrated in the magnified views in Fig. 10E, F, G, and H. Adequate motion correction was also achieved in areas outside the VOI, as illustrated by the sagittal view in Fig. 10N and by the axial slice in Fig. 10J, which did not include any of the estimation VOI. The amplitude of the motion was estimated to be approx. 8 mm.

Reduction of artifacts and improved visualization of the anatomy after motion compensation is further demonstrated by comparison with the motion-free NLB reconstruction in Fig. 10C, G, K, and O. Fig. 10D, H, L, and P show a difference image between the NLB volume and the motion compensated LB volume. Only minor differences are found inside the motion estimation VOI, indicating lack of any major deformation of the image after motion compensation. Outside of the VOI, slightly more pronounced deviation between the two volumes is apparent. This is consistent with increased residual motion artifacts outside the VOI (e.g. in Fig. 10J) and illustrates the local character of image-based motion estimation. Note that the large values observed in the difference map at the skin line and around the patella and the patellar tendon is a result of load bearing and not uncompensated patient motion.

4. Discussion and conclusions

We developed a purely image-based motion compensation algorithm and evaluated it in application to high-resolution extremity CBCT. The method estimates the motion trajectory by iterative optimization of a cost function that consists of an autofocus term that maximizes image sharpness and a regularization term that penalizes abrupt motions. A statistical algorithm (CMA-ES) was employed to provide robust optimization of the non-convex cost function. A restart strategy with adjustment of the size of the solution search space was shown to be essential to achieve satisfactory correction for cases with large motion amplitudes.

Successful motion compensation was achieved across a range of motion amplitudes, from sub-mm drifts that often do not result in gross artifacts, but may hamper quantitative assessment of trabecular structure, to centimeter motions, where the method restored images that were initially non-diagnostic. Reduction of artifacts and improved agreement with the true (i.e., static) volume were shown for a variety of motion patterns including relatively simple translations, simultaneous rotations and translations, and clinical patient data with an unknown and likely complex motion trajectory.

The benchtop experiments used a CMOS-based imaging chain, specifically designed for the next generation of extremity CBCT optimized for high resolution imaging of bone microarchitecture. Excellent results achieved for sub-mm motions in the benchtop studies indicate that the autofocus metric performs well even when the initial departure from the optimum (sharp image) is subtle. Studies of the effect of motion compensation on the accuracy of metrics of trabecular architecture are ongoing.

Analysis of the clinical data illustrates the performance of the algorithm for the complex, mm-range motion typically encountered in patient imaging on the current generation extremity CBCT. Streak artifacts were reduced and the visualization and integrity of the trabecular detail and bone boundaries was restored to that of a static scan. Due to factors such as the lack of independent measurement of patient motion and somewhat inferior spatial resolution of the current CBCT scanner compared to the CMOS-based benchtop, it was not possible to identify cases representing more subtle, sub-mm patient motion to complement the example of Fig. 10. Nevertheless, the patient dataset clearly illustrates the usefulness of the proposed algorithm for current clinical applications of extremity CBCT, in particular in diagnostic tasks in bone.

Further tests of the algorithm on patient data acquired on the extremity CBCT system are ongoing to assess the impact of motion compensation on expert observer performance in clinical tasks. The observer studies are beyond the scope of this paper, but the preliminary results are of interest to provide insight into the type and amplitude of motion patterns that are typically encountered in patient imaging. Visual inspection of the motion trajectories, obtained during motion compensation for 24 knee scans, showed a step-like trajectory in 58% of the cases, a drift-like trajectory in 30% of the cases, and a multimodal curve in 12 % of the cases. The median motion amplitude was 3.2 mm. A similar range of motion amplitudes was reported in studies involving C-arm imaging with knees flexed around 60°, even though the flex position is likely more challenging to maintain than the natural stance considered in our study. For the flexed position, (Berger et al 2016) showed rotation <= 1° and translation <= 2 mm, and (Choi et al 2013) found motion trajectories with rotation components <= 2.5°. This assessment indicates that both the amplitude and the type of the motion patterns considered in the evaluation studies presented here are representative of the motions typically encountered in patient imaging.

Motion compensation times of ~20 min with no restart and ~40 min with restart (required for >6 mm translational motion) were attained owing to the ability to limit the computation of the autofocus metric to a local VOI and by leveraging GPU for parallel reconstruction of the population of candidate solutions in CMA-ES (involving both a multi-threaded implementation of the filtering and backprojection operations in the FDK algorithm and simultaneous reconstruction of candidate solutions) and for parallel computation of the autofocus metrics. Further acceleration of the motion compensation code is possible. For example, the CMA-ES implementation could be optimized by parallel sampling of candidate motion patterns and by parallel computation of the covariance matrices, instead of the current sequential execution on a CPU. The increase in runtime due to the restart could be potentially avoided by parallel execution of multiple CMA-ES optimizations with different initial states (e.g., in a multi-GPU architecture). This approach could be used to simultaneously probe different values of σ, instead of performing a restart with larger σ only if the initial CMA-ES run fails to converge. In general, the computation time stated here is thus a conservative upper bound on the speed of the algorithm. Further optimization of the code is ongoing, and the work reported within the scope of this paper provides promising results on the initial implementation.

Among the autofocus metrics evaluated in this work, the gradient-based metrics were found to outperform entropy and variance for applications in motion estimation in high resolution extremity CBCT. While similar findings were reported in (Kingston et al 2011) for quantification of geometrical misalignment in CBCT, other authors have found entropy to be more appropriate both for geometric calibration (Wicklein et al 2012, Kyriakou et al 2008) and for compensation of motion in head CBCT (Wicklein et al 2013) and in angiographic applications (Hahn et al 2016). In some of these applications, however, the motion amplitudes are likely small enough (below ~10 mm) to remain within the range where the entropy shows the desirable monotonic decrease with decreasing motion. It was only above this amplitude that we found the undesirable decrease of entropy with increasing motion. Furthermore, the gradient-based metrics might be preferable in high-resolution orthopaedic CBCT because they better leverage the rich frequency content of trabecular bone. For other applications, where the images exhibit a more piecewise structure, such as in head imaging or in imaging of contrast-enhanced vessels, entropy may indeed be a superior metric of image sharpness (Atkinson et al 1997).

The studies of the sensitivity of motion compensation to the selection of the parameters of the objective function imply a somewhat narrow range of regularization strength, β, yielding optimal performance at large motion amplitudes. However, an approximate guess of the motion amplitude to guide the selection of β can be obtained by assessing the severity and patterns of motion artifacts in the uncompensated volume.

The presented method assumes that the structures in the motion estimation VOI only undergo rigid transformations. However, while the motion of individual bones might be assumed rigid, the deformation of the whole extremity might be more complex (e.g. knee flexion). Future work involves development of methods that combine rigid motion estimates from multiple VOIs into a deformable motion field for the entire volume, following an approach similar to that presented in (Berger et al 2016). Future work includes appropriate techniques for combination of the rigid motion trajectories into a non-rigid motion field for the whole volume. It is worth noting that in the initial application to clinical data, adequate correction was achieved throughout the whole field of view despite using a fairly localized VOI that included only one bone (the tibia). This is because typical motions in a natural standing pose (as opposed to a flexed stance) occurred as a mostly rigid shift and tilt of the entire extremity, with the joint locked at a fixed angle.

Previous work on motion compensation in extremity CBCT indicated that minor deformations of the object may emerge in the compensated volumes as an effect of inconsistencies in the motion pattern that might e.g. induce variable effective magnification throughout the scan (Choi et al 2014, Berger et al 2016). No significant distortions were found in the difference images for clinical data in Fig. 10. However, slight deformations are the likely culprit behind degraded performance of the compensation algorithm at motion amplitudes >5 mm. Future studies will evaluate the effect of such distortions on quantitative accuracy of measurements performed in the compensated image, in particular in assessment of bone microstructure. It is anticipated that high resolution imaging in this application will be performed using patient immobilization that will restrict the motion amplitudes to a sub-mm range. In this range, the excellent SSIM achieved with the compensation algorithm in the simulation and benchtop experiments indicates that little or no deformation was induced. In general, however, lack of deformation cannot be guaranteed because of the inherent degeneracy of the motion estimation problem (i.e. many motion patterns might yield images that appear free of motion artifacts, even if the shapes remain distorted). For the same reason, the compensation algorithm does not necessarily reproduce the true motion pattern, even when the correction appears to be successful, as in Fig. 6A. For example, the estimated motion trajectory may contain an erroneous rotational motion of the sample around the scan axis that is perfectly synchronized with the gantry rotation and thus results in an apparent change in magnification, but does not introduce any artifacts. Even assuming that this rotational motion began with the sample shifted towards the source by as much as 5 mm, the resulting apparent magnification is only 1% less than the actual magnification of the system (425 mm/540 mm with the erroneous rotation vs. 430 mm/540 mm without). For a 100 μm detail size, consistent with the target resolution of the system, the scaling of the object associated with this erroneous motion pattern is only ~1 μm, which is well below the voxel size. While this is just a theoretical example, it illustrates the fact that many motion patterns can yield images that are apparently free of artifacts and distortions at the resolution of the CBCT system and are thus equivalent from the point of view of the autofocus objective function. At the same time, the example in Fig. 6 illustrates that the compensation algorithm typically correctly recovers the approximate amplitude and location of the dominant component of the true motion pattern.

In conclusion, the proposed image-based technique achieved successful compensation of motion artifacts and recovery of bone trabecular structure in high-resolution extremity CBCT across a broad range of motion amplitudes. The algorithm does not rely on fiducial markers, external tracking devices, or prior data and thus avoids any disruptions to the imaging workflow and can be applied retrospectively to any scan contaminated by patient motion where projection data is available. The proposed methodology will be essential in enabling clinical high-resolution applications of CBCT, such as assessment of trabecular bone, where even subtle, sub-mm patient motion can be detrimental to quantitative accuracy.