Multiparametric MRI maps for detection and grading of dominant prostate tumors

Abstract

Purpose

To develop an image-based technique capable of detection and grading of prostate cancer, which combines features extracted from multiparametric MRI into a single parameter map of cancer probability.

Materials and Methods

A combination of features extracted from diffusion tensor MRI and dynamic contrast enhanced MRI was used to characterize biopsy samples from 29 patients. Support vector machines were used to separate the cancerous samples from normal biopsy samples and to compute a measure of cancer probability, presented in the form of a cancer colormap. The classification results were compared to the biopsy results and the classifier was tuned to provide the largest area under the Receiver Operating Characteristic (ROC) curve. Based solely on the tuning of the classifier on the biopsy data, cancer colormaps were also created for whole-mount histopathology slices from four radical prostatectomy patients.

Results

An area under ROC curve of 0.96 was obtained on the biopsy dataset and was validated by a “leave-one-patient-out” procedure. The proposed measure of cancer probability shows a positive correlation with Gleason score. The cancer colormaps created for the histopathology patients do display the dominant tumors. The colormap accuracy increases with measured tumor area and Gleason score.

Conclusion

Dynamic contrast enhanced imaging and diffusion tensor imaging, when used within the framework of supervised classification, can play a role in characterizing prostate cancer.

INTRODUCTION

As the second leading cancer-related cause of death among males (1), prostate cancer is the subject of research efforts worldwide. The improvements achieved in the screening techniques for prostate cancer have resulted in the diagnosis of a rising number of cases, among which lies a population with low risk and/or localized tumors. Nevertheless, radical prostatectomy remains the most common treatment for the disease. As a result, 30% of cases of radical prostatectomy are performed on patients with pathologically insignificant cancer (2), making them subject to complications such as sexual, urinary, and bowel morbidity after the surgery. These complications are associated with the techniques employed during surgery. Even though these have improved significantly in the past decade (3,4), further improvements are difficult to envisage without knowledge of the cancer location, which can determine the need for and extent of the surgical positive margins applied. Furthermore, focal treatment of the disease with associated sparing of sensitive structures such as the neuro-vascular bundles, are viable options only if accurate patient-specific maps of cancer grade and stage can be provided pre-operatively. In other words, the success of focal therapy relies on proper patient selection and adequate characterization of the tumor’s location, extent and histology. The most commonly used method to assess prostate cancer is biopsy under transrectal ultrasound (TRUS). Because TRUS cannot accurately image prostate cancer, biopsy protocols suffer from significant sampling errors, resulting in false negatives or under-sampling of major tumors (5).

Magnetic resonance imaging has a proven ability to visualize the prostate anatomy (6). However, the conventional T2 weighted MRI has insufficient specificity and sensitivity for diagnosis, and specially grading, of prostate cancer even at 3T (7–9). A number of MRI-based techniques that provide physiological information about tissue have been studied to improve the grading of cancer. Earlier studies focused on Magnetic Resonance Spectroscopy (MRS), which allows the creation of metabolite maps in the prostate region (10). However, the diagnostic improvements due to MRS were limited and inconclusive (11). A more recent development is the use of diffusion, both diffusion weighted imaging (DWI) and diffusion tensor imaging (DTI), which characterize the de-phasing of the MR signal caused by molecular diffusion. Prostate cancer causes a pathological change in the tissue in which the regular pattern of distribution of prostatic glands is disrupted by masses of malignant epithelial cells and glands that are irregularly distributed (12). The increased cellular density can cause a decrease in apparent diffusion coefficients (ADC) in DWI, and average diffusivity <D> values in DTI, measured in prostate tumors. The structural changes are also likely to alter the molecular level diffusion and to cause differences in fractional anisotropy (FA) between regular and normal cells, intensified by the progress of the disease. Diffusion imaging is fast and convenient without the need for contrast agents. Radiologists have reported that ADC can help differentiate central gland tumors from stromal and glandular hyperplasia (13). Studies in case of DTI, however, are also inconclusive and report increased, decreased, or even unchanged values of FA (14–16). Dynamic Contrast Enhanced MRI (DCE MRI) has also been studied for grading of prostate cancer. When combined with a pharmacokinetic model, DCE characterizes the changes in tissue microvasculature which are linked to cancer growth (17). However, DCE prostate studies report moderate to weak correlations between cancer grade and Gleason score with individual DCE parameters (18, 19). A review of the role of MRI in detection and staging of prostate cancer is recently published (20).

The inconclusive correlation of MRI-based physiologic parameters with the progression of the disease is partly due to the heterogeneous and complex nature of both the biological tissue and the physiologic process of cancer progression. It is difficult, if not impossible, to extract specific ranges for the values of the individual parameters matched to the cancer stage. In the absence of such statistics, the solution appears to be supervised classification of the multi-parametric MRI data to separate normal and cancer tissue (21–23). Therefore, in this work a machine learning approach based on support vector machine classification (SVM) is used.

The purpose of this work is to use machine learning to develop an image based technique capable of detection and grading of prostate cancer by combining features extracted from multiparametric MRI into a single parameter map of cancer probability. We also study the validity of this method by comparison of the probability maps with wholemount pathology.

MATERIALS AND METHODS

Data Collection Protocols

The data used in this work was obtained in two studies, both reviewed and approved by the Clinical Research Ethics Board of our institution. The data from a biopsy study was used for training the machine learning algorithm and leave-one-patient-out evaluation. A second dataset from patients scheduled for radical prostatectomy, with available whole mount histopathology analysis after surgery, was used for further validation of the trained classifier.

Biopsy Data

This data was used in order to train classifiers and quantitatively assess the performance of the DTI-DCE parameters for cancer detection. During 2009, 29 patients with a high clinical suspicion for prostate adenocarcinoma due to an elevated prostate specific antigen (PSA) and/or palpable prostatic nodule, with no prior treatment, were consecutively recruited to this study. Average PSA was 8.5 ng/ml (range: 0.94 – 15 ng/ml). Written consent was obtained from each patient prior to entering the study. To ensure that the biopsy process or result did not affect the assessment of MRI as a diagnosis tool, the MRI scans in the original study were completed prior to biopsy for all patients; the biopsy was done the same day within a couple of hours following MRI. We use the same data here, with the goal of training a classifier to detect and grade prostate cancer.

The biopsies were performed under local anesthetic and the number of biopsies obtained from the peripheral zone (PZ) was determined by prostate gland size. In patients with a prostate gland of 30 cc or less, eight biopsies (base: right and left; midgland: right lateral, left lateral, right medial, left medial; apex: right and left) were taken. For prostate glands ranging 31–60 cc, 10 biopsies (base: right lateral, left lateral, right medial, left medial; midgland and apex biopsies as above) were obtained. For prostate glands greater than 60 cc, 12 biopsies were obtained (apex: right lateral, left lateral, right medial, left medial, base and midgland biopsies the same as the 10 biopsy scheme).

The dataset included a total of 240 negative biopsy cores and 29 positive biopsy cores. The positive cores were from ten patients. Detailed information about the positive cases is provided in (23) and Table 1. In seven cases, the patients went on to radical prostatectomy as their treatment. In these cases, the Gleason scores reported from post-surgical analysis were used as the Gleason score of the tumor. The histology was interpreted with assignment of the Gleason score by a number of different experienced anatomic pathologists who practice general and subspecialty uropathology.

Table 1.

Clinical data for 10 patients with biopsy confirmed cancer.

Patient	age [years]	PSA [ng/mL]	number of positive biopsies (size in mm)	biopsy Gleason score	prostatectomy Gleason score	clinical stage
P003	62	5.3	5 (8, 6, 2, 2, 1)	3+4	4+3	cT2a
P004	67	7.1	4 (7, 5, 1, 1)	3+4	3+4	cT2b
P005	60	5.4	2 (1.5, 1)	3+3	n/a	n/a
P007	58	7.1	5 (2, 3, 1, 2, 2)	4+5	3+4	cT1c
P010	55	7.09	2 (0.5, 4)	3+3	n/a	cT1c
P015	72	12	3 (10, 1.5, <1)	4+4, 4+5	4+5	cT1c
P016	65	5.43	2 (<1, <1)	4+3, 3+3	3+4	cT1c
P020	64	6.8	2 (1, 7)	3+4	3+4	cT2a
P024	60	5.4	1 (3)	4+4	4+3	cT1c
P026	62	6.4	1 (not recorded)	3+3	n/a	cT2a

Prostatectomy Data

In 2010, we started a new study in which patients scheduled for radical prostatectomy consent to an MRI imaging session prior to the surgery. This is a different population than the biopsy cases described above. The patients recruited for this study have not received any therapy prior to radical prostatectomy. At the time of writing, four datasets were obtained, providing 40 cross sections.

To acquire the whole mount pathology analysis, the radical prostatectomy specimens were dissected and histopathologically examined in a uniform manner. The external surfaces of the specimens were inked and the seminal vesicles amputated. The specimens were dissected following a minimum of 16 hours fixation in 10% buffered formalin. The apical and bladder neck tissue was removed, using 5 mm thick layers. We developed a device (24) to cut the prostate gland in serial transverse cuts perpendicular to the posterior capsule, at 4 mm intervals, from inferior to superior. This procedure allowed us to obtain reasonably good correspondence between the pathology slices and the MR image slices. The processing and paraffin embedding were carried out in a routine fashion, except using oversized baskets and blocks to accommodate the intact prostate gland. Whole mount sections were cut using a Lieka RM2245 whole body rotary microtome, and were submitted as intact transverse sections mounted on oversize glass slides for H&E staining.

MR Imaging Protocol

For both the biopsy and the prostatectomy studies the MRI protocol was as follows. All MRI examinations were performed on a 3T MRI scanner (Achieva, Philips Healthcare, Best, The Netherlands). MRI signals were acquired with a combination of an endorectal coil (Medrad, Pittsburgh, PA, USA) and a cardiac phased-array coil (Philips Healthcare, Best, The Netherlands). Fast spin-echo T2-weighted images (repetition time TR = 1851 ms, effective echo time TE = 80 ms, field of view FOV = 14 cm, slice thickness = 4 mm with no gap, 284×225 matrix, 3 averages) were acquired in the axial and coronal planes to provide anatomical details of the prostate. From this sequence, 12 axial slices covering the entire gland were then selected and used for the DTI and DCE MRI scans. DTI data were acquired using a diffusion weighted single shot echo planar imaging (EPI) sequence (TR/TE = 2100/74 ms, FOV = 24 cm, slice thickness = 4 mm with no gap, 128×115 matrix, 6 non-collinear gradient directions, b-value = 0 and 600 sec/mm², 18 averages, total acquisition time of 8 minutes; the relatively low b-value of 600 sec/mm² was chosen to ensure sufficient SNR for quantitative measurements of DTI parameters).

DCE MRI was performed using a 3D T1-weighted spoiled gradient echo sequence (TR/TE = 3.4/1.06 ms, flip angle = 15°, FOV = 24 cm, 256×163 matrix, 2 averages). Initially, proton density (PD) images (TR/TE = 50/0.95 ms, flip angle = 4°) were acquired to allow calculation of the contrast agent concentrations in the prostate. Next, a series of 75 T1-weighted dynamics were acquired prior to (3 images) and following (72 images) a bolus injection of Gd-DTPA (Magnevist, Berlex Canada, 0.1 mmol/kg injected with a motorized power injector within 10 s at the rate if 2 ml/s, followed by a 20 ml flush of saline. This resulted in a time resolution of 10.6 s per 12 slices. Currently our scanner allows higher temporal resolution, however we kept the same protocol over the duration of the study for consistency. T1 values were calculated based on PD-weighted and T1-weighted images according to the procedure described in (25).

The total time of the MRI examination was approximately 45 minutes. The DTI data were processed off-line to calculate FA and average diffusivity (<D>) values. Diffusion weighted images were registered to the non-weighted b=0 image with a mutual information algorithm prior to calculating the eigenvalues of the diffusion tensor and generating maps of the average diffusivity <D> (i.e. trace of the diffusion tensor) and fractional anisotropy (FA) with the proprietary DTI processing toolbox PRIDE (Philips Healthcare, Best, The Netherlands).

DCE MRI data were processed off-line with software procedures developed in house using Matlab (Mathworks, Natick, MA, USA) and Igor Pro (WaveMetrics, Portland, OR, USA). Arterial Input Functions (AIFs) were extracted from voxels in the external iliac or femoral arteries in the central slice for each patient (26). Pharmacokinetic parameters: volume transfer constant, K^trans, fractional volume of the extra-vascular extra-cellular space, v_e, and fractional plasma volume, v_p, were calculated by fitting the contrast agent concentration vs. time curves to the extended Kety model. Fitting was carried out in every pixel of every slice within a region of interest (ROI) encompassing the prostate gland to generate maps of the pharmacokinetic parameter as described by Tofts et al (27).

T2-weighted images were used to identify the prostate gland, the peripheral zone, and other anatomical details that helped with matching MRI with histology. DCE MRI and DTI images were acquired with the slice thickness of 4 mm, location, and the same resolution; no interpolation was required. The vast majority of the glands were smaller than 48 mm and typically 8 – 10 slices were enough to cover the entire gland. We did not have any cases where the tumor was missed because of the insufficient MRI coverage.

Matching ROIs from MRI to Biopsy Cores

In the biopsy data, one ROI represented by one set of DCE and DTI parameters was defined for each biopsy core. To relate the DTI and DCE MRI parameters with biopsy results, we used the consensus in the literature on the values of <D> and K^trans in prostate tumors. It is widely reported that <D> is lower and K^trans is higher in the tumor than in normal PZ (19, 28).

The following correspondences between MRI slice locations and gland anatomy was assumed: slices 5 – 8 corresponded to midgland area, slices 1 – 4 (2 or 3 – 4 for smaller glands) corresponded to the apex, and slices 9 – 12 (9 – 10 or 11 for smaller glands) corresponded to the base. The tumor identification in the MRI data was based on a threshold value determined separately for the DTI and DCE MRI data. To determine the threshold, first the areas with low intensity on the <D> maps were manually segmented, based on visual inspection, in the areas corresponding to the positive biopsy locations. For example, left lateral midgland positive biopsy corresponded to any low <D> value areas, not smaller than 3×3 contiguous pixels (approximately 3 mm × 3 mm), in the left lateral peripheral zone within slices 5 – 8. The intensity threshold for the DTI data was defined as the average of all ROIs corresponding to positive biopsies plus one standard deviation. The addition of one standard deviation was applied to minimize the bias caused by manual segmentation. Similarly the intensity threshold for the DCE MRI data was determined as the average of the all high intensity areas on the K^trans maps corresponding to the positive biopsies, minus one standard deviation. Once the threshold values for the DTI and DCE MRI data were established across the dataset, the MRI data were analyzed again, and all the areas below the intensity threshold on the <D> maps and above the intensity threshold on the K^trans maps, corresponding to biopsy locations, were considered cancer. In the areas where no low <D> or high K^trans values were present, and also for negative cores, the average parameter values from the entire area corresponding to the biopsy location (e.g. average of the left lateral PZ in slices 5 – 8 corresponded to the left lateral midgland biopsy location) were calculated and used as the feature vector representing the biopsy core.

It should be noted that the ROIs from DCE and DTI were selected separately. This was to ensure that the selection criteria from one modality did not affect the selection in the other modality. Furthermore, the two datasets were not geometrically registered. Therefore matching was neither possible nor helpful. Since we classify an area generally corresponding to a biopsy, perfect geometric matching of the two image types is unnecessary.

Reference Standard in the Prostatectomy Data

The histology slides were examined and the regions of the prostatic carcinoma were outlined with assignment of the Gleason score by an anatomic pathologist with over 20 years of experience who practices general and subspecialty uropathology. The cancer probability maps acquired using the SVM-based measure of cancer probability (see the next section) were validated based on these histopathology results. Our cutting method and device ensured the matching of 2D MRI slices with pathology slides. However, the MRI slices and pathology slides were not deformed to be registered to each other.

Classification

The MRI data processing resulted in three DCE parameter maps (K^trans, v_e and v_p) and two DTI parameter maps (<D> and FA) per imaging plane. Each parameter map was of size 256×256 covering the field of view. In the biopsy data, each ROI constructed based on a biopsy core was represented by the 5 dimensional feature vector x = [K^trans, v_e, v_p, <D>, FA] consisting of values of the DCE and DTI parameters averaged over the ROI. To generate the colormaps, every pixel of the DTI-DCE image was represented and classified as a feature vector.

Support Vector Machines

In its most common form, the SVM classification approach depends on using a kernel function to map the input data to a higher dimension space where a hyperplane can be used to separate the data into different classes. The process of training a SVM classifier is equivalent to finding the optimal hyperplane that minimizes a classification error measure on the training dataset and maximizes the perpendicular distance between the decision boundary and the closest data points in the classes, a quality that makes SVM a maximum margin classifier. These closest data points that define the decision boundary are called “support vectors”. In a two-class case, if the training dataset consists of N feature vectors {x₁, ..., x_N} with class labels y_i ∈ {1,−1}, then the SVM training problem is equivalent to finding w and b such that:

$$\frac{1}{2}{w}^{T}w+c{\mathrm{\sum }}_{i=1}^{i=N}{\epsilon }_i$$ [1]

is minimized subject to

$$y_i(w^T\phi (x_i)+b)\ge 1-{\epsilon }_i$$ [2]

where b and w (the normal vector) define the hyperplane, ε_i ≥ 0 are the so-called slack variables that allow for misclassification of noisy and difficult data points, and c > 0 controls the trade-off between the slack variable penalty and the error margin, and φ(.) is the mapping function to a higher dimension. As shown in (29), w can be written as a linear combination of the transformed support vectors. In other words, w = Σ α_jφ(x_j), where x_j’s are the support vectors. This observation means that the decision hyperplane and the optimization equation [2] only contain the mapping function in its dot product format. Therefore, one does not need an explicit expression for φ(.) and the SVM optimization and decision hyperplane are defined fully given the kernel function of form K(x_i,x_j) = φ(x_i)^T . φ(x_j). The most common choice for the kernel function, also used in our work, is a Radial Basis Function (RBF) kernel defined as:

$$K\left(x_i,x_j\right)=e^{-\gamma {\mid \left|x_i-x_j\right|\mid }^2}$$ [3]

The use of this kernel is equivalent to mapping the data into an infinite dimensional Hilbert space (29). The RBF kernel has only one parameter (γ > 0) that can be adjusted. This means that the process of tuning the SVM classifier to a specific problem is limited to finding the appropriate values for just two parameters: c and γ. Once ε_i ≥ 0 are given, for a given choice of c and γ, w and b that solve [1] and [2] are obtained by solving a quadratic program (QP). The details of the solution can be found in (30) and in the publicly available C++ implementation of the SVM algorithms known as LIBSVM (http://www.csie.ntu.edu.tw/~cjlin/libsvm), which is the library that we have used.

SVM-based A Posteriori Class Probabilities

SVM is merely a decision machine: If f(x_n) = w^T φ(x_n) + b > 0, then the class label for x_n is y_n = 1. In other words, SVM does not provide a posteriori class probability. In order to generate the cancer distribution probability maps and also the Receiver Operating Characteristic (ROC) curves, one needs a posteriori probability of cancer of the form:

$$P_c(x_n)=p(y_n=1\mid f(x_n)=w^T\phi (x_n)+b)$$ [4]

where P_c(x_n) stands for probability of x_n being cancerous. To extend SVM for probability estimates, after the training step, we train the parameters of an additional sigmoid function of the form:

$$P_c(x_n)=p(y_n=1\mid f(x_n))=\frac{1}{1+exp(Af(x_n)+B)}$$ [5]

to map the values of f(x_n) to a posteriori probabilities. The values of parameters A and B are fitted using maximum likelihood estimation from the training set for which the actual labels are known (31, 32). We used class probabilities generated with this method for creating the probabilistic cancer maps.

Cross Validation and Tuning the Classifier

To tune the classifier, with appropriate values of c and γ, we exhaustively searched the parameter space 1 ≤ c ≤ 100, 1 ≤ γ ≤ 100 with steps of 0.1. For each set of parameters, we trained the SVM using data from 28 biopsy patients and tested it on the data from the 29^th patient, and repeated the process for all 29 datasets. This exhaustive search could be completed in less than 10 minutes on a typical PC. Note that this process was only completed once to set the parameters of the classifier. The classifier parameter set resulting in the best classification performance, as measured by the average area under the ROC curve for the 29 tests, was chosen.

The biopsy dataset was unbalanced, with more normal biopsy cores than cancerous cores (240 vs. 29). This could cause a bias towards the normal class during the optimization step of the SVM. To reduce the bias, we repeated the entire leave-one-patient-out training-testing cross validation 100 times, each time with a random subset consisting of half of the normal biopsies, and averaged the results to report the ROC curve. One-way analysis of variance (ANOVA) was used with the outcome of the 100 trials to compare the performance of DCE features alone, DTI features alone, and DCE-DTI combined.

ROCs and Colormaps

To generate the ROC curves, a posteriori cancer probability (P_c) was used to determine a decision boundary which we call t. A biopsy core was classified as cancerous if P_c > t. The value of t was incrementally increased from 0 to 1, with each t value yielding one point on the ROC curve (sensitivity vs. 1-specificity). To create the colormaps used to validate the methods by comparison with the histopathologic analysis of whole-mount slides from prostatectomy cases, each pixel in the entire surface of the prostate gland in DCE-DTI images was classified using the SVM tuned and trained on the biopsy data. The P_c values were plotted in standard Jet colormap, with hot colors representing high cancer probabilities.

RESULTS

The results reported here are acquired using the SVM classifier with parameter values set at c =0.6 and γ = 4, determined by the exhaustive search to improve the area under the ROC curve.

ROC Curves and Correlation with Gleason sScore on Biopsy Data

In order to study the role of DCE and DTI separately, we report three sets of ROC curves acquired using only the DCE features, [K^trans, v_e, v_p], only the DTI features [<D>, FA], and the combined feature vector, [K^trans, v_e, v_p,<D>, FA]. The summary statistics for the five parameters in the biopsy dataset is presented in Table 2, separately for biopsy normal and cancerous regions of interest.

Table 2.

Summary statistics in format of mean (standard deviation) for the five parameters used in the analysis. Values are reported for the normal and cancer biopsies.

	<D> (1000−3mm2/s)	FA	Ktrans (min−1)	ve	vp
Normal	1.662 (0.317)	0.207 (0.067)	0.070 (0.047)	0.227 (0.115)	0.017 (0.011)
Cancer	1.120 (0.174)	0.198 (0.051)	0.148 (0.071)	0.202 (0.049)	0.007 (0.007)

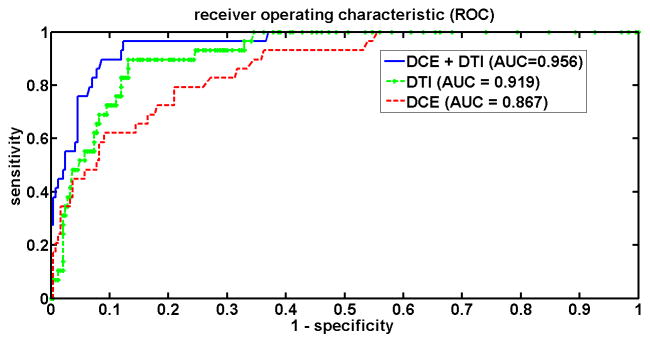
The area under ROC curve (AUC) was 0.867, 0.919 and 0.956 for DCE, DTI and the combined DCE-DTI features (Figure 1). The combined feature vector resulted in higher AUC than DCE (p=0.002) and DTI (p=0.01). With the combined feature vector, at the decision threshold of P_c =0.5, three of the 29 tumors were misclassified while a specificity of 91% was obtained (221 out of 243 normal biopsy samples were correctly classified). When P_c=0.3 was set as the threshold for cancer detection, only one tumor was misclassified, while the specificity of 87% was maintained (211 out of 243 normal biopsy samples were correctly classified).

Figure 1.

ROC curves for the biopsy data, for different groups of features acquired by changing the decision threshold, Pc, from 0 to 1.

We also noted a positive correlation between the P_c value and the Gleason score of the tumors. The average P_c value was 0.555 for tumors of grade 3+3 (number of tumors=7), 0.778 for tumors of grade 3+4 and 4+3 (n=19), and 0.963 for grade 4+5 (n = 3). The increase in P_c values was significant from Grade 6 to 7 (p=0.01). The small number of tumors in grade 4+5 did not warrant an analysis of statistical significance. None of the 4+5 tumors were misclassified in any of the experiments.

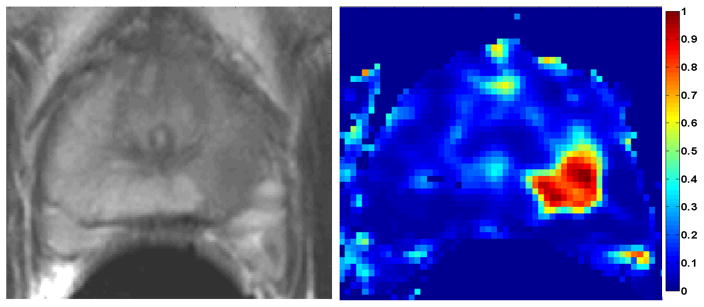
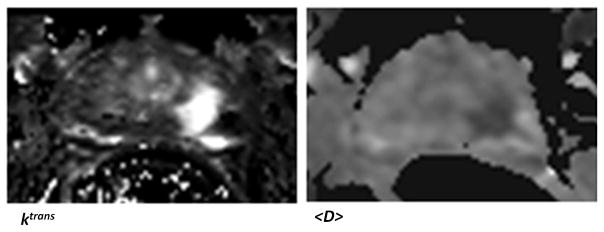
The T2-weighted image and the cancer probability map obtained for the mid slice MRI data of a patient with positive biopsy cores in the mid-left-lateral and mid-left-medial regions of the prostate are illustrated in Figure 2. This was acquired by treating every pixel of the DCE-DTI image as a feature vector and computing P_c. The tumor was of grade 4+5. For this case, the <D> and K^trans maps are also strong indicators of the existence of cancer. These maps are presented in Figure 3.

Figure 2.

Left: T2-weighted MRI of the mid-gland of a patient with biopsy confirmed cancer in mid-left region. Right: The SVM-based cancer probability map, with hot colors showing higher Pc. The Gleason score: 4+5, the average Pc in the tumor area: 0.9.

Figure 3.

The <D> and K^trans maps for the patient presented in Figure 2.

Cancer Colormaps Revealing Significant Pathologic Conditions

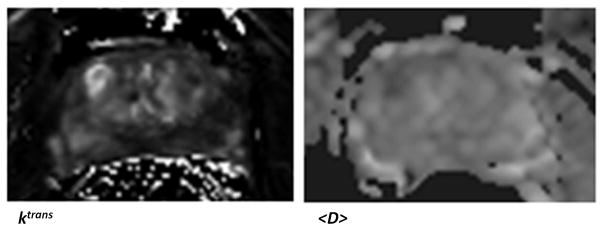
The trained classifier was used on the second data set from patients who underwent radical prostatectomy followed by whole-mount pathology analysis. In three of these four patients we found a “dominant tumor”. This is in agreement with previous studies that point out the existence of a single dominant tumor with several much smaller foci also present in many prostatectomy specimens (33). In a study involving 100 prostatectomy patients, it was shown that the Gleason score of the dominant tumor was identical to the primary Gleason score of the prostatectomy specimens in 97% of patients (34). Therefore, we believe a system designed to efficiently screen patients for possible focal therapy, can be assessed based on its ability to demonstrate the dominant tumor. Figure 4 shows the outcomes for case 1. For one of the prostate sections in this case, the parametric maps (K^trans and <D>) are presented in Figure 5. For case 2 and 3, samples of the probabilistic maps, along with pathology finding and T2 image are presented in Figures 6 and 7. As these Figures illustrate, in the cases with dominant tumors, the cancer colormaps created by pixel-wise computation of the P_c values demonstrate a visible tumor in the area validated by the histopathologic analysis. Note that the DTI and DCE data from these patients were not used in training the SVM classifier.

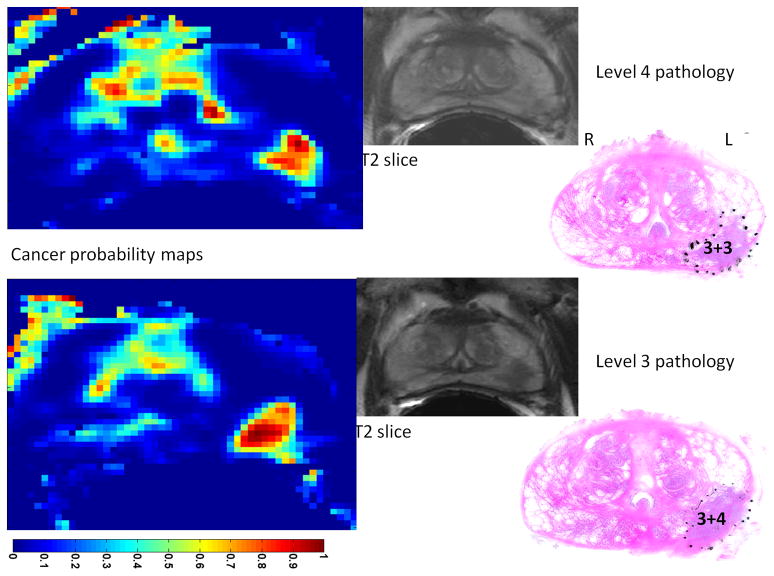
Figure 4.

Cancer colormaps and MRI images with corresponding histopathology slide for case 1. The main pathologic finding is a 3+4 tumor in the transition zone, visible in two consecutive cross sections.

Figure 5.

The <D> and K^trans maps corresponding to the case presented in Figure 4, row 1.

Figure 6.

Cancer colormaps and MRI images with corresponding histopathology slide for case 2. The main pathologic finding is a tumor that is of Gleason score 3+4 in one cross section and 3+3 in the neighbor cross section. The hot-spot in the transition zone of the prostate is a false positive detection. This is most likely due to the fact that our SVM is trained only on data from peripheral zone.

Figure 7.

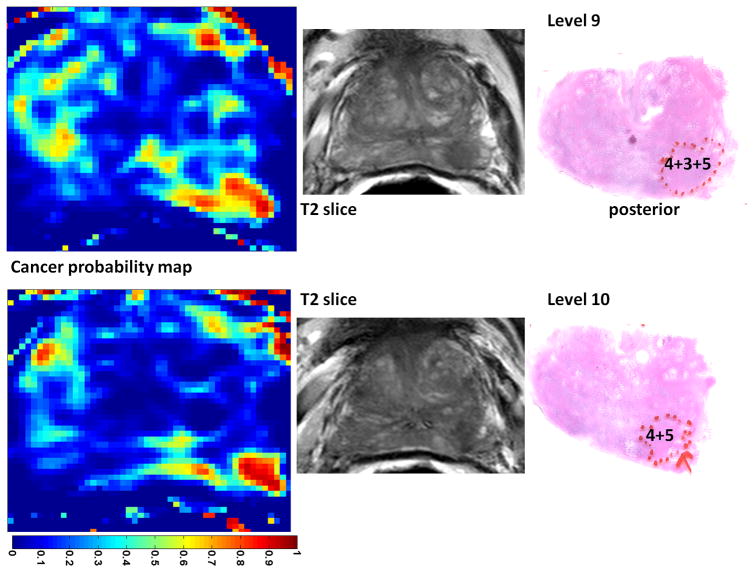
Cancer colormaps and MRI images with corresponding histopathology slide for case 3. The main pathologic finding is a tumor that is of Gleason score 4+3 (with considerable tertiary Gleason score of 5) in one cross section and 4+5 in the neighboring cross section.

Table 3 reports the surface area and the Gleason score of the tumors determined by the pathologist and compares them with the surface area of the tumor and P_c determined from the colormaps. To calculate the surface area, pixels with P_c >0.5 were considered part of the tumor. For each case, the data is presented for two consecutive cross sections (pathology levels) that best depict the dominant tumor. In cases with Gleason score > 3+3, the area of the tumor is very close in the pathology slide to the area depicted by the SVM-based cancer colormap resulting in an average difference of 2.8%. In case of the 3+3 tumor, level 4 in case 2, the area of the tumor as depicted in the probability map is 40% smaller than the pathology finding. As expected, the colormaps more accurately depict the tumor in the cases of tumor grades 3+4 and 4+5 than in tumor grade 3+3. In one case (level 10, case 3), a 4+5 tumor was identified. The average P_c in this case was 0.86, providing a distinct appearance to the tumor. Note that if one considers the effect of shrinking due to specimen fixation, the depicted tumor area in the colormaps is smaller than the expected size of the tumor even in case of 3+4 and 4+5 tumors.

Table 3.

Area and Gleason score of the tumors in six cross sections from the prostatectomy cases where a dominant tumor was present.

Patient	Tumor area (pathology)	Gleason Score	Tumor area (map)	Pc
Case 1, level 4	108 mm2	3+4	106 mm2	0.72
Case 1, level 3	94 mm2	3+4	92 mm2	0.70
Case 2, level 4	120 mm2	3+3	70 mm2	0.68
Case 2, level 3	93 mm2	3+4	88 mm2	0.75
Case 3, level 9	86 mm2	4+3	83 mm2	0.82
Case 3, level 10	72 mm2	4+5	71 mm2	0.86

For each tumor, the area of tumor in the colormaps and also the average P_c are given.

In one case, case 4, no dominant tumor could be identified. Cancer was bilateral involving all areas of the gland, occupying 25% of the overall volume of the prostate and up to 60% of the surface of certain cross sections. The highest grade reported by the pathologist was 3+3. The colormap showed many hot spots. However, no dominant tumor was identified. In the middle plane of this 3+3 case, the cancer area depicted on the probability map, with threshold of P_c >0.5, was 36% smaller than the area depicted by the pathologist.

DCE imaging is not always possible because contrast agents are contra-indicated in some cases. It was noted that DTI alone can also provide an efficient modality within our framework: for the three cases with a dominant tumor, using only DTI features we acquired maps showing an area difference with the combined DTI-DCE of approximately 6.1% in the dominant tumor.

DISCUSSION

We found that the combination of DTI and DCE provides an area under ROC curve of 0.96 and is more efficient in cancer detection than each method individually. DTI alone provides an area under ROC curve of 0.92 in the biopsy data. Using an extension of the standard SVM classification approach, we were able to compute a posteriori class probabilities that quantify the probability of cancer for each set of DCE-DTI parameters, based on the available training data. The average P_c value was 0.555 for tumors of grade 3+3, 0.778 for tumors of grade 3+4 and 4+3, and 0.963 for grade 4+5.

One distinction of our work compared to the previously published (21, 23) work on multiparametric MRI for cancer detection is our ability to combine DTI and DCE features and provide one reliable measure of cancer probability (P_c) that can be used for ROC curves and cancer probability maps. We also validate our cancer probability measure based on the reference standard of whole mount pathology on a second group of patients.

In the past, we have reported the performance of the five parameters in detection of prostate cancer individually, and the use of a statistical approach, namely logistic regression, for combining the DTI and DCE parameters for cancer detection (23). The use of SVM in the current work provides two main advantages. The first one is the fact that SVM is a maximum margin classifier and provides the ability to generalize the trained classifier. The second one is the ability of the proposed framework to provide a value for the probability of cancer.

In analyzing the presented colormaps, one should note that the training of the SVMs used to compute these probability values was entirely based on the data from our biopsy datasets. This means that the outcomes are most reliable on the peripheral zone of the gland, which is usually the target of the biopsy studies. Nevertheless, as visible in Figure 4, we have also been successful in detection of the dominant tumor in the transition zone. Additional data from the transition zone is required as we have also encountered false positive findings in this zone (Figure 6).

At this stage of our work, we decided not to use the data from prostatectomy patients for the training step of the SVM classification. This was due to several reasons, including the currently limited number of patients enrolled in the prostatectomy study, and the difficulty of accurately registering the pathology slides to MRI images to establish the reference standard for training. Also, our analysis does not target accurate delineation of the individual tumor contours at this stage. This is partly due to the fact that specimen deformation during fixation limits our ability for establishing a reference standard for the exact geometry of the tumor.

As described earlier, we used a special cutting device that allowed us to slice the prostate in correspondence with the position of the MRI slices. Further, we ensured the matching of the slices, visually, based on the anatomical details clearly visible in T2-weighted images and histology sections. We acknowledge that deformations caused by the fixation process and the potential slight shift of the slices in the axial direction exist and result in errors in the process of matching the MRI and histology reference. Investigators have reported attempts directed towards developing deformable registration of the histology and MRI images (35–38). However, the validation of the registration process requires maintaining visible markers throughout the imaging, surgery and laboratory work. This has led to the lack of a clinically viable method for quantitative registration of MR slices with histology. Due to this limitation, we have not used the data from prostatectomy patients in the training stage. Instead, we used this data as a second validation dataset. We looked for the existence of dominant tumors in the areas of the slides corresponding to areas of the cancer maps with high probability of cancer. We report the surface area and the average probability of cancer from the maps and study their correlation with the surface area and Gleason score of the tumor determined by the pathologist. In the absence of a method for quantitatively validated deformable registration of slices from MRI and histopathology, we have used these measures for qualitative validation. In our current setup, when most areas of the gland are invaded by carcinoma (such as case 4 in our prostatectomy study), the interpretation and validation of the colormaps is difficult due to the lack of quantitative registration. These cases, however, are unlikely to be missed during conventional biopsy. Furthermore, they are not candidates for focal therapy.

Similar to any other machine learning method, our algorithm can be improved by presenting more data in the training stage. We require more data to represent all levels of cancer progression, including very high grade and very low grade cases, and also all areas of the gland including the central zone. As we continue our study, such data will be incorporated into the system. We will also consider the detection of benign pathologies such as benign prostatic hyperplasia when such cases are represented in our data for training purposes.

We found that tumor classification is increasingly more accurate for higher Gleason scores (with 2–3% area difference in 3+4 and 4+5 tumors vs. 30–40% difference in 3+3 tumors). The sensitivity of our approach to the pathologically significant cases, accuracy in determining the dominant tumors with high Gleason score, and the correlation of the computed cancer probabilities with the Gleason score, are helpful features for treatment planning. This provides additional value to the routine radiological analysis of the images, even in cases where the tumor is visible on the T2-weighted image.

As it is evident from Figures 3 and 5, <D> and K^trans provide tumor contrast in many cases. Nevertheless, clinical challenges remain in dealing with false positive detections, and more importantly, separating indolent from aggressive tumors. This type of prognostic information is currently available only through pathology, which can be misleading due to undersampling of the clinically significant diseased areas during biopsy. Our computational framework is a step towards developing the ability to quantitatively characterize prostate tumors non-invasively. The clinical impact of such system, if achieved, will be significant. We propose an objective, quantitative method to radiologically characterize prostate cancer and replace the standard practice of visual evaluation by a radiologist.

We recognize a number of limitations in the current stage of the study. One limitation is the current lack of a quantitative registration mechanism between MRI and pathology. This has limited our quantitative analysis on the wholemount data to cases with a dominant tumor. As described earlier, tackling this issue is among our immediate research goals. The potential geometric distortion of diffusion images is another shortcoming. This limits our ability to pinpoint the exact location of a tumor. At the current stage, we have not detected significant distortion away from the rectum in the DTI images from the prostatectomy cases for which we have wholemount pathology. We will work towards a reliable technique to register DTI data to other MRI images as we progress. Finally, our current validation with wholemount pathology is limited to a small dataset and we need to expand this study to a sufficiently large group of patients who represent different stages of the disease.

In conclusion, a combination of DCE and DTI MRI features, when used along with a SVM-based machine learning approach, can provide helpful cancer probability maps for detection and grading of prostate cancer. The performance of the method is reported on a biopsy dataset of 29 patients, and validated for three additional cases by comparison of the generated probability maps with wholemount pathology in terms of the accuracy in depiction of the dominant prostate tumors.