Abstract
It is known that different amino acid residues have effects on the thermodynamic stability of an α-helix. The underlying mechanism for the thermodynamic helical propensity is not well understood. The major accepted hypothesis is the difference in the side-chain configurational entropy loss upon helix formation. However, the changes in the side-chain configurational entropy explain only part of the thermodynamic helical propensity, thus implying that there must be a difference in the enthalpy of helix–coil transition for different residues. This work provides an experimental test to this hypothesis. Direct calorimetric measurements of folding of a model host peptide in which the helix formation is induced by metal binding is applied to a wide range of residue types, both naturally occurring and nonnatural, at the guest site. Based on the calorimetric results for 12 peptides, it was found that indeed there is a difference in the enthalpy of helix–coil transition for different amino acid residues, and simple empirical rules that define these differences are presented. The obtained difference in the enthalpies of helix–coil transition complement the differences in configurational entropies and provide the complete thermodynamic characterization of the helix-forming tendencies.
Keywords: protein stability, thermodynamics, calorimetry
The structure of the α-helix in polypeptides was proposed more than a half-century ago (1). Nevertheless, some details of the thermodynamics of the helix–coil transition remain to be deciphered (see reviews in refs. 2–7 and references therein). From the basic consideration of the structure of an α-helix, the arrangement of the i to i + 4 hydrogen-bonding pattern by the peptide backbone is the driving force for helix formation, and is enthalpically favorable (8, 9). It is also known that, entropically, helix formation restricts the configurational freedom of the side chain (10–17). For example, the loss in configurational entropy for alanine will be very small because it has a very small side chain, while valine, because of the β-branching of the side chain, will have a large decrease in conformational entropy upon helix formation (14). Based on these observations, it was proposed that the loss in configurational entropy is a major factor that defines the helix-forming propensities of different amino acid residues (17). Later, it was noticed that the loss in configurational entropy explains only 50–70% of the difference in the thermodynamic propensity as measured by the difference in the Gibbs energy. This finding suggests that there is unaccounted entropy change or there is also a difference in the enthalpy of a helix–coil transition for different amino acid residues (18–20). Indirect estimates of the enthalpy of helix–coil transitions for just four amino acid residues further suggests the sequence dependence of the enthalpy (18, 19).
Direct calorimetric measurements of the enthalpy of helix–coil transition are very difficult, for numerous reasons, including the small absolute values, low cooperativity of the helix–coil transition, and the lack of simple model systems (21–23). Most of these shortcomings have been overcome recently by using a model system in which metal binding induces helix formation in a short helical peptide (24, 25), thus allowing the use of isothermal titration calorimetry (ITC) to monitor the enthalpy of helix–coil transition (26). By using different peptides, it was found that the enthalpy of the helix–coil transition for alanine is -0.9 ± 0.1 kcal/mol, and is independent of peptide length (26). This experimental setup is extended in the present work to incorporate 11 different amino acid residues at a host position. The nature of the guest residues was selected to represent differences in size, shape, hydrophobicity, hydrogen-bonding potential, and included both the natural amino acids alanine (A), glycine (G), valine (V), leucine (L), isoleucine (I), phenylalanine (F), asparagine (N), glutamine (Q), serine (S), and threonine (T), and the nonnatural amino acids norvaline (J) and 2-aminobutyric acid (B). Based on the calorimetric results for these 12 peptides, it was found that indeed there is a difference in the enthalpy of helix–coil transition for different amino acid residues and simple empirical rules that define these differences are presented. The obtained difference in the enthalpies of helix–coil transition complement the differences in configurational entropies and provide the complete thermodynamic characterization of the helix-forming tendencies.
Materials and Methods
Peptide Synthesis, Purification, and Sample Preparation. Peptides P1 (Ac-DKDGDGYISAAE-NH2), and P2X (Ac-DKDGDGYISAAEAXAQ-NH2) where X = A, L, I, V, S, T, F, N, Q, G, and the nonnatural amino acids J and B, were synthesized at the Penn State University College of Medicine Core Facility, by solid-phase procedures on a Milligen 9050 FMoc peptide synthesizer. Peptides were cleaved from the resin by using a trifluoroacetic acid procedure, followed by multiple ether extractions, and dried under nitrogen. Peptide identities were confirmed by MS (Voyager DE-PRO, Perseptive Biosystems/Applied Biosystems). Peptides were purified by using a C18 reverse-phase HPLC system (Waters, Milford, MA), single peaks were collected together and lyophilized, then dissolved in water and lyophilized again to remove residual trifluoroacetic acid. For titration experiments, fresh peptide stock solutions were prepared before each experiment and then diluted to either 50 or 100 μM and dialyzed extensively against 10 mM sodium cacodylate/100 mM NaCl, pH 6.9 (Buffer A). Spectrapor CE dialysis membranes with a molecular mass cutoff of 500 Da were used for all dialysis. Peptide concentrations were measured spectrophotometrically before the experiment by using a molar extinction coefficient of 1,450 M-1·cm-1 at 275 nm as determined (26). The LaCl3 (Alfa Aesar, Ward Hill, MA) stock was prepared by weight in water, and dilutions were made with dialysis buffer before the experiment. The LaCl3 concentrations for titration experiments were kept at 2 mM.
Fluorescence Measurements. Fluorescence intensity was measured by using a FluoroMax spectrophotometer with dm3000f software. A constant temperature of 25°C during the experiment was maintained by using a thermostated cell holder connected to a circulating water bath. The peptide concentration was 8 μM in Buffer A. Samples were exited at 280 nm and emission was recorded at 302 nm, the emission maximum for tyrosine. Samples were titrated with increasing amounts of LaCl3 until saturation. The measured intensity values were corrected for dilution and blanks were subtracted. A change in fluorescence intensity upon addition of LaCl3 was assumed to be proportional to the degree of binding. The degree of binding is expressed as a single-site binding equation
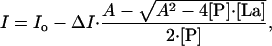 |
[1] |
where I is the intensity at each point of the titration upon addition of LaCl3, Io is the initial intensity, ΔI is the total change in intensity, A is [P] + [La] + Kd, [P] is the concentration of peptide, [La] is the concentration of LaCl3, and Kd is the apparent disassociation constant. Experimental data were fit to Eq. 1, using the nonlinear regression nlreg software.
CD Spectroscopy. The CD spectra of peptides in Buffer A with or without 2.5 mM LaCl3 were recorded in a 1-mm path length water-jacketed cuvette in a Jasco 715 spectropolarimeter (Jasco, Easton, MD) equipped with a Neslab RTE-111 temperature control unit. CD spectra were measured at three different concentrations (17, 85, and 170 μM) at 0°C. The sample was heated at a rate of 1°C per min and data were recorded every 0.2°C. Reversibility was checked by overlap of spectra before and after heating.
ITC. The overall procedure for ITC experiments was similar to that previously described (26). Experiments were carried out by using a VP-ITC titration calorimeter (Microcal, Northampton, MA). Three microliters of LaCl3 solution (≈2 mM) was injected into the cell containing a peptide at either 50 or 100 μM. The blank injections of LaCl3 into buffer A were used to account for the heats of mixing and dilution. In each experiment, 10–15 injections past saturation were made to ensure completion of binding. The heat of the reaction (Q) is obtained by integrating the peak after each injection of ligand using origin software provided by Microcal. The enthalpy (ΔHcal) was calculated by summing the individual heats, then correcting for dilution and dividing it by the total number of moles of peptide in the cell.
Data Analysis. The enthalpy measured experimentally for each peptide upon adding La3+ is related to the enthalpy of helix formation, on a per-residue basis, Δhα(P2X), as in ref. 26
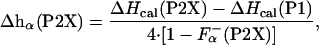 |
[2] |
where 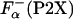 is the fraction of helical residues in peptide in the absence of La3+.
is the fraction of helical residues in peptide in the absence of La3+. 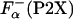 can be calculated from the experimentally measured ellipticity of these peptides, [Θ-(P2X)], as in ref. 26
can be calculated from the experimentally measured ellipticity of these peptides, [Θ-(P2X)], as in ref. 26
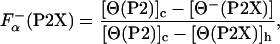 |
[3] |
where  is the fraction helix in the absence of La3+, [Θ-(P2)]c and [Θ-(P2X)]h are the ellipticity for the reference unfolded (coil) and fully helical states, respectively. [Θ-(P2)]c and [Θ-(P2X)]h are calculated from the experimentally measured ellipticities of peptides in the absence and presence of La3+ as described in details in refs. 26 and 27. The temperature dependence of [Θ-(P2)]c is taken to be the same for all peptides. The
is the fraction helix in the absence of La3+, [Θ-(P2)]c and [Θ-(P2X)]h are the ellipticity for the reference unfolded (coil) and fully helical states, respectively. [Θ-(P2)]c and [Θ-(P2X)]h are calculated from the experimentally measured ellipticities of peptides in the absence and presence of La3+ as described in details in refs. 26 and 27. The temperature dependence of [Θ-(P2)]c is taken to be the same for all peptides. The 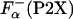 obtained this way refer only to those additional residues that are forming helical structure besides the first 12 residues of peptide P1. It should be noted that although Eq. 3 uses experimentally measured ellipticities to calculate
obtained this way refer only to those additional residues that are forming helical structure besides the first 12 residues of peptide P1. It should be noted that although Eq. 3 uses experimentally measured ellipticities to calculate 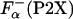 , ellipticity values are averaged properties and do not reflect the average helicity at the guest site. Thus, an alternative approach to get independent estimates for
, ellipticity values are averaged properties and do not reflect the average helicity at the guest site. Thus, an alternative approach to get independent estimates for 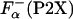 was used; the averaged helicity at the substitution (guest) site were calculated by using agadir (28). Calculations were made for a pH of 7.0, an ionic strength of 0.1 M, and a temperature of 5°C on the actual P2X sequences, to give the values of
was used; the averaged helicity at the substitution (guest) site were calculated by using agadir (28). Calculations were made for a pH of 7.0, an ionic strength of 0.1 M, and a temperature of 5°C on the actual P2X sequences, to give the values of 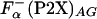 . In addition, the La3+ binding and helix initiation was modeled for agadir calculation by replacing the metal-binding sequence with a stretch of 57 alanine residues. Average helicity obtained in these calculations,
. In addition, the La3+ binding and helix initiation was modeled for agadir calculation by replacing the metal-binding sequence with a stretch of 57 alanine residues. Average helicity obtained in these calculations, 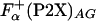 , was combined with the
, was combined with the  to get the
to get the 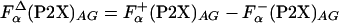 which was used instead of
which was used instead of 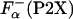 , in Eq. 2.
, in Eq. 2.
Numerical results of the experiments described above are reported in Table 1, which is published as supporting information on the PNAS web site.
Results
Design of the Guest Position in Peptides. Fig. 1A shows a cartoon representation of the three-dimensional structure of the P2A peptide that has the sequence Ac-DKDGDGYISAAEAAAQNH2. The first 12 residues are involved in the binding of La3+ ion, while the last 7–8 residues form an α-helix. The residue in position 14 was chosen as a guest site for substitutions. It is located on the solvent-exposed face of the helical segment, and thus, all potential side-chain–side-chain interactions will be minimized. It was shown previously that there is no difference in helix propensity for nonionizable amino acid residues at the solvent-exposed positions in the middle and at the C terminus of the α-helix. Twelve different amino acids were chosen to be incorporated at the guest position (Fig. 1B). The eight nonpolar amino acid residues included five naturally occurring aliphatic amino acids with increasing size of the side chain (G, A, V, I, and L), two nonnatural aliphatic amino acids (J and B), and one aromatic amino acid (F). The four polar amino acid residues contained hydroxyl (S and T) and amide (N and Q). Amino acids with ionizable side chains were not included in the studies because they can interfere with the metal binding.
Fig. 1.
Structure of the model peptide and of the residues incorporated at the guest position. (A) Cartoon representation of the structure of the P2A peptide in the presence of La3+ [Protein Data Bank (PDB) ID code 1NKF, ref. 24]. The side chain of Ala-14 is shown as a green sphere. (B) Ball-and-stick models of the amino acid residues that were used in this study.
CD Spectroscopy. The helical fraction in P2X peptides in the absence of La3+ was estimated from the experimentally measured ellipticities of the peptides by using a procedure described before (26, 27). As expected, the measured values of ellipticities vary for different peptides, indicating different amounts of the fractional helical structure in P2X (X = A, G, V, L, I, J, B, N, Q, S, T) series of peptides. Are these differences similar to those obtained in other peptide models? If the answer is yes, the P2X model possesses the general properties of helical peptides, and thus, the data obtained in the P2X model system will have general applicability. There are two sets of CD measurements of the host–guest peptides that include the nonnatural amino acids. Comparison of the ellipticity for the P2X peptide and those of Baldwin and coworkers (29, 30) and Kallenbach and coworkers (12, 31) are shown in Fig. 2. The correlation coefficients with these two model peptide systems are 0.88 and 0.76, respectively. Such good correlations suggest that the P2X peptide system is capturing the general model-independent helical properties.
Fig. 2.
Comparison of the ellipticities of the P2X peptides in the absence of La3+ with the ellipticities of peptide models used previously by Baldwin and coworkers (29, 30) and Kallenbach and coworkers (12, 31). Correlation coefficients are 0.88 and 0.76, respectively.
NMR study shows that upon La3+ binding, the P2A peptide folds into a structure in which the last eight residues are helical (24). These changes in the structure induced by La3+ binding can also be monitored by CD spectroscopy (26, 27). For example, upon La3+ binding, the ellipticity of the P2A peptide changes from -4,100 to -11,600 deg·cm2·dmol-1 at 25°C. Similar large changes in the ellipticity are observed for all P2X peptides. This step allows calculation of the fraction of helical residues in the P2X peptides in the absence of La3+, 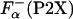 by using Eq. 3. Temperature dependence of
by using Eq. 3. Temperature dependence of 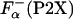 for selected peptides is shown in Fig. 3.
for selected peptides is shown in Fig. 3.
Fig. 3.
Temperature dependence of the fraction helix of selected P2X peptides in the absence of La3+ ions. □, P2G; ○, P2A; ⋄, P2N; ▵, P2V; ▿, P2B;  , P2T. The lines through the points are shown only to guide the eye.
, P2T. The lines through the points are shown only to guide the eye.
La3+ Binding Monitored by Fluorescence Spectroscopy. P1 and P2A peptides bind La3+ with relatively high affinities in the low micromolar range (24, 26). Analysis of La3+ binding to the P1 peptide monitored by fluorescence spectroscopy gave a dissociation constant, Kd, of 9.4 ± 0.9 μM, whereas the Kd for the P2A peptide was 2.4 ± 0.2 μM. The rest of the P2X (X = G, V, L, I, J, B, N, Q, S, T) showed a Kd lower than that of the P1 peptide but higher than that of the P2A peptide. The Kd estimates for the P2A peptide compare well with the previously reported values (24, 26, 32). Because La3+ binding leads to the folding of the P2X peptides, the La3+-binding affinities of the peptides will include contribution from the helix formation, thus allowing estimates of the thermodynamic helix propensity scale. For this step, the effect of La3+ binding is taken into account by correcting for the binding affinity of the P1 peptide that binds La3+ but does not form a helix as
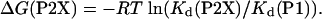 |
[4] |
Because the P2X peptides have certain helical structure in the absence of La3+ (24), the difference in the 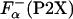 should be taken into account as
should be taken into account as
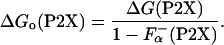 |
[5] |
Here, ΔGo (P2X) has the meaning of the apparent thermodynamic helix propensity because Eqs. 4 and 5 assume a two-state process. There is an indication that in a peptide system similar, but not identical, to P2X, there is some fraying at the helix end; however, it appears that the correction due to fraying is rather small, <5% (32). The values of 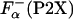 that are used in Eq. 5 were obtained by using experimentally measured ellipticities of the peptides. However, the ellipticity as measured by CD spectroscopy is an averaged property and does not specifically reflect the changes at the substitution site. To estimate the relative error introduced by a two-state assumption, the values of
that are used in Eq. 5 were obtained by using experimentally measured ellipticities of the peptides. However, the ellipticity as measured by CD spectroscopy is an averaged property and does not specifically reflect the changes at the substitution site. To estimate the relative error introduced by a two-state assumption, the values of 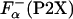 were also computed by agadir using two different approaches (see Materials and Methods for details). The values of ΔGo (P2X) calculated by using different estimates of ΔGo (P2X) are compared in Fig. 4A. Clearly, ΔGo (P2X) sets obtained by using
were also computed by agadir using two different approaches (see Materials and Methods for details). The values of ΔGo (P2X) calculated by using different estimates of ΔGo (P2X) are compared in Fig. 4A. Clearly, ΔGo (P2X) sets obtained by using 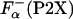 from Eq. 3 or computed using agadir are very similar, with the larger deviation on the order of 0.08 kcal/mol, which is smaller that the experimental error.
from Eq. 3 or computed using agadir are very similar, with the larger deviation on the order of 0.08 kcal/mol, which is smaller that the experimental error.
Fig. 4.
Comparison of helix propensity scales. (A) Comparison of the apparent thermodynamic helix propensity, ΔGo(P2X), calculated by using experimentally defined parameters according to Eq. 5, 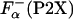 , or using
, or using 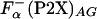 (○) and
(○) and 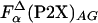 (▵) computed by agadir (see Materials and Methods for details). The dashed lines are the linear fits with the slopes of 1.02 and 1.05, and correlation coefficients of 0.990 and 0.991, respectively. (B) Comparison of the thermodynamic helix propensity scale obtained from La3+ binding to P2X peptides (Eq. 6), ΔΔGo(P2X), with the unified helix propensity scale of Pace and Scholtz (35), ΔΔGP&S (○). The ΔΔG data for nonnatural amino acids (□) are from ref. 31. The correlation coefficient is 0.92 and the slope is 0.9. Solid lines on A and B have a slope of 1.
(▵) computed by agadir (see Materials and Methods for details). The dashed lines are the linear fits with the slopes of 1.02 and 1.05, and correlation coefficients of 0.990 and 0.991, respectively. (B) Comparison of the thermodynamic helix propensity scale obtained from La3+ binding to P2X peptides (Eq. 6), ΔΔGo(P2X), with the unified helix propensity scale of Pace and Scholtz (35), ΔΔGP&S (○). The ΔΔG data for nonnatural amino acids (□) are from ref. 31. The correlation coefficient is 0.92 and the slope is 0.9. Solid lines on A and B have a slope of 1.
Most thermodynamic helical propensity scales are commonly expressed relative to the A (12, 13, 16, 33–35), a residue that has the highest helix propensity as
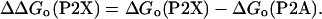 |
[6] |
Again, to assure the general applicability of the P2X peptides for study of the thermodynamic and structural basis of helix propensity, ΔΔGo (P2X) values must be compared with the existing helix propensity scales. Fig. 4B compares the values of ΔΔGo (P2X) with the unified helix propensity scale of Pace and Scholtz (35), ΔΔGP&S, which was derived from the analysis of several experimental helix propensity scales. The two data sets correlate very well (correlation coefficient of 0.92 and slope of 0.9), once again supporting the notion that the P2X peptide can serve as a universal model for the study of the thermodynamics of helix–coil transition.
ITC. Fig. 5A shows the temperature dependence of the experimental enthalpies, ΔHcal, that accompany La3+ binding to P1 and P2X peptides. The values of enthalpy are very different for the different peptides, both in sign and in the absolute magnitude. These experimentally measured enthalpies are used to calculate the enthalpy of helix formation, Δhα, by using Eq. 2. Fig. 5B shows the temperature dependencies of Δhα for a representative set of peptides. In agreement with a previous study (26), Δhα for all peptides is within experimental error independent of temperature. However, the absolute values of Δhα are very different for the different peptides ranging from -0.91 ± 0.09 kcal/mol for P2B and -0.40 ± 0.08 kcal/mol for P2G. The accuracy of the measurements is an important issue, and it is clear that the P2X system provides a very good measure of Δhα. For example, Δhα for P2A obtained is this work is -0.89 ± 0.08 kcal/mol, which is identical to the value of -0.9 ± 0.1 kcal/mol reported earlier (26), despite the fact that the P2A peptide was from two different sources and the experiments were performed at different locations and at different times. Additional source of inaccuracy in Δhα can come from  . To access the magnitude of these effects, Δhα was computed by using the
. To access the magnitude of these effects, Δhα was computed by using the 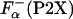 obtained from the experimentally measured ellipticities of the peptides using Eq. 3, or using the agadir-computed values (see Materials and Methods for details). Comparison of these estimates is given in Fig. 6 and clearly shows that the difference is smaller that the experimental error. Thus, the differences in the values of Δhα for different P2X peptides are significant and provide direct demonstration that the enthalpy of helix–coil transition is sequence-dependent.
obtained from the experimentally measured ellipticities of the peptides using Eq. 3, or using the agadir-computed values (see Materials and Methods for details). Comparison of these estimates is given in Fig. 6 and clearly shows that the difference is smaller that the experimental error. Thus, the differences in the values of Δhα for different P2X peptides are significant and provide direct demonstration that the enthalpy of helix–coil transition is sequence-dependent.
Fig. 5.
Enthalpies obtained from ITC experiments. (A) The temperature dependence of the experimental enthalpies, ΔHcal, that accompany La3+ binding to P1 and selected P2X peptides. (B) The temperature dependence of the enthalpies of helix–coil transition, Δhα, for the selected peptides. □, P2G; ○, P2A; ⋄, P2N; ▵, P2V; ▿, P2B;  , P1.
, P1.
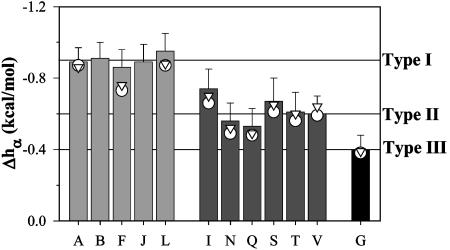
Fig. 6.
Comparison of the enthalpy of helix formation Δhα obtained from different peptides by using Eq. 3. Horizontal lines are drawn at -0.9 kcal/mol (type I), -0.6 kcal/mol (type II), and -0.4 kcal/mol (type III). For comparison, the values of Δhα calculated by using 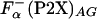 (○) and
(○) and 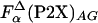 (▵) computed by agadir (see Materials and Methods for details) are also shown.
(▵) computed by agadir (see Materials and Methods for details) are also shown.
Discussion
The enthalpies of the helix–coil transition for the studied amino acid residues can be clustered into three distinct types (Fig. 6). Type I includes residues A, F, L, and nonnatural amino acids B and J, and are characterized by Δhα values of approximately -0.9 kcal/mol. Type II includes the β-branched I, T, and V, and also polar residues S, N, and Q, and are characterized by Δhα values of -0.6 kcal/mol. Type III is the residue G and has the lowest absolute value of Δhα, -0.4 kcal/mol.
Type III residue G has the lowest enthalpy, presumably because of the fact that it does not have a side chain. Two possible factors can be responsible. One factor is the ability of the glycine backbone to sample a much larger ϕ/Ψ-space on the Ramachandran plot. This factor affects the backbone accessibility to the solvent, an important contributor to the thermodynamics of helix formation (19, 36–39). Another factor is the presence of the Cβ atom in all other amino acids not only restricts the conformation of the peptide backbone but also adds some favorable van der Waals interactions that are known to have a significant enthalpic component (20). One, or most probably, both of these factors define very low enthalpy values for glycine residue. For the amino acid residues that have a side chain, two rules appear to define whether they will belong to type I or type II according to their enthalpy, Δhα.
Rule 1: If a Residue Is β-Branched, It Belongs to Type II. Comparison of the chemical nature and shape of the amino acid residues belonging to type II clearly indicates that the shape of the side chain, and specifically, β-branching, is very important because all β-branched side chains belong to type II (Fig. 6). It is not related to the overall size (i.e., number of heavy atoms) or the hydrophobicity of the side chain, because β-branched V has a very different enthalpy than J, which contains the same number of carbon atoms in the side chain. Similarly, the Δhα value for β-branched I is very different from that of L. Moreover, polar T that has the same shape as V, and also the same enthalpy. The β-branching of amino acid residues has been proposed to lead to a larger burial of the polar backbone in the helical state (19). This suggestion was later supported by experimental and theoretical considerations (6, 37, 38, 40, 41). The observed low enthalpy for the β-branched residues (Fig. 6) further supports this hypothesis. Indeed, hydration of the polar backbone is negative (20, 42), and thus, the more backbone is shielded from the solvent in the helical state because of β-branching, the smaller the total enthalpy change upon helix–coil transition will be. It must be noted that, at least in the case of a backbone that is polar but heterogeneous, the energetics of hydration does not seem to scale well with the geometrical/structural parameter widely used in the past, the solvent-accessible surface area (ASA) (37). Thus, direct demonstration of such effects using traditional approaches of comparing ASA is impossible.
Rule 2: If a Residue Is Not β-Branched, but Can Form Hydrogen Bonds, It Belongs to Type II. Another factor that defines the difference in Δhα values seems to be the ability to form hydrogen bonds. Polar residues S, N, and Q are not β-branched, yet they belong to type II (Fig. 6). For comparison, B has a similar shape to S, but does not possess the hydrogen-bonding capability, and is a type I residue. Similarly, L, which belongs to type I, has the same shape as N, but N can potentially form several hydrogen bonds by means of its amide moiety, and thus belongs to type II. What causes these differences in the enthalpies of helix–coil transition for the amino acid residues with hydrogen-bonding capabilities? It is probably related to the interaction with the solvent and intramolecular hydrogen bonding in the unfolded state. However, at the present time, there are no trivial ways of modeling the unfolded state and no simple explanation can be provided.
Importance of the Difference in Δhα Values for Understanding Helix Propensities. Since the first thermodynamic helix propensity scales were determined, the difference in the side-chain entropy in the helical and coiled states was brought up as one of the determinants (10–17). In 1992, Creamer and Rose (14) performed a simple Monte Carlo calculation to compute the side-chain configurational entropy for a series of nonpolar residues in the unfolded state and in the α-helical state. They found that there is very good correlation between helix propensities (ΔΔG relative to A) and entropy loss upon helix formation (ΔΔS relative to A). Based on this correlation Creamer and Rose (17) concluded “... that loss of side chain entropy is a major determinant of the helix-forming tendency of residues in both peptide and protein helices.” This conclusion was later questioned by Blaber et al. (16), who calculated the loss of side-chain configurational entropy for all residues using the distribution of the side-chain rotamers in the known three-dimensional structures of protein. The ΔΔS values computed by Blaber et al. (16) for nonpolar residues were similar to those of Creamer and Rose (14, 17), suggesting the overall applicability of both methods for calculation of entropy. However, Blaber et al. (16) found little correlation between helix propensity and entropy loss when considering both polar and nonpolar residues. Furthermore, Luo and Baldwin (19) noted that even for nonpolar residues, despite good correlation, the entropy explains only a 50–70% difference in ΔΔG. A possible explanation for this lack of correlation between ΔΔG and ΔΔS for all residues, and less than unity slope of the ΔΔG versus T·ΔΔS plot for nonpolar residues is that, since ΔG = ΔH - T·ΔS, there is a difference in the enthalpy of helix–coil transition for different amino acid residues. The measurements of enthalpy of helix–coil transition are very difficult. Nevertheless, the direct calorimetric measurements performed by different groups that used different model systems gave very comparable results (see e.g., refs. 22 and 23 and references therein). The only indication that there might be a difference in the enthalpy of helix–coil transition comes from the work of the Baldwin group (19). Using Lifson–Roig analysis, they showed that there is a difference in the enthalpy of helix–coil transition and the rank order is A>I>V>G. However, this order is shown by using an indirect way to calculate enthalpy and is performed for only four amino acid residues, all of them nonpolar.
In this work, we experimentally explore the hypothesis that different amino acid residues will have a different enthalpy of helix–coil transition. This work is performed by using direct calorimetric measurements of the folding of a model host peptide in which helix formation is induced by metal binding, and is applied to a wide range of residue types, not only nonpolar residue types but polar residue types as well. The observed differences in the enthalpies of helix–coil transition clearly add the missing part of thermodynamic analysis of the helix propensity. Fig. 7 compares the thermodynamic propensity scales from Pace and Scholtz (35), ΔΔGP&S, and obtained in this work by using the La3+ binding, ΔΔGo(P2X), with the entropy changes upon helix–coil transition, T·ΔΔS, as reported in refs. 14 and 16, and a sum of T·ΔΔS and ΔΔhα. It is clear that the T·ΔΔS + ΔΔhα describes the observed thermodynamic propensity scales much better. These data provide definite support to the idea that the thermodynamic helix propensity scale is defined by both enthalpic and entropic components. It appears that, for some amino acid residues, the entropy is indeed a major determinant in agreement with the earlier conclusion of Creamer and Rose (17). For other amino acid residues, it appears that the enthalpic component is more significant than the entropic component or both the enthalpic and entropic effects are equally important.
Fig. 7.
Comparison of two different helical propensity scales, ΔΔGP&S (gray bars) and ΔΔGo(P2X) (black bars), with the change in configurational entropy upon helix–coil transition. T·ΔΔS only (blue bars), or with the sum of T·ΔΔS and the enthalpy of helix formation ΔΔhα (red bars). The configurational entropy changes upon helix–coil transition are taken from Blaber et al. (16), with the exception of those for nonnatural amino acids B and J, which were taken from Creamer and Rose (14). All parameters are calculated relative to A.
Concluding Remarks. It remains unclear as to what are the interactions and structural determinants that define the difference in the enthalpies for helix–coil transition for different amino acid residues. There is not much more information that the experiment can provide. It is thus up to thorough computer simulations to provide the detailed picture of the contributions of different interactions to the thermodynamics of the helix–coil transition. Given the current state of the art of such simulations (7), it appears to be feasible.
Supplementary Material
Acknowledgments
We thank George Rose and Trevor Creamer for discussions, Timothy Keiffer for assistance with peptide purification, Dawn Richardson for the helpful comment on the manuscript, and the anonymous reviewer for suggesting the use of agadir as an alternative way of estimating 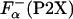 . This work was supported in part by National Institutes of Health Grant GM54537 (to G.I.M.).
. This work was supported in part by National Institutes of Health Grant GM54537 (to G.I.M.).
This paper was submitted directly (Track II) to the PNAS office.
Abbreviations: J, norvaline; B, 2-aminobutyric acid; ITC, isothermal titration calorimetry.
References
- 1.Pauling, L., Corey, R. B. & Branson, H. R. (1951) Proc. Natl. Acad. Sci. USA 37, 205-210. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Scholtz, J. M. & Baldwin, R. L. (1992) Annu. Rev. Biophys. Biomol. Struct. 21, 95-118. [DOI] [PubMed] [Google Scholar]
- 3.Chakrabartty, A. & Baldwin, R. L. (1995) Adv. Protein Chem. 46, 141-176. [PubMed] [Google Scholar]
- 4.Rohl, C. A. & Baldwin, R. L. (1998) Methods Enzymol. 295, 1-26. [DOI] [PubMed] [Google Scholar]
- 5.Baldwin, R. L. & Rose, G. D. (1999) Trends Biochem. Sci. 24, 26-33. [DOI] [PubMed] [Google Scholar]
- 6.Nymeyer, H. & Garcia, A. E. (2003) Proc. Natl. Acad. Sci. USA 100, 13934-13939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Gnanakaran, S., Nymeyer, H., Portman, J., Sanbonmatsu, K. Y. & Garcia, A. E. (2003) Curr. Opin. Struct. Biol. 13, 168-174. [DOI] [PubMed] [Google Scholar]
- 8.Schellman, J. A. (1955) C. R. Trav. Lab. Carlsberg Ser. Chim. 29, 223-229. [PubMed] [Google Scholar]
- 9.Schellman, J. A. (1955) C. R. Trav. Lab. Carlsberg Ser. Chim. 29, 230-259. [PubMed] [Google Scholar]
- 10.Sueki, M., Lee, S., Powers, S. P., Denton, J. B., Konishi, Y. & Scheraga, H. A. (1984) Macromolecules 17, 148-155. [Google Scholar]
- 11.Padmanabhan, S., Marqusee, S., Ridgeway, T., Laue, T. M. & Baldwin, R. L. (1990) Nature 344, 268-270. [DOI] [PubMed] [Google Scholar]
- 12.Lyu, P. C., Liff, M. I., Marky, L. A. & Kallenbach, N. R. (1990) Science 250, 669-673. [DOI] [PubMed] [Google Scholar]
- 13.O'Neil, K. T. & DeGrado, W. F. (1990) Science 250, 646-651. [DOI] [PubMed] [Google Scholar]
- 14.Creamer, T. P. & Rose, G. D. (1992) Proc. Natl. Acad. Sci. USA 89, 5937-5941. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lee, K. H., Xie, D., Freire, E. & Amzel, L. M. (1994) Proteins 20, 68-84. [DOI] [PubMed] [Google Scholar]
- 16.Blaber, M., Zhang, X. J., Lindstrom, J. D., Pepiot, S. D., Baase, W. A. & Matthews, B. W. (1994) J. Mol. Biol. 235, 600-624. [DOI] [PubMed] [Google Scholar]
- 17.Creamer, T. P. & Rose, G. D. (1994) Proteins 19, 85-97. [DOI] [PubMed] [Google Scholar]
- 18.Luo, P. & Baldwin, R. L. (1997) Biochemistry 36, 8413-8421. [DOI] [PubMed] [Google Scholar]
- 19.Luo, P. & Baldwin, R. L. (1999) Proc. Natl. Acad. Sci. USA 96, 4930-4935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ermolenko, D. N., Richardson, J. M. & Makhatadze, G. I. (2003) Protein Sci. 12, 1169-1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Scholtz, J. M., Marqusee, S., Baldwin, R. L., York, E. J., Stewart, J. M., Santoro, M. & Bolen, D. W. (1991) Proc. Natl. Acad. Sci. USA 88, 2854-2858. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Richardson, J. M., McMahon, K. W., MacDonald, C. C. & Makhatadze, G. I. (1999) Biochemistry 38, 12869-12875. [DOI] [PubMed] [Google Scholar]
- 23.Richardson, J. M. & Makhatadze, G. I. (2004) J. Mol. Biol. 335, 1029-1037. [DOI] [PubMed] [Google Scholar]
- 24.Siedlecka, M., Goch, G., Ejchart, A., Sticht, H. & Bierzynski, A. (1999) Proc. Natl. Acad. Sci. USA 96, 903-908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wojcik, J., Goral, J., Pawlowski, K. & Bierzynski, A. (1997) Biochemistry 36, 680-687. [DOI] [PubMed] [Google Scholar]
- 26.Lopez, M. M., Chin, D. H., Baldwin, R. L. & Makhatadze, G. I. (2002) Proc. Natl. Acad. Sci. USA 99, 1298-1302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Chin, D. H., Woody, R. W., Rohl, C. A. & Baldwin, R. L. (2002) Proc. Natl. Acad. Sci. USA 99, 15416-15421. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Lacroix, E., Viguera, A. R. & Serrano, L. (1998) J. Mol. Biol. 284, 173-191. [DOI] [PubMed] [Google Scholar]
- 29.Padmanabhan, S. & Baldwin, R. L. (1991) J. Mol. Biol. 219, 135-137. [DOI] [PubMed] [Google Scholar]
- 30.Padmanabhan, S., York, E. J., Stewart, J. M. & Baldwin, R. L. (1996) J. Mol. Biol. 257, 726-734. [DOI] [PubMed] [Google Scholar]
- 31.Lyu, P. C., Sherman, J. C., Chen, A. & Kallenbach, N. R. (1991) Proc. Natl. Acad. Sci. USA 88, 5317-5320. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Goch, G., Maciejczyk, M., Oleszczuk, M., Stachowiak, D., Malicka, J. & Bierzynski, A. (2003) Biochemistry 42, 6840-6847. [DOI] [PubMed] [Google Scholar]
- 33.Horovitz, A., Matthews, J. M. & Fersht, A. R. (1992) J. Mol. Biol. 227, 560-568. [DOI] [PubMed] [Google Scholar]
- 34.Rohl, C. A., Chakrabartty, A. & Baldwin, R. L. (1996) Protein Sci. 5, 2623-2637. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Pace, C. N. & Scholtz, J. M. (1998) Biophys. J. 75, 422-427. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Baldwin, R. L. (2003) J. Biol. Chem. 278, 17581-17588. [DOI] [PubMed] [Google Scholar]
- 37.Avbelj, F., Luo, P. & Baldwin, R. L. (2000) Proc. Natl. Acad. Sci. USA 97, 10786-10791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Avbelj, F. & Baldwin, R. L. (2003) Proc. Natl. Acad. Sci. USA 100, 5742-5747. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ghosh, T., Garde, S. & Garcia, A. E. (2003) Biophys. J. 85, 3187-3193. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Thomas, S. T., Loladze, V. V. & Makhatadze, G. I. (2001) Proc. Natl. Acad. Sci. USA 98, 10670-10675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Avbelj, F. & Baldwin, R. L. (2004) Proc. Natl. Acad. Sci. USA 101, 10967-10972. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Makhatadze, G. I. & Privalov, P. L. (1995) Adv. Protein Chem. 47, 307-425. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.