Regular multicharged transient soft matter in Coulomb explosion of heteroclusters

Abstract

Nanointerfaces of mobile, thin spherical shells of light ions that expand on the femtosecond time scale, can be produced by Coulomb explosion of extremely ionized molecular heteroclusters consisting of light and heavy ions, e.g., (D⁺I^q+)ⁿ (q = 7-35), which are generated in ultraintense laser fields (intensity, I, = 10¹⁶ to 10²⁰ W·cm^-2). Modeling, together with molecular dynamics simulations, reveals the expansion of 2D monolayers with high energies and narrow energy distributions [e.g., E_av ≃ 23 keV and ΔE/E_av = 0.16 for D⁺ from (D⁺I²⁵⁺)₂₁₇₁] arising from kinematic run-over effects. The expanding regular, monoionic, spherical nanointerfaces manifest the attainment of transient self-organization in complex systems driven by repulsive Coulomb interactions.

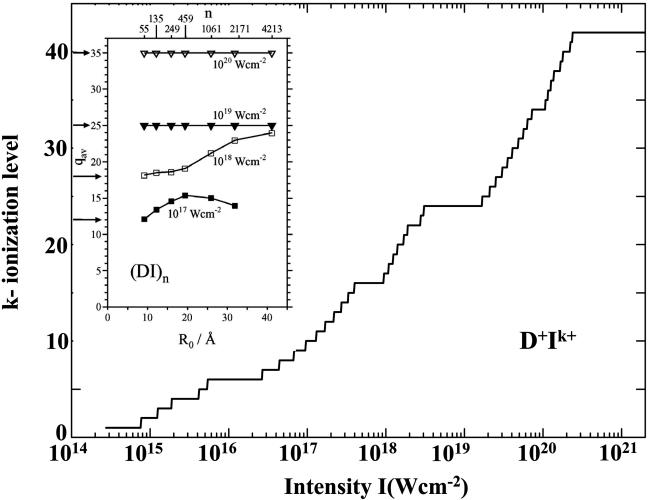
Rigid and soft interfaces between different forms of macroscopic matter play a central role in surface, polymer, and soft matter science (1). Nanointerfaces in finite systems, i.e., clusters and nanostructures, that are characterized by a large surface-to-volume ratio (2), can also be subdivided into two analogous categories: (i) Rigid nanointerfaces, involving the surfaces of metallic, ionic, molecular, semiconductor, or van der Waals clusters at sufficiently low temperatures (2), as well as monomolecular layers of fullerenes or of nanotubes (3), and (ii) soft nanointerfaces involving surfaces of liquid clusters above the (smeared out) phase transition temperature (4) or of helium clusters at zero temperature (2). We propose that nanointerfaces consisting of multicharged soft matter with radially expanding monomolecular mobile boundaries can be realized by Coulomb explosion (5-7) of some highly ionized molecular heteroclusters, whose constituents consist of light few-electron and heavy many-electron atoms, e.g., hydroiodic acid (AI)_n clusters or methyl iodide (CA₃I)_n clusters (with A = H, D, or T). Extreme multielectron heterocluster ionization in ultraintense laser fields (peak I = 10¹⁶ to 10²⁰ W·cm^-2) results in spectacular ionic clusters, e.g., (D⁺I^q+)_n (with an iodine heavy ion charge of q = 7-35). Such extreme ionization levels can be accomplished by the barrier suppression ionization mechanism (8) for a single molecule (Fig. 1). In the intensity domain I = 10¹⁷ to 10¹⁸ W·cm^-2, a further increase of the ionization level in the cluster is induced by the ignition mechanism (8, 9), whereas at the highest-intensity domain, I = 10¹⁹ to 10²⁰ W·cm^-2, which is of interest herein, the charges on individual cluster molecules are identical to the single-molecule q (Fig. 1 Inset). We demonstrate the formation of unique regular nanostructures (spatial dimensions of ∼100-500 Å) in the Coulomb explosion of light-heavy ionic heteroclusters, which gives rise to extremely mobile, transient, expanding boundary monolayers of A⁺ (H⁺, D⁺, or T⁺) ions. These transient spherical shells provide a case of soft matter expanding on the femtosecond time scale. The features of such a Coulomb exploding multicharged monolayer of soft matter are qualitatively distinct from the uniform Coulomb explosion of homonuclear multicharged clusters (10, 11), e.g., (A⁺)_n. Information emerges on transient structures, i.e., the mapping of all nuclear ionic coordinates involved in the dynamic process, unveiling facets of ultrafast structural dynamics that are of considerable interest in chemistry, physics, and biology (12, 13). Regarding energetics, interesting applications of Coulomb explosion of an assembly of deuterium containing heteroclusters involve dd nuclear fusion driven by Coulomb explosion (14-16) of heteroclusters (11, 15-17). For exploding light-heavy atom heteroclusters, e.g., (DI)_n, in ultraintense laser fields, the extremely charged I^q+ (q = 7-35) ions act as most effective energetic triggers for driving the expanding D⁺ ions, resulting in a dramatic enhancement of the nuclear fusion driven by Coulomb explosion yields.

Fig. 1.

The laser intensity dependence of the ionization level of the DI molecule calculated by the barrier suppression ionization mechanism (8). Ionization potentials of the ionic molecule were calculated by the procedure of ref. 8 with the ionization potentials of the iodine atom taken from ref. 26. The Inset shows the cluster size and laser intensity dependence of the average inner ionization level (q_av = 〈q〉) of I^q+ ions from (DI)_n heteroclusters (n = 55-4,213) calculated by molecular dynamics simulations for energetic electrons and ions (8, 9) in the intensity range I = 10¹⁷ to 10²⁰ W·cm^-2, with the intensities marked on the curves. The horizontal arrows mark the single molecule ionization levels at these intensities.

Methods

Coulomb explosion of (H⁺I^q+)_n and (D⁺I^q+)_n (n = 55-4,213) light-heavy heteroclusters was described by an electrostatic model. These analytical results were supplemented by molecular dynamics simulations performed under cluster vertical ionization (CVI) initial conditions (8-11,15) and by complete molecular dynamics simulations for energetic electrons and ions (8, 9) in these heteroclusters, which are subjected to a Gaussian laser field with a peak intensity of I = 10¹⁷ to 10²⁰ W·cm^-2 and a pulse duration of τ = 25 fs.

Results

Kinematic Effects and Ions Spatial Distribution. We explore some unique features of the spatial distribution, energetics, and temporal dynamics of this multicharged transient soft matter. Coulomb explosion constitutes a relatively simple process in the case of CVI when the time scales for inner and outer ionization processes are short on the time scale of ion expansion and outer ionization is complete (8-11,15). CVI is realized at high laser intensities (I = 10¹⁸ to 10²⁰ W·cm^-1). The CVI Coulomb explosion of (A_k^qA+B^qB+) ionic heteroclusters consisting of light A^qA+ ions of mass, m_A, and charge q_A, and of heavy B^qB+ ions with mass, m_B, and charge, q_B (with m_A << m_B and kq_A << q_B), is characterized by the kinematic parameter (11, 15, 16) η_AB = m_Bq_A/m_Aq_B > 1. For (AI)_n (A = H, D, or T) heteroclusters extremely charged (A⁺I²⁵⁺)_n clusters are generated at I = 10¹⁹ W·cm^-2 (Fig. 1), with η_HI = 5.1 for (H⁺I²⁵⁺)_n, η_DI = 2.5 for (D⁺I²⁵⁺)_n and η_TI = 1.7 for (T⁺I²⁵⁺)_n. η_AB > 1 results in the run-over process (11, 15, 16) of the light A^qA+ ions relative to the heavy B^qB+ ions. The expansion dynamics manifests a marked contraction of the spatial distribution of the light ions, resulting in a nearly monoionic expanding spherical shell.

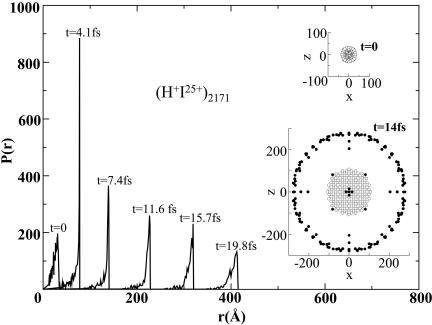
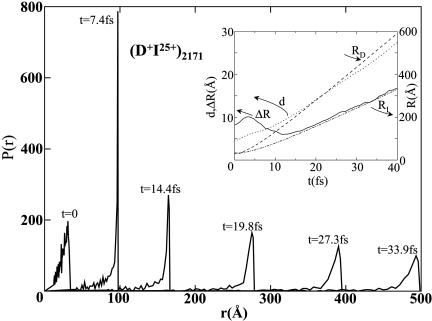
Molecular dynamics simulations of Coulomb explosion of (H⁺I²⁵⁺)₂₁₇₁ and (D⁺I²⁵⁺)₂₁₇₁ clusters under initial CVI conditions were performed with initial structures of the neutral (HI)₂₁₇₁ and (DI)₂₁₇₁ heteroclusters. The Coulomb explosion data portrayed in Figs. 2 and 3 demonstrate the run-over process with the formation of narrow expanding nanoshells of light ions, with spatial dimensions of R_H, R_D = 100-500 Å. Soon after the onset of the expansion (4.1 fs for H⁺ and 7.4 fs for D⁺), the ionic shells become very narrow (Fig. 2 Insets), with the radial distribution P(r) (containing 50% of the light ions) being characterized by the minimal widths of ΔR = 4 Å for H⁺ and ΔR = 5 Å for D⁺ (Fig. 3 Inset). For longer times, the width ΔR increases nearly proportionally to the ionic shell of the mean radius, R (R_D for D⁺ or R_H for H⁺), with ΔR remaining narrow, i.e., for D⁺, ΔR/R ≃ 0.025 at t = 15-40 fs (Fig. 3). The average interionic distances, d, inside the 50% ionic domain increase smoothly with 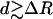(Fig. 3), providing a 2D monolayer expansion.

Fig. 2.

Molecular dynamics simulations under CVI initial conditions of Coulomb explosion of (H⁺I²⁵⁺)₂₁₇₁ heteroclusters, portraying the time-dependent narrow distributions P(r) of the H⁺ ions. The Insets show the 2D projections of the initial structure at t = 0 and of the narrow shell of light ions at t = 14 fs, with the x and z axes being given in Å. Open circules mark I²⁵⁺ ions, and black dots mark H⁺ ions.

Fig. 3.

Molecular dynamics simulations under CVI initial conditions of Coulomb explosion of (D⁺I²⁵⁺) heteroclusters, portraying the time-dependent narrow distribution of the D⁺ ions. The Inset shows the time dependence of the mean radii of the distributions of the D⁺ ions (R_D) and of the I²⁵⁺ ions (R_I), the distribution width ΔR, and the average interionic distance, d, for the D⁺ ions.

An Electrostatic Model. We supplemented the numerical exercises of simulations by a soluble analytical model, which provides further insight into the nature of the expansion of the narrow spherical shell of the light ions. The condition η_AB ≫ 1 allows for the separation of the time scales between the fast light ion motion and the slow heavy ion motion (Figs. 2 Insets and 3 Inset), so we ignore the heavy ion motion. Furthermore, as q_B ≫ 1, only A^qA+ - B^qB+ Coulomb interactions are considered. The temporal dynamics will be characterized by their Coulomb expansion time of the light A^qA+ ions. The time t(r;r₀) for an ion initially located at radius r₀ (<R₀) to reach radius r (>R₀) is

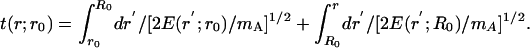[1]

The A^qA+ ions kinetic energy, E(x; y), calculated from the change in the potential energy from point y to point x, inside and outside the initial cluster configuration, is given by

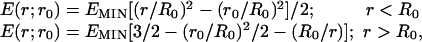[2]

where 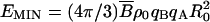, with ρ₀ being the molecular density (in Å^-3) and B = 14.385 eV·Å^-1 (1 eV = 1.602·10^-19 J). Eqs. 1 and 2 result in the expansion time

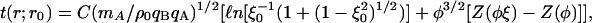[3]

where C = 1.310 fs·Å^-3/2, ξ₀ = r₀/R₀, ξ = R₀/r, 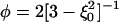, and the function Z(x) is given by (11)

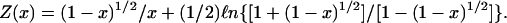[3a]

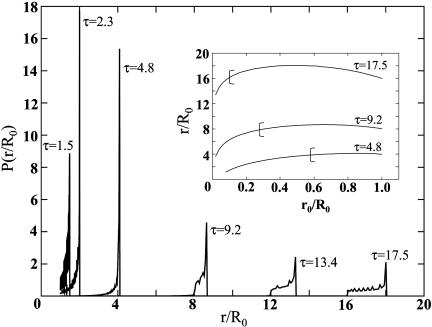
The dependence of the expansion distance, r/R₀, on the initial distance, r₀/R₀ (in reduced units), calculated from Eq. 3 for fixed reduced times, τ(ξ; ξ₀) = t(r; r₀)C^-1 (2m_A/ρ₀q_Aq_B)^-1/2, allows one to construct the histograms of the time-dependent radial distribution, P(r/R₀), of the light ions, which are portrayed in Fig. 4. Ions arrive to the same final distance, r, from two different initial r₀ radii (Fig. 4 Inset), manifesting the run-over process, which induces the transformation of the initially formed uniform sphere of A^qA+ ions into an expanding narrow shell. At the point where dr/dr₀ = 0 (Fig. 4 Inset), the light ion distribution diverges, manifesting the sharp spikes in P(r) (Fig. 4), where the narrow distribution peaks at a large, but finite, value, because of the finite r₀ steps used in the numerical calculations based on Eq. 3. The electrostatic model (Fig. 4) confirms the formation of an expanding soft narrow shell, which emerged from the simulations under CVI initial conditions (Figs. 2 and 3).

Fig. 4.

Histograms of the time-dependent radial distribution P(r/R₀) of the light ions calculated by the electrostatic model for Coulomb explosion of light-heavy (A_k^qA+B^qB+) heteroclusters, Eq. 3, with fixed times τ(ξ₀;ξ) (see text). The Inset shows the dependence of the expansion distance, r/R₀, on the initial distance, r₀/R₀, Eq. 3, for several times (in reduced units), with the vertical short lines marking the lower limit of r₀/R₀ for which light ions arrive to the same final distance from two different initial distances.

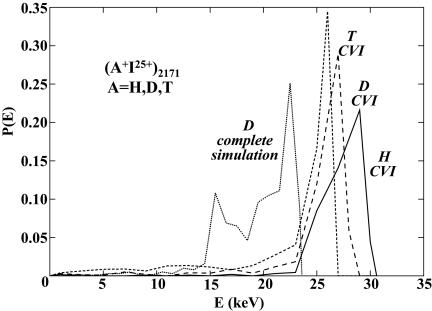
Simulations of Electron and Nuclear Dynamics. Our conclusions regarding expanding soft 2D nanointerfaces were confirmed by a complete simulation (8, 9), including both (high energy) electron and nuclear dynamics, which was performed for a (DI)₂₁₇₁ cluster subjected to a Gaussian laser pulse with a peak intensity of I = 10¹⁹ W·cm^-2. Extreme multielectron ionization of (DI)_n at I = 10¹⁹ W·cm^-2 results (Fig. 1) in a cluster-size-independent iodine charge q = 25 (Fig. 1 Inset), which allows for confrontation between the complete electronic-nuclear simulations with the molecular simulations of Figs. 2 and 3. The shell structure of the D⁺ ions for the complete simulations are somewhat broader (by a numerical factor of ∼2) than the CVI results. At an advanced stage of the expansion, the shell manifests a bimodal distribution reflecting the presence of faster and slower ions that is also exhibited in the kinetic energy distribution P(E) in Fig. 5. The electrostatic model, Eqs. 2 and 3, predicts the narrow distribution of the final kinetic energy

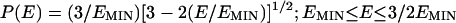[4]

and the average energy is E_av = (6/5)E_MIN. The simulations of the energetics of Coulomb explosion of (A⁺I²⁵⁺⁾₂₁₇₁ (A = H, D, or T) clusters performed for CVI initial conditions (Fig. 5) confirm the predictions of Eq. 4 for a narrow energy distribution. The energy distribution interval, which includes 75% of the light (A⁺ I⁺²⁵)_n ions, is impressively narrow with widths of 0.14 E_av for H⁺, 0.14 E_av for D⁺, and 0.16 E_av for T⁺ ions, as compared with the width of 0.25 E_av for the theoretical distribution (Eq. 4). The narrow energy distribution around a high value of E_av provides a marked advantage in the enhancement of the yields for dd nuclear fusion driven by Coulomb explosion in these heteroclusters due to energetic driving of deuterons by extremely multicharged heavy I^q+ (q = 25) ions. However, in the Coulomb explosion of first-row heteroclusters, e.g., 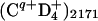(q = 4-6) (11) (where E_av = 5.8 keV), the neutron yields, Y, for dd fusion under the conditions of the Lawrence Livermore experiment (14) were calculated as Y = 10⁵ (10, 11), whereas the increased deuteron energies from (D⁺I²⁵⁺)₂₁₇₁ light-heavy heteroclusters (E_av = 23 keV, according to Fig. 5) result in three orders of magnitude increase of the dd fusion cross section and in Y ∼ 10⁸.

Fig. 5.

Kinetic-energy distributions P(E) of the A⁺ light ions from Coulomb explosion of (A⁺I²⁵⁺)₂₁₇₁ (A = H, D, or T) heteroclusters. The curves marked “H CVI” (—), “D CVI” (- -), and “T CVI” (- - -) represent the results of the CVI simulations for the three isotopes. The curve marked “D complete simulation” (· · ·) represents the results for simulations including both electron inner/outer ionization dynamics and nuclear dynamics in a (DI)₂₁₇₁ cluster subjected to a Gaussian laser field with I = 10¹⁹ W·cm^-2 and τ = 25 fs, using the procedure of ref. 8.

Discussion

The formation of spherical shells involving an ionic monolayer, expanding on the femtosecond time scale, introduces a family of regular, transient structures of exploding clusters. This ultrafast (5-40 fs) structural dynamics (with the time-dependent radial distribution function consisting of a subcluster of I^q+ ions located near the origin and a narrow distribution at R for the light ions) will become amenable to experimental interrogation by the ultrafast low-energy electron diffraction methods pioneered for the interrogation of transient molecular structures (12). As the characteristic distance scales are R ∼ 100-500 Å, low-energy (100-300 eV) electrons will be required for transient cluster structures. Alluding to other aspects of the transient structure, we also note that the large peak value, together with the narrow shell structure for P(r) (Figs. 2 and 3) and, consequently, the large apparent volume density does not imply shock wave phenomena in these soft nanointerfaces. This finding is in contrast with a claim advanced for shock waves in Coulomb explosion of homonuclear clusters with strongly decreasing periphery density (18). The condition for shock phenomena involves a significant decrease in the mean distance between the particles. In our simulation, the mean distance, d, between the light ions is comparable to the shell width ΔR (Fig. 3), whereupon the expansion is essentially 2D with the absence of shock wave phenomena.

From the point of view of methodology, when the narrow shell (R ≫ ΔR and 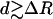) is formed at R (≫R₀), its potential energy, U, inferred from the extension of the electrostatic model, Eq. 2, to include repulsion between the light ions, is 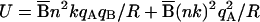. The potential energy corresponds to a sum of pressure-volume energy, with internal pressure p = n²kB̄q_Aq_B/4πR⁴ and of a surface tension-surface energy with the (negative) surface tension 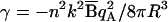. The expanding thin spherical shell of the light ions bears analogy to a “soap bubble” driven by Coulomb pressure, which originates from light-ion-heavy-ion repulsions, whereas the negative surface tension, due to light-ion-light-ions repulsions, is small.

The formation of a transient halo of an expanding, monoionic spherical shell involves spatial segregation of different constituents of the exploding light-heavy ionic heterocluster. The realization of a transient halo or a “soap bubble” of light ions raises the issue of self-organization included by conservative forces (19-21). Self-organization governs the structure, dynamics, and function of complex chemical, physical, astrophysical, and biological systems (19-21). Self-organization on the molecular level (20, 21) involves the formation of specific structures of matter, i.e., solids, clusters, biomolecules, and soft matter, resulting from electromagnetic interactions (21). This concept, which is relevant to the systems explored herein, is narrower than the general concept of self-organization driven by interactions and boundary conditions, which involves the capability of specific forms of matter to develop self-reproductive structures (19). An essential aspect of self-organization is provided by the specific nature of the interactions between the atomic, molecular, biomolecular, and cluster constituents, which determine the energy landscape of the complex system (4, 22). An important characteristic of these interactions pertains to their nature and strength, with the balance between attractive and repulsive interactions driving self-organization on the molecular level into a stable structure. The transient halos of expanding, regular, monoionic spherical nanointerfaces explored herein unveil aspects of transient self-organization on the molecular level in complex systems, which are driven by repulsive interactions.

Spatial segregation of different constituents of a finite system with the formation of a cloud, or halo, of one type of constituent prevails in nuclei (23, 24) and in clusters (25). This is the case for neutron halos in neutron rich nuclei, close to the neutron drip line (23, 24), which marks the boundary for the existence of these nuclei (e.g., ⁶He, ¹¹Li, and ¹¹Be), where a diffuse neutron cloud is induced by short-range nuclear forces (23, 24). Another example is the formation of diffuse surface states of an excess electron on (He)_n (n > 4·10⁵) clusters, which are induced by strong short-range repulsive pseudopotential and weak long-range attractive polarization interactions (25). Spatial segregation in one- or several-particle clouds (23-25) manifests stable structures. The transient halo of light ions in exploding light-heavy heteroclusters manifests a many-particles regular, dynamic structure where spatial segregation is driven by repulsive interactions.