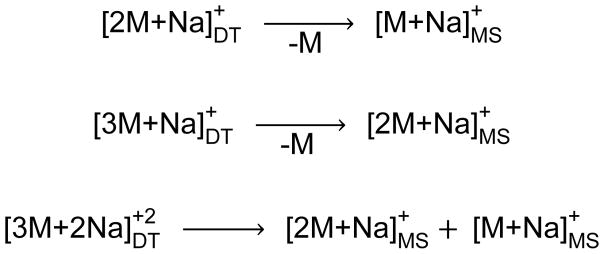Experimental and Theoretical Investigation of Sodiated Multimers of Steroid Epimers with Ion Mobility-Mass Spectrometry

Abstract

Ion mobility-mass spectrometry (IM-MS) has recently seen increased use in the analysis of small molecules, especially in the field of metabolomics, for increased breadth of information and improved separation of isomers. In this study, steroid epimers androsterone and trans-androsterone were analyzed with IM-MS to investigate differences in their relative mobilities. Although sodiated monomers exhibited very similar collision cross sections (CCS), baseline separation was observed for the sodiated dimer species (R_S = 1.81), with measured CCS of 242.6 and 256.3 Ų, respectively. Theoretical modeling was performed to determine the most energetically stable structures of solution- and gas-phase monomer and dimer structures. It was revealed that these epimers differ in their preferred dimer binding mode in solution-phase: androsterone adopts a R=O - - Na⁺ - - OH—R′ configuration, whereas trans-androsterone adopts a R=O - - Na⁺ - - O=R′ configuration. This difference contributes to a significant structural variation, and subsequent CCS calculations based on these structures relaxed in the gas-phase were in agreement with experimentally measured values (ΔCCS ~ 5%). Additionally, these calculations accurately predicted the relative difference in mobility between the epimers. This study illustrates the power of combining experimental and theoretical results to better elucidate gas-phase structures.

Graphical Abstract

Introduction

Ion mobility spectrometry (IMS) is a technique used to measure the velocity of gas-phase ions subjected to an electric field [1–6]. Classical drift tube ion mobility involves introduction of a temporally confined ion packet into a uniform field drift tube, where these ions travel at a constant drift velocity (v_d) proportional to their mobility constant (K) and the electric field strength (E), as v_d = KE. As the ions move through the drift tube, they experience interactions with buffer gas molecules that ultimately dictate the ion’s drift time, with smaller ions undergoing fewer collisions and thus traveling more quickly. Separation of ions can be achieved based on differences in mass, shape, and charge, collectively referred to as the rotationally averaged collision cross section (CCS, Ω), a property which describes an ion’s size under given experimental conditions (e.g., drift gas composition, temperature, and pressure) [1, 4, 5]. Experimentally measured drift times can be converted to cross sections using the Mason-Shamp equation [1, 4, 5], below:

$$\mathrm{\Omega }=\frac{{(18\mathrm{\pi })}^{1/2}}{16}\frac{\text{ze}}{{({\mathrm{k}}_{\mathrm{B}}\mathrm{T})}^{1/2}}{\left[\frac{1}{{\mathrm{m}}_{\mathrm{I}}}+\frac{1}{{\mathrm{m}}_{\mathrm{B}}}\right]}^{1/2}\frac{{\mathrm{t}}_{\mathrm{d}}\mathrm{E}}{\mathrm{L}}\frac{760}{\mathrm{P}}\frac{\mathrm{T}}{273.2}\frac{1}{\mathrm{N}}$$ (1)

where ze is the charge, k_B is the Boltzman constant, m_I is the analyte ion mass, m_B is the buffer gas molecule mass, t_d is the corrected drift time in milliseconds, E is the electric field strength in V·cm⁻², L is the drift tube length in cm, P is the drift tube pressure in Torr, T is the drift tube temperature in Kelvin, and N is the drift tube number density in cm⁻³.

Hyphenation of IMS with other analytical techniques, especially mass spectrometry (IM-MS) [3], allows improved specificity of analysis. Although historically IM-MS has been used for the study of large biomolecules such as proteins [7–10], recently this technique has been used increasingly for small molecule analysis, primarily due to its rapid millisecond separation capabilities that allow coupling with liquid chromatography [11, 12] and improved analysis of complex samples with mass spectrometry [13, 14]. Additionally, IM-MS offers great potential in rapid separation of isomers that cannot be resolved with mass spectrometry alone. First demonstrated for structural isomers of polycyclic aromatic hydrocarbons [15], this potential has been shown across numerous classes of biological molecules including carbohydrates [16–24], peptides [25, 26], oligonucleotides [19], lipids [19, 27–29], amino acids [29–31], fatty acids [32], glycans and glycopeptides [33], and other small molecules [34]. However, diastereomers and especially epimers, which differ in stereochemistry at a single chiral center, have very subtle structural differences that may contribute to only minor variation in CCS. To improve separation, several novel IMS strategies have been employed, including pre-analysis derivatization [35–37], use of alternative drift gases and chiral modifiers [38, 39], alkali and transition metal complexation [16–18, 29, 40–42], and multimer formation [30, 43].

In combination with IM-MS, theoretical modeling can aid in elucidating gas-phase three-dimensional structure and improving experimental design in separation of isomers. Generated theoretical structures can be used to calculate theoretical CCS values based on one of several methods, including the projection approximation (PA) [44], exact hard-sphere scattering (EHSS) [45], and the trajectory method (TM) [46]. In the literature it has been shown that theoretical results obtained using TM most closely agree with experimentally obtained values [45, 46]. All these approaches have been gathered in a software program MOBCAL, used to predict CCS based on three-dimensional structure [44–46]. Because nitrogen gas has also become increasingly popular with ion mobility analyses due to lower cost and greater availability, recently the MOBCAL software was modified [47, 48] to allow for trajectory method calculations in N₂ buffer gas, as well as to account for several other atoms found in biological molecules, such as fluorine.

Molecular modeling has been applied in several studies in the literature to compare theoretically- and experimentally-derived CCS values for the identification of gas-phase structures [48–51]. IM-MS experimental results provide information on the charge, atomic composition, and CCS of the molecules, but only a comparison of experimental and theoretical CCS can provide additional molecular structural information, which could not be achieved with experimental results alone. The CCS comparative approach has been used previously to determine structural information for small organic molecules such as crown ethers [52] and carbon clusters [53]; macromolecules such as polyethylene glycol polymers [7]; peptides including bradykinin [54–58]; proteins [7] and cytochrome C [8]; and small biologically-relevant molecules including vitamin D metabolites [51], amino acids [31, 59, 60], and carbohydrates [42]. Comparison of IMS and theoretical results can help identify isomer conformers that can lead to understanding of differences that contribute to separation, improving the potential for these applications. As examples, studies have compared theoretical and experimental IM-MS results for isomeric monosaccharide-transition metal complexes [42], amino acid-alkali metal complexes [31], and small molecule multimer complexes [18], each of which allowed resolution of isomers.

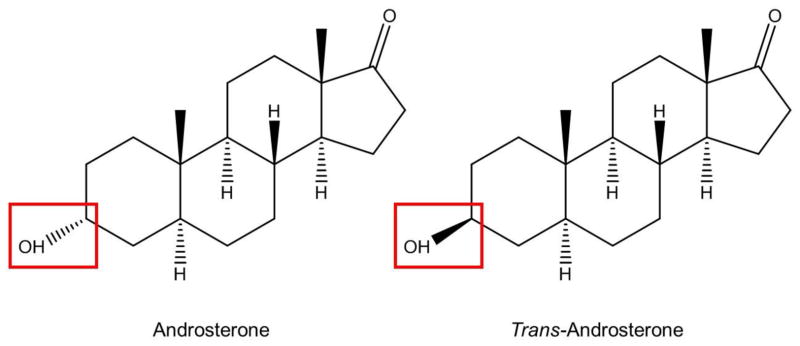
Here we compare theoretical and experimental IM-MS results for a model steroid epimer pair, androsterone and trans-androsterone. These endogenous androgens differ only in their chirality at the C3 position (Scheme 1), with androsterone containing an α-hydroxyl group and trans-androsterone a β-hydroxyl. Specifically, we address structural similarities and differences in the formation of the sodiated multimers of these isomers.

Scheme 1.

Androsterone (left) and trans-androsterone (right)

Experimental Methods

Standard Preparation

Androsterone and trans-androsterone were purchased from Sigma-Aldrich (St. Louis, MO). Solids were prepared as 10 μg/m solutions in Fisher Optima C-MS grade water (with 0.1% formic acid), purchased from Fisher Scientific (Pittsburgh, PA).

IM-MS Analysis

Standards were analyzed with an Agilent 6560 IM-QTOF ion mobility-mass spectrometer instrument (Santa Clara, CA). Standards were directly infused by syringe pump at a flow rate of 10 μ/min. An Agilent Jet Stream (AJS) source was used to perform electrospray ionization (ESI). The ESI source conditions were as follows: capillary voltage: +4000 V; nozzle voltage: +1000 V; drying gas: 325 °C at 5 L/min; sheath gas: 275 °C at 8 L/min.

Ion mobility analysis was performed with a 78 cm uniform field drift tube maintained at approximately 4 torr nitrogen drift gas and 32 °C. The IM trap fill time was 5000 μs and the trap release time was 150 μs. Drift time spectra were acquired over a 60 ms window. To calculate the corrected drift time (t_d), the field was varied over eight field strength steps from 9.6–18.6 V/cm (drift tube voltage 750–1450 V). Total drift time, t_D, was recorded and plotted versus the inverse of the drift tube voltage. This plot provided two points of information: (a) the linearity of the plot indicated that all experiments were performed under low-field conditions, and (b) the y-intercept provided a correction factor (t₀) to the drift time corresponding to the time ions spent in regions of the instrument outside of the drift tube. The Mason-Schamp equation (Eq. 1) [1, 4, 5], shown in Equation (1), was used to compute the collision cross section (Ω) for ions of interest based on corrected drift time. All drift spectra shown were acquired at 18.6 V/cm, unless otherwise noted; optimal peak resolving power was achieved at this field strength. Time of flight mass spectra were acquired in full scan high resolution mode over a range from m/z 100–1700. All IM-MS data processing was performed using Agilent IM-MS Browser B.06.00.

Theoretical Methods

Geometry optimizations and frequency calculations were performed at the B3LYP-D3/6-31G(d) level¹ using the Gaussian 09 [61] program, where D3 means that the Grimme’s empirical dispersion correction [62] was added to the B3LYP functional. In order to account for solvent effects, we used the SMD solvation model designed by Truhlar and coworkers [63]. For both androsterone and trans-androsterone the sodiated monomer optimizations were performed by initially placing the sodium ion (Na⁺) close to the oxygen of either the ketone or the hydroxyl group (see Scheme 1). This allowed comparison of the energetically favorable “binding mode”, which indicates the preference for the sodium ion to be associated with either the ketone (R=O - - Na⁺) or the hydroxyl group (R—HO - - Na⁺) of the steroid. The sodiated dimer optimizations were performed by taking the sodiated monomer and then adding a second monomer to it. The initial dimer structures were created by arranging three different binding modes of Na⁺, relative to the ketone and/or the hydroxyl groups, as follows: R=O - - Na⁺ - - O=R′, R=O - - Na⁺ - - OH—R′, and R—HO - - Na⁺ - - OH—R′. For each case, more than 18 initial configurations with different torsion angles between the monomers were submitted to gas-phase geometry optimization. The gas-phase optimized structures were then submitted to new geometry optimizations in solution-phase, followed by frequency calculations in order to obtain the Gibbs free energies. All the gas-phase optimized geometries were submitted to collision cross section (CCS) calculations using the trajectory method (TM) in the MOBCAL software package [49]. These calculations were performed using N₂ as the drift gas (used experimentally). For each structure, the atomic point charges needed for CCS calculations with TM were obtained using CHelpG [64] charges fitted to the electrostatic potential calculated at the B3LYP-D3/6-31+G(d,p) level using the Gaussian 09 [61] program.

Results and Discussions

Experimental Results

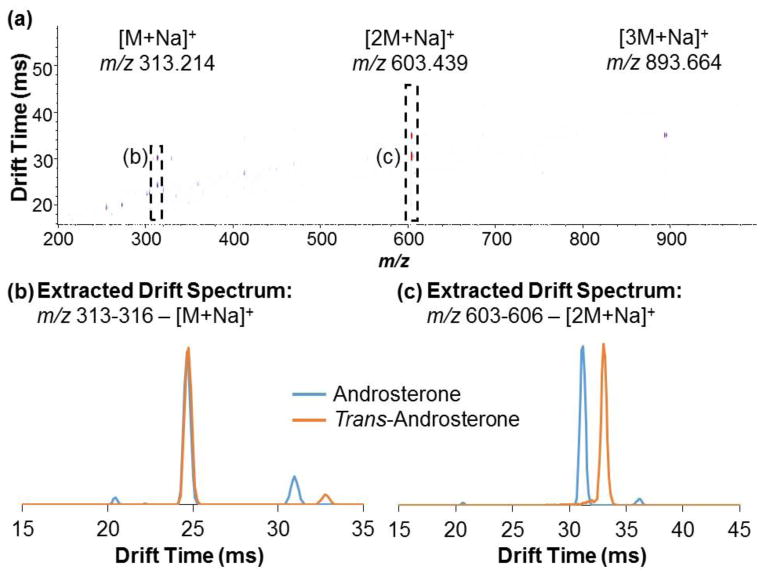
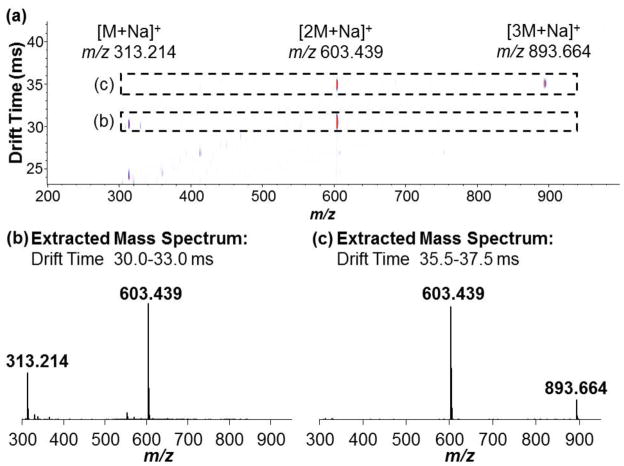
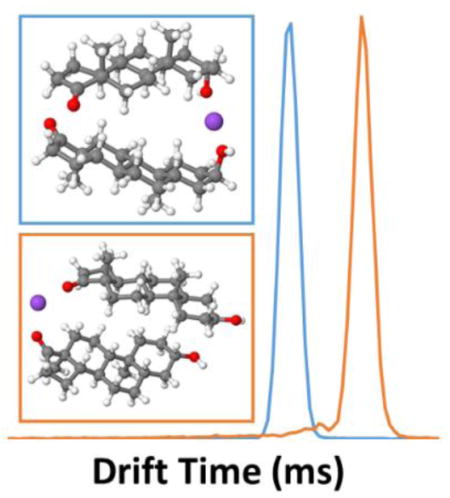
Ion mobility drift time spectra and mass spectra were acquired individually for androsterone and trans-androsterone. Because ionization efficiency for the [M+H]⁺ species of most steroids is typically low with ESI, the sodiated species were the focus of these experiments. Reconstruction of individual drift time spectra allowed comparison of these compounds at a given m/z value. An IM-MS spectrum of androsterone is shown in Figure 1a, indicating the primary sodiated species identified, with an extracted drift time spectrum overlay for the sodiated monomer of each species, [M+Na]⁺ at m/z 313.214 (Figure 1b), and the sodiated dimer of each species, [2M+Na]⁺ at m/z 603.439 (Figure 1c). Minimal separation (R_S = 0.06) was observed between the primary drift peaks (t_D ~ 24.50 ms) for the sodiated monomers (Figure 1b), indicating only very minor differences in their gas-phase structures. Collision cross sections (CCS) were measured as 197.1 ± 0.2 and 196.8 ± 0.2 Ų, respectively. All experimentally obtained CCS values are presented in Table 1. Although separation of the monomer drift peaks was minimal, differences in their overall drift spectra were observed. Notably, additional drift peaks were observed for each of the epimers at m/z 313.214. The presence of these drift peaks corresponds to unique drift tube species which are subsequently detected at that m/z; examples can include charge location isomers (more common with protonated species) which may differ in their CCS and drift time, or species that fragment to that given m/z after exiting the drift tube. The primary difference between the spectra of the epimers was the appearance of resolved drift peaks in the 30.0–33.0 ms range. Figure 2a shows an IM-MS spectrum with corresponding extracted mass spectrum for this drift time range (30.0–33.0 ms) indicating that these drift peaks correspond to the sodiated dimer [2M+Na]⁺ species at m/z 603.439 (Figure 2b). This instrumentation, which performs ion mobility analysis at intermediate pressure (4 torr) and roughly ambient temperature (~30 °C), represents a gentler environment than with those instruments that operate at atmospheric pressure and elevated temperature. Because of this, drift time detection of more labile species is possible, including dimers and trimers. However, these fragile species may fragment upon entering the high vacuum environment of the QTOF-MS, due to the pressure being much lower in this region (10⁻⁵ – 10⁻⁷ torr). This contributes to the presence of additional peaks in the drift spectra for lower m/z species.² An overlay of the drift time spectra for the sodiated dimers (Figure 1c) shows that the epimers exhibit baseline separation (R_S = 1.81). Differences in gas-phase structure for the sodiated dimers that account for this resolution are discussed in greater detail with the theoretical results in the next subsection.

Fig. 1.

(a) IM-MS spectrum of androsterone, indicating sodiated species at m/z 313.214 for [M+Na]⁺, 603.439 for [2M+Na]⁺, and 893.664 for [3M+Na]⁺. Extracted drift spectra overlays for androsterone and trans-androsterone are shown for the (b) sodiated monomer range (m/z 313–316) and (c) sodiated dimer range (m/z 603–606)

Table 1.

Measured collision cross sections (CCS) for all detected sodiated species of androsterone and trans-androsterone.

Drift Tube Ion Species	Androsterone CCS (Å2)	trans-Androsterone CCS (Å2)
[M+Na]+ -- m/z 313.214	197.1 ± 0.2	196.8 ± 0.2
[2M+Na]+ -- m/z 603.439	242.6 ± 0.3	256.3 ± 0.3
[3M+Na]+ -- m/z 893.664	284.0 ± 0.3	----
[3M+2Na]+2 -- m/z 458.327	315.0 ± 0.7	----

Fig. 2.

(a) IM-MS spectrum of androsterone with extracted mass spectra for the (b) 30.0–33.0 drift time range, corresponding to the sodiated dimer, and the (c) 35.5–35.7 ms drift time range, corresponding to the sodiated trimer

The drift spectrum for the androsterone sodiated dimer also exhibits unique drift peaks at 36.16 ms and 20.46 ms (Figure 1c); the latter is uniquely observed in the drift spectrum for the androsterone monomer as well (Figure 1b). Investigation of the mass spectrum for the 35.5–35.7 ms drift time range indicates that this peak corresponds to the singly sodiated trimer [3M+Na]⁺ species (Figure 2c) at m/z 893.664; the mass spectrum for the 21.0–21.1 ms drift time range indicates that this peak corresponds to the doubly sodiated trimer [3M+2Na]⁺² species at m/z 458.327 (mass spectrum not shown). Neither species was detected for trans-androsterone. In addition, the [2M+2Na]⁺² species was not observed for either compound. A summary of the identified drift tube ions for androsterone based on mass spectrometry, as well as the post-drift tube fragmentation patterns, is shown in Scheme 2. However, the unique presence of the sodiated trimer species for androsterone only will not be discussed further in this work. The relative stability of the sodiated dimer for both androsterone and trans-androsterone was investigated, based on several different experimental parameters, and these results are provided in the Supplementary Material. Overall, it was observed that the androsterone dimer was considerably more stable than that of trans-androsterone; this could contribute to the observation of larger complexes (i.e., singly and doubly sodiated trimers) for androsterone, but not for trans-androsterone.

Scheme 2.

Post-drift tube fragmentation of sodiated multimer species for androsterone

Theoretical versus Experimental Results: Monomers

To better understand the structural differences responsible for the mobility of the epimers, theoretical modeling was performed to determine the most energetically favorable ionic structures. Because of the connection between solution-phase ions and electrospray-formed gas-phase ions, optimized structures were determined for both solution- and gas-phase. The gas-phase energies and solution-phase Gibbs free energies for the optimized sodiated monomer structures of androsterone and trans-androsterone are reported in Table 2. The results indicate that the R=O - - Na⁺ binding mode is the most stable monomer configuration by ~0.3–0.5 kcal/mol for both epimers in solution. This is also the most stable binding mode in the gas-phase, with the energy difference between the two binding modes being ~4 kcal/mol for both epimers. Therefore, if we were to consider the sodiated monomers being formed in the gas-phase, only the binding mode in which Na⁺ binds to the ketone group would exist (approximately 99% of the sodiated monomer species would be of R=O - - Na⁺ type, as at room temperature k_bT = 0.592 kcal/mol ³); however, in solution the difference in Gibbs free energies is lower than k_bT; therefore, according to our theoretical results, both binding modes can be formed in solution.⁴ In this work we hypothesize that, once the molecules reach the drift tube in the gas-phase, they have enough time to relax their structures but they don’t change their solution binding mode. Changing the sodiated monomer binding mode in the gas-phase, for example, would involve a disassociation of the sodium ion followed by a reassociation on the other end of the molecule, which is unlikely in the gas-phase. Due to the fact that the gas-phase molecules are much more disperse than in solution, one can rationalize that the multimer formation is more likely in solution. Hence we hypothesize that all the multimers are being formed in solution.

Table 2.

Gibbs free energies (solution-phase) and energy differences (gas-phase) of the androsterone and trans-androsterone sodiated monomers, obtained at B3LYP-D3/6-31G(d) level. The differences are reported in kcal/mol and are with respect to the most stable sodiated monomer.

Binding mode	Gibbs Free Energy difference (Solution-Phase)	Energy difference (Gas-phase)
	Androsterone
Na+ binding at ketone	0.000	0.000
Na+ binding at hydroxyl	0.276	4.016
	trans-androsterone
Na+ binding at ketone	0.000	0.000
Na+ binding at hydroxyl	0.522	4.275

Table 3 presents collision cross sections (CCS) calculated with MOBCAL using the optimized geometries for the gas-phase sodiated monomers. These results indicate that the predicted CCS for the most stable binding modes show good agreement with the experimentally measured results. We see the theoretical CCS values underestimate the experimental ones by around 5% for both epimers. Despite the minor absolute difference between experimental and theoretical CCS, the CCS ratio of androsterone to trans-androsterone is very similar (within 0.2%) for experimental (1.0015) and theoretical (1.0038) results, demonstrating the ability for this approach to accurately predict relative differences in CCS by looking at the most stable binding modes.

Table 3.

Comparison of experimentally-measured and trajectory method-calculated gas-phase CCS. As several structures were optimized for the dimers with different initial torsional angles, the dimer results are averages weighted by the Boltzmann factors for T = 298 K with the respective energy of each optimized structure. Experimental errors and theoretical standard deviations are also shown.

Binding mode	Androsterone		Trans-Androsterone
	Theoretical CCS (Å2)	Experimental CCS (Å2)	Theoretical CCS (Å2)	Experimental CCS (Å2)
	Results for Sodiated Monomers:
Na+ binding at ketone	186.9 ± 2.1	197.1 ± 0.2	186.2 ± 1.2	196.8 ± 0.2
Na+ binding at hydroxyl	180.8 ± 0.9		190.2 ± 1.4
	Results for Sodiated Dimers:
R=O - - Na+ - - O=R′	250.4 ± 1.7	242.6 ± 0.3	245.7 ± 2.1	256.3 ± 0.3
R=O - - Na+ - - OH—R′	234.7 ± 2.3		246.0 ± 2.2
R—HO - - Na+ - - OH—R′	237.4 ± 3.2		257.4 ± 2.2

Another interesting aspect to notice is that, although the CCS values agree for the R=O - - Na⁺ binding mode, there is an evident difference between the CCS values for the R=OH - - Na⁺ binding mode. Androsterone and trans-androsterone differ from each other on the positioning of the hydroxyl group. Although this structural difference does not affect the R=O - - Na⁺ binding mode CCS values, when sodium binds at the hydroxyl group this difference leads the sodium to be placed in a significantly different position around the molecule (for androsterone sodium stays perpendicular to the molecular plane, and for trans-androsterone it stays inside the molecular plane), leading thus to different R=OH - - Na⁺ binding mode CCS values. Structures for the R=OH - - Na⁺ binding mode are shown in Figure S3.

Theoretical versus Experimental Results: Dimers

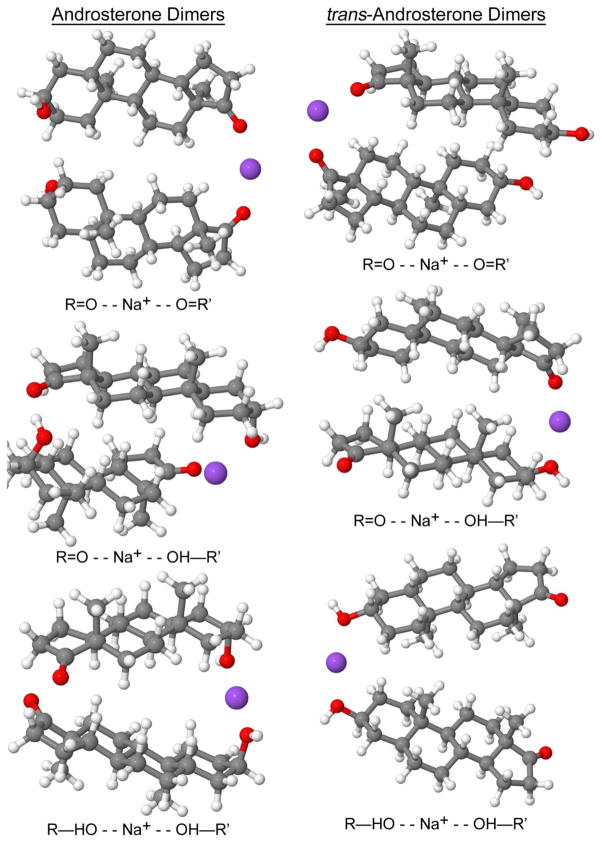
Consideration of sodium bound dimers first involved investigation of the solution-phase binding mode: Na⁺ binding at both ketone groups (R=O - - Na⁺ - - O=R′), Na⁺ binding at a ketone group and at a hydroxyl group (R=O - - Na⁺ - - OH—R′), or Na⁺ binding at both hydroxyl groups (R—HO - - Na⁺ - - OH—R′). The gas-phase optimized geometries for the sodiated dimers are shown in Figure 3. As shown in Table 5, the most stable solution-phase androsterone sodiated dimer is R—HO - - Na⁺ - - OH—R′, with the R=O - - Na⁺ - - OH—R′ being close in free energy. The most stable trans-androsterone sodiated dimer is R=O - - Na⁺ - - O=R′, with the R=O - - Na⁺ - - OH—R′ being close in free energy. The other sodiated dimer binding modes (R=O - - Na⁺ - - O=R′ for androsterone, and androsterone, and R—HO - - Na⁺ - - OH—R′ for trans-androsterone) are unlikely to be formed due to the high free energy difference in comparison to the most stable binding modes. However, the gas-phase results presented in Table 4 show that only the R=O - - Na⁺ - - OH—R′ binding mode for androsterone and the R=O - - Na⁺ - - O=R′ binding mode for trans-androsterone are energetically favorable in the gas-phase, due to the high free energy for the structures of the other binding modes. This comparison displays the importance of performing theoretical modeling in both solution- and gas-phase, especially when done in combination with ESI experiments.

Fig. 3.

Optimized gas-phase geometries for androsterone and trans-androsterone sodiated dimers

Table 4.

Gibbs free energies (solution-phase) and energy differences (gas-phase) of the androsterone and trans-androsterone sodiated dimers, obtained at B3LYP-D3/6-31G(d) level. The differences are reported in kcal/mol and are with respect to the most stable sodiated dimer.

Binding mode	Gibbs Free Energy difference (Solution-Phase)	Energy difference (Gas-phase)
	Androsterone
R=O - - Na+ - - O=R′	5.885	2.609
R=O - - Na+ - - OH—R′	0.560	0.000
R—HO - - Na+ - - OH—R′	0.000	6.497
	trans-androsterone
R=O - - Na+ - - O=R′	0.000	0.000
R=O - - Na+ - - OH—R′	0.539	3.516
R—HO - - Na+ - - OH—R′	4.893	11.266

It is interesting to note that the solution- and gas-phase most stable binding modes for androsterone are not the same. The relative energies have components of internal energy, interactions with solvent, and entropic effects coming from internal vibrations. Given all these variables, the correlation between energy ordering in the solution and gas phases is non-trivial, and there is nothing that requires them to be similar. On the Gaussian program [61], the entropic contribution to the Gibbs Free Energy is computed using information from the frequency calculation. Therefore, even disregarding major structural changes, the entropic contribution may significantly alter the stability in solution in respect to the stability in the gas-phase. Our results show that the difference ΔG-ΔE between the R—HO - - Na+ - - OH—R′ and R=O - - Na+ - - OH—R′ androsterone binding modes in solution is mostly entropic (TΔS=−5.183 kcal/mol). This large entropic difference for androsterone (that leads to a stability reordering) is possibly because the two structures are packed differently.

Table 3 presents CCS for the gas-phase sodiated dimers. As with the monomer calculations, the results indicate that the predicted CCS for the most stable binding modes show good agreement with the experimentally measured results, with theoretical values underestimating the experimental ones by 5% for both epimers. Again, the ratio of androsterone to trans-androsterone CCS is very similar (within 0.2%) for experimental (0.9662) and theoretical (0.9465) results, based on the values corresponding to the most stable binding modes in solution. This shows that the theoretical modeling approach can both accurately predict the significant difference in dimer CCS that is observed experimentally, while also determining the most energetically favorable structures and binding modes that contribute to this difference. It is also interesting to note that the binding modes that are close in free energy also have similar CCS, while the binding mode that is higher in free energy has a larger predicted CCS; this indicates that the CCS results are in agreement with the stability obtained in solution, not in the gas-phase.

Conclusions

Experimentally, androsterone and trans-androsterone sodiated monomers exhibited very similar mobility drift time and CCS; in contrast, baseline separation was observed for the sodiated dimers. Theoretical calculations were performed to determine the most stable conformations in solution- and gas-phase for the sodiated monomer and dimer species, which revealed that these epimers have different energetically favorable sodiated dimer binding modes. Calculation of CCS based on these energetically favorable structures was in good agreement with experimentally obtained values (ΔCCS ~ 5%). Additionally, the modeling approach was able to predict even more accurately the relative differences in CCS between the epimers, revealing the structural differences and binding mode preferences that contributed to significant separation between dimers in the experimental results. This work is an example of how the combination of experimental results and theoretical calculations is able to provide a higher level of understanding of the molecules studied that neither experimentation or theoretical modeling alone are able to achieve.

Supplementary Material

13361_2016_1525_MOESM1_ESM

Fig. S1 Instrumental schematic of the Agilent 6560 IM-QTOF, detailing instrumental parameters that were varied to change the energy applied for measure of dimer stability

Fig. S2 MS/MS spectra for androsterone and trans-androsterone, with the parent sodiated dimer at m/z 603 isolated. Fragmentation of the dimer can be seen (a,b) in the absence of collision energy, (c,d) at CE = 10 ev, and (e,f) at CE = 20 eV

Fig. S3 Androsterone and trans-androsterone structures for the R=OH - - Na⁺ binding mode

Table S1 Experimental parameters varied for measurement of dimer stability, including the standard experimental value and the range measured.