Gland segmentation in prostate histopathological images

Abstract.

Glandular structural features are important for the tumor pathologist in the assessment of cancer malignancy of prostate tissue slides. The varying shapes and sizes of glands combined with the tedious manual observation task can result in inaccurate assessment. There are also discrepancies and low-level agreement among pathologists, especially in cases of Gleason pattern 3 and pattern 4 prostate adenocarcinoma. An automated gland segmentation system can highlight various glandular shapes and structures for further analysis by the pathologist. These objective highlighted patterns can help reduce the assessment variability. We propose an automated gland segmentation system. Forty-three hematoxylin and eosin-stained images were acquired from prostate cancer tissue slides and were manually annotated for gland, lumen, periacinar retraction clefting, and stroma regions. Our automated gland segmentation system was trained using these manual annotations. It identifies these regions using a combination of pixel and object-level classifiers by incorporating local and spatial information for consolidating pixel-level classification results into object-level segmentation. Experimental results show that our method outperforms various texture and gland structure-based gland segmentation algorithms in the literature. Our method has good performance and can be a promising tool to help decrease interobserver variability among pathologists.

1. Introduction

The prostate gland is a functional conduit that allows urine to pass from the urinary bladder to the urethra and adds nutritional secretions to the sperm to form semen during ejaculation. Microscopically, the prostate is composed of glandular epithelium and fibrous stroma. Prostate cancer (PCa) occurs mostly in gland cells and hence is called prostate adenocarcinoma.

Gleason grade of prostate adenocarcinoma is an established prognostic indicator that has stood the test of time.^1,2 The Gleason system is based on the glandular pattern of the tumor. Architectural patterns are identified and assigned a pattern from 1 to 5, with 1 being the most differentiated and 5 being undifferentiated.^2,3

Increasing Gleason grade is directly related to a number of histopathological end points, including lympho-vascular space invasion by carcinoma, tumor size, positive surgical margins, and pathological stage, which includes risk of extraprostatic extension and metastasis. Histological grade of prostatic carcinoma is one of the most powerful, if not the dominant, predictor of clinical outcome for patients with this cancer. A number of clinical end points have been linked to histological grade. These clinical end points include clinical stage, response to different therapies, prostatic-specific antigen (biochemical) failure, progression to metastatic disease, PCa-specific survival, and overall survival.^2,4–7

Certain areas of the Gleason system have been modified over the years. Some aspects in the original scoring are interpreted differently in modern practice. Due to the changes in the Gleason scoring over the years, it is now known that a specimen that has received a Gleason score of $1+1=2$ in the area of Gleason would today be referred as adenosis (atypical adenomatous hyperplasia).⁸ It is therefore a grade that should not be diagnosed regardless of the type of specimen, with extremely rare exceptions. Also, a diagnosis of a lower score on needle biopsy is inaccurate because of

• 1.poor reproducibility among experts,
• 2.poor correlation with prostatectomy grade, with the majority of cases exemplifying higher grade at resection, and
• 3.the possibility of misguiding clinicians and patients into believing that the patient has an indolent tumor.

Hence, clinicians are no longer using these Gleason 1 and 2 cancers in managing PCa. As for Gleason 5, it is easily identified by pathologists, and hence in our study, we did not focus on it. Instead, our study concentrates on the difficulties and reliability in identifying Gleason 3 and 4 cancers, which will subsequently affect both pathology and actual clinical management of PCa.

In the International Society of Urological Pathology 2005 Modified Gleason System, Gleason pattern 3 includes discrete glandular units, glands that infiltrate in and among nonneoplastic prostate acini and showing marked variations in size and shape. Pattern 4 exhibits ill-defined glands with poorly formed glandular lumina, cribriform, and fused microacinar glands. Pattern 4 also shows hypernephromatoid structures.⁹

The Gleason grading system, like all histological grading methods, possesses an inherent degree of subjectivity. Intra-and interobserver variability do exist. Recent data suggest that, for needle biopsy grading, pathologist training and experience can influence the degree of interobserver agreement.^10–12 Manual diagnosis of PCa is a tedious and time-consuming process where the pathologist examines a prostate tissue under a microscope. Moreover, the diagnostic accuracy depends on the personal skill and experience of the pathologist.

While the Gleason system has been in use for many decades, its dependence on qualitative features leads to a number of issues with standardization and variability in diagnosis. Intermediate Gleason grades (3 or 4) are often under- or overgraded, leading to interobserver variability up to 48% of the time.¹² The main reason for undergrading (score 6 versus 7) was not recognizing relevant fusion of glands as a criterion for pattern 4.¹³

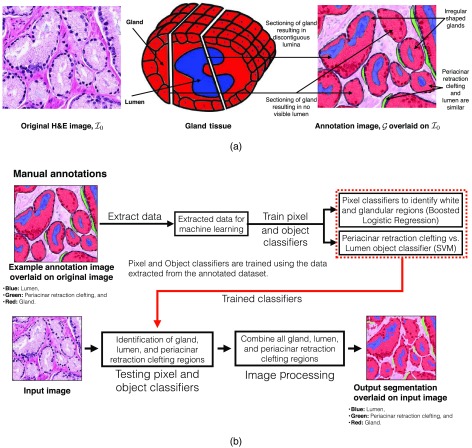
These problems motivate the research and development of assisting the diagnosis and prognosis processes through the use of software.¹⁴ Effective assistive diagnosis and prognosis tools have to be built in stages. First, basic tools, such as automated prominent nucleoli detection and gland segmentation tools, need to be developed. Second, these tools need to be put together in an effective way. We developed an effective prominent nucleoli detector in our previous work.¹⁵ In this paper, we present an effective method for gland segmentation. Gland segmentation is the first step for the analysis of gland shapes and architecture. We illustrate the main challenges we encountered in gland segmentation in a sample Gleason pattern 3 image in Fig. 1(a). The original hematoxylin and eosin (H&E) image ${\mathcal{I}}_0$ overlaid by annotation image $\mathcal{G}$ and the exhibiting potential issues in segmentation are shown in this figure.

Fig. 1.

(a) Example of Gleason pattern 3 H&E image, ${\mathcal{I}}_0$. We also show the annotations (image $\mathcal{G}$) overlaid on ${\mathcal{I}}_0$. For image $\mathcal{G}$, red: gland, blue: lumen, and green: periacinar retraction clefting. Both the gland section with discontiguous lumina and the gland section with no visible lumen generally result from tangential sectioning of well-formed glands. We illustrate these two cases by the schematic diagram of gland tissue with example section positions in the middle. (b) Overview of our gland segmentation system.

Glands are inherently three-dimensional (3-D) structures, but, when processed and sliced, we can only analyze the cross section of these 3-D structures. Glands are generally composed of a lumen in the center with epithelial nuclei at the boundary and cytoplasm filling in the intermediate space. Lumen can be identified as empty white spaces within the glandular structure. Periacinar retraction clefting resulting in clear spaces around the glandular area may be seen on the histological material as a random phenomenon in tissue fixation. These cleftings arise from tissue handling during the biopsy procedure, undue delay in fixation, and tissue fixation itself. These periacinar retraction clefting are also white and are very similar to lumen. Some of the white areas may be masked by other cellular components, such as blood cells, which may impede automated identification of lumen and periacinar retraction clefting objects. Tangential sectioning of well-formed glands leads to gland sections with no visible lumen and/or with discontiguous lumina in the histological tissue slides. These issues arise when the tangential section plane misses the lumen or passes through the lumen multiple times (see Fig. 1). The varying gland shapes and sizes impede segmentation algorithms, which rely on template shapes and structures. We have illustrated all of these issues in Fig. 1(a).

In this study, we aim to develop an automated system for gland segmentation in PCa tissue images of H&E-stained histology slides. We used a machine learning and image processing-based gland segmentation method. Machine learning methods used pixel neighborhood and object shape information for an empirical estimate of various regions of the image. Image processing methods were used to further refine these approximations to compute the final segmentation result. The workflow of our method is as follows:

• 1.Tissue images are manually extracted from whole slide images. These images are then segmented by our automated gland segmentation system.
• 2.Periacinar retraction clefting and lumen regions are automatically identified in the extracted tissue images.
• 3.All the glands lined by epithelial cells and surrounded by stromal cells are automatically segmented for the final result.

2. Related Work

Existing gland segmentation methods generally use texture and/or gland structure information. Farjam et al.¹⁶ used variance and Gaussian filters to extract roughness texture features in prostate histopathological images. They used $k$-means clustering for pixel-wise classification for nucleus and cytoplasm. This pixel information was then used for gland segmentation. Texture-only based approaches generally do not have access to lumen and epithelial nuclei’s spatial information and may perform badly, as discussed in Sec. 4.

To alleviate this problem in gland segmentation, algorithms have been developed to use gland morphology and lumen–epithelial nuclei relationships. Naik et al.¹⁷ used a level set method for gland segmentation. The initial level set is detected by a Bayesian classifier and surrounded the lumen region. The energy functional was developed for attaining minimum energy when the level set is around the epithelial nuclei. Xu et al.¹⁸ proposed a faster version of Naik et al.¹⁷ after modifying the energy functional in the geodesic general active contour model. These level set methods, when initialized correctly, would result in a reasonable segmentation. This property also defines their main limitation, which is level set initialization. These algorithms would also result in inaccurate segmentation due to incorrect or missing initial level sets.

Gunduz-Demir et al.¹⁹ proposed using object graphs for segmentation of colon histopathology images. Their algorithm first detects circular objects in the images and then identifies them as nuclei and lumen using object-graph information. A boundary of the gland was then constructed by connecting the centroids of nuclei objects. The identified lumen objects are then grown until they touch the gland boundary. This method will segment glands with lumen inside them but would fail to properly segment glands with no visible lumen and discontiguous lumina.

Nguyen et al.²⁰ used $k$-nearest neighbor classification based on CIELab color space information to classify pixels as stroma, lumen, nuclei, cytoplasm, or blue mucin. This method then unified the nuclei and cytoplasm pixels to extract gland boundaries. Similarly, Monaco et al.²¹ used luminance channel in the CIELab color space in conjunction with Gaussian kernels to find the gland centers. These gland centers were then expanded into glands using a region growing method²² in the RGB color space. This method will segment glands with lumen inside them but would fail to segment glands with no visible lumen and discontiguous lumina.

An improvement of Nguyen et al.²⁰ was suggested in Ref. 23 by finding nuclei and lumen object first and then using a local spatial search to connect the lumen to their nearby nuclei. Various points at the lumen boundary were sampled, and all the nearest nuclei points were connected to these points. The final gland segmentation was defined as the convex hull of various connected components, with each connected component being defined as a gland. Various lumen–nuclei connections were pruned using simple rules for reducing noise in the final result. This method will segment glands with lumen inside them but would fail to segment glands with no visible lumen and discontiguous lumina.

Nguyen et al.²⁴ proposed a nuclei-based gland segmentation method to address both issues of gland sections with no visible lumen and discontiguous lumina by building a graph of nuclei and lumina in an image. This paper then used the normalized cut method²⁵ to partition the graph into different components, each corresponding to a gland. The gland boundaries were then created by connecting nearby nuclei by straight lines. As such, the resultant glands would most likely cover most of the actual gland region. On the other hand, the resultant gland boundaries would be polygonal in shape, which may not follow the exact continuous shape of the gland.

Ren et al.²⁶ also proposed a region-based nuclei segmentation method. This paper used color map normalization²⁷ and subsequent color deconvolution²⁸ to get separate masks for nuclei and gland regions. This paper addressed the issues of gland sections with discontiguous lumina and no visible lumen by not using lumen as prior information. Local maxima points in the distance transform map for the binary gland mask were used to identify individual glands. Nuclei regions were grouped to these local maxima points, and their Delaunay triangulation was used for output gland segmentation. This method relied on local maxima points to identify individual glands objects. The output gland boundaries are polygonal in shape, which like Nguyen et al.²⁴ will not follow the continuous shape of gland.

Sirinukunwattana et al.²⁹ also proposed a solution for a similar problem of gland segmentation in colon histopathological images by suggesting a random polygons model. This model treats each glandular structure as a polygon of a random number of vertices, which in turn represent approximate locations of nuclei. Their algorithm used a reversible-jump Markov chain Monte Carlo (RJMCMC) method to infer all the maximum a posteriori polygons. This method relies on using pixel-based identification of lumen regions to infer the initial random polygons for RJMCMC. It addresses the issue of segmenting glands with discontiguous lumina by filtering the converged maximum a posteriori polygons using a heuristic criterion. The method then proceeds to rerun RJMCMC with the remaining maximum ‘a posteriori’ polygons as initial polygons. The subsequent polygon-shaped glands are then improved upon by cubic spine interpolation such that the segmented glands have a more similar shape to the actual glands. This paper, however, does not address the issue of segmenting glands with no visible lumen explicitly.

Various deep learning-based methods have also been developed for similar segmentation problems in various types of histopathological images.^30–36 Xu et al.³³ proposed a multichannel neural network for gland segmentation in colon histopathological images. Their method comprised three neural network channels. One channel was responsible for segmenting foreground pixels from background pixels. The second channel was responsible for detecting gland boundaries while the third channel was designed for gland detection. The outputs of these three channels were fused together by a convolutional neural network (CNN) for the final gland segmentation result. This paper, however, does not address the issue of segmenting glands with no visible lumen and discontiguous lumina explicitly.

Chen et al.³⁴ proposed a deep contour-aware network (DCAN) for gland segmentation in colon histopathological images. This network was designed to find the gland regions and gland boundaries (contours) simultaneously. DCAN was trained after initializing its weights, which were defined according to a DeepLab³⁷ model trained on the PASCAL VOC 2012 dataset.³⁸ DCAN fused the results for gland regions and their boundaries by a simple pixel-based binary operation. This paper, however, does not address the issue of segmenting glands with no visible lumen and discontiguous lumina explicitly by focusing on detecting gland boundaries along with gland regions.

Ren et al.³⁵ focused on the gland classification task while proposing a CNN for binary gland segmentation in prostate histopathological images. This CNN was designed in an encoding and decoding architecture with 10 layers in both of them. Using this approach, it was able to improve upon Nguyen et al.²³ and Ren et al.²⁶ on a dataset of 22 H&E images, each of $2400\times 1800\text{pixels}$, in the gland segmentation task. This paper, however, does not address the issues of segmenting glands with no visible lumen and discontiguous lumina explicitly.

Jia et al.³⁶ proposed a weakly supervised CNN framework with area constraints for segmenting histopathological images. The CNN was trained and tested on two separate datasets of colon histopathological images. Their main contribution is the introduction of area constraints as weak supervision. The dataset was created by annotating cancerous and noncancerous regions along with a rough estimation (in term of percentage area) of the relative size of the cancerous regions in each image. This rough estimate acted as a weak constraint for the proposed CNN. This paper, however, does not address the issues of segmenting glands with no visible lumen and discontiguous lumina explicitly as it was more focused on binary segmentation of cancerous and noncancerous regions.

3. Method

We propose a machine learning and image processing-based method to solve the gland segmentation problem while addressing the issues illustrated in Fig. 1(a). Figure 1(b) shows an overview of our gland segmentation system. We developed a set of pixel classifiers and object classifiers for identification of various regions in an image. Our classifiers are trained on the data extracted from the manual annotations of the pathologist. The trained pixel and object classifiers are tested on a given image for an estimate of various regions. Image processing methods are then used for refining these region estimates into the final segmentation result.

3.1. Obtaining Manual Annotations for Training Pixel and Object Classifiers

We describe our image acquisition and manual annotation steps below.

3.1.1. Annotation of images into gland, lumen, periacinar retraction clefting, and stroma regions by the research pathologist

The whole slide tissue images of prostate biopsies for 10 patients with PCa were downloaded from The Cancer Genome Atlas (TCGA).³⁹ The patients in this data set exhibit Gleason pattern 3 and/or 4. A total of 43 images from these whole slide images were extracted. Out of 43 images, 36 images were of $2720\times 2048\text{pixels}$ and 7 images were of $1360\times 1024\text{pixels}$ dimensions. All of these images were extracted at $40\times$ magnification with pixel resolution of $0.25\mu \mathrm{m}$ per pixel. Scanner and source institution information for these patients was not available on TCGA website. We give details of these TCGA images in Table 1. After image extraction, the annotation workflow of the research pathologist is as follows:

Table 1.

Description of extracted images.

Image	Gleason grade	Bounding box $(x_{\min },y_{\min }),(x_{\max },y_{\max })$
TCGA-2A-A8VO-01Z-00-DX1_L72702_T66921_W2720_H2048	3	(72,702, 66,921), (75,422, 68,969)
TCGA-2A-A8VO-01Z-00-DX1_L79545_T35778_W2720_H2048	3	(79,545, 35,778), (82,265, 37,826)
TCGA-2A-A8VO-01Z-00-DX1_L81449_T55250_W2720_H2048	$3+4$	(81,449, 55,250), (84,169, 57,298)
TCGA-2A-A8VO-01Z-00-DX1_L82247_T40015_W2720_H2048	3	(82,247, 40,015), (84,967, 42,063)
TCGA-2A-A8VO-01Z-00-DX1_L85502_T58665_W2720_H2048	3	(85,502, 58,665), (88,222, 60,713)
TCGA-HC-7075-01Z-00-DX1_L11216_T3583_W2720_H2048	$3+4$	(11,216, 3583), (13,936, 5631)
TCGA-HC-7075-01Z-00-DX1_L12975_T10686_W2720_H2048	3	(12,975, 10,686), (15,695, 12,734)
TCGA-HC-7075-01Z-00-DX1_L13921_T14013_W2720_H2048	3	(13,921, 14,013), (16,641, 16,061)
TCGA-HC-7075-01Z-00-DX1_L18204_T7968_W2720_H2048	3	(18,204, 7968), (20,924, 10,016)
TCGA-HC-7075-01Z-00-DX1_L25396_T4657_W2720_H2048	$3+4$	(25,396, 4657), (28,116, 6705)
TCGA-HC-7077-01Z-00-DX1_L31247_T4210_W1360_H1024	$3+4$	(31,247, 4210), (32,607, 5234)
TCGA-HC-7077-01Z-00-DX1_L33310_T6060_W1360_H1024	3	(33,310, 6060), (34,670, 7084)
TCGA-HC-7077-01Z-00-DX1_L34840_T5090_W1360_H1024	3	(34,840, 5090), (36,200, 6114)
TCGA-HC-7077-01Z-00-DX1_L35090_T6525_W1360_H1024	3	(35,090, 6525), (36,450, 7549)
TCGA-HC-7077-01Z-00-DX1_L36272_T3010_W1360_H1024	3	(36,272, 3010), (37,632, 4034)
TCGA-HC-7211-01Z-00-DX1_L30692_T17413_W1360_H1024_pattern4	4	(30,692, 17,413), (32,052, 18,437)
TCGA-HC-7211-01Z-00-DX1_L31053_T21217_W1360_H1024_pattern4	4	(31,053, 21,217), (32,413, 22,241)
TCGA-HC-7212-01Z-00-DX1_L23123_T10332_W2720_H2048_pattern3	$3+4$	(23,123, 10,332), (25,843, 12,380)
TCGA-HC-7212-01Z-00-DX1_L17555_T17714_ W2720_H2048_pattern4	4	(17,555, 17,714), (20,275, 19,762)
TCGA-HC-7212-01Z-00-DX1_L2051_T6465_ W2720_H2048_pattern4	4	(2051, 6465), (4771, 8513)
TCGA-HC-7212-01Z-00-DX1_L9643_T2160_ W2720_H2048_pattern4	4	(9643, 2160), (12,363, 4208)
TCGA-HC-7212-01Z-00-DX1_L6955_T4656_ W2720_H2048_pattern4	4	(6955, 4656), (9675, 6704)
TCGA-XJ-A9DQ-01Z-00-DX1_L58543_T10148_ W2720_H2048	3	(58,543, 10,148), (61,263, 12,196)
TCGA-G9-6364-01Z-00-DX1_L36428_T45944_ W2720_H2048	$3+4$	(36,428, 45,944), (39,148, 47,992)
TCGA-G9-6364-01Z-00-DX1_L43716_T42632_ W2720_H2048	$3+4$	(43,716, 42,632), (46,436, 44,680)
TCGA-G9-6365-01Z-00-DX1_L83292_T39235_ W2720_H2048	$3+4$	(83,292, 39,235), (86,012, 41,283)
TCGA-G9-6365-01Z-00-DX1_L84869_T37165_ W2720_H2048	$3+4$	(84,869, 37,165), (87,589, 39,213)
TCGA-G9-6364_L151748_T35850_W2720_ H2048	$3+4$	(151,748, 35,850), (154,468, 37,898)
TCGA-G9-6364_L131990_T52007_W2720_ H2048	$3+4$	(131,990, 52,007), (134,710, 54,055)
TCGA-G9-6364_L122615_T48695_W2720_ H2048	$3+4$	(122,615, 48,695), (125,335, 50,743)
TCGA-G9-6365_L80439_T8350_W2720_ H2048	$3+4$	(80,439, 8350), (83,159, 10,398)
TCGA-G9-6365_L83152_T15462_W2720_ H2048	$3+4$	(83,152, 15,462), (85,872, 17,510)
TCGA-G9-6365_L69172_T28814_W2720_ H2048	$3+4$	(69,172, 28,814), (71,892, 30,862)
TCGA-G9-6385_L23690_T17439_W2720_ H2048	$3+4$	(23,690, 17,439), (26,410, 19,487)
TCGA-G9-6385_L29600_T19834_W2720_ H2048	$3+4$	(29,600, 19,834), (32,320, 21,882)
TCGA-G9-6385_L26699_T26585_W2720_ H2048	$3+4$	(26,699, 26,585), (29,419, 28,633)
TCGA-G9-6385_L23524_T23766_W2720_ H2048	$3+4$	(23,524, 23,766), (26,244, 25,814)
TCGA-G9-6385_L26359_T23758_W2720_ H2048	$3+4$	(26,359, 23,758), (29,079, 25,806)
TCGA-XJ-A83H-01Z_L67058_T32077_ W2720_H2048	$3+4$	(67,058, 32,077), (69,778, 34,125)
TCGA-XJ-A83H-01Z_L69605_T30039_ W2720_H2048	$3+4$	(69,605, 30,039), (72,325, 32,087)
TCGA-XJ-A83H-01Z_L50723_T22263_ W2720_H2048	$3+4$	(50,723, 22,263), (53,443, 24,311)
TCGA-XJ-A83H-01Z_L55225_T17149_ W2720_H2048	$3+4$	(55,225, 17,149), (57,945, 19,197)
TCGA-XJ-A83H-01Z_L68817_T9948_ W2720_H2048	$3+4$	(68,817, 9948), (71,537, 11,996)

• 1.Segmentation of nontissue regions that appeared white in color, and these regions were labeled as periacinar retraction clefting.
• 2.Identification and segmentation of the glands lined by epithelial cells. Whether the glands appeared discrete, variable in size and shape, or fused were properly classified and annotated. If somewhat touching (not fused), glands have a discernible boundary, then they are annotated as separate glands.
• 3.Identification of the lumen region(s) of the gland. Note that lumen regions also appear white in the image. Special care has to be taken to prevent confusion between periacinar retraction clefting and lumen objects.

All the regions in the images that were not annotated as either parts of lumen or gland or periacinar retraction clefting are considered stroma. We show a sample H&E image and its corresponding manual annotation in Fig. 1(a). We use these manually annotated labels for training various pixel classifiers. Similarly, the annotated lumen and periacinar retraction clefting objects are used to train the periacinar retraction clefting versus lumen object classifier.

3.1.2. Distribution of images for training and subsequent testing

We did a twofold cross-validated study to gauge the performance of our gland segmentation system. The first fold has 24 images (from six patients) for training and 19 images (from four patients) for testing. The second fold has 19 images (from four patients) for training and 24 images (from six patients) for testing. For both folds, the training images are used to extract the pixel- and object-level data to train the pixel and object classifiers.

3.2. Pixel Classifiers

The manual annotations define four types of pixels, i.e., gland, stroma, lumen, and periacinar retraction clefting. They are used to extract the training data for the pixel classifiers. Various machine learning methods, such as $k$-means clustering, $k$-nearest neighbor classification, random forest, and support vector machine (SVM)⁴⁰ along with features generated from RGB color space, CIELab color space, texture, and pixel neighborhood, have been proposed in the literature for pixel-level identification.^{16–21,23,24,29} Similarly, Yap et al.¹⁵ also proposed using different intensity gradient-based features derived from various color spaces, including RGB and CIELab along with SVM,⁴⁰ standard logistic regression (LR), and AdaBoost,⁴¹ for prominent nucleoli detection; they also showed that usage of various color spaces emphasizes multiple aspects of pixel-level patterns from various regions in the histopathological images. In our pixel classifier, we use a similar approach of LR in various color spaces along with AdaBoost⁴¹ for the classifier combination. We discuss the generation of LR classifier ensemble and the subsequent combination for pixel classification later in this section.

3.2.1. Training data extraction from the annotated dataset

An image in our dataset contains at least a million pixels. It is then computationally infeasible to use all the pixels for training the pixel classifiers. Instead, we sampled a subset of pixels to train the pixel classifiers. Each sampled pixel is endowed with a feature that is derived from a variable image patch of size $s\times s$ pixels centered at that pixel. We define the periacinar retraction clefting and lumen regions as cavity regions as both of them appear white in the images. We also define gland and stroma regions as noncavity regions for their tissue content.

Sampling cavity pixels and noncavity pixels

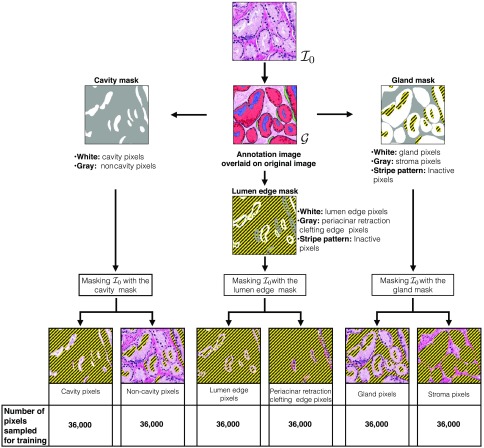
All the pixels whose corresponding square patches are in either periacinar retraction clefting or lumen are identified as cavity pixels. All the pixels whose corresponding patches are in either gland or stroma are identified as noncavity pixels. This definition of cavity and noncavity pixels is used for sampling the training dataset. The pixels that were very near the boundary of cavity and noncavity regions were not sampled for training purposes. Figure 2 shows an example of an annotated image $\mathcal{G}$ and the corresponding cavity pixels and noncavity pixels in the cavity mask. We sampled 36,000 cavity pixels and noncavity pixel pairs to train the cavity versus noncavity pixel classifier.

Fig. 2.

Gland and stroma regions are extracted from image $\mathcal{G}$ to the gland mask (right). Cavity and noncavity regions are extracted from image $\mathcal{G}$ to the cavity mask (left). Lumen edge and periacinar retraction clefting edge regions are extracted from image $\mathcal{G}$ to the lumen edge mask (bottom). We also separate the binary groupings in the three masks to show each grouping separately in six images at the bottom. In all of these images, the inactive pixels are shown in a stripe pattern. Active pixels are shown using the RGB values of the original image. In the six pixel grouping images, only the active pixels are used for sampling a particular group (type) of pixels. We also indicate the total number of pixels sampled from each grouping for training of pixel classifiers.

Sampling lumen edge pixels and periacinar retraction clefting edge pixels

We define another pixel classifier to extract neighborhood information of lumen and periacinar retraction clefting objects. Both types of objects have different characteristic surrounding regions. Lumen is always inside the gland and surrounded by cytoplasm. Periacinar retraction clefting may have any type of surrounding region.

All the pixels at the edge of lumen are considered lumen edge pixels, and all the pixels at the edge of periacinar retraction clefting are considered periacinar retraction clefting edge pixels. Figure 2 shows an example of an annotated image $\mathcal{G}$ and the corresponding lumen edge pixels and periacinar retraction clefting edge pixels in the lumen edge mask. We sampled 36,000 lumen edge pixels and periacinar retraction clefting edge pixel pairs to train the lumen edge versus periacinar retraction clefting edge pixel classifier.

Sampling gland and stroma pixels

All the pixels with their corresponding square patch inside the gland are considered gland pixels. All the pixels whose corresponding square patch is inside the stroma are considered stroma pixels. This definition of gland and stroma pixels is used for sampling the training dataset. The pixels that were very near the boundary for gland or stroma were not sampled for training purposes. Any pixel/information from the lumen and periacinar retraction clefting regions is not used. Figure 2 shows an example of an annotated image $\mathcal{G}$ and the corresponding gland pixels and stroma pixels in the gland mask. We sampled 36,000 gland pixels and stroma pixel pairs to train the gland versus stroma pixel classifier.

3.2.2. Training of pixel classifiers

We designed three pixel classifiers, i.e., cavity versus noncavity pixel classifier, gland versus stroma pixel classifier, and lumen edge versus periacinar retraction clefting edge pixel classifier, as part of our gland segmentation system. They are trained in two stages. In the first training stage, an ensemble of LR classifiers is trained using the training data. In the second stage, this ensemble of LR classifiers is combined using AdaBoost.⁴¹ We defined two disjoint subsets of training images (for a given fold) ${\mathrm{Set}}_{\text{weak}}$ and ${\mathrm{Set}}_{\text{AdaBoost}}$ corresponding to the two training stages.

For a given pixel classifier, the LR pixel classifier ensemble was trained on 20,000 pixels pairs sampled from ${\mathrm{Set}}_{\text{weak}}$, and the AdaBoost⁴¹ combination was trained on 16,000 pixel pairs sampled from ${\mathrm{Set}}_{\text{AdaBoost}}$. As such, we sampled a total of 36,000 cavity pixel, noncavity pixel pairs; 36,000 gland pixel, stroma pixel pairs; 36,000 lumen edge pixel, periacinar retraction clefting edge pixel pairs for training. We were able to use a total of 72,000 pixels ($=36000\times 2$) within a feasible training time for each of the three pixel-level classifiers.

Ensemble of logistic regression pixel classifiers

We use the standard LR with the L2 penalty (regularized) and the gradient descent method to train our LR pixel classifiers. We use the raw pixel values of $p_c(x,y)$ ($c\in \{\mathrm{1,2},3\}$) for a three-channel image patch $p$ of $s\times s$ pixels centered at the given pixel as the input to the LR pixel classifier. We have a total of $3s^2$ features that are the input to the LR. The pixel classification score by LR is within the interval [0, 1] and is linearly mapped to [0, 255] to create a grayscale prediction image from all the pixel-wise scores.

The grayscale LR pixel classification score can be thresholded to create a binary classifier. The binary classifier will predict a positive sample for score value higher than the threshold and a negative sample otherwise. As such, we can generate 256 binary classifiers from a single LR pixel classifier. We term the set of all binary classifiers as weak classifiers.

Yap et al.¹⁵ showed that it is effective to extend the RGB color space to other color spaces viz. HLS, HSV, CIELab, CIELuv, XYZ, and YCbCr. This paper also proposed using different image patch sizes to capture information at different resolutions for a given data sample, i.e., pixel. The original images in RGB color space were digitally extended to the other six color spaces indicated above. We also used image patch sizes of $2\times 2$, $4\times 4$, $6\times 6$, $8\times 8$, $12\times 12$, and $16\times 16\text{pixels}$ for LR pixel classifier training. The LR training with all 20,000 pixel pairs for patch sizes of $8\times 8$, $12\times 12$, and $16\times 16\text{pixels}$ can be time-consuming. We can reduce the training time of LR pixel classifiers with patch sizes of $8\times 8$, $12\times 12$, and $16\times 16\text{pixels}$ using subsets of 1000, 2000, 4000, 8000, and 16000 pixel pairs from the total of 20,000 pixel pairs instead of using all pixel pairs. We were able to train the LR pixel classifiers with patch sizes of $2\times 2$, $4\times 4$, and $6\times 6\text{pixels}$ using all the 20,000 pixel pairs within feasible time.

A weak binary classifier is considered to be unique according to image patch size ($s\times s$), number of training samples, color space of input images that the underlying LR pixel classifier is trained on, and the threshold for the grayscale LR pixel classification score. We have a total of six image patch sizes ($2\times 2$, $4\times 4$, $6\times 6$, $8\times 8$, $12\times 12$, and $16\times 16$), six possible subset cases (1000, 2000, 4000, 8000, 16000, and 20000 pixel pairs), seven color spaces (RGB, HLS, HSV, CIELab, CIELuv, XYZ, and YCbCr), and 256 (0 to 255) thresholds to define a unique weak binary classifier. As such, there are $\mathrm{64,512}(=6\times 6\times 7\times 256)$ possible weak classifiers.

Out of all possible 64,512 weak binary classifiers, we were able to train 35,840 within reasonable computing time. We generated three ensembles of 35,840 weak binary classifiers for each of the three pixel classifiers. These three ensembles correspond to cavity versus noncavity pixel classification, gland versus stroma pixel classification, and lumen edge versus periacinar retraction clefting edge pixel classification.

Logistic regression pixel classifier ensemble combination by boosting

The results of weak classifiers were combined by AdaBoost.⁴¹ Each of the three ensembles was combined using the AdaBoost⁴¹ trained on the corresponding 16,000 pixel pairs sampled from ${\mathrm{Set}}_{\text{AdaBoost}}$ images. The boosted combination result for a pixel is a weighted sum ($H$) of the votes by all the weak classifiers. A positive $H$ indicates a positive sample prediction while a negative $H$ indicates a negative sample prediction.

Our subsequent steps in the segmentation pipeline require the pixel-level classification output as a probability map, i.e., in the interval [0, 1]. We mapped the weighted sum $H$ to [0, 1] using $f(H)=1/1+e^{-H}$. After mapping, the outputs for all three pixel classifiers are within the same interval of [0, 1]. This mapping also allows usage of image processing methods without any extra pixel value scaling operations.

3.3. Periacinar Retraction Clefting Versus Lumen Object Classifier

The manual annotations define periacinar retraction clefting and lumen objects. The annotated lumen and periacinar retraction clefting objects along with the two pixel classifiers, i.e., gland versus stroma pixel and lumen edge versus periacinar retraction clefting edge, are used to extract the training data for the object classifier.

3.3.1. Training data preparation for periacinar retraction clefting versus lumen object classifier

We used the neighborhood and shape-based information with SVM⁴⁰ for object classification. Vanderbeck et al.⁴² proposed using morphological and textural features along with nuclei density for automated white region (regions that look like cavity objects in our dataset) classification in liver biopsy images. Nguyen et al.²³ also proposed using morphological features for gland classification in histopathological images. We use similar feature extraction methods for our dataset and the periacinar retraction clefting versus lumen object classification problem.

Our object feature extraction process comprises three independent subprocesses. Two of these subprocesses pertain to the object’s neighborhood information while the third one pertains to shape (morphology) information.

We have defined gland versus stroma pixel to differentiate between gland and stroma pixels and lumen edge versus periacinar retraction clefting edge pixel classifier to differentiate between lumen edge and periacinar retraction clefting edge pixels. Both of these pixel classifiers use information in the square patch surrounding a given pixel. We wish to extract an object’s neighborhood information that comprises the distribution of different types of pixels.

Our above two pixel classifiers after training can aid in approximation of an object surrounding the pixels’ distribution information. The gland versus stroma pixel classifier can quantify the distribution of gland and stroma pixels in the neighborhood. The lumen edge versus periacinar retraction clefting edge pixel classifier does a more sophisticated prediction and provides the distribution information about the surrounding pixels if they belong to a lumen edge or periacinar retraction clefting edge. The lumen objects are more likely to be surrounded by gland (predicted) pixels and lumen edge (predicted) pixels. On the other hand, the periacinar retraction clefting objects will most likely be surrounded by stroma (predicted) pixels and periacinar retraction clefting edge (predicted) pixels. Both of the above pixel classifiers’ responses are hence important for quantification of the given object’s neighborhood information. Our two subprocesses (1) and (2) use these two pixel classifiers for extracting the object’s neighborhood information.

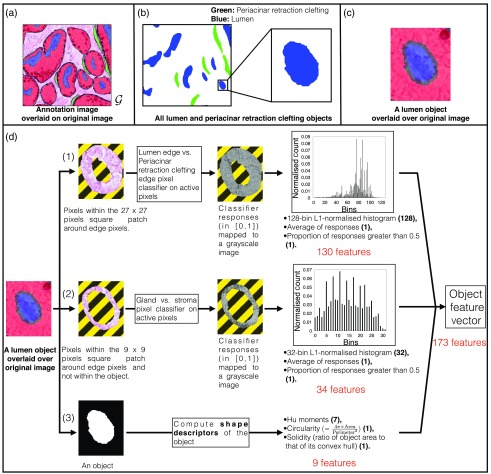
The third subprocess is computation of the given object’s shape descriptors. We illustrate the object feature extraction process in Fig. 3. In panel (d) of this figure, we illustrate the three subprocesses for feature extraction from an annotated lumen object. We marked the subprocess (1) for lumen edge versus periacinar retraction clefting edge classification based-subfeature, (2) for gland versus stroma classification based-subfeature, and (3) for shape descriptor subfeature. In both (1) and (2), a histogram is computed from the classifier responses. These histograms are subsequently $L1$-normalized such that the resultant bin height is a normalized count and the sum of all the bin heights is unity. In panel Fig. 3(d), for both (1) and (2), we first show the pixels that are tested by the corresponding pixel classifier followed by the classifier response and the $L1$-normalized histogram.

Fig. 3.

Object feature extraction from manual annotations. (a) Example of an annotated image $\mathcal{G}$ overlaid over the original image. (b) All annotated lumen and periacinar retraction clefting objects in example image. We also show a zoomed-in image of a lumen object. (c) A lumen object (annotation) is overlaid over the original image. (d) Object feature extraction process (three independent subprocesses). In (1) and (2) subprocesses, lumen edge versus periacinar retraction clefting edge classifier and gland versus stroma classifier are used to test the pixels around the given object. All the inactive pixels (not tested by the pixel classifiers) are shown in a stripe pattern. In (3) subprocess, shape descriptors are computed for the object. The final concatenated object feature vector is of 173 ($=130+34+9$) dimensions. We show the number of dimensions of each computed value by the three subprocesses in parenthesis.

• 1.All the pixels within the $27\times 27\text{pixels}$ patch around any edge pixel are tested by a pretrained lumen edge versus periacinar retraction clefting edge pixel classifier. These classifier responses ($\in [\mathrm{0,1}]$) are binned into a 128-bin $L1$-normalized histogram. The average value of these classifier responses and proportion of responses that are greater than 0.5 are also computed. This generates 130 feature values for the given object.
• 2.All the pixels within the $9\times 9\text{pixels}$ patch around any edge pixel and not within the annotated object are tested by a pretrained gland versus stroma pixel classifier. These classifier responses ($\in [\mathrm{0,1}]$) are binned into a 32-bin $L1$-normalized histogram. If a pixel being tested is within the annotated stroma region, then its response is considered fixed at zero. The average value of these classifier responses and proportion of responses that are greater than 0.5 are also computed. This generates 34 feature values for the given object.
• 3.We compute the object shape descriptors, i.e., Hu moments (seven-dimensional),⁴³ solidity (ratio of the object area to that of its convex hull), and circularity ($=4\pi \times \text{Area}/{\text{Perimeter}}^2$). This generates nine feature values for the given object.

The subfeatures from (1), (2), and (3) are concatenated to create a 173 ($=130+34+9$)-dimensional object feature vector. For both (1) and (2), various values of square patch size and number of histogram bins were tried, and the combination with the best object classification performance was chosen for the final system. All the periacinar retraction clefting and lumen objects except the ones being cut at the border of the images were used to train the periacinar retraction clefting versus lumen object classifier.

3.3.2. Training of periacinar retraction clefting versus lumen object classifier

We used the lumen and periacinar retraction clefting objects in all the images of ${\mathrm{Set}}_{\text{weak}}$ and ${\mathrm{Set}}_{\text{AdaBoost}}$ to train our object classifier and ensure usage of the same images for training both object and pixel classifiers. Both Nguyen et al.²³ and Vanderbeck et al.,⁴² along with proposing morphological features for object classification as discussed, also proposed using a SVM⁴⁰ classifier. They finalized SVM⁴⁰ for classification after comparing various classification methods, such as naive Bayes classifier, LR, decision trees, neural networks, etc., and using various subset of features. For our gland classification system, an object classifier SVM⁴⁰ with radial basis function kernel, $C=512$, and $\gamma =0.0195312$ (found using cross-validation) was trained on the 173-dimensional feature space. The object classifier was trained on 810 lumina, 451 periacinar retraction clefting objects in the first fold, 553 lumina, and 222 periacinar retraction clefting objects in the second fold.

3.4. Testing of the Trained Pixel and Object Classifiers and Subsequent Usage of Image Processing Methods to Compute Final Segmentation from Their Predictions

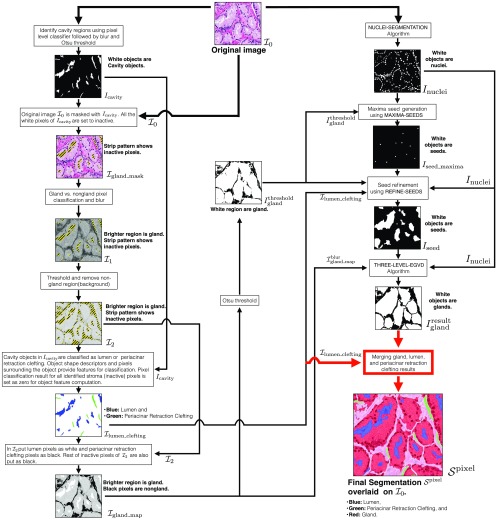
Once we have trained the pixel and object classifiers, we can use them on the input test image for identifying various regions. This testing provides a rough estimate for various regions. These estimates are refined and improved upon by the image processing methods discussed in the following sections. We illustrate the complete segmentation process in Fig. 4. The input image is denoted by ${\mathcal{I}}_0$, and the subsequent images in the pipeline are denoted by an “$I$” (for binary images) and “$\mathcal{I}$” (for nonbinary images) symbol with a subscript format. Binary images are single-channel monochrome images, while nonbinary images are single-channel grayscale or three-channel RGB images.

Fig. 4.

Complete work flow for segmenting an image into gland, lumen, periacinar retraction clefting, and stroma regions. Input image is ${\mathcal{I}}_0$, and final segmentation is ${\mathcal{S}}^{\text{pixel}}$.

We used some of the basic image processing methods, including Gaussian blur, median blur, image thresholding, erosion, and dilation, in our segmentation pipeline. We use Gaussian blur to reduce noise in grayscale images. We used median blur along with erosion and dilation to reduce noise in binary images. A dilation operation was also used to enlarge small objects in our images as part of various algorithms discussed later in this section. For both Gaussian blur and median blur, we fixed the kernel size at $5\times 5\text{pixels}$. Image thresholding methods, including Otsu,⁴⁴ moments preserving,⁴⁵ percentile,⁴⁶ maxentropy,⁴⁷ and Shanbhag⁴⁸ methods, were implemented. These image thresholding methods were used to generate binary images from the grayscale images in the segmentation pipeline. We tried various combinations of thresholding methods and Gaussian kernels with different values of $\sigma$ at various stages of the pipeline. The configuration with the best performance was chosen for the final system.

3.4.1. Image processing methods to compute final segmentations using pixel and object classifiers’ prediction

Given the input test image ${\mathcal{I}}_0$, all the pixels in the image are tested by a cavity versus noncavity pixel classifier. The pixel-wise classification score is within the interval [0, 1], and this is linearly mapped to [0, 255] to create a grayscale prediction image. This prediction image is blurred by a Gaussian kernel of $\sigma =10$ and thresholded by Otsu’s method⁴⁴ to separate the cavity and noncavity regions. The resultant binary mask $I_{\text{cavity}}$ indicates cavity regions in white on black noncavity regions (see Fig. 4). The Gaussian blur reduces noise in the prediction (cavity versus noncavity) image and prevents various false positive (FP) (small) cavity objects in $I_{\text{cavity}}$.

The original image ${\mathcal{I}}_0$ is masked by $I_{\text{cavity}}$. All the white pixels of $I_{\text{cavity}}$ are set inactive to create ${\mathcal{I}}_{\text{gland}\_\text{mask}}$. The remaining active pixels in the image are tested by the gland versus stroma pixel classifier. These predictions are also mapped into a grayscale prediction image. This prediction image is blurred by a Gaussian kernel of $\sigma =2$ to create ${\mathcal{I}}_1$ (see Fig. 4). In ${\mathcal{I}}_1$, the brighter grayscale regions indicate glands, while darker grayscale regions indicate stroma with inactive pixels being indicated by a stripe pattern. During the method development, we found that a slight amount of Gaussian blur with $\sigma =2$ was needed to enhance the gland boundaries in the prediction image and to compute ${\mathcal{I}}_1$. ${\mathcal{I}}_1$ is then thresholded by a moment preserving method⁴⁵ to separate the gland and stroma regions.

The grayscale values of ${\mathcal{I}}_1$ in the identified gland regions are copied over to another image ${\mathcal{I}}_2$. In ${\mathcal{I}}_2$, all stroma, periacinar retraction clefting/lumen regions are inactive with their pixel intensity set at zero. We indicate these inactive regions by a stripe pattern and the remaining active pixels by a grayscale value (see Fig. 4).

The binary mask $I_{\text{cavity}}$ contains all the detected cavity objects. ${\mathcal{I}}_2$ contains the neighborhood information of these cavity objects. Object shape information from $I_{\text{cavity}}$ and neighborhood information from ${\mathcal{I}}_2$ are used for the classification of cavity objects as either lumen or periacinar retraction clefting. The object classification result is stored in ${\mathcal{I}}_{\text{lumen}\_\text{clefting}}$ (see Fig. 4), where lumen and periacinar retraction clefting objects are indicated in blue and green, respectively, on a white background.

We augment ${\mathcal{I}}_2$ by putting all identified lumen pixels as white (255) and all identified periacinar retraction clefting /stroma pixels as black (0). The resultant image is ${\mathcal{I}}_{\text{gland}\_\text{map}}$ (see Fig. 4). This grayscale gland probability map is a rough estimate of glandular regions as the gland boundaries of nearby/touching glands may not be prominent. ${\mathcal{I}}_{\text{gland}\_\text{map}}$ is thresholded by Otsu’s method⁴⁴ to compute $I_{\text{gland}}^{\text{threshold}}$, indicating gland regions in white on a black background (see Fig. 4).

So far, we have identified gland, lumen, stroma, and periacinar retraction clefting regions. The next step is to further segment the gland regions into unique gland objects. The gland regions at this stage in the segmentation pipeline have many merged gland objects (as indicated by $I_{\text{gland}}^{\text{threshold}}$ in Fig. 4). The epithelial nuclei generally line the glandular boundary; hence, once identified, they can aid in estimating gland boundaries. We use a seed-based segmentation algorithm to find the unique gland objects in ${\mathcal{I}}_{\text{gland}\_\text{map}}$. These algorithms use the seed locations as initial objects. These initial objects are grown pixel wise into glands with each seed defining only one gland. Optimal positions for the seed for an object are generally inside its central region. Lumen objects being in this region are hence a natural choice for seeds. There are some glands sections with no visible lumen inside them. Nuclei being at the gland border can aid in finding a seed for these types of glands. There are also glands with discontiguous lumina. These lumen objects need to be merged into one seed to avoid oversegmentation. We use the nuclei objects’ and lumen objects’ spatial distribution to find unique seeds for glands with discontiguous lumina. We first discuss the nuclei object segmentation using H&E stain information.

Stain separation for identification of nuclei objects

Nuclei are stained in blue by the hematoxylin stain in the H&E (RGB) image. This H&E image is separated into hematoxylin (blue) and eosin (pink) channels using ImageJ plugin implementation of Ruifrok et al.⁴⁹ The separated channels of eosin and hematoxylin are in grayscale, indicating the respective channel’s color intensity distribution. The hematoxylin grayscale image is denoised using Gaussian blur, thresholding, and median blur operations. The final binary mask $I_{\mathrm{nuclei}}$ (see Fig. 4) indicates nuclei regions in white on a black background. The NUCLEI-SEGMENTATION algorithm shows this process in detail (Algorithm 1).

Algorithm 1.

Nuclei segmentation algorithm (NUCLEI-SEGMENTATION).

Input:

- ${\mathcal{I}}_0$ is the original H&E image.

Output:

- $I_{\mathrm{nuclei}}$ is the binary nuclei mask. White regions are nuclei on a black background.

Function and variable description:

- BLUR($\mathcal{I},{\sigma }_s$) is the Gaussian blur function with kernel with $\sigma ={\sigma }_s$. Output is a grayscale image.

- Stain separation method is described by Ruifrok et al.49

- MOMENTS-THRESHOLD($\mathcal{I}$) thresholds $\mathcal{I}$ using the moments preserving image thresholding method.45 Output is a binary image.

- Median filter (blur) replaces each pixel intensity by the median of all the pixel intensities in its kernel neighborhood.

Parameters:

- Select Gaussian kernel with $\sigma =3$ for the blur operation. This value for sigma was optimized empirically.

1:  Procedure NUCLEI-SEGMENTATION(${\mathcal{I}}_0$)

2:   Separate the haemotoxylin and eosin channels of ${\mathcal{I}}_0$ into ${\mathcal{I}}_{\mathrm{Hematoxylin}}$ and ${\mathcal{I}}_{\mathrm{Eosin}}$.       ⊳ Both ${\mathcal{I}}_{\text{Hematoxylin}}$ and ${\mathcal{I}}_{\mathrm{Eosin}}$ are grayscale images.

3:   ${\mathcal{I}}_{\text{Hematoxylin}}^{\text{blur}}=\mathrm{BLUR}({\mathcal{I}}_{\text{Hematoxylin}},3)$.

4:   $I_{\text{Hematoxylin}}^{\text{threshold}}=\mathrm{MOMENTS}-\mathrm{THRESHOLD}({\mathcal{I}}_{\text{Hematoxylin}})$.

5:   Remove noise in $I_{\text{Hematoxylin}}^{\text{threshold}}$ to compute $I_{\mathrm{nuclei}}$ by median blur.

6:   return nuclei mask $I_{\mathrm{nuclei}}$.

7: end procedure

Seed generation for glands with no visible lumen using nuclei objects

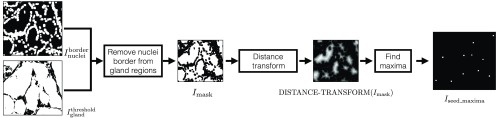
The thresholded gland probability map $I_{\text{gland}}^{\text{threshold}}$ and $I_{\mathrm{nuclei}}$ are used to find the seeds for the gland with no visible lumen inside them. We illustrate this process in Fig. 5. The nuclei mask $I_{\mathrm{nuclei}}$ is dilated 8 times using a $3\times 3\text{pixel}$ dilation window to compute $I_{\mathrm{nuclei}}^{\text{border}}$. The nuclei border image $I_{\mathrm{nuclei}}^{\text{border}}$ is subtracted from $I_{\mathrm{gland}}^{\text{threshold}}$ to extract nonnuclei gland regions and compute $I_{\text{mask}}$ (see Fig. 5). A Euclidean distance map is computed for $I_{\text{mask}}$, and ImageJ’s “Find Maxima” function is used for finding intensity (distance) peaks in this distance map. These peaks approximate the centroids of the glands and hence can be used as seeds for these glands. The MAXIMA-SEEDS (Algorithm 2) algorithm shows this process in detail, and its output is $I_{\text{seed}\_\text{maxima}}$ (see Fig. 5, also shown in Fig. 4). We identify the seeds in $I_{\text{seed}\_\text{maxima}}$ as maxima seeds.

Fig. 5.

Seed generation for glands without any visible lumen by MAXIMA-SEEDS (Algorithm 2).

Algorithm 2.

Maxima-seeds generation algorithm (MAXIMA-SEEDS).

Input:

- $I_{\text{gland}}^{\text{threshold}}$ is the binary gland mask. White regions are glands on a black background.

- $I_{\mathrm{nuclei}}$ is the binary nuclei-border mask. White regions are nuclei borders on a black background.

Output:

- $I_{\text{seed}\_\text{maxima}}$ is the binary maxima-seed mask. White regions are centroid locations of the gland objects.

Function and variable description:

- DILATE($I,d$) conducts “$d$” dilation operations on binary image $I$ with a $3\times 3$ pixels dilation window. Output image is also binary.

- DISTANCE-TRANSFORM($I$) computes the Euclidean distance map of image $I$. Output image is grayscale.

- FIND-MAXIMA($\mathcal{I}$) computes the local intensity maxima pixels in the $\mathcal{I}$. Output is a binary image indicating the maxima pixels in white.

- Given a binary image $I$, $\overline{I}$ is a binary image with corresponding inverted pixel values.

- $I_a\wedge I_b$ is a Boolean operation defining pixel-wise AND operation between $I_a$ and $I_b$.

Parameters:

- Select number of dilation operations $d=8$. This value for $d$ was optimized empirically.

1:  Procedure MAXIMA-SEEDS ($I_{\text{gland}}^{\text{threshold}}$, $I_{\mathrm{nuclei}}$)

2:   $I_{\mathrm{nuclei}}^{\text{border}}=\text{DILATE}(I_{\mathrm{nuclei}},8)$.

3:   $I_{\text{mask}}=I_{\text{gland}}^{\text{threshold}}\wedge \overline{I_{\mathrm{nuclei}}^{\text{border}}}$.    ⊳ Remove nuclei borders from gland regions.

4:   $I_{\text{seed}\_\text{maxima}}=\mathrm{FIND}-\mathrm{MAXIMA}(\mathrm{DISTANCE}-\mathrm{TRANSFORM}[I_{\text{mask}})]$.    ⊳ Find the centers of the glandular objects.

5:   return maxima-seed mask $I_{\text{seed}\_\text{maxima}}$.

6: end procedure

Seed generation for glands with discontiguous lumina using nuclei and lumen objects

The maxima seeds in $I_{\text{seed}\_\text{maxima}}$ and lumen objects in ${\mathcal{I}}_{\text{lumen}\_\text{clefting}}$ provide different sets of seeds for segmentation. After incorporating both maxima seeds and lumen, some gland objects may have multiple potential seeds inside them. These potential seeds need to be merged into one unique seed to avoid oversegmentation.

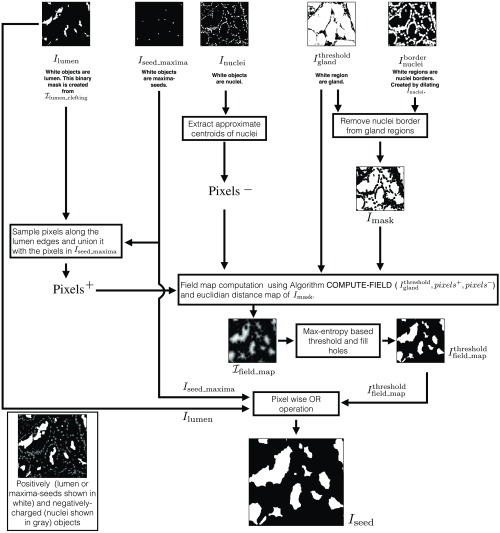
We use an electric potential field-based approach for refining the gland seeds. We developed REFINE-SEEDS (Algorithm 3) for this task, illustrated in Fig. 6. REFINE-SEEDS algorithm treats lumen and maxima seeds as positively charged objects and the nuclei as negatively charged objects. We defined COMPUTE-FIELD algorithm (Algorithm 4) to compute the electric potential field distribution in an image according to the charge distribution. All lumen and maxima seeds inside a gland will be in a region with high magnitude of potential field due to their positive charge. Given the field image according to a given charge distribution, it can be thresholded to identify regions with high magnitude of field. The lumen objects and maxima seeds, which are inside one gland, will be inside one of the high-field magnitude regions. This identified region can act as a single unique seed for the corresponding gland and hence help prevent oversegmentation.

Algorithm 3.

Seed-refining algorithm (REFINE-SEEDS).

Inputs:

- $I_{\text{gland}}^{\text{threshold}}$ is the binary gland mask. White regions are glands on a black background.

- $I_{\mathrm{nuclei}}$ is binary the nuclei mask. White regions are nuclei on a black background.

- $I_{\text{seed}\_\text{maxima}}$ is the binary maxima-seed mask. White regions are centroid locations of the gland objects.

- ${\mathcal{I}}_{\text{lumen}\_\text{clefting}}$ is the lumen-clefting RGB image. Blue objects are lumen and green objects are periacinar retraction clefting on a white background.

Output:

- $I_{\text{seed}}$ is the binary seed mask. White regions are seed objects on a black background.

Function and variable description:

- PIXEL-IN($I$) returns all the white pixels in the binary image $I$. DILATE($I,d$) and DISTANCE-TRANSFORM($I$) are the same functions as defined in Algorithm 2.

- Given a binary image $I$, $\overline{I}$ defines a binary image with corresponding inverted pixel values. $I_a\wedge I_b$ and $I_a\vee I_b$ are the Boolean operations defining pixel-wise AND and OR operations between $I_a$ and $I_b$, respectively.

- ${\text{pixels}}^{+}$ and ${\text{pixels}}^{-}$ are two sets containing positive and negative charged particles (pixels).

- MAX-ENTROPY-THRESHOLD($\mathcal{I}$) thresholds $\mathcal{I}$ using the entropy-based image thresholding method.47 Output is a binary image.

Parameters:

- Select number of dilation operations $d=8$. This value for $d$ was optimized empirically.

1:  Procedure REFINE-SEEDS ($I_{\text{gland}}^{\text{threshold}}$, $I_{\mathrm{nuclei}}$, $I_{\text{seed}\_\text{maxima}}$, $I_{\text{lumen}\_\text{clefting}}$)

2:   $I_{\mathrm{nuclei}}^{\text{border}}=\mathrm{DILATE}(I_{\mathrm{nuclei}},8)$.

3:   Create binary lumen mask $I_{\text{lumen}}$ from ${\mathcal{I}}_{\text{lumen}\_\text{clefting}}$.    ⊳ $I_{\text{lumen}}$ indicate lumen in white.

4:   Sample some pixels along the edges of lumen objects ($I_{\text{lumen}}$) into ${\text{pixels}}^{+}$.

5:   ${\text{pixels}}^{+}={\text{pixels}}^{+}\cup \mathrm{PIXELS}-\mathrm{IN}(I_{\text{seed}\_\text{maxima}})$.    ⊳ All the maxima seeds are added to ${\text{pixels}}^{+}$.

6:   Extract approximate centroids of nuclei in $I_{\mathrm{nuclei}}$ into ${\text{pixels}}^{-}$.    ⊳ Remove nuclei from the gland regions.

7:   $I_{\mathrm{mask}}=I_{\mathrm{gland}}^{\mathrm{threshold}}\wedge \overline{I_{\mathrm{nuclei}}^{\mathrm{border}}}$.

8:   ${\mathcal{I}}_{\mathrm{field}}=\mathbf{COMPUTE}\mathbf{-}\mathbf{FIELD}(I_{\mathrm{gland}}^{\mathrm{threshold}},{\text{pixels}}^{+},{\text{pixels}}^{-})$.

9:   ${\mathcal{I}}_{\mathrm{field}\_\mathrm{map}}={\mathcal{I}}_{\mathrm{field}}\times \mathrm{DISTANCE}-\mathrm{TRANSFORM}(I_{\mathrm{mask}})$.    ⊳ Pixel-wise multiplication of two real valued images.

10:   Linearly rescale ${\mathcal{I}}_{\text{field}\_\text{map}}$ to values within [0, 255] for further numerical operations.

11:   $I_{\text{field}\_\text{map}}^{\text{thershold}}=\mathrm{MAX}-\text{ENTROPY}-\text{THRESHOLD}({\mathcal{I}}_{\text{field}\_\text{map}})$.

12:   Fill holes in $I_{\text{field}\_\text{map}}^{\text{threshold}}$ image.

13:   $I_{\text{seed}}=I_{\text{seed}\_\text{maxima}}\vee (I_{\text{field}\_\text{map}}^{\text{threshold}}\vee I_{\text{lumen}})$.    ⊳ Unify all the seeds.

14:   return seed mask $I_{\mathrm{seed}}$.

15: end procedure

Fig. 6.

Seed refinement using REFINE-SEEDS (Algorithm 3). The distribution of positively and negatively charged objects is shown in black box. Nuclei constitute negatively charged particles. Lumen and maxima seeds constitute positively charged objects.

Algorithm 4.

Field computation algorithm (COMPUTE-FIELD).

Inputs:

- $I_{\text{gland}}^{\text{threshold}}$ is the binary gland mask. White regions are glands on a black background. Field is computed inside gland regions only.

- ${\text{pixels}}^{+}$ is a set of pixels with an assigned positive charge.

- ${\text{pixels}}^{-}$ is a set of pixels with an assigned negative charge.

Output:

- ${\mathcal{I}}_{\text{field}}$ is the grayscale field image. Pixel intensity is directly proportional to field magnitude at its location. Pixel intensities are within [0, 255].

Parameters:

- Define +ve and −ve charges as $+1$ and $-1$, respectively. Set decay rate for +ve and −ve charges as 1.0 and 1.6, respectively. These charge values and decay rates were optimized empirically.

1:  Procedure COMPUTE-FIELD($I_{\text{gland}}^{\text{threshold}}$, ${\text{pixels}}^{+}$, ${\text{pixels}}^{-}$)

2:   Initialize all pixels in ${\mathcal{I}}_{\text{field}}$ to zero.

3:   for All pixels $(x,y)\in I_{\text{gland}}^{\text{threshold}}$do

4:   ${\mathcal{I}}_{\text{field}}(x,y)=\sum _{(x_j,y_j)\in {\text{pixels}}^{+}}\frac{(1.0)}{{[{(x-x_j)}^2+{(y-y_j)}^2]}^{\frac{1}{2}}}+\sum _{(x_k,y_k)\in {\text{pixels}}^{-}}\frac{(-1.0)}{{[{(x-x_k)}^2+{(y-y_k)}^2]}^{\frac{1.6}{2}}}$.

5:   end for

6:   Linearly rescale ${\mathcal{I}}_{\text{field}}$ to values within [0, 255] for further numerical operations.

7:   return field image ${\mathcal{I}}_{\mathrm{field}}$.

8: end procedure

Instead of using all pixels inside nuclei, lumen, or maxima seeds, we sample some pixels for computing electric potential field image, ${\mathcal{I}}_{\text{field}}$, thereby saving computational time. In REFINE-SEEDS (Algorithm 3), we first sample the set of positive pixels “${\text{pixels}}^{+}$” from the lumen edges and union it with the maxima seeds pixels. We extract approximate centroids of nuclei objects to compute the set of negative pixels, “${\text{pixels}}^{-}$”. COMPUTE-FIELD algorithm (Algorithm 4) uses the pixel sets ${\text{pixels}}^{+}$, ${\text{pixels}}^{-}$, and the binary gland mask $I_{\text{gland}}^{\text{threshold}}$ to compute the image’s electric potential field image ${\mathcal{I}}_{\text{field}}$. Electric potential field for nongland regions is not computed.

We define a binary mask $I_{\text{mask}}$ that indicates the nonnuclei-border glandular regions. The Euclidean distance map of $I_{\text{mask}}$ will have low pixel values around the nuclei regions compared with high pixel values in the central region of the glands. Field map image ${\mathcal{I}}_{\text{field}\_\text{map}}$ is computed by pixel-wise multiplication of ${\mathcal{I}}_{\text{field}}$ and the Euclidean distance map of $I_{\text{mask}}$. It will have low pixel values around the nuclei regions and high pixel values in the central region of the glands. The multiplication operation enhances the electric field distribution image from ${\mathcal{I}}_{\text{field}}$ to ${\mathcal{I}}_{\text{field}\_\text{map}}$. The high electric potential field regions are identified by thresholding ${\mathcal{I}}_{\text{field}\_\text{map}}$ using Maxentropy image thresholding method.⁴⁷ All the seeds from thresholded field image ${\mathcal{I}}_{\text{field}\_\text{map}}^{\text{threshold}}$, lumen object image $I_{\text{lumen}}$, and maxima-seed image $I_{\text{seed}\_\text{maxima}}$ are unified by a pixel-wise OR operation to compute $I_{\text{seed}}$ (see Figs. 4 and 6).

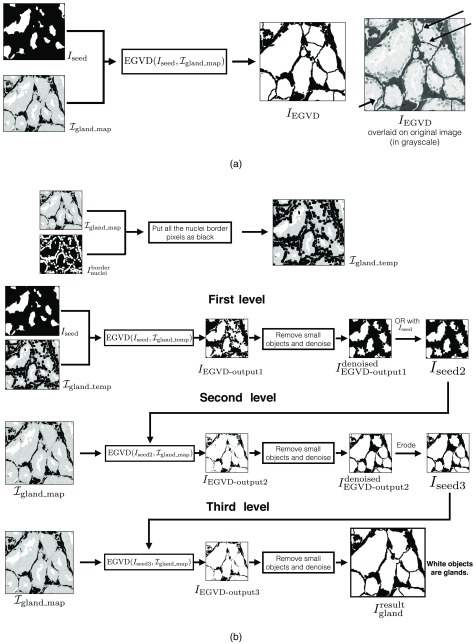
Evolving generalized Voronoi diagram-based binary gland segmentation

We use the evolving generalized Voronoi diagram (EGVD)-based segmentation method to define gland boundaries of touching or nearby glands in ${\mathcal{I}}_{\text{gland}\_\text{map}}$. The EGVD-based binary segmentation uses a seed (binary) image and a grayscale image. The grayscale image defines background regions in black and foreground (gland) regions by a grayscale value. The output binary segmentation is created by growing all the seed objects defined in the seed image until they touch each other or meet the background region as defined in the input grayscale image.⁵⁰

We show an example of EGVD output image $I_{\mathrm{EGVD}}$ when we use seed image $I_{\text{seed}}$ and grayscale image ${\mathcal{I}}_{\text{gland}\_\mathrm{map}}$ in Fig. 7(a). For a good gland segmentation result, the seed growing should stop at the gland boundaries lined by epithelial nuclei. The output glands should also not have their boundary defined within cytoplasm. The seed growing iterations in EGVD treat both cytoplasm and nuclei regions in the foreground equally. The black arrows on $I_{\mathrm{EGVD}}$ in Fig. 7(a) show the gland boundaries being defined in cytoplasm. We also observe that some of the seeds in $I_{\text{seed}}$ are extraneous and do not belong to any gland object. The bottom-left black arrow indicates the segmented gland that has been grown across nuclei and hence leads its boundary to be defined in cytoplasm. It also indicates one of the glands grown from the extraneous seed.

Fig. 7.

(a) Example of EGVD output with $I_{\text{seed}}$ and ${\mathcal{I}}_{\text{gland}\_\text{map}}$ as inputs. Top-right black arrows indicate gland boundaries being predicted within the cytoplasm. Bottom-left black arrow indicates one of the glands that was grown from extraneous seed. (b) Complete workflow for the THREE-LEVEL-EGVD algorithm (Algorithm 5).

We developed a THREE-LEVEL-EGVD method (Algorithm 5) to solve the issues of extraneous seeds and gland boundaries being predicted within cytoplasm. We illustrate the method in Fig. 7(b). We first put all nuclei border pixels indicated by $I_{\mathrm{nuclei}}^{\text{border}}$ in ${\mathcal{I}}_{\text{gland}\_\text{map}}$ as black to compute ${\mathcal{I}}_{\text{gland}\_\text{temp}}$. $I_{\text{seed}}$ is used as the seed image and ${\mathcal{I}}_{\text{gland}\_\text{temp}}$ as the grayscale image to compute the binary EGVD result, $I_{\mathrm{EGVD}-\text{output}1}$. Nuclei border pixels are put as black in ${\mathcal{I}}_{\text{gland}\_\text{temp}}$ to prevent the gland object from growing across the nuclei by EGVD. As black pixels are defined as background, EGVD will stop growing the seed objects once they touch the nuclei border regions. Hence, the grown seed objects will not cover the nuclei regions. $I_{\mathrm{EGVD}-\text{output}1}$ is cleaned up by removing small gland objects and noise to compute $I_{\mathrm{EGVD}-\text{output}1}^{\text{denoised}}$. A pixel-wise OR operation is done on $I_{\text{seed}}$ and $I_{\mathrm{EGVD}-\text{output}1}^{\text{denoised}}$ to retain all the initial seeds in $I_{\text{seed}}$, for they may have been removed during previous denoising step. The resultant image is $I_{\text{seed}2}$.

Algorithm 5.

Three level EGVD algorithm (THREE-LEVEL-EGVD).

Inputs:

- $I_{\text{seed}}$ is the binary seed mask. White regions are seed objects on a black background.

- ${\mathcal{I}}_{\text{gland}\_\text{map}}$ is the grayscale gland image. Grayscale regions are glands on a black background.

- $I_{\mathrm{nuclei}}$ is the binary nuclei mask. White regions are nuclei on a black background.

Output:

- $I_{\text{gland}}^{\text{result}}$ is the binary gland mask. White regions depict gland on a black background.

Function and variable description:

- DILATE($I,d$) conducts “$d$” dilation operations on binary image $I$ with a $3\times 3$ pixels dilation window. Output image is also binary.

- EGVD($I_s,{\mathcal{I}}_f$) is the image segmentation algorithm described by Yu et al.50 where $I_s$ is the seed image and ${\mathcal{I}}_f$ is the grayscale image. It returns the binary segmentation result.

- $I_a\vee I_b$ is a Boolean operation defining the pixel-wise OR operation between $I_a$ and $I_b$.

Parameters:

- Select number of dilation operations $d=8$. This value for $d$ was optimized empirically.

1:  Procedure THREE-LEVEL-EGVD($I_{\text{seed}}$, ${\mathcal{I}}_{\text{gland}\_\text{map}}$, $I_{\mathrm{nuclei}}$)

2:    $I_{\mathrm{nuclei}}^{\text{border}}=\mathrm{DILATE}(I_{\mathrm{nuclei}},8)$.    ⊳ $I_{\mathrm{nuclei}}^{\text{border}}$ indicates nuclei border pixels in white.

3:    Put all white pixels indicated by $I_{\mathrm{nuclei}}^{\text{border}}$ in ${\mathcal{I}}_{\text{gland}\_\text{map}}$ as black to compute ${\mathcal{I}}_{\text{gland}\_\text{temp}}$.

4:    $I_{\mathrm{EGVD}-\mathrm{output}1}=\mathrm{EGVD}(I_{\text{seed}},{\mathcal{I}}_{\text{gland}\_\text{temp}})$.

5:    Remove small objects and noise in $I_{\mathrm{EGVD}-\mathrm{output}1}$ and then save it to $I_{\mathrm{EGVD}-\mathrm{output}1}^{\mathrm{denoised}}$.

6:    $I_{\text{seed}2}=I_{\mathrm{EGVD}-\text{output}1}^{\text{denoised}}\vee I_{\text{seed}}$.

7:    $I_{\mathrm{EGVD}-\text{output}2}=\mathrm{EGVD}(I_{\text{seed}2},{\mathcal{I}}_{\text{gland}\_\text{map}})$.

8:    Remove small objects and noise in $I_{\mathrm{EGVD}-\text{output}2}$ and then save it to $I_{\mathrm{EGVD}-\text{output}2}^{\text{denoised}}$.

9:    Erode $I_{\mathrm{EGVD}-\text{output}2}^{\text{denoised}}$ to compute $I_{\text{seed}3}$.

10:   $I_{\mathrm{EGVD}-\text{output}3}=\mathrm{EGVD}(I_{\text{seed}3},{\mathcal{I}}_{\text{gland}\_\text{map}})$.

11:   Remove small objects and noise in $I_{\mathrm{EGVD}-\text{output}3}$ and then save it to $I_{\mathrm{gland}}^{\mathrm{result}}$.

12:   return binary gland mask $I_{\mathrm{gland}}^{\mathrm{result}}$.

13: end procedure

In the second level of EGVD, $I_{\text{seed}2}$ and ${\mathcal{I}}_{\text{gland}\_\text{map}}$ are used as the seed image and the grayscale image, respectively. The EGVD result is $I_{\mathrm{EGVD}-\text{output}2}$. As illustrated in Fig. 7(b), we can observe that the objects in $I_{\mathrm{EGVD}-\text{output}2}$ cover a major portion of the respective gland regions. The extraneous seeds are generally in the stroma regions near the gland boundaries. The seed growing iterations for these seeds will lead to small gland objects as they touch the background regions or other gland objects earlier than the seeds, which are in the central regions of actual glands. The gland objects generated by extraneous seeds of $I_{\text{seed}2}$ are identified by their relatively smaller size and are removed from $I_{\mathrm{EGVD}-\text{output}2}$. The resultant denoised EGVD output, $I_{\mathrm{EGVD}-\text{output}2}^{\text{denoised}}$, is eroded to compute the seed image for the third level, $I_{\text{seed}3}$.

In the third level of EGVD, $I_{\text{seed}3}$ and ${\mathcal{I}}_{\text{gland}\_\text{map}}$ are used as the seed image and the grayscale image, respectively. The EGVD result is $I_{\mathrm{EGVD}-\text{output}3}$. The seed objects in $I_{\text{seed}3}$ cover a major portion of the respective gland regions. In many cases, the seed objects’ boundaries are next to the corresponding epithelial nuclei. These type of seed objects will lead the seed growing iterations to terminate within the nuclei regions as the neighboring grown seed objects would be touching each other when they grow into the nuclei regions. This step allows THREE-LEVEL-EGVD to define the gland boundaries in the nuclei regions and not in cytoplasm [see $I_{\mathrm{EGVD}-\text{output}3}$ in Fig. 7(b)]. $I_{\mathrm{EGVD}-\text{output}3}$ is then cleaned up similarly as in the previous steps to compute the final result $I_{\text{gland}}^{\text{result}}$.

Merging all detected gland, lumen, and periacinar retraction clefting objects for final segmentation

The binary gland output $I_{\text{gland}}^{\text{result}}$ and object classification result ${\mathcal{I}}_{\text{lumen}\_\text{clefting}}$ are merged to compute the final segmentation result ${\mathcal{S}}^{\text{pixel}}$. We have illustrated the complete segmentation process starting from pixel classifiers testing to the last EGVD-based segmentation step in Fig. 4.

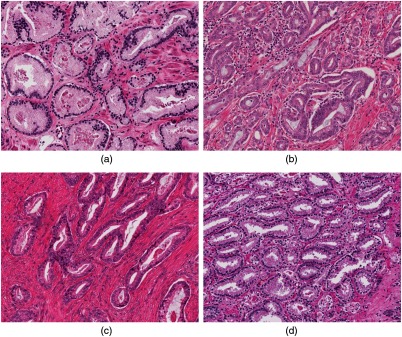
As discussed in this section, the binary nuclei mask, $I_{\mathrm{nuclei}}$, that is computed by NUCLEI-SEGMENTATION (Algorithm 1) is used by algorithms MAXIMA-SEEDS (Algorithm 2), REFINE-SEEDS (Algorithm 3), COMPUTE-FIELD (Algorithm 4), and THREE-LEVEL-EGVD (Algorithm 5) either directly as input or indirectly as ${\text{pixels}}^{-}$. $I_{\mathrm{nuclei}}$ may have noisy segmentation result when the nuclei are crowded and/or have margination of chromatin. The sole purpose of $I_{\mathrm{nuclei}}$ is to provide an approximate location of gland boundaries and approximate location of negatively charged pixels in our gland segmentation pipeline. This pipeline has been developed such that it dilates the $I_{\mathrm{nuclei}}$ to counter noisy nuclei segmentation. Along with number of dilation operations, the value for “−ve” charge and the corresponding decay rate in the COMPUTE-FIELD (Algorithm 4) were also empirically estimated to keep the gland segmentation pipeline robust to noisy nuclei segmentation. Another possible concern in our gland segmentation pipeline is how the color variations of a given image will affect the final result. We have used the images from 10 patients in TCGA dataset. These images were extracted such that they had color variations. Our pixel classifier training sets were sampled randomly from different patient images to ensure heterogeneity. We show four images from our dataset depicting four color variations in Fig. 8. We have also defined the usage of Ruifrok et al.⁴⁹ in conjunction with tunable blur and threshold operations in NUCLEI-SEGMENTATION (Algorithm 1) to reduce the effect of color variations. The empirical estimation of various parameters in our segmentation pipeline was also done for robust performance.

Fig. 8.

(a)–(d) Four images from our dataset illustrating different color variations. Our gland segmentation pipeline was developed using 43 images with different color variations for robust and generalizable performance.

4. Experiments and Results

4.1. Dataset and Experiments

H&E-stained images of the PCa were used to demonstrate the effectiveness of our method. This dataset consisted of 43 images extracted from 10 patients’ tissue whole slide images. These whole slide images were hosted by TCGA. We did a twofold cross-validation study of our gland segmentation system. We trained and tested our system as discussed in Sec. 3. We have compared our segmentation method with base-line methods as discussed by Farjam et al.,¹⁶ Naik et al.,¹⁷ and Nguyen et al.²³ We implemented these methods and tuned the parameters to maximize their segmentation performance. We evaluated all the gland segmentation methods’ results according to our manual annotations. As discussed in Sec. 3.1.1, we annotated almost touching nearby glands according to their discernible boundaries. This lead to a design where we have not tried to incorporate any ambiguity with respect to boundaries between different glands.

4.1.1. Evaluation of image segmentation

We evaluate the segmentation performance using pixel-wise metrics, such as precision, recall, accuracy, $F$-score, and omega index (OI),⁵¹ and object-wise metrics, such as Jaccard index (JI), Dice index (DI), and Hausdorff distance (HD). We do image-wise comparison of the segmentation results. We denote a manual annotation image by $\mathcal{G}$ and a corresponding segmented image generated using method “$t$” by ${\mathcal{S}}^t$.

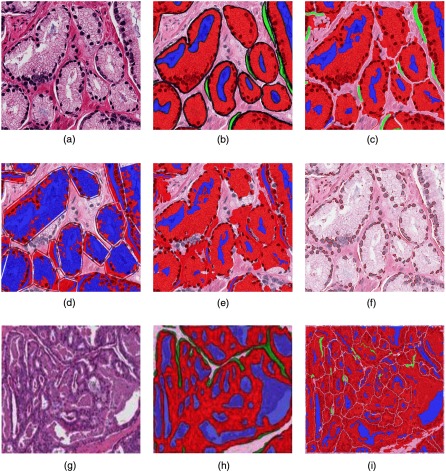
We show an example H&E image ${\mathcal{I}}_0$, corresponding annotation $\mathcal{G}$, and various segmentation results ${\mathcal{S}}^t$ in Figs. 9(a)–9(f). Our method as shown in ${\mathcal{S}}^{\text{pixel}}$ correctly identifies major portions of various gland objects defined in $\mathcal{G}$. It is also able to segment glands with no visible lumen inside them and glands with discontiguous lumina inside them. The result image ${\mathcal{S}}^{\mathrm{Nguyen}}$ for Nguyen et al.²³ has many segmented lumen objects that are much larger than the actual lumen objects. This method was able to estimate the gland boundaries at the epithelial nuclei. The result image ${\mathcal{S}}^{\mathrm{Naik}}$ for Naik et al.¹⁷ shows many nearby glands being merged into one. This method also estimated the gland boundaries at the epithelial nuclei. The result image ${\mathcal{S}}^{\mathrm{Farjam}}$ for Farjam et al.¹⁶ shows that only the nuclei regions were identified as gland objects. This method predicted all the other regions as stroma.

Fig. 9.

We compare various methods in (a)–(f). (a) Original H&E image ${\mathcal{I}}_0$, (b) annotation image $\mathcal{G}$, (c) image ${\mathcal{S}}^{\text{pixel}}$ by our method, (d) image ${\mathcal{S}}^{\mathrm{Nguyen}}$ by Nguyen et al.,²³ (e) image ${\mathcal{S}}^{\mathrm{Naik}}$ by Naik et al.,¹⁷ and (f) image ${\mathcal{S}}^{\mathrm{Farjam}}$ by Farjam et al.¹⁶ We also illustrate a failure case for our method in (g)–(i). (g) Another input H&E image, (h) corresponding annotation image, overlaid on image in (g), and (i) our result ${\mathcal{S}}^{\text{pixel}}$. All the annotation/segmented images are shown overlaid on the corresponding original image ${\mathcal{I}}_0$ and red: gland, blue: lumen, green: periacinar retraction clefting, and white: stroma.

Pixel-wise metrics

For each type of classification of gland, lumen, or periacinar retraction clefting, we can compute true positive (TP), FP, true negative (TN), and false negative (FN) pixels predictions. We can then report precision, recall, $F$-score, and accuracy using TP, FP, FN, and TN values. Higher values of these metrics indicate better performance of a given segmentation method.

The current image segmentation problem can also be viewed as a clustering problem where we want to cluster the pixels into gland, lumen, clefting, or stroma pixels. We can quantify the agreement between $\mathcal{G}$ and ${\mathcal{S}}^t$ by OI, which indicates the ratio of how many pairs of pixels out of all the pixels were put in the same cluster by both $\mathcal{G}$ and ${\mathcal{S}}^t$. Given $L$ pixels in image $\mathcal{G}$, OI is computed by going through all the corresponding ${}^L{C}_2$ pixel pairs. It is computationally infeasible to calculate OI from all the pixels in our dataset as each image has at least a million pixels. Hence, we approximated OI using a subset of pixels in the images. While sampling pixels, we ensure that we sample the same number of pixels from each pixel type for unbiased estimation. The number of sampled pixels in image $\mathcal{G}$ is constrained by the smallest total area spanned by a single pixel type. If the smallest number of pixels of one type in an image is $l_p$, then we can only sample $l_p$ pixels from each of the four types in this image. The maximum possible value of $l_p$ was chosen as 2217 by going through all the images in the dataset. This was done to ensure OI computation is done using the same number of pixel pairs. We sampled 2217 pixels in each of the four pixel types, namely, gland, lumen, periacinar retraction clefting, and stroma, and then approximated OI by going through ${}^{8868}{C}_2$ pixel pairs.

Object-wise metrics

We define three types of objects in our segmentations, namely, gland, lumen, and periacinar retraction clefting. We first find all the gland objects in $\mathcal{G}$ and ${\mathcal{S}}^t$. All the gland objects in $\mathcal{G}$ are identified as $G_1,G_2,\dots ,G_i,\dots ,G_m$. We put these objects in $O_{\mathcal{G}}$ such that $G_i\in O_{\mathcal{G}}$. Similarly, all the gland objects in ${\mathcal{S}}^t$ are identified as $S_1^t,S_2^t,\dots ,S_j^t,\dots ,S_k^t$. We put these objects in $O_{{\mathcal{S}}^t}$ such that $S_j\in O_{{\mathcal{S}}^t}$. All the objects $G_i$ are matched to an object $M_i\equiv S_j^t$ (say) using the Gale–Shapley algorithm.⁵² The set of all matched objects is $M$, i.e., $(G_i,M_i)\in M$. We compute the object-wise JI, DI, and HD as

$$\mathrm{JI}(G_i,M_i)=\frac{|G_i\cap M_i|}{|G_i\cup M_i|},$$ (1)

$$\mathrm{DI}(G_i,M_i)=\frac{2|G_i\cap M_i|}{|G_i|+|M_i|},$$ (2)

$$\mathrm{HD}(G_i,M_i)=\max \{\underset{x\in G_i}{\sup }\underset{y\in M_i}{\inf }\Vert x-y\Vert ,\underset{y\in M_i}{\sup }\underset{x\in G_i}{\inf }\Vert x-y\Vert \},$$ (3)

where $|·|$ denotes the number of pixels of a given object. Both JI and DI evaluate the overlap of two matched objects while HD evaluates the shape similarity between them. Higher values of HD indicate large deviations of shape between the two objects. For evaluating any segmentation algorithm’s result ${\mathcal{S}}^t$ at the object level, we need to evaluate

• i.how well the segmented objects in $O_{{\mathcal{S}}^t}$ overlap the objects in $O_{\mathcal{G}}$ and
• ii.how well the ground truth objects in $O_{\mathcal{G}}$ overlap the objects in $O_{{\mathcal{S}}^t}$.

We compute weighted averages of JI, DI, and HD for a given image as follows:

$${\mathrm{JI}}_{\text{weighted}}(O_{\mathcal{G}},O_{{\mathcal{S}}^t})=\frac{1}{2}[\sum _{j=1}^k{w}_j\mathrm{JI}(G_j,S_j^t)+\sum _{i=1}^m{w}_i^{\prime }\mathrm{JI}(G_i,M_i)],$$ (4)

$${\mathrm{DI}}_{\text{weighted}}(O_{\mathcal{G}},O_{{\mathcal{S}}^t})=\frac{1}{2}[\sum _{j=1}^k{w}_j\mathrm{DI}(G_j,S_j^t)+\sum _{i=1}^m{w}_i^{\prime }\mathrm{DI}(G_i,M_i)],$$ (5)

$${\mathrm{HD}}_{\text{weighted}}(O_{\mathcal{G}},O_{{\mathcal{S}}^t})=\frac{1}{2}[\sum _{j=1}^k{w}_j\mathrm{HD}(G_j,S_j^t)+\sum _{i=1}^m{w}_i^{\prime }\mathrm{HD}(G_i,M_i)],$$ (6)

where $w_j=\frac{|S_j^t|}{\sum _j^k|S_j^t|}$ and $w_i^{\prime }=\frac{|G_i|}{\sum _i^m|G_i|}$. The first and second term in the above equations take care of the evaluation criterions (i) and (ii), respectively, as discussed above. These object-level metrics were derived from the ones discussed by Sirinukunwattana et al.²⁹ Better segmentation algorithms will have higher values of ${\mathrm{JI}}_{\text{weighted}}$, and ${\mathrm{DI}}_{\text{weighted}}$ and a lower value of ${\mathrm{HD}}_{\text{weighted}}$.

Some of the objects in $O_{\mathcal{G}}$ and $O_{{\mathcal{S}}^t}$ will remain unmatched due to very low or no intersection with all the objects in the other set. A higher number of unmatched objects in $O_{\mathcal{G}}$ and $O_{{\mathcal{S}}^t}$ indicates lower performance of the segmentation algorithm. We evaluate the object matching by computing the $F$-score, which is a harmonic mean of the percentage of objects matched in $O_{\mathcal{G}}$ and the percentage of objects matched in $O_{{\mathcal{S}}^t}$. The higher this object matching F-score is, the better is the segmentation algorithm. We also defined the metrics unmatched object area of $\mathcal{G}$ (${\mathbf{U}}_{\mathcal{G}}$) and unmatched object area of ${\mathcal{S}}^t$ (${\mathbf{U}}_{\mathcal{S}}$) [see Eqs. (7) and (8)]. We calculate total area of all unmatched objects and then divide it by the area of the image $\mathcal{G}$. Area of $\mathcal{G}$ and corresponding ${\mathcal{S}}^t$ will always be the same. A better segmentation algorithm will result in lower values for ${\mathbf{U}}_{\mathcal{G}}$ and ${\mathbf{U}}_{\mathcal{S}}$ metrics.

$${\mathbf{U}}_{\mathcal{G}}=\frac{\sum _l\text{Area of unmatched object}{G}_l\in O_{\mathcal{G}}}{\text{Area of Image}}$$ (7)

$${\mathbf{U}}_{\mathcal{S}}=\frac{\sum _l\text{Area of unmatched object}{S}_l^t\in O_{{\mathcal{S}}^t}}{\text{Area of Image}}$$ (8)

Comparison and discussion

The evaluation metrics discussed above were computed on the test results of our method (${\mathcal{S}}^{\text{pixel}}$), active contour-based method (${\mathcal{S}}^{\text{Naik}}$¹⁷), texture-based method (${\mathcal{S}}^{\text{Farjam}}$¹⁶), $k$-means clustering, and nuclei–lumen association-based method (${\mathcal{S}}^{\mathrm{Nguyen}}$²³). For the active contour-based method by Naik et al.,¹⁷ the initial level set was defined from the white regions detected by our method. We compared the pixel-wise metrics of our method with the other three methods. We report image-wise averages of precision, recall, accuracy, and $F$-score for the three cases of gland, lumen, and clefting classification in Table 2. Image-wise averaged OI is reported in Table 2.

Table 2.

Pixel-wise metrics for testing. The reported values are average value $\pm \text{standard error}$ over the set of 37 images. ${\mathcal{S}}^{\text{pixel}}$: our method, ${\mathcal{S}}^{\mathrm{Nguyen}}$: $k$-means clustering and nuclei–lumen association-based method by Nguyen et al.,²³ ${\mathcal{S}}^{\mathrm{Naik}}$: active contour method by Naik et al.,¹⁷ and ${\mathcal{S}}^{\mathrm{Farjam}}$: texture-based method by Farjam et al.¹⁶

Pixel type	Method	Precision	Recall	$F$-score	Accuracy
(a) Pixel-wise metrics for each pixel type
Gland	${\mathcal{S}}^{\text{pixel}}$	$0.64\pm 0.017$	$\mathbf{0}.\mathbf{90}\pm \mathbf{0}.\mathbf{004}$	$\mathbf{0}.\mathbf{74}\pm \mathbf{0}.\mathbf{01}$	$\mathbf{0}.\mathbf{72}\pm \mathbf{0}.\mathbf{01}$
	${\mathcal{S}}^{\mathrm{Nguyen}}$	$\mathbf{0}.\mathbf{66}\pm \mathbf{0}.\mathbf{015}$	$0.30\pm 0.02$	$0.39\pm 0.02$	$0.59\pm 0.01$
	${\mathcal{S}}^{\mathrm{Naik}}$	$0.61\pm 0.019$	$0.41\pm 0.02$	$0.47\pm 0.02$	$0.59\pm 0.01$
	${\mathcal{S}}^{\mathrm{Farjam}}$	$0.54\pm 0.01$	$0.08\pm 0.0003$	$0.15\pm 0.005$	$0.54\pm 0.01$
Lumen	${\mathcal{S}}^{\text{pixel}}$	$\mathbf{0}.\mathbf{82}\pm \mathbf{0}.\mathbf{02}$	$0.55\pm 0.02$	$\mathbf{0}.\mathbf{64}\pm \mathbf{0}.\mathbf{02}$	$\mathbf{0}.\mathbf{94}\pm \mathbf{0}.\mathbf{004}$
	${\mathcal{S}}^{\mathrm{Nguyen}}$	$0.49\pm 0.03$	$\mathbf{0}.\mathbf{69}\pm \mathbf{0}.\mathbf{02}$	$0.54\pm 0.02$	$0.86\pm 0.01$
	${\mathcal{S}}^{\mathrm{Naik}}$	$0.65\pm 0.02$	$0.62\pm 0.02$	$0.60\pm 0.01$	$0.90\pm 0.01$
	${\mathcal{S}}^{\mathrm{Farjam}}$	NA
Periacinar retraction clefting	${\mathcal{S}}^{\text{pixel}}$	$0.42\pm 0.05$	$0.15\pm 0.02$	$0.18\pm 0.026$	$0.97\pm 0.003$
	${\mathcal{S}}^{\mathrm{Nguyen}}$	NA
	${\mathcal{S}}^{\mathrm{Naik}}$	NA
	${\mathcal{S}}^{\mathrm{Farjam}}$	NA
(b) OI for comparing all pixel types
Method			OI
${\mathcal{S}}^{\mathrm{pixel}}$			$\mathbf{0.48}\pm \mathbf{0.01}$
${\mathcal{S}}^{\mathrm{Nguyen}}$			$0.36\pm 0.01$
${\mathcal{S}}^{\mathrm{Naik}}$			$0.36\pm 0.01$
${\mathcal{S}}^{\mathrm{Farjam}}$			$0.18\pm 0.01$

Note: The best results are shown in bold.

Our method identified all four regions, i.e., gland, lumen, periacinar retraction clefting, and stroma, in the images. Hence, we show our pixel-wise metrics for the three regions in Table 2. Our method used pixel-level information for empirical estimates of the regions and then improved it using object-level information.

Nguyen et al.²³ used $k$-means clustering to identify the lumen regions and nuclei regions first. After identification, the nuclei regions were associated to nearby lumen regions. The output segmented glands were computed using the convex hull of some pixels sampled from the associated lumen and nuclei regions. We observed many instances with identified lumen regions indicating surrounding cytoplasm as lumen region. The output convex hull may not follow the shape of gland as it would connect the adjacent nuclei points by a straight line. This lead to incorrect predictions of both gland and stroma pixels. Nguyen et al.²³ also do not differentiate between lumen and periacinar retraction clefting regions, which explains this method’s low pixel-wise accuracy, $F$-score, and OI as illustrated in Table 2.

Our implementation of Naik et al.¹⁷ used the cavity objects provided by our method as the initial level set for the glands. These level sets after energy minimization converged around the epithelial nuclei. In the case of nearby and touching glands, the final level sets merged, leading to one gland instead of two or more adjacent gland segments. This merging lead to incorrect predictions for both gland and stroma pixels and, hence, the low pixel-wise $F$-score, accuracy, and OI as illustrated in Table 2.

Farjam et al.¹⁶ used a texture-based approach to first segment nuclei regions and then segmented stroma, cytoplasm, and lumen regions together. The nuclei regions were used to identify the gland boundaries to obtain gland regions. This method used $k$-means clustering in the grayscale images for identifying these regions. The nuclei regions were being identified correctly. In many instances, the combined stroma and lumen regions were not being identified properly. The identified stroma, cytoplasm, and lumen regions did not contain the actual lumen, stroma, or cytoplasm completely. This lead to most of the cytoplasm being predicted as background with only nuclei and surrounding pixels being predicted as gland regions. This explains the low pixel-wise $F$-score, accuracy, and OI as shown in Table 2.

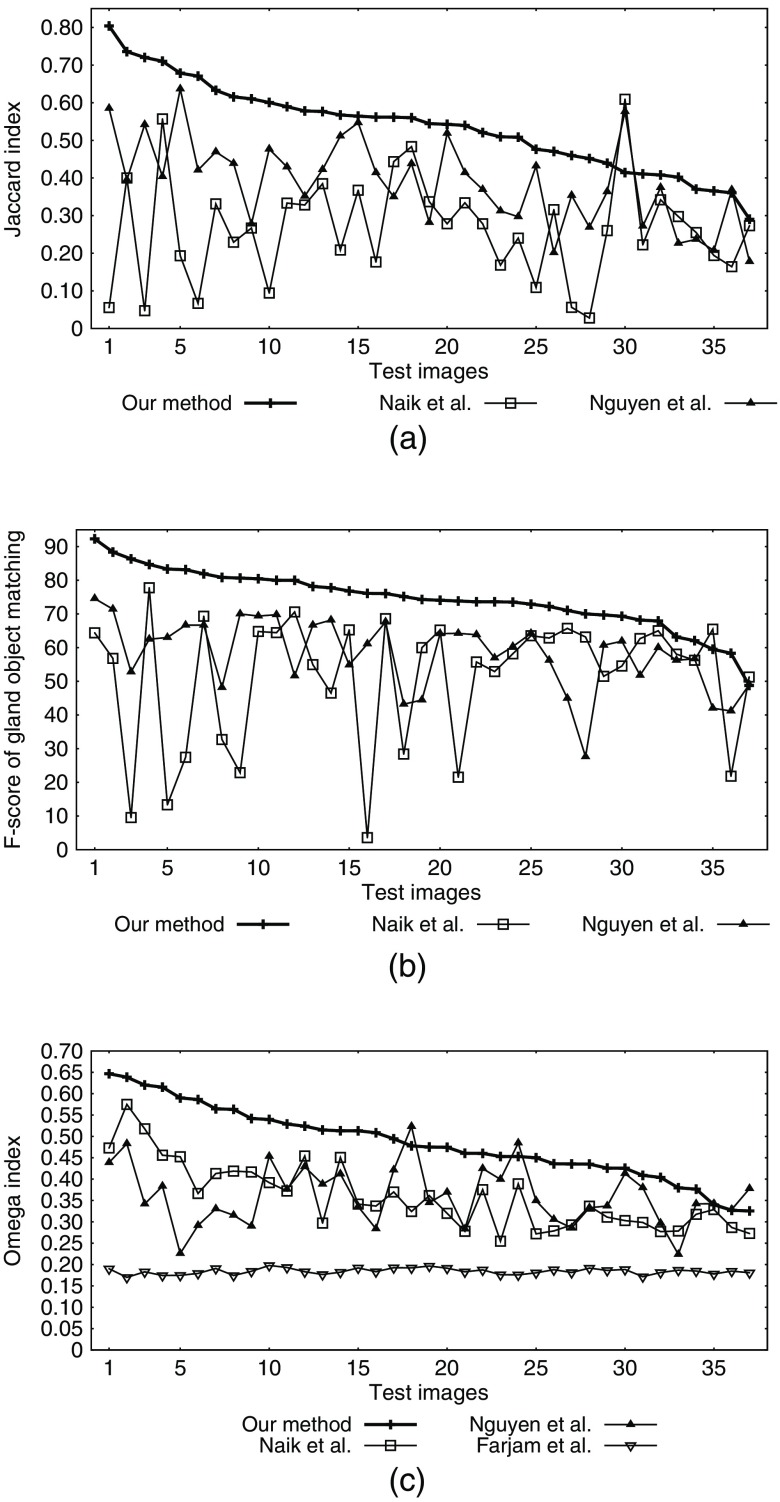
We computed ${\mathrm{JI}}_{\text{weighted}}$, ${\mathrm{DI}}_{\text{weighted}}$, ${\mathrm{HD}}_{\text{weighted}}$, $U_{\mathcal{G}}$, and $U_{\mathcal{S}}$ for gland objects in each image result. We report the image-wise average of these object-wise metrics for all four methods in Table 3. Figure 10 illustrates the evaluated JI (${\mathrm{JI}}_{\text{weighted}}$ for gland objects), gland object matching $F$-score, and pixel-wise OI for all the images.

Table 3.

Object-wise metrics for testing (for gland objects). The reported values are average value $\pm \text{standard error}$ over the set of 37 images. ${\mathcal{S}}^{\text{pixel}}$: our method, ${\mathcal{S}}^{\text{Nguyen}}$: $k$-means clustering and nuclei–lumen association-based method by Nguyen et al.,²³ ${\mathcal{S}}^{\text{Naik}}$: active contour method by Naik et al.,¹⁷ and ${\mathcal{S}}^{\text{Farjam}}$: texture-based method by Farjam et al.¹⁶

Method	JI (${\mathrm{JI}}_{\text{weighted}}$)	DI (${\mathrm{DI}}_{\text{weighted}}$)	${\mathbf{U}}_{\mathcal{G}}$	${\mathbf{U}}_{\mathcal{S}}$	HD (${\mathrm{HD}}_{\text{weighted}}$)	Object matching $F$-score
${\mathcal{S}}^{\text{pixel}}$	$\mathbf{0}.\mathbf{54}\pm \mathbf{0}.\mathbf{01}$	$\mathbf{0}.\mathbf{65}\pm \mathbf{0}.\mathbf{01}$	$\mathbf{0}.\mathbf{04}\pm \mathbf{0}.\mathbf{006}$	$0.11\pm 0.02$	$189.98\pm 13.27$	$\mathbf{74}.\mathbf{54}\pm \mathbf{1}.\mathbf{42}$
${\mathcal{S}}^{\mathrm{Nguyen}}$	$0.38\pm 0.01$	$0.49\pm 0.01$	$0.10\pm 0.02$	$0.17\pm 0.01$	$\mathbf{177}.\mathbf{83}\pm \mathbf{13}.\mathbf{58}$	$58.24\pm 1.68$
${\mathcal{S}}^{\mathrm{Naik}}$	$0.26\pm 0.02$	$0.37\pm 0.03$	$0.20\pm 0.02$	$\mathbf{0}.\mathbf{02}\pm \mathbf{0}.\mathbf{002}$	$497.04\pm 57.47$	$51.26\pm 3.14$
${\mathcal{S}}^{\mathrm{Farjam}}$	$0.01\pm 0.0008$	$0.02\pm 0.0002$	$0.00\pm 0$	$0.12\pm 0.004$	$228.46\pm 14.55$	$1.101\pm 0.078$

Note: The best results are shown in bold.

Fig. 10.

Results for all 37 images. (a) JI (${\mathrm{JI}}_{\text{weighted}}$) for gland segmentation (object-wise metric), (b) $F$-score for gland object matching (%age) (object-wise metric), and (c) OI (pixel-wise metric). Object-wise results for texture-based method by Farjam et al.¹⁶ are not shown due to low performance.

Our method identified the lumen, periacinar retraction clefting, and nuclei regions based on the object-level information. The spatial distribution of lumen and nuclei regions was used to obtain the gland objects. The usage of lumen and nuclei objects for seed estimation allowed fewer false gland detections; hence, we obtained a high gland object matching $F$-score as shown in Table 3. Seed-based growing also helped attain high overlap between the actual gland regions and the segmented gland regions and hence the high values of object-wise metrics ${\mathrm{JI}}_{\text{weighted}}$ and ${\mathrm{DI}}_{\text{weighted}}$. There were some cases of segmented glands indicating surrounding stroma as gland region and hence having a different shape, leading to a high value of the object-wise metric ${\mathrm{HD}}_{\text{weighted}}$ as shown in Table 3.

Nguyen et al.²³ obtained gland objects by convex hulls of the same pixels in the detected lumen and nuclei objects. The convex hulls lead to shape differences between the actual glands and detected glands. Also, the detected glands (convex hulls) sometimes included adjoining stroma regions and/or excluded some the glandular region, leading to low values of object-wise metrics ${\mathrm{JI}}_{\text{weighted}}$ and ${\mathrm{DI}}_{\text{weighted}}$ as shown in Table 3. The shape differences lead to a high value of the object-wise metric ${\mathrm{HD}}_{\text{weighted}}$ as shown in Table 3.

Our implementation of Naik et al.,¹⁷ as discussed, merged nearby/touching glands into one gland. This lead to low overlap and drastic shape differences between the actual gland regions and detected gland regions. Due to low overlap, we obtained low values of object-wise metrics ${\mathrm{JI}}_{\text{weighted}}$ and ${\mathrm{DI}}_{\text{weighted}}$, and huge shape differences lead to a high value of the object-wise metric ${\mathrm{HD}}_{\text{weighted}}$ as shown in Table 3.

Farjam et al.,¹⁶ as discussed, identified the nuclei and surrounding regions as glands. It essentially identified a lot of false gland objects. These objects did not cover the actual gland regions and led to low overlap and substantial shape difference between the matched objects. This led to very low values of object-wise metrics ${\mathrm{JI}}_{\text{weighted}}$ and ${\mathrm{DI}}_{\text{weighted}}$, and huge shape differences led to a high value of the object-wise metric ${\mathrm{HD}}_{\text{weighted}}$ as shown in Table 3.

4.2. Failure Cases

In our dataset of 43 images, we have a total of six images with a cribriform pattern. Our method resulted in inaccurate segmentation for these six cribriform pattern cases. We show an example image in Figs. 9(g)–9(i). In these cribriform cases, the glands have multiple lumen and they are surrounded by nuclei instead of just cytoplasm. Our method REFINE-SEEDS (Algorithm 3) failed in merging them as it relies on cytoplasm to define the inside region of the gland and on nuclei to define the gland boundary. REFINE-SEEDS assumes the regions with high nuclei density as the border regions and keeps the multiple lumina disconnected. Due to inaccurate seed refining, subsequent THREE-LEVEL-EGVD results in oversegmentation as shown in Fig. 9(i). Other methods, such as Farjam et al.,¹⁶ Naik et al.,¹⁷ and Nguyen et al.,²³ also generated final segmentation similar to that of our method (oversegmented) for these six cribriform pattern cases.

5. Conclusion

We developed an automated method for gland segmentation in prostate histopathological images using machine learning and image processing methods. We used a dataset of Gleason pattern 3 and 4 PCa images for developing this system. Our method outperformed texture- and gland structure-based methods by Farjam et al.,¹⁶ Naik et al.,¹⁷ and Nguyen et al.²³ Our method, however, fails in the images with the cribriform pattern. The cribriform pattern contains a lot of glands fused into one and hence contains a lot of nuclei clusters inside a gland. These clusters, in turn, impede our method during the seed-refining step, resulting in inaccurate segmentation.

A possible extension of our work can be the development of a practical user-friendly interface with efficient image acquisition and dataset preparation systems. Another future research can be the development of automated systems to analyze the segmented glands for grading purposes. The architecture, shape, and size of glands are some of the important features in the diagnostics of PCa. A good quality gland segmentation enables the computer to elucidate these features correctly. As such, a gland segmentation system may work as a base for future expert systems that analyze gland architectures.

Biographies

Malay Singh is a PhD student in the Department of Computer Science, School of Computing, National University of Singapore. He received his BTech degree in information technology from the Indian Institute of Information Technology-Allahabad, India, in 2012.

Emarene Mationg Kalaw is a research scientist at Bioinformatics Institute. She received her BSc (Hons) degree in biology in 1997 and her MD degree in 2001 from De La Salle University Philippines. She later obtained her MSc degree in medical research from Griffith University in 2007. She has worked as a research pathologist/scientist at Singapore General Hospital and National Cancer Centre, Singapore. Her research interests include histopathology for prostate cancer (PCa), kidney cancer, and bladder cancer.

Danilo Medina Giron is a senior pathologist at the Tan Tock Seng Hospital, a tertiary hospital in Singapore. He is a medical graduate from the University of the Philippines and finished his pathology residency at the State University of New York at Buffalo. He is board certified by the American Board of Pathology and the Royal College of Physicians and Surgeons of Canada. He practiced pathology in Canada, the Philippines, and Singapore.

Kian-Tai Chong is the consultant, adjunct assistant professor, codirector of urologic oncology, and director of research in the Department of Urology. He also manages the prospective urology cancer clinical databases and tissue repository in Tan Tock Seng Hospital. He completed his full-time clinical urologic-oncology fellowship at Memorial-Sloan Kettering Cancer Center, New York. His key professional interests are the prevention, diagnosis, treatment, and management of PCa, kidney cancer, bladder cancer, testis cancer, and penile cancer.

Chew Lim Tan is a professor in the Department of Computer Science, School of Computing, National University of Singapore. He received his BSc (Hons) degree in physics from the University of Singapore in 1971, his MSc degree in radiation studies from the University of Surrey, UK, in 1973, and his PhD in computer science from the University of Virginia, USA, in 1986. His research interests include document image analysis, text and natural language processing, and neural networks.

Hwee Kuan Lee is a senior principal investigator of the Imaging Informatics Division in Bioinformatics Institute. His current research work involves computer vision algorithms for clinical and biological studies. He obtained his PhD in theoretical physics from Carnegie Mellon University in 2001. He then held a joint postdoctoral position with Oak Ridge National Laboratory and University of Georgia. He worked at Tokyo Metropolitan University and Data Storage Institute before joining Bioinformatics Institute in 2006.

Disclosures

The authors, Malay Singh, Emarene Mationg Kalaw, Danilo Medina Giron, Kian-Tai Chong, Chew Lim Tan, and Hwee Kuan Lee, have no financial disclosures or conflicts of interest.