A “Beheaded” TAML Activator: A Compromised Catalyst that Emphasizes the Linearity between Catalytic Activity and pK_a

Abstract

Studies of the new tetra-amido macrocyclic ligand (TAML) activator [Fe^III{(Me₂CNCOCMe₂NCO)₂CMe₂}OH₂]⁻ (4) in water in the pH range of 2–13 suggest its pseudo-octahedral geometry with two nonequivalent axial H₂O ligands and revealed (i) the anticipated basic drift of the first pK_a of water to 11.38 due to four electron-donating methyl groups alongside (ii) its counterintuitive enhanced resistance to acid-induced iron(III) ejection from the macrocycle. The catalytic activity of 4 in the oxidation of Orange II (S) by H₂O₂ in the pH range of 7–12 is significantly lower than that of previously reported TAML activators, though it follows the common rate law (v/[Fe^III] = k_Ik_II[H₂O₂][S]/(k_I[H₂O₂] + k_II[S]) and typical pH profiles for k_I and k_II. At pH 7 and 25 °C the rate constants k_I and k_II equal 0.63 ± 0.02 and 1.19 ± 0.03 M⁻¹ s⁻¹, respectively. With these new values for pK_a, k_I and k_II establishing new high and low limits, respectively, the rate constants k_I and k_II were correlated with pK_a values of all TAML activators. The relations log k = log k⁰ + α × pK_a were established with log k⁰ = 13 ± 2 and 20 ± 4 and α = −1.1 ± 0.2 and −1.8 ± 0.4 for k_I and k_II, respectively. Thus, the reactivity of TAML activators across four generations of catalysts is predictable through their pK_a values.

Graphical abstract

Introduction

Designed over the last three decades,^1,2 tetra-amido macrocyclic ligand (TAML) activators 1, 2, and 3 (Chart 1), which are catalysts of the first, fourth, and fifth generations,³ respectively, are particularly effective for the catalyzed degradation of micropollutants by hydrogen peroxide in aqueous media and therefore are extremely promising for the purification of environmental and drinking waters. These catalysts function at the parts per billion (ppb) to parts per trillion (ppt) concentration range and direct the oxidizing power of H₂O₂ at a wide spectrum of environmental threats,⁴ among which endocrine disruptors such as steroid hormone derivatives are particularly hazardous.⁵ Additionally, TAML activators are successfully used in fine organic synthesis.^6–9

Chart 1. TAML Activators Applicable to Water Treatment.

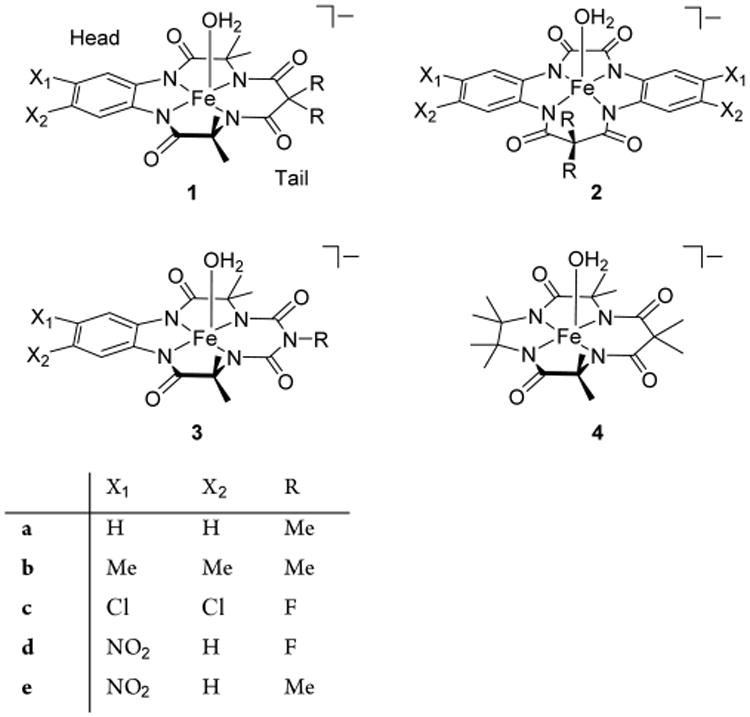
Catalysis by TAML activators is kinetically and mechanistically similar to that by peroxidase enzymes including issues related to operational instability of fragile biomolecules.^10–12 The recently emphasized importance of understanding the inactivation of man-made biorelevant catalysts in terms of “causes, avoidance, and cure” has been among our top TAML research priorities.^13–15 On the basis of the results of earlier work¹⁴ we hypothesized that suicidal degradation of oxidized forms of TAML activators could start with electron transfer from the aromatic ring or “head” of 1, because electron-withdrawing aryl substituents enhanced the operational stability of TAML activators. The mechanistic knowledge acquired¹⁴ has been successfully applied for the synthesis of “ideal” TAML activator 1d.¹⁶ Even though TAML activators of later generations, specifically, of fourth (2)^17,18 and fifth (3),^3,19 have been designed, the first generation activator 1d remains one of the most efficient catalysts for environmental⁵ and other²⁰ applications.

In the pursuit of an exceedingly operationally stable activator, it has been decided to eliminate all aryl rings from the TAML ligand system, that is, to design a “beheaded” catalyst with a nonexisting electron transfer pathway from the aromatic moiety. This is how the idea of making new TAML activator 4 emerged, and here we report on the characterization, properties, and reactivity of 4 in aqueous solution. A correlation was found between the pK_a of the axially ligated water molecule of TAML activators across all generations and the rate constants k_I and k_II. This allows for the effortless and straightforward estimation of catalytic activity of TAML activators for the oxidative degradation of organic substrates at neutral pH. A part of this work has been recently communicated.²¹

Results and Discussion

Properties of 4 in the Solid State and in Solution

TAML activator 4 with different counter cations (tetramethylammonium and bis(triphenyphosphine)iminium (PNP)) readily forms yellow needlelike crystals on diffusion of diethyl ether into acetonitrile. Unfortunately, these do not diffract X-rays well enough for structural characterization. The absence of a rigid aromatic moiety in the ligand system could increase nonplanarity of the complex with respect to the four deprotonated amide nitrogens. In turn, enhanced nonplanarity results in instability of iron TAML activators,²² which compromises catalysis. Therefore, the structural features of 4 were tested by density functional theory (DFT) calculations, and the results are presented in Figure 1.

Figure 1.

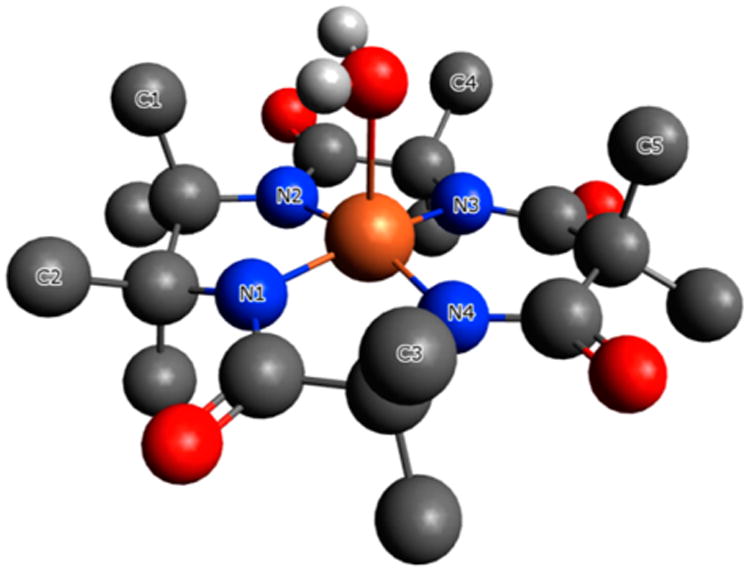
Results of DFT optimization of the structure of 4 in the form [FeL(OH₂)]⁻ in vacuum. H atoms other than those of H₂O ligand are omitted for clarity. Selected bond distances: Fe–O, 2.285; Fe–N(1–4) 1.878, 1.872, 1.886, and 1.888 Å, respectively.

It was particularly interesting to analyze the effects brought about by the (CMe₂)₂ unit of 4, which replaced the traditional phenylene ring in TAML activators of previous generations (cf. structures 1–4). The aromatic ring is referred to as the “head” part of TAML activators.²² The calculated geometry of beheaded 4 was compared with the X-ray structural data collected for 1a.²² There is a noticeably elongated Fe–O bond 2.285 Å in 4 versus 2.097 Å in 1a perhaps due to the electron-donating effect of the (CMe₂)₂ unit. The C(Me₂)₂ units are rotated around the Me₂C–CMe₂ bond, the dihedral angle C(1)C₂C(2) being 36.9°. Iron lies just 0.20 Å above the average plane of the four amide nitrogens versus 0.36 Å in 1a. In turn, this places the C(1)H₃ group very close to the oxygen of the axial water ligand, the C(1)…O separation being 3.415 Å. On the one hand, the latter value matches the sum of the van der Waals radii of CH₃ (2.0) and O (1.4 Å). On the other hand, the average Fe–N distance in 4 (1.881) is close to that in 1a (1.885 Å) suggesting that the (CMe₂)₂ unit translates its influence primarily at the axial ligand. As it will be shown below, the Fe–O bond elongation agrees perfectly with a pronounced increase in the pK_a of coordinated water.

It is worth noting that the carbon atom periplanar to C1 sits close to Fe, the separation being 3.415 Å. This suggests a steric repulsion between the C atom and the sixth (aqueous) ligand in water, where previous TAML activators are octahedral with two axial H₂O ligands ([FeL(OH₂)₂]⁻).²² Optimization of [FeL(OH₂)₂]⁻ for 4 by DFT in vacuum confirmed this hypothesis. The calculated Fe–O bonds appeared very different, specifically, of 2.273 and 3.418 Å, suggesting that one of the water ligands should be much more weakly bound to iron(III).

Compound 4 is moderately soluble in methanol and water, where its properties were tested in some detail. In methanol, 4 has an absorption maximum at 379 nm (ε = 7.8 × 10³ M⁻¹ cm⁻¹), and Beer's law holds in the concentration range of (0.11 – 1.2) × 10⁻⁴ M ruling out significant aggregation under these conditions. In pure water the maximum is at 368 nm (ε = 7.2 × 10³ M⁻¹ cm⁻¹) in the concentration range of (0.13–5.4) × 10⁻⁴ M. As mentioned above, iron TAML activators are octahedral diaqua or aqua/hydroxo species in aqueous solution,²² which was also confirmed for 4 by electron paramagnetic resonance (EPR) measurements (see below). The diaqua species typically dominate under neutral conditions and transform into aqua/hydroxo derivatives under basic conditions. The acid–base equilibria are accompanied by profound spectral changes in the UV–vis region, which for 4 are demonstrated in Figure 2. The spectral changes are fully pH-reversible, occur within two pH units, and there are isosbestic points at 343 and 407 nm. This all is consistent with the single-proton acid–base equilibrium:

Figure 2.

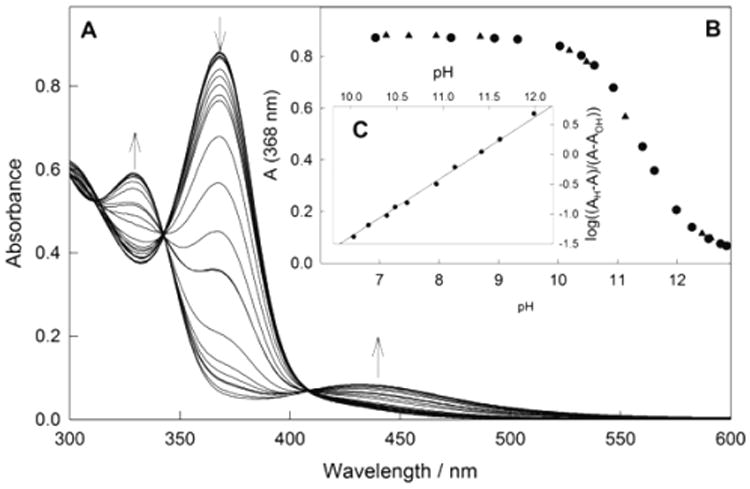
(A) Spectral changes of 4 at pH 7–13. Circles and triangles are the data obtained by changing the pH from 7 to 13 and from 13 to 7, respectively. (B) Absorbance (368 nm) vs pH. (C) Linearization of the data using eq 2. Conditions: 1.2 × 10⁻⁴ M 4, 25 °C, Carmody buffer.

$${[\text{FeL}{({\text{OH}}_2)}_2]}^{-}\rightleftharpoons {[\text{FeL}(\text{OH})({\text{OH}}_2)]}^{2-}+{\mathrm{H}}^{+}$$ (1)

The pK_a of 4 (11.38 ± 0.01) was calculated using eq 2, where A_H, A_OH, and A are absorbances at neutral, basic, and intermediate pH, respectively, (Figure 2C).

$$log\frac{A_{\mathrm{H}}-A}{A-A_{\text{OH}}}=\text{pH}-\mathrm{p}{K}_{\mathrm{a}}$$ (2)

The pK_a value of 11.38 for 4 is the highest ever reported for iron TAML activators. The low acidity of the coordinated water reflects a profound decrease of the Lewis acidity of the central metal due to the combined donor effect of four methyl groups in the beheaded part of 4. It agrees also with predictions by DFT. The pK_a value closest to 11.38, of 10.32, has been recently measured for N-tailed “biuret” TAML activator 3a.³ Such distinct variance prompted us to measure pK_a for 1b. A similar approach as described above for 4 (see Figure S1) resulted in the value of 10.35 ± 0.02, which is not significantly higher than that for 3a and 1a (pK_a values of both equal 10.3). The latter value indicates that the phenylene ring is a decent “buffer” that neutralizes the electron-donating properties of the methyl groups.

EPR spectra of the TAML species in solutions with pH above and below the pK_a reveal the difference in speciation between the protonated and deprotonated forms of 4. Figure 3 shows the EPR spectra of samples prepared in pH 2, 10.5, and 13 buffer solution with 10% glycerol. All samples revealed intermediate spin, S = 3/2, iron(III) complexes. The spectra recorded for the samples at pH below the pK_a of 4 are nearly identical. The simulation overlaid for the pH 10.5 spectrum is calculated for S = 3/2, D = 1.2 cm⁻¹, and E/D = 0.22. The g-values for the ±1/2 doublet and the g_z-value of the ±3/2 doublet are indicated in Figure 3. The spectrum of the pH 13 sample showed a significant change in symmetry to a more axial species. The spectrum at pH 13 showed a 50% conversion to the higher pH species. The difference spectrum of pH 13 minus pH 10.5 is also shown in Figure 3. The simulation overlaid on the difference spectrum is calculated for S = 3/2, D = 1.3 cm⁻¹, and E/D = 0.11. The g-values for the ±1/2 doublet and the g_z-value of the ±3/2 doublet are indicated on Figure 3. For a pK_a value of 11.4, 95% of the complex should be the deprotonated species at pH 13. The different ratio of the deprotonated species is attributed to a change in pK_a and/or pH of aqueous solutions upon freezing of the EPR sample.^23,24

Figure 3.

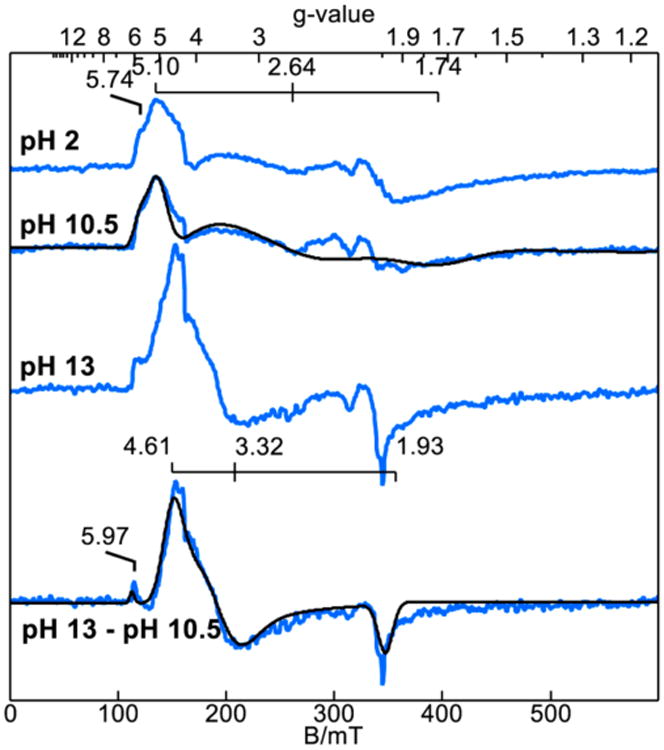
EPR spectra of iron(III) complex 4 (5 × 10⁻⁴ M) at pH 2, 10.5, and 13. Samples were prepared in Carmody buffer with 10% glycerol.

Mössbauer spectra of the pH 2 and 13 samples were recorded at 100 K. For this temperature the magnetic spectra essentially collapsed to doublets. At pH 2, the parameters of the doublet were the isomer shift (δ) 0.14 mm s⁻¹ and the quadrupole splitting (ΔE_Q) 3.59 mm s⁻¹. At pH 13, the doublets are broad due to residue magnetic effects, but a doublet was observed from the deprotonated species with δ = 0.11 mm s⁻¹ and ΔE_Q = 2.94 mm s⁻¹.

Kinetics of Acid-Induced Iron Ejection from 4

At pH 4 and below TAML acctivator 1a undergoes proton-induced demetalation, which occurs according to eq 3.²² The process is kinetically interesting due to its rate law, specifically, k_obs = k₁[H⁺] + k₃[H⁺]³.²² The third-order term in H⁺ was rationalized by the peripheral protonation of the tail amide oxygens of 1a, because its 1c analogue with the fluorine tail appeared to be 9 orders of magnitude more resistant to demetalation.²²

$${[\text{FeL}{({\text{OH}}_2)}_2]}^{-}+4{\mathrm{H}}^{+}\to {\text{Fe}}^{\text{III}}+{\mathrm{H}}_4\mathrm{L}+2{\text{OH}}_2$$ (3)

As far as 4 is concerned, the increased electron-donating capacity of the four methyl units should greatly increase the rate of demetalation. Therefore, it has been thrilling to probe this concept through the kinetic investigation of reaction 3 with complex 4, as we have found just the opposite effect. It should be emphasized first that 4 is markedly more resistant to H⁺ than 1a, since we were able to manipulate 4 at pH 2 for a span of 8 h without any evidence for its collapse. Correspondingly, the acid-induced demetalation of 4 was studied in the range of [H⁺] 0.003–0.250 M by following the exponential decrease in absorbance at 368 nm at 25 °C. Pseudo-first-order rate constants k_obs depend strictly linearly on [H⁺] with the corresponding second-order rate constant k₁ of (3.41 ± 0.05) × 10⁻⁴ M⁻¹ s⁻¹ (Figure 4). There is no evidence for higher-order terms in the acid concentration suggesting that peripheral protonation does not assist the iron ejection from 4 and the rate-limiting step involves a proton attack at one the Fe–N bonds as previously proposed.²² Since the beheaded (tetramethylated) part of 4 could be more susceptible to the electrophilic attack compared to its “tail” part, it is likely that proton attacks Fe–N(1) or Fe–N(2) bond (Figure 1). Peripheral protonation of 1 was considered to involve the tail part of TAML activators.²² If similar tail protonation occurs in the case of 4, the actual reactive Fe–N(1) or Fe–N(2) sites are too far away from the protonation site, and therefore the peripheral phenomena do not affect the speed of reaction 3 in the case of 4.

Figure 4.

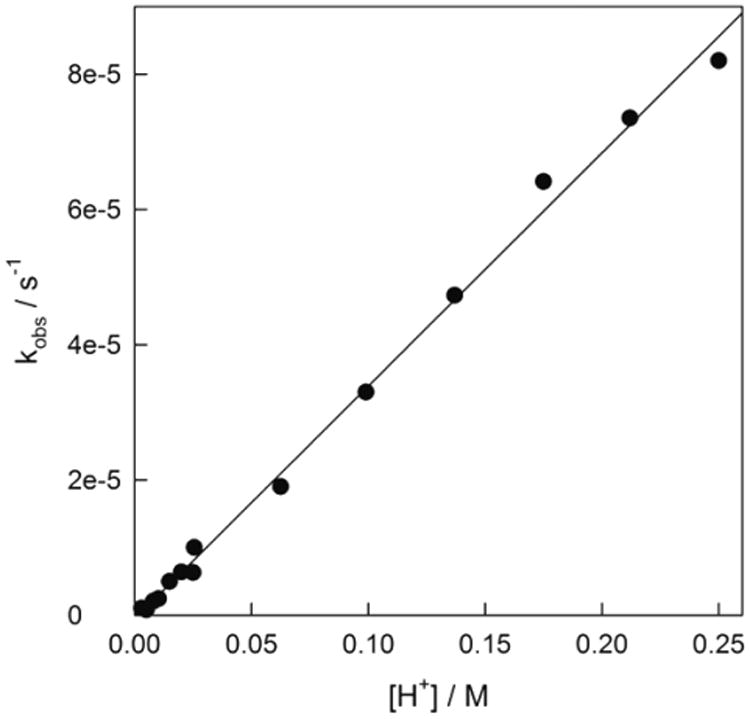
Pseudo-first-order rate constants k_obs vs [H⁺] for the demetalation of 4 at 25 °C.

The value of k₁ displays 10 000 and 10-fold resistance of 4 to acid compared to TAML activators 1a and 3a, with k₁ values of 2.2 ± 0.7 and (3.7 ± 0.5) × 10⁻³ respectively.^19,22 This increased resistance to acid-induced demetalation is counter-intuitive, because 4 is more electron-rich than 1a or 3a and therefore should be more prone to electrophilic demetalation. Therefore, the retardation might have steric origin. The methyl groups of the (CMe₂)₂ unit may function as a fence that prevents the proton attack at Fe–N(1) or Fe–N(2) sites revealing a rare case of steric retardation of the reaction involving specific acid catalysis.²⁵ This may also explain why there is no indication of third-order dependence on [H⁺] in this concentration range.

Catalytic Activity of 4 versus Lewis Acidity

The catalytic intrigue was how the high value of pK_a for 4 would affect its activity in catalyzed oxidations by hydrogen peroxide. We^3,17,18,26 and others^27–29 employ Orange II dye for catalyzed oxidations by H₂O₂ and other primary oxidants. Measurements were initiated at pH 7 because of our long-term goal of using TAML activators for purification of water in the environment. The steady-state rate of fading of the Orange II band at 484 nm is a linear function of [4] in a range from 1 × 10⁻⁵ to 1 × 10⁻⁴ M at [H₂O₂] = 5 × 10⁻³ M and [Orange II] = 4 × 10⁻⁵ M. The rate law is typical of catalysis by TAML activators. There is a hyperbolic dependence on concentration of H₂O₂ (Figure 5A), which agrees with common rate law 4 (with negligible k_I) and is consistent with the general two-step mechanism of catalysis shown in Scheme 1.^4,12

Figure 5.

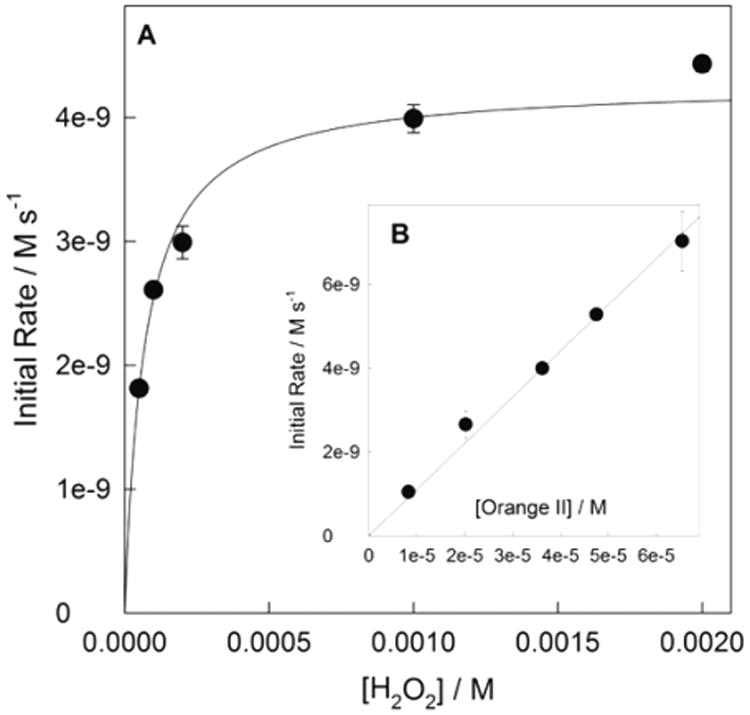
(A) Initial rate of 4-catalyzed Orange II degradation by H₂O₂ as a function of H₂O₂ concentration. Conditions: pH 7 (0.01 M phosphate buffer), 1.0 × 10⁻⁴ M 4, 3.6 × 10⁻⁵ M Orange II, 25 °C. (B) Linear dependence of initial rate on [Orange II] at 1 × 10⁻³ M H₂O₂ and 1 × 10⁻⁴ M 4 (see text for details).

Scheme 1. General Stoichiometric Mechanism of Catalysis by TAML Activators^4,12.

$$\frac{\text{rate}}{[{\text{Fe}}^{\text{III}}]}=\frac{k_{\mathrm{I}}{k}_{\text{II}}[{\mathrm{H}}_2{\mathrm{O}}_2][\text{substrate}]}{k_{-\mathrm{I}}+k_{\mathrm{I}}[{\mathrm{H}}_2{\mathrm{O}}_2]+k_{\text{II}}[\text{substrate}]}$$ (4)

Equation 4 implies that when the reaction rate levels off at high H₂O₂ concentrations, it should be a linear function of [Orange II], which is confirmed in Figure 5B. Though the kinetic data in Figure 5 are normal for TAML activators, the absolute concentrations of 4 used to generate the data are by ca. 3–4 orders magnitude higher than usually employed implying that the rate constants k_I and k_II should be markedly lower. In fact, the values k_I and k_II obtained by fitting the data in Figure 5A to eq 4 equal 0.63 ± 0.02 and 1.19 ± 0.03 M⁻¹ s⁻¹, respectively, and k_II calculated from the slope of the line in Figure 5B equals 1.10 ± 0.02 M⁻¹ s⁻¹. These values are significantly lower than those for the prototype TAML activator 1a (31.4 and 4.95 × 10³ M⁻¹ s⁻¹, respectively).^19,22 An additional unusual feature of 4 is that k_I and k_II are very close to each other, whereas the relation k_I ≪ k_II usually holds for TAML activators and other man-made iron-containing peroxidase mimetics, though the opposite relation is typical of peroxidase enzymes.^4,12

To check whether or not the relation k_I ≈ k_II is valid at pH other than 7, the corresponding rate constants were obtained at pH from 7 to 12 (Figure 6). The normal trend, that is, k_I ≪ k_II, reappears at pH above 9, though the gap between k_I and k_II is not as large as for 1–3 TAML activators. If compared with the data for 1–3, the bell-shaped pH profile for k_I is moved to the alkaline region with the maximum around 11.75, which reflects the highest pK_a value of 4. Its quantification is based on the mechanistic model in Scheme 2, which leads to the pH dependence of k_I (eq 5).

Figure 6.

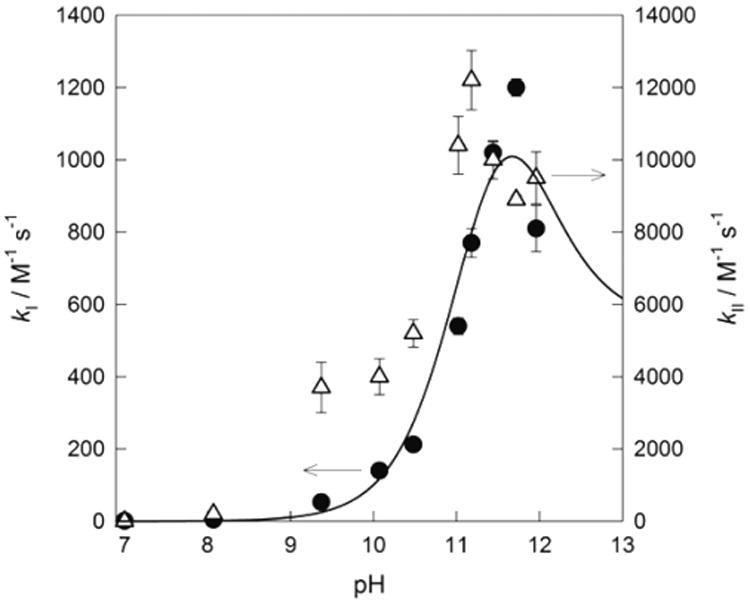
Values of k_I (●, k_I axis) and k_II (Δ, k_II axis) as a function of pH. The solid line was calculated for k_I (see text for details).

Scheme 2. Typical TAML Activator Mechanism for k_I Step that Accounts for the pH Profile as in Figure 6^a.

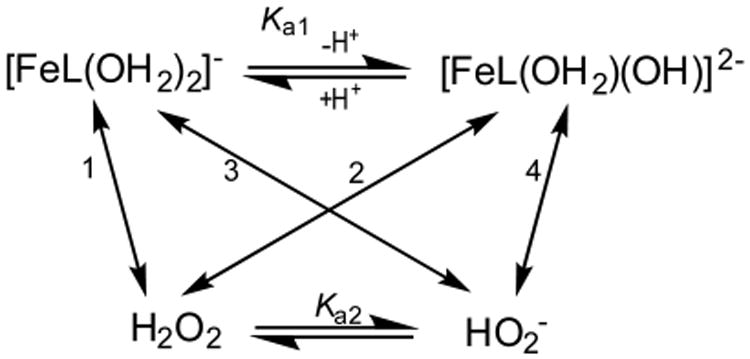
^aNumerals at the two-sided arrows 1–4 correspond to the rate constants k₁–k₄, respectively (eq 5).

$$k_{\mathrm{I}}=\frac{k_1{[{\mathrm{H}}^{+}]}^2+(k_2{K}_{\mathrm{a}1}+k_3{K}_{\mathrm{a}2})[{\mathrm{H}}^{+}]+k_4{K}_{\mathrm{a}1}{K}_{\mathrm{a}2}}{{[{\mathrm{H}}^{+}]}^2+(K_{\mathrm{a}1}+K_{\mathrm{a}2})[{\mathrm{H}}^{+}]+K_{\mathrm{a}1}{K}_{\mathrm{a}2}}$$ (5)

It is important to note that in the case of 4 eq 5 reduces to eq 6, because (i) pK_a of 4 (pK_a1) is essentially equal to pK_a of H₂O₂ (pK_a2) and (ii) one of the kinetically indistinguishable rate constants (k₂ or k₃) is considerably larger than the other.¹⁰

$$k_{\mathrm{I}}=\frac{k_1{[{\mathrm{H}}^{+}]}^2+k_{2/3}{K}_{\mathrm{a}}[{\mathrm{H}}^{+}]+k_4{K_{\mathrm{a}}}^2}{{[{\mathrm{H}}^{+}]}^2+2K_{\mathrm{a}}[{\mathrm{H}}^{+}]+{K_{\mathrm{a}}}^2}$$ (6)

Here K_a = K_a1 = K_a2 and k_2/3 = k₂ or k₃. The data in Figure 6 were fitted to eq 6 assuming K_a = 1 × 10^−11.5 M. The fitting procedure was similar to such used by us previously.^3,10 The value of 0.63 ± 0.03 M⁻¹ s⁻¹, which was measured at pH 7, can be assumed to be the upper limit for the intrinsic rate constant k₁, as fitting the data gives greater than 100% error for this parameter. The low value of this intrinsic rate constant means that the reaction between [FeL(OH₂)₂]⁻ and HOOH is by far the slowest of the four possible reaction pathways. The value of k₄, for the reaction between [FeL(OH₂)(OH)]²⁻ and HOO⁻, was determined to be 550 ± 70 M⁻¹ s⁻¹, which is 3 orders of magnitude higher than k₁, due to the higher electron density of iron species. The value for k_2/3, 1600 ± 200 M⁻¹ s⁻¹ is, in turn, threefold higher than k₄ indicating that perhaps the electrostatic repulsion of the two deprotonated species at higher pH mitigates the higher reactivity due to increased electron density. The dominant reaction pathway described by k_2/3, either [FeL(OH₂)₂]⁻ + HOO⁻ or [FeL(OH₂) (OH)]²⁻ + HOOH, is kinetically indistinguishable; however, the increased electron density on the metal center of the [FeL(OH₂) (OH)]²⁻ complex would probably favor the k₂ pathway. The comparison with the values of 4.0 × 10², 1.8 × 10⁴, and 1.5 × 10₃ M⁻¹ s⁻¹ for k₁, k₂, and k₄ respectively, previously reported for 1c,¹⁰ suggests that even though the reactivity of 4 in terms of k_I does increase under alkaline conditions, it is nevertheless much lower than that of TAML activators of earlier generations. For the reasons outlined previously, no attempt was made to quantify the pH profile for k_II in Figure 6. Semiquantitatively, k_II for 4 is ca. 10 times lower than that for 3a.³

The results of our recent work³⁰ on characterization of iron(V)oxo species derived from 4 in pure water allow to hypothesize that iron(V)oxo is most likely the reactive intermediate in catalysis by 4. It has been demonstrated that iron(IV)oxo species is stable at pH ≈ 13. If the solution pH is decreased to 10.6 and below, iron(IV)oxo disproportionates rapidly to form iron(III) and iron(V)oxo derivatives of 4.³⁰ Therefore, iron(V)oxo is the only plausible oxidized species in the pH range shown in Figure 6. This feature is unique for TAML activators, because just iron(IV) state could be generated in pure water for all previously known activators (generations 1–5).

pK_a of TAML Activators Is What Controls Reactivity

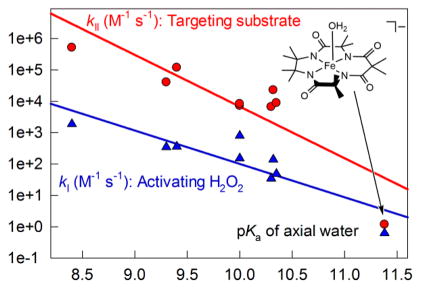
Regardless of their structural variations, TAML activators of generation 1 to 5³ all include iron(III) coordinated by four deprotonated amide nitrogens, which form a pseudo plane. The same is true for a new activator 4, the properties of which in aqueous media are described in this work. It is always a challenge to find a parameter (property) of a catalyst that assists in predicting its catalytic activity. The highest value of pK_a of the axial water ligand in the family of all TAML activators reported here (11.35) and the lowest of 8.4 for 2e reported previously¹⁸ extend the available gap in pK_a to three units, which is trustworthy for linear free energy correlations. Both rate constants k_I and k_II (eq 4) are essential for the oxidative catalysis by TAML activators, and therefore the dependencies of log k_I and log k_II versus pK_a are demonstrated in Figure 7. Here the rate constants k_I and k_II at pH 7 and 25 °C correspond to reactions with H₂O₂ and Orange II, respectively. As seen, both k_I and k_II increase with a decrease in pK_a. The rate constants k_II are more sensitive than k_I to variations in pK_a. This agrees with earlier results that revealed poor sensitivity of the k_I values to electronic effects.^4,12 Dependencies of both rate constants on pK_a could be satisfactorily linearized as log k = log k⁰ + α × pK_a with log k⁰ = 13 ± 2 and 20 ± 4 and α = −1.1 ± 0.2 and −1.8 ± 0.4 for k_I and k_II, respectively. There is a single data point that deviates more noticeably from the straight line, and this is k_II for 4. This we attribute to the steric effect imposed by the tetramethylated part of 4. The steric retardation for k_I is obviously less evident than for k_II, because the H₂O₂ molecule is smaller than that of Orange II.

Figure 7.

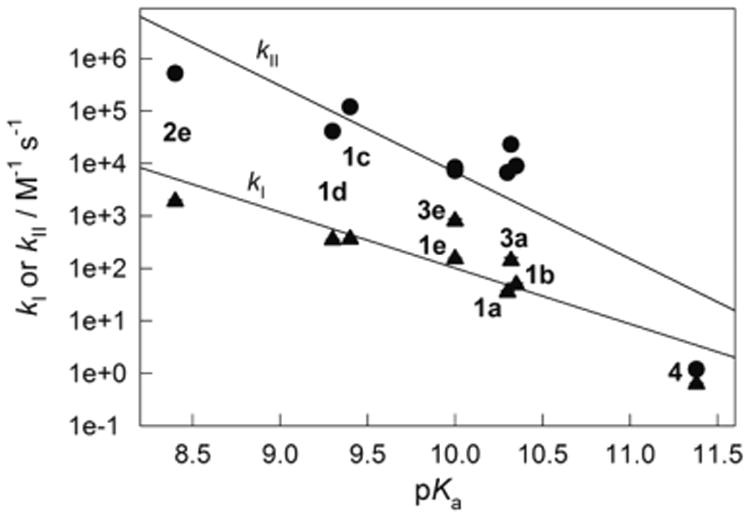
Linear free energy relationships for k_I and k_II (measured at pH 7 and 25 °C) for selected TAML activators 1–4 as a function of their pK_a (see text for details). The data for activators other than 4 and pK_a of 1b are reported elsewhere: 2e;¹⁸ 3a and 3e;³ 1a and 1e,³ 1d,¹⁶ 1f;²² other values of k_II are from ref 21.

A decrease in pK_a parallels the increasing Lewis acidity of the iron(III) center of TAML activators. Correspondingly, both k_I and k_II increase with increasing Lewis acidity. Because of this it is possible to predict the rate constants k_I and k_II for TAML activators using the equations log k = log k⁰ + α × pK_a provided the pK_a is known. And since the pK_a values could be effortlessly measured using the UV–vis spectroscopy as it is shown in Figure 2, estimating the catalytically relevant rate constants k_I and k_II becomes a painless routine.

Operational Stability of 4

Oxidized forms of TAML activators (active catalyst in Scheme 1) undergo suicidal inactivation, which is quantified by first-order rate constant k_i.¹⁴ This catalyst inactivation is an attribute of all oxidative catalysts including enzymes.^4,13 Values of k_i are available through the universal eq 7 provided an oxidant is used in excess with respect to a substrate, and the substrate conversion should be incomplete, which is easily achieved by using low catalyst concentrations.¹⁵

$$ln\frac{S_0}{S_{\infty }}=\frac{k_{\text{II}}}{k_{\mathrm{i}}}{[{\text{Fe}}^{\text{III}}]}_0$$ (7)

Here S₀ and S_∞ are substrate concentrations at time t = 0 and ∞, that is, degradation of S is incomplete. The value of k_i was obtained using k_II = 1.19 M⁻¹ s⁻¹ at pH 7 and 25 °C of (4.1 ± 0.1) × 10⁻⁷ s⁻¹. It is the lowest measured value to date. However, the ratio k_II/k_i is comparable to the other TAML activators.¹⁴ This implies that the “beheading” of TAML activators to produce 4 does not bring about additional operational stability. This argues against the main degradation pathway by aromatic oxidation, making more probable the degradation via tail group units, as it was postulated earlier.³¹

Conclusion: Structural and Reactivity Consequences

The novel beheaded TAML activator 4 added several new features to the already rich chemistry of this family of catalysts.^1,2,4,11,12 These new features, the most prominent being the lack of phenylene unit in the ligand architecture, the highest pK_a of coordinated water, enhanced resistance to the acid-induced iron ejection plus unprecedented aqueous iron-(V)oxo chemistry, which is currently under investigation, allow us to classify 4 as a Generation 6 TAML activator.

Experimental Section

Materials

Synthesis of 4 has recently been communicated.²¹ Orange II was obtained from Sigma-Aldrich and purified by recrystallization. Hydrogen peroxide was obtained from Fisher Scientific and standardized using the absorbance at 230 nm.³² All other reagents used in this study of at least ACS reagent grade were used as received.

Spectrophotometric Titration

Carmody buffer, consisting of 0.1 M boric acid, 0.025 M citric acid, and 0.05 M K₃PO₄, was used to prepare a 0.12 mM solution of 4 at pH 7.³³ Concentrated KOH and H₃PO₄ were used for further pH adjustments. The spectral data were collected using a double-beam Shimadzu UV-1800 instrument.

Kinetic Studies

Kinetic studies were conducted at 25 °C in 0.01 M phosphate buffer. Stock solutions of 4, Orange II, and H₂O₂ were prepared in HPLC-grade water. Appropriate volumes of the buffer, compound 4, and Orange II were added to polystyrene cuvettes, and the reactions were initiated by the addition of an aliquot of H₂O₂. Reaction progress was assayed by measuring a decrease in absorbance at 484 nm (λ_max for Orange II, ε = 2.1 × 10⁴ M⁻¹ cm⁻¹ at pH 7–10) using an HP 8453 diode array spectro-photometer with a thermostated eight-cell changer. Above pH 10 the following values of ε were used: 17 180, 14 850, 12 750, and 11 230 M⁻¹ cm⁻¹ at pH 10.5, 11.0, 11.4, and 11.7, respectively. The initial rates were calculated from linear plots of Orange II concentration versus time when the conversion of the dye did not exceed 10%. Each data point reported is a mean value of at least three measurements.

Electron Paramagnetic Resonance and Mössbauer Measurements

EPR X-band EPR spectra were recorded on a Bruker spectrometer equipped with an Oxford ESR-910 liquid helium cryostat. The signal was quantified relative to a CuEDTA spin standard. For both instruments, the microwave frequency was calibrated with a frequency counter, and the magnetic field was calibrated with an NMR gaussmeter. A modulation frequency of 100 kHz was used for the EPR spectra. The EPR simulation software (Spin Count) was written by one of the authors.³⁴ The software diagonalizes the spin Hamiltonian. The quantitative simulations were least-squares fits of the experimental spectra generated with consideration of the intensity factor, which allows the computation of simulated spectra for a specified sample concentration. Mössbauer spectra were recorded with a spectrometer using a Janis Research dewar. The isomer shifts were reported relative to Fe metal. Mössbauer spectra were obtained as described previously.³⁵

Density Functional Theory Calculations

Density functional theory calculations were performed using Becke's three parameter hybrid functional (B3LYP) and basis set 6-311G provided by the Gaussian 09 software package.³⁶ The geometry optimization for complex 4 was terminated upon reaching the default convergence criteria. The optimizations did not impose any symmetry. Geometry optimizations for each species were performed in the absence of a solvent (in vacuum).