Abstract
The computer-assisted analysis for better interpreting images have been longstanding issues in the medical imaging field. On the image-understanding front, recent advances in machine learning, especially, in the way of deep learning, have made a big leap to help identify, classify, and quantify patterns in medical images. Specifically, exploiting hierarchical feature representations learned solely from data, instead of handcrafted features mostly designed based on domain-specific knowledge, lies at the core of the advances. In that way, deep learning is rapidly proving to be the state-of-the-art foundation, achieving enhanced performances in various medical applications. In this article, we introduce the fundamentals of deep learning methods; review their successes to image registration, anatomical/cell structures detection, tissue segmentation, computer-aided disease diagnosis or prognosis, and so on. We conclude by raising research issues and suggesting future directions for further improvements.
Keywords: Medical image analysis, deep learning, unsupervised feature learning
1. INTRODUCTION
Over the last decades, we have witnessed the importance of medical imaging, e.g., computed tomography (CT), magnetic resonance (MR), positron emission tomography (PET), mammography, ultrasound, X-ray, and so on, for the early detection, diagnosis, and treatment of diseases (1). In the clinic, the medical image interpretation has mostly been performed by human experts such as radiologists and physicians. However, due to large variations in pathology and potential fatigue of human experts, researchers and doctors have recently begun to benefit from computer-assisted interventions. While, compared to the advances in medical imaging technologies, it is belated for the advances in computational medical image analysis, it has recently been improving with the help of machine learning techniques.
In the stream of applying machine learning for data analysis, meaningful feature extraction or feature representation lies at the heart of its success to accomplish target tasks. Conventionally, meaningful or task-related features were mostly designed by human experts based on their knowledge about the target domains, which thus made it challenging for non-experts to exploit machine learning techniques for their own studies. However, deep learning (2) has relieved such obstacles by absorbing the feature engineering step into a learning step. That is, instead of extracting features in a hand-designed manner, deep learning requires only a set of data with minor preprocessing, if necessary, and then discovers the informative representations in a self-taught manner (3, 4). So, now the burden of feature engineering has shifted from a human-side to a computer-side, thus allowing non-experts in machine learning to effectively use deep learning for their own researches and/or applications, especially in medical image analysis.
The unprecedented success of deep learning arises mostly from the following factors: (1) advancements of high-tech central processing units (CPUs) and graphics processing units (GPUs); (ii) availability of a huge amount of data (i.e., big data); (iii) developments of learning algorithms (5, 6, 7, 8, 9). Technically, deep learning can be regarded as an improvement of the conventional artificial neural networks (10) by building networks with multiple (more than two) layers. It is empirically shown that deep neural networks can discover hierarchical feature representations such that the higher level features can be derived from the lower level features (4). Thanks to its nice characteristic of learning hierarchical feature representations solely from data, deep learning has achieved record-breaking performance in a variety of artificial intelligence applications (11, 12, 13, 14, 15, 16, 17, 18) and grand challenges (19, 20, 21). Particularly, great improvements in computer vision inspired its use to medical image analysis such as image segmentation (22, 23), image registration (24), image fusion (25), image annotation (26), computer-aided diagnosis and prognosis (27, 28, 29), lesion/landmark detection (30, 31, 32), and microscopic imaging analysis (33, 34), to name a few.
Deep learning methods are highly effective when the number of available samples are large during a training stage. For example, in ImageNet Large Scale Visual Recognition Challenge (ILSVRC), more than 1 million annotated images were provided (19). However, as for medical applications, we usually have a very limited number of images, e.g., less than 1,000 images. Therefore, one of the main challenges in applying deep learning to medical images arises from the limited small number of available training samples to build deep models without suffering from overfitting. To this end, research groups have devised various strategies, such as (i) to take image patches either 2D or 3D as input (25, 35, 36, 37, 38, 39, 40, 41), rather than the full-sized images, to reduce the input dimensionality, thus the number of model parameters; (ii) to expand their dataset by artificially generating samples via affine transformation (i.e., data augmentation) and then train their network from scratch with the augmented dataset (35, 36, 37, 38); (iii) to use deep models trained over a huge number of natural images in computer vision as ‘off-the-shelf’ feature extractor and then train the final classifier or output layer with the target-task samples (39, 41); (iv) to initialize model parameters with those of pre-trained models from non-medical or natural images and then fine-tune the network parameters with the task-related samples (42, 43); (v) to use models trained with small-sized inputs for arbitrarily-sized inputs by transforming weights in the fully connected layers into convolutional kernels (32, 44).
In terms of the input types, we can categorize deep models as typical multi-layer neural networks that take input values in vector form (i.e., non-structured) and convolutional networks that takes 2D or 3D shaped (i.e., structured) values as input. Because of the structural characteristic of images (i.e., the structural or configural information among neighboring pixels or voxels is another important source of information), convolutional neural networks have gained great interest in medical image analysis (33, 45, 32, 46, 22, 44, 31). However, networks with vectorized inputs were also successfully applied to different medical applications (47, 25, 27, 29, 48, 24, 49, 50). Along with deep neural networks, deep generative models (51) such as deep belief networks and deep Boltzmann machines that are the probabilistic graphical models with multiple layers of hidden variables have also been successfully applied to brain disease diagnosis (43, 25, 52, 29), lesion segmentation (53, 45, 32, 54), cell segmentation (33, 55, 34, 56), image parsing (57, 58, 59), and tissue classification (31, 46, 22, 44).
In this article, we first explain the computational theories of neural networks and deep models (e.g., stacked auto-encoder, deep belief network, deep Boltzmann machine, convolutional neural network) and their fundamentals of extracting high-level representations from data in Section 2. Section 3 introduces recent studies that exploited deep models for different applications in medical imaging by covering image registration, anatomy localization, lesion segmentation, object/cell detection, tissue segmentation, and computer-aided detection and diagnosis. Finally, we conclude this article by summarizing research trends and suggesting directions for further improvements in Section 4.
2. DEEP MODELS
In this section, we explain the fundamental concepts of feed-forward neural networks and basic deep models in the literature. The contents are specifically focused on learning hierarchical feature representations from data. It is also described how to efficiently learn parameters of deep architecture by reducing overfitting.
2.1. Feed-forward neural networks
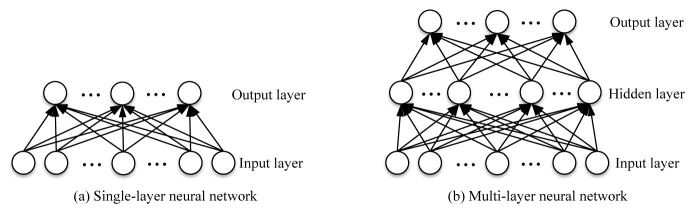
In machine learning, artificial neural networks are a family of models that mimic the structural elegance of the neural system and learn patterns inherent in observations. The perceptron (60) is the earliest trainable neural network with a single-layer architecture1, composed of an input layer and an output layer. The perceptron or modified perceptron with multiple output units in Fig. 1(a) is regarded as a linear model, which prohibits their applications for tasks of involving complicated data patterns, despite the use of non-linear activation functions in the output layer.
Figure 1.
Architectures of feed-forward neural networks.
Such limitation is successfully circumvented by introducing the so-called ‘hidden’ layer between the input layer and the output layer. Note that in neural networks the units of the neighboring layers are fully connected to each other, but there are no connections among the units in the same layer. For a two-layer neural network in Fig. 1(b), also called as multi-layer perceptron, given an input vector v = [vi] ∈ ℝD, we can write the estimation function of an output unit yk as a composition function as follows
| (1) |
where the superscript denotes a layer index, f(1)(·) and f(2)(·) denote non-linear activation functions of units at the specified layers, M is the number of hidden units, and Θ = {W(1),W(2),b(1),b(2)}2 is a parameter set. Conventionally, the hidden units’ activation function f (1)(·) is commonly defined with a sigmoidal function such as a ‘logistic sigmoid’ function or a ‘hyperbolic tangent’ function, while the output units’ activation function f(2) (·) is dependent on the target task. Since the estimation is proceeded in a forward manner, this type of network is also called feed-forward neural network.
When regarded the hidden layer in Eq. (1) as feature extractor ϕ(v) = [ϕj(v)] ∈ ℝM from an input v, the output layer is nothing but a simple linear model
| (2) |
where . The same interpretation holds when we have a more number of hidden layers. Thus, it is intuitive to understand that the role of hidden layers are to find features informative for the target task.
For the practical use of neural networks, it is required to learn model parameters Θ from data. This parameter learning problem can be formulated as error function minimization. From an optimization perspective, an error function E for neural networks is highly non-linear and non-convex. Thus, there is no analytic solution of the parameter set Θ. Instead, it is possible to resort to a gradient descent algorithm by updating the parameters iteratively. To utilize a gradient descent algorithm, it is required for a way to compute a gradient ∇E (Θ) evaluated at the parameter set Θ.
For a feed-forward neural network, the gradient can be efficiently evaluated by means of error backpropagation (61). Once we obtain the gradient vector of all the layers, the parameters θ ∈ {W(1),W(2),b(1),b(2)} are updated as follows
| (3) |
where η is a learning rate and τ denotes an iteration index. The update process repeats until convergence or reaching to the predefined number of iterations. As for the parameter update in Eq. (3), the stochastic gradient descent with a small subset of training samples, thus called as mini-batch, is commonly used in the literature (62).
2.2. Deep Models
Under a mild assumption on the activation function, a two-layer neural network with a finite number of hidden units can approximate any continuous function (63), and thus it is regarded as universal approximator. However, it is also possible to approximate complex functions to the same accuracy using a ‘deep’ architecture, i.e., more than two layers, with much fewer number of units in total (3). Hence, it is possible to reduce the number of trainable parameters, thus allowing to train with a relatively small dataset (64).
2.3. Unsupervised feature representation learning
Compared to shallow architectures that require a ‘good’ feature extractor, mostly designed in a handcrafted manner based on domain expert knowledge, deep models are useful to discover informative features from data in a hierarchical manner, i.e., fine-to-abstract. Here, we introduce three deep models widely used in different applications for unsupervised feature representation learning.
2.3.1. Stacked Auto-Encoder
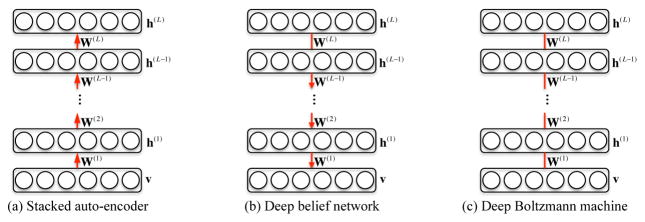
An auto-encoder, also known as auto-associator (65), is a special type of two-layer neural network that learns a latent or compressed representation of the input by minimizing the reconstruction error between the input and the output values of the network, i.e., reconstruction of the input from the learned representations. Note that due to its simple shallow structural characteristic, the representational power of a single-layer auto-encoder is known to be very limited. But when stacking multiple auto-encoders as shown in Fig. 2(a), which is thus called as stacked auto-encoder (SAE), by taking the activation values of hidden units of an auto-encoder as the input to the following upper auto-encoder, it is possible to improve the representational power greatly (66). Thanks to the hierarchical nature in structure, one of the most important characteristics of the SAE is to learn or discover highly non-linear and complicated patterns such as the relations among input values. When an input vector is presented to an SAE, the different layers of the network represent different levels of information. That is, the lower the layer in the network, the simpler patterns; the higher the layer, the more complicated or abstract patterns inherent in the input vector.
Figure 2.
Three representative deep models with vectorized inputs for unsupervised feature learning. The red links, whether they are directed or undirected, denote the full connections of units in two consecutive layers but no connections among units in the same layer. Note the differences among models in directed/undirected connections and directions of connections that depict the conditional relationships.
With regard to training parameters of the weight matrices and the biases in SAE, a straightforward way is to apply backpropagation with the gradient-based optimization technique starting from random initialization by regarding the SAE as a conventional feed-forward neural network. Unfortunately, it is generally known that deep networks trained in that manner perform worse than networks with a shallow architecture, suffering from falling into a poor local optimum (67). To circumvent this problem, it is good to consider a greedy layer-wise learning (5, 68). The key idea in a greedy layer-wise learning is to pre-train one layer at a time. That is, we first train parameters of the 1st hidden layer with the training data as input, and then train parameters of the 2nd hidden layer with the outputs from the 1st hidden layer as input, and so on. That is, the representation of the l-th hidden layer is used as input for the (l + 1)-th hidden layer. The important feature of such pre-training technique is that it is conducted in an unsupervised manner with a standard backpropagation algorithm, thus allowing to increase the dataset size by exploiting unlabelled samples for training.
2.3.2. Deep Belief Network
A restricted Boltzmann machine (RBM) (69) is a single-layer undirected graphical model with a visible layer and a hidden layer. It assumes symmetric connectivities between visible and hidden layers, but no connections among units within the same layer. Because of the symmetry of the connectivities, it is allowed to generate input observations from hidden representations. Therefore, an RBM naturally becomes an auto-encoder (5, 69) and their parameters are usually trained using a contrastive divergence algorithm (70) so as to maximize the log-likelihood of observations. Similar to SAE, it is possible to stack multiple RBMs for deep architecture construction, which results in a single probabilistic model, called a deep belief network (DBN). A DBN has one visible layer v and a series of hidden layers h(1), ···, h(L) as shown in Fig. 2(b). Note that once stacking multiple RBMs hierarchically, while the top two layers still form an undirected generative model, i.e., RBM, the lower layers form directed generative models. Hence, the joint distribution of the observed units v and the L hidden layers h(l) (l = 1, …, L) in DBN is given as follows
| (4) |
where h(0) = v, P(h(l−1)|h(l)) corresponds to a conditional distribution for the units of the layer l − 1 given the units of the layer l, and P(h(L−1),h(L)) denotes the joint distribution of the units in the layers L − 1 and L.
As for the parameters learning, the greedy layer-size pre-training scheme (5) can also be applied as follows:
Train the first layer as an RBM with v = h(0).
Use the first hidden layer to obtain the representation of inputs with either the mean activations of P(h(1) = 1|h(0)) or samples drawn according to P(h(1)|h(0)), which will be used as observations for the second hidden layer.
Train the second hidden layer as an RBM, taking the transformed data (mean activations of samples) as training examples (for the visible layer of the RBM).
Iterate steps (ii) and (iii) for the desired number of layers, each time propagating upward either mean activations of samples.
After the greedy layer-wise procedure is completed, it is possible to apply the wake-sleep algorithm (71) to further increase the log-likelihood of observations. But in most practice, no further procedure is made to train the whole DBN jointly.
2.3.3. Deep Boltzmann Machine
A deep Boltzmann machine (DBM) (51) is also constructed by stacking multiple RBMs in a hierarchical manner. However, unlike the DBN described above, all the layers in DBM still form an undirected generative model after stacking RBMs as illustrated in Fig. 2(c). Thus, for the hidden layer l except for the case of l = 1, its probability distribution is conditioned by its two neighboring layers l + 1 and l − 1, i.e., P(h(l)|h(l+1),h(l−1)). The incorporation of information from both the upper and the lower layers improves a DBM’s representational power to be more robust to noisy observations.
Let us consider a three-layer DBM, i.e., L = 2 in Fig. 2(c). Given the values of the units in the neighboring layer(s), the probability of the binary visible or binary hidden units being set to 1 is computed as follows
| (5) |
| (6) |
| (7) |
where σ(·) denotes a logistic sigmoid function. In order to learn the parameters Θ = {W(1),W(2)}, we maximize the log-likelihood of the observed data. The derivative of the log-likelihood of the observed data with respect to the model parameters takes the following simple form
| (8) |
where 𝔼data [·] denotes the data-dependent statistics obtained by sampling the model conditioned on the visible units v(= h(0)) and 𝔼model [·] denotes the data-independent statistics obtained by sampling from the model. When the model approximates the data distribution well, it can be reached for the equilibrium of data-dependent and data-independent statistics.
2.4. Fine-tuning deep models for target tasks
Note that during the feature representation learning for the three deep models described above, the target values either discrete labels or continuous real-values of observations were never involved. Therefore, there is no guarantee that the learned representations by SAE, DBN, or DBM are discriminative for a classification task, for example. To tackle this problem, generally the so-called fine-tuning step is followed after the unsupervised feature representation learning.
For a certain task of either classification or regression, it is straightforward to convert the feature representation learning models into a deep neural network by stacking another output layer on top of the highest hidden layer in SAE, DBN, or DBM with an appropriate output function. Here, one noticeable thing for the case of DBM is that for each input vector, they first should be augmented with the marginals of the approximate posterior of the second hidden layer as by-product when converting a DBM to a deep neural network (51). The top output layer is then used to predict the target value(s) of an input. To fine-tune the parameters in a deep neural network, we first take the pre-trained connection weights of the hidden layers as their initial values, randomly initilize the connection weights between the top hidden layer and the output layer, and then train the whole parameters jointly in an supervised (i.e., end-to-end) manner by gradient descent with a backpropagation algorithm. It is empirically proved that the initialization of the parameters via pre-training helps the supervised optimization reduces the risk of falling into local poor optima (5, 67).
2.5. Convolutional neural networks
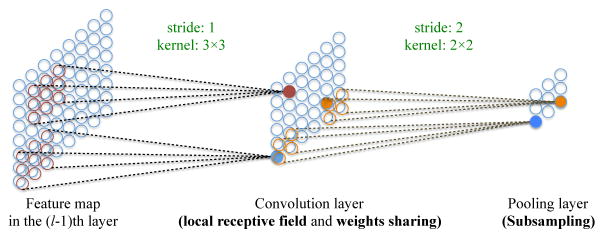
In deep models of SAE, DBN, and DBM described above, the inputs are always in vector form. However, for (medical) images, the structural information among neighboring pixels or voxels is another importance source of information. Hence, the vectorization inevitably destroys such structural and configural information in images. A convolutional neural network (CNN) (72) is designed to better utilize spatial and configuration information by taking 2D or 3D images per se as input. Structurally, CNNs have convolutional layers interspersed with pooling layers, followed by fully connected layers as in a standard multi-layer neural network. Unlike deep neural networks, a CNN exploits three mechanisms of local receptive field, weights sharing, and subsampling as illustrated in Fig. 3 that help greatly reduce the degrees of freedom of a model.
Figure 3.
A graphical illustration of three key mechanisms (i.e., local receptive field, weights sharing, and subsampling) in convolutional neural networks.
The role of a convolution layer is to detect local features at different positions in the input feature maps with learnable kernels , i.e., connection weights between the feature map i at the layer l − 1 and the feature map j at the layer l. Specifically, the units of the convolution layer l compute their activations based only on a spatially contiguous subset of units in the feature maps of the preceding layer l − 1 by convolving the kernels as follows:
| (9) |
where M(l−1) denotes the number of feature maps in the layer l − 1, * denotes a convolution operator, is a bias parameter, and f (·) is a non-linear activation function. Due to the mechanisms of weight sharing and local receptive field, when the input feature map is slightly shifted, the activation of the units in the feature maps are also shifted by the same amount.
A pooling layer follows a convolution layer to down-sample the feature maps of the preceding convolution layer. Specifically, each feature map in a pooling layer is linked with a feature map in the convolution layer; each unit in a feature map of the pooling layer is computed based on a subset of units within a local receptive field from the corresponding convolution feature map. Similar to the convolution layer, the receptive field that finds a representative value, e.g., maximum or average, among the units in its field. Usually, a stride of the size of the receptive field in pooling layers is set equal to the size of the receptive field for sub-sampling, which thus helps a CNN to be translation invariant.
Theoretically, the gradient-descent method combined with a backpropagation algorithm is also applied for learning parameters of a CNN. However, due to the special mechanisms of weights sharing, local receptive field, and pooling, it needs slight changes accordingly, i.e., to sum the gradients for a given weight over all the connections using the kernel weights, to figure out which patch in the layer’s feature map corresponds to a unit in the next layer’s feature map, and to up-sample the feature maps of the pooling layer to recover the reduced size of maps.
2.6. Reducing overfitting
A critical challenge in training deep models arises mostly from the limited number of training samples, compared to the number of learnable parameters. Thus, it has always been an issue to reduce overfitting. In this regard, recent studies have devised nice algorithmic techniques to better train deep models. Some of the techniques are as follows:
Initialization and momentum (73, 74): to use a well-designed random initialization and a particular schedule of slowly increasing the momentum parameter as iteration passes
Rectified linear unit (ReLU) (7, 75, 76): to apply for non-linear activation function
Denoising (6): to stack layers of denoising auto-encoders, which are trained locally to reconstruct the original ‘clean’ inputs from the corrupted versions of them
Dropout (8), dropconnect (77): to randomly deactivate a fraction of the units or connections, e.g., 50%, in a network on each training iteration
Batch normalization (9): to perform normalization for each mini-batch and backpropagating the gradients through the normalization parameters.
For the further details, refer to the respective references.
3. APPLICATIONS IN MEDICAL IMAGING
Impressive improvements by deep learning, over other machine learning techniques in the literature, have been demonstrated. Those successes have been attractive enough to draw an attention of researchers in the field of computational medical imaging to investigate the potential of deep learning in medical images acquired with CT, MRI, PET, and X-ray, for example. In the following, we introduce the practical applications of deep learning in medical images for image registration/localization, anatomical/cell structures detection, tissue segmentation, and computer-aided disease diagnosis/prognosis.
3.1. Deep feature representation learning in medical images
Many existing medical image processing methods rely on morphological feature representations to identify the local anatomical characteristics. However, such feature representations were mostly designed by human experts, i.e., handcrafted, requiring intensive dedicated efforts. Moreover, the designed image features are often problem-specific and hardly reusable, i.e., not guaranteed to work for other image types. For instance, the methods of image segmentation and registration designed for 1.5-Tesla T1-weighted brain MR images are not applicable to 7.0-Tesla T1-weighted MR images (48, 24), not to mention to other modalities or different organs. Further, as demonstrated in (78), 7.0-Tesla MR images can reveal the brain’s anatomy with the resolution equivalent to that obtained from thin slices in vitro. Thus, researchers are able to observe clearly the fine brain structures in μm unit, which was only possible with in vitro imaging in the past. However, lack of efficient computational tools substantially hinders the translation of new imaging technique into medical imaging arena.
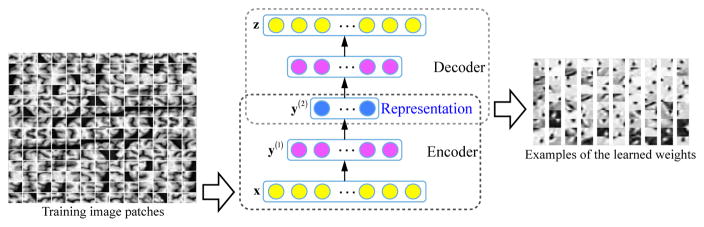
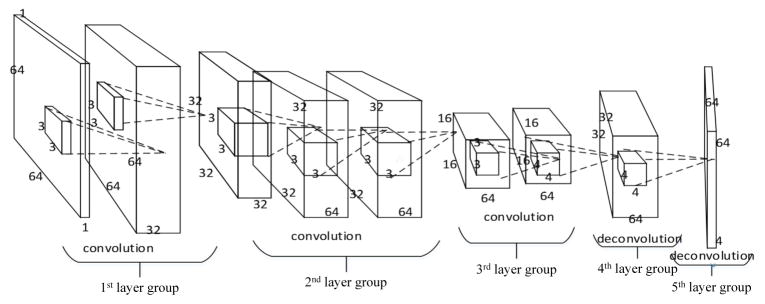
Although current state-of-the-art methods use supervised learning to find the most relevant and essential features for target tasks, they require a significant amount of manually labeled training data, while the learned features may be superficial and may misrepresent the complexity of anatomical structures. More critically, the learning procedure is often confined to the particular template domain, with a certain number of pre-designed features. Therefore, once template or image features change, the entire training process has to start over again. To address these limitations, Wu et al. (48, 24) have developed a general feature representation framework that (i) can sufficiently capture the intrinsic characteristics of anatomical structures for accurate brain region segmentation and correspondence detection; (ii) can be flexibly applied to different kinds of medical images. Specifically, they used an SAE with a sparsity constraint, thus they called it sparse auto-encoder, to hierarchically learn feature representations in a layer-by-layer manner. As shown in Fig. 4, their SAE model consisted of encoding and decoding modules hierarchically. In the encoding module, given an input image patch x, it first mapped the input to an activation vector y(1) through a non-linear deterministic mapping. Then they repeated this procedure by using the y(1) as the input to train the second layer and so forth until they obtained the high-level feature presentations (blue circles in Fig. 4). The decoding module was used to validate the expressive power of the learned feature representations by minimizing the reconstruction errors between the input image patch x and the reconstructed patch z after decoding.
Figure 4.
Construction of a deep encoder-decoder via SAE and visualization of the learned feature representations.
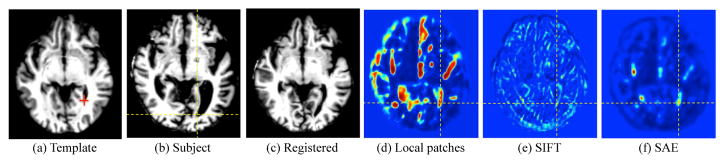
The power of feature representations learned by deep learning is demonstrated in Fig. 5, where the first three images show a typical image registration result for the elderly brain images and the last three images compare the use of different feature representations for finding a correspondence of a template point, indicated by the red cross in Fig. 5(a). In the last images, the different colors of voxels indicate their likelihood of being selected as correspondence in the respective location. From the figure, it is obvious that the deformed subject image in Fig. 5(c) is far from being well registered with the template image in Fig. 5(a), especially for ventricles. Noticeably, it is very difficult to learn meaningful features given such inaccurate correspondences derived from imperfect image registration, as suffered by many supervised learning methods (79, 80, 81). Further, we can observe that for the cases of using handcrafted features, i.e., local patches and SIFT (scale-invariant feature transform) (82), they either detect too many non-corresponding points when using the entire intensity patch as the feature vector as shown in Fig. 5(d) or have too low responses and thus miss the correspondence when using SIFT features as shown in Fig. 5(e). Meanwhile, the SAE-learned feature presentations reveal the least confusing correspondence information for the subject point under consideration, thus making it easy to locate the correspondence of the red-cross template point in the subject image domain.
Figure 5.
The similarity maps of identifying the correspondence for the red-crossed point in the template (a) w.r.t. the subject (b) by handcraft features (d–e) and the SAE learned features by unsupervised deep learning (f). The registered subject image is shown in (c). It is clear that the inaccurate registration results might undermine the supervised feature representation learning that highly relies on the correspondences across all training images.
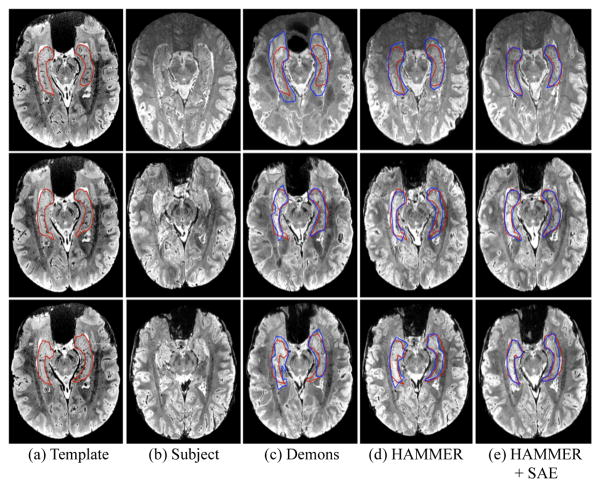
In order to qualitatively evaluate the registration accuracy, they further showed deformable image registration results over various public datasets, as presented in Fig. 6, where the manually labeled hippocampus on the template image and the deformed subject’s hippocampus by different registration methods are marked by red and blue contours, respectively. Compared to the state-of-the-art registration methods of intensity-based diffeomorphic Demons (83) and feature-based HAMMER (84) for 1.5- and 3.0-Tesla MR images, the method of using the SAE-learned feature representation in Fig. 6(e) presents better performance in terms of overlapping between the red contour and the blue contour.
Figure 6.
Typical registration results on 7.0-Tesla MR brain images by Demons (83), HAMMER (84), and HAMMER combined with SAE-learned feature representations, respectively. Three rows represent three different slices in the template, subject, and registered subjects.
Another successful medical application is to localize a prostate from MR images (85, 86). Accurate prostate localization in MR images is difficult due to the following two main challenges: (i) the appearance patterns vary a lot around the prostate boundary across patients and (ii) the intensity distributions highly vary across different patients and do not often follow the Gaussian distribution. To address these challenges, Guo et al. (86) applied SAE to learn the hierarchical feature representations from MR prostate images. Their learned features were integrated in a sparse patch matching framework to find the corresponding patches in the atlas images for label propagation (87). Finally, a deformable model was adopted to segment the prostate by combining the shape prior with the prostate likelihood map derived from sparse patch matching. Fig. 7 gives the typical prostate segmentation results of different patients produced by four different feature representations. For better understanding, 3D visualization of the segmentation results is also presented below each 2D segmentation results. For each 3D visualization, the red surface indicates automatic segmentation results with different features, such as intensity, handcrafted, and SAE-learned feature representations, respectively. The transparent grey surfaces indicate the ground-truth segmentations.
Figure 7.
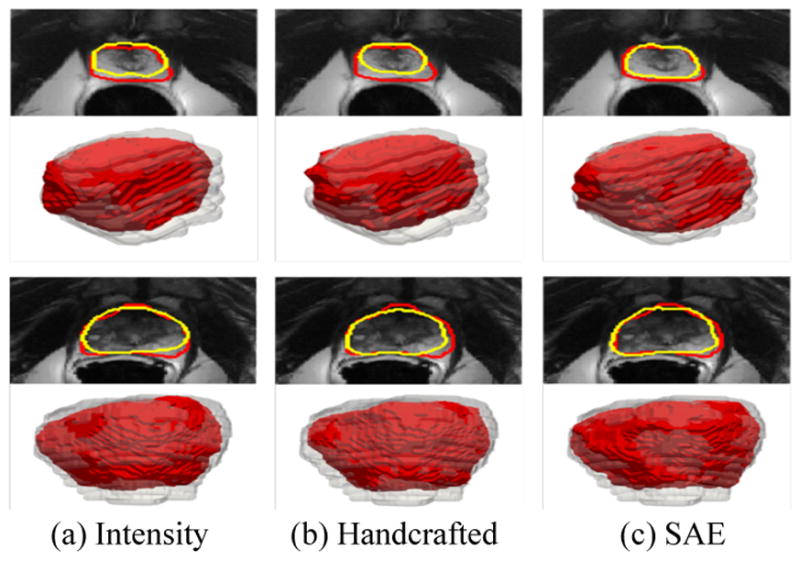
Typical prostate segmentation results of two different patients produced by three different feature representations. Red contours indicate the manual ground-truth segmentations, and yellow contours indicate the automatic segmentations. The second and fourth rows show the 3D visualization of the segmentation results corresponding to the images above. For each 3D visualization, the red surfaces indicate the automatic segmentation results using different features, such as intensity, handcrafted, and deep learning, respectively. The transparent grey surfaces indicate the ground-truth segmentations.
From the applications described above, we observe that (i) the latent feature representations inferred by deep learning can well describe the local image characteristics; (ii) we can rapidly develop image analysis methods for new medical imaging modalities by using deep learning framework to learn the intrinsic feature representations; and (iii) the whole learning-based framework is fully adaptive to learn the image data and reusable to various medical imaging applications, such as hippocampus segmention (88) and prostate localization in MR images (85, 86).
3.2. Deep learning for structures detection
Localization and interpolation of anatomical structures in medical images is a key step in radiological workflow. Radiologists usually accomplish this task by identifying some anatomical signatures, i.e., image features that can distinguish one anatomy from others. Is it possible for a computer to automatically learn such anatomical signatures as well? The success of computational methods is essentially dependent on how many anatomy signatures can be well extracted by the computational operations. While earlier studies often crafted specific image filters to extract anatomy signatures, more recent research trends show the prevalence of deep learning-based approaches thanks to two facts: (i) deep learning technologies become mature to solve real-world problems; (ii) more and more medical image datasets become available to facilitate the exploration of big medical image data.
3.2.1. Organ/bodypart detection
Shin et al. (47) demonstrated the applications of SAEs for separately learning both visual and temporal features, based on which they detected multiple organs in a time series of 3D dynamic contrast-enhanced MRI scans over datasets from two studies of liver metastases and one study of kidney metastases. Unlike the conventional SAEs, they applied a pooling operation after each layer so that features of progressively larger input regions were essentially compressed. According to the fact that different organ classes have different properties, they trained multiple models for tasks of separating each of the organs from all the other organs in a supervised manner.
In the mean time, Roth et al. (89) presented a method for organ- or bodypart-specific anatomical classification of medical images using deep convolutional networks. Specifically, they trained their deep network by using 4,298 axial 2D CT images to learn 5 anatomical classes, i.e., neck, lungs, liver, pelvis, and legs. In their experiments, they achieved an anatomy-specific classification error of 5.9% and an area under the receiver operating characteristic curve (AUC) value of 0.998, on average, in testing. However, real-world applications may require a finer grained differentiation beyond 5 body-parts, e.g., aortic arch vs cardiac sections. To address this limitation, Yan et al. (90, 91) used CNN in slice-based body part recognition, aiming to know which body part it came from a transversal slice of MR scan. Since each slice may contain multiple organs (enclosed in the bounding boxes), their CNN was trained in multi-instance fashion (92), where the objective function in CNN was adapted to in a way that as long as one organ was correctly labeled, the corresponding slice was considered as correct. In that way, the pre-trained CNN was sensitive to the discriminative bounding boxes. Based on the responses of the pre-trained CNNs, discriminative and non-informative bounding boxes were selected to further boost the representation power of the pre-trained CNN. At run-time, a sliding window approach was employed to apply the boosted CNN to the subject image. As the CNN only had peaky responses on discriminative bounding boxes, it essentially identified body parts by focusing on the most distinctive local information. Compared to the global image context-based approaches, their local approach was more accurate and robust. Their bodypart recognition method was tested to recognize 12 bodyparts on 7,489 CT slices, collected from scans of 675 patients with highly varying ages (1–90 years old). The whole dataset was divided into 2,413 (225 patients) training, 656 (56 patients) validation, and 4,043 (394 patients) testing subjects. They achieved the classification accuracy at 92.23%, which was already acceptable in some use cases.
3.2.2. Cell detection
Recently, it has become amenable to use digitized tissue histopathology for microscopic examination and automatic disease grading. One of the main challenges in microscopic image analysis comes from the need of analyzing all individual cells for accurate diagnosis, because the differentiation of most disease grades highly depends on the cell-level information. To tackle this challenge, deep CNN has been investigated to robustly and accurately detect and segment cells from histopathological images (33, 93, 94, 95, 49, 50, 34), which can significantly benefit the cell-level analysis for cancer diagnosis.
As the pioneering work, Cireşan et al. (33) used deep CNN to detect mitosis in breast histology images. Their networks were trained to classify each pixel in the images from a patch centered on the pixel. Their method won the 2012 ICPR Mitosis Detection Contest3, outperforming other contestants by a significant margin. Ever since their work, different groups used different deep learning methods for detection in histology images. For example, Xu et al. (50) used SAE to detect cells on breast cancer histopathological images. For training their deep model, they utilized a denoising auto-encoder for improving robustness to outliers and noises. Su et al. (49) also used SAE and sparse representation to detect and segment cells from microscopic images. Sirinukunwattana et al. (96) proposed a spatially constrained CNN (SC-CNN) to detect and classify nuclei in histopathological images. Specifically, they used SC-CNN to estimate the likelihood of a pixel being the center of a nucleus, where high probability values were spatially constrained to locate in the vicinity of the center of nuclei. To determine the nuclei type, they also developed a neighboring ensemble predictor coupled with CNN to more accurately predict the class label of detected cell nuclei. Chen et al. (34) designed deep cascaded CNN by leveraging the fully CNN (97). They first trained a coarse retrieval model to identify and locate the candidates of mitosis while preserving a high sensitivity. Based on the retrieved candidates, a fine discrimination model was then utilized by transferring knowledge from cross-domain to further single out mitoses from hard mimics. Their cascaded CNN achieved the best detection accuracy in 2014 ICPR MITOS-ATYPIA challenge4.
3.3. Deep learning for segmentation
Automatic segmentation in brain images is a prerequisite for quantitative assessment of the brain at all ages, ranging from infant to elderly. One of the main steps in brain image preprocessing involves removing non-brain regions, such as skull. While current methods demonstrate good results on non-enhanced T1-weighted images, they still struggle for other modalities and pathologically altered tissues. To circumvent such limitations, Kleesiek et al. (23) presented the use of 3D convolutional deep learning architecture for skull extraction, not limited to non-enhanced T1-weighted MR images. While training their 3D-CNN, they constructed mini-batches of multiple cubes, whose size was larger than the actual size of an input to their 3D-CNN for computational efficiency. Specifically, their deep model could take an arbitrary-sized 3D patch as input by building a fully convolutional CNN (97), and thus the output could be a block of predictions per input, rather than a single prediction as a conventional CNN has. Over four different datasets, their method achieved the highest average specificity measures, while the sensitivity displays about average results.
Regarding to accurate tissue segmentation, Moeskops et al. (98) devised a multi-scale CNN to enhance the robustness by ensuring segmentation details and spatial consistency. As the name says, their network used multiple patch sizes and multiple convolution kernel sizes to acquire multi-scale information about each voxel. Their method with multi-scale CNN attained promising segmentation results on eight tissue types with the Dice ratio averaging from 0.82 to 0.91 over five different datasets.
In human brain development, the first year of life is the most dynamic phase of the postnatal human brain development, with the rapid tissue growth and development of a wide range of cognitive and motor functions. Accurate tissue segmentation of infant brain MR images into white matter (WM), gray matter (GM), and cerebrospinal fluid (CSF) in this phase is of great importance in studying the normal and abnormal early brain development. It is well-known that the segmentation of infants’ brain MRI is considerably more difficult than adults’ brain MRI, because of the reduced tissue contrast (99), increased noise, severe partial volume effect (100), and ongoing WM myelination (99, 101) in the infant brain. Specifically, the WM and GM exhibit almost the same intensity level (especially in the cortical regions), resulting in the low image contrast. Although many methods have been proposed for infant brain image segmentation, most of those focused on segmentation of either neonatal images (~3 months) or infant images (>12 months) using a single T1-weighted or T2-weighted image (102, 103, 104, 105, 106). Few studies have addressed the difficulties in segmentation of the isointense-phase images.
To overcome the above-mentioned difficulties, Zhang et al. (22) designed four CNN architectures to segment infant brain tissues based on multi-modality MR images. Specifically, their CNN architecture contained three input feature maps corresponding to T1-weighted, T2-weighted, and fractional anisotropy (FA) image patches of 13×13 in size. It then applied three convolutional layers and one fully connected layer, followed by an output layer with a softmax function for tissue classification. In comparison with the commonly used segmentation methods on a set of manually segmented isointense stage brain images, they validated the effectiveness of their CNN significantly outperforming the competing methods. More recently, Nie et al. (44) proposed a multiple fully convolutional networks (mFCNs), illustrated in Fig. 8, to segment the isointense-phase brain image with T1-weighted, T2-weighted and FA modality information. Instead of simply combining three modality data from the original (low-level) feature maps, they proposed a deep architecture to effectively fuse their high-level information from three modalities. They assumed that high-level representations from different modalities were more complementary to each other. They first trained one network for each modality, in order to effectively employ information from multiple modalities, and then fused multiple-modality features from high-layer of each network, as shown in the top of Fig. 8. In their experiments, mFCNs could achieve the average Dice ratios of 0.852 for CSF, 0.873 for GM, and 0.887 for WM from 8 subjects, outperforming FCNs and other competing methods.
Figure 8.
An architecture of the fully convolutional network used for tissue segmentation in (44).
3.4. Deep learning for computer-aided detection (CADe)
Computer-aided detection (CADe) is to find or localize abnormal or suspicious regions, and thus to alert clinicians for attention. The primary goal of CADe is to increase the detection rate of diseased regions while reducing the false negative rate possibly due to mistake or fatigue of observers. While CADe is regarded as a well established area in the medical imaging field, deep learning methods have recently further improved performance in different clinical applications.
Typically, the conventional pipeline of CADe is as follows: (i) the candidate regions are first detected by means of image processing techniques; (ii) the candidate regions are represented by a set of features such as morphological or statistical information; (iii) the features are fed into a classifier, e.g., support vector machine (SVM), to output a probability or make a decision of being diseased. As explained in Section 1, the handcrafted feature representations can be absorbed into deep learning. Many groups have successfully applied their own deep models for applications such as pulmonary nodules detection, lymph nodes detection, interstitial lung disease classification in CT, cerebral microbleeds detection, multiple sclerosis lesion detection in MRI, for example. Noticeably, most of the methods in the literature exploited deep convolutional models to maximally utilize structural information in 2D, 2.5D, or 3D.
Ciompi et al. (39) used a pre-trained OverFeat (107) out-of-the-box as feature extractor and empirically showed that the CNN learned from a completely different domain of natural images could provide useful feature descriptions for pulmonary peri-fissural nodules classification. Roth et al. (36) focused on training deep models from scratch. To tackle the problem of data insufficiency in training deep CNNs, they expanded their dataset by scaling, translation, and rotation in random over training samples. They also augmented the test samples in a similar way, obtained the CNN outputs for every augmented test samples, and finally took the average of the outputs of the randomly transformed/scaled/rotated patches for lymph nodes and colonic polyps detection. In the meantime, to better utilize volumentric information in images, Ciompi et al. (39) and Roth et al. (36) considered 2.5D information with 2D patches of three orthogonal views (axial, saggital, and coronal). Setio et al. (38) considered three sets of orthogonal views, in total 9 views from a 3D patch and used ensemble methods to fuse information from different views for pulmonary nodule detection.
Gao et al. (108) focused on the holistic classification of CT patterns for interstitial lung disease with a deep CNN. They borrowed the network architecture from (109) with 6 units at the output layer for their target application of classifying patches into one of normal, emphysema, ground glass, fibrosis, micronodules, and consolidation. In order to overcome the overfitting problem, they utilized a data augmentation strategy by generating images by randomly jittering and cropping 10 subimages per original CT slice. At the testing stage, they generated 10 jittered images and then fed those into the trained CNN. Finally, they predicted the input slice by aggregation, similar to Roth et al.’s work (36).
Shin et al. (41) conducted experiments on datasets of thoraco-abdominal lymph node detection and interstitial lung disease classification to explore how the CNN performance changes according to factors of CNN architectures, dataset characteristics, and transfer learning. They considered 5 deep CNNs of CifarNet (110), AlexNet (109), Overfeat (107), VGG-16 (111), and GoogLeNet (112) that achieved state-of-the-art performances in various computer vision applications. From their extensive experiments, they drew some interesting findings: (i) It was consistently beneficial for CADe problems to transfer-learning from the large scale annotated natural image datasets (ImageNet); (ii) Applications of off-the-shelf deep CNN features to CADe problems could be improved by exploring the performance-complementary properties of handcrafted features.
Unlike the studies above that used deterministic deep architectures, van Tulder and de Bruijne (31) exploited a deep generative model with convolutional RBM as basic building blocks for interstitial lung disease classification. In particular, they used a discriminative RBM that has an additional label layer along with input and hidden layers to improve the discriminative power of learned feature representations. From their experiments, they showed the advantages of combining generative and discriminative learning objectives by achieving higher performance than that of purely generative or discriminative learning methods.
In applications of using brain images, Pereira et al. (30) studied for brain tumor segmentation using CNNs in MR images. In particular, they explored small-sized kernels to have the fewer number of parameters but deeper architectures. They trained different CNN architectures for low and high grade tumors and validated their method in 2013 Brain Tumor Segmentation (BRATS) Challenge5, where they ranked the top for the complete, core, and enhancing regions for the challenge dataset. Brosch et al. (45) applied deep learning for multiple sclerosis lesion segmentation on MR images. Their model was a 3D-CNN, composed of two interconnected pathways, i.e., convolutional pathway that learned hierarchical feature representations as other CNNs did and deconvolutional pathway that consisted of deconvolutional and unpooling layers with shortcut connections to the corresponding convolutional layers. Specifically, the deconvolutional layers were designed to calculate abstract segmentation features from the features represented from the convolutional layers and the activations of the previous deconvolutional layer, if exist. In comparison with five publicly available methods for multiple sclerosis lesion segmentation, their method achieved the best performance in the metrics of Dice similarity coefficient, absolution volume difference, and lesion-wise false positive rate.
One of the main limitations of the typical deep CNNs arises from the fixed architecture of the model themselves. That is, when the size of an input observation is larger than that of the unit in the input layer, the straightforward way is to apply a sliding window strategy. However, it is computationally very expensive and time/memory consuming. Due to this kind of scalability issue in CNNs, Dou et al. (32) devised a 3D fully connected network by transforming units in the fully connected layers into 3D (1×1×1) convolutionable kernel that allowed to process an arbitrary-sized input efficiently (97). The outputs of their 3D fully connected network could be re-mapped back into the original input, and thus it was possible to interpret the network output more intuitively. For cerebral microbleeds detection in MRI, they designed a cascade framework. Specifically, they first screened the inputs with the proposed 3D fully connected network to retrieve candidates with high probabilities of being cerebral microbleeds, and then applied a 3D CNN discrimination model for final detection. In their experiments, they validated the effectiveness of their method by removing massive redundant computations and dramatically speeding up the detection process.
3.5. Deep learning for computer-aided diagnosis (CADx)
Computer-aided diagnosis (CADx) provides a second objective opinion for an assessment of a disease from image-based information. The major applications of CADx are the discrimination of being malignant or benign for lesions and the identification of certain diseases from image(s). Conventionally, CADx systems were mostly developed to use handcrafted features that were engineered by domain experts. Recently, similar to other applications, deep learning methods have been successfully applied to CADx systems, too.
Cheng et al. (35) exploited SAE with a denoising technique (SDAE) for the differentiation of breast ultrasound lesions and lung CT nodules. Specifically, the image regions of interest (ROIs) were first resized into 28×28, where all pixels in each patch were treated as the input to the SDAE. At the pre-training step, they corrupted the input patches with random noises to enhance noise-tolerance of their model. Later, at the fine-tuning step, they further included the resized scale factors of the two ROI dimensions and the aspect ratios of the original ROIs to preserve the original information. Shen et al. (37) proposed a hierarchical learning framework with a multi-scale CNN to capture varying sizes of lung nodules. In their CNN architecture, three CNNs that took nodule patches from different scales as inputs were assembled in parallel. To reduce overfitting, they set the parameters of three CNNs to be shared during training. The activations of the top hidden layer in three CNNs, one for each scale, were concatenated to form a feature vector. For classification, they used SVM with radial basis function kernel and random forest, which were trained to minimize “companion objectives” defined as the combination of overall hinge loss function and sum of the companion hinge loss functions (113).
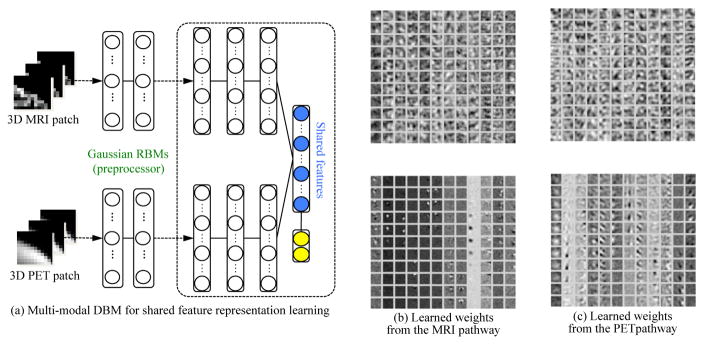
In applications of brain disease diagnosis, Suk et al. (27) used SAE to identify Alzheimer’s disease or mild cognitive impairment by fusing neuroimaging and biological features. In particular, they extracted gray matter volume features from MRI, regional mean intensity values from PET, and three biological features (Aβ42, p-tau, and t-tau) from CSF. After training modality-specific SAEs, for each modality, they constructed an augmented feature vector by concatenating the original features with the outputs of the top hidden layer of the respective SAEs. For clinical decision, a multi-kernel SVM (114) was trained. The same authors extended their work to find hierarchical feature representations by combining heterogeneous modalities during the feature representation learning, rather than in the classifier learning step (25). Specifically, they exploited DBM to find a latent hierarchical feature representation from a 3D patch, and then devised a systematic method for a joint feature representation, blue circles in Fig. 9(a), from the paired patches of MRI and PET with a multi-modal DBM. To enhance diagnostic performance, they also used a discriminative DBM by injecting a discriminative RBM (115) on top of the highest hidden layer. That is, the top hidden layer was connected to both the lower hidden layer and the additional label layer that indicated the label of the input patches, yellow circles in Fig. 9(a). In this way, they could train a multi-modal DBM to discover hierarchical and discriminative feature representations by integrating the process of discovering features of inputs with their use in classification. Fig. 9(b) and Fig. 9(c) visualize, respectively, the learned connection weights from the MRI pathway and the PET pathway, where each column with 11 patches in the upper block and the lower block composes a 3D volume patch.
Figure 9.
An illustration of (a) the shared feature learning from patches of the heterogeneous modalities, e.g., MRI and PET, with discriminative multi-modal DBM and (b, c) visualization of the learned weights in Gaussian RBMs (bottom) and those of the first hidden layer (top) from MRI and PET pathways in multi-modal DBM (25).
Plis et al. (116) applied DBN to MR images and validated feasibility of the application by investigating if a building block of deep generative models was competitive with independent component analysis, mostly widely used method for functional MRI (fMRI) analysis. They also examined the effect of the depth in deep learning analysis of structural MRI over schizophrenia dataset and Huntington disease dataset. Inspired by Plis et al.’s work, Kim et al. (117) and Suk et al. (29), independently, studied applications of deep learning for fMRI-based brain disease diagnosis. Kim et al. adopted an SAE for whole-brain resting-state functional connectivity pattern representation for schizophrenia (SZ) diagnosis and identification of aberrant functional connectivity patterns associated with SZ. They first computed Pearson’s correlation coefficients between every pairs of 116 regions based on their regional mean blood-oxygenation-level-dependent (BOLD) signals. After performing Fisher’s r-to-z transformation to the coefficients and Gaussian normalization sequentially, the pseudo z-scored levels were fed into their SAE. More recently, Suk et al. (29) proposed a novel framework of fusing deep learning with hidden Markov model (HMM) for functional dynamics estimation in resting-state fMRI and successfully applied for MCI diagnosis. Specifically, they devised a deep auto-encoder (DAE) by stacking multiple RBMs to discover hierarchical non-linear functional relations among brain regions. Fig. 10 visualizes examples of the learned connection weights in the form of functional networks. Their DAE was used to transform the regional mean BOLD signals into an embedding space, whose bases were understood as complex functional networks. After embedding functional signals, they then used HMM to estimate dynamic characteristics of functional networks inherent in rs-fMRI via internal states, which could be inferred from observations statistically. By building a generative model with an HMM, they estimated the likelihood of the input features of rs-fMRI as belonging to the corresponding status, i.e., MCI or normal healthy control, based on which they finally determined the clinical label of a testing subject.
Figure 10.
Functional networks learned from the first hidden layer of Suk et al.’s deep auto-encoder (29). Functional networks on the left column, from top to bottom, correspond to the default-mode network, executive attention network, visual network, subcortical regions, and cerebellum. On the right column, these show the relations among regions of different networks, cortices, and cerebellum.
There were also studies that exploited CNNs for brain disease diagnosis. Brosch et al. (43) performed manifold learning from down-sampled MR images using a deep generative model, which was composed of three convolutional RBMs and two following RBM layers. To speed up the calculation of convolutions, computational bottleneck of the training algorithm, they performed training in frequency domain. By generating volume samples from their deep generative model, they validated the effectiveness of deep learning for manifold embedding with no explicitly defined similarity measure or proximity graph. Li et al. (40) constructed a three-layer CNN with two convolutional layers and one fully connected layer. Specifically, they proposed to use CNNs for completing and integrating multiple-modality neuroimaging data by designing a 3D CNN architecture that received one volumetric MR patch as input and another volumetric PET patch as output. When trained end-to-end on subjects with both data modalities, the network captured the nonlinear relationship between two modalities. In their experiments, they demonstrated to predict and estimate the PET data given the input MRI data and evaluated the proposed data completion method quantitatively by comparing the classification results based on the true and the predicted PET images.
4. CONCLUSION
Computational modeling for medical image analysis has great impacts on both clinical applications and scientific researches. Recent progresses in deep learning have shed new light on medical image analysis by allowing discovering morphological and/or textural patterns in images solely from data. As deep learning methods have achieved the state-of-the-art performance over different medical applications, its use for further improvement can be the major step in the medical computing field. However, there are still rooms for improvements. First, lessoned in computer vision, where breakthrough improvements were achieved by exploiting large amounts of training data, e.g., more than 1 million annotated images in ImageNet (19), it would be one direction to build such big publicly available dataset of medical images, by which deep models can find more generalized features in medical images, thus allowing making a leap in performance. Second, while the data-driven feature representations, especially in an unsupervised manner, helped enhance accuracy, it is also desirable to devise a new methodological architecture, with which it becomes possible to reflect or involve the domain-specific knowledge. Third, it is also necessary to develop algorithmic techniques to efficiently handle images acquired with different scanning protocols, by which there is no need to train modality-specific deep models. Last but not least, when applying deep learning to investigate the underlying patterns in images such as fMRI, due to the black-box like characteristics of deep models, it still remains challenging to understand and interpret the learned models intuitively.
Acknowledgments
This work was supported by Institute for Information & communications Technology Promotion (IITP) grant funded by the Korea government (MSIP) (No.B0101-16-0307, Basic Software Research in Human-level Lifelong Machine Learning (Machine Learning Center)). This work was also supported by Basic Science Research Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science, ICT & Future Planning (NRF-2015R1C1A1A01052216), NIH grants (EB006733, EB008374, EB009634, MH100217, MH108914, AG041721, AG049371, AG042599, DE022676).
Footnotes
In general, the input layer is not counted.
For details, refer to http://ludo17.free.fr/mitos_2012/index.html.
For details, refer to http://mitos-atypia-14.grand-challenge.org/.
For details, refer to http://martinos.org/qtim/miccai2013/.
DISCLOSURE STATEMENT
The authors are not aware of any affiliations, memberships, funding, or financial holdings that might be perceived as affecting the objectivity of this review.
LITERATURE CITED
- 1.Brody H. Medical imaging. Nature. 2013;502:S81–S81. doi: 10.1038/502s81a. [DOI] [PubMed] [Google Scholar]
- 2.Schmidhuber J. Deep learning in neural networks: An overview. Neural Networks. 2015;61:85–117. doi: 10.1016/j.neunet.2014.09.003. [DOI] [PubMed] [Google Scholar]
- 3.Bengio Y. Learning deep architectures for ai. Foundations and Trends in Machine Learning. 2009;2:1–127. [Google Scholar]
- 4.LeCun Y, Bengio Y, Hinton G. Deep learning. Nature. 2015;521:436–444. doi: 10.1038/nature14539. [DOI] [PubMed] [Google Scholar]
- 5.Hinton GE, Salakhutdinov RR. Reducing the dimensionality of data with neural networks. Science. 2006;313:504–507. doi: 10.1126/science.1127647. [DOI] [PubMed] [Google Scholar]
- 6.Vincent P, Larochelle H, Lajoie I, Bengio Y, Manzagol PA. Stacked denoising autoencoders: Learning useful representations in a deep network with a local denoising criterion. Journal of Machine Learning Research. 2010;11:3371–3408. [Google Scholar]
- 7.Nair V, Hinton GE. Rectified linear units improve restricted boltzmann machines. Proceedings of International Conference on Machine Learning (ICML) 2010 [Google Scholar]
- 8.Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R. Dropout: A simple way to prevent neural networks from overfitting. Journal of Machine Learning Research. 2014;15:1929–1958. [Google Scholar]
- 9.Ioffe S, Szegedy C. Batch normalization: Accelerating deep network training by reducing internal covariate shift. Proceedings of International Conference on Machine Learning (ICML) 2015 [Google Scholar]
- 10.Bishop CM. Neural networks for pattern recognition. Oxford University Press, Inc; 1995. [Google Scholar]
- 11.Collobert R, Weston J. A unified architecture for natural language processing: Deep neural networks with multitask learning. Proceedings of International Conference on Machine Learning (ICML) 2008 [Google Scholar]
- 12.Sutskever I, Martens J, Hinton GE. Generating text with recurrent neural networks. Proceedings of International Conference on Machine Learning (ICML) 2011 [Google Scholar]
- 13.Hinton GE, Deng L, Yu D, Dahl GE, Mohamed A, et al. Deep neural networks for acoustic modeling in speech recognition: The shared views of four research groups. IEEE Signal Processing Magazine. 2012;29:82–97. [Google Scholar]
- 14.Szegedy C, Toshev A, Erhan D. Deep neural networks for object detection. Proceedings of Neural Information Processing Systems (NIPS) 2013:2553–2561. [Google Scholar]
- 15.Taigman Y, Yang M, Ranzato M, Wolf L. Deepface: Closing the gap to human-level performance in face verification. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2014 [Google Scholar]
- 16.Zhang J, Zong C. Deep neural networks in machine translation: An overview. IEEE Intelligent Systems. 2015;30:16–25. [Google Scholar]
- 17.Karpathy A, Li F. Deep visual-semantic alignments for generating image descriptions. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2015 doi: 10.1109/TPAMI.2016.2598339. [DOI] [PubMed] [Google Scholar]
- 18.Silver D, Huang A, Maddison CJ, Guez A, Sifre L, et al. Mastering the game of Go with deep neural networks and tree search. Nature. 2016;529:484–489. doi: 10.1038/nature16961. [DOI] [PubMed] [Google Scholar]
- 19.Russakovsky O, Deng J, Su H, Krause J, Satheesh S, et al. ImageNet Large Scale Visual Recognition Challenge. International Journal of Computer Vision. 2015;115:211–252. [Google Scholar]
- 20.Everingham M, Van Gool L, Williams CKI, Winn J, Zisserman A. The PASCAL Visual Object Classes Challenge 2012 (VOC2012) Results. 2012 http://www.pascal-network.org/challenges/VOC/voc2012/workshop/index.html.
- 21.Roux L, Racoceanu D, Capron F, Calvo J, Attieh E, et al. MITOS-ATYPIA-14. 2014 http://mitos-atypia-14.grand-challenge.org/
- 22.Zhang W, Li R, Deng H, Wang L, Lin W, et al. Deep convolutional neural networks for multi-modality isointense infant brain image segmentation. NeuroImage. 2015;108:214–224. doi: 10.1016/j.neuroimage.2014.12.061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Kleesiek J, Urban G, Hubert A, Schwarz D, Maier-Hein K, et al. Deep MRI brain extraction: A 3D convolutional neural network for skull stripping. NeuroImage. 2016;129:460–469. doi: 10.1016/j.neuroimage.2016.01.024. [DOI] [PubMed] [Google Scholar]
- 24.Wu G, Kim M, Wang Q, Munsell BC, Shen D. Scalable high-performance image registration framework by unsupervised deep feature representations learning. IEEE Transactions on Biomedical Engineering. 2016;63:1505–1516. doi: 10.1109/TBME.2015.2496253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Suk HI, Lee SW, Shen D. Hierarchical feature representation and multimodal fusion with deep learning for AD/MCI diagnosis. NeuroImage. 2014;101:569–582. doi: 10.1016/j.neuroimage.2014.06.077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Shin H, Roberts K, Lu L, Demner-Fushman D, Yao J, Summers RM. Learning to read chest x-rays: Recurrent neural cascade model for automated image annotation. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2016 [Google Scholar]
- 27.Suk HI, Lee SW, Shen D. Latent feature representation with stacked auto-encoder for AD/MCI diagnosis. Brain Structure and Function. 2015;220:841–859. doi: 10.1007/s00429-013-0687-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Suk HI, Shen D. Deep learning in diagnosis of brain disorders. Recent Progress in Brain and Cognitive Engineering. 2015:203–213. [Google Scholar]
- 29.Suk HI, Wee CY, Lee SW, Shen D. State-space model with deep learning for functional dynamics estimation in resting-state fMRI. NeuroImage. 2016;129:292–307. doi: 10.1016/j.neuroimage.2016.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Pereira S, Pinto A, Alves V, Silva CA. Brain tumor segmentation using convolutional neural networks in MRI images. IEEE Transactions on Medical Imaging. 2016;35:1240–1251. doi: 10.1109/TMI.2016.2538465. [DOI] [PubMed] [Google Scholar]
- 31.van Tulder G, de Bruijne M. Combining generative and discriminative representation learning for lung CT analysis with convolutional restricted boltzmann machines. IEEE Transactions on Medical Imaging. 2016;35:1262–1272. doi: 10.1109/TMI.2016.2526687. [DOI] [PubMed] [Google Scholar]
- 32.Dou Q, Chen H, Yu L, Zhao L, Qin J, et al. Automatic detection of cerebral microbleeds from MR images via 3D convolutional neural networks. IEEE Transactions on Medical Imaging. 2016;35:1182–1195. doi: 10.1109/TMI.2016.2528129. [DOI] [PubMed] [Google Scholar]
- 33.Cireşan DC, Giusti A, Gambardella LM, Schmidhuber J. Mitosis detection in breast cancer histology images with deep neural networks. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2013:411–418. doi: 10.1007/978-3-642-40763-5_51. [DOI] [PubMed] [Google Scholar]
- 34.Chen H, Qi X, Cheng JZ, Heng PA. Deep contextual networks for neuronal structure segmentation. Proceedings of AAAI Conference on Artificial Intelligence 2016 [Google Scholar]
- 35.Cheng JZ, Ni D, Chou YH, Qin J, Tiu CM, et al. Computer-aided diagnosis with deep learning architecture: Applications to breast lesions in US images and pulmonary nodules in CT scans. Scientific Reports. 2016;6:24454EP. doi: 10.1038/srep24454. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Roth HR, Lu L, Liu J, Yao J, Seff A, et al. Improving computer-aided detection using convolutional neural networks and random view aggregation. IEEE Transactions on Medical Imaging. 2016;35:1170–1181. doi: 10.1109/TMI.2015.2482920. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Shen W, Zhou M, Yang F, Yang C, Tian J. Multi-scale convolutional neural networks for lung nodule classification. Proceedings of Information Processing in Medical Imaging (IPMI) 2015:588–599. doi: 10.1007/978-3-319-19992-4_46. [DOI] [PubMed] [Google Scholar]
- 38.Setio AAA, Ciompi F, Litjens G, Gerke P, Jacobs C, et al. Pulmonary nodule detection in CT images: False positive reduction using multi-view convolutional networks. IEEE Transactions on Medical Imaging. 2016;35:1160–1169. doi: 10.1109/TMI.2016.2536809. [DOI] [PubMed] [Google Scholar]
- 39.Ciompi F, de Hoop B, van Riel SJ, Chung K, Scholten ET, et al. Automatic classification of pulmonary peri-fissural nodules in computed tomography using an ensemble of 2D views and a convolutional neural network out-of-the-box. Medical Image Analysis. 2015;26:195–202. doi: 10.1016/j.media.2015.08.001. [DOI] [PubMed] [Google Scholar]
- 40.Li R, Zhang W, Suk HI, Wang L, Li J, et al. Deep learning based imaging data completion for improved brain disease diagnosis. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2014:305–312. doi: 10.1007/978-3-319-10443-0_39. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Shin HC, Roth HR, Gao M, Lu L, Xu Z, et al. Deep convolutional neural networks for computer-aided detection: CNN architectures, dataset characteristics and transfer learning. IEEE Transactions on Medical Imaging. 2016;35:1285–1298. doi: 10.1109/TMI.2016.2528162. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Gupta A, Ayhan M, Maida A. Natural image bases to represent neuroimaging data. Proceedings of International Conference on Machine Learning (ICML) 2013 [Google Scholar]
- 43.Brosch T, Tam R. Manifold learning of brain MRIs by deep learning. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2013:633–640. doi: 10.1007/978-3-642-40763-5_78. [DOI] [PubMed] [Google Scholar]
- 44.Nie D, Wang L, Gao Y, Sken D. Fully convolutional networks for multi-modality isointense infant brain image segmentation. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI) 2016 doi: 10.1109/ISBI.2016.7493515. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Brosch T, Tang LYW, Yoo Y, Li DKB, Traboulsee A, Tam R. Deep 3D convolutional encoder networks with shortcuts for multiscale feature integration applied to multiple sclerosis lesion segmentation. IEEE Transactions on Medical Imaging. 2016;35:1229–1239. doi: 10.1109/TMI.2016.2528821. [DOI] [PubMed] [Google Scholar]
- 46.Chen H, Dou Q, Wang X, Qin J, Heng P. Mitosis detection in breast cancer histology images via deep cascaded networks. Proceedings of AAAI Conference on Artificial Intelligence 2016 [Google Scholar]
- 47.Shin HC, Orton MR, Collins DJ, Doran SJ, Leach MO. Stacked autoencoders for unsupervised feature learning and multiple organ detection in a pilot study using 4D patient data. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2013;35:1930–1943. doi: 10.1109/TPAMI.2012.277. [DOI] [PubMed] [Google Scholar]
- 48.Wu G, Kim M, Wang Q, Gao Y, Liao S, Shen D. Unsupervised deep feature learning for deformable registration of MR brain images. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2013:649–656. doi: 10.1007/978-3-642-40763-5_80. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Su H, Xing F, Kong X, Xie Y, Zhang S, Yang L. Robust cell detection and segmentation in histopathological images using sparse reconstruction and stacked denoising autoencoders. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2015:383–390. doi: 10.1007/978-3-319-24574-4_46. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Xu J, Xiang L, Liu Q, Gilmore H, Wu J, et al. Stacked sparse autoencoder (SSAE) for nuclei detection on breast cancer histopathology images. IEEE Transactions on Medical Imaging. 2016;35:119–130. doi: 10.1109/TMI.2015.2458702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Salakhutdinov R. Learning deep generative models. Annual Review of Statistics and Its Application. 2015;2:361–385. [Google Scholar]
- 52.Munsell BC, Wee CY, Keller SS, Weber B, Elger C, et al. Evaluation of machine learning algorithms for treatment outcome prediction in patients with epilepsy based on structural connectome data. NeuroImage. 2015;118:219–230. doi: 10.1016/j.neuroimage.2015.06.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Maier O, Schrder C, Forkert ND, Martinetz T, Handels H. Classifiers for ischemic stroke lesion segmentation: A comparison study. PLoS ONE. 2015;10:1–16. doi: 10.1371/journal.pone.0145118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Havaei M, Davy A, Warde-Farley D, Biard A, Courville A, et al. Brain tumor segmentation with deep neural networks. Medical Image Analysis. 2017;35:18–31. doi: 10.1016/j.media.2016.05.004. [DOI] [PubMed] [Google Scholar]
- 55.Ronneberger O, Fischer P, Brox T. U-net: Convolutional networks for biomedical image segmentation. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2015:234–241. [Google Scholar]
- 56.Fakhry A, Peng H, Ji S. Deep models for brain EM image segmentation: novel insights and improved performance. Bioinformatics. 2016 doi: 10.1093/bioinformatics/btw165. [DOI] [PubMed] [Google Scholar]
- 57.Farag A, Lu L, Roth HR, Liu J, Turkbey E, Summers RM. A bottom-up approach for pancreas segmentation using cascaded superpixels and (deep) image patch labeling. CoRR. 2015 doi: 10.1109/TIP.2016.2624198. abs/1505.06236. [DOI] [PubMed] [Google Scholar]
- 58.Ghesu FC, Krubasik E, Georgescu B, Singh V, Zheng Y, et al. Marginal space deep learning: Efficient architecture for volumetric image parsing. IEEE Transactions on Medical Imaging. 2016;35:1217–1228. doi: 10.1109/TMI.2016.2538802. [DOI] [PubMed] [Google Scholar]
- 59.Wang CW, Huang CT, Lee JH, Li CH, Chang SW, et al. A benchmark for comparison of dental radiography analysis algorithms. Medical Image Analysis. 2016;31:63–76. doi: 10.1016/j.media.2016.02.004. [DOI] [PubMed] [Google Scholar]
- 60.Rosenblatt F. The perceptron: A probabilistic model for information storage and organization in the brain. Psychological Review. 1958:65–386. doi: 10.1037/h0042519. [DOI] [PubMed] [Google Scholar]
- 61.Rumelhart DE, Hinton GE, Williams RJ. Learning representations by back-propagating errors. Nature. 1986;323:533–536. [Google Scholar]
- 62.Le QV, Ngiam J, Coates A, Lahiri A, Prochnow B, Ng AY. On optimization methods for deep learning. Proceedings of International Conference on Machine Learning (ICML) 2011 [Google Scholar]
- 63.Hornik K. Approximation capabilities of multilayer feedforward networks. Neural Networks. 1991;4:251–257. [Google Scholar]
- 64.Schwarz G. Estimating the Dimension of a Model. The Annals of Statistics. 1978;6:461–464. [Google Scholar]
- 65.Bourlard H, Kamp Y. Auto-association by multilayer perceptrons and singular value decomposition. Biological Cybernetics. 1988;59:291–294. doi: 10.1007/BF00332918. [DOI] [PubMed] [Google Scholar]
- 66.Bengio Y, Lamblin P, Popovici D, Larochelle H. Greedy layer-wise training of deep networks. Proceedings of Neural Information Processing Systems (NIPS) 2007:153–160. [Google Scholar]
- 67.Larochelle H, Bengio Y, Louradour J, Lamblin P. Exploring strategies for training deep neural networks. Journal of Machine Learning Research. 2009;10:1–40. [Google Scholar]
- 68.Hinton GE, Osindero S, Teh YW. A fast learning algorithm for deep belief nets. Neural Computation. 2006;18:1527–1554. doi: 10.1162/neco.2006.18.7.1527. [DOI] [PubMed] [Google Scholar]
- 69.Smolensky P. Information processing in dynamical systems: Foundations of harmony theory. Parallel distributed processing: Explorations in the microstructure of cognition. 1986:194–281. [Google Scholar]
- 70.Hinton GE. Training products of experts by minimizing contrastive divergence. Neural Computation. 2002;14:1771–1800. doi: 10.1162/089976602760128018. [DOI] [PubMed] [Google Scholar]
- 71.Hinton G, Dayan P, Frey B, Neal R. The “wake-sleep” algorithm for unsupervised neural networks. Science. 1995;268:1158–1161. doi: 10.1126/science.7761831. [DOI] [PubMed] [Google Scholar]
- 72.Lecun Y, Bottou L, Bengio Y, Haffner P. Gradient-based learning applied to document recognition. Proceedings of the IEEE. 1998;86:2278–2324. [Google Scholar]
- 73.Glorot X, Bengio Y. Understanding the difficulty of training deep feedforward neural networks. Proceedings of International Conference on Artificial Intelligence and Statistics (AISTATS) 2010 [Google Scholar]
- 74.Sutskever I, Martens J, Dahl GE, Hinton GE. On the importance of initialization and momentum in deep learning. Proceedings of International Conference on Machine Learning (ICML) 2013;28 [Google Scholar]
- 75.Glorot X, Bordes A, Bengio Y. Deep sparse rectifier neural networks. Proceedings of International Conference on Artificial Intelligence and Statistics (AISTATS) 2011 [Google Scholar]
- 76.Maas AL, Hannun AY, Ng AY. Rectifier Nonlinearities Improve Neural Network Acoustic Models. 2013. [Google Scholar]
- 77.Wan L, Zeiler MD, Zhang S, LeCun Y, Fergus R. Regularization of neural networks using dropconnect. Proceedings of International Conference on Machine Learning (ICML) 2013;28 [Google Scholar]
- 78.Cho ZH, Kim YB, Han JY, Min HK, Kim KN, et al. New brain atlas - mapping the human brain in vivo with 7.0 T MRI and comparison with postmortem histology: Will these images change modern medicine? International Journal of Imaging Systems and Technology. 2008;18:2–8. [Google Scholar]
- 79.Wu G, Qi F, Shen D. Learning-based deformable registration of MR brain images. IEEE Transactions on Medical Imaging. 2006;25:1145–1157. doi: 10.1109/tmi.2006.879320. [DOI] [PubMed] [Google Scholar]
- 80.Ou Y, Sotiras A, Paragios N, Davatzikos C. Dramms: Deformable registration via attribute matching and mutual-saliency weighting. Medical Image Analysis. 2011;15:622–639. doi: 10.1016/j.media.2010.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Sotiras A, Davatzikos C, Paragios N. Deformable medical image registration: A survey. IEEE Transactions on Medical Imaging. 2013;32:1153–1190. doi: 10.1109/TMI.2013.2265603. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Lowe DG. Object recognition from local scale-invariant features. Proceedings of IEEE International Conference on Computer Vision (ICCV) 1999 [Google Scholar]
- 83.Vercauteren T, Pennec X, Perchant A, Ayache N. Diffeomorphic demons: Efficient non-parametric image registration. NeuroImage. 2009;45:S61–S72. doi: 10.1016/j.neuroimage.2008.10.040. [DOI] [PubMed] [Google Scholar]
- 84.Wu G, Kim M, Wang Q, Shen D. S-hammer: Hierarchical attribute-guided, symmetric diffeomorphic registration for MR brain images. Human Brain Mapping. 2014;35:1044–1060. doi: 10.1002/hbm.22233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Liao S, Gao Y, Oto A, Shen D. Representation learning: A unified deep learning framework for automatic prostate MR segmentation. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2013:254–261. doi: 10.1007/978-3-642-40763-5_32. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Guo Y, Gao Y, Shen D. Deformable MR prostate segmentation via deep feature learning and sparse patch matching. IEEE Transactions on Medical Imaging. 2016;35:1077–1089. doi: 10.1109/TMI.2015.2508280. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Liao S, Gao Y, Shi Y, Yousuf A, Karademir I, et al. Automatic prostate MR image segmentation with sparse label propagation and domain-specific manifold regularization. Proceedings of Information Processing in Medical Imaging (IPMI) 2013:511–523. doi: 10.1007/978-3-642-38868-2_43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kim M, Wu G, Shen D. Unsupervised deep learning for hippocampus segmentation in 7.0 tesla MR images. Proceedings of Machine Learning in Medical Imaging (MLMI) 2013:1–8. [Google Scholar]
- 89.Roth HR, Lee CT, Shin HC, Seff A, Kim L, et al. Anatomy-specific classification of medical images using deep convolutional nets. Proceedings of IEEE International Symposium on Biomedical Imaging (ISBI) 2015 [Google Scholar]
- 90.Yan Z, Zhan Y, Peng Z, Liao S, Shinagawa Y, et al. Bodypart recognition using multi-stage deep learning. Proceedings of Information Processing in Medical Imaging (IPMI) 2015:449–461. doi: 10.1007/978-3-319-19992-4_35. [DOI] [PubMed] [Google Scholar]
- 91.Yan Z, Zhan Y, Peng Z, Liao S, Shinagawa Y, et al. Multi-instance deep learning: Discover discriminative local anatomies for bodypart recognition. IEEE Transactions on Medical Imaging. 2016;35:1332–1343. doi: 10.1109/TMI.2016.2524985. [DOI] [PubMed] [Google Scholar]
- 92.Maron O, Lozano-Pérez T. A framework for multiple-instance learning. Proceedings of Neural Information Processing Systems (NIPS) 1998:570–576. [Google Scholar]
- 93.Liu F, Yang L. A novel cell detection method using deep convolutional neural network and maximum-weight independent set. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2015:349–357. [Google Scholar]
- 94.Xie Y, Xing F, Kong X, Su H, Yang L. Beyond classification: Structured regression for robust cell detection using convolutional neural network. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2015:358–365. doi: 10.1007/978-3-319-24574-4_43. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Xie Y, Kong X, Xing F, Liu F, Su H, Yang L. Deep voting: A robust approach toward nucleus localization in microscopy images. Proceedings of Medical Image Computing and Computer-Assisted Intervention (MICCAI) 2015:374–382. doi: 10.1007/978-3-319-24574-4_45. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Sirinukunwattana K, Raza SEA, Tsang YW, Snead DRJ, Cree IA, Rajpoot NM. Locality sensitive deep learning for detection and classification of nuclei in routine colon cancer histology images. IEEE Transactions on Medical Imaging. 2016;35:1196–1206. doi: 10.1109/TMI.2016.2525803. [DOI] [PubMed] [Google Scholar]
- 97.Long J, Shelhamer E, Darrell T. Fully convolutional networks for semantic segmentation. Proceedings of IEEE Conference on Computer Vision and Pattern Recognition (CVPR) 2015 doi: 10.1109/TPAMI.2016.2572683. [DOI] [PubMed] [Google Scholar]
- 98.Moeskops P, Viergever MA, Mendrik AM, de Vries LS, Benders MJNL, Iśgum I. Automatic segmentation of MR brain images with a convolutional neural network. IEEE Transactions on Medical Imaging. 2016;35:1252–1261. doi: 10.1109/TMI.2016.2548501. [DOI] [PubMed] [Google Scholar]
- 99.Weisenfeld NI, Warfield SK. Automatic segmentation of newborn brain MRI. NeuroImage. 2009;47:564–572. doi: 10.1016/j.neuroimage.2009.04.068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Xue H, Srinivasan L, Jiang S, Rutherford M, Edwards AD, et al. Automatic segmentation and reconstruction of the cortex from neonatal MRI. NeuroImage. 2007;38:461–477. doi: 10.1016/j.neuroimage.2007.07.030. [DOI] [PubMed] [Google Scholar]
- 101.Gui L, Lisowski R, Faundez T, HPS Morphology-driven automatic segmentation of MR images of the neonatal brain. Medical Image Analysis. 2012;16:1565–1579. doi: 10.1016/j.media.2012.07.006. [DOI] [PubMed] [Google Scholar]
- 102.Warfield S, Kaus M, Jolesz FA, Kikinis R. Adaptive, template moderated, spatially varying statistical classification. Medical Image Analysis. 2000;4:43–55. doi: 10.1016/s1361-8415(00)00003-7. [DOI] [PubMed] [Google Scholar]
- 103.Prastawa M, Gilmore JH, Lin W, Gerig G. Automatic segmentation of MR images of the developing newborn brain. Medical Image Analysis. 2005;9:457–466. doi: 10.1016/j.media.2005.05.007. [DOI] [PubMed] [Google Scholar]
- 104.Wang L, Shi F, Lin W, Gilmore JH, Shen D. Automatic segmentation of neonatal images using convex optimization and coupled level sets. NeuroImage. 2011;58:805–817. doi: 10.1016/j.neuroimage.2011.06.064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Wang L, Shi F, Li G, Gao Y, Lin W, et al. Segmentation of neonatal brain MR images using patch-driven level sets. NeuroImage. 2014;84:141–158. doi: 10.1016/j.neuroimage.2013.08.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Wang L, Gao Y, Shi F, Li G, Gilmore JH, et al. Links: Learning-based multi-source integration framework for segmentation of infant brain images. NeuroImage. 2015;108:160–172. doi: 10.1016/j.neuroimage.2014.12.042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Sermanet P, Eigen D, Zhang X, Mathieu M, Fergus R, LeCun Y. Overfeat: Integrated recognition, localization and detection using convolutional networks. CoRR. 2013 abs/1312.6229. [Google Scholar]
- 108.Gao M, Bagci U, Lu L, Wu A, Buty M, et al. Holistic classification of CT attenuation patterns for interstitial lung diseases via deep convolutional neural networks. Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization. 2016;0:1–6. doi: 10.1080/21681163.2015.1124249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Krizhevsky A, Sutskever I, Hinton GE. Imagenet classification with deep convolutional neural networks. Proceedings of Neural Information Processing Systems (NIPS) 2012:1097–1105. [Google Scholar]
- 110.Krizhevsky A. Tech rep. University of Toronto; 2009. Learning multiple layers of features from tiny images. [Google Scholar]
- 111.Simonyan K, Zisserman A. Very deep convolutional networks for large-scale image recognition. CoRR. 2014 abs/1409.1556. [Google Scholar]
- 112.Szegedy C, Liu W, Jia Y, Sermanet P, Reed S, et al. Going deeper with convolutions. Proceedings of Computer Vision and Pattern Recognition (CVPR) 2015 [Google Scholar]
- 113.Lee CY, Xie S, Gallagher PW, Zhang Z, Tu Z. Deeply-supervised nets. Proceedings of International Conference on Artificial Intelligence and Statistics (AISTATS) 2015;38 [Google Scholar]
- 114.Gönen M, Alpaydin E. Multiple kernel learning algorithms. Journal of Machine Learning Research. 2011;12:2211–2268. [Google Scholar]
- 115.Larochelle H, Bengio Y. Classification using discriminative restricted boltzmann machines. Proceedings of International Conference on Machine Learning (ICML) 2008 [Google Scholar]
- 116.Plis SM, Hjelm D, Salakhutdinov R, Allen EA, Bockholt HJ, et al. Deep learning for neuroimaging: a validation study. Frontiers in Neuroscience. 2014;8 doi: 10.3389/fnins.2014.00229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Kim J, Calhoun VD, Shim E, Lee JH. Deep neural network with weight sparsity control and pre-training extracts hierarchical features and enhances classification performance: Evidence from whole-brain resting-state functional connectivity patterns of schizophrenia. NeuroImage. 2016;124(Part A):127–146. doi: 10.1016/j.neuroimage.2015.05.018. [DOI] [PMC free article] [PubMed] [Google Scholar]