Abstract
The work of molecular machines such as the ribosome is accompanied by conformational changes, often characterized by relative motions of their domains. The method we have developed seeks to quantify these motions in a general way, facilitating comparisons of results obtained by different researchers. Typically there are multiple snapshots of a structure in the form of pdb coordinates resulting from flexible fitting of low-resolution density maps, from X-ray crystallography, or from molecular dynamics simulation trajectories. Our objective is to characterize the motion of each domain as coordinate transformations using moments of inertia tensor, a method we developed earlier. What has been missing until now are ancillary tools that make this task practical, general, and biologically informative. We have provided a comprehensive solution to this task with a set of tools implemented on the VMD platform. These tools address the need for reproducible segmentation of domains, and provide a generalized description of their motions using Principal axes of inertia. Although this methodology has been specifically developed for studying ribosome motion, it is applicable to any molecular machine.
Keywords: Segmentation, Inertia Tensors, Domain motion, Absolute Orientation, Quaternions, Ribosome
Graphical Abstract
INTRODUCTION
To analyze the mechanism underlying a biophysical process it is often necessary to characterize the dynamics of the macromolecular machine responsible for this process, using simple and biologically meaningful motion parameters. Our study was motivated by the need for a common framework for describing domain motions in the ribosome during the process of mRNA-tRNA translocation, but the problem we are addressing is quite general and of increasing importance as structural knowledge on molecular machines in various states rapidly accumulates. For this reason we will state the problem and the approach we have taken in a general way, and then proceed to exemplify it with the ribosome.
The structures of macromolecules to be characterized may arise from a variety of sources: X-ray crystallography, cryo-EM, or molecular dynamics (MD) simulations. They are represented in the form of atomic coordinates and are usually stored as pdb files for individual models derived from experiments, or dcd files for MD trajectories. In the case of cryo-EM the coordinates may be obtained by flexible fitting1–2 of existing structures, or, resolution permitting, by de novo modeling3. We opted to use VMD4, a popular software package for molecular dynamics simulations and visualizations, as a platform to develop a toolset to analyze the domain motions of molecular machines.
There are numerous studies in the literature describing motions in molecular machines, for instance ribosomes3, 5–19, RNA polymerase20–22, ATP-synthase23–24, and GroEL25–26, but only few of these make use of a general method or tool14–19. In this work we sought to address some shortcomings of existing methods, such as the need for a domain segmentation tool that makes allowance for inconsistencies in the residues, and the lack of an integrated platform for segmentation, computation and display of coordinate transformations.
First, in order to quantify domain motions, it is necessary to properly define the domains in the molecule that are structurally and functionally distinct – i.e., domains that at least in approximation behave like rigid bodies. Given the lack of tools in VMD to accomplish this task in a straightforward way, we have developed an automated segmentation method on the VMD platform for extracting the major domains from any macromolecular structure whose atomic coordinates are given. The challenge posed by the comparison of two realizations of a domain in two different structures has been noted by Whitford et al.15: The coordinate transformation for a given residue is usually not representative for other residues in the domain. Rather, positions of residues are subject to random local fluctuations but also additional changes that are functionally relevant. For expediency, these local fluctuations are often ignored, and the motion is approximated by a collective rigid-body motion with a set of global parameters. Whitford et al.15 developed an approach where global motion of a domain from one structure to the other is calculated from the average of the local displacements between corresponding atoms in the two structures. Compared to the problem these authors addressed – comparison of structures along MD trajectories -- experimentally derived structures may present an additional problem because of gaps in coverage, as residues in one structure may not be all matched to those in the other. Here, we have used and expanded a more general method based on Inertia tensor with Principal axes and the associated angles to describe the motion in a global way. This method was introduced by us to characterize the domain motion of the ribosome 27 and later on applied in two additional studies of its dynamics28–29.
We aim to describe the macromolecular domain motion in a compact and precise manner. Typically, a rigid body motion is measured with the aid of a set of three Euler angles obtained from the transformation or rotation matrices. The problem with such representation is that different orders in a sequence of rotations will generate different sets of Euler angles and so the reported results may be inconsistent and not comparable, although one can circumvent this problem by using the angle-axis representation derived from the rotation matrix12, 14. We propose an alternative approach for a unique representation and characterization of the macromolecular rotations, by using unit quaternions. Some of the interesting features of unit quaternions for 3D rotations are smooth interpolation between two quaternions and smaller round-off errors with unit normalization.
THE APPROACH
A molecule may exist in a series of conformations, such that each of its domains (modeled in approximation as rigid bodies) undergoes a series of coordinate transformations. We sought to develop a toolset aimed at defining the domains and describing these transformations. For the purpose of this exposition, it is sufficient to consider the case of a molecule in two states, A and B, whose domains undergo coordinate transformations in the process of going from A to B.
The following description is divided into three sections. One deals with the practical problem of defining the domains in a structure given by its atomic coordinates. The second sketches out the method of determining the Principal axes of the inertia tensor for a domain thus defined. The third describes the way to use these systems of Principal axes to track the motion of the domain in 3D.
1. Domain Segmentation – Overall Strategy
Our aim has been to develop a general method for segmentation of structural models represented by pdb coordinates that will not depend on the type of structures and residues (protein or RNA). Our approach to this problem is to perform the segmentation not on the atomic structure, but on a 3D density map generated from that structure. This step renders the segmentation virtually insensitive to minor inconsistencies in residue counts and relative gaps. The boundaries of the resulting volume segments are then used as masks for extracting the enclosed residues for the corresponding domain.
1.1. Automated 3D Volume Segmentation
For segmentation, we use a method known as the Watershed Algorithm widely used in computer vision for segmenting 2D images and 3D volumetric images (or density maps). We will first briefly describe the basic concept of the Watershed Algorithm 30–32 and then summarize the segmentation method making use of it 33.
Watershed Algorithm
The algorithm we use in the implementation of our segmentation method is part of the Matlab toolbox (see Text S8), so we will only briefly mention the general working principle 33. Its schematic for the 1D case is illustrated in the Supplementary Material (Fig. S1), but the underlying idea remains the same for a 2D image or a 3D density map. A density map is treated as a topographical surface with peaks and valleys, or ‘catchment basins’ where the elevation level is given by the density values in each voxel. There are two ways to perform Watershed segmentation. One is the top-down approach, where the water flow is simulated from regions of higher elevation, or peaks, to the lower level, or valleys, following the path of steepest descent. The other way, which we have used, is the bottom-up approach where we first find the local minima or catchment basins. Each of the local minima is treated as an independent water source which floods the associated catchment basin up to the point that it spills into the neighboring basin. This level defines the boundary between the two basins, and is considered as a boundary between two segments. Instead of the original density maps, we have applied the Watershed Algorithm to the Distance Transform30, 32, 34 of the binary map (i.e., the thresholded density map in Section 1.2). The idea to apply the Watershed method to the Distance Transform of the binary map is that the peaks (regional maxima) of the Distance Transform map provides the initial markers for the foreground objects of interest (domains in our case) we wish to identify.
Distance Transform
The Distance Transform (see general description provided in Text S1) of a density map is defined as the distance of every voxel X from its nearest non-zero valued voxel, and is given by
| 1.1 |
where X ∈ O ∪ Oc, O is the set of object voxels, and Oc is the set of background voxels. The distance function is given by
| 1.2 |
where X = (x1, x2, x3), Y = (y1, y2, y3) are voxel coordinates.
To obtain a proper initial segmentation one can try different distance functions, combined with a proper region merging method as will be sketched out below.
Region Merging
Application of the Watershed Algorithm to real density maps often produces severe over-segmentation due to the existence of numerous regional minima. Therefore it is necessary to take additional steps either in pre-processing (by smoothening the map) or post-processing, or both, to produce fewer and more meaningful segments using region merging methods 35–40. The basic approach is to use some type of region similarity or dissimilarity metric in a statistical sense based on the intensity or contour variation and then merge the neighboring regions, for example using a region adjacency graph, in a hierarchical manner. As we go higher in the hierarchical order (merging level), more regions are merged with one another and we obtain fewer over-segmented regions.
The full segmentation method we employed for a pdb structure, represented by a set of pdb coordinates, is summarized below
1.2. Segmentation Steps
Convert pdb structure into the corresponding 3D density map : Mvol
Apply a Gaussian filter to Mvol to obtain a smooth map Mf
-
Obtain a binary map:
where k is the number of the voxel.
For simulated maps (derived directly from a pdb structure as in our case), with no background noise, we use threshold = 0, otherwise we can choose a higher value for experimental density maps with noise. We can inspect the binary map for proper thresholding (Fig. 1A). Alternatively, we can also use an automatic thresholding method41 based on density values.
Generate the Distance Transform of the complementary binary map: ~Mbin → DT where the elements of DT are obtained from equation 1.1 using the distance function d (equation 1.2).
Invert the Distance Transform matrix to convert the high-density regions (potential object location) into catchment basins: DT ≔ −DT
Make the background or non-object voxels (~object_voxels) for Mbin in DT (from step (e)) as −inf ; i.e., force the background to be its own catchment basin.
Apply the Watershed Algorithm (Section 1.1) on DT (from step (f)) to obtain segments Sr.
Apply the region merging step as described above to merge over-segmented regions Sr into Sm (m < r). It may be possible to obtain a pre-specified number of segments through iterative application of the merging criteria (maximum merging size and merging level) but at present we have chosen to use the merging criteria already tested on the first input dataset and were able to get the expected segmentation for the subsequent datasets.
Once we have the segmentation parameters from one input dataset, we perform the segmentation on the fly for multiple input pdb structures by using the residue list from the first input pdb structure so as to obtain consistent segmented domains on all pdb structures, assuming the subsequent structures are obtained from the same source such as a simulation trajectory. However, if the structures originate from mixed sources then we can use the initial segments derived from the first pdb structure as masks for each of the subsequent structures, potentially with missing residues, to extract the enclosed residues.
Figure 1.
Density Map Segmentation. A. Binary maps, generated by application of a threshold to the density map (central Z-axis slice shown); threshold = 0 (left) is appropriate while threshold = 0.5 (right) is unsuited for segmentation. B. Distance Transform (DT) of the complementary binary map ~Mbin (central Z-axis slice shown). C. Same map as in (B) but showing central X-axis slice (top) and Y-axis slice (bottom). D. Inverted distance transform map DT ≔ − DT. E. Same map as in (D) but showing central X-axis slice (top) and Y-axis slice (bottom). F. Distance Transform map with voxels corresponding to the background voxels of Mbin, labeled as −infinity, so that the background voxels becomes inaccessible. G. Same map as in (F) but showing central X-axis slice (top) and Y-axis slice (bottom). H. Segmentation of the volume maps after applying the Watershed Transform with region merging. I. Same map as in (F) but showing central X-axis slice (top) and Y-axis slice (bottom).
2. Inertia Tensor and Principal Axes
The original idea of using moment of Inertia Tensor and Principal Axes to characterize the motions of ribosomal domains was first introduced in a cryo-EM study, focused on the role of L1 stalk and tRNA interaction, whose aim was to analyze the dynamics of the translation elongation cycle 27. We have used this method as part of our toolset as it is a general method to compute the Principal axes for any macromolecular structure represented by a set of atomic coordinates. We have provided a brief recapitulation of the concepts of Moment of Inertia and Principal Axes in the Supplementary Material (Text S2), since they form the basis of our approach.
2.1. Domain Motion Using Principal Axes
Once we have the individual domains segmented and selected, we can compute the Inertia Tensors and hence the Principal Axes for each individual domain, as outlined in the previous section. The task of characterizing the domain motions is now reduced to one of quantifying the transformation (i.e., rotation, translation) of the Principal Axes coordinate system of a particular domain from one state to the other. We can measure the domain rotation in different ways as implemented in the toolset (Text S6). In addition to the conventional Euler angles, another method we have employed here to describe the domain motions is to compute the absolute orientation using unit quaternion which characterizes the rotation (unambiguously) between two coordinate systems with one unique rotation axis and the corresponding rotation angle. The details are illustrated in Section 3.
2.2. Example
In the following we go through the basic steps for setting up the descriptor using Principal Axes for domain motions, using the ribosome as an example.
For calculating the domain motion of the small subunit (SSU) with respect to the large subunit (LSU) going from State A to State B, we align the Principal Axes of the LSU of structure #1 with the Cartesian coordinate system XYZ. First the Principal axis 3 is aligned with the Z axis, then the Principal axis 2 is aligned with the Y axis and, since both XYZ and the Principal axes form orthogonal coordinate systems, the Principal axis 1 would be already aligned to the X axis at this stage. The Principal axes of the LSU for the subsequent structures are also aligned to XYZ and consequently the LSU of both structures are aligned to one another. Then we compute the transformation of the Principal Axes of the SSU body from State A to B.
For computing the domain motion of the SSU head, we align the Principal axes of the SSU body to XYZ in the same way as mentioned above (a) and calculate the rotation for the head domain.
There is an option to either use all atoms for computing the Inertia Tensors for all the domains or just a subset of particular atoms such as phosphorus. Using all atoms takes typically several minutes on a single processor per ribosome model compared to using just phosphorus atoms, which just takes several seconds, at the expense of accuracy.
3. Characterization of Domain Motion with Absolute Orientation
Once we have the Principal Axes for each domain, the transformation between the Principal axes coordinate system for a particular domain from one state to the next (Fig. 4A, 4B) will determine the unique rotation (Fig. 4C) for that domain with a single rotation axis and rotation angle (Fig. 4D). A similar idea of characterizing the molecular motion was presented in a recent method12, 14 which uses the Euler-Rodrigues (E-R) formula to calculate the inter-domain rotation relative to a reference model. This method provides a single E-R rotation axis and rotation angle for one pair of molecules at a time. However, these authors measure the rotation by computing the transformation matrix for the whole domain, whereas we are dealing with the transformation of the domain Principal axes only.
Figure 4.
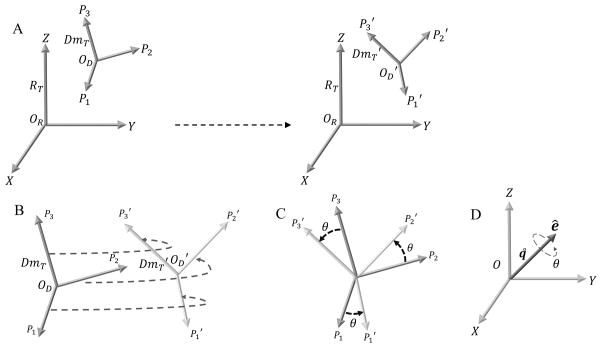
Coordinate Axes Transformation using Absolute Orientation. A. Fixed reference frame denoted by the Principal axes of Inertia tensor RT. The domain moving relative to the fixed reference frame is denoted by the Principal axes of Inertia tensors DmT and DmT′ on the left hand side (lhs) and right hand side (rhs), respectively. The Principal axes P1, P2 & P3 (lhs) move to P1′, P2′ & P3′ (rhs), respectively. B. Schematic illustrating the Absolute Orientation problem for coordinate axes transformation between DmT and DmT′. There is a unique rotation and also a translation (given by the difference between the corresponding centers OD − OD′) to obtain the complete coordinate axes transformation. C. Special case where the origins for DmT & DmT′ coincide and the coordinate axes transformation is achieved just by rotating DmT by an angle θ about an axis perpendicular to the plane of rotation, to be transformed into DT′. D. Angle-axis representation for the unit quaternion q˚. The solution to the rotation for the coordinate axes transformation in B or C is given by q˚. The axis of rotation is given by ê and the angle of rotation is given by θ.
The problem of describing the transformation of coordinate axes and, in general, the least squares fitting of two sets of points has several closed-form solutions42–44. We have chosen to use the more classical approach for absolute orientation algorithm proposed by Horn42. In this approach, a closed-form solution to the least-square problem of absolute orientation is determined using unit quaternions. The basics of quaternions and the least square problem of absolute orientation using unit quaternion are briefly outlined in the Supplementary Material (Text S3 and S4, respectively). Here we merely present the implementation steps, in Section 3.1 below.
3.1. Absolute Orientation Algorithm
We summarize the absolute orientation algorithm for coordinate axes transformation in simple implementable steps as follows.
- Compute the centroids of the input coordinate systems 1 and 2, as shown in Supplementary equation S4.4
- Next we subtract the centroids from the respective coordinate systems so that we only deal with measurements relative to the centroids (eq. S4.5).
- Then we compute the matrix M (S4.25).
Having the matrix M, we can use its element values to assign the elements Sxx, Sxy, Sxz and so on (eq. S4.26).
Using the matrix elements from step (d), we compute the matrix N (eq. S4.27).
Finally, we perform eigen-decomposition of N and determine the eigenvector emax with the largest positive eigenvalue. The unit quaternion q˚ (representing the rotation) in the direction of emax is the required solution to the absolute orientation problem.
3.2. Component of Rotation Around a Specified Axis
The unit quaternion (Section 3.1) along with a unique rotation axis and a rotation angle (Text S3), provides us with precise information about the domain’s rigid-body rotation. However, in certain situations, it may be necessary to obtain the component of the rotation around a specified axis v⃗ that is different from the true rotation axis. This can be achieved through the decomposition45 (see Text S5 for detailed description) of the unit quaternion q˚ into two components, q˚s and q˚t, such that q˚ = q˚sq˚t.
Let the unit quaternion q˚ = (qw, qx, qy, qz) represent the complete rotation and the specified axis be the vector v⃗ = (vx, vy, vz)T. The rotation axis component of q˚ is r⃗q = (qx, qy, qz)T. The projection of the rotation axis r⃗q along the vector v⃗ is given by:
| 3.1 |
where is a unit vector along v⃗.
Using the projection vector P→rqv and the scalar part of q˚, we construct (Text S5, equation S5.3) the unit quaternion q˚t as :
| 3.2 |
Therefore, q˚t, as defined above, is a unit quaternion and represents the component of the rotation around the specified vector v⃗. We can determine the other component as q˚s = q˚q˚t−1.
RESULTS AND DISCUSSION
We have applied our method to a cryo-EM dataset from a sample of translating eukaryotic ribosomes. The details of the results and detailed biological implications will be provided in a separate research article (XX, YY, ZZ, in preparation). Here we aim to illustrate the application of our toolset to compute the domain rotation between two structures representing the ribosome in two different states (labeled as A(class2.pdb) and B(class5.pdb); see movies MS1, MS2, MS3 in Supplementary Material).
Segmentation
We demonstrate the segmentation method (Section 1.2) with an example of the ribosome structure. To begin with, we generated a simulated density map (Mvol) from the ribosome pdb structure and applied a Gaussian filter to the density map in order to obtain a smooth map (Mf) (see description of the filter parameter used in Text S8). Next, we converted the smooth map into a binary map using thresholding (Section 1.2 step (c)). Since, the initial density map does not contain any background noise, we chose a threshold of zero to obtain the binary map (Mbin). Through visual inspection of the 3D volume, we can confirm that the binary map is contiguous and the thresholding was performed properly and here, we just show the 3D binary map with representative central slice along Z-axis (Fig. 1A left). In contrast, another choice of the threshold (higher value) produced a severely fragmented binary map (central Z-axis slice shown in Fig. 1A right).
In the next step, we converted the complement of the binary map into a Distance Transform map (DT) as shown with a representative central volume slice along the Z-axis (Fig. 1B). The Distance Transform map makes it simpler, compared to the original density map, to find the regional minima or catchment basins. We also show central slices along X-axis (Fig. 1C top) and Y-axis (Fig. 1C bottom). Next, we computed the inverted Distance Transform map (−DT ) (representative central Z-axis slice, Fig. 1D) and the corresponding two other orthogonal slices (Fig. 1E). Then we labeled the voxels, belonging to the set of background voxels in the original binary map (Mbin) as inaccessible (Section 1.2 step (f)) in the inverted Distance Transform map obtained in the previous step. The resulting Distance Transform map is shown with representative orthogonal central slices (Figs. 1F, 1G).
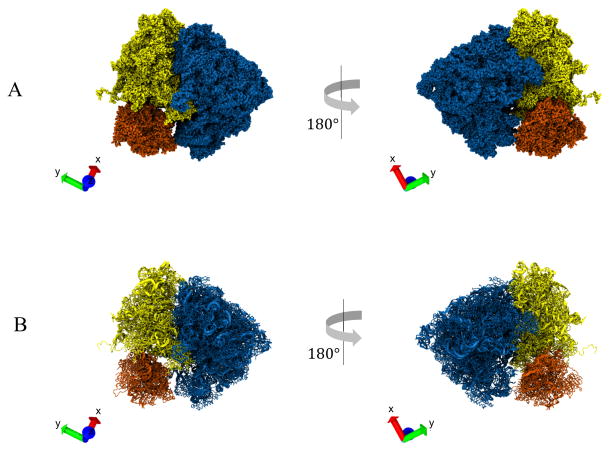
Next, we applied the Watershed algorithm (Section 1.2 step (g) & (h)) to the final Distance Transform map obtained in the last step. Using our segmentation approach on this map, together with the specific set of parameter values (Text S8), the Watershed method initially produced 396 segments before the application of region merging (i.e., merging level is set to 0). The maximum merging size was set to 503. Higher merging levels produced less over-segmentation and we settled at a merging level (11) that generated three volume segments corresponding to the three major domains in the ribosome. We can inspect representative orthogonal slices of the segmented density map (Figs. 1H, 1I) to determine if the segmentation was performed properly. The map (Fig. 2A) shows the three relevant domains, large subunit (blue), small subunit body (yellow) and small subunit head (orange). Finally, using the individual segments as mask for extracting the residues from the whole ribosome structure, we obtained the segmented pdb structure (Fig. 2B).
Figure 2.
Segmentation of Ribosome Structure. A. Segmentation of the 3D density map of a ribosome structure into its three relevant domains: large subunit (LSU) (blue), small subunit (SSU) body (yellow), and SSU head (orange). B. Segmented atomic model of the ribosome. The segments were obtained by extracting the residues contained within the individual volume segments obtained from (A). VMD axes X(red), Y(green), Z(blue) are shown on the bottom left inset of each panel.
Inertia Tensor and Principal Axes Calculation
After we had the relevant domains segmented out, we proceeded to set up the platform for characterizing the motion of the relevant domains of the ribosome. For each of the domain of interest (approximated as a rigid body) we computed the Inertia tensor and Principal axes (Section 2 and Text S2) using all atoms. As described in the Supplementary (Text S2), we can observe from the example of ribosome structures (Figs. 3, S2C), how the distribution of mass of a rigid body determines the order of the three Principal axes. From the eigen-decomposition of the Inertia tensor matrix for any domain of the ribosome structure, we obtained the eigenvalues (Principal moments), I11, I22, I33 which are ordered as I11 > I22 > I33 (numerical data not shown). This implies that the distribution of mass should be most elongated along Principal axis 3, the eigenvector corresponding to the smallest moment I33 and the least elongated along Principal axis 1. We see that for each of the domain (LSU, SSU, SSU body, etc.) (Figs. 3, Fig. S2C), the distribution of mass is indeed most elongated along Principal axes 3, followed by Principal axis 2, and the least elongated along Principal axis 1. For any ribosome domain approximated as a rigid body, the order of the three Principal axes and their orientation should be consistent at all points during the motion. By consistent orientation, we mean that if the rigid body has only translation and no rotation moving from state A to B, then the pair of Principal axes at A and B should align with each other only by translation.
Figure 3.
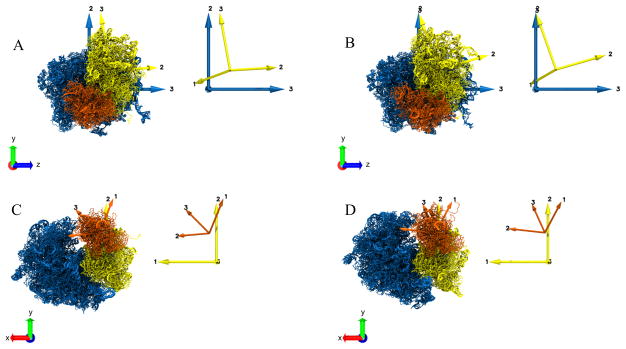
Principal axes computation for the segmented domains (Fig 2) of the ribosome structures in two states, “A” and “B”. The Principal axes for individual domains are shown with the same color as the corresponding domain. The inset on the right of each panel shows the Principal axes only. A. Principal axes of LSU (blue) and SSU body (yellow) for the structure in state “A”. B. Principal axes of LSU (blue) and SSU body (yellow) for the structure in state “B”. C. Principal axes of SSU body (yellow) and SSU head (orange) for the structure in state “A”. D. Principal axes of SSU body (yellow) and SSU head (orange) for the structure in state “B”. For panels (A) and (B), the LSU is fixed and aligned to the Cartesian VMD coordinate system axes XYZ. For panels (C) and (D), the SSU body is fixed and aligned to the Cartesian coordinate system axes XYZ.
For the purpose of demonstrating the characterization of domain motion with Principal axes, we measured two types of motion for the pair of structures A and B - (a) inter-subunit motion, which is motion of the entire SSU or SSU body (target) relative to the LSU (reference) and (b) head rotation, which is motion of the SSU head (target) relative to the SSU body (reference).
For measuring the inter-subunit rotation we first computed the Principal axes of the reference LSU of structure A (RT in Fig. 4A left) and aligned it to the Cartesian coordinate axes XYZ (see Section 2.2 for the detailed alignment procedure). Then we computed the Principal axes of the SSU body of A (DmT in Fig. 4A, Fig. 3A). After that, we computed and aligned the Principal axes of the LSU of structure B (RT in Fig. 4A right) with XYZ and, as a result, the Principal axes of the LSU of both structures A and B were aligned to each other. Next, we computed the Principal axes of the SSU body of B (DmT′ in Fig. 4A, Fig. 3B). The coordinates of the Principal axes of the SSU body for both A and B are now expressed relative to the fixed coordinate system (Principal axes) of the LSU of A and B.
For the head rotation we followed the same alignment procedure for the Principal axes of the SSU body as in case above with LSU as the reference. In this case, the coordinates of the Principal axes of the SSU head for A and B are now expressed relative to the fixed coordinate system of the SSU body of A and B (Fig 3C, 3D).
Measuring the rotation of a domain (SSU, SSU body, SSU head) at this stage is equivalent to tracking the associated Principal Axes from one state to the other (Fig. 4B). The rotation of Principal Axes is estimated by solving the least squares problem of absolute orientation, i.e., by calculating the transformation of the coordinate axes between state A and B (Fig. 4C) using unit quaternions. The angle-axis representation (Fig. 4D) of the unique quaternion gives us the rotation axis and the corresponding rotation angle, although the unit quaternion by itself is a sufficient descriptor of the rotation.
Coordinate Axes Transformation/Absolute Orientation
We demonstrate the working principle of the Absolute Orientation algorithm (Section 3.1) using a simple example in the Supplementary (Text S9). Here we show its application by calculating the transformation of the Principal axes computed for SSU body and SSU head from state A (class2) to B (class5) and the rotation measurements are tabulated below (Table 1). The rotation of SSU body from state A (Fig. 3A) to B (Fig. 3B) (movie MS1) is characterized by the unit quaternion q˚body and the corresponding rotation angle θbody around the native rotation axis given by the unit vector êbody.
Table 1.
The unit quaternion q˚ and the corresponding axis-angle estimates obtained by solving the absolute orientation problem for the Principal Axes computed for the domains (SSU Head, SSU Body, Full SSU and the reference SSU) in the two states A and B.
| Domain | q˚ = (qw, qx, qy, qz) | ||||
|---|---|---|---|---|---|
| SSU Head | q˚head | 0.989429 | −0.007936 | −0.100939 | 0.103817 |
| SSU Body | q˚body | 0.992263 | −0.091447 | −0.073468 | 0.040654 |
| SSU | q˚SSU | 0.996006 | −0.085232 | −0.007273 | 0.025572 |
| SSU Ref | q˚SSU_ref | 0.995708 | −0.089049 | −0.005387 | 0.024636 |
| ê = (ex, ey, ez) | θ (degree) | ||||
| SSU Head | êhead | −0.054727 | −0.696057 | 0.715898 | 16.68 |
| SSU Body | êbody | −0.736592 | −0.591778 | 0.327462 | 14.26 |
| SSU | êSSU | −0.954637 | −0.081456 | 0.286415 | 10.24 |
| SSU Ref | êSSU_ref | −0.962162 | −0.058203 | 0.266189 | 10.62 |
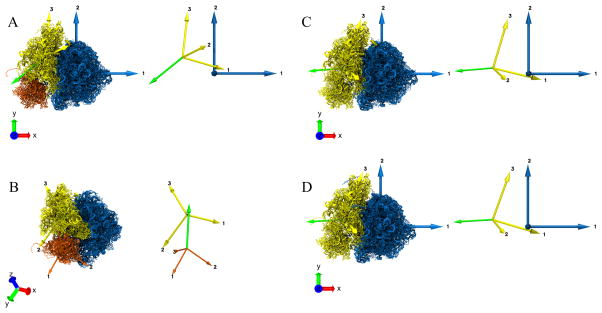
We calculated the rotation of SSU head, full SSU and reference SSU from state A (Fig. 3C) to B (Fig. 3D) (movies MS2, MS3) in the same way. The graphical visualization of the rotation axis for the SSU body, SSU head, full SSU (head and body combined) and the reference SSU is shown as a green arrow (Fig. 5A, 5B, 5C, 5D). One can validate the above rotation axis and angle by visual inspection of the change in the two models (movies MS1, MS2, MS3).
Figure 5.
Characterization of domain motion between two structures “A” and “B” (Fig. 3) using the Absolute Orientation algorithm for the Principal Axes transformation from “A” to “B”. The resulting unit quaternion describing the rotation, is expressed in its axis-angle representation. The Principal axes for individual domains are shown with the same color as the corresponding domain, and the rotation axis is shown in green. The inset on the right of each panel shows the Principal axes and the rotation axis. A. Rotation of SSU body (yellow) from state “A” to “B”. The LSU remains fixed here. The green arrow represents the axis of rotation of the SSU body between states “A” and “B” and is drawn overlayed on model “B” B. Rotation of SSU head (orange) from state “A” to “B”. The SSU body remains fixed. The green arrow represents the axis of rotation of the SSU head between the states “A” and “B” and is drawn overlayed on model “B”. C. Rotation for the full SSU (yellow) from state “A” to “B”. The LSU remains fixed. The green arrow represents the axis of rotation of the SSU body between states “A” and “B” and is drawn overlayed on model “B”. D. Rotation of the full SSU (yellow) from state “A” to “B”. The LSU remains fixed here. The LSU and SSU, in this case, are obtained from a reference segmentation. The green arrow represents the axis of rotation of the SSU body between states “A” and “B” and is drawn overlayed on model “B”.
The rotation axis not only tells us about the directionality (clockwise or anticlockwise sense) of the rotation, but also provides us with a way to categorize the rotation into different types, as described in the literature for macromolecular motion, depending on the alignment of the rotation axis and the Principal axes of the reference molecule. For example, in our case (Fig. 5A), the acute angles between the rotation axis êSSU and the three Principal axes, (1 0 0)T, (0 1 0)T, (0 0 1)T of the fixed LSU are 17.3°,85.3° and 73.4° respectively. We can see that the rotation axis êSSU is more closely aligned with the Principal axis 1 of LSU compared to the other two axes. Since Principal axis 1 is approximately perpendicular to the inter-subunit interface (Fig. 5A), we can refer this SSU rotation as ‘inter-subunit rotation’. If the rotation axis êSSU was closely aligned with Principal axis 2 of LSU, which is approximately parallel to the Principal axis 3 of SSU, then the SSU rotation would be described as ‘rolling’ and so on. Similar motions (head rotation, swiveling, etc.) can be described for the rotation of the SSU head relative to SSU body. In general, the true rotation axis may not be closely aligned to a pre-specified axis of rotation and, in certain cases, it may be necessary to know the rotation around such chosen axis.
Given a unit quaternion representing the rotation of a domain with a unique rotation axis and rotation angle, we can obtain the component of the rotation around a specified axis using the decomposition of the unit quaternion (Section 3.2). As an illustration, we chose to find the component of SSU body rotation (q˚body), around the Principal axis 1 of LSU, i.e. v⃗ = (1 0 0)T. From the decomposition (equation 3.2) of q˚body, we obtained the component q˚t = (0.995780 −0.091771 0.0 0.0)T. The corresponding rotation angle θt = 10.53° and the rotation axis is êt = (−1, 0, 0)T = −v⃗ i.e, êt is aligned with v⃗. These measurements will help us to validate our rotation estimates with those reported in the literature where the rotation is calculated around a chosen axis.
Error analysis
Since the absolute orientation provides a closed-form solution to the problem of determining coordinate axes transformations, the major source of error in the measurement of the rotation is the uncertainty in the segmentation of the domains as it affects the subsequent computation of their Principal axes.
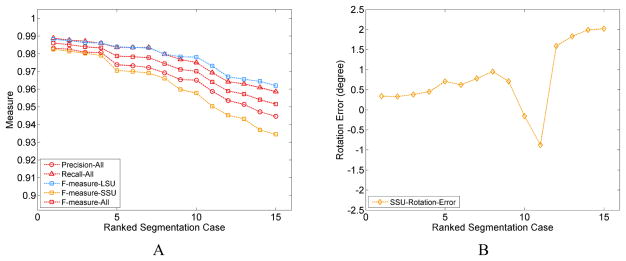
In order to characterize the magnitude of errors, we have investigated several instances of segmentations with small variations in the parameters, and in each instance evaluated the segmentation quality with regard to a reference structure using Precision, Recall and F − measure calculated based on the atoms included or excluded in the segmentation, (see Supplementary Text S10). As there is no differentiation between SSU body versus head in the coordinates of the reference model, we only used the SSU and LSU domains in this error assessment. Since the segmented density map has no background noise, the error in the segmentation stems primarily from errors in assignment at the interface of the two subunits and the neighboring regions. The incorrectly segmented atoms, in the above-mentioned regions, constitute a very small fraction (Text S10, Table S3) of the total number of atoms in the two subunits. Consequently, the Precision, Recall and F − measure values are quite high ~ 0.90 – 0.99 (Fig. 6A, S6) for the two individual subunits and overall structure. The resulting error in the rotation angle of the SSU is lower than ±0.5° (Tables S1, S3; Fig. 6B) for the highest-quality segmentation cases 1 – 4 (Table S1, S4) with small segmentation error (in terms of all three quality measures including Precision ≥ 0.97, for individual subunits and combined). Indeed, visual assessment (Fig. S3) confirms that segmented domains for the cases 1 – 4 appear to be closest to the corresponding reference domains. However, one additional case (case 6) with low rotation angle error presents an anomaly as the segmentation error is much larger (Precision = 0.92) (Tables S3, S4; Figs. S5, S6). A possible explanation for this discrepancy is that the error in the segmentation from different regions of the inter-subunit interface (Fig S5) is being averaged out to a considerable extent due to the nature of Principal axes calculation over a large number of atoms.
Figure 6.
Characterizing the Error in Domain Segmentation and Domain Rotation. A. Segmentation quality measures, with Precision, Recall calculated for the full structure and F − measure calculated for the individual domains and also the full structure, in all the segmentation cases listed in Table S1. The plotted values are ranked based on the F-measure of the SSU (Table S4). B. Errors in rotation angle of the SSU for the segmentation cases and ranked in the same manner as in A.
The rotation angles are close for cases 1 – 4, when we measured the SSU body and SSU head separately (Fig. 6C, Table S2). As references for the SSU body and head domains are not available, the error in their respective rotation angles could not be calculated. Therefore, it was not possible to compare the error in the SSU body and head rotation angles with the error in rotation angles for the full SSU, which could have provided us with an estimate about the sensitivity (see Text S10, S10.1) of the SSU rotation measurements to segmentation error.
From our earlier discussion, we know that the error in segmentation is mainly at the periphery of the subunits. We should note that this is the worst-case scenario where the wrongly assigned atoms are farthest away from the axis and thus have larger contribution in the calculation of the Principal axes. Consequently, the rotation measurements are more affected, compared to contributions by the inner atoms.
As our calculations show, the computation of rotation angles is robust to small segmentation errors (Precision > 0.97) (Table S4), but the domain segmentation should be carefully verified prior to the Principal axes calculations in order to accurately measure small rotations.
CONCLUSIONS
We have developed an integrated platform for segmentation and computation of coordinate system transformations to characterize the motion of individual domains of biomolecules. We have demonstrated the application of our toolset on a specific example of a ribosome dataset. Measuring the rotational motion of the macromolecules using a single rotation axis and the associated rotation angle through the use of quaternions is a straightforward, unambiguous way to characterize the domain motions. The methodology we have presented here is very general and applicable to any macromolecule. Therefore, we anticipate that inertia tensor and the absolute orientation with unit quaternions (or rotation matrix), from which we can compute the native axis of rotation and the rotation angle, will prove to be a useful toolset. Its use by the community would make the characterization of macromolecular domain motions comparable, compact and biologically informative.
Supplementary Material
Fixed LSU with SSU body rotation from state “A” to “B.”
Fixed SSU Body with SSU head rotation from state “A” to “B.”
Fixed LSU with Full SSU rotation from state “A” to “B.”
Figure S1. Illustration of classical watershed flooding algorithm for a 1D image. The idea remains the same for a 2D image or 3D density map. ‘s’ denotes the flooding level or intensity (density) (arbitrary values here). Colored regions are catchment basins and the vertical lines are the watershed lines demarcating the boundaries between the basins. The flooding starts from a source at the catchment basin at the minimum intensity level for the and gradually fills up the basins with increasing flooding levels until it reaches the maximum level. In the process of flooding, the watershed is marked between two neighboring basin at the moment when the flood water starts to spill into the neighboring basin.
Figure S2. Inertia Tensor and Principal Axes of a Rigid Body. A. An arbitrary rigid body with an axis of rotation P passing through the origin O (center of mass). An infinitesimally small element with mass dm is situated at X with position vector r⃗. The rigid body is rotating with an angular velocity of ω→. B. An example of a disc with radius r (and radial vector r⃗) rotating around Z axis passing through the center of the disc. C. Three Principal axes computed for each of the two domains of the ribosome. The two domains shown are LSU (blue) and SSU body (yellow). The Principal axes for individual domains are shown with the same color as the corresponding domain. The inset on the right panel shows the Principal axes only.
Figure S3. Segmentation Error for the Segmentation Case 1 in Tables 1, S1, S3. A. Initial segmentation of the three relevant domains LSU (blue), SSU Body (yellow), SSU Head (orange). The red segment could not be automatically segmented out. Part of the red segment belongs to SSU (highlighted region) and the other part to LSU (highlighted region). B. The false positive (incorrectly identified; pink) and false negative (incorrectly rejected; green) atoms are shown on the segmented LSU domain (blue). The third panel shows the interface view of the LSU. C. The false positives (pink) and false negatives (green) are shown on the segmented SSU domain (yellow). The residues belonging to the red segment are not shown in (B) and (C) and were excluded from the LSU and SSU residues in subsequent calculations.
Figure S4. Segmentation Error for the Segmentation Case 14 in Tables S1, S2, S3. A. The false positives (pink) and false negatives (green) are shown on the segmented LSU domain (blue). The third panel shows the segmentation error in the interface view of the LSU. B. The false positives (pink) and false negatives (green) are shown on the segmented SSU domain (yellow). The residues belonging to the red segment were excluded from the LSU and SSU residues in subsequent calculations.
Figure S5. Segmentation Error for the Segmentation Case 6 (top row) and Case 8 (bottom row) in Tables S1, S2, S3. A. The false positives (pink) and false negatives (green) are shown on the segmented LSU domain (blue). The third panel shows the interface view of the LSU. B. The false positives (pink) and false negatives (green) are shown on the segmented SSU domain (yellow). The residues belonging to the red segment were excluded from the LSU and SSU residues in subsequent calculations.
Figure S6. Characterizing the Error in Domain Segmentation and Domain Rotation Angle. A. Segmentation quality measures with Precision, Recall, F − measure calculated for the individual domains and the full structure, in all the segmentation cases listed in Table S1. The plotted values are ranked based on the F − measure of the SSU (Table S4). Across all the segmentation cases, the Precision and Recall values for the individual subunit seemed to vary more than the corresponding measures for the full structure and the F − measure. B. The rotation angle for SSU, SSU body and SSU head for the corresponding segmentation cases and the plotted angles are ranked in the same manner as in A.
Acknowledgments
We would like to thank Wen Li, Amedee Des Georges and Hstau Liao for helpful discussions. The authors also acknowledge the computer time provided by the National Science Foundation (NSF)-funded Extreme Science and Engineering Discovery Environment (XSEDE) MCA93S028, and a Blue Waters Illinois allocation, which is part of the Blue Waters sustained-petascale computing project supported by the NSF (awards OCI-0725070 and ACI-1238993) and the state of Illinois.
Funding Sources
Supported by HHMI and NIH R01 GM29169 (to J.F.); NSF PHY1430124 and NIH 9P41GM104601 (to K.S.).
Footnotes
Notes
The authors declare no competing financial interest.
Software availability
Software will be made available upon request.
Details of the various methods used in the toolset. This material is available free of charge via the Internet at http://pubs.acs.org.
References
- 1.Trabuco LG, Villa E, Schreiner E, Harrison CB, Schulten K. Molecular dynamics flexible fitting: a practical guide to combine cryo-electron microscopy and X-ray crystallography. Methods. 2009;49(2):174–80. doi: 10.1016/j.ymeth.2009.04.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Trabuco LG, Villa E, Mitra K, Frank J, Schulten K. Flexible fitting of atomic structures into electron microscopy maps using molecular dynamics. Structure. 2008;16(5):673–83. doi: 10.1016/j.str.2008.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Noel JK, Levi M, Raghunathan M, Lammert H, Hayes RL, Onuchic JN, Whitford PC. SMOG 2: A Versatile Software Package for Generating Structure-Based Models. PLoS computational biology. 2016;12(3):e1004794. doi: 10.1371/journal.pcbi.1004794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Humphrey W, Dalke A, Schulten K. VMD: visual molecular dynamics. Journal of molecular graphics. 1996;14(1):33–8. 27–8. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 5.Behrmann E, Loerke J, Budkevich TV, Yamamoto K, Schmidt A, Penczek PA, Vos MR, Burger J, Mielke T, Scheerer P, Spahn CM. Structural snapshots of actively translating human ribosomes. Cell. 2015;161(4):845–57. doi: 10.1016/j.cell.2015.03.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Spahn CM, Gomez-Lorenzo MG, Grassucci RA, Jorgensen R, Andersen GR, Beckmann R, Penczek PA, Ballesta JP, Frank J. Domain movements of elongation factor eEF2 and the eukaryotic 80S ribosome facilitate tRNA translocation. The EMBO journal. 2004;23(5):1008–19. doi: 10.1038/sj.emboj.7600102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Wriggers W, Agrawal RK, Drew DL, McCammon A, Frank J. Domain motions of EF-G bound to the 70S ribosome: insights from a hand-shaking between multi-resolution structures. Biophysical journal. 2000;79(3):1670–8. doi: 10.1016/S0006-3495(00)76416-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Agirrezabala X, Lei J, Brunelle JL, Ortiz-Meoz RF, Green R, Frank J. Visualization of the hybrid state of tRNA binding promoted by spontaneous ratcheting of the ribosome. Mol Cell. 2008;32(2):190–7. doi: 10.1016/j.molcel.2008.10.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ratje AH, Loerke J, Mikolajka A, Brunner M, Hildebrand PW, Starosta AL, Donhofer A, Connell SR, Fucini P, Mielke T, Whitford PC, Onuchic JN, Yu Y, Sanbonmatsu KY, Hartmann RK, Penczek PA, Wilson DN, Spahn CM. Head swivel on the ribosome facilitates translocation by means of intra-subunit tRNA hybrid sites. Nature. 2010;468(7324):713–6. doi: 10.1038/nature09547. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Agirrezabala X, Frank J. Elongation in translation as a dynamic interaction among the ribosome, tRNA, and elongation factors EF-G and EF-Tu. Quarterly reviews of biophysics. 2009;42(3):159–200. doi: 10.1017/S0033583509990060. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Taylor DJ, Nilsson J, Merrill AR, Andersen GR, Nissen P, Frank J. Structures of modified eEF2 80S ribosome complexes reveal the role of GTP hydrolysis in translocation. The EMBO journal. 2007;26(9):2421–31. doi: 10.1038/sj.emboj.7601677. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Guo Z, Noller HF. Rotation of the head of the 30S ribosomal subunit during mRNA translocation. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(50):20391–4. doi: 10.1073/pnas.1218999109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ermolenko DN, Majumdar ZK, Hickerson RP, Spiegel PC, Clegg RM, Noller HF. Observation of intersubunit movement of the ribosome in solution using FRET. Journal of molecular biology. 2007;370(3):530–540. doi: 10.1016/j.jmb.2007.04.042. [DOI] [PubMed] [Google Scholar]
- 14.Mohan S, Donohue JP, Noller HF. Molecular mechanics of 30S subunit head rotation. Proceedings of the National Academy of Sciences of the United States of America. 2014;111(37):13325–30. doi: 10.1073/pnas.1413731111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Whitford PC, Blanchard SC, Cate JH, Sanbonmatsu KY. Connecting the kinetics and energy landscape of tRNA translocation on the ribosome. PLoS computational biology. 2013;9(3):e1003003. doi: 10.1371/journal.pcbi.1003003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Poornam GP, Matsumoto A, Ishida H, Hayward S. A method for the analysis of domain movements in large biomolecular complexes. Proteins. 2009;76(1):201–12. doi: 10.1002/prot.22339. [DOI] [PubMed] [Google Scholar]
- 17.Matsumoto A, Ishida H. Global Conformational Changes of Ribosome Observed by Normal Mode Fitting for 3D Cryo-EM Structures. Structure. 2009;17(12):1605–1613. doi: 10.1016/j.str.2009.09.017. [DOI] [PubMed] [Google Scholar]
- 18.Tama F, Valle M, Frank J, Brooks CL., 3rd Dynamic reorganization of the functionally active ribosome explored by normal mode analysis and cryo-electron microscopy. Proceedings of the National Academy of Sciences of the United States of America. 2003;100(16):9319–23. doi: 10.1073/pnas.1632476100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Paci M, Fox GE. Centers of motion associated with EF-Tu binding to the ribosome. RNA biology. 2016;13(5):524–30. doi: 10.1080/15476286.2015.1114204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Nudler E. RNA polymerase active center: the molecular engine of transcription. Annual review of biochemistry. 2009;78:335–61. doi: 10.1146/annurev.biochem.76.052705.164655. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Steitz TA. Visualizing polynucleotide polymerase machines at work. Embo Journal. 2006;25(15):3458–3468. doi: 10.1038/sj.emboj.7601211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Hahn S. Structure and mechanism of the RNA polymerase II transcription machinery. Nature structural & molecular biology. 2004;11(5):394–403. doi: 10.1038/nsmb763. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yoshida M, Muneyuki E, Hisabori T. ATP synthase--a marvellous rotary engine of the cell. Nature reviews. Molecular cell biology. 2001;2(9):669–77. doi: 10.1038/35089509. [DOI] [PubMed] [Google Scholar]
- 24.Boyer PD. The ATP synthase--a splendid molecular machine. Annual review of biochemistry. 1997;66:717–49. doi: 10.1146/annurev.biochem.66.1.717. [DOI] [PubMed] [Google Scholar]
- 25.Horwich AL, Farr GW, Fenton WA. GroEL-GroES-mediated protein folding. Chemical reviews. 2006;106(5):1917–30. doi: 10.1021/cr040435v. [DOI] [PubMed] [Google Scholar]
- 26.Horwich AL, Fenton WA, Chapman E, Farr GW. Two families of chaperonin: physiology and mechanism. Annual review of cell and developmental biology. 2007;23:115–45. doi: 10.1146/annurev.cellbio.23.090506.123555. [DOI] [PubMed] [Google Scholar]
- 27.Trabuco LG, Schreiner E, Eargle J, Cornish P, Ha T, Luthey-Schulten Z, Schulten K. The role of L1 stalk-tRNA interaction in the ribosome elongation cycle. Journal of molecular biology. 2010;402(4):741–60. doi: 10.1016/j.jmb.2010.07.056. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Agirrezabala X, Schreiner E, Trabuco LG, Lei JL, Ortiz-Meoz RF, Schulten K, Green R, Frank J. Structural insights into cognate versus near-cognate discrimination during decoding. Embo Journal. 2011;30(8):1497–1507. doi: 10.1038/emboj.2011.58. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Agirrezabala X, Liao HY, Schreiner E, Fu J, Ortiz-Meoz RF, Schulten K, Green R, Frank J. Structural characterization of mRNA-tRNA translocation intermediates. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(16):6094–9. doi: 10.1073/pnas.1201288109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Meyer F. Topographic Distance and Watershed Lines. Signal Process. 1994;38(1):113–125. [Google Scholar]
- 31.Vincent L, Soille P. Watersheds in Digital Spaces - an Efficient Algorithm Based on Immersion Simulations. Ieee T Pattern Anal. 1991;13(6):583–598. [Google Scholar]
- 32.Meyer F, Beucher S. Morphological segmentation. Journal of Visual Communication and Image Representation. 1990;1(1):21–46. [Google Scholar]
- 33.Roerdink JBTM, Meijster A. The Watershed Transform: Definitions, Algorithms and Parallelization Strategies. Fundam Inf. 2000;41(1,2):187–228. [Google Scholar]
- 34.Paglieroni DW. Distance Transforms - Properties and Machine Vision Applications. Cvgip-Graph Model Im. 1992;54(1):56–74. [Google Scholar]
- 35.Bleau A, Leon LJ. Watershed-based segmentation and region merging. Comput Vis Image Und. 2000;77(3):317–370. [Google Scholar]
- 36.Haris K, Efstratiadis SN, Maglaveras N. Watershed-based image segmentation with fast region merging. 1998 International Conference on Image Processing - Proceedings. 1998;3:338–342. doi: 10.1109/83.730380. [DOI] [PubMed] [Google Scholar]
- 37.Pires RLVPM, De Smet P, Philips W. Watershed segmentation and region merging. P Soc Photo-Opt Ins. 2004;5308:1127–1135. [Google Scholar]
- 38.Wang J, Lu HQ, Eude G, Liu QS. A fast region merging algorithm for watershed segmentation. 2004 7th International Conference on Signal Processing Proceedings. 2004;1–3:781–784. [Google Scholar]
- 39.Beucher S. Watershed, Hierarchical Segmentation and Waterfall Algorithm. In: Serra J, Soille P, editors. Mathematical Morphology and Its Applications to Image Processing. Vol. 2. Springer Netherlands; 1994. pp. 69–76. [Google Scholar]
- 40.Crespo J, Schafer RW, Serra J, Gratin C, Meyer F. The flat zone approach: a general low-level region merging segmentation method. Signal Process. 1997;62(1):37–60. [Google Scholar]
- 41.Sezgin M, Sankur B. Survey over image thresholding techniques and quantitative performance evaluation. J Electron Imaging. 2004;13(1):146–168. [Google Scholar]
- 42.Horn BKP. Closed-form solution of absolute orientation using unit quaternions. J Opt Soc Am A. 1987;4(4):629–642. [Google Scholar]
- 43.Umeyama S. Least-squares estimation of transformation parameters between two point patterns. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1991;13(4):376–380. [Google Scholar]
- 44.Arun KS, Huang TS, Blostein SD. Least-Squares Fitting of Two 3-D Point Sets. Pattern Analysis and Machine Intelligence, IEEE Transactions on. 1987;PAMI-9(5):698–700. doi: 10.1109/tpami.1987.4767965. [DOI] [PubMed] [Google Scholar]
- 45.Dobrowolski P. Swing-twist decomposition in Clifford algebra. 2015 arXiv preprint arXiv:1506.05481. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.
Supplementary Materials
Fixed LSU with SSU body rotation from state “A” to “B.”
Fixed SSU Body with SSU head rotation from state “A” to “B.”
Fixed LSU with Full SSU rotation from state “A” to “B.”
Figure S1. Illustration of classical watershed flooding algorithm for a 1D image. The idea remains the same for a 2D image or 3D density map. ‘s’ denotes the flooding level or intensity (density) (arbitrary values here). Colored regions are catchment basins and the vertical lines are the watershed lines demarcating the boundaries between the basins. The flooding starts from a source at the catchment basin at the minimum intensity level for the and gradually fills up the basins with increasing flooding levels until it reaches the maximum level. In the process of flooding, the watershed is marked between two neighboring basin at the moment when the flood water starts to spill into the neighboring basin.
Figure S2. Inertia Tensor and Principal Axes of a Rigid Body. A. An arbitrary rigid body with an axis of rotation P passing through the origin O (center of mass). An infinitesimally small element with mass dm is situated at X with position vector r⃗. The rigid body is rotating with an angular velocity of ω→. B. An example of a disc with radius r (and radial vector r⃗) rotating around Z axis passing through the center of the disc. C. Three Principal axes computed for each of the two domains of the ribosome. The two domains shown are LSU (blue) and SSU body (yellow). The Principal axes for individual domains are shown with the same color as the corresponding domain. The inset on the right panel shows the Principal axes only.
Figure S3. Segmentation Error for the Segmentation Case 1 in Tables 1, S1, S3. A. Initial segmentation of the three relevant domains LSU (blue), SSU Body (yellow), SSU Head (orange). The red segment could not be automatically segmented out. Part of the red segment belongs to SSU (highlighted region) and the other part to LSU (highlighted region). B. The false positive (incorrectly identified; pink) and false negative (incorrectly rejected; green) atoms are shown on the segmented LSU domain (blue). The third panel shows the interface view of the LSU. C. The false positives (pink) and false negatives (green) are shown on the segmented SSU domain (yellow). The residues belonging to the red segment are not shown in (B) and (C) and were excluded from the LSU and SSU residues in subsequent calculations.
Figure S4. Segmentation Error for the Segmentation Case 14 in Tables S1, S2, S3. A. The false positives (pink) and false negatives (green) are shown on the segmented LSU domain (blue). The third panel shows the segmentation error in the interface view of the LSU. B. The false positives (pink) and false negatives (green) are shown on the segmented SSU domain (yellow). The residues belonging to the red segment were excluded from the LSU and SSU residues in subsequent calculations.
Figure S5. Segmentation Error for the Segmentation Case 6 (top row) and Case 8 (bottom row) in Tables S1, S2, S3. A. The false positives (pink) and false negatives (green) are shown on the segmented LSU domain (blue). The third panel shows the interface view of the LSU. B. The false positives (pink) and false negatives (green) are shown on the segmented SSU domain (yellow). The residues belonging to the red segment were excluded from the LSU and SSU residues in subsequent calculations.
Figure S6. Characterizing the Error in Domain Segmentation and Domain Rotation Angle. A. Segmentation quality measures with Precision, Recall, F − measure calculated for the individual domains and the full structure, in all the segmentation cases listed in Table S1. The plotted values are ranked based on the F − measure of the SSU (Table S4). Across all the segmentation cases, the Precision and Recall values for the individual subunit seemed to vary more than the corresponding measures for the full structure and the F − measure. B. The rotation angle for SSU, SSU body and SSU head for the corresponding segmentation cases and the plotted angles are ranked in the same manner as in A.