Mutation and catastrophe in the aging genome

Abstract

In the 1960s, Leslie Orgel proposed what is now known as the error catastrophe theory of aging, arguing that errors in protein translation that reduce the fidelity of the protein-translating enzymes would lead to a feedback loop of increasingly inaccurate protein synthesis, terminating in the death of the organism. This mechanism of aging would be consistent with the exponential increase of mortality observed in humans, but the error catastrophe theory of aging has been generally disregarded by researchers due to a lack of evidence for an age-related increase in protein errors. Another theory of aging, proposed at roughly the same time, is Leo Szilard’s two-hit model of somatic mutation accumulation, which assumed a linear increase in mutations over time but explained the nonlinear pattern of human mortality through a mechanism of genetic and cellular redundancy which kept mortality low until the redundancy was exhausted, at which point mortality rapidly rose. Here, we synthesize the two theories, along with the latest advances in genomics research. We propose a new catastrophe theory of aging, this time with somatic mutations as the primary agent of the feedback loop. Similar to protein errors affecting translation itself, somatic mutations in genes involved in DNA replication and repair would lead to a feedback loop of exponentially increasing mutation load. The difference from protein errors is that somatic mutations would mainly affect gene regulatory regions rather than the much smaller part of the genome encoding protein-coding information. Although the self-stimulating accumulation of somatic mutations is not mutually exclusive with the Szilard-based loss of redundancy, we present evidence that suggests that the accumulated mutations themselves could be numerous enough to cause mortality. Finally, we acknowledge the limits of our current knowledge and propose a course of research practices that will help to confirm or refute our model and advance the field of aging research as a whole.

1. Introduction: two models of aging

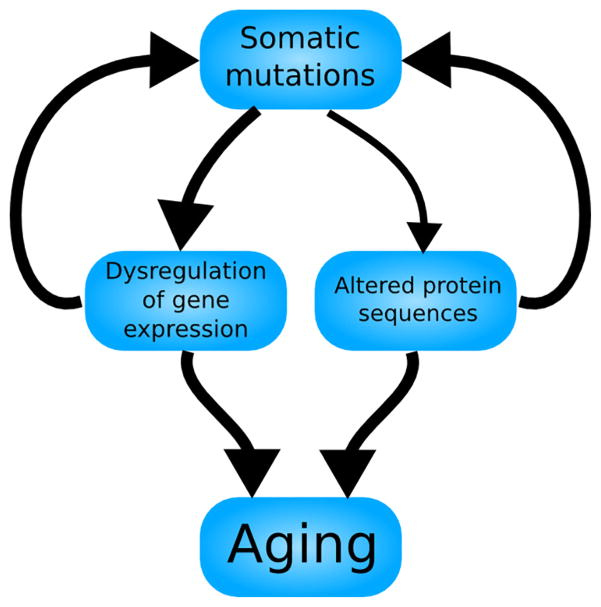
Over the years, many different processes have been hypothesized to cause aging (Medvedev, 1990) Although none is universally accepted, some are more popular than others. One enduring hypothesis is Leo Szilard’s two-hit model (Fig. 1), which has enjoyed widespread appeal since its proposal in the middle of the twentieth century. Seeking to explain why the number of deaths peaked around the age of eighty, Szilard proposed a model in which cells suffer aging “hits” destroying or inactivating chromosomes at a constant rate. A cell becomes nonfunctional upon receiving a hit when the homologous chromosome has either suffered an earlier hit or inherited a faulty allele of one of its genes. Mortality is low until the number of “surviving” cells—i.e. those not rendered nonfunctional from suffering a hit on both copies of a homologous chromosome or a hit on a chromosome whose homolog has a faulty allele—reaches a critical value, estimated by Szilard to be somewhere between 1/3 and 1/12 of all cells, at which point the risk of mortality rapidly rises (Szilard, 1959).

Fig. 1.

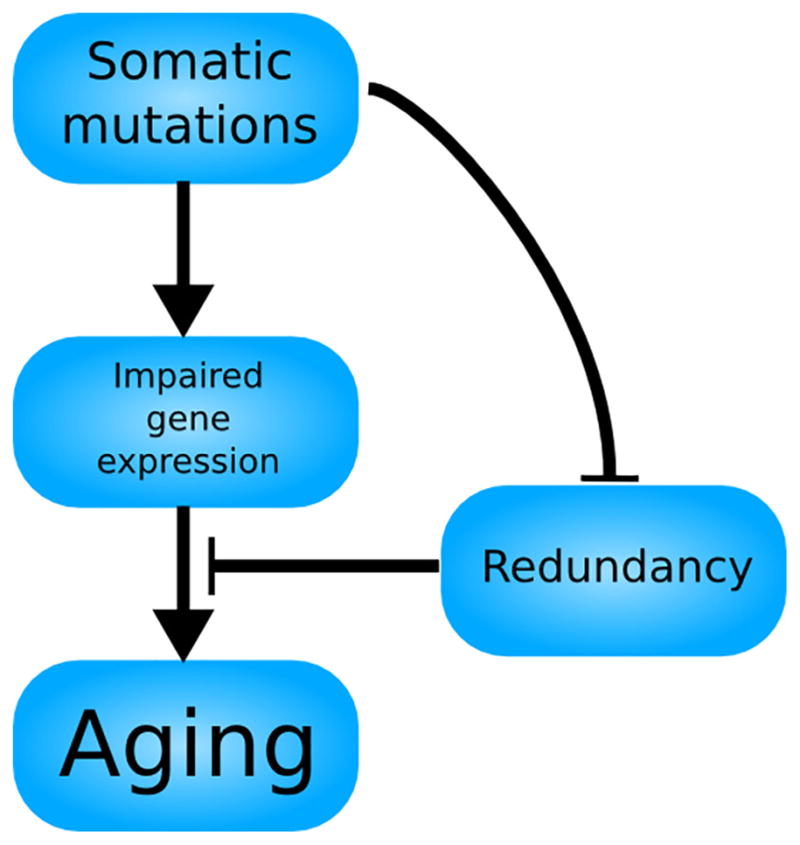
A schematic representation of the Szilard model of aging. Somatic mutations accumulate, interfering with the proper expression of genes, but the genetic and cellular redundancy of the organism prevents the impaired gene expression from leading to aging. However, the accumulation of somatic mutations also wears down the redundancy of the organism, causing an aging phenotype to manifest upon its exhaustion. Thus, the Szilard model is a feedforward loop, resulting in a phenotype after a period of latency.

The assumption that organisms receive hits—in essence, somatic mutations—at a constant rate over time and across all individuals is questionable and appears to be at odds with the exponentially accelerating trend of mortality with age, but Szilard reconciles this apparent contradiction with his model through the assumption that cells function optimally until their genetic redundancy (in the form of diploidy) is exhausted, and organisms are healthy until their cellular redundancy is exhausted. Combining this biologically plausible mechanism with some reasonable values for the rate of hits and critical value of surviving cells, Szilard arrives at an estimate of age-dependent human mortality that closely matches empirical observations. Despite its back-of-the-envelope nature, Szilard’s model has stood up well to modern scrutiny (Zetterberg et al., 2009). It is also notable that Szilard was able to derive an exponential mortality curve from a linear accumulation of age-related damage, a task that has proven difficult with other biomarkers of aging (Finch and Crimmins, 2016).

Around the same time as the physicist Szilard’s foray into biology, Leslie Orgel proposed a different theory of aging (Fig. 2). In contrast to Szilard’s implication of a constant rate of DNA mutation, Orgel attributed aging to an exponential rise of errors in proteins. In Orgel’s model, errors in the translation of a protein responsible for protein translation itself, reducing its fidelity, would lead to a feedback loop of mistranslation. Escalating exponentially until the cell becomes overwhelmed, such increased mistranslation was considered by Orgel to causally contribute to aging (Orgel, 1963).

Fig. 2.

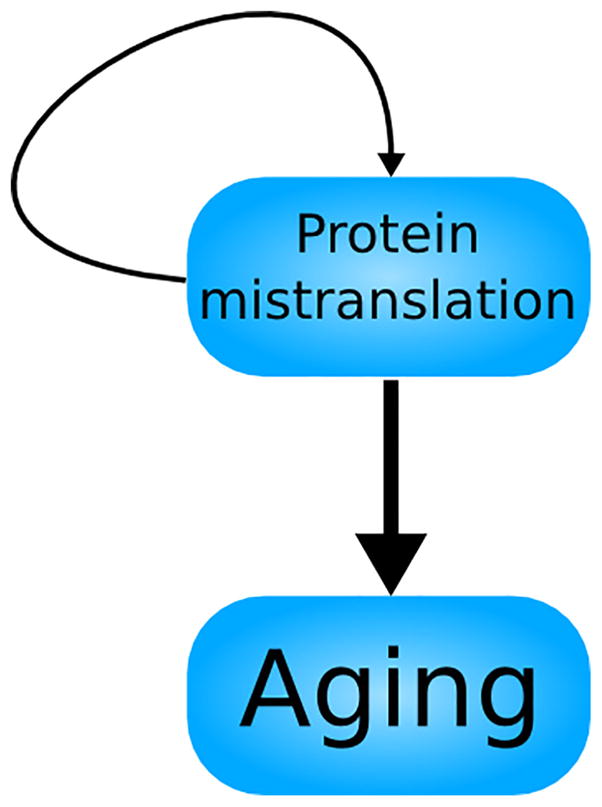
A schematic representation of the Orgel model of aging. Protein mistranslations lead to aging, while also propagating more protein mistranslations. This feedback loop could account for the acceleration of mortality with age, but subsequent research has cast doubt on whether the self-stimulating nature of protein mistranslation is sufficient to perpetually increase its rate; this uncertainty is reflected in the thinner arrow representing the feedback loop of protein mistranslation.

Since then, multiple attempts were made to test this “error catastrophe theory of aging”. A study measuring the accumulation of mistranslations in E. coli by tracking the incorporation of cysteine into flagellin found that the translational error rate in E. coli tends to converge to an elevated but stable value if perturbed by the mistranslation-promoting antibiotic streptomycin (Edelmann and Gallant, 1977). This finding presented evidence that protein translation errors would not necessarily increase without bound and might not have a role in aging. Another important piece of evidence against the error catastrophe theory of aging came from a study that used two-dimensional gel electrophoresis (size separation and isoelectric focusing) of radiolabelled proteins to examine the frequency of mistranslated proteins in cultured fibroblasts from fetal, young and old individuals, as well as from individuals suffering from the segmental progeroid syndromes Hutchinson-Gilford or Werner syndromes. They found that protein mistranslation did not increase with age or cell passage number and was not elevated in cells from progeroid individuals (Harley et al., 1980). Negative results like these resulted in error catastrophe being largely disregarded as a cause of aging.

After his initial proposal of his protein error catastrophe theory, Orgel himself conceded that the rate of mistranslation would converge to a stable value if the constant describing the proportionality between the number of existing mistranslations and the number of new mistranslations fell below a certain value (Orgel, 1970). In the light of modern knowledge about translation, the protein error catastrophe theory may have been undone by the robustness and highly redundant nature of the protein synthesis machinery. The ribosome is largely composed of RNA, so there are relatively few ways in which its function can be affected by mistranslation. Furthermore, a single E. coli cell can contain over 70,000 ribosomes (Philips, n.d.), and eukaryotic cells, being larger, may have even more. Thus, even a mistranslation in a ribosomal protein that dramatically increases the rate of translational infidelity would only affect that ribosome, which would account for a fraction of a percent of all translation in the cell. Considering the minute impact of each defect in a ribosomal protein, it is likely that the constant of proportionality is very low; and the failure to find any experimental evidence of a protein catastrophe only confirms this possibility. However, it should be noted that the negative experimental results merely indicate that the frequency of high-abundance protein changes is very low; similar to DNA mutations, low-abundance protein changes could be very important but are undetectable in bulk tissue or whole cell populations unless the type of change is exactly known. Thus, the lack of evidence for Orgel’s model of protein error catastrophe may be due to technical limitations, i.e. the lack of technology allowing the detection of low-abundance protein errors. Nevertheless, the combination of theoretical considerations ruling it out as a cause of aging and a complete lack of evidence as to its actual involvement make the protein error catastrophe model an unlikely candidate for explaining aging.

2. Somatic mutations, but not Szilard’s model

Genome instability—i.e., the tendency of genomes to accumulate sequence changes, usually due to errors made during repair or replication of a DNA template that is damaged by breakage or other physicochem-ical changes—is considered to be one of the hallmarks of aging (López-Otín et al., 2013). As we have seen, this was already recognized in the 1950s by Szilard and another physicist, Gioacchino Failla (Failla, 1958), but recent advances in genomics allowed for much more accurate methods to assess DNA damage and mutations in cells and tissues of aging organisms.

Initially, attention was focused on DNA damage rather than mutations as the possible cause of aging (Alexander, 1967; Gensler and Bernstein, 1981), but a more detailed examination of the kinetics of DNA damage reveal that DNA damage is unlikely to the primary cause of aging. The human genome is thought to be subjected to tens of thousands of lesions per cell per day (Ames et al., 1993; Lindahl and Nyberg, 1972), but the overwhelming majority of these must be rapidly repaired; otherwise the genome would soon become saturated with damage and life would cease. There is some evidence that DNA damage accumulates with age in some tissues (Maslov et al., 2013), but the exact nature of the damage remains unclear. Indeed, even these low levels of spontaneous DNA damage may represent a steady state due to continuous repair and induction of new damage. However, DNA damage can cause certain aging phenotypes by activating cellular responses, such as apoptosis and cellular senescence, which are also hallmarks of aging (White et al., 2015a). With notable exceptions, therefore, DNA damage is largely a transient phenomenon, and its most important endpoint is the mutations in sequence that arise as a consequence of errors during repair.

Such mutations, which can vary from base substitutions to large chromosomal aberrations, are not only inevitable but also irreversible. Indeed, once the original template is lost, the original can never be restored. In contrast to DNA damage, there is now a strong body of literature showing that various types of mutations accumulate with age in different cells and tissues of humans and experimental animals. Historically, these findings have relied primarily on detection of somatic mutations using selectable markers (Dollé et al., 2000; Lee et al., 1994; Ono et al., 2000), but they are of sufficient strength to warrant an inclusion of somatic mutations among the hallmarks of aging (López-Otín et al., 2013) and have been vindicated by recent sequencing-based experiments, such as the detection of an age-related increase in somatic mutations in human organoids (Blokzijl et al., 2016). The evidence is mainly correlative, but a causal role is suggested by the fact that many progeroid syndromes in humans are the result of a mutation in a DNA-repair gene (Vijg, 2007). Other results from model organisms find much the same: deficiency of the DNA repair enzyme Ku80 (Busuttil et al., 2008b) or Ercc1 in mice (Dollé et al., 2006) leads to an increased somatic mutation frequency and premature aging, while overexpression of Myc in flies causes both an increase in the somatic mutation frequency and a decrease in lifespan (Greer et al., 2013).

Somatic mutations, then, appear to be the strongest candidates for a cause of aging. This does not, however, mean ultimate triumph for Szilard’s model. Indeed, it is now clear that the genetic and cellular redundancies in this model are insufficient to explain the diversity and malleability of mortality curves. However, Szilard’s and Orgel’s models can be synthesized into a unified somatic mutation catastrophe theory of aging based on recent advances in measuring the actual frequency of somatic mutations in tissues of aging mammals and new insight into redundancy of the functional genome. As we will show, somatic mutations accumulate with age in an exponential fashion, analogous to the exponential increase in protein mistranslation posited by Orgel. We will now review the evidence that this is indeed the case and that the resulting somatic mosaicism contributes to age-related decline.

3. Somatic mutations increase exponentially with age

Studies of the age-related accumulation of somatic mutations have generally examined the relationship between the two variables, age and mutation frequency, with either a simple test for difference between two groups (“young” and “old”, whose boundary varies from study to study) or a linear regression when data on multiple age groups were available. They have generally met with success, finding an increase between young and old or a linear increase with age, but the existence of a significant linear relationship does not preclude the existence of a significant exponential relationship. Indeed, the latter may prove to be a better fit for the data. However, many studies of somatic mutation frequency are conducted with a relatively small number of time points and samples, making it difficult, if not impossible, to fit anything other than a line to the data.

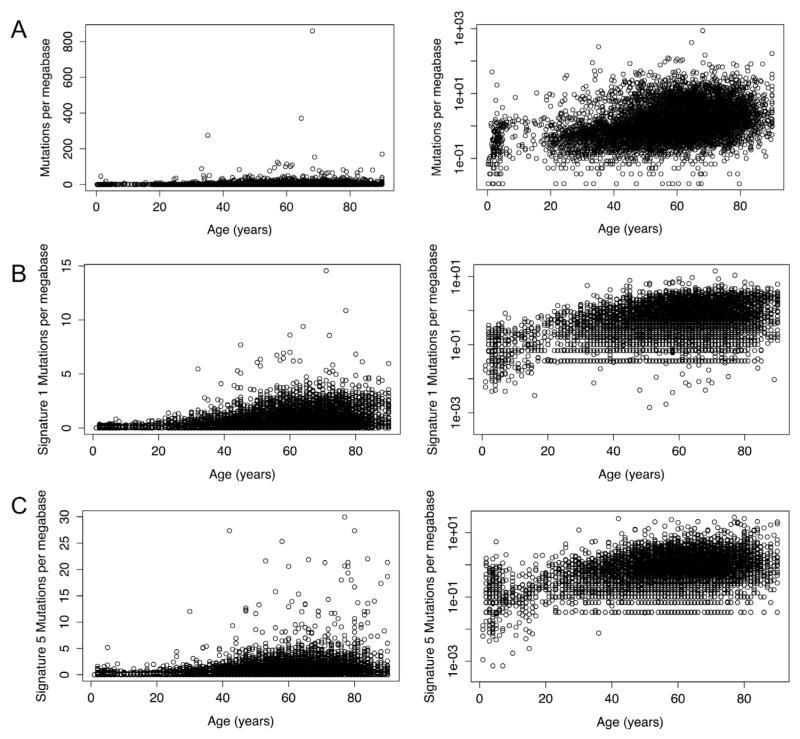
These limitations did not apply to a study examining the age-related increase in somatic mutations in nearly 7000 cancer genomes (Milholland et al., 2015); in this study, an exponential regression was found to fit the data much better than a linear regression (Fig. 3A; r = 0.36 vs r = 0.07). A short time after that study was published, another group published a paper which identified two mutational signatures, referred to as signature 1 and signature 5 and consisting of primarily C>T mutations and a broad mix of all mutation types respectively, as being associated with age in tumors (Alexandrov et al., 2015). They found sig-nificant linear correlations between those signatures and age, but re-analysis of their data reveals that an exponential correlation would fit the data even better (Fig. 3B and C). Another study looked for clonally expanded somatic mutations in blood using high-coverage sequencing of 160 genes; they found an age-related increase in the prevalence of somatic mutations that was clearly exponential, although they did not explicitly identify it as such (Jaiswal et al., 2014). These findings were anticipated by findings from the germline mutation rate: a paper examining de novo germline mutations in humans by whole-genome sequencing of family trios found that the increase in mutation frequency with the age of the father was better fit by an exponential regression than a linear regression (Kong et al., 2012). Since every germline mutation begins in the soma of one of the parents, this finding may be taken as evidence that somatic mutations increase exponentially with age.

Fig. 3.

Linear and exponential mutation accumulation. (A) Mutations in whole exomes per megabase in tumors vs age of patient at diagnosis. The increase is better modeled as an exponential relationship (right) than as a linear one (left) (r = 0.36 vs r = 0.07). (B) Signature 1 (age-associated), exome mutations in tumors per megabase vs age of patient at diagnosis. The frequency of somatic mutations belonging to mutation signature 1 as identified by Alexandrov et al. is better modeled as an exponential relationship than as a linear one (r = 0.296 vs r = 0.4). (C) Signature 5 mutations per megabase vs age of patient at diagnosis. Like signature 1 mutations, the frequency of somatic mutations belonging to mutation signature 5, as identified by Alexandrov et al., is better modeled as an exponential relationship than as a linear one (r = 0.23 vs r = 0.43). Data for (A) is from Milholland et al. (2015); data for (B) and (C) is from Alexandrov et al. (2015). Plots and correlation coefficients calculated using R (R Core Team, 2014).

It should be noted that the results described above have served to confirm earlier evidence for an exponential increase in mutation frequency found by methods not based on sequencing. The earliest result was a study of mutations in the hprt gene, which showed an exponential increase in the frequency of TG-resistant clones from kidney cells with the age of the donor (Martin et al., 1996). A study which used a restriction enzyme-based assay to investigate point mutation rates in the mitochondrial genome (Vermulst et al., 2007) found their increase with age was best fit by an exponential regression, as did an investigation using fluorescence in situ hybridization to detect chromosomal translocations (Sigurdson et al., 2008). Finally, two studies examined genome-wide patterns of somatic mosaicism using microarrays: in both of them, the proportion of individuals with detectable somatic mosaicism increased slowly and then more quickly in old age, consistent with an exponential increase with age (Jacobs et al., 2012; Laurie et al., 2012).

The exponential nature of the accumulation of somatic mutations was most recently demonstrated by whole genome sequencing of organoids derived from a variety of tissues (Blokzijl et al., 2016). A linear correlation between age and mutation frequency had an r² of 0.83 as compared to an exponential correlation with an r² of 0.86; linear and exponential models taking into account the tissue type and gender of the donor had adjusted r² values of 0.88 and 0.93, respectively. Thus, multiple experimental approaches have all found evidence supporting an exponential increase in the somatic mutation frequency.

The evidence reviewed above is far from definitive, but the concordance between a variety of sequencing- and non-sequencing-based assays and analyses strongly suggests that the age-related increase in somatic mutations is exponential, not linear. Meanwhile, evidence for some aspects of the Szilard model has been lacking. For example, Szilard’s model assumes a diploid organism, in which both copies of a chromosome must be inactivated before the cell suffers deleterious consequences. If this is the case, then the cells of triploid or tetraploid organisms would age according to a three- or four-hit model, affording them a much longer lifespan, while haploid organisms would follow a one-hit model and age more quickly. However triploid flies have not been found to live longer than diploid ones (Gowen, 1931), and haploid wasps do not suffer from a reduced lifespan compared to diploid individuals from the same species (Clark et al., 1963). Senescence is not even delayed in tetraploid human cells grown in culture (Thompson and Holliday, 1978). With the exception of the earliest paper, each of these findings was reported as evidence against the somatic mutation theory of aging. Since then, alternative explanations have arisen. The results in cultured cells can be explained by our knowledge that telomere attrition is generally the limiting factor for in vitro cell proliferation (and would affect all chromosomes more or less equally), while the validity of the findings in insects has been questioned on the grounds that a lack of appropriate gene dosage compensation nullified any longevity advantage gained through polyploidy (Finch, 1994). This latter line of reasoning may hold for the flies, but appears specious with regards to the wasps. First, haplodiploid inheritance is universal in wasps, so it is hard to imagine a species which has not evolved a way to handle variations in ploidy; even if the particular species studied had not, one must wonder why the haploid wasps, saddled with the double burden of reduced ploidy and improperly dosed genes, do not have a reduced lifespan. The lack of evidence for an influence of ploidy upon lifespan stands in contradiction to Szilard’s theory of aging due to its reliance on a chromosomally-based biological redundancy as the mechanism by which mutations lead to an accelerating increase in mortality, but, as we will explain later, it is still possible to formulate a theory of aging in which mutations play a prominent causal role.

It is conceivable that some modifications to Szilard’s model could salvage it: perhaps the genomes of haploid wasps possess mechanisms of redundancy not based on ploidy, such as homologous genes that perform the same role. But aside from the issues discussed above, Szilard’s model suffers from other inadequacies, especially when extending it beyond its original context to explain patterns of longevity in nonhuman species. Lifespan varies by orders of magnitude between species; for example between humans, mice and naked mole-rats, even all three are diploid and the latter two species are identical in mass. Indeed, longevity differences between these species may be due to differences in DNA repair (MacRae et al., 2015), suggesting that a model that focuses on the kinetics of somatic mutation, rather than the exhaustion of redundancy, will be better at predicting longevity.

To summarize, Szilard’s model, which predicts an exponential rise in mortality from a linear increase in somatic mutations, neither adequately explains the diversity of lifespans observed in nature nor successfully predicts the factors that modulate lifespan. In addition, one of its key assumptions, a constant rate of somatic mutation, appears to be false. Nonetheless, somatic mutations, by dint of their age-related increase and apparent association with progeria syndromes, could well be causally related to aging. In order to salvage the somatic mutation theory of aging, therefore, it is necessary to combine it with the error catastrophe theory to produce a new theory: the somatic mutation catastrophe theory of aging.

4. The somatic mutation catastrophe theory of aging

The somatic mutation catastrophe theory of aging (Fig. 4) explains why somatic mutations increase exponentially with age and how they might play a role in promoting aging. We will state the theory and then explain why it is more likely to be true than Orgel’s protein error catastrophe theory.

Fig. 4.

The somatic mutation catastrophe theory of aging. Somatic mutations lead primarily to a dysregulation of gene expression, but also to alterations in protein sequences, reflected in the relative weights of the arrows. Both of these consequences of somatic mutations contribute to aging, while also leading to further somatic mutations. This feedback loop could explain the age-related exponential increase in both somatic mutations and mortality with a mechanism more robust than Orgel’s.

DNA replication is imperfect and may lead to permanent changes in the sequence of the genome, i.e. mutations. Mutations may also result from damage to the DNA, lesions, that are either improperly repaired or not repaired quickly enough, as an abnormal residue or a basic site resulting from a lesion is unlikely to correctly convey the genomic information to a DNA polymerase and will almost certainly cause a mutation when encountered by the replication machinery. Mutations increase in frequency with time, but if one happens to interfere with one of the genes responsible for DNA repair, the rate of mutation will increase. The increased rate of mutation will make the occurrence of another DNA repair-disrupting mutation more likely, leading to a feedback loop of exponentially increasing mutation frequency. Assuming that risk of mortality is proportional to the somatic mutational burden of an organism, the exponential increase in mutation frequency will lead to an exponential increase in mortality.

The replacement of proteins with DNA as the agent of the positive feedback loop gives our model an important advantage over the protein catastrophe theory of aging. As discussed above, the thousands of ribosomes present in the cell put a damper on the propagation of protein mistranslations, but such massive redundancy does not exist in the genome. Instead, a mutation that acts to decrease the fidelity of a DNA polymerase or repair enzyme will affect around half of all copies of that polymerase. In other words, the constant of proportionality relating the number of existing mutations and the rate of mutation is likely to be higher than the constant relating the number of mistranslations and the rate of mistranslation.

Another one of the issues with Orgel’s model is that it relies on a very specific, subtle class of translation error: those errors that reduce the fidelity of the translational apparatus without completely obliterating its function. A mistranslated protein that has its function severely or completely disrupted will contribute few or no future mistranslations. By contrast, a much broader class of DNA mutations can increase the rate of somatic mutation. The genome is only able to maintain its sequence stability through the constant activity of hundreds of repair enzymes. In addition to the obvious, but rare, case of a mutation that reduces the fidelity of a DNA polymerase, any sort of mutation that affects either the fidelity or the efficiency of one of the many DNA repair enzymes could increase the mutation rate, as would a mutation in a regulatory region or transcription factor gene resulting in a decreased expression of one of those enzymes. To illustrate just how many types of mutations may themselves contribute to further somatic mutations, we will discuss the example of DNA polymerase η. DNA pol η performs translesion synthesis at UV-damaged sites with a higher fidelity than other polymerases; a loss of its expression or activity would increase the mutation rate, as evidenced by the fact that mutations in DNA pol η cause the condition xeroderma pigmentosum. Indeed, a knockout of DNA pol η has been found to cause greater UV-induced mutagenesis in mouse embryonic fibroblasts (Busuttil et al., 2008a). However, DNA pol η performs DNA replication at non-lesion sites with lower fidelity than other polymerases, so, hypothetically, a mutation causing overex-pression of DNA pol η could cause ectopic replication at sites where it is not needed, leading to an increase in the mutation rate. Therefore, almost any conceivable type of mutation in DNA pol η has the potential to increase the mutation rate: those that reduce the fidelity of DNA pol η, those that reduce its activity or expression, and even those that increase its expression.

The greater number of ways by which somatic mutations, as compared to protein mistranslations, can contribute to more mutations gives us confidence that the exponential increase in mutation frequency observed is due to a positive feedback loop. The propensity of cells to enter this feedback loop is evident by the prevalence of mutator phenotypes in cancers (Loeb, 2001); presumably mutator phenotypes may arise in other cells in the absence of oncogenic mutations and cause dysfunction in normal tissue as well. Recent advances in next-generation sequencing has now provided evidence that the number of mutations in a given somatic cells is very high, i.e., from several hundreds to thousands of base substitutions per average cell (Blokzijl et al., 2016; Milholland et al., 2015; Dong et al., 2017). Indeed, we recently showed that somatic mutation rates in both mice and humans are 1–2 orders of magnitude higher than the germline mutation frequency (Milholland et al., 2017) underscoring the disposable nature of the soma.

One further issue remains: if the massive levels of mistranslated proteins predicted by Szilard’s model were never observed, how can we posit somatic mutation catastrophe as a cause of aging? Surely the somatic mutations would manifest themselves in the form of aberrant proteins? We resolve this apparent contradiction by postulating that gene expression level changes, not protein sequence changes, are the primary functional consequence of somatic mutations. It has been known for quite some time that the fraction of the genome dedicated to regulation is much larger than the fraction that codes for amino acids, so it is time we gave the regulatory region its due. Indeed, it is now becoming apparent that not only does gene expression become increasingly disordered between cells with age (Bahar et al., 2006) but also that both natural aging and DNA damage-induced premature aging are accompanied by large-scale transcriptomic alterations, including increased variation in gene expression (White et al., 2015a, 2015b).

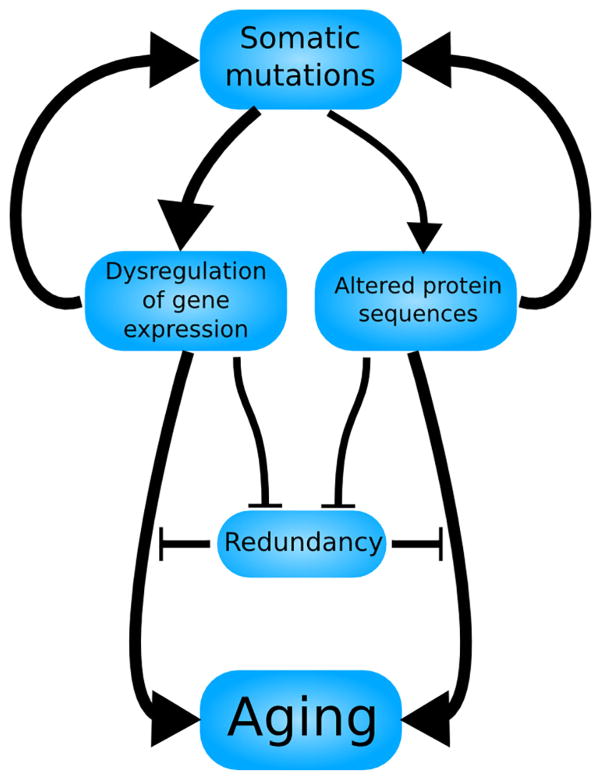
Finally, we wish to mention that we do not completely discount a role for Szilard’s genetic and cellular redundancy in modulating the relationship between somatic mutation frequency and mortality. The human mortality rate spans 4 orders of magnitude with age (Human Mortality Database, n.d.), while in the cancer dataset mentioned previously, 95% of the somatic mutation frequencies fall within a range of only 2 orders of magnitude. Therefore, in proposing a nonlinear increase of mutations with age, we do not want to risk implying an oversimplified 1:1 correspondence between mutation frequency and risk of mortality. Rather, we seek to convey a sophisticated model (Fig. 5) with both a nonlinear increase in somatic mutations with age and a nonlinear increase in mortality with somatic mutation frequency.

Fig. 5.

A more sophisticated model of the somatic mutation catastrophe theory of aging. Borrowing elements from both Szilard’s and Orgel’s models, somatic mutations increase at an accelerating rate with age, a feedback loop mediated partially by altered protein sequences but primarily by a dysregulation of gene expression. The redundancy of the organism, both cellular and genetic, may inhibit these consequences of somatic mutations from directly contributing to aging, but is itself subject to degradation by somatic mutations. This model may most accurately reflect human aging, predicting both a period of latency (reflecting the lack of an aging phenotype during development and early adulthood) and an accelerating decline afterwards (reflecting the slow-then-rapid deterioration that begins in middle age).

5. Conclusion: how to test the model

In this paper, we have proposed a new model to explain how somatic mutations, by increasing exponentially with age, may provide a mechanism for the aging process. We have also discussed the evidence for our model, which is convincing but by no means conclusive. That being said, we would like to suggest some guidelines for how to test our model. Even if our hypothesis turns out to be false, following these guidelines will advance the field as a whole and increase our understanding of aging.

First, experimental design should incorporate multiple time points. Two points may define a line, but they do not provide enough information to derive a curve. As we have demonstrated, a key aspect of our model is an exponential increase in mutation frequency with age. A simple comparison between a “young” and “old” group will never be able to test our hypothesized kinetics of a possible driver of aging. When recruiting human subjects, an effort should be made to select people from many ages, not just those under 30 and over 70. For experiments involving mice, it is often convenient to use two litters, which both ensures genetic homogeneity within groups and simplify the analysis. We suggest switching to staggered groups of mice occupying a wide range of ages, including multiple points within middle age. The resulting genetic heterogeneity of the mice may make the experiments slightly less tractable, but it will increase their applicability to genetically heterogeneous humans. In short, the benefits of this approach are worth the trouble. Simply reporting differences between the case and control groups will no longer be sufficient. Age is a continuous, quantitative variable, and investigators should make use of it as such. In addition, investigators should be on the lookout for any nonlinear relationships between variables. Ideally, multiple measurements should be recorded and their interactions analyzed using machine learning techniques. The somatic mutation frequency, for example, is modulated not just by age, but by tissue and environmental factors (Milholland et al., 2015); and while aging may be strongly influence by the somatic mutation frequency, other factors are bound to play a role as well. In short, less effort should be focused on trying to find the one gene, biomarker or variable that causes aging and on trying to understand the nature of the gestalt that leads to aging.

Finally, scientists should appreciate that aging is more than just age. Instead of using chronological age as the independent variable, efforts should be made to instead focus on mortality, either by following up with human subjects or by longer-term observation of animal models. The diverse level of health among people of the same age should indicate that chronological and biological age levels are largely decoupled. Ultimately, studies that seek to extend life and delay aging will need to focus on mortality risk, as chronological age will be rendered meaningless.

Taking advantage of advances in genomics and bioinformatics, we have used the evidence available to argue for a new theory of aging. To test that theory, still more sophisticated experiments and analyses will be necessary, but we are sure that the talented and dedicated scientists of the future will rise to the challenge. Regardless of what they find, we are now seeing the dawn of a new age in aging research.