Abstract
Conventional imaging of the human cornea with optical coherence tomography (OCT) relies on telecentric scanning optics with sampling beams that are parallel to the optical axis of the eye. Because of the shape of the cornea, the beams have in some areas considerable inclination to the corneal surface which is accompanied by low signal intensities in these areas and thus an inhomogeneous appearance of corneal structures. In addition, alterations in the polarization state of the probing light depend on the angle between the imaging beam and the birefringent axis of the sample. Therefore, changes in the polarization state observed with polarization-sensitive (PS-) OCT originate mainly from the shape of the cornea. In order to minimize the effects of the corneal shape on intensity and polarization-sensitive based data, we developed a conical scanning optics design. This design provides imaging beams that are essentially orthogonal to the corneal surface. Thus, high signal intensity throughout the entire imaged volume is obtained and the influence of the corneal shape on polarization-sensitive data is greatly reduced. We demonstrate the benefit of the concept by comparing PS-OCT imaging results of the human cornea in healthy volunteers using both scanning schemes.
OCIS codes: (170.4500) Optical coherence tomography, (260.5430) Polarization, (170.4470) Ophthalmology
1. Introduction
The human cornea shows a layered structure which was studied in vitro by various different approaches like histology [1], electron microscopy [2] and X-ray scattering [3–6] and is well known today. The outmost layer, the corneal epithelium, is separated from the stroma by Bowman’s layer. The stroma itself is composed of about 200 stacked lamellae organized parallel to the surface. Each of those lamellae has a thickness of 1.5 μm to 2.5 μm and contains highly organized parallel collagen fibrils which subtend large angles with fibrils in adjacent lamellae. The backside of the cornea is delimited by the Descemet’s membrane and the corneal endothelium [7]. Various corneal diseases such as keratoconus lead to changes of this regular structure.
Optical coherence tomography (OCT) provides high resolution cross-sectional images at short acquisition times and therefore is a powerful tool to non-invasively image the human cornea in vivo. Previous studies have shown the effectiveness of this method to image the anterior segment [8–11]. However, the axial resolution and contrast of standard OCT is not sufficient to resolve stromal lamellae and the underlying fibril structure. Nevertheless, these fibrils cause form birefringence which can be detected using polarization-sensitive (PS) methods, such as Mueller matrix ellipsometry [12], scanning laser polarimetry [13], liquid-crystal imaging polariscopes [14] and PS-OCT [15]. Thus, the organization of fibrils can be indirectly assessed through the investigation of changes in birefringence.
PS-OCT is a functional extension of OCT and was first introduced by Hee et al. [16] for one-dimensional imaging and by de Boer et al. [17] for two-dimensional cross sectional imaging. The initial method was extended in order to measure the cumulative retardation and axis orientation of tissue within one single A-scan per measurement location [18]. When imaging the human cornea with PS-OCT, distinct patterns in retardation and axis orientation can be observed, as shown by previous studies [19–23], that arise from the corneal shape and the corresponding fibril orientation. These patterns are distorted in case of diseases like keratoconus [24,25], making this technique a promising method for corneal diagnostics.
The analysis of the corneal structure is mostly limited to the central region or the periphery at the corneal-scleral interface because of the low signal-to-noise ratio (SNR) of the paracentral region. This low SNR is due to the large inclination of the incident beam to the surface of the cornea. In order to obtain sufficient signal intensity over the entire cornea, a different scanning strategy is needed, which makes the sampling beam impinge at an almost perpendicular angle throughout the entire surface of the cornea. Recently, a different scanning strategy has been proposed in order to image the iridocorneal angle [26]. However, this method requires a contact lens and was limited to the peripheral region of the cornea.
The aim of this work was to introduce a conical scanning optics design that enables scanning of the cornea with a large field of view (FoV) and perpendicular incident angles onto the corneal surface in order to enhance the signal intensity in the paracentral region and to reduce the influence of the corneal shape on PS-OCT data. We present the design of the conical scanning optics, analyze associated image distortions and present an approach to correct for them. Furthermore, we demonstrate the performance of the conical scanning scheme in comparison to the telecentric scanning geometry by measurements in phantoms and in eyes of five healthy volunteers. Enhanced SNR in reflectivity images of the paracentral cornea is obtained, which improves the reliabillity of PS-OCT data [27,28]. By minimizing the influence of the corneal curvature on PS data, we are able to identify additional birefringent structures in the corneal periphery that might be related to preferentially aligned, reinforcing collagen fibrils [4–6].
2. Methods
2.1. Polarization-sensitive single mode fiber based SS-OCT setup
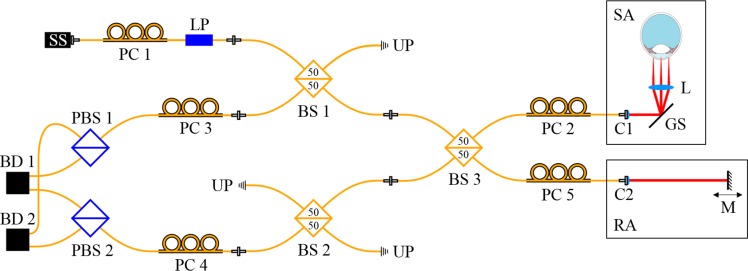
A previously developed [29] all single-mode (SM) fiber based Mach-Zehnder interferometer setup was adapted to a symmetrical Michelson interferometer setup [30] to improve the balanced detection of the system and to reduce the presence of image artifacts. A basic sketch of the setup is shown in Fig. 1.
Fig. 1.
Schematic diagram of the all SM fiber based SS-PS-OCT setup: SS, swept source; PC, polarization control paddles; LP, linear polarizer; BS, beam splitter; UP, unused port; SA, sample arm; RA, reference arm; C, collimator; GS, galvo-scanner; L, scanning lens; M, mirror; PBS, polarizing beam splitter; BD, balanced detection unit.
The light source is a tunable laser source (Axsun Technologies Inc., 1060 Swept Laser Engine) with a central wavelength of 1045 nm, a sweep range of 100 nm and a sweep rate of 100 kHz. The illumination power at the sample is set by adjusting the polarization state before the linear polarizer (LP, OZ Optics Ltd.) using fiber polarization control paddles (PC1). The light passes the first SM fiber based, non-polarizing beam splitter, BS1 (FOBS-22P-1111-6/125-SSSS-980/1100-50/50-40-3A3A3A3A-1-2, OZ Optics Ltd.) and is then split into sample and reference arm in BS3 (50/50). In the sample arm, after being reflected by the galvo-scanner, the light beam is focused onto the sample. In the reference arm, the collimated beam is reflected by a mirror (M), which is mounted on a translation stage. The backscattered light from the sample interferes with the light returning from the reference arm in BS3 and reaches the polarizing beam splitters (PBS1 and PBS2, FOBS-12P-111-6/125-SSS-1060-PBS-50-3A3A3A-1-1, OZ Optics Ltd.) after traversing BS1 or BS2, respectively. In PBS1 and PBS2 the interfered light is split into a horizontal and vertical polarization channel. The two corresponding interference signals are then detected by the balanced photo detectors (BD1 and BD2, Thorlabs Inc., PDB 460C) with a bandwidth of 200 MHz. The balanced signals are digitized using a dual channel digitizer (AlazarTech Inc., ATS9350) with 12-bit resolution at a variable frequency of up to 500 MHz. We measured an axial resolution of 6.3 μm in tissue and a depth range of 5.9 mm in air. For one volume acquisition we recorded 150 B-scans each containing 1024 A-scans in less than two seconds using a raster scan pattern. An illumination power of 1.8 mW at the cornea was used, which is below the laser safety limits [31]. Using a mirror as a sample, we measured a sensitivity of 97.1 dB close to the zero delay which is 2.8 dB below the calculated shot-noise-limit of 99.9 dB.
The polarization state of light in the different arms of the system is set manually using PC2 – PC5. The alignment of the system was done according to the protocol of the previous setup as reported in [29]. The sample was illuminated with circular polarized light. This allows to calculate reflectivity R, phase retardation δ and axis orientation θ according to:
| (1) |
| (2) |
| (3) |
with a single A-scan per measurement location [18], where A1 and A2 represent the amplitudes accessible from the complex signals obtained by the Fourier transform of the spectral data of the two polarization channels, Δϕ is the phase difference between the complex signals of the two channels at the same sample position, θ0 is an axis offset introduced by the fiber optics and z is the depth coordinate [29,32]. Before calculating the polarization-sensitive data, the images were intensity thresholded (only data above this threshold is used for further analysis). The threshold was chosen to be 5 dB above the noise floor. The degree of polarization uniformity (DOPU) was calculated by Stokes vector analysis [33] with a window size of 4 × 12 pixels (axial × lateral = 25 × 128 μm2), which roughly corresponds to 4 times the transverse and axial resolution of the system.
2.2. Scanning optics design
In order to achieve similar signal strength over the entire cornea, a sampling beam with perpendicular incident angle on the corneal surface is required. We simulated different scanning optics with the optical design software OpticStudio (Zemax LLC.) and found an aspheric condenser lens (ACL) with a focal length of 40 mm (Thorlabs Inc., ACL5040U-B) to be suitable for providing an almost perpendicular incident angle and a focal plane similar to the shape of a normal human cornea (11 mm diameter and a radius of curvature of 7.8 mm) (cf. Fig. 2(a)), with a distance of 219 mm between the galvo-scanner (GS) and the ACL.
Fig. 2.
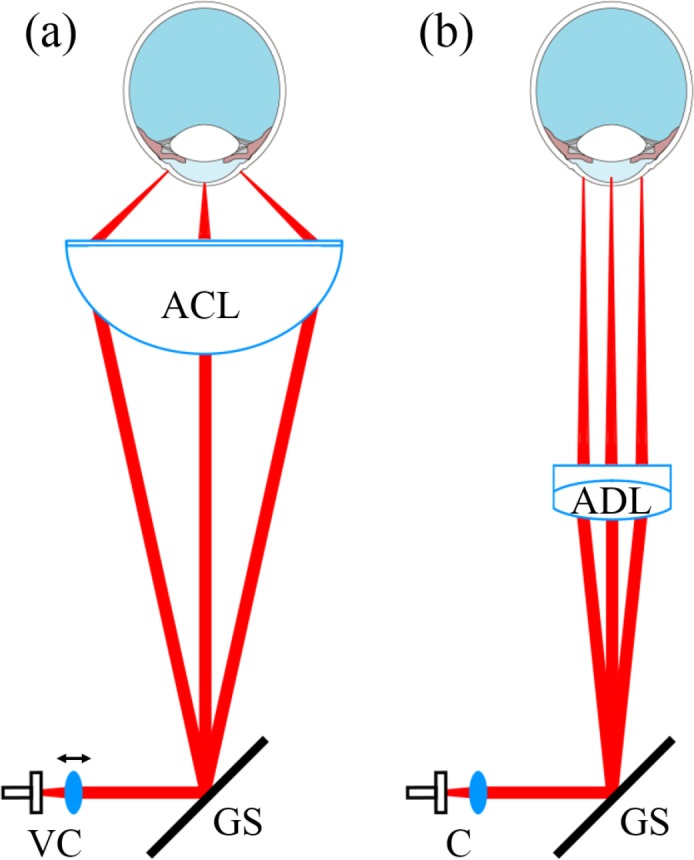
Sketch of the different scanning optics geometries: (a) Conical setup for perpendicular scanning, using an aspheric condenser lens (ACL) and (b) telecentric setup with sampling beams parallel to the optical axis, using an achromatic doublet lens (ADL). The position of the collimator lens (VC) is variable, to adjust the focal plane onto the surface of the cornea in the conical setup.
The transverse resolution of this configuration was measured to be 33 μm (1/e2 diameter) when using a collimated beam incidence on the lens. Using a collimator lens with a focal length of 10 mm (Thorlabs Inc., AC080-010-B), the beam diameter was measured to be 2.2 mm (1/e2). The FoV of the ACL is dependent on the distance between lens and eye. The focal length of the ACL is 40 mm but the distance between cornea and lens for the optimal FoV is 25 mm. So the focus of the sampling beam lies posterior to the cornea. To be able to shift the focus of the scanning beam onto the cornea, the position of the collimator lens is variable which results in a non collimated beam incidence on the ACL.
For telecentric scanning (cf. Fig. 2(b)) an achromatic doublet (ADL, Thorlabs Inc., AC254-125-B) was used. To be able to switch between the different scanning optics, without having to adjust the axial position of the sample, a focal length of 125 mm was chosen which resulted in a transverse resolution of 82 μm (1/e2).
2.3. Compensation of image distortions
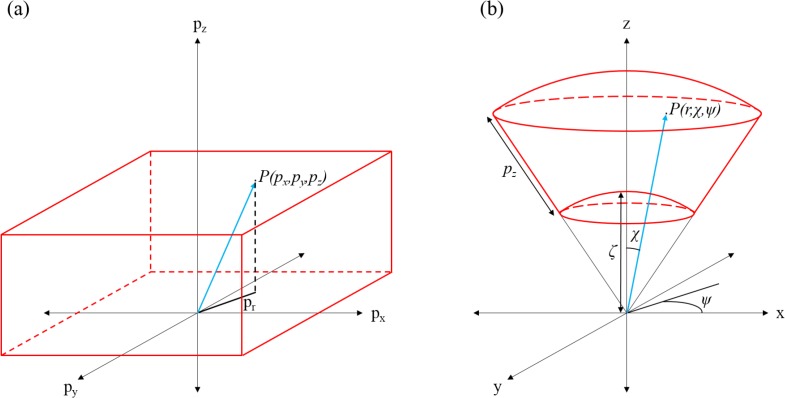
Due to the conical scanning optics the acquired images of the sample appear distorted. These distortions arise from the nearly perpendicular incidence of the imaging beam onto the sample as well as from field distortions introduced by the lens. In a first approximation, we considered the distortions introduced by the conical scanning geometry only (and neglect field distortions). Figure 3 shows the underlying geometrical context that was used for the distortion correction.
Fig. 3.
Conceptual representation of the image transformation: (a) shows a point P(px, py, pz) in the original data volume. (b) shows the same point P(pr, χ, ψ) with new dependencies in the transformed volume. The values used for the transformation are indicated.
The original, acquired data set had the pixel coordinates px, py, pz with px describing the current A-scan number (1 to 1024), py the current B-scan number (1 to 150) and pz the depth pixel number (1 to 1184). The geometry of this pixel coordinate system was distorted with respect to the laboratory coordinate system. px and py were normalized according to
| (4) |
with px,max being the number of A-scans and py,max the number of B-scans.
In a first correction step, we assigned spherical coordinates P(r, χ, ψ) to every point P(px, py, pz) of the original 3D data set (pixel coordinate system). Then every spherical coordinate is transformed into a Cartesian coordinate system that corresponds to the true laboratory system.
| (5) |
First the azimuthal angle ψ and the polar angle χ were calculated with
| (6) |
and
| (7) |
χmax is the aperture angle of the ACL and was calculated to be 68° (cf. Fig. 3). px,max is the number of A-scans per B-scan. The transformation into the laboratory coordinate system was done according to
| (8) |
| (9) |
| (10) |
Taking into account the scanning geometry, every pixel pz of an A-scan is corrected with an offset ζ, which was empirically determined to be 1100 pixels. A-scans as well as B-scans are fanned out by this transformation which causes gaps between adjacent A-scans and B-scans, respectively. These gaps are filled by linear interpolation of the neighboring pixels.
3. Results
3.1. Test sample imaging
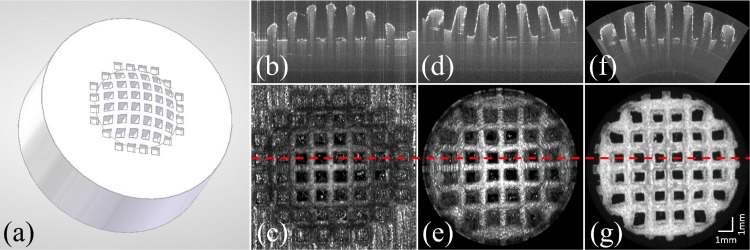
In order to test the conical scanning configuration, measurements were performed on a custom designed, 3D-printed test target. This target was made from a white colored acrylic-based photo-polymer and has a shape and size comparable to an average human cornea (diameter: 11 mm, radius of the anterior surface: 7.8 mm). A checkerboard pattern (the bridges were 0.6 mm thick and the square cavities were 1 mm × 1 mm in size) was introduced into the target’s surface (cf. Fig. 4(a)) in order to measure image distortions that may be introduced by the conical scanning optics.
Fig. 4.
(a) 3D model of the test object. (b) B-scan of the test target and (c) en-face projection imaged with the standard scanning optics as shown in Fig. 2(b). (d) B-scan of the same feature as in (b) and the en-face projection (e) of the test target imaged with the conical setup shown in Fig. 2(a). (f) and (g) show the corresponding B-scan and the en-face map of the surface of the test target after correcting for the distortions introduced by the scan pattern (but not for field distortions introduced by the lens, which are responsible for the remaining distortions at the periphery). The red dashed line represents the position of the corresponding B-scans.
Figure 4 shows imaging results obtained from the test target using both scanning schemes. A clear difference between the different scanning optics is the flattened appearance of the surface of the test target when using the conical scanning configuration. The FoV is limited by the aperture of the lens, and thus is smaller than the one achieved with the conventional method. The en-face image shows pillow shaped image distortions.
The scanning beam is impinging on the ACL under steep angles which cause slight polarization changes due to refraction at the surface of the lens. This slight polarization changes can be eliminated using a similar approach as for compensating retinal images for anterior segment birefringence [34]. The data is compensated with a previously recorded reference of a polarization preserving target (made of white colored acrylic-based photo-polymer) in post processing. This compensation algorithm relies on the measured retardation and axis orientation values at the surface of the test target. To reduce the noise we used a floating average based filter algorithm with a window size of 100 (x) × 14 (y) data points, which roughly corresponds to 1 mm × 1 mm. Thus, small changes of the polarization state at the surface can be accounted for, including variations with scanning. En-face images of the axis orientation at the surface of a polarization preserving test target with the shape and size of a normal human cornea before and after the compensation are shown in Fig. 5. The random axis orientation retrieved after this post processing step indicates the effectiveness of the method. The corresponding retardation values are close to 0° (not shown), thus the axis orientation is not defined and will be random.
Fig. 5.
En-face image of the axis orientation of a test target surface before (a) and after (b) the compensation for polarizing effects introduced by the scanning lens.
When imaging an object with a defined axis orientation using different incident angles, the interpretation of the measured axis orientation might be difficult as changes arise depending on the incident angle. To investigate the influence of the conical scanning optics geometry on the measurement of the axis orientation, a polarization preserving target behind a transparent retarder with defined retardation and axis orientation was imaged.
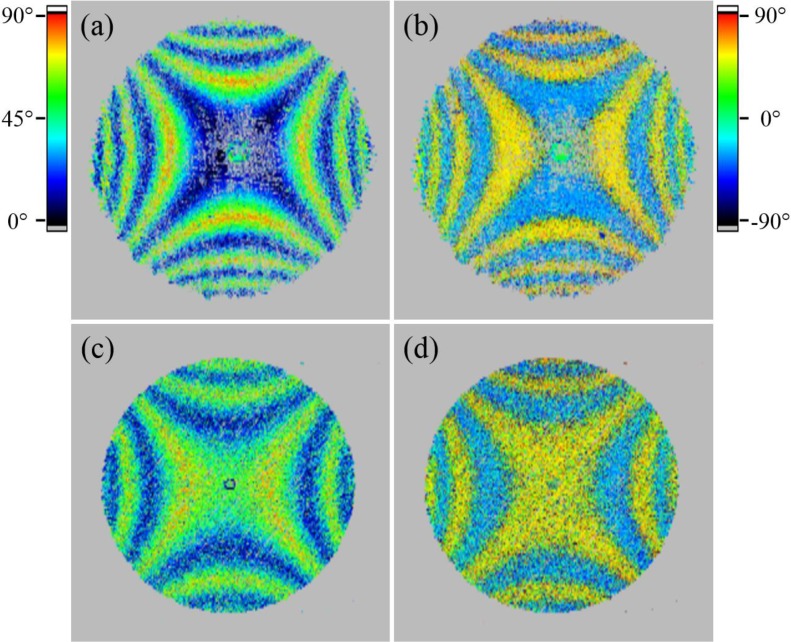
First, we put a zero order achromatic half wave plate (HWP, ACWP-700-1100-10-2, Laser Components GmbH) for wavelengths of 700–1000 nm in front of a polarization preserving, flat test target and imaged it with the conical scanning optics scheme. Then, surface maps of retardation and axis orientation were computed as described in the methods section, which are displayed in Fig. 6. The axis orientation offset θ0 was measured to be 58°, but was not compensated in the images in Fig. 6. To achieve zero order retardation of λ/2, the HWP consists of two birefringent crystals of slightly different thickness. The birefringent axes of the crystals are orthogonal to each other and are parallel to the surface of the crystal. The central area shows low retardation. With increasing incident angle an increase in retardation can be observed (apart from the ±45° orientation) (cf. Fig. 6(a)). The birefringent axis of each crystal is oriented along the x- and y-axis of the image, respectively. Without losing generality we assume that the first crystal has a horizontal axis orientation. In the central part of the image the incident light beam is orthogonal to both birefringent axes. Thus, a net retardation of λ/2 (caused by the differing thickness of the crystals) is introduced. With increasing distance from the center of the image, the incident angle of the light beam on the surface of the HWP decreases and there will be different angles of the beam with respect to the birefringent axes of the crystals. When the beam is scanned along the horizontal axis, the angle of the beam to the axis of the first crystal (horizontal axis orientation) will change and less retardation will be introduced by this crystal. However, the angle of the beam to the axis of the second crystal (with vertical axis orientation) will stay constant as will be the retardation introduced by this plate. Thus, the net retardation observed will be dominated by the second crystal and increases along the horizontal axis starting from the center of the image to the periphery. The oscillation of the colors from blue to red and blue again is caused by the algorithm that can only measure retardation values in between 0° and 90° [18]. Larger retardation values will be projected into this value range. When the beam is scanned along the vertical axis the situation is similar as before but the retardation will be dominated by the first crystal. When the beam is scanned along directions that are oriented at 45° to the horizontal and vertical axes, the beam will be incident on both birefringent axes under the same angle. Thus, the net retardation will not be changed along these directions. Scanning along all other directions will result in a different change of the incident angle to both axis orientations of the crystals which finally results in the observed retardation pattern (cf. Fig. 6(a)). The axis orientation image (cf. Fig. 6(b)) shows only two different axis orientations. In the central part of the image the upper and lower part shows a light blue color corresponding to the axis orientation of the first crystal. At these locations this crystal contributes more to the net retardation. On the left and right parts the contribution to the retardation from the second crystal is dominating. Thus, the axis orientation of this crystal (indicated by yellow color) is observed. The banding structure in horizontal and vertical direction is an artifact that is caused by the algorithm for calculating the axis orientation. Whenever the retardation value exceeds 90° or multiples thereof, a jump in axis orientation by 90° is observed [18].
Fig. 6.
Surface maps of retardation and axis orientation of a flat test target behind different retarders using the conical scanning optics. (a) Retardation and (b) axis orientation when the test target was imaged behind a HWP. (c) Retardation and (d) axis orientation when the test target was imaged behind a QWP, respectively. The axis orientation offset was not compensated.
In a second experiment we measured a zero order quarter wave plate (QWP, D-λ/4-1300/15, LINOS) for a wavelength of 1300 nm. As expected, we measured high retardation at the center (cf. Fig. 6(c)) which then changes with increasing incident angles in a similar way as in the case of the HWP. However, the second crystal of the QWP introduces a net retardation of ∼70°. Thus, the entire central part of the scan will be dominated by this crystal which can be observed by the constant axis orientation in this area (cf. Fig. 6(d)). Only for larger incident angles of the beam with respect to the birefringent axis of the second crystal, the retardation will be dominated by the first crystal and the corresponding axis orientation will be measured. This can be observed by the first change of axis orientation along the vertical direction that occurs at a location with 0° retardation. The next change in this direction is caused by the algorithm, as mentioned previously and occurs at a location with 90° reatardation. Along the horizontal direction, the change in axis orientation is caused by the artifact originating from the algorithm.
These experiments show that the measured retardation is dependent on the angle between the beam and the birefringent axis, whereas the measured axis orientation is independent from this angle with the exception of the artifact caused by the ambiguity at retardation values >90°.
3.2. Imaging human eyes in vivo
After simulating and testing of the conical scanning optics design we performed in vivo measurements. The ethics committee of the Medical University of Vienna approved all measurements following the tenets of the Declaration of Helsinki. Informed consent was obtained from all volunteers before each measurement. Both eyes of five healthy human volunteers were measured (four male and one female). Figure 7 shows representative B-scans of the cornea of a healthy volunteer recorded with both scanning configurations. The conventional scanning scheme produces high signal intensity at the central and peripheral (limbus and chamber angle) part of the cornea. Due to the large inclination of the beam, paracentral areas show low signal intensities. Compared to the conventional scanning optics, the conical scheme produces images with good signal intensity throughout the entire FoV. The vertical line in the image is an artifact, arising from backreflections within the system. The horizontal line in Fig. 7(a) arises from the strong backreflection at the apex of the cornea. The central part shows random retardation values in the stroma, while the back surface of the cornea shows low retardation values (cf. Fig. 7(b)). So only the backscattered light from the stroma indicates depolarization while the transmitted light is in a defined polarization state. This can also be observed in the DOPU image (cf. Fig. 7(d)) where depolarization is displayed in blue color (DOPU ≪ 1) and a defined polarization state is indicated in yellow/red color (DOPU close to 1). In the periphery of the cornea a strong increase of retardation with depth can be observed, which indicates high birefringence in this area. In this area the backscattered light is in a defined polarization state. The anterior part of the iris consists of polarization preserving tissue and the light backscattered there resembles the polarization state at the backside of the cornea [20]. The pigment epithelium of the iris depolarizes the light, which can be seen as a random retardation and axis orientation, as well as the low DOPU values in this area.
Fig. 7.
Comparison of representative B-scans of a human cornea using the conventional scanning optics (a–d), the conical scanning optics before (e–h), and also after the coordinate transformation (i–l). The reflectivity is shown in (a), (e) and (i), the retardation in (b), (f) and (j), the axis orientation in (c), (g) and (k) and the DOPU images in (d), (h) and (l). All polarization-sensitive images were intensity thresholded as described in the methods section (sub-threshold pixels were set to grey).
Figures 7(e–h) show image results obtained with the conical scanning optics. The low signal artifact at the central part of the cornea (cf. Fig. 7(e)) is due to shadowing from an eyelash. The corneal epithelium as well as Bowman’s layer can be resolved throughout the entire FoV (cf. Fig. 8). Also the backside of the cornea shows good signal quality. In the images produced with the conical scanning scheme, epithelium, Bowman’s layer and endothelium show low retardation values (cf. Fig. 7(f)) which indicate polarization preserving tissue. This uniform polarization state is also indicated by yellow/red colors in the DOPU image (cf. Fig. 7(h)). However, the light backscattered from the corneal stroma is depolarized (cf. low DOPU values and random retardation and axis orientation values). Figures 7(i–l) show the B-scans after the geometric transformation.
Fig. 8.
Comparison of regions of interest (ROI) of red rectangles in Fig. 7. The ROI of the image recorded with the standard scanning optics (a) shows less signal than the ROI of the image recorded with the conical scanning scheme (b). (c) shows the ROI of the distortion corrected image. For (a)–(c) the aspect ratio was changed to better visualize features of the corneal layer structure. (d) shows a different ROI as indicated in the red rectangles of Fig. 7(f–h) of retardation, (e) axis orientation and (f) DOPU.
To better visualize features of the corneal layer structure regions of interest marked with red boxes in Fig. 7 were magnified and are displayed in Fig. 8. The aspect ratio of the Figs. 8(a–c) was changed to enhance the depth information and show a comparison between the standard scanning protocol and the conical one before and after the geometric transformation. To quantify the gain in signal quality, the SNR on the surface of 10 corneas was measured in paracentral regions and averaged. The gain was calculated to be 14.5±1.8 dB. Figures 8(d–f) show the ROI of retardation, axis orientation and DOPU as marked by red boxes in Fig. 7.
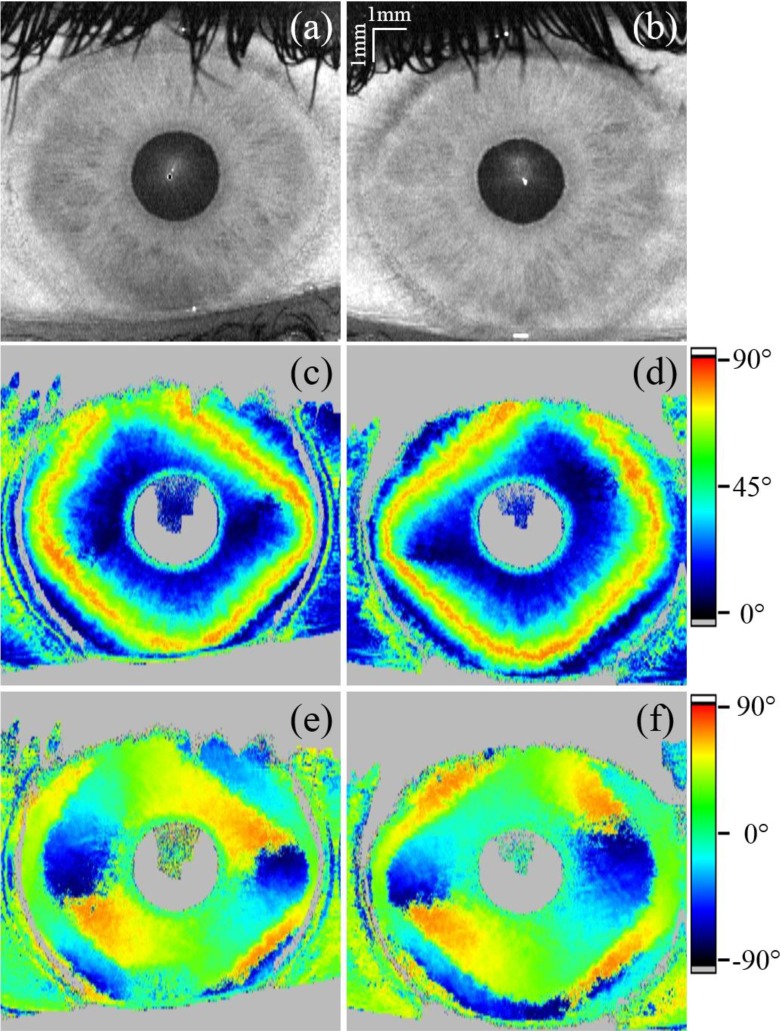
To further investigate the influence of the different scanning patterns on the polarization-sensitive measurement, en-face maps of retardation and axis orientation were generated. Because of the low signal intensity at the backside of the cornea in the case of conventional scanning, the top part of the iris and a part of the lens were segmented by intensity thresholding. The polarization-sensitive data was retrieved from this segmented area and averaged over ten pixels in depth [35] to generate the en-face maps. The fibrils of the cornea introduce form birefringence, which is dependent on the incident angle of the probing beam onto the fibril orientation within the cornea [19]. The visible patterns of retardation and axis orientation (cf. Fig. 9) can be explained by the corneal shape. With increasing incidence angle the retardation increases, which at some point results in oscillations in retardation (similar to the wave plates in Fig. 6). The algorithm only retrieves retardation values between 0° and 90°. Larger values will be projected into this range, which results in oscillations of the measured retardation values. Thus, starting from the center of the cornea towards the periphery, oscillating retardation values (indicated by the color change from blue to red and blue again) can be observed in Fig. 9. Also, a deviation of the 90° retardation line (orange-red color) from a perfectly circular shape is observable similar to a previous report [21]. The axis orientation images show the en-face projection of accumulated dominating fibril orientation with respect to the laboratory system. As can be seen by the color changes, the fibril orientation changes in the periphery of the cornea. Along a full circle around the corneal apex the fibril orientation changes by 360°, corresponding to two full color oscillations.
Fig. 9.
En-face projections generated from a 3D data set recorded in a right (a, c and e) and left (b, d and f) eye with the conventional scanning optics (polarization data retrieved from the iris). (a) and (b) show the reflectivity projections of the total depth, (c) and (d) the retardation and (e) and (f) the axis orientation. The axis orientation was not corrected for the offset θ0.
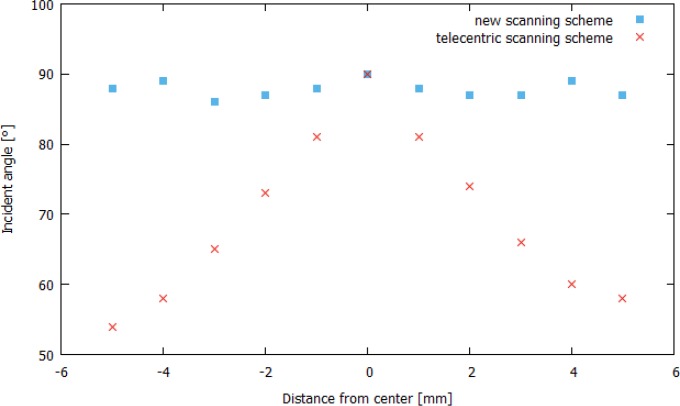
To reduce the influence of the corneal shape on the polarization-sensitive data, the incident angle has to be perpendicular to the corneal surface. Figure 10 shows a comparison of the incident angles, calculated from central B-scans, which were recorded with both scanning schemes. One can see that the conical scanning scheme provides an incident angle of almost 90° throughout the scan field.
Fig. 10.
Comparison of the incident angles on the corneal surface calculated for central B-scans recorded with both scanning schemes.
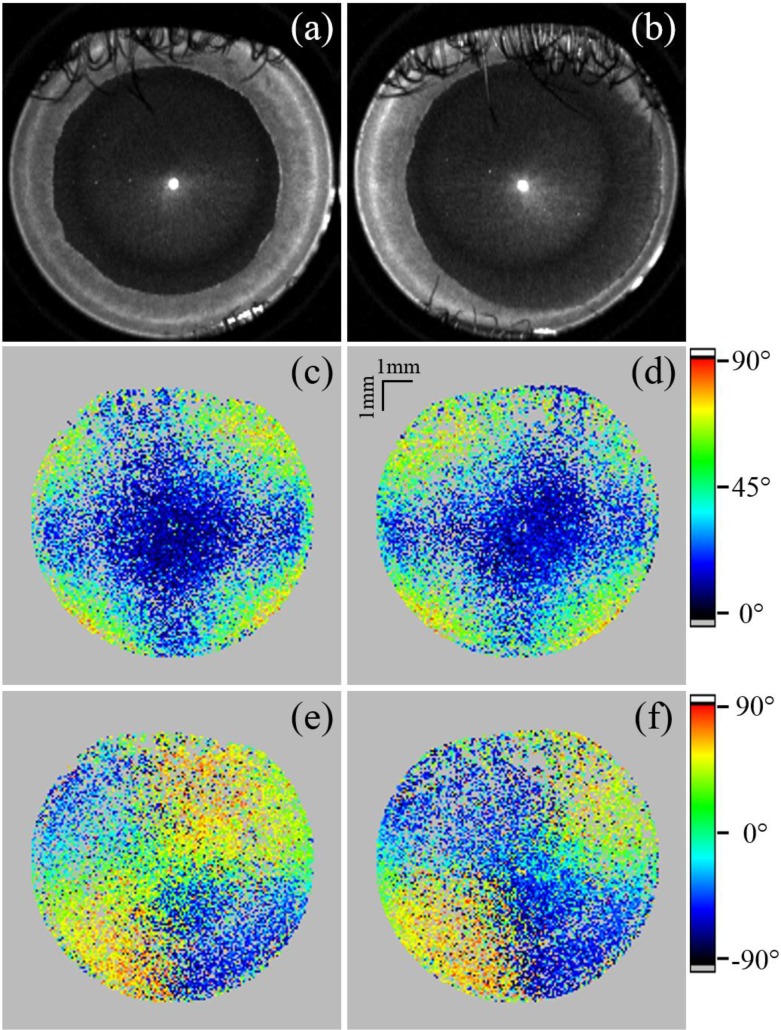
For the conical scanning geometry the signal quality was sufficient to extract the polarization-sensitive information at the backside of the cornea to generate en-face maps. These maps are then smoothed by averaging [35] over the nearest neighbors to compensate for missing pixels. The en-face projections of these segmented areas are displayed in Fig. 11. The retardation and axis orientation en-face maps of the backside of the cornea, recorded with the conical scanning optics, were scaled to match their size in relation to the reflectivity en-face images, which were calculated by applying the transformation algorithm. Figure 11 shows en-face maps of reflectivity, retardation and axis orientation. The reflectivity en-face image is a projection of the entire depth. The artifact at the center of the cornea is due to the strong specular reflex at the center. The upper third of the images shown in Fig. 11 are partly obstructed by eyelashes. Due to the smoothing of the polarization-sensitive data the effect of shadowing due to eyelashes is reduced but still visible in the corresponding Figs. 11(c–f). The central area of the cornea shows low retardation. Towards the periphery of the cornea increased retardation can be observed, with the exception towards the nasal direction where the retardation remains low. Patterns in retardation and axis orientation shown in Fig. 11 are severely different to the ones recorded with the telecentric scanning pattern shown in Fig. 9. Furthermore, a distinct midline symmetry between left and right eyes is observable.
Fig. 11.
En-face projections generated from a 3D data set recorded in a right (a, c and e) and left (b, d and f) eye with the conical scanning optics design (retardation and offset compensated axis orientation retrieved from the posterior corneal surface). (a) and (b) show the reflectivity projections of the total depth, (c) and (d) the retardation and (e) and (f) the axis orientation.
4. Discussion
We demonstrated a conical scanning optics design for imaging the human cornea in vivo, which produced good signal quality over the entire recorded area of the cornea because the sampling beam is almost perpendicular to the corneal surface throughout the FoV. The gain in SNR in the paracentral area was measured to be 14.5±1.8 dB.
To determine the size of the recorded area we applied a coordinate transformation on the recorded B-scans and compared the result with images that were recorded with conventional scanning optics. This comparison showed that it is possible to image the human cornea using a conical scan pattern from limbus to limbus.
The achievable FoV is currently limited by the aperture of the ACL and depends on the distance between cornea and ACL. This requires a precise (within a millimeter) alignment of the subject’s eye in axial direction, which can be achieved using the coherence gating provided by OCT. However, because of the large diameter of the lens and the short working distance to the eye, lateral subject alignment can be quite difficult. In order to determine the lateral position in real time the en-face projection of OCT data is used.
Because of the convergent scanning geometry, eyelid and eyelashes may obscure up to a third of the cornea, as can be seen in Fig. 11. In principle this can be avoided by using a cotton bud to push the eyelid away. For the proof of principle measurements presented here we decided not to use this option as the applied pressure might cause distortions of the corneal shape or might change the birefringent properties of the cornea.
The enhanced (and homogeneous) signal quality of corneal images using the conical scanning approach will facilitate thickness measurements of the different corneal layers such as epithelium, Bowman’s layer and stroma as these can be clearly observed in the entire FoV (cf. Figs. 7 and 8) in contrast to the standard scanning pattern. In addition, refraction at the corneal surface can be essentially neglected for the determination of layer thickness. Thus, the method might be a valuable tool for the diagnostics, investigation and follow up of corneal dystrophies like keratoconus.
The conical scan pattern probes corneal birefringence at angles that are approximately orthogonal to the corneal surface. Strong specular reflections occur at incident angles of 90°, which might disturb the recorded images. However, because of slight deviations from a perfectly perpendicular incidence due to curvature variations between different corneas (cf. Fig. 10), we observe a disturbing specular reflection only at a single location near the apex of the cornea (cf. Figs. 9 and 11). Furthermore this nearly perpendicular incident angle has several implications on the polarization-sensitive data. First of all we observe that the light that is backscattered from the stroma is depolarized, while the transmitted light is in a defined polarization state (cf. Fig. 8(d) and (f)). Using the standard scan pattern, similar depolarization can only be observed within the central part of the cornea. The origin of depolarization remains unclear but is certainly related to the orientation of the scanning beam with respect to the lamellae of the stroma. This possibly indicates that multiple reflections at interfaces of lamellae or fibrils are the cause for depolarization. We want to point out that in vitro measurements of the cornea did not show depolarization from within the stroma [19,20,24]. This effect can only be observed when imaging is performed in vivo which has been outlined in a previous study using a time-domain PS-OCT instrument [36]. We believe that this discrepancy originates from increased scattering that can be observed in vitro from the corneal stroma. After excising the cornea, the tissue is stored in a nutrient solution which results in a slight degeneration of the cornea and thus in an increase of scattering (which is already visible by the naked eye). Thus, the depolarizing character of the cornea is greatly attenuated and the increased scattering (which is polarization preserving) dominates the measured OCT signal.
At the endothelium of the cornea a defined polarization state can be observed and the influence of corneal birefringence on the polarization state can be measured in corresponding en-face maps (cf. Figs. 9 and 11). With the conventional scanning optics the signal at the endothelium is too weak in order to retrieve reliable polarization-sensitive information and the map is generated from data measured at the stroma of the iris. The retrieved retardation and axis orientation patterns are quite different. The retardation map obtained with the standard scanning pattern shows low retardation in the central part of the cornea while towards the periphery retardation strongly increases. This was attributed to cumulative retardation introduced by fibrils with nearly perpendicular orientation to each other and their corresponding varying angle with respect to the imaging beam because of the corneal shape [19, 21]. Using the conical scan pattern, this influence is greatly reduced. Nevertheless, distinct retardation patterns are visible, which might indicate the presence of additional birefringent structures.
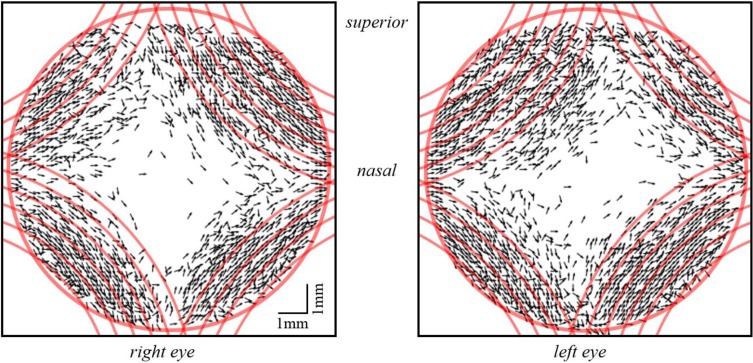
In order to determine the orientation of these structures with respect to the laboratory coordinate system, axis orientation maps can be used. However, this requires the compensation of the axis offset (θ0, cf. Eq. 3) introduced by the fiber optics. The offset was determined prior to the in vivo corneal measurements and was then used to calculate the true axis orientation. For a better visualization of the result we plotted the axis orientation as vectors only in areas of high retardation (>25°). As can be seen in Fig. 12, axis orientation is plotted only in the periphery of the image (the red circle indicates the limbus of the cornea) where increased retardation can be observed. In contrast to the axis orientation that is measured with the standard scanning pattern, the orientation of these birefringent structures are not oriented approximately tangentially along circles that are centered at the apex of the cornea. Indeed, the location and orientation of these structures is very similar to the model of preferentially aligned, reinforcing collagen fibrils suggested by Meek and coworkers based on X-ray scattering measurements [4–6]. These preferentially aligned, reinforcing collagen fibrils are thought to take up the stress exerted on the cornea by the ocular motor muscles and thereby maintain the corneal shape [5]. In order to show the similarity of the orientation of the birefringent structures and the reinforcing fibers, the vector plots in Fig. 12 have been superimposed with theoretical plots of these fibers (cf. red lines). It should be noted, that the proposed midline symmetry between left and right eye [4–6] is also clearly visible in the polarization-sensitive images. The presence of these fibrils might also explain the deviation from a radially symmetrical shape of the retardation pattern (cf. Fig. 9(c) and (d)) as the birefringence introduced by these fibers will add to the birefringence of the corneal fibrils. In vitro images of the human cornea do not show deviations from this radially symmetric shape [19,20]. Possibly, these reinforcing collagen fibrils are cut when excising the cornea and lose their birefringent property. The in vivo determination of the location of reinforcing collagen fibrils could be important for deciding on the location of incisions made in various surgical procedures of the anterior segment. It is well known that such surgical procedures may induce astigmatism [37–39]. One reason could be a distortion of the regular arrangement of those fibrils because of the incision which severely affects the shape of the cornea.
Fig. 12.
Vector representation of axis orientation measured at the backside of the cornea in areas of high retardation. Red lines show the idealized, theoretical orientation of preferentially aligned, reinforcing collagen fibrils, which are superimposed on the in vivo measurement data. The red circle represents the limbus region and therefore the FoV.
5. Conclusion
To summarize, we presented a conical scanning optics design for corneal imaging that uses a sampling beam with almost perpendicular incidence on the corneal surface. We demonstrated that the human cornea can be measured with good overall signal quality from limbus to limbus. Polarization-sensitive data can be retrieved from the entire recorded area. Furthermore, we detected additional birefringent structures in the cornea that might correspond to preferentially aligned reinforcing collagen fibrils.
Acknowledgements
The authors would like to thank Andreas Hodul for technical workshop assistance. Furthermore, we wish to thank Marco Augustin, Danielle J. Harper, Pablo Eugui and Antonia Lichtenegger from the Center for Medical Physics and Biomedical Engineering (Medical University of Vienna) for their assistance and helpful discussions.
Funding
Christian Doppler Laboratory (CDL) (OPTIMA); Austrian Science Fund (FWF) (P26553-N20).
Disclosures
CKH: Canon (F,P), MP: Canon (F,P), others: none
References and links
- 1.Meek K. M., Fullwood N. J., “Corneal and scleral collagens - A microscopist’s perspective,” Micron 32(3), 261–272 (2001). 10.1016/S0968-4328(00)00041-X [DOI] [PubMed] [Google Scholar]
- 2.Komai Y., Ushiki T., “The three-dimensional organisation of collagen fibrils in the human cornea and sclera,” Invest. Ophthalmol. Vis. Sci. 32(8), 2244–2258 (1991). [PubMed] [Google Scholar]
- 3.Daxer A., Fratzl P., “Collagen fibril orientation in the human corneal stroma and its implication in keratoconus,” Invest. Ophthalmol. Vis. Sci. 38(1), 121–129 (1997). [PubMed] [Google Scholar]
- 4.Aghamohammadzadeh H., Newton R. H., Meek K. M., “X-Ray Scattering Used to Map the Preferred Collagen Orientation in the Human Cornea and Limbus,” Structure 12(2), 249–256 (2004). 10.1016/j.str.2004.01.002 [DOI] [PubMed] [Google Scholar]
- 5.Meek K. M., Boote C., “The use of X-ray scattering techniques to quantify the orientation and distribution of collagen in the corneal stroma,” Prog. Retin. Eye Res. 28(5), 369–392 (2009). 10.1016/j.preteyeres.2009.06.005 [DOI] [PubMed] [Google Scholar]
- 6.Meek K. M., Knupp C., “Corneal structure and transparency,” Prog. Retin. Eye Res. 49, 1–16 (2015). 10.1016/j.preteyeres.2015.07.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.DelMonte D. W., Kim T., “Anatomy and physiology of the cornea,” J. Cataract Refract. Surg. 37(1), 588–598 (2011). 10.1016/j.jcrs.2010.12.037 [DOI] [PubMed] [Google Scholar]
- 8.Asrani S., Sarunic M., Santiago C., Izatt J., “Detailed Visualization of the Anterior Segment Using Fourier-Domain Optical Coherence Tomography,” Arch Ophthalmol. 126(6), 765–771 (2008). 10.1001/archopht.126.6.765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Ortiz S., Sielecki D., Grulkowski I., Remon L., Pascual D., Wojtkowski M., Marcos S., “Optical distortion correction in optical coherence tomography for quantitative ocular anterior segment by three-dimensional imaging,” Opt. Express 18(3), 2782–2796 (2010). 10.1364/OE.18.002782 [DOI] [PubMed] [Google Scholar]
- 10.Tan A. N., Sauren L. D. C., de Brabander J., Berendschot T. T. J. M., Lima Passos V., Webers C. A. B., Nuijts R. M. M. A., Beckers H. J. M., “Reproducibility of Anterior Chamber Angle Measurements with Anterior Segment Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 52(5), 2095–2099 (2011). 10.1167/iovs.10-5872 [DOI] [PubMed] [Google Scholar]
- 11.Poddar R., Cortés D. E., Werner J. S., Mannis M. J., Zawadzki R. J., “Three-dimensional anterior segment imaging in patients with type 1 Boston Keratoprosthesis with switchable full depth range swept source optical coherence tomography,” J. Biomed. Opt. 18(8), 86002 (2013). 10.1117/1.JBO.18.8.086002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Van Blokland G. J., Verhelst S. C., “Corneal polarization in the living human eye explained with a biaxial model,” J. Opt. Soc. Am. A 4(1), 82–90 (1987). 10.1364/JOSAA.4.000082 [DOI] [PubMed] [Google Scholar]
- 13.Zhou Q., Weinreb R., “Individualized compensation of anterior segment birefringence during scanning laser polarimetry,” Invest. Ophthalmol. Vis. Sci. 43(7), 2221–2228 (2002). [PubMed] [Google Scholar]
- 14.Bueno J. M., Vargas-Martín F., “Measurements of the corneal birefringence with a liquid-crystal imaging polariscope,” Appl. Opt. 41(1), 116–124 (2002). 10.1364/AO.41.000116 [DOI] [PubMed] [Google Scholar]
- 15.Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., “Polarization sensitive optical coherence tomography in the human eye,” Prog. Retin. Eye Res. 30(6), 431–451 (2011). 10.1016/j.preteyeres.2011.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Hee M. R., Huang D., Swanson E., Fujimoto J. G., “Polarization-sensitive low-coherence reflectometer for birefringence characterization and ranging,” J. Opt. Soc. Am. B 9(6), 903–908 (1992). 10.1364/JOSAB.9.000903 [DOI] [Google Scholar]
- 17.de Boer J. F., Millner T. E., van Gemert M. J. C., Nelson J. S., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett. 22(12), 934–936 (1997). 10.1364/OL.22.000934 [DOI] [PubMed] [Google Scholar]
- 18.Hitzenberger C. K., Goetzinger E., Sticker M., Pircher M., Fercher A., “Measurement and imaging of birefringence and optic axis orientation by phase resolved polarization sensitive optical coherence tomography,” Opt. Express 9(13), 780–790 (2001). 10.1364/OE.9.000780 [DOI] [PubMed] [Google Scholar]
- 19.Götzinger E., Pircher M., Sticker M., Fercher A., Hitzenberger C. K., “Measurement and imaging of birefringent properties of the human cornea with phase-resolved, polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(1), 94–102 (2004). 10.1117/1.1629308 [DOI] [PubMed] [Google Scholar]
- 20.Pircher M., Götzinger E., Leitgeb R., Hitzenberger C. K., “Transversal phase resolved polarization sensitive optical coherence tomography,” Phys. Med. Biol. 49(7), 1257 (2004). 10.1088/0031-9155/49/7/013 [DOI] [PubMed] [Google Scholar]
- 21.Fanjul-Vélez F., Pircher M., Baumann B., Götzinger E., Hitzenberger C. K., “Polarimetric analysis of the human cornea measured by polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 15(5), 056004 (2010). 10.1117/1.3486540 [DOI] [PubMed] [Google Scholar]
- 22.Lim Y., Yamanari M., Fukuda S., Kaji Y., Kiuchi T., Miura M., Oshika T., Yasuno Y., “Birefringence measurement of cornea and anterior segment by office-based polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 2(8), 2392–2402 (2011). 10.1364/BOE.2.002392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Yamanari M., Tsuda S., Kokubun T., Shiga Y., Omodaka K., Yokoyama Y., Himori N., Ryu M., Kunimatsu-Sanuki S., Takahashi H., Maruyama K., Kunikata H., Nakazawa T., “Fiber-based polarization-sensitive OCT for birefringence imaging of the anterior eye segment,” Biomed. Opt. Express 6(2), 369–389 (2015). 10.1364/BOE.6.000369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Götzinger E., Pircher M., Dejaco-Ruhswurm I., Kaminski S., Skorpik C., Hitzenberger C. K., “Imaging of Birefringent Properties of Keratoconus Corneas by Polarization-Sensitive Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 48(8), 3551–3558 (2007). 10.1167/iovs.06-0727 [DOI] [PubMed] [Google Scholar]
- 25.Fukuda S., Yamanari M., Lim Y., Hoshi S., Beheregaray S., Oshika T., Yasuno Y., “Keratoconus Diagnosis Using Anterior Segment Polarization-Sensitive Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 54(2), 1384–1391 (2013). 10.1167/iovs.12-10979 [DOI] [PubMed] [Google Scholar]
- 26.McNabb R. P., Challa P., Kuo A. N., Izatt J. A., “Complete 360° circumferential gonioscopic optical coherence tomography imaging of the iridocorneal angle,” Biomed. Opt. Express 6(4), 1376–1391 (2015). 10.1364/BOE.6.001376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Schoenenberger K., Colston B.W., Maitland D. J., Silva L. B. D., Everett M. J., “Mapping of Birefringence and Thermal Damage in Tissue by use of Polarization-Sensitive Optical Coherence Tomography,” Appl. Opt. 37(25), 6026–6036 (1998). 10.1364/AO.37.006026 [DOI] [PubMed] [Google Scholar]
- 28.Makita S., Yamanari M., Yasuno Y., “Generalized Jones matrix optical coherence tomography: performance and local birefringence imaging,” Opt. Express 18(2), 854–876 (2010). 10.1364/OE.18.000854 [DOI] [PubMed] [Google Scholar]
- 29.Trasischker W., Zotter S., Torzicky T., Baumann B., Haindl R., Pircher M., Hitzenberger C. K., “Single input state polarization sensitive swept source optical coherence tomography based on an all single mode fiber interferometer,” Biomed. Opt. Express 5(8), 2798–2809 (2014). 10.1364/BOE.5.002798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Klein T., Wieser W., Eigenwillig C. M., Biedermann B. R., Huber R., “Megahertz OCT for ultrawide-field retinal imaging with a 1050nm Fourier domain mode-locked laser,” Opt. Express 19(4), 3044–3062 (2011). 10.1364/OE.19.003044 [DOI] [PubMed] [Google Scholar]
- 31.International Electrotechnical Commission , “Safety of laser products - Part 1: Equipment classification and requirements,” IEC-60825–1-(2), (IEC,2014). [Google Scholar]
- 32.Götzinger E., Pircher M., Hitzenberger C. K., “High speed spectral domain polarization sensitive optical coherence tomography of the human retina,” Opt. Express 13(25), 10217–10229 (2005). 10.1364/OPEX.13.010217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Götzinger E., Pircher M., Geitzenauer W., Ahlers C., Baumann B., Michels S., Schmidt-Erfurth U., Hitzenberger C. K., “Retinal pigment epithelium segmentation by polarization sensitive optical coherence tomography,” Opt. Express 16(21), 16410–16422 (2008). 10.1364/OE.16.016410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Pircher M., Götzinger E., Baumann B., Hitzenberger C. K., “Corneal birefringence compensation for polarization sensitive optical coherence tomography of the human retina,” J. Biomed. Opt. 12(4), 041210 (2007). 10.1117/1.2771560 [DOI] [PubMed] [Google Scholar]
- 35.Sugita M., Pircher M., Zotter S., Baumann B., Roberts P., Makihira T., Tomatsu N., Sato M., Vass C., Hitzenberger C. K., “Retinal nerve fiber bundle tracing and analysis in human eye by polarization sensitive OCT,” Biomed. Opt. Express 6(3), 1030–1054 (2015). 10.1364/BOE.6.001030 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Pircher M., Goetzinger E., Leitgeb R. A., Sattmann H., Hitzenberger C. K., “Ultrahigh resolution polarization sensitive optical coherence tomography,” SPIE Proc. 5690, 257–262 (2005). 10.1117/12.592700 [DOI] [Google Scholar]
- 37.Kohnen T., Dick B., Jacobi K. W., “Comparison of the induced astigmatism after temporal clear corneal tunnel incisions of different sizes,” J. Cataract Refract. Surg. 21(4), 417–424 (1995). 10.1016/S0886-3350(13)80532-9 [DOI] [PubMed] [Google Scholar]
- 38.Woo S., Lee J., “Effect of central corneal thickness on surgically induced astigmatism in cataract surgery,” J. Cataract Refract. Surg. 29(12), 2401–2406 (2003). 10.1016/S0886-3350(03)00254-2 [DOI] [PubMed] [Google Scholar]
- 39.Borasio E., Mehta J. S., Maurino V., “Surgically induced astigmatism after phacoemulsification in eyes with mild to moderate corneal astigmatism,” J. Cataract Refract. Surg. 32(4), 565–572 (2006). 10.1016/j.jcrs.2005.12.104 [DOI] [PubMed] [Google Scholar]