Abstract
The sensitive detection and quantitative measurement of biological nanoparticles such as viruses or exosomes is of growing importance in biology and medicine since these structures are implicated in many biological processes and diseases. Interferometric reflectance imaging is a label-free optical biosensing method which can directly detect individual biological nanoparticles when they are immobilized onto a protein microarray. Previous efforts to infer bio-nanoparticle size and shape have relied on empirical calibration using a ‘ruler’ of particle samples of known size, which was inconsistent and qualitative. Here, we present a mechanistic physical explanation and experimental approach by which interferometric reflectance imaging may be used to not only detect but also quantitatively measure bio-nanoparticle size and shape. We introduce a comprehensive optical model that can quantitatively simulate the scattering of arbitrarily-shaped nanoparticles such as rod-shaped or filamentous virions. Finally, we optimize the optical design for the detection and quantitative measurement of small and low-index bio-nanoparticles immersed in water.
OCIS codes: (280.1415) Biological sensing and sensors; (310.6845) Thin film devices and applications; (110.3175) Interferometric imaging; (290.5850) Scattering, particles
1. Introduction
Many biological processes in health, disease, and modern medicine are mediated by nanoparticles 20–1000nm in diameter that present specific molecules on their surface that are critical to their function. Exosomes - a class of extracellular vesicles of size 30–100 nm - carry complex molecular payloads and are thought to have roles in cell-cell signaling, antigen presentation, immune suppression and inflammation [1]. Exosomes are also secreted by cancer cells, and are implicated in metastasis, tumor growth and angiogenesis [2]. Unfortunately, optical characterization of exosomes in liquid media has proven extremely difficult due to their very small size and refractive index similarity to the solvent [3]. Viruses, another category of biological nanoparticle, have specific surface antigens that drive attachment and penetration of the host cell surface. Virus morphologies can be highly diverse, yet mutations that cause defective morphologies also significantly reduce both replication and infectivity, suggesting a causal link [4–6].
Most commonly, sensitive direct detection or characterization of viruses is performed with plaque assays, or otherwise with molecular techniques based upon either (i) nucleic acid amplification via polymerase chain reaction of the viral genome, or (ii) immunoassays for capsid proteins [7]. However, these molecular techniques discard any information about virion shape or size, and may be unable to differentiate infectious virions from virus-like particles that do not contain genetic material but may still elicit immune response [8]. Biological nanoparticle characterization is often performed using not one but a suite of tests. Electron microscopy is by far the highest-resolution imaging method, yet proposals for rapid identification of viral pathogens have gone unrealized due to high cost, complexity and the requirement for high concentrations of virions [9]. The limitation in throughput is in general shared by all high-resolution approaches, such as near-field scanning optical microscopy and atomic force microscopy [10, 11]. It is also still difficult to image delicate particles such as exosomes with electron microscopy, since the requisite vacuum desiccates them and results in structures which are likely different from native ones [1]. Darkfield optical methods such as Nanoparticle Tracking Analysis (Nanosight) are in general much simpler, more rapid and allow indirect measurements of particle size but are often unable to detect bio-nanoparticles smaller than 100 nm without fluorescent labeling due to their weak scattering and also require a high concentration (picomolar) of particles.
In contrast to nanoparticle detectors based on liquid-phase optical scattering, solid-phase detectors which utilize a sensor surface have several advantages. First, the sensor surface is almost always functionalized with a molecular coating that confers a specific molecular affinity. Preparing hundreds of arrayed regions of varied molecular affinity, in the form of a microarray, is an industry-standard technology that confers this family of sensors with high multiplexing capability. Second, the heterogeneity of the substrate-medium interface can be exploited to amplify the local electromagnetic field and enhance the captured nanoparticle’s optical scattering. Unfortunately, optically enhancing structures in the literature are usually highly heterogeneous, so particle binding does not confer the same effect in all places on the sensor. For example, in a recent study, surface plasmon resonance was utilized to detect the binding of individual exosomes in real time using a gold film patterned with a periodic nanopore array, but since the optical signal from an exosome was a strong function of its precise position with respect to the pore, particle size could not be measured [12]. Micro-ring and whispering-gallery-mode optical resonator sensors share this problem of sensor heterogeneity, as do most extremely high-Q optical detectors in general [13].
The Single Particle Interferometric Reflectance Imaging Sensor (SP-IRIS) is an optical biosensing technology that combines a flat multilayer dielectric substrate such as thermally-grown oxide on silicon with a wide-field reflection microscope to count and classify single immobilized nanoparticles. SP-IRIS is one of a growing family of optical sensors which can precisely enumerate individual nanoparticles bound to a planar surface, either for characterization of synthetic nanoparticles [14–17], label-free enumeration of virus or exosome vesicles from complex media such as blood serum [18–21], or single-molecule detection where synthetic nanoparticles are used as specific labels [22]. Proof-of-concept demonstrations have shown that SP-IRIS can be used for the sensitive detection of both viruses and exosomes from complex media such as serum or cerebrospinal fluid [23, 24]. Previous studies have also shown qualitative correlations between the size of a captured nanoparticle and the corresponding visibility of that particle, and utilized reference particle samples of known size to calibrate an empirical sizing ‘ruler.’ [24–26] Recently, quantitative optical simulations using the dipole approximation have been developed and used to improve optical sensitivity to small, spherical nanoparticles [27–29]. However, this approach cannot be used to simulate larger, asymmetric or irregularly shaped nanoparticles.
In this article, we introduce a mechanistic physical explanation for understanding SP-IRIS as a modified common-path homodyne interferometer, in which the objective focus position may be used to adjust the phase angle between signal and reference. We also describe a complete optical model that utilizes the boundary element method to support simulations of nanoparticles of arbitrary size and shape. Finally we use the framework and model to optimize several optical parameters of the sensor for quantitative sizing of bio-nanoparticles.
2. Methods
2.1. Preparation of nanoparticle samples
Polished silicon wafers with 100 nm SiO2 thermal oxide films were ordered from Silicon Valley Microelectronics (Santa Clara, CA). To create fiducial markings, the wafer was patterned with standard photolithography and wet etching. Wafers were diced into 1 cm square chips. Bare gold nano-spheres and nanorods were purchased from Nanopartz, Inc (Loveland, CO). Vendors provided accurate measurements of average particle dimensions with transmission electron microscopy. To immobilize nanoparticles onto the substrate, SP-IRIS chips were treated with oxygen plasma for 5 minutes and spin-coated with particles diluted to about 1 pM in DI water.
2.2. Physical model of arbitrary particles imaged with SP-IRIS
The problem of numerically simulating the steady-state optical scattering of an arbitrary particle involves finding a self-consistent and time harmonic numerical solution to Maxwell’s equations throughout a region of interest with relevant boundary conditions. Beyond special cases where the symmetry of the problem permits an analytical solution via Mie scattering theory, problems in nanoparticle scattering are most often solved via discrete numerical methods such as the boundary element method (BEM) or discrete dipole approximation [30].
In the case of a particle embedded in a homogeneous and isotropic medium, Maxwell’s equations can be simplified to a surface integral equations at the nanoparticle-medium interface [31]. BEM simulations therefore only require that the two-dimensional interface be meshed, which greatly speeds up the solver compared to Finite-Different Time Domain or other volume-element methods. Several implementations of the boundary element method have been published and made freely available for academic use. We used the Magnetic Nanoparticle Boundary Element Method (MNPBEM) implementation because (a) it was implemented in MATLAB, our preferred language, (b) it included formulation for the scattered far fields of a particle on layered media, as described by Novotny [32], which simplified our implementation, and (c) it provided excellent published documentation and examples [33, 34].
The overall optical simulation essentially consists of three parts. First, we define the system geometry and use the MNPBEM toolbox to calculate the surface charge distributions on the nanoparticle-medium interface in response to a monochrome incident plane wave Einc(r), and compute from them the resulting far field scattering, E∞. The scattered far fields are expressed as the complex-valued magnitudes of plane wave components (i.e., far field components of the angular spectrum): E∞ = E∞(kx, ky). The unmagnified image formed by the microscope may therefore be obtained simply by evaluating the canonical angular spectrum integral over the microscope objective’s collection solid angle, with the appropriate prefactors [32, 35]:
| (1) |
Second, the reflected field is calculated using the equivalent complex Fresnel reflection coefficients of the thin film structure rs, rp, which are calculated using a full vector implementation of the matrix transfer method: [36]
| (2) |
Here ŝinc, , ŝref, are the polarization unit vectors defined as in Figure 1, where kxy is the component of the wave-vector k in the (x, y) plane:
| (3) |
| (4) |
| (5) |
| (6) |
Fig. 1.
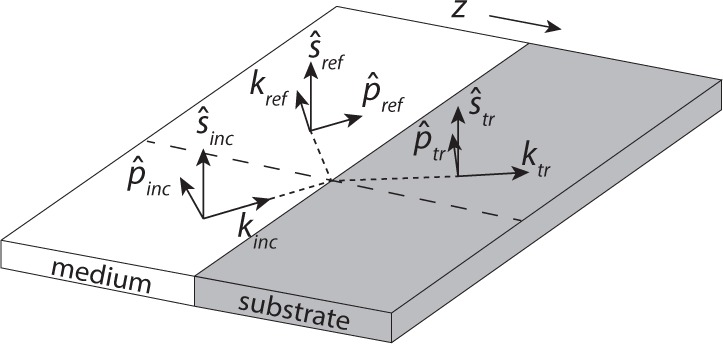
Coordinate system used to calculate the reflected field, showing the plane of incidence and coordinate unit vectors (Eqs. 2–6). An incident plane wave with kinc is decomposed into components perpendicular (ŝ) and parallel to the plane of incidence.
Third and finally, the resulting image formed at the detector I(r) is determined by coherently adding the scattered and reflected fields at the image plane position r
| (7) |
In many cases, the illumination cannot be approximated by a single plane wave. Then, the illumination profile at the surface is decomposed into a discrete sum of plane wave components via the angular spectrum representation, and summed incoherently:
| (8) |
In the case of Köhler illumination using an LED, these plane wave components are incoherent since each component corresponds with a different physical position on the diode and therefore an independent, uncorrelated photon emission event. The final image, therefore, consists of the incoherent superposition of the responses caused by each illumination component, where each reflected plane wave is coherent with its corresponding induced scattered field but no others [37].
2.3. Software availability
All codes used in this article have been made freely available online at https://www.github.com/derinsevenler/SP-IRIS-BEM/.
3. Results and discussion
3.1. Nanoparticle detection with interferometric reflectance imaging
The SP-IRIS substrate (Figure 2a) enhances the visibility of an immobilized nanoparticle through two synergistic yet highly coupled mechanisms of light interference, when imaged with a reflection microscope (Figure 2b). The first mechanism of enhancement is that the substrate reflects much of the forward-scattered light, which then constructively interferes with back-scattered light and increases the total back-scattering as compared to a transmitting substrate such as glass. Here, we denote the total far field back-scattered field with Escat. In Figure 3a–c) we simulate in three dimensions the Poynting vector magnitude (i.e. radiation pattern) of Escat of a 100 nm spherical virus (n=1.5). Note that Escat is a spherical wave, and that the radiation pattern changes shape with film thickness as the reflection coefficient of the substrate varies. The radiation patterns do not have rotational symmetry because the linearly-polarized plane wave illumination excites primarily only a single dipole mode in the particle, which does not radiate parallel to its orientation.
Fig. 2.
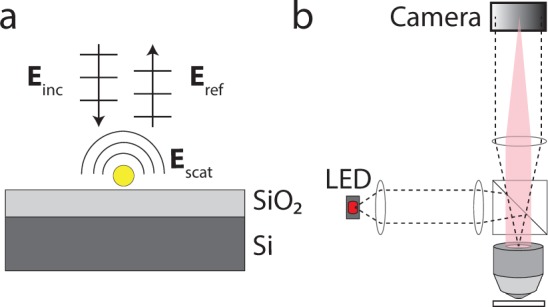
(a) The SP-IRIS substrate consists of a thin film of thermally grown oxide on polished silicon. Incident light (Einc) is both reflected by the substrate (Eref) and scattered by the immobilized nanoparticle (Escat). (b) Schematic of the reflection microscope. The LED source is imaged to the objective back pupil, providing Köhler illumination (dashed lines). Collected scattered light from a particular particle is indicated by red shadow.
Fig. 3.
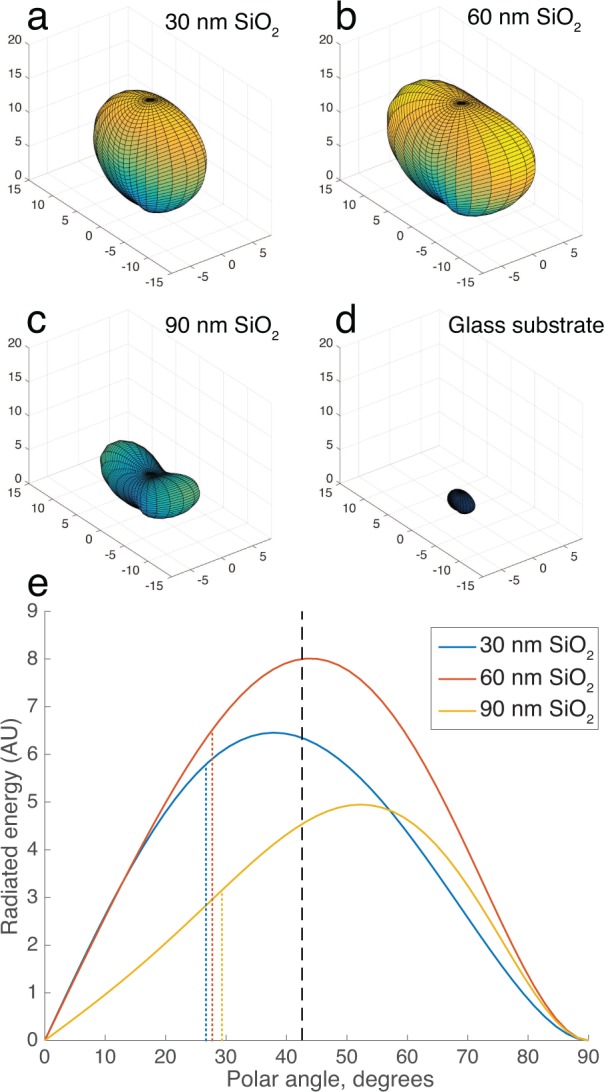
(a–c) 3D simulated plots of the radiation pattern (Poynting vector magnitude) of total back-scattered light Escat of a 100 nm virus particle (n=1.5) on SP-IRIS substrates with a range of film thicknesses, compared with (d) a glass substrate (arbitrary units). Illumination is a normal-incident linearly polarized plane wave with λ = 530 nm. (e) Distribution function of back-scattered radiation vs polar angle (i.e, from surface normal) for the cases shown in (a–c). The dashed line indicates the maximum collection angle of a 0.9 NA water-immersion objective. Dotted lines indicate the mean polar angle of the collected light, for each case.
The second mechanism of enhancement is that the scattered fields are detected interferometrically instead of directly. In interferometric detection, rather than directly detecting the faint scattered light against a dark background, the scattered light is interfered with a reference light beam and the interference pattern is recorded:
| (9) |
Here, ϕ is the difference in phase between the scattered (signal) and reference light. This method is also called optical homodyning, and allows measurements of the signal’s amplitude (|Escat|) instead of intensity (|Escat|2). In the context of detecting faint light scattering, this has two advantages over direct measurement: one theoretical and one practical. Theoretically, interferometric measurements of light amplitude are useful for detecting small nanoparticles since the scattering intensity of a nanoparticle with diameter D scales with D6, yet scattering amplitude scales with D3 [14]. Experimentally, interferometric detection avoids some sources of noise associated with measurements of faint light, including not just dark current and read noise in the sensor (which can be mitigated by using high performance photon counting sensors) but also stray light scattering and reflections in the optical path. In interferometric detection the reference field |Eref| can usually be increased until measurements of I(r) are limited only by shot noise of the signal.
To perform interferometric detection in SP-IRIS, the specular reflection by the substrate Eref (Figure 2) is also imaged onto the camera, and used as the reference light beam. Light scattered from a nanoparticle forms a diffraction-limited perturbation to the reflected field image (Figure 4a). The difference between the optical paths traversed by Escat and Eref to the sensor is < 1 µm, enabling the use of a partially-coherent LED instead of a highly-coherent laser beam, which are more common.
Fig. 4.
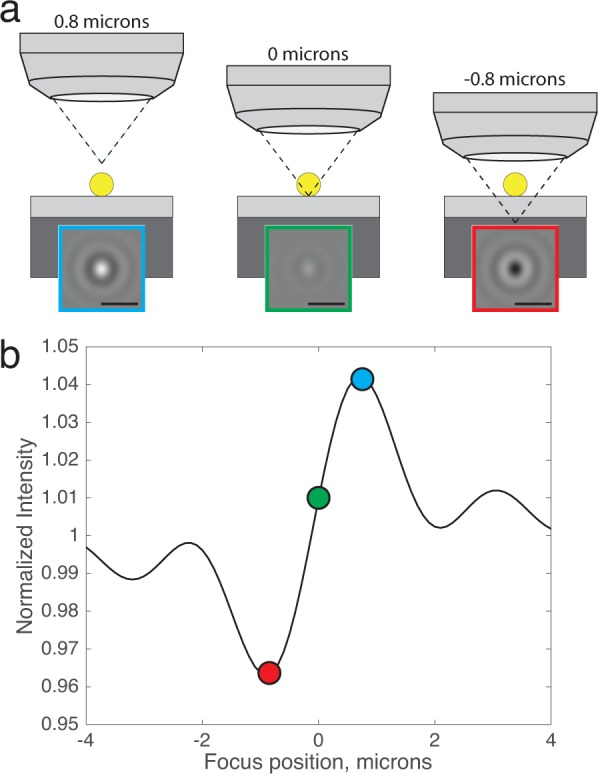
(a) Simulated images of a 100 nm virus with the microscope focal plane at three different positions with respect to the substrate top surface (NA = 0.9), scale bars are 1 1 µm). (b) The ‘defocus profile’: simulated normalized intensity at the center of the diffraction-limited image is plotted as a function of focus position, with the three focus positions labeled.
The final optical setup for SP-IRIS is therefore advantageously simple compared to other interferometric nanoparticle detectors, since removing the requirement for coherent illumination avoids many of the challenges inherent to coherent light imaging such as laser speckle and stray reflections [20, 38, 39]. However, this simplicity comes at the expense that the path length (i.e., phase) of the reflected field cannot be adjusted independently from that of the scattered field. Rather, it turns out that the phase angle ϕ between the two fields at the image plane is a strong function of the focus position of the microscope objective, provided that the illumination is limited to normal-incidence rays by radically under-filling the back aperture of the objective. This is because a particle illuminated with a normal-incidence plane wave will scatter light in all directions (as described earlier) yet the specularly reflected field only travel in one direction: back along the optical axis. Indeed, the vast majority of the scattered light is not back along the optical axis but at oblique angles (Figure 3e). Since the scattered and reflected fields are traveling (mostly) in different directions, changing the focus position of the objective alters the phase angle (ϕ) between them. Equivalently: within the angular spectrum representation, the plane wave components of the reflected field consists of rays that are mostly along the optical axis z (kz:ref ≈ |k|), while the majority of the scattered light is in plane wave components which are traveling at a significant polar angle (kz:scat < |k|). Crucially, changing the focus position the microscope objective by dz changes the path length of the reflected reference field by |k|dz, and the off-normal scattered fields by less: kz:scatdz = |k| cosθdz, where θ is the polar angle of a particular off-axis ray.
To elucidate this, consider the intensity at the center of the diffraction-limited image of a 100 nm virus (n=1.5) on an SP-IRIS substrate (100 nm of SiO2) as the focus position z is swept - we term this the ‘defocus profile’. If only |Escat|2 were collected (as in darkfield microscopy) this curve would trace out the axial point spread function of the microscope, which would be approximately a Gaussian centered at the medium-substrate interface and that decreases to 0 as the particle moves out of focus. However, when the specular reflected light is also collected, the background intensity (when out of focus) is not 0 but |Eref|2, and fringing is observed in the defocus profile (Figure 4). Since the reflected light is much brighter, the scattered fields are detected as a faint perturbation (about 4% in this case). Here we should define ‘normalized intensity’ as the ratio of the intensity of the combined scattered and reflected fields with that of the reference field alone, (i.e. when out of focus, or in the absence of a particle):
| (10) |
In this example, the normalized intensity fluctuates between 0.96 (darker than the background) to 1.04 (brighter than the background) along the defocus profile (Figure 4b), as the particle moves into and out of the focus and the phase angle ϕ is processed.
The defocus profile is a crucial measurement for quantitatively determining |Escat| since the fringe amplitude can not be determined directly from any single image. Indeed, accurately measuring |Escat| from the defocus profile is still nontrivial since the axial point spread function effectively acts as a modulating envelope. Depending on the elevation or size of a particle, the defocus profile may have a single large antinode at z = 0, or a node at z = 0 with two antinodes as in Figure 4b, or something in between. This is due to the fact that increasing the size of the particle will increase the elevation of its centroid, and a change the centroid position by as little as λ/20 will result in a noticeable shift in the position (in z) of the fringe peaks with respect to the axial point spread function [28].
In almost all previous work with SP-IRIS, the focus plane at which the highest number of particles were visibly brightest was chosen either by eye or by a custom auto-focus algorithm, and a single image was saved for later analysis. It should now be clear however that such a process cannot hope to accurately measure |Escat| for a population of nanoparticles of heterogeneous or otherwise unknown size. Indeed, this likely explains why attempts to generate empirical sizing ‘rulers’ using reference particles of known dimensions has been of limited efficacy, and resulted in different size-calibration curves from publication to publication despite modest changes in design.
Altogether, this paints a picture of SP-IRIS as a highly-coupled interferometric system which must be designed and optimized as a whole. We therefore use a perturbation approach to optimization, in which a measurement is simulated while sweeping one system parameter at a time, to develop an intuition for the problem along with optimal design.
3.2. Validation of the model
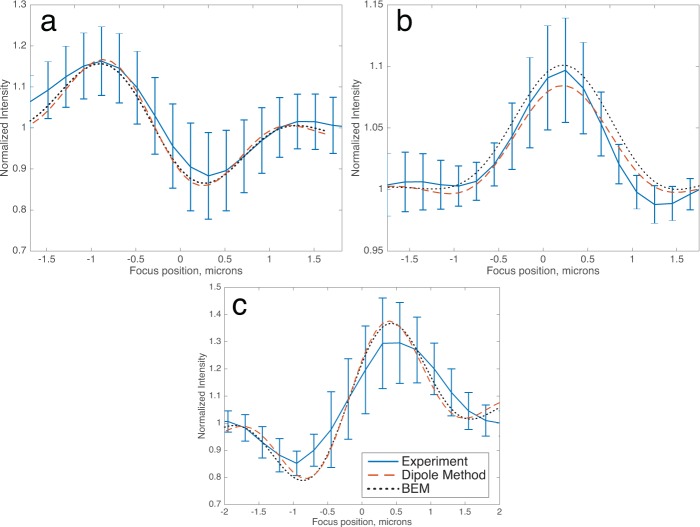
To validate our model we compared the results of simulations to both experimental measurements and the results of the dipole-approximation method published previously [27]. 60 nm diameter gold, 100 nm polystyrene (n=1.60) and 145 nm polystyrene spheres were diluted in DI water and spin-coated onto an SP-IRIS substrate with 100 nm oxide film. Note that nanoparticles on the substrate must be sufficiently far apart so that their diffraction-limited images would not overlap (at minimum about 2 µm). Z-stacks of images were taken over a 4 µm range of focus positions (z) in 200 nm increments, resulting in a data-cube I(x, y, z). High-pass spatial filtering followed by thresholding was used to identify the centroid of the diffraction-limited image of each particle, and the normalized intensity of the centroids were measured as a function of focal position z to measure experimental defocus profiles. Simulations of the defocus profile of these particles were generated using both the BEM and dipole methods and found to be in agreement with each other as well as with the average experimental curve (Figure 5).
Fig. 5.
Validation of BEM simulations against the dipole approximation method and experimental measurements, in the case of (a) 60 nm gold spheres (34 particles), (b) 100 nm diameter polystyrene (n=1.60) spheres (63 particles), and (c) 145 nm polystyrene spheres (24 particles), showing good agreement amongst all three for the entire range of particle sizes. (NA = 0.8, λ = 525 nm in (a–b), λ = 630 nm in (c)).
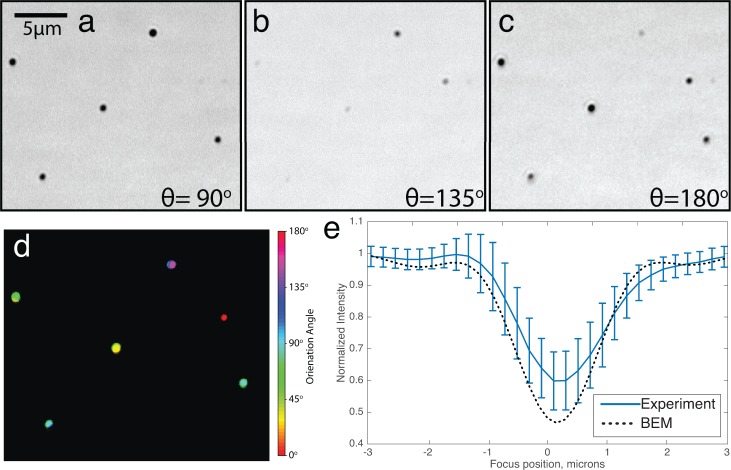
We then investigated if whether the BEM approach could be used to correctly predict the image of asymmetric particles such as nanorods. 25 × 71 nm gold nanorods were spun onto an SP-IRIS substrate using the same method described earlier, resulting in individually immobilized particles with random orientations. To account for the distribution of orientations, a linear polarizer in the illumination path was rotated over θ = (0°, 180°) in 15° increments (Figure 6a–c). As before, a z-stack was acquired for each position of the polarizer, resulting in a data-hypercube of I (x, y, z, θ). A sinusoid with form I(x, y, z0, θ) = V sin(2πθ + H) + 1 was fit to every image pixel (x, y) in a particular plane z = z0 at which particles were most visible to the eye. Fitted coefficients H(x, y) and V(x, y) were then represented respectively as the Hue (color) and Value (brightness) of an HSV image, in which particles of similar orientation are represented with similar false colors (Figure 6d). The average defocus profiles of a nanorod illuminated along its longitudinal axis were found to be in agreement with corresponding BEM simulations (Figure 6e).
Fig. 6.
Validation of BEM simulations of gold nanorods. (a–c) Cropped slices from the 25x71 nm gold nanorod dataset described in text, where θ is the illumination polarization angle. (d) Hue-Saturation-Value representation after fitting a sinusoid to each spatial position pixel as a function of illumination polarization angle. Value (i.e., brightness) indicates the presence of a particle and Hue (i.e., color) indicates particle orientation. (e) Comparison of simulated and measured normalized intensity of a 25x71 nm gold nanorod aligned parallel to the illumination polarization direction, as a function of defocus (59 particles, 50 × 0.8 NA, λ = 630 nm).
3.3. Design optimization for bio-nanoparticle detection and sizing
Many bio-nanoparticles of interest are in the range of 50 and 150 nm in diameter, with a refractive index of about n = 1.5 for virus-like particles and as low as n = 1.38 for exosome vesicles [40–42]. Our objective is to maximize the visibility of this category of bio-nanoparticles while immersed in water. Specifically, we wish to design an acquisition process that can not only detect but also accurately measure the size of bio-nanoparticles within the range 50–150 nm.
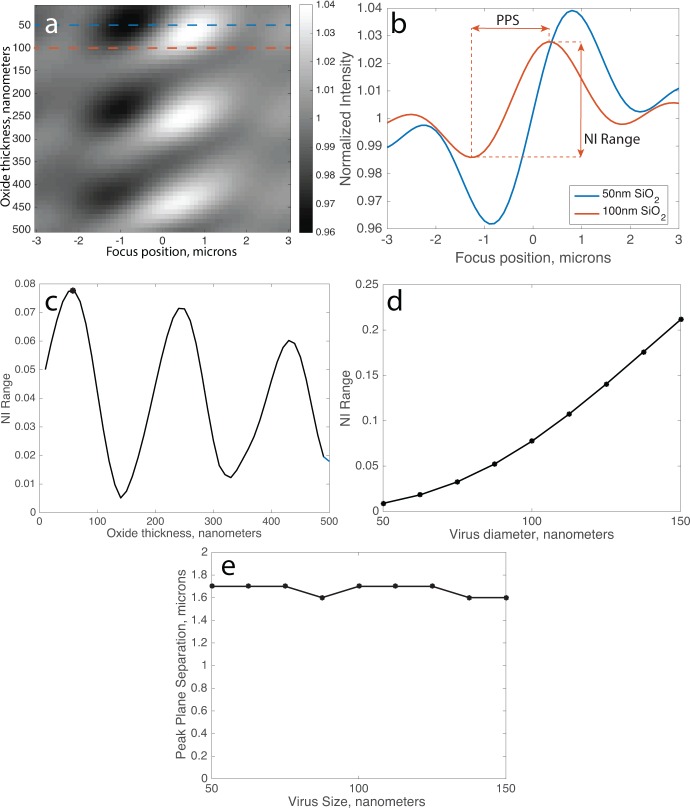
Towards this end, we simulated the defocus profile of a 100 nm virus (n = 1.5) on SP-IRIS substrates with a range of oxide film thicknesses (Figure 7). Here, the illumination is modeled as a normal-incident plane wave with λ = 530 nm, and the objective NA is 0.9. As expected, constructive self-interference of forward- and back-scattered light depends strongly on the correct selection of oxide film thickness, and it is periodic with . Rather than selecting the thickness at which the normalized intensity is simply either maximum or minimum, we use the normalized intensity range (NI Range, Figure 7b) as the objective function. This parameter is selected as an engineering trade-off; the ideal case would be to perform numerical fitting of the defocus profile at every pixel in the image to accurately measure |Escat|, but this is prohibitively computationally expensive. By comparison, NI Range is an approximation that can be calculated rapidly. Another useful metric is the peak plane separation, which is the distance (in z) between the two planes of maximum and minimum NI. The peak plane separation is an approximate measurement of the period, which like NI Range can be calculated rapidly. When the NI Range is optimized, the optimal oxide film thickness turns out to be about 50 nm (Figure 7c). When this oxide film thickness is used, the NI Range is a strong monotonic function of particle size (Figure 7d). However, the peak plan separation is nearly constant for a wide range of particle sizes, as would be expected (Figure 7e).
Fig. 7.
(a) Simulations of normalized intensity (at image center) of a 100 nm virus as a function of oxide film thickness and objective focus position. Two slices of this simulation where the film thickness is 50 or 100 nm are indicated by the dotted lines and plotted in (b) as defocus profiles. (c) NI Range for the range of oxide film thicknesses. (d) NI Range and (e) Peak plane separation are simulated for spherical virus between 50 and 150 nm in diameter on a 50 nm oxide film.
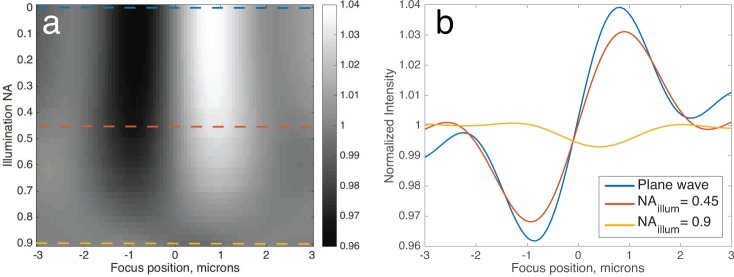
As mentioned earlier, SP-IRIS uses Köhler illumination to provide approximately flat and uniform illumination over the objective field of view. In Köhler illumination, the illumination source is imaged to the back pupil of the objective using two lenses in a 4-f configuration. However, this poses a challenge since in order to illuminate the surface with approximately plane wave illumination, the source should be focused onto a pinhole spatial filter and this pinhole should be imaged to the objective back pupil. This approach is inefficient from a power perspective since it will discard the vast majority of the source’s light [43]. It would be advantageous to know the rate at which fringe visibility decreases with increasing illumination numerical aperture (NA), so that a trade-off may be made. We therefore simulated the the defocus profile of a 100 nm virus on the optimal oxide film thickness of 50 nm, in water, while sweeping the illumination NA from 0–0.9 (Figure 8a). The collection NA is constant (0.9) for all cases, and the illumination is modeled as having uniform intensity over the chosen solid angle. As expected, illuminating with the full NA of the objective greatly decreases fringe visibility. However, we find that an illumination NA as high as 0.45 (i.e., objective fill factor f0 ~ 0.5) may be used while still retaining ~ 80% of the NI Range signal (Figure 8b).
Fig. 8.
(a) Simulations of normalized intensity (at image center) of a 100 nm virus as a function of illumination NA and focus position. (b) The defocus profiles when illumination angles are restricted to a single plane wave (NA = 0), or NA = 0.45 or NA = 0.9.
Finally, we considered the impact of using a different film material, instead of thermally grown oxide. Silicon nitride can also be deposited on polished silicon in very flat films, and has a higher refractive index (n=2.0–2.3 depending on the deposition protocol). To investigate the impact of changing the film material, we simulated the defocus profile of a 100 nm virus, as before, on SP-IRIS substrates with a range of nitride film thicknesses where n=2.05 (Figure 9).
Fig. 9.
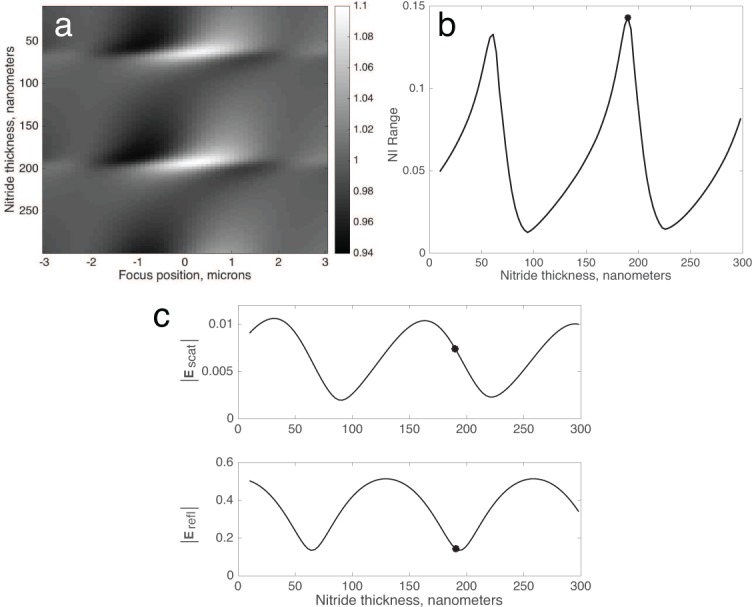
(a) Simulated defocus profiles of a 100 nm virus on a range of nitride films (n=2.05). (b) Optimal NI Range is achieved with a film thickness of 190 nm. (c) The field magnitudes |Escat| (top) and |Eref| (bottom) are plotted individually, with the optimal nitride thickness indicated.
As expected, the results are qualitatively similar to those with an oxide film. However, the peak NI Range is nearly twice that of optimized oxide (0.14 vs. 0.08). The reason for this improvement is that the refractive index of nitride is closer to the geometric mean of silicon and water, which means it forms an efficient anti-reflection coating when the thickness is an integer multiple of (Figure 9c). The minimization of |Eref|, rather than the maximization of |Escat|, is now the driving factor in increasing particle visibility. Since the scattered fields propagate mainly at high angles, and since the reflectivity is a function of incidence angle, it may be possible with this approach to find a configuration in which |Eref| is attenuated to the minimum required level while |Escat| is simultaneously large.
4. Conclusions
Biological and medical research into the structure and function of biological nanoparticles have revealed their multifaceted roles in molecular sorting, homeostasis, cell signaling and various types of disease. As the most abundant biological agents on earth, viruses exhibit an enormously diverse range of evolutionary strategies and morphologies which are still being elucidated [4]. At the molecular level, tools for investigation of these agents has grown tremendously. We believe the technique presented here is complementary to other single-particle characterization methods which have exquisite resolution but low throughput. By providing morphology information at single-particle resolution with high throughput and molecular specificity, SP-IRIS fills a niche between high-resolution approaches and the ensemble measurement techniques described earlier. We look forward to immediate application of the advances described herein to the high-throughput characterization of genetically modified viruses for cancer therapy, and multiplexed exosome detection and classification for biomarker discovery.
Acknowledgments
The authors would like to thank Jacob Trueb for helpful and interesting discussion.
Funding
National Institute of Allergy and Infectious Diseases (NIAID) (R21Al113715).
References and links
- 1.Kourembanas S., “Exosomes: Vehicles of intercellular signaling, biomarkers, and vectors of cell therapy,” Ann. Rev. Physiol. 77, 13–27 (2015). 10.1146/annurev-physiol-021014-071641 [DOI] [PubMed] [Google Scholar]
- 2.van der Pol E., Böing A. N., Harrison P., Sturk A., Nieuwland R., “Classification, functions, and clinical relevance of extracellular vesicles,” Pharmacol. Rev. 64, 676–705 (2012). 10.1124/pr.112.005983 [DOI] [PubMed] [Google Scholar]
- 3.van der Pol E., Coumans F., Varga Z., Krumrey M., Nieuwland R., “Innovation in detection of microparticles and exosomes,” J. Thromb. Haemostatis 11, 36–45 (2013). 10.1111/jth.12254 [DOI] [PubMed] [Google Scholar]
- 4.Lawrence C. M., Menon S., Eilers B. J., Bothner B., Khayat R., Douglas T., Young M. J., “Structural and functional studies of archaeal viruses,” J. Biol. Chem. 284, 12599–12603 (2009). 10.1074/jbc.R800078200 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Berthoux L., Pèchoux C., Darlix J.-L., “Multiple effects of an anti-human immunodeficiency virus nucleocapsid inhibitor on virus morphology and replication,” J. Virol. 73, 10000–10009 (1999). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Clavel F., Orenstein J. M., “A mutant of human immunodeficiency virus with reduced rna packaging and abnormal particle morphology,” J. Virol. 64, 5230–5234 (1990). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Darling A. J., Boose J. A., Spaltro J., “Virus assay methods: Accuracy and validation,” Biologicals 26, 105–110 (1998). 10.1006/biol.1998.0134 [DOI] [PubMed] [Google Scholar]
- 8.Lichty B. D., Power A. T., Stojdl D. F., Bell J. C., “Vesicular stomatitis virus: re-inventing the bullet,” Trends Mol. Med. 10, 210–216 (2004). 10.1016/j.molmed.2004.03.003 [DOI] [PubMed] [Google Scholar]
- 9.Doane F. W., “Virus morphology as an aid for rapid diagnosis,” Yale J. Biol. Med. 53, 19–25 (1980). [PMC free article] [PubMed] [Google Scholar]
- 10.Lange F. d., Cambi A., Huijbens R., Bakker B. d., Rensen W., Garcia-Parajo M., Hulst N. v., Figdor C. G., “Cell biology beyond the diffraction limit: near-field scanning optical microscopy,” J. Cell Sci. 114, 4153–4160 (2001). [DOI] [PubMed] [Google Scholar]
- 11.Kuznetsov Y. G., Victoria J. G., Robinson W. E., McPherson A., “Atomic force microscopy investigation of human immunodeficiency virus (hiv) and hiv-infected lymphocytes,” J. Virol. 77, 11896–11909 (2003). 10.1128/JVI.77.22.11896-11909.2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Im H., Shao H., Park Y. I., Peterson V. M., Castro C. M., Weissleder R., Lee H., “Label-free detection and molecular profiling of exosomes with a nano-plasmonic sensor,” Nature Biotech. 32, 490–495 (2014). 10.1038/nbt.2886 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Vollmer F., Arnold S., “Whispering-gallery-mode biosensing: label-free detection down to single molecules,” Nat. Methods 5, 591–596 (2008). 10.1038/nmeth.1221 [DOI] [PubMed] [Google Scholar]
- 14.Lindfors K., Kalkbrenner T., Stoller P., Sandoghdar V., “Detection and spectroscopy of gold nanoparticles using supercontinuum white light confocal microscopy,” Phys. Rev. Lett. 93, 037401 (2004). 10.1103/PhysRevLett.93.037401 [DOI] [PubMed] [Google Scholar]
- 15.van Dijk M. A., Lippitz M., Orrit M., “Far-field optical microscopy of single metal nanoparticles,” Acc. Chem. Res. 38, 594–601 (2005). 10.1021/ar0401303 [DOI] [PubMed] [Google Scholar]
- 16.van Dijk M. A., Lippitz M., Stolwijk D., Orrit M., “A common-path interferometer for time-resolved and shot-noise-limited detection of single nanoparticles,” Opt. Express 15, 2273–2287 (2007). 10.1364/OE.15.002273 [DOI] [PubMed] [Google Scholar]
- 17.Nie S., Emory S. R., “Probing single molecules and single nanoparticles by surface-enhanced raman scattering,” Science 275, 1102–1106 (1997). 10.1126/science.275.5303.1102 [DOI] [PubMed] [Google Scholar]
- 18.Wang S., Shan X., Patel U., Huang X., Lu J., Li J., Tao N., “Label-free imaging, detection, and mass measurement of single viruses by surface plasmon resonance,” Proc. Natl. Acad. Sci. 107, 16028–16032 (2010). 10.1073/pnas.1005264107 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Boccara M., Fedala Y., Bryan C. V., Bailly-Bechet M., Bowler C., Boccara A. C., “Full-field interferometry for counting and differentiating aquatic biotic nanoparticles: from laboratory to tara oceans,” Biomed. Opt. Express 7, 3736–3746 (2016). 10.1364/BOE.7.003736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Kukura P., Ewers H., Müller C., Renn A., Helenius A., Sandoghdar V., “High-speed nanoscopic tracking of the position and orientation of a single virus,” Nature Methods 6, 923–927 (2009). 10.1038/nmeth.1395 [DOI] [PubMed] [Google Scholar]
- 21.McLeod E., Dincer T. U., Veli M., Ertas Y. N., Nguyen C., Luo W., Greenbaum A., Feizi A., Ozcan A., “High-throughput and label-free single nanoparticle sizing based on time-resolved on-chip microscopy,” ACS Nano 9, 3265–3273 (2015). 10.1021/acsnano.5b00388 [DOI] [PubMed] [Google Scholar]
- 22.Patskovsky S., Meunier M., “Reflected light microspectroscopy for single-nanoparticle biosensing,” J. Biomed. Opt. 20, 097001 (2015). 10.1117/1.JBO.20.9.097001 [DOI] [PubMed] [Google Scholar]
- 23.Scherr S. M., Daaboul G. G., Trueb J., Sevenler D., Fawcett H., Goldberg B., Connor J. H., Ünlü M. S., “Real-time capture and visualization of individual viruses in complex media,” ACS Nano 10, 2827–2833 (2016). 10.1021/acsnano.5b07948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Daaboul G. G., Gagni P., Benussi L., Bettotti P., Ciani M., Cretich M., Freedman D. S., Ghidoni R., Ozkumur A. Y., Piotto C., Prosperi D., Santini B., Ünlü M. S., Chiari M., “Digital detection of exosomes by interferometric imaging,” Sci. Rep. 6, 37246 (2016). 10.1038/srep37246 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Daaboul G. G., Yurt A., Zhang X., Hwang G. M., Goldberg B. B., Ünlü M. S., “High-throughput detection and sizing of individual low-index nanoparticles and viruses for pathogen identification,” Nano Lett. 10, 4727–4731 (2010). 10.1021/nl103210p [DOI] [PubMed] [Google Scholar]
- 26.Daaboul G. G., Lopez C. A., Chinnala J., Goldberg B., Connor J. H., Ünlü M. S., “Digital sensing and sizing of vesicular stomatitis virus pseudotypes in complex media; a model for ebola and marburg detection,” ACS Nano 8, 6047–6055(2014). 10.1021/nn501312q [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Avci O., Adato R., Ozkumur A. Y., Ünlü M. S., “Physical modeling of interference enhanced imaging and characterization of single nanoparticles,” Opt. Express 24, 6094 (2016). 10.1364/OE.24.006094 [DOI] [PubMed] [Google Scholar]
- 28.Trueb J., Avci O., Sevenler D., Connor J., Ünlü M. S., “Robust visualization and discrimination of nanoparticles by interferometric imaging,” IEEE Journal of Selected Topics in Quantum Electronics 23, 6900610 (2016). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Avci O., Campana M. I., Yurdakul C., Ünlü M. S., “Pupil function engineering for enhanced nanoparticle visibility in wide-field interferometric microscopy,” Optica 4, 247–254 (2017). 10.1364/OPTICA.4.000247 [DOI] [Google Scholar]
- 30.Sorgenfrei S., Chiu C.-y., Gonzalez R. L., Jr, Yu Y.-J., Kim P., Nuckolls C., Shepard K. L., “Label-free single-molecule detection of dna-hybridization kinetics with a carbon nanotube field-effect transistor,” Nature Nanotechn. 6, 126–132 (2011). 10.1038/nnano.2010.275 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.García de Abajo F. J., “Retarded field calculation of electron energy loss in inhomogeneous dielectrics,” Phys. Rev. B 65, 115418 (2002). 10.1103/PhysRevB.65.115418 [DOI] [Google Scholar]
- 32.Novotny L., Hecht B., Principles of Nano-optics (Cambridge University Press, 2006). 10.1017/CBO9780511813535 [DOI] [Google Scholar]
- 33.Hohenester U., Trügler A., “Mnpbem - a matlab toolbox for the simulation of plasmonic nanoparticles,” Comput. Phys. Commun. 183, 370–381 (2012). 10.1016/j.cpc.2011.09.009 [DOI] [Google Scholar]
- 34.Waxenegger J., Trügler A., Hohenester U., “Plasmonics simulations with the mnpbem toolbox: Consideration of substrates and layer structures,” Computer Physics Communications 193, 138–150 (2015). 10.1016/j.cpc.2015.03.023 [DOI] [Google Scholar]
- 35.Mandel L., Wolf E., Optical Coherence and Quantum Optics (Cambridge University Press, 1995). 10.1017/CBO9781139644105 [DOI] [Google Scholar]
- 36.Saleh B. E. A., Teich M. C., Fundamentals of Photonics, Wiley series in pure and applied opticsWiley Inter-science, 2007), 2nd ed [Google Scholar]
- 37.Bohren C. F., Huffman D. R., Absorption and Scattering of Light by Small Particles (John Wiley & Sons, 2008). [Google Scholar]
- 38.Mitra A., Novotny L., “Real-time optical detection of single nanoparticles and viruses using heterodyne interferometry,” in “Nano-Optics for Enhancing Light-Matter Interactions on a Molecular Scale,” Bartolo B. D., Collins J., eds. (Springer; Netherlands, 2013), NATO Science for Peace and Security Series B: Physics and Biophysics, pp. 3–22. 10.1007/978-94-007-5313-6_1 [DOI] [Google Scholar]
- 39.Mudanyali O., McLeod E., Luo W., Greenbaum A., Coskun A. F., Hennequin Y., Allier C. P., Ozcan A., “Wide-field optical detection of nanoparticles using on-chip microscopy and self-assembled nanolenses,” Nature Photon. 5, 247–254 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Mitra A., Ignatovich F., Novotny L., “Real-time optical detection of single human and bacterial viruses based on dark-field interferometry,” Biosens. Bioelectron. 31, 499–504 (2012). 10.1016/j.bios.2011.11.025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Van Der Pol E., Van Gemert M. J. C., Sturk A., Nieuwland R., Van Leeuwen T. G., “Single vs. swarm detection of microparticles and exosomes by flow cytometry,” J. Thromb. Haemostasis 10, 919–930 (2012). 10.1111/j.1538-7836.2012.04683.x [DOI] [PubMed] [Google Scholar]
- 42.Gardiner C., Shaw M., Hole P., Smith J., Tannetta D., Redman C. W., Sargent I. L., “Measurement of refractive index by nanoparticle tracking analysis reveals heterogeneity in extracellular vesicles,” J. Extracell. Vesicles 3, 25361 (2014). 10.3402/jev.v3.25361 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Büttner A., Zeitner U. D., “Wave optical analysis of light-emitting diode beam shaping using microlens arrays,” Opt. Eng. 41, 2393–2401 (2002). 10.1117/1.1499975 [DOI] [Google Scholar]