Regression-based algorithm for bulk motion subtraction in optical coherence tomography angiography

Abstract

We developed an algorithm to remove decorrelation noise due to bulk motion in optical coherence tomography angiography (OCTA) of the posterior eye. In this algorithm, OCTA B-frames were divided into segments within which the bulk motion velocity could be assumed to be constant. This velocity was recovered using linear regression of decorrelation versus the logarithm of reflectance in axial lines (A-lines) identified as bulk tissue by percentile analysis. The fitting parameters were used to calculate a reflectance-adjusted upper bound threshold for bulk motion decorrelation. Below this threshold, voxels are identified as non-flow tissue, their flow values are set to zeros. Above this threshold, the voxels are identified as flow voxels and bulk motion velocity is subtracted from each using a nonlinear decorrelation-velocity relationship previously established in laboratory flow phantoms. Compared to the simpler median-subtraction method, the regression-based bulk motion subtraction improved angiogram signal-to-noise ratio, contrast, vessel density repeatability, and bulk motion noise cleanup in the foveal avascular zone, while preserving the connectivity of the vascular networks in the angiogram.

1. Introduction

Optical coherence tomography angiography (OCTA) is a noninvasive blood flow imaging technique [1–5] that allows depth-resolved visualization of functional vasculatures with capillary resolution. It has become an important clinical tool in ophthalmology [6–14] and exhibits great potential for dermatology [15, 16] and neurology [17]. To obtain flow signal, OCTA algorithms [1, 3, 18–20] rely on mathematical operations that quantify variations in the amplitude and/or the phase of optical coherence tomography (OCT) signal between at least two consecutive B-scans acquired at the same raster position. However, since the inter-scan time cannot be extremely small without affecting sensitivity to slow-speed blood flow [21, 22], OCTA of the retina is sensitive to involuntary eye motion between B-scans.

Software and hardware solutions exist to remove the effects of eye motion on OCTA. Microsaccadic motion can be corrected by registration methods [23–27] that retrieve the signal missing in corrupted frames from other scans. In addition, tracking-assisted scanning schemes [28–32] have been implemented in commercial systems to prevent data recording during a microsaccade. Also, inter-volume optical microangiography [33] operates at an ultra-high volumetric imaging rate in order to detect flow by recognizing signal variations between adjacent volumes instead of consecutive frames, showing potential to reduce the prevalence of motion artifacts. Yet, small-amplitude bulk motion caused by ocular drift, pulsation, tremors, or OCT system mechanical instabilities is currently undetectable by tracking systems and only partially attenuated by averaging registered images.

One way to reduce the effect of bulk motion is to co-register the reflectance images at each scanning position before computing the flow image. Methods that iteratively maximize cross-correlation of successive B-scans prior to OCTA processing have been used to estimate displacement and compensate bulk image shifts as well as global phase variations in the axial and lateral directions [34–36]. However, the actual three-dimensional nature of eye motion during scanning challenges this approach, which is limited to in-plane shifts. Another approach to solve the bulk motion problem is to approximate its velocity to the spatial average (along A-scan and B-scan directions) of the reflectance OCT signal variation between consecutive scans [37]. This solution requires acquisition of many frames of the same B-scan and assumes a low capillary density on the imaged sample.

In our split-spectrum amplitude decorrelation angiography (SSADA) algorithm, a simple bulk motion subtraction method was introduced to minimize the noise caused by motion between two consecutive B-scans. The decorrelation caused by bulk motion is estimated by the median decorrelation value within retinal tissue region, and then subtracted from all pixels at each B-frame of SSADA [9]. Although the median subtraction method improves the image quality, it constitutes an inaccurate approximation of the actual bulk motion contribution to flow signal.

In this paper, we propose a more accurate mechanism to remove the noise introduced by bulk motion. Using regression analysis; we first define the relationship between background bulk motion decorrelation and the logarithm of the OCT reflectance in a group of A-lines devoid of flow voxels within a segment of a B-frame. Then, we assign zero decorrelation values to the non-flow pixels in each segment where the respective voxels have values below a certain threshold derived from the relation between bulk motion and reflectance. A nonlinear model that relates decorrelation and flow velocity [38] is used to subtract estimated bulk-motion velocity from the measured velocity inflow voxels. Compared to the median subtraction algorithm, we demonstrate reduced bulk motion at avascular regions, improved image quality and vessel density repeatability while preserving vascular connectivity.

2. Methods

2.1 Data acquisition

Volumetric OCTA scans of the macula and the optic disc of healthy subjects were acquired using a wide-field 200-kHz OCT system. The system relies on a swept-source configuration that utilizes a tunable laser (Axsun, Inc., Billerica, MA, USA) operating at 1044 nm center wavelength with a 104 nm tuning range. It has a lateral resolution of 12 µm and an axial resolution of 7.5 µm, which is increased to 22.5 µm on the flow image. Participants were recruited at the Casey Eye Institute of OHSU and informed consent was obtained. The protocol was approved by the Institutional Review Board/Ethics Committee of OHSU and adhered to the tenants of the Declaration of Helsinki in the treatment of human participants. The scan pattern consisted of 800 B-frames composed of 850 A-lines and located at 400 raster positions (y-priority), covering an 8x6mm² area. Each B-scan was completed in 4.75 ms.

2.2 Data processing

Data was processed using the Matlab 2013a release (Mathworks, Natick, MA, USA). Cross-sectional OCT images were generated and B-frames acquired at the same raster position were averaged. OCTA data was calculated using the SSADA algorithm [1]. Segmentation of the vitreous and inner limiting membrane (ILM) interface, outer plexiform layer (OPL) and outer nuclear layer (ONL) interface as well as Bruch’s membrane and choroid interface was automatically performed by a directional graph-search algorithm developed by Zhang et al. [39]. The region contained between ILM and OPL is the vascularized inner retina. En face images were generated by maximum projection of the flow signal within the inner retinal slab. An expert grader manually corrected segmentation errors.

Frames affected by microsaccadic artifacts were recognized on the en face OCTA image by simply identifying summed flow signal above a threshold [28], and excluded from analysis. Then, we recognized the relationship between bulk motion contribution to decorrelation signal and the local reflectance. Because decorrelation is not linearly related to velocity, the subtraction of the bulk motion contribution must be performed on the velocity domain rather than in the decorrelation domain. Non-microsaccadic frames were divided into 5 segments where local reflectance does not vary abruptly. The segments are small enough that the axial-lines within them could be acquired within a small enough time frame (less than 1 millisecond) that bulk motion could be considered to be approximately constant within the segments. Then, we developed a method to estimate the bulk motion velocity from frame segments.

At each segment, we selected a group of A-lines devoid of inner retinal flow voxels. For this purpose, A-lines crossing large vessels were first identified by a binary large vessel mask of the en face angiogram and excluded from the following analysis. The mask was constructed by successively applying amplitude thresholding to remove the majority of capillary pixels, a morphological opening (erosion followed by dilation) to cleanup dispersed pixels, a Gaussian convolution filter to prevent holes in the middle of large vessels and a final binarization step. From the remaining A-lines, the first 10 percentile with the lowest decorrelation signal were selected, assuming these are composed by non-flow voxels only. The threshold chosen is approximately the upper boundary of inner retinal vessel densities among the healthy subjects that participated in the study. The decorrelation and natural logarithm of the reflectance data selected in the segment were converted into vectors and sorted by increasing order of reflectance values. Then, the vectors were divided into 20 equally sized bins and the reflectance and decorrelation values in each bin were averaged, forming the new vectors $D_{bin},R_{bin}$. The slope$(m{}_k)$ and intercept $(n{}_k)$ of the$D_{bin}=f(R_{bin})$linear relationship were identified and recorded for all k = 2000 segments. The slope of the linear fit was larger at frames with larger prevalence of motion, as shown in Figs. 1(A)-(C). The RMS deviation ($S_{BM}$) of the un-binned data was also recorded at each segment. Another linear regression fitting was performed to recognize the relationship between the deviation$S_{BM}$and the slopes$m_k$of all segments forming a volumetric scan, expressed as$S_{BM}=a+b{m}_k$(Fig. 1D). Then, the voxels in the k^th segment with decorrelation below the threshold defined in Eq. (1) were set to zero. In frames affected by microsaccadic artifacts no A-lines were selected, the regression analysis step was skipped and the decorrelation values of all voxels were also set to zero. Fitting parameters in segments with less than five A-lines selected for regression analysis were substituted by the parameters of the neighboring segment within the same B-frame.

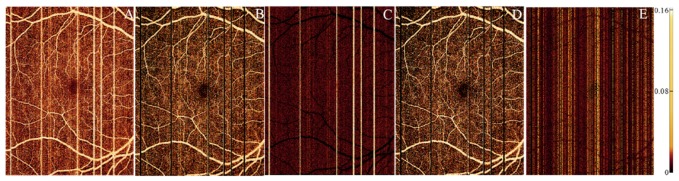
Fig. 1.

Linear regression of decorrelation signal (D_BM) due to bulk motion as a function of the natural logarithmic tissue reflectance (R). Panel A shows a 6mm × 8mm (horizontal x vertical) OCT angiography scan (400B-frames × 850pixels) from which frames 134, 208, and 336 were selected as examples for moderate, low, and high bulk motion. Panel B shows the cross-sectional B-scans of frames 134 (subtle bulk motion), 208 (moderate bulk motion) and 336 (high bulk motion near microsaccade). SSADA decorrelation signal in red color is overlaid on top of the reflectance OCT signal. Panel C shows the corresponding linear fit of the binned R vs. D_BM for the central segment indicated by a red arrow in B. In panel D it is observed that the RMS deviation of un-binned D of non-flow voxels from the fitting curve found at each segment exhibit a linear dependence on the corresponding segment’s slope, shown for all segments forming a volumetric scan.

$$D_{TH}=(m{}_{k}R+n{}_k)+1.96(a+bm{}_k)$$ (1)

Vascular voxels remain after thresholding, and the contribution of bulk motion$D_{BM,blood}$to their flow signal was obtained using the median reflectance of the flow voxels within the frame segment ($R_{blood}$in Fig. 2A). An estimate of bulk motion velocity was calculated by a nonlinear model that related decorrelation and velocity in laboratory blood flow phantoms [38] (Eq. (2).

Fig. 2.

Removal of bulk motion from voxels within each B-frame segment. (A) Decorrelation due to bulk motion (D_BM) is modeled as a function of logarithmic reflectance R based linear regression coefficients m_k and n_k from the regression analysis of the k^th frame segment. Voxels with decorrelation value below threshold D_TH set at the 97.5 percentile of bulk motion (assuming normal distribution) are classified as non-flow voxels (D set to zero). The bulk motion-induced decorrelation in blood D_BM,blood is calculated using the reflectance of blood$R_{blood}$obtained from the median reflectance of flow voxels (voxel with D above D_TH). Bulk motion velocity v_BM is obtained from D_BM,blood using Eq. (2). (B) The bulk motion velocity is subtracted from a voxel with uncorrected decorrelation value D₀ and corresponding velocity v₀ that is high relative to the saturation velocity according to the nonlinear curve relating flow signal D to velocity. Therefore subtracting v_BM from v₀ to obtained corrected velocity v₁and corrected flow signal D₁ has little effect. (C) The bulk motion velocity is subtracted from a voxel with uncorrected decorrelation value D₀ and corresponding velocity v₀ that is lower than the saturation velocity. Here subtracting v_BM from v₀ to obtained corrected velocity v₁and corrected flow signal D₁ has a larger effect than the previous example.

$$v_{BM}=-\frac{1}{3}{v}_{sat}\ln \left(1-\frac{D_{BM,blood}-D_{brownian}}{D_{sat}-D_{brownian}}\right)$$ (2)

The saturation value$D_{sat}$was calculated as 0.95 times the 99th percentile of the flow signal in the en face angiogram. $D_{brownian}$was estimated assuming that it maintains the same proportion to$D_{sat}$as the one reported previously [38]. The value of the saturation velocity$v_{sat}$was approximated utilizing the experimental data obtained in Ref [38], adjusting for the difference in inter-scan period between the Avanti RTVue-XR (Optovue, Inc. Fremont, CA, USA) and the wide-field system used here. Equation (2) was also used to calculate a velocity$v_0$ for each original decorrelation value$D_0$. Voxels with decorrelation above $D_{sat}$ cannot be converted to velocity domain by Eq. (2) and were assigned $D_{sat}$and $v_{sat}$values. The calculated$v_{BM}$was subtracted from $v_0$at every vascular voxel and the bulk motion-free decorrelation$D_1$was obtained by Eq. (3). By this mechanism we prevented excessive subtraction from voxels representing high-speed flow; where the impact of bulk motion on decorrelation value is significantly lower (Figs. 2 B-C).

$$D_1=\left(D_{sat}-D_{brownian}\right)\exp \left(-3\frac{v_0-v_{BM}}{v_{sat}}\right)+D_{brownian}$$ (3)

A flow diagram of the algorithm is shown in Fig. 3.

Fig. 3.

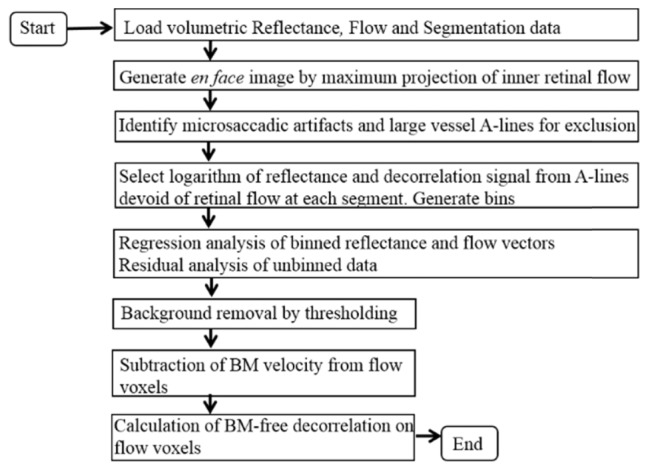
Flow diagram of the bulk-motion (BM)removal algorithm.

2.3 Comparison to median subtraction algorithm

The regression-based bulk motion subtraction method was compared with an earlier method in which the median decorrelation value of the segmented retinal region was subtracted from all retinal voxels within the B-frame segments defined above. The threshold used to distinguish vascular from non-flow pixels in original and median-subtracted angiograms was obtained from the decorrelation at the foveal avascular zone (FAZ) of en face projections by$D_{flow}={\overline{D}}_{FAZ}+2.33{\sigma }_{D_{FAZ}}$, where $\overline{D}$and $\sigma$represent mean value and standard deviation.

2.4 Comparison to inter-B-scan registration algorithm

An alternative approach to bulk motion removal a posteriori is to compensate the bulk motion between consecutive B-scans prior to computing OCTA flow signal. The benefits and tradeoffs of this pre-processing step in improving the artifact removal efficacy by the regression-based bulk-motion subtraction algorithm were evaluated.

For inter-B-scan registration we applied in SSADA a method similar to the one proposed by Lee et al [34]. Briefly, OCT images were first up-sampled by a factor of two in lateral (x) and axial (z) dimensions. An iterative routine maximizes the cross-correlation of the OCT signal of the two B-scans acquired at each position by rigid displacements of the second B-scan in two directions. After recognizing the optimal shift, it was applied to the second OCT image of each the 11 pairs generated by spectrum splitting [40]. Finally, the OCT images were down-sampled and the amplitude decorrelation signal was computed.

2.5 Image quality assessment

Bulk motion subtraction efficiency was assessed by the percentage of average FAZ signal remaining within the segmented retinal slab after processing the original data.

Parafoveal signal-to-noise ratio (SNR) was calculated by Eq. (4). The parafoveal annulus is concentric with the fovea, has an outer diameter of 2.5 mm and an inner diameter of 0.6 mm.

$$SNR=\frac{{\overline{D}}_{parafoveal}-{\overline{D}}_{FAZ}}{{\sigma }_{D_{FAZ}}}$$ (4)

Vessel density was defined for en face projection as the percentage of area occupied by vascular pixels within the parafovea. Its coefficient of variation was used to assess inter-scan vessel density repeatability.

The RMS image contrast was defined as the standard deviation of the en face flow image, expressed in Eq. (5):

$$C_{RMS}=\sqrt{\frac{1}{A}\times {{\displaystyle \sum _{(x,y)\in A}(D(x,y)-\overline{D})}}^2}$$ (5)

Preservation of the vascular integrity after bulk motion subtraction was assessed by the vascular connectivity, defined in a skeletonized version of the en face angiogram by the percentage of flow pixels contained in groups larger than five. Skeletonization of en face OCTA is the process of converting vessels into lines with a one-pixel width. It was performed by the function bwmorph included in Matlab’s Image Processing Toolbox. This function relies on an algorithm that iteratively removes pixels on boundaries of objects recognized on a binary image until the objects remain unchanged [41]. Since en face retinal angiograms contain vasculature of different dimensions (Fig. 4A), skeletonization was performed separately for large vessels and capillaries. If vessels with different calibers were not skeletonized separately, inaccuracies in the recognition of large vessels sometimes might be manifest (Figs. 4B-C).

Fig. 4.

Skeletonization of an en face angiogram. Close up of the foveal region is shown for better visualization. (A) Original angiogram. (B) Skeletonized version by applying the algorithm described in [41] separately on vessels of different calibers. This algorithm is executed by the function bwmorph in Matlab’s Image Processing Toolbox. (C) Inaccurate skeletonization obtained by the same algorithm applied directly on the original en face angiogram. Vessels of larger caliber on the upper left corner are almost indistinguishable.

The p-value of a paired sample t-test evaluated the statistical significance of the results.

3. Results

Optic disc and macula from eight healthy volunteers were imaged. Scans containing microsaccadic artifacts crossing the parafoveal annulus were processed by the algorithm but excluded from the quantitative analysis.

A-lines containing microsaccadic artifacts and large vessels were successfully recognized (Fig. 5). The background A-lines selected at each segment avoided those containing vascular information (Fig. 5C). Segments where the fitting parameters had to be obtained from adjacent segments due to the small number of background A-lines available never represented more than 3% of the total. Segments with no A-lines selected were located at the microsaccadic artifacts.

Fig. 5.

Selection of the background A-lines. (A) 6 × 8mm en face inner retinal angiogram on macula.(B) Identification of A-lines containing large vessel flow signal or microsaccadic artifacts. (C) Map of the A-lines contained within the lowest 10 percentile of maximum projection values (green) after removing the large vessel mask in (B) overlaid on top of the en face angiogram (purple). (D) Distribution of the number of A-lines selected for regression analysis in the 2000 segments.

Changes in bulk motion background signal could be observed by simple inspection of wide-field frames affected by moderate bulk motion on en face images (Fig. 6A). The fitting parameters varied significantly along a B-scan (Fig. 6B), showing that segment partitioning helped reduce the effect of variations in local reflectance, allowing a more accurate bulk motion removal.

Fig. 6.

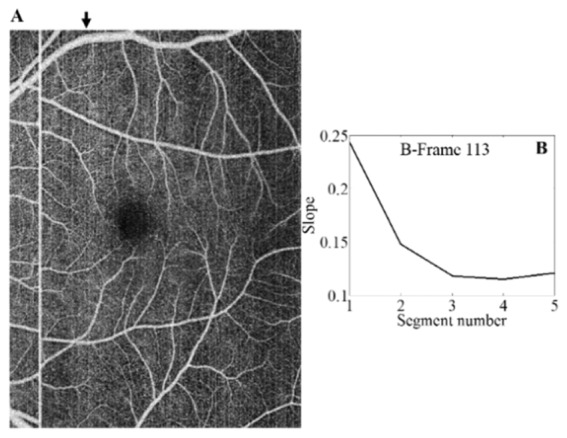
Within-frame variation of bulk motion. En face image of an unprocessed macular scan is shown in (A). A black arrow indicates the position of a frame of interest. Appearance of artefactual frames varied along the vertical axis due to changes in local reflectance. Fitting slope of each of the five segments into which the frame is partitioned is shown in (B).

Background signal at FAZ and bulk motion artefactual frames were effectively removed by the thresholding step (Figs. 7A-C), resulting in improved contrast between capillaries and background. Then, the brighter appearance of vascular pixels contained at artefactual lines was corrected by the step of bulk motion velocity subtraction (Fig. 7D). Larger subtraction from vascular voxels occurred in (non-microsaccadic) artefactual frames and smaller subtraction occurred at the flow voxels with decorrelation values near saturation (Fig. 7E).

Fig. 7.

Removal of bulk motion signal from a macular OCTA scan. (A) Unprocessed en face retinal angiogram. (B) After removal of decorrelation signal from bulk motion voxels using a reflectance-adjusted threshold. (C) Difference between images A and B. (D) After subtraction of bulk motion velocity from the vascular voxels. (E) Difference between images B and D.

Compared to the prior median subtraction algorithm (Table 1 ), the regression-based bulk motion subtraction algorithm removed a larger percentage of decorrelation noise from the FAZ, achieved a greater improvement in vessel density measurement repeatability, a better signal to noise ratio for flow detection and a better RMS contrast. Two methods preserved similar vascular continuity. No improvement of RMS contrast was observed between median-subtracted and original angiograms (p > 0.05), but significant improvement was found after regression-based subtraction. The vessel density did not see significant reduction from the original to the regression-based motion subtracted angiograms (p = 0.0687). The median-based algorithm running time was 4.6 seconds while the regression-based algorithm took 20.3 seconds on CPU. A qualitative comparison of the two bulk motion subtraction methods is shown for en face angiograms of the macula and optic disc in Fig. 8 and for one representative cross-sectional B-frame in Fig. 9.

Table 1. Performance Evaluation of Two Bulk Motion Subtraction Methods.

	Percentage of FAZ signal remaining after subtraction*	Mean vessel density (coefficient of variation)	Vascular connectivity*	Flow SNR*	RMS contrast*
Original (No subtraction)	N/A	87% (4.4%)	0.920 ± 0.003	10.6 ± 1.1	0.051 ± 0.002
Median subtraction	11.9% ± 1.0%	88% (3.3%)	0.921 ± 0.006	16.0 ± 1.7	0.051 ± 0.002
Regression-based bulk motion subtraction	9.6% ± 0.8%	85% (0.9%)	0.926 ± 0.003	19.7 ± 1.8	0.060 ± 0.001
p-value**	0.0034	0.0081	0.1783	<0.01	<0.01

^*Mean ± standard error.

^**Values correspond to the comparison between the two subtraction methods; n = 8.

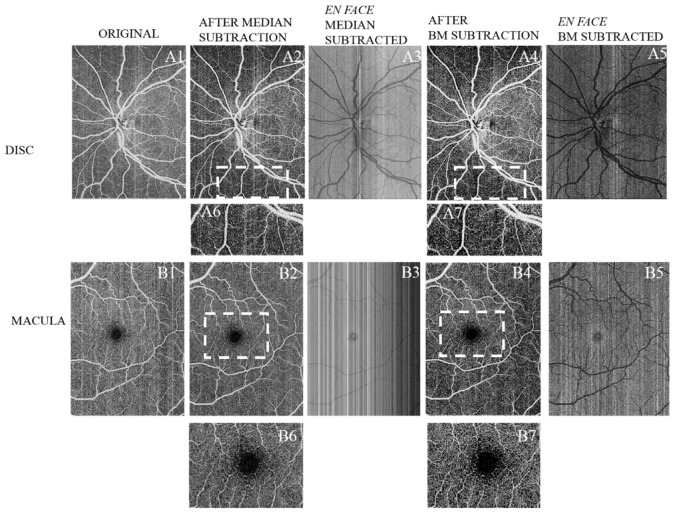
Fig. 8.

Qualitative comparison between median subtraction and regression-based bulk motion subtraction in an optic disc scan (A1-A7) and a macular scan (B1-B7).A1, B1 Unprocessed en face images. A2, B2 Scans after subtracting the median of the frame’s retinal region. A3, B3 are obtained by subtracting A1-A2 and B1-B2 respectively. A4, B4 Scans after regression-based bulk motion subtraction. A5, B5 are obtained by subtracting A1-A4 and B1-B4 respectively. A6 and A7 are close-ups of the 3.8mm × 1.7mm sections enclosed by dashed lines on A2 and A4 respectively.B6 and B7 are close-ups of the 3.4mm × 2.5mm sections enclosed by dashed lines on B2 and B4 respectively.

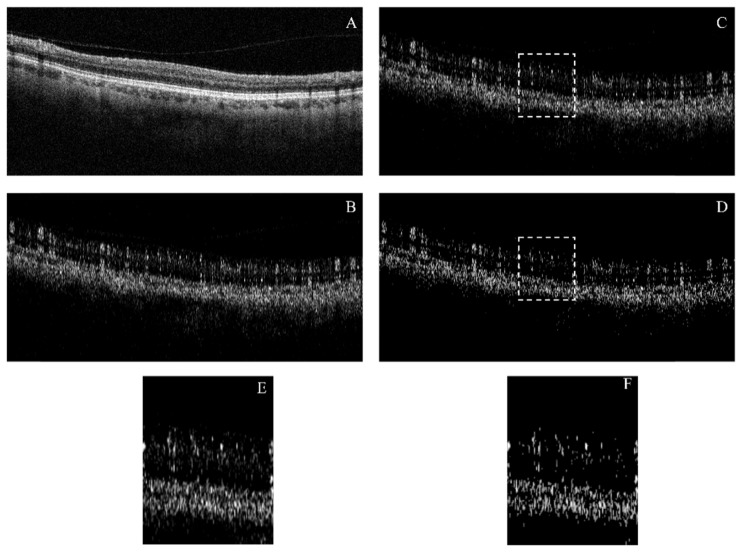
Fig. 9.

Qualitative comparison between two bulk motion subtraction algorithms applied to a non-microsaccadic B-frame with large contribution of bulk-motion. Projection artifacts are not corrected. A Reflectance image. B Unprocessed flow image. C Flow image after median subtraction. D Flow image after regression-based bulk motion subtraction. E and F are close-ups of the 1.3 mm B-scan sections enclosed by dashed lines in C and D respectively.

The pre-compensation performed by inter-B-scan registration could help improve the artifact removal efficiency of the bulk motion subtraction algorithm (Fig. 10(B) vs. Figure 10(D)). Addition of this step represented an average increase of 9 second of raw data processing per frame on CPU. Bright artifacts were reduced but not completely removed by inter-B-scan registration alone (Fig. 10C) and a background threshold was still necessary to identify vascular pixels. The pre-compensation could not remove the vessel density dependency on local reflectance by simple thresholding, while the regression-based thresholding proposed in this manuscript provided a correct spatial distribution of vascular pixels (Fig. 10(G) vs. Fig. 10(H)). Additionally, the background-capillary contrast of the resulting image was slightly degraded compared to the case where no displacements are implemented prior to SSADA (Figs. 10(E) vs. Fig. 10(F)).

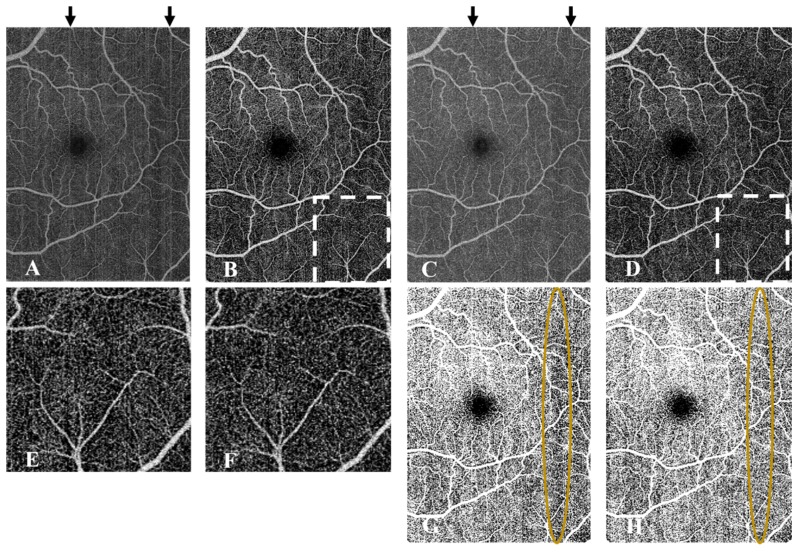
Fig. 10.

Investigation of the benefits of bulk motion pre-compensation by optimization of the bulk image shifts of the OCT images previous to OCTA processing by SSADA. A En face original OCTA without pre-compensation. B En face OCTA after regression-based bulk motion subtraction from the data set used in A. C Original en face non-thresholded OCTA after inter-B-scan registration. D Result of applying the regression-based bulk motion subtraction on the data set used for C. The residual artifacts still observed in B are better removed in D. E and F are close-ups of the regions enclosed by dashed lines in B and D respectively. Better capillary-background contrast was observed in E. G is a binary vessel mask obtained by imposing a fixed threshold on C while H is obtained by imposing a local regression-based threshold at each segment of a frame. Region enclosed shows that pre-compensation by inter-B-scan registration does not correct the vessel density dependence on local signal strength. Contrastingly, by a regression-based local thresholding a more homogeneous perfusion is identified for the whole scan in H.

4. Discussion

Currently, correction of bulk motion contribution to flow signal in SSADA is performed by a median subtraction algorithm that underestimates the real bulk motion background and ignores the saturation of decorrelation at vascular voxels. In this manuscript, we propose a new method to increase the accuracy of bulk motion subtraction, improving image quality and enhancing the repeatability of vessel density quantification while preserving vascular integrity. This could improve image interpretation by reducing bright line artifacts, and make quantification of vessel density more accurate. Moreover, unlike in the median subtraction algorithm, vascular recognition from background does not require referencing to an avascular region such as the FAZ, allowing computation of the vessel density on scans outside the macula such as the optic nerve head and anterior segment. Although this algorithm is demonstrated for SSADA, it can be potentially applied to other OCTA implementations such as speckle variance [20] and optical microangiography [3].

The algorithm is based on three main steps: (1) regression analysis of the background decorrelation vs. reflectance curves, (2) reflectance-dependent thresholding and (3) subtracting bulk motion velocity from the vascular voxels to retrieve bulk motion-free decorrelation values. Both the thresholding step and the estimation of$v_{BM}$rely on the accuracy of the linear regression routine, which assumes only background A-lines are selected. If voxels containing real flow signal were mistakenly chosen, they would contribute to larger flow signal at large reflectance voxels, overestimating the slope of the fitting curve. This would cause larger subtracted values, underestimation of the vessel density and degradation of the vascular integrity. We chose the first 10 percentile of A-lines with lower flow signal after removing the large vessel mask, given that the mean vessel density of macular scans did not exceed 90% for healthy subjects. This assumption underestimates the number of flow voxels. In optic disc scans, where some regions have a larger vessel density, the first five percentile of A-lines contained in the whole B-frame were selected. Averaging of voxel values in bins before regression analysis helped to minimize inaccuracies caused by occasional outliers.

Implementation of inter-B-scan registration prior to SSADA alone could not correct the disadvantages inherent to fixed thresholding. On the other hand, implementation of the regression-based algorithm alone was more successful in recognizing vasculature from background and did so in a shorter time. If inter B-scan registration could be optimized to preserve or improve capillary contrast, it can be a supplementary step to further improve the BM removal efficacy.

This algorithm uses information available in a single scan to remove bulk motion background and small-amplitude artifacts. However, given the high prevalence of microsaccadic artifacts in OCTA, it would not eliminate the need for registration of more scans [23] in a clinical scenario. Although commercial systems have adopted various forms of real-time tracking to prevent the recording of microsaccadic motion [28, 32], drifts between frames before and after microsaccades remain uncorrected, still necessitating registration of at least two volumes for truly artifact-free OCTA.

5. Conclusion

In summary, we have demonstrated a method that accurately subtracts bulk motion contribution to decorrelation of background and vascular voxels without affecting vascular integrity. The method recognizes the bulk motion decorrelation dependence on reflectance signal for background voxels; filters out background by a reflectance-dependent thresholding step, subtracts a bulk motion velocity value calculated by a nonlinear model that relates decorrelation and velocity, and finally retrieves the bulk motion-free decorrelation value. The regression-based bulk motion subtraction algorithm improved image quality, vessel density measurement repeatability and accuracy of bulk motion noise removal compared to an earlier median subtraction algorithm. Pre-compensation by OCT inter-B-scan registration before OCTA could improve the efficacy in removing visible artifacts at the cost of increased processing time and reduced capillary-background contrast. The regression-based algorithm takes into account the dependence of decorrelation on reflectance signal and hence, it shows potential to reduce the effect of signal strength on vessel identification. Furthermore, it can be used to identify flow voxels without the need for an avascular reference area. Finally, since it corrects flow signal on voxels of the three-dimensional OCTA data set, it might improve capillary flow index quantification accuracy and image quality on projection-resolved OCTA.

Funding

National Institutes of Health (NIH)(DP3 DK104397, R01 EY024544, R01 EY023285, P30 EY010572; Research to Prevent Blindness (New York, NY).