Abstract
Single-molecule-localization-based super-resolution microscopic technologies, such as stochastic optical reconstruction microscopy (STORM), require lengthy runtimes. Compressed sensing (CS) can partially overcome this inherent disadvantage, but its effect on super-resolution reconstruction has not been thoroughly examined. In CS, measurement matrices play more important roles than reconstruction algorithms. Larger measurement matrices have better restricted isometry properties (RIPs). This paper proposes, analyzes, and compares uses of higher resolution cameras and interpolation to achieve better outcomes. Statistical results demonstrate that super-resolution reconstructions is significantly improved by interpolating low-resolution STORM raw images and using point-spread-function-based measurement matrices with better RIPs. The analysis of publically accessible experimental data confirms this conclusion.
OCIS codes: (170.2520) Fluorescence microscopy, (100.6640) Superresolution, (100.3010) Image reconstruction techniques
1. Introduction
Optical microscopic techniques have played significant roles as tools for conducting cell studies. In recent years, developments in some microscopic techniques have broken the diffraction limit. These developments include reversible saturable optical linear fluorescence transitions (RESOLFT) [1], saturated structured illumination microscopy [2], stochastic optical reconstruction microscopy (STORM) [3,4], and (fluorescence) photoactivated localization microscopy ((f)PALM) [5–9]. Both STORM and (f)PALM are based on the imaging of sparsely distributed molecules and single-molecule localizations (SMLs). In these SML-based microscopic techniques, only a portion of the sparsely distributed molecules is imaged and localized in each raw image. Each final super-resolution image requires thousands of raw images [3,9,10]. Therefore, if more molecules can be identified and localized in each captured image, fewer raw images would be needed to generate the final super-resolution image. However, in these conventional localization methods, the diffraction limit restricted the maximum density of fluorescent molecules in a raw image. Some recently developed approaches have increased this density limitation. These approaches include the Dominion Astrophysical Observatory stochastic optical reconstruction microscopy [11], the structured sparse model and Bayesian information criterion [12], and compressed sensing (CS) in two dimensions (2D) [13,14] and three dimensions (3D) [12,15,16]. Among these methods, CS can increase the maximum density of fluorescent molecules in a raw image, even if these fluorophores are not distributed so sparsely that their images overlap with one another. Moreover, CS offers many other advantages, such as quick and simple image acquisition and reconstruction, simple management of images, and high temporal and spatial resolution.
To take full advantage of CS in SML-based microscopic techniques, one critical factor, namely, the restricted isometry property (RIP) of the CS measurement matrix based on the point-spread function (PSF), must be considered. However, the RIP of the PSF-based measurement matrix in previous CS-based methods [13,14] is not ideal for CS. Thus, the performance of CS was affected when it was applied to the image reconstruction of molecules with high density. A random matrix with a good RIP has been studied extensively in CS [17]. However, research on PSF-based measurement matrices is seldom reported. Currently, research on super-resolution imaging based on CS is more focused on specific applications and experiments, reconstruction algorithms in 2D [13] and 3D [16,18,19], and improvements to algorithm calculation speeds [14,20]. In the present paper, we propose a new processing method that uses interpolation and a PSF-based measurement matrix with lower coherence to yield a better RIP. Simulations and experimental results demonstrate that, compared to the CS method without interpolation or using a measurement matrix with higher coherence, the reconstruction results obtained using the proposed method are markedly better.
2. Compressed sensing and super-resolution microscopic imaging
The theory of CS asserts that if a signal x is sparse and the measurement matrix Φ satisfies the RIP, the signal x can be reconstructed exactly or approximately with high probability by solving
| (1) |
where , y denotes the measurement data, , Φ is the measurement matrix, , M < N, is the objective function, and y = Φx is the constraint function. Compared with the Nyquist–Shannon sampling theorem, CS requires fewer measurement data [21–23]. If the objective function is rather than , Eq. (1) is transformed to a convex optimization problem [24]. Super-resolution images can be treated as signals as well.
Both better reconstruction algorithms [17] and better measurement matrices [25] can improve reconstruction results. When a measurement matrix has a good RIP, its columns and rows have good incoherence, its row and column norms are approximately equal, and the elements of columns and rows are random to a certain degree. The incoherence of columns plays a leading role in the RIP of the measurement matrix [25–29]. Existing research results indicate that a measurement matrix with good column incoherence can improve the reconstruction results of various reconstruction algorithms. However, lower-quality measurement matrices would lead to worse reconstruction results no matter which reconstruction algorithm was used.
The PSF is the light-intensity distribution function at work in the image plane when light from an infinitely small point object passes through an optical system, such as a microscope [30]. The imaging process of the optical system is the convolution of the object function and PSF. The one-dimensional vectors y and x consist of row-wise concatenations of the raw and super-resolution images, respectively. The measurement matrix Φ is determined by the PSF of the imaging system. The ith column of Φ corresponds to the acquired raw image only if one molecule emits fluoroscopic photons at the position index i of x [13].
The final super-resolution image can be reconstructed using CVX, a Matlab optimization package [31], with Eq. (1) in which the objective function is . Thus, more fluorescent molecules can be activated simultaneously in real experiments compared to conventional STORM, and the requirements of sparse excitation and time-consuming imaging in conventional STORM can be avoided. Moreover, the number of acquired frames can be reduced [13]. Higher spatial and temporal resolution as well as greater acquisition and reconstruction efficiency of raw images are possible.
Equation (1) is suitable for noiseless situations. If a raw image contains background noise, this equation should be replaced by Eq. (2). If there is background noise in a raw image, better reconstruction results can be acquired by adding a noise-related column vector in the measurement matrix Φ. All elements in the noise-related column vector are set to 1. Correspondingly, one additional element is introduced in x. The corresponding element in c is set to 0. The value of this extra element in x represents a uniform image background with no sparsity constraint imposed on it [13]. Thus,
| (2) |
where the weight vector c is introduced to account for the differing contributions to the raw image from one single fluorescent molecule at different locations. The value of the ith element in c equals the summation of the ith column of Φ. The minimization term cTx is equivalent to a weighted L1 norm of x because x is non-negative [13]. In addition, ε is set to 1.5 as the universal setting for this study’s analyses of simulated and real data, as modeled in Ref [13].
3. Point-spread-function-based measurement matrix and relational analysis
The microscope used in Ref [13] was a Nikon Plan Apo VC. STORM raw images were recorded using an electron-multiplying charge-coupled device (EMCCD) camera (iXon DV897DCS-BV, Andor Technology Ltd., Belfast, Northern Ireland) with a 16-µm pixel size. Each pixel was divided into an 8 × 8 grid to support the acquisition of super-resolution images. A super-resolution image of 64 × 64 grids was reconstructed with the CVX optimization package [31] from a raw image of 7 × 7 pixels aligned with the central region of the 64 × 64 grids. The measurement matrix was ΦLR, and its size was 49 × 4096 because 49 = 7 × 7 and 4096 = 64 × 64. When the STORM raw image was recorded with a high-resolution EMCCD camera (FA285-CL, Raptor Photonics, Larne, Northern Ireland) with an 8-µm pixel size or was interpolated, the corresponding measurement matrix was ΦLI_HR in which the size was 169 × 4096, where 169 = 13 × 13. If the resolution of the EMCCD camera were to be doubled again, the corresponding measurement matrix would be ΦHI in which the size was 625 × 4096, where 625 = 25 × 25.
Our simulation and real experiment were based on data obtained from the EPFL website [32]. The full width at half maximum (FWHM) of the PSF in the EPFL website was 258.2 nm, and the effective pixel size of ΦLR was 100 nm. This paper’s code, experimental conditions, and parameters match those in Ref [13]. The only differences are in the variations of measurement matrices (ΦLI_HR and ΦHI), effective pixel size, and FWHM. All elements of the noise-related column vectors of ΦLI_HR and ΦHI are 1/4 and 1/16, respectively. ΦLR, ΦLI_HR, and ΦHI have 4097 real columns because a noise-related column was added. All detailed parameters are listed in Table 1. The grid sizes corresponding to ΦLR, ΦLI_HR, and ΦHI are 12.5nm. The super-resolution image sizes corresponding to ΦLR, ΦLI_HR, and ΦHI are 64 × 64 grids. The raw image sizes corresponding to ΦLR, ΦLI_HR, and ΦHI are 7 × 7, 13 × 13 and 25 × 25 pixels, respectively. The effective pixel sizes corresponding to ΦLR, ΦLI_HR, and ΦHI are 100, 50 and 25nm, respectively. The measurement matrix sizes (without the noise-related column) corresponding to ΦLR, ΦLI_HR, and ΦHI are 49 × 4096, 169 × 4096 and 625 × 4096, respectively.
Table 1. Parameters of Three Measurement Matrices, Raw Images and Super-resolution Images.
| ΦLR | ΦLI_HR | ΦHI | |
|---|---|---|---|
| |μmax| | 0.999561 | 0.999394 | 0.999382 |
| Measurement matrix size (without the noise-related column) |
49 × 4096 | 169 × 4096 | 625 × 4096 |
| Elements of the noise-related column | 1 | 1/4 | 1/16 |
| Raw image size | 7 × 7 | 13 × 13 | 25 × 25 |
| Effective pixel size (nm) | 100 | 50 | 25 |
| Super-resolution image size | 64 × 64 | 64 × 64 | 64 × 64 |
| Grid size (nm) | 12.5 | 12.5 | 12.5 |
CS theory implies that different measurement matrices have different RIPs. The measurement matrices ΦLR, ΦLI_HR, and ΦHI based on the EMCCD cameras of three different resolutions are studied here.
The column incoherence of ΦHI is the best, that of ΦLI_HR follows, and that of ΦLR is the worst, as listed in Table 1. The |μmax| of ΦLI_HR is less than that of ΦLR by 0.000167, and the |μmax| of ΦHI is less than that of ΦLI_HR by 0.000012. Therefore, according to CS theory, each of the reconstruction effects of ΦLR, ΦLI_HR, and ΦHI, in turn, should be better than the effect preceding it in that ranked order.
Because of the high column coherence of the PSF-based measurement matrix ΦLR, its RIP is the worst. Hence, the reconstruction results based on ΦLR are not optimal. If a high-resolution or super-high-resolution EMCCD camera was used, a better reconstruction effect could be expected. Therefore, we used the bicubic interpolation method with the high-resolution and low-resolution STORM raw images based on ΦLI_HR and ΦLR, respectively, to simulate super-high-resolution and high-resolution STORM raw images based on ΦHI and ΦLI_HR. Then, the reconstruction effects were compared to validate this method experimentally. Because interpolation processing correspondingly increased the number of photons in the STORM raw images artificially, normalized processing was used to keep the number of photons unchanged in the STORM raw images.
4. Comparison and analysis of reconstructed results based on different measurement matrices
Figure 1 presents comparable results from four different situations: low resolution (LR), high resolution (HR), low interpolation (LI), and high interpolation (HI). The LR and HR results represent cases in which the STORM raw images were acquired using low-resolution and high-resolution EMCCD cameras, respectively, and reconstructed using the CVX package based on ΦLR and ΦLI_HR, respectively. The LI and HI results represent cases in which the raw STORM images were acquired with the same low-resolution and high-resolution EMCCD cameras used to obtain the LR and HR results, respectively, and interpolated and reconstructed using the CVX package based on ΦLI_HR and ΦHI.
Fig. 1.
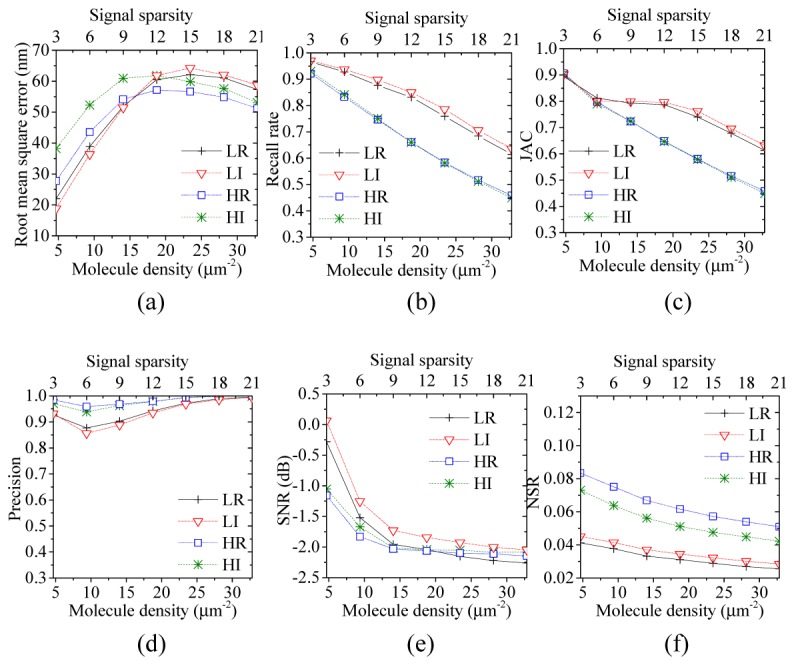
STORM image simulation analysis for LR, LI, HR, and HI based on CS and EPFL website data. The x axes represent molecule density and signal sparsity. (a) Comparison of measures of localization precision. (b) Comparison of recall rates. (c) Comparison of the JAC values. (d) Comparison of precision measures. (e) Comparison of SNRs. (f) Comparison of NSRs.
In CS, sparsity, defined as the number of fluorescence molecules, is used more often than molecule density because sparsity is related to the size of the measurement matrix. Sparsity is convenient for judging the reconstruction effect in CS. Hence, in Fig. 1, the x axis represents both molecule density and signal sparsity, and the y axes of Figs. 1(a) through 1(f) represent root-mean-square error (hereafter called localization precision), recall rate, precision, Jaccard index (JAC), SNR, and noise-to-signal ratio (NSR), respectively.
The signal x is a sparse signal of the fluorescent molecules that follows the log–normal distribution (peak (i.e. the single-molecule photon counts which corresponds to the peak of probability density function of the log-normal distribution): 3000; mean: 3896; standard deviation: 1700) [13]. The fluorescence signals of different molecule densities were tested 500 times. For each simulation, we created a sample consisting of point-like emitters distributed both uniformly and randomly. STORM raw images with Poisson noise and background noise were simulated. The background was 70 and 18 photons per pixel for LR and HR, respectively. Then, the mean of the results for each density was calculated and plotted, as shown in Fig. 1. The reconstruction algorithm used in Ref [13], CVX, was employed here.
In STORM, the raw image has a linear and shift-invariant relationship with the true molecule distribution. To model this relationship as in Eq. (2), a discrete grid is introduced to describe the molecule positions instead of using a list of molecule coordinates which is typically done to represent super-resolution images. The grid spacing (one-eighth the pixel size) is kept much smaller than the raw pixel size to ensure sufficient accuracy. In Eq. (2), both the raw image y, and the super-resolution image x are pixelated images. Unlike the single-molecule fitting method, compressed sensing algorithm does not directly return a list of molecule coordinates. Instead, it returns a pixelated super-resolution image. Hence, we convert the compressed sensing results into a list of molecule positions by identifying clusters of nonzero grid points, treating a group of adjacent nonzero grids as one identified molecule and calculating its ‘position’ from the center of mass [13].
Statistical measures of detection rates and localization precision were established by finding a pairing between the localized molecules and ground-truth molecules [33]. The nearest-neighbor search method was misleading if two ground-truth molecules were within the FWHM of the PSF. Hence, the Hungarian matching algorithm was used for detecting and matching molecules [34].
Each localized molecule that successfully paired with a ground-truth molecule was categorized as a true positive (TP). The remaining unpaired localized molecules were farther than the FWHM, and they were assigned to the category of false positive (FP). The remaining ground-truth molecules not associated with any localized molecule received the category designation of false negative (FN). The detection rate involves the sensitivity (recall rate r), positive predictive value (precision p), and JAC [34]. Thus,
| (3) |
Then, the formula for SNR is [34]
| (4) |
where x is a real signal, ; is the norm, in general, of a vector; and denotes the reconstruction result of x.
The reconstruction results of CS methods include not only the detection rate and localization precision but also the gray intensity, that is, the photon counts, of super-resolution images. SNR indicates the overall quality of the reconstructed image. The SNR of the super-resolution image can be considered definitively better only if its detection rate, localization precision, and gray intensity are all improved. If only one factor shows improvement, the SNR may be better or worse. The SNR in CS is a better evaluation parameter than localization precision, r, p, and JAC. In contrast, gray-intensity information of super-resolution images in SML fields has either been discussed only briefly or been neglected [13,16,18]. Previous reports on SML fields describe in detail only the detection rate and localization precision.
4.1 Comparison and analysis of reconstructed results based on the signal-to-noise ratio
CS theory indicates that higher-quality measurement matrices can lead to better reconstruction results that are evaluated mainly by SNR. However, noise can lead to lower-quality reconstruction results. Noise includes Poisson noise, background noise, and interpolation error if the raw image is interpolated. Because background noise is assumed to be uniform, and a noise-related column is added to the measurement matrix in Eq. (2), background noise cannot be regarded as noise. Thus, Fig. 1(f) depicts the noise-signal ratio (NSR) curves that originate from the expression
| (5) |
Here, in the LR and HR cases, the values of y are the real measurement data with background noise, and ynoi denotes the measurement data with both Poisson and background noise. In contrast, for the LI and HI cases, y denotes the real measurement data with background noise obtained with a higher-resolution camera compared to that used for obtaining ynoi, which denotes the measurement data with Poisson noise, background noise, and interpolation error.
As Table 1 indicates, the measurement matrix ΦLI_HR of LI shows much higher-quality than does ΦLR. At the same time, the NSR of LR and LI are both similar and close, as shown in Fig. 1(f). Thus, the overall SNR of LI is much better than the SNR of LR, as Fig. 1(e) shows. The values of NSR of HR are much higher than the NSR of LI in Fig. 1(f), while the measurement matrices of LI and HR are the same, namely ΦLI_HR. Thus, the SNR of HR is lower than that of LI, as shown in Fig. 1(e). The measurement matrix ΦHI of HI is slightly better than ΦHI, while the values of NSR of HI are lower than those of NSR of HR, as Fig. 1(f) shows. Thus, the SNR of HI is better than that of HR. These experimental results demonstrate that higher-quality measurement matrices and lower noise can lead to better reconstruction results. The obtained results demonstrate that LI and HI are better than LR and HR.
In Fig. 1(f), the overall NSR of HI is lower than that of HR, while the NSR of LI is higher than that of LR. These results are reasonable. After interpolation, new pixels are generated. The ratio of new to old pixels is approximately 2.5. The line segment of the Gaussian PSF between two old, adjacent pixels is closer to a straight line in a high-resolution raw image and is a curve in a low-resolution raw image. Some of the interpolated pixels (that is, new pixels) are very close to their true values in the positions in a high-resolution raw image where one of the two old, adjacent pixels contains positive noise (that is, the value of noise is positive) and the other contains negative noise (that is, the value of noise is negative). Thus, the NSR of HI is lower than that of HR. However, such cases rarely occur because the line segment of the Gaussian PSF between two old, adjacent pixels is a curve in a low-resolution raw image. Interpolation, in this circumstance, would lead to additional errors. Thus, the NSR of LI is higher than that of LR.
4.2 Comparison and analysis of reconstructed results based on detection rate and localization precision
Better SNRs of reconstruction results for CS do not imply better detection rates and localization precision for STORM. The SNR indicates the overall quality of the reconstruction image. The improvement of SNR alone does not imply improved localization precision.
Although the precision of HR and HI are higher than that of LR and LI, as shown in Fig. 1(d), the recall rates of LR and LI are higher than those of HR and HI, as shown in Fig. 1(b). The recall rates of HR and HI are almost the same. JAC is more objective and comprehensive indicator than precision and recall rate. The JACs of LR and LI are higher than those of HR and HI. As shown in Fig. 1(a), the curves of HI, HR, LR, and LI intersect at the point where the molecule density is approximately 17 μm−2. This result means that the measures of localization precision of HI, HR, LR, and LI are better in turn before this cross point. As shown in Fig. 1(b), the recall rates of HI, HR, LI, and LR after that point are very low. A discussion of the reconstruction results with such a low recall rate would be meaningless. Some of the curves in Fig. 1 are very close. In order to provide a more quantitative description, all the results and errors (i.e. standard deviation) of LR and LI before this cross point are presented in Table 2. There are three sets of data at three different molecule densities, 4.69 μm−2, 9.38 μm−2, and 14.06 μm−2. The average of the three recall rates of LI is 0.01 higher than that of LR. In addition, the JACs of LI and LR are almost the same.
Table 2. Simulation Analysis Results for LR and LI from Fig. 1.
| LR | LI | LR | LI | LR | LI | ||
|---|---|---|---|---|---|---|---|
| Molecule density (μm−2) |
4.69 | 9.38 | 14.06 | ||||
|
| |||||||
| Localization precision /Error (nm) |
21.99/3.76 | 18.86/3.2 | 38.92/7.78 | 36.4/7.01 | 51.89/9.79 | 51.49/9.38 | |
| Recall rate/Error | 0.97/0.03 | 0.97/0.02 | 0.93/0.03 | 0.94/0.02 | 0.88/0.03 | 0.90/0.02 | |
| Precision/Error | 0.93/0.03 | 0.93/0.03 | 0.88/0.03 | 0.86/0.03 | 0.90/0.03 | 0.89/0.03 | |
| JAC/Error | 0.89/0.04 | 0.90/0.04 | 0.81/0.03 | 0.80/0.03 | 0.79/0.03 | 0.80/0.03 | |
| SNR/Error (dB) | −0.28/0.56 | 0.06/0.42 | −1.52/0.24 | −1.26/0.3 | −2.0/0.16 | −1.73/0.26 | |
As is shown in Table 2, the average localization precision of LI is 2.02 nm better than that of LR, and the average SNR of LI is 0.29 dB better than that of LR. Higher SNR implies better image reconstruction quality. For example, the gray intensities of fluorescent molecules are closer to their true gray intensities (i.e., the photon counts). In general, the reconstruction result of LI is much better than that of LR and is the best for CS and SML before approximately 17 μm−2.
5. Simulated results of an observation and reconstruction
Figure 2 shows the simulated results of an observation and reconstruction. Figures 2(a) to 2(e) correspond to Figs. 2(f) to 2(j) and depict the results after taking the logarithms of Figs. 2(f) to 2(j) based on real data. This approach, a frequently used data possessing method in vibration mechanics [35] and digital image processing [36], provides easily performed checks and observations of data. Moreover, it preserves the relative scale of data. A comparison of Figs. 2(a) and 2(f) reveals that, within the areas highlighted by red ellipses, the white spots of Fig. 2(a) are clearer than those in Fig. 2(f). In addition, the brightnesses values of all white spots in Figs. 2(a) through 2(e) are different.
Fig. 2.
STORM image simulation analysis using CS to demonstrate its capability for identifying molecules efficiently at high densities. The scale bar in (e) is 200 nm. (a) The reconstructed result of an LR raw image. (b) The reconstructed result of an LI raw image. (c) The reconstructed result of an HR raw image. (d) The reconstructed result of an HI raw image. (e) True positions of six molecules. In (a)–(e), results were obtained after taking the logarithm of (f)–(j) based on real data. Thus, (f)–(j) correspond to (a)–(e). (k) A low-resolution raw image of STORM. The grid size of (a)–(j) equals 1/8 pixel of (k). (l) An interpolated low-resolution raw image of STORM. (m) A high-resolution raw image of STORM. (n) An interpolated high-resolution raw image of STORM.
Figure 2(e) shows the true positions and gray intensities of six molecules, where the molecule density is 9.37 μm−2. Figure 2(k) shows a simulated low-resolution STORM raw image of the same six molecules acquired with a low-resolution EMCCD camera based on the matrix ΦLR. Figure 2(m) is a simulated high-resolution STORM image of the same six molecules generated with a high-resolution EMCCD camera based on the matrix ΦLI_HR. Figure 2 (l) is an interpolated image of Fig. 2(k). Finally, Fig. 2(n) is an interpolated image of Fig. 2(m).
Figure 2(a) is the image reconstructed based on ΦLR and CVX. For this image, the SNR is −1.81 dB, and the localization precision is 43.18 nm. Figure 2(b) shows the image reconstructed based on ΦLI_HR and the interpolated image in Fig. 2(l). In this case, the SNR is −1.12 dB, and the localization precision is 28.48 nm. Figure 2(c) shows the image reconstructed based on ΦLI_HR and Fig. 2(m). Figure 2(d) shows the image reconstructed based on ΦHI and the interpolated image in Fig. 2(n). The red crosses in Figs. 2 (a) through 2(d) and Figs. 2(f) through 2(i) represent the true positions of the fluorescent molecules.
When we examined the results, we noticed that while four white spots appeared in the high-resolution STORM image in Fig. 2(c), there were at least six white spots in Figs. 2(a) and 2(b). The recall rate of Fig. 2(c) was worse than in Figs. 2(a) and 2(b). Although the SNR of Fig. 2(c) was higher than the SNR of Fig. 2(d), only a portion of the molecules was detected.
On comparing the results shown within the circles and rectangles in Figs. 2(a) and 2(b), we noticed that the fluorescent molecule was split into multiple white spots in the low-resolution STORM image in Fig. 2(a). In contrast, the white spots representing the same molecule in the interpolated low-resolution STORM image in Fig. 2(b) were closer each other. Thus, the localization precision of the interpolated low-resolution image is better than that of the low-resolution image. The localization precision and reconstruction quality of the interpolated low-resolution image in Fig. 2(b) are better than the reconstruction result of the low-resolution image in Fig. 2(a). The simulated results demonstrate that image reconstruction quality and localization precision can be improved greatly by using interpolated low-resolution STORM raw images.
6. Experimental data analysis
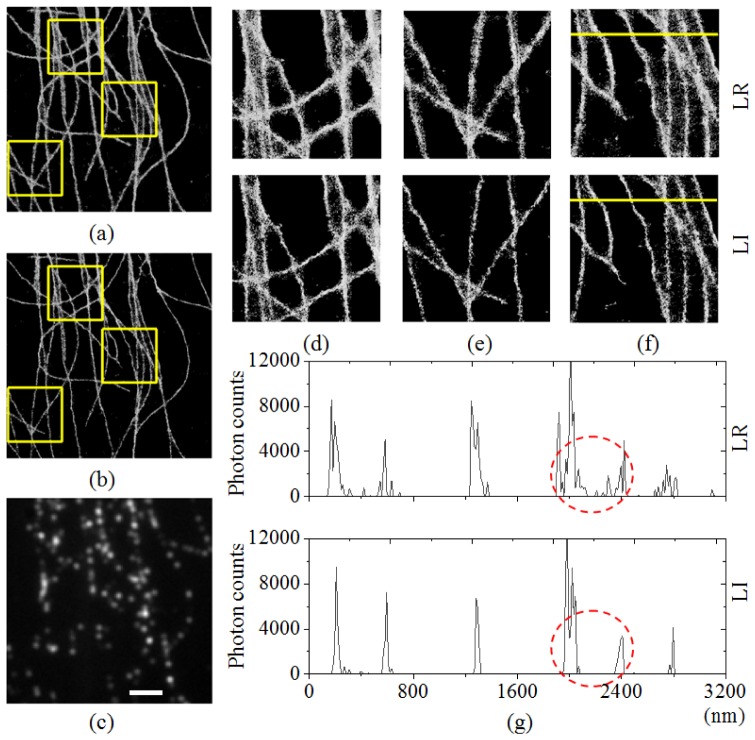
We used a publicly accessible data set from the EPFL website [32] to support the evaluation of the quality of 2D image reconstruction using LR and LI. The Tubulins high-density data set comprises 500 raw images of 128 × 128 pixels. The performances of LI and LR are compared in Fig. 3. The super-resolution image reconstructed using LI (Fig. 3(b)) was sharper than that reconstructed using LR (Fig. 3(a)). This distinction is apparent in the regions indicated by the yellow squares in Figs. 3(a) and 3(b) and enlarged in Figs. 3(d) through 3(f). A further evaluation of LI was performed by plotting and comparing photon profiles along the yellow line segments in Fig. 3(g).
Fig. 3.
Comparison of LR and LI based on experimental 2D high-density data (500 raw images) from the EPFL website. The yellow squares in (a) and (b) are 3200 × 3200 nm, and the scale bar in (c) indicates 2000 nm. (a) A reconstructed result of LR. (b) A reconstructed result of LI. (c) A frame of a raw STORM images. (d) Enlarged LR and LI images from the top areas marked by yellow squares in (a) and (b), respectively. (e) Enlarged LR and LI images from the middle areas marked by yellow squares in (a) and (b), respectively. (e) Enlarged LR and LI images from the bottom areas marked by yellow squares in (a) and (b), respectively. (g) Plots of photon-count profiles obtained by measurements made along the yellow lines in (f).
Six microtubules can be resolved in both the LI and LR images, as shown in Fig. 3(f). However, LI is clearly better, as shown in Fig. 3(g), because no photons should appear between adjacent microtubules. In the LI image, photons are hardly detectable at the positions between the first two microtubules or between the fourth and fifth tubules. LI offers better estimations of distances between microtubules and shows fewer spurious and noisy peaks compared to LR, as shown in the two red circles in Fig. 3(g). This observation and conclusion are consistent with the expectations from the results of simulations.
Figures 3(c) and 3(g) present the results of real data rendered in Matlab using the imshow and plot functions. Figures 3(a) and (b) and Figs. 3(d) through 3(f) show the results after taking the logarithms of the corresponding real data, a reliable and time-tested data-possessing method. When such processing is absent, a black and vague image will result.
7. Theoretical limit analysis and discussion
This section presents a discussion of the theoretical limits of this method. An important factor is the column incoherence of the measurement matrix. As Table 1 indicates, measurement matrices using higher-resolution cameras generally have better column incoherence. However, this trend is not always the case. As is well known, if the camera resolution is sufficiently high, the maximum values |μmax| of the coherence coefficients between the columns of the measurement matrices will be approximately 1. Thus, a higher resolution camera based on a certain microscope will not always improve the column incoherence of the measurement matrix. At some point, further improvement is impossible.
Poisson noise is related to the number of photons received by a camera pixel. Larger pixels can receive more photons. Poisson noise is reduced when the pixel size is increased. Thus, the NSR of HR is much higher than that of LR, as Fig. 1(f) illustrates. Noise is another factor that prevents higher-resolution cameras from being used in SML-based microscopic techniques in CS.
We gained insight into the computational complexity of this method by measuring and comparing the execution times for LR, LI, HR, and HI using the simulation data depicted in Fig. 1 and the experimental data used in Fig. 3. This analysis was performed using a stand-alone installation of Matlab running on a standard PC with an Intel Core i5-4440 3.1 GHz CPU and an AMD Radeon HD 8500M Series GPU. Data processing was performed in four parallel threads (one per CPU core). The mean execution time for HI was 72.73 times that for LR. The mean execution time for LI was 6.84 times that for LR. Reconstructing a high-density STORM raw image of 8 × 8 pixels with a sparsity of 21, based on the simulation data sets, required mean execution times of 1.43 s, 9.79 s, and 102.59 s for LR, LI, and HI, respectively. The mean execution times of LI and HR were almost equal because they employed identical 169 × 4096 measurement matrices and because execution runtimes mainly depend on the matrix size.
Although the |μmax| of ΦHI in Table 1 is better than the |μmax| of ΦLI_HR, HI and HR are worse than LI in localization precision, as shown in Fig. 1. Moreover, the computation cost for HI increased 10.6 times those for HR and LI. Thus, a high-resolution camera is not an optimal choice for working with data obtained from the EPFL website.
8. Conclusion
This paper proposed a method based on low-resolution raw images, interpolation, and PSF-based measurement matrices with higher incoherent coefficients to improve the performance of CS in STORM. The implementation of this method involves several steps. First, low-resolution microscopic STORM raw images were obtained with a low-resolution EMCCD camera. Then, the low-resolution STORM raw images were interpolated using CVX in Matlab to reconstruct the super-resolution image with better measurement matrices. The method can improve not only the localization precision and detection rate but also the overall reconstructed-image quality as measured by SNR.
Improvements to the incoherent coefficients of measurement matrices are the fundamental reason for the better reconstruction results obtained with interpolation. The incoherent coefficient of a measurement matrix tends to reach its peak and then decrease with increase in the raw-image resolution. Although the use of higher-resolution cameras is one possible way to increase the raw-image resolution, such cameras are unavailable at times. We can reach the same aim by means of optical magnification (e.g. zoom lens). However, the field of view will shrink accordingly. And only a part of the image can be seen. Furthermore, the small pixels of a high-resolution camera can lead to more Poisson noise because EMCCD units will receive few photons per pixel. Interpolation is easier to be implemented than using a higher-resolution camera or optical magnification because it 's a post-processing method.
It should be noted that computation costs increase exponentially with increase in the measurement matrix size. For a certain application, three factors, namely the RIP of the measurement matrix, noise, and computation cost, should be balanced and optimized. The method we proposed here uses a low-resolution camera to achieve better reconstruction effects compared to those provided by a higher-resolution camera. The quantity of acquired data needed to implement the proposed interpolation-based methods is only approximately 25% of the data needed for methods that utilize higher-resolution cameras. Moreover, our method simplifies experimental conditions and reduces experimental costs.
Funding
National Natural Science Foundation of China (61335001, 61235012, 61378091, 81660296, 41461082); Specially Funded Program on National Key Scientific Instruments and Equipment Development (2012YQ15009203); Guangdong Natural Science Foundation research team project (2014A030312008); Shenzhen Science and Technology Planning Project (JCYJ20150324141711698, JCYJ20160308104404452); Major National Basic Research Program of China (973) (2015CB352005); China Postdoctoral Science Foundation (2016M592525).
References and links
- 1.Hofmann M., Eggeling C., Jakobs S., Hell S. W., “Breaking the diffraction barrier in fluorescence microscopy at low light intensities by using reversibly photoswitchable proteins,” Proc. Natl. Acad. Sci. U.S.A. 102(49), 17565–17569 (2005). 10.1073/pnas.0506010102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Heintzmann R., Jovin T. M., Cremer C., “Saturated patterned excitation microscopy--a concept for optical resolution improvement,” J. Opt. Soc. Am. A 19(8), 1599–1609 (2002). 10.1364/JOSAA.19.001599 [DOI] [PubMed] [Google Scholar]
- 3.Rust M. J., Bates M., Zhuang X., “Sub-diffraction-limit imaging by stochastic optical reconstruction microscopy (STORM),” Nat. Methods 3(10), 793–796 (2006). 10.1038/nmeth929 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Min J., Vonesch C., Kirshner H., Carlini L., Olivier N., Holden S., Manley S., Ye J. C., Unser M., “FALCON: fast and unbiased reconstruction of high-density super-resolution microscopy data,” Sci. Rep. 4, 4577 (2014). 10.1038/srep04577 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Hess S. T., Girirajan T. P., Mason M. D., “Ultra-high resolution imaging by fluorescence photoactivation localization microscopy,” Biophys. J. 91(11), 4258–4272 (2006). 10.1529/biophysj.106.091116 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Cox S., Rosten E., Monypenny J., Jovanovic-Talisman T., Burnette D. T., Lippincott-Schwartz J., Jones G. E., Heintzmann R., “Bayesian localization microscopy reveals nanoscale podosome dynamics,” Nat. Methods 9(2), 195–200 (2011). 10.1038/nmeth.1812 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Burnette D. T., Sengupta P., Dai Y., Lippincott-Schwartz J., Kachar B., “Bleaching/blinking assisted localization microscopy for superresolution imaging using standard fluorescent molecules,” Proc. Natl. Acad. Sci. U.S.A. 108(52), 21081–21086 (2011). 10.1073/pnas.1117430109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mukamel E. A., Babcock H., Zhuang X., “Statistical deconvolution for superresolution fluorescence microscopy,” Biophys. J. 102(10), 2391–2400 (2012). 10.1016/j.bpj.2012.03.070 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Betzig E., Patterson G. H., Sougrat R., Lindwasser O. W., Olenych S., Bonifacino J. S., Davidson M. W., Lippincott-Schwartz J., Hess H. F., “Imaging intracellular fluorescent proteins at nanometer resolution,” Science 313(5793), 1642–1645 (2006). 10.1126/science.1127344 [DOI] [PubMed] [Google Scholar]
- 10.Min J., Holden S. J., Carlini L., Unser M., Manley S., Ye J. C., “3D high-density localization microscopy using hybrid astigmatic/ biplane imaging and sparse image reconstruction,” Biomed. Opt. Express 5(11), 3935–3948 (2014). 10.1364/BOE.5.003935 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Holden S. J., Uphoff S., Kapanidis A. N., “DAOSTORM: an algorithm for high- density super-resolution microscopy,” Nat. Methods 8(4), 279–280 (2011). 10.1038/nmeth0411-279 [DOI] [PubMed] [Google Scholar]
- 12.Quan T., Zhu H., Liu X., Liu Y., Ding J., Zeng S., Huang Z.-L., “High-density localization of active molecules using Structured Sparse Model and Bayesian Information Criterion,” Opt. Express 19(18), 16963–16974 (2011). 10.1364/OE.19.016963 [DOI] [PubMed] [Google Scholar]
- 13.Zhu L., Zhang W., Elnatan D., Huang B., “Faster STORM using compressed sensing,” Nat. Methods 9(7), 721–723 (2012). 10.1038/nmeth.1978 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Babcock H. P., Moffitt J. R., Cao Y., Zhuang X., “Fast compressed sensing analysis for super-resolution imaging using L1-homotopy,” Opt. Express 21(23), 28583–28596 (2013). 10.1364/OE.21.028583 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Zhang S., Chen D., Niu H., “3D localization of high particle density images using sparse recovery,” Appl. Opt. 54(26), 7859–7864 (2015). 10.1364/AO.54.007859 [DOI] [PubMed] [Google Scholar]
- 16.Ovesný M., Křížek P., Švindrych Z., Hagen G. M., “High density 3D localization microscopy using sparse support recovery,” Opt. Express 22(25), 31263–31276 (2014). 10.1364/OE.22.031263 [DOI] [PubMed] [Google Scholar]
- 17.Wei D., Milenkovic O., “Subspace pursuit for compressive sensing signal reconstruction,” IEEE Trans. Inf. Theory 55(5), 2230–2249 (2009). 10.1109/TIT.2009.2016006 [DOI] [Google Scholar]
- 18.Gu L., Sheng Y., Chen Y., Chang H., Zhang Y., Lv P., Ji W., Xu T., “High-density 3D single molecular analysis based on compressed sensing,” Biophys. J. 106(11), 2443–2449 (2014). 10.1016/j.bpj.2014.04.021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Huang J., Sun M., Chi Y., “Super-resolution image reconstruction for high-density 3D single-molecule microscopy,” in IEEE International Symposium on Biomedical Imaging, (IEEE, 2016), 241–244. 10.1109/ISBI.2016.7493254 [DOI] [Google Scholar]
- 20.Huang J., Gumpper K., Chi Y., Sun M., Ma J., “Fast two-dimensional super-resolution image reconstruction algorithm for ultra-high emitter density,” Opt. Lett. 40(13), 2989–2992 (2015). 10.1364/OL.40.002989 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Donoho D. L., “Compressed sensing,” IEEE Trans. Inf. Theory 52(4), 1289–1306 (2006). 10.1109/TIT.2006.871582 [DOI] [Google Scholar]
- 22.Baraniuk R. G., “Compressive sensing [Lecture Notes],” IEEE Signal Process. Mag. 24(4), 118–121 (2007). 10.1109/MSP.2007.4286571 [DOI] [Google Scholar]
- 23.Tsaig Y., Donoho D. L., “Extensions of compressed sensing,” Signal Process. 86(3), 549–571 (2006). 10.1016/j.sigpro.2005.05.029 [DOI] [Google Scholar]
- 24.Cheng T., “Directional remote sensing,” Geodetski List 36, 251–262 (2015). [Google Scholar]
- 25.Y. Lifeng, L. Gang, and C. Liping, “Optimizing projection matrix for compressed sensing systems,” in International Conference on Information, Communications and Signal Processing, (IEEE 2011), 1–5. 10.1109/ICICS.2011.6174310 [DOI] [Google Scholar]
- 26.Rauhut H., “Circulant and Toeplitz matrices in compressed sensing,” arXiv preprint arXiv:0902.4394 (2009).
- 27.Park J. Y., Yap H. L., Rozell C. J., Wakin M. B., “Concentration of measure for block diagonal matrices with applications to compressive signal processing,” IEEE Trans. Signal Process. 59(12), 5859–5875 (2011). 10.1109/TSP.2011.2166546 [DOI] [Google Scholar]
- 28.Duarte-Carvajalino J. M., Sapiro G., “Learning to sense sparse signals: Simultaneous sensing matrix and sparsifying dictionary optimization,” (DTIC Document, 2008). [DOI] [PubMed] [Google Scholar]
- 29.Elad M., “Optimized projections for compressed sensing,” IEEE Trans. Signal Process. 55(12), 5695–5702 (2007). 10.1109/TSP.2007.900760 [DOI] [Google Scholar]
- 30.Zhengle M., Chen W., Ya C., “Superresolution far-field fluorescence bio-imaging: breaking the diffraction barrier,” Chin. J. Lasers 9, 002 (2008). 10.3788/CJL20083509.1283 [DOI] [Google Scholar]
- 31.Grant M., Boyd S., “CVX: Matlab software for disciplined convex programming,” (http://cvxr.com/cvx, 2015).
- 32.Biomedical Imaging Group, Ecole Polytechnique Fédérale de Lausanne (EPFL), Lausanne, “Benchmarking of Single-Molecule Localization Microscopy Software,” (http://bigwww.epfl.ch/smlm/, 2015).
- 33.Sun Z., “3D Tracking of Quantum Dots and Endosomes in Drosophila Melanogaster (Leiden University, 2007), 1–36. [Google Scholar]
- 34.Sage D., Kirshner H., Pengo T., Stuurman N., Min J., Manley S., Unser M., “Quantitative evaluation of software packages for single-molecule localization microscopy,” Nat. Methods 12(8), 717–724 (2015). 10.1038/nmeth.3442 [DOI] [PubMed] [Google Scholar]
- 35.Pedro M. D., Pahud P., Vibration Mechanics (Springer; Netherlands, 1991). [Google Scholar]
- 36.Sacerdoti F. M., Digital Image Processing (Springer, 2016). [Google Scholar]