STED imaging performance estimation by means of Fourier transform analysis

Abstract

Due to relatively high powers used in STED, biological samples may be affected by the illumination in the process of image acquisition. Similarly, the performance of the system may be limited by the sample itself. Optimization of the STED parameters taking into account the sample itself is therefore a complex task as there is no clear methodology that can determine the image improvement in an objective and quantitative manner. In this work, a method based on Fourier transform formalism is presented to analyze the performance of a STED system. The spatial frequency distribution of pairs of confocal and STED images are compared to obtain an objective parameter, the Azimuth Averaged Spectral Content Spread (AASCS), that is related to the performance of the system in which the sample is also considered. The method has been first tested on samples of beads, and then applied to cell samples labeled with multiple fluorescent dyes. The results show that a single parameter, the AASCS, can be used to determine the optimal settings for STED image acquisition in an objective way, only by using the information provided by the images from the sample themselves. The AASCS also helps minimize the depletion power, for better preservation of the samples.

1. Introduction

Using STED microscopy [1,2], super-resolution images of different samples can be generated. Reports of images showing resolution down to 6nm when imaging nitrogen-vacancy centers in diamond have been presented [3], while typical values for resolution are around 20-70nm on biological applications [4–6], including in-vivo studies [7,8].

Theoretically, the resolution that can be achieved using STED improves without limit increasing the depletion laser power [9]. In practice, high depletion laser power can have a negative effect on the sample and on the quality of the final image. This is because high depletion power can result in increased photobleaching, blinking, re-excitation or two-photon effects [9–14]. All these interactions of the excitation and depletion beams with the sample are specific to the fluorescent molecule used and the sample itself, and they may affect the quality of the image. Thus, in biological samples (sensitive to high light intensities), a higher depletion power may not always be the optimal way to acquire the best STED image. To choose the appropriate acquisition parameters, assessment of the imaging performance taking into account the sample itself is required.

It is usually accepted that the point spread function (PSF) of an imaging system completely characterizes its performance, and that this function can be used to easily determine the resolution that the system can achieve. In order to acquire the PSF of a microscopy system experimentally, it is necessary to generate an image of a sample that can be considered as a point source. This is usually performed using fluorescent beads or other kinds of calibrated samples [15–18]. However, these methods may not be as accurate as expected, since as already explained, the dependence of the performance of a STED system depends strongly on the sample itself, and this dependence is neglected when using beads or calibrated samples [19].

STED system performance is an important issue: there are many parameters that have to be considered, like the quality of the zero in the depleting beam [20]. STED resolution has been traditionally determined by quantifying the size of a particular feature in the image. However, the selection of this feature is a subjective process. Furthermore, noise can have a great impact on the conclusions.

Thus, there is a need for an easy to use and objective method to assess the imaging system performance where the effect of the sample itself is considered [21]. The work presented in this paper aims at producing a tool that can provide information related to the performance of the STED imaging system in the context of the experiment itself in order to optimize the imaging protocol. This method provides a solution to solve controversies presented in the past [22].

2. Materials and methods

It is widely accepted that an image of an object can be expressed as the light distribution at this object convolved with the PSF of the system:

$$I(x,y)=O\left(x,y\right)\ast PSF(x,y)$$ (1)

where I is the light intensity distribution at the image, and O is the light distribution at the object.

Ĩ, is the Fourier transform (FT) of the image I, which is defined in Fourier space by u and v, the spatial frequencies along the x and y directions:

$$\tilde{I}(u,v)=FT\left\{O\left(x,y\right)\right\}·FT\left\{PSF(x,y)\right\}=\tilde{O}(u,v)·OTF(u,v)$$ (2)

where Õ is the FT of the light distribution in the object, and OTF is the optical transfer function, or the FT of the PSF. The sharper or narrower the PSF, the wider the OTF will be, and the better the resolution of the microscopy system.

Mathematical model

Consider the situation in which an image of a sample of beads is generated using an imaging system. Assuming that all the beads in the sample are identical and homogeneously distributed with no overlap, the intensity distribution of such image is described as follows:

$$I(x,y)={\displaystyle \sum _i{I}_{bead}(x-x_i,y-y_i)}+N(x,y)$$ (3)

where (x_i, y_i) are the positions at which each bead, i, can be found in the image, I_bead(x,y) is the image of a single bead, and N(x,y) is a term related to noise.

According to Eq. (2), the FT of the image described in Eq. (3) is:

$$\begin{array}{l}\tilde{I}(u,v)={\tilde{I}}_{bead}(u,v){\displaystyle \sum _i{C}_i{e}^{-j{x}_{i}u}{e}^{-j{y}_{i}v}}+\tilde{N}(u,v)=\\ ={\tilde{O}}_{bead}(u,v)·OTF(u,v){\displaystyle \sum _i{C}_i{e}^{-j{x}_{i}u}{e}^{-j{y}_{i}v}}+\tilde{N}(u,v)\end{array}$$ (4)

where Ĩ_bead is the FT of the image of a single bead. Ĩ_bead is calculated as the light intensity distribution in the object, Õ_bead, multiplied by the OTF of the optical system, and a phase shift related to the position of the sample in the image. Finally, Ñ is the FT of the noise term.

In polar coordinates, where k² = u² + v² and $\phi$ = tan⁻¹(v/u), Eq. (4) can be written as:

$$\tilde{I}(k,\phi )={\tilde{O}}_{bead}(k)·OTF(k){\displaystyle \sum _i{C}_i{e}^{-jk{x}_i\cos \phi }{e}^{-jk{y}_i\sin \phi }}+\tilde{N}(k,\phi )$$ (5)

where it can be seen that the phase term, introduced by the beads spatial distribution, and the noise term break the radial symmetry. In fact, although the beads are randomly distributed in the image, there may be some spatial arrangement at some specific directions that may appear as peaks in the FT of the image. In addition, in real samples, not all the beads are exactly spherical and with the same size. To circumvent this effect, Eq. (5) can be averaged around the azimuth angle, $\phi$.

In this work we will numerically calculate the FT of confocal and STED images, comparing them to the expression in Eq. (5).

Validation in samples of beads

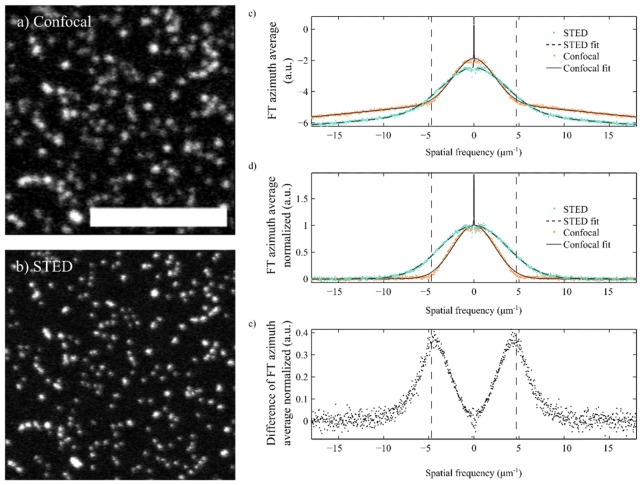
Figure 1(a) shows a confocal image of a sample with 70nm diameter beads, while Fig. 1(b) shows the same image acquired using STED. Both of these images where obtained using our TCS 5 STED CW microscope (Leica Microsystems, Germany) in confocal and STED modes, respectively. In the confocal mode, diffraction limit is ~180 nm, which is significantly larger than the size of the beads.

Fig. 1.

Confocal (a) and STED (b) images of the same sample of Chromeo 488 beads (70nm diameter). Scale bar is 5µm. (c) Radial average of the FT of the confocal and STED images shown in a) and b). (d) The data in c) has been normalized following the procedure described in this article. (e) Difference between the normalized data for the confocal and STED images. The difference is maximum on the spatial frequencies around the diffraction limit, which is shown in the plots as a vertical dotted line, the value of this difference is a measure of the contrast improvement.

Figure 1(c) shows plots of the logarithm of the FT of those images once they have been averaged around $\phi$. Since the frequency axis shows positive and negative components, strictly speaking averaging has been performed in the range [0°, 180°) for positive frequencies, and [180, 360°) for the negative ones. The resulting plots are symmetric about k = 0, as expected. From these plots, 3 different parts can be identified in each of its sides. A first part is found around k = 0, where the plot seems very irregular around a peak. The irregularities are the reminiscence of the lack of cylindrical symmetry of the term ${\displaystyle \sum C_i{e}^{-jk{x}_i\cos \phi }{e}^{-jk{y}_i\sin \phi }}$ . The peak is related to the average power in the image and appears because the intensity is real and positive. Note that there is a certain width of the peak, which is also related to the fact that, although the beads are very similar, they have slightly different dimensions.

A second part is found on the high spatial frequencies region. In the case of the confocal image, the values of k for this region are those beyond the corresponding diffraction limit (shown in the plot as vertical dotted lines). The FT in this area for the confocal image decays linearly and is related to noise, since there should be no spatial information encoded on those values of k. In fact, it fits very well a linear function, making it compatible with some source of electronic noise, such as 1/f noise.

Finally, a third region is found between the ones just described, where there is a bell shaped decay related to the product Õ_bead(k)·OTF(k). The intersection between the bell-shaped region and the noise region in Fig. 1(c) determines the effective cut-off frequency of the image, and in the case of the confocal one, it coincides with the spatial resolution of the system, i.e., the diffraction limit of the confocal system. Note that in the case of the STED image, the bell-shaped region extends beyond the diffraction limit of the confocal microscope, which is to be expected for super-resolution images. From now on, we will refer to this bell shaped region, as the azimuth averaged spectral content (AASC), which contains all the relevant information in the image. Its quantification will help determine the system performance.

Mathematically, the PSF of a confocal system is described using Bessel functions, while in the case of a STED system a Lorentzian function is accepted. The OTF of these systems is therefore described by the FT of these two functions. In our model, we opted for a Gaussian function to describe the AASC in both the confocal and the STED system. Although it is not describing strictly the two different theoretical models, it is a good approximation that allows us to compare them in an easy way, while still having a statistical model that we can rely on.

According to the above description, the data on the plot shown in Fig. 2(b) could be fitted to a function described by:

$$\log \left[\tilde{I}(k)\right]\approx A-B{e}^{\left(-\frac{{\left(k-k_0\right)}^2}{2{\sigma }^2}\right)}+C{e}^{\left(-\lambda \left|k-k_0\right|\right)}+D\left|\left(k-k_0\right)\right|$$ (6)

where A is a constant term; a Gaussian function multiplied by the constant B describes the AASC; the exponential term multiplied by the constant C describes the broadening of the peak due to different sizes of beads in the real image; D is related to noise.

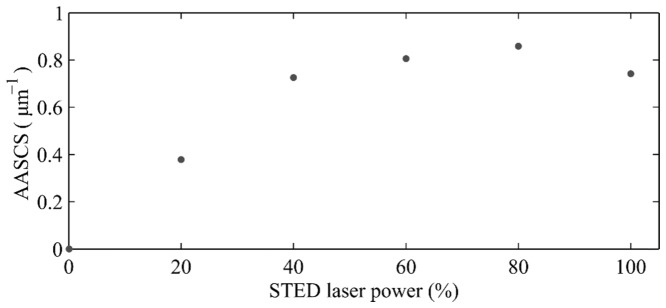
Fig. 2.

Variation of the AASCS with STED laser beam power (in arbitrary units) for images of Chromeo 488 beads.

Figure 1(c) shows the resulting data from the confocal and STED images of beads in Fig. 1(a) and Fig. 1(b), and the corresponding fits of the model described in Eq. (6). These have been determined, according to the model section, as follows: we calculate the FT of the image, take the logarithm, integrate around the azimuth angle, ϕ, and fit Eq. (6), where A, B, C, D, k₀, σ and λ have been adjusted using a simplex algorithm. The figure shows that the mathematical description in Eq. (6) is in good agreement with the results obtained for both the confocal and STED images of beads.

Figure 1(d) shows the same data and the calculated fits, once these have been normalized for better visualization and comparison. Normalization was performed by subtracting the terms A + D|(k-k₀)|, and then the height of the Gaussian function fitted, B, was normalized to 1, and C rescaled appropriately. As expected, the fit shows a larger value of σ (wider Gaussian function) for the STED image compared to the confocal one.

Figure 1(e) shows the difference between the normalized azimuth averaged FT of the confocal and STED images. This plot shows clearly that spatial frequencies beyond the diffraction limit are present in the STED image. Also, the maximum difference is found on the cut off frequency for the confocal image, plotted using dotted lines [23]. The magnitude of this difference is related to the increase in contrast in the STED image.

It is expected that, when acquiring STED images of beads, the PSF of the system becomes narrower than that of a confocal image, and so does the image of each bead, as it can be observed in Fig. 1(a) and Fig. 1(b). Therefore, an increase in the contribution of the higher spatial frequencies of the OTF beyond the corresponding diffraction limit should be translated to a widening of the AASC. Once electronic or other sources of noise are contemplated and taken into account, the only differences between these images should be introduced by the changes in the OTF of the system. At this point, we assess the performance of the STED system by calculating the difference in width between the fits of the AASC for the confocal and corresponding STED image. From now on, we refer to this metric as the Azimuth Averaged Spectral Content Spread (AASCS).

Figure 2 shows the AASCS calculated for several pairs of confocal and STED images of fluorescent beads where the intensity of the depletion beam was varied from 20% to 100%, being this last value the maximum available. As it is expected, the AASCS initially increased with the power of the STED laser.

Theoretically, in STED there is no limit to the increase in resolution with the depletion beam intensity as long as there are no unwanted interactions between the light and the sample, such as heat transfer or two photon excitation fluorescence. However, in the plot shown in Fig. 2, the AASCS increases with the depletion laser power up to a value of 80%. Further increase in depletion laser power reduces the resulting AASCS value. This is probably because increasing the intensity of the depletion source reduces the signal to noise ratio due to generation of a smaller fluorescent spot.

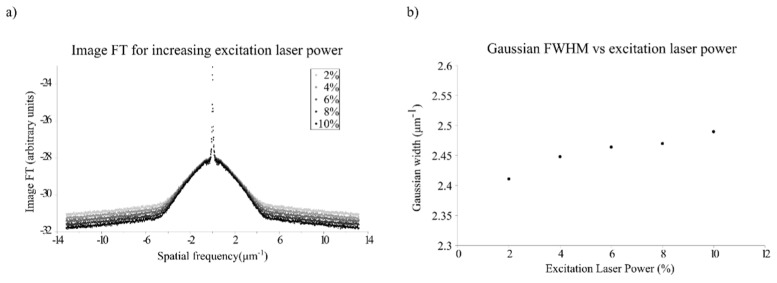
To corroborate this, we have taken confocal images of the same set of beads changing only the intensity of the excitation laser. Figure 3(a) shows plots for the azimuth average of the FT of these images, in this case without normalization. The width of the OTF in this case does not change, since all of the images are confocal images. However, the noise floor is reduced as the excitation laser power is increased. This is translated in our model into an increase in the width of the AASC, as it is shown in Fig. 3(b), where the width of the Gaussian fit, σ, is plotted.

Fig. 3.

a) FT of confocal images of beads averaged around the azimuth, showing the reduction in noise level as excitation laser power increases. b) Width of the Gaussian function fitting the AASC for confocal images of beads acquired at excitation laser powers of 2, 4, 6, 8 and 10%. Higher values of the excitation laser power produced saturation on the image and were discarded.

The results shown in Fig. 2, obtained using bead samples, suggest that, in order to optimize the performance of the system, it may be interesting not to use the full power of the depletion laser. Although the STED theory indicates that an increase in depletion power can increase the resolution, it is also true that this also can lead to increased noise, affecting the overall image quality. Maximizing the AASCS can be a way to objectively reach a compromise on the depletion laser power taking into account the SNR of the final image.

Images in cell samples

In order to validate the method in cell samples, we have extended our studies using the AASCS to samples of fixed cells tagged with different fluorescent dyes.

Figure 4 shows a pair of confocal and STED images of a Hela cells sample, where secretory vesicles and endoplasmic reticulum have been tagged using Oregon Green 488 and BD Horizon V500 respectively. This combination of dyes was used to produce multi-color STED images of the sample on our TCS 5 STED CW Leica microscope [24]. The dyes are chosen so that their emission spectra overlap and the same depletion source can be used; however, their absorption peaks are far enough from each other and different laser lines can be used to excite each dye minimizing cross talk between them. In this configuration, multi-color imaging is performed sequentially.

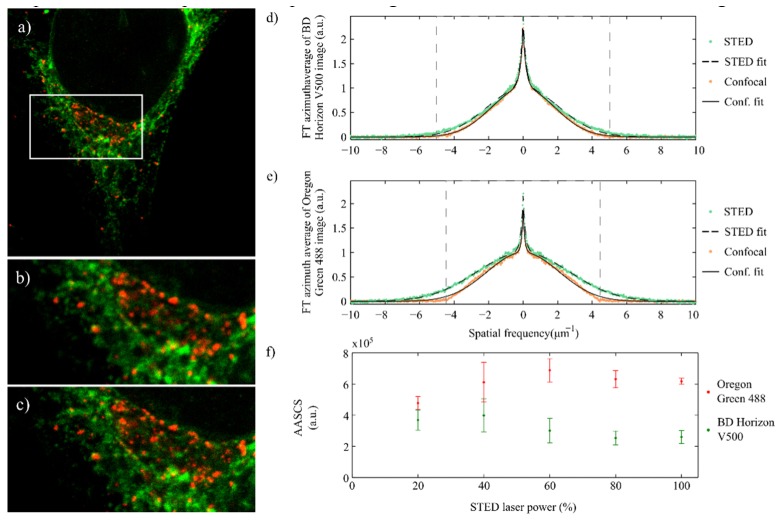
Fig. 4.

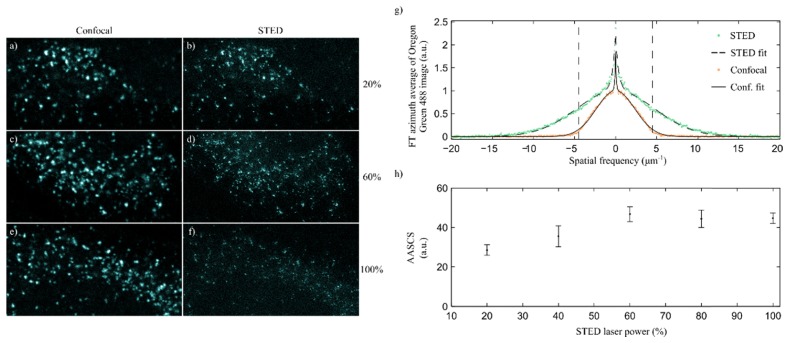
(a) Confocal image of a HeLa cell sample where endoplasmic reticulum has been tagged with BD Horizon V500 (green) and secretory vesicles with Oregon Green 488 (red). Image is 30.4x30.4µm in size. (b) and (c) are smaller sections of the image in a) acquired with confocal, b), and STED, c). (d) Azimuth average of the FT of the confocal and STED images in b) and c) for the BD Horizon V500 channel. Green markers show the data of the STED images, and orange the confocal ones. Corresponding fits of the data (dotted line for STED and solid for confocal) using the method described are also shown in the plots. (e) Similar to d) for the Oregon Green 488 channel. (f) AASCS calculated for the BD Horizon V500 and Oregon Green 488 channels of the HeLa samples described. The maximum AASCS is achieved at 60% depletion laser power for the Oregon Green 488, and 40% in the case of the BD Horizon V500.

In a double stained sample, each of the sequential acquisitions has to be optimized separately, and possible effects of acquisition of the image of one color on the image of the second color need to be considered.

Confocal and STED pairs of images of the sample were acquired using the 453nm line to excite BD Horizon V500, and 514nm line to excite Oregon Green 488.

The plots in Fig. 4(d)-4(e) show the azimuth averaged FT of the STED and confocal images in each channel after normalization. As in the case of randomly distributed beads, the contribution at higher frequencies is larger in the STED images than it is in the confocal ones. The fits to this data obtained using the model described in this paper are also shown in the plots, and are in agreement with the experimental data.

As in the case of beads, we also calculated the AASCS for different pairs of images that were acquired changing the depletion laser source power. The results are shown in Fig. 4(f).

When increasing the depletion laser power, the fluorescence signal is reduced. This is often compensated with by increasing the excitation laser power in the STED imaging protocol [25]. In these measurements, we increased the excitation laser power linearly with the depletion laser power. As an example, consider the case in which the excitation laser power used to acquire the confocal image was 1%. For the STED image with the depletion laser power at 100% the excitation power used was 2%, to compensate for this fluorescence reduction. For intermediate values, this excitation power increased linearly, e.g., we used 1.2 in the STED image with the depletion laser power at 20%, 1.4 at 40%, and so on. The plot in Fig. 4(f) shows that the AASCS is always positive, i.e., for all the depletion laser powers used the STED images have a higher contribution of the higher spatial frequencies when compared to the confocal ones. However, the AASCS increases with the power of the depletion laser source up to a certain value, and decreases for higher values. This maximum AASCS value is around 60% in the case of Oregon Green 488 and 40% in the case of BD Horizon V500. We observed this behavior systematically in all the experiments we performed. At this point, it would be unclear whether this behavior depends only on the fluorescent dye or also the structure tagged in the sample (notice that each fluorescent dye was used to tag different structures in the cell). To clarify this, we performed a second experiment, where we tagged the same structure, the secretory vesicles, in two different samples using only one of the dyes in each of the samples. The results observed for the AASCS show that each of the dyes present the same behavior as described before, i.e., the AASCS peaks at different depletion laser power values for each dye. Furthermore, the optimal AASCS calculated for BD Horizon has been consistently a half of the value for Oregon Green 488. This indicates that the performance of the STED system depends strongly on the dye used.

The differences in the behavior of the two dyes may be related to the effect of the high power depletion source may have on the sample, and also on the fluorescent molecule itself. It has been observed before that loss of fluorescence may be accelerated by the presence of a depletion source [12,26]. This may eventually affect the SNR that can be achieved in the images.

We have also studied the behavior of the AASCS in a gated STED microscope [27], and the results are shown in Fig. 5. In this case, incompatibilities with the excitation lines available in the microscope did not allow for multicolor experiments to be performed, and only images using Oregon Green 488 were used. Gated STED systems require lower depletion laser power levels, however, the same behavior as in the case of CW STED is observed in these experiments. In the case of gated STED, the AASCS peaks at a value of 60% of the depletion laser power. As it is expected, the values of the AASCS for gated STED are 4 times higher than those obtained by means of CW STED in comparable examples.

Fig. 5.

(a-f) Confocal and STED pairs of images from HeLa cell samples where secretory vesicles have been tagged with Oregon Green 488. A gated STED system from Leica was used on this experiment. STED images have been acquired setting the depletion laser power to 20%, b), 60%, d) and 100%, f). The images are acquired using photon counting settings, and the confocal (a,c, and e) and STED (b, d and f) images are shown using the same color scale to minimize display effects. (g) Azimuth average of the FT of the confocal and STED images in c) and d). Green markers show the data from the STED images, and orange from the confocal ones. Corresponding fits of the data using the method described are also shown in the plots, dotted line for STED and solid for confocal. (h) AASCS obtained using different excitation powers in the STED laser on the same sample. The data have been calculated using the images a-f), amongst others. The AASCS is maximum for values of the depletion laser power of around 60%.

It is interesting to note that the values at which the AASCS peaks coincides with the opinion of a trained eye as to which are the best images, both in the case of CW STED and also gated STED. Trained eyes tend to choose the images with higher AASCS when given a choice for different depletion laser powers. An example can be found in Fig. 5(a)-5(f), where different pairs of confocal and STED images acquired with different depletion laser powers are presented, so that the reader can compare them knowing the AASCS values obtained for each pair.

3. Discussion and conclusion

We present here a method that can be used for calibration and assessment of the quality of any STED system and helps in determining the best STED parameters for a given sample. The AASCS parameter provides information about the improvement achieved by using STED over a traditional confocal system.

Methods like Fourier Ring Correlation (FRC) can provide the resolution of the images acquired, taking into account the correlation of two identical images [21]. However, these methods do not consider other parameters that may affect the global quality of the image. The AASCS provides an objective metric for this, and has been successfully used to optimize acquisition parameters. However, although the resolution may be linked to the AASCS, it is not a direct readout of the resolution of the system.

Contrary to what STED theory predicts, we have observed that increasing the depletion intensity not always maximizes the value of the AASCS. This is because when more fluorophores are depleted, less fluorescence photons are generated. This results in reduced SNR, the image becomes noisier, and dimmer features are lost. In addition, high depletion powers can cause photobleaching, blinking, re-excitation or two-photon absorption that further reduce the quality of the final image. The AASCS is an objective and robust metric to optimize the performance of the STED imaging system as it can be used to maximize SNR in the image while minimizing unnecessary high depletion powers, helping preserve sample integrity. Futhermore, it has helped us reduce unnecessary high depletion power, minimizing the effect on the overall image quality.

It is necessary to point out the fact that this method relies on images where one cannot observe a specific spatial arrangement of the fluorescent molecules. If an arrangement of the molecules along a particular spatial direction was present, that would translate on a peak at specific spatial frequencies related to that direction and frequency. The azimuth average proposed in the model is intended to reduce any effect of periodicity of the image in its FT. However, if not considered, these peaks may produce artifacts on the fitting process that may be misleading. This may be the case of images of microtubules, where they are oriented preferentially along a certain direction. A similar situation can arise in the case of images that have been post processed by means of deconvolution methods: these methods may affect the spatial frequency distribution of the images, and the model suggested may not be suitable for fitting on those cases.

Finally, in this work only results related to confocal and STED images have been presented. However, the authors are confident that the use of this method could be extended to any technique that is able to produce pairs of uncorrected-corrected images of the exact same sample, e.g, adaptive optics or structured illumination.

Funding

The authors acknowledge financial support from Laserlab-Europe (EU-H2020 654148), The Foundation La Marató de TV3 (20141730), The Spanish Ministry of Economy and Competitiveness, through grants FIS2016-80455-R, the “Severo Ochoa” Programme for Centres of Excellence in R&D (SEV- 2015-0522), the CERCA Programme/Generalitat de Catalunya and the EU H2020-FET OPEN-2014-2015-RIA.