Performance of a differential contrast sensitivity method to measure intraocular scattering

Abstract

Increased intraocular scatter degrades quality of vision, especially in the presence of glare sources. Standard tests, such as visual acuity, are not well suited to capture this condition. There are specific methods to measure intraocular scatter, but require dedicated instruments. In this work, we propose a method to estimate the amount of scatter by combining to sequential measurements of the contrast sensitivity function for two conditions, with and without a glare source. We applied the approach in a group of young subjects with no know ocular pathology fitted with photographic diffusing filters. The straylight estimates were compared with those provided by two alternative techniques, one based on the compensation comparison method and the other the optical integration. The results obtained with the three approaches were in a good agreement, demonstrating the feasibility of the proposed method.

1. Introduction

High contrast visual acuity is not a complete descriptor of the visual function [1,2]. In several circumstances, even when visual acuity is normal, the contrast sensitivity function (CSF) can reveal abnormalities in vision [3–6]. In particular, one of the instances that visual acuity may fail to detect an abnormal situation is when intraocular scattering or straylight increases [7,8]. Common cases where scatter increases are related to anterior segment pathologies such as cataract [9]. Increased scattered light in the eye has a direct impact on the CSF, with the effect depending significantly on the luminance of surrounding where the gratings are presented. While the measurement of the CSF in a laboratory environment is well established, it usually requires significant dedication from the subjects, what is, often, inadequate for the clinical practice. Various methods for the estimation of the CSF in clinical settings exist, most commonly involving printed test charts. These methods are usually condensed and provide limited spatial frequency information to be more convenient and useful both for the clinicians and the patients. Recently, a computerized method was developed, named “quick CSF” [10] (q-CSF) where stimuli are presented by a computer monitor, providing precise and repetitive measurements [11] of the CSF for a broad range of spatial frequencies in relatively short time.

The estimation of intraocular scatter is an important and complementary option to complete the analysis of the quality of vision. Although, there are several approaches both based on psychophysical and optical techniques to the direct measurements [12–14], they are not yet well integrated in the routine clinical visual testing. Since, the CSF is very dependent on the presence of scatter if glare sources are present [15], we suggest an alternative approach based on the sequential measurement of the CSF for different glare situations (with and without glare). With proper analysis, scatter could be evaluated without the need of additional devices, just those required for the CSF testing.

In this study, a modified version of the q-CSF method, implementing a glare source for differential tests, was used to estimate intraocular scattering. A group of subjects was tested with photographic diffusers, introducing in this way specific amounts of straylight. The results were compared with those provided by two independent devices, a device providing psychophysically subjective measurements of the intraocular straylight [16] and an objective instrument [17] based on the optical integration principle [14,18] to optically quantify the amount of intraocular straylight.

2. Methods

Subjects

Seven normal subjects aged 31 ± 4 years old, all emmetropes and without any known ocular pathologies, participated as volunteers in the study. After being informed of the nature of the study, all subjects enrolled provided an informed consent, according to the tenets of the Declaration of Helsinki. Measurements were done monocularly, on the dominant eye of each participant. Intraocular scattering was induced by two different photographic diffuser filters (Black ProMist 1/4 and 1, Tiffen, USA) that have been also used in previous studies [16,17,19,20].

Procedure

The CSF was estimated for a range of spatial frequencies between 2 and 20 cycles per degree (c/deg). A uniform and bright annulus was placed concentrically to the test area, where the gratings were presented, to produce the glare effect. The task for each subject was the recognition of the orientation (left for 45° or right for 315°) of a sinusoidal grating of different contrast and spatial frequency, appearing for 0.3 seconds on a computer monitor, followed by an acoustic signal. The subject was seated at a distance of 1 meter from the screen with the test area subtending 7.36 degrees of the optical field and the glare annulus placed 1.39 degrees away from the test area, with a thickness 1.6 deg (Fig. 1).

Fig. 1.

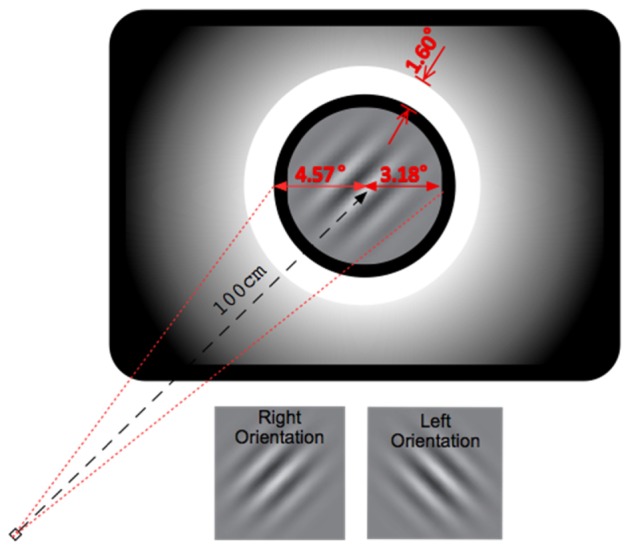
Schematic representation of the test screen.

The mean luminance of the test area (L) was 40 cd/m² and the luminance of the glare (E) annulus was 8030 cd/m². Each subject underwent 4 measurement sessions, two without and two with the glare annulus illuminated, for each conditions of induced scattering. Each session consisted of 100 recognition tasks and the average CSF was obtained for each glare condition. The procedure was applied monocularly for each subject, initially without any photographic diffuser, and, consecutively with the Black ProMist (BPM) 1/4 and the Black ProMist 1.

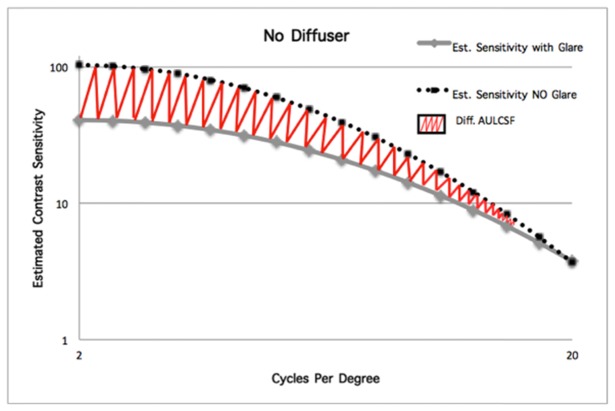
Two metrics were calculated from the estimated CSFs. The first metric was the Difference of the area Under the Logarithmic values of CSF (Diff. AULCSF) which was used as a means of comparison between glare conditions. Figure 2 shows an example of the CSF measured with and without glare and the meaning of this parameter.

Fig. 2.

Difference of the area Under the Logarithmic values of CSF (Diff. AULCSF) from the measurement with the glare source on and off.

The second metric was the amount of straylight described by the value S directly retrieved from the contrast sensitivity at 2 c/deg with (CS_on) and without (CS_off) the presence of glare. The method of calculating the S value is described in detail below.

Following the formalism of Paulsson et al [21], and assuming that the psychophysical effects, such as adaptation and pupil size can be neglected, the relationship between the contrast sensitivity (i.e., the inverse of the contrast threshold) for each glare condition can be written in terms of luminance parameters as:

$$\frac{C{S}_{on}}{C{S}_{off}}=\frac{L}{L+I_g}.$$ (1)

where I_g is the intensity from the glare source superimposed over the central area where the sinusoidal patterns are displayed, and L is the mean luminance of the grating stimulus.

Assuming that the lamp has a uniform intensity equal to E and α_min and α_max its minimum and maximum angular radius respectively (where α_min = 4.57 degrees and α_max = 6.17), the intensity Ig at the center of the ring lamp is given by the equation:

$$I_g=E \underset{{\alpha }_{min}}{\overset{{\alpha }_{max}}{\int }}2\pi \alpha PSF\left(\alpha \right)da.$$ (2)

where α is the visual angle and the PSF is the Point Spread Function for the eye or the coupled eye-diffuser filter system.

For further simplification, the PSF expression from the Stiles-Holladay equation was adopted (PSF = S/α², α units in degrees). Replacing this expression into the integral of the Eq. (2) and developing it, the intensity provided by the glare source becomes directly proportional to S [22]:

$$I_g=2\pi ESln\left[\frac{{\alpha }_{max}}{{\alpha }_{min}}\right].$$ (3)

Finally, S can be calculated replacing Ig from the Eq. (3) in (1):

$$S=\frac{1}{2\pi }\frac{L}{E}{\left(ln\left[\frac{{\alpha }_{max}}{{\alpha }_{min}}\right]\right)}^{-1}\left(\frac{C{S}_{off}}{C{S}_{on}}-1\right).$$ (4)

This expression provides a direct procedure to determine S from the contrast thresholds measures with and without glare.

Comparison with visual and optical scatter measurements

Two additional instruments were used to measure straylight. The C-Quant device (Oculus, Wetzlar, Germany) was used to assess the intraocular straylight under the same conditions measured with the differential CSF approach. All measurements with the C-Quant were performed with the diffuser placed in front of the dominant eye while the other eye was occluded. This device uses the compensation comparison method [23]. In this method, the central part of the test area is divided into two halves, surrounded by an annular, flickering, glare source. During the measurement, compensation light is added only to one half, while one half is flickering counter-phase with the glare source and the other half not. During each trial, the subject’s task was to detect the half with the highest flickering amplitude. Eventually, the compensation intensity is adjusted accordingly resulting the two halves appear equally illuminated. The calculated metric is the logarithmic straylight value (Log(S)). The measurement was accepted if and only if the estimated standard deviation was below 0.08 and the quality factor over 1.00 [16].

The second was a prototype device based on the optical integration technique [14] for the measurement of intraocular straylight [17,24]. The procedure does not require the subjects’ response. During the measurement, an extended source consisting of a uniform disk and an annulus are projected onto the retina, and, by appropriately placed diaphragms, only the forward-scattered light is sensed by a photo-detector. The logarithm of the straylight parameter (Log(S)) for each measurement is calculated from the ratio of the light’s intensity that is returning to the detector from the two different regions of illumination (the central and the peripheral). Each subject’s eye was measured initially bare and with the two different diffusers consecutively.

3. Results

The repeatability of the CSF method for calculating the intraocular straylight parameter was evaluated by calculating the Pearson’s correlation coefficient for the test-retest (relative reliability) [25] results. In particular, the Pearson’s correlation coefficient was 0.592 and the test-retest plot is shown in Fig. 3.

Fig. 3.

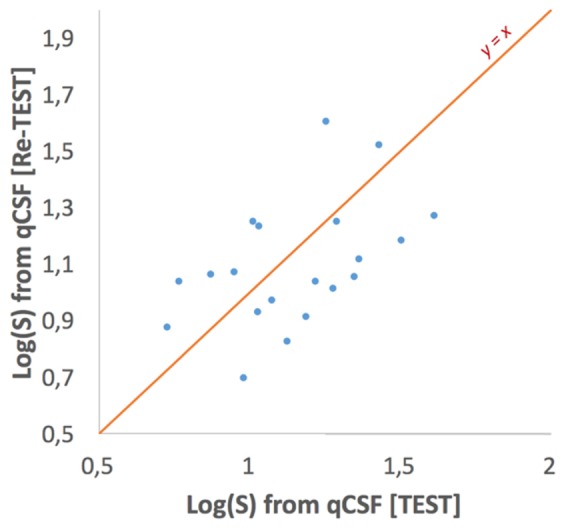
The test-retest comparison for the evaluation of the relative reliability of the method.

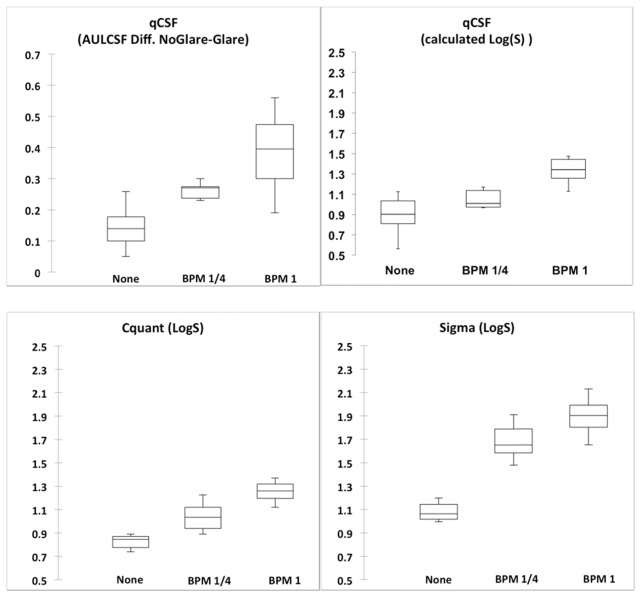
The average values of intraocular scattering for the 3 situations as measured with the differential CSF method, C-Quant and Sigma devices are presented in Fig. 4.

Fig. 4.

The median (central line inside each box), minimum and maximum values (whiskers) and the Q1 and Q4 quartiles (lower and higher borders of each box, respectively) of the Diff. AULCSF (upper left box) and the intraocular scatter, as measured by the three different methods.

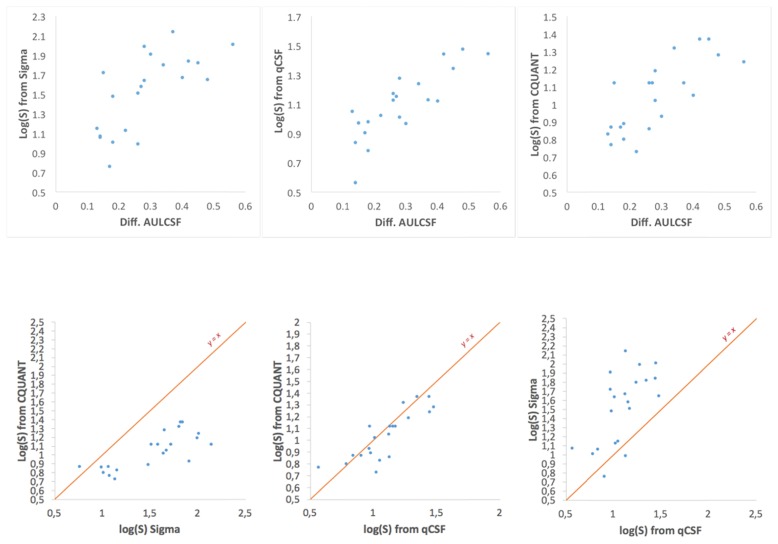
The Pearson correlation coefficient was calculated to compare the results recorded by the differential CSF method with the ones retrieved from the C-Quant and the Sigma devices. The results are presented on Fig. 5 and Table 1.

Fig. 5.

Scatter plots depicting the inter-agreement between all the different metrics acquired from the measurements. Each data point denotes a different subject in all of the three different scatter conditions.

Table 1. Pearson Correlation Coefficients among different methods.

Methods	Diff. AULCSF	C-Quant	Sigma	S from qCSF
Diff. AULCSF	1	0.766	0.693	0.834
C-Quant	0.766	1	0.771	0.833
Sigma	0.693	0.771	1	0.638
S from qCSF	0.834	0.833	0.638	1

4. Discussion

The sequential measurement of the CSF under the conditions described in the presend work allows the calculation of intraocular straylight. The approach was validated by comparison with the results obtained using two other different methods, optical and psychophysical, that were similar in the values of the Log(S).

It needs to be noted that in all measurements the mean luminance of the test area remained constant and all measurements were performed in photopic luminance conditions, preventing any detectable changes in the pupil size that could occur with the presence of the glare source. Moreover, preliminary trials did not reveal any measurable effect of adaptation or training of the method. Thus, the formalism introduced by Paulsson et al. [21] could safely be applied.

In a previous study [26], a Pearson correlation coefficient of 0.500 was reported between measurements of contrast threshold at 2 cycles per degree (measured by a custom made test device without the presence of glare) and the Log(S) (measured by the C-Quant device) in patients with two different kinds of cataract. In the present study, stronger correlation coefficients were recorded (0.833 and 0.766) among the C-Quant and the differential CSF method. The comparison of those coefficients demonstrates that the addition of an intense glare source, relatively close to the test area, may improve the sensitivity of a metric based on CSF for detecting small changes on the forward scattered light.

The stronger agreement between the estimated Log(S) from the CSF and the C-Quant compared to the agreement between the measurements taken with the Sigma and the CSF, can be attributed to the fact that both psychophysical methods quantify the amount forward scattered light as perceived by the subject, while the Sigma device is based on the evaluation of scattering at the optics of the eye. Additionally, it cannot be excluded that back reflections from the diffusers influence the measurements with the Sigma device, which is designed to suppress reflections only near the pupil plane.

In conclusion, we presented a simple method, based on a commonly used clinical test, to estimate the amount of straylight in patients. The performance of this method was compared with two well-established approaches showing good correlation. The repeatability, the ease of use for both the clinician and the subject are proofs that the differential CSF method can potentially be applied to detect changes in the scattering properties and transparency of the eye. We envision that this can be especially useful for a quick, cost-effective screening of cataract or other age related pathologies associated with elevated intraocular scattering.

Funding

European Research Council (ERC) Advanced Grant (AdG) −2013 −339228 (SEECAT); Secretaría de Estado e Investigación, Desarrollo e Innovación (SEIDI) FIS2013-41237-R; Fundación Séneca-Agencia de Ciencia y Tecnología de la Región de Murcia 19897/GERM/15