TuebingenCSTest – a useful method to assess the contrast sensitivity function

Abstract

Since contrast sensitivity (CS) relies on the accuracy of stimulus presentation, the reliability of the psychophysical procedure and observer’s attention, the measurement of the CS-function is critical and therefore, a useful threshold contrast measurement was developed. The Tuebingen Contrast Sensitivity Test (TueCST) includes an adaptive staircase procedure and a 16-bit gray-level resolution. In order to validate the CS measurements with the TueCST, measurements were compared with existing tests by inter-test repeatability, test-retest reliability and time. The novel design enables an accurate presentation of the spatial frequency and higher precision, inter-test repeatability and test-retest reliability compared to other existing tests.

1. Introduction

Contrast vision is fundamental for visual perception. The human visual system is more sensitive to local luminance contrast than absolute luminance [1]. Contrast is defined as relative difference between two color or luminance values e.g. between dark and bright. Objects with a large difference in luminance or color are better distinguishable from each other displaying a high contrast. The relative difference in luminance is usually expressed by the difference between maximum and minimum values divided by the sum of them, which Michelson called visibility [2]. Today the so called Michelson contrast is used to define the contrast of periodic pattern such as sine wave gratings including the so-called ‘Gabor Patches’, sinusoidal luminance patterns named after D. Gabor [3]. The contrast sensitivity (CS) is the reciprocal of the minimum contrast required for detection [4], and this contrast is called threshold contrast. Contrast sensitivity plotted against the spatial frequency of the Gabor Patch reveals the contrast sensitivity function (CSF) of the eye.

Reliable contrast sensitivity measurements are essential to describe precisely the visual function. The resultant CSF reveals the visual performance at different spatial frequencies including visual acuity, which corresponds to the cutoff-frequency on the high frequency end of the CSF [5].

Clinically, contrast sensitivity becomes relevant for several eye diseases such as cataract [6–8], glaucoma [9, 10], amblyopia [11, 12], multiple sclerosis [13–15], macular degenerations [16, 17], and diabetic retinopathy [18, 19]. The knowledge of the smallest perceivable contrast is also essential in order to verify the success of ocular surgeries e.g. laser-assisted in situ keratomileusis or intraocular lens implantation [20], by characterizing the entire visual function of the patient, using the CSF.

To measure contrast sensitivity, computer-based stimulus presentations nowadays replace paper-based charts like the traditional Pelli-Robson chart [21]. Therefore, display technologies such as cathode ray tube (CRT), liquid crystal display (LCD) or organic light emitting diode (OLED) need to be set up properly to present contrast pattern accurately. Although several methods have been developed in order to assess the contrast sensitivity function, little attention has been paid to a method which combines a precise stimulus presentation, a time-efficient psychophysical method and an accurate presentation of the spatial frequency resulting in repeatable and reliable results. In a view of time efficiency, the method of constant stimulus suffers from long measurement duration because of large trial numbers. Although methods of constant stimuli are probably highly accurate, they are less time-efficient than adaptive staircase procedures. Adaptive procedures use an algorithm to select the next stimulus intensity automatically which makes them time-efficient, by calculating and reducing the uncertainty [22].

The aim of the current research was to develop a new contrast sensitivity test that includes a time-efficient four-alternative forced choice (4AFC) staircase method together with a high resolution of the contrast levels while incorporating the magnification of currently worn prescriptions leading to repeatable and reliable contrast sensitivity measurements.

2. Methods

2.1 Development of the TuebingenCSTest

2.1.1 The Ψ method – a Bayesian adaptive staircase procedure

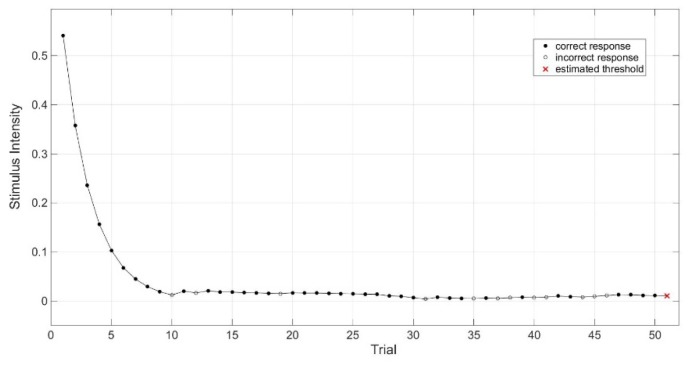
A Bayesian adaptive method that is called Ψ (psi) method was used for the acquisition of the threshold contrast of the psychometric function [23]. The Ψ method was implemented into the Palamedes Toolbox [24], which can be controlled by the software MATLAB (Matlab R2010b, MathWorks Inc., Natick, USA) running on Mac OSX, version 10.9.5, using 4AFC. For this experiment, the slope of the psychometric function was fixed and set to 2.74 with a lapse rate of 4%, as suggested used by Hou [25]. To be time efficient, 50 trials were used to determine the threshold contrast of the participants’ eye. The Ψ method considered the range of possible stimuli for each trial and calculated the probability and the uncertainty of correct and incorrect response [22]. To select the next stimulus, the expected uncertainty for all discrete stimuli was calculated and the stimulus intensity with the lowest calculated uncertainty was automatically selected in order to maximize the expected information [22]. A typical course of 50 trials is shown in Fig. 1, which ends in the estimated threshold contrast.

Fig. 1.

The Ψ (psi) method estimates the threshold contrast (red x) after 50 trials. Closed circles indicate correct responses and open circles an incorrect response. Stimulus intensity is defined in Michelson contrast.

2.1.2 The 16-bit gray-level resolution

A LCD-Display (ViewPixx 3D, VPixx Technologies, Saint-Bruno, Canada) with a mean luminance of 40 cd/m² and a pixel resolution of 1920 x 1080 was used for the presentation of the stimuli (Gabor Patch gratings), with a gray-level resolution of 16 bits (2¹⁶ levels). Since Lu and Dosher recommended a gray-level resolution of at least 12.4 bits [26], the current gray-level resolution of the used setup is high enough to assess high sensitivities to contrast. This keeps true even if the gray-level resolution is reduced by ca. 1 bits by gamma correction and by ca. 3 bits by the need for at least eight steps to draw a sine wave, ending up about 12 bits which corresponds to a stimulus presentation with contrast as low as 0.025% (3.61 log CS). Gamma correction and luminance was checked with a luminance meter (Konica Minolta LS-110, Konica Minolta, Inc., Tokyo, Japan).

2.1.3 The incorporation of lens magnification

Positive and negative lenses were used to correct ametropic eyes, but these lenses usually change the retinal image size. The total magnification (N_G) depends on the thickness (d) and the refractive index (n) of the lens, the distance between eye and lens (e), distance between corneal vertex and the first principal point of the eye (e’), and the front surface power of the lens (D) and the back vertex power (S’) in Eq. (1) [27].

$$N_G=\frac{1}{(1-\frac{d}{n}D)}·\frac{1}{(1-(e+e\text{'})S\text{'})}$$ (1)

with d = 0.0005 m for negative lenses and d = 0.001 m for positive lenses; e = 0.012 m, e’ = 0.001348 m and n = 1.52. The magnification of the lens was corrected by changing the size and the spatial frequency of the stimulus, so that both were rearranged. Without this correction of magnification each participant would have been presented slightly different spatial frequencies.

2.2 Validation of the TuebingenCSTest

Contrast sensitivity was measured by the four following tests: Functional Acuity Contrast Test (F.A.C.T.), Freiburg Acuity and Contrast Test (FrACT), quick CSF (qCSF) and the newly developed Tuebingen Contrast Sensitivity Test (TuebingenCSTest). The FrACT Version 3.9.3 was used with auditory feedback ‘with info’ setting and 8-bit gray-level resolution [28, 29], F.A.C.T. (Stereo optical co., inc., Chicago, IL, USA, developed by Ginsburg et al. [30]) was used as described in the manufacturer’s recommended testing procedure. The qCSF method was originally developed for 2AFC grating orientation identification task [31], while we used 4AFC with 50 trials for the qCSF. The TuebingenCSTest was used with 4AFC grating orientation identification task which means that one stimulus was presented per trial and four keyboard response choices were available. The incorporation of magnification of the lens was done in the new TuebingenCSTest and qCSF.

As mentioned before, Gabor patches (TuebingenCSTest, qCSF) and circular grating patches (FrACT, F.A.C.T.) were used as stimuli and presented by a Mac OSX, version 10.9.5 using the Psychophysics Toolbox Version 3.0.9 [32–34]. The possible orientations of both stimuli were depending on the test that was used – either 3AFC (orientation: 90°, 75° and 105°) for F.A.C.T. or 4AFC (orientation: 0°, 90°, 45° and 135°) for FrACT, qCSF and TuebingenCSTest. Since the visual angle of the stimuli is fixed to 1.7° in the F.A.C.T., the visual angle of the stimuli, used for the other test, was adapted to the same size. In case of the TuebingenCSTest, the FrACT and the qCSF, the stimuli were presented with a presentation time of 300 milliseconds (ms), while in the F.A.C.T. the stimuli are presented the whole time. The qCSF and TuebingenCSTest used technical 16-bit gray-level resolution whereas the FrACT can use only 8-bit.

To provide feedback to the participants, a tone was implemented into the TuebingenCSTest that played a high tone after correct responses and a deep tone after wrong responses, similar to the feedback ‘with info’ in FrACT. Additionally, the participants performed a short training with high contrast stimuli including each spatial frequency before the TuebingenCSTest begun to measure contrast sensitivity. In FrACT, the internal feedback was switched on. No feedback was provided in the qCSF whereas a neutral tone was played when a stimulus was presented.

Twelve participants were enrolled in the validation study of the TuebingenCSTest. The average age was 27 ± 3 years and habitual refractive errors (mean spherical refractive error: −2.06 ± 4.10 D) were corrected to normal vision using trial lenses. The study followed the tenets of the Declaration of Helsinki and was approved by the Institutional Review Board of the medical faculty of the University of Tuebingen. Informed Consent was obtained from all participants after the content and possible consequences of the study had been explained. The participants were placed in 6.1 m (20 feet) in front of the LCD-Display in a darkened room using a chin rest. Threshold contrast measurements were done monocular (right eye) for spatial frequencies of 1.5, 3, 6, 12 and 18 cycle per degree (cpd), while the order of spatial frequencies was randomized. The contrast sensitivity was measured for each spatial frequency separately. The whole block of the contrast sensitivity measurements was measured two times, separately for each test (FrACT, F.A.C.T., qCSF, TuebingenCSTest), with randomized order of the tests.

Statistics were performed with a statistics software (IBM SPSS Statistics 22, IBM Deutschland GmbH, Ehningen, Germany), using a Friedman test and two-way mixed intraclass correlation coefficient with absolute agreement. For post-hoc analysis a Dunn-Bonferroni test was used. Bland-Altman analysis were analyzed using a spreadsheet software (Microsoft Office Excel 2016, Microsoft, Redmond, USA) [35].

Inter-test repeatability was assessed using the Bland-Altman analysis and the test-retest reliability was evaluated via intraclass correlation coefficient (ICC) [36, 37]. Bland-Altman analysis included the coefficient of repeatability (COR) which is the 1.96 times the standard deviation of the difference between the test and the retest scores [35], which are contrast sensitivity measurements within one participant in the analysis.

3. Results

In order to verify the measurement of the CSF with the newly developed TuebingenCSTest (TueCST), we compared the obtained contrast sensitivity measures with three established contrast sensitivity tests (FrACT, F.A.C.T. and qCSF). Repeatability and reliability of contrast measurements for every contrast sensitivity test due to repeated measurements was investigated. Table 1 contains mean and standard deviation (SD) for test and retest contrast sensitivity in log CS of twelve participants.

Table 1. Mean and standard deviation (SD) for the FrACT, F.A.C.T., TueCST and qCSF using repeated contrast sensitivity measurements in log CS.

		Spatial Frequency (cpd)
		1.5		3		6		12		18
		Test	Retest	Test	Retest	Test	Retest	Test	Retest	Test	Retest
Contrast Sensitivity (log CS)	FrACT	1.93 (0.18)	1.91 (0.13)	1.96 (0.14)	1.88 (0.16)	1.78 (0.29)	1.74 (0.29)	1.36 (0.24)	1.31 (0.25)	1.02 (0.25)	0.94 (0.35)
	F.A.C.T.	1.89 (0.11)	1.93 (0.10)	2.16 (0.07)	2.17 (0.07)	2.13 (0.18)	2.16 (0.13)	1.81 (0.27)	1.90 (0.21)	1.26 (0.24)	1.40 (0.35)
	TueCST	1.85 (0.15)	1.84 (0.18)	1.91 (0.15)	1.96 (0.14)	1.74 (0.20)	1.77 (0.22)	1.29 (0.24)	1.31 (0.26)	0.93 (0.31)	0.95 (0.26)
	qCSF	1.67 (0.27)	1.58 (0.24)	1.88 (0.22)	1.76 (0.30)	1.71 (0.24)	1.68 (0.22)	1.16 (0.42)	1.19 (0.25)	0.73 (0.49)	0.74 (0.30)

3.1 Accordance of different contrast sensitivity tests

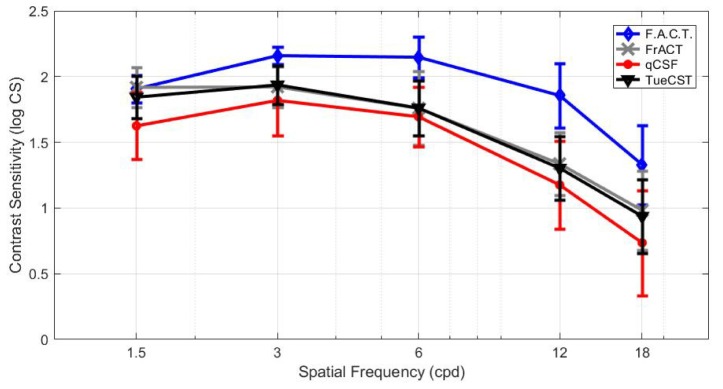
From each contrast sensitivity test, the CSFs were plotted along the measured contrast sensitivities at five spatial frequencies, and are presented in Fig. 2. A typical form of a CSF curve with a shape of an inverted ‘U’ was measured with all of the four tests. The CSF of F.A.C.T. showed its maximum at 6 cpd, FrACT at 3 and 6 cpd, qCSF and the TuebingenCSTest at 3 cpd. The shapes of the inter-individual mean CSFs were similar among the FrACT and the TuebingenCSTest. The standard deviation (SD) of the two repeated measurements varied with spatial frequency and reached smallest at 3 cpd within F.A.C.T., FrACT or TuebingenCSTest. In contradiction when the qCSF assessed the CSF, the smallest SD was obtained at 6cpd within qCSF.

Fig. 2.

Mean and standard deviation (SD) of contrast sensitivity measurements in log CS for TueCST, FrACT and qCSF for a luminance of L = 40 cd/m², and for F.A.C.T for L = 85 cd/m².

Kolmogorow-Smirnow test revealed that the measured contrast sensitivity data of FrACT, TuebingenCSTest and qCSF were normally distributed, but not those of F.A.C.T. (p<0.05). Statistical analysis of the contrast sensitivities demonstrated a significant difference among the four methods (χ² (3) = 165.43, p < 0.001, n = 120, Friedman Test). The post-hoc analysis found a significant difference between qCSF and the TuebingenCSTest (p < 0.001), between qCSF and FrACT (p < 0.001), between qCSF and F.A.C.T. (p < 0.001), between FrACT and F.A.C.T. (p < 0.001) and between F.A.C.T. and TuebingenCSTest (p < 0.001). But the post-hoc test showed no significant difference between FrACT and TuebingenCSTest (p = 0.92).

3.2 Inter-test repeatability – coefficient of repeatability

Table 2 contains mean and standard deviation (SD) and the Bland-Altman coefficients of repeatability (COR) for test and retest contrast sensitivity in log CS. High inter-test repeatability is indicated by a lower COR. Compared to already established test for the measurement of the CS, the CORs were lowest at 1.5, 6, 12 and 18 cpd for the new TuebingenCSTest, when compared to FrACT, F.A.C.T. and qCSF. Only repeated measurements at the spatial frequency of 3 cpd showed a slightly lower COR for F.A.C.T. compared to the TuebingenCSTest (COR 0.15 log CS vs. COR 0.18 log CS). The highest agreement between two measurements of contrast sensitivity using the TuebingenCSTest was at 6 cpd with a COR of 0.15 log CS.

Table 2. Coefficient of repeatability (COR) for the FrACT, F.A.C.T., TueCST and qCSF using repeated contrast sensitivity measurements in log CS.

		Spatial Frequency (cpd)
		1.5	3	6	12	18
COR (log CS)	FrACT	0.23	0.20	0.26	0.33	0.48
	F.A.C.T.	0.22	0.15	0.39	0.29	0.47
	TueCST	0.17	0.18	0.15	0.23	0.38
	qCSF	0.64	0.55	0.40	0.66	0.81

Although the COR values of F.A.C.T. were robust at 1.5, 3 and 12 cpd, the F.A.C.T. had a COR of 0.39 log CS at 6 cpd, while the TuebingenCSTest and the FrACT showed a better repeatability. The FrACT test demonstrated a marginal better average COR value with 0.30 log CS compared to F.A.C.T. with COR 0.31 log CS, but the repeatability for qCSF turned out in a poor agreement with COR of 0.61 log CS. On average the TuebingenCSTest revealed a COR of 0.22 log CS indicating that the developed test showed a higher repeatability when compared to FrACT, F.A.C.T. and qCSF.

3.3 Test-retest reliability - intraclass correlation coefficient

Table 3 contains intraclass correlation (ICC) for the test and retest of the contrast sensitivity in log CS. The ICC were highest for the TuebingenCSTest compared to FrACT, F.A.C.T. and qCSF. According to Cicchetti ICC between 0.75 and 1.00 are interpreted as excellent, between 0.60 and 0.74 as good, between 0.40 and 0.59 as fair and smaller than 0.4 as poor [38]. An ICC of 0.31 for qCSF at 1.5 cpd and an ICC of 0.33 for F.A.C.T. at 6 cpd indicated almost poor reliability, nevertheless on average the qCSF and F.A.C.T. demonstrated a good reliability with ICC of 0.61 and 0.63, respectively. The FrACT and the TuebingenCSTest came up with excellent reliability at all tested spatial frequencies. However, the developed TuebingenCSTest revealed always higher ICCs with a range between 0.88 and 0.96 ICC, representing the best reliability among all four contrast sensitivity tests.

Table 3. The Intra-class correlation (ICC) for the FrACT, F.A.C.T., TueCST and qCSF using repeated contrast sensitivity measurements.

	Spatial Frequency (cpd)
	1.5	3	6	12	18
FrACT	0.83	0.82	0.94	0.86	0.81
F.A.C.T.	0.60	0.59	0.33	0.87	0.76
TueCST	0.93	0.88	0.96	0.94	0.88
qCSF	0.31	0.58	0.77	0.70	0.67

3.4 Time duration

The TuebingenCSTest was performed with a mean duration ( ± SD) of 10.17 ± 1.52 minutes, while qCSF took 2.17 ± 0.87 minutes, FrACT 9.08 ± 1.35 minutes and F.A.C.T. 5.17 ± 1.37 minutes. Since all these tests need some time to instruct the participant, an average instruction time of 1-2 minutes can be estimated, depending on the age of the participant as well as whether the participant is naïve to these kinds of measurements or not. This instruction has to be conducted before the measurements start and has to be added to the actual measurement time.

4. Discussion

The newly developed contrast sensitivity test was designed to be able to work with a sufficiently high gray-level resolution, using an effective staircase procedure and accurate presentation of the spatial frequency by incorporating the magnification of spectacle lenses. Good agreement with the FrACT confirmed that the new TuebingenCSTest is measuring contrast sensitivity at the correct range of log CS values. Although the coefficients of repeatability (COR) were lowest at 3 cpd for F.A.C.T., the CORs were lowest in the TuebingenCSTest separately at 1.5, 6, 12 and 18 cpd indicating the TuebingenCSTest to have a better repeatability compared to the FrACT, the F.A.C.T. and the qCSF for measuring contrast sensitivity. Conformingly, the intraclass correlation coefficients (ICC) were highest for TuebingenCSTest when compared to FrACT, F.A.C.T. and qCSF.

One reason why F.A.C.T. showed significant higher contrast sensitivities compared to FrACT, qCSF and TuebingenCSTest is simply explained by the fact that the contrast sensitivities are higher with higher luminance because F.A.C.T. used 85 cd/m², but whereas the other tests used the ViewPixx monitor that had a luminance of 40 cd/m². Compared to the F.A.C.T and FrACT test, the TuebingenCSTest and qCSF used Gabor patches with Gaussian edge while the other two tests used circular grating patches with abrupt edges. Due to the Gaussian filtering of the edge, a Gabor Patch also contains low spatial frequencies compared to a circular grating. But since abrupt edges have a sharper transition from stimulus to background, this ‘edge sharpening’ can induce contrast enhancement in images for example [39], and hence a Gaussian edge is preferred for the test of the threshold contrast and was therefore applied in the qCSF and the TuebingenCSTest. The influence on the perception of the edge itself of the stimuli can be assumed as small, because a Gaussian edge of 0.1° was used, whereas the stimulus size was 1.7°. Furthermore, the F.A.C.T. did not present the stimuli with 300 ms and also all nine contrast levels were presented at the same time as long the participant wanted to look at them. In addition, due to the fact that the F.A.C.T. uses a 3-AFC, the probability for the participant to reach one step above their threshold (also called guess rate) is 33%, while the probability to score two steps above the threshold is 11% [40]. By using a 4AFC in the other tests, the guess rate to measure higher thresholds is 25% for one step and 6.25% for two steps. Although the F.A.C.T. holds all these advantages, its repeatability and its reliability was worse than the TuebingenCSTest for all spatial frequencies, excluding the COR at 3 cpd. The ICC of the FrACT ended up better when compared to the F.A.C.T. for almost all spatial frequencies, whereas the repeatability was similar. Due to the total number of only 50 trials, the main advantage of the qCSF is the very short duration of the measurement, but the test suffers from a low repeatability, reliability and came up with significant poorer contrast sensitives than FrACT and the TuebingenCSTest. The repeatability of the qCSF could be probably increased by increasing the number of trials, as shown by Dorr [41].

It is well known that the test of the CS has advantages especially in the detection and monitoring of ocular pathologies. Because such a test takes commonly long, especially in older and untrained participants or patients, most practitioners avoid the test of the CS. Possible solutions to reduce the time needed for this CS measurement, especially while using the TuebingenCSTest, are: On the one hand, a faster computer with more random-access memory (RAM) can be used, while on the other hand, it is also possible to reduce the number of presentation of the used stimuli. The experiments were conducted on a computer with limited random-access memory (RAM), which prolongs the inter stimulus interval leading to a longer duration of the measurement. With more RAM memory, we were able to achieve a time duration of 55 ± 11 seconds (mean ± SD) per spatial frequency. With initial instruction, the whole test would take at least 6 minutes, which would roughly halve the current duration of ca. 10 minutes of the TuebingenCSTest. While the use of a fast personal computer only requires an investment of money, the use of fewer trials has some disadvantages that need to be additionally addressed. Most likely, the repeatability and as well as the reliability will be affected in case fewer trials are used.

The measurement with the TuebingenCSTest is more time-efficient if the slope is fixed, since in that case, the threshold contrast can be assessed within only 50 trials. Hou and colleagues showed that the slope is constant within individuals, but varies among individuals [42]. To estimate both, the slope and the threshold, the Ψ (psi) method needs more than 250 trials for a 2AFC [23]. Our 4AFC procedure might need less trials than for 2AFC to determine the slope, but still probably more than 50 trials. For future experiments, the slope can be estimated with the TuebingenCSTest to use individual slopes for each participant in order to increase the accuracy of the threshold contrast determination.

The Ψ method of Kontsevich and Tyler was indicated as the best method for getting both thresholds and slopes [23, 43]. Relevant for the TuebingenCSTest, pro and contra arguments for and against the Ψ method are listed in Table 4.

Table 4. The Ψ (psi) method: arguments pro and contra.

Pro	Contra
Ψ adapts fast near to coarse threshold and then slowly and precisely to the threshold [23], like other adaptive procedures, see Fig. 1.	Lapses and biases (e.g. serial dependencies [44]) affect adaptive procedures regarding the accuracy of threshold estimation.
Threshold and slope of the psychometric function can be determined within the same measurement [23].	Lapses can have an impact rather on adaptive procedures than method of constant stimuli for example.
Adaptive procedures are more time-efficient than the method of constant stimulus, in which the stimulus presentation is repeated at exactly the same intensity level multiple times.	Lapses can occur for example due to pressing button wrongly [45], or not fixating on the stimulus by eye blinks or involuntary saccades.
	To estimate the threshold and especially the slope, the Ψ algorithm needs a lot of computational power, especially RAM memory, for calculating the uncertainty [45].
	Calculations in real-time can unintentionally prolong the inter stimulus interval leading to longer duration of the measurement [45].

One disadvantage of adaptive procedures like the Ψ method is the fact that errors in the first trials affect the further procedure [23, 25]. This can occur because observers make for example lapses such as occasional finger errors which are considered as stimulus-independent [46]. Obviously, also eye blinks or involuntary saccades would lead to less fixations on the stimulus that would lead to errors in the measurement of the contrast sensitivity. Therefore, to partly overcome such attentional-caused lapses by eye movements, a gaze contingent presentation of the used stimulus can be implemented in the TuebingenCSTest. Another disadvantage are biases, such as serial dependencies e.g. that right-handed observers may be biased to press the right button on the response keyboard [47].

Since perceptual learning can change the slope [48], a threshold measurement should be done in trained observers. Because the participants in the current study were naïve observers, we used the following method to overcome this effect: a short training with feedback was presented in the TuebingenCSTest and a constant slope was assumed. Feedback was provided for every trial to reduce the chance for biases and lapses. As described for visual acuity measurements using the FrACT, systematic feedback does not affect reproducibility and also offers advantages such as greater comfort [49].

To accurately present stimuli for a contrast sensitivity measurement, a sufficiently high gray-level resolution as well as an accurate presentation of the spatial frequency are needed. The sufficiently high gray-level resolution was achieved by using the ViewPixx monitor with a 16-bit gray-level resolution. The advantage of using 16-bit gray-level resolution is the fact that the Gabor Patch can be presented smoothly, which means that the sine wave consists of additional but smaller steps. Since the human eye is able to perceive contrasts up to 0.15% (2.82 log CS) [50–52], the second advantage of a 16-bit gray-level resolution is the fact that the minimum amplitude of the sine wave stimuli (the lowest contrast level) can be smaller compared to the 8-bit gray-level resolution. In the current experiment, the FrACT was presented with a gray-level resolution of 8 bits. Due to the loss by gamma correction and by a smooth oscillating presentation of the Gabor Patch, this would lead to a 4-bit gray-resolution that corresponds to a minimal presentable contrast of 6.25% (1.20 log CS). In case the contrast levels are defined, the staircase procedure would continue in order to approach further threshold contrasts lower than 1.20 log CS. In this case, an 8-bit resolution would not present a Gabor Patch with smooth oscillating sine waves. Thus, the Gabor Patch would rather convert to square wave stimulus. These steps of the square wave can appear as sharp edges in the gray-level dimensions and it was shown that this ‘edge sharpening’ can induce contrast enhancement in images for example [39]. Such gray-level edges would become more obvious for Gabor Patches with lower spatial frequencies, because they cover more pixels in-between one cycle which can be filled with more gray-levels than in Gabor Patches with higher spatial frequencies. Furthermore, these gray-level edge sharpening will increase detectability: This increased sensitivity to edges can be explained by the antagonistic receptive fields of retinal ganglion cells and their lateral inhibitory connections which seemingly enhances contrast perception [53]. At 1.5 cpd, the FrACT showed a higher contrast sensitivity compared to the TuebingenCSTest (1.94 vs. 1.84 log CS). This difference was not significant, but could be explained by contrast enhancement through sharpening of edges in the 8-bit gray-level resolution.

As Blackwell described in his criteria called ‘sensory-determinacy’, methods that lead to lower threshold are preferred [54], since higher thresholds may indicate that the used method would lead to more unwanted extrasensory influences on the observer [47]. But the FrACT with an 8-bit gray-level resolution should be not preferred, although thresholds were lower than in the TuebingenCSTest because the observers were predisposed to lower threshold values due to increased gray-level edges.

Also an accurate presentation of the spatial frequency was achieved by incorporating the magnification of spectacle lenses. Other authors like Radhakrishnan corrected for spectacle magnification by altering the test distance [55]. For the new TuebingenCSTest, the correction for magnification was accomplished before recording the response. Therefore, with the TuebingenCSTest, measured contrast sensitivity for a certain spatial frequency may afford a better comparison over participants with different prescriptions.

Furthermore, another advantage of the TuebingenCSTest and the FrACT is that it can be used for detecting notches in the CSF, which are selective spatial frequency losses due to optical defocus [56]. Tests such as qCSF tend to overlook these notches because they estimate the CSF with a given function that is not able to reflect selective spatial frequency losses.

5. Conclusion

We have successfully implemented the time-efficient Ψ method to measure the contrast sensitivity of the human eye with a sufficiently high gray-level resolution that allows a smooth oscillating Gabor Patch presentation. Correcting the presented spatial frequencies and the stimulus size to overcome the magnification of worn spectacle lenses helps to gain comparable threshold contrasts for participants with different habitual refractive errors. The new presented method, called TuebingenCSTest, can be set up customized and shows high precision, repeatability and reliability over a wide range spatial frequencies regarding contrast sensitivity measurements.

Funding

Eberhard-Karls-University Tuebingen (ZUK 63) as part of the German Excellence Initiative from the Federal Ministry of Education and Research (BMBF).