Abstract
Optical coherence tomography (OCT) has become an important imaging modality with numerous biomedical applications. Challenges in high-speed, high-resolution, volumetric OCT imaging include managing dispersion, the trade-off between transverse resolution and depth-of-field, and correcting optical aberrations that are present in both the system and sample. Physics-based computational imaging techniques have proven to provide solutions to these limitations. This review aims to outline these computational imaging techniques within a general mathematical framework, summarize the historical progress, highlight the state-of-the-art achievements, and discuss the present challenges.
OCIS codes: (110.4500) Optical coherence tomography, (110.1758) Computational imaging, (100.3175) Interferometric imaging, (100.3190) Inverse problems, (110.1085) Adaptive imaging
1. Introduction
Since its introduction in the early 1990s, optical coherence tomography (OCT) has become an invaluable modality with widespread biomedical applications [1–8]. In particular, it is now a standard of clinical care in ophthalmology [9]. OCT is the optical analogue of ultrasound imaging and measures the backscattered light to probe the three-dimensional (3D) structures of scattering samples. One attractive advantage of OCT is the decoupling of axial and transverse resolution, which makes it possible to achieve rapid volumetric imaging with millimeter-scale imaging depth and micrometer-scale axial resolution by using a low numerical aperture (NA) optical system. The use of low-NA optics, however, comes at the expense of low transverse resolution. In many medical and surgical scenarios, however, higher transverse resolution for visualizing cellular features in vivo is desirable. Therefore, the long-standing trade-off between transverse resolution and depth-of-field (DOF) limits further development of OCT.
As a broadband interferometry-based imaging technique, dispersion mismatch between the sample and reference paths negatively affects the axial resolution in OCT. Fully compensating for dispersion leads to the highest image quality, but this is often difficult to achieve in practice. Likewise, in some cases it is not desirable, or perhaps not possible, to achieve high-quality aberration-free imaging optics. In this case, aberrations can severely degrade the OCT image quality. Together, these limitations of dispersion mismatch, DOF, and optical aberration lead to restricted performance of an otherwise powerful imaging technology.
Across all imaging modalities, the exponential growth of computing power has enabled a revolution of imaging systems by improving image quality, accelerating the imaging speed, and offering more analysis and insight into the acquired data. Advanced computing power also provides more flexibility in hardware system design due to the fact that physical measurements can rapidly be inverted mathematically, and the substantial amount of data processing required to do this is now possible. Digital reconstructions based on physical models of imaging and multiplex object-to-data relations are other important features of computational imaging. Historical precedents include the evolution of X-ray projections into computed tomography [10,11], nuclear magnetic resonance into magnetic resonance imaging [12], and radar imaging into synthetic aperture radar (SAR) [13]. Following this historical trend, computational imaging techniques have been playing an increasingly important role in optical imaging, for example, incoherent fluorescence imaging [14], coherent digital holography [15], and OCT.
Optical computational imaging techniques have been proposed and developed in recent years to overcome the above limitations in OCT [16,17]. These techniques have been adapted to various types of OCT instruments and demonstrated as powerful tools in many applications, showing better performance than standard OCT alone. The post-processing nature of these methods provides more flexibility and dramatically decreases the time of the imaging session. In this paper, we review the physical models of these problems, their related computational imaging solutions, the current applications and challenges, and future directions.
2. General theoretical model of OCT
OCT is a broadband interferometric imaging technique which measures the backscattering light from the sample to reconstruct the depth-resolved structures [18,19]. Depending on the implementation scheme, OCT can be categorized into time-domain OCT (TD-OCT) and Fourier-domain OCT (FD-OCT). FD-OCT can be realized by different configurations of light sources and detectors, such as point-scanning spectral domain OCT (SD-OCT), and point-scanning and full-field swept source OCT (SS-OCT). The collected data is equivalent, or equivalent under a Fourier transform along the axial/wavenumber axis. Without loss of generality, we begin the discussion based on a point-scanning FD-OCT system similar to Fig. 1. As the detector is a square-law device, the signal we obtain for transverse scanning position (x, y) and wavenumber k can be described as
| (1) |
whereandare the light fields from the sample arm and the reference arm, respectively, and the superscript asterisk (*) indicates complex conjugation.denotes the complex cross-correlation term, which contains the object field information we are interested in.
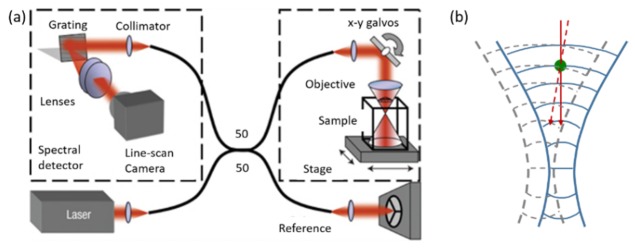
Fig. 1.
Schematic of a point-scanning spectral-domain OCT system. (a) A fiber-based Michelson interferometer is used to measure the spectral interference from the sample arm and reference arm with a spectrometer. In the sample arm, light is focused into the sample and scanned by the scanners. (b) A scatterer is probed by a Gaussian beam traveling at different angles. Figure adapted from [16].
3. Axial resolution improvement by computational techniques
Because the light travels through different optical materials in the sample arm and reference arm, the backscattering field at each wavelength may experience different delays due to the material dispersion.can therefore be rewritten as, whereanddescribe the additional accumulated phase deviation in the sample and reference arm due to the dispersion along the light path. For brevity, we define.
The mismatched phase distortion affects the axial resolution because it effectively results in a convolution between the ideal reflectivity profile with the Fourier transform of the mismatched phase,
| (2) |
wheredescribes a Fourier transform from the spectral to spatial domain, and the operator describes a convolution in the axial direction. By taking a Taylor expansion of the phase distortion,the effect of the convolution can be described as a combined effect from each order. The 0th and 1st order result in a phase shift and a circular spatial shift in the image, which does not usually pose a significant concern. However, the higher orders correspond to blurring effects and must be corrected to restore optimum axial resolution. For a system with well-matched dispersion, the higher order derivatives are close to zero, and as a result, the axial resolution is not affected. For a system with unmatched dispersion, however, degraded axial resolution can be observed.
The dispersion mismatch can be eliminated either experimentally by inserting and adjusting a variable thickness glass block in the reference arm, or by numerical computational methods in post processing. The former, however, cannot always remove the exact dispersion and is lacking in flexibility. Many different computational dispersion correction algorithms for OCT have been developed and demonstrated for the improvement of the axial resolution. Some early work [21] used the CLEAN algorithm for OCT dispersion correction, which is an iterative point-deconvolution algorithm that was previously used by the radio astronomy community. Fercher et al. proposed a method [22,23] to use depth-dependent phase correction for each windowed region to achieve numerical dispersion compensation. A similar phase cancellation method was used by Cense et al. who extracted and fitted the phase distortion up to the 9th order from the coherence function obtained from a strongly-reflecting reference point [24]. Work by de Boer [25] applied a quadratic phase shift in the Fourier domain of the interference signal to eliminate the group-velocity dispersion.
Another method was proposed by Marks et al. [26] that enabled the correction of dispersion within a dispersive homogeneous media or stratified media using a spectral resampling scheme,
| (3) |
where N is the total number of points in each axial scan, n is any integer between 0 and N-1, is the resampling array,is a number between 0 and 1, and,are the dispersion parameters. The numerical dispersion correction for both fixed system dispersion and sample material dispersion was automated using an autofocus algorithm by Marks et al. through iteratively minimizing the Renyi entropy of the corrected axial-scan image [27]. Another automated dispersion compensation method was proposed by Wojtkowski et al. which functioned by iteratively updating the 2nd and 3rd parameters, thereby maximizing a sharpness metric function such as one over the total number of pixels with intensity above a threshold [28]. With these numerical dispersion compensation algorithms, dispersion in OCT images can be flexibly and effectively corrected, resulting in near-optimal axial resolution, and at the same time, reducing the hardware complexity in the experimental setup. However, because of defocus and possible aberrations of the beam, transverse resolution of the image can still be sub-optimal. In the following sections, additional computational approaches will be introduced to address these concerns.
4. Trade-off between transverse resolution and depth-of-field
In OCT, the axial coherence gate causes the transverse and axial resolutions to be decoupled. The axial resolution is mainly affected by the light source. In a modern dispersion-corrected OCT system, good axial resolution in scattering tissues can be achieved by using a broadband light source. Improving the transverse resolution of OCT, however, is more challenging. The transverse resolution is determined by the effective NA of the objective and scales linearly with 1/NA. A higher NA system, e.g. optical coherence microscopy (OCM), generates a tighter focal spot, which provides higher transverse resolution. Unfortunately, the increase of NA also leads to the reduction of depth-of-focus, which is inversely proportional to the square of NA (1/NA2). Figure 2 is an illustration of focusing in OCT and the trade-off between resolution and depth-of-focus. In standard OCT using low NA optics, the light is implicitly assumed to be perfectly collimated in a pencil beam. In reality, the propagation of a Gaussian beam must converge before and diverge away from the focus. Only a portion of the 3D image volume within the DOF exhibits the desired transverse resolution, while the regions at out-of-focus depths are blurred. In low NA systems, the beam width w0 (related to transverse resolution) and the confocal parameter b (related to DOF) are both large, while in high NA systems, a tight focal width or spot size implies a small DOF.
Fig. 2.
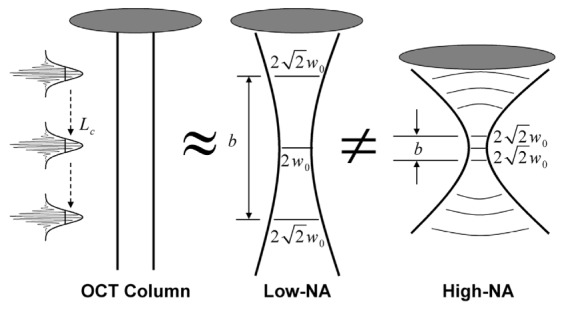
Geometry of a Gaussian beam for low- and high-numerical-aperture (NA) lenses. These geometries are contrasted with the assumption of a collimated axial OCT scan. The confocal parameter, b, is the region within which the beam is approximately collimated, and w0 is the beam radius at the focus, which is related to the transverse resolution (2w0). The axial resolution depends on the coherence length of the source, Lc. Figure adapted from [20].
To obtain a large DOF image with high transverse resolution for the visualization of finer structures, much work has been done to overcome this inherent trade-off and problem. Some attempts have been based on hardware methods, such as mechanical depth scanning [29,30], dynamic focus shifting [31–33], multi-beam focusing [34], and wavefront engineering for non-Gaussian beam illumination [35–40]. Hardware-assisted computational imaging approaches have also been proposed. Examples are complex wavefront shaping [41,42] and depth-encoded synthetic apertures [43,44]. The hardware-related methods require special hardware set-up configurations in the system design, which can complicate and increase the cost of the OCT system. In this paper, we focus on the computational imaging solutions to this trade-off between transverse resolution and DOF in OCT/OCM.
4.1 Deconvolution
The first attempt of using computational approaches to mitigate the transverse blurring outside the confocal parameter is amplitude-based deconvolution, which estimates the point spread function (PSF) and is popular in incoherent microscopy. Schmitt [21] derived the CLEAN deconvolution algorithm to sharpen the image in both the lateral and depth dimensions. Unlike the early deconvolution methods that only applied to single A-scans to improve the axial resolution, Ralston et al. [45] proposed a Gaussian optics model to incorporate information from adjacent A-scans. An iterative expectation-maximization algorithm, the Richardson-Lucy algorithm, with a beam-width-dependent iteration scheme, was developed for Gaussian beam deconvolution to improve the transverse resolution in OCT. An improvement in the transverse PSF for sparse scattering samples (tissue phantom with microparticles) in regions up to two times larger than the confocal region of the lens was achieved. The work in Ref [46] compared Wiener and Richardson-Lucy OCT image restoration algorithms and showed that the Richardson-Lucy algorithm provided better contrast and quality. Later, several Richardson-Lucy-based deconvolution approaches [47–50] and a Maximum-a-Posterior reconstruction framework [51] were proposed to improve the lateral resolution in OCT.
These methods rely on intensity-based models, and are not sufficiently accurate because phase information is neglected. For example, the interference fringes on an en face image produced by two closely adjacent scatterers outside the confocal region cannot be resolved by these real-valued PSF estimation methods. In addition, the optical transfer function of these incoherent processing methods is, in general, complicated with varying magnitudes and may contain small or even zero values, which make these methods sensitive to speckle and noise [52]. Therefore, these methods have rarely been used for imaging scattering tissue. We classify these above methods as computational image-processing methods. In the following two sections, we review what we term computational imaging methods based on the physical model of wave propagation, which utilizes the full complex field information that is naturally obtained from the broadband interferometric measurement in OCT.
4.2 Interferometric synthetic aperture microscopy
The OCT experiment can be considered as an inverse scattering problem [53,54]. To discuss the physics-model-based relationship between the detected data and the object structure, and the related computational imaging solutions, we begin with the dispersion-corrected complex 3D signal,, which can be given by a convolution of the (complex) system PSF,,with the sample scattering potential [16,55,56]
| (4) |
The axial origin of the coordinate systemis set at the focal plane without loss of generality. For a point-scanning system, the transverse information is acquired through the two-dimensional (2D) scanning of the focused beam. For full-field OCT systems, the lateral spatial information can be acquired by a 2D camera simultaneously, while the wavenumber is scanned. In both cases, the lateral sampling step should obey the Nyquist sampling requirement. Therefore, the 3D information can be coherently synthesized as long as the phase between each scanning step satisfies the stability requirement (discussions in Section 6) within the optical interrogation time. Utilizing the convolution theorem, Eq. (4) can then be rewritten in the transverse spatial frequency domain as
| (5) |
whererepresents the 2D transverse Fourier transform,is spatial frequency, and denotes the (depth-dependent) transverse band-pass response of the effective PSF. Under the asymptotic approximations for both the near-focus and far-from-focus cases, Eq. (5) can be simplified to the forward model [55] as
| (6) |
with
| (7) |
whererepresents the 3D Fourier transform, and the factor of 2 is introduced because of the double-pass geometry.denotes the space-invariant axial and transverse spatial frequency response of the system, which is related to the generalized pupil function derived in Fourier optics [57] and proportional to the optical power spectral density (detailed discussion can be found in Ref [55]). This frequency response of the system takes slightly different forms for the regimes within and beyond one Rayleigh range, and in theory, it should be inverted to fully recover the scattering potential [16]. When inverting the system PSF, it is important to regularize the inverse operator to avoid amplifying noise. This can be done using a Tikhonov-regularized pseudo-inverse filter with an appropriate regularization parameter [20]. However, in the common cases where aberration-free scalar Gaussian beam are used for illumination,is generally smooth within the pass-band and is a real Fourier-domain weighting factor, which will not introduce significant image distortions [55,58,59]. Therefore, it is sensible to compute the unfiltered solution of the scattering potential in the frequency domain,
| (8) |
Spatial domain structures can then be retrieved by the 3D inverse Fourier transform
| (9) |
The resampling stepin Eq. (8) corrects the depth-dependent defocus and is crucial for the performance of the algorithm. This coordinate warping in the Fourier domain of the signal was originally developed in the field of geophysics, and is known as the Stolt mapping [60]. This reduces the many-to-one mapping [one relates to many at different] in Eq. (5) to a one-to-one mapping between the spatial frequency domain of the object and the detected data, providing the capability to bring all the depths into focus simultaneously. This technique of defocus correction for the entire 3D OCT data set by solving the inverse problem is termed interferometric synthetic aperture microscopy (ISAM), and was first proposed by Ralston et al. [16,20,61] based on a point-scanning paraxial SD-OCT system. ISAM has been extended to different imaging geometries for both structural and functional imaging (e.g. full-field ISAM [62,63], rotationally-scanned ISAM [56], vector-field ISAM [55], and polarization-sensitive ISAM [64]), and has been successfully implemented by various research groups with different system configurations [65–72]. An example showing how ISAM corrects the defocus blur for different depths and the related warping of spatial frequency domain structures can be seen in Fig. 3.
Fig. 3.
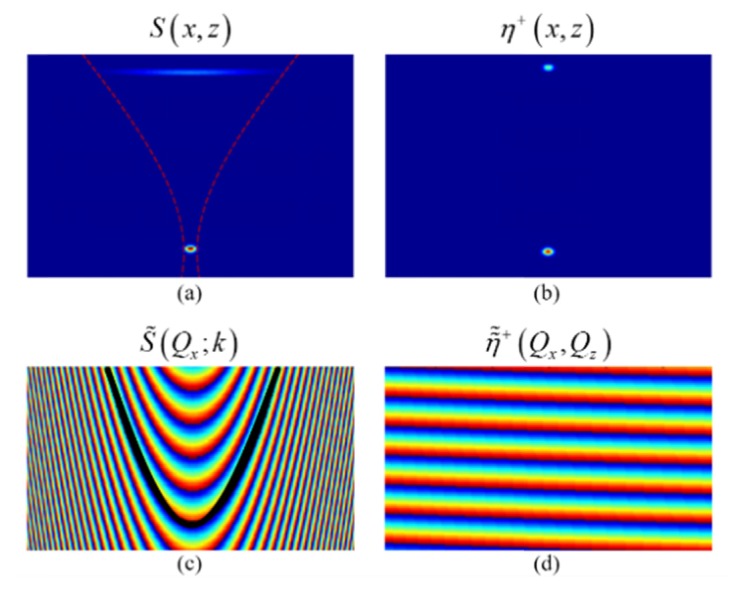
Simulation of two scattering particles which are in-focus and far-from-focus, respectively. (a) Cross-section image of the standard OCT reconstruction showing strong defocus for the far-from-focus particle. (b) ISAM reconstruction showing depth-invariant high transverse resolution. (c) Phase of the original complex data in the frequency-domain. Black line illustrates ISAM resampling curve. (d) Resampled phase in the frequency-domain, corresponding to the ISAM reconstruction. Adapted from [73].
Just as the name suggests, ISAM has much in common with SAR in both the physics and mathematics of the problem [74]. A heuristic illustration in Fig. 1(b) shows that a scatterer outside the focus region is probed by the scanning Gaussian beam multiple times at different angles during the scan. This acquisition scheme is very similar to SAR, although a divergent beam instead of a focusing beam is used in SAR. Computationally, SAR uses Fourier domain reconstruction methods that synthesize a very large aperture from continuous scan data to achieve high resolution radar images. These methods were independently developed by Wiley at the Goodyear Aircraft Company [75] and Sherwin et al. at the University of Illinois at Urbana-Champaign in the 1960s [76]. Interestingly, as the digital computational power at that time was far from sufficient for processing radar data, Fourier optical methods were used for radar data processing [77–79]. Further insightful comparisons and connections between SAR and ISAM were discussed in Ref [74]. In addition to SAR, ISAM also shares a broad commonality with other systems applying computational imaging to multi-dimensional data collected using both spatial multiplex and time-of-flight measurements from a spectrally-broad temporal signal, such as synthetic aperture sonar [80], seismic migration imaging [81], and certain modalities in ultrasound [82] and photoacoustic imaging [83].
ISAM brings the power of computational imaging into OCT and enhances the diagnostic capabilities. Many biomedical applications of OCT could benefit from the unique feature of spatially invariant reconstructions, which offers both high lateral resolution and extended DOF. One application example is for optical biopsy, as shown in Fig. 4. Resected human breast tissue was imaged by a point-scanning SD-OCT system with 0.05 NA. A volumetric ISAM rendering is presented and en face sections from regions far from (Section A) and nearer to (Section B) the focus are selected to compare histology, standard OCT processing, and ISAM reconstruction. It is evident that the out-of-focus images in standard OCT are blurry and the tissue features are more difficult to distinguish [Fig. 4(b), 4(e)]. The ISAM reconstruction provides transverse resolution improvement and exhibits comparable cellular features with respect to the histological section [Fig. 4(c), 4(f) and 4(a), 4(d)]. As a result, significantly more information regarding the tissue can be extracted within a shorter imaging time, without depth scanning.
Fig. 4.
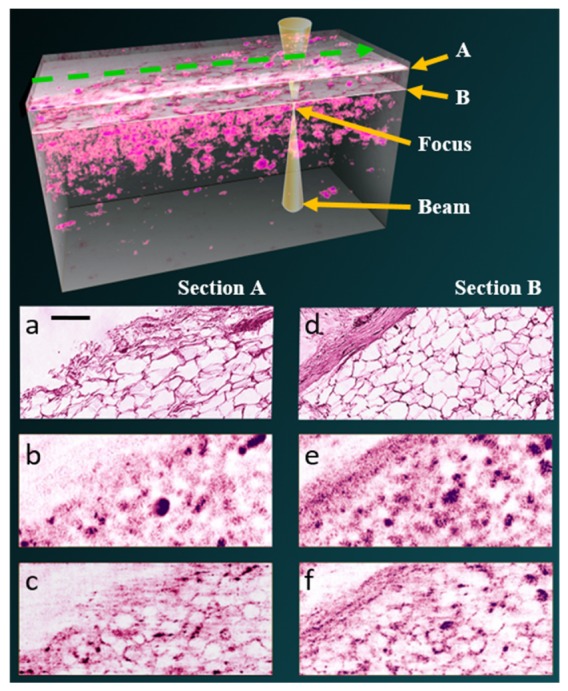
Human breast tissue imaged with Fourier-domain OCT according to the geometry illustrated in the top. En face images are shown at two different depths above the focal plane, 591 µm (section A) and 643 µm (section B). ISAM reconstructions (c,f) resolve structures in the tissue which are not decipherable from the standard OCT processing (b,e), and exhibit comparable features with respect to the histological section (a,b). The scale bar indicates 100 µm. Figure adapted from [16].
Because more underappreciated and neglected information in the OCT data is utilized in ISAM for improving image quality, the data manipulation and signal processing is much more intensive than standard OCT processing. Because of the rapid development of microelectronic devices, computational imaging has benefited greatly from the increasingly powerful computing resources and imaging sensors. Physics-based approximation models were proposed for high-speed parallel algorithms, which led to real-time visualization of ISAM reconstructions by using a multi-core CPU [58], graphics processing units (GPUs) [59] (examples can be seen in Fig. 5), and portable digital signal processers (DSPs) [84]. As a result of these and other technological advancements, ISAM technology has been commercialized by Diagnostic Photonics, Inc. in a system platform that includes a hand-held probe [85].
Fig. 5.
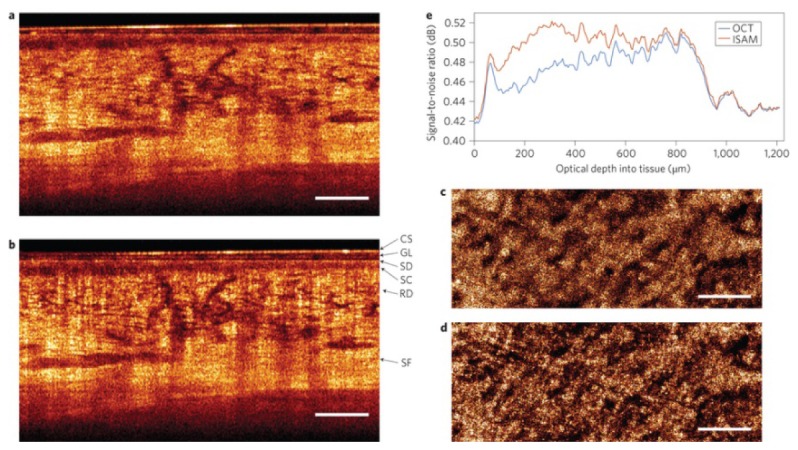
Real-time ISAM visualization of highly-scattering in vivo human skin from the wrist region acquired using a 0.1 NA OCT system, after placing the focus 1.2 mm beneath the skin surface. Cross-sectional results of (a) OCT and (b) ISAM. En face planes of (c) OCT and (d) ISAM at an optical depth of 520 µm into the tissue. (e) Variation of SNR with depth shows the improvement of ISAM, which was computed using the 20% (noise) and 90% (signal) quantiles of the intensity histograms. Compared to OCT, ISAM shows significant improvement over an extended depth range. CS, coverslip; GL, glycerol; SD, stratum disjunction; SC, stratum corneum; RD, reticular dermis; SF, subcutaneous fat. Scale bars represent 500 µm. Adapted from [59].
As ISAM provides depth-invariant transverse resolution, it has been discovered that the strategy of placing the focus deep in the tissue can dramatically improve the SNR from the sample surface to the focus [59]. Figure 5 shows an example of signal and resolution improvement of in vivo ISAM visualization by placing the focus deep, to 1.2 mm beneath the surface of highly-scattering human skin. The DOF was extended by over an order-of-magnitude (24 Rayleigh ranges) in real time.
ISAM has become user-friendly and provides real-time feedback, which is crucial for time-sensitive situations such as image-guided procedures or optical biopsies in clinical screening applications. Intraoperative ISAM imaging during thyroidectomy has been demonstrated, in which the extended depth-of-field provides better resolution of the thyroid follicle structure [86]. Another key clinical application is intraoperative imaging of cancer margins during breast conserving surgery. A recent clinical study demonstrated that a majority of reoperations could potentially be prevented through the use of intraoperative computational OCT imaging [87].
4.3 Digital refocusing
As there is a close connection between SAR and holography [88], it has also been recognized that an SD-OCT system, in principle, is performing digital holographic tomography synthesized by a series of wavenumbers, despite the detector being in the imaging or Fourier/Fresnel plane [72,89–92]. This can also be mathematically understood from the forward model. Applying the standard OCT processing (Fourier transform along k) to Eq. (6) and extracting a specific layer,
| (10) |
The scaling by a factor of two along depth is due to the double-pass nature of the OCT measurement. Replacingwithwhereis the central wave number andis the difference between the wavenumber and. Making theis small enough to be neglected,can be expanded under the paraxial approximation as
| (11) |
Equation (10) can then be rewritten as
| (12) |
where denotes convolution along depth. For different imaging systems, there may be different scaling factors [72,93]. Now, it can be seen that the term inside the brace in Eq. (12) is the scalar diffraction formula [57]. Therefore, it is clear that the defocus at a specific depth is caused by the quadratic phase term. Thus, digital refocusing methods that are based on scalar diffraction models and widely used in digital holography can also be applied to OCT data to cancel out this defocus term, such as the Fresnel propagation [94] or the angular spectrum method [93,95,96]. For a specific 2D en face plane, the out-of-focus OCT image is digitally refocused by simulating field propagation to the focal plane during post-processing. Equation (12) also implies the fact that it is equivalent to apply the conjugated quadratic phase term to eitheror for digital refocusing.
Figure 6 is an example that shows the image improvement by digital refocusing. Images of an onion sample were acquired using a point-scanning SD-OCT system. In Fig. 6(a), the en face OCT image from outside the focal region suffers from defocus. After digitally propagating the appropriate distance (estimated by optimizing the information entropy as an image metric), the same en face image is brought into focus [Fig. 6(b)]. Finally, Fig. 6(c) shows a representative en face image of the onion within the focal region for comparison.
Fig. 6.

Digital refocusing of OCT data from an onion. (a) En face plane from outside the focal region. (b) Digital refocusing result for (a). (c) A typical en face image within the focal region. Figure adapted with permission from [96].
Digital refocusing has been demonstrated not only in the point-scanning geometry but also with line-field SD/SS-OCT [97,98] and full-field SS-OCT [72,99–101]. In these systems, the data are acquired in the imaging plane. Holoscopy is another OCT technique combing a swept source laser and 2D camera with the detector in a plane within the Fresnel regime [92]. Digital refocusing is necessary for this technique, but this digital refocusing operation can only bring one 2D en face image into focus at a time, and the calculation is time consuming. Soon after, Hillmann et al. solved the inverse problem by resampling the data in the frequency domain, which can significantly reduce the processing time for the entire volume into a single computationally efficient step, which is very similar to full-field ISAM [102]. Example holoscopy images are shown in Fig. 7.
Fig. 7.

Holoscopic reconstruction of a grape comparing digital refocusing to the one-step reconstruction. (a) Cross-section from the volume refocued in one layer. (b) En face image at the virtual focus after the digital refocusing. (c) En face plane after the same digital recofusing operation as (b), 160 μm above the virtual focus. Since each depth is not independently brought into focus, defocus blur is still visible away from each virtual focus. (d) B-scan of the one-step reconstruction. (e) En face image at same location as (b). (f) En face image at same location as (f). Defocus is corrected since the one-step reconstruction brings every plane into focus. The NA was 0.14 (confocal parameter was 28 μm). Figure adapted with permission from [102].
The realization of ISAM and digital refocusing in various scanning systems demonstrates that computational imaging is versatile and not restricted to specific hardware configurations. It can be a powerful complementary tool for the existing hardware system and provides significant improvement over standard OCT processing. Different scanning geometries, however, have dissimilar effects on the data, such as the phase stability requirements (will be discussed in Section 6) and the signal strengths. Point-scanning systems usually have a confocal-type detection, which rejects undesirable multiply scattered light and provides better SNR around the focal volume, while the signal strength will decrease for the far-from-focus regions. Full-field OCT and holoscopy do not have the confocal gate, which makes these techniques more vulnerable to multiple scattering noise. However, these techniques have better photon-efficiency for detecting the out-of-focus light.
Although both ISAM and digital refocusing can correct the defocus blur, it should be stressed that they are different in theory. ISAM is a reconstruction technique that solves the inverse scattering problem for OCT and directly manipulates the 3D spatial frequencies, which brings all the depths into focus simultaneously and rearranges the 3D energy distribution of the data set (Fig. 4 and Fig. 5 in Ref [55], and Fig. 5 in [74]). Digital refocusing, in contrast, only deals with one 2D en face plane at a time, and cannot concentrate the energy spreading along the axial direction, which is caused by the quadratic phase migration. To achieve a space-invariant volume, processing needs to be carried out for all the depth layers separately, which leads to increased computational complexity [102].
5. Aberration correction
Aberration, which causes a deviation of an ideal wavefront, is an important issue affecting image quality in many imaging modalities. With increased NA for higher transverse resolution, the optical wavefront is more susceptible to being distorted by the imperfections of the imaging optics and the sample itself. As a result, the resolution may decrease, as well as the contrast and the signal-to-noise ratio. OCT/OCM also share this limitation are directly affected by aberrations in the system optics or the sample. Although OCT is usually performed at relatively low NA, it has been found that aberrations could still play a significant role in the disruption of the PSF in the far-from-focus regions [103]. Sophisticated optical designs can supress the static system aberrations [104,105], but they are not versatile for complex biological tissues that introduce unique, often dynamically changing, sample aberrations [106]. Hardware-based adaptive optics (HAO) has been introduced to correct the aberrations in incoherent imaging systems, such scanning laser ophthalmoscopy (SLO) [107] and fluorescence microscopy [108,109]. Integrated with OCT, HAO operates by using a wavefront sensor and wavefront corrector to dynamically measure and correct aberrations, has been developed for ophthalmology to study cellular details of the living human retina [110,111]. Recently, coherence-gated sensor-less adaptive optics has also been proposed and successfully applied to microscopy [112] and in vivo imaging of the human photoreceptor mosaic [113,114]. In spite of this success, HAO systems remain expensive and complex. In addition, the aberration compensation can only be valid for one isoplanatic patch during the imaging procedure, which extends the time of the imaging session for the application of large volumetric imaging.
Adie et al. [17] proposed a computational aberration correction technique, termed computational adaptive optics (CAO), to utilize the tomographic OCT data itself to compensate for the aberrations through post-processing. High-resolution 3D tomography was thereby achieved. Since then, CAO has become an active research field. In the following sections, we focus on CAO and review the theory, implementation, and recent progress of CAO applications.
5.1 CAO theory
Based on Fourier optics principles, the complex generalized pupil function is proportional to the scaled amplitude transfer function, which is related to the PSF through the Fourier transform. Aberrations can be described as a phase term inside the generalized pupil function in a single-pass system [57]. From Section 4.2, we learned that three-dimensional complex information can be obtained from the interferometric synthetic aperture acquisition, which make the direct connection from complex data to the complex generalized pupil function possible. ISAM was introduced in Section 4.2 as a solution to the inverse problem of the forward model of OCT and corrects defocus for all depths. However, it does not account for aberrations of the system. CAO theory is introduced here as an extension of the forward model.
The aberration in an OCT image is mainly induced by two factors, the system aberration and the sample aberration. The system aberration is generally fixed, while the sample-induced aberration in complex biological tissue samples is in general spatially variant [106] and can be dynamically changing over time, because the wavefront is distorted differently when passing through different micro-structures that are often moving. However, for a sufficiently small volume, and over a sufficiently short period of time, the aberration can be considered constant, thus allowing us to use the same sets of parameters for wavefront correction. In astronomical adaptive optics, such a region is called an isoplanatic patch, or volume of stationarity [115].
In each of such volume V, for each wavenumber k and each plane-wave component described by spatial frequency, aberration can be modelled as a multiplicative complex exponential that causes a phase shift in Eq. (6),
| (13) |
whereis the location dependent phase shift term, andis the image with aberration. Ideally, ifis known, it is possible to use phase conjugation to cancel the effect of aberration and recover the aberration-free image,
| (14) |
In traditional HAO, is measured by a wavefront sensor and physically corrected by a computer-controlled deformable mirror. CAO, on the contrary, utilizes the depth-resolved tomographic data itself to detect and cancel the aberrations numerically during post-processing. The scheme ofestimation is very similar to the techniques in sensor-less HAO but the feedback is digital instead of physical and the processing can be accomplished even after the imaging session. The aberration correction filteris related to both spatial frequency and spectral domains, so it can correct both monochromatic as well as chromatic aberrations [55,116]. In CAO, for the scenarios dominated by the fixed system aberrations, a reasonable assumption is that each depth plane contains similar aberration, thus a CAO filter can be determined at the focal plane and then be applied to all depths. ISAM is implemented at the end to correct the aberrations and defocus for all the depths simultaneously. In the cases where aberrations are significantly different from region to region, even in the same depth layer, it is possible to divide the volume into multiple regions and use different aberration correction filters for each piece, and then reassemble them to reconstruct the composite image [117]. A further simplification is the assumption of an achromatic system, where the k-dependence of the aberration correction filter can be dropped, effectively making this term a monochromatic aberration correction filter. As a result, CAO for each depth layer becomes an element-wise multiplication of spatial frequency domain 2D arrays,
| (15) |
In this case, aberration-free image in the spatial domain can therefore be achieved by applying the 2D inverse Fourier transform to.
5.2 Implementation of CAO
In this section, we will introduce several common methods of estimating the suitable aberration correction filter for the unknown aberrations introduced by the optics and/or tissue samples.
One method is through the use of image metrics for determining the best aberration correction filter. This method is similar to the sensor-less HAO techniques [118], but instead of optimizing the deformable mirror shape to cancel the wavefront distortion, this method optimizes the weights of a series of mathematical bases, such as Zernike polynomials, that compose the digital aberration correction filter, according to some computational image metric(s). Some useful example metrics are sharpness, entropy, maximum intensity, and spatial frequency content of the image. This approach was realized by manually adjusting the Zernike coefficients when CAO was first developed [17,119]. GPU-based implementation has also been achieved [120]. Recently, several iterative optimization algorithms have been independently proposed by Yang et al. [121], Pande and Liu et al. [122], and Hillmann et al. [52], for automatic aberration correction.
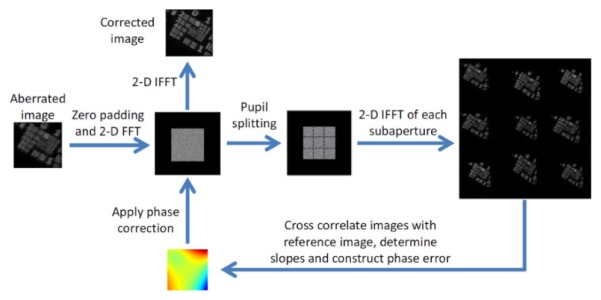
Another method is sub-aperture correlation, proposed by Kumar et al. [123], which implemented a computational method that mimics the Shack-Hartmann wavefront sensor for estimating the shape of the wavefront. The method divides each en face Fourier plane into multiple sub-apertures, and uses the cross-correlation between the reconstructed images from each sub-aperture to estimate the local wavefront slopes. Figure 8 shows the implementation steps of this method. Image improvement has been demonstrated for scattering samples which have a uniform Fourier spectrum, although only low-order aberrations can be corrected due to the trade-off between cross-correlation accuracy (sub-aperture size) and wavefront precision (sub-aperture number).
Fig. 8.
Sub-aperture cross-correlation method for estimation of the aberration correction filter. Reconstructions from each sub-pupil function are compared to the central reference sub-aperture to determine the slope of the wavefront. Reproduced with permission from [123].
The third common method in CAO is the guide-star (GS) method [116], originally developed by the astronomy community. This method is suitable for samples containing many point-like scatterers, such as individual photoreceptors in the retina. The basic steps include selection of a bright point-scatterer as the guide-star, and calculating the 3D PSF according to the guide-star. A complex deconvolution in the form of a frequency domain division is then performed on the whole volumetric image using the PSF obtained from the guide-star. In this deconvolution process, the aberration is cancelled and the optimum resolution can be restored to the image [124]. If the aberrations are spatial variant, multiple guide-stars across the whole field-of-view (2D) or volume (3D) can be picked to correct their local aberrations within each isoplanatic patch.
Of these three approaches, image metric optimization is the most general method. If desired, the image metric can be tuned to the expected image features [125]. The sub-aperture technique can be used to quickly calculate defocus in heterogeneous samples using only two sub-apertures [72]. Although the guide-star method may not be applicable for many biological samples, some sub-resolution biological features such as photoreceptors can be used as guide-stars.
5.3 Applications of CAO
CAO was first demonstrated in non-biological and ex vivo samples. Adie et al. [17] showed PSF improvement after CAO processing when imaging a silicone phantom with subresolution microparticles in an astigmatic system. CAO has been successfully applied to scattering biological samples imaged by different scanning geometries, such as ex vivo rat lung tissue [17] and 3D rabbit muscle tissue [116] by point scanning FD-OCT, and grape skin [123] and ex vivo mouse adipocytes by full-field SS-OCT [117].
As with ISAM, in vivo imaging is challenging because one must consider if there is any phase disruption due to the sample (or sometimes the system) motion (more detailed discussion can be found in the next section). Liu et al. [119] incorporated CAO and ISAM with a point-scanning SD-OCM system with NA 0.6 and an A-scan rate of 60 kHz for high-speed volumetric cellular imaging. Figure 9 demonstrates this capability for 3D in vivo cellular human skin imaging using only 2D scanning. A rigid holder to bring the skin into direct contact with the imaging system dramatically reduced the motion artifacts. Since many OCT/OCM systems with this A-scan rate are currently available, CAO can be readily applied to many existing systems with appropriate mounting for in vivo volumetric cellular imaging and cell tracking.
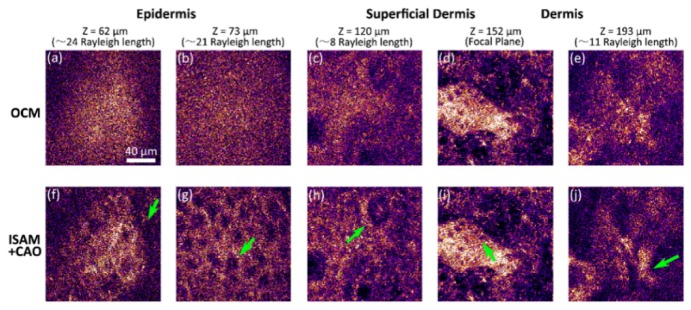
Fig. 9.
Volumetric cellular-resolution imaging of in vivo human skin acquired using a 0.6 NA point-scanning SD-OCM system without depth scanning. (a-e) En face results at different depths based-on the standard OCT processing. (f-j) ISAM and CAO processing for (a-e), respectively. Arrows indicate (f) boundary of the stratum corneum and epidermis, (g) granular cell nuclei, (h) dermal papillae, (i) basal cells, and (j) connective tissue. Scale bar represents 40 µm. Adapted from [119].
A key application of CAO is for retina imaging, which is currently the most widespread application of OCT and HAO. Cellular-resolution imaging of the photoreceptors is likely to be an important tool in early diagnosis and understanding of many diseases such as macular degeneration [111]. However, the imperfections of the eye optics limit the achievable transverse resolution and make aberration compensation very important. It should be noted that although photoreceptors have been imaged without adaptive optics when the subject’s eye has very low aberrations [105,126,127], in general, this is not the case [128].
Imaging the human eye poses more challenges for computational techniques because the eye exhibits frequent and inevitable motion [129]. Unlike imaging skin, direct contact of the imaging system with the eye is uncomfortable for subjects, and impractical. Therefore, high imaging speeds and motion correction techniques are necessary. Techniques such as en face OCT [130], full-field SS-OCT [131], and line-field SS-OCT [132] all provide high-speed retinal imaging.
The first published demonstration of CAO in the living human retina was reported by Shemonski et al. using an en face OCT imaging system, which operated at a 0.4 MHz point-scanning rate (4 kHz en face line rate) [124]. This high en face frame rate avoided transverse motion of the eye. An axial motion correction algorithm was also developed to stabilize the phase. Figure 10 shows a set of images spanning the foveal and parafoveal regions. In Fig. 10(b), few distinguishable features are visible in the original en face OCT image mosaic. After CAO aberration correction [Fig. 10(c)], individual cone photoreceptors become clearly visible throughout the full field-of-view. Later, the same en face OCT system was used to image retinal fibers as well [73].
Fig. 10.
Fovea images of the living human retina. (a) A fundus image showing the location of the acquired en face OCT data. (b) Original en face OCT data. (c) En face OCT data after CAO. N, nasal; S, superior. Scale bars represent 2 degrees in (a) and 0.5 degrees in (b, c). Figure adapted from [124].
For the sake of capturing an accurate historical timeline, Hillmann et al. [133] presented work at the same time as Shemonski et al. [134] demonstrating computational aberration correction in the living retina far from the fovea using a full-field SS-OCT system. A recent publication from Hillmann et al. [52] was the first realization of CAO for phase-stable three-dimensional volumetric imaging of the living human retina. The remarkably high speed full-field SS-OCT with 10 billion voxels per second guaranteed sufficiently stable phase to apply CAO to the entire coherent 3D tomograms. This imaging technique provides a unique approach to research the in vivo physiological responses to photostimulation in human photoreceptors [135]. Due to the high imaging speed and high resolution achieved by CAO, clear changes in the optical path lengths of the photoreceptor outer segments as a response to an optical stimulus in the living human eye were temporally and spatially resolved at the single cone level (Fig. 11). This may offer new diagnostic options in ophthalmology and neurology, and provide insights into visual phototransduction in humans.
Fig. 11.
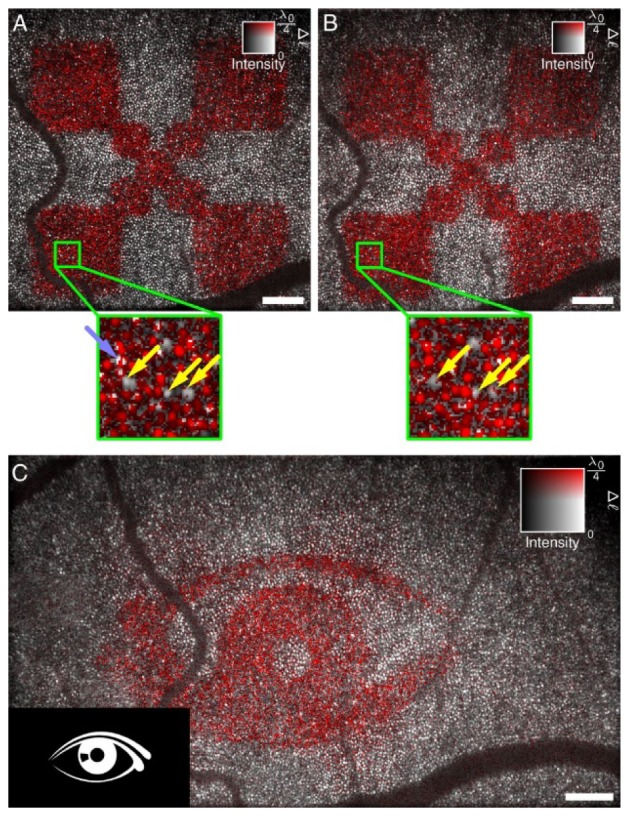
Retinal imaging and response to an optical stimulus. After computational aberration correction, optical path length changes Δℓ can be resolved in individual cones. (A and B) Measurements of independent responses were about 10 min apart. Light stimulus was 3 s for both cases. Most cones reacted to the stimulus, but some exhibited only a small or no response and are indicated by yellow arrows. Some locations pointed by the light blue arrow show abrupt phase changes within a single cone. (C). The proposed technique shows the capability of identifying more complicated stimulation patterns and indicating which photoreceptors contribute to an image seen by the test person. Scale bars represents 200 μm. Figure adapted from [135].
The research of CAO in high resolution retina imaging has become very active. At a recent conference, Fechtig et al. also reported that they had successfully applied computational aberration corrections to the 3D tomogram of retinal photoreceptors acquired from a high-speed line-field parallel SD-OCT system [136]. Anderson et al. proposed a far-field OCT spectral domain computational approach that combines a 2D lenslet array and a low cost 2D CCD for in vivo high speed volumetric imaging of retina [137]. These CAO techniques, and others in the future, will enable many new research directions in the biological and medical sciences, as well as in future clinical applications.
6. Stability
Computational image formation in OCT relies upon accurate measurement of the phase of the backscattered signal, which guarantees the coherent aperture synthesis. This places restrictions on the stability of the imaging experiment beyond that of standard OCT imaging. In the following section, the stability requirements are outlined, and solutions to the stability problem are summarized.
6.1 Phase stability requirements
In general, stability of the OCT amplitude image is critical for accurate imaging of sample structure. However, computational OCT imaging has the additional requirement of phase stability. Phase stability is achieved if there is a stable phase relationship between each measurement during which a point is being interrogated by the imaging beam. This duration of time over which a point is measured is termed the interrogation time [138]. For a point-scanned system, this is the duration of time between the first and last A-lines in which a point is illuminated by the scanning beam. Note that for a focused Gaussian beam, the interrogation time will be greater for points far from focus than for points near the focus. This is because the beam waist is broader away from focus, and will therefore illuminate a point for a longer period of time. For a full-field imaging system, the interrogation time covers the acquisition of the entire imaging volume. Because of this, full-field imaging is expected to have stricter phase stability requirements when compared to point-scanning methods.
The phase measurement is sensitive to motion in both the axial and transverse dimensions. Reconstruction artifacts introduced by various types of motion along each axis are reproduced here in Fig. 12. In the transverse dimension, the measurement is sensitive to motion on the order of the diffraction-limited transverse resolution. However, the measurement is much more sensitive to motion along the axial dimension. For axial displacements smaller than the axial resolution of the imaging system, the amplitude image will remain relatively unchanged. However, the phase of the backscattered light will change by a factor of, where ,is the central wavelength, and is the subresolution axial displacement. This indicates that even axial motion much less than the wavelength will contribute significant error in the phase measurement. Detailed thresholds for acceptable motion are outlined in [138].
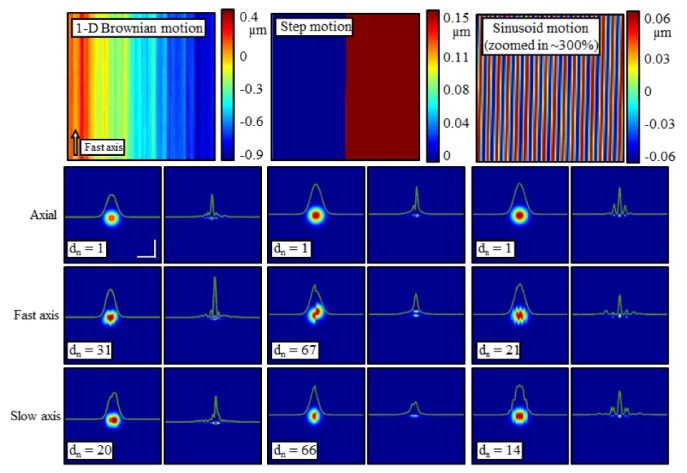
Fig. 12.
Simulation of a single point scatterer showing the impact of 1-D Brownian motion (left column), step motion (middle column), and sinusoidal motion (right column). The motion maps in the top row were applied along the axial dimension (second row), fast axis (third row), and slow axis (final row). Within each column, the left image shows the OCT en face plane, while the right image shows the result of computational refocusing. The magnitude of the motion applied is scaled by dn for each image to achieve a representative artifact. The simulation was performed at a central wavelength of λ0 = 1.33 µm. Scale bars represent 50 µm. Reproduced from [138].
Although the most common source of phase instability is sample motion, instability can also arise from the OCT system itself, including from the operator or user of the OCT system [139]. Any variation in the reference arm position will lead to apparent variations in optical path length that can corrupt the phase of the signal. Jitter of high-speed scanning mirrors used in point-scanning systems can be a source of instability [140], and the rotational scanning mechanisms in catheter-based OCT imaging are typically very unstable [141]. The imprecise triggering of swept-source lasers can also lead to phase instability within and between scan lines [142,143].
6.2 Hardware methods for phase stabilization
One possible method for overcoming the phase instability associated with sample motion is to image at very high speeds, such that the sample appears stationary. The sample may also be physically coupled to the imaging system, such that the system and sample move as one unit. A combination of these two techniques enabled the real-time, in vivo use of computational OCT [59]. However, care must be taken to ensure that high-speed beam scanning does not introduce its own inherent motion artifacts. Full-field imaging techniques do not require scanning mirrors, so phase-stable imaging at high-speeds might be more easily achieved with such techniques [131].
Axial motion can be tracked by placement of a phase reference object near the sample, such as a coverslip or catheter sheath, so that it appears in the OCT image [141,144]. Using this reference object, the phase of each A-line can be aligned in post-processing to restore phase stability. To account for unstable triggering of a swept-source sweep, a fiber Bragg grating can be used to generate a wavelength-dependent trigger to synchronize each A-line [142], while instabilities within the wavelength sweep can be calibrated out using a reference interferometer [143].
Computational reconstruction is sensitive to transverse motion on the order of the diffraction-limited spot size. When imaging with an aberrated beam, the acquired image is blurred and does not have features at the scale required to correct the transverse motion. However, using an additional speckle-tracking imaging sub-system, the transverse motion can be measured [145].
6.3 Post-processing methods for phase stabilization
In many cases, hardware solutions are not feasible or desirable. Additionally, the scanning speed is often insufficient to entirely overcome sample motion. An example is in retinal imaging, where stabilization via physical contact causes severe discomfort, and involuntary eye motion is rapid and difficult to overcome via high-speed scanning alone. For conditions such as these, post-processing methods have been developed to correct phase instability after the data has been acquired.
Due to the difficulty in correcting transverse motion without additional imaging hardware, a useful approach is to increase the imaging speed so that transverse motion is below the required stability threshold. Alternatively, additional hardware can be added to track transverse motion [145]. The following processing techniques can then be used to remove residual axial motion.
In swept-source full-field imaging, data is acquired simultaneously from all locations while the wavelength is varied over time. Axial motion will cause the sample to be at a different optical path length for each wavelength measurement. As a result, the phase relationship between each wavelength will be corrupted. This can be restored to a linear phase relationship by using a short-time Fourier transform to determine the approximate phase shift at each wavelength [146].
In a point-scanning imaging system, axial motion causes phase variation between adjacent A-lines. With line rates commonly in the hundreds of kilohertz, phase between A-lines along the fast-axis is relatively stable. However, the time difference between A-lines along the slow-axis is often an order-of-magnitude longer, making phase correction necessary along this dimension. The phase difference between A-lines along the slow-axis can be calculated by complex conjugate multiplication of adjacent fast-axis frames. By taking the complex average along depth, an en face phase map can be generated. This phase map can then be conjugated and multiplied throughout the three-dimensional OCT volume, correcting the phase at every depth. This process is outlined in Fig. 13, along with a rendering of the computational reconstruction with and without phase correction.
Fig. 13.
(a) Illustration of the axial motion correction algorithm implemented without an external phase reference. (b) Three-dimensional OCT and computationally-refocused reconstruction of an in vivo human sweat duct. Prior to phase correction, the computational refocusing fails dramatically. Following phase correction, the refocusing succeeds. Adapted from [145].
7. Discussion and summary
Various ex vivo, in vitro, and in vivo studies have demonstrated that computational OCT imaging techniques have matured to improve both the axial and transverse resolution, as well as overcome both limited depth-of-field and optical aberrations. In addition to lower cost and simpler system configurations, the post-processing nature of computational imaging also allows more flexible measurement and image improvement. For example, the advantages of high-speed volumetric imaging with high 3D resolution would not only shorten the precious time required for imaging in surgery or in clinical applications, but also shows great potential for fundamental research, such as tracking highly dynamic cell behaviors in 3D. The separation of image acquisition and aberration correction make the correction of spatially-variant aberrations more accurate in a shorter acquisition time than HAO, which has to sense the aberrations in each small isoplanatic volume and then execute each correction while imaging the subject. Another benefit of the computational OCT techniques is that the magnitude and accuracy of the measured wavefront aberrations in CAO are not limited by the wavefront sensor design (e.g. the well-known non-common path errors, and the trade-off between measurement sensitivity and dynamic range), and the correction is not restricted to the number and the stroke range of physical actuators, as in HAO. Furthermore, the inherent coherence gate of CAO has the ability to achieve a depth-resolved aberration correction, which is particularly important in microscopy.
Increasingly, researchers have been pushing the limit of computational OCT imaging. Despite the advantages noted above, computational OCT techniques are notoriously more sensitive to motion, compared to standard OCT. Addressing this challenge was a significant barrier that limited the translation of these techniques from the experimental benchtop to clinical practice. Fortunately, this problem has been overcome recently through the development of ultrahigh-speed hardware systems and advanced motion correction techniques. The resulting new hardware systems also create other new applications, such as in retinal photo-physiology [135], and many yet to come. This complementary development between computational imaging techniques and hardware development can further advance the applications of OCT, which has already been seen analogously in other imaging modalities such as X-ray and nuclear computed tomography, MRI, and likely more in the near future in ultrasound imaging.
Another limitation that exists among the post-processing techniques is the decreased signal in highly aberrated systems. The combination of new hardware design and computational imaging techniques can be a solution. The system can now be designed to optimize signal collection over an extended volume rather than minimizing aberrations at a given depth [17]. In high-resolution imaging of the retina, early evidence has shown that the physical compensation of defocus (a simple way is to adjust beam collimation) could provide sufficient SNR for CAO to achieve good performance. A practical strategy for volumetric aberration correction for the retina could be implemented by first determining the CAO wavefront filter at the depth which contributed the highest signal (e.g. inner segment/outer segment junction in retina), and then combining ISAM or digital refocusing to correct aberrations at other depths.
In summary, computational imaging techniques integrated with OCT present new opportunities for high-resolution volumetric imaging in many biological and clinical applications beyond standard OCT alone. Future studies will expand the imaging of different diseases in collaboration with medical specialists to assess the true clinical impact of these computational imaging techniques.
Acknowledgments
The authors thank former members of the Biophotonics Imaging Laboratory who have helped pioneer, develop, and demonstrate computational dispersion correction, ISAM, and CAO techniques including Tyler Ralston, Daniel Marks, Bryn Davis, Adeel Ahmad, Steven Adie, and Nathan Shemonski. Stephen A. Boppart and P. Scott Carney are co-founders of Diagnostic Photonics, Inc., which is licensing intellectual property from the University of Illinois at Urbana-Champaign related to ISAM. Stephen A. Boppart also receives royalties from MIT for patents related to OCT.
Funding
The research presented here from the Biophotonics Imaging Laboratory at the University of Illinois at Urbana-Champaign was supported by multiple grants from NIH, NSF, and private foundations over the last decade. Recent research was funded in part by the National Institutes of Health (NIH) (1 R01 CA166309, 1 R01 EB013723, S.A.B).
References and links
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical Coherence Tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Fujimoto J. G., Brezinski M. E., Tearney G. J., Boppart S. A., Bouma B., Hee M. R., Southern J. F., Swanson E. A., “Optical biopsy and imaging using optical coherence tomography,” Nat. Med. 1(9), 970–972 (1995). 10.1038/nm0995-970 [DOI] [PubMed] [Google Scholar]
- 3.Tearney G. J., Brezinski M. E., Bouma B. E., Boppart S. A., Pitris C., Southern J. F., Fujimoto J. G., “In vivo endoscopic optical biopsy with optical coherence tomography,” Science 276(5321), 2037–2039 (1997). 10.1126/science.276.5321.2037 [DOI] [PubMed] [Google Scholar]
- 4.Boppart S. A., Bouma B. E., Pitris C., Southern J. F., Brezinski M. E., Fujimoto J. G., “In vivo cellular optical coherence tomography imaging,” Nat. Med. 4(7), 861–865 (1998). 10.1038/nm0798-861 [DOI] [PubMed] [Google Scholar]
- 5.Nguyen C. T., Jung W., Kim J., Chaney E. J., Novak M., Stewart C. N., Boppart S. A., “Noninvasive in vivo optical detection of biofilm in the human middle ear,” Proc. Natl. Acad. Sci. U.S.A. 109(24), 9529–9534 (2012). 10.1073/pnas.1201592109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Graf B. W., Bower A. J., Chaney E. J., Marjanovic M., Adie S. G., De Lisio M., Valero M. C., Boppart M. D., Boppart S. A., “In vivo multimodal microscopy for detecting bone-marrow-derived cell contribution to skin regeneration,” J. Biophotonics 7(1-2), 96–102 (2014). 10.1002/jbio.201200240 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Mesiwala N. K., Shemonski N., Sandrian M. G., Shelton R., Ishikawa H., Tawbi H. A., Schuman J. S., Boppart S. A., Labriola L. T., “Retinal imaging with en face and cross-sectional optical coherence tomography delineates outer retinal changes in cancer-associated retinopathy secondary to Merkel cell carcinoma,” J. Ophthalmic Inflamm. Infect. 5(1), 25 (2015). 10.1186/s12348-015-0053-0 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Erickson-Bhatt S. J., Nolan R. M., Shemonski N. D., Adie S. G., Putney J., Darga D., McCormick D. T., Cittadine A. J., Zysk A. M., Marjanovic M., Chaney E. J., Monroy G. L., South F. A., Cradock K. A., Liu Z. G., Sundaram M., Ray P. S., Boppart S. A., “Real-time imaging of the resection bed using a handheld probe to reduce incidence of microscopic positive margins in cancer surgery,” Cancer Res. 75(18), 3706–3712 (2015). 10.1158/0008-5472.CAN-15-0464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Fujimoto J. G., Swanson E. A., “The development, commercialization, and impact of optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 57(9), OCT1–OCT13 (2016). 10.1167/iovs.16-19963 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Cormack A. M., “Representation of a function by its line integrals, with some radiological applications. II,” J. Appl. Phys. 35(10), 2722–2727 (1964). 10.1063/1.1713127 [DOI] [Google Scholar]
- 11.Hounsfield G. N., “Computerized transverse axial scanning (tomography). 1. Description of system,” Br. J. Radiol. 46(552), 1016–1022 (1973). 10.1259/0007-1285-46-552-1016 [DOI] [PubMed] [Google Scholar]
- 12.Lauterbur P. C., “Image formation by induced local interactions: examples employing nuclear magnetic resonance,” Nature 242(5394), 190–191 (1973). 10.1038/242190a0 [DOI] [PubMed] [Google Scholar]
- 13.Gough P. T., Hawkins D. W., “Unified framework for modern synthetic aperture imaging algorithms,” Int. J. Imaging Syst. Technol. 8(4), 343–358 (1997). [DOI] [Google Scholar]
- 14.Kam Z., Hanser B., Gustafsson M. G. L., Agard D. A., Sedat J. W., “Computational adaptive optics for live three-dimensional biological imaging,” Proc. Natl. Acad. Sci. U.S.A. 98(7), 3790–3795 (2001). 10.1073/pnas.071275698 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Colomb T., Montfort F., Kühn J., Aspert N., Cuche E., Marian A., Charrière F., Bourquin S., Marquet P., Depeursinge C., “Numerical parametric lens for shifting, magnification, and complete aberration compensation in digital holographic microscopy,” J. Opt. Soc. Am. A 23(12), 3177–3190 (2006). 10.1364/JOSAA.23.003177 [DOI] [PubMed] [Google Scholar]
- 16.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Interferometric synthetic aperture microscopy,” Nat. Phys. 3(2), 129–134 (2007). 10.1038/nphys514 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Adie S. G., Graf B. W., Ahmad A., Carney P. S., Boppart S. A., “Computational adaptive optics for broadband optical interferometric tomography of biological tissue,” Proc. Natl. Acad. Sci. U.S.A. 109(19), 7175–7180 (2012). 10.1073/pnas.1121193109 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Fercher A. F., Drexler W., Hitzenberger C. K., Lasser T., “Optical coherence tomography – principles and applications,” Rep. Prog. Phys. 66(2), 239–303 (2003). 10.1088/0034-4885/66/2/204 [DOI] [Google Scholar]
- 19.Fercher A. F., “Optical coherence tomography - development, principles, applications,” Z. Med. Phys. 20(4), 251–276 (2010). 10.1016/j.zemedi.2009.11.002 [DOI] [PubMed] [Google Scholar]
- 20.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Inverse scattering for optical coherence tomography,” J. Opt. Soc. Am. A 23(5), 1027–1037 (2006). 10.1364/JOSAA.23.001027 [DOI] [PubMed] [Google Scholar]
- 21.Schmitt J. M., “Restroation of optical coherence images of living tissue using the clean algorithm,” J. Biomed. Opt. 3(1), 66–75 (1998). 10.1117/1.429863 [DOI] [PubMed] [Google Scholar]
- 22.Fercher A., Hitzenberger C., Sticker M., Zawadzki R., Karamata B., Lasser T., “Numerical dispersion compensation for partial coherence interferometry and optical coherence tomography,” Opt. Express 9(12), 610–615 (2001). 10.1364/OE.9.000610 [DOI] [PubMed] [Google Scholar]
- 23.Fercher A. F., Hitzenberger C. K., Sticker M., Zawadzki R., Karamata B., Lasser T., “Dispersion compensation for optical coherence tomography depth-scan signals by a numerical technique,” Opt. Commun. 204(1-6), 67–74 (2002). 10.1016/S0030-4018(02)01137-9 [DOI] [Google Scholar]
- 24.Cense B., Nassif N., Chen T., Pierce M., Yun S.-H., Park B., Bouma B., Tearney G., de Boer J., “Ultrahigh-resolution high-speed retinal imaging using spectral-domain optical coherence tomography,” Opt. Express 12(11), 2435–2447 (2004). 10.1364/OPEX.12.002435 [DOI] [PubMed] [Google Scholar]
- 25.de Boer J. F., Saxer C. E., Nelson J. S., “Stable carrier generation and phase-resolved digital data processing in optical coherence tomography,” Appl. Opt. 40(31), 5787–5790 (2001). 10.1364/AO.40.005787 [DOI] [PubMed] [Google Scholar]
- 26.Marks D. L., Oldenburg A. L., Reynolds J. J., Boppart S. A., “Digital algorithm for dispersion correction in optical coherence tomography for homogeneous and stratified media,” Appl. Opt. 42(2), 204–217 (2003). 10.1364/AO.42.000204 [DOI] [PubMed] [Google Scholar]
- 27.Marks D. L., Oldenburg A. L., Reynolds J. J., Boppart S. A., “Autofocus algorithm for dispersion correction in optical coherence tomography,” Appl. Opt. 42(16), 3038–3046 (2003). 10.1364/AO.42.003038 [DOI] [PubMed] [Google Scholar]
- 28.Wojtkowski M., Srinivasan V., Ko T., Fujimoto J., Kowalczyk A., Duker J., “Ultrahigh-resolution, high-speed, Fourier domain optical coherence tomography and methods for dispersion compensation,” Opt. Express 12(11), 2404–2422 (2004). 10.1364/OPEX.12.002404 [DOI] [PubMed] [Google Scholar]
- 29.Huber R., Wojtkowski M., Fujimoto J. G., Jiang J. Y., Cable A. E., “Three-dimensional and C-mode OCT imaging with a compact, frequency swept laser source at 1300 nm,” Opt. Express 13(26), 10523–10538 (2005). 10.1364/OPEX.13.010523 [DOI] [PubMed] [Google Scholar]
- 30.Aguirre A. D., Sawinski J., Huang S.-W., Zhou C., Denk W., Fujimoto J. G., “High speed optical coherence microscopy with autofocus adjustment and a miniaturized endoscopic imaging probe,” Opt. Express 18(5), 4222–4239 (2010). 10.1364/OE.18.004222 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lexer F., Hitzenberger C. K., Drexler W., Molebny S., Sattmann H., Sticker M., Fercher A. F., “Dynamic coherent focus OCT with depth-independent transversal resolution,” J. Mod. Opt. 46(3), 541–553 (1999). 10.1080/09500349908231282 [DOI] [Google Scholar]
- 32.Divetia A., Hsieh T. H., Zhang J., Chen Z., Bachman M., Li G. P., “Dynamically focused optical coherence tomography for endoscopic applications,” Appl. Phys. Lett. 86(10), 103902 (2005). 10.1063/1.1879096 [DOI] [Google Scholar]
- 33.Lee K.-S., Zhao H., Ibrahim S. F., Meemon N., Khoudeir L., Rolland J. P., “Three-dimensional imaging of normal skin and nonmelanoma skin cancer with cellular resolution using Gabor domain optical coherence microscopy,” J. Biomed. Opt. 17(12), 126006 (2012). 10.1117/1.JBO.17.12.126006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Standish B. A., Lee K. K. C., Mariampillai A., Munce N. R., Leung M. K. K., Yang V. X. D., Vitkin I. A., “In vivo endoscopic multi-beam optical coherence tomography,” Phys. Med. Biol. 55(3), 615–622 (2010). 10.1088/0031-9155/55/3/004 [DOI] [PubMed] [Google Scholar]
- 35.Ding Z., Ren H., Zhao Y., Nelson J. S., Chen Z., “High-resolution optical coherence tomography over a large depth range with an axicon lens,” Opt. Lett. 27(4), 243–245 (2002). 10.1364/OL.27.000243 [DOI] [PubMed] [Google Scholar]
- 36.Leitgeb R. A., Villiger M., Bachmann A. H., Steinmann L., Lasser T., “Extended focus depth for Fourier domain optical coherence microscopy,” Opt. Lett. 31(16), 2450–2452 (2006). 10.1364/OL.31.002450 [DOI] [PubMed] [Google Scholar]
- 37.Liu L., Gardecki J. A., Nadkarni S. K., Toussaint J. D., Yagi Y., Bouma B. E., Tearney G. J., “Imaging the subcellular structure of human coronary atherosclerosis using micro-optical coherence tomography,” Nat. Med. 17(8), 1010–1014 (2011). 10.1038/nm.2409 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Blatter C., Weingast J., Alex A., Grajciar B., Wieser W., Drexler W., Huber R., Leitgeb R. A., “In situ structural and microangiographic assessment of human skin lesions with high-speed OCT,” Biomed. Opt. Express 3(10), 2636–2646 (2012). 10.1364/BOE.3.002636 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Liu L., Liu C., Howe W. C., Sheppard C. J. R., Chen N., “Binary-phase spatial filter for real-time swept-source optical coherence microscopy,” Opt. Lett. 32(16), 2375–2377 (2007). 10.1364/OL.32.002375 [DOI] [PubMed] [Google Scholar]
- 40.Sasaki K., Kurokawa K., Makita S., Yasuno Y., “Extended depth of focus adaptive optics spectral domain optical coherence tomography,” Biomed. Opt. Express 3(10), 2353–2370 (2012). 10.1364/BOE.3.002353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Jang J., Lim J., Yu H., Choi H., Ha J., Park J.-H., Oh W.-Y., Jang W., Lee S., Park Y., “Complex wavefront shaping for optimal depth-selective focusing in optical coherence tomography,” Opt. Express 21(3), 2890–2902 (2013). 10.1364/OE.21.002890 [DOI] [PubMed] [Google Scholar]
- 42.Yu H., Jang J., Lim J., Park J.-H., Jang W., Kim J.-Y., Park Y., “Depth-enhanced 2-D optical coherence tomography using complex wavefront shaping,” Opt. Express 22(7), 7514–7523 (2014). 10.1364/OE.22.007514 [DOI] [PubMed] [Google Scholar]
- 43.Mo J., de Groot M., de Boer J. F., “Focus-extension by depth-encoded synthetic aperture in Optical Coherence Tomography,” Opt. Express 21(8), 10048–10061 (2013). 10.1364/OE.21.010048 [DOI] [PubMed] [Google Scholar]
- 44.Mo J., de Groot M., de Boer J. F., “Depth-encoded synthetic aperture optical coherence tomography of biological tissues with extended focal depth,” Opt. Express 23(4), 4935–4945 (2015). 10.1364/OE.23.004935 [DOI] [PubMed] [Google Scholar]
- 45.Ralston T. S., Marks D. L., Kamalabadi F., Boppart S. A., “Deconvolution methods for mitigation of transverse blurring in optical coherence tomography,” IEEE Trans. Image Process. 14(9), 1254–1264 (2005). 10.1109/TIP.2005.852469 [DOI] [PubMed] [Google Scholar]
- 46.Liu Y., Liang Y., Mu G., Zhu X., “Deconvolution methods for image deblurring in optical coherence tomography,” J. Opt. Soc. Am. A 26(1), 72–77 (2009). 10.1364/JOSAA.26.000072 [DOI] [PubMed] [Google Scholar]
- 47.Woolliams P. D., Ferguson R. A., Hart C., Grimwood A., Tomlins P. H., “Spatially deconvolved optical coherence tomography,” Appl. Opt. 49(11), 2014–2021 (2010). 10.1364/AO.49.002014 [DOI] [PubMed] [Google Scholar]
- 48.Liu G., Yousefi S., Zhi Z., Wang R. K., “Automatic estimation of point-spread-function for deconvoluting out-of-focus optical coherence tomographic images using information entropy-based approach,” Opt. Express 19(19), 18135–18148 (2011). 10.1364/OE.19.018135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bousi E., Pitris C., “Lateral resolution improvement in Optical Coherence Tomography (OCT) images,” in Proceedings of the 2012 IEEE 12th International Conference on Bioinformatics & Bioengineering (IEEE, 2012), pp. 598–601. 10.1109/BIBE.2012.6399740 [DOI] [Google Scholar]
- 50.Hojjatoleslami S. A., Avanaki M. R. N., Podoleanu A. G., “Image quality improvement in optical coherence tomography using Lucy-Richardson deconvolution algorithm,” Appl. Opt. 52(23), 5663–5670 (2013). 10.1364/AO.52.005663 [DOI] [PubMed] [Google Scholar]
- 51.Boroomand A., Shafiee M. J., Wong A., Bizheva K., “Lateral resolution enhancement via imbricated spectral domain optical coherence tomography in a maximum-a-posterior reconstruction framework,” Proc. SPIE 9312, 931240 (2015). 10.1117/12.2081494 [DOI] [Google Scholar]
- 52.Hillmann D., Spahr H., Hain C., Sudkamp H., Franke G., Pfäffle C., Winter C., Hüttmann G., “Aberration-free volumetric high-speed imaging of in vivo retina,” Sci. Rep. 6, 35209 (2016). 10.1038/srep35209 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Fercher A. F., “Inverse scattering and aperture synthesis in OCT,” in Optical Coherence Tomography Technology and Applications, Drexler W., Fujimoto J. G., eds. (Springer, 2015), pp. 143–164. [Google Scholar]
- 54.Fercher A. F., Bartelt H., Becker H., Wiltschko E., “Image formation by inversion of scattered field data: experiments and computational simulation,” Appl. Opt. 18(14), 2427–2439 (1979). 10.1364/AO.18.002427 [DOI] [PubMed] [Google Scholar]
- 55.Davis B. J., Schlachter S. C., Marks D. L., Ralston T. S., Boppart S. A., Carney P. S., “Nonparaxial vector-field modeling of optical coherence tomography and interferometric synthetic aperture microscopy,” J. Opt. Soc. Am. A 24(9), 2527–2542 (2007). 10.1364/JOSAA.24.002527 [DOI] [PubMed] [Google Scholar]
- 56.Marks D. L., Ralston T. S., Carney P. S., Boppart S. A., “Inverse scattering for rotationally scanned optical coherence tomography,” J. Opt. Soc. Am. A 23(10), 2433–2439 (2006). 10.1364/JOSAA.23.002433 [DOI] [PubMed] [Google Scholar]
- 57.Goodman J. W., Introduction to Fourier Optics, 2nd ed. (McGraw-Hill, San Francisco, 1996). [Google Scholar]
- 58.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Real-time interferometric synthetic aperture microscopy,” Opt. Express 16(4), 2555–2569 (2008). 10.1364/OE.16.002555 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Ahmad A., Shemonski N. D., Adie S. G., Kim H.-S., Hwu W.-M. W., Carney P. S., Boppart S. A., “Real-time in vivo computed optical interferometric tomography,” Nat. Photonics 7(6), 444–448 (2013). 10.1038/nphoton.2013.71 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Stolt R. H., “Migration by Fourier-Transform,” Geophysics 43(1), 23–48 (1978). 10.1190/1.1440826 [DOI] [Google Scholar]
- 61.Ralston T. S., Marks D. L., Boppart S. A., Carney P. S., “Inverse scattering for high-resolution interferometric microscopy,” Opt. Lett. 31(24), 3585–3587 (2006). 10.1364/OL.31.003585 [DOI] [PubMed] [Google Scholar]
- 62.Marks D. L., Ralston T. S., Boppart S. A., Carney P. S., “Inverse scattering for frequency-scanned full-field optical coherence tomography,” J. Opt. Soc. Am. A 24(4), 1034–1041 (2007). 10.1364/JOSAA.24.001034 [DOI] [PubMed] [Google Scholar]
- 63.Marks D. L., Davis B. J., Boppart S. A., Carney P. S., “Partially coherent illumination in full-field interferometric synthetic aperture microscopy,” J. Opt. Soc. Am. A 26(2), 376–386 (2009). 10.1364/JOSAA.26.000376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.South F. A., Liu Y.-Z., Xu Y., Shemonski N. D., Carney P. S., Boppart S. A., “Polarization-sensitive interferometric synthetic aperture microscopy,” Appl. Phys. Lett. 107(21), 211106 (2015). 10.1063/1.4936236 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Ralston T. S., Adie S. G., Marks D. L., Boppart S. A., Carney P. S., “Cross-validation of interferometric synthetic aperture microscopy and optical coherence tomography,” Opt. Lett. 35(10), 1683–1685 (2010). 10.1364/OL.35.001683 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Chen X., Li Q., Lei Y., Wang Y., Yu D., “Approximate wavenumber domain algorithm for interferometric synthetic aperture microscopy,” Opt. Commun. 283(9), 1993–1996 (2010). 10.1016/j.optcom.2009.12.053 [DOI] [Google Scholar]
- 67.Chen X., Li Q., Lei Y., Wang Y., Yu D., “SD-OCT image reconstruction by interferometeric synthetic aperture microscopy,” J. Innov. Opt. Health Sci. 3(1), 17–23 (2010). 10.1142/S1793545810000812 [DOI] [Google Scholar]
- 68.Sheppard C. J. R., Kou S. S., Depeursinge C., “Reconstruction in interferometric synthetic aperture microscopy: comparison with optical coherence tomography and digital holographic microscopy,” J. Opt. Soc. Am. A 29(3), 244–250 (2012). 10.1364/JOSAA.29.000244 [DOI] [PubMed] [Google Scholar]
- 69.Heimbeck M. S., Marks D. L., Brady D., Everitt H. O., “Terahertz interferometric synthetic aperture tomography for confocal imaging systems,” Opt. Lett. 37(8), 1316–1318 (2012). 10.1364/OL.37.001316 [DOI] [PubMed] [Google Scholar]
- 70.St. Marie L. R., An F. A., Corso A. L., Grasel J. T., Haskell R. C., “Robust, real-time, digital focusing for FD-OCM using ISAM on a GPU,” Proc. SPIE 8934, 89342W (2014). 10.1117/12.2041686 [DOI] [Google Scholar]
- 71.Moiseev A. A., Gelikonov G. V., Shilyagin P. A., Terpelov D. A., Gelikonov V. M., “Interferometric synthetic aperture microscopy with automated parameter evaluation and phase equalization preprocessing,” Proc. SPIE 8934, 893413 (2014). [Google Scholar]
- 72.Kumar A., Drexler W., Leitgeb R. A., “Numerical focusing methods for full field OCT: a comparison based on a common signal model,” Opt. Express 22(13), 16061–16078 (2014). 10.1364/OE.22.016061 [DOI] [PubMed] [Google Scholar]
- 73.South F. A., Liu Y.-Z., Carney P. S., Boppart S. A., “Computed optical interferometric imaging: methods, achievements, and challenges,” IEEE J. Sel. Top. Quantum Electron. 22(3), 6800911 (2016). 10.1109/JSTQE.2015.2493962 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Davis B. J., Marks D. L., Ralston T. S., Carney P. S., Boppart S. A., “Interferometric synthetic aperture microscopy: computed imaging for scanned coherent microscopy,” Sensors (Basel) 8(6), 3903–3931 (2008). 10.3390/s8063903 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Lasswell S. W., “History of SAR at Lockheed Martin (previously Goodyear Aerospace),” Proc. SPIE 5788, 1–12 (2005). 10.1117/12.603927 [DOI] [Google Scholar]
- 76.Sherwin C. W., Ruina J. P., Rawcliffe R. D., “Some early developments in synthetic aperture radar systems,” IRE Trans. Mil. Electron. 6(2), 111–115 (1962). 10.1109/IRET-MIL.1962.5008415 [DOI] [Google Scholar]
- 77.Cutrona L., Leith E., Palermo C., Porcello L., “Optical data processing and filtering systems,” IRE Trans. Inf. Theory 6(3), 386–400 (1960). 10.1109/TIT.1960.1057566 [DOI] [Google Scholar]
- 78.Cutrona L. J., Leith E. N., Porcello L. J., Vivian E. W., “On the application of coherent optical processing techniques to synthetic-aperture radar,” Proc. IEEE 54(8), 1026–1032 (1966). 10.1109/PROC.1966.4987 [DOI] [Google Scholar]
- 79.Brown W., Porcello L., “An introduction to synthetic-aperture radar,” IEEE Spectr. 6(9), 52–62 (1969). 10.1109/MSPEC.1969.5213674 [DOI] [Google Scholar]
- 80.Hayes M. P., Gough P. T., “Broad-band synthetic aperture sonar,” IEEE J. Oceanic Eng. 17(1), 80–94 (1992). 10.1109/48.126957 [DOI] [Google Scholar]
- 81.Gray S. H., Etgen J., Dellinger J., Whitmore D., “Seismic migration problems and solutions,” Geophysics 66(5), 1622–1640 (2001). 10.1190/1.1487107 [DOI] [Google Scholar]
- 82.Nelson T. R., Pretorius D. H., “Three-dimensional ultrasound imaging,” Ultrasound Med. Biol. 24(9), 1243–1270 (1998). 10.1016/S0301-5629(98)00043-X [DOI] [PubMed] [Google Scholar]
- 83.Li M.-L., Zhang H. E., Maslov K., Stoica G., Wang L. V., “Improved in vivo photoacoustic microscopy based on a virtual-detector concept,” Opt. Lett. 31(4), 474–476 (2006). 10.1364/OL.31.000474 [DOI] [PubMed] [Google Scholar]
- 84.Ahmad A., Ali M., South F., Monroy G. L., Adie S. G., Shemonski N., Carney P. S., Boppart S. A., “Interferometric synthetic aperture microscopy implementation on a floating point multi-core digital signal processer,” Proc. SPIE 8571, 857134 (2013). 10.1117/12.2006876 [DOI] [Google Scholar]
- 85.“Diagnostic Photonics, Inc,” http://diagnosticphotonics.com.
- 86.Wax A., Backman V., eds., “Interferometric Synthetic Aperture Microscopy,” in Biomedical Applications of Light Scattering (McGraw-Hill Professional, 2010). [Google Scholar]
- 87.Zysk A. M., Chen K., Gabrielson E., Tafra L., May Gonzalez E. A., Canner J. K., Schneider E. B., Cittadine A. J., Scott Carney P., Boppart S. A., Tsuchiya K., Sawyer K., Jacobs L. K., “Intraoperative assessment of final margins with a handheld optical imaging probe during breast-conserving surgery may reduce the reoperation rate: Results of a multicenter study,” Ann. Surg. Oncol. 22(10), 3356–3362 (2015). 10.1245/s10434-015-4665-2 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Leith E. N., “Quasi-holographic techniques in the microwave region,” Proc. IEEE 59(9), 1305–1318 (1971). 10.1109/PROC.1971.8406 [DOI] [Google Scholar]
- 89.Yu L., Chen Z., “Digital holographic tomography based on spectral interferometry,” Opt. Lett. 32(20), 3005–3007 (2007). 10.1364/OL.32.003005 [DOI] [PubMed] [Google Scholar]
- 90.Schnars U., Jueptner W., Digital Holography (Springer, 2010). [Google Scholar]
- 91.Kim M. K., “Principles and techniques of digital holographic microscopy,” SPIE Rev. 1(1), 18005 (2010). [Google Scholar]
- 92.Hillmann D., Lührs C., Bonin T., Koch P., Hüttmann G., “Holoscopy - holographic optical coherence tomography,” Opt. Lett. 36(13), 2390–2392 (2011). 10.1364/OL.36.002390 [DOI] [PubMed] [Google Scholar]
- 93.Moiseev A. A., Gelikonov G. V., Terpelov D. A., Shilyagin P. A., Gelikonov V. M., “Digital refocusing for transverse resolution improvement in optical coherence tomography,” Laser Phys. Lett. 9(11), 826–832 (2012). 10.7452/lapl.201210102 [DOI] [Google Scholar]
- 94.Yasuno Y., Sugisaka J., Sando Y., Nakamura Y., Makita S., Itoh M., Yatagai T., “Non-iterative numerical method for laterally superresolving Fourier domain optical coherence tomography,” Opt. Express 14(3), 1006–1020 (2006). 10.1364/OE.14.001006 [DOI] [PubMed] [Google Scholar]
- 95.Yu L., Rao B., Zhang J., Su J., Wang Q., Guo S., Chen Z., “Improved lateral resolution in optical coherence tomography by digital focusing using two-dimensional numerical diffraction method,” Opt. Express 15(12), 7634–7641 (2007). 10.1364/OE.15.007634 [DOI] [PubMed] [Google Scholar]
- 96.Liu G., Zhi Z., Wang R. K., “Digital focusing of OCT images based on scalar diffraction theory and information entropy,” Biomed. Opt. Express 3(11), 2774–2783 (2012). 10.1364/BOE.3.002774 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Nakamura Y., Sugisaka J. I., Sando Y., Endo T., Itoh M., Yatagai T., Yasuno Y., “Complex numerical processing for in-focus line-field spectral-domain optical coherence tomography,” Jpn. J. Appl. Phys. 46(4A), 1774–1778 (2007). 10.1143/JJAP.46.1774 [DOI] [Google Scholar]
- 98.Fechtig D. J., Kumar A., Drexler W., Leitgeb R. A., “Full range line-field parallel swept source imaging utilizing digital refocusing,” J. Mod. Opt. 62(21), 1801–1807 (2015). 10.1080/09500340.2014.990938 [DOI] [Google Scholar]
- 99.Labiau S., David G., Gigan S., Boccara A. C., “Defocus test and defocus correction in full-field optical coherence tomography,” Opt. Lett. 34(10), 1576–1578 (2009). 10.1364/OL.34.001576 [DOI] [PubMed] [Google Scholar]
- 100.Min G., Choi W. J., Kim J. W., Lee B. H., “Refractive index measurements of multiple layers using numerical refocusing in FF-OCT,” Opt. Express 21(24), 29955–29967 (2013). 10.1364/OE.21.029955 [DOI] [PubMed] [Google Scholar]
- 101.Grebenyuk A., Federici A., Ryabukho V., Dubois A., “Numerically focused full-field swept-source optical coherence microscopy with low spatial coherence illumination,” Appl. Opt. 53(8), 1697–1708 (2014). 10.1364/AO.53.001697 [DOI] [PubMed] [Google Scholar]
- 102.Hillmann D., Franke G., Lührs C., Koch P., Hüttmann G., “Efficient holoscopy image reconstruction,” Opt. Express 20(19), 21247–21263 (2012). 10.1364/OE.20.021247 [DOI] [PubMed] [Google Scholar]
- 103.Adie S. G., Graf B. W., Ahmad A., Darbarsyah B., Boppart S. A., Carney P. S., “The impact of aberrations on object reconstruction with interferometric synthetic aperture microscopy,” Proc. SPIE 7889, 78891O (2011). 10.1117/12.875592 [DOI] [Google Scholar]
- 104.Hu Z., Rollins A., “Quasi-telecentric optical design of a microscope-compatible OCT scanner,” Opt. Express 13(17), 6407–6415 (2005). 10.1364/OPEX.13.006407 [DOI] [PubMed] [Google Scholar]
- 105.LaRocca F., Nankivil D., DuBose T., Toth C. A., Farsiu S., Izatt J. A., “In vivo cellular-resolution retinal imaging in infants and children using an ultracompact handheld probe,” Nat. Photonics 10(9), 580–584 (2016). 10.1038/nphoton.2016.141 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Ji N., Milkie D. E., Betzig E., “Adaptive optics via pupil segmentation for high-resolution imaging in biological tissues,” Nat. Methods 7(2), 141–147 (2010). 10.1038/nmeth.1411 [DOI] [PubMed] [Google Scholar]
- 107.Liang J., Williams D. R., Miller D. T., “Supernormal vision and high-resolution retinal imaging through adaptive optics,” J. Opt. Soc. Am. A 14(11), 2884–2892 (1997). 10.1364/JOSAA.14.002884 [DOI] [PubMed] [Google Scholar]
- 108.Booth M. J., “Adaptive optical microscopy: the ongoing quest for a perfect image,” Light Sci. Appl. 3(4), e165 (2014). 10.1038/lsa.2014.46 [DOI] [Google Scholar]
- 109.Wang K., Milkie D. E., Saxena A., Engerer P., Misgeld T., Bronner M. E., Mumm J., Betzig E., “Rapid adaptive optical recovery of optimal resolution over large volumes,” Nat. Methods 11(6), 625–628 (2014). 10.1038/nmeth.2925 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Hermann B., Fernández E. J., Unterhuber A., Sattmann H., Fercher A. F., Drexler W., Prieto P. M., Artal P., “Adaptive-optics ultrahigh-resolution optical coherence tomography,” Opt. Lett. 29(18), 2142–2144 (2004). 10.1364/OL.29.002142 [DOI] [PubMed] [Google Scholar]
- 111.Jonnal R. S., Kocaoglu O. P., Zawadzki R. J., Liu Z., Miller D. T., Werner J. S., “A review of adaptive optics optical coherence tomography: technical advances, scientific applications, and the future,” Invest. Ophthalmol. Vis. Sci. 57(9), OCT51–OCT68 (2016). 10.1167/iovs.16-19103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Rueckel M., Mack-Bucher J. A., Denk W., “Adaptive wavefront correction in two-photon microscopy using coherence-gated wavefront sensing,” Proc. Natl. Acad. Sci. U.S.A. 103(46), 17137–17142 (2006). 10.1073/pnas.0604791103 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Cua M., Wahl D. J., Zhao Y., Lee S., Bonora S., Zawadzki R. J., Jian Y., Sarunic M. V., “Coherence-gated sensorless adaptive optics multiphoton retinal imaging,” Sci. Rep. 6, 32223 (2016). 10.1038/srep32223 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Wong K. S. K., Jian Y., Cua M., Bonora S., Zawadzki R. J., Sarunic M. V., “In vivo imaging of human photoreceptor mosaic with wavefront sensorless adaptive optics optical coherence tomography,” Biomed. Opt. Express 6(2), 580–590 (2015). 10.1364/BOE.6.000580 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Marchetti E., Brast R., Delabre B., Donaldson R., Fedrigo E., Frank C., Hubin N., Kolb J., Lizon J.-L., Marchesi M., Oberti S., Reiss R., Santos J., Soenke C., Tordo S., Baruffolo A., Bagnara P., Consortium C., “On-sky testing of the multi-conjugate adaptive optics demonstrator,” Messenger (Los Angel.) 129, 8–13 (2007). [Google Scholar]
- 116.Adie S. G., Shemonski N. D., Graf B. W., Ahmad A., Carney P. S., Boppart S. A., “Guide-star-based computational adaptive optics for broadband interferometric tomography,” Appl. Phys. Lett. 101(22), 221117 (2012). 10.1063/1.4768778 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Kumar A., Kamali T., Platzer R., Unterhuber A., Drexler W., Leitgeb R. A., “Anisotropic aberration correction using region of interest based digital adaptive optics in Fourier domain OCT,” Biomed. Opt. Express 6(4), 1124–1134 (2015). 10.1364/BOE.6.001124 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Hofer H., Sredar N., Queener H., Li C., Porter J., “Wavefront sensorless adaptive optics ophthalmoscopy in the human eye,” Opt. Express 19(15), 14160–14171 (2011). 10.1364/OE.19.014160 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Liu Y.-Z., Shemonski N. D., Adie S. G., Ahmad A., Bower A. J., Carney P. S., Boppart S. A., “Computed optical interferometric tomography for high-speed volumetric cellular imaging,” Biomed. Opt. Express 5(9), 2988–3000 (2014). 10.1364/BOE.5.002988 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Tang H., Mulligan J. A., Untracht G. R., Zhang X., Adie S. G., “GPU-based computational adaptive optics for volumetric optical coherence microscopy,” Proc. SPIE 9720, 97200O (2016). 10.1117/12.2213949 [DOI] [Google Scholar]
- 121.Xu Y., Liu Y.-Z., Boppart S. A., Carney P. S., “Automated interferometric synthetic aperture microscopy and computational adaptive optics for improved optical coherence tomography,” Appl. Opt. 55(8), 2034–2041 (2016). 10.1364/AO.55.002034 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Pande P., Liu Y.-Z., South F. A., Boppart S. A., “Automated computational aberration correction method for broadband interferometric imaging techniques,” Opt. Lett. 41(14), 3324–3327 (2016). 10.1364/OL.41.003324 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Kumar A., Drexler W., Leitgeb R. A., “Subaperture correlation based digital adaptive optics for full field optical coherence tomography,” Opt. Express 21(9), 10850–10866 (2013). 10.1364/OE.21.010850 [DOI] [PubMed] [Google Scholar]
- 124.Shemonski N. D., South F. A., Liu Y.-Z., Adie S. G., Carney P. S., Boppart S. A., “Computational high-resolution optical imaging of the living human retina,” Nat. Photonics 9(7), 440–443 (2015). 10.1038/nphoton.2015.102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Fienup J. R., Miller J. J., “Aberration correction by maximizing generalized sharpness metrics,” J. Opt. Soc. Am. A 20(4), 609–620 (2003). 10.1364/JOSAA.20.000609 [DOI] [PubMed] [Google Scholar]
- 126.Miller D. T., Williams D. R., Morris G. M. M., Liang J., “Images of cone photoreceptors in the living human eye,” Vision Res. 36(8), 1067–1079 (1996). 10.1016/0042-6989(95)00225-1 [DOI] [PubMed] [Google Scholar]
- 127.Pircher M., Baumann B., Götzinger E., Hitzenberger C. K., “Retinal cone mosaic imaged with transverse scanning optical coherence tomography,” Opt. Lett. 31(12), 1821–1823 (2006). 10.1364/OL.31.001821 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Thibos L. N., Hong X., Bradley A., Cheng X., “Statistical variation of aberration structure and image quality in a normal population of healthy eyes,” J. Opt. Soc. Am. A 19(12), 2329–2348 (2002). 10.1364/JOSAA.19.002329 [DOI] [PubMed] [Google Scholar]
- 129.Martinez-Conde S., Macknik S. L., Hubel D. H., “The role of fixational eye movements in visual perception,” Nat. Rev. Neurosci. 5(3), 229–240 (2004). 10.1038/nrn1348 [DOI] [PubMed] [Google Scholar]
- 130.Felberer F., Kroisamer J.-S., Baumann B., Zotter S., Schmidt-Erfurth U., Hitzenberger C. K., Pircher M., “Adaptive optics SLO/OCT for 3D imaging of human photoreceptors in vivo,” Biomed. Opt. Express 5(2), 439–456 (2014). 10.1364/BOE.5.000439 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Spahr H., Hillmann D., Hain C., Pfäffle C., Sudkamp H., Franke G., Hüttmann G., “Imaging pulse wave propagation in human retinal vessels using full-field swept-source optical coherence tomography,” Opt. Lett. 40(20), 4771–4774 (2015). 10.1364/OL.40.004771 [DOI] [PubMed] [Google Scholar]
- 132.Fechtig D. J., Kumar A., Ginner L., Drexler W., Leitgeb R. A., “High-speed, digitally refocused retinal imaging with line-field parallel swept source OCT,” Proc. SPIE 9312, 931203 (2015). 10.1117/12.2081924 [DOI] [Google Scholar]
- 133.Hillmann D., Spahr H., Franke G. L., Hain C., Sudkamp H. M., Hüttmann G., “Numerical aberration correction in optical coherence tomography and holoscopy by optimization of image quality,” Presented at SPIE Photonics West, San Francisco, CA, February. (2015). [Google Scholar]
- 134.Shemonski N. D., Adie S. G., Liu Y.-Z., South F. A., Carney P. S., Boppart S. A., “A computational approach to high-resolution imaging of the living human retina without hardware adaptive optics,” Proc. SPIE 9307, 930710 (2015). 10.1117/12.2078308 [DOI] [Google Scholar]
- 135.Hillmann D., Spahr H., Pfäffle C., Sudkamp H., Franke G., Hüttmann G., “In vivo optical imaging of physiological responses to photostimulation in human photoreceptors,” Proc. Natl. Acad. Sci. U.S.A. 113(46), 13138–13143 (2016). 10.1073/pnas.1606428113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Fechtig D. J., Ginner L., Kumar A., Pircher M., Schmoll T., Wurster L. M., Drexler W., Leitgeb R. A., “Retinal photoreceptor imaging with high-speed line-field parallel spectral domain OCT,” Proc. SPIE 9697, 969704 (2016). 10.1117/12.2214719 [DOI] [Google Scholar]
- 137.Anderson T., Segref A., Frisken G., Ferra H., Lorenser D., Frisken S., “3D-spectral domain computational imaging,” Proc. SPIE 9697, 96970Z (2016). 10.1117/12.2214801 [DOI] [Google Scholar]
- 138.Shemonski N. D., Adie S. G., Liu Y.-Z., South F. A., Carney P. S., Boppart S. A., “Stability in computed optical interferometric tomography (Part I): Stability requirements,” Opt. Express 22(16), 19183–19197 (2014). 10.1364/OE.22.019183 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 139.Shemonski N. D., Ahmad A., Adie S. G., Liu Y.-Z., South F. A., Carney P. S., Boppart S. A., “Stability in computed optical interferometric tomography (Part II): in vivo stability assessment,” Opt. Express 22(16), 19314–19326 (2014). 10.1364/OE.22.019314 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Vakoc B. J., Tearney G. J., Bouma B. E., “Statistical properties of phase-decorrelation in phase-resolved Doppler optical coherence tomography,” IEEE Trans. Med. Imaging 28(6), 814–821 (2009). 10.1109/TMI.2009.2012891 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Sun C., Nolte F., Cheng K. H. Y., Vuong B., Lee K. K. C., Standish B. A., Courtney B., Marotta T. R., Mariampillai A., Yang V. X. D., “In vivo feasibility of endovascular Doppler optical coherence tomography,” Biomed. Opt. Express 3(10), 2600–2610 (2012). 10.1364/BOE.3.002600 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.Vakoc B. J., Yun S. H., de Boer J. F., Tearney G. J., Bouma B. E., “Phase-resolved optical frequency domain imaging,” Opt. Express 13(14), 5483–5493 (2005). 10.1364/OPEX.13.005483 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Braaf B., Vermeer K. A., Sicam V. A. D. P., van Zeeburg E., van Meurs J. C., de Boer J. F., “Phase-stabilized optical frequency domain imaging at 1-µm for the measurement of blood flow in the human choroid,” Opt. Express 19(21), 20886–20903 (2011). 10.1364/OE.19.020886 [DOI] [PubMed] [Google Scholar]
- 144.Ralston T. S., Marks D. L., Carney P. S., Boppart S. A., “Phase stability technique for inverse scattering in optical coherence tomography,” in 3rd IEEE International Symposium on Biomedical Imaging: Macro to Nano (IEEE, 2006), pp. 578–581. 10.1109/ISBI.2006.1624982 [DOI] [Google Scholar]
- 145.Shemonski N. D., Ahn S. S., Liu Y.-Z., South F. A., Carney P. S., Boppart S. A., “Three-dimensional motion correction using speckle and phase for in vivo computed optical interferometric tomography,” Biomed. Opt. Express 5(12), 4131–4143 (2014). 10.1364/BOE.5.004131 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 146.Hillmann D., Bonin T., Lührs C., Franke G., Hagen-Eggert M., Koch P., Hüttmann G., “Common approach for compensation of axial motion artifacts in swept-source OCT and dispersion in Fourier-domain OCT,” Opt. Express 20(6), 6761–6776 (2012). 10.1364/OE.20.006761 [DOI] [PubMed] [Google Scholar]