Abstract
Optical coherence tomography (OCT) is now a well-established modality for high-resolution cross-sectional and three-dimensional imaging of transparent and translucent samples and tissues. Conventional, intensity based OCT, however, does not provide a tissue-specific contrast, causing an ambiguity with image interpretation in several cases. Polarization sensitive (PS) OCT draws advantage from the fact that several materials and tissues can change the light’s polarization state, adding an additional contrast channel and providing quantitative information. In this paper, we review basic and advanced methods of PS-OCT and demonstrate its use in selected biomedical applications.
OCIS codes: (170.4500) Optical coherence tomography, (110.5405) Polarimetric imaging
1. Introduction
Optical coherence tomography (OCT) was introduced 25 years ago as a new modality for high-resolution cross-sectional imaging of transparent and translucent samples and tissues [1]. Within the past 25 years, OCT was improved in several aspects, comprising imaging speed, sensitivity, functional extensions, application fields, etc. This feature issue of Biomedical Optics Express describes these developments in several invited reviews and original research papers.
One of the remaining shortcomings of conventional, intensity based OCT is the lack of tissue specific contrast which frequently makes it difficult to directly differentiate between tissues. However, light has additional properties, beyond intensity, that can be exploited to generate tissue specific contrast and for quantitative measurements. Functional extensions of OCT, like Doppler OCT or spectroscopic OCT strive to exploit such additional light properties. The first of these functional extensions was polarization sensitive (PS) OCT, reported for one-dimensional measurements as early as 1992 [2]. Since then, PS-OCT was expanded to full 3D imaging at high speed and sensitivity and applied to various fields.
The aim of this review is to describe the principles of PS-OCT and some selected applications. Because of the limited space available, we had to restrict the content to the main principles and concepts, and to some selected applications in the biomedical field. Readers with a broader interest in other aspects of the technology are referred to our book chapters in the recent edition of the comprehensive 3-volume book “Optical Coherence Tomography – Technology and Applications” [3–5], to previous reviews [6, 7], and to the extensive original literature on PS-OCT. Readers with an interest in non-medical applications of PS-OCT are referred to a related review [8].
The remainder of this review is organized as follows: Chapter 2 describes the polarization properties of light and their representation and transformations in the Jones and the Mueller-Stokes calculus; chapter 3 discusses polarization changing light-tissue interaction mechanisms, as well as concepts and methods of how the corresponding properties can be measured. The methods section (chapter 4) applies the Jones formalism to describe birefringence measurements by a basic bulk-optics PS-OCT system (following the historic development of PS-OCT), followed by a description of how Jones and Stokes vectors are measured. The next sub-chapters discuss fiber optic versions of PS-OCT, polarization mode dispersion, and advanced data processing schemes. Finally, chapter 5 covers selected applications of PS-OCT to tissue imaging.
2. Polarization properties of light
Light is a transverse wave, the electromagnetic field oscillates perpendicular to the propagation direction, which gives rise to the polarization state of light, i.e., the direction of the field perpendicular to the propagation direction. Assuming that the light propagates in the z-direction, the polarization state of light can be described by the complex valued field strength along the x (horizontal) and y (vertical) direction, and , respectively. For a homogeneous monochromatic electromagnetic wave propagating in the z-direction with angular frequency ω = 2πc/λ and wave number k = ωN/c, where N = n + iκ represents the complex refractive index and λ and c are the wavelength and the speed of light, respectively, in vacuo, the wave can be described by its complex electric field , given by:
| (1) |
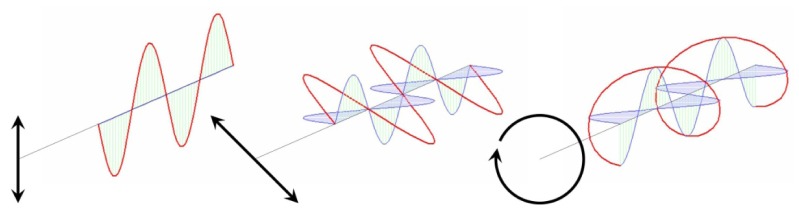
And . Three variables, the amplitude of the fields and , and their relative phase completely describe the polarization state of light, examples of which are given in Fig. 1.
Fig. 1.
Vibrational ellipses (from left to right) for vertically linear polarized light , linear polarized light oriented at 45° with respect to the vertical and horizontal orientations , and circularly polarized light . Reprinted from Ref [3].
The effect of light propagation through a material with a complex index of refraction, , can be seen through expansion of Eq. (1) to yield:
| (2) |
The imaginary part of the complex refractive index, κ, determines the attenuation of the wave as it propagates through the medium and that the real part, n, determines the phase velocity. There are a wide variety of media in which the index of refraction is independent of the polarization state of light. In these cases, light can propagate with no change of its polarization state. However, there are also many materials for which this is not the case. The goal of PS-OCT is to determine these light-polarization changing properties of a sample.
Jones vectors
A convenient way to describe polarization changes in materials and tissues is by the Jones formalism [9]. The electromagnetic field vector is a two dimension complex Jones vector. Changes to the polarization state can be described by a complex 2x2 dimensional Jones matrix . The polarization properties of any non-depolarizing optical system can be described using a Jones matrix. The transmitted polarization state as a result of an optical system represented by a Jones matrix acting on an incident polarization state can be determined by
| (3) |
Subsequent transmission of through an optical system results in a polarization state . As a result, the combined polarization effect of a cascade of optical elements, , can be described by the product .
A Jones matrix has 8 variables (4 complex numbers), of which 7 are independent variables that describe polarization effects in materials, and one is a common phase factor. These 7 independent parameters describe linear and circular birefringence (3 parameters, i.e., phase retardation and orientation of the optical phase retarder) and linear and circular diattenuation (4 parameters, i.e., two attenuation coefficients and orientation of the optical diattenuation). As an example, Eq. (4) gives the Jones matrix for a birefringent material that induces a phase retardation between electric field components parallel and orthogonal to a polarization state characterized by an orientation angle and a circularity related to [10].
| (4) |
where and . The Jones matrix of a dichroic material with attenuation coefficients and for electric field components parallel and orthogonal, respectively, to a polarization state given by an orientation angle and a circularity has the form [10]
| (5) |
The optic axis and the birefringence and diattenuation parameters can be extracted from the Jones matrix by an eigenvector and eigenvalue decomposition, as described in Section 3. The limitation of the Jones formalism is that it cannot describe depolarization, as Jones vectors describe pure polarization states.
An alternative method is the Stokes vectors and Mueller matrices formalism. A Stokes vector is a four component real vector , where , that does describe intensities. This allows for characterization of an optical system with a real matrix , known as a Mueller matrix, that relates an incident Stokes vector to a transmitted Stokes vector such that
| (6) |
Since Stokes vectors can be used to describe depolarized and partially polarized light, Mueller matrices have the advantage over Jones matrices of being able to describe depolarization effects. The Jones and Mueller matrix formalisms are closely related. Vector and matrix quantities in the Jones formalism can be converted into Stokes parameters and Mueller matrices using the relations [11]:
| (7) |
where represents the Kronecker tensor product.
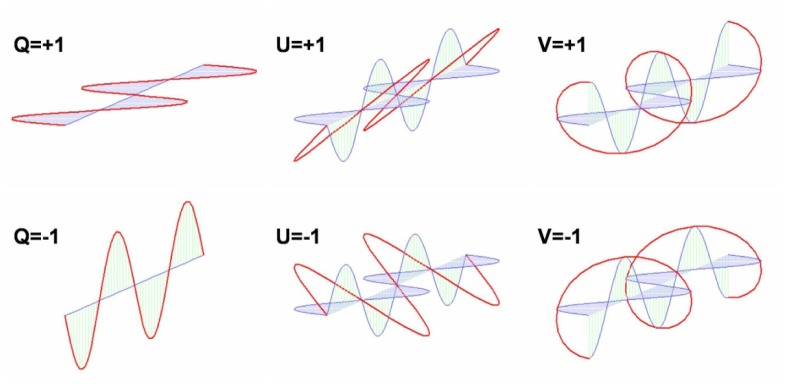
The polarization state of any monochromatic beam can be described using these four parameters, as shown in Fig. 2.
Fig. 2.
Electric fields components for various polarization states corresponding to the different Stokes parameters. Reprinted from Ref [3].
In the Stokes-Mueller formalism the degree of polarization can now be defined by
| (8) |
The degree of polarization of a beam of light can range from unity for purely polarized light to zero for unpolarized light.
Poincaré sphere
The Poincaré sphere is a three-dimensional representation of polarization states that allows for a more intuitive depiction of polarization phenomena. The -, -, and -components of the Stokes parameters are sufficient to describe the polarization state of light. For a partially polarized beam, the -Stokes parameter additionally provides only the degree of polarization. In the case of a fully polarized beam, . Thus, an explicit parameter to describe only the intensity of a beam is unnecessary, and the Stokes parameters can be expressed as a real 3-vector of the form
| (9) |
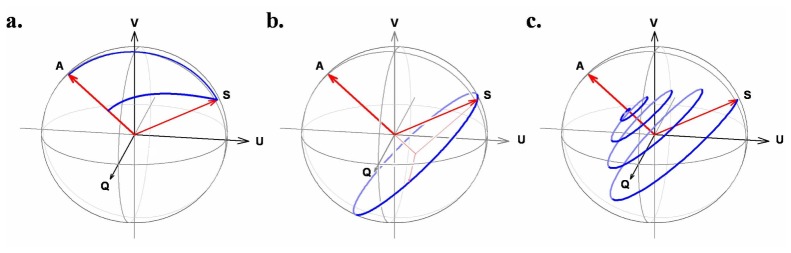
Such vectors can be pictured in a 3-dimensional space known as a Poincaré sphere [12]. The convenience of the Poincaré sphere is that e.g., the effect of birefringence can be visualized as rotations in this sphere, and that polarization properties of tissue can be analyzed in this framework (see e.g., Ref [6, 13–19].). As an example, Fig. 3 shows the transformation of a Stokes vector S in the Poincare sphere for three cases, pure diatteniation, birefringence, and the combined effect of diattenuation and birefringence having an orientation defined by the vector A in the Poincare sphere.
Fig. 3.
Poincaré sphere representations of the effects of (a) diattenuation, (b) birefringence, and (c) the combined effect about a common optic axis A on a polarization state S. The “pulling” effect of diattenuation is evident from the trace (inner arc) of the transmitted polarization state as diattenuation increases (the normalized trace along the surface of the sphere is also shown). Birefringence is equivalent to a rotation in the Poincaré sphere. The combined effect has the appearance of a spiral. Reprinted from Ref [3].
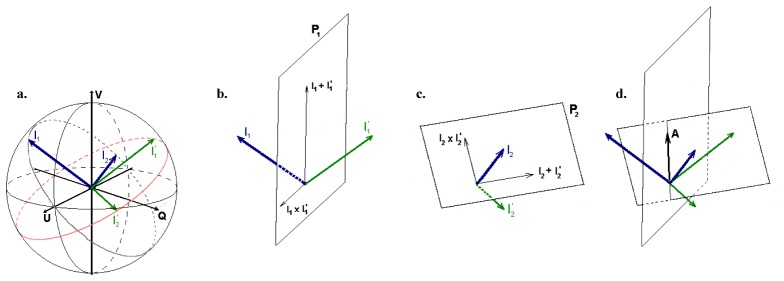
Birefringence can be calculated by analyzing the amount of rotation of 2 independent incident polarization states about a common optical axis. Figure 4 shows a graphical presentation of this method [13].
Fig. 4.
Birefringence calculation illustrating (a): the surface states, I1 and I2, in blue and the reflected states, I’1 and I’2, in green, (b, c) the planes P1 and P2 that span all possible rotation axes, and (d): the intersection of the planes resulting in determination of the optic axis. Reprinted from Ref [13].
Jones and Stokes formalism and the degree of polarization
The polarization properties of tissue can be analyzed in both mathematical frameworks, the Jones formalism or the Stokes formalism. In this review we will focus on the Jones formalism, noting the close mathematical connection between the Jones and Stokes formalism, where at least the Jones formalism can be mapped onto the Stokes formalism (Jones vectors can be converted to Stokes vectors, Jones matrices can be converted to Mueller matrices).
There are two weaknesses of the Jones formalism: the inability to describe partially polarized light, and the inability to describe the processes that lead to depolarization. These shortcomings are addressed by Stokes parameters and Mueller matrices [11], which are quantities based on irradiance, a measure of the energy per unit area and time of a light beam.
For PS-OCT these weaknesses are of limited relevance since OCT is a coherent detection technique, only the sample arm light that interferes with the reference, i.e. which is coherent with the reference arm light is detected. PS-OCT is not capable of measuring the degree of depolarization, the degree of polarization of the Jones vector is always unity, thus PS-OCT is not able to measure partially polarized light or depolarization processes directly. There are, however, two exceptions:
Firstly, depolarization can be observed as a function of wavelength by considering polychromatic light. The Jones vector for a single wavelength (k-vector) is unity. For polychromatic light (like an OCT light source), individual monochromatic Jones vectors (and their corresponding Stokes vectors) will have a degree of polarization of unity, but summing these Stokes vectors over the spectrum of the source could yield a Stokes vector with a degree of polarization less than unity because the polarization state could evolve with the wavelength [6].
Secondly, depolarization can be observed as a function of spatial location in the form of polarization scrambling, i.e., in the form of a variation of the polarization state on a very narrow spatial scale (from speckle to speckle) [20].
In the section on signal processing the Jones and Stokes formalism will be discussed again in the context of signal averaging. The quantification of polarization scrambling in a PS-OCT measurement will be discussed in a sub-section of chapter 3.
3. Determining the polarization properties of tissue
Various light-tissue interaction mechanisms can change the polarization state of backscattered light and therefore form the basis for tissue specific contrast generation by PS-OCT. Accessible to the OCT detection scheme based on a coherent detection of backscattered light are linear birefringence, linear diattenuation, and, in an indirect way, depolarization.
Birefringent materials are characterized by a refractive index that depends on the polarization orientation and on the propagation direction of light within the material. If polarized light enters a birefringent material, it is decomposed into two orthogonally polarized beam components that travel at different speeds. After transiting through a sheet of birefringent material, one polarization state of the light beam is retarded with respect to the other, depending on the amount of birefringence Δn (refractive index difference for the two orthogonal polarization states) and on the thickness of the sheet. This effect can be found in anisotropic crystals or in fibrous materials that consist of long, parallel fibrils embedded in a matrix of different refractive index (form birefringence) [21]. Form birefringence can be observed in several fibrous tissues like muscle, nerve fiber tissue, and tissues that contain collagen.
Diattenuation (or dichroism) describes the property of some materials to absorb light of different polarization states differently. While diattenuation seems to be rather negligible in tissues analyzed so far [16, 19, 22–24], it might be a problem when interpreting results solely due to birefringence. Therefore, a method for simultaneous determination of sample birefringence and diattenuation is desirable.
Depolarization can be caused by multiple scattering or scattering at non-spherical particles [25]. It is observed in pigmented tissue, where the depolarizing effect was shown to be caused by melanin granules [26].
To obtain birefringence and diattenuation related parameters, we will use the Jones formalism to determine the Jones matrix of a sample slice with a particular thickness. The round trip Jones matrix of a sample slice can be determined by probing the tissue with two different incident polarizations states and determining the Jones vectors , reflected from location and incident polarization state 1 and 2, respectively, and Jones vectors , reflected from location and incident polarization state 1 and 2, respectively. The Jones vectors for are given by,
| (10) |
This equation can be cast as a matrix equation,
| (11) |
and the Jones matrix is easily found as,
| (12) |
provided that the two Jones vectors , are independent, i.e., the matrix should be a non-singular matrix in order to calculate the inverse matrix .
The sample polarization properties can now easily be determined from the Jones matrix , as shown by Park et al. [16] and Makita et al. [27], by minimizing the off diagonal elements or performing an eigenvalue and eigenvector decomposition of this matrix. The phase retardation is given by the phase difference between two eigenvalues, and the diattenuation by the contrast of the squared power of the eigenvalues. The optic axis orientation is determined as the directions of the eigenvectors of the round-trip Jones matrix of the sample. The eigenvalues are given by:
| (13) |
where and are the trace and the determinant of the Jones matrix . The phase retardation, diattenuation, and relative optic-axis orientation are then determined by these eigenvalues and eigenvectors as described in the following subsections.
Phase retardation
The phase retardation over the length is determined by the phase difference between the two eigenvalues as
| (14) |
this phase retardation is a cumulative double-path phase retardation from depth position to the depth position of the sample. It should be noted that the selection of and from the two numerically obtained eigenvalues is arbitrary, the phase-retardation value has an ambiguity of rad. The phase retardation is aliased into a to rad range as
| (15) |
where is the aliased double-path phase retardation.
Diattenuation
The diattenuation over the length is defined as the contrast of the square of the absolute value of the amplitudes of the eigenvectors as [28, 29]
| (16) |
Optic-axis orientation
The effective optic axes of the sample can be derived from the eigenvalue and eigenvector decomposition of the sample Jones matrix . The optic-axis orientation is defined by the eigenvector, which is an Eigen Jones vector of the sample matrix that describes a polarization state that is unaltered by the round trip sample matrix. Using Eq. (7) this eigen Jones vector can be mapped to a Stokes vector that gives the optic axis orientation in a Poincaré sphere representation. As we will see later, in fiber based PS-OCT systems the sample matrix cannot be determined directly, in general it is a product of the sample Jones matrix and the Jones matrices of the (fiber) optical elements of the system, leading to a similarity transformation of the sample Jones matrix. The eigenvector of the similarity transformation is not an eigenvector of the round-trip Jones matrix of the sample but that of the similar matrix, and the optic-axis orientation of the similar matrix is not identical to that of the sample but only a relative axis orientation [17].
Quantification and imaging of depolarization
A direct measurement of depolarization is not possible by the coherence based detection scheme of OCT. The degree of polarization (DOP), as defined in classical polarization optics, is always equal to 1 in a single speckle obtained by PS-OCT, i.e., the light of a single speckle is fully polarized [30]. This can be illustrated by the way the Stokes vector elements are calculated from the measured signals:
| (17) |
where A0;x, A0;y are the amplitudes measured in the two orthogonal polarization channels of the PS-OCT instrument, and ΔΦ is their phase difference (see section 4, Eqs. (23) and 24). Inserting the Stokes vector elements into the classical definition of the DOP (cf. Equation (8), we see that DOP will be equal to 1 by definition of Eqs. (8) and (17). However, if we include several speckles in the analysis, the situation changes. If adjacent speckles have different polarization states (i.e., the polarization states are scrambled), an averaging of their corresponding Stokes vector elements will provide quantities whose square sum can be lower than 1. In analogy to the DOP, we can define a quantity that describes the degree of polarization uniformity (DOPU) within an averaging window or kernel:
| (18) |
where the index m indicates the mean value of the corresponding normalized Stokes vector elements within the evaluation kernel. In other words, DOPU can be regarded as a spatially averaged DOP. It is closely related to the apparent degree of polarization obtained by temporal averaging in liquids [30], to the quantity that was used to analyze local correlations of polarization states for detection of multiply scattered light [31], and to the laterally averaged DOP used to study depolarization by depth-dependent light scattering in a non-imaging experiment [32]. In case of a sample that backscatters light in a well-defined polarization state (polarization preserving or birefringent), DOPU is close to 1, in case of a depolarizing sample, DOPU is lower than 1. If we slide the evaluation kernel across a 2D or 3D data set and assign the DOPU value calculated within the kernel to the pixel at the kernel center, we can generate images of depolarization.
The original DOPU algorithm was later refined to improve it and optimize it for different applications. The spatial resolution, which is given by the kernel size, was improved by using smaller speckles (higher resolution) [33], analyzing temporal kernels [34], 3D kernels [35], and an optimum combination of those for imaging the retinal pigment epithelium (RPE) [36]. Other improvements comprise corrections for additive noise that reduce noise sensitivity [37], and the introduction of advanced metrics, the depolarization index [38] and the differential depolarization index [39] that are independent of the input polarization state used to image the sample.
4. Methods
Basic PS-OCT system
In this chapter, we introduce the concepts of PS-OCT by describing a basic version of a bulk optics PS-OCT system and analyzing the propagation of polarization states within the system by the Jones calculus. The system described is based on the PS low coherence interferometer first introduced in 1992 by Hee et al. [2]. Starting in 1997 de Boer et al demonstrated a PS-OCT imaging system showing accumulated phase retardation images and an overall optic axis orientation [40–42]. The first images of optic axis orientation were presented by Hitzenberger et al. [43]. The basic PS-OCT system illuminates the sample by a single, circular polarization state and is capable of measuring reflectivity and birefringence related parameters (retardation and optic axis orientation). The analysis follows a similar path as in previous work [40–44].
Figure 3 shows a sketch of the instrument. A broadband light source (e.g., a super luminescent diode) emits a light beam of short coherence length that is vertically polarized by polarizer P before entering the Michelson interferometer. The Jones vector of this beam can be written as:
| (19) |
where is the electric field vector, the scalar electric field, the field amplitude, the angular frequency, and the time. For simplicity, we ignore the oscillating term and set in the following.
The polarization insensitive beam splitter BS splits the light into a sample and a reference beam of equal amplitude. The reference beam passes through a quarter wave plate (QWP1) oriented at 22.5° to the vertical, is reflected at the reference mirror and propagates back through QWP1 and the beam splitter which directs half of its intensity towards the detection arm. After the double pass through BS, the beam’s intensity is reduced by a factor of 4, corresponding to an amplitude reduction by a factor of 2. The Jones vector of the reference beam in the detection arm can now be calculated by multiplying the input Jones vector twice by the Jones matrix of QWP1 [45], and accounting for the amplitude reduction, resulting in (see e.g., [43]):
| (20) |
where zr is the reference arm length and k0 the center wave number of the source spectrum. Equation (20) describes a linearly polarized beam with polarization orientation at 45°. The polarizing beam splitter PBS in the detection arm splits this beam into horizontally and vertically polarized reference beam components of equal power.
The sample beam transits QWP2 (oriented at 45°) and is thereby circularly polarized, enabling retardation measurements independent of the sample’s axis orientation. The beam is backscattered by the sample (reflectivity R), transits QWP2 a second time, and is directed towards the detection arm by BS. The double pass of BS again reduces the amplitude by a factor of 2. Depending on the birefringence of the sample (which is assumed to be a homogenous linear retarder with retardation δs and axis orientation θs, which is assumed to be constant in depth), the sample beam component reflected at depth z is in an arbitrary (in general elliptical) polarization state as it enters the detection arm of the interferometer. Its Jones vector is given by [41–43, 46]:
| (21) |
with z being the distance between the BS and a reflection site in the sample (neglecting any air gap in the sample arm), the mean refractive index of ordinary and extraordinary beams, and δs(z) = Δn·z·k0 (Δn, refractive index difference between ordinary and extraordinary beams).
In the detection arm, the interfering reference and sample beams are separated into a horizontal (x) and a vertical (y) polarization state by the polarizing beam splitter PBS, and their corresponding interference signals, recorded by the photodetectors, can be written as:
| (22) |
with
| (23) |
and
| (24) |
with and describing the envelopes of the interference signals that rapidly oscillate with path difference (cf. cosine terms of the phase functions ). is the modulus of the complex degree of coherence of the light beams and describes the width of the interferometric signal (depth resolution). The cosine and sine terms of Eq. (23) oscillate slowly with depth , yielding intensity oscillations in the two polarization channels that are 90° out of phase, and whose frequency is proportional to .
From the signals described by Eqs. (22)-(24), we can calculate various sample parameters. For simplicity, we omit the dependence (i.e. we assume a coherence function of infinitesimal width, equivalent to a non-zero amplitude only for ). Reflectivity and retardation can be derived from the signal amplitudes, while the axis orientation θs is encoded in the phase difference of the two signals:
| (25) |
The unambiguous ranges of retardation and axis orientation are 90° and 180°.
Figure 6 shows PS-OCT images recorded with a basic PS-OCT system as described above in a chicken myocardium [43]. The intensity image (Fig. 6(a)) shows very little structure and contains the least information. The retardation image (Fig. 6(b)) shows rather constant color with depth near the (transversal) central third of the image, and about two full color oscillations (indicating a phase shift of ~360°) in the right and left thirds of the image. This is caused by the birefringence of the fibrous structure of the muscle tissue (areas shown in gray indicate regions of low intensity where noise would severely distort the polarization information). The low birefringence in the central area of the image is probably caused by a steeper orientation of the muscle fibers in this area. The optic axis image (Fig. 6(c)) shows that the muscle fibers are differently oriented in the right and left hand parts of the tomogram (the 90° color change in axial direction at depth positions where the retardation (Fig. 6(b)) passes the 90° and 180° values are caused by the data processing algorithm and do not indicate layers of different orientation).
Fig. 6.
PS-OCT images recorded in a chicken myocardium in vitro. Image dimensions: horizontal: 14 mm, vertical: 5 mm (optical distance). (a) Intensity image (color bar: logarithmic intensity scale); (b) phase retardation image (color bar: 0 – 90°); (c) axis orientation image (color bar: −90° – + 90°). (Adapted from [43])
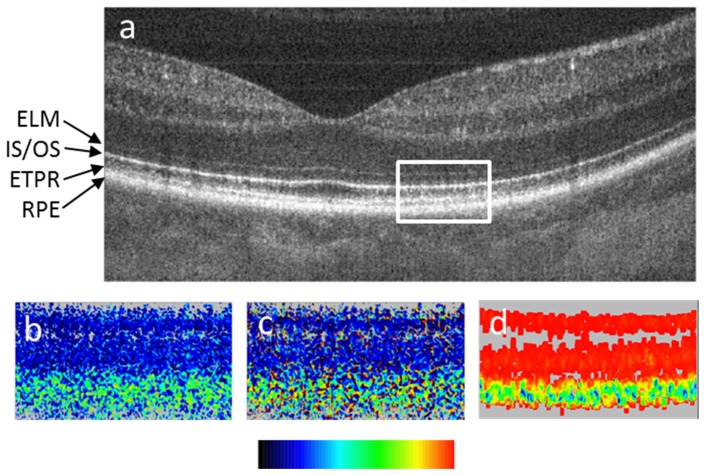
Figure 7 shows an example of imaging a depolarizing tissue in the human retina by PS-OCT [33]. Figure 7(a) shows an intensity based (reflectivity) B-scan through the fovea. Four layers of the outer retina are marked: the external limiting membrane (ELM), the boundary between inner and outer photoreceptor segments (IS/OS), the end tips of the photoreceptors (ETPR), and the RPE. The latter three of these layers show approximately similar intensity. Figures 7(b), 7(c) and 7(d) show zoom-ins into the corresponding retardation, axis orientation, and DOPU images. While IS/OS and ETPR preserve the polarization state (cf. their constant colors in figs. b and c), the RPE appears to have random retardation and axis values (random colors), i.e., their polarization state is scrambled. The DOPU image (Fig. 7(d)) clearly shows that DOPU is reduced (< 0.7) in the RPE (green color).
Fig. 7.
PS-OCT B-scan of healthy human fovea. (a) Reflectivity (log scale), the white rectangle shows approximate areas of the zoom-ins (b)-(d); (b) retardation (color bar: 0°-90°); (c) optic axis orientation (color bar: 0°-180°); (d) DOPU (color bar: 0-1). ELM, external limiting membrane; IS/OS, boundary between inner and outer photoreceptor segments; ETPR, end tips of photoreceptors; RPE, retinal pigment epithelium. (Adapted from [33])
Mueller matrix determination in PS-OCT
Yao et al. [47] and Jiao et al. [30] have presented a method by which the full Mueller matrix of a biological sample can be obtained based on irradiances, i.e., intensities. The determination of a Stokes vector based on irradiances requires four measurements for each incident polarization state. Their systems used variable wave plates and polarizers to sequentially obtain the four irradiance measurements for each of four different input polarization states, requiring 16 measurements in total. This yielded sufficient information to completely determine the Mueller matrix of a sample. A main disadvantage is that it requires a large number of sequential measurements from any location in a sample, significantly increasing the measurement time, without adding information that could not be obtained by determination of the Jones matrix, due to the coherent nature of the OCT detection principle.
A number of subsequent publications have also determined the Mueller matrix for a sample using faster systems with a more traditional two-channel detection scheme similar to that shown in Fig. 5 [48–50]. However, these studies measured the Jones vectors for light incident on and reflected back from a sample to first determine the sample Jones matrix, which is used to derive a corresponding Mueller matrix (e.g., see Eq. (7)). The coherent detection of OCT and the nature of Jones vectors necessarily dictates that the degree of polarization be unity. Unless these calculations are performed in a wavelength-dependent manner, any resultant Mueller matrices can only be used to determine the non-depolarizing polarization properties of a sample, negating any potential advantage over the Jones formalism.
Fig. 5.
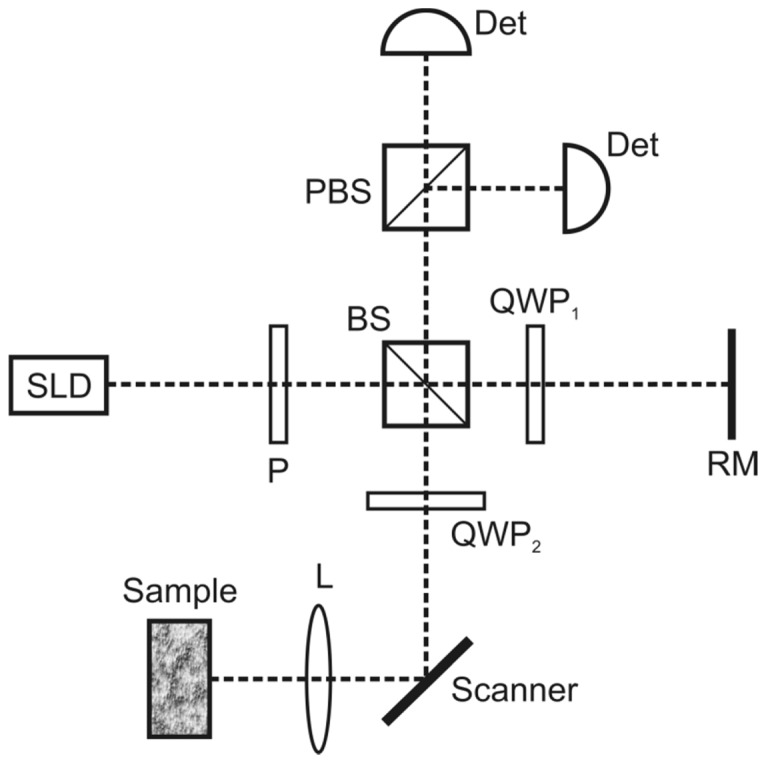
Sketch of basic PS-OCT system. BS, beam splitter; Det, detector; P, polarizer; PBS, polarizing beam splitter; QWP, quarter wave plate; RM, reference mirror; SLD, super luminescent diode.
Determination of the Jones vector and Stokes vector
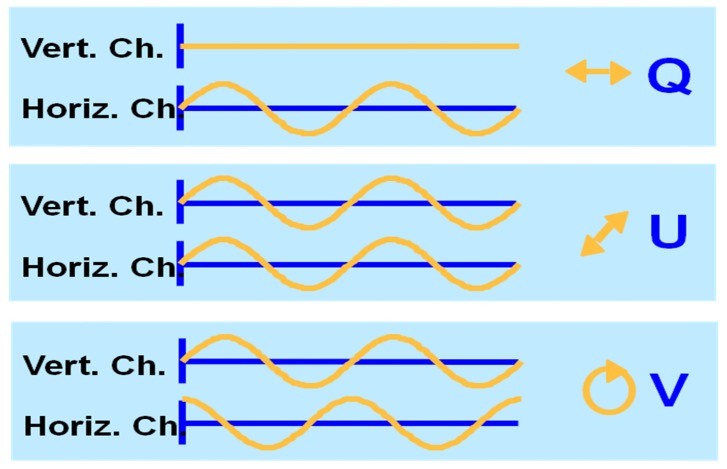
The Jones and Stokes vector can be directly determined by a polarization sensitive system as shown in Fig. 5. The two orthogonal polarization detectors measure the interference between sample and reference arm light in two orthogonally polarized channels. As described earlier (see Eq. (1)), three variables, the amplitude of the fields and , and their relative phase completely describe the polarization state of light. These variables can be directly determined by the amplitude of the interference in each channel, and the relative phase of the interference signal in the two orthogonal channels, as first shown by de Boer et al. [42, 51] and allow determination of the Jones vector, from a PS-OCT measurement. From the Jones vector the Stokes vector can be calculated according to Eq. (7). Figure 8 illustrates the principle and shows an example of the amplitude and phase of the interference in two orthogonal polarization channels over two cycles of the interference pattern. For each of three fundamental possibilities, the corresponding Stokes vector is given. Thus, the polarization state can be completely determined by the amplitude and relative phase of the interference fringes.
Fig. 8.
Example of the interference fringes measured in the horizontal and vertically polarized channel. If the amplitude in the vertical channel is zero, the light must be horizontally polarized (Q-state in Stokes vector notation). If the interference fringes are of equal magnitude and are in phase, the polarization state is linear at 45 degrees (U-state in Stokes vector notation). If the interference fringes are of equal magnitude and are 90 degrees out of phase, the polarization state is circular (V-state in Stokes vector notation) .
Limits of basic systems, fiber optic implementation and the depth resolved axis
Bulk PS-OCT systems provide a convenient framework to analyze the PS-system and tissue polarization properties, because the incident polarization state is fully under control. To determine birefringence a circular incident polarization state would always be altered by linear tissue birefringence, regardless of the orientation of the optic axis. However, bulk systems are prone to systematic errors, as analyzed in detail by Schoenenberger et al. [46]. A more important drawback is that they are impractical in clinical settings; fiber based systems would provide much more convenience.
Two types of optical fibers are in use for OCT applications: regular single mode (SM) fibers and polarization maintaining (PM) fibers. The most straightforward extension of the concepts presented above for a bulk optics PS-OCT system towards fiber technology is to use PM fibers. PM fibers have an elliptic core with different refractive indices for two orthogonal polarization modes aligned along the two axes of the ellipse. Thereby, a PM fiber can guide two linear orthogonal polarization states independently of each other, maintaining their relative amplitudes. If the orientation of the core’s ellipse is properly aligned with the orientation of the axes of the polarizing elements, the free-space and bulk-optic beam paths of Fig. 5 can be replaced by PM fibers and PM fiber based beam splitters. The same parameters as with the bulk optic system can be measured, similar equations are used. However, since the PM fiber just maintains the amplitude relation between the two orthogonal polarization states but not their phase relation, additional measures have to be taken to correct for the phase offset. Both, hardware [52] and software [33] based solutions have been reported. The main advantages of the PM fiber approach are its relatively simple implementation and the possibility to work with a single (circular) input polarization state. The disadvantages are that PM fibers and PM fiber components are more expensive than SM fibers, and that, because of their non-rotational symmetric core, they cannot be used in rotating endoscopic or catheter probes.
Conventional SM fibers avoid these drawbacks and are better compatible with existing commercial OCT technology. Unfortunately, single mode optical fiber changes the polarizations state during propagation due to stress and non perfect circular symmetry of the fiber core. Thus the incident polarization state on the tissue becomes arbitrary. For example, the polarization could be linear AND aligned with the optical axis of the sample. In that case, the reflected light from the sample would not change, even in the presence of birefringence, and a PS-OCT measurement would not render reliable information about tissue birefringence.
One way to solve this problem is to place polarization controllers in the source, sample, reference, and detector arm fibers and align them to mimic the wave plates used in the bulk setup of Fig. 5 [53]. A refined method requires the calibration of only one fiber transformation [54]. In these cases, the sample is illuminated again by circularly polarized light, and the corresponding equations used for the bulk system can be used. However, the method only works if the fibers are not moved after polarization controller alignment, i.e., the method does not work for flexible sample arms or endoscopes. A general solution that works with flexible probes overcomes this problem, and actually was the first demonstration of a fiber based PS-OCT system which solved this problem by probing the tissue with 4 different input polarization states [15]. This principle was universally adopted in a variety of modulation schemes for the input polarization states that were developed [52, 55–60].
Two main approaches evolved over time. In the first method, the tissue was probed consecutively with two polarization states orthogonal in the Poincare representation (e.g., a linear and a circular polarization state) [13, 15, 61]. The rationale was that for any orientation of the optical axis and for any induced change of the polarization state in the fiber, the tissue polarization properties could be determined. In a lossless fiber, the orthogonal states would remain orthogonal. Because the measurements of the reflected two states are delayed in time, no reliable phase relation exists between the fields measured for the two consecutive input polarization states. A method to extract the birefringence in the Poincaré representation using Stokes vectors was illustrated in Fig. 4. In the second approach the sample is (nearly) simultaneously probed with two polarization states. In this case a stable phase relation can be established between the detected fields of two different polarization states. This allowed also the use of two orthogonal polarized input states, e.g., linear horizontal and linear vertical. The simultaneous two-polarization probe was first performed by modulation multiplexing of two polarization states [52, 55]. A more recently popular approach to generate these two input states is by a passive Polarization Delay Unit (PDU) in the sample arm [58–60]. In a PDU two orthogonal polarization states are generated that have a small delay on the order of half the ranging depth of the OCT system. In a single A-line (depth profile), two simultaneous measurements with different input polarization states of the sample are performed, which are encoded in depth in the depth profile (e.g., the first half of the depth profile represents the first incident state, the second half of the depth profile represents the second incident state).
To determine the sample polarization properties with a fiber based PS-OCT system the system polarization properties need to be included in the analysis of the measurements. In general terms, a PS-OCT system sends polarized light from a source into the sample and reference arms of an interferometer, and reflected light from both arms is recombined and detected. Following Park et al. [16], the system can be separated into three sections, each described by a Jones matrix as shown in Fig. 9.
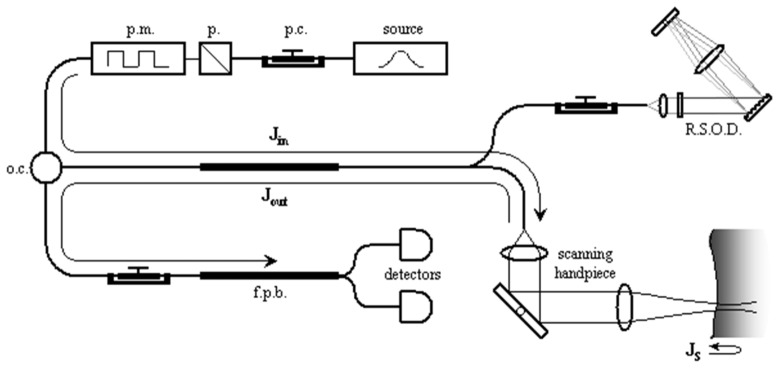
Fig. 9.
Schematic of the fiber-based PS-OCT system (p.c., polarization controller; p, polarizer; pm, polarization modulator; oc, optical circulator; RSOD, rapid scanning optical delay; fpb, fiber polarizing beamsplitter). Jin, Jout, and JS are the Jones matrix representations for the one-way optical path from the polarization modulator to the scanning handpiece, the one-way optical path back from the scanning handpiece to the detectors, and the round-trip path through some depth in the sample, respectively. Reprinted from [16].
We define as the Jones matrix representing the optical path from the polarized light source to the sample surface, as that going from the sample surface to the detectors, and as the round-trip Jones matrix for light propagation through a sample [16]. This nomenclature can be applied to all PS-OCT systems, ranging from bulk-optic systems [2, 40,43, 47, 62, 63], to those with fibers placed such that they are traversed in a round-trip manner [50], to time-domain [15, 61], spectral-domain [64] and swept source PS-OCT [55, 57, 58] systems. This approach is applicable to the use of optical fibers and non-diattenuating fiber components, and even for retinal systems [65], where the polarization effects of the cornea can be included in and . The electric field of light reflected from the sample surface, , can be expressed as , where represents a common phase of the E-fields associated with the propagation distance and represents the electric field of light coming from the polarized source. Likewise, the electric field of light reflected from some depth within the tissue may be described by . These two measurable polarization states can be related to each other such that , where and . is the measured Jones matrix as determined from the reflected fields from location and shown in Eq. (11).
If the optical system representing is non-diattenuating, can be treated as a unitary matrix with unit determinant after separating out a common attenuation factor. can be decomposed into a diagonal matrix , containing complete information regarding the amount of sample diattenuation and phase retardation, surrounded by unitary matrices with unit determinant that define the sample optic axis. can be reformed such that , where . Since unitary matrices with unit determinant form the special unitary group SU(2) [66], must also be a unitary matrix with unit determinant by closure. Thus, is given by,
| (26) |
with a diagonal matrix containing complete information regarding the amount of sample diattenuation and phase retardation, and a unitarian matrix that describes the optic axis orientation of the sample, , multiplied with a unitarian matrix that describes a rotation of the reference frame in the optical fiber.
Since the reference frame is rotated in the optical fiber, only a relative optic axis can be derived from . Determination of this relative optic axis in a fiber-based system has a fundamental ambiguity. All members of the SU(2) group can be mapped to rotations in SO(3), and so , , and all represent rotations in a Poincaré sphere representation. This means that , , and are related by unitary transforms and are equivalent except for their respective coordinate systems. Therefore, the amount of phase retardation and diattenuation in , , and is the same. The three matrices have the same eigenvalues and differ only in their eigenvectors, and their optic axis equivalents, in a well-defined manner dictated by . In other words, the optic axis of is the product of the sample optic axis defined by and the fiber transformations represented by . Due to the round-trip nature of detected light propagation in tissue, the circular components of birefringence and diattenuation in the sample cancel. Only the linear components of these properties can be measured using PS-OCT. In mathematical terms, the optic axes of , defined by its eigenvectors, can represent only linear birefringence and diattenuation. The sample optical properties (diattennuation and birefringence) can be extracted from by determining the eigenvalues as shown in Eqs. (13)-(16).
Polarization mode dispersion
Fiber optical components including optical fiber and circulators can have different wavelength-dependent refractive index between two eigen-polarizations. It results in a different dispersion of eigen-polarizations, so denoted as polarization mode dispersion (PMD). In PS-OCT, PMD can become significant with long optical fiber sections in the system and the presence of circulators, which can have a significant PMD [67]. It results in a differential delay and a different shape of the point spread functions for orthogonal polarization channels, and errors in phase retardation and other polarization property measurements [67, 68].
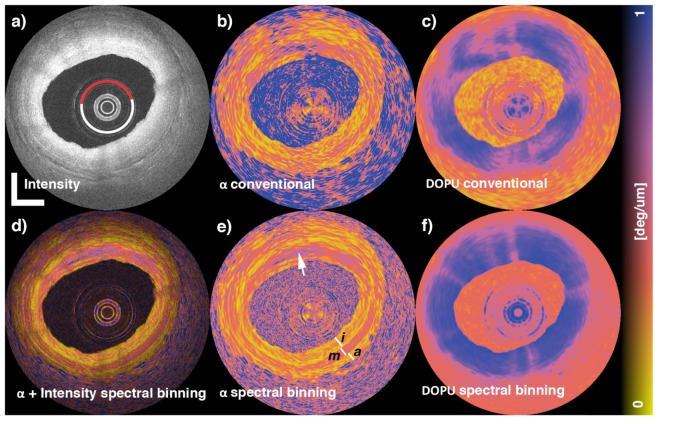
PMD can be classified into two types; PMD in non-common paths or in a common path of the interferometer. The first type of PMD occurs in probe and reference arms, whose lengths are typically a few meters. It mainly appears as a small additional dispersive phase in the OCT signals. Although this small dispersive phase is not a problem in non-PS-OCT, it can degrade the image quality and polarimetric accuracy of PS-OCT [68]. So far, several methods have been devised to eliminate this type of PMD. For instance, Zhang et al. demonstrated numerical compensation of PMD with three calibration signals obtained from the tip of the sample arm [69], and Villiger et al. numerically mitigated PMD artifacts by spectral binning [70]. Braaf et al. also demonstrated another sophisticated numerical correction method [71].
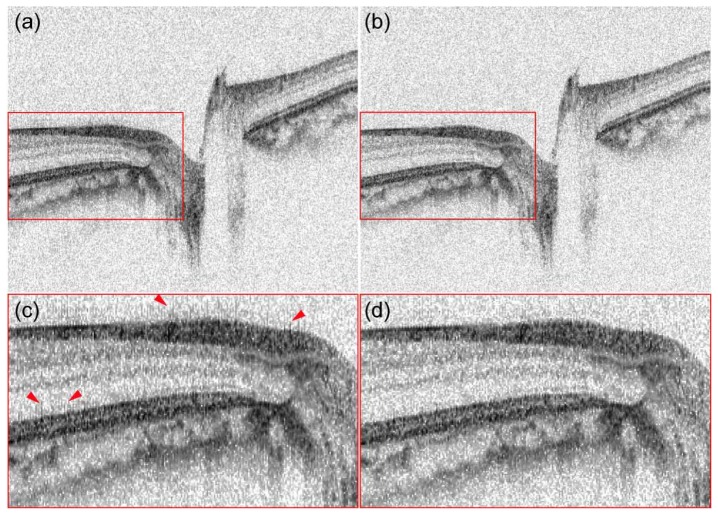
The second type of PMD becomes problematic if the interferometer consists of a very long optical fiber of the order of a few hundreds to thousands of meters in its common path. Optically buffered swept-source OCT is a typical example. This PMD is substantial and affects not only the phase but also the envelope of the spectrum if the OCT is equipped with polarization-sensitive components such as polarizers, polarizing beam splitters, or polarization-sensitive semiconductor optical amplifiers (SOAs). Hence, it significantly degrades the imaging performance of PS-OCT. Hong et al. demonstrated a combined hardware-software combination method in which the phase modulation occurred by PMD was converted into spectral envelope modulation by polarizers, and the envelope modulation was corrected by a fringe processing method [72].
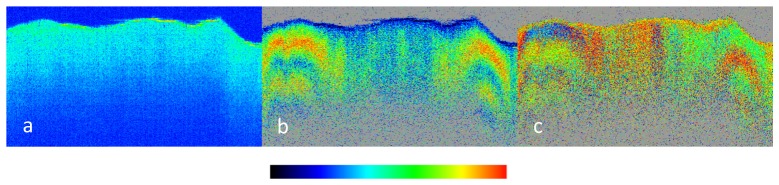
Figures 10 and 11 exemplify the PMD corrections in practical clinical images. Figure 10 demonstrates numerical correction of non-common-path PMD by the spectral binning method applied to cadaveric human coronary artery PS-OCT images [70]. The first row shows OCT intensity, local retardation, and DOPU without PMD correction (left to right), while the second row shows PMD corrected images; composition of intensity and local retardation (d), local retardation (e), and DOPU (f). Granular appearance in the non-PMD-corrected local retardation image hides the real birefringent structures appearing in the PMD-corrected local retardation image (e). Figure 11 is an example of correction of common-path PMD [72]. The left column [(a) and (c)] are retinal OCT intensity images taken by an optically buffered PS-OCT system without PMD correction. The optical buffering uses a long common-path fiber, and every two A-lines are suffering from severe PMD by the buffered fiber. This PMD results in fine comb-shaped artifacts as, for example, indicated by arrowheads in the magnified image (c). These artifacts were removed by a fringe processing method as shown in (b) and (d).
Fig. 10.
Cadaveric human coronary artery PS-OCT images with and without numerical non-common-path-PMD correction by a spectral binning method. The first row shows intensity, local retardation, DOPU without PMD correction (left to right). The second row shows intensity-local retardation composite, local retardation, DOPU with PMD correction (left to right.) The images were reprinted from [70].
Fig. 11.
Retinal intensity OCT images taken by an optically buffered PS-OCT system without (a) and with (b) common-path-PMD correction. (c) and (d) are magnified images of (a) and (b), respectively. The comb-like artifacts in (a) and (c) were suppressed in (b) and (d). The figure was reprinted from [72].
Advanced data processing
OCT measurements are always affected by noise, the measured signal deviates from the true value. For example, the complex OCT signal is affected by symmetric complex Gaussian noise, the distribution of measured complex OCT signals becomes complex Gaussian centered at the true signal value. Since the distribution of the measured signal is symmetric and centered at the true value, averaging of multiple signals is a maximum likelihood estimation (MLE) of the true value. It asymptotically approaches to the true value as the number of signals to be averaged increases. In other words, a mean estimator can provide an MLE of the complex OCT signal.
However, this optimistic scenario cannot be applied to phase retardation and birefringence measurement. These values are derived from a set of OCT signals through highly nonlinear operations. The nonlinear operation does not preserve the symmetry of the distribution [27]. For example, the distribution of measured phase retardations is no longer Gaussian or symmetric, and neither the mean nor the mode of the distribution correspond to the true phase retardation. So, the mean estimator of phase retardation does not provide a correct estimation of true phase retardation even with large number of measured values. In order to have a reliable estimate of the phase retardation, several more sophisticated estimators were proposed.
As discussed above, complex averaging provides an MLE of OCT signals. Although the phase retardation derived from the complex averaged OCT signals is not the MLE of phase retardation, it asymptotically approaches to the true phase retardation as the number of averaged signals increases. This fact has motivated researchers to explore several averaging methods of measured Jones matrix, i.e., a set of measured complex OCT signals.
If we can assume that a set of Jones matrices possess the same phase retardation, axis orientation, and common phase offset, complex averaging of each entry of the matrices provides a good estimation of the Jones matrix. However, for the image processing of PS-OCT, the averaging is frequently performed in a small but spatially extended kernel and for this spatially extended kernel the above mentioned assumption is not true.
The assumption is especially incorrect for the common phase offset in a Jones matrix. To mitigate this problem, common-phase correction was used for Jones matrix averaging with both a rectangular kernel [60, 73, 74] and gradually weighted Gaussian kernel [75]. Here it should be noted that these averaging methods are not technically the averaging of Jones matrix but complex averaging of measured OCT signals. Hence, it was a natural extension of averaging of non-Jones matrix OCT signals. This approach assumes that the polarization properties of the tissue are homogeneous in the kernel.
The averaging of a general Jones matrix, namely, averaging of polarization properties within an inhomogeneous tissue region, is still an open issue. Wang et al. demonstrated complex averaging of eigenvalues of Jones matrices [76]. An alternative and more complex approach of Jones matrix averaging is based on the Cloude-Pottier decomposition [77]. In this method, first an MLE of a covariance matrix of the Jones matrix is obtained. Then an estimation of the Jones matrix is obtained by using Cloude-Pottier decomposition. And finally, a reasonable estimation of phase retardation is obtained from the estimated Jones matrix.
Non-complex (intensity) averaging is also useful for phase retardation imaging. One widely accepted method is Stokes vector averaging [14]. Here the measured polarization sensitive OCT signals are first converted to a Stokes vector. A set of Stokes vectors distributes around its true value in Poincare sphere, the mean of the Stokes vectors is a good estimation of the true Stokes vector, which has the advantage that these are irradiances and in the averaging process reduce the effect of speckle. A good estimation of phase retardation is then obtained from two Stokes vector estimates at two depth positions. The intensity averaging is also useful for PS-OCT based on Hee’s method [2] in which the phase retardation is computed only from intensity (without phase information). It was shown that the phase retardation derived from the intensity-averaged OCT signals provides good image quality [78]. Villiger et al. [70] extended the Stokes vector averaging method by spectral binning.
Besides the approaches to obtain the phase retardation through a good estimation of OCT signals, Stokes vector, Jones vector, or Jones matrix, direct estimation methods of phase retardation have also been widely explored.
For more quantitative understanding, Makita et al studied how the Gaussian noise of a complex OCT signal affects the phase retardation measured by Jones matrix OCT. In this study, it was shown that the measured phase retardation was affected by only three independent parameters: a combined SNR of the measured OCT signals used for phase retardation computation, so-called effective SNR (ESNR), the true phase retardation value, and the relative angle of incident polarization states used for Jones matrix measurement [27]. The last parameter is a constant in practice, the distribution of phase retardation was affected by only two parameters; ESNR and true phase retardation.
Duan et al. designed a phase retardation estimation function based on this model, which takes measured phase retardation and ESNR as inputs and gives an estimation of phase retardation [79]. Kasaragod et al. further improved this estimator by using full information of probability distribution functions of measured and true phase retardations. It provides a maximum a-posteriori (MAP) estimation of true phase retardation (birefringence) from a set of measured phase retardations and ESNRs [80, 81]. An advantage of this approach is that the estimate obtained by this method is the MLE or MAP of phase retardation, while the phase retardation obtained from the MLE of Jones matrix is not an MLE of phase retardation.
5. Application of PS-OCT
Anterior eye segment imaging
Anterior segment PS-OCT is potentially useful for two applications in glaucoma treatment. One promising application is evaluation of the bleb which is created by trabeculectomy surgery. The other is the evaluation of the trabecular meshwork.
A bleb is a structure which was created by trabeculectomy surgery. The only effective strategy for the suppression of glaucoma progression is the reduction of intra-ocular pressure (IOP). While pharmacological interventions to reduce IOP are effective in the early stage, surgical intervention, including trabeculectomy, trabeculotomy, and laser iridotomy, are required in advanced or some specific cases. In trabeculectomy surgery, an artificial tissue structure, a so called filtering bleb, is created. The bleb bypasses the drainage of the aqueous humor and reduces IOP.
Since a bleb is an artificially created wound, it is gradually healed and scared. This healing of the bleb results in a dysfunction of the bleb. So, a frequent monitoring of the bleb’s structure and wound healing is important to maintain its functionality. Since scaring is associated with proliferation of collagen, it can be monitored by PS-OCT. At the same time, the structure of the bleb can be monitored by intensity image obtained by PS-OCT.
The progression of scaring in bleb was first visualized by phase retardation [82]. Lim et al validated the relationship between the phase retardation appearance and scar formation by comparing PS-OCT and histology in a rabbit [73]. Fukuda et al showed that phase retardation is a reasonable indicator of the functionality of the bleb [83, 84].
With the introduction of local phase retardation (birefringence) imaging, more accurate evaluation of scar formation becomes available [75, 85]. Among them, Yamanari et al showed histological correlation with birefringence image [75]. Kasaragod et al demonstrated a metric computed from the birefringence of the bleb, and it can be utilized for classification of functional and non-functional blebs [85]. Figure 12 exemplifies the birefringence imaging of trabeculectomy blebs (adapted from [85]). Each column represents a case of bleb. The first and second rows represent intensity cross section and birefringence cross section. High birefringent areas (red pixels) are overlaid on the intensity image. The dashed lines indicate the interface of sclera and conjunctiva. The values at the top left of the images represent the fraction of the high birefringence area in the conjunctiva, which correspond to the severity of the scaring and is denoted as fibrosis score.
Fig. 12.
Examples of birefringence imaging of blebs. (a) and (b) are intensity OCT and (c) and (d) are birefringence cross-sections. In (e) and (f), the high birefringence pixels (red) are overlaid on intensity image. The numbers at the top left indicate the areal fraction of high birefringence regions in the conjunctiva (adapted from [85]).
PS-OCT can be utilized for subjective observation of bleb status, and also for objective evaluation of its functionality. PS-OCT would be useful for optimization of trabeculectomy and its post-surgical maintenance.
The trabecular meshwork is a circular meshwork structure at the iridocorneal angle of the anterior eye chamber. The liquid filling the anterior eye chamber, aqueous humor, is drained throughout the trabecular meshwork. And hence, its blockage by the iris triggers the acute ocular hypertension and glaucomatous attack. In addition, malfunction of its drainage also causes chronic ocular hypertension and subsequent glaucoma. So, it is important to identify the location of the trabecular meshwork in OCT images and also to assess the abnormality in its micro-structural tissue.
Since the trabecular meshwork consists of collagen, it has specific birefringence properties, and it can be visualized by PS-OCT. Its polarization contrast was accidentally found by non-PS-OCT as a polarization artifact imitating Schlemn’s canal [86]. Conventional OCT also has some polarization contrast, although it is regarded as an artifact. So, the trabecular meshwork frequently appeared with a dark-band artifact in conventional anterior eye segment OCT images. Yasuno et al. performed a systematic comparison of visibility of trabecular meshwork by conventional OCT and PS-OCT, and have shown that PS-OCT provides better visibility [87].
Although it is under researchers’ consensus that PS-OCT is useful for selectively visualizing the trabecular meshwork, its detailed polarization and birefringence properties are still controversial. Some studies show high and some others show low birefringence [75, 80]. So, detailed investigations are required in the future.
Keratoconus is an ectatic thinning of the cornea. It is characterized by progressive conical protrusion of the cornea, and results in severe dysfunction of visual acuity. Although the mechanism of keratoconus is still unclear, it is reasonable to assume it is associated with microstructural tissue abnormalities of the cornea. Since the cornea consists of well organized collagen and has specific polarization properties [73, 88–90], its abnormality can be assessed by PS-OCT. The first application of PS-OCT to keratoconus was performed by Götzinger et at [91]. and it was found that the keratoconic cornea appears with an abnormal phase retardation pattern. Fukuda et al. showed that PS-OCT has high sensitivity to detect the keratoconus and is useful for grading the disease based on systematic clinical studies [92]. PS-OCT is a promising tool for screening and treatment control of keratoconus and also other corneal diseases [93].
Posterior eye segment imaging
The dominating application field of OCT in general and also of PS-OCT is imaging of the posterior eye segment. Several layers of the ocular fundus can change the light’s polarization state: the retinal nerve fiber layer (RNFL), Henle’s fiber layer, the sclera, as well as fibrotic lesions are birefringent, the RPE (and to a lesser extent the choroid) are depolarizing [7]. These properties can be used for various diagnostic applications, and only the most important can be presented here.
Imaging and quantification of the retinal nerve fiber layer
The axons of the ganglion cells of the retina make up the RNFL. These axons carry the electrical signals generated by the visual process via the optic nerve into the brain. The fibrous structure of the RNFL causes its birefringence [94].
In glaucoma, one of the leading causes of blindness in the world, the RNFL gets damaged, leading to vision loss. In many cases, such RNFL damages can be observed before a visual field loss is detected [95]. The damage leads to a thinning of the RNFL which is associated with a reduced retardation introduced by this layer to a sampling beam, and it has been shown in animal models that the birefringence is reduced at an even earlier stage of the disease [96]. These findings are the basis for the use of polarimetric techniques for glaucoma diagnosis. While an earlier technique, scanning laser polarimetry (SLP) [97–99] was quite successfully used as a glaucoma screening tool, it has some shortcomings that cause imaging artifacts in a considerable subset of eyes [100, 101]. These are caused by the lack of depth information, leading to scleral signals interfering with RNFL signals, thereby distorting the results [102]. PS-OCT can avoid these problems.
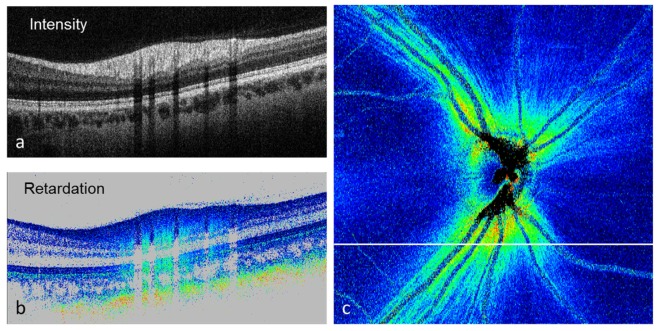
Retardation and birefringence measurement and imaging of the RNFL were among the first applications of PS-OCT in the eye [65, 103–109]. Figure 13 shows an example of PS-OCT retardation imaging in the optic nerve head (ONH) region. Figure 13(a) shows a reflectivity B-scan recorded inferior to the ONH. The RNFL is observed as the topmost, thick hyperreflective layer. Figure 13(b) shows a corresponding retardation image. The birefringence of the RNFL can be observed by the color gradient (color change from dark blue to cyan with increasing depth). In addition, the polarization scrambling RPE can be observed, as well as the strongly birefringent sclera (color gradient from blue to orange beneath the retina). If we extract the retardation value beneath the RNFL, e.g. within the strongly reflecting photoreceptors (they maintain the polarization state of the light they reflect, so the polarization state corresponds to that generated by the overlying RNFL), we can quantify the RNFL retardation and, by applying this method to the entire 3D data set from which the B-scans were taken, we can generate an en-face retardation map of the RNFL (Fig. 13(c)). In a healthy eye, this map shows a characteristic butterfly-shaped pattern that clearly shows the increased retardation caused by the thick RNFL in the vicinity of the ONH and along the arcuate nerve fiber bundles.
Fig. 13.
PS-OCT images recorded in the optic nerve head region of a healthy human eye. (a) Reflectivity B-scan; (b) retardation B-scan; (c) en-face RNFL retardation map. The white line indicates the position of the B-scans.
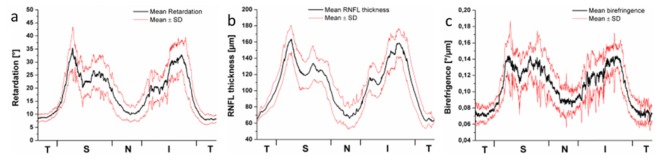
Figure 14 shows a quantitative evaluation of the RNFL retardation, thickness, and birefringence obtained around the ONH of 10 healthy eyes [110]. The respective quantities were measured along a circle around the ONH, ranging from the temporal position (T) over the superior (S), the nasal (N), the inferior (I), and back to the T position. The black curves show the mean values measured in the 10 eyes, the red curves indicate the range distribution (standard deviation). As can be seen, not just the retardation and thickness, but also the birefringence varies as a function of position, ranging from ~0.07 to 0.14°/µm on average. For a wavelength of 840 nm, this corresponds to a dimensionless birefringence Δn of 1.6 - 3.3·10−4 which is in the range of RNFL birefringence values reported in other studies [104, 108, 109].
Fig. 14.
Circumpapillar profiles of (a) RNFL retardation, (b) RNFL thickness, (c) RNFL birefringence. T, temporal; S, superior; N, nasal; I, inferior. Black line: mean value of 10 healthy eyes; red lines: mean value ± standard deviation. (Adapted from [110] by permission of the Association for Research in Vision and Ophthalmology)
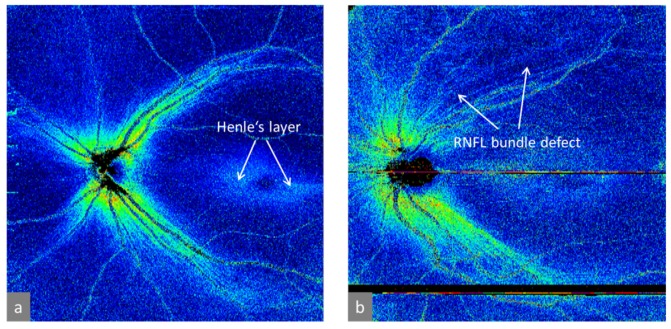
Figure 15 shows a comparison of retardation maps obtained in a healthy eye (Fig. 15(a)) and a glaucomatous eye (Fig. 15(b)) [111]. The latter image shows an RNFL bundle defect in the superior hemisphere, indicating the potential value of PS-OCT for glaucoma diagnostics. In addition to the RNFL retardation, the somewhat weaker retardation caused by Henle’s fiber layer can be seen as a doughnut-shaped retardation elevation. A more detailed analysis of the birefringence of this layer by PS-OCT can be found in ref [112].
Fig. 15.
Wide field RNFL retardation maps obtained in human eyes. (a) Healthy eye; (b) glaucomatous eye. (Adapted from [111])
Although the limited space does not allow to discuss these applications and results in more detail, it should be mentioned that several papers have reported interesting and useful results of PS-OCT imaging of birefringent structures in animal eyes (cf., e.g., [63, 113–116]).
Imaging of macular lesions
The macula is located near the center of the retina, at the posterior pole of the eye. Near the center of the macula, at the fovea centralis, the density of photoreceptor cells is highest, associated with the sharpest vision. Any damage to the fovea and the macula will therefore have a severe impact on vision. A variety of retinal diseases affect the macula, the most important being age related macular degeneration (AMD), the most frequent cause of irreversible vision loss in the developed world.
PS-OCT can be used in the diagnosis of various stages of AMD. One of the earliest indicators of AMD are drusen, localized elevations of the RPE, beneath which extracellular debris is accumulated. Drusen represent a major risk factor for disease progression. Therefore, an automated drusen detection and quantification is important for disease management. Since the RPE depolarizes backscattered light (cf. section 4), it can directly be segmented by PS-OCT by thresholding retinal DOPU images [20]. In further data processing steps, the area and volume of drusen can be automatically determined [117].
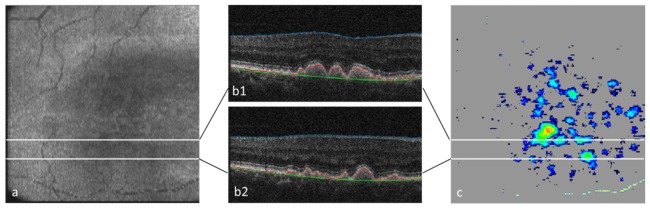
Figure 16 shows an example of drusen segmentation based on PS-OCT imaging. Figure 16(a) is an en-face intensity (reflectivity) projection image of a 3D PS-OCT data set acquired in the macula of a patient with drusen. Figure 16(b)1,2 are two reflectivity B-scans where three segmentation lines are drawn [117]. The inner limiting membrane (blue) is obtained by intensity thresholding, the RPE (red) is assumed to coincide with the lowest DOPU value within the depolarizing band in the corresponding DOPU image (not shown here), the green line indicates the position where the RPE should be (found by an iterative algorithm that uses the red line as a backbone). Figure 16(c) shows the drusen thickness map (distance between red and green line in the B-scans). From this map, area and volume of drusen can easily be quantified. Based on this method, characteristic growth patterns of drusen over time were identified [118].
Fig. 16.
Drusen segmentation by PS-OCT. (a) En face reflectivity projection image (pseudo SLO); (b1, b2) B-scans with segmentation lines: blue, inner limiting membrane; red, RPE; green, original position of RPE. (c) drusen map. (adapted from [117])
In addition to drusen quantification, PS-OCT is also able to differentiate between different types of drusen [119, 120]. Figure 17 shows a comparison of drusen imaged by PS-OCT and intensity based OCT [119]. In the PS-OCT image, the depolarizing material (tissue areas that meet the DOPU segmentation threshold) is shown in red, overlaid on the reflectivity data. Different types of drusen are observed, e.g., normal drusen with a continuous RPE above the exudative deposit, drusen filled completely with depolarizing material, and drusen with holes in the RPE or with a complete loss of the RPE. Ongoing studies investigate whether drusen type has an influence on the progression of the disease.
Fig. 17.
Drusen imaging by PS-OCT (a) and intensity based OCT (b) in the same eye of a patient with AMD. Various forms of drusen can be differentiated in the PS-OCT image, where depolarizing tissue (red) has been segmented by its low DOPU value. Blue arrow: druse filled with depolarizing material; white arrowheads: small atrophic lesions; yellow arrow: drusenoid structure with complete loss of RPE. (Reproduced from [119] by permission of the Association for Research in Vision and Ophthalmology)
Two forms of advanced stages of AMD can be differentiated: dry and wet (neovascular) AMD. In dry AMD, large areas of atrophic zones develop where the RPE and photoreceptors are lost. These geographic atrophies (GA) can also be segmented by PS-OCT by algorithms that have similarities to the drusen segmentation algorithm described above [117, 121]. In addition to GA quantification, PS-OCT also allows to judge whether the fovea still has intact RPE areas (foveal sparing) in cases with central GA, a condition difficult to judge by other imaging modalities [122].
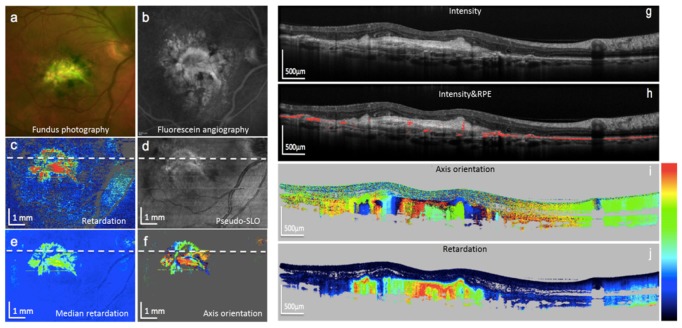
In the neovascular form of AMD, new vessel membranes grow beneath the retina or the RPE, and leakage of these vessels can lead to hemorrhage and fibrosis as an end stage. For therapy decisions, it is very important to judge whether the lesion is still active or in a fibrotic stage, a decision difficult to make based on reflectivity images. However, fibrotic tissue shows form birefringence and can therefore be identified by PS-OCT [123, 124]. A recent study using a PS-OCT system with an integrated retinal tracker [125] – which is important since the fixation capability of affected patients is usually poor, leading to heavy motion artifacts – demonstrated that fibrotic lesions can be readily identified and in the majority of cases also segmented by their characteristic birefringence patterns, showing column-like axis orientation patterns in PS-OCT B-scans (cf. Figure 18) [126]. The combination of PS-OCT with OCT angiography provides further insights into neovascular lesions in AMD patients [127].
Fig. 18.
Images of an eye with fibrotic neovascular AMD. (a) Color fundus photo; (b) fluorescein angiography; (c) PS-OCT mean retardation map; (d) PS-OCT reflectivity projection map; (e) PS-OCT median retardation map; (f) PS-OCT axis orientation map; (g) PS-OCT reflectivity B-scan; (h) same B-scan with segmented RPE (red); (i) PS-OCT axis orientation B-scan, fibrotic tissue generates column-like color pattern (color bar: −90 - + 90°); (j) PS-OCT retardation B-scan, fibrotic tissue is strongly birefringent (color bar: 0 – 90°). (Adapted from [126])
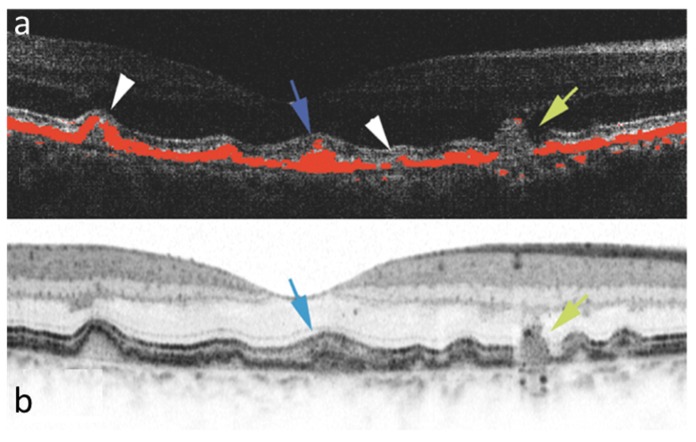
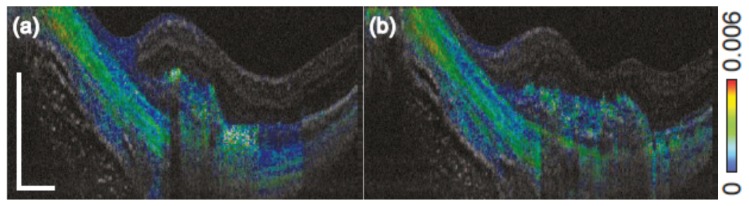
Figure 19 demonstrates the additional information obtained by depth resolved local birefringence imaging provided by PS-OCT [128]. Two cross sections through a neovascular lesion of a patient with myopic choroidal neovascularization are shown. Contrary to Fig. 18 that shows cumulative phase retardation, the local birefringence is displayed by the color coding. Elevated birefringence is observed in parts of the neovascular lesion as well as in the sclera, where alternating layers of higher and lower birefringence are observed which would not be discernible in cumulative retardation images.
Fig. 19.
Birefringence cross sectional B-scans extracted from a three dimensional data set acquired with Jones Matrix OCT in a patient with myopic choroidal neovascularization. A layered structure is visible in the sclera, as well as varying birefringence in the neovascular region. (Adapted from [128])
Several other diseases that affect the macula have been successfully studied by PS-OCT like diabetic retinopathy [129], central serous chorioretinopathy [130], telangiectasia [131], or hereditary diseases like albinism [132] and Stargardt’s disease [133]. Moreover, related studies in animal models have been performed [116, 134, 135]. A detailed description of these results is, however, beyond the scope of this paper.
Endoscopic PS-OCT
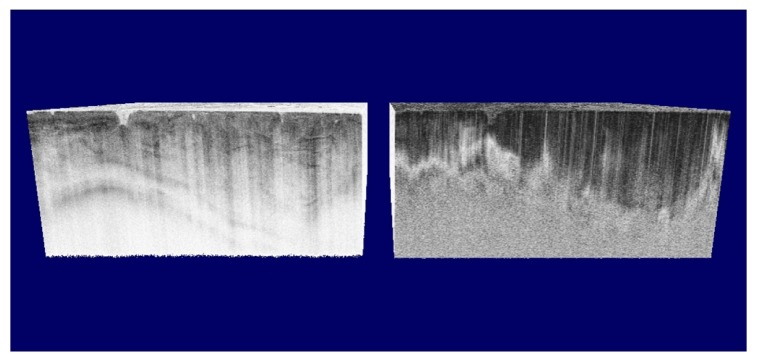
With the fiberoptic implementation of PS-OCT, also endoscopic applications come within reach of the technology. In endoscopic applications, the scanning mechanism provides an additional hurdle. In general either a whole fiber catheter rotates inside a protective sheet, or at the tip a micromotor provides a circumferential scan. In both approaches, the polarization incident on the sample changes due to the rotation mechanism, and these changes need to be taken into account to properly calculate the tissue birefringence [70, 136, 137]. In cardiovascular OCT, polarization sensitivity has found application in the assessment of collagen in the fibrous cap of atherosclerotic plaques [138], the determination of collagen and smooth muscle cell content in atherosclerotic plaques [139, 140], RF ablation monitoring of the endocardium [141], and the in human in vivo assessment of plaque rupture [142]. Figure 10 shows a PS-OCT example of ex-vivo human coronary artery. In pulmonology, endoscopic OCT is still at its infancy [137], an ex-vivo study has shown the potential for biopsy guidance in lung carcinoma [143], and recently PS-OCT results demonstrated the potential to visualize airway smooth muscle (ASM) cells ex vivo and imaging and volumetric assessments of ASM in humans in vivo [144].
Dermatology, collagen and nerves, cartilage and the reduced birefringence in tumors
Outside of ophthalmology the application of PS-OCT is focused on the birefringence caused by fibrous structures such as nerves, muscles and collagen, ligaments, tendons, cartilage, bones, blood vessels, intervertebral discs and the dentin in teeth.
PS-OCT has been applied to a wide variety of dermatological problems [145]. One of the first clinical applications of PS-OCT in particular was for the assessment of burn depth [13]. Burns are classified by depth into first-, second-, and third-degree injuries. First-degree burns cause redness and pain (e.g., sunburn). Second-degree burns are marked by blisters (e.g., scald by hot liquid). In third degree burns, both the epidermis and dermis are destroyed and the underlying tissue may also be damaged. A second-degree burn will heal if given proper care. However, a third-degree burn will not heal and requires a skin graft. Making the distinction between the two is difficult; a burn surgeon will often observe the injury over the course of several days before making an educated guess regarding burn depth [146]. Initial studies [13] have indicated the potential for PS-OCT to solve this problem by taking advantage of the fact that skin contains collagen, a birefringent material [40, 62]. At temperatures between 56 and 65°C, collagen begins to denature and lose its birefringence [41, 147]. It should be expected that normal and burned skin differ in their natural collagen content, which leads to a reduction in the ability of burned skin to alter the polarization state of light that has passed through and been reflected back from some depth. A good deal of work has been done towards establishing baselines for the polarization properties of normal human skin as PS-OCT technology has progressed [15, 145, 148–150]. This work has helped pave the way towards assessment of burns in humans [49, 151–153], and the assessment of scars [145, 153, 154]. In dermatology PS-OCT has also been used to asses dermal photo-ageing [155], and for the identification and delineation of basal cell carcinoma [156]. In osteoarthritis, PS-OCT has been used for the assessment of cartilage [157–161].
A relatively unexplored but potentially important field is the use of PS-OCT in the delineation of tumor tissue, which is based on the local destruction of collagen. Several papers have demonstrated the reduction of birefringence in tumor tissue in an animal model, and human esophagus, skin, vocal fold, breast and bladder [57, 76, 156, 162–170]. An example of PS-OCT images of a hamster cheek pouch cancer model is shown in Fig. 20, demonstrating the reduced birefringence in tumor tissue.
Fig. 20.
Structural intensity (left) and polarization sensitive image (right) of a hamster cheek pouch cancer model. In the intensity image the features of the tumor tissue are visible, however, the PS image shows significant contrast between normal (left) and tumor tissue (right) based on the banding pattern. The normal cheek pouch tissue shows a much higher birefringence than the cancer tissue. (Adapted from [57])
PS-OCT could also find an application in the study of the regeneration of nerves after injury or to visualize nerves intraoperatively during e.g., prostatectomy, due to the contrast PS-OCT images provide over structural intensity images for nerves due to their birefringent properties [171–173].
Disclosures
JFdB: Heidelberg Engineering (F,P); CKH: Canon (F,P); YY: Topcon (F), Tomey Corp. (F), Nidek (F)
Acknowledgement
The authors would like to acknowledge funding support over the past decades from government agencies, private donations and industrial partners. We would like to thank Martin Villiger for helpfull comments on the draft manuscript. Indispensable contributions from B. Hyle Park as a co-author on previous reviews, Bernhard Baumann, Erich Götzinger, Michael Pircher, Shuichi Makita, Masahiro Yamanari and numerous other graduate students, postdocs and colleagues, as well as from clinical partners, Ursula Schmidt-Erfurth and her team, are acknowledged. This review is in part based on previous reviews by the authors [3-7], and despite revisions might contain significant overlap.
References
- 1.Huang D., Swanson E. A., Lin C. P., Schuman J. S., Stinson W. G., Chang W., Hee M. R., Flotte T., Gregory K., Puliafito C. A., Fujimoto J. G., “Optical coherence tomography,” Science 254(5035), 1178–1181 (1991). 10.1126/science.1957169 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Hee M. R., Huang D., Swanson E. A., Fujimoto J. G., “Polarization-sensitive low-coherence reflectometer for birefringence characterization and ranging,” J. Opt. Soc. Am. B 9(6), 903–908 (1992). 10.1364/JOSAB.9.000903 [DOI] [Google Scholar]
- 3.Park B. H., de Boer J. F., “Polarization sensitive optical coherence tomography,” in Optical Coherence Tomography - Technology and Applications, Drexler W., Fujimoto J. G., eds. (Springer, Cham, 2015), pp. 1055–1101. [Google Scholar]
- 4.Hitzenberger C. K., Pircher M., “MUW approach of PS OCT,” in Optical Coherence Tomography - Technology and Applications, Drexler W., Fujimoto J. G., eds. (Springer, Cham, 2015), pp. 1103–1136. [Google Scholar]
- 5.Yasuno Y., Ju M. J., Hong Y. J., Makita S., Lim Y., Yamanari M., “Jones matrix based polarization sensitive optical coherence tomography,” in Optical Coherence Tomography - Technology and Applications, Drexler W., Fujimoto J. G., eds. (Springer, Cham, 2015), pp. 1137–1162. [Google Scholar]
- 6.de Boer J. F., Milner T. E., “Review of polarization sensitive optical coherence tomography and Stokes vector determination,” J. Biomed. Opt. 7(3), 359–371 (2002). 10.1117/1.1483879 [DOI] [PubMed] [Google Scholar]
- 7.Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., “Polarization Sensitive Optical Coherence Tomography in the Human Eye,” Prog. Retin. Eye Res. 30(6), 431–451 (2011). 10.1016/j.preteyeres.2011.06.003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Stifter D., “Beyond biomedicine: a review of alternative applications and developments for optical coherence tomography,” Appl. Phys. B 88(3), 337–357 (2007). 10.1007/s00340-007-2743-2 [DOI] [Google Scholar]
- 9.Jones R. C., “A new calculus for the treatment of optical systems I. Description and discussion of the calculus,” J. Opt. Soc. Am. A 31(7), 488–493 (1941). 10.1364/JOSA.31.000488 [DOI] [Google Scholar]
- 10.Gil J. J., Bernabeu E., “Obtainment of the polarizing and retardation parameters of a non-depolarizing optical system from the polar decomposition of its Mueller matrix,” Optik (Stuttg.) 76, 67–71 (1987). [Google Scholar]
- 11.Bohren C. F., Huffman D. R., Absorption and Scattering of Light by Small Particles (Wiley Interscience, New York, NY, 1983). [Google Scholar]
- 12.Shurcliff W. A., Ballard S. S., Polarized Light (Van Nostrand, New York, 1964). [Google Scholar]
- 13.Park B. H., Saxer C., Srinivas S. M., Nelson J. S., de Boer J. F., “In vivo burn depth determination by high-speed fiber-based polarization sensitive optical coherence tomography,” J. Biomed. Opt. 6(4), 474–479 (2001). 10.1117/1.1413208 [DOI] [PubMed] [Google Scholar]
- 14.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Real-time multi-functional optical coherence tomography,” Opt. Express 11(7), 782–793 (2003). 10.1364/OE.11.000782 [DOI] [PubMed] [Google Scholar]
- 15.Saxer C. E., de Boer J. F., Park B. H., Zhao Y., Chen Z., Nelson J. S., “High-speed fiber based polarization-sensitive optical coherence tomography of in vivo human skin,” Opt. Lett. 25(18), 1355–1357 (2000). 10.1364/OL.25.001355 [DOI] [PubMed] [Google Scholar]
- 16.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Jones matrix analysis for a polarization-sensitive optical coherence tomography system using fiber-optic components,” Opt. Lett. 29(21), 2512–2514 (2004). 10.1364/OL.29.002512 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Park B. H., Pierce M. C., Cense B., de Boer J. F., “Optic axis determination accuracy for fiber-based polarization-sensitive optical coherence tomography,” Opt. Lett. 30(19), 2587–2589 (2005). 10.1364/OL.30.002587 [DOI] [PubMed] [Google Scholar]
- 18.Kemp N. J., Park J., Zaatari H. N., Rylander H. G., Milner T. E., “High-sensitivity determination of birefringence in turbid media with enhanced polarization-sensitive optical coherence tomography,” J. Opt. Soc. Am. A 22(3), 552–560 (2005). 10.1364/JOSAA.22.000552 [DOI] [PubMed] [Google Scholar]
- 19.Kemp N. J., Zaatari H. N., Park J., Rylander Iii H. G., Milner T. E., “Form-biattenuance in fibrous tissues measured with polarization-sensitive optical coherence tomography (PS-OCT),” Opt. Express 13(12), 4611–4628 (2005). 10.1364/OPEX.13.004611 [DOI] [PubMed] [Google Scholar]
- 20.Götzinger E., Pircher M., Geitzenauer W., Ahlers C., Baumann B., Michels S., Schmidt-Erfurth U., Hitzenberger C. K., “Retinal pigment epithelium segmentation by polarization sensitive optical coherence tomography,” Opt. Express 16(21), 16410–16422 (2008). 10.1364/OE.16.016410 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Haskell R. C., Carlson F. D., Blank P. S., “Form birefringence of muscle,” Biophys. J. 56(2), 401–413 (1989). 10.1016/S0006-3495(89)82686-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.van Blokland G. J., “Ellipsometry of the human retina in vivo: preservation of polarization,” J. Opt. Soc. Am. A 2(1), 72–75 (1985). 10.1364/JOSAA.2.000072 [DOI] [PubMed] [Google Scholar]
- 23.Klein Brink H. B., van Blokland G. J., “Birefringence of the human foveal area assessed in vivo with Mueller-matrix ellipsometry,” J. Opt. Soc. Am. A 5(1), 49–57 (1988). 10.1364/JOSAA.5.000049 [DOI] [PubMed] [Google Scholar]
- 24.Todorović M., Jiao S., Wang L. V., Stoica G., “Determination of local polarization properties of biological samples in the presence of diattenuation by use of Mueller optical coherence tomography,” Opt. Lett. 29(20), 2402–2404 (2004). 10.1364/OL.29.002402 [DOI] [PubMed] [Google Scholar]
- 25.Schmitt J. M., Xiang S. H., “Cross-polarized backscatter in optical coherence tomography of biological tissue,” Opt. Lett. 23(13), 1060–1062 (1998). 10.1364/OL.23.001060 [DOI] [PubMed] [Google Scholar]
- 26.Baumann B., Baumann S. O., Konegger T., Pircher M., Götzinger E., Schlanitz F., Schütze C., Sattmann H., Litschauer M., Schmidt-Erfurth U., Hitzenberger C. K., “Polarization sensitive optical coherence tomography of melanin provides intrinsic contrast based on depolarization,” Biomed. Opt. Express 3(7), 1670–1683 (2012). 10.1364/BOE.3.001670 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Makita S., Yamanari M., Yasuno Y., “Generalized Jones matrix optical coherence tomography: performance and local birefringence imaging,” Opt. Express 18(2), 854–876 (2010). 10.1364/OE.18.000854 [DOI] [PubMed] [Google Scholar]
- 28.Chipman R. A., “Polarization analysis of optical systems,” Opt. Eng. 28, 280290 (1989). [Google Scholar]
- 29.Lu S. Y., Chipman R. A., “Interpretation of Mueller matrices based on polar decomposition,” J. Opt. Soc. Am. A 13(5), 1106–1113 (1996). 10.1364/JOSAA.13.001106 [DOI] [Google Scholar]
- 30.Jiao S., Yao G., Wang L. V., “Depth-resolved two-dimensional stokes vectors of backscattered light and mueller matrices of biological tissue measured with optical coherence tomography,” Appl. Opt. 39(34), 6318–6324 (2000). 10.1364/AO.39.006318 [DOI] [PubMed] [Google Scholar]
- 31.Adie S. G., Hillman T. R., Sampson D. D., “Detection of multiple scattering in optical coherence tomography using the spatial distribution of Stokes vectors,” Opt. Express 15(26), 18033–18049 (2007). 10.1364/OE.15.018033 [DOI] [PubMed] [Google Scholar]
- 32.Lee S. W., Kang J. H., Yoo J. Y., Kang M. S., Oh J. T., Kim B. M., “Quantification of scattering changes using polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 13(5), 054032 (2008). 10.1117/1.2976430 [DOI] [PubMed] [Google Scholar]
- 33.Götzinger E., Baumann B., Pircher M., Hitzenberger C. K., “Polarization maintaining fiber based ultra-high resolution spectral domain polarization sensitive optical coherence tomography,” Opt. Express 17(25), 22704–22717 (2009). 10.1364/OE.17.022704 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Götzinger E., Pircher M., Baumann B., Schmoll T., Sattmann H., Leitgeb R. A., Hitzenberger C. K., “Speckle noise reduction in high speed polarization sensitive spectral domain optical coherence tomography,” Opt. Express 19(15), 14568–14585 (2011). 10.1364/OE.19.014568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Bonesi M., Sattmann H., Torzicky T., Zotter S., Baumann B., Pircher M., Götzinger E., Eigenwillig C., Wieser W., Huber R., Hitzenberger C. K., “High-speed polarization sensitive optical coherence tomography scan engine based on Fourier domain mode locked laser,” Biomed. Opt. Express 3(11), 2987–3000 (2012). 10.1364/BOE.3.002987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Sugita M., Pircher M., Zotter S., Baumann B., Saito K., Makihira T., Tomatsu N., Sato M., Hitzenberger C. K., “Analysis of optimum conditions of depolarization imaging by polarization-sensitive optical coherence tomography in the human retina,” J. Biomed. Opt. 20(1), 016011 (2015). 10.1117/1.JBO.20.1.016011 [DOI] [PubMed] [Google Scholar]
- 37.Makita S., Hong Y. J., Miura M., Yasuno Y., “Degree of polarization uniformity with high noise immunity using polarization-sensitive optical coherence tomography,” Opt. Lett. 39(24), 6783–6786 (2014). 10.1364/OL.39.006783 [DOI] [PubMed] [Google Scholar]
- 38.Lippok N., Villiger M., Bouma B. E., “Degree of polarization (uniformity) and depolarization index: unambiguous depolarization contrast for optical coherence tomography,” Opt. Lett. 40(17), 3954–3957 (2015). 10.1364/OL.40.003954 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Ortega-Quijano N., Marvdashti T., Ellerbee Bowden A. K., “Enhanced depolarization contrast in polarization-sensitive optical coherence tomography,” Opt. Lett. 41(10), 2350–2353 (2016). 10.1364/OL.41.002350 [DOI] [PubMed] [Google Scholar]
- 40.de Boer J. F., Milner T. E., van Gemert M. J. C., Nelson J. S., “Two-dimensional birefringence imaging in biological tissue by polarization-sensitive optical coherence tomography,” Opt. Lett. 22(12), 934–936 (1997). 10.1364/OL.22.000934 [DOI] [PubMed] [Google Scholar]
- 41.De Boer J. F., Srinivas S. M., Malekafzali A., Chen Z. P., Nelson J. S., “Imaging thermally damaged tissue by polarization sensitive optical coherence tomography,” Opt. Express 3(6), 212–218 (1998). 10.1364/OE.3.000212 [DOI] [PubMed] [Google Scholar]
- 42.de Boer J. F., Milner T. E., Nelson J. S., “Determination of the depth-resolved Stokes parameters of light backscattered from turbid media by use of polarization-sensitive optical coherence tomography,” Opt. Lett. 24(5), 300–302 (1999). 10.1364/OL.24.000300 [DOI] [PubMed] [Google Scholar]
- 43.Hitzenberger C. K., Goetzinger E., Sticker M., Pircher M., Fercher A. F., “Measurement and imaging of birefringence and optic axis orientation by phase resolved polarization sensitive optical coherence tomography,” Opt. Express 9(13), 780–790 (2001). 10.1364/OE.9.000780 [DOI] [PubMed] [Google Scholar]
- 44.Fercher A. F., Hitzenberger C. K., “Optical coherence tomography,” Prog. Opt. 44, 215–302 (2002). 10.1016/S0079-6638(02)80017-8 [DOI] [Google Scholar]
- 45.Gerrard A., Burch J. M., Introduction to Matrix Methods in Optics (John Wiley & Sons, 1975). [Google Scholar]
- 46.Schoenenberger K., Colston B. W., Maitland D. J., Da Silva L. B., Everett M. J., “Mapping of birefringence and thermal damage in tissue by use of polarization-sensitive optical coherence tomography,” Appl. Opt. 37(25), 6026–6036 (1998). 10.1364/AO.37.006026 [DOI] [PubMed] [Google Scholar]
- 47.Yao G., Wang L. V., “Two-dimensional depth-resolved Mueller matrix characterization of biological tissue by optical coherence tomography,” Opt. Lett. 24(8), 537–539 (1999). 10.1364/OL.24.000537 [DOI] [PubMed] [Google Scholar]
- 48.Jiao S., Wang L. V., “Two-dimensional depth-resolved Mueller matrix of biological tissue measured with double-beam polarization-sensitive optical coherence tomography,” Opt. Lett. 27(2), 101–103 (2002). 10.1364/OL.27.000101 [DOI] [PubMed] [Google Scholar]
- 49.Jiao S., Yu W., Stoica G., Wang L. V., “Contrast mechanisms in polarization-sensitive Mueller-matrix optical coherence tomography and application in burn imaging,” Appl. Opt. 42(25), 5191–5197 (2003). 10.1364/AO.42.005191 [DOI] [PubMed] [Google Scholar]
- 50.Jiao S., Yu W., Stoica G., Wang L. V., “Optical-fiber-based Mueller optical coherence tomography,” Opt. Lett. 28(14), 1206–1208 (2003). 10.1364/OL.28.001206 [DOI] [PubMed] [Google Scholar]
- 51.de Boer J. F., Milner T. E., Nelson J. S., “Two dimensional birefringence imaging in biological tissue using phase and polarization sensitive optical coherence tomography,” in Trends in Optics and Photonics (TOPS): Advances in Optical Imaging and Photon Migration, Patterson J. G. F. a. M. S., ed. (Optical Society of America, Washington, DC, 1998, Orlando, USA, 1998), pp. 321–324. [Google Scholar]
- 52.Al-Qaisi M. K., Akkin T., “Polarization-sensitive optical coherence tomography based on polarization-maintaining fibers and frequency multiplexing,” Opt. Express 16(17), 13032–13041 (2008). 10.1364/OE.16.013032 [DOI] [PubMed] [Google Scholar]
- 53.Trasischker W., Zotter S., Torzicky T., Baumann B., Haindl R., Pircher M., Hitzenberger C. K., “Single input state polarization sensitive swept source optical coherence tomography based on an all single mode fiber interferometer,” Biomed. Opt. Express 5(8), 2798–2809 (2014). 10.1364/BOE.5.002798 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Lippok N., Villiger M., Jun C., Bouma B. E., “Single input state, single-mode fiber-based polarization-sensitive optical frequency domain imaging by eigenpolarization referencing,” Opt. Lett. 40(9), 2025–2028 (2015). 10.1364/OL.40.002025 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Yamanari M., Makita S., Yasuno Y., “Polarization-sensitive swept-source optical coherence tomography with continuous source polarization modulation,” Opt. Express 16(8), 5892–5906 (2008). 10.1364/OE.16.005892 [DOI] [PubMed] [Google Scholar]
- 56.Oh W. Y., Yun S. H., Vakoc B. J., Shishkov M., Desjardins A. E., Park B. H., de Boer J. F., Tearney G. J., Bouma B. E., “High-speed polarization sensitive optical frequency domain imaging with frequency multiplexing,” Opt. Express 16(2), 1096–1103 (2008). 10.1364/OE.16.001096 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Kim K. H., Park B. H., Tu Y., Hasan T., Lee B., Li J., de Boer J. F., “Polarization-sensitive optical frequency domain imaging based on unpolarized light,” Opt. Express 19(2), 552–561 (2011). 10.1364/OE.19.000552 [DOI] [PubMed] [Google Scholar]
- 58.Baumann B., Choi W., Potsaid B., Huang D., Duker J. S., Fujimoto J. G., “Swept source/Fourier domain polarization sensitive optical coherence tomography with a passive polarization delay unit,” Opt. Express 20(9), 10229–10241 (2012). 10.1364/OE.20.010229 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lim Y., Hong Y.-J., Duan L., Yamanari M., Yasuno Y., “Passive component based multifunctional Jones matrix swept source optical coherence tomography for Doppler and polarization imaging,” Opt. Lett. 37(11), 1958–1960 (2012). 10.1364/OL.37.001958 [DOI] [PubMed] [Google Scholar]
- 60.Ju M. J., Hong Y.-J., Makita S., Lim Y., Kurokawa K., Duan L., Miura M., Tang S., Yasuno Y., “Advanced multi-contrast Jones matrix optical coherence tomography for Doppler and polarization sensitive imaging,” Opt. Express 21(16), 19412–19436 (2013). 10.1364/OE.21.019412 [DOI] [PubMed] [Google Scholar]
- 61.Pierce M. C., Hyle Park B., Cense B., de Boer J. F., “Simultaneous intensity, birefringence, and flow measurements with high-speed fiber-based optical coherence tomography,” Opt. Lett. 27(17), 1534–1536 (2002). 10.1364/OL.27.001534 [DOI] [PubMed] [Google Scholar]
- 62.Everett M. J., Schoenenberger K., Colston B. W., Jr, Da Silva L. B., “Birefringence characterization of biological tissue by use of optical coherence tomography,” Opt. Lett. 23(3), 228–230 (1998). 10.1364/OL.23.000228 [DOI] [PubMed] [Google Scholar]
- 63.Ducros M. G., de Boer J. F., Huang H. E., Chao L. C., Chen Z. P., Nelson J. S., Milner T. E., Rylander H. G., “Polarization sensitive optical coherence tomography of the rabbit eye,” IEEE J. Sel. Top. Quantum Electron. 5(4), 1159–1167 (1999). 10.1109/2944.796342 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Park B. H., Pierce M. C., Cense B., Yun S. H., Mujat M., Tearney G. J., Bouma B. E., de Boer J. F., “Real-time fiber-based multi-functional spectral-domain optical coherence tomography at 1.3 microm,” Opt. Express 13(11), 3931–3944 (2005). 10.1364/OPEX.13.003931 [DOI] [PubMed] [Google Scholar]
- 65.Cense B., Chen T. C., Park B. H., Pierce M. C., de Boer J. F., “In vivo depth-resolved birefringence measurements of the human retinal nerve fiber layer by polarization-sensitive optical coherence tomography,” Opt. Lett. 27(18), 1610–1612 (2002). 10.1364/OL.27.001610 [DOI] [PubMed] [Google Scholar]
- 66.Tung W. K., Group Theory in Physics (World Scientific, 1985). [Google Scholar]
- 67.Villiger M., Zhang E. Z., Nadkarni S., Oh W. Y., Bouma B. E., Vakoc B. J., “Artifacts in polarization-sensitive optical coherence tomography caused by polarization mode dispersion,” Opt. Lett. 38(6), 923–925 (2013). 10.1364/OL.38.000923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Zhang E. Z., Vakoc B. J., “Polarimetry noise in fiber-based optical coherence tomography instrumentation,” Opt. Express 19(18), 16830–16842 (2011). 10.1364/OE.19.016830 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Zhang E. Z., Oh W. Y., Villiger M. L., Chen L., Bouma B. E., Vakoc B. J., “Numerical compensation of system polarization mode dispersion in polarization-sensitive optical coherence tomography,” Opt. Express 21(1), 1163–1180 (2013). 10.1364/OE.21.001163 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Villiger M., Zhang E. Z., Nadkarni S. K., Oh W. Y., Vakoc B. J., Bouma B. E., “Spectral binning for mitigation of polarization mode dispersion artifacts in catheter-based optical frequency domain imaging,” Opt. Express 21(14), 16353–16369 (2013). 10.1364/OE.21.016353 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Braaf B., Vermeer K. A., de Groot M., Vienola K. V., de Boer J. F., “Fiber-based polarization-sensitive OCT of the human retina with correction of system polarization distortions,” Biomed. Opt. Express 5(8), 2736–2758 (2014). 10.1364/BOE.5.002736 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 72.Hong Y. J., Makita S., Sugiyama S., Yasuno Y., “Optically buffered Jones-matrix-based multifunctional optical coherence tomography with polarization mode dispersion correction,” Biomed. Opt. Express 6(1), 225–243 (2015). 10.1364/BOE.6.000225 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 73.Lim Y., Yamanari M., Fukuda S., Kaji Y., Kiuchi T., Miura M., Oshika T., Yasuno Y., “Birefringence measurement of cornea and anterior segment by office-based polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 2(8), 2392–2402 (2011). 10.1364/BOE.2.002392 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Li J., de Boer J. F., “Coherent signal composition and global phase determination in signal multiplexed polarization sensitive optical coherence tomography,” Opt. Express 22(18), 21382–21392 (2014). 10.1364/OE.22.021382 [DOI] [PubMed] [Google Scholar]
- 75.Yamanari M., Tsuda S., Kokubun T., Shiga Y., Omodaka K., Yokoyama Y., Himori N., Ryu M., Kunimatsu-Sanuki S., Takahashi H., Maruyama K., Kunikata H., Nakazawa T., “Fiber-based polarization-sensitive OCT for birefringence imaging of the anterior eye segment,” Biomed. Opt. Express 6(2), 369–389 (2015). 10.1364/BOE.6.000369 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Wang Z., Lee H.-C., Ahsen O. O., Lee B., Choi W., Potsaid B., Liu J., Jayaraman V., Cable A., Kraus M. F., Liang K., Hornegger J., Fujimoto J. G., “Depth-encoded all-fiber swept source polarization sensitive OCT,” Biomed. Opt. Express 5(9), 2931–2949 (2014). 10.1364/BOE.5.002931 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Yamanari M., Tsuda S., Kokubun T., Shiga Y., Omodaka K., Aizawa N., Yokoyama Y., Himori N., Kunimatsu-Sanuki S., Maruyama K., Kunikata H., Nakazawa T., “Estimation of Jones matrix, birefringence and entropy using Cloude-Pottier decomposition in polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 7(9), 3551–3573 (2016). 10.1364/BOE.7.003551 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 78.Götzinger E., Pircher M., Baumann B., Schmoll T., Sattmann H., Leitgeb R. A., Hitzenberger C. K., “Speckle noise reduction in high speed polarization sensitive spectral domain optical coherence tomography,” Opt. Express 19(15), 14568–14585 (2011). 10.1364/OE.19.014568 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Duan L., Makita S., Yamanari M., Lim Y., Yasuno Y., “Monte-Carlo-based phase retardation estimator for polarization sensitive optical coherence tomography,” Opt. Express 19(17), 16330–16345 (2011). 10.1364/OE.19.016330 [DOI] [PubMed] [Google Scholar]
- 80.Kasaragod D., Makita S., Fukuda S., Beheregaray S., Oshika T., Yasuno Y., “Bayesian maximum likelihood estimator of phase retardation for quantitative polarization-sensitive optical coherence tomography,” Opt. Express 22(13), 16472–16492 (2014). 10.1364/OE.22.016472 [DOI] [PubMed] [Google Scholar]
- 81.Kasaragod D., Sugiyama S., Ikuno Y., Alonso-Caneiro D., Yamanari M., Fukuda S., Oshika T., Hong Y.-J., Li E., Makita S., Miura M., Yasuno Y., “Accurate and quantitative polarization-sensitive OCT by unbiased birefringence estimator with noise-stochastic correction,” Proc. SPIE 9697, 96971I (2016). 10.1117/12.2214527 [DOI] [Google Scholar]
- 82.Yasuno Y., Yamanari M., Kawana K., Oshika T., Miura M., “Investigation of post-glaucoma-surgery structures by three-dimensional and polarization sensitive anterior eye segment optical coherence tomography,” Opt. Express 17(5), 3980–3996 (2009). 10.1364/OE.17.003980 [DOI] [PubMed] [Google Scholar]
- 83.Fukuda S., Beheregaray S., Kasaragod D., Hoshi S., Kishino G., Ishii K., Yasuno Y., Oshika T., “Noninvasive evaluation of phase retardation in blebs after glaucoma surgery using anterior segment polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 55(8), 5200–5206 (2014). 10.1167/iovs.14-14474 [DOI] [PubMed] [Google Scholar]
- 84.Fukuda S., Fujita A., Kasaragod D., Ueno Y., Hoshi S., Kishino G., Beheregaray S., Yasuno Y., Oshika T., “Quantitative evaluation of phase retardation in filtering blebs using polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 57(14), 5919–5925 (2016). 10.1167/iovs.16-19548 [DOI] [PubMed] [Google Scholar]
- 85.Kasaragod D., Fukuda S., Ueno Y., Hoshi S., Oshika T., Yasuno Y., “Objective evaluation of functionality of filtering bleb based on polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 57(4), 2305–2310 (2016). 10.1167/iovs.15-18178 [DOI] [PubMed] [Google Scholar]
- 86.Asrani S., Sarunic M., Santiago C., Izatt J., “Detailed visualization of the anterior segment using fourier-domain optical coherence tomography,” Arch. Ophthalmol. 126(6), 765–771 (2008). 10.1001/archopht.126.6.765 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Yasuno Y., Yamanari M., Kawana K., Miura M., Fukuda S., Makita S., Sakai S., Oshika T., “Visibility of trabecular meshwork by standard and polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 15(6), 061705 (2010). 10.1117/1.3499421 [DOI] [PubMed] [Google Scholar]
- 88.Pircher M., Goetzinger E., Leitgeb R., Hitzenberger C. K., “Transversal phase resolved polarization sensitive optical coherence tomography,” Phys. Med. Biol. 49(7), 1257–1263 (2004). 10.1088/0031-9155/49/7/013 [DOI] [PubMed] [Google Scholar]
- 89.Fanjul-Vélez F., Pircher M., Baumann B., Götzinger E., Hitzenberger C. K., Arce-Diego J. L., “Polarimetric analysis of the human cornea measured by polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 15(5), 056004 (2010). 10.1117/1.3486540 [DOI] [PubMed] [Google Scholar]
- 90.Götzinger E., Pircher M., Sticker M., Fercher A. F., Hitzenberger C. K., “Measurement and imaging of birefringent properties of the human cornea with phase-resolved, polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(1), 94–102 (2004). 10.1117/1.1629308 [DOI] [PubMed] [Google Scholar]
- 91.Götzinger E., Pircher M., Dejaco-Ruhswurm I., Kaminski S., Skorpik C., Hitzenberger C. K., “Imaging of Birefringent Properties of Keratoconus Corneas by Polarization-Sensitive Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 48(8), 3551–3558 (2007). 10.1167/iovs.06-0727 [DOI] [PubMed] [Google Scholar]
- 92.Fukuda S., Yamanari M., Lim Y., Hoshi S., Beheregaray S., Oshika T., Yasuno Y., “Keratoconus Diagnosis Using Anterior Segment Polarization-Sensitive Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 54(2), 1384–1391 (2013). 10.1167/iovs.12-10979 [DOI] [PubMed] [Google Scholar]
- 93.Fukuda S., Kishino G., Hoshi S., Beheregaray S., Ueno Y., Fukuda M., Kasaragod D., Yasuno Y., Oshika T., “Repeatability of Corneal Phase Retardation Measurements by Polarization-Sensitive Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 56(5), 3196–3201 (2015). 10.1167/iovs.14-16327 [DOI] [PubMed] [Google Scholar]
- 94.Huang X. R., Knighton R. W., “Microtubules contribute to the birefringence of the retinal nerve fiber layer,” Invest. Ophthalmol. Vis. Sci. 46(12), 4588–4593 (2005). 10.1167/iovs.05-0532 [DOI] [PubMed] [Google Scholar]
- 95.Zangwill L. M., Bowd C., “Retinal nerve fiber layer analysis in the diagnosis of glaucoma,” Curr. Opin. Ophthalmol. 17(2), 120–131 (2006). [DOI] [PubMed] [Google Scholar]
- 96.Fortune B., Burgoyne C. F., Cull G., Reynaud J., Wang L., “Onset and Progression of Peripapillary Retinal Nerve Fiber Layer (RNFL) Retardance Changes Occur Earlier Than Rnfl Thickness Changes in Experimental Glaucoma,” Invest. Ophthalmol. Vis. Sci. 54(8), 5653–5661 (2013). 10.1167/iovs.13-12219 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Weinreb R. N., Dreher A. W., Coleman A., Quigley H., Shaw B., Reiter K., “Histopathologic validation of Fourier-ellipsometry measurements of retinal nerve fiber layer thickness,” Arch. Ophthalmol. 108(4), 557–560 (1990). 10.1001/archopht.1990.01070060105058 [DOI] [PubMed] [Google Scholar]
- 98.Dreher A. W., Reiter K., Weinreb R. N., “Spatially resolved birefringence of the retinal nerve fiber layer assessed with a retinal laser ellipsometer,” Appl. Opt. 31(19), 3730–3735 (1992). 10.1364/AO.31.003730 [DOI] [PubMed] [Google Scholar]
- 99.Bagga H., Greenfield D. S., Feuer W., Knighton R. W., “Scanning laser polarimetry with variable corneal compensation and optical coherence tomography in normal and glaucomatous eyes,” Am. J. Ophthalmol. 135(4), 521–529 (2003). 10.1016/S0002-9394(02)02077-9 [DOI] [PubMed] [Google Scholar]
- 100.Bagga H., Greenfield D. S., Feuer W. J., “Quantitative assessment of atypical birefringence images using scanning laser polarimetry with variable corneal compensation,” Am. J. Ophthalmol. 139(3), 437–446 (2005). 10.1016/j.ajo.2004.10.019 [DOI] [PubMed] [Google Scholar]
- 101.Mai T. A., Reus N. J., Lemij H. G., “Structure-function relationship is stronger with enhanced corneal compensation than with variable corneal compensation in scanning laser polarimetry,” Invest. Ophthalmol. Vis. Sci. 48(4), 1651–1658 (2007). 10.1167/iovs.06-1003 [DOI] [PubMed] [Google Scholar]
- 102.Götzinger E., Pircher M., Baumann B., Hirn C., Vass C., Hitzenberger C. K., “Analysis of the origin of atypical scanning laser polarimetry patterns by polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 49(12), 5366–5372 (2008). 10.1167/iovs.08-2081 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Cense B., Chen T. C., Park B. H., Pierce M. C., de Boer J. F., “In vivo birefringence and thickness measurements of the human retinal nerve fiber layer using polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(1), 121–125 (2004). 10.1117/1.1627774 [DOI] [PubMed] [Google Scholar]
- 104.Cense B., Chen T. C., Park B. H., Pierce M. C., de Boer J. F., “Thickness and birefringence of healthy retinal nerve fiber layer tissue measured with polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 45(8), 2606–2612 (2004). 10.1167/iovs.03-1160 [DOI] [PubMed] [Google Scholar]
- 105.Pircher M., Götzinger E., Leitgeb R., Sattmann H., Findl O., Hitzenberger C., “Imaging of polarization properties of human retina in vivo with phase resolved transversal PS-OCT,” Opt. Express 12(24), 5940–5951 (2004). 10.1364/OPEX.12.005940 [DOI] [PubMed] [Google Scholar]
- 106.Götzinger E., Pircher M., Hitzenberger C. K., “High speed spectral domain polarization sensitive optical coherence tomography of the human retina,” Opt. Express 13(25), 10217–10229 (2005). 10.1364/OPEX.13.010217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Mujat M., Park B. H., Cense B., Chen T. C., de Boer J. F., “Autocalibration of spectral-domain optical coherence tomography spectrometers for in vivo quantitative retinal nerve fiber layer birefringence determination,” J. Biomed. Opt. 12(4), 041205 (2007). 10.1117/1.2764460 [DOI] [PubMed] [Google Scholar]
- 108.Yamanari M., Miura M., Makita S., Yatagai T., Yasuno Y., “Phase retardation measurement of retinal nerve fiber layer by polarization-sensitive spectral-domain optical coherence tomography and scanning laser polarimetry,” J. Biomed. Opt. 13(1), 014013 (2008). 10.1117/1.2841024 [DOI] [PubMed] [Google Scholar]
- 109.Götzinger E., Pircher M., Baumann B., Hirn C., Vass C., Hitzenberger C. K., “Retinal nerve fiber layer birefringence evaluated with polarization sensitive spectral domain OCT and scanning laser polarimetry: a comparison,” J. Biophotonics 1(2), 129–139 (2008). 10.1002/jbio.200710009 [DOI] [PubMed] [Google Scholar]
- 110.Zotter S., Pircher M., Götzinger E., Torzicky T., Yoshida H., Hirose F., Holzer S., Kroisamer J., Vass C., Schmidt-Erfurth U., Hitzenberger C. K., “Measuring retinal nerve fiber layer birefringence, retardation, and thickness using wide-field, high-speed polarization sensitive spectral domain OCT,” Invest. Ophthalmol. Vis. Sci. 54(1), 72–84 (2013). 10.1167/iovs.12-10089 [DOI] [PubMed] [Google Scholar]
- 111.Zotter S., Pircher M., Torzicky T., Baumann B., Yoshida H., Hirose F., Roberts P., Ritter M., Schütze C., Götzinger E., Trasischker W., Vass C., Schmidt-Erfurth U., Hitzenberger C. K., “Large-field high-speed polarization sensitive spectral domain OCT and its applications in ophthalmology,” Biomed. Opt. Express 3(11), 2720–2732 (2012). 10.1364/BOE.3.002720 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Cense B., Wang Q., Lee S., Zhao L., Elsner A. E., Hitzenberger C. K., Miller D. T., “Henle fiber layer phase retardation measured with polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 4(11), 2296–2306 (2013). 10.1364/BOE.4.002296 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Ducros M. G., Marsack J. D., Rylander H. G., 3rd, Thomsen S. L., Milner T. E., “Primate retina imaging with polarization-sensitive optical coherence tomography,” J. Opt. Soc. Am. A 18(12), 2945–2956 (2001). 10.1364/JOSAA.18.002945 [DOI] [PubMed] [Google Scholar]
- 114.Dwelle J., Liu S., Wang B., McElroy A., Ho D., Markey M. K., Milner T., Rylander H. G., 3rd, “Thickness, phase retardation, birefringence, and reflectance of the retinal nerve fiber layer in normal and glaucomatous non-human primates,” Invest. Ophthalmol. Vis. Sci. 53(8), 4380–4395 (2012). 10.1167/iovs.11-9130 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 115.Baumann B., Rauscher S., Glösmann M., Götzinger E., Pircher M., Fialová S., Gröger M., Hitzenberger C. K., “Peripapillary rat sclera investigated in vivo with polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 55(11), 7686–7696 (2014). 10.1167/iovs.14-15037 [DOI] [PubMed] [Google Scholar]
- 116.Fialová S., Augustin M., Glösmann M., Himmel T., Rauscher S., Gröger M., Pircher M., Hitzenberger C. K., Baumann B., “Polarization properties of single layers in the posterior eyes of mice and rats investigated using high resolution polarization sensitive optical coherence tomography,” Biomed. Opt. Express 7(4), 1479–1495 (2016). 10.1364/BOE.7.001479 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Baumann B., Götzinger E., Pircher M., Sattmann H., Schuutze C., Schlanitz F., Ahlers C., Schmidt-Erfurth U., Hitzenberger C. K., “Segmentation and quantification of retinal lesions in age-related macular degeneration using polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 15(6), 061704 (2010). 10.1117/1.3499420 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Schlanitz F. G., Baumann B., Kundi M., Sacu S., Baratsits M., Scheschy U., Shahlaee A., Mittermüller T. J., Montuoro A., Roberts P., Pircher M., Hitzenberger C. K., Schmidt-Erfurt U., “Drusen volume development over time and its relevance to the course of age-related macular degeneration,” Br. J. Ophthalmol. 101(2), 198–203 (2017). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Schlanitz F. G., Baumann B., Spalek T., Schütze C., Ahlers C., Pircher M., Götzinger E., Hitzenberger C. K., Schmidt-Erfurth U., “Performance of Automated Drusen Detection by Polarization-Sensitive Optical Coherence Tomography,” Invest. Ophthalmol. Vis. Sci. 52(7), 4571–4579 (2011). 10.1167/iovs.10-6846 [DOI] [PubMed] [Google Scholar]
- 120.Schlanitz F. G., Sacu S., Baumann B., Bolz M., Platzer M., Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., “Identification of Drusen characteristics in age-related macular degeneration by polarization-sensitive optical coherence tomography,” Am. J. Ophthalmol. 160(2), 335–344 (2015). 10.1016/j.ajo.2015.05.008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Schütze C., Bolz M., Sayegh R., Baumann B., Pircher M., Götzinger E., Hitzenberger C. K., Schmidt-Erfurth U., “Lesion size detection in geographic atrophy by polarization-sensitive optical coherence tomography and correlation to conventional imaging techniques,” Invest. Ophthalmol. Vis. Sci. 54(1), 739–745 (2013). 10.1167/iovs.11-7877 [DOI] [PubMed] [Google Scholar]
- 122.Sayegh R. G., Zotter S., Roberts P. K., Kandula M. M., Sacu S., Kreil D. P., Baumann B., Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., “Polarization-sensitive optical coherence tomography and conventional retinal imaging strategies in assessing foveal integrity in geographic atrophy,” Invest. Ophthalmol. Vis. Sci. 56(9), 5246–5255 (2015). 10.1167/iovs.14-15114 [DOI] [PubMed] [Google Scholar]
- 123.Michels S., Pircher M., Geitzenauer W., Simader C., Götzinger E., Findl O., Schmidt-Erfurth U., Hitzenberger C. K., “Value of polarisation-sensitive optical coherence tomography in diseases affecting the retinal pigment epithelium,” Br. J. Ophthalmol. 92(2), 204–209 (2008). 10.1136/bjo.2007.130047 [DOI] [PubMed] [Google Scholar]
- 124.Miura M., Yamanari M., Iwasaki T., Elsner A. E., Makita S., Yatagai T., Yasuno Y., “Imaging polarimetry in age-related macular degeneration,” Invest. Ophthalmol. Vis. Sci. 49(6), 2661–2667 (2008). 10.1167/iovs.07-0501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 125.Sugita M., Zotter S., Pircher M., Makihira T., Saito K., Tomatsu N., Sato M., Roberts P., Schmidt-Erfurth U., Hitzenberger C. K., “Motion artifact and speckle noise reduction in polarization sensitive optical coherence tomography by retinal tracking,” Biomed. Opt. Express 5(1), 106–122 (2013). 10.1364/BOE.5.000106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Roberts P., Sugita M., Deák G., Baumann B., Zotter S., Pircher M., Sacu S., Hitzenberger C. K., Schmidt-Erfurth U., “Automated identification and quantification of subretinal fibrosis in neovascular age-related macular degeneration using polarization-sensitive OCT,” Invest. Ophthalmol. Vis. Sci. 57(4), 1699–1705 (2016). 10.1167/iovs.15-18694 [DOI] [PubMed] [Google Scholar]
- 127.Hong Y. J., Miura M., Ju M. J., Makita S., Iwasaki T., Yasuno Y., “Simultaneous investigation of vascular and retinal pigment epithelial pathologies of exudative macular diseases by multifunctional optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 55(8), 5016–5031 (2014). 10.1167/iovs.14-14005 [DOI] [PubMed] [Google Scholar]
- 128.Sugiyama S., Hong Y. J., Kasaragod D., Makita S., Uematsu S., Ikuno Y., Miura M., Yasuno Y., “Birefringence imaging of posterior eye by multi-functional Jones matrix optical coherence tomography,” Biomed. Opt. Express 6(12), 4951–4974 (2015). 10.1364/BOE.6.004951 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Lammer J., Bolz M., Baumann B., Pircher M., Gerendas B., Schlanitz F., Hitzenberger C. K., Schmidt-Erfurth U., “Detection and Analysis of hard exudates by polarization-sensitive optical coherence tomography in patients with diabetic maculopathy,” Invest. Ophthalmol. Vis. Sci. 55(3), 1564–1571 (2014). 10.1167/iovs.13-13539 [DOI] [PubMed] [Google Scholar]
- 130.Roberts P., Baumann B., Lammer J., Gerendas B., Kroisamer J., Bühl W., Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., Sacu S., “Retinal pigment epithelial features in central serous chorioretinopathy identified by polarization-sensitive optical coherence tomography,” Invest. Ophthalmol. Vis. Sci. 57(4), 1595–1603 (2016). 10.1167/iovs.15-18494 [DOI] [PubMed] [Google Scholar]
- 131.Schütze C., Ahlers C., Pircher M., Baumann B., Götzinger E., Prager F., Matt G., Sacu S., Hitzenberger C. K., Schmidt-Erfurth U., “Morphologic characteristics of idiopathic juxtafoveal telangiectasia using spectral-domain and polarization-sensitive optical coherence tomography,” Retina 32(2), 256–264 (2012). 10.1097/IAE.0b013e31821edfb0 [DOI] [PubMed] [Google Scholar]
- 132.Schütze C., Ritter M., Blum R., Zotter S., Baumann B., Pircher M., Hitzenberger C. K., Schmidt-Erfurth U., “Retinal pigment epithelium findings in patients with albinism using wide-field polarization-sensitive optical coherence tomography,” Retina 34(11), 2208–2217 (2014). 10.1097/IAE.0000000000000224 [DOI] [PubMed] [Google Scholar]
- 133.Ritter M., Zotter S., Schmidt W. M., Bittner R. E., Deak G. G., Pircher M., Sacu S., Hitzenberger C. K., Schmidt-Erfurth U. M., Macula Study Group Vienna , “Characterization of Stargardt disease using polarization-sensitive optical coherence tomography and fundus autofluorescence imaging,” Invest. Ophthalmol. Vis. Sci. 54(9), 6416–6425 (2013). 10.1167/iovs.12-11550 [DOI] [PubMed] [Google Scholar]
- 134.Baumann B., Schirmer J., Rauscher S., Fialová S., Glösmann M., Augustin M., Pircher M., Gröger M., Hitzenberger C. K., “Melanin pigmentation in rat eyes: in vivo imaging by polarization-sensitive optical coherence tomography and comparison to histology,” Invest. Ophthalmol. Vis. Sci. 56(12), 7462–7472 (2015). 10.1167/iovs.15-17742 [DOI] [PubMed] [Google Scholar]
- 135.Augustin M., Fialová S., Himmel T., Glösmann M., Lengheimer T., Harper D. J., Plasenzotti R., Pircher M., Hitzenberger C. K., Baumann B., “Multi-functional OCT enables longitudinal study of retinal changes in a VLDLR knockout mouse model,” PLoS One 11(10), e0164419 (2016). 10.1371/journal.pone.0164419 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Pierce M. C., Shishkov M., Park B. H., Nassif N. A., Bouma B. E., Tearney G. J., de Boer J. F., “Effects of sample arm motion in endoscopic polarization-sensitive optical coherence tomography,” Opt. Express 13(15), 5739–5749 (2005). 10.1364/OPEX.13.005739 [DOI] [PubMed] [Google Scholar]
- 137.Li J., Feroldi F., de Lange J., Daniels J. M. A., Grünberg K., de Boer J. F., “Polarization sensitive optical frequency domain imaging system for endobronchial imaging,” Opt. Express 23(3), 3390–3402 (2015). 10.1364/OE.23.003390 [DOI] [PubMed] [Google Scholar]
- 138.Kuo W. C., Chou N. K., Chou C., Lai C. M., Huang H. J., Wang S. S., Shyu J. J., “Polarization-sensitive optical coherence tomography for imaging human atherosclerosis,” Appl. Opt. 46(13), 2520–2527 (2007). 10.1364/AO.46.002520 [DOI] [PubMed] [Google Scholar]
- 139.Nadkarni S. K., Pierce M. C., Park B. H., de Boer J. F., Whittaker P., Bouma B. E., Bressner J. E., Halpern E., Houser S. L., Tearney G. J., “Measurement of collagen and smooth muscle cell content in atherosclerotic plaques using polarization-sensitive optical coherence tomography,” J. Am. Coll. Cardiol. 49(13), 1474–1481 (2007). 10.1016/j.jacc.2006.11.040 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 140.Nadkarni S. K., Bouma B. E., de Boer J., Tearney G. J., “Evaluation of collagen in atherosclerotic plaques: the use of two coherent laser-based imaging methods,” Lasers Med. Sci. 24(3), 439–445 (2009). 10.1007/s10103-007-0535-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 141.Fu X., Wang Z., Wang H., Wang Y. T., Jenkins M. W., Rollins A. M., “Fiber-optic catheter-based polarization-sensitive OCT for radio-frequency ablation monitoring,” Opt. Lett. 39(17), 5066–5069 (2014). 10.1364/OL.39.005066 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 142.van der Sijde J. N., Karanasos A., Villiger M., Bouma B. E., Regar E., “First-in-man assessment of plaque rupture by polarization-sensitive optical frequency domain imaging in vivo,” Eur. Heart J. 37(24), 1932 (2016). 10.1093/eurheartj/ehw179 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 143.Hariri L. P., Villiger M., Applegate M. B., Mino-Kenudson M., Mark E. J., Bouma B. E., Suter M. J., “Seeing beyond the bronchoscope to increase the diagnostic yield of bronchoscopic biopsy,” Am. J. Respir. Crit. Care Med. 187(2), 125–129 (2013). 10.1164/rccm.201208-1483OE [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.D. C. Adams, L. P. Hariri, A. J. Miller, Y. Wang, J. L. Cho, M. Villiger, J. A. Holz, M. V. Szabari, D. L. Hamilos, R. S. Harris, J. W. Griffith, B. E. Bouma, A. D. Luster, B. D. Medoff, and M. J. Suter, “Birefringence microscopy platform for assessing airway smooth muscle structure and function in vivo,” Sci. Transl. Med. 8, 359ra131–359ra131 (2016). 10.1126/scitranslmed.aag1424 [DOI] [PMC free article] [PubMed]
- 145.Pierce M. C., Strasswimmer J., Park B. H., Cense B., de Boer J. F., “Advances in optical coherence tomography imaging for dermatology,” J. Invest. Dermatol. 123(3), 458–463 (2004). 10.1111/j.0022-202X.2004.23404.x [DOI] [PubMed] [Google Scholar]
- 146.Brigham P. A., McLoughlin E., “Burn incidence and medical care use in the United States: estimates, trends, and data sources,” J. Burn Care Rehabil. 17(2), 95–107 (1996). 10.1097/00004630-199603000-00003 [DOI] [PubMed] [Google Scholar]
- 147.Maitland D. J., Walsh J. T., Jr., “Quantitative measurements of linear birefringence during heating of native collagen,” Lasers Surg. Med. 20(3), 310–318 (1997). [DOI] [PubMed] [Google Scholar]
- 148.Yasuno Y., Makita S., Sutoh Y., Itoh M., Yatagai T., “Birefringence imaging of human skin by polarization-sensitive spectral interferometric optical coherence tomography,” Opt. Lett. 27(20), 1803–1805 (2002). 10.1364/OL.27.001803 [DOI] [PubMed] [Google Scholar]
- 149.Pierce M. C., Strasswimmer J., Hyle Park B., Cense B., De Boer J. F., “Birefringence measurements in human skin using polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 9(2), 287–291 (2004). 10.1117/1.1645797 [DOI] [PubMed] [Google Scholar]
- 150.Pircher M., Goetzinger E., Leitgeb R., Hitzenberger C., “Three dimensional polarization sensitive OCT of human skin in vivo,” Opt. Express 12(14), 3236–3244 (2004). 10.1364/OPEX.12.003236 [DOI] [PubMed] [Google Scholar]
- 151.Pierce M. C., Sheridan R. L., Hyle Park B., Cense B., de Boer J. F., “Collagen denaturation can be quantified in burned human skin using polarization-sensitive optical coherence tomography,” Burns 30(6), 511–517 (2004). 10.1016/j.burns.2004.02.004 [DOI] [PubMed] [Google Scholar]
- 152.Kim K. H., Pierce M. C., Maguluri G., Park B. H., Yoon S. J., Lydon M., Sheridan R., de Boer J. F., “In vivo imaging of human burn injuries with polarization-sensitive optical coherence tomography,” J. Biomed. Opt. 17(6), 066012 (2012). 10.1117/1.JBO.17.6.066012 [DOI] [PubMed] [Google Scholar]
- 153.Gong P., Chin L., Es’haghian S., Liew Y. M., Wood F. M., Sampson D. D., McLaughlin R. A., “Imaging of skin birefringence for human scar assessment using polarization-sensitive optical coherence tomography aided by vascular masking,” J. Biomed. Opt. 19(12), 126014 (2014). 10.1117/1.JBO.19.12.126014 [DOI] [PubMed] [Google Scholar]
- 154.Lo W. C. Y., Villiger M., Golberg A., Broelsch G. F., Khan S., Lian C. G., Austen W. G., Jr, Yarmush M., Bouma B. E., “Longitudinal, 3D imaging of collagen remodeling in murine hypertrophic scars in vivo using polarization-sensitive optical frequency domain imaging,” J. Invest. Dermatol. 136(1), 84–92 (2016). 10.1038/JID.2015.399 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 155.Kuwahara T., Strasswimmer J., de Boer J., Anderson R., “Noninvasive measurements of the photodamaged human skin in vivo by polarization-sensitive optical coherence tomography,” J. Am. Acad. Dermatol. 52(3), 163 (2005). 10.1016/j.jaad.2004.10.661 [DOI] [Google Scholar]
- 156.Strasswimmer J., Pierce M. C., Park B. H., Neel V., de Boer J. F., “Polarization-sensitive optical coherence tomography of invasive basal cell carcinoma,” J. Biomed. Opt. 9(2), 292–298 (2004). 10.1117/1.1644118 [DOI] [PubMed] [Google Scholar]
- 157.Xie T., Guo S., Zhang J., Chen Z., Peavy G. M., “Determination of characteristics of degenerative joint disease using optical coherence tomography and polarization sensitive optical coherence tomography,” Lasers Surg. Med. 38(9), 852–865 (2006). 10.1002/lsm.20394 [DOI] [PubMed] [Google Scholar]
- 158.Shyu J. J., Chan C. H., Hsiung M. W., Yang P. N., Chen H. W., Kuo W. C., “Diagnosis of articular cartilage damage by polarization sensitive optical coherence tomography and the extracted optical properties,” Prog. Electromagnetics Res. 91, 365–376 (2009). 10.2528/PIER09022602 [DOI] [Google Scholar]
- 159.Ugryumova N., Jacobs J., Bonesi M., Matcher S. J., “Novel optical imaging technique to determine the 3-D orientation of collagen fibers in cartilage: variable-incidence angle polarization-sensitive optical coherence tomography,” Osteoarthritis Cartilage 17(1), 33–42 (2009). 10.1016/j.joca.2008.05.005 [DOI] [PubMed] [Google Scholar]
- 160.Lu Z., Kasaragod D. K., Matcher S. J., “Optic axis determination by fibre-based polarization-sensitive swept-source optical coherence tomography,” Phys. Med. Biol. 56(4), 1105–1122 (2011). 10.1088/0031-9155/56/4/014 [DOI] [PubMed] [Google Scholar]
- 161.Brill N., Wirtz M., Merhof D., Tingart M., Jahr H., Truhn D., Schmitt R., Nebelung S., “Polarization-sensitive optical coherence tomography-based imaging, parameterization, and quantification of human cartilage degeneration,” J. Biomed. Opt. 21(7), 076013 (2016). 10.1117/1.JBO.21.7.076013 [DOI] [PubMed] [Google Scholar]
- 162.Kim K. H., Burns J. A., Bernstein J. J., Maguluri G. N., Park B. H., de Boer J. F., “In vivo 3D human vocal fold imaging with polarization sensitive optical coherence tomography and a MEMS scanning catheter,” Opt. Express 18(14), 14644–14653 (2010). 10.1364/OE.18.014644 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Burns J. A., Kim K. H., deBoer J. F., Anderson R. R., Zeitels S. M., “Polarization-Sensitive Optical Coherence Tomography Imaging of Benign and Malignant Laryngeal Lesions: An In Vivo Study,” Otolaryngol. Head Neck Surg. 145(1), 91–99 (2011). 10.1177/0194599811403078 [DOI] [PubMed] [Google Scholar]
- 164.Burns J. A., “Optical coherence tomography: imaging the larynx,” Curr. Opin. Otolaryngol. Head Neck Surg. 20(6), 477–481 (2012). 10.1097/MOO.0b013e3283582d7d [DOI] [PubMed] [Google Scholar]
- 165.Mogensen M., Joergensen T. M., Nürnberg B. M., Morsy H. A., Thomsen J. B., Thrane L., Jemec G. B. E., “Assessment of Optical Coherence Tomography Imaging in the Diagnosis of Non-Melanoma Skin Cancer and Benign Lesions Versus Normal Skin: Observer-Blinded Evaluation by Dermatologists and Pathologists,” Dermatol. Surg. 35(6), 965–972 (2009). 10.1111/j.1524-4725.2009.01164.x [DOI] [PubMed] [Google Scholar]
- 166.Patel R., Khan A., Quinlan R., Yaroslavsky A. N., “Polarization-Sensitive Multimodal Imaging for Detecting Breast Cancer,” Cancer Res. 74(17), 4685–4693 (2014). 10.1158/0008-5472.CAN-13-2411 [DOI] [PubMed] [Google Scholar]
- 167.South F. A., Chaney E. J., Marjanovic M., Adie S. G., Boppart S. A., “Differentiation of ex vivo human breast tissue using polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 5(10), 3417–3426 (2014). 10.1364/BOE.5.003417 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Villiger M., Lorenser D., McLaughlin R. A., Quirk B. C., Kirk R. W., Bouma B. E., Sampson D. D., “Deep tissue volume imaging of birefringence through fibre-optic needle probes for the delineation of breast tumour,” Sci. Rep. 6, 28771 (2016). 10.1038/srep28771 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Gladkova N., Streltsova O., Zagaynova E., Kiseleva E., Gelikonov V., Gelikonov G., Karabut M., Yunusova K., Evdokimova O., “Cross-polarization optical coherence tomography for early bladder-cancer detection: statistical study,” J. Biophotonics 4(7-8), 519–532 (2011). 10.1002/jbio.201000088 [DOI] [PubMed] [Google Scholar]
- 170.Kiseleva E., Kirillin M., Feldchtein F., Vitkin A., Sergeeva E., Zagaynova E., Streltzova O., Shakhov B., Gubarkova E., Gladkova N., “Differential diagnosis of human bladder mucosa pathologies in vivo with cross-polarization optical coherence tomography,” Biomed. Opt. Express 6(4), 1464–1476 (2015). 10.1364/BOE.6.001464 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 171.Islam M. S., Oliveira M. C., Wang Y., Henry F. P., Randolph M. A., Park B. H., de Boer J. F., “Extracting structural features of rat sciatic nerve using polarization-sensitive spectral domain optical coherence tomography,” J. Biomed. Opt. 17(5), 056012 (2012). 10.1117/1.JBO.17.5.056012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Henry F. P., Wang Y., Rodriguez C. L. R., Randolph M. A., Rust E. A. Z., Winograd J. M., de Boer J. F., Park B. H., “In vivo optical microscopy of peripheral nerve myelination with polarization sensitive-optical coherence tomography,” J. Biomed. Opt. 20(4), 046002 (2015). 10.1117/1.JBO.20.4.046002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 173.Yoon Y., Jeon S. H., Park Y. H., Jang W. H., Lee J. Y., Kim K. H., “Visualization of prostatic nerves by polarization-sensitive optical coherence tomography,” Biomed. Opt. Express 7(9), 3170–3183 (2016). 10.1364/BOE.7.003170 [DOI] [PMC free article] [PubMed] [Google Scholar]