A Neural Interpretation of Exemplar Theory

Abstract

Exemplar theory assumes that people categorize a novel object by comparing its similarity to the memory representations of all previous exemplars from each relevant category. Exemplar theory has been the most prominent cognitive theory of categorization for more than 30 years. Despite its considerable success in providing good quantitative fits to a wide variety of accuracy data, it has never had a detailed neurobiological interpretation. This article proposes a neural interpretation of exemplar theory in which category learning is mediated by synaptic plasticity at cortical-striatal synapses. In this model, categorization training does not create new memory representations, rather it alters connectivity between striatal neurons and neurons in sensory association cortex. The new model makes identical quantitative predictions as exemplar theory, yet it can account for many empirical phenomena that are either incompatible with or outside the scope of the cognitive version of exemplar theory.

Introduction

Exemplar theory assumes that categorization is a process of learning about the exemplars that belong to the category. When an unfamiliar stimulus is encountered, its similarity is computed to the memory representation of every previously seen exemplar from each potentially relevant category. The probability that the stimulus is assigned to each category increases with the sum of these similarities (Brooks, 1978; Estes, 1986, 1994; Kruschke, 1992; Lamberts, 2000; Medin & Schaffer, 1978; Nosofsky, 1986).

Exemplar theory has been the most prominent cognitive theory of categorization for more than 30 years. Despite its considerable success in providing good quantitative fits to accuracy data from a wide variety of experiments, it has never had a detailed neurobiological interpretation. This article corrects that shortcoming of the literature. We propose a neural version of exemplar theory in which category learning is mediated by synaptic plasticity at cortical-striatal synapses. The neural version makes identical quantitative predictions to the exemplar model, yet it can account for many empirical phenomena that are either incompatible with or outside the scope of the cognitive version of exemplar theory.

One challenge to interpreting exemplar theory at the neural level is to separate the quantitative predictions of the theory from the cognitive interpretations that are used to justify those predictions. At the cognitive level, exemplar theory assumes that people access the memory representations of all previously seen exemplars. The standard interpretation is that these are detailed replicas of each exemplar (filtered by attentional processes) that do not typically include contextual information (e.g., details about the experimental room). The closest match in the memory literature to such representations is probably provided by semantic memory.

This cognitive version of exemplar theory has been a challenge to interpret at the neural level. First, the memory processes postulated by exemplar theory appear qualitatively different from all of the memory systems that have been identified by memory researchers. For example, within the memory systems literature, semantic memory is assumed to be declarative. In contrast, exemplar theorists are careful to assume that people do not have conscious awareness that they are accessing exemplar memories when making categorization decisions. Thus, the cognitive version of exemplar theory appears to postulate a unique memory system that has not yet been discovered by memory researchers.

It is important to note, however, that other instance-based theories postulate more traditional memory systems. For example, RULEX (Nosofsky, Palmeri, & McKinley, 1994) assumes people use explicit rules during categorization but they memorize exceptions. Presumably, people are aware of these exceptions, so this form of memory seems identical to semantic memory.

Previous attempts at providing a neural interpretation of the cognitive processes postulated by exemplar theory have assigned key roles to the hippocampus and surrounding medial temporal lobe structures (e.g., Pickering, 1997; Sakamoto & Love, 2004). The problem with these attempts is that the evidence supporting a major role for medial temporal lobe structures in category learning is weak.

First, medial temporal lobe interpretations of exemplar theory predict that patients with damage to medial temporal lobe structures should be impaired in category learning. We know of three studies that reported category-learning deficits in amnesiacs (Hopkins, Myers, Shohamy, Grossman, & Gluck, 2004; Kolodny, 1994; Zaki, Nosofsky, Jessup, & Unversagt, 2003), one that reported normal performance on the first 50 trials but impaired performance later on (Knowlton, Squire, & Gluck, 1994), and one that reported normal categorization by amnesiacs when the stimuli were faces, but impaired performance when the stimuli were virtual reality scenes (Graham et al., 2006). On the other hand, many more studies have reported intact category-learning performance in patients with amnesia (e.g. Bayley, Frascino, & Squire, 2005; Filoteo, Maddox, & Davis, 2001b; Janowsky, Shimamura, Kritchevsky, & Squire, 1989; Knowlton & Squire, 1993; Kolodny, 1994; Leng & Parkin, 1988; Squire & Knowlton, 1995; Zaki et al., 2003). For example, Filoteo et al. (2001b) reported normal performance by amnesiacs in a difficult information-integration categorization task with nonlinearly separable categories that required hundreds of training trials. In fact, in the Filoteo et al. (2001b) study, one (medial temporal lobe) amnesiac and one control participant completed a second day of testing. Despite lacking an explicit memory of the previous session, the patient with amnesia performed slightly better than the control on the first block of day 2. This result suggests that amnesiacs do not necessarily rely on working memory to perform normally in category-learning tasks (because working memory cannot be used to retain category knowledge across days).

A second set of problematic results come from neuroimaging studies of unstructured category-learning tasks. Unstructured categories are those in which the stimuli are assigned to each contrasting category randomly, and thus there is no rule- or similarity-based strategy for determining category membership. Introspection seems to suggest that the only way arbitrary categories of this type could be learned is via explicit memorization, so if medial temporal lobe structures play a critical role in any categorization task, then unstructured categorization tasks seem like a good candidate. Even so, fMRI studies of unstructured-category learning have found task-related activity in the striatum, but typically not in the hippocampus or other medial temporal lobe structures (Lopez-Paniagua & Seger, 2011; Seger & Cincotta, 2005; Seger, Peterson, Cincotta, Lopez-Paniagua, & Anderson, 2010). In addition, unstructured category learning includes a motor component that is more typical of striatal-mediated procedural learning than hippocampal-mediated declarative learning (Crossley, Madsen, & Ashby, 2012).

Third, a number of behavioral dissociations have been reported that seem more consistent with a striatal locus for the learning of similarity-based categories than a medial temporal lobe locus (for a review, see Ashby & Valentin, 2016). This work has contrasted rule-based (RB) and information-integration (II) category-learning tasks. In RB tasks, the categories can be learned via some explicit reasoning process (Ashby, Alfonso-Reese, Turken, & Waldron, 1998). In the most common applications, only one stimulus dimension is relevant, and the participant’s task is to discover this relevant dimension and then to map the different dimensional values to the relevant categories. A variety of evidence suggests that success in RB tasks depends on declarative memory and especially on working memory and executive attention (Ashby et al., 1998; Maddox, Ashby, Ing, & Pickering, 2004; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006). In II category-learning tasks, accuracy is maximized with a similarity-based strategy in which information from two or more incommensurable stimulus components is integrated at some predecisional stage (Ashby & Gott, 1988; Ashby et al., 1998). Evidence suggests that success in II tasks depends on procedural memory (Ashby, Ell, & Waldron, 2003; Ashby & Ennis, 2006; Filoteo, Maddox, Salmon, & Song, 2005; Knowlton, Mangels, & Squire, 1996; Maddox, Bohil, & Ing, 2004). Exemplar theory assumes a similarity-based categorization strategy so it seems especially tenable for II tasks. Furthermore, many researchers have argued that learning in RB tasks is mediated by an explicit, rule-learning process that is incompatible with exemplar theory (e.g., Ashby et al., 1998; Erickson & Kruschke, 1998; McDaniel, Cahill, Robbins, & Wiener, 2014; Nosofsky et al., 1994; Rouder & Ratcliff, 2006).

Currently, at least 25 separate empirical dissociations between RB and II category learning have been reported (Ashby & Valentin, 2016). Two of these are especially important for the present purposes. First, II but not RB tasks are extremely sensitive to feedback timing (Maddox, Ashby, & Bohil, 2003; Maddox & Ing, 2005; Worthy, Markman, & Maddox, 2013). In particular, II learning is better when the feedback is delivered 500 ms after the response than when the feedback is immediate or delivered after a 1 sec delay (Worthy et al., 2013), whereas feedback delays of 2.5 sec or longer completely abolish almost all II learning (Maddox et al., 2003; Maddox & Ing, 2005). In contrast, delays of up to 10 sec have no effect on RB learning. The II results are consistent with the effects on cortical-striatal synaptic plasticity of delays between dopamine (DA) release and Ca²⁺ influx into the spines of medium spiny neurons (Yagishita et al., 2014), and inconsistent with the hypothesis that II learning is mediated by medial temporal lobe structures. Another important dissociation is that switching the locations of the response keys interferes with performance of II tasks but not with performance of one-dimensional RB tasks (Ashby, Ell, & Waldron, 2003; Maddox, Bohil, & Ing, 2004; Maddox, Glass, O’Brien, Filoteo, & Ashby, 2010; Spiering & Ashby, 2008). This is relevant because a similar result has been reported for the most widely studied procedural-learning task – namely the serial reaction time task (Willingham, Wells, Farrell, & Stemwedel, 2000), and procedural learning is thought to depend on the striatum – not on the hippocampus.

This article describes a neural interpretation of exemplar theory that easily accounts for all of these problematic results. First though, we define the exemplar model more explicitly.

The Exemplar Model

Many researchers have tested exemplar models of categorization (e.g., Estes, 1986, 1994; Medin & Schaffer, 1978; Nosofsky, 1986, 2011). These various versions are all highly similar, but to establish mathematical equivalence it is necessary to focus on one specific version of exemplar theory. The model has evolved somewhat from its initial description, so our focus will be on the exemplar model known as the generalized context model (GCM; Nosofsky, 1986, 2011).

The equivalence result established below holds for any number of categories, but to keep the notation simpler we will assume a standard categorization experiment with two categories A and B. Under these conditions, the exemplar model assumes that the probability that a participant assigns stimulus k to category A equals

$$P(\mathrm{A}\mid k)=\frac{{\beta }_A{\displaystyle \sum _{i\in C_A}}{V}_{iA}{\eta }_{ik}}{{\beta }_A{\displaystyle \sum _{i\in C_A}}{V}_{iA}{\eta }_{ik}+{\beta }_B{\displaystyle \sum _{i\in C_B}}{V}_{iB}{\eta }_{ik}},$$ (1)

where C_A and C_B are sets containing the stimuli in categories A and B, respectively, η_ik is the similarity between stimuli i and k, β_A and β_B are constants reflecting the participant’s bias toward responding A and B, respectively, and V_iJ represents the memory strength of stimulus i with respect to category J. The memory strengths V_iJ are not free parameters, but instead are usually “set equal to the relative frequency with which each exemplar i is provided with Category J feedback during the classification training phase” (Nosofsky, 2011). Most categorization experiments present all stimuli equally often, and in this case note that all V_iJ are equal and therefore can be canceled from Eq. (1).

Similarity is assumed to be inversely related to the distance between the perceptual representations of the stimuli. More specifically, the distance between the perceptual representations of stimuli i and k, denoted δ_ik, is computed from the weighted Minkowski metric:

$${\delta }_{ik}={\left(\sum _{j=1}^m{w}_j{\mid x_{ij}-x_{kj}\mid }^r\right)}^{1/r},$$ (2)

where m is the number of perceptual dimensions, w_j is the proportion of attention allocated to dimension j, x_ij is the coordinate value of stimulus i on the j^th perceptual dimension, and r determines the nature of the distance metric. In particular, r = 1 produces city-block distance and r = 2 produces Euclidean distance. Similarity is inversely related to distance via:

$${\eta }_{ik}=exp(-c{\delta }_{ik}^{\omega })$$ (3)

where c and ω are constants. The parameter c is a measure of stimulus sensitivity, which increases with the overall discriminability of the stimuli. The constant ω defines the nature of the similarity function. In virtually all applications ω = 1 or 2. A value of ω = 1, which produces the exponential similarity function (Shepard, 1987), is typically combined with a city-block distance metric, whereas a value of ω = 2, which produces the Gaussian similarity function, is typically combined with a Euclidean distance metric.

The Neural Model

Although the evidence does not favor medial temporal lobe structures as the most important regions for category learning, it does favor a critical role for the basal ganglia, and especially the striatum – a major input region within the basal ganglia that includes the caudate nucleus and the putamen (for reviews, see e.g., Ashby & Ennis, 2006; Seger, 2008; Seger & Miller, 2010). A complete review is beyond the scope of this article, but briefly, in addition to the dissociations between RB and II categorization mentioned above, patients with striatal dysfunction are highly impaired in category learning (e.g., Ashby, Noble, Filoteo, Waldron, & Ell, 2003; Filoteo, Maddox, & Davis, 2001a; Filoteo et al., 2005; Knowlton et al., 1996; Sage et al., 2003; Shohamy, Myers, Onlaor, & Gluck, 2004; Witt, Nuhsman, & Deuschl, 2002), and almost all fMRI studies of category learning have reported significant task-related activity in the striatum (e.g., Nomura et al., 2007; Poldrack et al., 2001; Seger & Cincotta, 2002, 2005; Waldschmidt & Ashby, 2011).

So the evidence is good that the striatum plays a key role in category learning – at least in the learning of II and unstructured categories (i.e., rather than RB categories). The problem for exemplar theory is that basal ganglia neuroanatomy does not favor traditional interpretations of exemplar representations. Virtually all of cortex (except V1) sends excitatory (glutamatergic) projections to the striatum (Reiner, 2010). These cortical inputs, which synapse on medium spiny neurons (MSNs), are massively convergent, with estimates that somewhere between 50,000 and 350,000 cortical neurons converge onto a single striatal MSN (Bolam et al., 2006; Kincaid, Zheng, & Wilson, 1998; C. J. Wilson, 1995). In contrast, each of these cortical neurons might synapse onto as few as 10–100 MSNs (Wickens & Arbuthnott, 2010). Thus, it appears that the resolution of the striatal MSNs is not dense enough to allocate one MSN for every exemplar in any arbitrary category, especially when exemplar similarity is high.

As a result, we propose a reconceptualization of ‘exemplar representation’. To our knowledge, there are three existing process-level interpretations of exemplar theory –ALCOVE (Kruschke, 1992), the EBRW (Nosofsky & Palmeri, 1997), and the information-accumulation model (Lamberts, 2000). In each of these, the presentation of a new stimulus adds a new node to the network, and this node serves as the exemplar representation of that stimulus on all future trials. We propose instead that the presentation of a stimulus either changes the synaptic strength at an existing cortical-striatal synapse or creates a new synapse. As a result, categorization training does not recruit any new nodes, rather it alters connectivity between MSNs and units in sensory association cortex.

In the remainder of this section, we show that under appropriate conditions, such a model is mathematically equivalent to the exemplar model described by Eqs. (1), (2), and (3).

Model Architecture

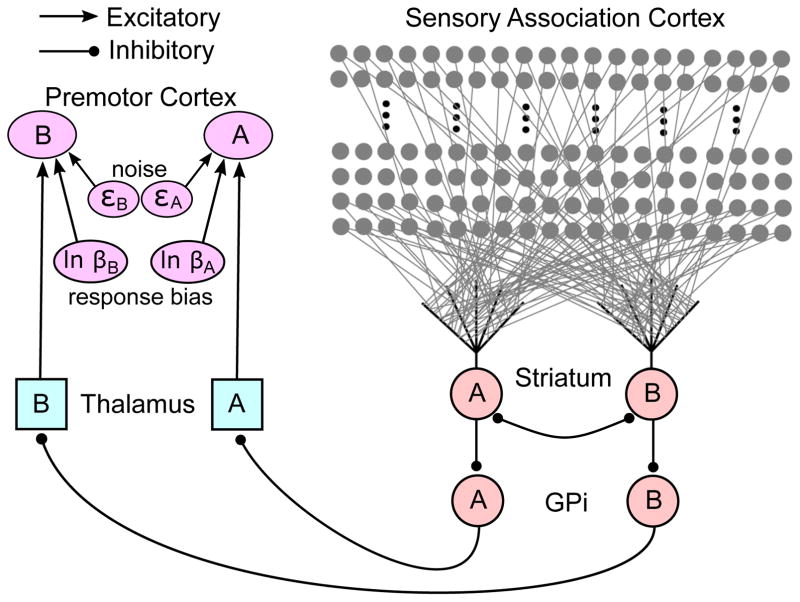
The architecture of the proposed model is shown in Figure 1. Essentially this just reproduces the well-known direct pathway through the basal ganglia, and is identical to the simplest version of the procedural-learning system of the COVIS model of category learning (Ashby et al., 1998; Ashby & Waldron, 1999; Ashby, Paul, & Maddox, 2011; Ashby & Crossley, 2011).

Figure 1.

Architecture of the model that is computationally equivalent to exemplar theory.

Sensory association cortex is modeled in the same way as in Ashby, Ennis, and Spiering (2007). Briefly, this means we assume an ordered array of many units in sensory cortex, each tuned to a different stimulus. Neurons in sensory cortex respond not only to a preferred stimulus, but also more weakly to similar stimuli. In perceptual neuroscience this phenomenon is described by the neuron’s tuning curve. We model the tuning curve of each sensory cortical unit in the Figure 1 model via radial basis functions – that is, we assume that each unit responds maximally when its preferred stimulus is presented and that its response decreases with the distance in perceptual space between the stimulus preferred by that unit and the presented stimulus. The equivalence to exemplar theory holds for any number of these units, so long as every perceptually distinct stimulus maximally excites a different unit. Given the known cortical-striatal convergence, with the two MSNs shown in Figure 1 we would expect the relevant regions of sensory cortex to include somewhere between 10,000 and 60,000 neurons.

The equivalence result established below assumes a standard categorization experiment in which the stimulus is presented at constant intensity and without a mask until the participant responds. Under these conditions, activation in each sensory unit is 0 during periods when no stimulus is displayed and is either 0 or equal to some positive constant value during the duration of stimulus presentation. More specifically, consider a trial when stimulus k is presented. Then the response of sensory unit i during the time when the stimulus is present will equal:

$$I_{i\mid k}=exp(-{\delta }_{ik}^{\omega }/\gamma ),$$ (4)

where δ_ik is the distance in perceptual space between the representations of stimuli i and k as defined by Eq. 2. When ω = 2, Eq. 4 describes a Gaussian radial basis function and when ω = 1, Eq. 4 describes a Laplacian radial basis function. Either way, Eq. 4 is a popular method for modeling the receptive fields of sensory units, both in models of categorization (e.g., Ashby & Crossley, 2011; Kruschke, 1992) and in other tasks (e.g., Er, Wu, Lu, & Toh, 2002; Oglesby & Mason, 1991; Riesenhuber & Poggio, 1999; Rosenblum, Yacoob, & Davis, 1996).

The key insight that links exemplar theory to cortical-striatal synaptic plasticity comes from Ashby and Alfonso-Reese (1995), who showed that exemplar models are equivalent to a classifier that estimates each category distribution via a Parzen (1962) kernel density estimator. Parzen kernels are known today as radial basis functions, so the key to the Ashby and Alfonso-Reese (1995) result was to recognize that the similarity function proposed by exemplar theory (i.e., Eq. 3) could be interpreted as a radial basis function. This reinterpretation of exemplar similarity provides a natural link between exemplar theory and models such as COVIS that use radial basis functions to model the response properties of sensory cortical units.

The second key feature of exemplar theory is that similarities are summed to determine category membership (i.e., see Eq. 1). Radial basis functions are summed in two different ways in neural models such as COVIS. First, each MSN responds to a weighted sum of the radial basis functions that model activation in sensory cortex¹, and second, the rules that govern synaptic plasticity (i.e., learning) dictate that the current synaptic strength is a weighted sum of previous activations. This latter sum is especially important when establishing equivalence to exemplar theory because it depends on all previously seen exemplars, whereas the former sum does not. So both exemplar theory and COVIS assign a key role to weighted sums of radial basis functions of all previously seen exemplars, and we believe it is this common feature of both theories that cause such similar behavior in the two conceptually different accounts of categorization. The mathematical equivalence established below only requires the latter of these two neural summing operations. Later however, we show that if both neural summing operations are allowed and if many of the ancillary assumptions required for exact mathematical equivalence are relaxed, numerical equivalence is barely affected. We believe this is because in both theories, behavior depends fundamentally on sums of radial basis functions that are activated by stimulus presentation.

At the outset of a new experimental session, we assume that the sensory cortical units are fully interconnected with the two striatal MSNs. Specifically, every unit in sensory cortex synapses with a dedicated spine on each of the two MSNs. Thus, if there are 40,000 units in sensory cortex there are 40,000 spines on each MSN.

Activation in each MSN is modeled using a firing-rate model (Dayan & Abbott, 2001; Ermentrout & Terman, 2010; H. R. Wilson & Cowan, 1972, 1973). Thus, the two MSNs shown in Figure 1 could be viewed as two identical populations of MSNs, or the activations produced could be viewed as average firing rates over many repetitions of the stimulus conditions. Firing-rate models are described by two equations. The first, typically written as a differential equation, describes how presynaptic input generates postsynaptic activation. This equation typically describes within-trial temporal dynamics and it integrates all sensory input², but in the present application, only a very simple model is needed. In particular, there is no need to model the temporal dynamics of within-trial activation or the summing of sensory inputs. Specifically, it suffices to simply assume that the postsynaptic activation in each MSN equals the presynaptic activation at the most active spine weighted by the relevant synaptic strength. The most active spine will be the one synapsing with the cortical unit that responds most strongly to the stimulus. Let A_J(n) denote the activation in striatal unit J (where J = A or B) on trial n. Then if stimulus k is presented on trial n

$$\begin{array}{l}{A}_J(n)=w_{Jk}(n)I_{k\mid k}\\ =w_{Jk}(n),\end{array}$$ (5)

where w_Jk(n) is the strength of the synapse between sensory unit k and MSN J on trial n. The latter equality holds because no matter how distance is defined, the distance from a point to itself must be zero. As a result δ_kk = 0, and so I_k|k = 1 (i.e., for an ω and any γ).

The second firing-rate equation converts the postsynaptic activation into postsynaptic firing rate. This equation models nonlinearities in the neural response (e.g., response compression). Following the standard approach, we assume that the postsynaptic firing rate in unit J, denoted by R_J(n) equals

$$R_J(n)=F[A_J(n)],$$ (6)

where F is a monotonically increasing function known as the activation function.

Equivalence to exemplar theory requires that F behaves as a natural log. Thus³,

$$\begin{array}{l}{R}_J(n)=ln[A_J(n)]\\ =ln[w_{Jk}(n)].\end{array}$$ (7)

Figure 1 shows the major neuroanatomical projections from the MSNs to regions in premotor cortex that control the motor response. However, the equivalence result established here treats these as simple relays that convey the signals generated within the striatum to motor output units. Therefore, there is no need to model activity in each of these regions separately. Instead, we simply assume that the MSN firing rates are unaltered as they pass through these relays. However, mathematical equivalence requires that two important processes must occur within premotor cortex. First, independent noise is added to each output unit. We assume that the most active output unit controls the response on each trial, so noise is needed to account for probabilistic responding. Second, a response bias term is added to each MSN output. For equivalence to the exemplar model the additive bias must equal B = ln β_J (see Figure 1). So if we denote the activation in output unit J on trial n as Y_J(n) then

$$Y_J(n)=R_J(n)+ln{\beta }_J+{\epsilon }_J.$$ (8)

We assume that response A is made on trial n if Y_A(n) > Y_B(n) and that response B is made if the opposite ordering occurs.

Learning

DA is known to have pronounced effects on cortical-striatal synaptic plasticity (e.g., Centonze, Picconi, Gubellini, Bernardi, & Calabresi, 2001; Shen, Flajolet, Greengard, & Surmeier, 2008). Much evidence suggests that strengthening of cortical-striatal synapses (and long-term potentiation) requires strong pre- and postsynaptic activation and DA levels above baseline. More specifically, the postsynaptic activation must be strong enough to activate NMDA receptors (a high-threshold glutamate receptor). In contrast, cortical-striatal synapses are weakened (and long-term depression occurs) if pre- and postsynaptic activation are strong and DA is below baseline (e.g., Arbuthnott, Ingham, & Wickens, 2000; Ronesi & Lovinger, 2005). DA levels rise above baseline following unexpected rewards and fall below baseline following the failure to receive an expected reward (Hollerman & Schultz, 1998; Mirenowicz & Schultz, 1994; Schultz, 1998). As a result, a number of researchers have proposed that synaptic plasticity at cortical-striatal synapses follows reinforcement-learning rules (Doya, 2000; Houk, Adams, & Barto, 1995).

Suppose every sensory-cortical neuron has one synapse onto each striatal MSN. A biologically motivated form of reinforcement learning assumes that if stimulus S_k is presented on trial n, then the strength of the synapse between striatal unit J (for J = A or B) and sensory-cortical unit k on trial n + 1 equals (e.g., Ashby & Crossley, 2011):

$$\begin{array}{l}{w}_{Jk}(n+1)=w_{Jk}(n)\\ +{\alpha }_w{I}_{k\mid S_n}{[R_J(n)-{\theta }_{\mathit{NMDA}}]}^{+}{[D(n)-D_{\mathit{base}}]}^{+}\\ -{\beta }_w{I}_{k\mid S_n}{[R_J(n)-{\theta }_{\mathit{NMDA}}]}^{+}{[D_{\mathit{base}}-D(n)]}^{+},\end{array}$$ (9)

where α_w and β_w are the constant learning and unlearning rates, respectively, [f(n)]⁺ = f(n) if f(n) > 0 and 0 if f(n) ≤ 0, θ_NMDA is a constant specifying the threshold for NMDA receptor activation, D(n) is the amount of DA released on trial n, and D_base is the baseline DA level. Note that this model assumes that the amount of synaptic strengthening (i.e., the plus term) is proportional to the product of 1) presynaptic activation, 2) the amount that the postsynaptic activation is above the NMDA threshold, and 3) the amount that DA is above baseline. In contrast, the amount of synaptic weakening (i.e., the minus term) is proportional to the product of 1) presynaptic activation, 2) the amount that the postsynaptic activation is above the NMDA threshold, and 3) the amount that DA is below baseline.

Solving Eq. (9) iteratively produces

$$\begin{array}{l}{w}_{Jk}(n+1)=w_{Jk}(0)\\ +{\alpha }_w\sum _{i=1}^n{I}_{k\mid S_i}{[R_J(i)-{\theta }_{\mathit{NMDA}}]}^{+}{[D(i)-D_{\mathit{base}}]}^{+}\\ -{\beta }_w\sum _{i=1}^n{I}_{k\mid S_i}{[R_J(i)-{\theta }_{\mathit{NMDA}}]}^{+}{[D_{\mathit{base}}-D(i)]}^{+}.\end{array}$$ (10)

Note that this solution includes a sum of radial basis functions activated by all previously seen exemplars. Since the exemplar model includes a similar such sum, this is the key feature of the neural model that allows it to mimic the exemplar model.

Assumptions

Proving that this model is equivalent to the exemplar model requires the following extra assumptions.

A1. Error trials do not change synaptic strengths

This assumption implies that β_w = 0 in Eq. (9). Although this assumption is biologically implausible (e.g., Calabresi, Maj, Pisani, Mercuri, & Bernardi, 1992), it is not necessarily imcompatible with exemplar theory. As noted above, exemplar theory assumes that the memory strength of exemplar i in category J is strengthened when a categorization response to exemplar i is provided with category J feedback during classification training (Nosofsky, 2011). On trials when the response is correct this is clear. Positive feedback unambiguously signals that the stimulus belongs to the category associated with the participant’s response. However, on error trials this is not so clear. Negative feedback typically only signals that the stimulus does not belong to the responded category. In the two-category case an inference can be made about the correct category membership of the stimulus, but when there are more than two categories, then no such inference is possible. As a result, exemplar theory also seems to predict no learning on error trials – at least in experiments with more than two categories.

A2. Only the spines on the striatal unit associated with the most active motor unit are eligible for synaptic plasticity

Assumptions A1 and A2 are clearly over-simplifications. However, note that they tend to offset each other – at least to a certain extent. Together they tend to ensure that active synapses on the MSN associated with the incorrect response (call this the incorrect MSN) never change strength. In the absence of these two assumptions, those synapses would get strengthened on trials when the correct MSN controls the response and weakened on trials when the incorrect MSN controls the response. Another interpretation of Assumptions A1 and A2, therefore, is that this strengthening and weakening cancel each other out.

A3. All initial synaptic strengths are negligible – just large enough to allow postsynaptic activation to the first stimulus presentation, but small enough so that mathematically we can assume that w_Ai(0) = w_Bi(0) = 0, for all i

A justification for this assumption is that the presentation of a novel stimulus that has no previous reward association causes DA release (e.g., Horvitz, Stewart, & Jacobs, 1997; Wickelgren, 1997), and increased DA levels potentiate the postsynaptic effects of glutamate (Ashby & Casale, 2003). Thus, available evidence suggests that the first presentation of a stimulus during an experimental session is likely to cause an uncharacteristically large striatal response.

It is also important to note that even without this assumption the contribution of w_Ai(0) and w_Bi(0) to w_Ai(n) and w_Bi(n) decreases as n increases. In other words, the effects of the initial weights on the asymptotic performance of the model are negligible. This is important because the exemplar model is a model of asymptotic performance – it was never proposed as a model of initial learning. So although Assumption A3 is necessary for strict mathematical equivalence, at the practical level this assumption is not critical.

A4. In whichever unit controls the response, [R_J(n) − θ_NMDA]⁺[D(n) − D_base]⁺ = K for all n, where K is a constant

In general, we expect [R_J(n) − θ_NMDA]⁺ to increase with n because the synaptic strength associated with its sensory input should increase as a result of training. In contrast, virtually all current models predict that [D(n) − D_base]⁺ will decrease with n because the rewards become more predictable as training progresses. The evidence is good that DA neurons respond to the reward prediction error (Schultz, 2002; Schultz, Dayan, & Montague, 1997) – defined as the value of the obtained reward minus the value of the predicted reward. Thus, as learning progresses, accuracy rises and so does the ability to predict the feedback valence. As a result, the amount by which DA levels rise following positive feedback should decrease. Thus, an alternative interpretation of assumption A4 is that [R_J(n) − θ_NMDA]⁺ increases with n at the same rate that [D(n) − D_base]⁺ decreases with n.

A5. The noise terms ε_J in Eq. (8) are independent random samples from identical double exponential distributions

A double exponential distribution is required for equivalence because probabilities associated with the maximum of double exponentially distributed random variables satisfy the relative goodness rule of Eq. (1) (Yellott, 1977). In particular, suppose ε₁, ε₂, …, ε_n are a set of independent random variables with identical double exponential distributions. Then (Yellott, 1977)

$$P\left(u_k+{\epsilon }_k=\underset{i=1}{\overset{n}{max}}\{u_i+{\epsilon }_i\}\right)=\frac{{\mathrm{e}}^{u_k}}{{\displaystyle \sum _{i=1}^n}{\mathrm{e}}^{u_i}}.$$ (11)

Equivalence to the Exemplar Model

In this section, we show that the model sketched in Figure 1 makes identical quantitative predictions as the exemplar model described by Eqs. (1), (2), and (3), given the reinforcement-learning model described earlier and under the assumptions outlined in the previous section. To keep the notation simple, we will demonstrate the equivalence for a two-category task, but the equivalence holds for any number of categories.

Consider a two-category task in which category A contains the M_A exemplars C_A = {a₁, a₂, …, aM_A} and category B contains the MB exemplars C_B = {b₁, b₂,…, bM_B}. Note that there are four kinds of trials: correct A response trials, correct B response trials, incorrect A response trials, and incorrect B response trials. By assumption 1, neither type of incorrect response trial will change any synaptic weights. So first consider correct A response trials – that is, trials when the stimulus belongs to the set C_A and motor unit A is more active than motor unit B. By assumption 2, no synaptic strengths on unit B will change. So correct A response trials will only cause changes in the strength of synapses on unit A. Similarly, correct B response trials will only cause changes in the strength of cortical-striatal synapses on unit B.

By assumptions A1 – A4, the reinforcement-learning model described by Eq. (10) predicts that the strength of the synapse between sensory unit k and striatal unit A reduces to

$$w_{Ak}(n_A+1)={\alpha }_{w}K\sum _{i=1}^{n_A}{I}_{k\mid S_i},$$ (12)

where i = 1, …, n_A denotes the first n_A correct A response trials. Suppose that of these n_A trials, stimulus a_i was presented n_aj times (so ${\sum }_{i=1}^{M_A}{n}_{a_i}=n_A$, where MA is the number of exemplars in category A). Note that I_k|Si equals the response of sensory unit k on a trial when stimulus S_i is presented. By Eq. (4) this equation becomes

$$\begin{array}{l}{w}_{Ak}(n_A+1)={\alpha }_{w}K\sum _{i=1}^{n_A}exp(-{\delta }_{k{S}_i}^{\omega }/\gamma )\\ ={\alpha }_{w}K\sum _{j=1}^{M_A}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )\\ ={\alpha }_{w}K\sum _{j\in C_A}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma ).\end{array}$$ (13)

Of course, by identical reasoning, a similar equation will hold for the synapses on striatal unit B.

Now consider the very next trial after all this training. Suppose some stimulus k is presented. Then by Eq. (7) the firing rate in striatal unit A will equal

$$\begin{array}{l}{R}_A=ln[w_{Ak}]\\ =ln\left[{\alpha }_{w}K\sum _{j\in C_A}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )\right].\end{array}$$ (14)

Similarly,

$$R_B=ln\left[{\alpha }_{w}K\sum _{j\in C_B}{n}_{b_j}exp(-{\delta }_{kj}^{\omega }/\gamma )\right].$$ (15)

By Eq. (8), activation in the output units will equal

$$\begin{array}{l}{Y}_A=R_A+ln{\beta }_A+{\epsilon }_A\\ =ln\left[{\alpha }_{w}K\sum _{j\in C_A}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )\right]+ln{\beta }_A+{\epsilon }_A\\ =ln\left[{\alpha }_{w}K{\beta }_A\sum _{j\in C_A}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )\right]+{\epsilon }_A,\end{array}$$ (16)

and

$$Y_B=ln\left[{\alpha }_{w}K{\beta }_B\sum _{j\in C_B}{n}_{b_j}exp(-{\delta }_{kj}^{\omega }/\gamma )\right]+{\epsilon }_B.$$ (17)

Finally, by assumption A5

$$\begin{array}{l}P(\mathrm{A}\mid k)=\frac{{\alpha }_{w}K{\beta }_A{\displaystyle \sum _{j\in C_A}}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )}{{\alpha }_{w}K{\beta }_A{\displaystyle \sum _{j\in C_A}}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )+{\alpha }_{w}K{\beta }_B{\displaystyle \sum _{j\in C_B}}n{b}_{j}exp(-{\delta }_{kj}^{\omega }/\gamma )}\\ =\frac{{\beta }_A{\displaystyle \sum _{j\in C_A}}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )}{{\beta }_A{\displaystyle \sum _{j\in C_A}}{n}_{a_j}exp(-{\delta }_{kj}^{\omega }/\gamma )+{\beta }_B{\displaystyle \sum _{j\in C_B}}{n}_{b_j}exp(-{\delta }_{kj}^{\omega }/\gamma )},\end{array}$$ (18)

which is clearly equivalent to the the exemplar model described by Eqs. (1), (2), and (3), with n_aj = V_jA, n_bj = V_jB, and γ = 1/c.

Effects of Relaxing Assumptions

As is generally always the case, proving exact mathematical equivalence requires strong assumptions. In particular, assumptions A1, A2, and A4 seem biologically unreasonable, and assumption A5 seems arbitrary. A natural question to ask therefore is to what extent equivalence depends on these assumptions. As mentioned earlier, we believe that the most important condition for equivalence is that both models assume that categorization responses are largely determined by weighted sums of radial basis functions of all previously seen exemplars. According to this view, relaxing the ancillary assumptions needed for equivalence might affect the initial learning trajectory of the neural model, but is unlikely to profoundly affect the model’s predictions about asymptotic performance. This section tests that prediction.

To examine the importance of assumptions A1, A2, A4, and A5 we conducted a number of simulations of the neural model in the absence of those assumptions. We call the model that satisfies all assumptions and is mathematically equivalent to exemplar theory the exemplar-equivalent model, and the more biologically realistic version that satisfies all assumptions of the exemplar-equivalent model except assumptions A1, A2, A4, and A5 the biologically-plausible model. Specifically, the biologically-plausible model was essentially identical to the procedural-learning component of the COVIS model described by Ashby et al. (2011). It differs from the exemplar-equivalent model in the following ways:

1. The biologically-plausible model changed synaptic strengths on all trials. So this version of the model was not constrained by assumption A1. The amount of synaptic weakening on error trials was set equal to the amount of synaptic strengthening on correct trials (i.e., β was set equal to α in Eq. 9).

2. All cortical-striatal spines were eligible for synaptic plasticity on every trial. In particular, synaptic strengths on both MSNs were modified on every trial. So this version was not constrained by assumption A2.

3. No assumptions were made about the relationship between the striatal and DA responses. So this version was not constrained by assumption A4. In particular, DA release was set to the same piecewise linear function of reward prediction error as in Eqs. 11 – 13 of Ashby et al. (2011).

4. In the exemplar-equivalent model, double-exponentially distributed noise was added to the activations of the premotor units. In the biologicaly-plausible model, no noise was added to the premotor units and normally distributed noise was added to the MSN activations.

Our general goal was to compare asymptotic performance of the exemplar-equivalent and biologically-plausible models, and if these differed, to ask whether the altered structure of the biologically-plausible model was consistent or inconsistent with the predictions of exemplar theory. To begin, it was important to set parameter values in the exemplar-equivalent model to values that are typical of previous applications of exemplar theory. To satisfy this constraint, we did a crude search to find parameter values that allowed the exemplar-equivalent model to reproduce the 16 × 2 confusion matrices predicted by the GCM in the Dimensional, Criss-Cross, Interior-Exterior, and Diagonal transfer conditions reported by Nosofsky (1986)⁴.

The critical question now is how much these predictions will change when we switch to the biologically more plausible version of the model. It turns out that the predictions change only a small amount. The r² between the predictions of the exemplar-equivalent and biologically-plausible models was .999, .998, .981, and .955, for the Dimensional, Criss-Cross, Interior-Exterior, and Diagonal conditions respectively. Thus, the only condition where the predictions changed by a non-negligible amount was the Diagonal condition. There are two possibilities here. Either the biologically-plausible model fundamentally changed the structure of the data in a way this is incompatible with the exemplar model, or it changed the predictions in a way that is consistent with exemplar theory but best accounted for by some slight change in one or more parameter values. To answer this question, we fit the GCM to the confusion matrices predicted by the biologically-plausible model. If the biologically-plausible model changed the structure of the data in a way that is incompatible with exemplar theory, then the GCM will fit poorly. In fact, the GCM provided excellent fits in all four conditions. The r² between the predictions of the biologically-plausible model and the GCM was .999, .999, .981, and .990, for the Dimensional, Criss-Cross, Interior-Exterior, and Diagonal conditions, respectively.

In summary, although exact mathematical equivalence requires all assumptions described above, assumptions A1, A2, A4, and A5 have little numerical effect on the asymptotic predictions of the model.

Discussion

The neural model described in this article makes very different psychological assumptions than are usually associated with exemplar theory, yet it is mathematically equivalent to the exemplar model. The cognitive version of exemplar theory assumes people retrieve memory representations of previously seen exemplars and that they compare the presented stimulus to these stored memories. Every new stimulus creates a new memory representation. In contrast, the neural version assumes that no memory representations are retrieved. For example, the neural model assumes that stimulus presentation always activates two striatal MSNs (in two-category tasks), regardless of the number of exemplars in each category and regardless of the number of training trials. Instead of adding a new exemplar memory representation, the neural version of exemplar theory assumes that presentation of a new stimulus either modifies the strength of an existing cortical-striatal synapse or creates a new synapse (e.g., by adding a new spine to an existing MSN). Thus, the exemplar representation in the neural version of exemplar theory is either the strength of a cortical-striatal synapse or perhaps it could be interpreted as a dedicated spine on an MSN. The more important point however, is that stimulation of that MSN (or that dendritic spine) would not retrieve an exemplar memory, but rather create an urge to respond either A or B, and in this sense the neural version makes different psychological assumptions than classical accounts of exemplar theory⁵.

Mathematical equivalence to the (GCM) exemplar model requires a number of strong assumptions that in some cases are biologically implausible. Even so, we showed via simulation that these assumptions have little effect on the asymptotic predictions of the model. Thus, the neural model described here mimics the numerical predictions of exemplar theory when the biologically implausible assumptions are replaced by assumptions that are more biologically realistic. We believe that the predictions of the neural model are robust with respect to violations of these ancillary assumptions because in both models the probability that a stimulus is assigned to a particular category increases with the weighted sum of radial basis functions activated by all previously seen exemplars from that category. The ancillary assumptions do not change this fundamental property of the neural model, and since this same property is shared by exemplar theory, the two psychologically different models make similar (or even identical) quantitative predictions.

Because the two models make identical or nearly identical quantitative predictions, any previous evidence in favor of the exemplar model that is based on its success in providing good quantitative fits to categorization data is also evidence in favor of the neural model. But in addition, the neural model is able to account for many empirical phenomena that are either incompatible with or outside the scope of the cognitive version of exemplar theory. This includes all the problematic data reviewed earlier in this article.

First, because the neural model assumes that the critical site of category learning is at cortical-striatal synapses, it easily accounts for the many reports that patients with striatal dysfunction are impaired in category learning. Second, for the same reason, it accounts for the common fMRI finding of categorization-related activation in the striatum (Lopez-Paniagua & Seger, 2011; Nomura et al., 2007; Poldrack et al., 2001; Seger & Cincotta, 2002, 2005; Seger et al., 2010; Waldschmidt & Ashby, 2011). Third, it accounts for the many empirical dissociations that have been reported between RB and II categorization tasks. For example, it accounts for the sensitivity of II category learning to feedback delays because of the known sensitivity of cortical-striatal plasticity to delays between DA release and activity at cortical-striatal synapses (Valentin, Maddox, & Ashby, 2014; Yagishita et al., 2014). It also accounts for the interference that occurs in II and unstructured categorization performance when the location of the response buttons is switched – because the terminal nodes in the Figure 1 model are in premotor cortex, rather than prefrontal cortex. Fourth, it accounts for deficits by patients with Parkinson’s disease in II and unstructured category learning (Hélie, Paul, & Ashby, 2012).

If more anatomical details are added into the model of the striatum (as in Ashby & Crossley, 2011; Cantwell, Crossley, & Ashby, 2015; Crossley, Ashby, & Maddox, 2013), then the neural version of exemplar theory can also account for a wide variety of other phenomena including i) single-unit recordings from MSNs and TANs during instrumental conditioning (Ashby & Crossley, 2011); ii) many behavioral phenomena from instrumental conditioning experiments, including fast reacquisition after extinction, the partial reinforcement extinction effect, spontaneous recovery, and renewal (Crossley, Horvitz, Balsam, & Ashby, 2016); iii) the result that recovery from a full reversal is quicker than learning new categories constructed from the same stimuli (Cantwell et al., 2015); and iv) unlearning and failures of unlearning (e.g., renewal) during II categorization (Crossley et al., 2013; Crossley, Ashby, & Maddox, 2014).

David Marr (1982) famously described three levels of mathematical modeling, which he referred to as computational, algorithmic, and implementational. Computational models (often called descriptive models in psychology) make quantitative predictions, but do not describe the algorithms that produce those predictions. Algorithmic models (often called process models in psychology) describe the algorithms, but not the architecture that implements those algorithms. At the lowest level, implementational models describe the architecture that implements the algorithms that produce the quantitative predictions. The original versions of exemplar theory – for example, the version described by Eqs. (1), (2), and (3) – were computational-level descriptions of asymptotic categorization behavior (i.e., the theory made no attempt to account for learning). Cognitive process was used to motivate the quantitative predictions, but no attempt was made to model those processes. To see this, note for example, that Eq. (1) makes no predictions about what response a participant will make on any single trial of a categorization experiment. Rather it simply describes the relative proportion of times the participant will give every possible response under the ideal conditions in which the same categorization trial is repeated an infinite number of times.

As one moves down Marr’s hierarchy, it is generally true that more than one interpretation is possible. For example, we know of three different algorithmic-level versions of exemplar theory (Kruschke, 1992; Lamberts, 2000; Nosofsky & Palmeri, 1997), which all make slightly different assumptions. The neural model proposed here is the first known implementational-level version, and it shows that some qualitatively different psychological assumptions are compatible with the quantitative predictions of computational-level versions of exemplar theory. One of the main reasons for developing lower-level versions of any theory is to account for more data. The algorithmic-level versions of exemplar theory can account for response time and learning data that are outside the scope of the computational-level version. And the neural version proposed here can account for many phenomena that are outside the scope of the algorithmic-level versions. Although many other neural versions may be theoretically possible, the many extra constraints provided by all these neuroscience-related phenomena would seem to narrow the set of candidate neural interpretations to a model that assigns a major role to the striatum. If so, then any alternative neural interpretation that is also consistent with the available neuroscience-related data should look qualitatively similar to the version proposed here (e.g., since both models would be constrained by the same basal ganglia neuroanatomy).

The neural version of exemplar theory is essentially a simplified version of the procedural-learning component of the COVIS model of category learning⁶ (Ashby & Crossley, 2011; Ashby et al., 2007; Cantwell et al., 2015). The COVIS model includes much more biological detail (e.g., spiking MSNs, striatal cholinergic interneurons), other brain areas (e.g., interlaminar thalamic nuclei), a more sophisticated reinforcement-learning model (e.g., with rate-limiting terms that constrain synaptic strengths to a fixed interval [0, w_max]), and it does not make any of assumptions A1 – A5. Even so, it is important to note that the equivalence established here greatly benefits both theories. Of course it provides exemplar theory access to a huge range of neuroscience-related phenomena that generally are outside the scope of any purely cognitive theory. But it also greatly benefits COVIS. First, it means that successes of the exemplar model in providing good quantitative fits to categorization data imply that COVIS should be equally successful at accounting for those data. Second, it provides a method to quickly fit COVIS to asymptotic response proportions collected in the course of a categorization experiment. Fitting the COVIS model currently requires time-consuming Monte Carlo simulations and therefore, exploring its predictions is a challenging computational process. In contrast, the exemplar model is simple enough that it can quickly be fit to data in a straightforward manner using standard optimization algorithms. Therefore, because of the equivalence established here, asymptotic behavioral predictions of COVIS can be quickly tested by fitting the exemplar model to the empirical confusion matrices.

Finally, this article makes one more equally important contribution. The equivalence of exemplar theory and the procedural-learning component of COVIS means that it is probably fruitless to attempt to test between these two models by comparing goodness-of-fits in any categorization experiment. Instead, the two historically disparate approaches to categorization modeling should be used together to create a more powerful armamentarium that can be used to improve our overall understanding of categorization behavior.