Bayesian adaptive design for targeted therapy development in lung cancer – a step toward personalized medicine

Abstract

Background

With the advancement in biomedicine, many biologically targeted therapies have been developed. These targeted agents, however, may not work for everyone. Biomarker profiles can be used to identify effective targeted therapies. Our goals are to characterize the molecular signature of individual tumors, offer the best-fit targeted therapies to patients in a study, and identify promising agents for future development.

Methods

We propose an outcome-based adaptive randomization trial design for patients with advanced stage non-small cell lung cancer. All patients have baseline biopsy samples taken for biomarker assessment prior to randomization to treatments. The primary endpoint of this study is the disease control rate at 8 weeks after randomization. The Bayesian probit model is used to characterize the disease control rate. Patients are adaptively randomized to one of four treatments with the randomization rate based on the updated disease control rate from the accumulated data in the trial. For each biomarker profile, high-performing treatments have higher randomization rates, and vice versa. An early stopping rule is implemented to suspend low-performing treatments from randomization.

Results

Based on extensive simulation studies, with a total of 200 evaluable patients, our trial has desirable operating characteristics to: (1) identify effective agents with a high probability; (2) suspend ineffective agents; and (3) treat more patients with effective agents that correspond to their biomarker profiles. Our trial design continues to update and refine the estimates as the trial progresses.

Limitations

This biomarker-based trial requires biopsible tumors and a two-week turn around time for biomarker profiling before randomization. Additionally, in order to learn from the interim data and adjust the randomization rate accordingly, the outcome-based adaptive randomization design is applicable only for trials when the endpoint can be assessed in a relative short period of time.

Conclusion

Bayesian adaptive randomization trial design is a smart, novel, and ethical design. In conjunction with an early stopping rule, it can be used to efficiently identify effective agents, eliminate ineffective ones, and match effective treatments with patients’ biomarker profiles. The proposed design is suitable for the development of targeted therapies and provides a rational design for personalized medicine.

Introduction

In recent years, the use of adaptive design methods based on interim observed data from on-going trials has become popular in clinical development due to their flexibility in the trial conduct. The outcome-based adaptive randomization (AR) design can be used to adjust the treatment assignment probabilities according to the performance of each treatment during the trial. As the trial progresses, more patients can be treated with more promising regimens based on the updated data. Several AR designs have been reported under names such as ‘play the winner,’ ‘biased coin,’ and ‘urn design.’ By incorporating early stopping rules for efficacy and/or futility, AR designs can be more efficient in selecting effective treatments or eliminating ineffective ones. The resulting designs are also more ethical because more patients are treated with effective treatments [1,2]. The use of AR designs in clinical trials can be found in many articles and books [3–8].

AR was first developed in the frequentist’s context, but has recently been expanded to the Bayesian framework. The Bayesian approach provides a natural way to incorporate prior information to the available data to form current knowledge. Furthermore, the Bayesian design allows for continuous updating and improving of the model estimates based on cumulative data observed over time. The Bayesian design is more flexible in trial conduct because even when the trial deviates from the original design, the inference remains unchanged because Bayesian inference is based on the data likelihood and not constrained to a preset, fixed design. Excellent introduction to the Bayesian clinical trial methods including Bayesian AR can be found in recent literature [9–16].

In this article, we design a clinical trial by using an AR design with an underlying hierarchical Bayes model to provide estimations for the treatment effect and the covariate effect. In many randomized designs, the baseline covariate is considered as prognostic (i.e., a covariate can impact the outcome but the effect is constant across all treatments) [17–19]. However, our AR design allows the covariate effect to be predictive (i.e., the effect of covariate on treatment outcome may vary with specific treatment). It offers an alternative to model all the treatment by covariate interactions when the covariate is predictive. The predictive model setting is consistent with the current knowledge of targeted agent development [20–22]. Furthermore, the addition of the hierarchical Bayes structure in the AR model allows ‘borrowing strength’, or information-sharing across patients receiving the same treatment but with different covariate profiles. Specifically, the information obtained in one subset of patients provides indirect information for patients with similar characteristics. When subsets of patients behave similarly, more information is shared. Conversely, when subgroups behave differently, less information is shared. Major goals for our trial design are: (1) to characterize the molecular signature of each tumor, (2) to offer the best-fit targeted therapy to patients in the trial, and (3) to identify promising targeted agents and their corresponding predictive signatures for future development. An overview of our clinical trial is given in Section Biomarker-integrated approaches of targeted therapy of lung cancer elimination (BATTLE), while the details of the hierarchical Bayes model are described in Section Hierarchical probit model. In Section AR and decision results the AR and decision rules of our trial design are specified. The operating characteristics of our trial design, illustrated by different scenarios of simulation studies are presented and compared in Section Simulation results, with a discussion in Section Discussion.

Biomarker-integrated approaches of targeted therapy of lung cancer elimination (BATTLE)

With the advancement of molecular biology and genomic research, many target-based agents that offer mechanism-based therapy have been developed in the past decade [23–26]. Because targeted agents are developed to address specific disease-causing defects, they offer hope for increasing treatment efficacy while reducing toxicity. Many targeted agents, however, do not work in all patients. The challenge of trial design is to screen for effective drugs and identify which patient groups will or will not benefit from the drugs. We use the BATTLE project, a phase II design in patients with advanced non-small cell lung cancer (NSCLC), to illustrate our trial design methodology.

The BATTLE project consists of one umbrella trial and four parallel phase II studies with biomarker-based targeted therapies in patients with advanced NSCLC previously treated with chemotherapy but subsequently failed. The four targeted therapies are erlotinib (Treatment 1), sorafenib (Treatment 2), vandetanib (Treatment 3), and the combination of erlotinib and bexarotene (Treatment 4). It is assumed that each treatment may be more efficacious in patients with a certain biomarker profile matching the agent’s mechanism of action. Therefore, the goal of this project is to establish a clinical trial prototype towards the development of targeted therapy that tests the efficacy of molecular targeted agents in advanced NSCLC patients by utilizing their biomarker profiles.

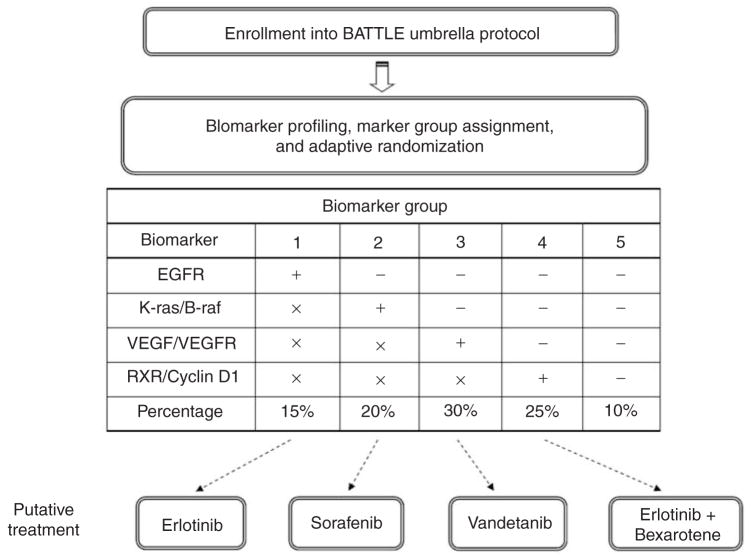
A total of 200 evaluable patients are expected to be enrolled into the study. All eligible patients will be required to have baseline core biopsy samples taken for biomarker profile assessment before randomization. Four types of biomarker classes (EGFR mutation/amplification, K-ras and/or B-raf mutation, VEGF and/or VEGFR expression, and RXR and/or cyclin D1 expression) will be assessed. Each patient will be assigned to one of the five marker groups (MGs) based on his or her profile. The priority of the marker group assignments and the associated distributions are shown in Figure 1. For example, if a patient has an EGFR mutation, he or she will be assigned to MG 1 regardless of the status of other biomarkers. Otherwise, a patient will be assigned to MG 2 if there is a K-ras and/or B-raf mutation. Similarly, MG 3 patients will have a positive VEGF and/or VEGFR expression, and MG 4 patients will have a positive RXR and/or cyclin D1 expression. Patients will be assigned to MG 1 through MG 4 in a sequential order. If none of the biomarkers are positive, the patient will be assigned to MG 5. The formation of the five biomarker groups reduces the total number of all possible biomarker combinations (2⁴ = 16). Based on our preliminary data, it is estimated that 15, 20, 30, 25, and 10 percent patients will belong to MGs 1, 2, 3, 4, and 5, respectively. The order of the assignment was derived based on the strength of the predictive markers evidence with respect to the corresponding treatments. Given four treatments and five marker groups, there are 20 treatment by marker subgroups – a substantial reduction from 64 all possible combinations.

Figure 1.

Schematic diagram of the flow of the BATTLE trial. All eligible patients will be enrolled in the Umbrella protocol first. Tissue biopsy will be taken for biomarker profiling. According to the characteristics of the four biomarker categories, patients will be assigned to the biomarker group 1 to 5 in a sequential order. The symbols ‘+’, ‘−’, and ‘x’ correspond to the positive, negative, and either positive or negative biomarker status, respectively. Patients will be adaptively randomized to one of the four treatments according to their biomarker groups. The dashed arrow indicates the putative effective treatment for each of the biomarker groups

Prior studies in this advanced, chemotherapy-treated NSCLC patient population have demonstrated the median time to progression of 2 to 3 months [27,28]. Hence, we consider a treatment successful if a patient reaches disease control status (i.e., progression-free) at 8 weeks. The 8-week disease control rate has been shown to be a good predictor for clinical benefit including survival in patients with advanced NSCLC [29]. The main objective of this study is to estimate and test the disease control rate for each treatment given patients’ tumor biomarker profiles. The primary endpoint is the 8-week disease control rate, which is defined as the fraction of patients who show no sign of objective disease progression at 8 weeks after randomization. The null and target disease control rates are set at 0.3 and 0.5, respectively.

Hierarchical probit model

The Bayesian probit model [30] is used to characterize the disease control rate for each treatment by marker subgroup. A probit model is a popular specification of a generalized linear model using the probit link function to model categorical or ordinal data. A latent continuous variable is introduced to model the relationship between response data and covariates. Let j and k denote the treatment and marker group, respectively. There are a total of four treatments and five marker groups. Let i be the index for the patient, from 1 to n_jk, where, n_jk is the total number of patients in the combination of treatment j and marker group k. Let, y_ijk be the random variable of disease control (progression-free at 8 weeks). It takes the value of 0 if patients experience progression or die within 8 weeks of the treatment. Otherwise, it equals to 1. A latent continuous variable z_ijk is introduced to model the disease control rate. Let

$$y_{\mathit{ijk}}=\{\begin{array}{ccc}0& \text{if}& z_{\mathit{ijk}}\le 0\\ 1& \text{if}& z_{\mathit{ijk}}>0\end{array}$$ (1)

The disease control rate for treatment j, MG k, is the probability that the latent variable is greater than 0, defined as γ_jk = P(y_ijk = 1) = P(z_ijk > 0). For each subgroup, we assume that z_ijk follows a normal distribution with a location parameter μ_jk. Note that because only the sign of z_ijk matters for determining y_ijk, the model can be identified up to a multiplicative constant on z_ijk. For the purpose of identifiability, we set the variance of z_ijk as 1 [31]. For a given marker group, a normally distributed hyper prior N(ϕ_j, σ²) is imposed on the location parameters μ_jk of the latent variable. The parameter ϕ_j is also normally distributed with mean 0 and variance τ², which allows for the exchange of information across different treatments. This hierarchical model setting allows borrowing information across different marker groups (k) within a treatment (j).

$$\begin{array}{ll}\hfill z_{\mathit{ijk}}& ~N({\mu }_{jk},1),\text{for}i=1,\dots ,n_{jk}\hfill \\ \hfill {\mu }_{jk}& ~N({\varphi }_j,{\sigma }^2),\text{for}k=1,\dots ,5\hfill \\ \hfill {\varphi }_j& ~N(0,{\tau }^2),\text{for}j=1,\dots ,4\hfill \end{array}$$ (2)

The parameters σ² and τ² control the extent of the borrowing across marker groups within each treatment and across all treatments, respectively. Our default configuration is to use the vague prior with σ² = 10⁶ and τ² = 10⁶. The details for computing the posterior distributions via Gibbs sampling from the full conditional distributions are given in the Appendix.

AR and decision rules

An outcome-based AR scheme is proposed for the BATTLE project. Because patients with distinct biomarker statuses may respond differently to different treatments, the biomarker status must be taken into consideration when assigning patients into various treatments. For example, if patients with EGFR mutation are more likely to respond to erlotinib than other treatments, it is desirable to assign more these types of patients to erlotinib. Because the true disease control rate for each of the treatment by marker combinations is unknown when the trial begins, ER is applied in the first part of the trial until at least one patient is enrolled in each subgroup with a known disease control status. Then, patients are adaptively randomized thereafter. Bayesian adaptive design can help to refine the estimation and randomize the patients accordingly as the trial progresses. Under the Bayesian probit model described above, all data are used in computing the posterior disease control rate and thus in determining the randomization ratio. The model gains efficiency by combining the data from all subgroups.

The randomization rate is computed based on the estimated posterior mean of the disease control rate of each treatment in each marker group. To ensure a certain minimal probability of randomization for each nonsuspended treatment, if the estimated disease control rate is < 10%, 10% is used in calculating the randomization ratio. AR will be carried out until the last patient is enrolled, unless the trial is stopped early because all four treatments are suspended due to futility. The randomization ratio for a patient in MG k to receive treatment j is proportional to the estimated mean disease control rate in MG k with treatment j. This is mathematically defined as:

$${\widehat{\gamma }}_{jk}/\sum _{\omega \in \mathrm{\Omega }}{\widehat{\gamma }}_{\omega k},$$ (3)

where γ̂ corresponds to the posterior mean of the disease control rate and Ω indicates the subset of all eligible and nonsuspended treatments for that patient at the time of randomization. For example, let us assume that the next patient to be randomized is in MG 1. If the current estimated disease control rates of treatments 1, 2, 3, and 4 in MG 1 are 0.6, 0.3, 0.2, and 0.1, the randomization rates to treatments 1, 2, 3, and 4 are 0.50, 0.25, 0.17, and 0.08, respectively.

An early stopping rule can be added to our trial design. If the current data shows that a treatment is unlikely to be beneficial to patients with certain biomarker profiles, randomization to that treatment is suspended. Specifically, denote the target disease control rate by θ₁ and the critical probability for early stopping, i.e., suspension of randomization due to futility by δ_L. Recall that the estimated disease control rate of the jth treatment for the kth marker group is Pr [z_ijk>0|Data]. Therefore, the trial will be suspended for the j^th treatment and k^th marker group if the chance that the estimated disease control rate greater than θ₁ is less than or equal to δ_L, i.e., :

$$Pr(Pr[z_{\mathit{ijk}}>0\mid \text{Data}]>{\theta }_1)\le {\delta }_L.$$ (4)

We choose 0.5 and 0.1 for θ₁ and δ_L, respectively, so that if given the current data, there is less than a 10% chance that the disease control rate in this treatment by marker subgroup is greater than 0.5, the treatment is suspended for this subgroup. The stopping rule will be applied after AR begins. Note that the early stopping criterion will be updated when each new outcome is observed. The suspension of a treatment in a certain marker group is only temporary and is reversible. If the updated data shows that the early stopping (suspension) criterion no longer holds, the treatment can be reopened to patients in that marker group.

Let θ₀ and δ_U be the disease control rate for standard treatment and the critical probability for declaring an effective treatment, respectively. The treatment will be considered a success at the end of a trial if the probability that the estimated disease control rate is equal to or greater than θ₀ is at least δ_U, i.e.,

$$Pr(Pr[z_{\mathit{ijk}}>0\mid \text{Data}]>{\theta }_0)\ge {\delta }_U.$$ (5)

In this study, we set θ₀ and δ_U at 0.3 and 0.8, respectively, which means that if the probability of a disease control rate greater than 0.3 is 80% or higher, the treatment will be declared effective for this treatment by marker subgroup. Please note that our trial design has no early stopping rule for effective treatments. If a treatment shows early signs of efficacy, patients will continue to be enrolled under the AR scheme and the declaration of efficacy will occur at the end of the trial. The above design parameters were chosen via extensive simulation studies to ensure that the design possessed desirable operating characteristics (shown in Section Simulation results).

Simulation results

We evaluate the operating characteristics of our trial design under various scenarios through simulations. In this phase II trial with five marker groups, four treatments, and a limited sample size of 200 evaluable patients, our target is to achieve a 20% false positive rate (i.e., claiming the non-effective treatment effective, which corresponds to the frequentist’s type I error rate), and an 80% power (i.e., claiming the effective treatment effective). A higher false positive rate is allowed so that we will not miss any potentially effective treatments. Once effective treatments are identified, they will be confirmed by larger studies in the future.

We conducted simulations with 1000 runs for each scenario. We assumed that for MG 1, the true DCR for Treatment 1 was 80%, but only 30% for all other treatments. We assumed that for MG 2, the true DCR for Treatment 2 was 60%, with 30% for all other treatments. Similarly, MG 3 and MG 4 had only one effective treatment, but there was no effective treatment in MG 5. In Scenario 1, both equal randomization (ER) and AR were studied without an early stopping rule. Scenario 2 depicted the same situation as Scenario 1, but applying an early stopping rule. Vague priors with σ² = τ² = 10⁶ were used in Scenarios 1 and 2. The effect of prior specification with varying treatment effect was examined in Scenario 3. We also studied the null case when the disease control rate was 0.30 for all subgroups and verified that the false positive rate were all under 20% (between 15% and 19%, data not shown).

Scenario 1: one effective treatment for MGs 1– 4, no effective treatment for MG 5; with no early stopping rule; and with vague priors

Table 1 shows the simulation results for Scenario 1 with both ER and AR. The top section of the table gives the observed mean and the model-based posterior mean of disease control rates. Under ER, the true disease control rates could be estimated unbiasedly. In this case, the observed rates were exactly the same as the true rates, i.e., the disease control rates for Treatments 1–4 were 0.8, 0.3, 0.3, 0.3 in MG 1; 0.3, 0.6, 0.3, 0.3 in MG 2; 0.3, 0.3, 0.6, 0.3 in MG 3; 0.3, 0.3, 0.3, 0.6 in MG 4; and 0.3, 0.3, 0.3, 0.3 in MG 5, respectively. The model-based posterior disease control rates also provided accurate estimates of the true rates. Conversely, with AR, the observed and the model-based rates were slightly lower than the corresponding true rates. This finding agrees with a well known result that AR causes bias in estimating the true parameters [5,6]. As expected, the average sample sizes for the four treatments were approximately the same within a given marker group when ER was applied. ER lacks the flexibility to allocate more patients into more effective treatments even when there is clear evidence that some treatments outperform the others. Conversely, after the initial ER phase, AR allocated patients into treatments based on the model-based disease control rates. As a result, of the 30.6 patients in MG 1, 11.0 (35.9%) were randomized to Treatment 1 but only 6.7 (21.9%), 6.3 (20.6%), and 6.6 (21.6%) were randomized to Treatments 2 through 4, respectively. The results showed that larger proportions of patients were randomized into more effective treatments for MGs 1–4 under AR. For MG 5, there was no allocation preference because none of the treatments were effective. The total numbers of patients reaching disease control status were 76.3 (38.2% of 200 randomized patients) using ER and 80.9 (40.5%) using AR. The results show that more patients reached disease control status with the AR design.

Table 1.

Operating characteristics for Scenario 1 with both equal randomization and adaptive randomization: one effective treatment for marker groups 1–4; no effective treatment for marker group 5; with no early stopping rule; and with vague priors

Marker group
Treatment	1	2	3	4	5
	ER | AR1	ER | AR	ER | AR	ER | AR	ER | AR
Disease control rate {1/2}2
1	0.80/0.79 | 0.78/0.78	0.30/0.31 | 0.26/0.27	0.30/0.31 | 0.28/0.29	0.30/0.31 | 0.26/0.27	0.30/0.31 | 0.24/0.25
2	0.30/0.31 | 0.27/0.28	0.60/0.60 | 0.57/0.56	0.30/0.30 | 0.28/0.29	0.30/0.31 | 0.28/0.29	0.30/0.31 | 0.25/0.27
3	0.30/0.31 | 0.25/0.26	0.30/0.31 | 0.27/0.28	0.60/0.60 | 0.59/0.58	0.30/0.31 | 0.27/0.28	0.30/0.31 | 0.25/0.26
4	0.30/0.31 | 0.27/0.28	0.30/0.31 | 0.27/0.28	0.30/0.31 | 0.28/0.29	0.60/0.60 | 0.58/0.58	0.30/0.31 | 0.25/0.26
Average sample size (column percentage)
1	7.6 (25.0) | 11.0 (35.9)	10.1 (25.0) | 9.1 (22.3)	15.2 (25.0) | 13.4 (22.0)	12.7 (25.0) | 11.2 (22.1)	5.1 (25.0) | 5.1 (25.2)
2	7.6 (25.0) | 6.7 (21.9)	10.1 (25.0) | 13.2 (32.4)	15.2 (25.0) | 13.5 (22.2)	12.7 (25.0) | 11.4 (22.5)	5.1 (25.0) | 5.0 (24.8)
3	7.6 (25.0) | 6.3 (20.6)	10.1 (25.0) | 9.2 (22.5)	15.2 (25.0) | 20.2 (33.2)	12.7 (25.0) | 11.4 (22.5)	5.1 (25.0) | 5.0 (24.8)
4	7.6 (25.0) | 6.6 (21.6)	10.1 (25.0) | 9.2 (22.5)	15.2 (25.0) | 13.7 (22.5)	12.7 (25.0) | 16.6 (32.8)	5.1 (25.0) | 5.1 (25.2)
Total	30.5 | 30.6	40.5 | 40.8	60.9 | 60.8	50.8 | 50.6	20.3 | 20.2
Probability of declaring effective treatment
1	0.96 | 0.97	0.20 | 0.16	0.20 | 0.17	0.19 | 0.16	0.19 | 0.16
2	0.19 | 0.18	0.85 | 0.85	0.20 | 0.17	0.20 | 0.16	0.19 | 0.16
3	0.20 | 0.15	0.19 | 0.17	0.93 | 0.94	0.20 | 0.17	0.20 | 0.16
4	0.19 | 0.18	0.19 | 0.18	0.19 | 0.17	0.90 | 0.88	0.19 | 0.16

¹ER: equal randomization; AR: adaptive randomization.

²For disease control rate, 1/2 indicate the observed disease control rate (1) and the model-based posterior mean of the disease control rate (2).

The probability of declaring an effective treatment for each biomarker group was also explored. This probability was at least 85% for effective treatments but 20% or less for ineffective treatments. The highest probabilities of declaring an effective treatment were 0.96 for ER and 0.97 for AR in patients with MG 1 and assigned to Treatment 1. Higher statistical power could be found in effective treatment by marker subgroups. The probability of declaring an effective treatment was about the same between the ER and AR designs when the treatment was effective. However, when the treatments were not efficacious, the probabilities of declaring an effective treatment were lower for AR (between 15% to 18%) than those for ER (between 19% to 20%).

Scenario 2: One effective treatment for MGs 1–4, no effective treatment for MG 5; with an early stopping rule; and with vague priors

The operating characteristics for the ER and AR designs when applying an early stopping rule (i.e., suspending inefficacious treatments from randomization) were shown in Table 2. Compared with the results in Scenario 1, the observed disease control rates for ER were no longer unbiased when an early stopping rule was implemented. For both ER and AR, the observed and model-based disease control rates under estimated the true rates. The bias for the model-based posterior mean estimates were smaller than that of the observed mean estimates. The standard errors for the posterior mean estimates ranged from 0.15 to 0.26 for the AR design.

Table 2.

Operating characteristics for scenario 2 with both equal randomization and adaptive randomization: one effective treatment for marker groups 1–4; no effective treatment for marker group 5; with early stopping rule; and with vague priors

Marker group
Treatment	1	2	3	4	5
	ER | AR1	ER | AR	ER | AR	ER | AR	ER | AR
Disease control rate {1/2}2
1	0.76/0.76 | 0.77/0.77	0.24/0.27 | 0.22/0.26	0.24/0.27 | 0.24/0.27	0.24/0.28 | 0.22/0.25	0.21/0.26 | 0.20/0.24
2	0.22/0.26 | 0.21/0.24	0.55/0.57 | 0.54/0.56	0.24/0.27 | 0.24/0.27	0.24/0.27 | 0.24/0.27	0.20/0.25 | 0.18/0.22
3	0.22/0.25 | 0.22/0.26	0.23/0.27 | 0.22/0.25	0.57/0.58 | 0.57/0.58	0.23/0.26 | 0.23/0.26	0.20/0.25 | 0.19/0.24
4	0.23/0.27 | 0.22/0.25	0.23/0.26 | 0.23/0.26	0.25/0.28 | 0.24/0.27	0.56/0.57 | 0.55/0.56	0.19/0.24 | 0.19/0.24
Average sample size (column percentage)
1	11.4 (38.1) | 13.0 (43.2)	8.2 (20.4) | 7.6 (19.1)	11.3 (18.9) | 10.8 (17.9)	10.0 (19.9) | 9.0 (18.1)	4.7 (23.7) | 4.6 (22.9)
2	6.0 (20.1) | 5.4 (17.9)	14.8 (36.9) | 15.4 (38.8)	11.3 (18.9) | 11.1 (18.4)	9.8 (19.5) | 9.3 (18.7)	4.5 (22.7) | 4.3 (21.4)
3	6.0 (20.1) | 5.7 (18.9)	8.1 (20.2) | 7.7 (19.4)	24.4 (40.7) | 25.9 (43.0)	9.6 (19.1) | 9.3 (18.7)	4.5 (22.7) | 4.4 (21.9)
4	6.2 (20.7) | 5.7 (18.9)	7.9 (19.7) | 7.6 (19.1)	11.5 (19.2) | 10.9 (18.1)	19.5 (38.8) | 20.7 (41.6)	4.3 (21.7) | 4.5 (22.4)
None	0.2 (0.7) | 0.3 (1.0)	1.1 (2.7) | 1.4 (3.5)	1.5 (2.5) | 1 .7 (2.8)	1.3 (2.6) | 1.5 (3.0)	1.8 (9.1) | 2.2 (10.9)
Total	29.9 | 30.1	40.1 | 39.7	59.9 | 60.3	50.2 | 49.8	19.8 | 20.1
Prob(A)/Prob(B)3
1	0.94/0.05 | 0.95/0.04	0.19/0.55 | 0.14/0.56	0.14/0.61 | 0.14/0.63	0.15/0.58 | 0.12/0.61	0.17/0.53 | 0.14/0.57
2	0.15/0.54 | 0.13/0.56	0.83/0.11 | 0.82/0.12	0.14/0.61 | 0.14/0.61	0.15/0.59 | 0.14/0.58	0.15/0.55 | 0.14/0.61
3	0.15/0.56 | 0.17/0.54	0.16/0.56 | 0.15/0.58	0.89/0.07 | 0.90/0.07	0.14/0.61 | 0.14/0.60	0.17/0.57 | 0.13/0.57
4	0.17/0.52 | 0.14/0.53	0.15/0.57 | 0.14/0.56	0.15/0.62 | 0.14/0.62	0.87/0.09 | 0.86/0.09	0.14/0.58 | 0.15/0.57

¹ER: equal randomization; AR: adaptive randomization.

²For disease control rate, 1/2 indicate the observed disease control rate (1) and the model-based posterior mean of the disease control rate (2).

³Prob(A)/Prob(B) correpond to probability of declaring an effective treatment/probability of suspending an ineffective treatment, respectively.

When an early stopping rule was applied to ER, the average sample size was larger for effective treatments and smaller for ineffective treatments. For example, for patients in MG 1, the average sample size for Treatment 1 was 11.4 but was only about 6 for Treatments 2, 3, and 4. Similarly, more patients were randomized into effective treatments in MGs 2, 3, and 4. This was a result of suspending ineffective treatments early. For AR, applying an early stopping rule provided further improvement on randomizing more patients into effective treatments. Comparing Scenario 1 versus Scenario 2, the percentage of patients receiving effective treatments increased from 35.9% to 43.2% for MG 1, 32.4% to 38.8% for MG 2, 33.2% to 43.0% for MG 3, and 32.8% to 41.6% for MG 4. The percentage of patients receiving effective treatments were also higher in AR compared to ER when an early stopping rule was applied. For patients in MG 5, since there were no effective treatments, percentages of patients randomizing into Treatments 1–4 were about the same for both ER and AR.

The additional row of ‘None’ indicates the average number of patients who were not randomized due to lack of efficacy in all treatments. In MGs 1–4, less than 4% of the patients were in the ‘None’ category because there was one effective treatment in each MG. However, for MG 5, 9.1% and 10.9% of the patients using ER and AR were not randomized due to no effective treatments for this marker group. These patients might receive other treatments off protocol.

The probabilities of declaring effective treatments were comparable between ER and AR. When the treatment was efficacious, the lowest power was 83% for ER and 82% for AR (in Treatment 2, MG 2). The probabilities of identifying effective treatments were slightly lower with an early stopping rule than without it, but were still above the pre-specified target of 80%. The false positive rates for declaring ineffective treatments as effective, were between 0.14 and 0.19 for ER and were between 0.12 and 0.17 for AR. The probabilities of suspending treatments were also comparable between ER and AR designs. When the treatments were effective, the probabilities of suspending were no larger than 0.11 for ER and 0.12 for AR (in Treatment 2, MG 2). Conversely, for ineffective treatments, the probabilities of suspending were at least 0.52 for ER and 0.53 for AR (in Treatment 4, MG 1). The probabilities of reopening the suspended treatments ranged from 0.13 to 0.31 in these cases. (data not shown)

When an early stopping rule was applied to the ER design, the operating characteristics were shaped to be similar to those in the AR design. The AR design, however, still randomized more patients into effective treatments compared to the ER design. Consequently, the total number of patients reaching disease control status was 81.4 (41.9% of an averaged 194.1 randomized patients) for the ER design, which was lower than 83.0 (43.0% of an averaged 192.9 randomized patients) for the AR design. For the AR design, the median (mean) number of patients required before starting AR was 85 (92), corresponding to almost half of the patients were in the ER phase before AR.

Scenario 3: Varying effectiveness for Treatments 1–4; AR utilized without an early stopping rule; and with varying informative priors on σ²

Scenario 3 was constructed to assess the impact of the prior distribution on the operating characteristics of the AR design. We assumed that the disease control rates varied from 0.3 to 0.8 for Treatment 1 and from 0.3 to 0.6 for Treatment 3 in different MGs. On the other hand, the disease control rates for Treatments 2 and 4 were 0.6 (effective) and 0.3 (ineffective) across all MGs, respectively. From (2), we let the variance of μ_jk, σ², vary at 100, 10, and 1 across all MGs. To avoid assuming that treatments had similar efficacy, the variance of ϕ_j, τ², remained at 10⁶. In Table 3, the results for σ² = 100 and 10 were closer than that of σ² = 10 and 1, indicating that there was little borrowing across MGs when σ² = 100 and 10, and much borrowing when σ² = 1. The amount of borrowing can be easily identified by examining the model-based posterior mean estimation of the disease control rates. As σ² went from 100 to 1, the model-based disease control rates for Treatment 1 decreased from 0.77 to 0.74 in MG 1 and from 0.78 to 0.75 in MG 2. In the meantime, the corresponding disease control rate for Treatment 1 increased substantially from 0.27 to 0.42 in MG 5. We saw a similar trend in Treatment 3 across different MGs, where estimated disease control rates for effective treatment by marker subgroups decreased, but estimated disease control rates for ineffective subgroups increased. The amount of borrowing was also reflected from the probability of declaring an effective treatment. One prominent finding was that Treatment 1 in MG 5 had a 15% chance of being declared effective when σ² = 100 and a 33% chance of being declared effective when σ² = 1. The increase in the probability can be attributed to (1) the treatment being very effective in all other MGs and, (2) a small σ² dictating that the variation of the disease control rates across all MGs would be small. In this case, too much borrowing led to a higher chance of the false conclusion that Treatment 1 worked in MG 5 in the situation of heterogeneous disease control rates across MGs. When the treatment effect was homogeneous across MGs, more borrowing yielded better results with respect to less biased estimates of disease control rate and more accurate declarations of effective treatments. For example, when the treatment is working, the probability of declaring it effective for Treatment 2, MG 5 increased from 68% for σ² = 100 and 10 to 75% for σ² = 1. On the other hand, when treatment is not working, the probability of declaring it effective reduced from 19% for σ² = 100 to 16% and 11% when σ² = 10 and σ² = 1, respectively in Treatment 4, MG 5.

Table 3.

Operating characteristics for Scenario 3: varying effectiveness for treatments 1 and 3. Treatment 2 is equally effective and Treatment 3 is equally ineffective for marker groups 1–5; adaptive randomization utilized with no early stopping rule; and with varying informative priors σ²=100, 10, 1, and τ²=10⁶

Marker group
Treatment	1	2	3	4	5
True disease control rate/Observed disease control rate {1/2/3}
1	0.8/0.78/0.80/0.79	0.8/0.79/0.80/0.79	0.6/0.58/0.58/0.59	0.6/0.58/0.58/0.59	0.3/0.24/0.24/0.29
2	0.6/0.55/0.57/0.58	0.6/0.58/0.57/0.58	0.6/0.59/0.60/0.59	0.6/0.58/0.58/0.59	0.6/0.55/0.54/0.56
3	0.6/0.58/0.55/0.57	0.3/0.27/0.26/0.28	0.6/0.58/0.58/0.60	0.3/0.27/0.28/0.28	0.3/0.24/0.25/0.27
4	0.3/0.26/0.27/0.28	0.3/0.28/0.26/0.27	0.3/0.28/0.28/0.28	0.3/0.27/0.27/0.28	0.3/0.25/0.24/0.26
Model-based posterior mean of the disease control rate {1/2/3}
1	0.77/0.78/0.74	0.78/0.78/0.75	0.58/0.58/0.59	0.58/0.58/0.59	0.27/0.29/0.42
2	0.55/0.57/0.58	0.57/0.57/0.58	0.59/0.59/0.59	0.58/0.59/0.58	0.55/0.55/0.57
3	0.58/0.55/0.53	0.28/0.28/0.32	0.58/0.57/0.57	0.28/0.29/0.32	0.26/0.28/0.34
4	0.27/0.29/0.30	0.29/0.27/0.29	0.29/0.29/0.29	0.28/0.28/0.29	0.27/0.27/0.29
Average sample size {1/2/3}
1	9.3/9.4/9.1	13.4/13.6/12.8	16.5/16.5/16.5	14.9/15.0/14.9	4.6/4.6/5.1
2	7.6/7.7/7.9	11.1/11.0/11.3	16.4/16.5/16.5	14.6/14.9/15.0	6.6/6.8/6.2
3	7.8/7.6/7.4	8.0/7.9/8.5	16.3/16.0/16.1	10.6/10.5/10.8	4.5/4.7/4.7
4	5.7/5.8/5.8	8.2/7.8/7.8	11.8/11.8/12.0	10.5/10.4/10.3	4.5/4.4/4.3
Total	30.5/30.5/30.2	40.7/40.4/40.4	61.0/60.9/61.1	50.5/50.7/50.9	20.2/20.5/20.3
Probability of declaring effective treatment {1/2/3}
1	0.95/0.96/0.97	0.98/0.99/0.99	0.91/0.91/0.93	0.89/0.89/0.92	0.15/0.16/0.33
2	0.71/0.75/0.79	0.83/0.80/0.86	0.91/0.92/0.95	0.89/0.88/0.91	0.68/0.68/0.75
3	0.76/0.71/0.71	0.18/0.15/0.19	0.90/0.89/0.91	0.16/0.18/0.19	0.16/0.17/0.17
4	0.18/0.18/0.17	0.17/0.17/0.14	0.17/0.19/0.18	0.16/0.15/0.16	0.19/0.16/0.11

¹The entries {1/2/3} correspond to σ²=100(1); σ²=10(2); and σ²=1(3), respectively.

Discussion

Randomized clinical trials have become the gold standard for comparing treatment regimens in the past 50) years [32–35]. Randomization is essential in controlling both known and unknown biases including patient selection bias, treatment allocation bias, outcome evaluation bias, etc. The majority of trials use a fixed randomization ratio (e.g., 1 : 1 or 1 : 2 between the two treatments). A design with a fixed randomization ratio is simple but rigid. It does not allow for changing the randomization ratio during the trial to favor treatments that are more likely to be effective. It also does not take an individual patient’s disease characteristics into consideration when determining treatment assignments. In this article, we propose an AR trial design under the framework of a hierarchical Bayes model. Based on extensive simulation studies, we have shown that with a total of 200 evaluable patients, our trial design has desirable operating characteristics that: (1) select clinically effective agents with a high probability and ineffective agents with a low probability; (2) treat more patients with effective agents according to their tumor biomarker profiles; and (3) suspend ineffective agents from enrollment with a high probability by applying an early stopping rule. The Bayesian AR design is a smart, novel, and ethical design. In conjunction with an early stopping rule, it can be applied to efficiently identify effective agents and eliminate ineffective ones. By aligning effective treatments with patients’ biomarker profiles, more patients are treated with effective therapies, and hence, more patients could reach disease control status. AR design with early stopping is ideally suitable for the development of targeted therapy. Our trial design continues to ‘learn’ by updating the posterior distribution and improves the estimates as the trial progresses. It is a ‘smart’ design that matches patients with the drugs best suited for them. However, there are still important issues that require further discussion.

Prior specifications

In Bayesian data analysis, it is customary to take several priors, each reflecting a different degree of optimism or uncertainty, to assess their effect on posterior inferences. In our model, σ² controls the amount of borrowing from across different MGs for the same treatment. The amount of borrowing is limited when σ² is 10 or larger. However, when σ² is 1, there may be too much borrowing and thus result can in wrong conclusion in determining treatment efficacy. The other parameter τ² governs the variation of treatment effect across all treatments. A small τ² indicates that the treatment efficacy is similar while a large τ² allows treatment efficacy to be different among treatments. In our simulation studies, we also found that a small τ² is not desirable. (data not shown) Because little is known about the treatment effect for patients with particular biomarker profiles, vague priors such as σ² = 10⁶ and τ² = 10⁶ are reasonable choices for our trial design and yield desirable operating characteristics.

Adaptive randomization versus equal randomization

Our simulation studies showed that both the ER and AR designs controlled the type I and type II error rates but the AR design allocated more patients into effective treatments, hence, more patients reached disease control status. This result held in designs with and without an early stopping rule. AR is a rational choice for the development of predictive markers. Bayesian AR paradigm provides an ideal framework to align patients with better treatments. The concept of selecting proper patient groups for evaluating targeted therapies is consistent with the idea of enriching the patient population. It has been shown that choosing patients who are more likely to benefit from the targeted therapy can increase the efficiency of the trial design [36,37]. One known ramification of the AR design is that it results in biased estimates due to dependent samples. The magnitude of such bias can be quantified and corrected [38,39].

Another important consideration is when to start AR. If AR starts early, the randomization ratio is largely determined by the early results from a few patients and can vary greatly. If AR starts late, the result is more similar to ER. In our proposed trial, we start AR after observing at least one response outcome in all treatment by marker subgroups. Consequently, approximately 90 patients were enrolled in the ER part of the study before AR. This contributes to the fact that only a moderate difference was found in the operating characteristics between ER and AR designs. When adequate prior information becomes available, the AR process can start earlier. The issue of determining the best time to start the AR process remains an open question, and is a topic of future research.

Early stopping rules

When evidence accumulates that a treatment does not work in patients with certain biomarker profiles, we have devised an early stopping rule that suspends the randomization of patients with the same biomarker profiles into that treatment. The suspension is not permanent, however. Due to the dynamic nature of our trial design, the model continues to update when new outcomes are observed. At any given time, if the treatment efficacy exceeds the threshold of the stopping rule, the suspension is lifted. As much as researchers like to see success, only a small number of new treatments are truly effective. Therefore, applying an early stopping rule can increase the study efficiency by terminating ineffective treatments early, saving resources, and enhancing the study ethics [40]. Applying an early stopping rule improves the operating characteristics for both ER and AR designs. When an early stopping rule is applied to the ER design, ineffective treatments are suspended early and patients are randomized into effective treatments. It produces a similar effect as in the AR design. The percentages of randomized patients reaching disease control status were 38.2% in the ER design with no early stopping rule, 40.5% in the AR design with no early stopping rule, 41.9% in the ER design with an early stopping rule, and 43.0% in the AR design with an early stopping rule in scenarios 1 and 2. The AR design with an early stopping rule has the highest proportion of patients reaching disease control status.

Challenges in trial conduct

There are several challenges associated with the conduct of this biomarker driven, outcome-based AR trial. First, the time for a patient’s biomarker assessment needs to be short because the patient’s treatment assignment depends on the determination of the marker profile. For the BATTLE project, we have assembled a designated molecular pathology laboratory. The turn around time is usually within 1 week but cannot be longer than 2 weeks as stipulated in the protocol. Second, the time for outcome assessment must be relatively short as well, so that the decision based on up-to-date data can provide appropriate guidance for subsequent treatment assignments. If a trial has a fast accrual rate, many patients may have been enrolled into the trial before the outcome data becomes available to provide useful information for the AR. Therefore, quick and easily assessable endpoints and slow to moderate accrual rates (relative to the outcome assessment time) are most suitable for outcome-based AR designs.

In clinical settings, not every patient has a biopsiable tumor, nor has the desire to undergo an additional biopsy procedure. Also, the amount and quality of tissue samples may vary, leading to an incomplete biomarker panel for some patients. Shall patients with no or partial biomarker results be enrolled in the study? If so, how? Biomarker diagnostic tools may have varying sensitivity and specificity. Hence, the assignment of a patient to a biomarker group may not be 100% accurate. These practical considerations pose challenges to the trial design and requires further investigation.

In the midst of many challenges, we have derived an AR design to achieve our goals. Our trial design presents a step towards personalized medicine. With the advancement of medical knowledge and molecular, genomic biomarker tools, an efficient and flexible design such as ours will enable us continue to learn more about new agents’ clinical activities and molecular underpinning. Researchers can then apply this knowledge to better treat patients enrolled in a trial. The success of such trials require an integrated multi-disciplinary research team consisting of clinical investigators, who see patients and perform biopsies, basic scientists, who run the biomarker analysis, computer programmers, who build web-based database applications to capture data in real time, and statisticians who provide the statistical design and implement AR.

Abbreviations

AR

adaptive randomization

BATTLE

biomarker-integrated approaches of targeted therapy of lung cancer elimination

EGFR

epidermal growth factor receptor

ER

equal randomization

MG

biomarker group or marker group in short

NSCLC

non-small cell lung cancer

RXR

retinoid X receptor

VEGF

vascular endothelial growth factor

VEGFR

vascular endothelial growth factor receptor

Appendix: full conditional distributions for the model

We present the full conditional distributions for the hierarchical probit model in this section. Gibbs sampling method is applied to compute the posterior distributions. Denote L_ijk as the likelihood for the ith patient in kth marker group receiving jth treatment. Assuming independence across patients, the overall likelihood is a product,

$$\begin{array}{l}L=\prod _j\prod _k\prod _{i=1}^{n_{jk}}{L}_{\mathit{ijk}}\\ L_{\mathit{ijk}}={\left(Pr(z_{\mathit{ijk}}\ge 0\mid {\mu }_{jk},{\varphi }_j,{\sigma }^2,{\tau }^2)\right)}^{I(y_{\mathit{ijk}}=1)}\\ {\left(Pr(z_{\mathit{ijk}}<0\mid {\mu }_{jk},{\varphi }_j,{\sigma }^2,{\tau }^2)\right)}^{I(y_{\mathit{ijk}}=0)}\\ ={\left\{\underset{0}{\overset{\infty }{\int }}f(z_{\mathit{ijk}}\mid {\mu }_{jk},1)\right\}}^{I(y_{\mathit{ijk}}=1)}{\left\{\underset{-\infty }{\overset{0}{\int }}f(z_{\mathit{ijk}}\mid {\mu }_{jk},1)\right\}}^{I(y_{\mathit{ijk}}=0)}\end{array}$$

The full conditional distributions of the parameters are proportional to the product of the likelihood of data and the prior distributions. Therefore, they follow normal distributions given the use of conjugate priors. The mean of the posterior distribution is the weighted average of the mean of the prior distribution and the mean of data. The latent variable z_ijk follows a truncated normal distribution. If y_ijk = 0, z_ijk can be sampled from the normal distribution centering at μ_jk and the variance of 1 and bounded in the region of less than 0. Otherwise, z_ijk can be sampled from the same normal distribution but bounded in the region of greater than 0.

$$\begin{array}{ll}\hfill z_{\mathit{ijk}}\mid y_{\mathit{ijk}},{\mu }_{jk}& \propto \{\begin{array}{ll}N({\mu }_{jk},1)I(-\infty ,0)\hfill & \text{if}{y}_{\mathit{ijk}}=\mathit{0}\hfill \\ N({\mu }_{jk},1)I(0,\infty )\hfill & \text{if}{y}_{\mathit{ijk}}=\mathit{1}\hfill \end{array}\\ \hfill {\mu }_{jk}\mid z_{\mathit{ijk}},{\varphi }_j& \propto N\left(\sum _{i=1}^{n_{jk}}{z}_{\mathit{ijk}}+{\varphi }_j/{\sigma }^2,1/(n_{jk}+1/{\sigma }^2)\right)\\ \hfill {\varphi }_j\mid {\mu }_{jk}& \propto N\left(\sum _{k=1}^5{\mu }_{jk},1/(5+1/{\tau }^2)\right)\end{array}$$