Abstract
Relapsing fever agents like Borrelia hermsii undergo multiphasic antigenic variation that is attributable to spontaneous DNA non-reciprocal transpositions at a particular locus in the genome. This genetic switch results in a new protein being expressed on the cell surface, allowing cells with that phenotype to escape prevailing immunity. But the switch occurs in only one of several genomes in these spirochetes, and a newly-switched gene is effectively “recessive” until homozygosity is achieved. The longer that descendants of the switched cell expressed both old and new proteins, the longer this lineage risks neutralization by antibody to the old protein. We investigated the implications for antigenic variation of the phenotypic lag that polyploidy would confer on cells. We first experimentally determined the average genome copy number in daughter cells after division during mouse infection with B. hermsii strain HS1. We then applied discrete deterministic and stochastic simulations to predict outcomes when genomes were equably segregated either linearly, i.e. according to their position in one-dimensional arrays, or randomly partitioned, as for a sphere. Linear segregation replication provided for a lag in achievement of homozygosity that was significantly shorter than could be achieved under the random segregation condition. For cells with 16 genomes, this would be a 4-generation lag. A model incorporating the immune response and evolved matrices of switch rates indicated a greater fitness for polyploid over monoploid bacteria in terms of duration of infection.
Keywords: Lyme disease, plasmid, relapsing fever, spirochete, tick, vector-borne disease
Introduction
Borrelia hermsii and other species that cause relapsing fever are noted for their evasion of the host’s adaptive immunity through multi-phasic antigenic variation [1]. A change in antigenic identity, or serotype, of a cell is the consequence of a spontaneous, non-reciprocal transposition, in which a previously silent allele for a surface protein supplants another allele occupying an expression site through a stochastic recombination [2]. We call this genetic event and the accompanying change in phenotype a “switch.” The serotype of a cell is determined by the expression of one out of several Variable Major Proteins (VMP) [3]. The serotype-specific antibodies that are elicited by cells expressing the prevailing VMP over time rise to a concentration sufficiently high to clear that particular serotype from the blood, i.e. at ~107 bacteria per milliliter [4]. The minority of cells expressing a different VMP, to which the vertebrate host has not previously been exposed, continue to proliferate in the presence of the initial immune response. But as numbers of cells expressing the different VMP increase, adaptive immunity to that serotype follows in turn. Other serotypes and the immune responses to them succeed until either the host dies, or the VMP repertoire is exhausted and the host recovers (reviewed in [4]).
These events occur among linear plasmids, which are each in approximate equal numbers with chromosomes in a cell [4-6]. A single chromosome and each of the several types of linear and circular plasmids constitute a single genome. Inactive, or silent versions of genes for VMPs occur on five different plasmids, while the expression site, defined by a particular promoter and an upstream enhancer, occurs on only one plasmid [7,8]. If there was one genome per cell, which is the case for most bacteria under natural conditions, the daughter cell with the recently switched VMP gene may go through a transitional period where the both the remaining VMP molecules and the newly-made VMPs are represented at the cell’s surface. But given the turnover of membranes in Borrelia spp. [9], this phenotypic lag would probably be less than the generation time of 5 to 8 hours [4]. But what if there were several genomes in the cell, as is the case for the several Borrelia species that cause relapsing fever, as well as the agents of Lyme disease [10,11]? These genomes are tandemly-arrayed along the lengths of these filamentous cells. As Hinnebusch and Bendich described it, the “DNA content of a borrelia is not contained within a central condensed nucleoid, as it is for E. coli, but instead is distributed throughout the approximately 20-µm length of the spirochete during most stages of growth” [12]. The rate of switching from expression of one VMP was estimated as 10-4 to 10-3 per cell per generation [13,14], so the likelihood of two or more independent genetic switches occurring the same cell is very low. How then do cells contend with their hazardous environment containing antibodies targeted to them if only one of its several genomes has undergone a switch? We address this question here.
We follow the Oxford English Dictionary in defining a cell as “polyploid” when it contains “more than two homologous sets of chromosomes” [15]. When there are two or more haploid genomes in a cell, we have to consider whether relationships of “recessive” and “dominant” apply [16]. All microbes, no matter how many genomes, have to contend with the inevitable phenotypic lag while proteins turnover [17]. But our interest here is the delay is imposed on polyploid organisms by “segregation lag,” that is, the number of generations that elapse before identical genomes with respect to the genotype of interest is achieved [18].
For this study, we apply “homozygous” to a cell in which all copies of its genomes are identical at the locus of interest, in this case the expression site of gene for a VMP, which, for an example, we name VMP1. “Heterozygous” refers then to a cell in which at least one of its genomes has a different allele at the specified locus. This definition also holds for cells in which all but one of its genomes has the variant allele. It would apply to any genome copy number of ≥ 2, of course. But the cases of greatest interest for us have genome copy numbers ≥ 4, since there may be four complete or near-complete dichotomously replicating chromosomes during rapid growth of bacteria, e.g. Escherichia coli, that have only a single chromosome under slow growth conditions [19,20]. For this study we also assume that a recently switched gene for a different VMP, which we name VMP2, is “recessive.” That is, the antigenic identity of cell is dominated by the original VMP—VMP1 in the example—until that protein is absent from the cell’s surface. Plausibly, some VMP1 molecules persist on the surface but so sparsely that the circulating specific antibodies to VMP1 have no effect on the cells. In other words, the cell may still be strictly heterozygous in genotype but the phenotype is effectively pure VMP2, not a mélange of new VMP2 and retained VMP1. But for simplicity, we specify that the newly-transposed vmp2 allele is strongly recessive and that only when identity of all genomes at this locus is achieved can the cell evade specific immunity to VMP1-expressing cells in its environment.
Conceivably, a newly-switched expression site (e.g. with vmp2) somehow either silences or out-expresses the unsubstituted expression loci in the cell’s other genomes. An epigenetic phenomenon like this could effect a phenotype change sooner than expected in post-switch lineages. This may be the case for Azotobacter vinelandii, which may have up to 80 copies of its chromosome per cell [21]. But lacking evidence to the contrary, we here assume that in Borrelia cells all the vmp expression sites in the cell have equivalent transcriptional activity.
Two other assumptions for the modeling are, first, random pool replication, i.e. each of the genomes is replicated once per generation [22], and, second, equal-number segregation of genomes at division through a faithful partitioning mechanism [23]. The reports of Hinnebusch et al. and Lopez et al. on plasmid stability in Borrelia spp. over long periods of serial cultivation provide justification for these assumptions [10,24].
We are left then with these three specifications for the model: (1) The polyploid cell has to be homozygous for vmp2 (or another VMP gene), if it is to avoid the immunity that has been elicited by its VMP1-expressing (VMP1+) predecessors. (2) Replicons are equably reproduced and distributed. (3) The post-switch, newly-activated allele is recessive, and there is no silencing or other expression bias favoring newly-switched loci. Under these conditions the question then is how soon—measured in number of generations—can homozygosity be achieved? Presumably, the longer a bacterium and its descendants retain a complete or partial VMP1+ phenotype, either as a homozygote or heterozygote, the longer it is at risk of neutralization or clearance by the prevailing immunity against VMP1.
How genomes segregate at division is an important factor. The two options we consider are, first, random but equable segregation of unimpeded genomes in a 3-dimensional space, like a sphere, and, second, segregation outcomes that depend on genome locations in a linear or 1-dimensional array. The latter circumstance, termed “linear segregation,” would seem to apply to Borrelia spp., what with their filamentous shapes and tandemly-arrayed genomes in single file. But the consequences of this or other arrangement for antigenic variation have not been fleshed out. Accordingly, our starting point is this null hypothesis: random segregation is indistinguishable from linear segregation in terms of number of generations to achieve homozygosity. By “indistinguishable” we mean within one generation. This hypothesis was addressed through simulations, after first carrying out an empirical study of the number of genomes per cell during infection of a mouse.
Materials and Methods
Strain and culture conditions. The “Browne Mountain” isolate of B. hermsii strain HS1 (BioSample SAMN04481062) was originally obtained by Willy Burgdorfer in 1968 from an Ornithodoros hermsi tick collected in eastern Washington in 1968 [25]. Twenty-five different serotypes, each identified by a single number, e.g. serotype 21, were isolated from this population by Stoenner et al. [14] and further characterized by Restrepo et al. [26]. The complete genome of this isolate of B. hermsii has been sequenced [8]. All serotype stocks in plasma from infected mice were kept frozen at -80°C. For the present study, serotype 7 was cloned again by limiting dilution in immunodeficient mice [27]. Serotype identity was confirmed by sequencing of the expression site for the VMP genes on plasmid as described [26]. Cells of strain HS1’s serotype 33 were cultivated in BSK II broth medium supplemented with 12 percent rabbit serum at 34°C [28].
Cell counts by microscopy. Spirochetes were counted by phase-contrast microscopy of a Petroff-Hausser counting chamber with a depth of 20 µm (Hausser Scientific) and under 400x magnification. A volume of 4.5 μl plasma or culture medium was placed in the chamber, and spirochetes in 400 squares were counted. Lengths of spirochetes were determined from digital photographs of phase-contrast microscopy fields that included for calibration the 50 µm divisions of the counting chamber. Each spirochete was measured 10 times by tracing along its length with ImageJ (http://rsb.info.nih.gov/ij/) and converting pixels to µm.
Mouse infection. Five adult female CB17-Prkdcscid/J mice with severe combined immunodeficiency (SCID) (Jackson Laboratories) were inoculated intraperitoneally with serotype 7 cells in 100 μl of infected plasma diluted in phosphate-buffered saline with 5 mM MgCl2. The group of mice were monitored daily for the presence of spirochetes by phase-contrast microscopy of a wet mount of tail vein blood. Once spirochete densities had reached their peak, the mice were terminally bled under anesthesia by cardiac puncture with heparin-coated syringes. Blood samples were briefly centrifuged at 93 x g for 1 min in a table top centrifuge to reduce the concentration of erythrocytes prior to microscopy of the plasma and DNA extractions.
Quantitative PCR. DNA was extracted with the Qiagen QIAmp DNA kit from plasma depleted of erythrocytes and erythrocytes and with the Qiagen DNeasy kit from B. hermsii cells of in vitro cultures. PCR reactions were carried out as described [13]. The forward primer, reverse primer, and probe for the single-copy 16S ribosomal RNA gene were 5’-GGTCAAGACTGACGCTGAGTCA-3’, 5’-GGCGGCACACTTAACACGTTAG-3’, and 5’-TCTACGCTGTAAACGATGCACACTTGGTG-3’, respectively. The DNA standard was total genomic DNA extracted using a phenol-chloroform protocol, as described [29]. Genome copies in the standard were calculated from the total DNA concentration, as determined by spectrometry, with a mass for a single B. hermsii genome size of 1.5 fg [8]. The qPCR result was the mean of three replicates. The linear slope of 16S ribosomal RNA gene copies regressed on cells counted by microscopy was ~1 over a 100-fold range [4].
Statistics. Descriptive statistics, frequency distributions, and linear regressions were carried out with SYSTAT v. 13 (SYSTAT Software, Inc.). Unless otherwise specified, variances were 95 percent confidence intervals (95 percent CI). Confidence intervals for ratios were calculated with SAS/STAT v. 9.2 (SAS Institute, Inc.). Probabilities of different outcomes for linearly-segregated genomes were exact. The likelihoods of specified genome compositions in a growing population of cells undergoing random segregations were inferred using Excel v. 14.7 (Microsoft, Inc.) and the hypergeometric function HYPGEOM.DIST.
Computer models. Two Python programs were written for each of the types of genome segregation under consideration: linear and random. The endpoints for both programs were the number of generations that elapse before at least one cell in the population was homozygous with respect to a variant allele for a new serotype. The independent variable was the number of genomes in a cell. In the linear segregation model the outcomes vary according to the randomly-determined position of the switched genome in a linear array. But from that initial state onwards, i.e., as cells divide and the population expands, the probabilities were exact. In the random segregation model, stochasticity applied both for the initial state and then the distribution of genomes within cells as the population increased. For both models means and variances (standard error) from 1000 runs of the program were calculated.
Another Python program simulated both the growth of the pathogen and antibody response to it. It was derived from Frank’s model for African trypanosome infections [30]. The serotype-specific antibody concentration, a, in Frank’s equation 1 was replaced by a(1 + a/b) where a is the serotype-specific antibody concentration and the b parameter represents synergy between antibodies in their effect on the bacteria as their concentrations increase. Other parameters in the model were the following: the number of possible serotypes, the range of switch rates, the amount of specific antibody to the serotype at time 0, the number of cells of a given serotype that would elicit a half maximal antibody response, the loss of specific antibody by degradation, the carrying capacity (maximum density) of the host for the bacterium, a constant that represents the rate of death of the bacteria in the presence of specific antibody, the growth rate of bacteria, and the accumulation rate for the specific antibody. We solved this system of equations using a distribution of Python from Enthought (Austin, TX), and a finite difference method with forward Euler time steps [31], which are specified in their number and length. Rather than supplying a random matrix of switch rates, we evolved sets of switch rates within specified ranges [30,32]. The program starts with matrix of random switch rates within the given range (e.g. 10-6 to 10-3 per generation) in a (n-1) by (n-1) matrix, where n is the number of serotypes. For each set of conditions the program is run 1000 times and each matrix is evaluated for the sum of bacterial cells at each time step. The duration of infection after 1000 runs was recorded. To account for more than one genome in a cell, the switch rate was multiplied by the number of cells that were present g number of generations earlier, where g is the number of generations for a polyploid cell to become homozygous for a new allele. Each simulation with a given set of values was replicated 5 to 10 times.
The three programs (linear_segregation, random_segregation, and infection_model) are available at https://github.com/borrelialab/Borrelia-genome-copy.
Results
Genome copy number. We first revisited the question of the number of genomes in a Borrelia cell. Kitten et al., using both hybridization with probes and intercalation of a dye into double-stranded DNA, estimated that the mean copy number per cell was 16 (11-20) for the chromosome and 14 (11-18) for the plasmid bearing the expression site for VMP genes for spirochetes in the blood of infected mice [11]. The ratio of ~1 expression site plasmid for each chromosome holds for different spirochete densities in culture and phases of growth (unpublished findings). For the present study we used quantitative PCR of a stably-maintained, single-copy chromosomal gene and microscopic counts of whole cells to estimate genome copy numbers. A possible confounder for this analysis were agglomerates of organisms. Spirochetes divide by binary transverse fission [33], so it was possible that a fraction of the cells in the population were in chains of two or more cells. There could also be entangled spirochetes [28]. If these were counted as single cells, genome copy numbers could be overestimated. We assessed the frequency of these forms for B. hermsii growing in broth medium. This was preferable to blood, because of greater accuracy of length measurements in the absence of other cellular elements, such as platelet and fibrin strands. In a previous study of cells growing in culture or mouse blood we did not observe a difference in the distributions of lengths of B. hermsii under these two conditions [11]. Since this strain of B. hermsii does not grow as colonies on solid medium, we could not perform colony counts.
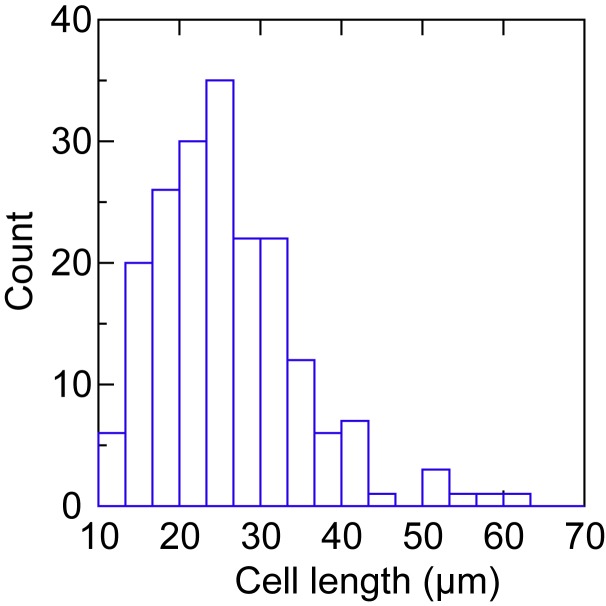
The spirochetes were cultivated in the broth medium at 34°C and were studied in log-phase of growth, when the cell density was ~106/ml. The lengths of 193 randomly-selectedcells were determined by image analysis of photomicrographs and calibration of the pixels with a scale in µm in the photographs. The lengths were measured end-to-end without adjustment for amplitude of the tightly helical cells. Figure 1 shows the frequency distribution of the cell lengths. A similar distribution of lengths of another relapsing fever species was found by Bates et al. in their study of the blood of an animal model [34]. In the present study the mean length was 25.9 µm, the standard deviation was 8.9, the standard deviation interval was 17.0 to 34.9 µm, and the median length was 24.7 µm. Only 6 (3 percent) of the 193 cells were greater than 2 standard deviations than the mean in length. Some of these appeared to be daughter cells that had physically-separate protoplasmic cylinders but retained a transient attachment by a residual fusion of outer membranes. Occasional pairs of tethered cells may have counted as single cells but this false assignment would have had a negligible (≤ 3 percent) effect on determinations of genome copies per cell.
Figure 1.
Frequency distribution of the lengths of a log-phase population of Borrelia hermsii cells by phase contrast microscopy.
To estimate the number of genomes per cell, five SCID mice were each inoculated with ~50 cells of serotype 7, and then the infection was monitored by microscopy of tail vein blood. As soon as the density of spirochetes in the blood reached its expected peak [4], anti-coagulated blood was obtained. After a brief centrifugation, plasma from each sample was pooled, mixed, and then divided into 6 aliquots. These were individually subjected to microscopic quantitation of cells and qPCR for respective determinations of cell and genome counts per milliliter. The mean cell count was 3.3 (2.9-3.7) x 107, and the mean genome count was 75 (47-100) x 107. From this we calculated that there were a mean of 22 (12-32) genomes per cell in this population in the blood. If the genomes were distributed along the length of the cell, as previous studies of Borrelia spp. indicated [11,12], there would ~1 genome for every micron of cell length. The copy genome copy number by qPCR was somewhat higher than our previous estimate for bacteria in the blood [11], but the confidence intervals overlapped.
For this simulation-based investigation of the consequences of polyploidy for B. hermsii, the simplest case is of a cell just after division. Among the genomes of this hypothetical cell, there is single one that that has different expressed VMP allele. For the simulation we assume that the switch occurred during replication in the parent, resulting in distribution of the switched genome to the one daughter cell but not the other. If the mean number of genomes per cell in the population is 22, then the mean number genomes immediately after the division is 22 divided by loge 2, or 32 [35]. Each daughter cell then would have on average ~16 genomes.
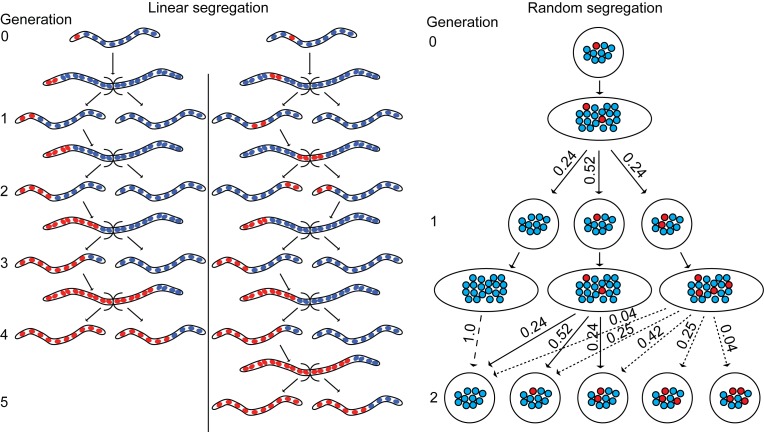
Segregation of genomes. Figure 2 shows schematically three examples of daughter cells with 10 genomes per cell. Each was bequeathed a single switched genome from the parent. (The second daughter cell did not have a switched genome and is not shown.) The leftmost and center cells are shown as filaments, have tandemly-arrayed genomes, and segregate linearly. The two cells differ in the position of the newly-switched genome in the line of genomes. Counting from the left, when the switched genome is in position one, at least one cell of the progeny is homozygous for the new VMP by generation 4. However, if the variant genome is at position three, then not until generation 5 could a homozygous cell for the new VMP be expected.
Figure 2.
Schematic representation of outcomes of linear and random segregation of genomes in a hypothetical polyploid spirochete. Under both conditions at the outset (generation 0) one genome (red) of the has a different gene at the expression site and other 9 genomes (blue) have the prevalent gene of the ancestors. In the linear segregation model two different states at generation 0 are shown. These differ by the location of the genome with the switched gene in the 1-dimensional array. All possible daughter cells of the subsequent 4 generations are shown. In the random segregation model the genome with the switched gene is distributed among the cells of the subsequent 2 generations with probabilities shown.
The rightmost cell is shown as a sphere rather than as a filament for convenience of presentation, but the genomic arrangement it depicts is plausibly possible for cylindrical cell as well as a spherical one. The point is that the initial position of the switched genome in this daughter cell does not matter. According to this model, the genomes are equably but randomly distributed to daughter cells during subsequent divisions in that population. The likelihood for each of the possible configurations of switched and non-switched genomes can be exactly calculated, as exemplified in Figure 2. The state only through generation 2 is shown, but it is apparent that it may be several more generations before homozygosity for the new VMP is achieved under these conditions.
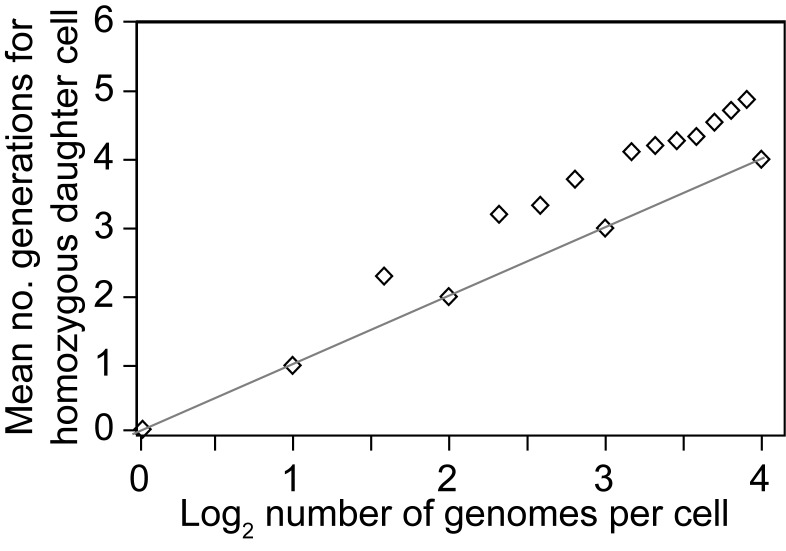
The effect of genome copy number and position on the outcome of linear segregation is summarized in Figure 3. This shows the mean number of generations for a population to achieve at least one homozygous cell for the new VMP by genome copy number. As an example, consider two cells, one with 7 genomes and the other with 8, each with one switched genome right after a division. In the 7-genome cell, a homozygous cell for the variant could be achieved in three generations for two of the possible 7 positions and in four generations for the other 5 positions, for a mean of 3.71 generations for all permutations. In contrast, for the lineage of 8-genome cells homozygosity is achieved in four generations, no matter what the position of switched genome is in the cell. Cells with other integer exponents of 2 (2n), e.g. 16 (24), for genome copy number faster achievement of homozygosity than cells with fewer genomes but not in powers of 2.
Figure 3.
Scatter plot of the mean number of generations for the appearance of a homozygous daughter cells with a new protein to occur in a population of bacteria undergoing linear segregation of genomes in different copy numbers. The linear regression curve for genomes numbering 2n, where n is an integer ranging from 0 to 4, is shown.
The greater variation in outcomes and the greater lag to homozygosity for populations with randomly-segregating genomes is shown in Figure 4. This summarizes the outputs of two simulation programs: one for randomly-segregating genomes (top) and the other for linearly-segregating genomes (bottom). Both cases specify cells with 16 genomes after division. By generation 14 (i.e. 16,384 cells) of a population beginning from one cell, 1024 cells in population with linearly-segregating genomes are homozygous for the new VMP and 15,360 are homozygous for the old VMP. There are no heterozygotes. On the other hand, after generation 14 in the population with the randomly-segregating genomes there are about the same number of cells with no switched genes, but on average only 10 cells are homozygous for the new VMP after 14 generations. The rest of the descendants of the switch genome are distributed in various numbers among the other heterozygous cells, all of which would presumably be expressing the old VMP and be susceptible to immunity elicited by that VMP. A simulation of outcomes for populations featuring randomly- and linearly-segregating genomes in 10 copies revealed a similar pattern. However, there are still expected to be a few heterozygous cells in the population of linearly-segregating cells, because of the asymmetries at divisions for genome copy numbers that are not powers of 2 (Figure S1 of Supplementary Material, Appendix A).
Figure 4.
Frequency distributions of the number of cells with different proportions of genomes with a switched VMP gene in descendent populations 14 generations after the genetic switch in the ancestor. The cells in these populations have 16 genomes. The top panel shows the results under the condition of random segregation of genomes. The bottom panel shows the results under the condition of linear segregation. Error bars denote the standard errors.
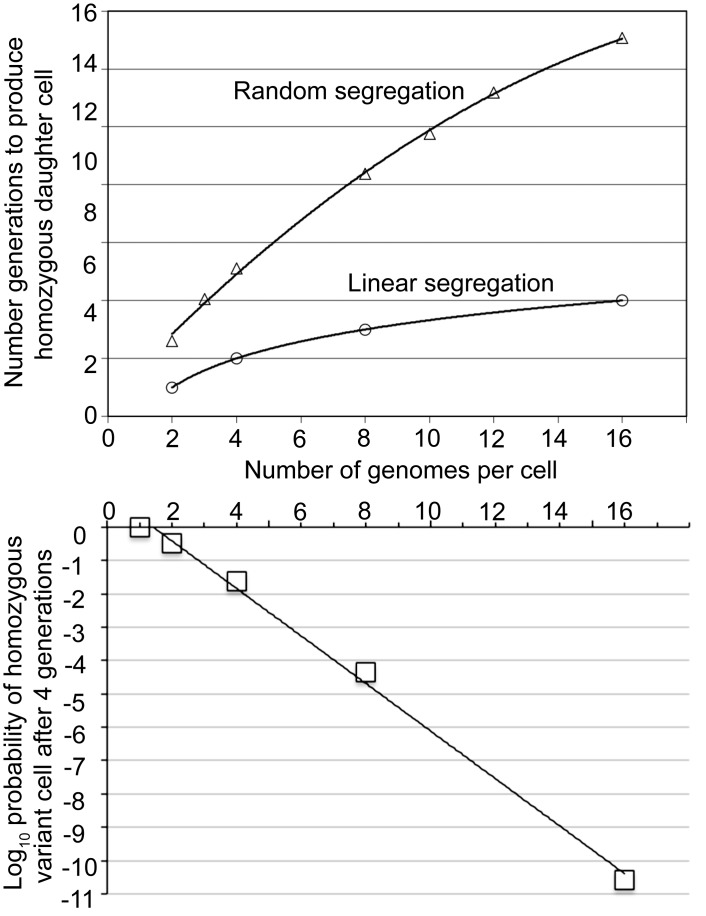
Figure 5 summarizes results of applying the hypergeometric distribution for inferring probabilities of outcomes for populations with randomly-segregating genomes of different copy numbers. In the top panel of the figure the dependent variable is the number of generations to produce a homozygous daughter cell for the new VMP. It was 15 generations by this analysis. This compares with 4 generations for the population of cells with 16 linearly-segregating genomes. For lower panel of the figure the dependent variable is the probabilities of a homozygous variant cell in the population with randomly-segregating genomes by different copy number.
Figure 5.
Differences in outcomes in the generations until homozygosity for a switch gene is achieved under the random segregation and linear segregation models. The top panel gives the number of generations by number of genomes per cell. For the random segregation condition the plotted values are means calculated from a hypergeometric distribution. The best-fit curve (R2 = 0.998) is a second-order quadratic polynomial. For the linear segregation model the values are exact for genomes numbering 2n, where n is an integer ranging from 0 to 4. The best-fit curve (R2 = 1.0) is a logarithmic function. The bottom panel gives probability of a homozygous variant cell after four generations by the number of genomes per cell and when there is random segregation.
Infection model with different genome copy numbers. The theoretical advantage of linear segregation for expeditiously achieving homozygosity of an otherwise recessive allele is clear. But does polyploidy make any difference for the infection itself, such as for the duration of infection? For a polyploid organism there are more genomes in which a “mutation” or gene switch might occur each generation, but weighed against this advantage is the consequent generational lag before a descendent cell achieved homozygosity for new serotype. We first examined the consequences of polyploidy with a discrete deterministic model under the following initial conditions: an expanding population starting from a single cell of one serotype, a switch rate to a new serotype that ranged from 10-3 to 10-6 per genome per generation, a number of genomes per cell that ranged from 1 to 32, and a constant cell density at which the immune response to the infecting serotype clears cells with that phenotype. In this case, this was generation 25 of binary reproduction. This would be 16,777,216 (~2 x 107) bacteria per milliliter, which is the approximate density achieved by B. hermsii in immunocompetent Mus musculus before clearance by antibody begins [4,36]. The endpoint for this simulation was the number of cells that were homozygous for the new serotype at the generation of peak density. We also examined the relative fitness, or fold increase, of polyploid cells over cells with single genomes under these various conditions.
For each specified switch rate, the number of cells homozygous for the new serotype increased with greater numbers of genomes for each of the specified switch rates (Figure 6). The comparative advantages over a single genome cell, as the numbers of genomes per cell increased, was greatest for a switch rate of 10-6 and least for a switch rate of 10-3. But under a switch rate of 10-6 and at time when immune clearance commenced in this simulation, homozygous switched cells were rarer than in populations with higher switch rates. In population sizes of a hundred or less, variants may be vulnerable to extinction by bottlenecks imposed by non-immune mechanisms, such as filtering by the spleen [37,38]. In contrast, when the switch rates were 10-5 or higher and when there were 8 or 16 genomes per cell, there would be 103 to 105 cells of the new serotype circulating at the time of antibody clearance of cells of the original serotype. These estimates from the simulations were similar to the experimental finding of 1300-2500 bacteria remaining in the blood after clearance of cells of the infecting serotype by the serotype-specific immune response in infected mice [4,36].
Figure 6.
3-dimensional scatter plots with regression of the interaction of genome copy number (x-axis) and genetic switch rate (grouping variable) on the number of homozygous cells for the switch gene after 25 generations (y-axis). The relative fold-increase by in the proportion of switched cells. The designated switch rates shown are 10-6, 10-5, 10-4, and 10-3 per genome per generation. The copy number of genomes range from 1 (log2 0) to 32 (log2 5).
We next included the immune response of the host and selected parameters associated with that, such as rate of increase in serotype-specific antibody levels and degradation of antibody. The segregation of genomes was assumed to be linear, and genome number cashed out in the model as “generation lag”, i.e., the number of generations for a daughter cell to be homozygous for a new VMP gene after a switch in one of the genomes at time 0. The lag was the n exponent value when 2n were the genome copies. The lag ranged from 0 for lineage of one genome cells to 8 for a more improbable lineage of cells each with 256 genomes. The model also applied a matrix of randomly-applied switch rates that were bounded at their upper and lower limits within a range specified at input and were then evolved over a 1000 runs for the specific set of conditions to maximize duration of infection. While this was designed to “select” for an optimal matrix, the particular characteristics of an output matrix depended on stochastic events, i.e. the timing of a randomly-generated switch in an expanding population. For this reason up to 10 replicates of the simulation were carried out for each set of conditions.
Figure 7 summarizes the results of this simulation for three different ranges of switch rates per genome per generation: 10-6 to 10-3, 10-7 to 10-4, and 10-8 to 10-5. The number of serotypes was 12. Specific antibody appeared after there were at least 100 bacteria and then accumulated at a rate equivalent to the doubling rate for the bacteria, as we had noted [4]. The values for other parameters are given in the legend for the figure. The dependent variable was the duration of infection in arbitrary time units over continuous scale. When there were no switches and, consequently, no antigenic variation, the duration of infection was ~50 time steps. This was the outcome when the generation lag was long and the switch rate was low. When antigenic variation occurred at a high enough frequency for variant cells to appear before antibody accumulations reached a neutralizing level, the infection was extended. Infection duration was least for cells with only one genome. It increased in time for all sets of switch rates as genome copies increased, up to the point when there was too much generation lag for a given switch rate range (e.g. 7 when the switch range was 10-7 to 10-4). As the critical nexus of long generation lag and low switch rate was approached, the variances of the outcomes among the replicates increased (e.g. a generation lag of 7 for a switch range of 10-6 to 10-3). For genome copies in range of 8 to 32 per cell the durations of infection were comparatively robust and were at or near its maximum—about 3-fold the durations for cells incapable of immune evasion—for all three sets of switch rates. As detailed in the next section, the overall range of 10-8 to 10-3 for switch rates encompassed rates that were observed in experimental infections [13].
Re-evaluation of VMP switch rate in B. hermsii. The estimate of the switch in serotype rate by Stoenner et al. was 10-4 to 10-3 per cell per generation [14]. We examined in more detail the data of that paper’s Table V, which provided the frequencies of new serotypes in populations in mouse blood after immunosuppressed mice had been treated with serotype-specific antisera to the infecting serotype, in that case serotype 7. We applied a simple estimate of mutation rate (equivalent here to switch rate) that is based on the Poisson distribution and the proportions of the null class, i.e. no detectable variants in the replicate [39]. The frequencies of null class replicates were 20 of 20 for sample sizes of 333 cells, 14 of 20 for 1,000 cells, 4 of 20 for 10,000 cells, and none of 20 for 100,000 cells. On this basis, the switch rate for a population serotype 7 to any other serotype could more precisely be estimated as between 0.7 x 10-4 and 3.3 x 10-4 per cell per generation based.
We also analyzed data from our previous study of serotype 7 and serotype 19 B. hermsii infections in mice [13]. Table 2 of the Supplementary Information for that paper provided 9 replicates each of infected mouse bloods for the quantitative determinations of the frequencies of serotype 7 in a growing population of serotype 19 cells and of serotype 19 in a growing population of serotype 7 cells. Although differential growth rates between wildtype and mutant can confound mutation rates estimates [18], our observation of mixtures of the two serotypes was that serotype 7 and serotype 19 grew at the same rate in mice [13]. A fluctuation analysis using FALCOR [40] was applied. The estimated switch rate (with 95 percent CI) for serotype 19 to serotype 7 was 1.5 (0.7-2.2) x 10-4 per cell per generation. The corresponding rate for cells of serotype 19, an infrequently observed serotype in mice during relapses [13], in a population of serotype 7 cells was 2.5 (2.3-4.9) x 10-7, a thousand-fold lower. If the count of cells with a new serotype for the population size when we measured it actually was the result of switches that occurred in genomes 3-4 generations earlier in the population’s history, then the genome switch rates per generation in the blood of mice from serotype 19 to serotype 7 or from serotype 7 to any other serotype was ~10-3.
Discussion
Ryan and Wainwright noted in 1954 that a mutation in only one of the “nuclei” of a bacterium with four chromosomes could result in a two-generation delay in the growth of a mutant clone in an environment selecting against the parent phenotype and called this phenomenon “segregation delay” [41]. Our observations from experiments and from computer simulations lead us to a similar conclusion about Borrelia species. There likely is a delay of a few generations in the complete change of phenotype of cells after a switch has occurred in one among the many tandemly-arrayed genomes, but it is not nearly so long as would be expected if the segregation of genomes was random.
By the criterion of duration of infection, there appear to be advantages of polyploidy over monoploidy for organisms with the adaptation of antigenic variation, and possibly for other forms of genetic variation in the face changing environment, such as transmission from one species of vertebrate host to another species. However, the advantage accrues only for the contingency of linear segregation. Under this mode of replication, there is the accumulation in the bacterial population of many heterozygotes, some descendants of which will be homozygotic for an antigen that is novel in the context of an the infected animal. As Lark remarked about organisms with multiple chromosomes, “...non-random segregation can be viewed as a mechanism for preserving cell lineages with useful adaptation” [42].
Our studies focused on relapsing fever and one species, B. hermsii, in particular. Under the limits of the model, the favorable range of switch rates for linearly-segregating polyploid cells undergoing antigenic was similar to what was empirically observed in infected mice [14,27]. Other Borrelia species of relapsing fever agents, such as B. duttonii and B. turicatae, have multiple VMP genes which sequentially manifest during relapses [1], so presumably the same circumstances apply. But what about that other clade in the family Borreliaceae, the agents of Lyme disease? There are multiple genomes in these spirochetes as well [12]. An antigenic variation system in Borreliella (Borrelia) burgdorferi involves the VlsE gene, which is located on a linear plasmid [43]. Instead of a complete or near-complete replacement of the antigen gene at an expression site, as occurs in B. hermsii, in B. burgdorferi there is the accumulation of more localized conversions that are sequentially templated by partial vlsE sequences at another locus. But the same challenge exists for B. burgdorferi: achieving homogeneous expression of the converted vlsE gene after a conversion event as soon as possible in an environment of circulating antibodies to the unaltered VlsE protein.
Figure 7.
Box whisker plots of durations in arbitrary time units of infection by different generation lags in achievement of homozygosity for a switched gene in simulations that incorporate parameters for the host antibody response (see text). Matrices of evolved switch rates were in the ranges of 10-6 to 10-3, 10-7 to 10-4, and 10-8 to 10-5 per genome per generation. There were 300 time steps, each step being 0.1 in arbitrary time units. Serotype-specific antibody appeared and began to accumulate once there were at least 100 cells and at doubling rate equal to the doubling rate for the bacteria. The antibody synergy parameter (b) was 0.5. The antibody loss rate was 0.001. The carrying capacity, i.e. the maximum cell density, was 107 cells per milliliter. The death rate constant for the bacteria once serotype-specific antibody appeared was 0.001. For each condition there were a 1000 runs and in 5 or 10 replicates. If the coefficient of variation was >0.05 after 5 replicates, another 5 replicates of 1000 runs were carried out.
Acknowledgments
The work was supported National Institute of Health grant AI-24424. We thank Steven Frank for helpful discussions in the past and his suggestion for incorporation of antibody synergy in the model. We also thank the several colleagues who over the years at conferences and seminars asked about the implications of polyploidy for antigenic variation. These questions finally spurred us to examine the possible consequence of multiple genomes for this pathogen.
Glossary
- SCID
severe combined immunodeficiency
- VMP
variable major protein
Appendix A.
Author Contributions:
C.D.C., R.L.D., and A.G.B. planned and carried out the studies, analyzed the data, and wrote the paper. R.L.D. wrote the computer programs. The work of all authors was supported by National Institute of Health grant AI-24424. R.L.D. was also supported by a scholarship from King Abdullah University of Science and Technology.
References
- Barbour AG, Guo BP. The pathogenesis of relapsing fever. In: Radolf JD, Samuels DS, editors. Borrelia: Molecular Biology, Host Interaction and Pathogenesis. Norfolk, UK: Caister Academic Press; 2010. pp. 333–358. [Google Scholar]
- Kussell E, Leibler S. Phenotypic diversity, population growth, and information in fluctuating environments. Science. 2005;309(5743):2075–2078. doi: 10.1126/science.1114383. [DOI] [PubMed] [Google Scholar]
- Barbour AG, Tessier SL, Stoenner HG. Variable major proteins of Borrellia hermsii. J Exp Med. 1982;156(5):1312–1324. doi: 10.1084/jem.156.5.1312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Crowder CD, Ghalyanchi Langeroudi A, Shojaee Estabragh A. et al. Pathogen and host response dynamics in a mouse model of Borrelia hermsii relapsing fever. Vet Sci. 2016;3(3):19. doi: 10.3390/vetsci3030019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitten T, Barbour AG. Juxtaposition of expressed variable antigen genes with a conserved telomere in the bacterium Borrelia hermsii. Proc Natl Acad Sci U S A. 1990;87(16):6077–6081. doi: 10.1073/pnas.87.16.6077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Plasterk RH, Simon MI, Barbour AG. Transposition of structural genes to an expression sequence on a linear plasmid causes antigenic variation in the bacterium Borrelia hermsii. Nature. 1985;318(6043):257–263. doi: 10.1038/318257a0. [DOI] [PubMed] [Google Scholar]
- Barbour A, Burman N, Carter C. et al. Variable antigen genes of the relapsing fever agent Borrelia hermsii are activated by promoter addition. Mol Microbiol. 1991;5:489–493. doi: 10.1111/j.1365-2958.1991.tb02132.x. [DOI] [PubMed] [Google Scholar]
- Barbour AG. The chromosome and plasmids of the tick-borne relapsing fever agent Borrelia hermsii. Genome Announc. 2016;4(3):e00528. doi: 10.1128/genomeA.00528-16. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bergström S, Zückert WR. Structure, function and biogenesis of the Borrelia cell envelope. In: Samuels DS, Radolf JD, editors. Borrelia: Molecular Biology, Host Interaction, and Pathogenesis. Norfolk, UK: Caister Academic Press; 2010. pp. 139–166. [Google Scholar]
- Hinnebusch J, Barbour AG. Linear- and circular-plasmid copy numbers in Borrelia burgdorferi. J Bacteriol. 1992;174(16):5251–5257. doi: 10.1128/jb.174.16.5251-5257.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitten T, Barbour AG. The relapsing fever agent Borrelia hermsii has multiple copies of its chromosome and linear plasmids. Genetics. 1992;132(2):311–324. doi: 10.1093/genetics/132.2.311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinnebusch BJ, Bendich AJ. The bacterial nucleoid visualized by fluorescence microscopy of cells lysed within agarose: comparison of Escherichia coli and spirochetes of the genus Borrelia. J Bacteriol. 1997;179(7):2228–2237. doi: 10.1128/jb.179.7.2228-2237.1997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbour AG, Dai Q, Restrepo BI. et al. Pathogen escape from host immunity by a genome program for antigenic variation. Proc Natl Acad Sci U S A. 2006;103(48):18290–18295. doi: 10.1073/pnas.0605302103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stoenner HG, Dodd T, Larsen C. et al. Antigenic variation of Borrelia hermsii. J Exp Med. 1982;156(5):1297–1311. doi: 10.1084/jem.156.5.1297. [DOI] [PMC free article] [PubMed] [Google Scholar]
- OED Online [Internet] Oxford: Oxford University Press; 2016. [cited 2017 March]. “polyploid, adj. and n.”. Available from: http://www.oed.com/view/Entry/147327?redirectedFrom=polyploid . [Google Scholar]
- Lieb M. Forward and reverse mutation in a histidine-requiring strain of Escherichia coli. Genetics. 1951;36(5):460. doi: 10.1093/genetics/36.5.460. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Newcombe HB. Delayed phenotypic expression of spontaneous mutations in Escherichia coli. Genetics. 1948;33(5):447–476. doi: 10.1093/genetics/33.5.447. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kissling GE, Grogan DW, Drake JW. Confounders of mutation-rate estimators: selection and phenotypic lag in Thermus thermophilus. Mut Res. 2013;749(1-2):16–20. doi: 10.1016/j.mrfmmm.2013.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schaechter M, Maaloe O, Kjeldgaard NO. et al. Dependency on medium and temperature of cell size and chemical composition during balanced grown of Salmonella typhimurium. J Gen Microbiol. 1958;19(3):592–606. doi: 10.1099/00221287-19-3-592. [DOI] [PubMed] [Google Scholar]
- Cooper S, Helmstetter CE. Chromosome replication and the division cycle of Escherichia coli B/r. J Mol Biol. 1968;31(3):519–540. doi: 10.1016/0022-2836(68)90425-7. [DOI] [PubMed] [Google Scholar]
- Maldonado R, Jimenez J, Casadesus J. Changes of ploidy during the Azotobacter vinelandii growth cycle. J Bacteriol. 1994;176(13):3911–3919. doi: 10.1128/jb.176.13.3911-3919.1994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jacob F, Brenner S, Cuzin F, et al., editors. On the regulation of DNA replication in bacteria. Cold Spring Harbor Symposia on Quantitative Biology. Cold Spring Harbor: Cold Spring Harbor Laboratory Press; 1963. [Google Scholar]
- Novick R, Wyman L, et al. Plasmid life cycles in Staphylococcus aureus. In: Schlessinger D, editor. Microbiology-1974. Washington, DC: American Society for Microbiology; 1975. pp. 115–129. [Google Scholar]
- Lopez JE, Schrumpf ME, Raffel SJ. et al. Relapsing fever spirochetes retain infectivity after prolonged in vitro cultivation. Vector Borne Zoonotic Dis. 2008;8(6):813–820. doi: 10.1089/vbz.2008.0033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thompson RS, Burgdorfer W, Russell R. et al. Outbreak of tick-borne relapsing fever in Spokane County, Washington. JAMA. 1969;210(6):1045–1050. [PubMed] [Google Scholar]
- Restrepo BI, Kitten T, Carter CJ. et al. Subtelomeric expression regions of Borrelia hermsii linear plasmids are highly polymorphic. Mol Microbiol. 1992;6(22):3299–3311. doi: 10.1111/j.1365-2958.1992.tb02198.x. [DOI] [PubMed] [Google Scholar]
- Dai Q, Restrepo BI, Porcella SF. et al. Antigenic variation by Borrelia hermsii occurs through recombination between extragenic repetitive elements on linear plasmids. Mol Microbiol. 2006;60(6):1329–1343. doi: 10.1111/j.1365-2958.2006.05177.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barbour AG. Isolation and cultivation of Lyme disease spirochetes. Yale J Biol Med. 1984;57(4):521–525. [PMC free article] [PubMed] [Google Scholar]
- Meier JT, Simon MI, Barbour AG. Antigenic variation is associated with DNA rearrangements in a relapsing fever Borrelia. Cell. 1985;41(2):403–409. doi: 10.1016/s0092-8674(85)80013-1. [DOI] [PubMed] [Google Scholar]
- Frank SA. A model for the sequential dominance of antigenic variants in African trypanosome infections. Proc Biol Sci. 1999;266(1426):1397–1401. doi: 10.1098/rspb.1999.0793. [DOI] [PMC free article] [PubMed] [Google Scholar]
- LeVeque RJ. Finite Difference Methods for Ordinary and Partial Differential Equations: Steady-state and Time-dependent Problems. Philadelphia: Siam; 2007. [Google Scholar]
- Frank SA, Barbour AG. Within-host dynamics of antigenic variation. Infect Genet Evol. 2006;6(2):141–146. doi: 10.1016/j.meegid.2004.10.005. [DOI] [PubMed] [Google Scholar]
- Holt SC. Anatomy and chemistry of spirochetes. Microbiol Rev. 1978;38:114–160. doi: 10.1128/mr.42.1.114-160.1978. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bates LB, Dunn LH, St John J. Relapsing fever in Panama. The human tick, Ornithodoros Talaje, demonstrated to be the transmitting agent of relapsing fever in Panama by human experimentation. Am J Trop Med. 1921;1(4):183–210. [Google Scholar]
- Koch A. The variability and individuality of the bacterium. In: Neidhardt F, editor. Escherichia coli and Salmonella typhimurium: Cellular and Molecular Biology. Washington DC: American Society for Microbiology; 1987. p. 1606. [Google Scholar]
- Crowder CD. Infection dynamics of the relapsing fever agent Borrelia hermsii. Irvine, CA: University of California Irvine; 2007. [Google Scholar]
- Alugupalli KR, Gerstein RM, Chen J. et al. The resolution of relapsing fever borreliosis requires IgM and is concurrent with expansion of B1b lymphocytes. J Immunol. 2003;170(7):3819–3827. doi: 10.4049/jimmunol.170.7.3819. [DOI] [PubMed] [Google Scholar]
- Meleney HE. Relapse phenomena of Spironema recurrentis. J Exp Med. 1928;48:65–82. doi: 10.1084/jem.48.1.65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Foster PL. Methods for determining spontaneous mutation rates. Meth Enzymol. 2006;409:195–213. doi: 10.1016/S0076-6879(05)09012-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hall BM, Ma CX, Liang P. et al. Fluctuation analysis CalculatOR: a web tool for the determination of mutation rate using Luria-Delbruck fluctuation analysis. Bioinformatics. 2009;25(12):1564–1565. doi: 10.1093/bioinformatics/btp253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ryan FJ, Wainwright LK. Nuclear segregation and the growth of clones of spontaneous mutants of bacteria. J Gen Microbiol. 1954;11(3):364–379. doi: 10.1099/00221287-11-3-364. [DOI] [PubMed] [Google Scholar]
- Lark KG. Discovering non-random segregation of sister chromatids: the naive treatment of a premature discovery. Front Oncol. 2012;2:211. doi: 10.3389/fonc.2012.00211. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang JR, Norris SJ. Genetic variation of the Borrelia burgdorferi gene vlsE involves cassette-specific, segmental gene conversion. Infect Immun. 1998;66(8):3698–3704. doi: 10.1128/iai.66.8.3698-3704.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]