Assessing Model Selection Uncertainty Using a Bootstrap Approach: An update

Abstract

Model comparisons in the behavioral sciences often aim at selecting the model that best describes the structure in the population. Model selection is usually based on fit indices such as AIC or BIC, and inference is done based on the selected best-fitting model. This practice does not account for the possibility that due to sampling variability, a different model might be selected as the preferred model in a new sample from the same population. A previous study illustrated a bootstrap approach to gauge this model selection uncertainty using two empirical examples. The current study consists of a series of simulations to assess the utility of the proposed bootstrap approach in multi-group and mixture model comparisons. These simulations show that bootstrap selection rates can provide additional information over and above simply relying on the size of AIC and BIC differences in a given sample.

Introduction

Model selection can have different goals. Examples are selection of a model that optimally predicts an outcome in new data, selection of a regression model that includes the most important predictors (i.e., variable selection), or selection of a model that adequately describes the interrelations of the variables of interest. This study focuses on the latter, more specifically on model selection in the area of latent variable (mixture) model comparisons. Model selection in empirical studies in this area often relies on one or more fit indices of choice together with suggested cutoff-criteria for these indices to select a single best-fitting model. The best-fitting model is then used for inference regarding model structure and parameter estimates. This practice has been criticized for not taking into account the uncertainty of model selection: in a different sample drawn from the same population, a different model might be selected due to sampling fluctuation (Burnham & Anderson, 2002; Efron, 2014; Preacher & Merkle, 2012). Inference regarding parameter estimates and model implied structural relations should therefore be made in the context of model selection uncertainty.

However, model selection uncertainty is not directly quantifiable if only a single sample is available. To improve on the practice of focusing on a single best-fitting model a previous study proposed to use a bootstrap approach to gauge model selection uncertainty (Lubke & Campbell, 2016). Two empirical examples illustrated that conducting model comparisons in bootstrap samples drawn with replacement from the original sample can serve to compute bootstrap model selection rates, which in turn can caution against focusing on a single best-fitting model. The current study aims at assessing the performance of this bootstrap approach with simulated data. In particular, we want to establish whether bootstrap selection rates can add information on model uncertainty over and above the information coming from selection criteria AIC (Akaike Information Criterion) or BIC (Bayesian Information Criterion) of competing, potentially non-nested models.

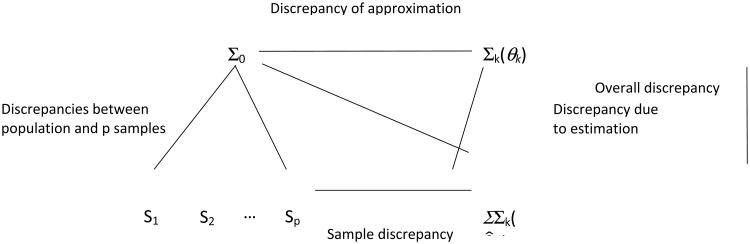
Linhart and Zucchini (1986; see also Cudeck & Henly, 1991; Preacher, Zhang, Kim, & Mels, 2013) provide a useful framework for investigating model selection uncertainty and the potential utility of bootstrapping model comparisons. The framework is illustrated in Figure 1 (based on Figure 1 of Cudeck & Henly, 1991), which shows the population covariance matrix Σ₀, sample covariance matrices S₁, S₂, …, S_p, computed in repeated samples from the population, the model-implied covariance matrix Σ_k(θ) at the population level for model k, and the estimated model implied covariance matrix Σ_k(θ̂_k). Different discrepancies between pairs of these matrices can be defined. First, the difference between the population covariance matrix Σ₀ and the model-implied covariance matrix Σ_k(θ) of an approximating model M_k is called the “discrepancy due to approximation”. This discrepancy is a constant, as it involves the difference between two covariance matrices that are fixed, and depends only on the level of misspecification of M_k. Second, the difference between the model-implied covariance matrix Σ_k(θ) and its estimated counterpart is termed, “discrepancy due to estimation”. This discrepancy is a random variable because it depends on model estimation in a sample. For a given finite sample size, it increases with the number of estimated parameters, and decreases with increasing sample size. Third, the “sample discrepancy” is the difference between an observed sample covariance matrix S_i and the estimated model implied matrix Σ_k(θ̂_k). This discrepancy is the observed counterpart of the discrepancy due to approximation. It is the only quantity that is directly calculable in a single sample, and is the basis of model evaluation in an empirical study. Fourth, the overall discrepancy is the difference between Σ₀ and Σ_k(θ̂_k). For the purpose of this paper, it is useful to add the discrepancy between the population covariance matrix and the sample covariance matrix (see Figure 1), which we call PS-discrepancy. As N approximates the population size, the PS-discrepancy vanishes as a result of the sample becoming more and more representative of the target population.

Figure 1.

Although Cudeck and Henly (1991) describe the different discrepancies in the context of covariance structure analysis, the framework is useful more generally (see Linhart & Zucchini, 1986). It can be used to connect the concepts of model selection uncertainty and power to discriminate between alternative models, and it provides a relevant background to assess the performance of different fit indices and the necessary sample size to select an appropriate model.

Model selection uncertainty refers to the situation where different models are selected as the best-fitting model when fitting a set of k models to multiple, equal sized samples from the population (S₁, … S_p in Figure 1). Model selection uncertainty is not directly estimable if only a single sample is available. It can be quantified in a simulation by computing model selection rates across multiple samples generated under a population model. Model selection uncertainty is likely to increase with increasing PS-discrepancy, especially if the fitted models imply relatively similar structures. Since the PS-discrepancy decreases with increasing sample size, model selection uncertainty is expected to decrease as well. In the extreme case that the sample contains the entire the population, model selection uncertainty is zero, with the effect that the best-fitting model is the model with the smallest discrepancy due to approximation. Model selection is usually done based on one or more selection criteria. Note that different model selection criteria have different objectives, and employ different model parsimony penalties. Consequently, different fit criteria can result in different model selection rates. Note also that although the best model would be the model with the smallest discrepancy due to approximation, in a model selection based on fit criteria the best model is not necessarily the same as the best-fitting model because of the parsimony penalties. For a given choice of fit index, model selection and the power to discriminate between different models depends on the discrepancies due to approximation of the models as well as the discrepancies due to estimation. As with the PS-discrepancy, the discrepancy due to estimation for a given model decreases with increasing sample size, with the effect that the discrepancy due to approximation becomes more important in determining the power to discriminate between models.

The comparison of latent variable models in the behavioral sciences is most commonly aimed at finding the model that is most appropriate to describe the structure in the population. In practice, usually only a single sample (i.e., only an empirical distribution) is available, making it impossible to directly assess discrepancies of approximation of the candidate models or model selection uncertainty. A previous paper illustrated a resampling approach aimed at quantifying selection uncertainty using two empirical data sets (Lubke & Campbell, 2016). Generally, resampling observed sample values with replacement (“naïve bootstrapping”) from a representative sample can be used to obtain the distribution of a statistic of interest (Efron, 1979). Naïve bootstrapping, however, does not necessarily always work well.

Bollen and Stine (1992) illustrate the inadequacy of naïve bootstrapping when the procedure is used to obtain the critical value in a one-sided null-hypothesis test of the mean of a squared normally distributed variable with known variance 1. They show that, in this example, neither the expected value nor the variance of the chi-square distributed test statistic computed across bootstrap samples equals the expected value or variance under the null hypothesis, and therefore the bootstrapped distribution does not provide a correct critical value for statistical testing. The key problem is that any given sample will likely deviate from the (in this case hypothetical) population where the null hypothesis is true, that is, the empirical distribution does not have mean zero. The Monte Carlo distribution derived by naïve bootstrapping will consequently also not center at zero. In addition, Bollen and Stine (1992) show that the variance of the bootstrapped test statistic is also inflated due to the PS-discrepancy.

Similarly, consider drawing a sample from a multivariate normal distribution followed by computing the sample covariance matrix for that particular sample, S_i, and fitting model A to S_i. As stated above, a sample covariance matrix computed in a finite sample drawn from the population deviates from the population covariance matrix Σ₀. Resampling from the empirical distribution with replacement provides the Monte Carlo distribution of the sample covariance matrix S_i, and fitting model A to each bootstrap sample covariance matrix results in the bootstrap estimate of the sample discrepancy S_i− Σ_A(θ̂_A). This estimate depends on a single observed S_i, which deviates from Σ₀ by the PS-discrepancy. The bootstrap estimate is expected to center around S_i, and therefore to differ from the true model selection uncertainty in repeated samples from the population because multiple S_i, i=1, … p center around Σ₀. In other words, the difference is due to the fact that naïve bootstrapping reuses in-sample data, whereas model selection uncertainty is defined for out-of-sample data. However, to the extent that a sample is representative of the structure in the population this difference is expected to be small.

Bollen and Stine (1992) and others (Yuan, Hayashi, & Yanagihara, 2007) have proposed improved bootstrap methods in order to test the fit of a given model. Instead of naïvely resampling from the empirical distribution, the central idea behind these methods is to resample not directly from the observed sample data, but from modified data or a modified covariance matrix. The modifications can, for instance, be based on available theory concerning the data, and generally aim at a better representation of the desired population. The proposed resampling schemes are suitable to assess the performance of a given model relative to the population of interest but are not suitable for the comparison of non-nested models. Furthermore, the methods are designed for covariance structure models rather than the raw data analyses that are necessary when fitting and comparing mixture models.

Model selection in mixture model comparisons is especially challenging due to the fact that a higher level of within class model complexity can be counterbalanced by fewer classes (or vice versa) to achieve a similar fit. As a consequence of the interdependency of the number of classes and the within class parameterization it is common in practice to compare a very large number of mixture models. Information regarding the replicability of results over and above currently used fit criteria would be beneficial in this field.

The question then arises to what extent naïve bootstrapping can be useful to gauge model selection uncertainty, that is, to assess whether more than one model would be selected with considerable non-zero probability in repeated samples from the population. Resampling from observed sample data with replacement followed by model comparisons in each bootstrap sample provides the bootstrap estimate of model selection rates using the information provided by a single sample drawn from a population. Based on the discussion above, these bootstrap selection rates are not expected to provide unbiased estimates of the model selection rates that would be observed in repeated samples from the population due to the bias introduced by the PS-discrepancy. However, comparing a set of different models in bootstrap samples drawn from a representative sample should to some extent reflect the true degree of model selection uncertainty. Therefore bootstrap selection rates should provide useful information about the confidence one should assign to the best-fitting model.

In a series of simulations, we focus on the situation that BIC or AIC differences between the two best-fitting models provide “strong” or “very strong evidence” in favor of the best-fitting model according to suggested guidelines (Burnham & Anderson, 2004; Kass & Raftery, 1995). We consider these scenarios because researchers might be particularly tempted to base inference only on the best-fitting model when AIC or BIC differences between the two best fitting models are large. The first part of the simulation study concerns the comparison of 2-group factor models, and the second part concerns 1- and 2-class mixture models. The aim of both parts is to investigate whether bootstrap selection rates are indicative of model selection uncertainty and to what extent they can provide useful information over and above suggested guidelines regarding AIC or BIC differences between the top two models.

Methods

Data Generation and Fitted Models

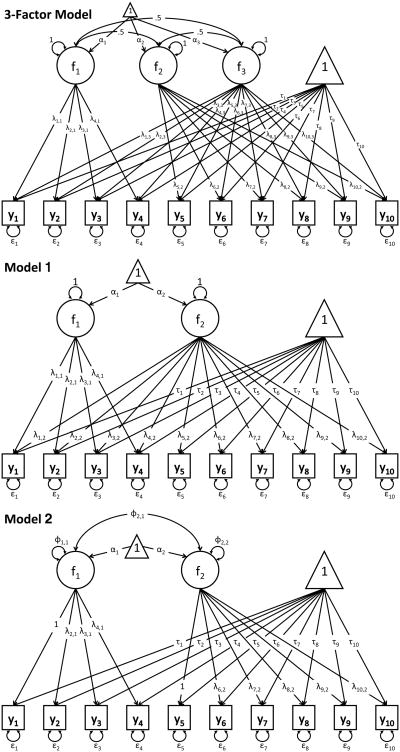
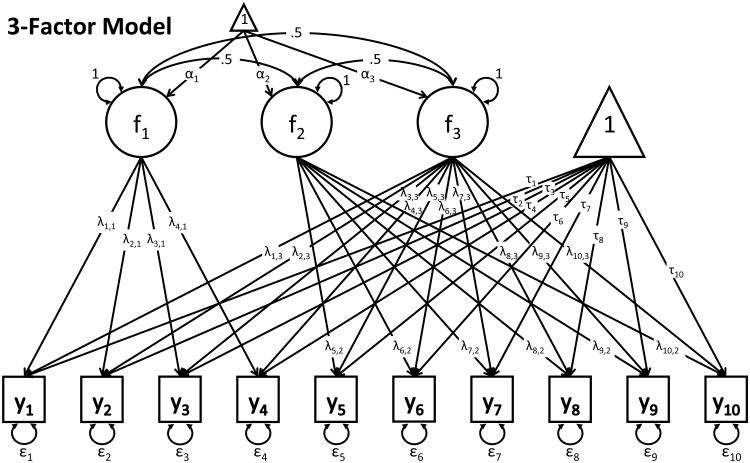
Data-generating processes are commonly more complex than the structure specified in the models that are fitted to sample data. In this study, data are generated under a 2-group, 3-factor model for ten observed variables (see Figure 2), which has 83 parameters, and is more complex than any of the fitted models. Data were generated for total sample sizes of N=200, 350, 700, and 1500 with equal-sized groups. The Mahalanobis distance (MD) between the two groups in the population was 1.792. The average MD in samples of N=350 was 1.875 with a standard deviation of 0.123. These values were similar for N=700, averaging at 1.939 with a standard deviation of 0.09. Note that the model implied MD's of the fitted models can differ from these values.

Figure 2.

We compare the fit of different 2-group (or 2-class) 2-factor models to the simulated data. The 2-group models are part of the set of 2-factor models used in the analysis of the Holzinger-Swineford (Holzinger & Swineford, 1939) data presented in Lubke and Campbell (2016). Model 1 was a bi-factor model (54 parameters), model 2 was a 2-factor model with correlated factors with group (or class) specific loadings (62 parameters), and model 3 had the same factor structure as model 2 but loading invariance across groups or classes was imposed (also 54 parameters, see Figure 2). Note that models 1 and 3 had the same number of parameters but differed with respect to the model implied mean and covariance structure. The set of mixture models included two single class models, namely the bi-factor model (34 parameters) and the model with two correlated factors (31 parameters). Note that when fitting single class models model 3 was identical to model 2. In addition, we fit the 2-class versions of models 1 through 3 (55 parameters for the 2-class versions of models 1 and 3, and 64 parameters for model 2). While the two-group models utilize the correct grouping variable, the 2-class mixture models were fitted to the same data without this information.

Model fit criteria AIC and BIC

The fitted models are not all nested, and were therefore compared using the AIC as well as the BIC. For the mixture models, we provide results concerning the sample-size adjusted BIC, which represents a compromise between AIC and BIC in terms of the parsimony penalty. While the main focus of this paper is not on the comparison of fit criteria, it is clear that the choice of criterion has a direct effect on model selection. AIC and BIC have been derived within different philosophies but, more importantly, they have different objectives regarding model selection.

The objective of the AIC can be described as the selection of the model that minimizes the overall discrepancy for a given sample size by finding a compromise between the discrepancy due to approximation and the discrepancy due to estimation. The latter (for a given N) is a monotonically increasing function of p (Bozdogan, 1987; Burnham & Anderson, 2004). The AIC is based on the Kullback-Leibler divergence I which quantifies the distance between two distributions as the difference between their expected log likelihoods (Kullback & Leibler, 1951). Denote the distribution in the population as f(y|θ*) with true parameter vector θ*, and an approximating distribution implied by a model M_k as f(y|θ_k), then I(θ*; θ_k) = E[log] f(y|θ*)− E[log f(y|θ_k)], where the expectation is with respect to the true population distribution. Note that this measure is a quantification of the discrepancy due to approximation. The first term depends on the true population parameters, and the second term depends on the parameter vector θ_k of M_k. The AIC is a sample based estimator of 2E[I(θ*; θ_k)], where estimates of θ_k are obtained by maximum likelihood (see Bozdogan, 1987, or Burnham & Anderson, 2004, for an accessible description of the derivation of AIC). Writing the average overall discrepancy, as quantified by 2nE[I(θ*; θ̂_k)], as the sum of the expected approximation error and the expected estimation error, one can show that the latter equals the df of the approximating model. The first term depends on the true and approximating model; however, when comparing different models, the interest is in finding the model that minimizes 2nE[I(θ*; θ̂_k)], so the constant term pertaining to the population can be omitted, leading to the formula AIC = −2 log L (θ̂_k) +2p.

Importantly, AIC represents a tradeoff between bias due to using an approximating model and variance due to estimation. The optimal tradeoff depends on sample size because with increasing sample size, the AIC for a given model is increasingly dominated by the maximized log likelihood. This can result in the selection of increasingly complex models as sample size increases. That is, AIC is not asymptotically consistent (for examples, see Linhart & Zucchini, 1986).

The objective of BIC is to select the model with the highest posterior probability. It is derived as an approximation of the Bayes factor. Suppose r=1, …, k,…, R models are considered. Using Bayes' theorem, the posterior probability of M_k equals $m_k/{\sum }_{r=1}^R{m}_r$ where m_r is the likelihood of the model times the prior of the parameters integrated over the parameter space (see for instance Wasserman, 2000). Assuming that each model has the same prior selection probability, a Bayes factor for two models M_i and M_j is simply m_i/m_j. Bayes factors are easy to interpret in terms of how likely M_i is relative to M_j. Bayes factors depend on the choice of priors for the parameters. That is, different priors result in different Bayes factors. In addition, their calculation can be cumbersome, especially in case of highly parameterized models, due to the necessity to solve multiple integrals. Instead, Kass and Wasserman (1995) showed that m_k can be approximated by m̂_k, where log m̂_k = log L (θ̂_k) −p/2*log N. The approximation is “fairly accurate” (Wasserman, 2000) if the prior for the parameters is a specific type of non-informative prior. Multiplying log m_k by −2 gives BIC= −2 log L (θ̂_k) +p*log N.

BIC is asymptotically consistent, which means that BIC-based selection converges to the model with the highest posterior probability in the long run, given sufficient sample size. If sample size is not sufficient, however, selection using BIC will result in adopting overly simple models.

Regarding the use of the AIC in empirical analyses, Burnham and Anderson (2004) state that empirical support for the second best fitting model is substantial if the AIC difference between the best and second best fitting models is between 0 and 2, is considerably less given differences between 4 and 7, and is essentially absent if differences are larger than 10. Kass and Raftery (1995) provide very similar guidelines for BIC differences based on Jeffrey's (1961) guidelines for the interpretation of Bayes factors, namely that a BIC difference between 0 and 2 is not worth more than a bare mention, that a difference between 2 and 6 provides positive evidence against the second best fitting model, a difference between 6 and 10 provides strong, and a difference larger than 10 provides very strong evidence against the second best model.

Preliminary Analyses

To determine a priori which of the fitted models has the smallest discrepancy due to approximation, we fit the three 2-group models to the model-implied covariance matrices and mean vectors of the 2-group 3-factor population model that were computed with the true parameter values. Using the model-implied covariance and mean structure rather than generating data under a model eliminates sampling error. In this situation, if the fitted models are only mildly misspecified, the value of the chi-square test of model fit (i.e., the likelihood ratio test between the fitted and the saturated model) equals the non-centrality parameter (Satorra & Saris, 1985). Although the scale of the obtained chi-square test of model fit statistics depend on sample size, the ordering of the three fitted models with respect to this statistic does not, and therefore provides the correct order of the discrepancies due to the approximation of the models. The 2-factor model without loading invariance (Model 2) had the smallest chi-square test of model fit, followed by models 3 and 1. The values for N=700 were 31.466, 0.995, and 25.443 for model 1 through 3, respectively.¹ Recall that the two-group model 2 is the most complex model with 62 estimated parameters, whereas models 1 and 3 both have 54 estimated parameters. The two more restricted models might be favored at smaller sample sizes due to parsimony penalties implemented in the AIC and BIC. Note that out of these two, model 3 should be selected more often because of its smaller discrepancy due to approximation. The selection rate of model 2 is expected to increase with increasing sample size because model selection in a given sample (estimation method and fit index being equal) depends on the discrepancy due to approximation as well as the discrepancy due to estimation. The latter is expected to decrease with increasing sample size, and therefore the relative impact of the discrepancy of approximation becomes more important, favoring the selection of model 2.

Bootstrap Method

Part 1 of the simulation concerns the comparison of the three 2-group models, and consisted of drawing 1000 samples from the population (for each of the 4 sample sizes) followed by fitting the three models to each sample. We obtained (1) the AIC and BIC differences between the best and second best-fitting model in each sample, and (2) the AIC and BIC-based model selection rates across samples to quantify model selection uncertainty. Next, B=2000 bootstrap samples were drawn from each of these samples (called “population sample” to clarify the distinction with “bootstrap sample”) and the models were compared in each bootstrap sample (i.e., a total of 8,000,000 model comparisons). In each set of 2,000 bootstrap samples, the bootstrap model selection rates for the three models were computed based on the AIC as well as based on BIC. This setup permits relating the AIC or BIC difference between the best and second best fitting models in a population sample to the bootstrap selection rates in that same population sample. This in turn permits assessing the additional value of naïve bootstrapping over and above rules-of-thumb regarding the size of the AIC or BIC differences advocated by, for instance, Burnham and Anderson (2004) and Kass and Raftery (1995).

In the second part of the simulation, five mixture models were fitted as single class and 2-class versions of the two-group models. The single class models did not account for the presence of the groups present in the data. The simulation involving the comparison of mixture models was more limited in size due to the computational burden of estimating mixture models. The five mixture models were fitted to 100 of the population samples with sample sizes N=350 and N=700, respectively. The number of bootstrap samples drawn from each population sample was set to 100 as well, resulting in a total of 20,000 comparisons of the five models. AIC, BIC, and saBIC differences between the best and second best fitting models were recorded for each sample from the population and were compared to the bootstrap selection rates, similar to the process described above for the two-group models.

Results

The results for the 2-group analyses are presented first, followed by the mixture results. Both sections have two main parts: (a) the results pertaining to model selection in repeated samples from the population, which provide the basic information about model selection uncertainty under the different conditions, and (b) the results concerning model comparisons in the bootstrap samples drawn from each of the repeated samples from the population.

In the analyses of the bootstrap comparisons, the focus is on whether bootstrap selection rates are smaller than unity for the best-fitting model especially when the AIC or BIC differences in the population were larger than 8 while model selection uncertainty is evident in repeated samples from the population. Large AIC or BIC differences are considered as strong or very strong evidence in favor of the best fitting models. Relying on these cutoffs would not be advised if there is evidence of model selection uncertainty. Therefore the interest of the simulations is to investigate whether bootstrap selection rates can protect against undue confidence under those conditions.

Part 1a: Two group models fitted to repeated samples from the population

Table 1 shows the model selection rates for models 1 through 3 for sample sizes N=200, N=350, N=700, and N=1500 using either the lowest AIC or lowest BIC as a criterion to determine the best fitting model. As can be seen, both AIC and BIC lead to non-zero selection rates for the more constrained models 1 and 3 at smaller sample sizes. At N=1500, the model with the smallest discrepancy due to approximation (model 2) is selected in all samples, independent of the selection criterion. These results are in line with the expectation that model selection uncertainty decreases with increasing sample size.

Table 1. Overall model selection rates for the 3 fitted 2-group models in P=1000 samples drawn from the population.

	N=200	N=350	N=700	N=1500
	AIC
model 1	0.089	0.055	0.005	0
model 2	0.794	0.905	0.995	1
model 3	0.117	0.04	0	0
	BIC
model 1	0.306	0.359	0.156	0
model 2	0.029	0.065	0.511	1
model 3	0.665	0.576	0.333	0

Note: Model 1-3 were compared using either AIC or BIC to determine the best-fitting model. Model selection rates are computed as the proportion of selecting a given model in P=1000 model comparisons.

Using the AIC as a criterion results in higher selection rates of model 2 already at smaller sample sizes compared to BIC. This result highlights the fact that although asymptotically BIC-based model selection results in selecting the model with the highest posterior probability, it can lead to adopting overly constrained models if sample size is too small. Specifically, for sample sizes N=200 and N=350, using BIC as a criterion almost always resulted in selecting models 1 and 3 rather than the more appropriate model 2. Model 3 was selected more often than model 1 at these sample sizes, in line with the different discrepancies due to approximation of these two equally parsimonious models.

Comparing results in smaller samples to the results in larger sample sizes, it is obvious that the AIC and BIC differences between the top 2 models generally increase with sample size. This is expected, and shows the higher power to discriminate between models in larger samples. As can be seen in Table 2 and Table 3, for N=200, in 168 of the 1,000 samples the AIC difference was smaller or equal to 2, whereas for the BIC it was 364 of the 1,000 samples. For N=350, 100 samples had AIC differences smaller than or equal to 2, and 397 samples had BIC differences smaller than or equal to 2 (see Table 2 and Table 3, column #samp). But even with N=200 or N=350, there were multiple samples in which the model comparisons resulted in larger AIC or BIC differences. For N=200, 371 samples had AIC differences larger than 10, and 73 samples had BIC differences larger than 10. In those cases, AIC-based selection was almost always in favor of the more appropriate, but also more highly parameterized, model 2 (369 out of 371, note though the high probability of selecting model 2 overall). Comparisons in samples that showed larger BIC differences were in favor of model 3, which is closer to the true data generating mechanism than model 1 (67 out of 73, note that model 2 was not often selected in general at that sample size). With sample size at N=700, BIC-based selection resulted in more samples in which model 2 was selected overall. Importantly, there were also more samples with BIC differences larger than 10 and larger than 15 favoring model 2 (276 out of 1000 resulted in selection of model 2) than samples with these larger differences favoring models 1 or 3 (28 out of 1000).

Table 2. Median bootstrap selection rates for AIC and BIC based selection.

	AIC: model 1	AIC: model 2	AIC: model 3	BIC: model 1	BIC: model 2	BIC: model 3
N=200	0.28805	0.8899	0.25305	0.4865	0.674	0.606
N=350	0.30350	0.9590	0.18075	0.5360	0.734	0.550
N=700	0.34750	0.9995	NA	0.4250	0.842	0.412

Note: The P=1000 population samples and corresponding bootstrap samples were first grouped according to which model was the best fitting model based on either AIC or BIC for each sample size. The median bootstrap selection rates were then computed within each group. For instance, if AIC-based selection in the population sample with N=200 resulted in model 1 as the best fitting model, then the median bootstrap selection rate for model 1 in the corresponding bootstrap samples was 0.28805.

Table 3. Minimum and maximum bootstrap selection model selection rates of the 3 fitted 2-group models in relation to AIC differences observed in samples drawn from the population.

Δ AIC	Model 1			Model 2			Model 3
	N=200
	min	max	#samp	min	max	#samp	min	max	#samp
0-2	0.136	0.518	53	0.564	0.862	59	0.112	0.457	56
2-4	0.181	0.538	20	0.501	0.908	89	0.196	0.515	37
4-6	0.265	0.606	6	0.619	0.906	81	0.255	0.623	17
6-8	0.297	0.509	4	0.534	0.935	105	0.436	0.544	3
8-10	0.37	0.783	3	0.694	0.968	88	0.388	0.651	3
10-12	0.643	0.643	1	0.514	0.974	73	NA	NA	0
12-15	0.643	0.643	1	0.55	0.982	102	NA	NA	0
15-20	NA	NA	0	0.683	0.992	100	NA	NA	0
>20	NA	NA	0	0.687	0.996	94	NA	NA	0
	N=350
0-2	0.179	0.353	25	0.69	0.862	48	0.084	0.319	27
2-4	0.242	0.449	20	0.688	0.9	67	0.165	0.443	8
4-6	0.348	0.487	7	0.783	0.943	71	0.262	0.371	4
6-8	0.47	0.542	2	0.824	0.954	74	0.459	0.459	1
8-10	0.511	0.511	1	0.859	0.967	64	NA	NA	0
10-12	NA	NA	0	0.898	0.981	81	NA	NA	0
12-15	NA	NA	0	0.787	0.988	97	NA	NA	0
15-20	NA	NA	0	0.914	0.996	151	NA	NA	0
>20	NA	NA	0	0.815	1	252	NA	NA	0
	N=700
0-2	0.274	0.348	2	0.734	0.734	1	NA	NA	0
2-4	0.317	0.364	3	0.79	0.868	3	NA	NA	0
4-6	NA	NA	0	0.842	0.855	2	NA	NA	0
6-8	NA	NA	0	0.907	0.954	4	NA	NA	0
8-10	NA	NA	0	0.875	0.968	6	NA	NA	0
10-12	NA	NA	0	0.91	0.964	8	NA	NA	0
12-15	NA	NA	0	0.922	0.988	22	NA	NA	0
15-20	NA	NA	0	0.932	0.996	54	NA	NA	0
>20	NA	NA	0	0.962	1	895	NA	NA	0

Note: Δ AIC is the AIC difference between the best and second-best fitting model in samples drawn from the population. Min and max are the minimum and maximum bootstrap selection rates for samples within a given range of Δ AIC presented for each winning model, and #samp is the number of samples within that range favoring that model. For instance, for N=200, there were 53 samples (out of P=1000) with an AIC difference between 0 and 2 favoring model 1, and the minimum and maximum bootstrap selection rates for model 1 were 0.136 and 0.518, respectively.

To summarize the results concerning model selection uncertainty in repeated samples from the population, smaller samples have, as expected, higher selection uncertainty. AIC-based selection resulted in less selection uncertainty than BIC (model 2 was selected 80% of the time using AIC with N=200, increasing to 0.995 with N=700 where as the BIC selection rate for any model and sample size remained below 0.7). Using BIC as a criterion model selection shifted from models 1 and 3 towards the selection of model 2 as sample size increased. In addition to higher levels of uncertainty when sample size is small, there was also a larger proportion of samples from the population resulting in small AIC or BIC differences. In other words, there is a higher probability of having lower power to discriminate between models. Higher probability does not mean certainty, and in some of the smaller samples the AIC or BIC differences were, in fact, substantial. In an empirical setting this would be interpreted as strong or very strong evidence in favor of the best model. Given the observed model selection in our simulated data, focusing on the single best fitting model would not be adequate in this case. In the next part we investigate whether under these conditions bootstrap selection rates can guard against undue confidence in the best model.

Part 1b: Bootstrap selection rates of 2-group models in relation to AIC and BIC differences in the corresponding population samples

Throughout this section, results for N=1500 are not shown due to the absence of model selection uncertainty (see Table 1) for this sample size. As expected bootstrap selection rates computed over all P=1000 × B=2000 bootstrap samples did not provide unbiased estimates of the model selection rates presented in Table 1. The bootstrap selection rates depended on which model was the best-fitting model in the sample drawn from the population, and, as might be expected, on the AIC or BIC differences between the first and second best-fitting models in the sample.

To provide some more detail, Table 2 shows the median bootstrap selection rates for best-fitting models for sample sizes N=200, 350, and 700, conditional on which model was selected as the best fitting model in the sample generated under the population model. The median bootstrap rates were computed as follows. For each sample size, the P=1000 population samples were first grouped according to which model was the best fitting model based on either AIC or BIC for each sample size. The median bootstrap selection rate was then determined for each group. The bootstrap selection rates need to be evaluated in the light of the model selection rates presented in Table 1. For instance, at N = 200 the median BIC bootstrap rate for model 2 was .674, but model 2 was only selected 2.9% of the time at that sample size. This means that the few times model 2 was selected according to BIC, it had a relatively high median bootstrap selection rate at the given sample size. AIC-based selection favored model 2 for all sample sizes with a low level of uncertainty. BIC-based selection had a higher level of uncertainty, favoring model 1 and 3 at the smaller sample sizes, and model 2 at N=700.

Interestingly, for all sample sizes and for both the AIC and BIC-based selection, the bootstrap selection rates were generally higher for model 2 conditional on its selection than were the bootstrap selection rates for models 1 or 3 given their selection in the population sample. Generally, AIC-based bootstrap selection rates followed the pattern of model selection rates in the population, with higher rates for the best-fitting model when sample size is larger. BIC bootstrap selection rates remained generally lower than AIC rates. This is in line with the higher model selection uncertainty when using BIC in this simulation.

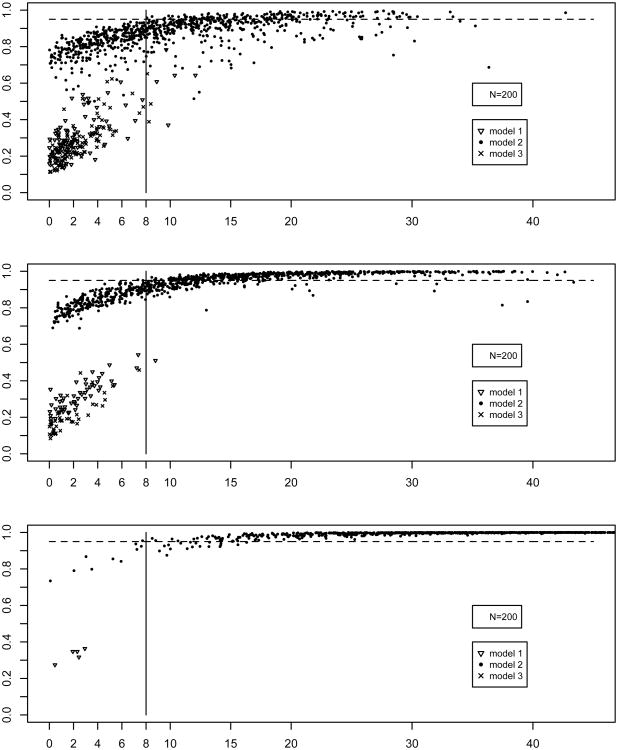
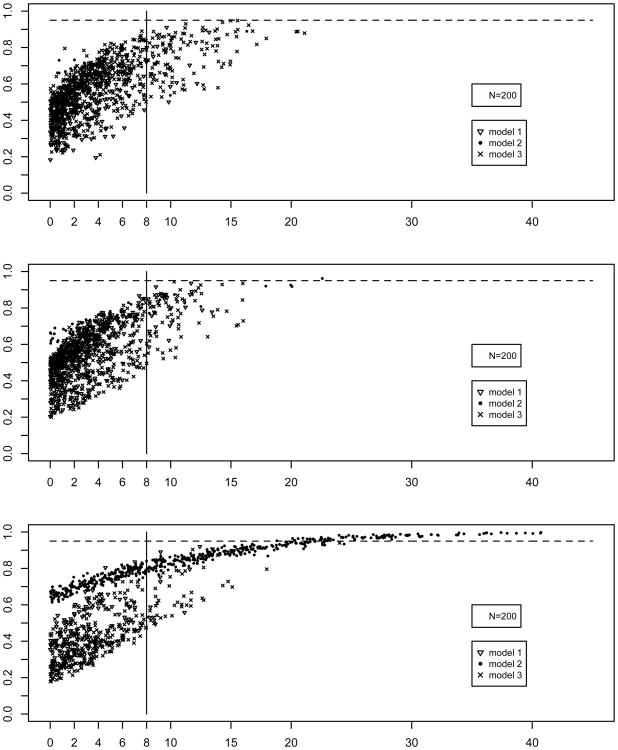
Figures 3 and 4 are plots of the AIC and BIC differences between the two best fitting models fitted to a given sample (x-axis) against the bootstrap selection rates for the best-fitting model in that same sample (y-axis). The panels correspond to sample sizes 200, 350, and 700. As can be seen in Figure 3, AIC-based bootstrap selection rates for the suboptimal models 1 and 3 remain below 0.80 for N=200, and decrease as sample size increases. Importantly, in the samples in which the AIC difference in the population sample was larger than 10 favoring models 1 or 3, the bootstrap selection rates were below 0.8. In samples with large AIC differences favoring model 2 the bootstrap selection rates were high, and overestimated the model selection rates for for this model presented in Table 2. Especially for the smaller sample sizes of N=200 and N=350, BIC-based selection was mostly in favor of models 1 or 3. For all sample sizes, bootstrap selection rates for samples with large BIC differences did not exceed 0.95 unless BIC differences were larger than 20. This shows that in a given sample the BIC difference between the two top models can (incorrectly) inspire great confidence in the best fitting model (e.g., a BIC difference as large as 20), however, the bootstrap rates provide evidence that other models can also appropriately describe the structure in such a sample.

Figure 3.

Figure 4.

The results plotted in Figures 3 and 4 are quantified in Tables 3 (AIC) and 4 (BIC) to provide a more direct connection to the suggested guidelines concerning AIC and BIC differences. The tables are built as follows. First, the P population samples are grouped according to the best-fitting model using either the AIC or BIC. Then AIC or BIC differences between the best and second best fitting are binned for each best fitting model, and minimum and maximum bootstrap selection rates for all three models are computed within each bin. For instance, Table 3 shows in the first row that there were 53 population samples favoring model 1 with AIC differences between 0 and 2, and the bootstrap selection rates of model 1 computed across the B=2,000 bootstrap samples drawn from those 53 population samples were between 0.138 and 0.518.

Table 4. Minimum and maximum bootstrap selection model selection rates of the 3 fitted 2-group models in relation to BIC differences observed in samples drawn from the population.

Δ BIC	Model 1			Model 2			Model 3
	N=200
	min	max	#samp	min	max	#samp	min	max	#samp
0-2	0.183	0.636	158	0.532	0.73	10	0.221	0.795	196
2-4	0.195	0.714	72	0.471	0.732	12	0.304	0.784	156
4-6	0.311	0.79	43	0.696	0.696	1	0.211	0.823	128
6-8	0.358	0.789	18	0.693	0.78	3	0.425	0.89	74
8-10	0.501	0.91	10	0.537	0.722	2	0.528	0.888	44
10-15	0.602	0.884	5	NA	NA	0	0.552	0.947	55
15-25	NA	NA	0	0.889	0.889	1	0.778	0.948	12
>25	NA	NA	0	NA	NA	0	NA	NA	0
	N=350
0-2	0.204	0.654	171	0.582	0.712	20	0.2	0.693	206
2-4	0.272	0.728	96	0.674	0.762	11	0.251	0.752	156
4-6	0.333	0.774	54	0.668	0.786	12	0.338	0.792	85
6-8	0.49	0.867	16	0.6	0.829	10	0.403	0.85	62
8-10	0.586	0.916	14	0.662	0.845	4	0.496	0.88	33
10-15	0.722	0.936	8	0.808	0.876	4	0.528	0.944	29
15-25	NA	NA	0	0.918	0.962	4	0.702	0.935	5
>25	NA	NA	0	NA	NA	0	NA	NA	0
	N=700
0-2	0.198	0.552	73	0.614	0.752	53	0.178	0.59	96
2-4	0.328	0.680	42	0.668	0.773	47	0.236	0.644	96
4-6	0.374	0.804	14	0.704	0.82	54	0.32	0.77	59
6-8	0.459	0.836	15	0.738	0.84	52	0.39	0.797	39
8-10	0.494	0.891	8	0.766	0.868	39	0.498	0.846	19
10-15	0.558	0.92	4	0.808	0.924	89	0.54	0.904	21
15-25	NA	NA	0	0.868	0.982	117	0.698	0.94	3
>25	NA	NA	0	0.957	0.998	60	NA	NA	0

Note: ΔBIC is the BIC difference between the best and second-best fitting model in samples drawn from the population. Min and max are the minimum and maximum bootstrap selection rates for samples within a given range of ΔBIC presented for each winning model, and #samp is the number of samples within that range favoring that model. For instance, for N=700, there were 42 samples (out of P=1000) with a BIC difference between 0 and 2 favoring model 1, and the minimum and maximum bootstrap selection rates for model 1 in this bin were 0.328 and 0.680, respectively.

To evaluate the additional benefit of bootstrapping model selection rates over and above suggested guidelines concerning AIC and BIC differences, we focus on the maximum bootstrap selection rates. The main question is whether bootstrap selection rates can protect against unwarranted confidence in case AIC or BIC differences in a given population sample are large. The rationale to focus on the maximum bootstrap selection rates rather than, say, the median rates, is that bootstrap selection rates are only useful as a protection against undue confidence if the rates are below unity in all samples from the population.

As can be seen in Table 3, AIC-based model selection only rarely resulted in selecting suboptimal models 1 or 3 with an AIC difference between 8 and 10 (six samples) or above 10 (2 samples), and for these cases, the bootstrap selection rates had a maximum of 0.783. Considering BIC-based selection in sample of size N=200, there were 54 samples with BIC differences between 8 and 10 and 72 samples with BIC differences above 10 favoring either model 1 or 3. The maximum bootstrap selection rate were 0.947 and 0.948, respectively, in these two brackets. For N=350, models 1 or 3 were favored in 47 samples with a BIC difference between 8 and 10, and in 42 samples with a BIC difference larger than 10. The bootstrap selection rates did not differ substantially from N=200, with maxima equal to 0.944 and 0.935, respectively. For N=700, the results shifted in the expected direction, with fewer population samples leading to suboptimal model selection with BIC difference between 8 and 10 (27 samples) or above 10 (28 samples). The maximum bootstrap selection rates are also lower, 0.891, and 0.940, respectively.

In sum, BIC differences lead more often than AIC to decisions in favor of suboptimal models 1 and 3 with large BIC differences, especially when sample size was 200 or 350. The bootstrap selection rates never exceeded 0.95 in those cases, and were mostly considerably smaller (see Table 2 for median rates). AIC-based bootstrap selection rates of models 1 and 3 were below 0.8. For model 2 the maximum bootstrap rates were between 0.96 and 0.98 independent of sample size when AIC differences were between 10 and 12.

Part 2a: Mixture models fitted to repeated samples from the population

Mixture modeling has the additional burden of estimating the most likely grouping of subjects into classes while also estimating the mean and covariance structures within each class. Note that the factor covariance matrix of the bi-factor model is fixed to be an identity matrix within each class, whereas this matrix is fully estimated in the two models with correlated factors. Estimation of class-specific factor covariance matrices in addition to estimating class specific loadings can be challenging, especially in smaller samples, and can result in non-convergence. Bootstrap results can also be informative with respect to model stability in the form of bootstrap convergence rates. Therefore, convergence is reported in addition to model selection. Proper convergence was defined the same as in our previous paper (Lubke & Campbell, 2016), namely, in terms of absence of errors such as an ill-conditioned Fisher Information matrix or non-positive definite first order derivative matrix. In addition, proper convergences depended on the likelihood being replicated.

In the mixture part of the simulation, P_mix=100 population samples were analyzed for N=350 and N=700. In samples with N=350, the single class models had, as expected, no convergence problems, whereas the individual convergence rates for the 2-class versions of models 1, 2, 3 were 0.64, 0.45, and 0.50, respectively. The pattern of non-convergence is in line with the difficulty to estimate the latent factor variances and covariance compared to having these parameters fixed. In only 23 out of 100 population samples we observed proper convergence of all fitted models simultaneously. For N=700, the convergence rates were almost perfect with only the 2 class version of model 1 resulting in 3 out of 100 non-convergences, meaning that in 97 out of 100 population samples all models converged properly.

Model selection rates based on AIC, BIC, and sample-size adjusted BIC are given in Table 5 for both sample sizes. The selection rates should be viewed in the light of model complexity. The single class models 1 and 2 had 34 and 31 estimated parameters where as the two class versions of model 1 through 3 had 55, 63, and 55 estimated parameters, respectively. Note that for N=350, selection rates computed for samples in which all models converged differed considerably from the selection rates computed across all samples but only compare the converged models.

Table 5. Selection rates for the five mixture models for N=350 and N=700.

	AIC	BIC	saBIC	AIC	BIC	saBIC
N=350
1class Model 1	0	0	0 .04	0	0	0.043
1class Model 2	0.19	1	0.64	0	1	0.13
2class Model 1	0.41	0	0.08	0.13	0	0.13
2class Model 2	0.36	0	0.16	0.696	0	0.348
2class Model 3	0.04	0	0.08	0.174	0	0.348
N=700
1class Model 1	0	0	0	0	0	0
1class Model 2	0	1	0.36	0	1	0.36
2class Model 1	0.05	0	0.06	0.021	0	0.62
2class Model 2	0.9	0	0.36	0.928	0	0.371
2class Model 3	0.05	0	0.22	0.052	0	0.227

Note: the first 3 columns show results when comparing converged models in all 100 samples whereas columns 4-6 show results based on samples in which all models converged.

Notably, BIC-based model selection was in favor of the most parsimonious model (i.e., single class model 2) in all comparisons carried out in the population samples, both for N=350 and N=700. There is therefore no model selection uncertainty in BIC-based selection. However, BIC-based selection does not detect the group differences present in the population. The single class model 2 is substantially more parsimonious compared to its 2-class versions (with and without measurement invariant loadings). AIC-based selection is higher for the most appropriate (but also most complex) 2-class model 2, namely 0.36 for all comparisons of N=350, and 0.696 for the 23 comparisons in samples where all models converged. For N=700, the AIC selection rates are 0.9 and 0.928. The sample-size adjusted BIC provides an intermediate solution.

The BIC differences between the best and second-best fitting models in samples of N=350 were larger than 10 in all but 9 out of 100 samples, thus providing “very strong evidence against the second best model” (Kass & Rafery, 1995). The smallest BIC difference was 6.669, the largest difference was 17.547, with a median of 14.246. For N=700, the minimum BIC difference was 4.802, the maximum difference was 19.593, with a median of 16.92. Only 5 samples had BIC differences below 10. For AIC, these numbers were considerably larger, reflecting that a larger number of samples provided less evidence in favor of the selected model. For N=350, 81 out of 100 comparisons had BIC differences below 10, and for N=700 this was 47 out of 100.

Part 2b: Bootstrap selection rates of mixture models in relation to AIC, saBIC, and BIC differences in the corresponding population samples

The mixture model results are presented similar to the 2-group results. First, results in the population samples are grouped according to the best-fitting model, and are binned according to fit index differences between best and second best model. Note that bin cut points are selected with the aim of having multiple samples within bin, while also including the separation between differences smaller and larger than 10. For each bin, minimum and maximum bootstrap selection rates are presented for each model (see Tables 6-8 for the AIC, saBIC, and BIC).

Table 6. Minimum and maximum bootstrap selection model selection rates of the 5 fitted mixture models in relation to AIC differences observed in samples drawn from the population.

Δ AIC	1-class model 1			1-class model 2			2-class model 1			2-class model 2			2-class model 3
	min	max	#samp	min	max	#samp	min	max	#samp	min	max	#samp	min	max	#samp
N=350
0-2	NA	NA	NA	0.13	0.40	6	0.28	0.43	7	0.08	0.36	6	0.01	0.01	1
2-5	NA	NA	NA	0.19	0.60	10	0.23	0.47	7	0.01	0.18	9	0.00	0.00	2
5-10	NA	NA	NA	0.41	0.52	3	0.26	0.50	18	0.03	0.27	11	0.03	0.03	1
10-20	NA	NA	NA	NA	NA	NA	0.22	0.46	6	0.06	0.24	8	NA	NA	NA
20-26.4	NA	NA	NA	NA	NA	NA	0.29	0.37	3	0.10	0.27	2	NA	NA	NA
N=700
0-5	NA	NA	NA	NA	NA	NA	0.50	0.52	2	0.19	0.69	14	0	0.1	5
5-10	NA	NA	NA	NA	NA	NA	0.40	0.50	2	0.16	0.73	24	NA	NA	NA
10-15	NA	NA	NA	NA	NA	NA	NA	NA	NA	0.24	0.74	19	NA	NA	NA
15-20	NA	NA	NA	NA	NA	NA	NA	NA	NA	0.20	0.79	13	NA	NA	NA
20-40.2	NA	NA	NA	NA	NA	NA	0.43	0.43	1	0.38	0.80	20	NA	NA	NA

Table 8. Minimum and maximum bootstrap selection model selection rates of the 1-class model 2 in relation to BIC differences observed for this model in samples drawn from the population.

ΔBIC	1-class model 2
	min	max	#samp
N=350
0-10	0.61	0.85	9
10-13	0.69	0.95	23
13-15	0.70	0.99	27
15-17	0.75	1.00	36
17-17.6	0.92	0.99	5
N=700
0-10	0.59	0.83	5
10-15	0.58	0.98	25
15-17	0.58	0.99	23
17-18	0.62	1.00	17
18-19.6	0.44	0.99	30

Note: The 1-class model 2 was the only model selected using BIC as a criterion.

Given the much smaller size of this part of the simulation compared to the two-group part (100 bootstrap samples drawn from each of 100 population samples), the rates within each bin should be evaluated more tentatively. In general, similar to the 2-group results, AIC differences in model comparisons carried out in population samples were generally larger in samples in which the 2-class model 2 was selected. The same was true for saBIC. Bootstrap selection rates for the 2-class model 2 were also higher compared to the other models. AIC bootstrap selection rates for the other 4 models remained below 0.52 for N=350, and below 0.50 for N=700 when those less appropriate models were favored in the corresponding population sample.

In 19 out of 100 samples of size N=350, the AIC difference was larger than 10. The bootstrap selection rates remained below 0.50 (see Table 6, AIC-based selection rates for N=350), thus providing evidence for the model selection uncertainty that was observed in repeated sample from the population (maximum selection rate was 0.696, see Table 5). With larger samples, the AIC-based selection rates in repeated samples from the population were larger (i.e., 0.928 for the 2-class model 2), and corresponding bootstrap rates were also higher (i.e., maximally 0.8 for this model). As can be seen in Table 7, the saBIC provides an intermediate solution between AIC and BIC-based selection, tending more towards the AIC-based results.

Table 7. Minimum and maximum bootstrap selection model selection rates of the 5 fitted mixture models in relation to saBIC differences observed in samples drawn from the population.

ΔsaBIC	1-class model 1			1-class model 1			2-class model 1			2-class model 2			2-class model 3
	min	max	#samp	min	max	#samp	min	max	#samp	min	max	#samp	min	max	#samp
N=350
0-2	0.34	0.48	3	0.21	0.59	12	0.27	0.50	3	0.01	0.21	4	0.01	0.01	3
2-4	0.60	0.60	1	0.28	0.44	11	0.44	0.49	3	0.08	0.22	3	0.00	0.01	2
4-6	NA	NA	NA	0.27	0.66	22	0.30	0.30	1	0.05	0.24	3	0.03	0.05	2
6-8	NA	NA	NA	0.43	0.72	18	NA	NA	NA	0.16	0.16	1	0.02	0.02	1
8-15	NA	NA	NA	0.48	0.48	1	0.29	0.29	1	0.06	0.25	5	NA	NA	NA
N=700
0-2	NA	NA	NA	0.05	0.15	6	0.39	0.52	3	0.40	0.65	5	0.02	0.26	9
2-4	NA	NA	NA	0.11	0.25	7	0.48	0.52	2	0.33	0.57	5	0.04	0.18	6
4-7	NA	NA	NA	0.12	0.33	13	0.60	0.60	1	0.36	0.70	5	0.00	0.10	5
7-10	NA	NA	NA	0.14	0.41	9	NA	NA	NA	0.50	0.76	6	0.20	0.23	2
10-24.7	NA	NA	NA	0.20	0.20	1	NA	NA	NA	0.37	0.77	15	NA	NA	NA

The results for BIC are limited due to the absence of model selection uncertainty in both sample size settings of this simulation. BIC-based selection was always in favor of the most parsimonious model, 1-class model 2, and, consistent with this finding, bootstrap selection rates were high (see Table 8). These results are in line with the conclusion drawn from the 2-group analyses, namely, that BIC can result in the selection of overly constrained models when sample size is small. It is surprising that even when N=700, none of the other models were selected in any of the samples even though the MD between the 2 groups was 1.939 on average in the N=350 data generated under the population model. The only difference with other simulation studies covering BIC-based mixture model selection in similar mixture models is that here the data generating model is not included in the set of fitted models, and all fitted models are less complex models than the model that generated the data.

Discussion

This simulation study aimed at assessing the utility of obtaining bootstrap model selection rates in order to gauge model selection uncertainty. We considered the situation where model comparisons in a given sample result in large AIC or BIC differences between the two top models, which in an empirical study would be regarded as strong evidence in favor of the model with the lowest criterion value. However, large AIC or BIC differences can occur while there is considerable model selection uncertainty in repeated samples from the population. In this case confidence in the best-fitting model should be reduced because other models can be selected in different samples from the same population. We focused on this scenario because researchers might be especially tempted to base inference only on the best-fitting model when AIC or BIC differences are large, and disregard the effects of model selection uncertainty on inference (Preacher & Merkle, 2012; Rousseliere & Rousseliere, 2016; Song & Lee, 2002). We investigated whether bootstrap selection rates can be indicative of model selection uncertainty and therefore serve as a protection against undue confidence.

Several general results concerning model selection uncertainty were as expected, namely, that model selection uncertainty decreased with sample size while power to discriminate between competing models increased. In addition, model selection uncertainty depended on the fit index, with AIC resulting in the selection of more complex models at smaller sample sizes compared to BIC.

More interestingly, regarding the question whether bootstrap selection rates are useful over and above the information provided by the fit indices, our results showed that bootstrap selection rates were generally well below unity. This means that even if a model comparison in the sample from the population resulted in AIC or BIC differences between 8 and 10 or larger than 10 in favor of a given model, other models were selected in multiple bootstrap samples drawn from the original sample. In practice, such a finding can protect against focusing only on the single best-fitting model. The utility of bootstrap selection rates was especially evident in the mixture part of the simulation. In the mixture analyses, there was evidence of considerable model selection uncertainty for both N=350 and N=700 when using AIC or the sample size adjusted BIC. The bootstrap selection rates did not exceed 0.80 even if differences in the original sample were larger than 20, suggesting that other models can represent the population structure, showing that bootstrap selection rates can guard against undue confidence in the top model. In that case, not only the best-fitting model should be considered for inference. These results mirror the empirical results presented in our first paper on this topic (Lubke & Campbell, 2016). In Lubke and Campbell (2016), we found that the largest bootstrap selection rates for any of the fitted models did not exceed 0.258 in the Holzinger-Swineford analysis when the BIC difference between the two best-fitting models was 16.20. In the growth mixture analysis of the NLSY data, the highest bootstrap selection rate was 0.478 when the BIC difference was 12.04. This showed that bootstrap selection rates can caution against an interpretation of the results that focuses only on the best fitting model even when the observed AIC or BIC difference in the sample is large.

In mixture analyses, the proposed bootstrap approach is also useful to compute model convergence rates, which provide useful information regarding model instability. Rather than having to base the interpretation of a model comparison on the models that converged properly, bootstrapping provides convergence rates together with information concerning the potential causes of non-convergence in the bootstrap samples. We found that models that did not properly converge in the original sample can have substantial non-zero convergence rates in the bootstrap samples as well as, vice versa, that models that converged in the original sample had less than perfect bootstrap convergence rates. In addition to the information regarding model stability, results (e.g., parameter estimates, fit indices) of properly converged models in bootstrap samples can be useful in the general discussion of a given empirical analysis.

Regarding the differences in performance between the AIC and BIC in this simulation, it is important to note that our study was not designed to compare these two indices. It is known that AIC is not asymptotically consistent, and can lead to the selection of overly complex models when sample size increases (Linhart & Zucchini, 1986). The BIC, on the other hand, is known to be consistent but not efficient, potentially leading to the selection of overly simple models in smaller samples (Vrieze, 2012). The result in this study that AIC-based selection resulted in adopting the model with the smallest discrepancy due to approximation more often than BIC. Especially in smaller samples, this can be simply be due to the fact that the most complex fitted model was also the model with the smallest approximation discrepancy. AIC-based model selection in this study could therefore by design not result in the selection of a model that is too complex. The results of this study did confirm the tendency of BIC to select overly simple models in cases where the sample size is small.

It was surprising, however, that even for N=700, none of the BIC-based mixture model comparisons were in favor of one of the 2-class models. Compared to other mixture model simulation studies, the performance of BIC in our simulation was clearly inferior. This outcome could be due to the fact that the true model was not included in the set of fitted models, and that all fitted models were simplified approximations of the true structure (i.e., had considerably fewer parameters). In most simulations, the set of fitted models include the true model, that is, the data generating mechanism has the same complexity as one (or more) of the fitted models, and less as well as more complex models are fitted to the data. Under those conditions, given sufficient sample size, BIC will select the model with the highest posterior probability (i.e., the data generating model) while AIC has the tendency to select increasingly complex models with increasing sample size (Henson, Reise, & Kim, 2007; Li, Cohen, Kim, & Cho, 2009; Lubke & Neale, 2006, 2008; Lubke & Tueller, 2010; Nylund, Asparouhov, & Muthén, 2007; Vrieze, 2012; Yang & Yang, 2007). If all fitted models are less complex than the data generating mechanism, BIC-based selection is expected to favor the model with the smallest approximation discrepancy given sufficient sample size, but AIC-based selection might result in favoring this model already at smaller sample sizes. In other words, using the AIC might lead to selecting models that are more informative with respect to the more complex population structure than the BIC under those conditions. Clearly, more simulation work is needed to investigate the setting that the population model is not included in the set of fitted models, and that discrepancies due to approximation are large. Such simulations would mirror more closely empirical studies in the behavioral sciences, and would be helpful to update recommendations regarding necessary sample sizes as well as guide the choice of a fit index for model selection at a given sample size in this more realistic situation. In addition, not all of the currently available simulation studies comparing the performance of different fit indices necessarily include scenarios in which the investigated indices based on their respective objectives are expected to perform well and scenarios where performance is expected to deteriorate. More generally, the choice of information criterion in an empirical analysis should take into account their different objectives rather than exclusively relying on currently available simulation results.

Quantifying model selection uncertainty based on a single sample is a challenging task due to the fact that the structure in a sample deviates by an unknown degree from the true structure in the population, which, in turn, depends on sample size. To add to this challenge, model selection is contingent on the choice of selection criterion as well as other factors such as the number of fitted models and their level of complexity and similarity. Several interesting alternatives to model selection based on fit indices have been proposed, especially within the Bayesian framework. Particularly Bayesian nonparametric models (Hjort, Holmes, Müller, & Walker, 2010) seem to be promising. In the Bayesian nonparametric approach, instead of pre-specifying and fitting various models with different model implied structures and levels of complexity, only one model is fitted to the data. In this approach model complexity itself is an unknown quantity that is inferred by conditioning on the data. Applied to factor models, Bayesian non-parametric modeling in conjunction with the Indian Buffet Process prior (Griffiths & Ghahramani, 2005) can be used to infer the number of factors needed in a factor model. Similarly, the number of mixture components in a mixture analysis can be inferred using the Chinese Restaurant process prior (Gershman & Blei, 2012). It would be interesting to investigate in more detail the advantages and disadvantages of different approaches to model selection especially in the context of mixture models. In the meantime, the current study hopefully underlines the fact that model selection based on fit indices is probabilistic, and that results of model comparisons should be interpreted in the light of selection uncertainty.