The effects of external cues on individual and collective behavior of shoaling fish

We examine changes in interaction rules, predictability, and vigilance of x-ray tetras due to external food and alarm cues.

Abstract

Collective animal behavior is an emergent phenomenon arising from the local interactions of the members of animal groups. Considerable progress has been made in characterizing these interactions, particularly inferring rules that shape and guide the responses of animals to their near neighbors. To date, experimental work has focused on collective behavior within a single, stable context. We examine the individual and collective behavior of a schooling fish species, the x-ray tetra (Pristella maxillaris), identifying their response to changes in context produced by food cues or conspecific alarm cues. Fish exposed to alarm cues show pronounced, broad-ranging changes of behavior, including reducing speed and predictability in their movements. Alarmed fish also alter their responses to other group members, including enacting a smaller zone of repulsion and increasing their frequency of observation of, and responsiveness to, near neighbors. Fish subject to food cues increased speed as a function of neighbor positions and reduced encounter frequency with near neighbors. Overall, changes in individual behavior and the interactions among individuals in response to external cues coincide with changes in group-level patterns, providing insight into the adaptability of behavior to changes in context and interrelationship between local interactions and global patterns in collective behavior.

INTRODUCTION

The collective behavior of animal groups provides us with some of the most amazing spectacles in nature. In recent years, considerable steps have been made toward understanding how group-level patterns emerge from the local interactions of group members. One aspect that has been largely neglected, however, is to see how collective behavior adapts and changes according to context. Here, we present a broad-ranging and detailed analysis of how individuals adapt their behavior in response to changes in information, how they adjust the ways in which they interact with other group members, and the implications that these have for the collective behavior of the group as a whole.

The spectacle of large numbers of animals acting synchronously and coherently in groups is one of the most arresting sights in nature. This collective behavior is manifested by a wide and diverse range of organisms, from bacteria to humans. Moreover, it is an example of a complex system—a system composed of interacting units that are subject to feedback that exhibits emergent global patterns. In the context of collective animal behavior, patterns of group behavior are the outcome of the interactions between the members of that group.

Recent studies have used detailed data obtained from tracking animals in groups to deduce the rules that individuals apply to their interactions with other group members. Thus far, empirical examinations of local interactions in group movement have usually been of animals in a consistent biological context for the entirety of each observation period, for example, natural surface swimming of surf scoters (1), spontaneous or homing flights of pigeons (2), natural flocks of European starlings (3), and small, freely exploring shoals of fish under controlled laboratory conditions (4, 5).

Animals adapt their behavior to context; for example, animals behave very differently when they are foraging, compared to when they come under attack. For group-living animals, the clearest differences may be observed at the level of the group. Typically, a group of animals under attack contracts, whereas foraging groups tend to be more dispersed and less coherent. However, to understand these group-level patterns, it is essential to examine changes in behavior at an individual level and, in particular, changes in the ways that group members interact with one another. A study by Hoare et al. (6) described the tendency of shoals of banded killifish (Fundulus diaphanus) to disperse when food cues were detected and to contract when the group perceived danger. These changes occurred as individuals altered their distance to near neighbors according to context, potentially by adapting the range of their interaction zones. More recently, Bode et al. (7) examined the responses of groups of three-spined stickleback (Gasterosteus aculeatus) to a perceived threat. Under such conditions, groups of the fish behaved more synchronously. A model produced in parallel with this experimental work suggested that this synchronicity is driven by fish increasing their update frequency or the rate at which they acquire and apply information from near neighbors.

Despite these insights, however, more needs to be done if we are to claim a detailed understanding of collective behavior of animals across contexts. The empirical components of both Hoare et al. (6) and Bode et al. (7) focused on what can be thought of as measures of emergent properties of collective behavior—the size of distinct shoals of fish across different contexts and distributions of observed speeds and nearest-neighbor distances within shoals pooled across all group members. Zonal models [for example, see the study by Couzin et al. (8)] were then used to infer possible changes in individual-level interactions that could lead to similar changes in emergent behavior. Here, we take advantage of the recent advances in quantifying individual interactions from observational data (1–5) to quantify observed changes in both individual interactions and emergent behavior in an experiment where we manipulated the proximate conditions experienced by groups of a schooling fish, the x-ray tetra (Pristella maxillaris), in an annular arena. During the experiment, we added one of three different types of cue (food, alarm, or control) to the arena, causing the fish to adjust their behavior. Food cues were composed of macerated fish food added to conditioned water that was then filtered to remove particles, alarm cues were composed of macerated conspecifics mixed with conditioned water that was then filtered, and control cues were composed solely of conditioned water (see Materials and Methods for more details). Our experimental procedure allowed us to examine changes in individual and group behavior and in the rules of interaction applied by fish before and after the cues were added, and to compare across treatments. The results of this procedure allow us to show, for the first time, context dependence of the rules that animals use to structure their interactions when subject to food or alarm cues and the implications of such changes for group-level patterns from data obtained in a controlled laboratory environment.

In particular, we examined how the addition of cues affected the median and SD over time of basic measures of individual locomotion (speed, turning speed, and magnitude of acceleration) and group configuration [distance of individuals from the group’s center, nearest and mean neighbor distances, group expanse (see sections S1.3 and S2.2), and polarization of the direction of motion of group members] using standard bootstrap analysis. Initial statistical analysis suggested that alarm cues, in particular, had marked effects on most of these basic measures. We further examined how the addition of cues affected the probability of individual fish observing neighbors in different relative positions and the speed and relative alignment of individual fish as a function of relative partner location. We investigated how the external cues affected the average rules of interaction used by individual fish to adjust their speed and heading as a function of the relative location and speed of their groupmates using methods first fully developed in the studies by Herbert-Read et al. (4) and Katz et al. (5). We also adapted a Markov chain approach (9) to examine how the different cues affected the predictability of changes in displacement and velocity of fish, quantified using information theory measures of conditional entropy, mutual information, and entropy rate. Finally, inspired by the work of Strandburg-Peshkin et al. (10) and Rosenthal et al. (11), we examined how changes in group configuration (individual spacing and group polarization) that followed the application of cues affected the ability of both individuals and the group to maintain vigil over sections of open water, and the ability of individuals to see their groupmates, and thus receive information about potential threats or the availability of food (see sections S1.7 and S2.6).

During the course of our investigation, we also examined how the application of cues affected (i) how fish positioned themselves with respect to the boundaries of the annular arena, (ii) the frequency of direction changes by group members, (iii) the time delay associated with alignment in motion, (iv) responses to rapid turns of partner fish, (v) instances of isolation by group members, (vi) swapping position between the exterior and interior of the group, and (vii) the tendency to face toward the group’s center or the arena’s boundaries (details of this last analysis appear in sections S1.13 and S2.12). Details of these supplementary investigations are provided in the Supplementary Materials, with an overview of the results given at the end of the Results section here.

RESULTS

Basic measures of individual locomotion

Control groups

The magnitude of acceleration of fish in control groups decreased after cues were released, but there were no other significant changes to the basic measures of locomotion for individuals in control groups (see Table 1 and section S2.1). A priori, we expected that there may be temporal effects within control groups; such time effects were taken into account when evaluating the effects of food and alarm cues (see section S1.16).

Table 1. Basic bootstrap 95% confidence intervals for test statistics derived from the median and SD speed, s_i(t), turning speed, α_i(t), and magnitude of acceleration, a_i(t), of individual fish.

Statistically significant effects are marked with an asterisk (*) (that is, confidence intervals for the test statistics that lie entirely above or below 0). If a confidence interval lies entirely below zero, then the associated quantity decreased from the ante-cue interval (A) to the post-cue interval (P); if a confidence interval lies entirely above zero, then the associated quantity increased from A to P. Analysis of control group data revealed any underlying temporal effects; food and alarm cue effects were then adjusted to take into account these underlying effects of time.

Variable	Control	Food	Alarm
Median si(t) (mm/s)	−12.73 to 1.43	−0.40 to 21.28	−25.87 to −7.99*
SD si(t) (mm/s)	−3.83 to 2.46	−0.86 to 7.19	−7.86 to 0.04
Median αi(t) (rad/s)	−0.08 to 0.08	−0.14 to 0.08	0.22 to 0.74*
SD αi(t) (rad/s)	−0.82 to 1.15	−2.14 to 0.38	1.82 to 4.98*
Median ai(t) (mm/s2)	−26.80 to −2.27*	4.93 to 48.07*	−36.03 to −4.02*
SD ai(t) (mm/s2)	−29.62 to 51.57	−20.41 to 94.01	−54.03 to 45.03

Food cue groups

The magnitude of acceleration of fish increased after the release of food cues (Table 1 and section S2.1).

Alarm cue groups

The median speed of fish subject to alarm cues decreased after cues were released into the arena, whereas their median and SD in turning speed increased. In addition, the magnitude of acceleration decreased for fish in alarm groups (Table 1 and section S2.1).

Basic measures of group configuration

Control and food cue groups

There were no significant effects on the basic measures of group configuration for fish subject to food cues or members of control groups (see Table 2).

Table 2. Basic bootstrap 95% confidence intervals for test statistics derived from the median and SD distances of individual fish from the group centroid, d_i,c(t), distances of individual fish to its nearest neighbor, d_i,nn(t), the mean distance of all neighbors from individual fish, d_i,mn(t), and polarization of the direction of motion of group members, R(t).

Statistically significant effects are marked with an asterisk (*). If a confidence interval lies entirely below zero, then the associated quantity decreased from interval A to P; if a confidence interval lies entirely above zero, then the associated quantity increased from A to P. Analysis of control group data revealed any underlying temporal effects; food and alarm cue effects were then adjusted to take into account these underlying effects of time.

Variable	Control	Food	Alarm
Median di,c(t) (mm)	−3.88 to 4.37	−6.81 to 9.04	−13.91 to −3.45*
SD di,c(t) (mm)	−1.94 to 1.49	−7.41 to 2.86	−6.40 to −0.42*
Median di,nn(t) (mm)	−1.93 to 2.96	−2.28 to 7.21	−8.42 to −2.09*
SD di,nn(t) (mm)	−1.15 to 0.68	−1.96 to 2.45	−4.78 to −0.61*
Median di,mn(t) (mm)	−5.11 to 6.09	−5.87 to 15.97	−20.03 to −5.43*
SD di,mn(t) (mm)	−1.83 to 1.51	−10.48 to 1.33	−6.64 to 0.22
Median R(t)	−0.03 to 0.04	−0.05 to 0.07	−0.18 to −0.01*
SD R(t)	−0.04 to 0.003	−0.04 to 0.02	0.01 to 0.08*

Alarm cue groups

Median distances from fish to the group centroid, nearest neighbor distances and mean neighbor distances decreased after the release of alarm cues (see Table 2). There were shifts in the observed distributions of nearest and mean neighbor distances that suggested that a greater proportion of smaller distances were observed for fish subject to alarm cues (figs. S8 and S9). In addition, spacing between fish became less variable after deployment of alarm cues. Polarization of the direction of motion decreased for groups subject to alarm cues (see section S2.2 for further details).

Speed, relative alignment, and rules of interaction as a function of partner displacement and own speed

Observations common to all treatments

Our results before the introduction of cues are broadly in agreement with previous studies. As with other species of fish (4, 5), the tetras seemed to maintain a small zone of repulsion where there was a low probability of observing partners and where focal fish would reduce their speed if partners were located directly in front of them, increase their speed if partners were located directly behind them, and turn away from partners in this region (Figs. 1 to 3). Fish tended to travel at lower mean speeds when partner fish were located slightly in front or behind than when fish were located further away (Fig. 4).

Fig. 1. Mean changes in components of velocity as a function of the relative x or y coordinates of partner fish.

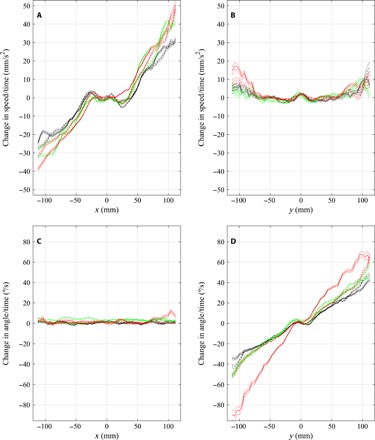
(A to D) Mean change in speed over time (the mean of $\frac{\mathrm{\Delta }\mathit{s}}{\mathrm{\Delta }\mathit{t}}(\mathit{t})$) (A and B) and mean change in angle of motion over time (the mean of $\frac{\mathrm{\Delta }\mathrm{\theta }}{\mathrm{\Delta }\mathit{t}}(\mathit{t})$) (C and D) of focal fish (located at the origin, moving parallel to the positive x axis) as a function of the relative x coordinates (A and C) or y coordinates (B and D) of all other partner fish. Curves corresponding to control trials are plotted in black, curves corresponding to food treatments are plotted in green, and curves corresponding to alarm cue treatments are plotted in red. Data before application of a cue are plotted as a dashed line; post-cue data are plotted as solid lines. Dotted lines are plotted one standard error above and below each curve. Note that in (B) and (D), the motion of focal fish is out of and perpendicular to the page, toward the reader. The calculations used to generate these plots are detailed in sections S1.2 and S1.5.

Fig. 3. Mean change in angle of motion over time as a function of relative groupmate locations.

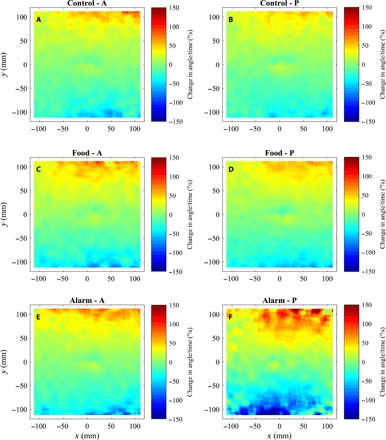
(A to F) Mean change in angle of motion over time (the mean of $\frac{\mathrm{\Delta }\mathrm{\theta }}{\mathrm{\Delta }\mathit{t}}(\mathit{t})$) of focal fish as a function of all other groupmate relative locations before (A, C, and E) and after (B, D, and F) application of cues for focal fish located at the origin, for fish subject to control (A and B), food (C and D), or alarm (E and F) treatments. The direction of motion of focal fish in each plot is parallel to the positive x axis. Extreme changes in angle have been truncated at 150°/s in these plots for visualization purposes. The calculations used to generate these plots are described in sections S1.2 and S1.5.

Fig. 4. Mean speed as a function of relative groupmate locations.

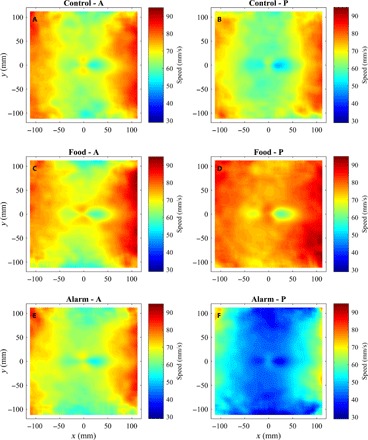
(A to F) Mean speed (the mean of s(t)) of focal fish as a function of all other groupmate relative locations before (A, C, and E) and after (B, D, and F) application of cues for focal fish located at the origin, for fish subject to control (A and B), food (C and D), or alarm (E and F) treatments. The direction of motion of focal fish in each plot is parallel to the positive x axis. The calculations used to generate these plots are described in sections S1.2 and S1.5.

Focal fish tended to exhibit a positive change in speed if partner fish were in front of them and outside the proposed zone of repulsion and a negative change in speed if partner fish were located behind them (Figs. 1A and 2). Such adjustments in speed suggest that the fish were acting to avoid being separated from their partners by too great a distance in a manner analogous to theoretical interactions in a zone of attraction [for example, see previous works (8, 12–25)]. Again, such attraction-like adjustments in speed have been observed in other species of shoaling fish (4, 5).

Fig. 2. Mean change in speed over time as a function of relative groupmate locations.

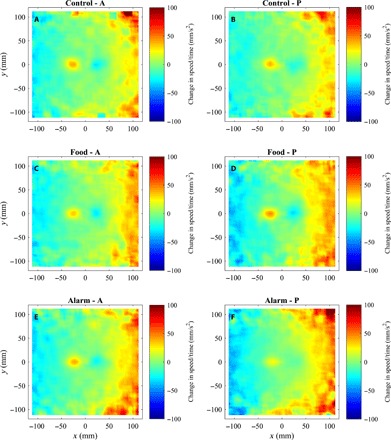
(A to F) Mean change in speed over time (the mean of $\frac{\mathrm{\Delta }\mathit{s}}{\mathrm{\Delta }\mathit{t}}(\mathit{t})$) of focal fish as a function of all other groupmate relative locations before (A, C, and E) and after (B, D, and F) application of cues for focal fish located at the origin, for fish subject to control (A and B), food (C and D), or alarm (E and F) treatments. The direction of motion of focal fish in each plot is parallel to the positive x axis. Extreme changes in speed have been truncated at 100 mm/s² in these plots for visualization purposes. The calculations used to generate these plots are detailed in sections S1.2 and S1.5.

In general, there was a greater probability of partner fish being located in small regions to the left and right of focal fish than to the front or back of focal fish at similar distances (Fig. 5, A and B, and hottest regions in Fig. 6). Beyond the putative repulsion zone, mean speed of focal fish tended to be relatively high when partner fish were located nearby and to the left or right of the focal fish. On average, focal fish tended to be reasonably well aligned with partners three to four body lengths in front and behind and two body lengths to either side (the x-ray tetras had a body length of approximately 30 mm).

Fig. 5. Relative observation frequency of groupmates at different relative x or y coordinates, and mean speed as a function of the relative x or y coordinates or partner fish.

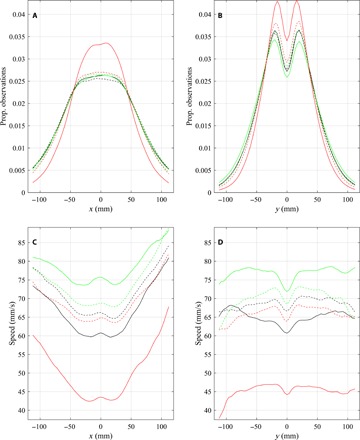
(A to D) Relative frequency that partner fish were observed at given (A) x coordinates or (B) y coordinates relative to focal fish located at the origin and the mean speed (the mean of s(t)) of focal fish as a function of relative (C) x coordinates or (D) y coordinates of all other partner fish. Curves corresponding to control trials are plotted in black, curves corresponding to food treatments are plotted in green, and curves corresponding to alarm cue treatments are plotted in red. Error bars are omitted in (C) and (D) as the error bars appear to lie directly on top of, and obscure, the mean curves at the scale that these plots are presented here. Data before application of a cue are plotted as a dashed line; post-cue data are plotted as solid lines. Note that in (B) and (D), the motion of focal fish is out of and perpendicular to the page, toward the reader. The calculations used to generate these plots are detailed in sections S1.2 and S1.5.

Fig. 6. Relative observation frequency of groupmates as a function of relative groupmate locations.

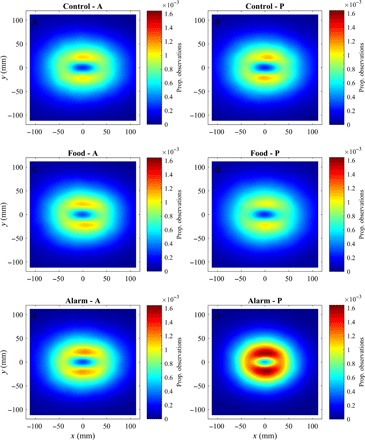
(A to F) Relative frequency of observations of all other groupmates before (A, C, and E) and after (B, D, and F) application of cues for focal fish located at the origin, for fish subject to control (A and B), food (C and D), or alarm (E and F) treatments. The direction of motion of focal fish in each plot is parallel to the positive x axis. The calculations used to generate these plots are detailed in sections S1.2 and S1.5.

Faintly visible in Fig. 3, there seems to be a tendency to turn away from nearby partners in the immediate vicinity of focal fish. Such a tendency is consistent with repulsion to nearby neighbors and has been observed for golden shiners (5). Beyond this, tetras tended to turn toward the location of partners (Figs. 1D and 3), as has been described in previous studies (4, 5). However, in addition to the above, our results show clear adjustments to the above measures in response to external cues.

Food cue groups

Fish subject to the food cue had slightly reduced probabilities of observing partners within approximately two body lengths after the release of cues, suggesting that food treatment groups spread out slightly. However, there were no significant changes in median measures of spacing for fish in food treatment groups, so any trend might be subtler (see Table 2).

There was also some evidence that fish subject to food cues exhibited relatively higher changes in speed over time, especially for focal fish swimming in a medium speed range (60 to 80 mm/s) (see figs. S20C and S23D). Thus, fish subject to food cues tended to speed up more and slow down less as a function of their own speed and relative partner location compared to fish in other treatment groups and their own earlier behavior (see section S2.4 for additional details).

Alarm cue groups

Fish subject to alarm cues showed strongly increased observation probabilities with neighbors within approximately two body lengths after the release of cues. These results relating to relative partner locations of alarm cue fish are consistent with our bootstrap analysis, all of which suggested that fish subject to alarm cues bunched up (see Table 2).

Fish subject to alarm cues tended to travel at lower speeds across the full range of relative partner locations, whereas fish subject to food cues tended to travel at higher speeds (Figs. 4 and 5, C and D). The reduction in speed did not seem to be driven by fish having to adopt slower speeds because their partners were closer to them, as fish subject to alarm cues tended to adopt lower mean speeds irrespective of the relative location of their partners over the entire plotted domain of relative partner locations.

Fish subject to alarm cues tended to be less aligned with their partners, especially when focal fish were traveling at relatively high speeds. This was consistent with the decrease in polarization of the direction of motion of alarm group fish observed in the measures of group configuration (Fig. 7).

Fig. 7. Mean relative directions of motion of groupmates as a function of relative groupmate locations.

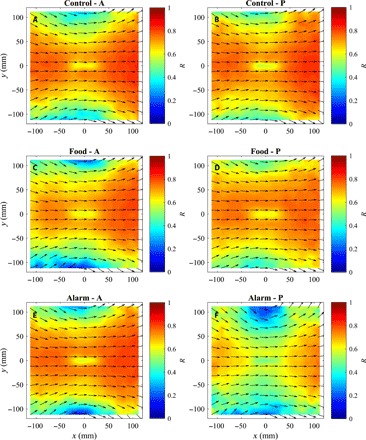
(A to F) The mean direction of motion of all other groupmates (indicated by arrows) relative to focal fish located at the origin before (A, C, and E) and after (B, D, and F) application of cues for focal fish located at the origin, for fish subject to control (A and B), food (C and D), or alarm (E and F) treatments. The direction of motion of focal fish in each plot is parallel to the positive x axis. The heat portion of these plots indicates the polarization of angles contained in each bin, R. The calculations used to generate these plots are detailed in sections S1.2 and S1.5.

Fish subject to alarm cues showed slightly depressed magnitudes of changes in speed when partner fish were very close, consistent with the idea of a reduced repulsion zone in these fish (Fig. 2F). Fish in alarm treatments also tended to exhibit slightly increased changes in magnitudes of changes in speed when partners were further away (Fig. 2F) and a marked increase in the magnitude of changes in angle over time toward partner fish (solid red line in Fig. 1D and regions beyond one body length in Fig. 3F).

Further analysis suggested that external cues can and do affect the average rules of interaction that fish use to adjust their velocity as a function of their own speed and the relative location of their partners (see section S2.4 for further details, where speed is also treated as an independent variable in determining rules of interaction).

Predictability of changes in displacement and velocity

According to measures of entropy, mutual information, and entropy rate, fish became less predictable in their movements following exposure to alarm cues, both in terms of changes in displacement and changes in velocity over short time periods. Decreased predictability of changes in displacement for alarmed fish was evidenced by an increase in associated conditional entropy (Fig. 8A), a decrease in the mutual information that one movement gave about the next movement to follow (following the same trend observed for fish subject to food cues but opposite to that observed for control groups; Fig. 8B), and an increase in entropy rate (Fig. 8C) after the release of cues. We also observed increases in the conditional entropy and entropy rate associated with changes in displacement of fish subject to alarm cues (Fig. 8, D and F). In general, fish subject to any treatment gave away very little mutual information about changes in velocity over short durations (Fig. 8E) (see section S2.5 for additional details).

Fig. 8. Entropy, mutual information, and entropy rate associated with changes in displacement and velocity.

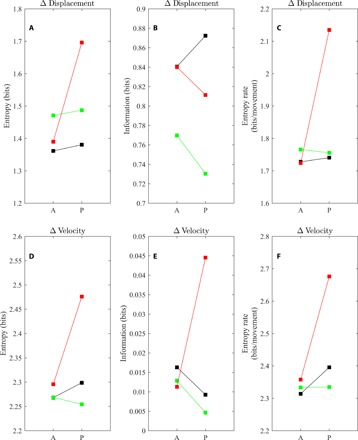
Entropy (left), mutual information (middle), and entropy rate (right) associated with changes in displacement (top) and velocity (bottom) over 20 frames (0.8 s) for control (black), food (green), and alarm (red) treatments before (A) and after (P) deployment of the relevant cue. The calculations used to generate these plots are detailed in section S1.6.

Open water under vigilance by individuals and groups and visibility of groupmates

Control groups

The SD of the intersection of the individual areas of open water visible to each fish (a measure of the area visible to the entire group) increased after the injection of cue-free water into the arena for control groups (see section S2.6, figs. S37 to S39, and table S6).

Food cue groups

There were no changes in measures of the area of open water visible to individuals or the group or to the number of individuals visible to individual fish after the injection of food cues (section S2.6, figs. S37 to S39, and table S6).

Alarm cue groups

After application of alarm cues, the SD of the area of open water visible to individual fish increased (see fig. S37 and table S6). However, there was no change in the median or SD of the area of open water visible to the entire group after application of alarm cues (fig. S38 and table S6). The overall response to alarm cues also reduced the median number of groupmates visible to each fish (fig. S39 and table S6) (see section S2.6 for a more detailed description and some further remarks).

Other measures affected by cues or time (reported in detail in the Supplementary Materials)

After the injection of cue-less water, fish in control groups decreased their median distance from the inner boundary of the arena and increased their median distance from the outer boundary of the arena (see section S2.3). Taking this change over observation interval into account, there was no significant effect of food cues on median distances to the boundaries, but fish subject to alarm cues significantly increased their median distance from the inner arena boundary. There were also significant reductions in the SD of the distances to both inner and outer annular boundaries for fish subject to alarm cues (section S2.3). Following directly from this analysis, we determined that fish subject to alarm cues tended to spend greater unbroken durations within two body lengths of the outer boundary of the annulus, whereas fish subject to food cues tended to spend shorter durations within two body lengths of the outer boundary (section S2.14).

X-ray tetras subject to alarm cues tended to change their sense of motion about the annular arena (clockwise or anticlockwise about the central circle) more frequently than they did before the injection of cues and more frequently than fish in other treatment groups (see section S2.7).

Application of cues did not affect the mean time taken to maximally align directions of motion of individual fish with earlier movements of other group members, but fish subject to alarm cues tended to be less aligned with their groupmates’ previous movements (section S2.8).

Fish subject to alarm cues increased the number of rapid turns they enacted per minute on average, whereas fish subject to food cues reduced the mean amount of time to align with rapidly turning groupmates (section S2.9).

Fish subject to food cues tended to spend slightly greater durations more than three body lengths from other groupmates than fish in control groups after the release of cue-less water (section S2.10).

There were complex results relating to the durations that fish spent on the edge of their group that suggested that fish subject to food and alarm cues spent shorter durations on the group exterior than fish in control groups, with fish subject to food cues spending the shortest durations on the group exterior (section S2.11). However, there were no significant differences between durations spent on the group exterior within each treatment group across the ante- and post-cue observation intervals; thus, it is possible that post-cue differences between the treatment groups were due to group composition rather than a response to the cues (section S2.11).

DISCUSSION

Our results show that fish respond to external cues by adjusting their rules of interaction. These changes in localized interactions in turn correlate with global properties of the groups. As a result, we are able to describe in detail how the ecological context shapes behavior both at the individual and group levels. Further, the observed rules of interaction of x-ray tetras before the release of cues were very similar to those previously observed for other species of shoaling fish. It might therefore be reasonable to expect qualitatively similar adjustments to these rules for other species responding to equivalent external cues (although this would have to be investigated in detail for each species of interest).

The strongest response was to alarm cues, which produced wide-ranging effects on the behavior of the fish. Detection of alarm cues caused the fish to decrease their speed but increase their turning speed. Alarmed fish also seemed to adapt their interactions with other group members in two main ways. First, there was an apparent reduction in the extent to which they were repulsed by very near neighbors, as evidenced by a greater relative frequency of observing partners at distances of 50 mm or less, and diminished magnitude of changes in speed to avoid near neighbors in front or behind. Second, they appeared to increase their attraction to neighbors at distances beyond 50 mm, markedly increasing their turning speed toward those neighbors and changing their speed in a manner consistent with reducing interindividual distances. The tendency to increase responsiveness to near neighbors may point to parallels between our findings and those of Bode et al. (7) in fish under a perceived threat. Overall, the effect of these changes is to produce more tightly clustered shoals, with smaller distances to their neighbors than under other observed circumstances (food or control treatments).

Following the detection of the alarm cue, individual tetras responded by reducing their speed, which was correlated with a reduction in group alignment. Such positive correlation between individual speed and group alignment has been observed for other species of fish, although the direction of causality between speed and alignment has not been established for real shoals (26, 27). However, the clustering of fish under these circumstances did not result in any reduction in vigilance at the group level, in terms of the median or SD of the area of open water visible to the group, suggesting that this response need not make them more vulnerable to an approaching predator (28). Fish subject to alarm cues responded by exhibiting increased levels of entropy in their movements (29, 30). This reduction in the predictability of their movements likely makes them less vulnerable to capture by an attacking predator (31–34). However, although increasing entropy in response to a threat may partially mitigate the immediate danger, it may also reduce the ability of animals to synchronize their behavior with near neighbors, making it harder for the group to mount a collective response and potentially decreasing the antipredator function of the group as a whole. Examining the role of entropy in the movements of grouping prey animals and reconciling the trade-off between predictability to predators and the maintenance of coherence in groups is an important future research goal.

In comparison to the fish subject to alarm cues, those in the food treatment showed a less marked response to their detection of the cues. There is some suggestion that they showed a reduced frequency of observing groupmates at close proximities and that they traveled at greater speed across almost the full range of partner locations based on Figs. 4 to 6. This is broadly in line with the dispersal of shoals of killifish on detecting food cues reported by Hoare et al. (6). The slight reduction in observation frequencies near to the focal individual may be driven by the increase in speed relative to partner positions and in the magnitude of acceleration, because groups that travel faster tend to increase their nearest-neighbor distances (27) [although see the study by Partridge (35)], potentially reducing the risk of collisions. Hence, in this case, it seems that individual speed may play some role in regulating the global structure of the group.

MATERIALS AND METHODS

Experimental subjects and protocol

We used x-ray tetras (P. maxillaris) as the study species in this experiment. X-ray tetras are a strongly shoaling characin species native to South America. The fish that we used were the progeny of individuals imported in 2009. Individuals used in the experiment measured 31 ± 3 mm. Before experiments, the x-ray tetras were held in 90-liter aquariums held at a temperature of 27° ± 0.5°C in the animal holding rooms at the University of Sydney and were fed daily on Wardley aquarium flake food. Fish were fed on the day of their experimental trial at 9:00 a.m., with experimental trials performed in the afternoon.

Groups of eight fish were transferred in small beakers to the experimental arena, an annulus constructed of white acrylic. The external and internal diameters of the annulus were 660 and 270 mm, respectively, at the water surface, giving the fish a channel of 195 mm to swim in. The annulus was filled to a depth of 7 cm with aged, conditioned water at the same temperature as the fish’s holding tanks. The fish were allowed to settle for 5 min. Following this, we recorded the behavior of the fish for a total of 15 min using a Canon G1X camera positioned 1 m about the arena and filming at 25 frames per second at a resolution of 1080p. Seven minutes after the conclusion of the acclimation period, we introduced one of three cues to the water (conspecific alarm cues, food cues, or a control cue) using two syringes attached to tubes. The cues were introduced simultaneously at two diametrically opposing positions. In total, we added 100 ml of cues gradually over a period of approximately 2 min. Pilot tests using dye revealed that the cues would spread throughout the annulus within this time frame. As a result, we were able to designate two separate periods of time in the experiment: from 0 to 7 min after the acclimation period, designated as the ante-cue (A) period; from 9 to 15 min, designated as the post-cue (P) period. We used three different types of cues. Alarm cue was produced by humanely euthanizing an x-ray tetra and then macerating the fish using a mortar and pestle. To this, we added 100 ml of aged, conditioned water and filtered the result through filter paper into a measuring cylinder. Food cue was produced by macerating one teaspoon of Wardley flaked fish food, adding 100 ml of aged, conditioned water, and again filtering it to remove particulate matter. Finally, the control was performed using 100 ml of filtered, aged, conditioned water. We performed a total of 30 experiments (10 experiments for each treatment) and used different fish for each replicate. Experimental work was performed blind with the experimentalist unaware of the hypotheses being tested. The experimental design allowed for a comparison of pre- and post-cue behavior that took into account any temporal effects observed within control groups when estimating the effects of food and alarm cues.

Data analysis

We constructed a time series of estimates of the speed, turning speed, and magnitude of acceleration of individual fish from trajectory data using standard finite difference approximations (see section S1.2). We determined the median and SD over time of each time series (for each fish) and then determined means within each group of each of these individual measures before the release of a cue (ante-cue) and after the release of a cue (post-cue), effectively collapsing the data down to single number measurements for each aspect of behavior measured for each group. We then applied bootstrap analysis to determine whether each summary measure of locomotion changed after application of cues, taking into account any effect of time observed within control groups (section S1.16). We applied the basic method outlined in the book by Davison and Hinkley (36) to determine 95% confidence intervals for ante- to post-cue differences in each averaged statistic. If the 95% confidence interval was completely below zero, then the corresponding statistic decreased significantly after application of a cue; if the confidence interval was completely above zero, then the corresponding statistic increased significantly after the cue was released.

We also constructed a time series of the distance between each fish and the group center, the distance between each fish and its nearest neighbor at a given instant, and the mean distance from each individual to its neighbors (section S1.3). Again, we determined the median and SD over time of each of these measures for each individual and then averaged the individual measures across all group members ante- and post-cue. We then applied the same method of bootstrap analysis previously used on measures of locomotion to our data on individual spacing (section S1.16). At the group level, we determined the expanse of the group (see sections S1.3 and S2.2 for details and results) (14, 37) and polarization of the direction of motion of the tetras as a function of time (section S1.3). We determined the median and SD of each of these group level measures over time (within each tracked observation period) and then averaged each measure across all three intervals before the release of cues and all three intervals after the release of cues. We then applied bootstrap analysis to the averaged measures of median and SD expanse and polarization (as per section S1.16).

We determined the relative frequency that each fish observed its partners at given relative coordinates, as well as the mean speed, mean relative alignment in the direction of motion, mean change in speed over time, and mean change in angle of motion (change in heading relative to the positive x axis) over time of fish as a function of the relative locations of all other group members [see section S1.5 and see the study by Lukeman et al. (1) for an important example of relative frequency and alignment heat maps, where they examine interactions in floating flocks of surf scoters (Melanitta perspicillata)]. We rendered these functions as heat maps in two dimensions, as well as examining each quantity as a function of the relative x or y coordinates of partner fish in isolation. Combined, the mean change in speed over time and the change in angle of motion over time describe how the fish, on average, adjusted their velocity as a function of relative partner location [via changes in the magnitude (speed) and heading (angle of motion) of the velocity vector]; we refer to this pair of measures as the rules of interaction (4, 5). An alternative method for examining component-wise changes in velocity is to determine the mean components of an individual’s acceleration vector that are parallel (tangential) and perpendicular (normal) to the individual’s velocity vector [as in the study by Katz et al. (5)]; either our polar component-based method or the Cartesian component-based method of the study by Katz et al. (5) is equally valid for describing changes in velocity in two dimensions. There is evidence that at least some species of fish [eastern mosquitofish (Gambusia holbrooki) and golden shiners (Notemigonus crysoleucas)] make adjustments to their velocity as a function of their own speed (4, 5), as well as the speed and relative direction of motion of their partners (5), in addition to the relative location of partner fish. We therefore further examined relative frequency of observations of partner fish, mean alignment in directions of motion, and rules of interaction as function of both relative partner location and speed of focal fish (see section S2.6 for full details).

We determined the conditional entropy, mutual information, and entropy rate (38) associated with changes in displacement and velocity of individual fish over short time intervals as proxies for the predictability of the motion of the fish. To do this, we assumed that individual changes in displacement and velocity could be treated as part of a Markov process, where the next change in displacement of change in velocity was only dependent on the previously observed change in displacement or velocity (section S1.6) (9).

We examined how changes in individual spacing and group polarization affected the open space seen by individual fish and the entire group (estimated in mm²) and the number of groupmates visible to each fish at a given time using a modified ray-casting method combined with grid-based methods for representing areas (section S1.7, with corresponding detailed results in section S2.6).

As discussed in the Introduction, we performed a number of supplementary investigations. An overview of the results of these investigations is given in the Results section, with details of the associated calculations given in sections S1.4 and S1.8 to S1.15.

Ethical approval

All applicable international, national, and/or institutional guidelines for the care and use of animals were followed. All procedures performed were in accordance with the ethical standards of the University of Sydney (where the experimental work was performed).

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/3/6/e1603201/DC1

section S1. Analysis

section S2. Results

fig. S1. The annular arena and estimated boundaries.

fig. S2. Durations of unbroken travel clockwise or anticlockwise about arena.

fig. S3. Distributions of observed speeds.

fig. S4. Distributions of observed acceleration magnitudes.

fig. S5. Distributions of observed changes in speed over time.

fig. S6. Distributions of observed turning speeds.

fig. S7. Distributions of observed individual distances to group centroid.

fig. S8. Distributions of observed nearest neighbor distances.

fig. S9. Distributions of observed mean neighbor distances.

fig. S10. Distributions of group expanse.

fig. S11. Distributions of polarization in direction of motion.

fig. S12. Distributions of polarization in facing direction.

fig. S13. Distributions of observed distances to inner boundary.

fig. S14. Distributions of observed distances to outer boundary.

fig. S15. Observation frequency of groupmates and changes in velocity as a function of relative groupmate positions for focal fish traveling at 0 to 20 mm/s (projections).

fig. S16. Observation frequency of groupmates as a function of relative groupmate positions for focal fish traveling at 0 to 20 mm/s (heat maps).

fig. S17. Relative directions of motion of groupmates as a function of relative groupmate positions for focal fish traveling at 0 to 20 mm/s (arrow and heat maps).

fig. S18. Mean change in speed over time as a function of relative groupmate positions for focal fish traveling at 0 to 20 mm/s (heat maps).

fig. S19. Mean change in heading as a function of relative groupmate positions for focal fish traveling at 0 to 20 mm/s (heat maps).

fig. S20. Observation frequency of groupmates and changes in velocity as a function of relative groupmate positions for focal fish traveling at 60 to 80 mm/s (projections).

fig. S21. Observation frequency of groupmates as a function of relative groupmate positions for focal fish traveling at 60 to 80 mm/s (heat maps).

fig. S22. Relative directions of motion of groupmates as a function of relative groupmate positions for focal fish traveling at 60 to 80 mm/s (arrow and heat maps).

fig. S23. Mean change in speed over time as a function of relative groupmate positions for focal fish traveling at 60 to 80 mm/s (heat maps).

fig. S24. Mean change in heading as a function of relative groupmate positions for focal fish traveling at 60 to 80 mm/s (heat maps).

fig. S25. Observation frequency of groupmates and changes in velocity as a function of relative groupmate positions for focal fish traveling at 120 to 140 mm/s (projections).

fig. S26. Observation frequency of groupmates as a function of relative groupmate positions for focal fish traveling at 120 to 140 mm/s (heat maps).

fig. S27. Relative directions of motion of groupmates as a function of relative groupmate positions for focal fish traveling at 120 to 140 mm/s (arrow and heat maps).

fig. S28. Mean change in speed over time as a function of relative groupmate positions for focal fish traveling at 120 to 140 mm/s (heat maps).

fig. S29. Mean change in heading as a function of relative groupmate positions for focal fish traveling at 120 to 140 mm/s (heat maps).

fig. S30. Relative frequency of partner observation and mean speed of focal fish for bins centered about the x or y axes.

fig. S31. Changes in velocity of focal fish for bins centered about the x or y axes.

fig. S32. Observation frequency of groupmates and changes in velocity as a function of relative groupmate positions for focal fish traveling at 0 to 20 mm/s for bins centered about the x or y axes.

fig. S33. Observation frequency of groupmates and changes in velocity as a function of relative groupmate positions for focal fish traveling at 60 to 80 mm/s for bins centered about the x or y axes.

fig. S34. Observation frequency of groupmates and changes in velocity as a function of relative groupmate positions for focal fish traveling at 120 to 140 mm/s for bins centered about the x or y axes.

fig. S35. Entropy, mutual information, and entropy rate associated with changes in displacement.

fig. S36. Entropy, mutual information, and entropy rate associated with changes in velocity.

fig. S37. Distributions of estimated areas sighted by individual fish.

fig. S38. Distributions of estimated area sighted by all group members.

fig. S39. Distributions of estimated number of groupmates seen by each individual.

fig. S40. Survival functions for durations between changes in sense of motion around the arena.

fig. S41. Distributions of observed isolation events per minute.

fig. S42. Survival functions for individual durations in isolation.

fig. S43. Distributions of the number of swaps between group exterior and interior.

fig. S44. Survival functions for durations spent on the group exterior.

fig. S45. Distributions of the group fraction facing outward from the nearest wall.

fig. S46. Survival functions for durations spent within one body length of the outer boundary.

fig. S47. Survival functions for durations spent within two body lengths of the outer boundary.

fig. S48. Survival functions for durations spent within one body length of the inner boundary.

fig. S49. Survival functions for durations spent within two body lengths of the inner boundary.

table S1. States associated with changes in displacement.

table S2. States associated with changes in velocity.

table S3. Bootstrap confidence intervals for median and SD change in speed over time.

table S4. Bootstrap confidence intervals for median and SD distances from individual fish to the group centroid, nearest and mean neighbor distances, and group expanse and polarization (in direction of motion or facing direction).

table S5. Bootstrap confidence intervals for median and SD distances to boundaries.

table S6. Bootstrap confidence intervals for median and SD estimates for areas and number of groupmates sighted.

table S7. Log-rank test comparison of survival functions for durations between individual changes in sense of motion around the arena.

table S8. Bootstrap confidence intervals associated with time lag to maximum mean correlation in direction of motion.

table S9. Bootstrap confidence intervals associated with the analysis of rapid turns.

table S10. Bootstrap confidence intervals for median and SD number of isolation events per fish per minute.

table. S11. Log-rank test comparison of survival functions for durations in isolation.

table S12. Bootstrap confidence intervals for mean and SD number of interior-exterior group position swaps per minute.

table S13. Log-tank test comparison of durations spent on the group exterior.

table S14. Bootstrap confidence intervals for the mean and SD group fraction facing outward with their right eye.

table S15. Bootstrap confidence intervals for the median SD group fraction facing outward from the nearest wall.

table S16. Log-rank test comparison of survival functions for durations within one body length of the outer boundary.

table S17. Log-rank test comparison of survival functions for durations within two body lengths of the outer boundary.

table S18. Log-rank test comparison of survival functions for durations within one body length of the inner boundary.

References (39–52)