Electron spin dynamics and spin–lattice relaxation of trityl radicals in frozen solutions

Abstract

Electron spin–lattice relaxation of two trityl radicals, d₂₄-OX063 and Finland trityl, were studied under conditions relevant to their use in dissolution dynamic nuclear polarization (DNP). The dependence of relaxation kinetics on temperature up to 100 K and on concentration up to 60 mM was obtained at X- and W-bands (0.35 and 3.5 Tesla, respectively). The relaxation is quite similar at both bands and for both trityl radicals. At concentrations typical for DNP, relaxation is mediated by excitation transfer and spin-diffusion to fast-relaxing centers identified as triads of trityl radicals that spontaneously form in the frozen samples. These centers relax by an Orbach–Aminov mechanism and determine the relaxation, saturation and electron spin dynamics during DNP.

Introduction

NMR belongs to a class of spectroscopies in which the energy, hv, of a transition is much less than the thermal energy, k_BT, of the sample. The NMR signal intensity is proportional to the population difference, or polarization, of the two levels in the transition and is generally a tiny fraction of the potential signal. The normalized population difference for ¹³C is hv/2k_BT, or ∼10⁻⁵ at room temperature in a 500 MHz (¹H) NMR (h and k_B are Planck’s constant and the Boltzmann constant, respectively). The NMR signal can be enhanced by increasing magnetic field (hv) or lowering sample temperature (k_BT). But there are practical limits to both tactics.

Hyperpolarization has blossomed in recent years as a third tactic to increase sensitivity by producing non-equilibrium states with population differences approaching ± 100%. The hyperpolarization method known as dynamic nuclear polarization, DNP, pumps electron spin transitions to convert their polarization into nuclear spin polarization.^1–4 DNP increases NMR and MRI sensitivity by modest factors of ∼10 to hundreds of thousands to benefit current NMR and MRI methods and spawn new applications.

However, the NMR or MRI measurement time is typically very much shorter than the time required for polarization. Such is the case in dissolution DNP where nuclei are hyperpolarized at low temperatures, then liquefied and measured at room temperature.¹ Measurement time is limited by nuclear spin– lattice relaxation, T_1n, to minutes but it can take hours to fully hyperpolarize the sample. There is considerable room for improving DNP efficiency in terms of the hyperpolarization achieved and the time required.

A popular class of free radicals for dissolution DNP are the triaryl methyl radicals, known as TAMs or trityls. They combine a narrow, intense EPR spectrum with good chemical stability, reasonable solubility and facile separation from hyperpolarized products. Improvement of the EPR and the molecular properties of trityls has helped in optimizing DNP of pyruvate.⁵ Recent progress in high-yield synthesis of TAMs promises a wide range of TAMs with diverse substituents.^6–8 But making full use of these advances in trityl synthesis requires a detailed understanding of how trityl radical properties affect DNP.

DNP overview

During the 1950–1960s, DNP was developed for the production of polarized targets and polarized beams in high-energy physics experiments where long measurement times made slow polarization rates tolerable. Semi-quantitative consideration of the nuclear and electron spin systems and their interactions could rationalize observed DNP trends.^4,9,10 Quantitative predictions became possible with development of the spin temperature model,^9,11,12 in which various properties of the spin system, e.g., electron spin polarization, nuclear spin polarization and two-spin order, are treated as separate thermal reservoirs with their own temperatures and heat capacities. Even when spin temperature theory does not apply, it is convenient to discuss DNP in terms of these reservoirs.

One beauty of the spin temperature model is its ability to predict asymptotic properties of the spin system from a few empirical relaxation rates without detailed consideration of the underlying spin dynamics. However, considerably greater understanding of the electron spin dynamics is needed to optimize DNP kinetics, particularly when the simplifying assumptions of spin temperature theory are not met.

Numerical modelling of DNP based on EPR properties of the radical and its interactions with other radicals, the nuclei and the microwave field have recently been used to predict kinetics and the extent of polarization.^13–20 Unfortunately, experimentally-determined data needed for this quantitative modelling are very sparse. Relaxation of electron spin polarization to the lattice, diffusion of polarization through the EPR spectrum and multiple-spin flip-flops are important determinants of the entire hyperpolarization process;^14,19–21 and experimental data for conditions relevant to DNP are sparse or inconsistent.

For instance, one basic parameter, the relaxation rate for the total electron spin polarization to the lattice, 1/T_1e or spin–lattice relaxation rate, has been reported a few times for trityl radicals at low temperatures. Some reports indicate that 1/T_1e is ∼1 s⁻¹ at 10 K^22–24 which extrapolate to considerably slower rates at 1–2 K.^22,23 Other reports suggest 1/T_1e > 20–200 s⁻¹ at 10 K^24–26 and 0.5–10 s⁻¹ at 1–2 K.^5,24,27–30 These results have been called ‘‘partially contradictory”,²⁹ which is not surprising because they come from different trityl radicals at concentrations between 0.2 and 45 mM in different solvents with EPR frequencies of 9.5–336 GHz. The two order-of-magnitude variation in these reported rates does highlight the critical need for better data to support quantitative modelling of DNP.

Some of that variation may be related to recent reports of dimers, larger aggregates and even fibrils of radicals in trityl solutions,^31,32 underscoring the need to understand the physical chemistry of trityl radicals in solution. Each aggregate size has different electron spin properties. It is quite possible that one size of aggregate may play an important role in electron spin–lattice relaxation of the sample while a different size of aggregate plays an important role in the transfer of polarization to the nuclear reservoir.

Pulse sequences used to generate nuclear coherences in pulsed EPR³³ can also produce nuclear polarization.³⁴ The microwave pulses can directly transfer electron spin polarization, via the hyperfine interaction, into nuclear polarization. Understanding the electron spin dynamics is even more important if microwave pulses are ever used for DNP as an alternative to cw pumping.

The role of electron spins

The total electron Zeeman polarization, given by ${\displaystyle \sum _i{m}_{\mathrm{S},i}}$, with the summation extending over all trityl radicals, i, corresponds to the Zeeman reservoir in spin temperature treatments^12,35 and to $E_{z_{\mathrm{e}}}$ in the modelling of Colombo Serra et al.¹⁹ The Zeeman polarization is maintained by spin– lattice relaxation involving lattice phonons or vibrations. A combination of microwave pumping, electron spin diffusion, electron spectral diffusion and electron cross-relaxation converts the Zeeman polarization into an EPR-frequency-dependent polarization corresponding to the dipolar reservoir. Only then does hyperpolarization of bulk nuclei arise by polarization transfer from the dipolar reservoir to the nuclear spin reservoir. If electron spin polarization transfer to the dipolar reservoir is not understood and optimized, no manipulation of nuclear spin dynamics can ever recover it.

Goals

This paper examines one important aspect of electron spin dynamics: the direct energy transfer between the electron spin polarization and the phonons of the lattice. This spin–lattice relaxation determines the extent and rate that the Zeeman reservoir is saturated by microwave pumping. We examine two trityl radicals: d₂₄-OX063 and Finland trityl, Scheme 1, at X- and W-bands, between 4–100 K, and at concentrations up to 60 mM. The entire trityl radical spectrum is saturated as uniformly as possible and the peak of the spin echo signal is used to measure the electron magnetization of the widest possible spectral range. This strategy is designed to eliminate artifacts from spectral diffusion or polarization transfer between the Zeeman and dipolar reservoirs. The measurements are isolated from redistribution of the polarization, P_e,i,¹⁹ across the EPR spectrum.³⁶ The dependence of electron spin–lattice relaxation on experimental DNP parameters, such as temperature, radical concentration, and magnetic field strength are examined. Other aspects of trityl radical spin dynamics are equally important and will be examined in subsequent papers.

Scheme 1.

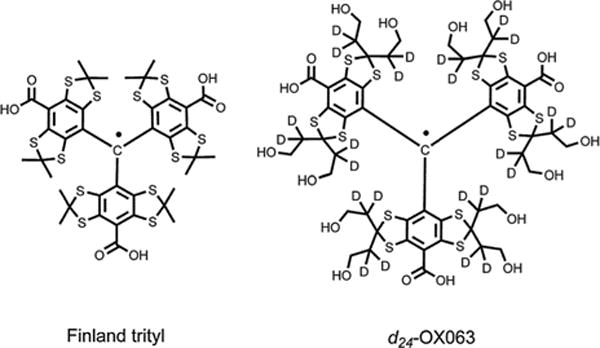
Molecular structures of Finland trityl and d₂₄-OX063 free radicals.

Although dissolution DNP is carried out at very low temperatures and high fields, measuring relaxation over a broad temperature and frequency range is very important for predicting spin dynamics under different conditions and for understanding the physical mechanisms underlying relaxation. Measurements over a small temperature range can give ad hoc functional forms that are impossible to relate to physical or chemical properties of the sample. The energy and statistics of the phonons involved in relaxation determine the temperature dependence^37,38 and can be very revealing of the species that actually transfer spin energy to the lattice. At the very low temperatures typical for dissolution DNP, electron spin–lattice relaxation is usually very simple because it involves only the lowest energy electron spin states and phonons. The spin–lattice relaxation is readily predicted at DNP temperatures, ESI,^† Section S2, avoiding phenomena that do not affect spin–lattice relaxation but do complicate its measurement, for example, the very low temperature physical annealing reported by Marin-Montesinos et al.³²

The recovery kinetics after a saturating or inverting pulse is usually idealized as a simple exponential with a single relaxation rate. Often, relaxation exhibits non-exponential kinetics with a distribution of relaxation rates reflecting the ‘random’ distribution of radicals in dilute solids. We find several clear indications that the properties of individual trityl radicals are not the major determinant of relaxation of the electron Zeeman reservoir with the lattice. Rather, a few fast-relaxing paramagnetic centers dominate the relaxation kinetics in samples with high trityl concentrations.

Results

Spin–lattice relaxation

The recovery of M_z to its equilibrium value of M_z,eq was measured between 4–100 K at concentrations up to 60 mM for both OX063 and Finland trityl, using the two-pulse electron spin echo to measure the EPR signal intensity in saturation-recovery experiments. Measurements are designed to quench any artifactual recovery caused by redistribution of energy among the electron spins.^38–41 A picket fence of pulses saturates >90% of M_z ^39,42,43 within ± 120 MHz of resonance (see ESI,^† Section S1), which far exceeds the width of the EPR spectrum. Consequently the signal recovery measures the transfer of energy from electron spins to the lattice but not redistribution of energy among the electron spins (which corresponds to the dipolar reservoir). We will refer to the recovery of signal due to transfer of spin energy to the lattice as spin–lattice relaxation.

OX063^‡

Recoveries of the spin echo signal following saturation in 1 mM OX063 samples are exponential (∝1− (1− δ)e^−bt) within ±1%, Fig. 1, where δ accounts for incomplete saturation of the electron spins. The rate b is the spin–lattice relaxation rate. In dilute samples b is assumed to be a characteristic of an individual trityl radical in that solvent and is referred to here as w_S or 1/T_1e. The values of b at X- and W-band are similar to the reported 1/T_1e for Finland trityl²³ but are roughly an order of magnitude slower than those reported at low temperatures for 15 mM OX063.²⁴

Fig. 1.

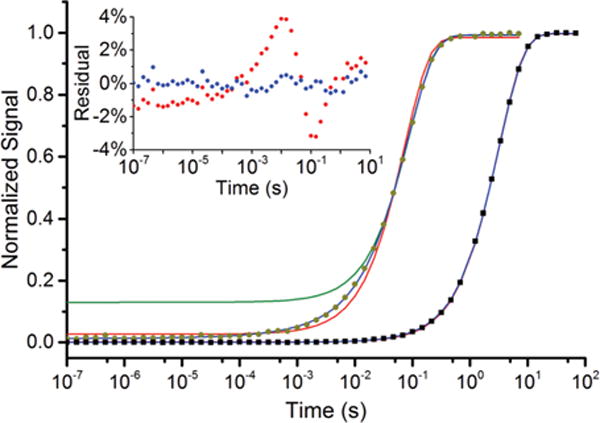
Experimental X-Band saturation-recovery data. The spin echo intensity is plotted as a function of time following a saturating picket fence of pulses for 1 mM (black squares) and 40 mM (dark yellow circles) OX063. Solid lines are least-squares fits to the data: exponential fit (red) and eqn (1) (blue). A fit to the tail of the recovery (for time > 0.05 s) at 40 mM OX063 (green) fails to catch the initial ∼12% of the recovery. The inset shows the residuals for 40 mM OX063 as a percentage of the fully-recovered signal for fits with a single exponential (red) and with eqn (1) (blue).

At higher OX063 concentration, the signal recovery becomes markedly faster, particularly below 40 K. The recovery is non-exponential at early times and systematic deviations much larger than noise are seen in the residuals from the exponential fits, Fig. 1 inset. Such behavior is repeatedly encountered in studies of spin–lattice relaxation in solids by EPR and NMR.^44–48 The initial signal recovery is the result of rapid cross-relaxation by a subset of the spins to nearby, rapidly-relaxing spins that serve as sinks to convert spin energy into lattice phonon energy. This cross-relaxation results in a distribution of relaxation rates and non-exponential kinetics.

Fits to the experimental signal recoveries improve dramatically using a well-established relaxation model.^44,49–55 Spin diffusion transports spin energy from most of the radicals to the fast-relaxing centers where cross relaxation transfers it to the lattice. Dzheparov derived the detailed kinetics in this model for I = 1/2 nuclei where the intrinsic nuclear spin–lattice relaxation is negligible.^54,55 His results are applicable to S = 1/2 trityl radicals once their intrinsic T_1e is included, so that relaxation occurs by three parallel routes: (1) cross-relaxation via dipolar interactions with a nearby, fast-relaxing, minority spin; (2) spin diffusion via flip-flops with other trityl radicals, eventually reaching a fast-relaxing spin; and (3) by its intrinsic 1/T_1e = w_S. For a frozen, isotropic solution of radicals, the relaxation kinetics of M_z can be written as

$$M_z\left(t\right)-M_{z,\mathrm{eq}}=(M_z\left(0\right)-M_{z,\mathrm{eq}})e^{-\sqrt{at}-bt}$$ (1)

The two terms in the exponent of eqn (1) have simple explanations. The first term in a comes from cross-relaxation of a radical in a single step via dipolar interactions with the nearest fast-relaxing center, analogous to Förster resonant energy transfer (FRET).⁴⁵ In the absence of this cross-relaxation, a = 0. Many radicals are too far from a fast-relaxing center for effective cross-relaxation, they can undergo spin diffusion in a series of electron-spin flip-flops with other trityl radicals. A saturated electron spin eventually comes near a fast-relaxing center and cross relaxation to it occurs. The second term, in b, is Dzheparov’s result for the combination of spin diffusion-cross relaxation plus the intrinsic w_S for an isolated radical.

Fits of recoveries for radical concentrations above 1 mM were much better with eqn (1). Systematic deviations in the residuals were reduced to the level of experimental noise, Fig. 1 inset. Some fits for 1 mM OX063 improved slightly with eqn (1), but in more than half of those, the improvement was not statistically significant in the F-test at the p = 0.05 level. Occasionally, non-exponential recoveries are treated by fitting only the tails of the recovery, which works well for the tails, but completely fails for a significant fraction of spins contributing to the initial recovery, Fig. 1.

Relaxation rates in each OX063 sample increase smoothly with temperature, Fig. 2. Considerable scatter was seen: for duplicate samples at higher concentration; for samples with different rates of freezing; or even for the same frozen sample following storage, Fig. 2. Scatter is greatest when b is large, suggesting that random events during sample preparation and handling affect the fast-relaxing centers. A recent report of self-assembly and annealing of OX063 capsules³² illustrates the complexity of concentrated solutions of OX063 and is consistent with the scatter we see among samples.

Fig. 2.

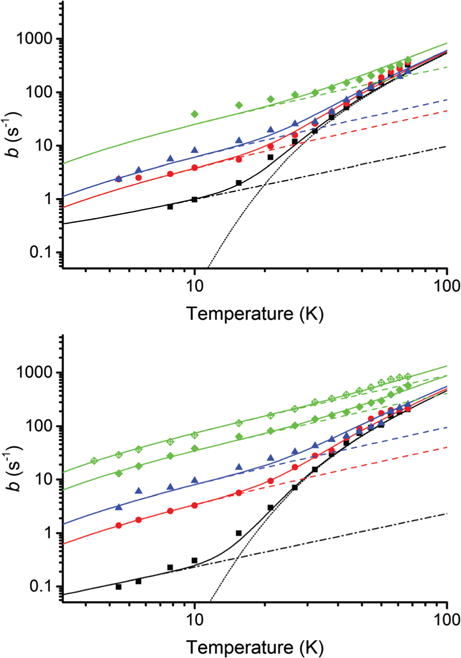
The temperature dependence of spin–lattice relaxation of OX063. The measured values of b are plotted as points and the fits of eqn (2) are plotted as solid lines. The concentration-independent direct and Raman terms are shown as dash-dot and dotted lines respectively while the Orbach–Aminov terms at each concentration are shown as dashed lines. Data for W-band (upper) are shown at radical concentrations of 1 mM (black, squares), 20 mM (red, circles), 40 mM (blue, triangles) and 60 mM (green, diamonds). Data for X-band (lower) are shown at radical concentrations of 1 mM (black, squares), 20 mM (red, circles), 40 mM (blue, triangles) and for the same 60 mM (green, diamonds) sample before and after storage. Uncertainties in b are generally smaller than the symbols.

Finland trityl

Relaxation of Finland trityl was studied, expecting that replacement of OX063’s 2-hydroxyethyl sidechains by methyl groups would simplify its behavior and make its electron spin–lattice relaxation more reproducible.

The 2.5 mM Finland trityl samples had nearly exponential recoveries, similar to 1 mM OX063 samples. Inclusion of the a term in eqn (1) failed to give a significantly better fit, in more than half the measurements, than the single-exponential at the p = 0.05 level for 2.5 mM Finland trityl. However, a is required at higher concentrations, as in OX063, to reduce residuals to the level of noise. Relaxation of Finland trityl samples was consistent among samples at both X- and W-bands, Fig. 3, with much better reproducibility than for OX063.

Fig. 3.

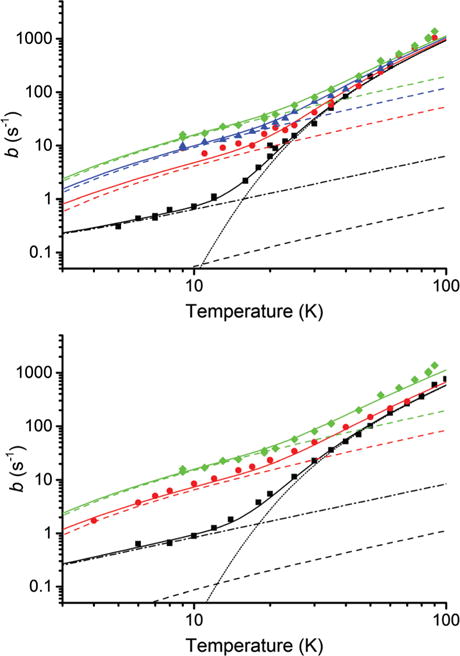
The temperature dependence of spin–lattice relaxation of Finland trityl. The measured values of b are plotted as points and the fits of eqn (2) are plotted as solid lines. The concentration-independent direct and Raman terms are shown as dash-dot and dotted lines respectively while the Orbach–Aminov terms at each concentration are shown as dashed lines. Data for W-band (upper) are shown at radical concentrations of 2.5 mM (black, squares), 26 mM (red, circles), 39 mM (blue, triangles) and 50 mM (green, diamonds). Data for X-band (lower) are shown at radical concentrations of 2.5 mM (black, squares), 26 mM (red, circles) and 50 mM (green, diamonds). Uncertainties in b are generally smaller than the symbols.

Temperature and concentration dependence

The OX063 and Finland trityl samples show similar trends. Relaxation rates increase smoothly and monotonically with temperature. Below ∼20 K, relaxation rates increase sharply with increasing radical concentration. The relatively large scatter noted for OX063 samples thwarted attempts at quantitative analysis of its concentration dependence. But the good reproducibility with Finland trityl allowed fitting of the temperature and concentration dependence of both a and b.

Temperature dependence of b

The spin relaxation described by the b coefficient involves spin flip-flops and spin–lattice relaxation of radicals and fast-relaxing centers. The values of b for individual OX063 and Finland trityl samples vary as much as four orders of magnitude over 4–100 K. The temperature dependence of every sample can be fit over its entire temperature range by three spin–lattice relaxation terms well-known from studies of materials for masers and polarized targets:^{44,48,49,52,53,56} a direct process, an Orbach–Aminov process and a Raman process.

$$b=A_{\mathrm{dir}}v\coth \frac{hv}{kT}+\frac{A_{\mathrm{Orb}}}{\left({\mathrm{e}}^{\frac{{\Theta }_{\mathrm{Orb}}}{T}}-1\right)}+A_{\text{Ram}}{\left(\frac{T}{{\Theta }_{\mathrm{D}}}\right)}^9{I}_8\left(\frac{T}{{\Theta }_{\mathrm{D}}}\right)$$ (2)

where A_dir, A_Orb and A_Ram are the coefficients of the direct, Orbach–Aminov and Raman processes, respectively; Θ_Orb is the Orbach temperature corresponding to the excited state energy specific for OX063 or Finland trityl; Θ_D is the Debye temperature of the solvent; and I₈() is the 8th transport integral, see for example.^37,38

The direct process and the Orbach–Aminov process have similar temperature dependences over this temperature range, with rates roughly proportional to T below 10 K. The higher concentration samples show a slightly stronger dependence at the lowest temperatures: a characteristic of an Orbach–Aminov process that is consistently fit better by the Orbach–Aminov term. The 1 and 2.5 mM samples seem to have a slightly weaker dependence at the lowest temperatures: a characteristic of the direct process. Many spin–lattice relaxation terms have a low-temperature region where the rate is roughly proportional to temperature and can be difficult to assign.^38,56–59 This is particularly true for the relaxation at low trityl concentrations which is not the focus of this paper. So purely for convenience, not intending to make an assignment, we call (and fit) that low-temperature relaxation as a direct process to clearly distinguish it from the concentration-dependent Orbach–Aminov process.

The electron spin–lattice relaxation has been studied for 15 mM OX063 in pyruvic acid between 1.7–4.2 K at W-band.²⁹ The relaxation rate is reported as 0.23 T^2.17 s⁻¹ and agrees well over that temperature range with the Orbach–Aminov term and the total relaxation rate for 50 mM Finland trityl in our solvent, ESI,^† Section S2.

Concentration dependence of b

Each individual OX063 sample is fit well with a different value of A_Orb, but with the same A_Ram and A_Dir, Table 1 and ESI,^† Section S3. The Orbach–Aminov term becomes stronger as the OX063 concentration increases: A_Orb = 1.5, 3.6, and 15–33 s⁻¹ at 20, 40 and 60 mM, respectively at X-band and 1.7, 2.7, and 11 s⁻¹ at W-band. The scatter among OX063 samples, most notable for the 60 mM OX063 sample after storage, makes it problematic to analyse the OX063 concentration dependence.

Table 1.

Spin–lattice relaxation rate parameters obtained from least-squares fitting of the concentration and temperature dependence of the rate b obtained from experimental saturation-recovery measurements. See text for details

	d24-OX063				Finland trityl
	X-band		W-band		X-band		W-band
ADir, S−1	23 ± 1 × 10−3		10 ± 1 × 10−2		84 ± 4 × 10−3		63 ± 3 × 10−3
Aorb,2, M−2 S−1	—		—		69 ± 9 × 102		44 ± 6 × 102
ARam, S−1	67 ± 2 × 102		77 ± 4 × 102		83 ± 7 × 102		13 ± 1 × 103
Θd				135 ± 3 K
ΘOrb		3.7 ± 0.6 K				5.4 ± 0.6 K

The consistent results for Finland trityl do support global fitting of the combined temperature and concentration dependence. All combinations of concentration dependences up to fourth-order in [trityl] were attempted for A_dir, A_Orb and A_Ram at X- and at W-bands. The best fits were obtained at each band with concentration-independent A_dir, and A_Ram but with a quadratic concentration dependence for A_Orb:

$$A_{\mathrm{Orb}}=A_{\mathrm{Orb},2}{[\mathrm{trityl}]}^2$$ (3)

Global fits of eqn (2) to X- and W-band Finland trityl data give good fits with similar values for the coefficients, Table 1 and ESI,^† Section S3.

Relaxation of these radicals has several similarities with that of transition metal ions in inorganic crystals studied in the context of masers and polarized targets.^{44,48,49,52,53,56} The temperature dependence shows a direct, an Orbach–Aminov, and a Raman process. The Orbach–Aminov coefficient depends on the square of the concentration of the paramagnetic ion, but the Raman coefficient is independent of concentration.

The a rate

The a coefficient primarily arises from trityl radicals that cross-relax to a nearby fast-relaxing center faster than they relax directly to the lattice and faster than they undergo flip-flops with other trityl radicals.^45,55 The uncertainties for a are larger than those for b because a comes from the deviation from exponential kinetics, typically 0–10%, described by b. The least scatter in the experimentally-determined a occurs in X-band measurements of Finland trityl; the a values clearly depend on both temperature and concentration, Fig. 4. Finland trityl at W-band and OX063 at X- or W-bands have greater scatter but are broadly consistent with the trends in Fig. 4.

Fig. 4.

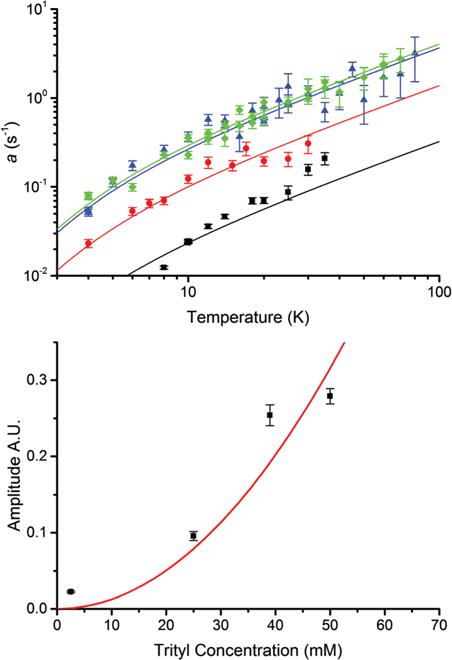
Temperature and concentration dependence of the a term for Finland trityl at X-band. The solid lines were obtained by fitting the amplitude of the Orbach–Aminov term to a (upper) at each concentration: 2.5 mM (black, squares), 26 mM (red, circles), 39 mM (blue, triangles) and 50 mM (green, diamonds). The amplitudes are fit by a quadratic concentration dependence (lower). Error bars are uncertainties from the fits.

The a seems to vary linearly with temperature above 10 K, and even more strongly below 10 K; a trend similar to that mentioned earlier for the Orbach–Aminov term. In fact, the temperature dependence of a for each Finland trityl sample, Fig. 4, is fit rather well by a ∝ (exp(Θ_Orb/T)−1) ⁻¹ from the Orbach–Aminov term of eqn (2) using the same Θ_Orb that fits b, Fig. 3. The amplitude of a seems to vary as [trityl]², Fig. 4.

The fast-relaxing centers

Trityl radicals provide the benchmarks for dissolution DNP. The experimental relaxation data in this paper indicate that their spin–lattice relaxation, below ∼40 K and at concentrations typical for DNP, is mediated by a small number of fast-relaxing centers. Because spin–lattice relaxation is an important part of the spin dynamics that produces hyperpolarization, identifying the fast-relaxing centers is essential for understanding DNP as it is currently carried out and for optimizing dissolution DNP. Whether or not the fast-relaxing centers are desirable for DNP, their identity, their origin, and their amount remain key questions.

The number of fast-relaxing centers

An important indication of the source and identity of the fast-relaxing centers lies in their number as estimated from b. The relaxation model underlying eqn (1) gives b as the combination of spin diffusion with cross-relaxation through the fast-relaxing centers acting in parallel with the intrinsic w_S of isolated radicals. Thus, b depends on the concentrations and relaxation rates of all spins: the trityls and the fast-relaxing centers.

The asymptotic relaxation rate corresponding to b has been derived for several limiting cases, based on kinetic^44,48,49,53 or spin temperature^60–62 considerations. In the limit that the rate w_d of spin diffusion is slow compared to the relaxation rate for the fast-relaxing centers, b → w_S + N_Fw_d where N are the concentrations of spins, w are the intrinsic 1/T_1e, and the F and S subscripts indicate fast- and slow-relaxing spins, respectively. This limit is reached for the lowest radical concentrations, yielding b = w_S. At higher concentrations, w_d ≫ w_F and,

$$b\to \frac{N_{\mathrm{F}}{w}_{\mathrm{F}}+N_{\mathrm{S}}{w}_{\mathrm{S}}}{N_{\mathrm{F}}+N_{\mathrm{S}}}$$ (4)

which is simply the weighted average of all relaxing species. For N_S ≫ N_F, eqn (4) reduces to b ≈ w_S + w_F(N_F/N_S).

At the lowest radical concentrations, a sum of the direct and Raman terms fits b quite well. Here b corresponds to w_S, or the spin–lattice relaxation intrinsic to an isolated trityl radical, so the direct and Raman terms are characteristics of the individual trityl radicals in this solvent. At high temperatures, b converges to the same Raman term for all concentrations, which implies that w_S ≫ w_FN_F/N_S in that range. The Orbach–Aminov term dominates b at the low temperatures and higher concentrations, so that b ≈ w_FN_F/N_S. Thus, the Orbach–Aminov relaxation is a characteristic of the fast-relaxing centers.

Although they have a significant influence on the relaxation of all radicals in the sample, the fast-relaxing centers are a small fraction of the total number of radicals: N_S ≈ [trityl] ≫ N_F. Eqn (2)–(4) can be combined when the Orbach–Aminov term dominates,

$$\begin{array}{l}b\approx w_{\mathrm{F}}\frac{N_{\mathrm{F}}}{N_{\mathrm{S}}}=\frac{A_{\text{Orb},2}{[\text{trityl}]}^2}{\left({\mathrm{e}}^{\frac{{\Theta }_{\text{Orb}}}{T}}-1\right)}\\ \frac{N_{\mathrm{F}}}{N_{\mathrm{S}}}=\frac{N_{\mathrm{F}}}{[\text{trityl}]}\propto {[\text{trityl}]}^2\\ N_{\mathrm{F}}\propto {[\text{trityl}]}^3\end{array}$$ (5)

showing that the number of fast-relaxing centers varies as the cube of the radical concentration.

The source of fast-relaxing centers

The fast-relaxing centers arise from the radicals used in preparing the samples. The number of fast-relaxing centers varies as the cube of the radical concentration, ruling out impurities or contaminants in sample tubes, solvents, etc. as the source of the fast-relaxing centers. Likewise, dissolved oxygen, O₂, is also ruled out. Although O₂ is paramagnetic and a potent relaxation agent in liquid trityl solutions,⁶³ the diffusional motion of O₂ and radical is a key factor in relaxation in liquids. Molecular diffusion and the consequent relaxation is virtually absent in frozen samples used here and for DNP. Indeed, we saw no difference in spin–lattice relaxation of rigorously-degassed, frozen samples versus those equilibrated with air, confirming that N_F is unrelated to O₂.

Eqn (5) indicates that the fast-relaxing centers come from the radicals added to the samples, but they cannot be simple impurities in the free radical compounds. In that case N_F ∝ [trityl]. The observed cubic dependence suggests that the fast-relaxing centers are clusters or aggregates of trityls that assemble in solution or as the sample freezes. If trityl solutions maintain an equilibrium between monomers and clusters during freezing, the cubic dependence would implicate a triad of radicals as the fast-relaxing species as proposed in other systems.^48,52,53

OX063 has been reported to form clusters called capsules in a similar solvent.³² The scatter in relaxation among samples and with sample handling for OX063 suggests that clusters of several different sizes are involved and that equilibrium is not reached. Our experience in purifying trityls by crystallization is that their rate of dissolution is quite slow so that the comparatively rapid preparation and freezing of samples may not allow them to reach equilibrium.

Calculations that neglect molecular size predict that a significant fraction of radicals would be closer than 1 nm at the trityl concentrations used in DNP.⁶⁴ OX063 and Finland trityl are each roughly 1 nm in diameter and would form a contact pair if separated by only 1 nm. So pairs and triads of trityl radicals in physical contact with each other are expected on the basis of statistics, and are likely candidates for the fast-relaxing centers. Pairs and other small aggregates would have weak ‘half-field’ lines near g = 4 from transitions with ΔM_S =±2. They can occur only from states with S ≥ 1, such as pairs, triads or larger aggregates of trityl radicals even if those aggregates have no exchange interaction separating the states with S = 1 from the S = 0 state. Such half-field lines are often assumed to indicate a triplet state with S = 1 having distinctly different energy from its corresponding singlet state with S = 0. In fact, half-field transitions can result from random pairs of radicals with no exchange interaction and with strongly mixed S = 0 and S = 1 states. Eaton et al.⁶⁵ showed that random radicals in frozen solution produce half-field lines detectable at sufficiently-high radical concentrations. We observe half-field lines at the higher concentrations of Finland trityl and OX063, ESI,^† Section S5, similar to those seen by Marin-Montesinos, et al.^31,32 Thus, our samples have an abundance of pairs and/or larger clusters of trityl radicals with appreciable dipolar interactions, as noted in other samples of concentrated trityl radicals.^31,32 We find that those abundant clusters are EPR-active, with spectra similar to that of an isolated radical, and contribute to the EPR signals measured in our experiments, ESI,^† Section S7.

Spin–lattice relaxation

The Orbach–Aminov term dominates relaxation at the low temperatures and high concentrations used for DNP. It is a defining characteristic of the fast-relaxing centers. Orbach–Aminov relaxation has a two phonon mechanism. Each phonon causes a transition involving an excited state whose energy, k_BΘ_Orb, is less than the limiting Debye energy of the solid, k_BΘ_D. Such is the case here, where Θ_D is 135 K for our frozen solvent and the excited states for fast-relaxing centers are at Θ_Orb = 3.7 K (2.6 cm⁻¹) and 5.4 K (3.8 cm⁻¹) in OX063 and Finland trityl, respectively.

These excited state energies are well below what one normally expects for vibrational or electronic states but are well within the range of exchange couplings, J, and splittings between the electronic spin states in biradicals, in nearest-neighbor and next-nearest-neighbor ions in inorganic crystals, and in radical pairs in crystals.⁶⁶ The classic study on the concentration dependence of electron spin–lattice relaxation of Ir⁴⁺ ions in single crystals by Harris and Yngvesson^52,67 found relaxation behaviour having strong parallels with our observations for trityl radicals. Four major conclusions are directly relevant to our work. (1) The electron spin–lattice relaxation of isolated Ir⁴⁺ ions has concentration-independent direct and Raman terms. (2) There is an Orbach–Aminov term whose coefficient is proportional to the square of the Ir⁴⁺ concentration, as is seen with Finland trityl. (3) The Θ_Orb in the two Ir⁴⁺ compounds are 6.2 and 10.2 K, identical to the spectroscopically-measured exchange interaction, J, between nearest-neighbor ions.^52,67 (4) A triad of three ions is the fast-relaxing center which provides an efficient relaxation conduit.

As radical concentration and sample temperature vary, the spin–lattice relaxation in our samples changes from being a molecular property of individual trityl radicals to being a bulk property of the sample. This change can be seen by decomposing the relaxation rate b into its component parts. At 1–2.5 mM, the samples seem to be in the regime of slow spin diffusion and b is equal to w_S.

At higher concentrations, eqn (4) applies at all temperatures. The increase in b with increasing concentration is due to the Orbach–Aminov term, but never exceeds 200 s⁻¹. This allows limits to be set on w_F because b−w_S = w_F(N_F/N_S) for small N_F according to eqn (4). Spin diffusion is fast, but requires several flip-flops at a rate w_ff for an average spin to reach a fast-relaxing center. This means that the rate of spin diffusion, w_d, to a fast-relaxing center is much slower than the phase memory decay rate 1/T_M ≈ 10⁶ s⁻¹ of the spin echo since one spin flip-flop can destroy the precession phase of more than one radical. Thus, w_F < w_d ≪ w_ff ≤ 1/T_M and, at ∼70 K, 200 s⁻¹ ≪ w_F ≪ 10⁶ s⁻¹. At lower temperatures, the limits scale together, so that at 10 K, 20 s⁻¹ ≪ w_F ≪ 10⁵ s⁻¹. Similarly, (N_F/N_S) > 10⁻³ for the 50–60 mM samples. None of these limits are very restrictive, but do set some boundaries. The limits for w_F are more consistent with relaxation of free radicals and molecular excited states than for transition metal ions.

Cross-relaxation

The relaxation of the free radicals requires rapid cross-relaxation of the trityl radicals to the fast-relaxing centers. This means that the EPR spectrum of the fast-relaxing center must have good overlap with that of the trityl radical to allow rapid resonance energy transfer. The CW EPR spectrum of dilute, frozen Finland trityl or OX063 is dominated by a single line with a peak-to-peak linewidth of about 6 MHz at X-band from the slight g-anisotropy and unresolved ¹H hyperfine couplings.^68,69 Dipolar interactions broaden the wings of the line at higher concentrations more than 15 MHz from the center, see Fig. S19 (ESI^†).

The EPR spectrum of the S = 1 state for a pair of nearest-neighbor S = 1/2 spins in inorganic crystals can be several GHz in width because of their mutual dipolar interaction (or zero-field splitting) at the short distances between ions. This huge width is usually assumed to preclude rapid cross-relaxation with monomers.^48,52,66,67 A triad of strongly coupled S = 1/2 ions consists of two S = 1/2 and one S = 3/2 states. Each of these states, at least to first order, has one EPR transition free of dipolar interactions and comparable in width to the isolated ion. The common expectation is for greater spectral overlap and faster cross-relaxation for an isolated spin with a spin-coupled triad, than for an isolated spin with a spin-coupled pair.^48,52,66,67 Calculations in random solid solutions support this greater overlap.^70,71

For the trityl radicals studied here, cross-relaxation to pairs may not be so unfavourable. The distance of closest approach for trityl radicals is much larger, ∼1 nm, than in crystals of inorganic ions, and the unpaired spin density is concentrated at the center of the radical.⁶⁹ We estimate the dipolar interaction in a contact pair to be on the order of 20 MHz; not that much larger than the EPR linewidth of isolated radicals, even at X-band. Unlike inorganic ions or even small radicals such as nitroxides, contact pairs of trityls may have spectral overlap and cross-relaxation rates with isolated radicals that are similar to those of triads.

Under conditions typical for DNP, the spin–lattice relaxation of trityl radicals is dominated by fast-relaxing centers that appear to consist of triads of radicals forming spontaneously in the frozen, concentrated solutions. The triads have a doublet ground state that is separated from its excited spin states with S = 1/2 and S = 3/2 by Θ_Orb ∼3–6 K. This does not mean that the exchange interactions J between pairwise members of the triad are necessarily equal. Such a case could be called a symmetric triad in which all three spins have identical interactions with other members of the triad.⁶⁶ Many exchange topologies are possible and the point at which a radical interacting weakly with a pair should be called a very asymmetric triad is rather arbitrary.

A spin-coupled pair has four energy levels, three levels in a triplet state with S = 1 and one level in a singlet state with S = 0. The average splitting between the singlet and triplet states is |J| or Θ_Orb. A radical interacting weakly with this spin-coupled pair forms a doublet S = 1/2 state with the singlet and, at an energy |J| away, some mixture of doublet and quartet S = 3/2 states with the triplet.

A triad has eight energy levels: four in a state with S = 3/2 and four in two states with S = 1/2 but the splitting between spin states, which appears in the Orbach–Aminov relaxation as Θ_Orb, is a complicated function of the J’s between all three radicals,^48,52,66 but Θ_Orb is usually comparable to |J|.

The complicated dependence of spin state energies on J causes the Orbach–Aminov relaxation for triads to be much faster than for pairs.^48,52,59,67 The spin–lattice relaxation of Ir⁴⁺ pairs is comparable to that of the Ir⁴⁺ ions in concentrated crystals. The relaxation of a pair is much too slow to account for the observed spin–lattice relaxation of single ions even if cross-relaxation were not prevented by the minimal spectral overlap. However, numerical estimates of relaxation rates find that relaxation for triads is fast enough that they can be fast-relaxing species.^48,52,67

Discussion

These spin–lattice relaxation measurements show just one aspect of a very dynamic spin system. Spin diffusion and cross relaxation with a few fast-relaxing centers dominate relaxation and have several implications for our understanding of hyperpolarization.

Trityl spin–lattice relaxation

At low concentrations, the spin–lattice relaxation of trityl radicals is described by a single exponential rate or time constant. However at higher concentrations typical of DNP applications, relaxation is non-exponential with a distribution of rates. The spectrum of rates n(ω)dω, in the sample is just the inverse Laplace transform of the relaxation kinetics given in eqn (1),

$$n\left(\omega \right)\mathrm{d}\omega =\frac{1}{2}\sqrt{\frac{a}{\pi {\left(\omega -b\right)}^3}}{\mathrm{e}}^{-\frac{a}{4\left(\omega -b\right)}}\mathrm{d}\omega$$ (6)

for ω ≥ b and is zero otherwise. This distribution of spin–lattice relaxation rates has a peak just above b and a tail toward higher frequencies that dies off as ω^−3/2, Fig. S20 (ESI^†). The rate in eqn (6) never quite reaches zero at large ω. In practice, the distribution of relaxation rates should not extend much beyond ∼10⁸ s⁻¹, the dipolar interaction for a contact pair of trityl radicals which we estimated to be on the order of (2π)20 MHz.

For a < b, the distribution is effectively a delta function at b. Trityl radicals should be saturated by a microwave pumping field as if they all had the same spin–lattice relaxation time. The fast-relaxing centers and the few radicals that cross-relax directly to them should be negligible as long as (N_F/N_S) ≪ 1, although they could very well be dominant in determining the effective relaxation rate b.

On the other hand, if a > b, there really are subsets of radicals with different relaxation times, yet still interacting with the other subsets. Such a population of radicals would have a very nonlinear response to microwave pumping and a wide distribution of Zeeman and dipolar temperatures at steady state. This would require much more complicated modelling than is currently done.

Trityl spin–lattice relaxation is amazingly similar at X- and W-bands despite a ten-fold change in magnetic field, B₀. The relaxation is certainly not dominated by rates that scale with B₀² or B₀⁴ 0 as often seen for S = 1/2 transition metal ions. This limits the kinds of couplings between spins and phonons that are responsible for relaxation. But it also suggests that for polarizers operating below ∼250 GHz, the electron spin–lattice relaxation is not a major factor in the variations in their DNP performance.

Relaxation is rather similar for OX063 and Finland trityl. We expected this because the electron spin is concentrated in the central core common to all trityls. On the other hand, the differences in the concentration-dependent relaxation and in Θ_Orb are expected because aggregate formation and interradical contacts that determine J involve chemical interactions of trityls with each other and with solvent. These interactions involve the different types of sidegroups on the surface of the trityls but isolated from the electron spin. The chemical properties of groups at the trityl surface could explain some of the sensitivity of DNP to changes in radical concentration, solvent or other solutes.

Spin dynamics

Spin diffusion plays a major role in the spin–lattice relaxation of the bulk of the trityl radicals in the samples with radical concentrations typical for DNP. The spin diffusion occurs by mutual flip-flops of radical spins. These flip-flops drive diffusion of electron spin polarization to the fast-relaxing centers where equilibration with the lattice can occur. Since these flip-flops couple the Δm_S,i = +1 transition of a radical, i, with the Δm_S,j = −1 transition of another radical, j, the net electron spin polarization, ${\displaystyle \sum _i{m}_{S,i}}$, is conserved. Consequently the flip-flops facilitate spin–lattice relaxation but are not the relaxation event itself.

Each radical, i, produces a dipolar field, d_i,j, affecting other radicals, j, and nuclear spins. The dipolar fields from the two radicals in a flip-flop transition are different at most points in space. So even though a flip-flop conserves spin polarization, it does not conserve the dipolar field. Most flip-flop transitions produce a net change in the dipolar field of (d_{i, j}−d_i′,j) ≠ 0 in their immediate vicinity. The flip-flop itself generally causes relaxation of the x and y components of the participating electron spins and of other nearby radicals, contributing to T_M and T₂ spin relaxation. The fluctuating dipole field may cause some electron spin–lattice relaxation. But the probability is on the order of ∼ (d/B₀)² or less, so that flip-flops primarily affect electron spin–lattice relaxation through their role in spin diffusion to fast-relaxing centers.

A radical, j, experiences a net dipolar field, $d_{\text{net},j}\left(t\right)={\displaystyle \sum _i{d}_{i,j}{m}_{\mathrm{S},i}\left(t\right)}$ that is the sum of contributions from all radicals around it. The d_net,j(t) clearly has a time dependence driven by the m_S,i(t) of the electron spins around it. The net dipolar field, along with the hyperfine fields and the applied magnetic field, determines the EPR frequency of radical j. It is generally overlooked that the net dipolar fields at different radicals are not the same, although often correlated statistically. Consequently, the difference in EPR frequencies of two radicals fluctuates as d_net,j(t)−d_{net, j′}(t). Thus, during hyperpolarization of a DNP sample, the fluctuating dipolar field can bring the radical into and out of resonance with applied microwave or rf fields and with other spins. The importance of fluctuating resonance frequencies is recognized in MAS-DNP where it has profound effects on spin dynamics and hyperpolarization kinetics^72–74 but has been ignored in modelling of dissolution DNP.

Salikhov and co-workers studied EPR spectral diffusion driven by modulation of the dipole field by spin–lattice relaxation^75,76 and by spin flip-flops.⁷⁷ They found that strong electron spin polarization decreases the rates of phase relaxation and spectral diffusion.⁷⁶ The electron spin flip-flops occur between two spins with opposite m_S, which are rare when spins are strongly polarized. One might expect that spectral diffusion and other phenomena driven by electron spin flip-flops are strongly suppressed at the low temperatures and high magnetic fields used for DNP. This may very well be true when the microwave pumping fields are off and the electron spins are fully relaxed. But the hyperpolarization process requires strong pumping by microwave fields that drive the electron spins far from equilibrium. The non-equilibrium state and its non-equilibrium spin polarization support electron spin flip-flops and spectral diffusion during hyperpolarization.

Nuclear spin–lattice relaxation

Nuclear spin–lattice relaxation opposes the nuclear spin polarization rate and limits the ultimate degree of polarization. The relaxation of I = 1/2 nuclei in low temperature solids is primarily due to cross relaxation with paramagnetic centers.^11,47 The nuclear spin– lattice relaxation rate is written, for example, by Abragam in chapter IX, eqn (40) as⁴⁷

$$w_{\mathrm{n}}=\frac{1}{T_{1\mathrm{n}}}\propto \frac{\tau }{1+{{\omega }_I}^2{\tau }^2}$$ (7)

where ω_I is the NMR frequency of that nuclear spin. τ is the correlation time for m_S and is often taken to be T_1e (or 1/b here). But at the high concentrations typical for DNP, m_S varies much more rapidly due to w_ff than by w_S or b. Thus, τ is closer to the spin echo decay time T_M than to T_1e.

Over the entire temperature range examined here, the spin echo signal decays indicate that τ ω_I (or ω_I/w_ff) ≫ 1, so that the majority of the trityl radicals contribute to the nuclear spin– lattice relaxation rate as w_n ∝ N_Sw_ff/ω_I². The fast-relaxing centers responsible for electron spin–lattice relaxation also contribute to nuclear relaxation as w_n ∝ N_Sw_F/ω_I². We find that N_F ∝ [trityl]³, but w_ff ∝ [trityl]. This means that nuclear relaxation may be mediated by electron spin flip-flops at moderate radical concentrations but by w_F of radical triads or fast-relaxing centers at higher concentrations. The crossover occurs when N_Sw_ff ≈ N_Fw_F and could lead to a rather complicated dependence of DNP on radical concentration and temperature.

Are clusters desirable?

Clusters form spontaneously in trityl solutions typical for dissolution DNP and need to be considered when modelling or trying to optimize DNP. An obvious question is whether the hyperpolarization process benefits from or is hindered by trityl cluster formation. The answer is not clear because detailed numerical simulations with parameters reflecting real samples have never been reported and the mechanism responsible for hyperpolarization with trityl radicals is still uncertain. However, some speculation based on our findings and general chemical and physical considerations is possible.

As shown here, triad clusters of three trityls have a great impact on spin–lattice relaxation rates. Preventing the formation of clusters would make it easier for microwaves to saturate resonant trityl radicals, leading indirectly to a larger asymptotic value for the hyperpolarization. On the other hand, each radical must absorb microwaves many times before the steady-state hyperpolarization is reached. The net microwave absorption rate equals the net spin–lattice relaxation rate, so with no clusters, the buildup of polarization would be much slower. Increasing radical concentration could compensate for the lack of clusters, but would also increase the nuclear spin–lattice relaxation rate, as just discussed, decreasing asymptotic hyperpolarization. Preventing triad clusters would probably degrade polarization for a fixed pumping time.

These considerations predict that agents, such as Gd(III) that increase spin–lattice relaxation when added to DNP samples, would enhance the rate of hyperpolarization, as observed. They also suggest that increasing trityl radical triad formation could preserve electron spin–lattice relaxation at lower total trityl radical concentrations. This would slow nuclear spin–lattice relaxation, as discussed earlier, and enhance hyperpolarization.

Nitroxide biradicals are better polarizing agents than nitroxide radicals, thought to be due to dipolar interactions within the biradical that enhance transfer of polarization to nuclei. It was something of a surprise that trityl biradicals showed no improvement over trityl radicals.²⁷ We can speculate that DNP samples with trityl radicals already contain sufficient self-assembled trityl dimers to be equivalent to the biradical DNP sample. And that dimers play a distinctly different role than triads. In this case, one would expect that preventing self-assembly of trityl dimers would impair hyperpolarization.

These speculations suggest that the self-assembly of trityl clusters does have a positive impact on DNP, but implies that controlling the amounts of individual clusters may allow much better control of the DNP process.

Experimental

Trityls and solutions

The Finland trityl and d₂₄-OX063 radicals were synthesized as previously described.⁷⁸ To prepare samples, the appropriate radical, as the sodium salt of Finland trityl or the acid form of OX063, was first dissolved in a mixture of ∼300 μL methanol (≥99.9% Sigma-Aldrich) and ∼0.2 μL aqueous ammonia solution (to help solubility and moderate pH). A 10 μL aliquot was added to 3 mL distilled water and the optical absorption was measured by a UV spectrometer (Shimadzu UV-1601). The trityl concentration was calculated using a nominal molar extinction coefficient of 16 000 M⁻¹ cm⁻¹.⁷⁹ The appropriate volume of the methanol solution to make a sample of the desired concentration was dried by a nitrogen gas flow, and re-dissolved in a degassed 60: 40(v/v) glycerol: water stock mixture. Samples were prepared in a nitrogen box to minimize dissolved O₂ although the relaxation of air-saturated samples is indistinguishable from that of samples degassed by repeated freeze–pump–thaw cycles.

Trityl solutions for X-band measurement were transferred (∼50 μL) to quartz tubes (Norell S-4-EPR-250s o.d. 4.0 mm) and immediately frozen and stored in liquid nitrogen unless otherwise noted. For W-band measurement, the 2.5 mM Finland trityl and 1 mM OX063 samples were placed in quartz tubes (Vitrocom Inc. CV7087Q (i.d. 0.70 mm o.d. 0.87 mm)). High concentration samples were loaded into capillaries (Vitrocom Inc. CV1525Q (i.d. 0.15 mm o.d. 0.25 mm)) which were then placed into the 0.87 mm o.d. quartz tubes. The W-band samples were stored at a nominal −40 °C until measurement.

Measurements

Spin–lattice relaxation rates, 1/T_1e, were measured between 4–100 K using a Bruker E680 W-/X-band spectrometer by the saturation-recovery method using a picket fence of 20 pulses, 3 μs apart, of 12 ns duration (3 π/8 turning angle). The two-pulse echo signal was measured with a 16 ns π/2 first pulse and the width of the second pulse was chosen between 8–32 ns to optimise echo intensity by reducing instantaneous diffusion. Each recovery occurs over a wide range of times, so every recovery was measured at six points per decade in time starting 100 ns after the end of the saturating picket fence of pulses and extending until recovery was complete, occasionally to delays of 100 s.

Fitting

Recovery and temperature/concentration dependence data were analyzed using Matlab (MathWorks). Figures were prepared using OriginPro 2015 and 2016 (Origin Labs).

Conclusions

Electron spin–lattice relaxation of the trityl free radicals, OX063 and Finland, at the multi-millimolar concentrations used for low-temperature DNP is mediated by spin diffusion to fast-relaxing paramagnetic centers where the spin energy is dissipated as lattice phonons by an Orbach–Aminov relaxation mechanism. The relaxation of electron spins to the lattice is non-exponential and is enhanced as the radical concentration increases. The spin–lattice relaxation is quite similar at X- and W-bands at all temperatures and concentrations studied.

The fast-relaxing centers seem to be exchange-coupled clusters of three radicals that form spontaneously in the frozen samples as a result of the solubility and large volume of the trityl radicals. Formation of these fast-relaxing centers and the spin–lattice relaxation of the final samples are quite sensitive to molecular properties of the trityl, the chemical composition of the solvent mixture, and the sample preparation procedure.

Spin diffusion among trityl radicals plays an important role in spin–lattice relaxation. But it also drives spectral diffusion of each radical and will affect the transfer of energy among the thermal reservoirs during the DNP process. The resonant frequency of an individual radical varies with time. This dynamic resonant frequency needs to be included in numerical modelling of the DNP process.