Benchmarking of participant-level confound regression strategies for the control of motion artifact in studies of functional connectivity

Abstract

Since initial reports regarding the impact of motion artifact on measures of functional connectivity, there has been a proliferation of participant-level confound regression methods to limit its impact. However, many of the most commonly used techniques have not been systematically evaluated using a broad range of outcome measures. Here, we provide a systematic evaluation of 14 participant-level confound regression methods in 393 young adults. Specifically, we compare methods according to four benchmarks, including the residual relationship between motion and connectivity, distance-dependent effects of motion on connectivity, network identifiability, and additional degrees of freedom lost in confound regression. Our results delineate two clear trade-offs among methods. First, methods that include global signal regression minimize the relationship between connectivity and motion, but unmask distance-dependent artifact. In contrast, censoring methods mitigate both motion artifact and distance-dependence, but use additional degrees of freedom. Importantly, less effective de-noising methods are also unable to identify modular network structure in the connectome. Taken together, these results emphasize the heterogeneous efficacy of proposed methods, and suggest that different confound regression strategies may be appropriate in the context of specific scientific goals.

Introduction

Resting-state (intrinsic) functional connectivity (rsfc-MRI) has evolved to become one of the most common brain imaging modalities (Craddock et al., 2013; Fox and Raichle, 2007; Power et al., 2014b; Smith et al., 2013; Van Dijk et al., 2010), and has been critical for understanding fundamental properties of brain organization (Damoiseaux et al., 2006; Fox et al., 2005; Power et al., 2011; Yeo et al., 2011), brain development over the lifespan (Di-Martino et al., 2014; Dosenbach et al., 2011; Fair et al., 2008), and abnormalities associated with diverse clinical conditions (Baker et al., 2014; Buckner et al., 2008; Fair et al., 2010). rsfc-MRI has numerous advantages, including ease of acquisition and suitability for a wide and expanding array of analysis techniques. However, despite knowledge that in-scanner motion can influence measures of activation from task-related fMRI (Friston et al., 1996), the impact of in-scanner motion on measures of functional connectivity was not explored for 16 years after its initial discovery (Biswal et al., 1995). However, since the near-simultaneous publication of three independent reports in early 2012 (Van Dijk et al., 2012; Power et al., 2012; Satterthwaite et al., 2012), it has been increasingly recognized that motion can have a large impact on rsfc-MRI measurements, and can systematically bias inference. This bias is particularly problematic in developmental or clinical populations where motion is correlated with the independent variable of interest (age, diagnosis) (Satterthwaite et al., 2012; Fair et al., 2012), and has resulted in the reevaluation of numerous published findings.

In response to this challenge, there has been a recent proliferation of participant-level confound regression and censoring methods aimed at mitigating the impact of motion on functional connectivity (Yan et al., 2013a; Power et al., 2015). These methods can be broadly grouped into several categories. First, high-parameter confound regression strategies use expansions of realignment parameters or tissue-compartment signals, often including derivative and quadratic regressors (Friston et al., 1996; Satterthwaite et al., 2013; Yan et al., 2013a). Second, principal component analysis (PCA) based methods (CompCor; Behzadi et al. (2007); Muschelli et al. (2014)) find the primary directions of variation within high-noise areas defined by anatomy (e.g., aCompCor) or temporal variance (tCompCor). Third, whole-brain independent component analysis (ICA; Beckmann et al. (2005)) of single-subject time series has increasingly been used for de-noising, with noise components selected either by a trained classifier (ICA-FIX; Griffanti et al. (2014); Salimi-Khorshidi et al. (2014)) or using a priori heuristics (ICA-AROMA; Pruim et al. (2015b,a)). Fourth, temporal censoring techniques identify and remove (or de-weight) specific volumes contaminated by motion artifact, often followed by interpolation. These techniques include scrubbing (Power et al., 2012, 2014a, 2015), spike regression (Satterthwaite et al., 2013), and de-spiking (Jo et al., 2013; Patel et al., 2014). Censoring techniques have been reported to attenuate motion artifact, but at the cost of a shorter time series and variably reduced degrees of freedom. Fifth, one recent report emphasized the relative merits of spatially-tailored confound regression using local white matter signals (wm-Local; Jo et al. (2013)). Finally, the inclusion of global signal regression (GSR) (Macey et al., 2004) in confound regression models remains a source of controversy (Fox et al., 2009; Murphy et al., 2009; Chai et al., 2012; Saad et al., 2012; Yan et al., 2013b; Murphy and Fox, in press). While several studies have suggested its utility in de-noising (Fox et al., 2009; Power et al., 2015; Satterthwaite et al., 2013; Yan et al., 2013a), other studies have emphasized the risk of removing a valuable signal (Yang et al., 2014; Hahamy et al., 2014), potentially biasing group differences (Gotts et al., 2013; Saad et al., 2012), or exacerbating distance-dependent motion artifact. Distance-dependent artifact (Power et al., 2012; Satterthwaite et al., 2012) manifests as increased connectivity in short-range connections, and reduced connectivity in long-range connections, which has the potential to impact measures of network topology (Yan et al., 2013b).

Substantial additional work has moved beyond use of realignment parameters and timeseries signal as regressors. Specifically, recent work has suggested that techniques such as MotSim may potentially track more signal variance related to motion (Patriat et al., 2017). Furthermore, while initial work suggested that voxel-wise motion regressors were not advantageous, work by Spisák et al. (2014) suggests that such information can be successfully utilized. Additionally, recent work has evaluated the impact of motion on timeseries smoothness (Scheinost et al., 2014), and suggested that uniform smoothing may ameliorate artifact. Finally, recent work has proposed geometric techniques for correcting motion artifact (e.g., median angle correction) (He and Liu, 2012) and investigated prospective correction techniques (Faraji-Dana et al., 2016).

This recent proliferation of de-noising techniques has prompted excitement but also sowed confusion. Unsurprisingly, new de-noising pipelines have often tended to emphasize outcome measures that suggest their relative superiority. As a result, investigators often anecdotally report substantial uncertainty regarding which pipeline should be used. Such uncertainty has been exacerbated by the lack of common outcome measures used across studies, which has hampered direct comparison among pipelines. While one review paper has summarized recent developments in this rapidly-evolving sub-field (Power et al., 2015), systematic evaluation of de-noising pipelines according to a range of benchmarks remains lacking.

Several prior papers have compared some of these confound regression strategies on selected benchmark measures. For example, Yan and colleagues evaluated a range of de-noising strategies based on realignment parameters (e.g., 6P, 12P, 24P), scrubbing, and GSR (Yan et al., 2013c). Subsequently, Pruim et al. (2015a) compared ICA-AROMA to the 24-parameter model, scrubbing, and aCompCor, among other techniques. Building on such work, Burgess et al. (2016) examined the relative added value of mean grayordinate time series regression, which is similar to GSR, as an addition to ICA-based de-noising (ICA-FIX). However, prior work has not directly evaluated several of the most commonly implemented de-noising methods, such as 36-parameter confound regression + censoring, using a broad range of benchmark measures.

Accordingly, in this report we compare 14 of the most commonly used confound regression strategies in a large (N = 393) dataset of adolescents and young adults. Pipelines evaluated include standard techniques, high-parameter confound regression, PCA-based techniques such as aCompCor and tCompcor, ICA-based approaches such as ICA-AROMA, spatially-tailored local white matter regression, and three different censoring techniques (spike regression, de-spiking, and scrubbing); GSR is included in many pipelines as well. It should be emphasized that this is not a comprehensive evaluation of all artifact-control strategies in use, and that models evaluated were limited to a subset of those commonly used at present. Critically, we compare these pipelines according to four intuitive benchmarks, including the residual relationship between functional connectivity and subject motion, the degree of distance-dependent artifact, the identifiability of network structure after de-noising, and the loss of temporal degrees of freedom. As described below, results underscore the relative strengths and weaknesses among these methods, and reveal clear trade-offs among commonly used confound regression approaches.

Materials and methods

Participants and data acquisition

The task-free BOLD data used in this study (N = 393) were drawn from the Philadelphia Neurodevelopmental Cohort (PNC) (Satterthwaite et al., 2014, 2016) on the basis of age, health, and data quality. Participants' ages ranged from 8 to 22 years. All participants selected for evaluation were ages 8–22, were free from medical conditions that could impact brain function (Merikangas et al., 2010), lacked gross structural brain abnormalities (Gur et al., 2013), were not taking psychotropic medication at the time of the scan, and had high quality imaging data free of gross motion. In total, N = 84 (44 females) participants were not included in this sample due to gross motion, defined as a mean relative RMS (root mean squared) displacement > 0:2mm, or > 20 volumes with framewise relative RMS displacement > 0:25mm. The exclusion of participants with gross in-scanner motion allowed us to evaluate the utility of confound regression strategies for the mitigation of artifact due to micro-movements.

Structural and functional subject data were acquired on a 3T Siemens Tim Trio scanner with a 32-channel head coil (Erlangen, Germany), as previously described (Satterthwaite et al., 2014, 2016). High-resolution structural images were acquired in order to facilitate alignment of individual subject images into a common space. Structural images were acquired using a magnetization-prepared, rapid-acquisition gradient-echo (MPRAGE) T1-weighted sequence (T_R = 1810ms; T_E = 3:51ms; FoV = 180 × 240mm; resolution 1mm isotropic). Approximately 6 minutes of task-free functional data were acquired for each subject using a blood oxygen level-dependent (BOLD-weighted) sequence (T_R = 3000ms; T_E = 32ms; FoV = 192 × 192mm; resolution 3mm isotropic; 124 spatial volumes). Prior to scanning, in order to acclimate subjects to the MRI environment and to help subjects learn to remain still during the actual scanning session, a mock scanning session was conducted using a decom-missioned MRI scanner and head coil. Mock scanning was accompanied by acoustic recordings of the noise produced by gradient coils for each scanning pulse sequence. During these sessions, feedback regarding head movement was provided using the MoTrack motion tracking system (Psychology Software Tools, Inc, Sharpsburg, PA). Motion feedback was only given during the mock scanning session. In order to further minimize motion, prior to data acquisition subjects' heads were stabilized in the head coil using one foam pad over each ear and a third over the top of the head. During the resting-state scan, a fixation cross was displayed as images were acquired. Subjects were instructed to stay awake, keep their eyes open, fixate on the displayed crosshair, and remain still.

Structural image processing

A study-specific template was generated from a sample of 120 PNC subjects balanced across sex, race, and age bins using the build Template Parallel procedure in ANTs (Avants et al., 2011a). Study-specific tissue priors were created using a multi-atlas segmentation procedure (Wang et al., 2014). Next, each subject's high-resolution structural image was processed using the ANTs Cortical Thickness Pipeline (Tustison et al., 2014). Following bias field correction (Tustison et al., 2010), each structural image was diffeomorphically registered to the study-specific PNC template using the top-performing SyN deformation (Klein et al., 2009). Study-specific tissue priors were used to guide brain extraction and segmentation of the subject's structural image (Avants et al., 2011b).

BOLD time series processing

Task-free functional images were processed using the XCP Engine (Ciric et al., In Preparation), which was configured to support the 14 pipelines evaluated in this study (see Figure 1). Each pipeline was based on de-noising strategies previously described in the neuroimaging literature. A number of preprocessing procedures were included across all de-noising pipelines. Common elements of preprocessing included (1) correction for distortions induced by magnetic field inhomogeneities using FSL's FUGUE utility, (2) removal of the 4 initial volumes of each acquisition, (3) realignment of all volumes to a selected reference volume using MCFLIRT (Jenkinson et al., 2002), (4) demeaning and removal of any linear or quadratic trends, (5) co-registration of functional data to the high-resolution structural image using boundary-based registration (Greve and Fischl, 2009), and (6) temporal filtering using a first-order Butterworth filter with a passband between 0.01 and 0.08 Hz. We did not apply slice timing correction during preprocessing, as recent data suggest that the interpolation that occurs may artificially reduce motion estimates (Power et al., under review). These preliminary processing stages were then followed by the confound regression procedures described below. In order to prevent frequency-dependent mismatch during confound regression (Hallquist et al., 2013), all regressors were band-pass filtered to retain the same frequency range as the data. As in our prior work (Satterthwaite et al., 2012, 2013), the primary summary metric of subject motion used was the mean relative RMS (root-mean-squared) displacement calculated during time series realignment using MCFLIRT.

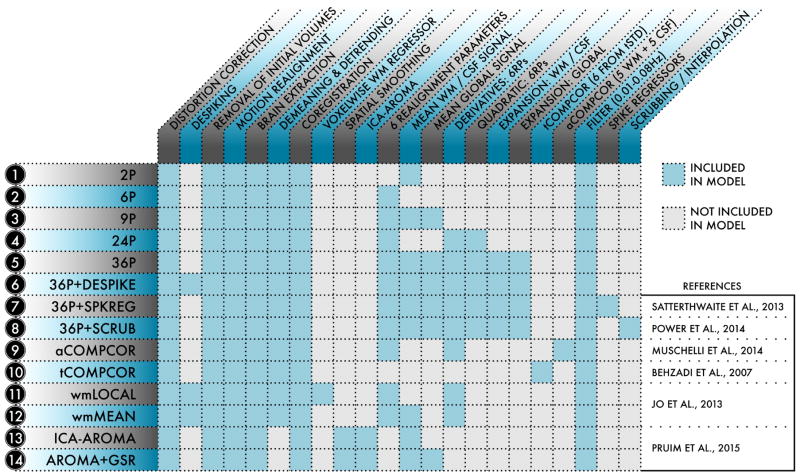
Figure 1. Schematic of the 14 de-noising models evaluated in the present study.

For each of the 14 models indexed at left, the table details what processing procedures and confound regressors were included in the model. De-noising models were selected from the functional connectivity literature and represented a range of strategies.

Overview of confound regression strategies

The primary objective of the current study was to evaluate the performance of common de-noising strategies. We selected 14 de-noising models, labelled 1–14 below, for evaluation (Figure 1). Models 1–5 used nuisance parameters derived from 6 movement estimates and 3 physiological time series, as well as their temporal derivatives and quadratic expansions.

• Model 1. (2P) Used only the 2 physiological time series: mean signal in WM and mean signal in CSF, and functioned as a base model for comparison to other more complex confound regression models.

• Model 2. (6P) Used only the 6 motion estimates derived from MCFLIRT realignment as explanatory variables.

• Model 3. (9P) Combined the 6 motion estimates and 2 physiological time series with global signal regression. This model has been widely applied to functional connectivity studies (Fox et al., 2005, 2009).

• Model 4. (24P) Expansion of model 2 that includes 6 motion parameters, 6 temporal derivatives, 6 quadratic terms, and 6 quadratic expansions of the derivatives of motion estimates for a total 24 regressors (Friston et al., 1996).

• Model 5. (36P) Similar expansion of model 3: 9 regressors, their derivatives, quadratic terms, and squares of derivatives (Satterthwaite et al., 2013).

Models 6–8 further expanded upon this maximal 36P strategy by incorporating censoring approaches.

• Model 6. (36P+despike) Included 36 regressors as well as despiking (Cox, 1996).

• Model 7. (36P+spkreg) Included 36 regressors as well as spike regression, as in Satterthwaite et al. (2013).

• Model 8. (36P+scrub) Included 36 regressors as well as motion scrubbing, as in Power et al. (2014a).

Models 9 and 10 adapted variants of the PCA-based CompCor approach.

• Model 9. (aCompCor) Used 5 principal components each from the WM and CSF, in addition to motion estimates and their temporal derivatives (Muschelli et al., 2014).

• Model 10. (tCompCor) Used 6 principal components from high-variance voxels (Behzadi et al., 2007).

Models 11 and 12 comparatively evaluated the efficacy of local and global-mean tissue-class regressors.

• Model 11. (wmLocal) Used a voxelwise, localised WM regressor in addition to motion estimates and their temporal derivatives and despiking (Jo et al., 2013).

• Model 12. (wmMean) Identical to model 11 except that it used the mean signal across the WM instead of a voxelwise, localised WM regressor (Jo et al., 2013). Models 13 and 14 evaluated subhect-specific ICA de-noising.

• Model 13. (ICA-AROMA) Used a recently developed ICA-based procedure for removal of motion-related variance from BOLD data, together with mean WM and CSF regressors (Pruim et al., 2015a,b).

• Model 14. (AROMA+GSR) Combined ICA-AROMA as implemented in model 13 with global signal regression, in a procedure somewhat analogous to Burgess et al. (2016).

We explicitly limited our scope to models that did not require training a classifier, and did not evaluate confound regression strategies that require extensive parameter optimization (Salimi-Khorshidi et al., 2014; Griffanti et al., 2014; Patel et al., 2014). Furthermore, in order to constrain the parameter space, we did not examine unpublished combinations of de-noising approaches.

Confound regression using realignment parameters

Time series of six realignment parameters (three translational and three rotational) for each subject were returned by MCFLIRT as part of time series realignment (motion correction). Additionally, the temporal derivative, quadratic terms, and quadratic of the temporal derivative of each of the realignment parameters were calculated, yielding 24 realignment regressors in total. The original six realignment parameters were included in confound regression models 2 and 3. Models 9 and 11 included 12 realignment regressors – the 6 realignment parameters and their temporal derivatives – while the full set of 24 expanded realignment regressors were included as part of confound regression models 4–8.

Global signal regression

The mean global signal was computed by averaging across all voxelwise time series located within a subject-specific mask covering the entire brain. The global signal was included in model 3, while the expanded models 5–8 included 4 global signal regressors: the global signal, its derivative, its square, and the derivative of its square.

Tissue class regressors

Mean white matter (WM) and cerebrospinal fluid (CSF) signals were computed by averaging within masks derived from the segmentation of each subject's structural image; these masks were eroded using AFNI's 3dmask tool (Cox, 1996) to prevent inclusion of gray matter signal via partial-volume effects. The WM mask was eroded at the 2-voxel level, while the CSF mask was eroded at the 1-voxel level. More liberal erosion often resulted in empty masks in our data. Temporal derivatives, quadratic terms, and squares of the derivative were computed as above. Two tissue class regressors (WM and CSF) were included in models 3 and 12, whereas their expansions (8 regressors) were included in models 4–8.

Local white matter regression

Model 11 used a local WM regressor (Jo et al., 2013). This was computed in AFNI using 3dLocalstat (Cox, 1996). Unlike the regressors described above, which were voxel-invariant, the value of the local WM regressor was computed separately at each voxel. For each voxel, a sphere of radius 45mm was first centered on that voxel; this sphere defined that voxel's local neighborhood. Next, this spherical neighborhood was intersected with an eroded WM mask to produce a local WM mask, which included only the fraction of the WM that was also in the voxel's neighborhood. The mean signal within this new local WM mask was then used to model the local WM signal at the voxel (Jo et al., 2013). This process was repeated at every voxel in order to generate the local WM regressor. This local WM regressor was included in model 11 along with realignment parameters and their derivatives (12 total); this model also included voxelwise de-spiking. In order to evaluate the efficacy of this local regressor in comparison with a more typical mean tissue regressor, model 12 was identical to model 11 with a mean WM regressor substituting for the local WM regressor.

CompCor

Principal component analysis (PCA) can be used to model noise in BOLD time series (Behzadi et al., 2007; Muschelli et al., 2014). Broadly, the use of PCA-derived regressors to model noise is called component-based correction (CompCor). Numerous variants of CompCor have been developed; here, our focus will be on anatomical CompCor (aCompCor, model 9) and temporal CompCor (tCompCor, model 10). In aCompCor, a PCA is performed within an anatomically defined tissue class of interest. We extracted 5 components for WM and CSF each, yielding 10 compcor components (Muschelli et al., 2014). As part of model 9, as in Muschelli et al. (2014), these 10 aCompCor components were combined with 12 re-alignment parameters (raw and temporal derivative). In tCompCor, the temporal variance of the BOLD signal is first computed at each voxel. Subsequently, a mask is generated from high-variance voxels, and principal components are extracted from the time series at these voxels. In confound regression model 10, tCompcor was implemented using ANTs, with 6 tCompCor components used as confound regressors for each participant.

ICA-AROMA

ICA-AROMA (automatic removal of motion artifact) is a recently-introduced, widely-used method for de-noising using single-subject ICA (Pruim et al., 2015a,b); we evaluated ICA-AROMA in confound regression models 13 and 14. In contrast to other ICA based methods (e.g., ICA-FIX: Salimi-Khorshidi et al. (2014)), it does not require dataset-specific training data. The input to ICA-AROMA is a voxelwise time series that has been smoothed at 6mm FWHM using a Gaussian kernel. After decomposing this time series using FSL's MELODIC (with model order estimated using the Laplace approximation) (Beckmann et al., 2005), ICA-AROMA uses four features to determine whether each component corresponds to signal or noise. The first 2 features are spatial characteristics of the signal source: (1) the fraction of the source that falls within a CSF compartment and (2) the fraction of the source that falls along the edge or periphery of the brain. The remaining features are derived from the time series of the source: (3) its maximal robust correlation with time series derived from realignment parameters and (4) its high-frequency spectral content. ICA-AROMA includes two de-noising steps. The first de-noising step occurs immediately after classification. All component time series (signal and noise) are included as predictors in the linear model, and the residual BOLD time series is obtained via partial regression of only the noise time series. A second confound regression step occurs after temporal filtering, wherein mean signals from WM and CSF (models 13 and 14) and the global signal (model 14 only) were regressed from the data.

Temporal censoring: de-spiking, spike regression, and scrubbing

In addition to regression of nuisance time series, a number of ‘temporal censoring' approaches were used to identify motion-contaminated volumes in the BOLD time series and reduce their impact on further analysis. These approaches included despiking, spike regression, and scrubbing. Despiking is a procedure that identifies outliers in the intensity of each voxel's detrended BOLD time series and then interpolates over these outliers. Despiking was implemented in AFNI using the 3dDespike utility (Cox, 1996) as part of confound regression model 6.

Unlike despiking, which identifies outliers on a voxel-wise basis, spike regression and scrubbing censor complete volumes based on metrics of subject movement defined a priori. For spike regression, as in Satterthwaite et al. (2013), volumes were flagged for spike regression if their volume-to-volume RMS displacement exceeded 0.25mm. Next, as part of confound regression model 7, k ‘spike' regressors were included as predictor variables in the de-noising model, where k equalled the number of volumes flagged (Satterthwaite et al., 2013). For each flagged time point, a unit impulse function that had a value of 1 at that time point and 0 elsewhere was included as a spike regressor.

For scrubbing, the framewise displacement (FD) (Power et al., 2012) was computed at each time point as the sum of the absolute values of the derivatives of translational and rotational motion estimates. If framewise displacement (FD) at any point in time exceeded 0.2mm, then that time point was flagged for scrubbing. It should be noted that the conversion of FD to RMS displacement is approximately 2:1, and thus the published criterion for scrubbing has a lower threshold for flagging high-motion volumes than does spike regression. Scrubbing of BOLD data was performed iteratively (Power et al., 2014a) as part of confound regression model 8. At any stage where a linear model was applied to the data (for instance, during detrending procedures), high-motion epochs were temporally masked out of the model so as not to influence fit. During temporal filtering, a frequency transform was used to generate surrogate data with the same phase and spectral characteristics as the unflagged data. This surrogate data was used to interpolate over flagged epochs prior to application of the filter. During confound regression, flagged timepoints were excised from the time series so as not to contribute to the model fit. For scrubbing (but not spike regression) if fewer than five contiguous volumes had unscrubbed data, these volumes were scrubbed and interpolated as well.

Overview of outcome measures

We evaluated each de-noising pipeline according to four benchmarks. Residual QC-FC correlations and distance-dependence provided a metric of each pipeline's efficacy, while loss of temporal DOF provided an estimate of each pipeline's efficiency. Finally, the modularity quality provided an estimate of network identifiability after de-noising.

Relationship between mean relative RMS displacement and functional connectivity (QC-FC correlations)

In order to estimate the residual relationship between subject movement and connectivity after de-noising, we computed QC-FC correlations (quality control / functional connectivity) (Power et al., 2015; Satterthwaite et al., 2012, 2013; Power et al., 2012). While other metrics have been used in prior reports, including FD-DVARS correlations, we favor QC-FC as the most useful metric of interest as it directly quantifies the relationship between motion and the primary outcome of interest (rather than two quality metrics, as in FD-DVARS). For an extended discussion of the rationale for this measure, see Power et al. (2015).

We evaluated QC-FC relationships within two commonly-used whole-brain networks, the first consisting of spherical nodes distributed across the brain (Power et al., 2011) and the second comprising an areal parcellation of the cerebral cortex (Gordon et al., 2016). For each network, the mean time series for each node was calculated from the denoised residual data, and the pairwise Pearson correlation coefficient between node time series was used as the network edge weight (Biswal et al., 1995). For each edge, we then computed the correlation between the weight of that edge and the mean relative RMS motion. To eliminate the potential influence of demographic factors, QC-FC relationships were calculated as partial correlations that accounted for participant age and sex. We thus obtained, for each de-noising pipeline, a distribution of QC-FC correlations. This distribution was used to obtain two measures of the pipeline's ability to mitigate motion artifact, including: 1) the number of edges significantly related to motion, which was computed after using the false discovery rate (FDR; Benjamini and Hochberg (1995)) to account for multiple comparisons; and 2) the median absolute value of all QC-FC correlations. All graphs were generated using ggplot2 in R version 3.2.3 (Wickham, 2009); brain renderings were prepared in BrainNet Viewer (Xia et al., 2013).

Distance-dependent effects of motion

Early work on motion artifact demonstrated that in-scanner motion can bias connectivity estimates between two nodes in a manner that is related to the distance between those nodes (Satterthwaite et al., 2012; Power et al., 2012). Under certain processing conditions, subject movement enhances short-distance connections while reducing long-distance connections. To determine the residual distance-dependence of subject movement, we first used the center of mass of each node to obtain a distance matrix D where entry D_ij indicates the Euclidean distance between the centers of mass of nodes i and j. We then obtained the correlation between the distance separating each pair of nodes and the QC-FC correlation of the edge connecting those nodes; this correlation served as an estimate of the distance-dependence of motion artifact.

Network modularity

Including additional regressors in a confound model has the potential to remove real signal in addition to motion-related noise. In order to evaluate this possibility, we computed modularity quality (Q), an explicit quantification of the degree to which there are structured sub-networks in a given network, in this case the de-noised connectome. Prior work has demonstrated a relationship between Q and subject motion (Satterthwaite et al., 2012) that is mitigated by participant-level de-noising approaches (Satterthwaite et al., 2013). If confound regression and censoring were removing real signal in addition to motion-related noise, we expect that Q would decline. To determine Q, community detection was performed on each subject's de-noised network using the Louvain heuristic (Blondel et al., 2008), which partitions the connectome into sub-networks in a manner that maximizes the value of Q. As functional connectomes included positive and negative weights, we used a version of the Louvain algorithm that accommodates signed data (Rubinov and Sporns, 2010), and did not threshold connectivity matrices. Because this approach to community detection is degenerate, a consensus partition was obtained over 100 Louvain optimizations (Lancichinetti and Fortunato, 2012). Finally, the modularity quality of the resultant consensus partition was estimated according to an established null model (Girvan and Newman, 2002); the mean of Q values across subjects provided an estimate of the sub-network definition still present in the connectome after de-noising. Furthermore, we also assessed whether (and to what extent) Q was correlated with motion; to do this, we computed the Pearson correlation coefficient between subjects' Q values and their motion estimates. These relationships were computed as partial correlations that accounted for participant age and sex.

Additional degrees of freedom lost in confound regression

Confound regressors and censoring both reduce the temporal degrees of freedom (DOF) in data. This loss in temporal DOF may introduce bias if it is variable across subjects. While removal of temporal DOF reduces the number of observations that sample the connectome, the current analysis is not biased by the concatenation of temporally discontinuous time series (i.e., after censoring) because the current analysis (1) uses a time-invariant measure of connectivity that is not dependent on any temporal autocorrelation structure (i.e., Pearson correlation) and (2) applies any procedures that are dependent upon temporal autocorrelation structure (e.g., temporal filtering) prior to concatenation. De-noising strategies ideally limit the loss of temporal DOF, for instance by including fewer, more efficacious regressors. In the present study, we assessed the number of temporal DOF lost in each confound regression approach.

As in previous work (Pruim et al., 2015a), we assumed that each time series regressed out and each volume excised from the data constituted a single temporal DOF. Consequently, the loss of temporal DOF was estimated as the sum of the number of regressors in each confound model and the number of volumes flagged for excision under that model. It should be emphasized that the values thus obtained are imperfect estimates. First, because functional MR time series typically exhibit temporal autocorrelation, the actual loss in DOF will be less than the estimated loss in DOF. Accordingly, censoring adjacent volumes does not remove the same number of DOF as does censoring volumes separated in time. Furthermore, a temporal bandpass filter was uniformly applied to all data prior to confound regression; this filtering procedure would itself have removed additional temporal DOF and elevated the autocorrelation of the data. Because this filter was uniform across all de-noising strategies, it was not considered when estimating the loss of additional temporal DOF in each model.

Results

Heterogeneity in confound regression performance

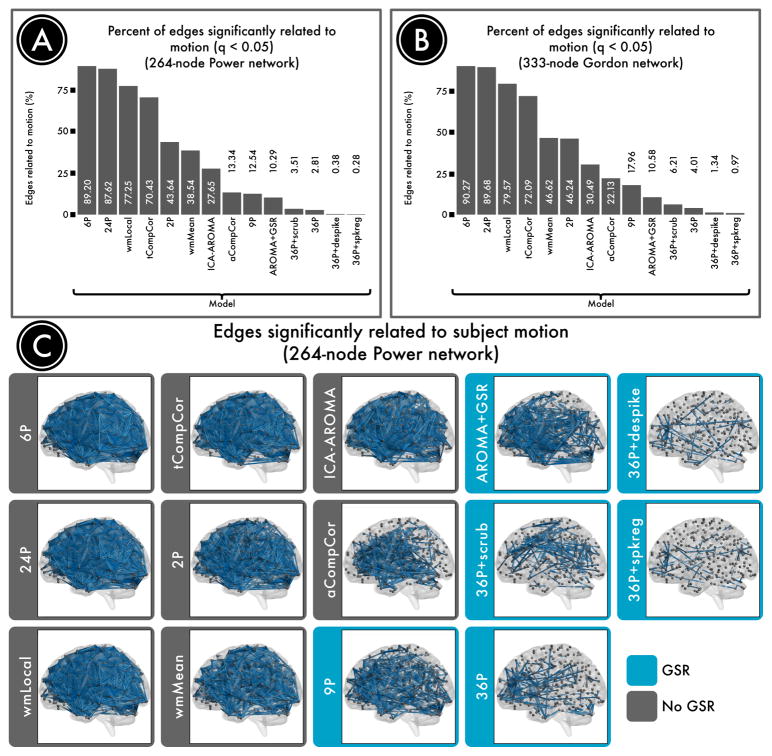
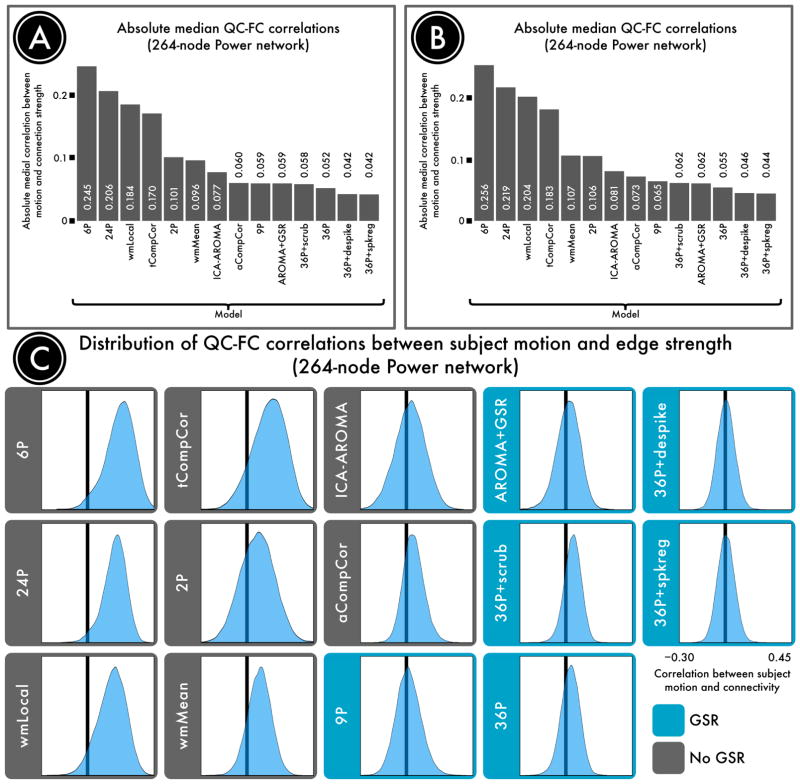
Confound regression strategies typically remove some, but not all, of the artifactual variance that head motion introduces into the BOLD signal. The motion-related artifact that survives de-noising can be quantified to provide a metric of pipeline performance. Here, our primary benchmark of confound regression efficacy was the residual relationship between brain connectivity and subject motion, or the QC-FC correlation. We measured QC-FC correlations using two metrics: the percentage of network connections where a significant relationship with motion was present (Figure 2), and the absolute median correlation (AMC) between connection strength and head movement across all connections (Figure 3).

Figure 2. Number of edges significantly related to motion after de-noising.

Successful de-noising strategies reduced the relationship between connectivity and motion. The number of edges (network connections) for which this relationship persists provides evidence of a pipeline's efficacy. A, The percentage of edges significantly related to motion in a 264-node network defined by Power et al. (2011). Fewer significant edges is indicative of better performance. B, The percentage of edges significantly related to motion in a second, 333-node network defined by Gordon et al. (2016). C, Renderings of significant edges with QC-FC correlations of at least 0.2 for each de-noising strategy, ranked according to efficacy. Strategies that include regression of the mean global signal are framed in blue and consistently ranked as the best performers.

Figure 3. Residual QC-FC correlations after de-noising.

The absolute median QC-FC correlation is another measure of the relationship between connectivity and motion. A, The absolute median correlation between functional connectivity and motion in a 264-node network defined by Power et al. (2011). A lower absolute median correlation indicates better performance. B, The absolute median correlation between functional connectivity and motion in a second, 333-node network defined by Gordon et al. (2016). C, Distributions of all edgewise QC-FC correlations after each de-noising strategy, ranked according to efficacy. Results largely recapitulated those reported in Figure 2, with GSR-based approaches (blue frame) collectively exhibiting the best performance. Whereas approaches that included more regressors generally yielded a narrower distribution, those approaches that included GSR tended to shift the distribution's center toward 0.

No preprocessing strategy was completely effective in abolishing the relationship between head movement and connectivity. However, different approaches exhibited widely varying degrees of efficacy. The top four confound regression strategies included 36 parameters, comprising an expansion of GSR, tissue-specific regressors (WM, CSF), and realignment parameters. Beyond this base 36-parameter model, all censoring techniques provided provided some additional benefit, reducing the number of edges that were significantly related to motion to less than 7%. Convergent results were present across both QC-FC measures (% edges, AMC) and networks (Power, Gordon) that were evaluated. The top-performing method, GSR+spike regression, yielded < 1% of edges that were significantly related to motion.

In contrast, many pipelines performed relatively poorly, leaving a majority of network edges with a residual relationship with motion. Specifically, 89% of edges were impacted by motion when the least effective method was used (6 realignment parameters). The commonly used 24-parameter expansion of realignment parameters originally suggested by Friston et al. (1996) did not provide much of an improvement (88% edges). Similarly, the local WM regressor model (77% edges) and tCompCor 70% edges) also resulted in substantial residual QC-FC correlations. In fact, these methods performed worse than a basic 2-parameter model composed of mean WM and CSF signals (44% edges). Notably, a local WM signal (77% edges) did not provide any benefit over the mean WM signal (39% edges) according to QC-FC metrics, and in fact performed considerably worse. Finally, several methods demonstrated intermediate performance, with 1–20% of edges impacted by motion. This middle group included methods as disparate as aCompCor (13% edges), ICA-AROMA (28% edges), ICA-AROMA with GSR (10% edges), and the classic 9-parameter confound regression model which included GSR (13% edges).

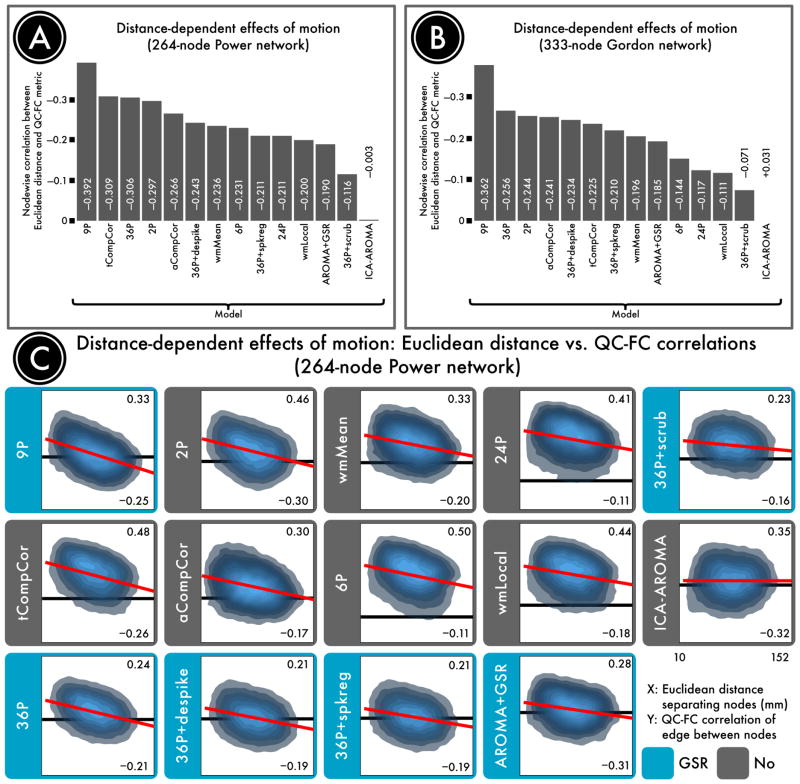
Variability in distance-dependent motion artifact after confound regression

Our second benchmark quantified the distance-dependent motion artifact that was present in data processed by each pipeline (Figure 4). We observed that distance-dependence was present even under conditions where artifact magnitude was attenuated. For example, though the 36-parameter model was among the most effective in attenuating QC-FC relationships, its application revealed strongly distance-dependent artifact. Examination of graphs that plot QC-FC by Euclidean distance (see Figure 4C) revealed that this is due to effective mitigation of motion artifact for long-range but not short-range connections.

Figure 4. Distance-dependence of motion artifact after de-noising.

The magnitude of motion artifact varies with the Euclidean distance separating a pair of nodes, with closer nodes generally exhibiting greater impact of motion on connectivity. A, The residual distance-dependence of motion artifact in a 264-node network defined by Power et al. (2011) following confound regression. B, The residual distance-dependence of motion artifact in a second, 333-node network defined by Gordon et al. (2016). C, Density plots indicating the relationship between the Euclidean distance separating each pair of nodes (x-axis) and the QC-FC correlation of the edge connecting those nodes (y-axis). The overall trend lines for each de-noising strategy, from which distance-dependence is computed, are indicated in red. For each plot, the ordinate is rescaled to the data; thus, the ordinate does not reflect the width of the distribution of QC-FC correlations. (The same data is plotted to a common ordinate in Supplemental Figure 1.) The best performing models either excised high-motion volumes (36-parameter + scrubbing) or used more localized regressors (ICA-AROMA and wmLocal). In general, approaches that made use of GSR without censoring resulted in substantial distance-dependence. This effect was driven by differential efficacy of de-noising, with effective de-noising for long range connections but not short-range connections.

Distance-dependence was highly prominent in models that included GSR, but did not include censoring (e.g., 9-parameter and 36-parameter models). However, despite the lack of global signal in the aCompCor and tCompcor models, data returned from both of these component-based approaches revealed substantial distance-dependent artifact. Notably, inclusion of censoring consistently reduced distance-dependence, although scrubbing was more effective than spike regression or voxelwise despiking.

The top performing method according to this benchmark was ICA-AROMA, which completely abolished any distance-dependence of residual motion artifact. In other words, the motion artifact that was still present in the data after ICA-AROMA impacted all connections in a manner that was not dependent on the spatial separation between nodes. Augmenting ICA-AROMA with GSR decreased QC-FC correlations but exposed distance-dependent artifact, suggesting that ICA-AROMA did not completely remove long-distance motion artifact.

There was similar lack of distance-dependence in the wmLocal model, although as noted above this model did not provide effective de-noising according to QC-FC benchmarks. Use of a local tissue regressor revealed less distance-dependent artifact than did the whole-tissue regressor.

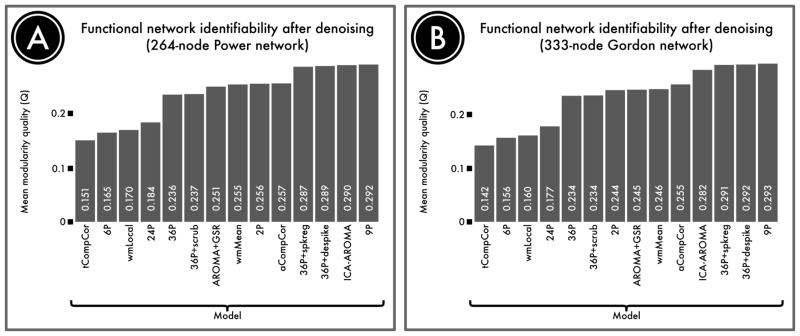
Confound regression strategies mitigate the impact of motion on network modularity

We next evaluated the degree to which de-noising strategies impacted sub-network identifiability, which was operationalized as the network modularity quality (Q; Figure 5). First and most notably, the 4 models that exhibited the poorest performance according to QC-FC measures (6P, 24P, wmLocal, and tCompCor) also suffered from an inability to identify structured functional sub-networks of the brain. This suggests that motion artifact impedes network identifiability. Second, the 36-parameter models did not uniformly out-perform lower order models. However, addition of any of the three censoring techniques evaluated (scrubbing, spike regression, or despiking) provided an improvement over and above the 36-parameter base model. Third, both AROMA and aCompCor performed well, at levels similar to that observed for 36-parameter models with censoring. However, addition of GSR to AROMA did not improve the observed Q value. Fourth and finally, the top-performing model was in fact the 9P model, which had a higher mean Q value than all 36-parameter models and ICA-AROMA.

Figure 5. Identifiability of network structure after de-noising.

Although de-noising approaches remove motion artifact from BOLD time series, it is possible that they also remove signal of interest. We quantified the retention of signal of interest as the modularity quality of the de-noised connectome. A, The modularity quality in a 264-node network defined by Power et al. (2011) following confound regression. B, The modularity quality in a second, 333-node network defined by Gordon et al. (2016). ICA-, GSR-, and tissue class-based models performed relatively well, while models that included realignment parameters alone did not remove enough noise to accurately identify network structure.

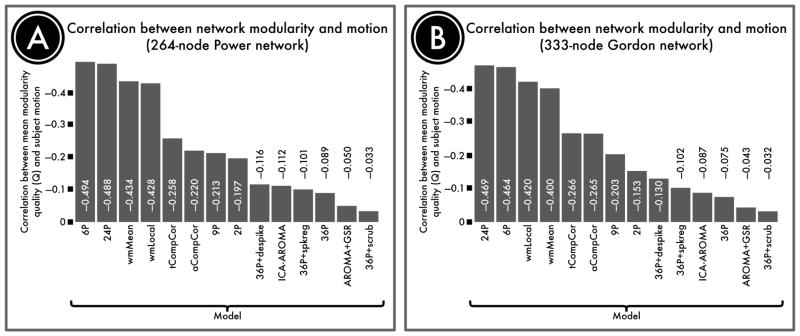
To ascertain whether network identifiability was systematically impacted by motion, we also evaluated the correlation between modularity quality and motion for each de-noising approach. In general, 36-parameter models and ICA-based models most effectively decoupled modular structure from subject motion, while models with high residual QC-FC correlations likewise left high correlations between motion and modularity (Figure 6). Notably, the 9P model that displayed the highest mean Q value nonetheless retained a substantial relationship with motion, as expected from the edgewise QC-FC analyses. Furthermore, addition of GSR to AROMA successfully reduced the relationship between motion and modularity.

Figure 6. Correlation between subject motion and modularity quality.

Motion affects network modularity to varying degrees for different de-noising approaches. We quantified the retention of signal of interest as the modularity quality of the de-noised connectome. A, The correlation between subject motion and modularity quality in a 264-node network defined by Power et al. (2011) following confound regression. B, The correlation between subject motion and modularity quality in a second, 333-node network defined by Gordon et al. (2016). In general, GSR- and ICA-based methods most effectively decoupled network structure from artifact.

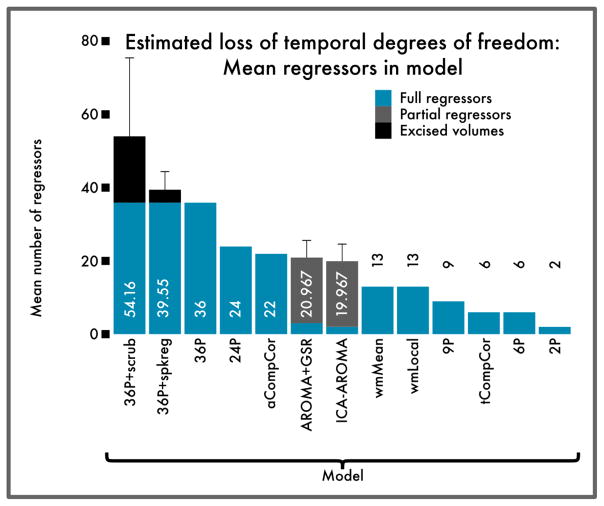
Effective preprocessing strategies use many additional degrees of freedom

Perhaps unsurprisingly, the preprocessing strategies that consistently reduced both QC-FC correlations and distance-dependence were also among the costliest in terms of loss of temporal degrees of freedom (Figure 7). By definition, the 36-parameter models included a high fixed number of regressors. Furthermore, models that additionally included censoring resulted in a substantial additional loss of data that varied across subjects. (Because the 36P+despike model censors data in a spatially adaptive manner, the DOF loss varied by voxel. Because of this spatial variability, the DOF loss is not explicitly estimated for this model.) ICA-AROMA also had a variable loss of DOF, but of a lower magnitude than censoring or high-parameter confound regression.

Figure 7. Estimated loss of temporal degrees of freedom for each pipeline evaluated.

Bars indicate mean number of additional regressors per confound model; error bars indicate standard deviation for models where the number of confound regressors varies by subject. High-parameter models and framewise censoring performed well overall on other benchmarks, but were also costliest in terms of temporal degrees of freedom. Despite this cost, augmenting a high-parameter model with censoring improved signal detection (see Figure 5), suggesting that the lost degrees of freedom corresponded largely to noise. Because the 36P+despike model censors data in a spatially adaptive manner, the DOF loss in this case varied by voxel, and is not displayed.

Discussion

In response to rapid evolution of confound regression strategies available for the mitigation of motion artifact, in this report we evaluated 14 commonly used pipelines. Results indicate that there is substantial heterogeneity in the performance of these confound regression techniques across all measures evaluated. The context, implications, and limitations of these findings are discussed below.

Confound regression techniques have substantial performance variability

We evaluated confound regression strategies according to four intuitive benchmarks that were selected to capture different domains of effectiveness. These included QC-FC associations, distance-dependence of motion artifact, modularity quality and its association with motion, and additional degrees of freedom lost in confound regression. Across each benchmark, there was a striking heterogeneity in pipeline performance. While no model completely abolished motion-related variance, 36-parameter models with censoring (Satterthwaite et al., 2013; Power et al., 2014a) performed well across a range of benchmarks, as did ICA-AROMA with GSR.

Notably, in terms of limiting QC-FC relationships, the top six confound regression approaches all included GSR. This effect was consistent in both networks we evaluated. The effectiveness of GSR is most likely due to the nature of motion artifact itself: in-scanner head motion tends to induce widespread reductions in signal intensity across the entire brain parenchyma (see Satterthwaite et al. (2013), Figure 4). As discussed in detail elsewhere (Power et al., 2016) this effect is highly reproducible across datasets, and is effectively captured by time series regression of the global signal.

For studies of individual difference where motion may be a substantial confounding factor, our results clearly support the use of models that utilize GSR. Across nearly every benchmark, models without GSR underperformed relative to similar models that included GSR. Whereas QC-FC correlations were relatively zero-centered for the case of GSR-based models, most models that omitted GSR – but particularly those that included realignment parameters alone – exhibited distributions that were shifted strongly to the right. Furthermore, augmentation of GSR-based models using either scrubbing or ICA-AROMA yielded better performance than RP-based models across all benchmarks. Thus, while our results cannot advocate for any single model in all scenarios, they suggest that (1) GSR is likely to be the single most effcacious strategy for de-noising and (2) RP-based models are comparably in-effective at de-noising. These results are convergent with recent data regarding the role of motion and physiological artifact in global signal (Power et al., 2016).

Beyond GSR, a second strategy that clearly minimizes QC-FC relationships is temporal censoring. We evaluated three censoring variants, including scrubbing, spike regression, and de-spiking. Compared to spike regression and de-spiking, scrubbing appears to be more effective in removing distance-dependent artifact in this dataset. This is most likely due to the explicit tension between data quality and data quantity: because of the lower threshold for scrubbing than spike regression (due to differences in FD vs. RMS measures of motion; see Figure 9C in Yan et al. (2013a)), more low-quality data was excised during scrubbing. Furthermore, scrubbing includes a criterion to not leave isolated epochs (< 5 volumes) of un-scrubbed data. Consequently, this leads to clear differences in the additional degrees of freedom lost by each method. In contrast to spike regression and scrubbing, which eliminate high motion volumes completely, time series de-spiking identifies and interpolates large changes in signal intensity on a voxelwise basis (Cox, 1996). This allows for spatial adaptivity (see Patel et al. (2014)) but also renders quantification of data loss and comparisons with volume-based censoring techniques more difficult.

Loss of temporal degrees of freedom should be interpreted with caution because temporal DOF may correspond in part or in whole to artifactual sources rather than signal of interest. For example, although removal of volumes contaminated by motion via censoring results in reduced temporal DOF, it improves network identification relative to the same model without any censoring. This can be explained by considering that the temporal DOF in each time series can be either primarily signal or primarily noise DOF; the DOF that censoring removes are primarily noise, and their removal thus increases the overall signal-to-noise ratio of the time series.

Another DOF-related concern about motion censoring is the potential for variable loss of temporal DOF to bias group-level analyses. One proposed solution involves excising a uniform number of volumes from all subject time series, regardless of the number of motion-contaminated frames. However, if motion results in more noise DOF, then the number of useful signal DOF is variable from the start. The extent to which each de-noising strategy removes temporal DOF (through either confound regression or volume excision) should thus not be considered in isolation, but in concert with the ability of that strategy to identify meaningful signal in the data, for instance as evidenced by the network identifiability benchmark.

Critically, while both GSR and censoring appeared effective in minimizing QC-FC relationships, they exhibited opposite effects on distance-dependence. While censoring techniques appear to consistently reduce the presence of distance-dependence, GSR is associated with increased distance-dependence. Thus, commonly used models that include GSR (9-parameter, 36-parameter) have among the greatest distance-dependence of the models we evaluated. However, it should be emphasized that the distance-dependence associated with GSR is not the result of worsening associations with motion in certain connections. Rather, the distance-dependence seen with GSR stems from differential de-noising efficacy, whereby motion artifact is more effectively minimized for long-distance connections than for short-range connections. Certain models such as the local WM regression approach (Jo et al., 2013) thus have minimal distance-dependence, but this is a consequence of lack of efficacy across all distances. In contrast, ICA-AROMA (Pruim et al., 2015b,a) reduced motion to a moderate degree over all connection distances, resulting in almost no distance-dependence. However, while clearly an improvement over some other methods, data processed using ICA-AROMA was noisier than other methods which included GSR or censoring, and resulting networks contained a substantial number of edges impacted by motion. As suggested by the work of Burgess et al. (2016), adding GSR to ICA-AROMA mitigates QC-FC relationships, but as expected exacerbates distance-dependence.

Somewhat to our surprise, benchmark results for aCompCor (Behzadi et al., 2007; Muschelli et al., 2014) were most similar to models that included GSR. Alone among models where GSR was not included, aCompCor both was relatively effective in the mitigation of residual motion (13% of edges impacted) and also exhibited substantial distance-dependence (e.g., r = −0:26). This suggests that while aCompCor does not explicitly include GSR, the practical results of its application are in fact quite similar.

Generally, the models that performed poorly in terms of residual QC-FC correlations also did not perform well in terms of ability to identify structured subnetworks in the connectome. This suggests that the removal of noise by more effective methods also unmasks structure. Although censoring substantially reduced the temporal degrees of freedom in the time series, it improved network identifiability in relation to the 36-parameter model alone, suggesting the possibility that the lost temporal degrees of freedom were largely contaminated and did not contain useful information regarding network topology.

Somewhat to our surprise, the very simple two-parameter model (WM, CSF) outperformed commonly used models based on re-alignment parameters alone (e.g., 6-parameter, 24-parameter), suggesting that the relative values of tissue signal regressors and realignment parameters are not equal. This is likely because the WM and CSF regressors capture, to varying extents, the global signal changes that are strongly associated with motion (Power et al., 2016).

Trade-offs of confound regression approaches: implications for investigators

The current results emphasize two clear trade-offs in the choice of confound regression strategy. First, pipelines that include global signal regression tend to be more effective at minimizing QC-FC relationships, but at the cost of some increase in distance-dependence. As noted above, for minimizing QC-FC relationships, nearly all of the top strategies (except aCompCor) included GSR. Conversely, the two techniques that had the most substantial distance-dependence (the 9-regressor and 36-regressor methods) both included GSR. Second, censoring techniques provide a clear benefit in reducing QC-FC relationships and additionally tend to attenuate distance-dependence. However, by definition, removing contaminated volumes results in less data and loss of degrees of freedom.

These trade-offs suggest that a single confound regression strategy is unlikely to be optimal for every study. For example, in studies of network organization, network identifiability may be of primary interest. Somewhat to our surprise, the classic 9P model displayed the highest network modularity, and thus remains a good choice for many such studies. However, the presence of anti-correlations, altered degree distribution (Yan et al., 2013b), and distance-dependent impact of motion that occurs with GSR-based models (including 9P) may make models without GSR more appealing for certain studies of network organization. In these cases, ICA-AROMA appears to be an excellent choice, as it has high network identifiability and low distance dependence.

In contrast, for studies of group or individual differences, minimizing QC-FC relationships is likely to be of paramount importance so as to limit the possibility that inference is driven by artifactual signals. This concern is particularly relevant for studies of brain development or clinical sub-groups where motion is systematically related to the subject-level variable of interest (e.g., age, disease status). For such studies, models that include GSR tend to perform best, including 36P+censoring models and ICA-AROMA + GSR. Our results accord with Burgess et al. (2016) and suggest that ICA-based de-noising alone without GSR does not provide maximal control of motion artifact. Co-varying for motion at the group level is unlikely to be a panacea for such studies when inadequate subject-level time series de-noising is employed, as prior work (Power et al., 2014a) has suggested that motion effects at the group level may potentially both be nonlinear and vary across sub-samples in a manner that is difficult to predict. However, aggressive volume censoring may be problematic in datasets with relatively brief acquisitions. In datasets where long time series are acquired, such as multi-band acquisitions (Feinberg et al., 2010) and intensive acquisitions of single subjects (Laumann et al., 2015), loss of temporal degrees of freedom is less likely to be a major concern. The 36-parameter models without volume censoring offer uniformity, as does randomly or systematically censoring additional volumes until all subjects retain approximately the same degrees of freedom.

Limitations

Several limitations of the current approach should be noted. One of the principal challenges in evaluating the performance of de-noising approaches is the lack of a noise-free ground truth. Our primary benchmark of confound regression performance assumes that mitigation of the relationship between QC (participant motion) and FC (i.e., the imaging measurement) is desirable. To the degree that in-scanner motion itself represents a biologically informative phenotype, this approach will mistake signal for noise. Indeed, prior data suggests that this may sometimes be the case. For example, Zeng et al. (2014) found specific changes in connectivity for participants who had generally high levels of motion, even on scans where motion was low. However, without multiple scans to allow such careful dissociation, most studies are incapable of disambiguating the large confounding effects of motion on connectivity. Second, in place of QC-FC relationships, one could focus on alternative benchmarks such as test-retest reliability (Zuo et al., 2014). Reliability is certainly of interest, but to the degree that motion tends to be highly correlated within individuals across scanning sessions, there is a substantial potential for the presence of consistent motion artifact across sessions to artificially inflate reliability, and diminish the biological relevance of observed results. A third and related concern is that certain de-noising methods could conceivably both minimize QC-FC relationships and even enhance reliability by aggressively removing both signal and noise, but in the process diminish sensitivity to meaningful individual differences. Indeed, one prior study demonstrated the association between canonical resting state networks and randomly generated confound parameters (Bright and Murphy, 2015). This concern is somewhat mitigated by prior work, which suggests that higher-order confound regressors improve the confound regression model fit (Yan et al., 2013a; Satterthwaite et al., 2013), while random regressors do not (see Figure 8 in Satterthwaite et al. (2013)). Furthermore, our results suggest that sub-network modularity is actually improved by effective de-noising. Fourth, while our evaluation included many of the most commonly used techniques, other approaches which require substantial training or parameter selection (i.e., ICA-FIX (Salimi-Khorshidi et al., 2014; Griffanti et al., 2014), wavelet de-spiking (Patel et al., 2014)) may be valuable and merit further consideration. Fifth, it is unknown whether the present results generalize to other datasets, which may have different acquisition parameters including much longer timeseries (Laumann et al., 2016) and multiband acquisition (Feinberg et al., 2010). In particular, the relatively short (6 min) scan time used in the current study is a potential limitation; replication of results in longer acquisitions would enhance confidence in the generalizability of the present results. However, the similar findings reported by Burgess et al. (2016)), which used the longer, multi-band time series data from the Human Connectome Project, suggest convergence with the present results. Furthermore, it is possible that the structure of motion artifact is population-dependent. In the present study, we examined the efficacy of de-noising strategies in a sample of young adults and adolescents. Consequently, the conclusions that we present here may not necessarily generalize to other populations, underscoring the importance of evaluating and reporting the residual confounding effects of motion in all studies of functional connectivity. While the current study was conducted in a combined sample of adolescents and young adults, it did not explore the extent to which the efficacy of each denoising strategy was age- or population dependent, which merits additional investigation in the future. Sixth and finally, it should be noted that while improvements in image acquisition (including multi-echo techniques) may not salvage existing motion-contaminated data, it is likely that they will change the methodological landscape of connectivity research moving forward (Kundu et al., 2012, 2013; Bright and Murphy, 2013).

Conclusions

Taken together, the present results underline the performance heterogeneity of recently-introduced, commonly-used confound regression methods. In selecting among these methods, investigators should be aware of the relative strengths and weaknesses of each approach, and understand how processing strategy may impact inference. Clearly, the relative merit of each approach will vary by research question and study design. Perhaps most importantly, as has been emphasized in nearly every other study of motion artifact, the choice of confound regression strategy is often dwarfed in importance by the need to transparently report and evaluate the impact of motion in each dataset. At a minimum, this includes reporting the relationship between motion artifact and not only subject phenotypes (e.g., group, age, symptom or cognitive score) but also the functional connectivity measures being considered. In the context of such data, the distinction between observed results and the impact of motion artifact can be understood. Such transparency bolsters confidence in reported findings, but also will likely tend to emphasize the remaining challenges for de-noising going forward. Especially when considered in the context of the the rapid evolution of available techniques since 2012, there is no doubt that innovations in post-processing confound regression strategies will continue.