Molecular dynamics simulations and free energy calculations of netropsin and distamycin binding to an AAAAA DNA binding site

Abstract

Molecular dynamics simulations have been performed on netropsin in two different charge states and on distamycin binding to the minor groove of the DNA duplex d(CGCGAAAAACGCG)·d(CGCGTTTTTCGCG). The relative free energy of binding of the two non-covalently interacting ligands was calculated using the thermodynamic integration method and reflects the experimental result. From 2 ns simulations of the ligands free in solution and when bound to DNA, the mobility and the hydrogen-bonding patterns of the ligands were studied, as well as their hydration. It is shown that even though distamycin is less hydrated than netropsin, the loss of ligand–solvent interactions is very similar for both ligands. The relative mobilities of the ligands in their bound and free forms indicate a larger entropic penalty for distamycin when binding to the minor groove compared with netropsin, partially explaining the lower binding affinity of the distamycin molecule. The detailed structural and energetic insights obtained from the molecular dynamics simulations allow for a better understanding of the factors determining ligand–DNA binding.

INTRODUCTION

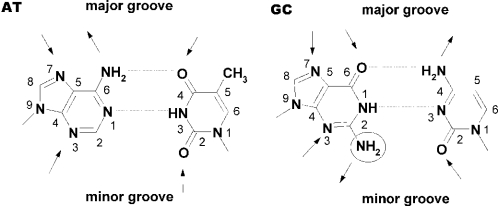
The DNA molecule is a target of various antitumour active drugs that form covalent and non-covalent molecular complexes when binding to the minor or major groove (1–5). The first DNA-interactive anticancer drugs belong to the family of the covalently binding DNA alkylating agents (6,7). In recent years, ligands that bind non-covalently in the minor groove have attracted considerable attention because of their pronounced sequence specificity (8). Netropsin and distamycin (Figure 1) are two naturally occurring amide-linked oligopyrole antibiotics with affinity for A-T rich regions of the DNA minor groove (9,10). Their interaction with the minor groove is non-covalent and non-intercalative, and it is based on hydrogen bonding (11,12), van der Waals contacts, hydrophobic effects and electrostatic effects of the charged ends with netropsin having two cationic charges and distamycin having one (13–18). Both molecules possess a crescent shape that is complementary to the shape of the minor groove. At least four consecutive A-T base pairs are involved in the interaction of DNA with one netropsin or distamycin molecule (13–17). The introduction of a G-C base pair in the A-T rich region disturbs the binding of the netropsin molecule due to sterical hindrance of the exocyclic C2 amino group of guanine (Figure 2) (9,10). However, distamycin can occupy such sites in a 2:1 side-by-side head to tail orientation (19–21). The formation of a 2:1 distamycin–DNA complex versus a 1:1 complex is known to be highly DNA sequence dependent (22). In case of oligomer duplexes with AAAAA binding sites, 1:1 complexes are formed at low distamycin:DNA ratios and 2:1 complexes are formed at the ratios >1 (22). On the contrary, AAGTT binding sites are occupied in a 2:1 manner even at low distamycin:DNA ratios (23), suggesting that the wider minor groove of these sites requires two ligand molecules to establish close contacts with the walls of the groove. Furthermore, the thermodynamics of the binding of netropsin and distamycin to DNA is strongly dependent on the binding sequence (24,25). It is well established, for example, that binding of netropsin to a homogenous A-T sequence is an entropy-driven process while binding of the same molecule to an alternating ATAT sequence is an enthalpy-driven process (24,25). The enthalpy–entropy compensation results in a similar favourable net free energy of binding in either case. Considering only the enthalpy of binding may, therefore, lead to poor correlations with the observed binding affinities. For an accurate determination of the DNA–drug binding strength, calculation of the free energy differences, which include entropic contributions, is required.

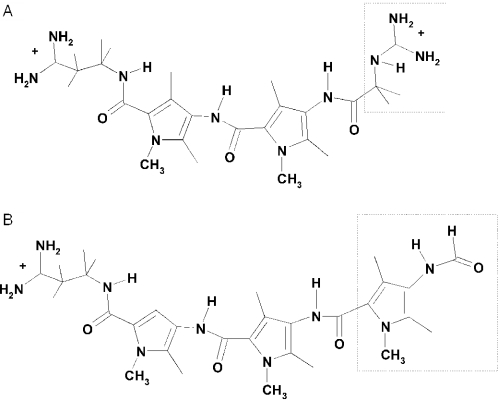
Figure 1.

Structures of netropsin (A) and distamycin (B). The netropsin molecule consists of two methylpyrole rings, three amide linkages, a guanidinium and a propylamidinium part. The components of distamycin are three methylpyrole rings, three amide linkages, a formamide and a propylamidinium part. Atoms within the rectangles are changed during the TI calculation.

Figure 2.

Schematic representations of A-T and G-C base pairs with hydrogen-bond donors and acceptors indicated. The exocyclic C2 amino group of guanine that interferes with netropsin binding in the minor groove is encircled and the major and minor groove positions are marked. The arrows indicate possible ligand–DNA hydrogen bonding.

In this paper, we present the calculation of relative free energies of binding of netropsin and distamycin to the oligonucleotide sequence d(CGCGAAAAACGCG) in a DNA duplex with its complement using molecular dynamics (MD) simulations in explicit aqueous solvent. Free energy calculations of binding for these and similar ligands to different DNA sequences have already been performed earlier (26–28). In our calculations, we have employed the thermodynamic integration (TI) approach (29) utilizing two different GROMOS force fields for the perturbed or changing part of the ligand. MD trajectories of 2 ns were generated for the ligands free in solution and for the ligands bound to DNA. Structural and hydration characteristics of the ligands in solution and of their complexes with DNA were analysed and the results were compared with the experimental data.

MATERIALS AND METHODS

System set-up

Since a crystal structure of either of the complexes is not available, spatial structures of the DNA duplex d((CG)₂A₅(CG)₂)–d((CG)₂T₅(CG)₂) in an ideal B-DNA conformation were obtained using the INSIGHTII software package (Accelrys Inc., San Diego, CA). Structures of netropsin and distamycin were taken from the crystal structures PDB ID 101D (30) and PDB ID 267D (31), in which netropsin and distamycin are complexed to slightly different DNA sequences. Initial structures of the DNA–drug complex were obtained by placing the netropsin and distamycin molecules (in their X-ray structures) into the minor groove. A dual topology and coordinates were obtained for a ligand that contained both sets of atoms that are shown within the rectangular boxes in Figure 1. The complex was solvated in a periodic truncated octahedron using 11 034 simple point charge (SPC) water molecules (32) with a minimum distance of 0.23 nm from any (non-hydrogen) solute atom to the water oxygen. The coordinates of water were optimized by steepest descent energy minimization in which DNA and ligand were positionally restrained using a harmonic interaction with a force constant of 2.5 × 10⁴ kJ mol⁻¹ nm⁻². Using the PROION utility of the GROMOS software package (33), 20 Cl⁻ and 43 Na⁺ ions were added to the system in order to obtain an overall neutral system at an experimental salt concentration of 110 mM NaCl. The same procedure as for the complex was employed for the ligand in water resulting in a computational box containing 3225 water molecules, 6 Na⁺ and 7 Cl⁻ ions.

Parameters

The parameters and the charges for netropsin and distamycin were selected in analogy to existing parameters in the GROMOS force field. At pH 7, netropsin has a total charge of +2 e, while distamycin has a charge of +1 e. In order to investigate the effect of ligand charge on the binding free energy differences, we decided to use two different sets of parameters for the perturbed part of the netropsin molecule, force-field parameters 45A4 and force-field parameters 45B4. The latter distinguishes itself from the 45A4 set by charged moieties being neutralized (33,34). When using force-field parameters 45A4, the charge of the perturbed part (atoms within the rectangular boxes in Figure 1) changed from +1 to 0 during the mutation of netropsin (Net) into distamycin (Dist). When using the force-field parameters 45B4, the perturbed part remained neutral throughout the calculation (NetN to Dist). The force-field parameters used for the ligands are available as Supplementary Information. For DNA, the GROMOS force-field parameters 45A4 were used (35). This parameter set was recently optimized resulting in modified nucleotide backbone torsional-angle parameters and explicit hydrogens and revised charge distributions on the nucleotide bases. This new parameter set leads to an improved DNA stability and smaller deviations between simulated and experimental observables.

Molecular dynamics simulations

All MD simulations were carried out using the GROMOS96 biomolecular simulation package (33). Prior to the free energy calculations, the solvated complex and ligand were each equilibrated in an 80 ps MD simulation. First, the system was heated at constant volume over 30 ps from 50 to 300 K, using the weak coupling approach (36) with a relaxation time of 0.1 ps. The solvent and the solute were coupled to separate temperature baths. During the heating, the DNA and ligand positions were harmonically restrained with a stepwise decreasing force constant, initially at 2.5 × 10⁴ kJ mol⁻¹ nm⁻². After this, the system was coupled to a constant temperature bath at 300 K and to a constant pressure bath of 1 atm with a relaxation time of 0.5 ps and an estimated isothermal compressibility of 4.575 × 10⁻⁴ (kJ mol⁻¹ nm⁻³)⁻¹. During all simulations, we used the SHAKE algorithm to keep all bonds rigid allowing for a time step of 2 fs (37). Non-bonded interactions were calculated using a triple-range cut-off scheme. Interactions within a short-range cut-off of 0.8 nm were calculated at every time step from a pair list that was generated every five steps. At these time points, interactions between 0.8 and 1.4 nm were also calculated and kept constant between updates. To account for a homogenous medium outside the long-range cut-off, a reaction-field contribution (38) was added to the electrostatic interactions and forces, using a relative permittivity of 61 (39).

Trajectory structures for analysis were saved at 0.2 ps intervals from 2 ns MD simulations of the ligands in solution and from the simulations of the complexes of the ligands with DNA. Atom-positional root-mean-square deviations (RMSDs) from the initial conformation were calculated for the DNA-backbone atoms, DNA-base atoms and the atoms of the ligand that were bound in the DNA minor groove. The DNA backbone atoms were used in the least-squares translational and rotational superposition. The flexibility of the ligands was investigated in terms of the atom-positional root-mean-square fluctuations (RMSFs) for all non-hydrogen atoms. In the analysis of interactions, the following geometrical criterion for hydrogen bonds was used: a donor–acceptor distance <0.25 nm and a donor–hydrogen–acceptor angle of at least 135°. Hydration shells around the atoms of a ligand in solution and when bound to the DNA were determined based on the radial distribution function g(r) for all ligand atoms with water oxygen atoms. The number of water molecules in the first hydration shell of a solute atom can be calculated as

$$N_{\text{w},\text{at}}^{\text{shell}}={\int }_0^{R_{\text{c}}}{\rho }_{\text{w}}g\left(r\right)4\pi r^2\text{d}r,$$ 1

where ρ_w is the number density of water in the computational box and R_c is a cut-off distance, set to 0.245 nm. The number of hydration shell water molecules of a molecule (ligand), $N_{\text{w}}^{\text{shell}}$ is just taken as the sum of $N_{\text{w},\text{at}}^{\text{shell}}$ over all atoms.

Free energy calculations

The TI method was used to calculate the relative free energy differences of binding of netropsin and distamycin to the d((CG)₂A₅(CG)₂)–d((CG)₂T₅(CG)₂) DNA duplex. In this method, the system is mutated from one state to another by changing the interaction parameters that define the Hamiltonian H as a function of a coupling parameter λ. The free energy difference, ΔG, between two states of a system, state A defined by a Hamiltonian H(λ = 0) = H_A and state B, defined by a Hamiltonian H(λ = 1) = H_B, is calculated as follows:

$$\Delta G_{\text{BA}}=G_{\text{B}}-G_{\text{A}}={\int }_0^1\frac{\text{d}G\left(\lambda \right)}{\text{d}\lambda }\text{d}\lambda ={\int }_0^1{\langle \frac{\partial H\left(\lambda \right)}{\partial \lambda }\rangle }_{\lambda }\text{d}\lambda ,$$ 2

where ${\langle \rangle }_{\lambda }$ denotes ensemble averaging at a given λ value. The system is perturbed from state A to state B in discrete steps. The Hamiltonian of the system at any intermediate state can be defined as

$$H\left(\lambda \right)=\left(1-\lambda \right)H_{\text{A}}+\lambda H_{\text{B}}.$$ 3

The integrand in Equation 2 is evaluated numerically from MD simulations at specified values of λ and the value of ΔG_BA is then calculated using the trapezoid rule.

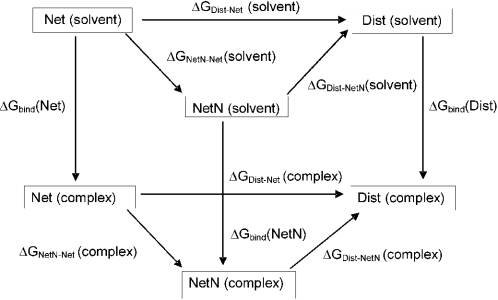
The TI method can be used to determine the relative binding free energies between two ligands as is shown in Figure 3. Net, NetN and Dist states refer to the netropsin (charge +2 e), netropsin (charge +1 e) and distamycin (charge +1 e) molecules, respectively, in solution (solvent) or in the complex with DNA. In this study, we report 12 TI simulations. Both netropsin with a net charge of +2 (Net) and netropsin with a net charge of +1 (NetN) were changed into Dist. To be able to close the thermodynamic cycles, the mutation from Net into NetN was performed as well. All mutations were performed in both directions in the solvated state of the ligand and in the complexed state (Figure 3). In addition, the four end-states involving Net and Dist in the free and the complexed state were simulated for 2 ns. Experimentally determined values for the free energy of binding of netropsin to DNA, ΔG_bind(Net), and the free energy of binding of distamycin to DNA, ΔG_bind(Dist) are available (25). Because these are virtually impossible to calculate directly, we use the fact that the free energy is a state function, so it follows that

$$\begin{array}{c}\Delta \Delta G_{\text{binding}}\left(\text{Net},\text{Dist}\right)=\Delta G_{\text{bind}}\left(\text{Net}\right)-\Delta G_{\text{bind}}\left(\text{Dist}\right)\\ =\Delta G_{\text{Dist}-\text{Net}}\left(\text{solvent}\right)-\Delta G_{\text{Dist}-\text{Net}}\left(\text{complex}\right),\end{array}$$ 4

where Net can also be replaced by NetN. To calculate the relative binding free energy ΔΔG_binding, free energy changes for conversion of netropsin into distamycin both in solution and when bound to the DNA minor groove need to be evaluated.

Figure 3.

Thermodynamic cycles used for the calculation of relative free energy of binding of netropsin and distamycin to the d(CGCGAAAAACGCG)·d(CGCGTTTTTCGCG) duplex. Net corresponds to the netropsin molecule with a net charge of +2 e parameterized with the force field 45A4. NetN corresponds to the same molecule but having a net charge of +1 e. The perturbation part of NetN (boxed atoms in Figure 1) is parameterized with force field 45B4 (non-charged version of the guanidinium group). Dist is the distamycin molecule. The abbreviations ‘solvent’ and ‘complex’ correspond to the ligand that is free in solution and to the one that is in complex with the DNA.

In our free energy calculations, we converted netropsin into distamycin by switching off the non-bonded interactions of the –CH₂–NH–C(NH₂)₂ group of the netropsin tail while simultaneously switching on the non-bonded interactions of the –Py–NH–COH group of the distamycin tail (Py indicates the methylpyrole ring). The perturbed parts of both molecules are shown within the rectangular boxes of Figure 1. During the conversion, the bonded interactions and atomic masses remain unchanged. The TI simulations were started after the system was equilibrated for 80 ps.

In the perturbation simulations, separate simulations were performed at 11 equally spaced λ values, from λ = 0 to λ = 1. At each point, the system was first equilibrated for 40 ps after which the data were collected during 80 ps simulations. Later, up to seven additional λ values were added and simulations at particular λ values were prolonged for 40 or 80 ps in order to obtain a smooth free energy profile and to reduce the error estimates per λ value. The hystereses of all the perturbations of one ligand into another were determined by performing the mutations in both the forward and the backward direction. In the backward calculations, the final coordinates of the forward set of runs were used as the starting points.

RESULTS AND DISCUSSION

Molecular dynamics simulations

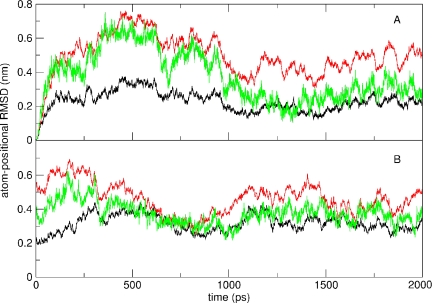
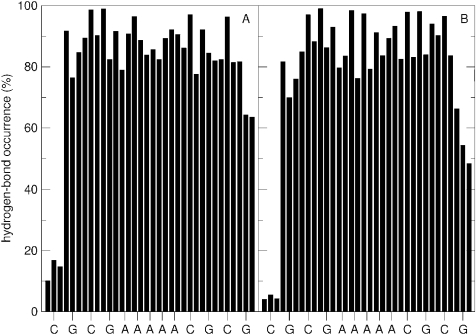
In Figure 4, the atom-positional RMSD of the DNA backbone, base and the ligand atoms in the trajectory structures from the initial structure is shown for the netropsin–DNA and distamycin–DNA complexes. The backbone and the ligand geometries diverge from the geometries of the starting structure in the first part of the simulation. However, after 1 ns, the RMSD returns to smaller values. The simulation of the DNA–Dist complex was started from the endpoint of the perturbation simulation that had changed netropsin into distamycin in the complex. Hence, for this simulation the RMSD values already have higher values at the starting time. These do not change much over the course of the simulation. Throughout the simulation, the double-helical DNA structure was well maintained. The occurrence of Watson–Crick hydrogen bonds between the base pairs in the end-state simulations of both complexes is shown in Figure 5. The hydrogen bonds are well preserved between all the base pairs except for the GC-base pairs at the end of the double helix. However, an increased flexibility of the first and last nucleotides is commonly observed in MD simulations of polynucleotides (35,40).

Figure 4.

Atom-positional RMSD of the DNA backbone, base and the ligand atoms in the trajectory structures from the initial structure, for the simulated DNA–Net (A) and DNA–Dist (B) complexes. The black line corresponds to base pair atoms, the red line to the backbone atoms and the green line to the ligand atoms.

Figure 5.

Occurrence of Watson–Crick hydrogen bonds in simulations of netropsin–DNA (A) and distamycin–DNA (B) complexes. For every GC-pair three hydrogen bonds and for every AT-pair two hydrogen bonds are given. Along the x-axis, the sequence of the primary DNA strand is given. For the definition of a hydrogen bond, see the caption to Table 1.

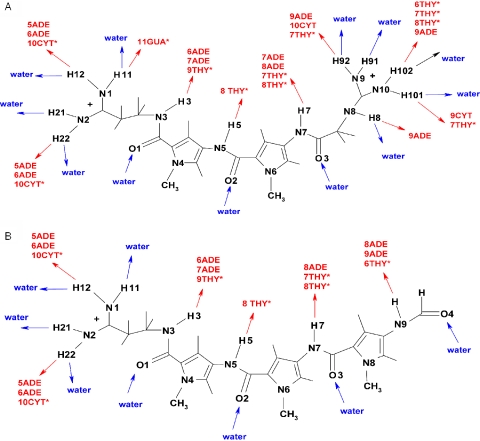
Table 1 lists the occurrence of hydrogen bonds involving the ligands in solution and when bound to the DNA minor groove. From a comparison of the hydrogen bonds, it can clearly be seen that both ligands were oriented with the amide hydrogens (H3, H5, H7) pointing towards the DNA double helix, while the amide carbonyl oxygens (O1, O2, O3) remain in contact with water. In fact, owing to the orientation of the ligands the carbonyl oxygens are exposed to bulk water and show slightly more hydrogen bonding with water in the complex than in the solution. The tails of both ligands are strongly involved in hydrogen bonds to both the DNA and the solvent. In the simulations, three-centred hydrogen bonds were also observed and they are listed in Table 2. A three-centred hydrogen bond is defined for a donor (D), hydrogen (H) and two acceptors (A1 and A2) if (i) the H–A1 and H–A2 distances are within 0.27 nm; (ii) the D–H–A1 and D–H–A2 angles are at least 90°; (iii) the sum of the angles D–H–A1, D–H–A2 and A1–H–A2 is at least 340°; and (iv) the dihedral angle defined by the planes through D, A1, A2 and H, A1, A2 is <15° (41). In accordance with the previous experimental studies (13,14,30), some of the three-centred hydrogen bonds form a bridge between the bases and riboses of the two DNA strands. Three-centred hydrogen bonds are also observed for the bases and riboses of the same strand. The different (normal) hydrogen bonds between both ligands and the DNA are displayed graphically in Figure 6. The average number of hydrogen bonds in which the ligands are involved are given in the one to last row of Table 1. It can be seen that upon binding each ligand replaces on an average 3 out of 11 hydrogen bonds to water with 3 to DNA. The average number of ligand–solvent hydrogen bonds for netropsin is slightly higher than for distamycin, both in solution as well as in the complex. The average number of hydrogen bonds that are formed to the DNA is very similar to both ligands and each ligand looses on an average half a hydrogen bond upon binding.

Table 1.

Occurrence of hydrogen bonds (%) to DNA and water, and hydration shell number of water molecules for netropsin and distamycin free in solution and in complex with DNA

Netropsin				Distamycin
Atoms	Free water	Complex		Atoms	Free water	Complex
		DNA	Water			DNA	Water
N1–H11→	76	1	76	N1–H11→	76	0	81
N1–H12→	82	35	31	N1–H12→	83	45	22
N2–H21→	72	0	81	N2–H21→	76	0	80
N2–H22→	82	46	26	N2–H22→	82	36	30
N3–H3→	59	41	0	N3–H3→	60	44	0
O1←	76	0	90	O1←	72	0	91
N4←	14	0	14	N4←	13	0	17
N5–H5→	58	33	0	N5–H5→	58	43	0
N5←	4	0	2	N5←	4	0	0
O2←	84	0	91	O2←	85	0	90
N6←	14	0	11	N6←	13	0	20
N7–H7→	77	61	0	N7–H7→	66	76	0
N7←	3	0	0	N7←	5	0	1
O3←	66	0	69	O3←	84	0	89
N8–H8→	79	13	56	N8←	14	0	16
N8←	0	0	0	N9–H9→	71	41	0
N9–H91→	67	0	68	N9←	6	1	4
N9–H92→	57	9	41	O4←	86	0	76
N10–H101→	67	1	73
N10–H102→	59	47	5
Total	11.9	3.1	8.1	Total	11.2	3.2	7.5
$N_{\text{w}}^{\text{shell}}$	10.2		5.5	$N_{\text{w}}^{\text{shell}}$	7.3		2.7

For every hydrogen bonding atom in the ligands, the occurrence of hydrogen bonds (>1%) to (→) and from (←) water and to and from DNA is given. A hydrogen bond is defined by a donor–acceptor distance <0.25 nm and a donor–hydrogen–acceptor angle >135°. The atom labelling is indicated in Figure 6. The average number of hydrogen bonds between ligands on the one hand and DNA and water on the other is given in the row labelled ‘Total’. The average number of water molecules within a shell of radius 0.245 nm around the atoms of the ligand is given in the row labelled $N_{\text{w}}^{\text{shell}}$.

Table 2.

Occurrence of three-centred hydrogen bonds (%) to DNA for netropsin and distamycin

Netropsin			Distamycin
Three-centred hydrogen bond		Occurrence (%)	Three-centred hydrogen bond		Occurrence (%)
N1–H12→	5Ade N3	5	N1–H12→	5Ade N3	11
	6Ade O4′			6Ade O4′
N2–H22→	5Ade N3	9	N1–H12→	5Ade N3	1
	6Ade O4′			10Cyt* O2
N2–H22→	5Ade N3	1	N2–H22→	5Ade N3	7
	10Cyt* O2			6Ade O4′
N3–H3→	6Ade N3	2	N2–H22→	5Ade N3	1
	7Ade O4′			10Cyt* O2
N3–H3→	6Ade N3	3	N3–H3→	6Ade N3	2
	9Thy* O2			7Ade O4′
N7–H7→	8Ade N3	7	N3–H3→	6Ade N3	6
	7Thy* O2			9Thy* O2
N7–H7→	7Thy* O2	2	N7–H7→	7Thy* O2	3
	8Thy* O4′			8Thy* O4′
N9–H92→	9Ade N3	1	N9–H9→	8Ade N3	2
	10Cyt O4′			9Ade O4′
N10–H102→	6Thy* O2	10	N9–H9→	9Ade O4′	2
	7Thy* O4′			9Ade N3
			N9–H9→	9Ade N3	1
				6Thy* O2

The occurrence of hydrogen bonds larger than 1% is given. Nucleotides in the second strand of the DNA duplex are marked with an asterisk after the nucleotide name and ribose atoms with a prime (′) after the atom name. Three-centred hydrogen bonds are defined for a donor atom D, hydrogen atom H, and two acceptor atoms A1 and A2 if (i) the distances H–A1 and H–A2 are within 0.27 nm; (ii) the angles D–H–A1 and D–H–A2 are >90°; (iii) the sum of the angles D–H–A1, D–H–A2 and A1–H–A2 is at least 340°; and (iv) the dihedral angle defined by the planes through the atoms D–A1–A2 and H–A1–A2 is at most 15°.

Figure 6.

A schematic representation of the hydrogen bonds that netropsin (A) and distamycin (B) form with the DNA and with water when they are bound to the minor groove of the d((CG)₂A₅(CG)₂)-d((CG)₂T₅(CG)₂) duplex in aqueous solution. The occurrence of hydrogen bonding in the simulation is given in Table 1. Hydrogen bonds with DNA are shown in red and hydrogen bonds with water are shown in blue. Nucleotides in the second strand of the DNA duplex are marked with the asterisks. Not all hydrogen bonds in Table 1 are displayed.

Geometrical parameters characterizing the spatial arrangement and conformation of the nucleotides along the DNA helix were calculated according to the 3DNA convention (42,43) over the simulations of the DNA–netropsin and DNA–distamycin complexes as well as for a very similar simulation of the uncomplexed DNA sequence in solution. Even though the structural parameters are not direct experimental observables, a comparison between uncomplexed DNA and DNA–netropsin or DNA–distamycin can be made. Some of the structural parameters for the binding site changed upon complexation of netropsin and distamycin. In particular, the roll was reduced from an average of 6.3° for uncomplexed DNA to 3.6° in the complexes, the propeller was reduced from −4.1° to −9.4°, the inclination was reduced from 12.2° to 6.6° and the x-displacement was increased from −0.32 to −0.20 nm. Interestingly, the opening for the 5Ade–9Thy base pair (forming hydrogen bonds with the charged side of the molecules; see Figure 6) changes from −4.2° in uncomplexed DNA to +4.3° in the complexes.

A stronger interaction of netropsin with water can also be observed from the number of water molecules that are in close contact with the ligands. The number of water molecules within a cut-off distance of 0.245 nm of the ligand were calculated according to Equation 1 and are given in the last row of Table 1. Netropsin is tightly bound to 10.2 water molecules in solution, which is being reduced to an average of 5.5 water molecules upon binding to the DNA. Distamycin looses a very similar amount (4.6) of short-distance water interactions upon binding, but is interacting with fewer short-distance water molecules than netropsin. This can be explained from the larger hydrophobicity of distamycin compared with netropsin.

From the simulation trajectories, the atom-positional RMSFs of both ligands in water and in complex with the DNA have also been calculated. The average flexibility per atom is reduced upon binding to DNA for both molecules. For netropsin, the average RMSF value is reduced from 0.088 nm in solution to 0.055 nm when bound to DNA. For distamycin, these values are 0.092 and 0.050 nm in solution and when bound to DNA, respectively, resulting in a larger loss of mobility for this ligand. In terms of binding affinities, this may indicate a higher entropic penalty for the binding of distamycin. This is in agreement with entropy determinations from recent experiments (25). Closer examination of the atom-positional RMSF values reveals that the most mobile parts of netropsin and distamycin are the tails of both molecules, while the central part is more rigid (44,45).

Relative binding free energies

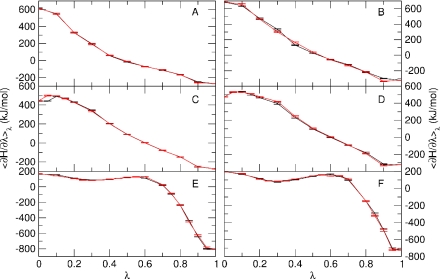
The values of ${\langle \partial H/\partial \lambda \rangle }_{\lambda }$ for the perturbation simulations performed in the present study are shown in Figure 7. All curves are relatively smooth and can be integrated quite accurately. The free energy differences as assigned in the thermodynamic cycles of Figure 3 are collected in Table 3. In the second column, the results for the perturbation of netropsin at a net charge of +2 e into distamycin are collected. The third column lists the free energy differences between the results obtained with the use of the 45B4 parameter set for the perturbed part of netropsin (resulting in a net charge of +1 e for the ligand). The fourth column presents the free energy change between the two descriptions of the netropsin molecule. Finally, the fifth column gives the free energy of the cycle defined as

$$\Delta G_{\text{cycle}}=\Delta G_{\text{Dist}–\text{Net}}-\Delta G_{\text{Dist}–\text{NetN}}-\Delta G_{\text{NetN}–\text{Net}}.$$ 5

Figure 7.

Free energy profiles for the changes of Net to Dist (A and B), NetN to Dist (C and D) and Net to NetN (E and F) when the ligand is free in solution (A, C and E) and when bound to the minor groove of DNA (B, D and F). The values of the integrand ${\langle \partial H/\partial \lambda \rangle }_{\lambda }$ are plotted as a function of the coupling parameter λ for the forward (black solid line) and backward (red solid line) perturbation of one ligand into another. The error bars correspond to statistical errors from block averaging (46).

Table 3.

Results of TI calculations for ligands free in solution and complexed to DNA

	ΔGDist–Net (kJ mol−1)	ΔGDist–NetN (kJ mol−1)	ΔGNetN–Net (kJ mol−1)	ΔGcycle (kJ mol−1)
Free (solvent)
Forward	69.2 ± 2.9	117.0 ± 2.8	−50.7 ± 2.6	2.9 ± 8.3
Backward	68.7 ± 4.7	119.0 ± 3.6	−50.7 ± 3.1	0.4 ± 11.4
Average	69.0 ± 3.8	118.0 ± 3.2	−50.7 ± 2.9	1.7 ± 9.9
Complex
Forward	108.3 ± 5.6	119.4 ± 5.3	−5.3 ± 5.3	−5.8 ± 16.2
Backward	105.6 ± 6.7	126.6 ± 4.5	−6.1 ± 4.2	−14.9 ± 15.4
Average	107.0 ± 6.2	123.0 ± 4.9	−5.7 ± 4.8	−10.3 ± 15.9
ΔΔGbinding
Simulation	−38.0 ± 10.0	−5.0 ± 8.1	−45.0 ± 7.7	12.0 ± 25.8
Experiment	−11.3 ± 1.2

For each of the free energy changes, ΔG, the results obtained from forward and backward simulations are reported as well as their average. Indicated free energies are defined in Figure 3. ΔG_cycle is defined as the free energy change along the closed triangles in Figure 3, in a clockwise sense. The relative free energy of binding for the two ligands, ΔΔG, was calculated as in Equation 4 and is compared to the experimental value (25). Errors on calculated values were obtained from block averaging of the integrand in Equation 2 according to Allen and Tildesley (46).

Theoretically, the value of ΔG_cycle should be equal to zero. For all perturbations the results from the forward and the backward perturbations are given, as well as their average values. It can be seen that for most perturbations the hysteresis (difference between forward and backward results) is of the order k_BT, except for the mutation of NetN to Dist in the complex, where it is 7.2 kJ mol⁻¹. The cycle closures (ΔG_cycle) that can be calculated are within the error bars of the theoretical value of 0 kJ mol⁻¹. These values are quite reasonable in view of the large change in ${\langle \partial H/\partial \lambda \rangle }_{\lambda }$ value in Figure 7.

The results for the relative free energies of binding of both the forms of netropsin with respect to distamycin do reflect the experimental results (25). For the simulations that involve the annihilation of a full charge (Net to Dist), the relative free energy of binding of −38 kJ mol⁻¹ overestimates the experimental value (−11 kJ mol⁻¹), while in the overall neutral perturbation a value of −5 kJ mol⁻¹ is obtained, which slightly underestimates the experimental value. For both simulations, netropsin is seen to bind more favourably than distamycin. It is interesting to note that the removal of a full charge in solution leads to a reduction in the free energy by ∼50 kJ mol⁻¹, while in the DNA complex, the effect of the charge accounts for a reduction of only 6 kJ mol⁻¹. The high-electrolytic environment of the DNA seems to have a reducing effect on the usually larger values involved with changes of a full charge. The many positively charged ions (43 Na⁺) present can easily compensate for local electrostatic effects on the removal of a charge in the ligand.

From the analysis of the end-state simulations of netropsin and distamycin in solution and when bound to DNA, it was determined that the DNA–ligand interactions and the changes in ligand–solvent interactions were very similar to both ligands. A slightly larger loss of mobility upon ligand binding was found for distamycin, giving rise to a larger entropic cost when binding this ligand to DNA. This agrees with the experimentally obtained relative entropy as well as with the relative free energy of binding of the two ligands.

CONCLUSIONS

The TI method was applied in a study of binding free energy differences of netropsin in two different charge states and distamycin to the oligonucleotide duplex d(CGCGAAAAACGCG)·d(CGCGTTTTTCGCG). The preferential binding of netropsin over distamycin was reproduced in agreement with the experimental data. Interestingly, the results that were obtained from a perturbation that did not involve a change of a full charge on netropsin, agreed closest to the experiment. Owing to the electrolytic nature of the system consisting of DNA, water and ions, the effect of removing a full charge is reduced significantly.

From four simulations of the ligands, in solution and when bound to the DNA minor groove, a comparison of the binding characteristics between the two ligands was performed. Overall, it was shown that distamycin interacts with fewer solvent molecules than netropsin, which corresponds to the higher hydrophobicity of the distamycin molecule. However, the loss of ligand–solvent hydrogen bonds upon DNA binding was very similar to both ligands and was almost exactly compensated by the formation of DNA–ligand hydrogen bonds. A corresponding result was obtained from an analysis of the number of water molecules in the first solvation shell around the ligand. Slight differences between the ligands were seen in the loss of mobility of the ligand atoms upon binding to DNA. This loss was more pronounced for distamycin, leading to a more unfavourable entropic contribution to the free energy of binding for this molecule, which partially explains its lower binding affinity and agrees with the experimental findings.

It has been shown that the energetic and structural information can be obtained from MD simulations of the two ligands bound to the AAAAA site of a duplex oligonucleotide with a thermodynamically calibrated biomolecular force field. The explicit treatment of solvent molecules ensures adequate solvation behaviour of DNA and ligands and allows for a close examination of the changes in solvation of the ligands. This would provide an improved basis for the design of DNA-binding drugs.

SUPPLEMENTARY MATERIAL

Supplementary Material is available at NAR Online.