Measuring the potential energy barrier to lipid bilayer electroporation

Abstract

Electroporation is a common tool for gene transfection, tumour ablation, sterilization and drug delivery. Using experimental methods, we explore the temperature dependence of electropore formation in a model membrane system (droplet-interface bilayers), using optical single-channel recording to image the real-time gating of individual electropores. We investigate the influence of the agarose substrate on electropores formed in this system. Furthermore, by examining the temperature-dependent kinetics of pore opening and closure we are able to estimate a barrier to pore opening in 1,2-diphytanoyl-sn-glycero-3-phosphocholine (DPhPC) membranes to be 25.0 ± 8.3 k_BT, in agreement with previous predictions. Overall these measurements help support the toroidal model of membrane electroporation.

This article is part of the themed issue ‘Membrane pores: from structure and assembly, to medicine and technology’.

1. Introduction

Lipid membranes provide the permeability barrier that keeps a cell's ‘insides’ in and their ‘outsides’ out—it is an understatement to say we have a vested interest in understanding exactly how this barrier is maintained. Preventing membrane permeabilization is not just important for cell viability, as controlled permeabilization is also required for all transport processes that occur across this membrane.

In general, lipid membranes are not spontaneously leaky, and in order to form a pore the energetic barrier to parting the lipid leaflets and making a hole must be overcome. This can be done through the action of transmembrane [1,2] or membrane-associated proteins or peptides [3,4], or even in a pure lipid bilayer through the modulation of surface tension [5] or the application of an external perturbation such as temperature [6,7 and references therein], pressure [8] or an applied potential [9].

Perhaps the simplest method to create pores is via the application of an applied potential, termed electroporation. Electroporation is most commonly used for gene transfection [10], but also has notable uses in sterilization [11,12], as a therapeutic cancer treatment [13–15], and for transdermal drug delivery [16]. For obvious reasons electroporation has been most widely studied using methods that record the ionic current across the membrane [7,17,18], and those that monitor uptake or leakage across the bilayer [19,20]. Experimental imaging studies of pore formation are extremely limited, apart from the visualization of very large pores in giant unilamellar vesicles (GUVs) where, for example, closure dynamics have been used to determine the pore line tension [21].

With regard to understanding the fundamental mechanics of electroporation, the principal limitation of electrical recording is that it is the sum total current across the bilayer that is measured. Electrical recording of electroporation cannot therefore resolve whether conductance events are due to individual or many pores. As a result, it is very difficult to construct a physical model that corresponds to this process based solely on information regarding the total ionic flux across the bilayer. It is also worth highlighting that stepwise ‘channel-like’ gating can also be generated in pure lipid bilayers using an applied potential [7]. To address these limitations, we recently used optical imaging of ionic flux to study the formation and properties of individual, mobile punctate defects in a lipid bilayer [22]. In the current paper, we expand on this work to further quantify the properties of individual electropores and explore the questions we raised in our initial observations.

Our previous work supported a toroidal pore mechanism, where lipids initially part in the plane of the membrane to form a hydrophobic pore, followed by rearrangement to form a hydrophilic (toroidal) pore lined with lipid head groups (figure 1a). Molecular dynamics simulations have shown that the local field at the headgroup–water interface generates depressions in the membrane, which protrude into the hydrophobic core and develop into single-file columns of water, termed ‘water wires’, that line the hydrophobic pores [23]. Enlargement of the pore and subsequent transit of ions across the membrane then takes place by molecular reorientation of the lipids to form an electrically conductive, headgroup-stabilized toroidal defect.

Figure 1.

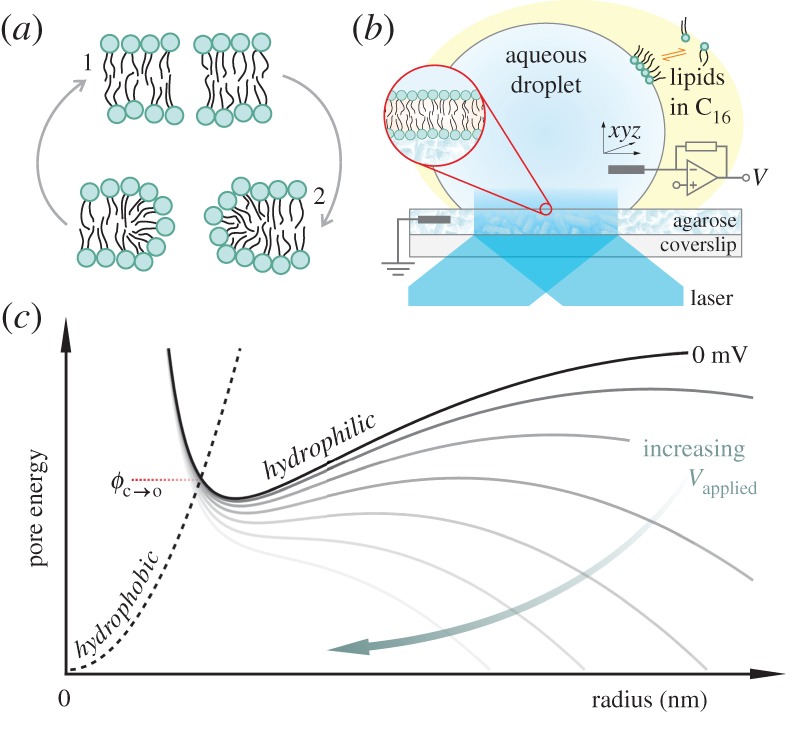
(a) Depiction of pore geometries: lipids in an intact bilayer may be parted by thermal fluctuations to form a hydrophobic pore (1). At larger radii, these defects rearrange to a toroidal (hydrophilic) pore (2) in order to minimize exposure of the hydrophobic membrane interior to water. (b) Cartoon of the droplet-interface bilayer setup. A bilayer is formed through contact between a droplet and a planar agarose hydrogel, both incubated in lipid in hexadecane (C₁₆). The bilayer is interrogated electrically by a patch-clamp amplifier connected via electrodes in the droplet and the agarose, and optically by a totally internally reflected laser beam. See §2b–d for details. (c) Illustrative energy curves for the two pore geometries. A hydrophobic pore that surmounts the energy barrier 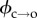(closed to open) will convert to a toroidal pore. The applied transmembrane potential lowers the pore free energy (increasing voltage from black to grey solid lines).

In the absence of a potential, parting of lipids due to thermal motion is insufficient to produce a pore of a size such that rearrangement to a hydrophilic (conducting) pore can take place [24]. If formed, the existence of a pore is largely dependent on the balance between the surface tension of the membrane, which works to enlarge a defect, and the line tension, which works to close it. A transmembrane voltage augments the surface tension, lowering the free energy of the hydrophilic pore, thus stabilizing it (figure 1c). Here we explore electropore formation using optical single-channel recording (oSCR) by imaging the Ca²⁺ flux through individual electropores in droplet-interface bilayers (DIBs, figure 1b).

2. Material and methods

(a). Materials

1,2-Diphytanoyl-sn-glycero-3-phosphocholine (DPhPC) was purchased from Avanti Polar Lipids (AL, USA) and Lipoid (Ludwigshafen, Germany), and were stored as chloroform stocks at −20°C. Aqueous solutions were prepared using doubly deionized 18.2 MΩ cm Milli-Q water. Potassium chloride solutions were treated with Chelex resin (200–400 mesh; Bio-Rad) to remove divalent cations and filtered using a 0.22 μm Steriflip filter (Millipore). Ca²⁺-sensitive Fluo-8 dye was purchased from AAT Bioquest (CA, USA) and stored at 1 mg ml⁻¹ in MilliQ at −20°C. All other chemicals were purchased from Sigma-Aldrich.

(b). Droplet-interface bilayers

DIBs were prepared as described in [25]. Briefly, O₂ plasma-cleaned coverslips were spin-coated with aqueous 0.75% (wt/vol) ultra-low gelling agarose, then affixed to a purpose-machined PMMA device with 16 wells. A channel within the device was then filled with 2% (wt/vol) hydrating agarose containing 750 mM CaCl₂, 10 mM HEPES. This provides a hydration reservoir, making contact with the hydrogel around the wells, but not covering the substrate within them. The device was incubated with 8.7 mg ml⁻¹ DPhPC in hexadecane for 15 min for monolayer formation. Aqueous droplets (∼50 nl) containing 1.5 M KCl, 10 mM HEPES, 370 μM EDTA and Fluo-8 dye (∼50 μM) were incubated in the same lipid-in-oil solution for 30 min. Droplets were added to the device, where they sank to make contact with the substrate and form a bilayer. (Further detail may be found in the electronic supplementary material, together with depictions of the device.) Devices were placed within a Faraday cage on an inverted microscope (Ti-E; Nikon). Ag/AgCl electrodes were placed in the hydrating agarose and into the top of the droplet via a micromanipulator and connected to a patch-clamp amplifier (Axopatch 200B; Molecular Devices, CA, USA) in voltage-clamp mode. The room temperature was 21°C.

(c). Electrical recording

Data for I–V curves were collected by exposing bilayers to a voltage protocol that applied 5 mV increments between ±5 and ±300 mV for 180 s, with each step in voltage separated by a 30 s period at 0 mV.

(d). Fluorescence imaging

Fluo-8 was excited by a totally internally reflected 473 nm laser beam (Vortran Laser Technology, CA, USA; 3–4 mW at the back focal plane of the objective) through a 60×, 1.49 NA TIRF oil-immersion objective lens (Nikon). Emitted light (Fluo-8 λ_{em. max.} = 514 nm) passed through a 525/39 nm emission filter (Brightline Basic; Semrock, NY, USA) and images were collected on an electron-multiplying CCD (iXon3 897; Andor, UK) at a frame rate of 120.34 Hz. The device was mounted on a temperature-controlled stage (PE94; Linkam, UK), and the objective was heated via a custom-built resistance heater. Temperature was monitored using a thermocouple placed in the well adjacent to that containing the imaged droplet.

(e). Imaging unsupported bilayers

For experiments where additional hydration was used to raise the bilayer (25–90 μm) relative to the substrate, a 60×, 1.20 NA water-immersion objective was used, and the laser was incident on the bilayer at a glancing angle, rather than totally internally reflected. A lower NA objective was selected in order to increase the working distance. The coverslip was marked with a pen before spin-coating the substrate agarose. This reference was used to measure the axial (z) position of the bilayer above the substrate. Images were recorded at 49.85 Hz.

(f). Data analysis

The oSCR signal from electropores was tracked using the Trackmate plugin in Fiji [26]. Detected tracks were then manually selected. Mean-squared displacements were calculated from the tracking data with a custom-written procedure in Igor Pro (Wavemetrics). Fluorescence versus time plots were obtained by drawing a circular region of interest (diameter 20 pixels = 7.846 μm) around the pore, and the mean intensity value within this area was determined for each frame.

Electropore kinetics were analysed by custom-written procedures in Igor Pro, with a transition between open and closed states defined as crossing a threshold set at 2.5 times the standard deviation of the background intensity (see electronic supplementary material, figure S2a). The periods that a fluctuating oSCR signal from a pore spent either above or below this threshold were counted (and defined as the open time and closed time, respectively). Histograms of these times were best fitted with double exponentials, yielding a pair of characteristic time constants for both the open and closed states, denoted τ_1/2,o and τ_1/2,c [22], with the subscripts 1 and 2 indicating the short and long values, respectively. The temperature used in calculations was taken to be that of experimental room temperature (294 K).

3. Results

(a). Effect of the agarose substrate

Our previous work exploited DIBs supported on an agarose hydrogel [22]. We observed free Brownian motion for these electropores and thus reasoned that any effect of the underlying substrate was negligible. In addition, for DIBs formed in this manner, we have previously reported diffusion coefficients from single-particle tracking of fluorescently labelled lipids that correspond to those seen in unsupported lipid bilayers [27]. However, we have also exploited dehydration of the agarose support to corral transmembrane proteins at a specific location on the bilayer [28]. To explore further if electropores are affected by the agarose substrate, DIBs were generated on an agarose substrate that was ‘over-hydrated’: following addition of the lipid-in-oil solution to form a monolayer at the agarose–oil interface, small (∼200 nl) droplets of buffer solution were fused with the interface. This increased the volume of buffer present on the agarose-facing side of the DIB and raised the bilayer away from the substrate by between 25 and 90 μm. These ‘over-hydrated’ DIBs were then used to measure the diffusional properties and gating kinetics of electropores.

Figure 2a shows an example of electropores formed following this procedure. Here the lipid bilayer is 32 μm above the glass coverslip. We find the single-channel activity, voltage dependence of ionic flux and diffusion of these pores to be largely similar to those observed when electropores are formed in a DIB where the bilayer is ∼200 nm from the glass coverslip.

Figure 2.

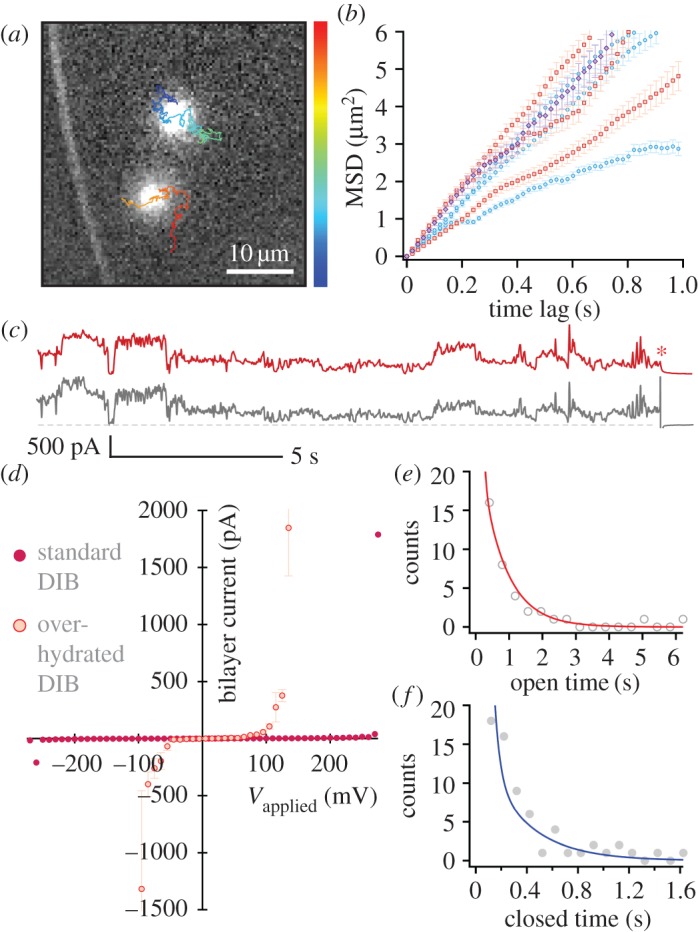
Electropores on an aqueous cushion. Cushion height varied from 25 to 90 μm. (a) Pores observed at 330 mV. The overlaid tracks show the trajectories of the pores, running from the start (blue) to the end (red) of the recording. Image is a single 20 ms exposure. (b) MSD versus t plots for pores at 250 mV (red), 330 mV (blue) and 415 mV (purple). The mean lateral diffusion coefficient was 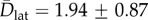μm² s⁻¹ (n = 8). Error bars are the standard error for each MSD value. (c) oSCR trace (red) and corresponding electrical recording (black) for a single electropore at 210 mV. The red asterisk indicates the point at which the voltage was switched off. The grey dashed line represents 0 pA. (d) Typical I–V curve for an over-hydrated (red) and standard DIB (purple). Over-hydrated bilayers were found to rupture at lower potentials compared with standard bilayers exposed to the same protocol. Data points are the mean bilayer current at each applied potential; error bars are one standard deviation. (e) Pore open and (f) pore closed lifetime histograms fitted with double exponentials; n = 12. The lifetimes derived from these fits (τ_1,o = 61.2 ± 0.5, τ_1,c = 42.9 ± 1.7, τ_2,o = 748.5 ± 11.1, τ_2,c = 328.1 ± 22.6 ms) are essentially unchanged from those found in standard DIBs.

Figure 2b shows mean-squared displacement versus time plots for such electropores on an over-hydrated substrate. As in our previous work, we see no obvious relationship between the applied potential and the lateral diffusion coefficient (D_lat) of the pores, the mean of which was 1.94 ± 0.87 μm² s⁻¹ (n = 8). Notably these mean D_lat values are around an order of magnitude larger for the over-hydrated bilayers (table 1), as expected for larger aqueous separations between the bilayer and the agarose [29].

Table 1.

Comparison of lateral diffusion coefficients of electropores under standard and over-hydrated DIB conditions.

Vapplied	mean Dlat/μm2 s−1 (n)
standard preparationa
260 mV	0.15 ± 0.1 (5)
330 mV	0.27 ± 0.3 (8)
over-hydrated bilayersb
250 mV	1.73 ± 0.5 (3)
330 mV	1.51 ± 0.5 (3)

^aData from [22].

^bThis work.

We also analysed the electrical characteristics and gating kinetics of the electropores to investigate whether the water cushion modulates their opening and closing behaviour. The electrical data and the corresponding oSCR traces show the same fluctuating behaviours indicative of rapidly changing radii, with the bilayer current and the oSCR signal showing complementary traces (figure 2c). To assess the ensemble electrical behaviour of these bilayers, a voltage protocol (see §2c) was applied and the corresponding I–V characteristic plotted (figure 2d). This protocol acts as a standard electrical treatment against which the behaviour of different membranes may be compared, which we parameterize by the potential at which the bilayer ruptures, V_rupture. Current fluctuations (formation of pores) begin at ∼60 mV; the number of pores, their size and the distribution sizes increase as the voltage is raised [22]. This continues until the bilayer ruptures. Bilayers without over-hydration rupture at a mean potential of 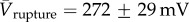(n = 7), whereas over-hydrated bilayers were destroyed at 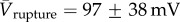(n = 5) when subjected to the same protocol. This would suggest that rather than potentially nucleating pores, the presence of an agarose substrate serves to stabilize the bilayer against rupture.

While the value of V_rupture gives us a good idea of the range of voltages over which reversible electroporation takes place, thus providing us with a guide to the potentials that can be applied without rupturing the membrane during an oSCR experiment, the membrane may survive at voltages higher than V_rupture. The duration of the applied potential is as important to the electroporation outcome as the magnitude of the applied field [30]. In the case of oSCR experiments, bilayers were exposed for a few tens of seconds in order to make a recording, shorter than for the I–V curves (180 s). We may speculate that in exposure over shorter periods, instances that bilayers survive above V_rupture result from the presence of multiple pores (relaxing the transmembrane voltage [31,32]) temporarily preventing the formation of larger, critical defects that would otherwise overcome the barrier to unbounded pore formation and destroy the membrane, or that the shorter exposure reduces the probability of pre-pore defects [18] existing within the membrane.

Although the I–V characteristic and rupture potential inform us about the stability of the entire bilayer, we were primarily interested in determining whether the dynamic behaviour of the pores had changed. It might be expected that if the agarose is influencing individual pore properties, we would observe a difference in gating kinetics when the bilayer is raised away from it. These kinetics were analysed by counting the period of time that pores were open and closed, as observed by oSCR, then fitting these lifetimes with double exponentials [22] (see §2f). Although we cannot conclusively attribute a mechanism to these two processes, the shorter-lived closed period may be the result of some non-conductive pre-pore state, a state that has a higher probability of pore formation [18]. Short-lived open states may be due to immediate relaxation of the local field upon pore formation [22,31,32]. We found that the characteristic lifetimes for pores in over-hydrated bilayers were essentially identical to those for standard DIBs (figure 2e,f). Further, the fact that these distributions were again best fit with double exponentials suggests that the short-time components observed here and previously reported do not result from any bilayer interaction with the substrate.

(b). Temperature dependence of electropore formation

The ability to access the gating kinetics of individual defects is an advantage of using Ca²⁺ flux imaging to monitor electroporation. We exploited this in order to determine the pore formation energy barrier. The rate at which hydrophilic pores are formed (that is, transition over the energy barrier 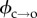; see figure 1c) is described by

3.1

where v is the frequency of lateral lipid fluctuations, S is the area of the membrane and a₀ is the area per lipid [33]. This rate will be proportional to the inverse of the closed lifetime, with an expression of the same form for open lifetimes. Taking logarithms

3.2

where C is the constant of proportionality linking k to τ. 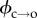has been experimentally estimated to be ∼45k_BT in asolectin black lipid membranes [33]. Equations (3.1) and (3.2) apply to a bilayer experiencing zero transmembrane potential. When a voltage is applied

3.3

where h is the membrane thickness, r_* is the radius at which a hydrophobic pore converts to a hydrophilic pore, ε_w and ε_m are the relative permittivities of water and the membrane, respectively, and ε₀ is the permittivity of free space. However, with a bilayer thickness of 4.8 nm and r_* given a value of 0.5 nm [22,33–35], the term (π/2h)r²_*(ε_w − ε_m)ε₀V² only becomes comparable to tens of k_BT (the predicted value of 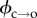) when V > 500 mV; this is far above the mean rupture potential for DPhPC DIBs. Furthermore, we and others have determined previously that electropore lifetimes do not vary significantly with the applied potential in the range 150–350 mV [18,22]. This implies that the energy barrier is relatively constant in this voltage range, and under these conditions equation (3.3) reduces back to equation (3.2).

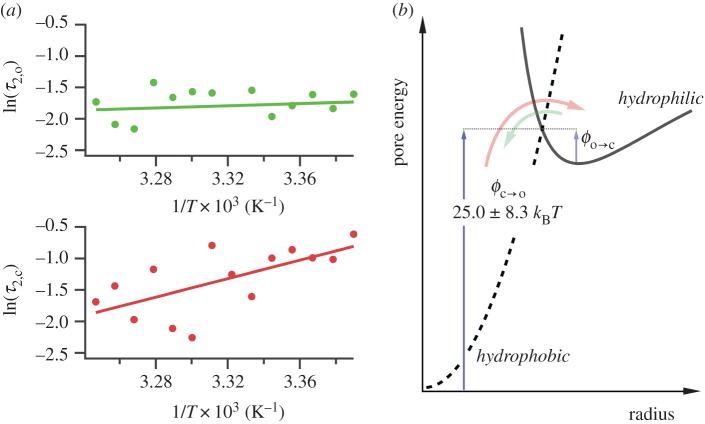
The barrier ϕ can therefore be determined by examining electropore gating as a function of temperature. As expected, electroporation and bilayer rupture were more likely as the temperature was raised; experiments were therefore carried out at 100 mV, a balance between a potential sufficient to observe electropores near room temperature, but one low enough to prevent rupture at elevated temperatures. Lipids at their phase transition have shown increased propensity towards pore formation [7]; however, DPhPC exhibits no phase transition in this range [36], and so these experiments probe electroporation of unperturbed bilayers. The results from the analysis of 754 pores are presented in figure 3a. Measurements were made from between 22 and 35°C. The Arrhenius plots are for the τ₂ lifetimes, which represent transitioning over the hydrophobic–hydrophilic barrier (figure 3b). The τ₁ lifetimes, suggested to be a result of either a pre-pore or extremely brief openings due to immediate relaxation of the local electric field upon pore opening, showed the same trends as the corresponding τ₂ (electronic supplementary material, figure S2b). We found that whereas τ_2,c decreased with increasing temperature, τ_2,o had no strong dependence on temperature. Linear regression to the τ_2,c data finds the barrier to pore opening in DPhPC to be 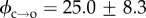k_BT, which is in agreement with the estimate made by Glaser et al. [33], and in very good agreement with the barriers calculated from molecular dynamics simulations of phosphatidylcholine bilayers by Majhi et al. [37], who based their calculations on pore initiation times and similar Arrhenius kinetics. Although within error, the barrier to pore collapse from a hydrophilic pore from our experiments is, as expected, smaller than that of 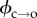(see figures 1c and 3b), with .

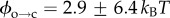Figure 3.

Temperature dependence of electroporation. (a) Arrhenius-type plots for electropore open (upper) and closed (lower) lifetimes. The data shown here are for the τ₂ lifetimes. τ_1,o and τ_1,c showed the same trend as their longer counterparts (electronic supplementary material, figure S2b). Each data point is derived from at least five pores (maximum 337, mean 54). Error bars, derived from the standard deviation of the fits that revealed the lifetimes, are obscured by the data points. (b) Detail of the hydrophobic–hydrophilic energy curves. The colours of the arrows correspond to the data in (a): τ_2,c is the period a pore spends attempting to overcome 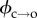(red); τ_2,o is the average time a pore resides in the hydrophilic regime before returning to a closed state via 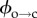(green).

4. Discussion

In the absence of a thick (tens of micrometres) hydrating layer, the DIB agarose substrate reduces the diffusion of electropores and increases V_rupture; however, the substrate does not influence the gating behaviour of individual electropores. This suggests that rather than nucleating pores, the presence of an agarose substrate serves to stabilize the bilayer against rupture, perhaps due to the agarose–membrane interactions that lead to a reduced diffusion coefficient. This is not inconsistent with the values of τ₁ and τ₂ remaining unchanged, however: these lifetimes are indicative of the transition over the initial hydrophobic–hydrophilic barrier, whereas rupture is initiated by a pore traversing a barrier at larger radii (see figure 1c). We might speculate that the agarose reduces the expansion of the larger pores [38], but has little effect on the lifetime of the smaller defects.

Measurements on the temperature dependence of electroporation are consistent with a toroidal pore model where the formation of hydrophilic pores takes place via a hydrophobic intermediate. This intermediate is simply a parting of lipids within the membrane with no molecular reorientation, a transient state generated by the thermal energy. In raising the bilayer temperature, the probability of surmounting this barrier to hydrophobic pore formation is increased. This is what we observe: τ_2,c decreases with increasing temperature. The open lifetime, however, appears to vary less strongly with temperature. This implies that the increased lipid fluctuations as a result of increased k_BT do not greatly aid in surmounting 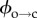. More likely, the lipid rearrangement that is required to close the pore—overcoming forces such as double-layer repulsion between the headgroups and the removal of interfacial water as the toroidal walls come together [24,39]—dominates the energetics of this return process.

The reason for our observation of two lifetimes for the open and closed states remains to be determined. It would be of interest to examine pore kinetics at lower ionic strengths, whereby the reduction of the local electric field at the site of a pore [31,32] would be lessened. We speculate in this case whether we would no longer observe the short open lifetime, but retain the short closed lifetime, if indeed the latter is the result of non-conductive defects. The fact that we observe that τ_1,c also decreases with temperature (electronic supplementary material, figure S2b) is consistent with this lifetime being the result of such defects within the membrane, which may be more prone to opening to a pore with increased thermal energy. Further work is needed to elucidate the origin of these short lifetimes.

This work provides further insight into the mechanism of electropore formation in lipid membranes, including a new experimental method for estimating the electroporation barrier. Although oSCR does not image pores directly, its ability to probe individual electroporation events occurring in a bilayer in real time is a valuable tool in probing this phenomenon.

Data accessibility

Supporting information, including further details of the experimental setup, may be found online.

Author's contributions

J.T.S and M.I.W. designed the research. J.T.S. performed the research and analysed the data. J.T.S. and M.I.W. wrote the paper.

Competing interests

We have no competing interests.

Funding

M.I.W. is supported by the European Research Council (ERC-2012-StG-106913, CoSMiC); J.T.S. is supported by the European Research Council and the Engineering and Physical Sciences Research Council.