Abstract
Cyclin-dependent kinases (CDKs) are vital in regulating cell cycle progression, and, thus, in highly proliferating tumor cells CDK inhibitors are gaining interest as potential anticancer agents. Clonogenic assay experiments are frequently used to determine drug efficacy against the survival and proliferation of cancer cells. While the anticancer mechanisms of drugs are usually described at the intracellular single-cell level, the experimental measurements are sampled from the entire cancer cell population. This approach may lead to discrepancies between the experimental observations and theoretical explanations of anticipated drug mechanisms. To determine how individual cell responses to drugs that inhibit CDKs affect the growth of cancer cell populations, we developed a spatially explicit hybrid agent-based model. In this model, each cell is equipped with internal cell cycle regulation mechanisms, but it is also able to interact physically with its neighbors. We model cell cycle progression, focusing on the G1 and G2/M cell cycle checkpoints, as well as on related essential components, such as CDK1, CDK2, cell size, and DNA damage. We present detailed studies of how the emergent properties (e.g., cluster formation) of an entire cell population depend on altered physical and physiological parameters. We analyze the effects of CDK1 and CKD2 inhibitors on population growth, time-dependent changes in cell cycle distributions, and the dynamic evolution of spatial cell patterns. We show that cell cycle inhibitors that cause cell arrest at different cell cycle phases are not necessarily synergistically super-additive. Finally, we demonstrate that the physical aspects of cell population growth, such as the formation of tight cell clusters versus dispersed colonies, alter the efficacy of cell cycle inhibitors, both in 2D and 3D simulations. This finding may have implications for interpreting the treatment efficacy results of in vitro experiments, in which treatment is applied before the cells can grow to produce clusters, especially because in vivo tumors, in contrast, form large masses before they are detected and treated.
Keywords: CDK inhibition, Cell cycle checkpoints, Agent-based model, Tumor cluster, Cell motility
1. Introduction
One of the hallmarks of cancer is uncontrolled proliferation, a consequence of loss of control over the normal cell cycle [1]. The mammalian cell cycle is a sequence of complex processes that ensures the faithful replication of DNA and the equal division of identical chromosomal copies between two daughter cells. The sequence of these processes is tightly regulated, thereby guaranteeing that the initiation of later events (such as physical cell division) is preceded by the completion of earlier events (such as cell organelle duplication or DNA synthesis). The cell cycle is usually divided into four general phases: G1 (gap phase), in which a cell increases in size and duplicates its organelles; S (synthesis phase), during which DNA is replicated; and G2 (gap phase), which involves cell preparation for chromosome separation and physical division into two offspring cells in the M (mitosis) phase. The successful completion of the cell cycle necessitates that these separate phases take place at the right sequence and at the right time. If a cell attempts mitotic division before its chromosomes have been fully replicated, the daughter cells will inherit incomplete DNA. Conversely, if the cell undergoes several rounds of DNA replication between mitoses, it will contain multiple copies of chromosomes. Moreover, a cell requires a sufficient interval between two consecutive cell divisions for it to double its mass and organelles; unless such a condition is satisfied, daughter cells become progressively smaller. In all of these cases, the emerging cell subpopulation loses its normal characteristics, and may acquire genomic or chromosomal instability [2].
Among the mechanisms that cells have developed to ensure the appropriate completion of the cell cycle are cell cycle checkpoints. These can actively halt progression through the cycle until the critical events of a particular cell cycle phase are finalized. These checkpoints can also respond to cell DNA damage by arresting the cell cycle, thereby providing time for DNA repair. Several cell cycle checkpoints respond to specific forms of stress, and impose arrest at specific points in the cell cycle [3]. For example, a checkpoint in the G1 phase ensures that a cell reaches an adequate size before it enters the S phase; small cells in a cell culture remain longer in the G1 phase, a behavior that enables the cells to continue growing [4]. The G2 checkpoint suspends the cell cycle if extensive DNA repair is required before a cell can initiate mitosis [5]. The specific checkpoint in the M phase, called the spindle assembly checkpoint, can delay the cell cycle to avoid the erroneous segregation of chromosomes [6,7].
Cyclin-dependent kinases (CDKs), a family of protein kinases, are critical regulators of cell cycle progression [2,8]. The activity of CDKs is modulated by several cyclins and functional inhibitors (e.g., Ink4, Cip, and Kip) [9]. Among the 13 CDKs expressed in human cells, CDK2, CKD4, and CKD6 are involved in the interphase, and CDK1 is involved in mitosis [2]. The cyclins associated with particular CDKs activate CDK catalytic abilities, and together are responsible for passing through the cell cycle checkpoints. Tumor-associated mutations frequently deregulate certain CDK-cyclin complexes, resulting in either continued proliferation or unscheduled reentry into the cell cycle [10]. This opens up possibilities for CDK inhibitors as relevant drug candidates for cancer therapy [10,11,12,13]. The selective inhibition of CDKs may limit the progression of a tumor cell through the cell cycle and facilitate the induction of an apoptotic pathway. Specific CDK-cyclin complexes that are modulated by CDK inhibitors may also be responsible for maintaining a quiescent state in different cell populations [2].
This paper focuses on two CDKs—CDK1 and CDK2—each involved in the control of cell cycle checkpoints. During the G1 phase, CDK2 forms a complex with the E-type cyclins (E1 and E2) that enables transition from the G1 to the S phase [9]. The CDK2-cyclin E complex can also prevent cells from passing the G1 checkpoint if it is diminished [14,15]. Upon entering into S phase, the E-type cyclins are gradually replaced by A-type cyclins (A1 and A2) that form complexes with CDK2 and enable progression through the S phase until the A-type cyclins start forming complexes with CDK1, which allows the cell to move to the G2 phase [9]. However, passage through the G2-phase checkpoint is also controlled by the phosphorylation and dephosphorylation of CDK1 via WEE1 and CDC25 [16,17]. Moreover, CDK1 stimulates the mechanism for repairing DNA double-stranded breaks [18], which enables the cells to reduce their DNA damage before entering into M phase. In the G2 phase the A-type cyclins are replaced by the B-type cyclins (B1 and B2), and the CDK1-cyclin B complexes are responsible for the transition from G2 to M phase (compare Fig. 8.12 in [9]).
We model the CDK-regulated cell cycle in individual cells in a simplified way. We do not consider separate cyclins, but do model the CDK-cyclin complexes together, as well as the total amounts of both CDKs, because our main goal is to investigate the influence of CDK1 and/or CDK2 inhibition on cell population behavior. There are more detailed models of CDK-cyclin kinetics [19,20,21]; however, they do not consider spatial interactions between cells in large populations, as we do in this paper. Therefore, to build a model that incorporates both intracellular and intercellular aspects of the cell-cycle control, we use a single-cell-based off-lattice hybrid model in which each cell is equipped with an individually regulated cell cycle, but the cells can interact physically with one another. To our knowledge, only the model developed by Powathil et al. [22,23] addresses both these aspects. However, our model uses a different mathematical framework to model individual cell dynamics and focuses on different components of the cell-cycle regulation mechanisms. In this paper, we discuss mainly the 2D version of our model as an analogue of an experimental clonogenic assay, and the simulated results may be compared to those derived from typical 2D in vitro experiments, as we show in Section 4.
The clonogenic survival assay is an in vitro experimental technique that can be used for verifying whether a potential anticancer agent has therapeutic effects. It is used to evaluate whether tumor cells can sustain indefinite proliferation and thereby form multicellular clones [24,25]. In this experimental setting, cells are cultured on 2D plates in a medium that contains the nutrients necessary for cell growth and survival. A constant concentration of the anticancer agent is added to the culture (the medium is changed periodically to keep conditions uniform). After a specific period, the cells are fixed, often stained, or counted. The results are usually reported after normalization using the cell number of the nontreated (control) cell culture. The findings may also be interpreted as cell growth inhibition relative to the growth of control cells. A similar protocol is used in our computational model, but for simplicity, we model only a small but representative part of an entire plate, which is typically visible under a microscope.
2. Model
We use an off-lattice hybrid model of growing cell colonies. In its 2D version, the model is a computational analogue of in vitro clonogenic assays [26,27], whereas the 3D version of the model is an analogue of a typical multicellular spheroid culture [28,29]. We model cells as individual entities: each equipped with an individually regulated cell cycle, individually controlled cell size, cell migration, cell–cell interactions, and individually defined cell response to environmental cues including the drugs inhibiting CDKs. These conditions enable us to investigate the emergent properties of an entire cell population. We incorporate sufficient morphological and physiological details about a single cell in the model to compare the model results with experimental data, but the cell representation is simple enough; thus, we can simulate the behavior of thousands (or more) of cells under a reasonable computational time. Each cell is mathematically represented by a disk and specified by a pair of variables (x, a), where x is the center of the disk and represents the physical location of a cell, and a is the cell radius (the reference cell radius is a0 = 5 μm). Both of them can dynamically adapt during the simulation. Cell location changes during cell movement, and cell radius changes during cell growth or shrinkage. Simultaneous consideration of both these variables is necessary to impose the volume exclusivity condition between cells. This is critical because cells compete for limited space during colony expansion. Each in silico cell is equipped with an individual cell cycle control mechanism that is defined by a set of ordinary differential equations. These features enable us to trace the cell progression through cell cycle phases, and to determine the roles of specific molecules (CDK1 and CDK2) in cell cycle control. We first describe the cell cycle control model, and then the mechanics of individual cell growth and migration, which are crucial to the development of tumor cell colonies under CDK inhibition. The pseudo-code of the fully integrated algorithm of cell cycle regulation, growth, migration, and cell–cell interactions is presented in Table 1.
Table 1.
Pseudo-code of the full algorithm of cell cycle regulation, growth, migration, and cell–cell interactions.
| Program cell cycle update for Δt |
| for i=1 to Number_of_cells |
| Update all Nprotein |
| Update Q, P |
| Update ai's |
| end of for |
| for i=1 to Number_of_cells |
| Calculate repulsive forces based on updated ai |
| Update location |
| end of for |
| Neighbor search |
| for i=1 to Number_of_cells |
| Apply growth rate compromise algorithm based on ai to settle aifinal |
| ai =aifinal |
| end of forfor i=1 to Number_of_cells |
| Update cell phase based on new variables |
| end of for |
| Calculate motility forces for each cell |
| for i=1 to Niteration |
| Update locations of all cells following the motility forces for Δt / Niteration |
| Calculate repulsive forces based on ai |
| Update location |
| Neighbor search |
| end of for |
| for i=1 to Number_of_cells |
| if cell qualifies for the cell division |
| Replace with two daughter cells |
| end of if |
| end of for |
2.1 Cell cycle regulation
Cell cycle regulation and control mechanisms are biologically complex and comprise many interconnected components. In this paper, we focus on cell cycle checkpoints and the roles of CDK1 and CDK2 in cell cycle regulation. Both kinases form complexes with the appropriate cyclins that are crucial in facilitating passage through cell cycle checkpoints. During the G1 phase, the newly born cell needs to first increase its volume and the amounts of all proteins necessary to survive and progress through the cell cycle. Two factors, cell size and the amount of CDK2-cyclin E complexes, determine whether a cell is ready to pass the G1 checkpoint and move on to the S phase. CDK2 can be inhibited from forming this complex, which may prolong the G1 phase indefinitely; we regard this phenomenon as G1 arrest. For the cells that pass the G1 checkpoint, CDK1 stimulates DNA repair (by the homologous recombination discussed below) and, when inhibited, significantly slows down the DNA repair process in the S and G2 phases. CDK1 also undergoes phosphorylation by the nuclear kinase WEE1 (at Tyr15 of CDK1) that is affected by the levels of DNA damage. The increased phosphorylated CDK1 prevents a cell from passing the G2/M checkpoint. The cell then stays in the G2 phase, which allows for DNA repair and, in turn, diminishes the amount of phosphorylated CDK1. Both the inhibited and phosphorylated CDK1s are subsets of CDK1, and they are not mutually exclusive. Some of the DNA repair processes are cell cycle specific; such processes include the homologous recombination (HR, amending double-stranded DNA breaks by using similar or identical molecules of DNA as templates) that is more pronounced in the S and G2 phases and the nonhomologous end-joining (connecting open ends in double-stranded DNA breaks without any template) that is active mostly in the G1 phase [30]. The other mechanisms of DNA repair that are active throughout the entire cell cycle are base excision repair, which fixes small, nonhelix–distorting base lesions by removing damage bases, and nucleotide excision repair, which restores bulky helix-distorting lesions by scanning through damage regions [30,31]. We also recognize the importance of spatial interactions between cells, especially cell volume exclusivity; thus, we trace the size of each cell (cell radius) during all the phases of the cell cycle.
The full list of model variables is listed in Table 2, the governing equations in Table 3, and the model parameters and their values in Table 4. Some of these equations are phase independent because the underlying kinetics occur throughout the entire cell cycle, and the others take different forms in different cell cycle phases because they describe phase-specific mechanisms. However, all of the equations are written in Table 2 in a unified format. Since the newly born cell upon division of the mother cell inherits half of its mass and protein contents, the total amounts of CDK1, CDK2, and WEE1 need to be increased during the G1 phase for the cell to function properly. We follow a simple kinetics of protein production and degradation where the total amount of each protein is normalized to 1 (Eqs. (1–3)), and the rCDK1, rCDK2, and rWEE1 denote the net increase rate (arising from combining both production and degradation rates) for CDK1, CDK2 and WEE1, respectively. Similarly, by combining the forward and reverse reaction rates and normalizing the total amounts of CDK inhibitors, their kinetics is described by Eqs. (4–5) with the net increase rates rCDK1i and rCDK2i, respectively. The kinetics of the CDK2-cyclin E complex formation in the G1 phase is controlled by the amount of uninhibited CDK2 (i.e. NCDK2 – NCDK2i) with net increase rate rCDK2E (Eq. (6)), since cyclin E is abundant during the G1 phase (compare [9] Fig. 8.10 and [19] Fig. 2). CDK2-cyclin E complex become degraded after the cell passes the G1 phase since CDK2 starts forming other complexes important for the cell-cycle progression. Thus, the CDK2-cyclin E complex is gradually diminished to zero after the G1 phase, which is represented in Eq. (6) as an appropriate decay term activated after the G1 phase. The mathematical form of this decay term is not crucial for our model as long as it depletes CDK2-E before the cell division.
Table 2.
Model variables.
| Symbol | Name |
|---|---|
| a | Cell radius |
| P (=Po+Pc) | DNA replication index |
| Q | DNA damage index |
| NCDK1 | Amount of CDK1 |
| NCDK1y | Amount of CDK1 with phosphorylation at Tyr 15 |
| NCDK1i | Amount of inhibited CDK1 (no contribution of DNA repair) |
| NCDK2 | Amount of CDK2 |
| NCDK2i | Amount of inhibited CDK2 (no contribution to CDK2E synthesis) |
| NWEE1 | Amount of WEE1 |
| NCDK2E | Amount of CDK2 and cyclin E complex |
Table 3.
Model equations including cell cycle control equations (1–11) and cell growth and migration equations (11–15).
| (1) |
|
|
| (2) |
|
|
| (3) |
|
|
| (4) |
|
|
| (5) |
|
|
| (6) |
|
|
| (7) |
|
|
| (8) |
|
|
| (9) |
|
|
| (10) |
|
|
| (11) |
|
|
| (12) |
|
|
| (13) |
|
|
| (14) |
|
|
| (15) |
|
Table 4.
Model parameters.
| Symbol | Name | Value |
|---|---|---|
| a0 | Typical cell size | 5 μm |
| ra | Cell radius growth rate (default) | 0.19 μm/s |
| rp | DNA replication rate | 0.44 h-1 |
| rbd | DNA damage rate (background) | 0.01 h-1 |
| rcd | DNA damage rate (copied part in S phase) | 0.015 h-1 |
| rbr | DNA repair rate (background) | 0.3 h-1 |
| rn | DNA repair rate (non-homologous end joining) | 0.1 h-1 |
| rh | DNA repair rate (homologous recombination) | 0.4 h-1 |
| ks | DNA repair suppress constant | 0.1 |
| rCDK1 | CDK1 production rate | 0.48 h-1 |
| rCDK1i | CDK1 inhibition rate | 0.045 h-1 |
| rCDK2 | CDK2 production rate | 0.48 h-1 |
| rCDK2i | CDK2 inhibition rate | 0.075 h-1 |
| rWEE1 | WEE1 production rate | 0.48 h-1 |
| rCDK1y | CDK1y synthesis rate | 2.4 h-1 |
| rCDK2E | MF synthesis rate | 0.48 h-1 |
| dCDK1y | CDK1y degradation rate in G2 phase | 1 h-1 |
| ath | Threshold for a in G1 phase | 0.95×21/2×a0 |
| NthCDK2E | Threshold for MF in G1 phase | 0.99 |
| NthCDK1y | Threshold for CDK1y in G2 phase | 0.1 |
| Qth | Threshold for Q in M phase | 0.02 |
| k | Repulsive spring constant | 5 [k] |
| η | Linear drag coefficient | 1 h·[k] |
During the S phase, the cell needs to double its DNA content, which we denote by the DNA replication index P. Thus P will increase from 1 (the initial DNA contents) to 2 (the original DNA and its copy) with a constant increase rate rp (Eq. (7)). This approach reflects the dynamics of DNA replication, which occurs simultaneously at multiple locations of replication origins [3], and, as the replication process is being completed, the number of active replication origins gradually reduces [32]. Since the cell DNA is constantly exposed to chemical products of various metabolic reactions that can cause DNA damage ([9] reports as many as 10,000 genome modifications in a single cell each day, that are removed by a highly effective DNA repair system), we introduce a variable Q as a DNA damage index that represents the cumulative effect of DNA damage and repair. Its dynamics (Eq. (8)) depend on the cell cycle phase and, in the S phase, on the stage of DNA replication. To consider this, we first decompose P into Pc, which represents the already duplicated DNA and Po, which is the part of the DNA to be duplicated (Pc is equal to zero during the G1 phase). The rates of DNA damage in Po and Pc are denoted by rbd and rcd, respectively. We assume that rcd is higher because, first, if the region to be duplicated is already damaged then the resultant copies also preserve or inherit this damage; second, DNA replication is a stressful process that causes additional damage to DNA [33]. We include three categories of DNA repair mechanisms in the model. The phase-independent mechanisms, such as base excision repair and nucleotide excision repair, take place throughout the cell cycle and are represented by background repair rate rbr. The two phase-specific mechanisms are nonhomologous end-joining, which is more active in the G1 phase (repair rate rn), and HR, which is more pronounced in the S and G2 phases (repair rate rh). We capture this phase specificity in the model by applying suppression multiplier ksp and cell cycle specificity function CST (where T denotes the cell cycle phase, Eq. (10)) to rh or rn, depending on the current cell cycle phase. To implement the stimulus from CDK1 to HR, we multiply the HR rate by the amount of uninhibited CDK1. Non-phosphorylated CDK1 (i.e., NCDK1 – NCDK1y) turns into phosphorylated CDK1 (NCDK1y) and the rate of change in phosphorylated CDK1 (NCDK1y) is proportional to the DNA damage index and the amount of WEE1 [12,30], with proportionality constant rCDK1y. The phosphorylated CDK1 is degraded during the G2 phase, when DNA damage rapidly decreases. We indicate this occurrence in Eq. (9) by using cell cycle specificity function CSG2 and degradation rate dCDK1y.
In addition to the changes in the amount of intracellular proteins, cell size increases during the cell cycle; such increase plays a crucial role in enabling passage through the cell cycle checkpoint and in regulating the cell cycle. The increase of cell size follows Eq. (11) when no physical interactions occur between cells. However, given that we are interested in studying the effects of physical constraints on cell cycle progression, additional laws and equations are necessary to capture cell–cell interactions and volume exclusivity. These are described in detail in the next section.
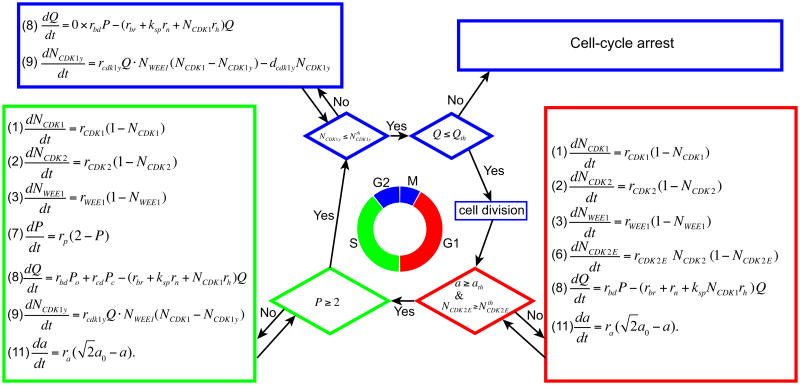
Progression from one phase of the cell cycle to the next is regulated by a series of checkpoints that are implemented using the threshold values of certain variables for each specific phase (Figure 1). They have been chosen such that the duration of each cell cycle phase is within the durations of the G1, S, and G2/M phases reported for many mammalian cells [3,9,27,34]. The G1 phase is completed when cell size a and the amount of CDK2-cyclin E (CDK2-E) complexes are higher than the prescribed threshold values. Both thresholds and the rate constants in the related equations are chosen, so that the duration of the G1 phase is 12 hours under the absence of both CDK2 inhibition and space competition among cells. Under CDK2 inhibition, however, the amount of CDK2-E increases more slowly, thereby prolonging the duration of the G1 phase. If cell size remains below the threshold because of spatial limitations, a cell may be prevented from passing the G1 checkpoint. Either of these cases may lead to an indefinite duration of the G1 phase (called G1 arrest). The S phase takes about 10 hours and ends when cell DNA is doubled. We model this phenomenon by choosing a threshold value of two for DNA replication index P and an appropriate DNA replication rate. The G2/M checkpoint is controlled by two threshold values (Figure 1) that should be reached in sequence. A cell will remain in the G2 phase until the amount of phosphorylated CDK1 reaches a level smaller than the prescribed threshold. This period is used for repairing damaged DNA; such repair, in turn, reduces the amount of phosphorylated CDK1. Once the first threshold is reached, the cell DNA damage index is immediately probed, and if this index is below the threshold, the mother cell will divide. If the DNA damage index is too high, a cell will undergo arrest in the G2/M phase. When no inhibitors are present and the cell can successfully divide, the span of the G2/M phase, typically 2 hours, is determined by the amount of phosphorylated CDK1 at the entrance to this phase. When CDK1 is inhibited from stimulating HR, however, the DNA damage index may remain at a level too high to enable successful passage through the second G2/M threshold. Moreover, if WEE1 is inhibited or its production is suppressed, the cell may enter the G2 phase with a diminished phosphorylated CDK1 that will result in shorter time for DNA repair. During cell division, all proteins are split equally between two daughter cells, except for CDK2-E, which has already been diminished such that its amount in each daughter cell is zero. Cell age is also reset to zero upon cell division. Certain tumor cells and embryonic cells may have much shorter doubling times, and we show in Section 4 how our model can be tuned to match the doubling time for a particular cell line.
Figure 1.
Schematic flowchart of the cell cycle regulation and checkpoints for a control case with no inhibitors.
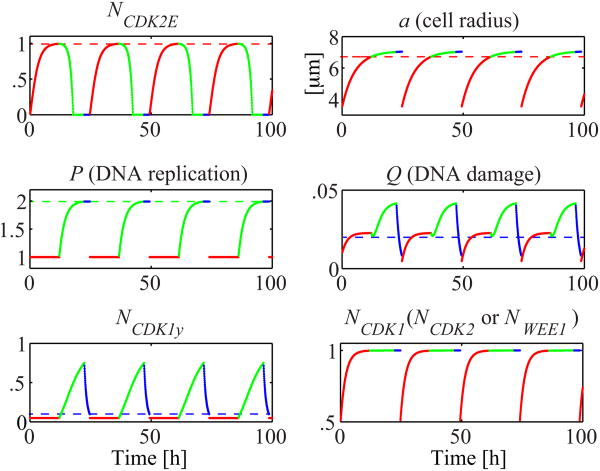
When enough space is available for cells to grow and when neither CDKs is inhibited, all intracellular proteins show cyclic behavior in every cell cycle, and all cells divide at about 24 hours of age. The evolution of the selected model variables over four consecutive cell cycles is shown in Figure 2. CDK2-E increases steadily and reaches the threshold level in G1 phase (red) and starts decay as soon as the cell enters the S phase (green). The majority of cell growth (a) is completed in the G1 phase because reaching a certain cell size is one of the conditions for passing the G1 checkpoint; however, a slight increase in cell size may occur during the other phases. P stays constant during the G1 phase and doubles in the S phase (green) in order to pass the S checkpoint. The main condition for cell division is the reduction of a cell's Q index to a level below the threshold value before the cell enters the M phase. The Q level is low after cell division and increases slightly in the G1 phase, but quickly stabilizes because, in this phase, P is constant but NCdk1 doubles. Q increases again in the S phase, in which DNA is duplicated and damaged with higher rates (rbd and rcd). During the G2 phase, Q rapidly decreases (blue) and reaches its threshold, but continues to decline because the duration of the G2 phase depends on whether the phosphorylated CDK1 falls below its threshold value. NCDK1y steadily rises during the S phase with increasing level of Q; in the G2 phase, NCDK1y rapidly decreases with Q and due to its own degradation. Both Q and NCDK1y fall below their thresholds, and the G2/M phase ends with cell division. The CDK1, CDK2, and WEE1 almost reach their saturation levels during the G1 phase (red) and then change only minimally during the rest of the cell cycle. The four discontinuity points in the graphs in Figure 2 represent the times of cell division.
Figure 2.
Evolution of the cell cycle regulation variables in the case of no spatial interactions between the cells and without cell cycle inhibitors. Dashed lines indicate the threshold levels and color codes show the cell cycle phases: G1 (red), S (green), and G2/M (blue). Governing equations are listed in Figure 1, and parameter values are: rCDK1 = 0.48 h-1; rCDK2 = 0.48 h-1; rWEE1 = 0.48 h-1 rCDK2E = 0.48 h-1; rbd = 0.01 h-1; rcd = 0.015 h-1; rbr = 0.3 h-1; rn = 0.1 h-1; rh = 0.4 h-1; ks = 0.1; rCDK1y = 3.84 h-1; dCDK1y = 1.08 h-1; ra = 0.19 μm/h; rp = 0.44 h-1; ath = 0.95×21/2×a0; NthCDK2E = 0.99; NthCDK1y = 0.1; and Qth = 0.02. All inhibition parameters from Table 4 are set to zero here, and the cell cycle specificity function CST values are explicitly assigned in Figure 1.
2.2 Cell growth and migration
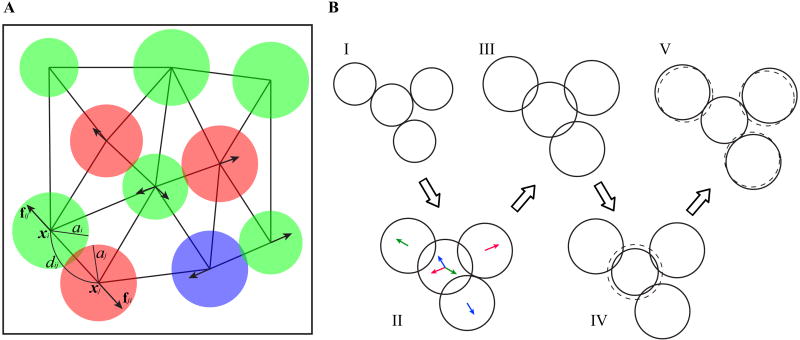
All cells, regardless of whether they are cultured in vitro or grown in vivo, inevitably interact with neighboring cells and with the environment. We recognize the importance of such spatial interactions and introduce repulsive forces between nearby cells as a mechanism for maintaining cell volume exclusivity. This mechanism prevents cell overlap during growth and migration. Among the cell physical properties included in our model are cell position, cell radius, repulsive forces between neighboring cells (identified by the nearest neighbor search), orientation of cell division, and direction and speed of cell migration. Figure 3A shows a small cluster of cells, together with the identified neighborhood relationship and selected physical properties.
Figure 3.
Model physical features. A. Each individual cell is characterized by its position xi, and a radius ai. dij denotes the physical distance between cells xi and xj. When cells overlap the repulsive forces fij (arrows) are exerted to restore volume exclusivity. B. Diagrams (I)–(V) illustrate the algorithm restoring volume exclusivity between four overlapping cells: the consecutive diagrams show how cell sizes evolve in one time step to ensure cell growth and volume exclusivity. The depicted overlapped sizes are greatly exaggerated for visual purposes. The initial cell configuration is shown in (I). When all cell sizes increase, following Eq. (11), the cells overlap and repulsive forces between them are activated (II). Arrows with matching colors indicate pairs of repulsive forces that will result in cell relocation along the corresponding force direction; note, that the middle cells experience three repulsive forces, and thus will be moved along the averaged direction—in the presented case this relocation is minimal. As a result, the overlapping sizes have been reduced but not eliminated (III). The middle cell is surrounded; therefore, following step (iv) of the algorithm, its size needs to be reduced (IV). The dashed circle in (IV) indicates cell size before reduction. The three other cells are not surrounded, thus according to step (ii′) of the algorithm, they will be pushed along the acting repulsive forces, away from the middle cell, without reducing their sizes (V). The dashed circles in (V) indicate previous locations of cells. The procedure described in diagrams (I)–(V) represents one time step in our simulation.
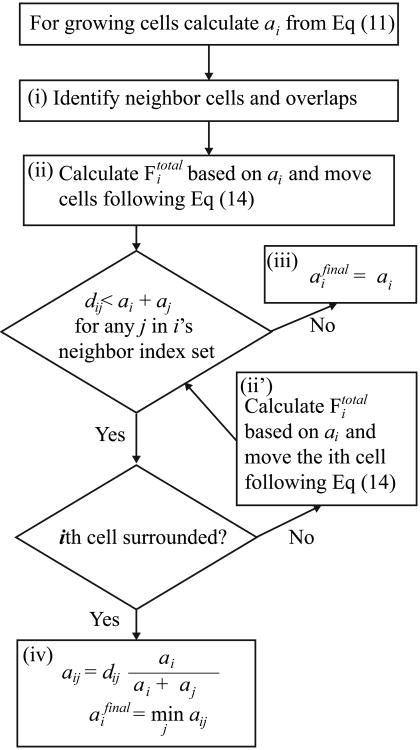
The cell size growth equation (Eq. (11)) describes a linear increase in cell radius at a constant rate ra with an imposed maximum cell size. We intend to model the in vitro cell culture, wherein cells are confined to a predetermined domain (such as a Petri dish) and compete for space to grow while interacting with one another. Given that cell–cell overlap is inevitable when Eq. (11) is applied to each cell independently, introducing additional mechanisms is necessary to resolve potential issues in cell volume exclusivity. First, to accommodate two nonoverlapping daughter cells within the space left by the mother cell just after its division, we increase cell size during a mother cell's lifespan from a0/21/2 (when the cell is born) to 21/2a0 (just before cytokinesis), where the cell reference radius is denoted by a0. Moreover, a straightforward numerical implementation of Eq. (11) for each individual cell (ai = a(t + Δt)), without consideration of the presence of its neighbors, may cause tiny overlaps between the cells (i.e., ai + aj > dij), as depicted in Figure 3A. In such a case, we deploy an algorithm that restores volume exclusivity for each cell (depicted in Figure 3B and summarized in Figure 4) as follows: (i) the nearest neighbor search is executed to determine cells with mutually infringed boundaries by comparing the distance dij between two cell centers and the sum of their corresponding radii. (ii) When a breach occurs, the repulsive forces are applied to eliminate or reduce the infringed volume. These forces are modeled using the linear elasticity formula (Eq. (12)). When a cell has multiple overlaps, more than one repulsive force may arise in different directions (including opposite directions), and cell relocation (Eq. (14)) follows the total repulsive force (i.e., Fi = Fitotal). (iii) In many cases, this is sufficient to resolve volume exclusivity issues (aifinal = ai in Figure 4(iii)). In some cases, however, a particular cell continues to exhibit overlaps, which may happen when the cell has more than one overlapping neighbor. In such a situation, we first examine whether we can move the cell in a direction that reduces overlaps. The absence of this direction is referred to as a surrounded case. (iv) If the cell is surrounded, we inspect all overlapping pairs and calculate their weighed reduced radii aij, and take the minimum over all overlapping pairs as the final radius (aifinal in Figure 4(iv)). This approach eliminates all overlaps. (ii′) If the cell is not surrounded, we reduce cell–cell overlaps by calculating the total repulsive force acting on that cell and move it along the direction of the force. Step (ii′) should be repeated until either the cell is surrounded or all the overlaps are resolved. The concept of the surrounded cell and step (ii′) are introduced to avoid compromising the growth rate of outermost cells when cells form clusters. In this algorithm, the calculated aifinal is not smaller than the cell radius in the previous time step.
Figure 4.
A comprehensive algorithm for cell radius growth ensuring volume exclusivity.
When cells overlap, equal but opposite repulsive forces are exchanged between two overlapping cells. Force magnitude is proportional to breached distance, with proportionality constant k (Eq. (12)). If a cell (with index i) overlaps with multiple neighbors, the total repulsive force exerted on it is calculated as in Eq. (13), where j runs over the index set Ni of all the neighbors of the ith cell. For the cell center, xi, its location is updated following Eq. (14) using the total repulsive force from Eq. (13), Fi = Fitotal, and η, which denotes the linear drag coefficient. In numerical calculations with a discrete time step size Δt, the moving distance is equal to FitotalΔt/η. We choose k, η, and Δt so that they satisfy 2kΔt = η, which is the condition imposed on two growing daughter cells placed right next to each other. This condition is necessary for the cells to increase their size precisely in accordance with Eq. (11) without any overlap; such an increase is achieved because the cells push each other and grow in a precisely orchestrated manner. In this case, volume exclusivity is realized at step (ii) of the algorithm shown in Figure 4, and no radius reduction (iv) is necessary. This choice of parameters generally ensures stable numerical implementation and warrants maximal volume exclusivity among all overlapping cells after the repulsive forces in step (ii) are applied.
Figure 3B shows an example of how to preserve volume exclusivity while the neighboring cells are growing. Diagram (I) shows the initial cell configuration; diagrams (II)–(IV) show the intermediate steps, and diagram (V) is the final configuration. The overlapping areas are greatly exaggerated to demonstrate our algorithm. Four neighboring cells (I) increase their sizes following Eq. (11), which causes cell overlapping and activation of repulsive forces (II). Cell relocation, that follows the repulsive forces, reduces but does not eliminate the overlaps (III). The middle cell is surrounded; therefore, following step (iv) of the above algorithm, the middle cell radius is reduced. Since the other three cells are not surrounded, they are pushed away from the middle cell following step (ii′) of the algorithm without reducing their sizes.
In our model, the cells can also actively move in a random fashion. The voluntary movement of the ith cell is implemented by applying a motility force, Fim, through Eq. (14) (i.e., Fi = Fim). The motility force Fim is a randomly chosen vector whose magnitude is selected from a uniform distribution between zero and a predefined maximum (b in Eq. (15)) We set the magnitude of a typical repulsive force m1 (m1=2kΔa, where Δa is a typical radius increment for Δt during the time at which a shows linear growth) as the reference value. By setting 100m1 as the predefined maximum (b = 100m1), we qualitatively reproduce the behavior of highly motile cells (as described in literature, e.g., in [27]). We refer to this as a “motility of 100” or m100. At every time step, the motility force is assigned to each cell and the cells move in accordance with the resultant velocity determined by Eq. (14). However, when this velocity is applied with the previously chosen time step Δt, it may generate a large relocation distance and significant overlaps with nearby cells. When the repulsive forces are reapplied in order to prevent cell overlap they may become a source of numerical instability. Therefore, we separate voluntary movements from relocation during cell growth and use fractionated time steps to prevent such instabilities. That is, once cell size and location are settled by the algorithm in Figure 4, the forces for voluntary movements are generated and time step Δt is divided into a predefined number of smaller time steps with empirically chosen fractions (the fractionated time step). The cell locations are then iteratively updated through the alternate application of the motility and repulsive forces (with the fractionated time step and Δt, respectively) to account for both cell movement and cell overlap prevention.
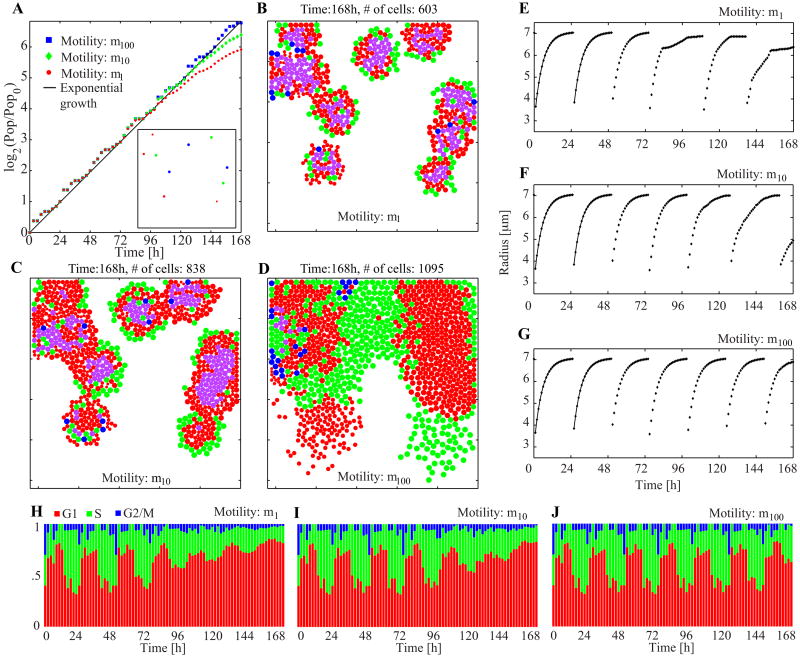
To illustrate the different collective behaviors, we consider three cell motility values (m1, m10, m100) and simulate growing cell colonies starting with identical initial conditions shown in the inset of Figure 5A. Each simulation is carried out in a representative 500 × 500 μm2 domain that corresponds to a typical image recording size of cell culture under a microscope [25]. The population-doubling curves normalized by the initial cell number and the snapshots taken at the end of each simulation (at 168 hours) are presented in Figure 5A–D. As expected, cells characterized by lower motility form tight clusters, while high motility cells spread freely and cover more than half of the available space (see Video 1). Most of the inner cells in the clusters also grow more slowly because they detect space limitations, and some stay in the G1 phase for more than 24 hours (denoted in magenta in Figure 5B–D, 38% for m1, 26% for m10, and negligible for m100). Also, the total final populations for all three cases are considerably different: m100 cell population is almost twice as big as the m1 population.
Figure 5.
Collective behavior and spatial organization of cells with different motilities. A. Population-doubling curves with the inset snapshot of the common initial condition at the time zero. B–D. Final snapshots from three simulations with different motilities. The video recording of these three simulations is shown in Video 1 in the Supplementary material. The initial population in the culture is ten cells and identical initial conditions are used in all three simulations. Colors are used to show the cell cycle phases: G1 (red), G1 older than 24 hours (magenta), S (green), and G2/M (blue). The coloration corresponding to the cell cycle phases follows the experimental FUCCI (fluorescent ubiquitination-based cell cycle indicator) method [26]. E–G. Traces of cell size from one particular cell (index nine out of ten). The solid lines in the first two cycles show the analytic solution of Eq. (11). H–J. Population cell cycle distributions. All cell cycle specific parameters are listed in Figure 2. Physical parameters used: k = 5 [k] and η = 1 h· [k]; [k] is an arbitrary unit for k.
To inspect in detail the cell cycle progression on an individual-cell level, we traced the same cell in each of the three simulations, and reported its size in Figure 5E–G. In all three cases cell size growth is identical during the first three cell cycles (i.e., until about 72 hours), but the cycles beyond this period exhibit substantial differences. At m1 (Figure 5E), the cell growth during the fourth cell cycle shows a significant slowdown because the cell is surrounded by the neighboring cells. However, no significant deviation from one cell cycle to another is observed at m100 (Figure 5G), and the evolution of cell size occurs strictly in accordance with Eq. (11). Similar trend can be noticed at the population level (Figure 5H–J). The observed oscillations in cell cycle phase distribution occur because (i) the cells' doubling times are assumed identical when no external limitations exist; (ii) two daughter cells are born simultaneously and are thus synchronized unless external influence is present; (iii) each cell in the M phase (blue) gives birth to two cells in the G1 phase (red). Thus, at m100, oscillations are present throughout the entire simulation since no space limitation occurs until confluence is reached. At lower cell motility, the oscillations disappear after several cell cycles because cell synchronization is broken as the growth rate of cell size slows down for the cells located inside the clusters: at around 80 hours (m1) and 110 hours (m10). This very closely corresponds to the times at which the graphs in Figure 5E and 5F deviate from the initial cell size growth dynamics.
3. Results
To investigate the effects of cell cycle inhibitors on cell population growth, we consider both intrinsic and extrinsic factors. These include the dynamics of intracellular factors that regulate the duration of each phase of the cell cycle in every individual cell, physical interactions between neighboring cells, and cell competition for space. In the previous section, we also showed that motility, as a property of each individual cell, influences the spatial organization of cell colonies at the population level. Thus, we want to examine whether the efficacy of cell cycle inhibitors is altered by emerging group traits. First, we present a control case in which no cell cycle inhibitors are used, the cells are quite motile, and they interact with one another. Initiating the simulation with a small number of cells enables us to observe the long-term evolution of growing cell populations until spatial confluence is reached. Second, we examine the effects of CDK1 and CDK2 inhibitors (separately and in combination) in comparison with those of the control. We again choose high cell motility to distinguish the effects of growth inhibition due to cell–cell interactions from those of the cell cycle inhibitors. Finally, we test the combined effects of the cell cycle inhibitors and cell–cell physical interactions on cell population growth by integrating various cell motilities and different cell cycle inhibitors.
3.1 Cell colony growth without cell cycle inhibitors
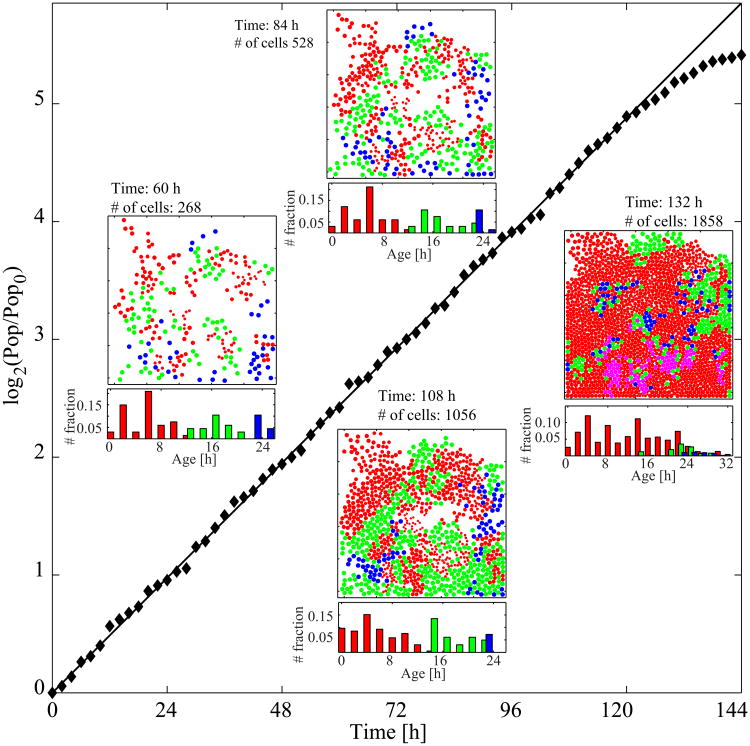
The simulation for the control case is initiated with 50 cells, which constitute about 2.5% of the maximum population capacity of the chosen domain size (500 × 500 μm2). The cell locations within the domain are randomly assigned. The age of each cell is drawn from a uniform distribution between 0 and 24 hours, which determines the values of all cell cycle-related variables (a, NCDK1, NCDK2, NWEE1, NCDK2E, NCDK1y, Q, and P) in accordance with the graphs in Figure 2. The chosen initial cell age also specifies the current phase of the cell cycle. Given the predefined durations of each cell cycle phase (12:10:2 hours for G1, S, and G2/M, respectively) and the random selection of cell ages, the cell population ratios of the G1, S, and G2/M phases are expected to be roughly 50%:42%:8% at the beginning of the simulation (such initial population ratios are frequently observed in laboratory experiments [34,35,36], but we show in Section 4 how our model can be tuned to other cell cycle phase distributions). The simulation is carried out over 144 hours until the growing cell colony reaches 94% of confluence. The population-doubling curve normalized by the initial number of cells in the log scale (diamonds) is shown in Figure 6. The straight solid line indicates the exponential population growth with a rate of (ln 2) / 24 per hour. The simulated population growth strictly occurs along this line for about 110 hours. Subsequently, it begins to plateau because cell competition for space becomes a limiting factor. The four inset figures show the simulation snapshots taken at 60, 84, 108, and 132 hours, as well as the corresponding cell age distributions. We assume that nutrients are abundant, and because the cells are highly motile, there is enough space for all the cells to grow in strict accordance with the graphs in Figure 2. With time, however, the cells start competing for space, and population growth slows down because some cells do not satisfy the required G1 checkpoint size (a) condition within the intended 12 hours of G1 duration. As the available space is diminished, therefore, an increasing number of cells become trapped in the G1 phase (the G1-arrested red cells dominate in the 132-hour snapshot); some of these cells have spent more than 24 hours in this phase (indicated in magenta in Figure 6, the 132-hour snapshot).
Figure 6.
Cell colony growth in the control case without inhibitors. A normalized population-doubling curve with four snapshots of the cell culture (domain size, 500×500 μm2; cell motility, m100) and corresponding cell age histograms. The video recording of simulation snapshots with the corresponding age histogram is shown in Video 2 in the Supplementary material. Cells are color-coded to show: G1 phase (red), G1 phase duration of more than 24 hours (magenta), S phase (green), G2/M phase (blue). Parameter values are the same as in Figure 5.
The four age distributions in Figure 6 confirm this trend. In the first two snapshots, the phase-wise age distributions are well separated and no cell is older than 25 hours, indicating that all the cells progress through the cell cycle without delay. At 108 hours, a small population of cells still in the G1 phase (red) but older than 12 hours begin to emerge (less than 1% of the total 625 cells in the G1 phase), implying that these cells cannot transition from the G1 to the S phase in a timely manner. At 132 hours, a large population of cells remain in the G1 phase for more than 12 hours (52% of the total 1576 cells in the G1 phase) with a widely spread age distribution (0 to 32 hours). This distribution is nearly threefold that seen in the typical G1 phase duration confirming the red cell domination observed in the 132-hour snapshot in Figure 6.
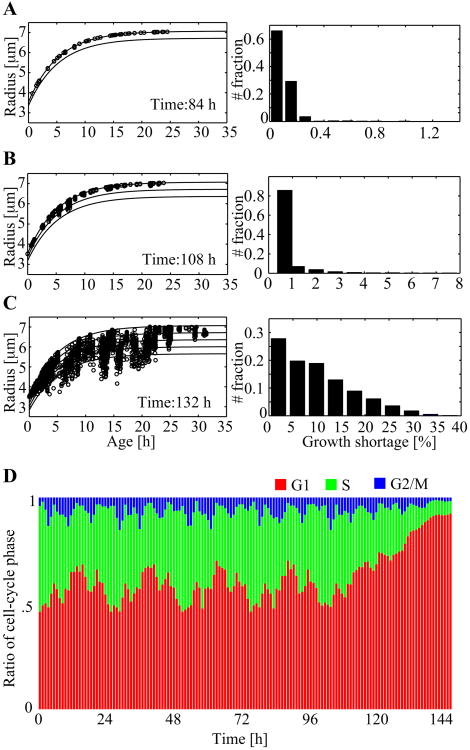
To look more closely into the effects of spatial competition, we consider the relationship between cell size (a) and cell age (Figure 7A–C) at three different time points. The top solid curve in each graph in the left column of Figure 7A–C is the plot of the analytic solution of Eq. (11). This plot dictates the expected increase in cell size over time when no spatial limitations exist (the subsequent lower lines are progressively decreasing percentile curves in 5% decrements). Each circle represents an individual cell in the culture, indicating its actual age (x-axis) and radius (y-axis). The graphs in the right column of the figure show the histograms of growth shortage, which is defined as the ratio of the difference between the expected and actual sizes normalized by the expected size. The data at 84 hours (Figure 7A) show that all the cells exhibit size growth in close accordance with the top growth chart (the analytic solution of Eq. (11)), and that growth shortage is very low (more than 98%) of cells stay within 99.5% of the expected size). As the population continues to increase over time, the competition for space becomes significant. At 108 hours (Figure 7B), several data points diverge from the analytic solution graph, and the corresponding histogram shows some cells with a growth shortage higher than 5%. However, no cell grows behind the expected size by more than 8%. The graph at 132 hours (Figure 7C) shows a considerably different situation. The cell size versus age data significantly deviate from the analytic solution, and the maximum growth shortage reaches 35%, with more than the half of the cells showing the growth shortage of 10% or higher.
Figure 7.
A-C. Cell growth charts and growth shortage (i.e., |aexpect - aactual| / aexpect, where the aexpect value is determined by Eq. (11).) histogram at three different times. Individual cell data points are shown by circles and the analytic solution for cell radius (Eq. (11)) are the top solid curves. Lower solid curves are progressively decreasing percentile curves in 5% decrements. D. The population cell-cycle distributions over the 144 hours of simulation.
Figure 7D illustrates the evolution of the cell cycle phase distribution recorded every hour over 144 hours. Throughout the entire simulation, the G2/M phase ratio remains small (1–15%). The characteristic G1-phase oscillations, visible for about 100 hours, reconfirm that most of the cells freely grow (and further divide). The change in the G1 phase distribution pattern that occurs at around 120 hours and the subsequent G1 phase domination are also consistent with the plateau in the population-doubling curve in Figure 6. These phenomena are due to the space limitations that arise as the computational culture becomes highly confluent. At the end of this simulation, the G1-phase ratio reaches 92%, reaffirming G1 phase cell arrest.
3.2 Effects of CDK1 and CDK2 inhibitors on cell colony growth
Here, we present the results of incorporating the CDK1 and CDK2 inhibitors to the model. We assume that the inhibitors act on all the cells during the entire simulation, i.e., their effects are temporally and spatially uniform. This assumption is consistent with the clonogenic assay setup, where the medium in which the cells are grown is periodically changed to keep the nutrients and the therapeutic agent uniformly dissolved and available to all the cells in the culture. We also assume that the cells in these simulations are highly motile (m100) to distinguish between the effects of cell cycle arrest due to CDK inhibition and those of growth arrest due to spatial limitations. CDK2 inhibition is expected to cause cell cycle arrest at the G1 phase because the inhibited CDK2 slows down the CDK2-E buildup that is crucial to enabling passage through the G1 checkpoint. CDK1 inhibition is expected to cause cell arrest at the G2/M checkpoint because the low amount of uninhibited CDK1 diminishes HR stimulation, which in turn may result in cell entry into the M phase with a DNA damage index that is too high to allow for cell reproduction.
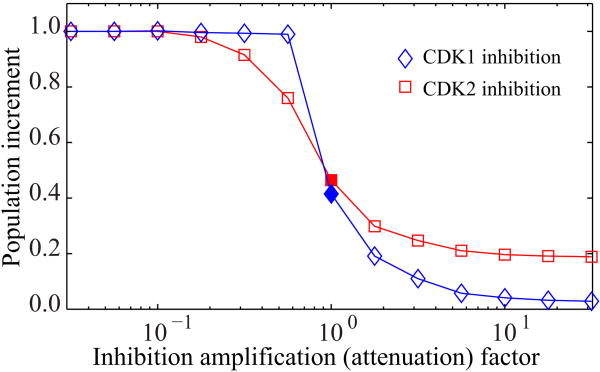
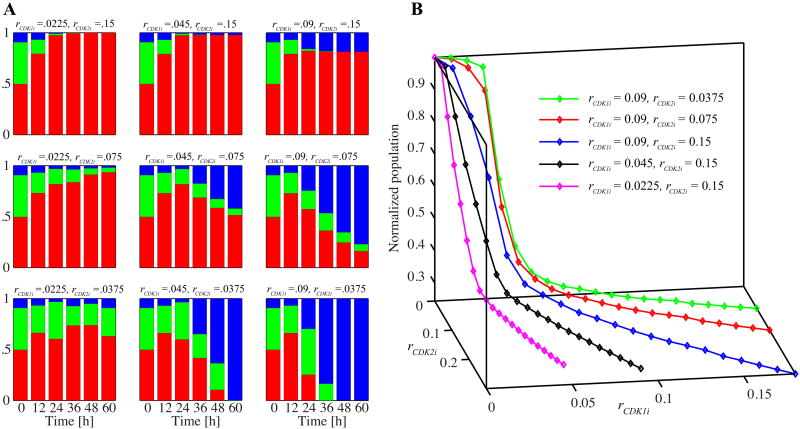
The effectiveness of the inhibitors as agents that suppress population growth depends on the choice of inhibition parameters (rCDK1i and rCDK2i). We examine the inhibition response curves of each inhibitor by comparing the relative increment in population size at 48 hours (Figure 8). The x-axis values represent the inhibition amplification factor; that is, the inhibition parameters of CDK1 and CDK2 normalized by the chosen rCDK1i and rCDK2i values (in the caption of Figure 8), respectively. The y-axis represents the increment in inhibited population with respect to the increment in control population reached at 48 hours. The initial cell configuration and cell age distribution are identical in all cases (with and without inhibitors), and the inhibitors are applied at the beginning of the simulation. Both curves show a decreasing logistic function that levels off at the top and bottom of the graphs. Small values of CDK1 and CDK2 inhibition parameters impose no noticeable effects on cell population growth. With high inhibition parameters, cell population growth significantly diminishes in both cases, but the final effects differ. With CDK1 inhibition, nearly complete termination of population growth is observed. Conversely, very strong CDK2 inhibition results in nonnegligible population growth (about 20%). This result is attributed to the fact that CDK2 inhibition cannot prevent cells from completing the first cell cycle and proliferating when cells at the beginning of simulations have already passed the G1 phase, as is the case for about half of the cells in our simulation. Therefore, at least 200 more cells would have born for 48 hours. CDK1 inhibition can stop some of the cells at the G2/M checkpoint and prevent them from completing the first proliferation. This prevention accounts for the differences at the population increment levels for the large amplification factors in Figure 8. We choose rCDK1i and rCDK2i around the 50% level of population increase as our basic parameters (the chosen values in the caption of Figure 8), and use them to analyze the effects of the CDK inhibitors.
Figure 8.
Inhibition response curves for CDK1 and CDK2 inhibitors. Each simulation starts with 400 cells with the same initial configuration and age distribution. The solid diamond and square corresponding to the amplification factor of one indicate the simulation results with the parameters rCDK1i = 0.045 h-1 and rCDK2i = 0.075 h-1, respectively.
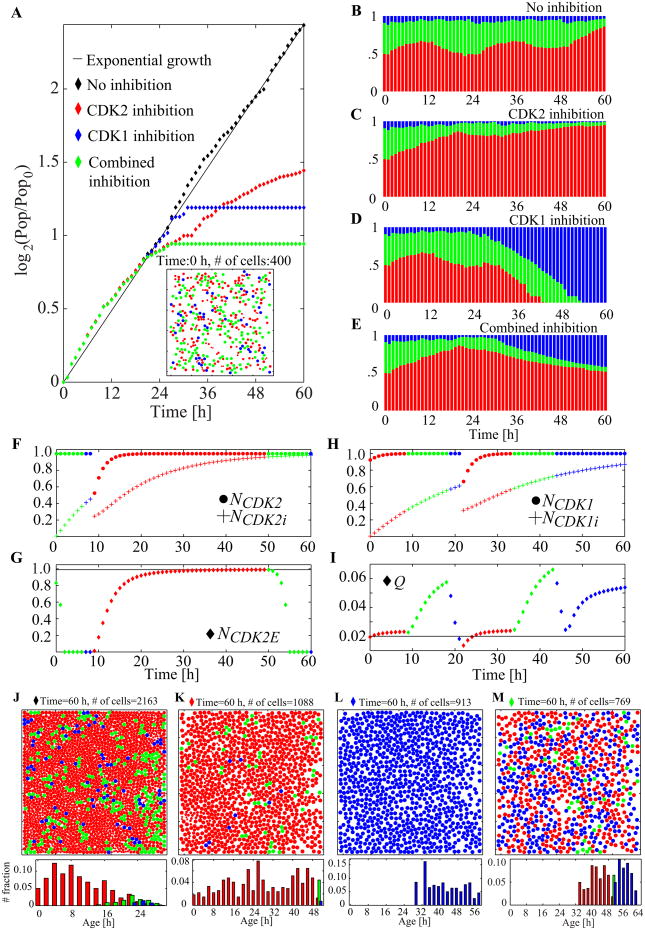
Figure 9 depicts the detailed analysis of four different simulations: scenarios without any treatment (control), with CDK2 inhibition, with CDK1 inhibition, and with the CDK1 and CDK2 combined inhibition. All simulations start with 400 cells (about 20% of confluence) and identical initial cell configurations (inset of Figure 9A; the initial conditions are set by the method used in the simulation in Figure 6). All the inhibitors are effective at the start of the simulation (from time 0). Inhibition parameters rCDK1i and rCDK2i are chosen as presented in Figure 8. The corresponding population growth curves in log scale over 60 hours for four cases (control, CDK2, CDK1, or combined inhibition) are shown in Figure 9A. The solid diagonal line indicates the exponential population growth; during the entire simulation, the control cells (black diamonds) exhibit an increase that follows the exponential population growth line. With our chosen parameters, the cell culture subjected to CDK2 inhibition (red diamonds) shows 50.3%) of the control population at the end of the simulation; the cell culture subjected to CDK1 inhibition (blue diamonds) reaches 42.2% of the control population. When the inhibitors are applied in combination (green diamonds), the final population size amounts to only 35% of the control size.
Figure 9.
The effects of CDKs inhibitors applied separately and in combination. A. The normalized population-doubling curves for all four cases with the inset snapshot of the common initial condition at the time zero (cell motility, m100, rCDK1i = 0.045 h-1, rCDK2i = 0.075 h-1; domain size, 500 × 500 μm2). Cells are color-coded to show: G1 phase (red), S phase (green), G2/M phase (blue). B–E. The population cell cycle distributions collected over 60 hours of simulations for all four cases. F–G. Evolution of the most relevant cell cycle regulation variables for the CDK2 inhibition. Colors correspond to the cell cycle phases. H–I. Evolution of the most relevant cell cycle regulation variables for the CDK1 inhibition. J–L. Snapshots taken at the end of each simulation and the corresponding phase-wise cell-age histograms. See Video 3 in the Supplementary material for the animated snapshots from each simulation. All the parameters identical as in Figure 6, additionally rCDK1i = 0.045 h-1 and rCDK2i = 0.075 h-1.
Although the populations at the end of each simulation differ considerably (Figure 9A), all four cases show almost identical growth for up to 22 hours; that is, for a period corresponding roughly to one cell cycle. This result is attributed to each inhibition taking place at a certain point in the cell cycle (at the cell cycle checkpoint); the cells need to reach this point for inhibition to have an effect. Further, the inhibitors become more effective after the first cell division is completed and the daughter cells start a new cell cycle without preaccumulated molecules. The CDK1-inhibited cell population reaches a sudden plateau, whereas the CDK2-inhibited cell culture continues to increase gradually, although at a much slower overall speed. This difference is a consequence of the distinct dynamics of each of the cell cycle checkpoints. The conditions in the G1 checkpoint are continuously tested for each cell in the G1 phase; thus, a cell has multiple chances to pass this checkpoint. By contrast, DNA damage is inspected only once in the M phase, preventing a second opportunity for cells to pass the G2/M checkpoint. When the inhibitors are combined, the population growth curve also reaches a plateau. However, this combined effect is subadditively synergistic, according to the fractional product concept [37], because the remaining population at a final time of 60 hours, (i.e., 35%) is larger than 21.2% (50.3% of 42.2%) of the control population. Since these two inhibitor treatments in our simulation cause cell cycle arrest at different phases, we do not expect super-additive synergy. The CDK2 inhibition that holds cells in the G1 phase can deprive cells of the opportunity to be arrested at the G2/M phase because of CDK1 inhibition. Nonetheless, given the fact that each inhibition allows for the completion of one cell cycle, our observations indicate that the maximal inhibition effect would be the termination of population growth before it is doubled.
The population cell cycle distributions of each of the four cases are shown in Figures 9B–E. The patterns are very similar during the first 12 hours, confirming that a lag time also exists in the cell cycle distributions before the effects of the inhibitors become observable. After this initial period, however, the population response is very different. In the control group, the cell cycle distributions exhibit two periodic fluctuations, indicating that most of the cells complete their cell cycles at least twice. This finding also confirms the exponential growth in cell population size shown in Figure 9A. Nevertheless, close inspection of the graph of cell cycle phase distribution (Figure 9B) at the end of the simulation indicates the emergent effects of spatial limitations (an increased population of G1 red cells), suggesting that the population-doubling graph in Figure 9A would deviate from the diagonal line at a longer simulation. By contrast, the three remaining simulations show no oscillations in cell cycle distribution. The CDK2 and CDK1 inhibitor treatments result in G1 and G2/M arrests, respectively (Figures 9C and 9D). Combining the inhibitors causes a mixed effect: cell population is roughly halved between the G1 and G2/M phases at 60 hours (Figure 9E). Over the final 24 hours, however, the observed trend is of a decreasing G1 population and an increasing G2/M population because the chosen CDK2 inhibition parameter enables the cells to pass the G1 checkpoint slowly and move on to the S and G2/M phases. Upon reaching the G2/M phase, the cells are permanently arrested, thereby keeping the population size constant. We expect the population ratio G1:G2/M to stabilize at around 50:50 if the simulation is run for an extended period. For the graphs in Figures 9F–G and Figures 9H–I, we choose two particular cells (one of each set of graphs) that fail to complete two full cell cycles. We then record the evolution of several specific intracellular variables. Figures 9F and 9G show three variables relevant to CDK2 inhibition (NCDK2, NCDK2i, and NCDK2E), and Figures 9H and I show three variables relevant to CDK1 inhibition (NCDk1, NCDK1i, and Q). The amount of inhibited CDK2 (NCDK2i, plus signs in Figure 9F) reaches more than 50%) of the total CDK2 amount soon after the beginning of the second cell cycle. This increase results in a slower progression of NCDK2E synthesis (Figure 9G). Thus, the cell reaches the threshold level (horizontal line) in 38 hours (it should take 12 hours normally) and transitions into the S phase. This result explains the lack of oscillation in the population cell cycle distributions shown in Figure 9C. Conversely, even if both the total CDK1 and the inhibited CDK1 (Figure 9H) show dynamics similar to that of CDK2 (Figure 9F) during the second cycle, the progression through the cell cycle reaches a phase that differs from that observed in CDK2 inhibition. The high amount of inhibited CDK1 does not prevent cell progression from the G1 to the S phase and from the S to the M phase. Nevertheless, because the level of DNA damage steadily increases to a level higher than that achieved in the first cycle over time (Figure 9I), the cells fail to reduce the damage below the threshold during the DNA repair phase in the second cycle. This failure causes cell arrest in the G2/M phase (Figure 9I). Figures 9J–M show the final snapshots from each simulation, with the corresponding phase-wise age distributions. The control case (Figure 9J) and the CDK2 inhibition case (Figure 9K) both show G1 phase (red) cell domination, but for different reasons. For the control case, the G1 phase arrest of cells is caused by spatial limitations, whereas for CDK2 inhibition case, such arrest is caused by slow CDK2-E synthesis. These phenomena are initiated at different times, as shown in the G1-phase age histograms. With CDK2 inhibition, most of the cells in the G1 phase are considerably older than those in the control case, indicating that the cells become G1 arrested early in the simulation and remain arrested for a long period. By contrast, the majority of the G1-phase cells in the control case are young but more densely packed, preventing them from progressing through their cell cycles. The complete G2/M phase (blue) cell domination shown in Figure 9L starts at 54 hours (shown in Figure 9D). This result is attributed to the implementation of G2/M arrest as a permanent cell arrest (not a prolonged process in a phase) and the fact that our choice of CDK1 inhibition parameter is high enough to allow only two cell divisions at most. Figure 9M shows the final simulation snapshot (at 60 hours) of the cell colony exposed to the combined inhibitors. Almost half of the cells are in the G1 phase (red), and the other half are in the G2/M phase (blue), with some cells occasionally found in the S phase (green). Given that our choice of parameter for CDK2 inhibition continues gradually to enable cells to escape from the G1 phase, we can expect slowly decreasing G1-phase cells. Nonetheless, because the G2/M phase-arrest is permanent, the entire population does not increase, as confirmed by the plateau in the population-doubling curve (Figure 9A).
3.3 Inhibitor efficacy depending on cell motility
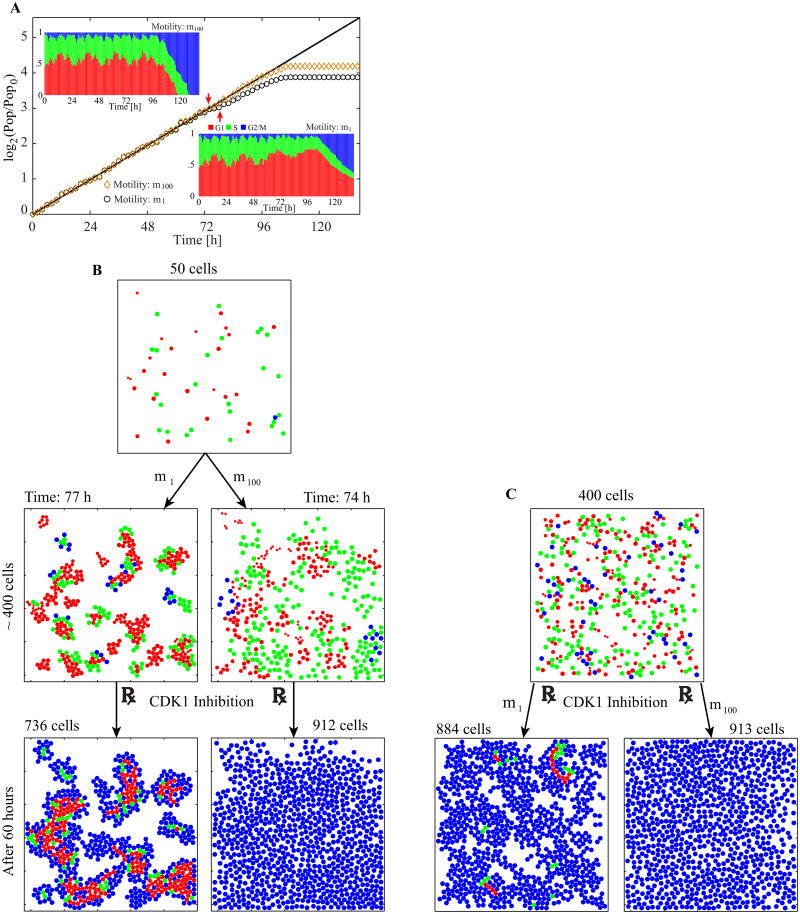
Thus far, we have investigated CDK inhibition in conjunction with high cell motility (m100) only. As shown in the cell growth and migration section, low cell motility leads to local overcrowding that influences cell cycle progression; our intention is to distinguish interruptions of the cell cycle due to CDK inhibitors from the overcrowding effects. In the previous section we demonstrate that cell arrest at different cell cycle phases is not necessarily synergistically super-additive, suggesting that the low cell motility in our model can alter the effects of CDK1 or CDK2 inhibitors. To explore this idea further, we compare the results of simulations in which two different motilities (low m1 and high m100) are used in conjunction with single and combined CDK inhibitors.
We aim to examine how the CDK inhibitors affect cells that have already formed clusters (as shown in Figure 5); thus, we start our simulations with 50 cells and allow these to grow without exposure to any inhibitors until the population reaches 400 cells. The cells with motilities of m100 and m1 take 74 and 77 hours, respectively, to reach the population of 400 (Figure 10B, middle panels). This waiting time enables the m1 cells to form small but tight clusters, and the m100 cells to spread across the computational domain. Such a scenario is typical for in vitro experiments that are always preceded by a period at which cells are allowed to attach and grow in fresh media. After this incubation time, the action of a chosen inhibitor is initiated (red arrows along the population-doubling curves in Figures 10A, also in Figures 11A and 11D), and the simulation is run for additional 60 hours. This extension enables comparison with the results in the previous section, in which each simulation is initiated with 400 cells and run for 60 hours.
Figure 10.
The effects of cell motility (m100 vs. m1) and cluster formation on CDK1 inhibition. A. Population-doubling curves of cells with motility m1 (black circles) and m100 (orange diamonds) with distributions of cell cycle phases (insets). Initially, cells are grown without inhibitors until they reach a population of 400 cells, then CDK1 inhibition is applied (74 hours for m100 and 77 hours for m1, shown by red arrows). B. Selected snapshots from both simulations from A. See Video 4 in the Supplementary material for the animated snapshots from each simulation. C. Two simulations starting with 400 cells of motility, either m1 or m100, grown for an additional 60 hours under the CDK1 inhibition.
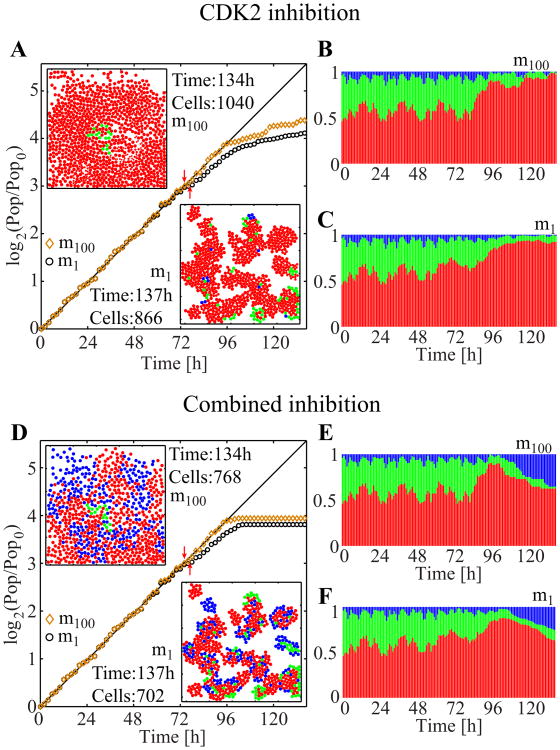
Figure 11.
CDK2 inhibition and combined inhibitions with the motility m100 or m1. A. Population-doubling curves with snapshots at the end of each simulation. Two red arrows indicate when the CDK2 inhibition was initiated for each case (i.e., at 74 hours for the motility m100, and at 77 hours for the motility m1). B–C. The corresponding population cell cycle distributions. D. Population-doubling curves with snapshots at the end of each simulation. Two red arrows indicate when the combined inhibition started for each case (i.e., at 74 hours for the motility m100, and at 77 hours for the motility m1). E–F. The corresponding population cell cycle distributions.
First, we investigate the effect of CDK1 inhibition (Figure 10). In both cases (m1 and m100), population size steadily increases for about 20 hours after the addition of the inhibitors. However, the population growth of m1 is slower, indicating that not all cells actively progress through their cell cycles and divide. Both populations reach (different) plateaus at about the same time (Figure 10A), but a clear distinction is observed in spatial distributions and phase structures, as shown in the final simulation snapshots (Figure 10B, bottom two panels) and in the cell cycle distribution (insets in Figure 10A). While the m100 cells are all arrested in the G2/M phase (similar to that depicted in Figure 9L), the m1 cells also exist in both the G1 and S phases. These cells are located inside the clusters, indicating that they are still in the G1 and S phases because of spatial limitations; they do not progress through their cell cycles and avoid the cell cycle arrest effect of CDK1 inhibition. Only the outer cells are arrested at the G2/M phase by CDK1 inhibition. The last 60 hours in the cell cycle distribution graphs in the insets of Figure 10A show patterns similar to those in Figures 9D and 9E, where the CDK1 and combined inhibitor treatments are applied to the m100 cells. The graphs in Figures 9D and the upper left inset of Figure 10A are similar because of the way both computational experiments are designed. The similarities in Figures 9E and the lower right inset of Figure 10A indicate that the low cell motility plays a role that is analogous to that of CDK2 inhibition through the confinement of cells in the G1 phase arrest. When the simulations are run without incubation time, that is, when the inhibitors are applied before the cells form clusters, no noticeable difference in inhibition efficacy was observed between the results obtained after 60 hours of both simulations (Figure 10C). In these cases, almost all cells, regardless of their motility, become arrested in the G2/M phase because the cells can undergo only a limited number of cell divisions and fail to form clusters large enough to contain an inner region where cells are constrained by space limitations.
Next, we investigate the effects of the CDK2 and combined inhibitor treatments on the cells of both motilities (Figure 11). All the simulations are conducted in a manner similar to the CDK1 inhibition case. For m100, the results observed during the final 60 hours in Figure 11 are comparable to those shown in Figure 9, both in terms of the shape of the population growth curves (compare Figures 9A, 11A, and 11D), and the evolution of cell cycle phase distributions (compare Figures 9C and 11B, and Figures 9E and 11E). In contrast to the results simulated in the sole CDK1 inhibition, the results of the CDK2 and combined inhibitor treatments are very similar regardless of cell motility; the population growth in Figures 11A and 11D); the cell cycle distributions in Figures 11B an 11C, and in Figures 11E and 11F. For CDK2 inhibition, this result may be attributed to the fact that both CDK2 inhibition and low cell motility cause cell G1 phase arrest. At the end of both simulations (Figures 11B and 11C), most of the cells are in the G1 phase. For m100, this result is attributed to CDK2 inhibition, but for m1, the effect stems from the combined effect of CDK2 inhibition (for the inner and outer cells) and spatial limitations due to low motility (for the cells in the clusters). Thus, the final population of m1 is slightly smaller than that of m100. For the combined inhibitors, the final populations in both cases contain cells that are present in all the cell cycle phases. The 137-hour snapshot of m1 (Figure 11D, bottom) shows that the cells in the G1 phase (red) are located on the edges of cell clusters, in contrast to the same motility and time snapshot in Figure 10A. These cells are arrested in the G1 phase because of CDK2 inhibition. The inner cells in the G1 phase (red) are affected by both CDK2 inhibition and low motility. The G2/M-arrested (blue) cell population is a result of CDK1 inhibition, and no blue cells are found in the inner regions of the clusters. Again, the m100 cells (Figure 11D, top snapshot) are scattered throughout the domain and arrested in either the G1 or the G2/M phase.
4. Discussion
In this paper, we presented a newly developed model that couples the dynamics of intracellular factors regulating the cell cycle with the mechanical interactions that occur during cell growth, division, and movement, taking particular care to assure cell volume exclusivity. We built the model to capture the essence of the CDK1 and CDK2 inhibition processes. In the construction, we used cell cycle checkpoints to model cell cycle progression and phase-specific cell arrest. We also incorporated physical constraints, such as repulsion forces, contact inhibition, and cell overcrowding to reproduce a typical setup of clonogenic assay experiments. Thus, this spatially explicit hybrid model of discrete cells equipped with individually controlled cell cycles enables the analysis of emerging behaviors at the cell population level, while allowing for modification of the properties of each cell independently.
Our model differs significantly from typical models of cell cycle control that are compartmental, that is an entire cell population is divided into several subgroups (compartments), each defining a different phase of the cell cycle. The progression through the cell cycle is modeled by transferring a small portion of cells from one phase to another following the predefined transition rates that may capture effects of particular drugs or cell line characteristics [38,39]. These models successfully reproduce experimental observations of the population cell cycle distributions, but as individual cell cycles progress, they miss certain detailed dynamic characteristics of cell cultures that comprise heterogeneous cells. Within a compartment, cell population is averaged, and the information on individual cell cycle progress within a phase is coarse-grained. The individual cell behavior, such as the extent to which the cell has progressed through the phase, or the time necessary to complete passage through a checkpoint and progression to the next phase, cannot be reproduced by simply multiplying transition rates with population size. One can overcome this downside by introducing more compartments and time-delay terms in governing equations [40], or by introducing a simultaneous time and age dependency [41]. As the number of compartments increases, however, the compartmental model converges to individual cell-based models, such as that described in this paper. Therefore, the individual cell model can be considered the ultimate form of the compartmental model.
In contrast to models that disregard spatial aspects in relation to cell population growth, in the discrete agent-based models the basic model components representing the cells act as independent but interacting agents. These models usually incorporate spatial aspects, such as cell locations, colony shapes, or resource distributions. Depending on the geometric degree of freedom, modeling styles can be divided into two classes: on-lattice and off-lattice models. On-lattice agent-based models are variations of the cellular automata models based on a square or hexagonal lattice [22,23,42,43,44,45,46,47,48,49,50] or Cellular Potts models, in which each cell is composed of several lattice sides [51,52,53,54]. These models adopt strict (lattice-based) rules regarding cell location and possible movement directions, thus their geometric setup is straightforward to program and relatively computationally inexpensive. However, Cellular Potts-type models can be highly complex depending on how many lattice points an individual cell can occupy. Conversely, off-lattice models have no restrictions on cell location and direction of cell movement. Among the off-lattice agent-based models of cell colony growth, the cell-centered models are probably the most utilized model frameworks [55,56,57,58,59,60,61,62,63,64], sometimes applied in combination with a continuum description to represent densities or populations of inactive cells, such as nonproliferating, quiescent, or necrotic cell regions [65,66]. More complex models trace cell membrane points or cell–cell boundary interface inputs, as in the vertex-based models [67,68], Voronoi-Delaunay cellular models [69,70], and fluid-based elastic cell models [43,48,71]. The subcellular element models [72,73] explore internal cell complexity by including not only the cell surface but also the intracellular components. In these modeling frameworks, cell–cell interactions and cell–cell neighborhood relationships are defined in a more realistic manner, however they require much more complex multistep-algorithms for tracing all cells, determining the cell's immediate neighbors, and assigning the axis of cell division to place new daughter cells. Despite the fact that agent-based models are naturally suited to equip each cell with individually regulated control mechanisms, only limited information regarding cell cycle progression has been incorporated in these frameworks [63,70,74]. In two recent papers adopting the cellular automata framework to model cell colonies [22,23] the emerging intracellular heterogeneity results from changes in cell cycle phases in response to cell cycle specific chemotherapeutic agents or to radiotherapy, respectively. This internal heterogeneity, in turn, influences cell response to these anticancer treatments, and may lead to cell cycle mediated drug resistance or to modified radiation sensitivity. Cell cycle synchronization during radiotherapy has been also investigated using the off-lattice agent based model [75].
The mathematical framework of our model is based on the mechanistic model introduced by Meineke et al. [60]. However, we extended this model by incorporating mechanisms of cell cycle inhibition responses, and by imposing significant constraints on cell–cell interactions during cell growth and migration. In our model the increment in size during cell growth is controlled by the available space to ensure cell volume exclusivity, and the cells with multiple neighbors may grow slower than sparsely placed cells. When cells are overcrowded their growth is suppressed until the space is available. The growing or moving cells can push on their neighbors and are, in turn, exposed to the counteracting forces exerted by the nearby cells. The final cell relocation is the result of force balancing. These features enable the derivation of quantitative results on both population and individual cell levels.
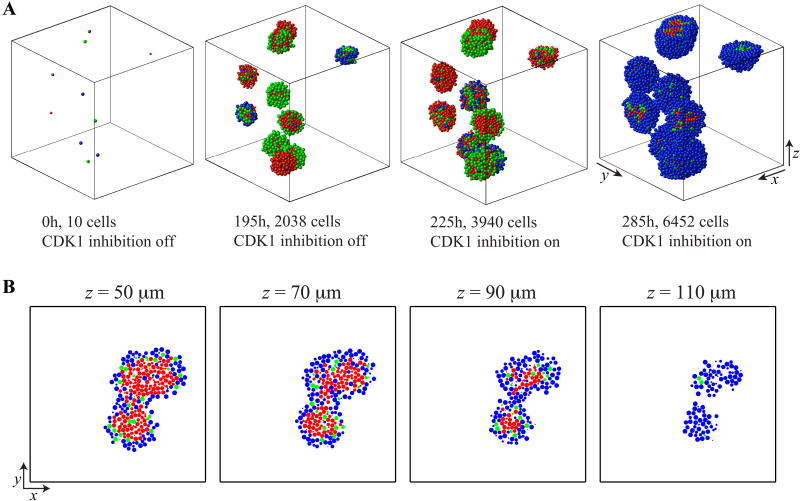
We investigated in this paper how individual cell responses to combinations of CDK inhibitors affect the growth of an entire cancer cell population. In particular, we were interested in inhibitors of CDK1 and CDK2, which are known to regulate passage through the G2/M and G1 checkpoints of the cell cycle, respectively. We examined more closely three cell cycle arrest mechanisms: (1) DNA damage that is linked to CDK1 inhibition and causes G2/M arrest; (2) CDK2-cyclin E complex formation that is associated with CDK2 inhibition and induces G1 arrest; and (3) cell growth dynamics and physical cell–cell interactions that may lead to G1 arrest as a result of cell competition for space and contact inhibition. We also looked into the combined effects of these mechanisms.
The first two mechanisms are related to a cell's intrinsic response to CDK1 and CDK2 inhibitors, and the last one considers extrinsic factors that growing cells encounter in either cell cultures or tissues. We simulated and compared four different computational experiments: a control case (without inhibitors), two cases in which one of the inhibitors was applied (either CDK1 or CDK2), and a case in which the inhibitors were simultaneously applied. In all the cases, the cells were assumed highly motile to distinguish the intra- and intercellular aspects of cell cycle arrest. We comprehensively analyzed all the computational experiments in terms of population-doubling curves and population cell cycle and age distributions, as well as provided snapshots and videos of the dynamic simulations. These quantitative measurements were chosen because they can also be collected from laboratory experiments (i.e., counting of viable cells, flow cytometry analysis, and time-lapse microscopy movies). Our simulations show that during the initial 12 hours, the effects of the three inhibitor treatments cannot be distinguished from one another and from the control case, as indicated by the cell cycle distribution graphs; and during the first 24 hours, these effects cannot be distinguished by inspecting the population-doubling curves or the configurations of growing cells from the colony assay. These findings may provide insight into when and how often data should be collected through laboratory experiments to obtain comparable results or results that are distinguishable. We also showed that cell cycle inhibitors that cause cell arrest at different cell cycle phases are not necessarily synergistically super-additive.
We studied whether the spatial patterns formed by growing cells affect the efficacy of cell cycle inhibitors. We first examined three cases, in which cells of increasing motile abilities were not exposed to inhibitors. We showed different emergent traits in colony structures, such as the formation of tight cell clusters versus uniform cell dispersal. These simulations reveal significant effects on cell cycle regulation. Different final population sizes with less motile cells produce the lowest number of offspring because of the G1 phase cell arrest within cell clusters. The cell cycle distribution dynamics show significant differences between the cases, with continuous oscillations in cell cycle distribution for highly motile cells; the cell cycles of the inner (surrounded) cells in the clusters are interrupted (G1 arrest) at low cell motility. Finally, the formation of tight clusters (due to low cell motility) alters the efficacy of cell cycle inhibitors by acting as the G1 arrest mechanism. As a result, a remarkable difference exists between the outcomes produced by cells of high and low motilities when they are exposed to CDK1 inhibitor. At high motility, all the cells are arrested in the G2/M phase. However, the low motility cells are arrested in the G1 and G2/M phases, and G1 arrest is attributed exclusively to cell contact inhibition in the inner cells surrounded by the G2/M-arrested cells.
The main reason for which the CDK1 efficacy is affected by tight cell cluster formation is slow overall dispersal of the cell colony because the peripheral cells limit movement and growth of the inner cells. We presented so far the results of our 2D simulations. However, it is essential to extend our model to the 3D space, because adding one spatial dimension increases the freedom in cell movement, In particular, the mean square displacement of a random motility in 3D is 50% larger than that in 2D. Similarly, sphere packing density in 3D is larger than in 2D; that may be an important factor in determining cell overcrowding. In order to examine whether CDK1 inhibitor efficacy affected by cell cluster formation is not a phenomenon limited to the 2D space, we extended our model to the full three dimensions. In the extended model cells are represented by spheres (that is, cell center location and its radius). All algorithms for cell growth, migration and determining the cell immediate neighbors are formulated identical as in the 2D model but extended to 3D. Several snapshots from a 3D simulation are shown in Figure 12 and confirm the formation of the G1-arrested core cluster and the G2/M-arrested cluster edge, similarly as in the 2D case shown in Figure 10. Here, the simulation is run in the domain of size 500 × 500 × 500 μm3 and is started with 10 initial cells (Figure 12A, 0 h). The CDK1 inhibition is turned on after 225 hours where the whole cell population count is 3940 (Figure 12A, 225 h). It is evident that after additional 60 hours all outer cells in each cluster are in the G2/M phase arrest (Figure 12A, 285 h). In order to show the inner cells, we use the cluster cross-sectional views. Four such cross sections (at z coordinates 50, 70, 90, and 110 μm from the bottom of the domain) are presented in Figure 12B. Two cross sections cutting roughly through the center of the cluster (z = 50 and 70 μm) show that all cells along the cluster edge are in the G2/M phase, but the majority of cells inside the cluster are arrested in the G1 phase with small number of cells in the S phase. As the cross sections move up and toward the cluster boundary (z = 90 and 110 μm) more cells are in the G2/M phase indicating that they were able to pass through the G1 and S phases and displayed the effect of CDK1 inhibition. Although the results in Figure 12 clearly show that this double-phase arrest in cell clusters exposed to the CDK1 inhibitor is not solely 2D phenomenon, they also suggest that 3D simulations require generation of larger clusters (and thus both larger numbers of cells and longer times of cluster growth) in order to observe cell separation into G1-arrested core and G2/M-arrested cluster edge. Since adding one spatial dimension enables cells to move around more easily and avoid being surrounded by other cells, even the cells in the middle of the cluster often find space to grow or move, and thus it takes more cells to create an environment where individual cells are trapped.
Figure 12.
CDK1 inhibition with the motility m1 in 3D. A. Selected simulation snapshots in the domain of 500×500×500 μm3. The simulation starts with ten cells without CDK1 inhibition. After waiting for 225 hours, when clusters are big enough, the CDK1 inhibition is initiated. Sixty hours later a majority of visible cells are blue, indicating that they are in G2/M phase. See Video 5 in the Supplementary material for the animated snapshots from the simulation. B. Selected cross-sections from the rightmost panel in A. are shown to display the cluster inside.
We demonstrated that spatial cellular organization at the time of drug administration is an important factor that influences the effects of cell cycle inhibitors, even when all cells are uniformly exposed to the drug, as in our model. Our findings may have implications for in vivo tumor growth, because drugs are typically applied after tumor masses have formed and have been detected. We illustrate this point with the following hypothetical scenario. If cell motility is low, the proliferating cell population will form clusters, with inner cells arrested in the G1 phase given space limitations. When these cells are exposed to the CDK1 inhibitor, the outer cells are G2/M-arrested (similar to that shown in Figures 10 and 12), and thus may incur high DNA damage. However, the inner cells sustain less DNA damage because they are already arrested in the G1 phase where the CDK1-stimulation requiring HR is not pronounced. Now, if chemotherapeutic treatment is scheduled weekly, the effects of CDK1 inhibition may be temporary and will diminish between consecutive treatments. On top of that, if the G2/M-arrested cells die because of high DNA damage clearing the nearby space, the previously trapped G1-arrested cells can resume their growth and progress through their cell cycles, thereby repopulating the tumor. A similar argument also applies to combined inhibitors. Figure 9 shows that when CDK1 and CDK2 inhibitors act in conjunction, the resultant cell population growth proceeds at a slower pace than that observed in single inhibition case; the final population is the smallest among the three treatments. The CDK1-inhibited population (in which all the cells are arrested due to high DNA damage) poses less of a threat than does the population grown under combined inhibition, even though the remaining population shown in Figure 9 is larger.
In order to increase practical and clinical importance of our model, it needs to be calibrated with experimental data acquired and measured by widely used laboratory techniques to fit not only various characteristics of particular cell lines of interest but also pharmacodynamic features of certain drugs. The typical cell size (parameter ao), cell motility (parameter m1-m100) and cell cycle length can be extracted from time-lapse microscopy movies [26,27,76]. In these experiments, sequences of images are taken to show regions of the dish in which the cells are growing. By tracing individual cells from one image to another one can record how cell position, shape, and size are changing over time, and how often the cells produce the offspring. Viable cell count is often monitored to determine the population doubling curves [27,35], that can be used to validate or adjust our results shown in Figure 5A or Figure 6. Additionally, the dynamic changes in cell cycle phase distributions, which can be measured from flow cytometry cell sorting experiments [77] or from microscopy images after FUCCI staining [26], can be compared with our dynamic simulations. Results of these experiments can be reported as bar-graphs with the ratios of cells being in the G1, S or G2/M phase, respectively, which can be directly compared with our simulated results shown in Figure 5H-J or 7D. Experimental results, however, rarely record high frequency data in contrast to our simulations [23,34,35]; therefore, by using the computational model we are able to supply the intermittent data points in the dynamics. Figure 13A shows an example of how the distributions of cell cycle phases under the drug treatment can be used to calibrate our model. Here, we consider a drug that inhibits both CDK1 and CDK2 but with unknown inhibition strengths. Nine panels in Figure 13A show simulated results of the cell cycle phase distributions up to 60 hours in 12-hour intervals using nine different combinations of inhibition parameters. All other parameters that control each cell cycle phase length, cell size growth rate, DNA replication rate, and the threshold levels for checkpoints are identical for every considered simulation. Each of the nine panels display different pattern of population cell cycle progression that depends on how strong the inhibitions are, and which of the two inhibitions is stronger. Hence, we can compare these simulated outcomes to the experimental results showing cell cycle phase distributions over time to pinpoint the right combination of model parameters or to narrow down the possible region in the model parameter space by eliminating unlikely combinations. The drug response curves, which are typically used in the drug testing experiments [78,79,80], can be used to further calibrate our model. Figure 13B displays dosage response curves of five different hypothetical drugs which are represented by five pairs of inhibition parameters (from Figure 13A). Again, by comparing these simulated outcomes to the drug response curves determined experimentally, we can identify model parameters for which the simulated results fit the experimental ones.
Figure 13.
Simulated responses to various drug characteristics and dosage. A. Population cell cycle distributions taken at 12-hour intervals between 0 and 60 hours. Each panel corresponds to cell population response to different sets of CDK1 and CDK2 inhibition parameters (representing hypothetical drugs). The center panel is the case referred to as the combined CDK1-CDK2 inhibition in Figure 9. B. Dosage response curve following five different hypothetical drugs. The markers on the graphs represent size of cell population after 60 hours of simulated time under the combined inhibition treatment. The size of cell population is normalized by the size of untreated cell population. The inhibition parameters are given by α · rCDK1i and α · rCDK2i, where α runs from 0 to 2 with a step size 0.1, and rcdk1i and rCDK2i are specified by the legend. Five different sets of parameters (rCDK1i, rCDk2i) correspond to the top row (magenta, black, blue; from left to right) and the right column (blue, red, green; from top to bottom) in Figure 13A. Having α equal to zero corresponds to the untreated case, therefore, all five graphs start with normalized value of 1 for α = 0.
The increased proliferative activity of cancer cells regulated by CDKs provides opportunities for developing new therapies that target CDKs with the reduced systemic toxicity that is typical of conventional chemotherapeutic agents. Several CDK inhibitors have already been developed and applied either in clinical trials or advanced preclinical testing. The most promising are flavopiridol, seliciclib, and dinaciclib [11,13,81,82]. However, no new therapies have been approved for clinical use. Most of the CDK inhibitors being developed have multiple targets. Whether selective inhibitors, called third-generation CDK inhibitors, will be therapeutically superior to multitarget CDK-inhibitor combinations remains unknown [81,82]. In this study, we regarded CDK1 and CDK2 inhibition as two separate mechanisms coming from two different inhibitors, enabling us to determine their individual activities and their combined effects on cell population behavior. This approach can be easily extended to the study of multitarget CDK inhibitors that are in trial, or used to propose new inhibitors that are more effective. We presented our results as a minimalistic framework that can be potentially extended to multiple CDK inhibitors or CDK inhibitors combined with other types of drugs.
We intentionally simplified certain elements of our model to reduce the number of model variables and parameters, but appropriate model extensions are being developed. In the current work, we did not explicitly include any of the numerous cyclin-CDK complexes that are known to change dynamically in normal proliferating cells. Instead, we focused only on CDKs as representative factors in cell cycle progression and in the passage of cell cycle checkpoints [19,21]. We also concentrated entirely on cell cycle arrest at both the G1 and G2/M checkpoints and did not introduce cell death to the model. This decision was born of the fact that different cell lines and different patients' tumors may be characterized by distinct sensitivities to DNA damage that trigger cell death. These cell line-specific characteristics should be part of model calibration.
We focused most of our efforts on modeling the 2D in vitro clonogenic assay. Such in vitro experiments are extensively conducted in cancer biology research because they provide relatively well-controlled environments in which to test hypotheses without compelling researchers to contend with the overwhelming number of unknown or redundant factors usually encountered in in vivo studies. With regard to controlled systems, in vitro cell line experiments and mathematical modeling share these advantages, making them a good combined approach. Quantitative experimental measurements for model parameterization and validation are the crucial building blocks of integrative mathematical models. Meanwhile, the experimentally testable predictions and hypotheses from mathematical models should be tested in laboratories. Having this positive feedback loop between experiments and simulations necessitates a mathematical model that is extendable and flexible, and at the same time, capable of producing results that are equivalent or comparable to experimental findings. In this paper, we have shown that our model is versatile and can produce results that are directly comparable to experimental measurements, including life-like image series, such as bright field microscopy or time-lapse imaging; fluorescent cell labeling that indicates cell cycle phases FUCCI; population-doubling curves acquired by counting viable cells over time; and cell cycle distributions obtained from flow cytometry analysis. Other experimental measurements and data, such as Western blots, microarrays, and image data also facilitate the parameterization of models and the validation of computational results.
We showed that our computational model is readily extendable to 3D experiments, such as multicellular spheroid cultures, or tumors that grow in vivo in tissue-like structure. We assumed that the CDK inhibitor-carrying drug is supplied uniformly to all cells, but the model can incorporate various chemical spatial and temporal gradients.
Since we model individual cells, we can derive quantitative results on both single-cell and population levels. We can also visualize spatial traits, such as cell colony formation or location-dependent cell cycle specificities, because our model has an explicit spatial component and because we trace the locations of all cells. We believe that the results obtained by deploying our hybrid approach with accurate implementation of physical interactions between cells reflect the versatility, extendibility, and potential of our model as a computational tool that provides feedback valuable to experimental and clinical studies.
Our research is greatly motivated by the sarcoma research at Moffitt Cancer Center. Preclinical sarcoma research at Moffitt Cancer Center has demonstrated promising results using small molecule inhibitors of the cell cycle, namely the CDK inhibitor dinaciclib and the WEE1 inhibitor MK1775. The latter has been shown to abrogate the G2/M checkpoint forcing cells with DNA damage to enter into unscheduled mitosis to undergo cell death, often referred to as mitotic catastrophe [83]. It has shown that this molecule also causes DNA damage and leads to apoptosis, an unexpected finding suggesting activity beyond affecting the G2/M checkpoint [12,80]. MK1775 has broad activity across sarcoma subtypes and lead to differentiation and necrosis in a xenograft model of osteosarcoma [12]. These agents are being further explored preclinically and clinically in osteosarcoma and other pediatric malignancies (NCT01748825, NCT01434316) [84]. Sarcomas are heterogeneous, mesenchymal tumors affecting both pediatric and adult populations [85,86]. Approximately 10% of childhood cancer and 8% of young adult cancers are sarcomas, compared to 1% of cancer incidence in people over 40 years of age. Ewing sarcoma, osteosarcoma and rhabdomyosarcoma affect about three quarter of all children with sarcomas whereas liposarcoma, leiomyosarcoma, undifferentiated sarcoma, neurofibrosarcoma, and synovial sarcoma represent some of the most common sarcoma types in the adult population [87,88]. The treatment of nonmetastatic sarcomas is frequently with curative intent with the use of multimodality therapy including surgery, radiation therapy with or without anthracycline-based, and chemotherapy. However and disappointingly, cure rates have only been very modestly improved for metastatic disease and recurrent sarcomas. Multiple attempts at increasing the doses of these conventional chemotherapeutic agents have increased toxicity without improved efficacy [89]. Thus, there is a pressing need to develop novel therapies to improve outcomes in sarcoma patients. Novel model systems, including mathematical and computational models, which can recapitulate critical elements of tumor biology would help speed up translation of basic research findings and traditional bench experiments and perhaps guide translation towards combinations of therapy, order of addition of therapies, or optimal length of exposure for optimal anticancer effect.
Supplementary Material
Highlights.
We developed a 2D/3D hybrid model of cell colony growth under cell cycle inhibition.
Our model integrates physical and physiological components of the cell cycle.
Our model captures population-level emergent properties.
Our model elucidates the characteristics of cell cycle-inhibiting drug.
Our model shows how cell colony morphology affects cell cycle inhibition efficacy.
Acknowledgments
This work was partially supported by the Miles for Moffitt Milestones Award grant from the Moffitt Foundation, and in part by the NIH Integrated Cancer Biology Program grant U54-CA113007.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Hanahan D, Weinberg RA. Hallmarks of cancer: the next generation. Cell. 2011;144:646–674. doi: 10.1016/j.cell.2011.02.013. [DOI] [PubMed] [Google Scholar]
- 2.Malumbres M, Barbacid M. Cell cycle, CDKs and cancer: a changing paradigm. Nature reviews Cancer. 2009;9:153–166. doi: 10.1038/nrc2602. [DOI] [PubMed] [Google Scholar]
- 3.Alberts B, Johnson A, Lewis J, Raff M, Roberts K, et al. Molecular biology of the cell. New York: Garland Science; 2008. [Google Scholar]
- 4.Zetterberg A, Larsson O. Coordination between cell growth and cell cycle transit in animal cells. Cold Spring Harbor symposia on quantitative biology. 1991;56:137–147. doi: 10.1101/sqb.1991.056.01.018. [DOI] [PubMed] [Google Scholar]
- 5.Gould KL, Nurse P. Tyrosine phosphorylation of the fission yeast cdc2+ protein kinase regulates entry into mitosis. Nature. 1989;342:39–45. doi: 10.1038/342039a0. [DOI] [PubMed] [Google Scholar]
- 6.Mikhailov A, Cole RW, Rieder CL. DNA damage during mitosis in human cells delays the metaphase/anaphase transition via the spindle-assembly checkpoint. Current biology : CB. 2002;12:1797–1806. doi: 10.1016/s0960-9822(02)01226-5. [DOI] [PubMed] [Google Scholar]
- 7.Rudner AD, Murray AW. The spindle assembly checkpoint. Current opinion in cell biology. 1996;8:773–780. doi: 10.1016/s0955-0674(96)80077-9. [DOI] [PubMed] [Google Scholar]
- 8.Morgan DO. Cyclin-dependent kinases: engines, clocks, and microprocessors. Annual review of cell and developmental biology. 1997;13:261–291. doi: 10.1146/annurev.cellbio.13.1.261. [DOI] [PubMed] [Google Scholar]
- 9.Weinberg RA. The biology of cancer. New York: Garland Science; 2007. [Google Scholar]
- 10.Lapenna S, Giordano A. Cell cycle kinases as therapeutic targets for cancer. Nature reviews Drug discovery. 2009;8:547–566. doi: 10.1038/nrd2907. [DOI] [PubMed] [Google Scholar]
- 11.Fu W, Ma L, Chu B, Wang X, Bui MM, et al. The cyclin-dependent kinase inhibitor SCH 727965 (dinacliclib) induces the apoptosis of osteosarcoma cells. Molecular cancer therapeutics. 2011;10:1018–1027. doi: 10.1158/1535-7163.MCT-11-0167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kreahling JM, Gemmer JY, Reed D, Letson D, Bui M, et al. MK1775, a selective Wee1 inhibitor, shows single-agent antitumor activity against sarcoma cells. Molecular cancer therapeutics. 2012;11:174–182. doi: 10.1158/1535-7163.MCT-11-0529. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Parry D, Guzi T, Shanahan F, Davis N, Prabhavalkar D, et al. Dinaciclib (SCH 727965), a novel and potent cyclin-dependent kinase inhibitor. Molecular cancer therapeutics. 2010;9:2344–2353. doi: 10.1158/1535-7163.MCT-10-0324. [DOI] [PubMed] [Google Scholar]
- 14.Koff A, Giordano A, Desai D, Yamashita K, Harper JW, et al. Formation and activation of a cyclin E-cdk2 complex during the G1 phase of the human cell cycle. Science. 1992;257:1689–1694. doi: 10.1126/science.1388288. [DOI] [PubMed] [Google Scholar]
- 15.Koledova Z, Kafkova LR, Calabkova L, Krystof V, Dolezel P, et al. Cdk2 inhibition prolongs G1 phase progression in mouse embryonic stem cells. Stem cells and development. 2010;19:181–194. doi: 10.1089/scd.2009.0065. [DOI] [PubMed] [Google Scholar]
- 16.O'Connell MJ, Raleigh JM, Verkade HM, Nurse P. Chk1 is a wee1 kinase in the G2 DNA damage checkpoint inhibiting cdc2 by Y15 phosphorylation. The EMBO journal. 1997;16:545–554. doi: 10.1093/emboj/16.3.545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Raleigh JM, O'Connell MJ. The G(2) DNA damage checkpoint targets both Wee1 and Cdc25. Journal of cell science. 2000;113(Pt 10):1727–1736. doi: 10.1242/jcs.113.10.1727. [DOI] [PubMed] [Google Scholar]
- 18.Ira G, Pellicioli A, Balijja A, Wang X, Fiorani S, et al. DNA end resection, homologous recombination and DNA damage checkpoint activation require CDK1. Nature. 2004;431:1011–1017. doi: 10.1038/nature02964. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Gerard C, Goldbeter A. Temporal self-organization of the cyclin/Cdk network driving the mammalian cell cycle. Proceedings of the National Academy of Sciences of the United States of America. 2009;106:21643–21648. doi: 10.1073/pnas.0903827106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gerard C, Tyson JJ, Novak B. Minimal models for cell-cycle control based on competitive inhibition and multisite phosphorylations of Cdk substrates. Biophysical journal. 2013;104:1367–1379. doi: 10.1016/j.bpj.2013.02.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Tyson JJ, Novak B. Temporal organization of the cell cycle. Current biology : CB. 2008;18:R759–R768. doi: 10.1016/j.cub.2008.07.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Powathil GG, Gordon KE, Hill LA, Chaplain MA. Modelling the effects of cell-cycle heterogeneity on the response of a solid tumour to chemotherapy: biological insights from a hybrid multiscale cellular automaton model. Journal of theoretical biology. 2012;308:1–19. doi: 10.1016/j.jtbi.2012.05.015. [DOI] [PubMed] [Google Scholar]
- 23.Powathil GG, Adamson DJ, Chaplain MA. Towards predicting the response of a solid tumour to chemotherapy and radiotherapy treatments: clinical insights from a computational model. PLoS computational biology. 2013;9:e1003120. doi: 10.1371/journal.pcbi.1003120. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Franken NA, Rodermond HM, Stap J, Haveman J, van Bree C. Clonogenic assay of cells in vitro. Nature protocols. 2006;1:2315–2319. doi: 10.1038/nprot.2006.339. [DOI] [PubMed] [Google Scholar]
- 25.Munshi A, Hobbs M, Meyn RE. Clonogenic cell survival assay. Methods in molecular medicine. 2005;110:21–28. doi: 10.1385/1-59259-869-2:021. [DOI] [PubMed] [Google Scholar]
- 26.Sakaue-Sawano A, Kurokawa H, Morimura T, Hanyu A, Hama H, et al. Visualizing spatiotemporal dynamics of multicellular cell-cycle progression. Cell. 2008;132:487–498. doi: 10.1016/j.cell.2007.12.033. [DOI] [PubMed] [Google Scholar]
- 27.Tyson DR, Garbett SP, Frick PL, Quaranta V. Fractional proliferation: a method to deconvolve cell population dynamics from single-cell data. Nature methods. 2012;9:923–928. doi: 10.1038/nmeth.2138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Godugu C, Patel AR, Desai U, Andey T, Sams A, et al. AlgiMatrix (TM) Based 3D Cell Culture System as an In-Vitro Tumor Model for Anticancer Studies. Plos One. 2013;8 doi: 10.1371/journal.pone.0053708. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Shaw KRM, Wrobel CN, Brugge JS. Use of three-dimensional basement membrane cultures to model oncogene-induced changes in mammary epithelial morphogenesis. Journal of Mammary Gland Biology and Neoplasia. 2004;9:297–310. doi: 10.1007/s10911-004-1402-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Branzei D, Foiani M. Regulation of DNA repair throughout the cell cycle. Nature reviews Molecular cell biology. 2008;9:297–308. doi: 10.1038/nrm2351. [DOI] [PubMed] [Google Scholar]
- 31.Curtin NJ. DNA repair dysregulation from cancer driver to therapeutic target. Nature reviews Cancer. 2012;12:801–817. doi: 10.1038/nrc3399. [DOI] [PubMed] [Google Scholar]
- 32.Brummer A, Salazar C, Zinzalla V, Alberghina L, Hofer T. Mathematical modelling of DNA replication reveals a trade-off between coherence of origin activation and robustness against rereplication. PLoS computational biology. 2010;6:e1000783. doi: 10.1371/journal.pcbi.1000783. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Burhans WC, Weinberger M. DNA replication stress, genome instability and aging. Nucleic acids research. 2007;35:7545–7556. doi: 10.1093/nar/gkm1059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Singhania R, Sramkoski RM, Jacobberger JW, Tyson JJ. A hybrid model of mammalian cell cycle regulation. PLoS computational biology. 2011;7:e1001077. doi: 10.1371/journal.pcbi.1001077. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Cai D, Latham VM, Jr, Zhang X, Shapiro GI. Combined depletion of cell cycle and transcriptional cyclin-dependent kinase activities induces apoptosis in cancer cells. Cancer research. 2006;66:9270–9280. doi: 10.1158/0008-5472.CAN-06-1758. [DOI] [PubMed] [Google Scholar]
- 36.Chaudhry MA. Base excision repair of ionizing radiation-induced DNA damage in G1 and G2 cell cycle phases. Cancer cell international. 2007;7:15. doi: 10.1186/1475-2867-7-15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Webb JL. Enzyme and metabolic inhibitors. 1-3 New York: Academic Press; 1963. [Google Scholar]
- 38.Eladdadi A, Isaacson D. A mathematical model for the effects of HER2 over-expression on cell cycle progression in breast cancer. Bulletin of mathematical biology. 2011;73:2865–2887. doi: 10.1007/s11538-011-9663-3. [DOI] [PubMed] [Google Scholar]
- 39.Roe-Dale R, Isaacson D, Kupferschmid M. A mathematical model of cell cycle effects in gastric cancer chemotherapy. Bulletin of mathematical biology. 2012;74:159–174. doi: 10.1007/s11538-011-9669-x. [DOI] [PubMed] [Google Scholar]
- 40.Simms K, Bean N, Koerber A. A mathematical model of cell cycle progression applied to the MCF-7 breast cancer cell line. Bulletin of mathematical biology. 2012;74:736–767. doi: 10.1007/s11538-011-9700-2. [DOI] [PubMed] [Google Scholar]
- 41.Basse B, Ubezio P. A generalised age- and phase-structured model of human tumour cell populations both unperturbed and exposed to a range of cancer therapies. Bulletin of mathematical biology. 2007;69:1673–1690. doi: 10.1007/s11538-006-9185-6. [DOI] [PubMed] [Google Scholar]
- 42.Anderson AR. A hybrid mathematical model of solid tumour invasion: the importance of cell adhesion. Mathematical medicine and biology : a journal of the IMA. 2005;22:163–186. doi: 10.1093/imammb/dqi005. [DOI] [PubMed] [Google Scholar]
- 43.Anderson AR, Rejniak KA, Gerlee P, Quaranta V. Microenvironment driven invasion: a multiscale multimodel investigation. Journal of mathematical biology. 2009;58:579–624. doi: 10.1007/s00285-008-0210-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Aubert M, Badoual M, Christov C, Grammaticos B. A model for glioma cell migration on collagen and astrocytes. Journal of the Royal Society, Interface / the Royal Society. 2008;5:75–83. doi: 10.1098/rsif.2007.1070. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Enderling H, Hlatky L, Hahnfeldt P. Tumor morphological evolution: directed migration and gain and loss of the self-metastatic phenotype. Biology direct. 2010;5:23. doi: 10.1186/1745-6150-5-23. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Gerlee P, Nelander S. The impact of phenotypic switching on glioblastoma growth and invasion. PLoS computational biology. 2012;8:e1002556. doi: 10.1371/journal.pcbi.1002556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Jiao Y, Torquato S. Emergent behaviors from a cellular automaton model for invasive tumor growth in heterogeneous microenvironments. PLoS computational biology. 2011;7:e1002314. doi: 10.1371/journal.pcbi.1002314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Kam Y, Rejniak KA, Anderson AR. Cellular modeling of cancer invasion: integration of in silico and in vitro approaches. Journal of cellular physiology. 2012;227:431–438. doi: 10.1002/jcp.22766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Alber MS, Kiskowski A. On aggregation in CA models in biology. J Phys A: Math Gen. 2001;34:10707–10714. [Google Scholar]
- 50.Dubois C, Farnham J, Aaron E, Radunskaya A. A multiple time-scale computational model of a tumor and its micro environment. Mathematical biosciences and engineering : MBE. 2013;10:121–150. doi: 10.3934/mbe.2013.10.121. [DOI] [PubMed] [Google Scholar]
- 51.Jiang Y, Pjesivac-Grbovic J, Cantrell C, Freyer JP. A multiscale model for avascular tumor growth. Biophysical journal. 2005;89:3884–3894. doi: 10.1529/biophysj.105.060640. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Poplawski NJ, Agero U, Gens JS, Swat M, Glazier JA, et al. Front instabilities and invasiveness of simulated avascular tumors. Bulletin of mathematical biology. 2009;71:1189–1227. doi: 10.1007/s11538-009-9399-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Shirinifard A, Gens JS, Zaitlen BL, Poplawski NJ, Swat M, et al. 3D multi-cell simulation of tumor growth and angiogenesis. Plos One. 2009;4:e7190. doi: 10.1371/journal.pone.0007190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Turner S, J AS, Cameron D. Tamoxifen treatment failure in cancer and the nonlinear dynamics of TGFbeta. Journal of theoretical biology. 2004;229:101–111. doi: 10.1016/j.jtbi.2004.03.008. [DOI] [PubMed] [Google Scholar]
- 55.D'Antonio G, Macklin P, Preziosi L. An agent-based model for elasto-plastic mechanical interactions between cells, basement membrane and extracellular matrix. Mathematical biosciences and engineering : MBE. 2013;10:75–101. doi: 10.3934/mbe.2013.10.75. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Drasdo D, Hohme S. A single-cell-based model of tumor growth in vitro: monolayers and spheroids. Physical biology. 2005;2:133–147. doi: 10.1088/1478-3975/2/3/001. [DOI] [PubMed] [Google Scholar]
- 57.Dunn SJ, Fletcher AG, Chapman SJ, Gavaghan DJ, Osborne JM. Modelling the role of the basement membrane beneath a growing epithelial monolayer. Journal of theoretical biology. 2012;298:82–91. doi: 10.1016/j.jtbi.2011.12.013. [DOI] [PubMed] [Google Scholar]
- 58.Galle J, Loeffler M, Drasdo D. Modeling the effect of deregulated proliferation and apoptosis on the growth dynamics of epithelial cell populations in vitro. Biophysical journal. 2005;88:62–75. doi: 10.1529/biophysj.104.041459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Macklin P, Edgerton ME, Thompson AM, Cristini V. Patient-calibrated agent-based modelling of ductal carcinoma in situ (DCIS): from microscopic measurements to macroscopic predictions of clinical progression. Journal of theoretical biology. 2012;301:122–140. doi: 10.1016/j.jtbi.2012.02.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Meineke FA, Potten CS, Loeffler M. Cell migration and organization in the intestinal crypt using a lattice-free model. Cell proliferation. 2001;34:253–266. doi: 10.1046/j.0960-7722.2001.00216.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Ramis-Conde I, Drasdo D, Anderson AR, Chaplain MA. Modeling the influence of the E-cadherin-beta-catenin pathway in cancer cell invasion: a multiscale approach. Biophysical journal. 2008;95:155–165. doi: 10.1529/biophysj.107.114678. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.van Leeuwen IM, Mirams GR, Walter A, Fletcher A, Murray P, et al. An integrative computational model for intestinal tissue renewal. Cell Proliferation. 2009;42:617–636. doi: 10.1111/j.1365-2184.2009.00627.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Fletcher AG, Breward CJ, Jonathan Chapman S. Mathematical modeling of monoclonal conversion in the colonic crypt. Journal of theoretical biology. 2012;300:118–133. doi: 10.1016/j.jtbi.2012.01.021. [DOI] [PubMed] [Google Scholar]
- 64.Szabo A, Unnep R, Mehes E, Twal WO, Argraves WS, et al. Collective cell motion in endothelial monolayers. Physical biology. 2010;7:046007. doi: 10.1088/1478-3975/7/4/046007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Kim Y, Othmer HG. A Hybrid Model of Tumor-Stromal Interactions in Breast Cancer. Bulletin of mathematical biology. 2013 doi: 10.1007/s11538-012-9787-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Kim Y, Stolarska MA, Othmer HG. A hybrid model for tumor spheroid growth in vitro I: Theoretical development and early results. Mathematical Models & Methods in Applied Sciences. 2007;17:1773–1798. [Google Scholar]
- 67.Mirams GR, Arthurs CJ, Bernabeu MO, Bordas R, Cooper J, et al. Chaste: an open source C++ library for computational physiology and biology. PLoS computational biology. 2013;9:e1002970. doi: 10.1371/journal.pcbi.1002970. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Osborne JM, Walter A, Kershaw SK, Mirams GR, Fletcher AG, et al. A hybrid approach to multi-scale modelling of cancer. Philosophical transactions Series A, Mathematical, physical, and engineering sciences. 2010;368:5013–5028. doi: 10.1098/rsta.2010.0173. [DOI] [PubMed] [Google Scholar]
- 69.Beyer T, Meyer-Hermann M. Modeling emergent tissue organization involving high-speed migrating cells in a flow equilibrium. Physical review E, Statistical, nonlinear, and soft matter physics. 2007;76:021929. doi: 10.1103/PhysRevE.76.021929. [DOI] [PubMed] [Google Scholar]
- 70.Schaller G, Meyer-Hermann M. Multicellular tumor spheroid in an off-lattice Voronoi-Delaunay cell model. Physical review E, Statistical, nonlinear, and soft matter physics. 2005;71:051910. doi: 10.1103/PhysRevE.71.051910. [DOI] [PubMed] [Google Scholar]
- 71.Rejniak KA. An immersed boundary framework for modelling the growth of individual cells: an application to the early tumour development. Journal of theoretical biology. 2007;247:186–204. doi: 10.1016/j.jtbi.2007.02.019. [DOI] [PubMed] [Google Scholar]
- 72.Sandersius SA, Newman TJ. Modeling cell rheology with the Subcellular Element Model. Physical biology. 2008;5:015002. doi: 10.1088/1478-3975/5/1/015002. [DOI] [PubMed] [Google Scholar]
- 73.Sandersius SA, Weijer CJ, Newman TJ. Emergent cell and tissue dynamics from subcellular modeling of active biomechanical processes. Physical biology. 2011;8:045007. doi: 10.1088/1478-3975/8/4/045007. [DOI] [PubMed] [Google Scholar]
- 74.Alarcon T, Byrne HM, Maini PK. A multiple scale model for tumor growth. Multiscale Modeling & Simulation. 2005;3:440–475. [Google Scholar]
- 75.Kempf H, Hatzikirou H, Bleicher M, Meyer-Hermann M. In silico analysis of cell cycle synchronisation effects in radiotherapy of tumour spheroids. PLoS computational biology. 2013;9:e1003295. doi: 10.1371/journal.pcbi.1003295. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Georgescu W, Wikswo JP, Quaranta V. CellAnimation: an open source MATLAB framework for microscopy assays. Bioinformatics. 2012;28:138–139. doi: 10.1093/bioinformatics/btr633. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Bartkova J, Horejsi Z, Koed K, Kramer A, Tort F, et al. DNA damage response as a candidate anti-cancer barrier in early human tumorigenesis. Nature. 2005;434:864–870. doi: 10.1038/nature03482. [DOI] [PubMed] [Google Scholar]
- 78.Bai Y, Li J, Fang B, Edwards A, Zhang G, et al. Phosphoproteomics identifies driver tyrosine kinases in sarcoma cell lines and tumors. Cancer research. 2012;72:2501–2511. doi: 10.1158/0008-5472.CAN-11-3015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Gray J, Cubitt CL, Zhang S, Chiappori A. Combination of HDAC and topoisomerase inhibitors in small cell lung cancer. Cancer biology & therapy. 2012;13:614–622. doi: 10.4161/cbt.19848. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Kreahling JM, Foroutan P, Reed D, Martinez G, Razabdouski T, et al. Wee1 inhibition by MK-1775 leads to tumor inhibition and enhances efficacy of gemcitabine in human sarcomas. Plos One. 2013;8:e57523. doi: 10.1371/journal.pone.0057523. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Malumbres M, Pevarello P, Barbacid M, Bischoff JR. CDK inhibitors in cancer therapy: what is next? Trends in pharmacological sciences. 2008;29:16–21. doi: 10.1016/j.tips.2007.10.012. [DOI] [PubMed] [Google Scholar]
- 82.Shapiro GI. Cyclin-dependent kinase pathways as targets for cancer treatment. Journal of clinical oncology : official journal of the American Society of Clinical Oncology. 2006;24:1770–1783. doi: 10.1200/JCO.2005.03.7689. [DOI] [PubMed] [Google Scholar]
- 83.De Witt Hamer PC, Mir SE, Noske DP, Van Noorden CJ, Wurdinger T. WEE1 kinase targeting combined with DNA damaging cancer therapy catalyzes mitotic catastrophe. Clinical cancer research : an official journal of the American Association for Cancer Research. 2011 doi: 10.1158/1078-0432.CCR-10-2537. [DOI] [PubMed] [Google Scholar]
- 84.Sampson VB, Gorlick R, Kamara D, Anders Kolb E. A review of targeted therapies evaluated by the pediatric preclinical testing program for osteosarcoma. Frontiers in oncology. 2013;3:132. doi: 10.3389/fonc.2013.00132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Ludwig J, Trent J. Targeted Therapy of Sarcoma. In: Kurzrock R, Markman M, editors. Targeted Cancer Therapy. Humana Press; 2008. pp. 317–334. [Google Scholar]
- 86.Reed D, Altiok S. Metastatic soft tissue sarcoma chemotherapy: an opportunity for personalized medicine. Cancer control: Journal of the Moffitt Cancer Center. 2011;18:8. doi: 10.1177/107327481101800306. [DOI] [PubMed] [Google Scholar]
- 87.Amankwah EK, Conley AP, Reed DR. Epidemiology and therapies for metastatic sarcoma. Clinical epidemiology. 2013;5:147–162. doi: 10.2147/CLEP.S28390. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Reynoso D, Subbiah V, Trent JC, Guadagnolo BA, Lazar AJ, et al. Neoadjuvant treatment of soft-tissue sarcoma: a multimodality approach. Journal of surgical oncology. 2010;101:327–333. doi: 10.1002/jso.21481. [DOI] [PubMed] [Google Scholar]
- 89.Thomas DM, Wagner AJ. Specific targets in sarcoma and developmental therapeutics. Journal of the National Comprehensive Cancer Network : JNCCN. 2010;8:677–685. doi: 10.6004/jnccn.2010.0050. quiz 686. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.