The development and modeling of devices and paradigms for transcranial magnetic stimulation

Abstract

Magnetic stimulation is a noninvasive neurostimulation technique that can evoke action potentials and modulate neural circuits through induced electric fields. Biophysical models of magnetic stimulation have become a major driver for technological developments and the understanding of the mechanisms of magnetic neurostimulation and neuromodulation. Major technological developments involve stimulation coils with different spatial characteristics and pulse sources to control the pulse waveform. While early technological developments were the result of manual design and invention processes, there is a trend in both stimulation coil and pulse source design to mathematically optimize parameters with the help of computational models. To date, macroscopically highly realistic spatial models of the brain as well as peripheral targets, and user-friendly software packages enable researchers and practitioners to simulate the treatment-specific and induced electric field distribution in the brains of individual subjects and patients. Neuron models further introduce the microscopic level of neural activation to understand the influence of activation dynamics in response to different pulse shapes. A number of models that were designed for online calibration to extract otherwise covert information and biomarkers from the neural system recently form a third branch of modeling.

1 What is TMS and how could modeling improve technology?

Transcranial magnetic stimulation (TMS) is an established method to activate neurons noninvasively in the brain using electromagnetic induction (Barker, Jalinous, & Freeston, 1985; Polson, Barker, & Freeston, 1982). The technique is unmatched in several applications ranging from experimental neuroscience to medical diagnosis and therapy (Aleman, 2013; Eldaief, Press, & Pascual-Leone, 2013; Wassermann & Zimmermann, 2012). Through time-varying current in a stimulation coil, TMS generates strong alternating magnetic field pulses that can permeate the electrically poorly conducting skull and evoke action potentials of neurons in the focus of the stimulation coil. Thus, unlike subthreshold neuromodulation techniques, TMS pulses can trigger a neuron’s endogenous signal transmission mechanism, which amplifies the stimulus and transmits the signal to other neurons (Di Lazzaro et al., 2004; Di Lazzaro et al., 2012; Volz, Hamada, Rothwell, & Grefkes, 2014).

However, the interaction of the brain tissue with the electromagnetic fields is not obvious. Accordingly, theoretical and modeling work has accompanied TMS since the invention of this technique (Durand, Ferguson, & Dalbasti, 1989; Guidi, Scarpino, Angeleri, Antili, & Leo, 1989; Lorenzen & Weyh, 1992; Maccabee, Amassian, Cracco, & Cadwell, 1988; McRobbie, 1985; Reilly, 1989; Reilly, 1992; Roth & Basser, 1990; Rudiak & Marg, 1994; Turner, 1986; Ueno, Tashiro, & Harada, 1988a; Yamaguchi et al., 1989). In terms of spatial distribution, the magnetic field that is generated by the current in the stimulation coil is almost independent from the specific head anatomy, whereas the induced electric fields in the brain and around the neurons are not (Esselle & Stuchly, 1992). The induced currents interact with both the macroscopic and microscopic anatomy as well as the varying electrical conductance. Both lead to charge accumulation and influence the distribution of the induced electric field. In terms of the temporal dynamics, neurons have various subtypes, with diverse geometry and membrane excitability, leading to differential response to the current pulse waveforms. The key motivation behind spatial and temporal modeling is to gain a better understanding of the mechanisms of action of TMS, design and optimize devices, and plan as well as guide TMS interventions.

2 What are the physical and physiological fundamentals of TMS?

2.1 Electromagnetism and the spatial aspect of TMS

In contrast to electrical stimulation, where current flows directly between two electrodes, a cathode and an anode, and generates a stimulating electric field, magnetic stimulation uses electromagnetism to induce currents across the skull into the brain without any direct electrical contact. The event chain starts in the stimulation coil, which during a pulse guides a strong alternating current that in turn generates a spatially extended magnetic field. According to Ampère’s circuital law, the magnetic field around the coil is proportional to the coil current strength. Although the magnetic field strength decreases rapidly with distance, it reaches into the brain if the coil is placed close enough to a subject’s head (Barker, 1991; Deng, Peterchev, & Lisanby, 2008). The alternating nature and briefness of the current pulse and therefore the magnetic field in the brain—which follows the same time course—cause a high time derivative of the magnetic field, i.e., a strong change of the magnetic field over time (Peterchev, Deng, & Goetz, 2015). According to Faraday’s law of induction, the time derivative of the current generates an electric field (Jackson, 1999; Maxwell, 1891).

To this point, the process primarily depends on the coil design, i.e., the shape of the conductors in the coil (see Figs. 2 and 4) as well as potentially implemented magnetically active materials, such as ferromagnetic iron cores (see Figs. 3 and 4), but not on the brain anatomy (Epstein & Davey, 2002; Lorenzen & Weyh, 1992; Tachas & Samaras, 2014). Since the brain is electrically conductive, the induced electric field causes a current that has to follow the brain anatomy and also local electrical conductivity differences caused by different tissue types or tissue compositions according to Ohm’s law (Ruohonen et al., 1996; Wagner, Zahn, Grodzinsky, & Pascual-Leone, 2004). At interfaces or gradients between different electrical conductivities, the current transiently builds up charge accumulations, which in turn generate an additional, often called secondary electric field according to Gauss’ law. This secondary electric field superimposes the induced electric field and strongly depends on the individual brain anatomy as well as the position of the coil orientation (D’Ostilio et al., 2014; Kammer, Vorwerg, & Herrnberger, 2007; Laakso, Hirata, & Ugawa, 2014; Mills, Boniface, & Schubert, 1992; Opitz, Windhoff, Heidemann, Turner, & Thielscher, 2011; Tofts, 1990). The result of that superposition is the electric field that is considered to cause neural activation in TMS (Esselle & Stuchly, 1992).

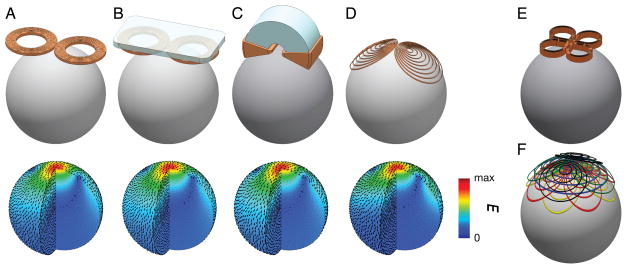
Figure 2.

Example illustrations of TMS coils (top) and the corresponding induced electric field distributions simulated in a spherical model (bottom). A. 70-mm figure-of-eight coil (The Magstim Ltd., Whitland, Wales). B. Figure-of-eight coil with soft-magnetic back-plate. C. C-core coil (Neuronetics, Inc., Malvern, PA). D. Minimum energy eccentric coil (Knäulein & Weyh, 1996). E. Cloverleaf coil. F. Multi-focal multi-layer coil, composed of two orthogonal layers of cloverleaf coils, a circular coil, and two orthogonal layers of figure-8 coils.

Figure 4.

Actual implementations of early magnetic stimulation coils: A. and B. early academic coils with C-shaped cores of a cobalt-steel alloy with high permeability and saturation level (Lorenzen & Weyh, 1992; Schmid, et al., 1993) (Courtesy of Dr. Thomas Weyh). C. Eccentric figure-of-eight coil. D. Cloverleaf coil (Courtesy of Dr. Eric Wassermann).

Figure 3.

Different approaches for improving stimulation coils with soft-magnetic materials: A. Commercial C-core coil (Neuronetics, Inc., Malvern, PA) and B. core-enhanced figure-of-eight coil with magnetic back-plate to reduce the field energy of the field as presented by A. Barker (A. T. Barker, 2001).

The overall process of induction in TMS is described by Maxwell’s equations, which summarize the physical laws given above. These equations or derivations thereof are in general the source for all spatial modeling of the electric fields induced by TMS.

2.2 Neurophysiology for the activation process and temporal aspects of TMS

Whereas Maxwell’s equations describe the physics of induction, they fall short in describing neural activation. The activation process is in the domain of neurophysiology. Neuron models of various types fill this gap. Neuron models are required, for instance, to estimate the local threshold of activation. For example, neuron models predict that similarly to supra-threshold electrical stimulation the TMS induced electric field may exclusively activate axons as was identified, e.g., by the neural time constant (Corthout, Barker, & Cowey, 2001; D’Ostilio et al., 2016; Nowak & Bullier, 1998a, 1998b; Peterchev, Goetz, Westin, Luber, & Lisanby, 2013). The axonal membrane contains electrically sensitive ion channels, most importantly for the excitation in the brain sodium channels such as Na_V1.1, Na_V1.2, Na_V1.3, and Na_V1.6, which respond to electric fields across their structure with nanomechanical conformation changes (Krishnan, Lin, Park, & Kiernan, 2009; Leterrier, Brachet, Dargent, & Vacher, 2011; Trimmer & Rhodes, 2004). The local density and genetic expression of types and subunits depends on both the neuron type and the location (Lai & Jan, 2006; Leterrier, Brachet, Fache, & Dargent, 2010; Trimmer & Rhodes, 2004). The membrane itself behaves electrically as a capacitance (Gentet, Stuart, & Clements, 2000; Howell, Medina, & Grill, 2015). Thus, neuron models are the key to understanding activation dynamics and studying pulse-shape effects. The temporal shape of pulses was reported to substantially affect efficiency and thus coil as well as device heating (Goetz et al., 2013; Goetz, Truong, et al., 2012; Niehaus, Meyer, & Weyh, 2000; Peterchev, Murphy, & Lisanby, 2011), to enable selective activation of certain neuron types or populations (Claus, Murray, Spitzer, & Flügel, 1990; Corthout, et al., 2001; Kammer, Beck, Thielscher, Laubis-Herrmann, & Topka, 2001; Kammer, et al., 2007; Ni et al., 2011; Peterchev, et al., 2013; Sommer, D’Ostilio, et al., 2014), and to increase neuromodulation strength compared to standard biphasic pulses in repetitive protocols (Antal et al., 2002; Arai et al., 2007; Arai et al., 2005; Goetz et al., 2016; Hannah, Ciocca, Sommer, Hammond, & Rothwell, 2014; Sommer, Ciocca, et al., 2014; Sommer, Lang, Tergau, & Paulus, 2002; Sommer et al., 2013). Finally, neuron models also explain and predict directionality effects of TMS, i.e., why the orientation of the coil affects the threshold and allows activation of different neuron populations (Goetz, et al., 2016; Niehaus, et al., 2000).

3 What are the major developments in TMS technology?

Magnetic stimulation devices typically consist of two components: a pulse source that generates the strong rapid current surge during a pulse (Fig. 1A), and a stimulation coil, which is placed over the neural target (Fig. 1B). In available technology, the pulse source determines the temporal shape of a pulse, i.e., the shape of the coil current over time, as well as the temporal sequence of pulse trains. The stimulation coil, on the other hand, is responsible for the spatial distribution of its magnetic field and consequently the spatial distribution of the induced electric field and the current flow in the brain.

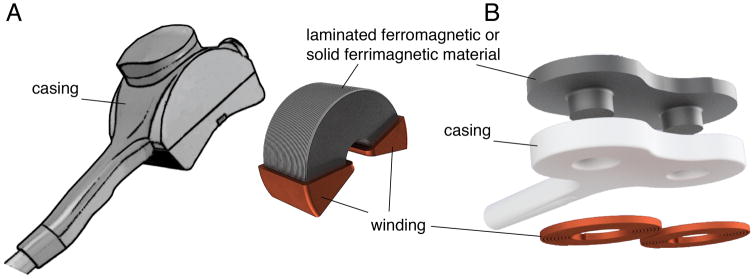
Figure 1.

A. Early repetitive stimulators such as the depicted monophasic stimulator with maximum repetition rates of more than 30 Hz, peak voltage of 5,000 V, and variable rise-time provided by adjustable capacitance between 40 μF and 200 μF allowed neuromuscular magnetic stimulation in the periphery and neuromodulatory protocols in the brain for the first time (Schmid, et al., 1993). B. Structure of a modern figure-of-eight coil, which is typically formed by a conductor loop, here a copper band, between the two pieces of the casing. The coil incorporates at least one, often two temperature sensors near the conductor that terminate stimulation when the coil exceeds the safe temperature range. It is usually filled with hardening resin for mechanical robustness, thermal conductivity, and electrical safety (modified from (Mould, 1998)).

3.1 Stimulation coils

3.1.1 Conventional coil designs

The stimulation coil forms the interface of the stimulation system to a subject or patient. Apart from material-related, mechanical, and thermal topics, the fundamental subject of coil design refers to the shape and position of the electrical conductor in the casing to generate a certain magnetic and in turn electric field distribution. As the electric field strength was found to correlate with activation, it should be large in the target area with minimum electric field strength elsewhere (Krings et al., 1997; Opitz et al., 2013). The portfolio of available specialized coils includes devices for small animals, peripheral neural and neuromuscular stimulation, as well as various cortical targets (see Fig. 2) (Bustamante et al., 2013; Bustamante, Gorostiza, López de Santa María Miró, & Iturri, 2007; Crowther et al., 2011; Deng, Lisanby, & Peterchev, 2013; Emrich et al., 2012; Goetz, Afinowi, Herzog, & Weyh, 2013; Goetz, Herzog, Gattinger, & Gleich, 2011; Knäulein & Weyh, 1996; Mueller et al., 2014; Ruohonen, Ravazzani, Grandori, & Ilmoniemi, 1999; Szecsi, Götz, Pöllmann, & Straube, 2010; Ueno, et al., 1988a). Importantly, despite the diversity of available stimulation coils, all coils—including coils that aim at deeper stimulation—induce a stronger electric field on the cortical surface than in deeper locations (Heller & van Hulsteyn, 1992). Furthermore, there is a general trade-off between focality and depths of stimulation so that focal stimulation implies a rather shallow field, whereas coils with deeper spread of the field are nonfocal (Deng, et al., 2013; Deng, Lisanby, & Peterchev, 2014). Mathematical optimization that included coil arrays by way of mathematical design of the solution space identified the Pareto front, which confirms this depth–focality trade-off, although the optimal trade-off curve has yet to be achieved with presently available coils (Gomez, Cajko, Hernandez-Garcia, Grbic, & Michielssen, 2013). Advances in high-power metamaterial research could enable more optimal coil design in the future.

Early magnetic stimulation coils were mostly circular (Barker, et al., 1985; Polson, et al., 1982). Some had modifications such as an angulated extension in the otherwise circular winding, which turned out to have limited impact on focality (Cohen et al., 1990). Figure-of-eight coils consist of two loops each with several wire turns that meet in the center to form a strong focus underneath (Fig. 1B, 2A–C) (Ueno, et al., 1988a). There are several strategies for increasing stimulation focality. The eccentric figure-of-eight coil has higher density of winding turns toward the center of the coil where the two loops meet (Fig. 2D, 4C); this coil has better focality compared to the conventional figure-of-eight coil with the same outer dimensions (Knäulein & Weyh, 1996). Coils with more than two loops, such as in the cloverleaf coil (Fig. 2E), were proposed and used for peripheral nerve stimulation, but did not gain popularity (Roth et al., 1994; Ruohonen, Ravazzani, & Grandori, 1998).

There has been tremendous interest in building small TMS coils for animal studies and in-vitro experiments (and exploration of multichannel systems, see Section 3.1.4). The fundamental challenge is that diminishing head sizes reduce coupling to the TMS coil (Weissman, Epstein, & Davey, 1992), thus prohibitively high coil currents are required to achieve suprathreshold stimulation. Although small circular current components, e.g., generated by small coil loops, would allow strong foci and high-definition control over spatial field distributions, their implementation is associated with difficulties. First, due to the spatial low-pass filtering behavior of distance, strong foci generated by small current loops attenuate rapidly with distance and do often hardly reach the cortex. Second, pulse sources require a certain minimum inductance of stimulation coils, whereas the inductance of presented micro-coils is typically small, and the available space is small to increase the number of turns and ensure necessary high-voltage insulation in between. Third, the required current for an approximately constant induced electric field strength grows approximately inversely to the squared diameter of a loop. Thus, for a micro-coil with only one fifth of the diameter of a loop of a conventional figure-of-eight coil, the necessary current increases about 25-fold, leading to a current in the multi-digit kilo-ampere range. At the same time, the space for a conductor with sufficient cross section to sustain such high currents without damage is rarely available. At present, micro coils, such as ones used in some rodent or in-vitro studies (Tang, Makowiecki, Bartlett, & Rodger, 2015), can only produce subthreshold field strengths that fall into the so-called low field magnetic stimulation realm, which can have different physiological effects and mechanisms from conventional suprathreshold TMS.

For concurrent TMS and functional magnetic resonance imaging (MRI), appropriate MRI-compatible stimulation coils and positioning systems have been developed (Bestmann, Baudewig, Siebner, Rothwell, & Frahm, 2005; Bohning et al., 1999; Moisa, Pohmann, Ewald, & Thielscher, 2009). For MRI compatibility, coils primarily have to withstand the additional forces caused by the Lorentz-type interaction of the strong coil currents with the external field of the MRI scanner and a preferably symmetric field, e.g., as in planar figure-of-eight coils, to avoid the generation of rotational momentum. Furthermore, to avoid conventional squirrel-cage-like MRI head detection coils, Navarro de Lara et al. presented a flat head MRI head coil that can be inserted between the stimulation coil and the head (Navarro de Lara et al., 2015; Navarro de Lara et al., 2013).

3.1.2 Use of ferromagnetic material

Although the use of magnetically active materials for the guidance of magnetic fields, such as iron, is state of the art in electrical engineering, e.g., for transformers, the majority of magnetic stimulation coils are air coils (Volz, et al.). Magnetic materials with high permeability can guide and concentrate magnetic fields with low resistance to reduce the stray field outside the intended target as was demonstrated during the early days of TMS (Lorenzen & Weyh, 1992). Well known examples for such materials are ferromagnetic iron, cobalt, nickel as well as a number of compounds, ferrimagnetics (also known as ferrites), and rarely antiferromagnetics (Jiles, 2016). Academic devices as well as commercial systems showed that the appropriate use of magnetic core material allows more flexible shaping of the magnetic field as well as a reduction of the required pulse current in the coil to achieve the same field as air coils (Al-Mutawaly & Findlay, 1998; Davey & Epstein, 2000; Davey & Riehl, 2005; Deng, et al., 2008; Epstein & Davey, 1994; Epstein & Davey, 2002; Lorenzen & Weyh, 1992; Salvador, Miranda, Roth, & Zangen, 2007 ). Most designs use a C-shaped core (Fig. 3A, Figs. 4A and 4B), which was derived from a ring transformer with an air gap (Davey & Riehl, 2005; Epstein & Davey, 1994; Lorenzen & Weyh, 1992; Riehl, 2004; Riehl & Ghiron, 2005). Nevertheless, magnetic flux guidance with magnetic materials was also described to reduce the magnetic stray flux of designs known from air coils, such as circular and figure-of-eight coils (Barker, 2001; Ghiron, Riehl, & Shipway, 2014; Kim, Loukaides, Sykulski, & Georghious, 2004). For instance, ferromagnetic or ferrimagnetic material on the back of a figure-of-eight coil concentrates the necessarily closed magnetic flux lines on the back closer to the conductors so that the field energy is smaller for the same or even larger field strength in the target area (Fig. 2B and 3B). Ideally, such a steel backplane can shunt up to half of the field to reduce the energy content of the stray flux.

However, the conditions of magnetic stimulation risk substantial magnetic loss in magnetic-core coils and require a careful design. The high frequency components of the TMS coil current of 1 kHz – 10 kHz are orders of magnitude higher than the typical frequencies of 50 Hz and 60 Hz in power engineering as well as ~500 Hz in electric vehicles. The high fundamental frequency of TMS can lead to substantial loss in the magnetic material in the form of eddy currents, static hysteresis, and anomalous loss. Importantly, the eddy current loss grows notably stronger with both frequency f and the magnetic flux density B than the other loss contributions and is approximately proportional to the squared frequency, f², as well as the squared magnetic flux density, B² (Krings & Soulard, 2010).

The material selection of iron cores involves at least three degrees of freedom. Due to the high magnetic flux densities of TMS (~2 T), the material should show a high magnetic saturation level. For flux densities above the magnetic saturation, the differential magnetic permeability falls from initially greater than 100 down to 1, i.e., the permeability of air. If pulses exceed that magnetic saturation level, the electric AC resistance drops by more than one order of magnitude, causing a sharp rise of the coil current and potentially undesirably loading the stimulator circuit. To avoid large eddy-current losses and associated heating due to the high fundamental frequency of TMS pulse currents, the electrical conductivity of the material should be small. Strong field amplification in the target demands a high magnetic permeability. Ferromagnetic materials such as iron or silicon steel provide both high saturation levels of up to approximately 2 T and high relative magnetic permeability of more than μ_r = 20,000, which both can be further improved by adding cobalt to the alloy, but are electrically conductive and require lamination to reduce eddy-current loss (Haiji, Okada, Hiratani, Abe, & Ninomiya, 1996; Littmann, 1967; Lorenzen & Weyh, 1992; Schmid, Weyh, & Meyer, 1993; Takada, Abe, Masuda, & Inagaki, 1988). Ferrites, on the other hand, are not electrically conductive and therefore present low loss, but saturate already at approximately 500 mT and offer lower relative permeabilities of ~1,000 (Gutfleisch et al., 2011; Ott, Wrba, & Lucke, 2003). Soft magnetic compounds (SMC), which contain small grains of soft-magnetic material in a nonconductive polymer matrix, may act as a compromise, but a use as a core material in magnetic stimulation coils has not been reported yet (Shokrollahi & Janghorban, 2007).

For the design and simulation process, various models for the nonlinear relationship of magnetic field strength H and the flux density B, which is also represented by the permeability μ, and magnetic loss in magnetic materials are known in the literature (Krings & Soulard, 2010). The Landau-Lifschitz equations as well as later modifications provide differential equations to describe the dynamics of domain-wall motion (Gilbert, 2004; Landau & Lifshitz, 1935). The Preisach, the Jiles-Atherton, and derived models describe B and H in relation of each other including hysteresis and can be incorporated into typical simulation systems used in TMS field modeling (Basso, Berlotti, Infortuna, & Pasquale, 1995; Bertotti, 1992; Bertotti, Basso, & Pasquale, 1994; Jiles & Atherton, 1986; Preisach, 1935). The simplest approach implements the nonlinearity as a look-up table and derives the magnetic loss in a post-processing step using the phenomenological approach by Bertotti et al. (Bertotti, 1988; Boglietti, Cavagnino, Lazzari, & Pastorelli, 2003).

3.1.3 Modified coil designs

Conventional coils induce electric fields with well-defined and temporally constant directionality. The local axes of the induced electric field at each location in the head stays the same throughout the entire duration of the pulse. The field of known coils thus has a fixed orientation relative to anatomic structures such as gyri and axons therein (Balslev, Braet, McAllister, & Miall, 2007). Rotem et al. presented a coil that rotates the induced electric field orientation during a pulse (Rotem et al., 2014). The demonstrated cloverleaf coil design is composed of two perpendicular figure-of-eight coils and requires two standard biphasic stimulators that are fired with a time delay that corresponds to a 90° phase shift of the underlying sinusoidal pulse. In experiments using conventional coils, neuronal activation is dependent on coil orientation; this directional sensitivity could be overcome with the rotating field coil design (D’Ostilio, et al., 2014; D’Ostilio, et al., 2016; Laakso, et al., 2014; Mills, et al., 1992; Rotem, et al., 2014).

The high loss of energy of a pulse of up to 100 J and the fast heating of stimulation coils has spurred work on superconducting coils. Superconducting stimulation coils would enable higher pulse amplitudes, faster pulse rhythms, and continuous long-term stimulation utilizing the latest protocols, such as theta burst (Friedman, Wolfus, Yeshurun, & Bar-Haim, 2004; Yang et al., 2010). However, the high currents of magnetic stimulation of up to 10 kA tend to be incompatible with the finite critical current densities of known superconductors (Lloberas, Sumper, Sanmarti, & Granados, 2014; Maeda & Yanagisawa, 2014). Above a few hundred Amperes per millimeter squared for the type-II high-temperature superconductor YBaCuO, depending on the cryogenic operating temperature and material properties such as grain structure, the current’s magnetic field influences the spin coupling of Cooper pairs—the essential charge carriers behind superconductivity—and renders superconductivity energetically unstable (Blatter, Feigel’man, Geshkenbein, Larkin, & Vinokur, 1994; Bugoslavsky et al., 2001; Palstra, Batlogg, van Dover, Schneemeyer, & Waszczak, 1989; Senoussi, 1992; Tixador et al., 2001). The effective cross section is further reduced due to screening currents that arise with the rapid alternating magnetic field during a pulse flow into the opposite direction of the intended coil current. These screening currents are also responsible for the diamagnetic behavior of superconductors, known as the Meissner effect (Larbalestier, Gurevich, Feldmann, & Polyanskii, 2001; Uglietti, Yanagisawa, Maeda, & Kiyoshi, 2010). Filamentation and Roebel structures, similar to Litz wires in conventional coils, can reduce such issues (Badcock et al., 2009; Hussennether, Oomen, Leghissa, & Neumüller, 2004; Long et al., 2008). Furthermore, most high-temperature superconductors are brittle and do not withstand the mechanical stress caused by the magnetic forces during a pulse without proper stabilization (Lloberas, et al., 2014). Due to further practicality issues in manufacturing and as the cooling effort is high and has to be implemented without substantially increasing the distance to the target, no successful superconducting TMS coil is known to date.

The high current surges during a pulse cause substantial mechanical forces in the pulse source, the cable, and the coil (Counter & Borg, 1992). These forces emit a loud clicking sound, which reaches the ears in two ways: through the air as well as bone conduction (Stenfelt & Goode, 2005). Due to its brevity, the clicking sound is typically underestimated with respect to its sound pressure level (Counter & Borg, 1992; Goetz et al., 2015; Starck, Rimpiläinen, Pyykkö, & Esko, 1996). There are reports of several cases of at least temporary hearing threshold shift and at least one case of permanent hearing loss associated with TMS in the literature (Counter, Borg, & Lofqvist, 1991; Loo et al., 2001; Pascual-Leone et al., 1993; Zangen, Roth, Voller, & Hallett, 2005). Even with earplugs for protection, the clicking sound distracts subjects and complicates the application of TMS during sleep. More importantly, despite earplugs, the TMS clicking sound activates auditory brain networks, which can dominate the intended TMS-induced brain activation (Bestmann, et al., 2005; Counter, 1994; Nikouline, Ruohonen, & Ilmoniemi, 1999; Siebner et al., 1999; Stenfelt & Goode, 2005; Tringali, Perrot, Collet, & Moulin, 2012). Modern coils use a stiff, rigid structure but could reduce the sound pressure only to a small amount. Vacuum casing as well as the use of shear coolants were proposed (Ghiron & Riehl, 2005; Ilmoniemi, Ruohonen, Kamppuri, & Virtanen, 1997). A recent solution implemented a coil structure with dedicated layers for acoustic decoupling and dissipation as well as pulses with its spectral content exclusively in the ultrasound range (Goetz, Murphy, & Peterchev, 2014; Peterchev, Murphy, & Goetz, 2015). For ultrasound, the sound impedances and absorption rates of most materials increase, the ear is less sensitive from a mechanical perspective, and safety levels are far higher (Howard, Hansen, & Zander, 2005; Möser & Kropp, 2010). In a demonstrator, the two-pronged approach reduced the sound pressure by more than 25 dB and the perceived psychoacoustic loudness of the coil click by 14-fold.

3.1.4. Inverse problem of optimum coils

Most coil simulation models analyze typically predefined coils and compared their performance (Deng, et al., 2013). Few analyses have been aimed at optimizing coil parameters such as winding thickness, radii, and other spatial characteristics in an analytical sense (Beyzavi & Nguyen, 2008; Jarmo Ruohonen, Virtanen, & Ilmoniemi, 1997). Recently, the computational TMS community increased its focus on numerical optimization of coils for specific objectives (Ilmoniemi, Koponen, Nieminen, & Järnefelt, 2013; Koponen, Nieminen, & Ilmoniemi, 2015; Starzynski, Szmurlo, & Sawicki, 2009). Most approaches embed physical electric field simulation models into iterative global optimization methods, such as genetic algorithms. Both realistic head models, e.g., solved with the finite element method, and idealized spherical models that allow accelerated semi-analytical solutions, such as spherical harmonics, can serve on the physics side (Gomez, et al., 2013; Starzynski, et al., 2009). A number of models parametrize coils, e.g., by radius, height, position, and overlap as well as cross section of individual coil components to maximize stimulation in a particular target (Starzynski, et al., 2009; Xu, Wang, Chen, Yang, & Yan, 2005). Alternative methods perform a widely unconstrained optimization without defining a certain parametric coil shape, but generate the extracranial current distribution required for the specific objectives almost freely (Gomez, et al., 2013; Ho et al., 2009; Koponen, et al., 2015). Koponen et al., for instance, decompose the field into basic components with increasing spatial frequency and varies the weights of each component in the superposed solution, i.e., the individual current, until the minimum energy objective is best met (Koponen, et al., 2015). The set of spatial components should span a more or less complete vector space and can use purely mathematical concepts such as Lissajous or Rose winding curves, discrete cosine modes as known from the JPEG image format, or Laplacian spherical harmonics for the current distribution. Alternatively, a multilayer coil can be constructed using a sequence of standard coils (e.g. Fig. 2F, layer 1: cloverleaf coil, layer 2: cloverleaf coil with a 45° rotation, layer 3: circular coil, layer 4: figure-of-eight coil in x-direction, layer 5: figure-of-eight coil in y-direction) (Ilmoniemi, Koponen, Nieminen, & Järneflt, 2014).

In the TMS community, numerical coil optimization seems to go hand-in-hand with another trend to design multi-focal or multi-channel micro-scale stimulation coils (Ho, et al., 2009; Laudani, Fulginei, & Salvini, 2015; Roth, Levkovitz, Pell, Ankry, & Zangen, 2014; Ruohonen & Ilmoniemi, 1998; Ruohonen, et al., 1999; Xiong, Shi, Hu, & Liu, 2016). Several approaches use a flat or curved grid of approximately equally sized loops (Han, Chun, Lee, & Lee, 2004; Ho, et al., 2009; Laudani, et al., 2015; Ruohonen & Ilmoniemi, 1998; Ruohonen, et al., 1999; X. Wang, Chen, Guo, & Wang, 2005). Alternatively, Ge et al. use a grid of vertical and horizontal lines mapped onto a head instead of loops (Ge, Wang, Tang, Xiao, & Wu, 2012). A ring current can be generated by controlling the current of two vertical and two horizontal lines appropriately. As such, the grid structure resembles address lines in TFT screens or historic computer memory. Optimization in such framework adjusts the current amplitude in the individual loops or the conductors of a linear grid to optimize certain objectives, such as the electric field in a predefined target while minimizing the overall field energy or co-activation elsewhere (Gomez, et al., 2013). Indeed, if the current share of each channel is fixed and not used to dynamically change between several neural targets, the currents of the individual channels of the multichannel coils can be mathematically converted into an overall planar current distribution and be approximated with an equivalent winding pattern that does not contain the regular grid of loops any more. However, many multichannel coil approaches are widely naïve to manufacturing coils and to the necessary high currents in the kilo-ampere range, which increase inversely to the square of the coil size. Other implementation challenges include: coupling between the channels that may distort the stimulator circuit operation; the heating and forces associated with small coil elements; and complex electronic control of independent channel currents. Accordingly, most articles on multichannel TMS still lack reports on a successful implementation and experimental data.

3.2 Stimulators and waveforms

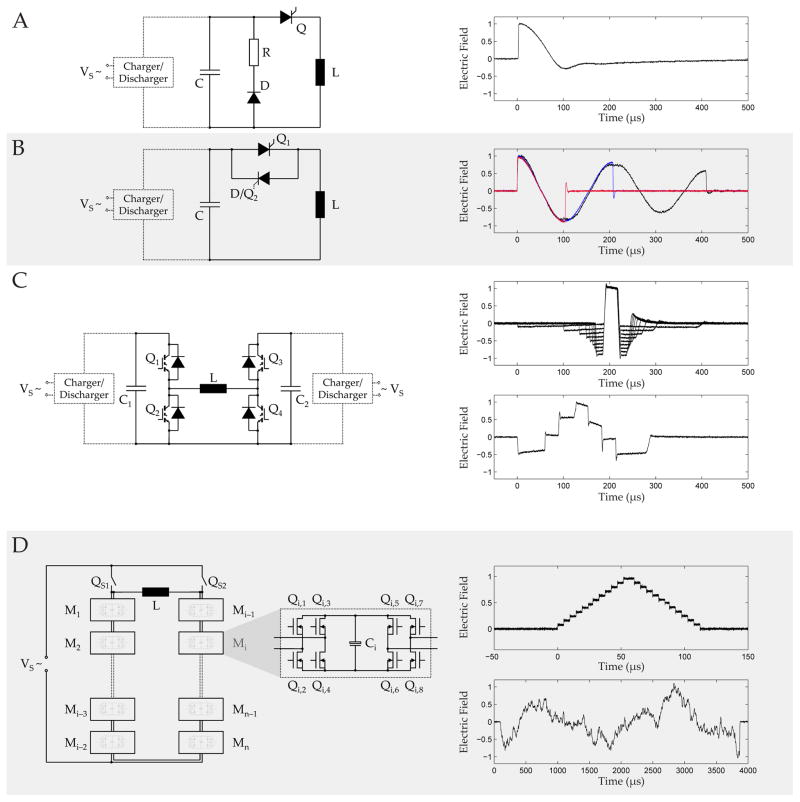
Whereas the stimulation coil determines the spatial field conditions, the stimulator or pulse source generates the pulse current and is responsible for the temporal aspects (see Fig. 5) (Jalinous, 1991). Because the electrical parameters of commercial systems have converged to very similar values, pulse sources are typically general-purpose devices that can feed a variety of coils. The challenge for pulse sources is the combination of very high currents and the briefness of stimulation pulses, which exceed the range of conventional electronics technologies such as amplifiers. Most pulse sources therefore exclusively use an electrical oscillator design with a pre-charged capacitor and a power switch in the device and an inductance represented by the stimulation coil to form a more or less damped sinusoidal current shape (Peterchev, et al., 2015; Polson, et al., 1982). Closing the switch establishes a current oscillation between the pre-charged capacitor and the stimulation coil, which can: be damped with a resistor to slowly return to zero and form so-called monophasic pulses (Fig. 6A); be terminated after one period to generate so-called biphasic pulses; or left oscillating for several periods to form polyphasic pulses (Fig. 6B) (Peterchev, et al., 2015). However, the oscillator that is formed by closing the switch depends on the components only and cannot be changed without reconfiguring the circuit. Several devices that could generate pulses different to these standard pulses, such as sinusoidal half-wave pulses with up to 400 μs duration as well as rectangular and trapezoidal pulses, were presented, but none of these could adjust the pulse shape over a wider range during operation (Havel et al., 1997; J. F. Nielsen, Klemar, & Kiilerich, 1995). The prevailing switch in TMS devices is the thyristor, a type of controllable electrical diode that can only be turned on but not actively turned off. From the time of triggering the pulse on, the circuit is no longer controlled from outside. In consequence, the pulses of most available TMS stimulators are fixed with respect to pulse duration and shape. Practical aspects for device implementation of prevailing conventional devices are discussed in detail in the literature (Al-Mutawaly & de Bruin, 2001; Cadwell, 1991; Jalinous, 1991; McRobbie, 1985; Wolf & Walker, 1991).

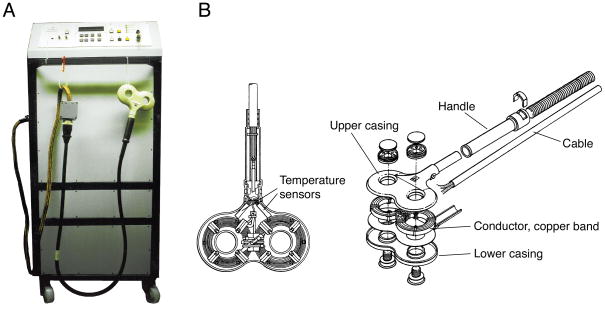
Figure 5.

A. First magnetic stimulator built by Drs. M. Polson and A. Barker in 1982, which was a single-pulse device primarily tested in animals and peripherally (Polson, et al., 1982) (Courtesy of Dr. Michael Polson). B. Modern repetitive pulse source with power supply, high-voltage pulse train, and control unit (Mag&More GmbH, Munich, Germany).

Figure 6.

Circuit topologies (left column) and typical pulse shapes (right column) of typical magnetic stimulation pulse sources. A. Monophasic stimulator, B. Biphasic and polyphasic stimulator, C. controllable parameter TMS (cTMS), D. Modular pulse synthesizer.

Recent developments have achieved overcoming the pulse-shape limitation and allow adjusting the shape during operation. Several refinements of a TMS technology that enables the configuration of pulse parameters (cTMS) have been demonstrated and are available commercially (Fig. 6C) (Peterchev, D’Ostilio, Rothwell, & Murphy, 2014; Peterchev, Jalinous, & Lisanby, 2008; Peterchev, et al., 2011). cTMS splits a pulse into few near-rectangular voltage segments, which can be adjusted in amplitude and duration. Modern high-voltage high-power semiconductor devices—specifically insulated gate bipolar transistors (IGBT)—let cTMS actively commutate the coil current between two capacitors with different capacitance and arbitrary initial charge level. A pulse can be assembled of phase segments selecting from three different electric field amplitude levels, while the three amplitude levels can be slightly changed between consecutive pulses in a train (Peterchev, D’Ostilio, Rothwell, & Murphy, 2014).

More flexibility and increased control over the pulse shape as well as the combination of pulses in a train require giving up a number of conventions of TMS electronics, including slow high-power switches and the oscillator design. A recently developed modular pulse synthesizer technology, for instance, does not implement an oscillator design but combines the output of multiple fast-switching lower power modules to generate practically any pulse shape as well as trains of rapidly changing pulse shapes (Fig. 6D) (Goetz et al., 2016; Goetz, Peterchev, & Weyh, 2015; Goetz, Pfaeffl, et al., 2012). In contrast to, for instance, conventional monophasic pulse sources, the principle of the modular pulse synthesizer is highly efficient and can recover most of the energy of any pulse shape for the next pulse. Thus, it can also generate the monophasic pulse shape at high repetition rates.

4 Models of the induced electric field distribution

4.1 Modeling approaches and technical aspects

The key phenomenon behind magnetic stimulation is electromagnetic induction. Mathematically, the induced electric field is derived through differential operators that act spatially and temporally on the magnetic field. In the operating frequencies of TMS (< 10 kHz), the quasi-static approximation allows that the spatial distribution of the magnetic field can be decoupled from its temporal dynamics (Bossetti, Birdno, & Grill, 2008). Numerically, the calculation of induced currents tends to instability as is known from other disciplines (Beck, Hiptmair, & Wohlmuth, 1999; Biro & Preis, 1990; Biro, Preis, Buchgraber, & Ticar, 2004; Clemens, Wilke, & Weiland, 2001; Hollaus & Biro, 2000; Soleimani, Lionheart, Peyton, Xiandong, & Higson, 2006; Wong & Cendes, 1989). In magnetic stimulation, stability is further complicated by the nonideal geometry in case of realistic models and because the coil currents and the induced currents in the brain differ by at least six orders of magnitude but are numerically tightly coupled in Maxwell’s equations as well as the double-curl equation that is derived from them using the Helmholtz decomposition. To enhance stability and increase speed, magnetic stimulation has been modeled with a variety of equation systems derived from Maxwell’s equations. Alternative equation systems are, for instance, the T-Ω formulation to enforce stability by a more appropriate choice of potentials, and various ways to decouple the coil and the induced currents so that the back-action of the small induced current on the coil current (Goetz, Afinowi, et al., 2013; Golestanirad, Mattes, Mosig, & Pollo, 2010; Miranda, Hallett, & Basser, 2003; Opitz, et al., 2011; Sawicki, Starzynski, & Wincenciak, 2006; Thielscher, Opitz, & Windhoff, 2011; Wagner et al., 2008; Wagner et al., 2014; Yang et al., 2006). The so-called A-V formulation of the magnetic field first solves the magnetic vector potential (A), then in a second step, derives the electric scalar potential (V). For the computational solution of these partial differential equations, researchers in the field use several different approaches, including finite difference methods (Fanjul-Vélez, Salas-García, Ortega-Quijano, & Arce-Diego, 2015; Toschi, Welt, Guerrisi, & Keck, 2008, 2009), finite volume methods (Goetz, Afinowi, et al., 2013; He & Liu, 2016), boundary element methods (Im & Lee, 2006; Nummenmaa et al., 2013; Salinas, Lancaster, & Fox, 2009), and impedance methods (De Geeter, Crevecoeur, & Dupre, 2011; De Geeter, Crevecoeur, Dupré, Van Hecke, & Leemans, 2012; De Geeter, Crevecoeur, Leemans, & Dupré, 2015; Nadeem, Thorlin, Gandhi, & Persson, 2003), while finite element methods (FEM) dominate (Bijsterbosch, Barker, Lee, & Woodruff, 2012; Chen & Mogul, 2009; Deng, et al., 2013; Janssen et al., 2013; Laakso & Hirata, 2012; Laakso, et al., 2014; W. H. Lee, Lisanby, Laine, & Peterchev, 2014; Miranda, et al., 2003; Opitz, et al., 2011; Masaki Sekino & Ueno, 2002; Thielscher, et al., 2011; Windhoff, Opitz, & Thielscher, 2013).

4.2 Simplified models

The early three-dimensional spatial models of magnetic stimulation were generally based on simplified and symmetric geometry, such as infinite half-planes and perfect spheres. For example, in a magnetic coil design study, the brain was approximated using a quasi-spherical volume conductor, enclosed by 58 planes (Ueno, Tashiro, & Harada, 1988b). In the theoretical model proposed by Rush and Driscoll (Rush & Driscoll, 1968), the head was modeled as three conducting concentric spherical shells consisting of the scalp, skull, and brain tissue. Each shell is considered as homogeneous with a dielectric property of the tissue it represents (Al-Mutawaly & Findlay, 1998; Deng, et al., 2013; Deng, Lisanby, & Peterchev, 2015; Deng, et al., 2008; Miranda, Lomarev, & Hallett, 2006; Ravazzani, Ruohonen, Grandori, & Tognola, 1996). With increasing computational power, progress in brain imaging, and available software tools, spherical head models were replaced by still idealized imaging-based head models (Fig. 8A) (Masaki Sekino & Ueno, 2002; Sekino & Ueno, 2004; Wagner, et al., 2008; Wagner, et al., 2004; Yang, et al., 2006) and finally gyri-precise realistic head models (Fig. 8B) (Cerri, De Leo, Moglie, & Schiavoni, 1995; Chen & Mogul, 2009; Im & Lee, 2006; Nadeem, et al., 2003; Salinas, et al., 2009). While spherical head models predict the absence of radial currents induced by TMS, which falsely justified the claim that only interneurons tangential to the cortical surface are stimulated during TMS, realistic head models showed otherwise. There were also gross discrepancies between spherical and realistic head models, and the differences are more pronounced for temporal and frontal targets (Nummenmaa, et al., 2013). Nevertheless, spherical models have been useful for TMS coil design (Davey & Riehl, 2006; Deng, Peterchev, & Lisanby, 2008; Ruohonen & Ilmoniemi, 1998) and evaluation of stimulation sites (Thielscher & Kammer, 2002).

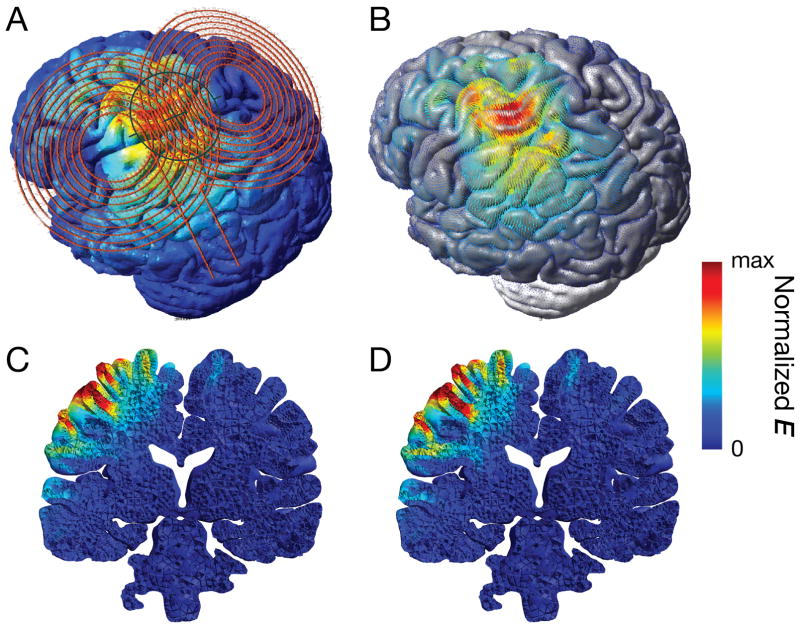
Figure 8.

Realistic head model of TMS: A. Figure-of-eight coil placed over the left primary motor cortex. B. Induced electric field distribution showing the effect of a focus spread out over several gyri. C. A coronal view at the level of the TMS hotspot, in a head model that assumes isotropic tissue conductivity for the white matter. D. The same view as in C in a head model that incorporated white matter anisotropy derived from diffusion tensor imaging data. The model shows slightly deeper reach of the electric field.

As a consequence of the macroscopic treatment of the problem, the representation of the head as an assembly of different materials forms abrupt material interfaces, e.g., between white and grey matter, where electrical parameters such as the conductivity can change by a factor of two (Bijsterbosch, et al., 2012). In simulation models, this abrupt step in conductivity leads to charge accumulation and therefore strong local electric fields at the interface (Kent Davey, Epstein, George, & Bohning, 2003; Silva, Basser, & Miranda, 2008). However, the brain microanatomy does not show such abrupt changes but is notably less defined and fringed. Furthermore, the currently prevailing model of neural activation by TMS considers the intra-axonal electric field responsible for neural activation, which is only peripherally affected by such extra-axonal interfaces (Roth & Basser, 1990). The interaction between macroscopic field modeling and the axonal membrane is not based on a consistent theory and may require more research in the future.

4.3 Models with increased level of detail

One way to increase the accuracy of the tissue-property representation introduces anisotropy, particularly of the electric conductivity. Due to the fibrous structure, white matter shows a by up to one order of magnitude higher conductivity along the dominant fiber orientation (Gabriel, Peyman, & Grant, 2009). Models implementing anisotropy extract the local fiber orientation from diffusion tensor imaging (DTI) and show minor changes for the electric field in the grey matter and the position of the stimulation focus, but local electric field amplitudes differ by up to approximately 20% (Fig. 8C and 8D) (De Geeter, et al., 2012; De Geeter, et al., 2015; De Lucia, Parker, Embleton, Newton, & Walsh, 2007; Lee et al., 2012; Lee, Lisanby, Laine, & Peterchev, 2016; Miranda, et al., 2003). Nummenmaa et al. further used DTI data to extract the local fiber orientation at the gyral crown in the focus to determine the optimal coil position for stimulation (Nummenmaa et al., 2014).

Due to cerebrospinal fluid (CSF) having a higher conductivity by a factor of approximately 5 to 20 times compared to other brain tissue, the exact location and the interface with the grey matter has a dominant influence on the field strengths in the grey matter and exceeds the influence of the interface between the grey and the white matter (Bijsterbosch, et al., 2012; Janssen, et al., 2013; Miranda, et al., 2003; Wagner, et al., 2008). Realistic head models found that the increase of the electric field in the gyral crowns is far beyond what the lower distance of these areas to the stimulation coil would explain (Bijsterbosch, et al., 2012). The highest electric fields in the brain emerge where the CSF is thinnest (Bijsterbosch, et al., 2012; Janssen, et al., 2013). With respect to modeling quality, an accurate segmentation of the surface between CSF and grey matter and a realistic representation of local thicknesses of the CSF layer therefore seems highly important. Both can suffer in automatic segmentation, which is known to show limited reliability particularly at these interfaces (de Boer et al., 2010; Eggert, Sommer, Jansen, Kircher, & Konrad, 2012; Klauschen, Goldman, Barra, Meyer-Lindenberg, & Lundervold, 2009). Janssen et al. studied the influence of a misestimated surface of the grey matter by eroding as well as growing the gyrus systematically starting from a reference segmentation and wound changes of electric field strength particularly in the surface of the grey matter and the vicinity (Janssen, et al., 2013). Importantly, CSF also affects focality. The more pronounced the sulci between gyri are modeled the wider the focus becomes spread over one or several gyri (see Fig. 8) (Janssen, Oostendorp, & Stegeman, 2015; Janssen, et al., 2013). Furthermore, CSF and its modeling can notably shift the actual focus of stimulation determined by the electric field magnitude vs. the assumed focus given by the coil axis (Bijsterbosch, et al., 2012). Several sensitivity analyses derived statistical information in which way important parameters, e.g., tissue conductivity, coil position and orientation, as well as uncertainties in such parameters influence the focus and the effective stimulation strength in the target (Gomez, Yücel, Hernandez-Garcia, Taylor, & Michielssen, 2015; Toschi, Keck, Welt, & Guerrisi, 2012). Such parameter sensitivity analyses typically use Monte-Carlo methods or models that do not process physical metrics but statistics, i.e., distributional information thereof.

Modern personal computers have reached sufficient computational power that the induced electric field can be estimated in real time. Consequently, highly simplified spatial field models can be introduced into frameless stereotactic neuronavigation systems, where they are overlaid with the brain anatomy (Comeau, 2014; Nummenmaa, et al., 2013; Ruohonen & Karhu, 2010). As realistic head models easily overwhelm computers, spherical head models with homogeneous tissue properties, i.e., one bulk conductivity, scaled to the specific head dimensions prevail. However, targeting with neuronavigation is usually performed on the gyral and sub-gyral level so that the missing anatomic fine structure and effects such as spreading of the focus across gyri could mislead (Sahlsten et al., 2015). A realistic model framework with substantially reduced spatial resolution of 3 mm that applies the admittance method and eliminates the back-action of the brain fields on the coil current was proposed to bring computation times to the order of ~20 s (Paffi et al., 2015). Fast parallel computation on graphics processors and Green’s function approaches may allow the use of more realistic anatomy in the future.

At present, electric field models in magnetic stimulation typically neglect the cellular structure of biological tissue as well as membranes but treat the brain as an assembly of homogeneous compartments of materials with average properties, such as electrical conductivity and permittivity. The electrical conductivity macroscopically describes the effective mobility of electric charge carriers through the cellular tissue (Gabriel, et al., 2009). A large permittivity results from the high number of thin cell membranes, which act as capacitors, and causes displacement currents. Whereas many TMS field simulation models neglect the permittivity (Bijsterbosch, et al., 2012; Goodwin & Butson, 2015; Janssen, et al., 2013), De Geeter et al. identified the permittivity to be responsible for about 20% of the field strength in the focus of the coil (De Geeter, et al., 2012). Furthermore, permittivity values used in TMS models are based on ex-vivo measurements, where membranes may have degraded, and have been suspected to underestimate in-vivo conditions (Gabriel, Lau, & Gabriel, 1996; Wagner, et al., 2014).

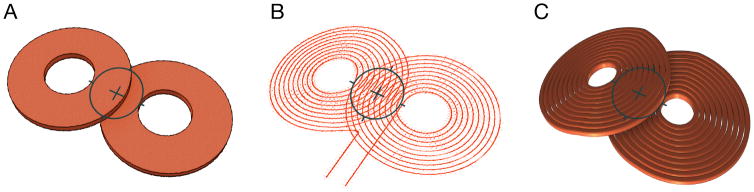
Finally, stimulation coils are often still represented by idealized geometries, such as single or double tori or hollow cylinders with only one loop in which the current either freely distributes in the simulation or with enforced constant current density (see Fig. 7). For an accurate estimation of the electric field distribution in the target, however, precise coil models need to incorporate the individual turns of a coil to account for proximity and skin effects, which can reduce the simulation error by up to 30% (Laakso & Hirata, 2012; Laakso, et al., 2014; Nadeem, et al., 2003; Salinas, et al., 2009).

Figure 7.

Coil models with: A. bulk conductor, B. individual turns with idealized line current, and C. individual turns with 3D representation of windings, demonstrating the increasing level of detail in induced-field modeling.

5 Models of the neural activation process

5.1 Phenomenological neuron models

Neuron models fill the deficiency that above-described spatial models can only describe the field distribution but do not include the actual neural response. A number of neuron models with different levels of detail are in use for simulating the neural response to TMS. These models include purely mathematical descriptions that mimic neural behavior as well as models reflecting the actual biological and physical mechanisms on the level of the neural membrane.

The simplest model in TMS research is the leaky integrate-and-fire neuron (Bostock, 1983; Corthout, et al., 2001; Lapicque, 1907; Peterchev, et al., 2011). This model describes the excitable neural membrane as a leaking electrical capacitor, i.e., a parallel connection of a capacitor C, which can be charged up by stimulation, and a resistor R, which discharges the capacitor with a time-constant of τ = RC. Some of these first-order models have a built-in resetting property, that is, when the depolarization exceeds a predefined threshold level, the model spikes and is reset to zero (Brunel & van Rossum, 2007; Izhikevich, 2004). By itself, the leaky integrate-and-fire neuron model is a low-pass filter with respect to the stimulator output amplitude and reflects the well-known strength-duration curve (Corthout, et al., 2001). Due to its low number of parameters, the leaky integrate-and-fire model can be noninvasively calibrated to real neurons in-vivo (Corthout, et al., 2001; D’Ostilio, et al., 2016; Peterchev, et al., 2013) (Deng, Lisanby, & Peterchev, 2011). The use of different coil orientations was reported to enable such system identification for specific neuron populations in the same cortical target volume (D’Ostilio, et al., 2014; D’Ostilio, et al., 2016). The leaky integrate-and-fire model may be sufficient for predicting trends and if the tested pulse shapes belong to the same class, i.e., that the pulses are typically related to each other by expansion and compression. However, as a highly simplified passive model with exclusively linear dynamics, it does not reflect the complex nonlinear active mechanisms of neurons. It is known to show deviations, e.g., when the pulse shape is substantially varied, for short pulses, and for double pulses as well as polyphasic pulses (Fang & Mortimer, 1991; Maccabee et al., 1998; Moffitt, McIntyre, & Grill, 2004). These deviations are also known in electrical stimulation (Bennie, Petrofsky, Nisperos, Tsurudome, & Laymon, 2002; Buetikofer & Lawrence, 1978, 1979; Dean & Lawrence, 1985; Gorman & Mortimer, 1983; Grill & Mortimer, 1995; A. Wongsarnpigoon, Woock, & Grill, 2010).

5.2 Biophysical neuron models

More accurate nonlinear neuron models include several purely mathematical representations without further biophysical meaning such as the FitzHugh-Nagumo, the Hindmarsh-Rose, and the Izhikevich models (d’Aloja, Lino, Maione, & Rizzo, 2005; d’Aloja, Lino, Maione, & Rizzo, 2007; FitzHugh, 1961; Hindmarsh & Rose, 1984; Izhikevich, 2003; Nagumo, Arimoto, & Yoshizawa, 1962; Suárez-Bagnasco, Armentano-Feijoo, & Suárez-Ántola, 2010; Xiu Wang, Wang, Deng, Wei, & Li, 2013). However, due to the high numbers of parameters of these models despite the limited mechanistic insight, biophysical models dominate at present. Biophysical models used in the TMS community typically follow the formalism of Hodgkin and Huxley, who described the neuron activation dynamics in electrical circuit models with nonlinear elements representing different ion conduction mechanisms, which were later discovered as ion channels (Hodgkin & Huxley, 1952). The Hodgkin-Huxley model describes the giant squid axon, which notably deviates from mammalian and particularly human neurons. The expansion of the formalism of equivalent electric circuits to add spatial characteristics of neurons initiated modern one-dimensional compartment models (McNeal, 1976; Scott, 1975). The concept of equivalent electrical circuits has been substantially expanded in computational neuroscience and led, for instance, to complex circuit models of entire motor units or for computational simulation of neuromodulation (Peasgood, Dissado, Lam, Armstrong, & Wood, 2003; Szlavik, 2008; Szlavik, Bhuiyan, Carver, & Jenkins, 2006; Szlavik & de Bruin, 1999).

Latest neuron models using the same formalism though different parameters are available for various mammalian neuron parts such as axon, soma, and dendrites as well as for their subsegments such as the axon initial segment, myelinated axon sections, and axonal nodes as these are known to differ with respect to expressed ion channel types and their densities on the membrane surface (Baker, Bostock, Grafe, & Martius, 1987; Bender & Trussell, 2012; Kole et al., 2008; McIntyre, Richardson, & Grill, 2002; Scholz, Reid, Vogel, & Bostock, 1993; Schwarz, Reid, & Bostock, 1995; Stephanova & Bostock, 1995). More complicated patterns of local accumulations that may affect excitability to TMS stimuli such as ion channel rafts have not been studied yet (Freeman, Desmazières, Fricker, Lubetzki, & Sol-Foulon, 2016; Kole & Stuart, 2012; Rasband & Peles, 2016; Vacher & Trimmer, 2012). In multi-compartment models, these segments and subsegments are combined to represent entire neurons (Kamitani, Bhalodia, Kubota, & Shimojo, 2001; McIntyre, et al., 2002; Salvador, Silva, Basser, & Miranda, 2011b).

Neuron models in TMS research have been set up as stand-alone models as well as implemented into spatial brain models. Stand-alone neuron models neglect the induction process as well as the spatial influence of the brain and can therefore not predict absolute thresholds without calibration but allow relative comparisons (Reilly, 1989). One important aspect of stand-alone neural models for TMS is the study of the neural activation process. A solid understanding of the neural activation process is, for instance, essential for the design of pulse shapes for effective activation of neurons (Corthout, et al., 2001).

5.3 Applications of neuron models

Important questions raised in the TMS community that could be solved by neuron models are the well-known experimental observations that biphasic pulses effectively stimulate, although they appear to compensate their depolarizing phase by their hyperpolarizing phase(s) and that polyphasic pulses even further decrease the threshold (Emrich, et al., 2012; Goetz, Weyh, & Herzog, 2009; Maccabee, et al., 1998; Pechmann et al., 2012). Similarly, neural models explain the higher threshold of monophasic relative to biphasic pulses as well as directional effects of the monophasic pulse shape (Salvador, et al., 2011b).

Head and single-neuron models well describe the spatial and temporal aspects of the initial activation process of single pulses. These models, however, cannot describe nor optimize neuromodulation effects. Neuromodulation phenomena as the basis of most cognitive research applications as well as therapeutic interventions of TMS emerge if several pulses are combined with certain timing constraints and trigger network effects. Esser et al. designed an appropriate large-scale thalamo-cortical model (Esser, Hill, & Tononi, 2005). The model includes > 30,000 neurons with > 5,000,000 synaptic connections in layers 2/3, 5, and 6 of the primary motor cortex and the thalamus with afferents from premotor and somatosensory circuits, but excludes spatial field calculations as well as activation dynamics, which were the center of above-described models. Each neuron is implemented as a simplified nonlinear single-compartment model with sodium and potassium channels to simulate physiological spiking behavior, though without the need for exact representation of the TMS activation process at the axonal membrane. Instead TMS pulses can be implemented by an activation of a predefined portion of synapses, while the portion increases for higher pulse amplitudes (Esser, et al., 2005). The model mimics the phenomenon that individual TMS pulses of sufficient amplitude cause several cortico-spinal responses, so-called I waves (Di Lazzaro, et al., 2012; Di Lazzaro, Ziemann, & Lemon, 2008; Esser, et al., 2005). With increasing pulse amplitude, the first wave, I1, is followed by up to three subsequently emerging additional responses, I2, I3, and I4, each ~ 1.5 ms apart. The model hypothesizes the multiple I waves to emerge from layer 5, where the density of inhibitory cells is considered and modeled lower than in upper cortical layers (Beaulieu, 1993).

An alternative model for the generation of I waves by d’Aloja et al. was implemented with a network of 500 cortical neurons and 100 corticospinal neurons, each of them represented by an Izhikevich spiking unit (d’Aloja, et al., 2005). The cortical neurons form a highly interconnected network, and each corticospinal neuron receives inputs from five cortical neurons. Rusu et al., in contrast, aim at explaining the I-wave generation in a model of a single pyramidal cell (Rusu, Murakami, Ziemann, & Triesch, 2014). The authors hypothesize that all could result from signal delays due to synaptic distance from the soma. However, general knowledge gaps of the mechanisms behind neuromodulation affect the predictive quality of corresponding models. As a consequence, essential outcomes in Rusu et al., e.g., the delays, are set as a-priori parameters, so that the model is not clearly falsifiable from an epistemological perspective and therefore risk a model without predictive qualities (Popper, 2005). Esser et al. rely on weaker assumptions, such as an increasing portion of excitatory neurons from layer 2 to layer 5 (Esser, et al., 2005).

More detailed models were designed to further describe and explain neuromodulation on the synaptic level. Huang et al. implemented a calcium-concentration based model (Huang, Rothwell, Chen, Lu, & Chuang, 2011). The model assumed a mixed effect of slow inhibition and fast facilitation dynamics to explain theta-burst stimulation. Since the dynamics of the development of inhibition and facilitation differ in this model, it further provides a potential explanation for the train-length-dependent neuromodulation effect of theta-burst stimulation.

Neuron models in TMS not only serve as an analytic tool to study existing technology and pulse shapes. Models are increasingly used to synthesize both novel pulse shapes and more effective pulse trains (Goetz, Truong, et al., 2013; Goetz, Truong, et al., 2012; Wilson, Goodwin, Brownjohn, Shemmell, & Reynolds, 2014). At present, new pulse shapes were studied and improved particularly with respect to their physical parameters, such as the specific stimulation threshold, associated coil heating, and acoustics. Parameter studies of pulse shapes started to explore ranges of pulse shapes that are not implemented in commercial TMS devices. Recent approaches freely synthesize TMS pulse shapes to find global optima by solving the underlying variational problem (Goetz, Truong, et al., 2013; Goetz, Truong, et al., 2012). Similar approaches are in progress for transcutaneous and invasive electrical stimulation (Jezernik, Sinkjaer, & Morari, 2010; Wongsarnpigoon & Warren, 2010; Wongsarnpigoon, et al., 2010). For the improvement of neuromodulation protocols, on the other hand, Wilson et al. performed parameter sweeps for continuous trains and bursts with a wide range of burst rates and no. of pulses (Fung, Haber, & Robinson, 2013; Robinson, 2011; Wilson, et al., 2014).

5.4 Integration of neuron models into spatial models

For the prediction of absolute stimulation thresholds and coil orientation effects, neuron models are incorporated into realistic head models (Goodwin & Butson, 2015; Salvador, et al., 2011b). Typically, such studies solve the spatial field distribution stationary sinusoidal or transient realistic pulse shape and subsequently feed the local electric field properties into a one-dimensional neuron model. This approach generates a loose forward coupling between the spatial as well as the neuron model and simplifies the interaction of the neural membrane and its surrounding. Salvador et al., for instance, combine a realistic spatial sulcus model with a dozen dynamical neuron models (Salvador, Silva, Basser, & Miranda, 2011a). In the coupling step, the electric field are extracted from a finite-element software tool and transferred to the Neuron stimulation environment (Yale University, New Haven, CT) to calculate the axonal response. Despite limitations because of the highly-simplified interface at the membrane, Salvador et al. could demonstrate the experimentally well-known threshold difference between mono- and biphasic and the threshold reduction for posterior-anterior induced current direction (Salvador, et al., 2011b). Agudelo-Toro et al., in contrast, presented a notable spatial model that avoids these simplifications, which are widely used for coupling neurons to spatial models, and incorporates the microscopic neuron with all its spatial characteristics including the membrane into a finite-element model (Agudelo-Toro & Neef, 2013). The necessary equations for such an approach are long known (Scott, 1975). However, Agudelo-Toro and colleagues simplified the equation system to achieve computation times in an acceptable range of minutes to few hours.

6. Model-based experimental methods

Most computational models in TMS are autonomously set up based on fundamental physical and physiological relationships, while simple calibration of parameters may be taken from experiments. There is an increasing trend of combining models and experiments. The combination of both can improve theoretical mechanistic insight as well as prediction abilities, for instance, when models are calibrated and validated in a closed-loop setup that optimally picks stimuli such that it decreases the parameter estimation errors most efficiently (Alavi, Goetz, & Peterchev, 2016; Goetz, Whiting, & Peterchev, 2011; Treutwein & Strasburger, 1999). Furthermore, the combination can enhance experimental abilities by the extraction of otherwise inaccessible quantities or information and by revealing underlying interactions in the brain, which may serve as novel diagnostic tools for psychiatry and neurology.

A prominent target of combined experimental-modeling methods is neural recruitment in the motor system. Stimuli in the motor cortex are known to evoke corticospinal responses that travel along the spine to a peripheral muscle and activate a peripheral muscle, which can be detected electrically as a motor-evoked potential (MEP). The response amplitude and latency of the MEP wave depends on several extrinsic parameters such as stimulation strength, stimulus properties, as well as pulse dynamics; there is further a large number of intrinsic anatomical and physiological factors that can be extracted with appropriate model learning techniques (Peterchev, et al., 2013; Rösler, 2001). The input–output behavior, including the sigmoid recruitment that is on average formed by the MEP size as a function of stimulation strength, is a sensitive marker for various pharmaceuticals as well as neurological disorders and a predictor for motor recovery (Boroojerdi, Battaglia, Muellbacher, & Cohen, 2001; Caramia et al., 1991; Carroll, Riek, & Carson, 2001; Julkunen, Ruohonen, Sääskilahti, Säisänen, & Karhu, 2011; Kaelin-Lang & Cohen, 2000; Malcolm et al., 2006; Pitcher, Ogston, & Miles, 2003; Thomas & Gorassini, 2005; van Kuijk et al., 2009; van Kuijk, Pasman, Hendricks, Zwarts, & Geurts, 2009).

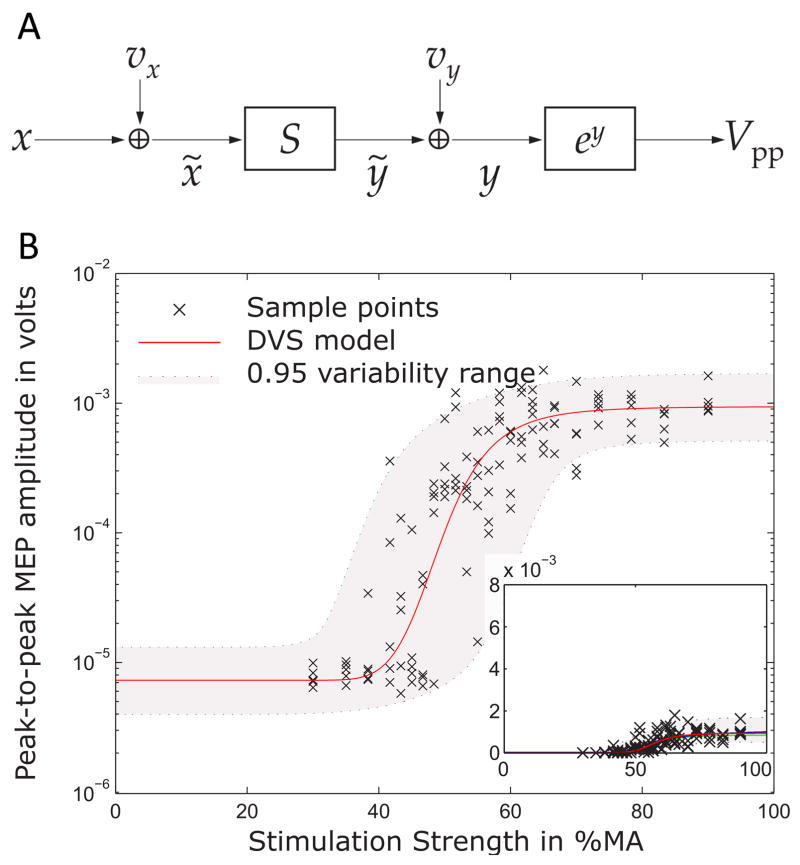
An underestimated component in the input–output behavior is the trial-to-trial variability of MEPs, which can vary by orders of magnitude, although there are no differences of extrinsic conditions or coil movements (Brouwer & Qiao, 1995; Ellaway et al., 1998; Gugino et al., 2001; Rösler, Roth, & Magistris, 2008). This variability was observed to show an intricate statistical distribution, to change in the presence of various drugs and brain injuries, and to be to a large part a correlate of ongoing endogenous neuromodulation on the cortical and spinal level (Darling, Wolf, & Butler, 2006; Devanne, Lavoie, & Capaday, 1997; Kaelin-Lang et al., 2002; Mitchell, Baker, & Baker, 2007; Moosavi, Ellaway, Catley, Stokes, & Haque, 1999; Nielsen, 1996; Choudhury et al., 2011; Zarkowski, Shin, Dang, Russo, & Avery, 2006). Model-based decomposition techniques were developed with the aim to turn TMS into a tool to observe ongoing signaling in a neural circuit, similar to the detection of postsynaptic potentials with patch-clamp techniques. The underlying models of the corticospinal input–output system incorporate various sources of variability and are designed to be calibrated to a subject (Fig. 9) (Goetz, Luber, Lisanby, & Peterchev, 2014; Goetz & Peterchev, 2012). By the calibration, the overall variability is decomposed so that for each MEP the contribution of the various variability sources can be quantified to reconstruct the inhibitory or excitatory input to the stimulated neurons at the time of stimulation.

Figure 9.

Model for describing the stimulus–response behavior of motor-evoked potentials. A. Each stimulus with strength x that activates the motor cortical target is perturbed by a variability source v_x, which describes ongoing endogenous neuromodulation and incoming signals to the activated neurons. A summation S represents the recruitment of the many parallel units. A second variability source v_y and an exponential function together describe the multiplicative output-side variability, which is caused by effects in the periphery, such as cellular fluctuations of calcium concentrations and fatigue, and measurement noise. B. The model (line and grey band) well describes the experimental behavior given by the crosses and allows splitting variability into its contributions to detect endogenous neuromodulation of the stimulated neurons in real-time.

Similarly, the triple-stimulation method is based on a high-level neural model of the spinal and peripheral pathway from signals from the brain to the muscle (Magistris, Rösler, Truffert, & Myers, 1998). This method applies an electrical stimulus, e.g., at the wrist shortly after the TMS stimulus in the motor cortex to cancel out the original stimulus by its antidromic signal. A third peripheral stimulus is applied proximally to the cancellation point, which only successfully passes on along those fibers where the previous antidromic signals have cancelled out already. This method can estimate the number of activated motor units and detect the phase relationship of descending MEP and can isolate the trial-to-trial variability of MEPs that results from phase desynchronization. In diagnostics, the triple stimulation technique showed more than two-times higher sensitivity for neural dysfunction than the measurement of MEP amplitudes and latencies (Magistris, Rösler, Truffert, Landis, & Hess, 1999).

The approach to combine experiment and modeling to extract otherwise covert information has further been expanded to TMS with concurrent electroencephalography (EEG). Cona et al. developed a neural mass model for TMS-evoked potentials (TEP) (Cona, Zavaglia, Massimini, Rosanova, & Ursino, 2011; Ursino, Cona, & Zavaglia, 2010). The model includes cortical columns with four neuron populations—pyramidal neurons, excitatory glutamatergic interneurons, fast GABA_A interneurons, and slow GABA_A interneurons—from three cortical sites—the occipital, the parietal, and the frontal lobes, while the pyramidal neurons implement the interconnection of the sites. Cona et al. calibrated the model to subjects to mimic the first 200 ms of TEPs with high correlation. The model predicts the TEP response including individual components at the site of stimulation as well as at the other sites to where it is relayed through projections. The calibrated model further reveals information about the connectivity of the used cortical areas as well as variability, both of which are not accessible directly (Cona, et al., 2011). However, these models do not currently distinguish different physiological sources of response to TMS, such as auditory and somatosensory contributions to the evoked potentials.

7. Conclusions

Computational modeling plays an important role throughout the entire field of magnetic stimulation for developing improved equipment and understanding how magnetic stimuli interact with the brain. Increasingly realistic and detailed models are unmatched in many aspects of TMS for uncovering mechanisms since the interaction of TMS with the brain is complex due to the high degree of positive and negative feedback as well as interference with endogenous brain activity. Since there is typically no access to internal processes, the response to TMS is hardly predictable or understandable without modeling. The importance of detailed models will further grow as experimental procedures increase in complexity, as devices give experimenters more control, e.g., over the pulse shape, and as easy-to-use simulation tools become available (Peterchev, et al., 2014; Windhoff, et al., 2013). For the foreseeable future, it appears likely that more and more experimenters will simulate their experiments to plan the procedure, analyze the outcome, and predict behavior.

However, modeling of TMS runs a serious risk that is often ignored, but harms scientific integrity. Due to the high complexity of neural interaction with TMS, inappropriate modeling easily becomes post-hoc and inductive. That occurs if models, particularly models with many parameters, are fit to an outcome, but are not able to predict more than the data they were fit to. To be scientifically sound, a model needs to always make predictions that go beyond the data used to set up the model—preferably predictions that the authors of the model cannot answer by the time the model is set up. Those predictions are the key to test, validate, potentially falsify the model or find limitations (Popper, 2005). Authors of models should therefore clearly report the data and observations used for model regression, assumptions their models were set up with, and how parameters were estimated and incorporated. Outcomes that are to be explained must not be implemented as parameters into the model. The risk for inductive modeling is further aggravated if models provide high complexity with multiple feedback loops and a large set of parameters. Furthermore, authors should be encouraged and always present testable predictions based on their models, which are clearly marked as such. The report of such predictions for validation is enforced in other disciplines that are particularly susceptible to nonobvious inductive models, such as statistics and machine learning (Babyak, 2004; Drummond & Japkowicz, 2010; Hawkins & Kraker, 2010; Langley, 1988). A number of models in the literature of magnetic stimulation thus far do not reach that quality level. Falsifiable and falsified models should lose their bad reputation in the community. The falsification of models might be the only path to scientific progress.