Human photoreceptor cone density measured with adaptive optics technology (rtx1 device) in healthy eyes

Abstract

The anatomic structures of the anterior segment of the eye enable correct reception of stimuli by the retina, which contains receptors that receive light impulses and transmit them to the visual cortex. The aim of this study was to assess the effect of the size of the sampling window in an adaptive optics (AO) flood-illumination retinal camera (rtx1) on cone density measurements in the eyes of healthy individuals and to investigate the differences in cone density and spacing in different quadrants of the retina. Thirty-three subjects with no ophthalmic or systemic disease underwent a detailed ophthalmologic examination. Photographs of retinal fragments 3 degrees from the fovea were taken using the rtx1 AO retinal camera. We used sampling windows with 3 sizes (50 × 50, 100 × 100, and 250 × 250 μm). Cone density, spacing, and shape were determined using AOdetect software. The median (interquartile range) cone density was 19,269 (4964) cones/mm². There were statistically significant differences between measurements taken with the 50/50 and 250/250-m windows. There were no significant differences in the cone spacing results between any of the windows examined, but the measurements differed according to location between the superior and temporal quadrants. The most common cone shape was hexagonal (47.6%) for all window sizes and locations. These findings may help in the development of a normative database for variation in cone density in healthy subjects and to allow the best window to be chosen for obtain the most correct values for eccentricity measurements of 3 degrees. In our study, the optimal sampling window was 100 × 100 μm.

1. Introduction

The anatomic structures of the anterior segment of the eye enable correct reception of stimuli by the retina, which has receptors that receive light impulses and transmit them to the visual cortex. Thus, the retina is one of the most important structures in the eye in terms of the visual process. However, because of its location in the posterior segment and its very small size (200–300 μm in thickness^[1]), the development of retinology has lagged behind that of diagnostic tools and treatment of diseases involving the anterior segment of the eye.

Starting in 1850, examination of the fundus of the human eye involved only a set of special, regularly improved speculums, triple mirrors, and contact lenses. New diagnostic (imaging) methods were gradually introduced in the second half of the 20th century and included color fundus photography, fluorescein and indocyanine angiography, scanning laser ophthalmoscopy, and optical coherence tomography. Optical coherence tomography, initially mirror, then spectral, and now also enabling deep analysis of the structures, including the choroid, is presently the gold standard for diagnosis of disease in the posterior segment of the eye.^[2,3]

The technological improvements made in the last 20 years, coupled with the pursuit of ever improved diagnostic capability, have enabled retinal imaging at the cellular and microvascular levels. Improvements in these ophthalmic procedures have been made possible by application of adaptive optics (AO), a technology proposed by Horace Babcock, a US astronomer, who first employed it in 1953 in telescopes used by astronomers to mitigate atmospheric turbulence. The concept behind this technology is that wavefront distortions can be measured and compensated for in real time by using deformable mirrors.^[4]

As in astronomy, the quality of retinal imaging in ophthalmology when captured with the existing devices is limited by wavefront distortions due to the optical irregularity of the structures of the human eye, including the cornea and lens, which induce higher level aberrations. Innovative AO technology enhances the image quality, eliminating wavefront distortions as early as at the time of performing the examination. The rtx1 (Imagine Eyes; Orsay, Paris, France) is the first microscope to use AO technology and show single retinal cells (photoreceptors) and the smallest blood vessels (arterioles). The image resolution achieved by this technology is by far superior (S) to that of any other known diagnostic tool.^[5,6]

The rtx1 uses en face reflectance imaging with flashed, noncoherent near-infrared illumination. The detector is a low-noise, charged-coupled device camera, and the pixel resolution of the camera is 1.6 μm at the fundus of the eye. The transverse optical resolution is 250 line pairs per millimeter, with an imaging field of view of 4 × 4 arc degrees. The total image acquisition time is 4 seconds, during which 40 individual images can be acquired. The rtx1 microscope includes image acquisition and object recognition software for image analysis oriented toward cones and vessels. Its graphical user interface allows for generation of a map of objects and statistical analysis of recognized and observed structures.^[7]

Examination using the rtx1 includes several parameters: the length of the eyeball, refractive error, pupil size, and the transparency of the ocular media. Customized analysis of the examination findings requires a biometric measurement. Changes in the transparency of the cornea, lens, and vitreous may prevent acquisition of sharp images.^[5,8] The advantages of the device are that it enables selection of any area of the retina for imaging and repeating of measurements in the same spot based on automatically saved coordinates of that spot in the form of an entire image. The rtx1 is particularly valuable for evaluating the progression of retinal changes. Further, it is possible to adjust the depth of the retinal region under evaluation. This enables visualization of individual photoreceptors (cones and rods), intraretinal deposits, neurosensory retinal atrophy, lamina cribrosa, microexudations, and microaneurysms.^[3]

Two computer programs are provided by the manufacturer for analysis of the examination findings, that is, AOdetect (for analysis of photoreceptors) and AOdetectArtery (for analysis of the retinal vasculature) (Imagine Eyes; Orsay, Paris, France). On conducting a retinal examination (image acquisition), taking into account the length of the eyeball, an image should be selected and sent to the analyzing software for automatic processing. The software calculates the mean and maximum–minimum numeric and percentage values of all parameters, as well as the standard deviation. Added to each visualization is a hot color scale, whereby the hotter the color, the greater the density of the photoreceptors. The results are automatically exported to an Excel sheet in the form of a table.^[7,9]

The available international literature offers few publications on examination findings using the rtx1, and there is no unequivocal information regarding standardization of these findings. The objective of this study was to compare scan fragments of varying sizes captured using the rtx1 during examination of healthy eyes in order to optimize the area analyzed and employ the adopted measurement window as a standard for further examinations in selected ophthalmic and systemic diseases.

2. Methods

Retinal examinations with an rtx1 device were conducted between May and July 2015 at the Department of Ophthalmology, Second Faculty of Medicine, Medical University of Warsaw, located in the Ophthalmic University Hospital in Warsaw. The study protocol was approved by the Bioethical Commission of the Medical University of Warsaw. Each patient received both oral and written information explaining the objective and design of the study, as well as the operating principles of the device and the course of the examination. In accordance with the Declaration of Helsinki, written informed consent was obtained from all subjects who participated in the study.

2.1. Eligibility criteria

Eyes were eligible for inclusion in the study if they were from healthy adults (aged older than 18 years) without a history of systemic disease, with full corrected visual acuity, and without a history of other ophthalmic disease as confirmed by a detailed slit-lamp examination and additional tests.

2.2. Study group

The study group consisted 33 subjects comprising 19 women (57.6%) and 14 men (42.4%), and there is no significant difference in the gender structure (P  =  .194). The overall mean (standard deviation) age was 43.0 ± 14.5 years (women, 43.8 ± 14.5 years; men, 42.0 ± 14.5 years, P  =  .732). The mean axial eyeball length of the right eye (OD) was 23.95 ± 1.33 mm and that of the left eye (OS) was 23.93 ± 1.34 mm (P  =  .978) and without any significant difference between women and men for both eyes (Table 1).

Table 1.

Demographic characteristics and axial length in the study group (n  =  33).

2.3. rtx1 examination procedure

Each patient underwent retinal imaging examination using the rtx1 AO retinal camera. Each rtx1 examination captured 4 × 4 arc degree scans of the 4 perifoveal areas of the retina 3 degrees off the center of the fovea (temporally, nasally, superiorly, and inferiorly). Most of the examinations did not require dilation of the pupils. In isolated cases, where the width of the pupil was less than 4 mm, 1 drop of 1% tropicamide was administered. Eyes in which no images of acceptable quality could be captured were excluded from the analysis.

Images were taken 3 degrees off the fixation point, that is, approximately 900 μm off the fovea and outside the foveal avascular zone. Thus, the scans captured also showed the capillaries (Fig. 1). However, the measurement frames were not set to include areas with blood vessels, so capture of these areas proved more difficult as the size of the frame increased.

Figure 1.

Image of a fragment of the retina captured with the rtx1 adaptive optics flood-illumination retinal camera.

The best fragments of images captured were selected on the basis of quality, that is, those in which the structures imaged could be identified in greatest detail. The size of the frame in that area was then selected (50 × 50, 100 × 100, or 250 × 250 μm). In each case, the smallest frame represented a fragment of a larger frame, which in turn was a fragment of the largest frame.

The scans captured were analyzed using the image processing and recognition software provided by the manufacturer (AOdetect v0.1). AOdetect is used to determine the thickness, distribution, and morphology of the photoreceptors. The area to be analyzed in detail is selected using a movable frame, the width and location of which is controlled by the investigator (Fig. 2). Algorithms based on segmentation and the Delaunay triangulation method of en face reflectance imaging illumination allow automatic determination of the number, shape, and location of the cones and calculation of the statistics for the selected values.

Figure 2.

Imaging of cones using AOdetect. This software calculates the mean, maximum, and minimum numeric and percentage values for all parameters, including the standard deviation. Added to each visualization is a hot color scale (i.e., the hotter the color, the greater the density of the photoreceptors).

2.4. Parameters evaluated

The mean (±standard deviation) cone density per mm² of retinal surface, the shape-based cone morphology, and location of the cones in terms of neighborhood and distribution were analyzed. Any differences in values for these parameters between the OD and OS were also analyzed. Comparisons were made between cone density and type captured using the different frame sizes (50 × 50, 100 × 100, and 250 × 250 μm) in the same eyes. Outcomes in the respective quadrants were recorded to check for any differences in the parameters evaluated relative to measurement location and frame size. To assess the repeatability defined as the variation in repeated measurements for 10 images made on the same study samples taken under identical conditions, the repeatability coefficient was calculated.

2.5. Statistical analysis

The statistical analysis was performed using IBM SPSS Statistics for Windows version 22.0 software (IBM Corp., Armonk, NY). Abnormally distributed continuous variables were analyzed using the Mann–Whitney nonparametric test. Fisher Exact test was used to analyze differences in categorical variables between groups. The Shapiro–Wilk test was applied to identify the distribution of the data. We used Friedman analysis of variance to analyze the variation in packing density, spacing, and Voronoi triangulation at different eccentricities and quadrants; a post hoc test with Bonferroni correction was applied for the significance level. The Mann–Whitney U test was used to check for interocular variability in cone packing density. A simple linear regression or multiple regression were applied to analyze the variation in cone density according to axial length and age. All analyses were 2-tailed and a P value of <.05 was considered to be statistically significant.

3. Results

In total, 996 findings were captured for the OD and OS in the different quadrants (T, temporal; N, nasal; S; I, inferior) using the different frame sizes (50, 100, and 250 μm).

The following aggregated data were analyzed for each eye separately: cone packing regularity (assessed by analysis of Voronoi domains of the selected regions of interest), percentage distribution of cone packing as a function of the neighborhood (N%), mean cone density (DM), standard deviation for cone density (DSD) cones per mm², mean cone spacing (SM), and standard deviation for cone spacing (SSD) in μm. The values were retrieved from the AO optical coherence tomography image measurement according to the cone recognition and count algorithm for the assumed frame area. The findings for all parameters are presented in Table 2.

Table 2.

Parameters measured for the entire study population (n  =  898).

Distribution of the DM and N%6 values was normal (P  =  .265 and.151, respectively, Shapiro–Wilk test), while for the other variables (DSD, SM, and SSD), there was a deviation from the normal distribution (P < .05, Shapiro–Wilk test). For this reason, the median and interquartile range (IQR  =  third–first quartile [Q3–Q1]) are reported instead of the mean and standard deviation conventionally reported for normal distributions.

No statistically significant difference in DM was found between the OD and OS. The median (IQR) DM for the entire study group (all eyes and measurement frames) was 19,269 ± 4964 with a Q1 to Q3 range of 16,995 to 21,959 cones/mm². A summary of the DM, DSD, SM, SSD, pentagonal, hexagonal, and septagonal shapes findings for the OD and OS is shown in Table 3.

Table 3.

Measurements in ODs (n  =  527) and OSs (n  =  371).

The relation between DM and age, and the eyeball length was very weak (1-way Analysis of Variance r  =  −0.209, P < .001, and r  =  −0.362, P < .001, respectively), as well as the DM variability explained by both covariants is of a very low level (R²  =  0.162, P < .001, multiple regression model).

On examination with 50 × 50, 100 × 100, and 250 × 250 μm frames, the median DM values were 19,616 ± 5124, 19,402 ± 4753, and 18,892 ± 4930 cones/mm², respectively, with median SM values of 7.83 ± 0.945, 7.88 ± 0.95, and 8.00 ± 1.00 μm. There was a statistically significant difference in DM values obtained using the 50 × 50 and 250 × 250 μm frames (H[2, N  =  898]  =  6.74; P  =  .034, Kruskal–Wallis test), while the SM values for the individual measurement frames did not show any statistically significant differences (H[2, N  =  877]  =  4.26; P  =  .119, Kruskal–Wallis test). A comparison of the findings captured with the 50 × 50 and 250 × 250 μm frames showed significant differences in DM values (P < .05, Mann–Whitney U test; Fig. 3). The average coefficient of repeatability for the quadrants had the lowest value for the 100 × 100 μm frame in comparison to the others 2223 (10.3%) versus 2427 (11.4%) and 2830 (13.7%).

Figure 3.

Cone density in the 50 × 50, 100 × 100, and 250 × 250 μm frames. Q1, first quartile; Q3, third quartile. ^†Mann–Whitney U test for the dimension variable of 50 versus 250.

The cone density and spacing values in the respective quadrants are shown in Figure 4. The highest density (19,894 ± 3860 cones/mm²) was observed in quadrant T and the lowest (18,740 ± 3626 cones/mm²) in quadrant S. There were statistically significant differences in findings for quadrants S versus T (P  =  .006) and S versus N (P  =  .01; H[3, N  =  898]  =  13.44, P  =  .0038, post hoc Kruskal–Wallis test). No statistically significant differences in DM were observed for the other quadrants.

Figure 4.

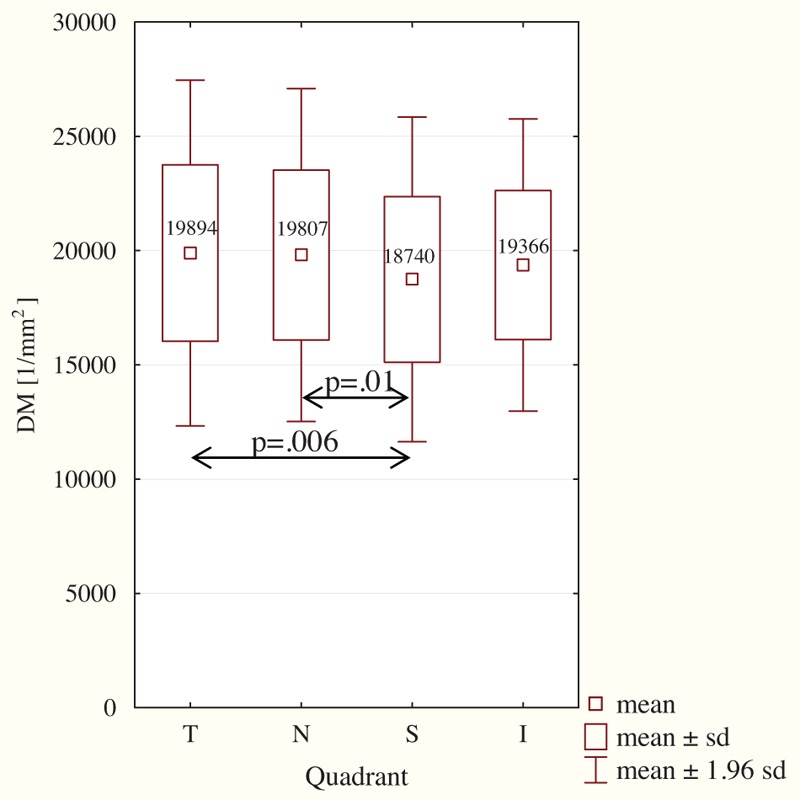
Mean cone density the respective quadrants (n  =  898). I  =  inferior quadrant, N  =  nasal quadrant, S  =  superior quadrant, T  =  temporal quadrant; post hoc Kruskal–Wallis test.

The longest SM distance (8.07 μm) was observed in quadrant S and the shortest (7.89 μm) in quadrant T; this difference was statistically significant (P  =  .006; (H[3, N  =  877]  =  10.32; P  =  .016, Kruskal–Wallis test). No statistically significant differences in SM distance were observed when comparing the other quadrants.

The prevalent cone shape was hexagonal (N%6; 47.6%, range of variability 26.3%–68.8%), followed by pentagonal (N%5; 25.0%) and septagonal (N%7; 20.7%). However, significant differences were observed in terms of the relative proportions of pentagonal and hexagonal cones in the respective frames as follows: 50 versus 250 μm (N%5^∗∗; P  =  .001; N%6^∗∗; P  =  .006) and 100 versus 250 μm (N%6^∗; P  =  .032), including respective sides (T: N%5^∗∗; P  =  .020) and locations (OD, N%6^∗, P  =  .040; OS, N%5^∗, P  =  .013).

4. Discussion

AO allows capture of high-resolution images of the retinal microstructures in vivo, with findings comparable to those seen on histologic examination. This is possible because of the correction for aberration arising from various refractive surfaces in the eye within the AO imaging system. At present, most publications focus on discussing findings for healthy individuals. This should pave the way to building a normative database that will provide clinicians with the ability to detect early changes in the course of various diseases of the retina and optic nerve as well as early damage to the retinal microcirculation.

Histopathology studies have demonstrated that the highest cone density area is 0.032 deg².^[10] The human retina contains on average 4.6 (range 4.08–5.29) million cones. The maximum number of cones (99,000 cones/mm² on average) is in the fovea. The rods are the other type of photoreceptor cells, and the retina contains on average about 92 (77.9–107.3) million rods. In the fovea, the mean horizontal measure of the rodless zone is 0.350 mm. The largest number closest to the fovea is found in the upper quadrants, with the count increasing at the slowest rate eccentrically from the N quadrant.^[11] This distribution of retinal photoreceptors in humans has been confirmed by histologic examination^[4] and in vivo techniques.^[9,12,13]

The cone density is known to change with distance from the center of the fovea. The DM at 0.5 mm from the fovea has been reported to be 32,199 cones/mm², which decreases significantly to 11,597 cones/mm² at 1.5 mm from the center.^[14] Histologic studies show that there is considerable variability in cone density (100,000–324,000 cones/mm²) between individuals.^[11] Lombardo et al^[12] reported that the cone density decreased from 51,000 cones/mm² at 250 μm to 14,000 cones/mm² at 1300 μm. In a study of the density and distribution of retinal photoreceptors in eyes taken from cornea donors, Jonas et al found that the cone density in the foveola center was up to 150,000 cones/mm² but decreased to 2500 cones/mm² on the retinal periphery near the ora serrata. The highest density of cones was found in the N segment of the retina. The diameter of the cones and the distance between them also increased with the distance from the fovea.^[15] The rod density was highest at 3 to 5 mm from the fovea, where it took the form of a ring-like area. The mean rod density was 72,246 ± 17,295/mm² and decreased peripherally to 30,000 to 40,000/mm².^[15]

Despite ongoing intensive studies, no standard has been established so far regarding procedures for measuring cone density using the rtx1 device. The measurement window most frequently chosen by investigators is 100 × 100 μm. Other frame sizes mentioned in the literature are 50 × 50^[17] and 240 × 240 μm.^[7] Our study aimed to determine which of the 3 frame sizes offers the most accurate measurement and to identify any statistically significant differences between measurements captured using these different frame sizes.

The 100 × 100 μm measurement window is frequently chosen because it correlates with the retinal area targeted by the Goldman III stimulus on functional perimetry.^[16] This allows functional changes to be displayed in a given area of the retina.^[16,17] Muthiah et al^[7] used a large measurement window, that is, 240 × 240 μm, in their study. In their opinion, this large area allowed measurement errors to be minimized. However, our study results do not support the conclusions of Muthiah et al, and the discrepancy may be explained by the fact that the measurement area (being outside the foveal avascular zone) includes blood vessels that could distort measurements of cone density. It is practically impossible to avoid inclusion of blood vessels in the examined field when using the larger measurement frame sizes. Another reason may be the decreased accuracy of the algorithm used by the software to calculate cone density as the measurement frame decreased in size; this has already been reported elsewhere.^[18,19]

Interestingly, our analyses showed statistically significant differences in cone density between the smallest (50 × 50 μm) and largest (250 × 250 μm) measurement areas. However, there was no difference between the frames of smallest and intermediate size (i.e., 100 × 100 μm) but the repeatability is the optimal for the latter. Cone density increased as the area examined became smaller.

Cone density measurements at distances smaller than 1 mm from the fovea, that is, 2 to 3 degrees, are considered to have limited reliability due to the high-cone packing density near the fovea.^[16,20] Like Chui et al, we analyzed the area about 3 degrees off the foveal center, which corresponds to 0.9 mm in terms of distance. Curcio et al^[11] concluded that the DM is 16,000 cones/mm² and the mean cone spacing is 7.4 μm at approximately 1 mm off the fovea. Similar findings were reported by Chui et al^[20] (mean 15,121 cones/mm² in emmetropic eyes with a mean spacing of 7.6 μm). Miller et al reported finding a DM of 23,000 cones/mm² at 2 degrees, but the range of values was wide (2800–32,000 cone/mm²).^[17] In our study, the DM was 19,453 cones/mm², which is comparable with the findings of other investigators.^[7,16]

Muthiah et al^[7] analyzed cone density in different quadrants of the retina at 2, 3, 5, and 7 degrees off the fovea and compared the values obtained by automatic and manual measurement. Cone density at 2 degrees was 26,500 and 24,200 cones/mm², respectively, when measured manually and automatically; 19,500 and 20,800 cones/mm² at 3 degrees; 13,800 and 15,600 cones/mm² at 5 degrees; and 11,200 and 12,900 cones/mm² at 7 degrees.^[7] In our study, all measurements were conducted using automatic software, with the selection of location verified by 2 investigators.

The average difference in photoreceptor density between the OD and OS in an individual patient is 8%, and there may be differences in distribution.^[11] In our study, the difference in cone density between the eyes was not statistically significant, but there were differences in terms of the percentages of cones with the most frequent shapes (pentagonal and hexagonal). Curcio et al^[11] demonstrated that cones become larger and their mosaic layout becomes distorted as the distance from the center increases. Chui et al^[20] confirmed that the most frequent cone shape is hexagonal. In our study, 47.6% of cones were hexagonal; packing of pentagonal and septagonal cones was present in 25% and 20.7% of eyes, respectively. As in our study, Muthiah et al^[7] found that hexagonal cones were the most numerous and at 5 degrees accounted for 49% of all cones. In their study, when pentagonal and heptagonal cones were included, the total proportion of cells with those shapes was 95%.^[7] In our study, hexagonal cones accounted for more than 93% of all cones. The hexagonal shape is best preserved at small distances from the center; the longer the distance, the lower the percentage of hexagonal cones due to emergence of cones with other shapes, which happens as early as 0.7 mm from the fovea.^[20] The distance between cones increases with the distance from the fovea, reaching 7.86 and 7.08 mm at 2 and 3 degrees, respectively.^[21] Our findings are consistent with this observation, that is, the mean distance between cones was 7.83 μm with no differences relative to the size of the area examined.

Cone density is affected by length of the eyeball and age.^[14] Cone density is highest during the early stages of eye development. However, the eyeball continues to grow until early adulthood. Therefore, a fixed number of cones are distributed in eyeballs of varying length, leading to differences of up to 60% in their distribution; this has been confirmed by measurements of cone density at 2 degrees off the fovea in emmetropic and myopic eyes.^[20] On average, the density decreases by 341 cones/mm² for each 1 mm of increasing eyeball length.^[14] When measurements are taken 0.5 mm from the fovea, there is no difference in cone density between myopes and emmetropes.^[14]

The difference in cone density between the T and N quadrants, measured at up to 2 mm from the fovea, may be as high as 10%. Cone density is also 10% higher when the cones are measured horizontally instead of vertically. The highest cone density is in the T quadrant, followed by the S, N, and I quadrants.^[14,16] Horizontal packing of cones is denser than vertical packing. We obtained similar findings in our study, that is, the highest density of cones was in the T quadrant and the lowest in the S quadrant. A study by Park et al^[14] did not find any statistically significant difference in cone density measured at 0.5 to 1.5 mm from the fovea in relation to patient age, that is, between 20 and more than 50 years of age. According to Song et al,^[13] the greatest difference in age-related cone density occurs at less than 0.5 mm from the fovea. Beyond that cutoff, there are no differences in cone density between older and younger patients.^[13]

There are differences in cone spacing (SM) in the respective retinal quadrants. In the study by Miller et al,^[17] the highest SM was found in the I and S quadrants. Significant differences were also found between those quadrants and the T and N quadrants. Similarly, we found the SM to be highest in the S quadrant and lowest in the T quadrant.^[17]

5. Conclusion

There has been no literature published thus far concerning the use of AO as a diagnostic tool in the Polish Caucasian population, and our study may help in the development of a normative database containing information on variations in healthy subjects in this population. This information would also allow us to choose the best window to achieve the most accurate measurements.