An interactive tool for rapid biventricular analysis of congenital heart disease

Summary

Cardiac malformations are the most common birth defect. Better interventions in early life have improved mortality for children with congenital heart disease, but heart failure is a significant problem in adulthood. These patients require regular imaging and analysis of biventricular (left and right ventricular) function. In this study, we describe a rapid method to analyse left and right ventricular shape and function from cardiac MRI examinations. A 4D (3D+time) finite element model template is interactively customized to the anatomy and motion of the biventricular unit. The method was validated in 17 patients and 10 ex‐vivo hearts. Interactive model updates were achieved through preconditioned conjugate gradient optimization on a multithread system, and by precomputing points predicted from a coarse mesh optimization.

Introduction

Congenital heart disease (CHD) comprises a suite of a cardiac defects present from birth. These comprise the most common form of severe birth defect with an incidence rate of approximately 75 in 1000 births (Fogel, 2005). These children now have reduced mortality due to improved medical treatment and surgical advances; however, heart failure is a significant problem in adulthood. The most common forms of CHD are ventricular septal defect, atrial septal defect and persistent ductus arteriosus (Roest & de Roos, 2012).

The role of the right ventricle (RV) in maintaining overall heart function is an important factor in heart disease (Anavekar et al., 2008). The RV contributes greatly to left ventricular (LV) function, particularly in CHD as many congenital lesions impact the RV either directly or indirectly (Haddad et al., 2008).

The current gold standard for evaluating LV and RV function in CHD is MRI (Grothues et al., 2004; Ntsinjana et al., 2011). Figure 1 shows four‐chamber long‐axis views, with the acquired short‐axis slice positions, for three different CHD lesions. MRI has the ability to image all parts of the heart at high resolution without the influence of other structures, unlike ultrasound (Grothues et al., 2004). MRI also has high reproducibility and does not use harmful radiation, unlike alternative imaging methods such as cardiac catheterization, X‐ray angiography, multidetector CT, and radionuclide ventriculography, which have increased risk.

Figure 1.

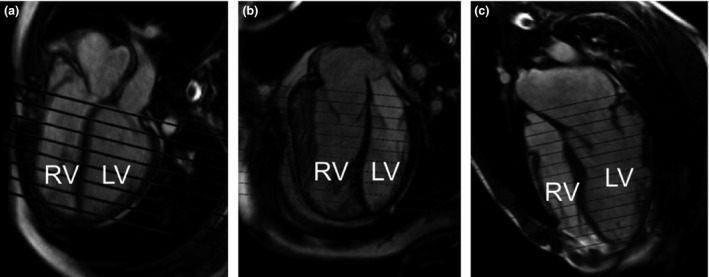
4‐chamber cine frame with the short‐axis planes of 3 patients with CHD. (a) Teratology of Fallot, (b) transposition of the great arteries with an atrial switch procedure, (c) Marfan's syndrome with Bentall procedure and a mitral valve repair.

However, the quantification of biventricular function from MRI takes significant time. Current practice is to manually contour the inner and outer boundaries of the left and right ventricular myocardium in short‐axis images at end diastole and end systole. The availability of fast, robust, and efficient evaluation of ventricular function using MRI would reduce the need for alternative, more risky, procedures.

While some semi‐automated methods (Wang et al., 2014b) for analysis of biventricular function have been developed, none appear to consider the additional challenges of CHD. Model‐based analysis methods have been proposed using subdivision surfaces (Hubka et al., 2002;Sheehan et al., 2008) and free‐form deformations (Perperidis et al., 2004), but these methods are not capable of interactive analysis.

A fast processing tool based on an interactive guide‐point modelling technique (Young et al., 2000; Li et al., 2010) was previously developed to analyse LV 4D (3D + time) shape and function throughout the cardiac cycle. Image features were tracked to warp the model between frames using a non‐rigid registration method (Li et al., 2010). In this study, we present modifications and extensions to this method to create a novel method to analyse biventricular function. The major improvements required to reduce the computation time included the introduction of a faster solution procedure with multithreading, and a novel way to compute the preconditioner using predicted model points based on a coarse mesh optimization. To the best of our knowledge, this is the only tool which can rapidly model both ventricles and all four valves.

Methods

The guide‐point modelling method, originally developed for analysing the LV (Young et al., 2000), was extended to interactively customize a biventricular model to the patient images. A finite element biventricular model created for biomechanical applications was constructed from an ex‐vivo porcine heart and comprised of 157 nodes and 88 hexahedral finite elements defining both the LV and RV, as well as the four valve (mitral, aortic, tricuspid, and pulmonary) orifices (Stevens & Hunter, 2003). The mesh had a total of 5981 geometric degrees of freedom and used a tricubic Hermite interpolation scheme (Lam, 2012). For the geometric interpolation, element coordinates ξ₁, ξ₂, and ξ₃ were defined in the circumferential, longitudinal, and transmural directions, respectively.

Reduction of complexity

The biomechanical model complexity was high as it was developed for solution of finite elasticity problems. In our application of interactive shape and motion estimation, fewer degrees of freedom are desirable to aid model customization. The complexity of the biomechanical biventricular model was therefore reduced by incorporating linear transmural variation, as analysis of volume, shape, and mass does not require higher order interpolation between surfaces. The interpolation scheme was also converted to Bézier basis functions (rather than Hermite), in order to have all shape parameters in the same units. This is desirable for principal component analysis and other dimension reduction techniques commonly used in atlas‐based population statistics (Fonseca et al., 2011). The workflow to create the finite element model is shown in Fig. 2.

Figure 2.

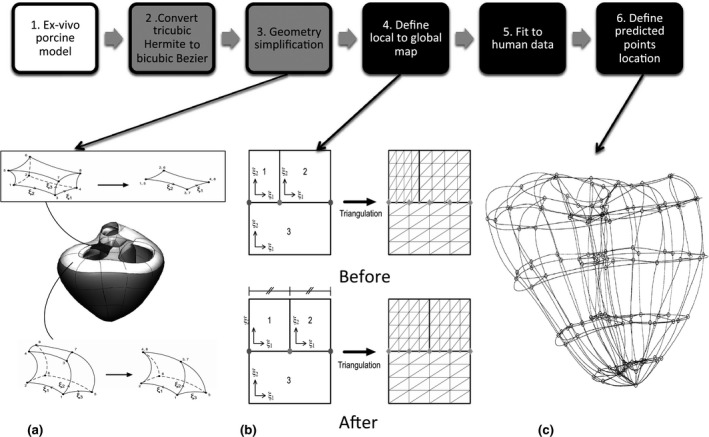
Workflow to develop a biventricular finite element model. The grey boxes show model simplification steps and the black boxes show the steps required for it to be a good prior for guide‐point modelling. (a) shows the simplification of basal geometry, by collapsing the element between the aortic and mitral valves (top) and collapsing elements along the valve annulus (bottom); (b) Relocation of a hanging node to align subdivision schemes; (c) Initial predicted points, shown on the 82‐element model.

The basal geometry was also simplified by removing degrees of freedom, as shown in Fig. 2a. The elements between the valves were collapsed to two dimensions by removing the ξ₃ variation (as shown in the top box of Fig. 2a). The elements around the outside of the valves were collapsed using the method shown in the box at the bottom of Fig. 2a. This removed nine nodes from the overall model. A general linear global‐to‐local parameter mapping scheme (Nielsen, 1987) was used to maintain continuity at element boundaries between different subdivision levels, as shown in Fig. 2b. The simplified mesh had 138 nodes and 82 bicubic‐linear Bézier elements, representing a reduction of geometric degrees of freedom by 70% to 1791.

To correct for differences between ex‐vivo porcine and in‐vivo human heart geometries, the new model was customized to a high‐resolution 3D MRI dataset acquired from a healthy volunteer. The acquisition parameters were as follows: navigator‐gated whole heart 3D sequence with a T2 preparation pulse, 50 short‐axis slices, each with 192 × 192 voxels of dimension 1·35 × 1·35 × 1·30 mm³, on a 1·5 T Siemens MRI scanner (Siemens Avanto). A large number of points were generated by manual segmentation of the epicardial and endocardial surfaces. The finite element model was fitted to these data by minimizing Eq. (1) by linear least squares. The resulting model of human anatomy, shown in the middle panel of Fig. 2, was then used as a template for interactive customization to patient images.

Guide‐point modelling

The guide‐point modelling method described by Li (Li et al., 2010) was employed to customize biventricular heart geometries to patient images. Briefly, the model parameters were optimized by least squares minimization of an objective function quantifying the difference in displacements between the model and the data:

$${\mathrm{M}}_{\mathrm{z}}={\mathrm{M}}_0\text{exp}(-\text{TE}/\text{T2*})+\mathrm{C}$$ (1)

where D is the total number of data points, w _d is the weight of the data point (d), and x ^finial(ξ _d), x ^initial(ξ _d) are the initial and final positions of the model points corresponding to the data point h _d. The data points included sparse guide points placed by the user, and densely sampled contour points generated by the non‐rigid registration image tracking process (Li et al., 2010). The three coordinate fields could be solved independently. E _s(u) was chosen to impose a standard Sobolev regularization:

$${\mathrm{M}}_{\mathrm{z}}={\mathrm{M}}_0\text{exp}(-\text{TE}/\text{T2*})+\mathrm{C}$$ (2)

The ζ _i smoothing weights were set to 0·01 for all cases. The first three terms penalized deviation from shape in the circumferential, longitudinal, and transmural directions, respectively. Terms 4 and 5 penalized change in curvatures and the final 3 penalized change in surface area. The interpolation in the ξ ₃ direction was linear, and thus, the second‐order derivative in this direction was zero.

This optimization problem resulted in a system of linear equations, Ax = b where A is a square matrix formed by

$${\mathrm{M}}_{\mathrm{z}}={\mathrm{M}}_0\text{exp}(-\text{TE}/\text{T2*})+\mathrm{C}$$ (3)

A _data contains information about the model points corresponding to the data and the basis function evaluations at their projections onto the model. In this work, A _smoothing was the Sobolev regularization matrix, although any similar regularization scheme could be used, provided it is quadratic in the model parameters. Minimizing Eq. (1) produces the displacements u which, when added to the template, become the customized finite element model. The solution was found using a preconditioned conjugate gradient method. This algorithm is designed for matrices which are positive definite and symmetric (Trefethen & Bau, 1997). However, efficient solution depends on the use of an effective preconditioner. In this application, approximation of the preconditioner derived from the inverse of the smoothing matrix does not produce an efficient preconditioner because the Sobolev smoothing matrix is singular. This is because the derivatives in Eq. (2) are invariant to a constant displacement.

Prediction

A set of predictor points was added to the optimization, to improve preconditioning. These points were assigned to fixed model positions (element coordinates), which were invariant for all customizations. This enabled the data matrix terms corresponding to the predictor points to be precalculated and included in the preconditioner, resulting in a well‐conditioned system which required considerably fewer iterations for convergence. The positions of the predictor points were set to correspond to the nodes of the finite elements in the biventricular model. The deformations of these points were then predicted by solving Eq. (1) using a coarse host mesh of reduced complexity. Figure 2c shows the initial node location, and Fig. 3 shows the host mesh deformation. Host mesh deformation is a variant of free‐form deformation (Sederberg & Parry, 1986), which minimizes the distance between landmark points and target points (Fernandez et al., 2004) using a simplified model geometry. In this work, we used a single trilinear hexahedral element which was constructed to encompass the entire 82‐element biventricular geometry. This simplified model contained affine deformations as a subset of the allowed trilinear deformation. The target points were defined as the guide points on the biventricular model. The landmarks were defined as the corresponding biventricular model surface points (i.e. the model point which was closest to the guide point). The host mesh deformation was solved using a minimization function similar to Eq. (1), where the nodal parameters were that of the host mesh. No smoothing term was required in this solution because the data were sufficient to constrain all degrees of freedom of the host mesh. As the embedded element coordinates of the predictor points did not change, the predicted point locations after the host mesh deformation were calculated from the corresponding deformed model points.

Figure 3.

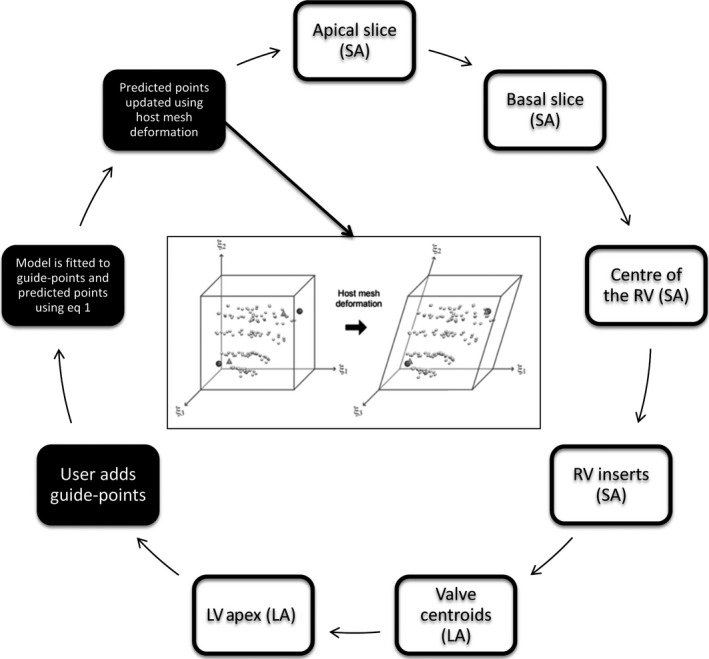
Workflow of creating a patient‐specific biventricular model. The White boxes show initialization steps and the black boxes show the interactive customization steps. The image in the middle shows host mesh deformation, with the initial model on the left and deformed on the right (bounding box: the host mesh; dark circles: guide points; triangles: model surface points corresponding to the guide points; light circles: predicted points).

The predicted points were calculated at the nodes of the full biventricular model and added to the A matrix (from Eq. (3)) as follows:

$${\mathrm{M}}_{\mathrm{z}}={\mathrm{M}}_0\text{exp}(-\text{TE}/\text{T2*})+\mathrm{C}$$ (4)

Terms arising from the predictor points were included the preconditioner, which was defined as

$${\mathrm{M}}_{\mathrm{z}}={\mathrm{M}}_0\text{exp}(-\text{TE}/\text{T2*})+\mathrm{C}$$ (5)

Fig. 2c shows the predicted points for the end‐diastolic frame. To ensure that the model preferentially fit user‐placed guide points over the automatically generated predicted points, each guide point was given a weighting of 2·5 and the predicted points were weighted at 0·01.

Initialization and landmarks

To initialize the customization of the model to each case, fiducial landmarks were defined by the user, including the apical and basal LV central axes; centroids of the mitral, aortic, tricuspid, and pulmonary valves; and left ventricular apical epicardium. The diagram in Fig. 3 shows the initialization steps. The valve centroid landmarks were optional because not all cardiac MRI examinations include slices through all four valves. These landmarks were used to calculate the pose and scale of the customized template. The valve centroids enabled the biventricular model to accurately model the location of the valves.

Solver improvement

Fast solution procedures were required to achieve fully interactive updates. Every update to a guide‐point placement required an update to the current frame, propagation of the current frame contours through all frames using non‐rigid image registration, and an update of the model on all other frames. The solution process was identified as a computationally expensive task that could be improved using more efficient numerical algorithms, optimized libraries, and parallel computing.

Math Kernel Library (MKL) is an optimized library for Intel processors, designed to solve engineering, science, and financial problems (Wang et al., 2014a). It contains packages to perform linear algebra (BLAS and LAPACK), fast Fourier transform, statistics, data fitting, and vector calculations. MKL was chosen as the numerical solver because of its speed and its ability to perform operations in parallel (Wang et al., 2014a).

We used the MKL preconditioned conjugate gradient solver with a reverse communication interface. Reverse communication enabled the A matrix described in Eq. (4) to be constructed algorithmically without ever computing the actual matrix elements. This is advantageous in the current application because the number of conjugate gradient iterations required for convergence is much less than the dimension of the matrix. Each iteration computed a new search direction, calculated a new solution vector, and then called a subroutine to compute A × x algorithmically. The result was then sent to be multiplied by the preconditioner which was precomputed. Finally, the convergence criteria were checked, and if the criteria were not met, the iteration continued. The fast BLAS functions of MKL were utilized in all steps.

MKL supports fast calculations for sparse matrices in compressed coordinate, compressed sparse row, and compressed sparse column formats. Compressed sparse row and compressed sparse column format required less memory than compressed coordinate format, and testing demonstrated that for the current application compressed sparse row format had faster performance.

Temporal behaviour

The temporal interpolation of the model consisted of Fourier basis with five harmonics to approximate the time‐varying periodic motion of the heart. After each guide‐point update, the current frame solution was updated. Contours from the current frame were then propagated to all other frames by non‐rigid registration (Li et al.,2010). Solutions for these frames were then updated according to Eq. (1). A temporal update was then performed which fitted each model parameter through time using the Fourier temporal basis functions. This uncoupling of temporal from spatial updates enabled the biventricular model to maintain interactive update rates.

Experiments

Ten ex‐vivo sheep hearts were obtained from a meat wholesaler and scanned using a steady‐state free precession (SSFP) imaging protocol on a MAGNETOM Skyra 3T scanner (Siemens, Germany). Short‐axis slices were taken parallel to the tricuspid valve, covering the left and right ventricles from base to apex. Long‐axis slices were taken through both ventricles and through the mitral, aortic, tricuspid, and pulmonary valves. Imaging parameters were as follows: 5 mm slice thickness with 10 mm interslice gap, 256 × 200 image matrix, flip angle of 73°, 10 frames, and 0·96 × 0·96 × 5 mm³ voxel size. At the completion of imaging, the hearts were dissected and LV and RV myocardial mass were measured by weight, as follows.

Each heart was cut down the RV free wall side along its long axis, perpendicular to and through the interventricular septum, to unfold in one piece with the LV free wall intact. The two half‐RV flaps were then separated from the interventricular septum junction, along with septal papillary muscle and trabeculae. The remaining bulk comprised the LV and the septum. For segmentation purposes, the septum was included in the measurement of LV mass. The atria were then removed along the mitral and tricuspid valve annuli, fatty tissue on the LV and RV epicardial surfaces was removed, leaving just the myocardium. The resulting LV piece and two RV pieces were then weighed separately on an electronic scale.

Ethics approval was granted from the institutional ethics committee, to recruit and image patients with congenital heart disease. There were 12 male and five female participants with an average age of 22·35 ± 15·57 years. The pathologies included transposition of the great arteries (n = 3), Tetralogy of Fallot (n = 7), Ebstein's anomaly (n = 1), Marfan's syndrome (n = 1), bicuspid aortic valve (n = 1), pulmonary atresia (n = 1), pulmonary atresia with intact ventricular septum (n = 1), and complex congenital cases with multiple defects (n = 2). Typical imaging parameters were as follows: 256 × 208 image matrix, 6 mm slice thickness, 360 × 360 mm field of view flip angle = 60°, TE = 1·6 ms, and TR = 30 ms. Seventeen participants were scanned with written informed consent, and the images were manually contoured using vendor software (Syngo MR 2004V, Siemens Medical Solutions, Erlangen, Germany). Guide‐point modelling results were compared against manual contours drawn on the end‐diastolic and end‐systolic frames, with mass and volumes of each chamber calculated using standard slice summation.

Results

The experiments were run on a Dell OptiPlex 990 running Windows XP using an Intel^® Core i5 3·30 GHz with 4GB of RAM. Multithreading was enabled for the analysis of the sheep hearts and patients with congenital heart disease.

Solver speed

We first compared the computation times of a solver which used a non‐optimized sparse conjugate gradient code (math.nist.gov/sparselib++), against the optimized MKL solver in single‐threaded and multithreaded configurations. The code was tested with three different tolerances for the convergence criterion: 1 × 10⁻⁴, 1 × 10⁻⁹, and 1 × 10⁻¹¹.

Table 1 shows that when the solver was converted to MKL and the MKL linear algebra package was added, the average update speed for the single‐threaded configuration was 4× faster (average 451%). With the addition of multithreading, the speed increased approximately 10× faster (1070%) compared with the non‐optimized solver.

Table 1.

Average speed test results for the solver for single thread and multithreading (four threads were used)

Tolerance	Solving time (s)
	Biventricular model with SparseLib	Biventricular model with MKL solver
		Single thread	Multithreads
1E‐11	0·484	0·11	0·05
1E‐9	0·422	0·09	0·04
1E‐4	0·187	0·04	0·02

Validation

The 10 sheep hearts were customized in a mean time of 12·5 ± 1·02 min per case. As the heart was stationary, it was not necessary to consider time points other than the first frame. The hearts had a mean mass and standard deviation of 93·36 ± 10·33 g and 34·01 ± 4·35 g for the LV and RV, respectively, by weight. Differences between the biventricular model and autopsy weights were 5·76 ± 3·68 g for the LV and 6·73 ± 4·41 g for the RV.

The 17 CHD cases took an experienced analyst between 4 and 5 h on average to contour the end‐diastolic and end‐systolic frames manually. The biventricular guide‐point modelling process took an average of 19·4 ± 4·18 min to analyse each case. End‐diastolic volume (EDV), the end‐systolic volume (ESV), myocardial mass, and the ejection fraction (EF), calculated as (EDV –ESV)/EDV *100%, were recorded for both the LV and RV. Table 2 shows the average difference and standard deviation of the differences between the biventricular model mass and volumes, and the values from manual contouring. Pearson product‐moment correlation coefficient (PPMCC) is a linear measure of correlation. PPMCC values were computed to assess correlation between the biventricular model and manual contours. Figure 4 shows one short‐axis cine frame from two cases, fitted with the biventricular model and manual analysis. 4(b) shows an example of a ‘bad’ fit by the biventricular model, where as 4(d) shows a ‘good’ fit.

Table 2.

Average difference in measures of heart function between manual contours and the biventricular model

	Biventricular model average	Manual average	Average difference (% difference)	Manual analysis interobserver error	PPMCC
LVEDV (ml)	150·23 ± 58·91	144·79 ± 54·96	5·44 ± 10·15 (3·78%)	−0·02 ± 2·29	0·987
LVESV (ml)	73·71 ± 41·74	55·96 ± 39·81	17·75 ± 10·62 (31·7%)	2·37 ± 5·30	0·967
LVEF (%)	52·46 ± 7·99	63·34 ± 12·06	−10·88 ± 6·27 (−17·18%)	−1·78 ± 3·88	0·882
LV Mass (g)	133·65 ± 48·30	104·88 ± 39·92	28·77 ± 13·96 (27·43%)	6·04 ± 5·7	0·937
RVEDV (ml)	238·65 ± 99·62	228·27 ± 101·34	10·37 ± 26·72 (4·54%)	−3·43 ± 10·91	0·965
RVESV (ml)	149·24 ± 75·02	125·08 ± 68·84	24·15 ± 17·62 (19·31%)	6·04 ± 5·57	0·974
RVEF (%)	39·39 ± 8·73	47·14 ± 9·67	−7·76 ± 7·74 (−16·46%)	−0·26 ± 3·60	0·651
RV Mass (g)	90·65 ± 43·31	68·41 ± 35·59	22·24 ± 10·92 (32·51%)	6·95 ± 5·50	0·981

Figure 4.

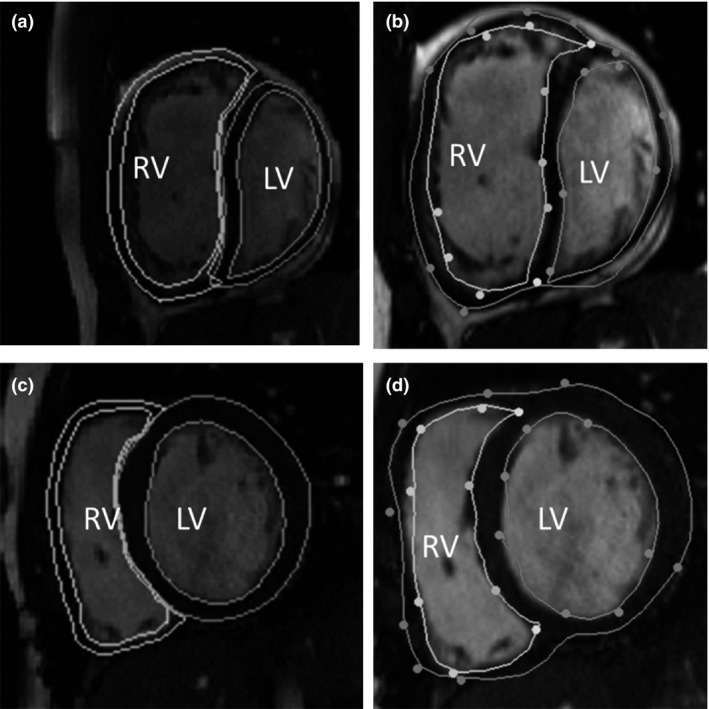
Short‐axis cine frames, with contours drawn by manual analysis (left) and contours from the biventricular model (right). (a) and (b) are from a participant with transposition of the great arteries, whom has had a mustard procedure. (c) and (d) are from a participant with coarctation of the aorta and a repaired ventricular septal defect. In images. The ventricles are notated on each images and the endocardial and epicardial surface are shown for both ventricles. Note, the manual contours have a separate epicardial surface drawn for each ventricle, where as the biventricular model has one contour.

Discussion

An interactive biventricular analysis procedure based on the guide‐point modelling method was developed. The variations and complexities of the shape of the RV are significantly more complex to model than that of the LV. A porcine model was simplified and fitted to digitized human cardiac data to create a template mesh. A set of predicted points, created from the nodes of the template mesh, was added to the model solution process to improve conditioning. The inclusion of MKL as the solver and linear algebra package significantly improved the computation time of the biventricular solver, making it a truly interactive tool.

The biventricular modelling method showed good correlation to the ex‐vivo heart results. It was significantly faster than the current clinical standard of manual contouring, while maintaining good correlation with clinical measures of heart function. The strong positive correlation, demonstrated by the PPMCC, and the reduced analysis time compared to manual contours suggest that the method could be useful in a clinical setting. While the PPMCC has shown good correlation, it is clear there are significant differences between the results of the two methods. The main reason for the bias between methods was the extent to which the manual contours were drawn up to the valves. The basal and apical extent of the ventricles are difficult to determine in the short‐axis images, due to partial voluming at the apex and the valves, which is a known limitation of manual contouring (Gentles et al., 2005; Hudsmith et al., 2005). The biventricular model has the advantage of being able to position the valves in both short‐ and long‐axis views, thus eliminating a major source of error in volume and mass calculations. Figure 1 shows the location of the short‐axis slices on the four‐chamber slice. Figure 1a shows that there was a significant volume of RV above the highest short‐axis slice in this case. This volume would not be taken into account in the manual analysis, while it would be included in the biventricular model. In Fig. 1b, some RV volume was excluded at both the basal and apical ends of the stack of short‐axis images. In Fig. 1c, there was some volume excluded at the LV apex. The images in Fig. 1 demonstrate how the different methods could be producing slight different results. The method did well with most CHD pathologies however; it was difficult to accurately assess the Ebstein's case, due to the significant different location of the tricuspid valve from normal anatomy. The number of guide points required was dependent on the amount of customization required, with an average of 318·1 ± 45·7 guide points.

Another source of difference between the analysis methods could be interventricular dyssynchrony. Jing et al. showed patients with repaired Tetralogy of Fallot have significant interventricular dyssynchrony (Jing et al., 2014), and as the biventricular model assumes that the ESV frame is the same for both the LV and RV, this could introduce an error. The correlation of EF for both ventricles, while still strong, is lower than other clinical measures. As shown in Fig. 1, the long‐axis slices add more information regarding ventricle size and volume. As EF is calculated from both EDV and ESV, the differences between the two methods would be compounded. The RV is most likely more pronounced due to the lack of accountability of dyssynchrony in the biventricular model, whereas the manual analysis did allow the RV to have a different ESV than the LV.

While the set of predicted points generated by the host mesh fit improved model conditioning, they were not a highly accurate prediction of heart motion and therefore could be further improved to reduce the amount of customization required by the user. It would also be advantageous to consider other smoothing schemes that are more suited to a biventricular shape.

Higher order interpolation between surfaces is required for deformation analysis (because strain is known to increase from endocardial to epicardial surfaces), and modelling of electrophysiological and mechanical processes. The simplified model used in the current work could easily be converted to tricubic Bezier basis functions after customization, for the purposes of solving these problems.

In conclusion, the biventricular modeller presented in this study rapidly produces accurate segmentations, which a major bottleneck in both clinical practice and research. While the tool has been specifically designed for the additional challenges of CHD, it could be used for assessing cardiac MRI, of those with acquired disease as well.

Conflict of interest

The authors have no conflict of interest.