Polarizable Force Field for DNA Based on the Classical Drude Oscillator: I. Refinement using Quantum Mechanical Base Stacking and Conformational Energetics

Abstract

Empirical force fields seek to relate the configuration of a set of atoms to its energy, thus yielding the forces governing its dynamics, using classical physics rather than more expensive quantum mechanical calculations that are computationally intractable for large systems. Most force fields used to simulate biomolecular systems use fixed atomic partial charges, neglecting the influence of electronic polarization, instead making use of a mean-field approximation that may not be transferable across environments. Recent hardware and software developments make polarizable simulations feasible, and to this end, polarizable force fields represent the next generation of molecular dynamics simulation technology. In this work, we describe the refinement of a polarizable force field for DNA based on the classical Drude oscillator model by targeting quantum mechanical interaction energies and conformational energy profiles of model compounds necessary to build a complete DNA force field. The parametrization strategy employed in the present work seeks to correct weak base stacking in A- and B-DNA and the unwinding of Z-DNA observed in the previous version of the force field, called Drude-2013. Refinement of base nonbonded terms and reparametrization of dihedral terms in the glycosidic linkage, deoxyribofuranose rings, and important backbone torsions resulted in improved agreement with quantum mechanical potential energy surfaces. Notably, we expand on previous efforts by explicitly including Z-DNA conformational energetics in the refinement.

Graphical abstract

Introduction

Empirical force fields employ classical mechanics to calculate the energy of an atomic configuration and the forces acting on each atom. Since the first molecular dynamics (MD) simulation of a protein,¹ force fields have advanced considerably, including all-atom, united-atom (in which nonpolar hydrogen atoms are combined with their parent carbon atoms), and coarse-grained (in which particles represent multiple atoms) forms. The most popular empirical force fields employ an additive model for electrostatics, in which each atom is assigned a fixed, partial charge and the total electrostatic force is as a summation over all interacting atom pairs. The most commonly used additive force fields for biomolecular simulations are AMBER,^2-3 CHARMM,^4-7 GROMOS,^8-9 and OPLS-AA.^10-11

While these force fields have been successfully employed for many years, known deficiencies are present in the additive representation of electrostatic interactions that limit their ultimate accuracy.^12-13 Recent quantum mechanical (QM) calculations have shown that the use of additive force fields for nucleic acids are particularly inadequate for accurately modeling base stacking,^14-16 hydrogen bonding,¹⁶ and ion interactions,¹⁷ all of which are important for the stability of DNA and RNA. Additionally, it has been shown that aromatic rings have considerable molecular polarizability due to the delocalization of π electrons,¹⁸ a property that increases the thermal stability of duplex DNA.¹⁹ Thus, the development and application of polarizable force fields is necessary to achieve better agreement with QM data and to more accurately simulate nucleic acids.

One method for modeling electronic polarization in a computationally efficient manner is the Drude oscillator model,²⁰ in which auxiliary (Drude) particles are attached to each non-hydrogen atom via a harmonic spring. The Drude oscillators carry a negative charge to represent the electronic degrees of freedom in the system. The functional form of the Drude oscillator model is described in detail elsewhere,²¹ but a brief description is appropriate here. This polarizable functional form is similar to traditional additive force fields in its treatment of internal (bonded) terms and its pairwise treatment of van der Waals interactions using the Lennard-Jones (LJ) form employed by most common additive force fields. The representation of electrostatics is extended to include the Drude oscillators, such that the unscreened Coulombic potential between atoms i and j and their Drude oscillators is calculated as:²²

$$U_{\mathit{\text{elec}}}=\sum _i\sum _{j>i}[\frac{q_i{q}_j}{|{\mathbf{r}}_i-{\mathbf{r}}_j|}+\frac{q_i{q}_{D,j}}{|{\mathbf{r}}_i-{\mathbf{r}}_j-{\mathbf{d}}_j|}+\frac{q_j{q}_{D,i}}{|{\mathbf{r}}_i+{\mathbf{d}}_i-{\mathbf{r}}_j|}+\frac{q_{D,i}{q}_{D,j}}{|{\mathbf{r}}_i+{\mathbf{d}}_i-{\mathbf{r}}_j-{\mathbf{d}}_j|}]$$ (1)

where r_i and r_j are the positions of atoms i and j, d_i and d_j are the Drude-bond lengths for atoms i and j, q_i and q_j are the partial charges on atoms i and j, and q_D,i and q_D,j are the partial charges on their respective Drude oscillators. These charges assigned to an atom i and its Drude oscillator are calculated from the atomic polarizability, α:

$${\alpha }_i=\frac{q_{D,i}^2}{k_D}$$ (2)

$$q_i=q_{\mathit{tot},i}-q_{D,i}$$ (3)

where k_D is the force constant of the bond between atom i and the Drude oscillator and q_tot,_i is the total charge of the Drude-atom pair for atom i.

The electrostatics explicitly include interactions between neighboring (i.e. 1-2 and 1-3 atom pairs) atomic dipoles, using a screening function proposed by Thole:²³

$$S_{ij}(r_{ij})=1-[1+\frac{a{r}_{ij}}{2{({\alpha }_i{\alpha }_j)}^{1/6}}]exp\left[\frac{a{r}_{ij}}{({\alpha }_i{\alpha }_j)}\right]$$ (4)

where a is a screening constant for the interaction, r_ij is the distance between atoms i and j, and α_i and α_j are their respective atomic polarizabilities. The same screening function can be applied to intermolecular interactions (called NBTHOLE for “nonbonded Thole”), which is particularly important in modeling the interactions involving ions.^24-25 The Drude model also allows for off-diagonal LJ interactions (NBFIX), which can be applied to achieve better agreement with intermolecular interaction energies and coordination geometries.

The first generation Drude-2013 polarizable force field for DNA^{21, 26-27} was shown to predict differential ion response among monovalent ions.^28-30 In addition, it more accurately models the energetics of base flipping in DNA than the additive CHARMM36 force field^31-32 due to mutual polarization between the flipping bases and water.³³ However, in performing extended simulations of DNA with Drude-2013, it was found that B-DNA sequences could become unstable after several hundred nanoseconds,³⁴ and that left-handed, Z-DNA unfolded in under 10 ns.²⁶ Subsequent analyses indicated that the causes of these phenomena were primarily due to inadequate descriptions of base stacking and backbone conformational energetics.

The deficiencies in the Drude-2013 DNA force field motivated the present study. Here, we seek to further improve upon the already successful first generation Drude-2013 DNA force field by targeting additional QM data, with an emphasis on base-stacking interactions and conformational energetics of the DNA backbone, including explicit targeting of Z-DNA conformational energetics.

Methods

Base Stacking Calculations

QM calculations were previously carried out to obtain interaction energies of all stacked monomers in DNA, with intermolecular degrees of freedom fixed to produce base orientations found in both A- and B-form helices.³⁵ The interaction energies were calculated using spin-component scaled (SCS)³⁶ second-order Møller-Plesset perturbation theory (MP2) with density fitting³⁷ (DF, synonymous with resolution of the identity, RI³⁸) level of theory (SCS-RIMP2) in conjunction with the aug-cc-pVTZ basis set³⁹ with counterpoise correction⁴⁰ for basis set superposition error (BSSE)⁴¹ for DNA stacked monomers (32 configurations, including both A- and B-DNA geometries, optimized at the MP2/aug-cc-pVDZ level of theory) produced by McDonald et al.³⁵ Indeed, the original Drude parameter set for nucleic acid bases⁴² yields interaction energies that, in many cases, differ significantly from these QM values and are systematically too weak (see below). Thus the stacked monomer interaction energies represent new and important target data for refining the force field.

Refinement was carried out by applying a Monte Carlo/simulated annealing (MC/SA) protocol⁴³ used previously in the development of the Drude-2013 force field.^44-45 The error function was defined as the root-mean-square difference (RMSD) between Drude and QM interaction energies, equally weighted among all stacked monomer configurations. To preserve the quality of the previous parameters in reproducing gas-phase dipole moments, molecular polarizabilities, and electrostatic surface potential maps, charges were allowed to deviate by ±0.05 e, α values by ±0.01 ų, and Thole screening factors by ±0.5 from their previously published values;⁴² these screening factors were constrained to positive values in cases where subtracting 0.5 would result in a negative value. Upon generation of each new parameter set, each stacked monomer pair was energy minimized. Intermolecular degrees of freedom between bases (rise, slide, shift, twist, tilt, and roll) were held fixed as previously described,³⁵ using the LONEPAIR facility within CHARMM to define virtual interaction sites for the constraints. Intramolecular degrees of freedom were allowed to relax freely. New parameter sets were accepted if the total RMSD decreased, or if the Metropolis criterion was satisfied in iterations in which the RMSD increased. The initial temperature was set to 500 K and was periodically scaled by a factor of 0.75. Convergence was achieved if the RMSD did not change by more than 0.001 between two consecutive cycles.

Parameters for the four bases (adenine, guanine, cytosine, and thymine) were adjusted simultaneously by targeting the 32 configurations described above. First, the electrostatic parameters of the base heavy atoms (charges, atomic polarizabilities, and Thole screening factors) were refined by targeting single-point HF/cc-pVDZ interaction energies of the MP2/aug-cc-pVDZ optimized geometries from McDonald et al.³⁵ Following electrostatic refinement, Lennard-Jones (LJ) parameters for non-hydrogen base atoms were adjusted by targeting the SCS-RIMP2/aug-cc-pVTZ energies calculated by McDonald et al.³⁵ The same MC/SA protocol was utilized in both refinement steps, with several optima identified in the fitting of the electrostatic parameters used as starting points for independent runs of LJ parameter fitting. Both the well depths (ε) and radii (R_min/2) of all heavy atoms in the purine and pyrimidine rings were varied, within windows of ±0.05 kcal mol^-1 and ±0.2 Å, respectively.

In total, several iterations of the MC/SA fitting protocol identified three potential electrostatic parameter sets by targeting HF/cc-pVDZ energies, resulting in eight total parameter sets after LJ fitting. These parameter sets were all evaluated using several criteria utilized in the original parametrization of the nucleic acid bases,⁴² namely base-pair hydrogen bonding of 15 pairs (canonical and noncanonical configurations), water interactions of methylated bases, dipole moments, molecular polarizabilities, heats of sublimation, and crystal lattice parameters. We expand upon this set of target data in the present work by also assessing nine base step (two stacked, Watson-Crick hydrogen bonded base pairs) interaction energies. Though several parameter sets were generated in the course of this work, here we present the results of only the final, fully optimized parameter set.

Base-Water Interactions

A central feature in the parametrization of both the additive CHARMM and polarizable Drude-2013 force fields is a correct description of interactions with water. In concert with base stacking and pairing interaction energies, the strength of interactions with water will dictate, in part, the stability of any nucleic acid structure. We assessed the interactions between water molecules placed at several locations relative to all four methylated DNA bases, both in-plane and out-of-plane, as was carried out previously.⁴² An example of these interactions for 9-methyladenine is shown in Figure 1. The target data were the distances between water oxygen atoms and base heavy atoms from geometry optimizations at the MP2/6-31G* level of theory, and interaction energies on these optimized structures at the RIMP2/cc-pVQZ level of theory with counterpoise correction⁴⁰ for BSSE.⁴¹

Figure 1.

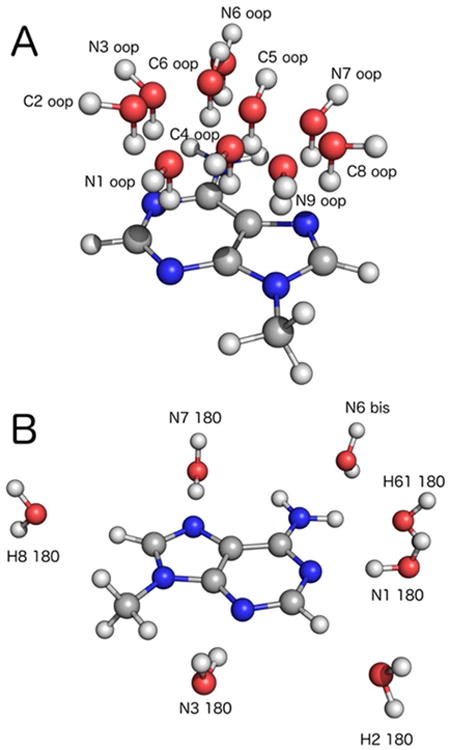
Geometries for (A) out-of-plane and (B) in-plane water interactions with 9-methyladenine. Note that each calculation was carried out on a bimolecular system (the base and one water); the composite images represent all of the interactions that were considered as part of parameter validation and refinement.

Base-Pair Hydrogen Bonding

The strength of hydrogen bonding between bases is an important factor in the stability of double-stranded DNA (dsDNA). To assess the ability of the Drude force field to model hydrogen bonding, we carried out interaction energy calculations between canonical and noncanonical geometries of the four DNA bases as described by Baker et al.,⁴² though here we include only the 15 pairs that contain only DNA bases. Briefly, the initial geometries of each base dimer (Supporting Figure S2) were taken from previous QM optimizations⁴⁶ and monomers from MP2/6-31G* optimizations performed during the course of the initial Drude nucleic acid base parametrization.⁴² Drude oscillators and lone pairs were added to these configurations in CHARMM,⁴⁷ which were subsequently minimized for 500 steps using the steepest descents algorithm and then for an additional 5000 steps using the Adopted-Basis set Newton-Raphson (ABNR) method. Base monomers were minimized using 1000 steps of steepest descent and an additional 200 steps of ABNR minimization. The interaction energy of the base dimers was calculated as the difference between the minimized dimer system energy and the sum of the individual minimized monomers. We note that in the Drude force field the energy minimization includes the Drude oscillators, thereby accounting for the self-consistent field condition required for polarizable force field calculations. Accordingly, calculating the interaction energy in this manner accounts for the polarization response upon the formation of hydrogen bonds.

Base Step Interaction Energies

Interaction energies for base steps (two stacked Watson-Crick base pairs) were calculated for the base steps studied previously by Parker et al.¹⁴ in a QM study that systematically varied intermolecular degrees of freedom. Coordinates of each base step were taken from the optimized geometry at the minimum value of twist and rise. In the case of AA:TT, missing hydrogen atoms were rebuilt using the internal coordinate builder of CHARMM. As with the stacked monomers, intermolecular degrees of freedom (in this case only twist and rise, to correspond to the QM calculations) were held in place via restraints between virtual sites constructed at the geometric center of the six-membered ring in each base. Intramolecular degrees of freedom were allowed to relax. Interaction energies were computed by taking the difference of the energy of the base step complex after energy minimization and the sum of the two energy-minimized Watson-Crick base pairs. Additionally, these interaction energy calculations were repeated with the real atoms fixed to match the calculations originally performed by Šponer et al.⁴⁸ and Hill and Platts,⁴⁹ who employed fixed base geometries when determining multi-body corrections for each system. This approach is also similar to that of Parker et al.,¹⁴ who enforced planarity in the bases while performing scans over other intermolecular degrees of freedom.

Base Crystal Simulations

As in previous work,⁴² the quality of the reoptimized nucleic acid base parameters was assessed by calculating heats of sublimation (ΔH_sub) and molecular volumes (V_m) for base crystals with available experimental data. Initial coordinates for each crystal were obtained from the Cambridge Structural Database.⁵⁰ For all crystals, the unit cell was replicated twice in each spatial dimension, to give eight unit cells containing between 16 and 64 molecules. Following energy minimization, 10 independent simulations of 500 ps were performed for each crystal starting from random initial velocities. The first 100 ps were discarded as equilibration. We note that extending simulations up to 10 ns did not yield any difference in the results; therefore using the shorter simulations was sufficient for assessing the quality of the base parameters. Electrostatic interactions were calculated with the particle mesh Ewald method (PME),^51-52 with the real-space contribution truncated at 12 Å. van der Waals interactions were switched to zero over 10 - 12 Å, with an isotropic long-range correction.⁵³ Neighbor lists were updated within 16 Å. For gas-phase systems, ten independent simulations of a single molecule were performed with infinite cutoffs for 2.5 ns, with the first 100 ps discarded. Increasing sampling to 100 independent simulations yielded no difference in the results. All simulations were performed with the extended Lagrangian algorithm²² and a dual Langevin thermostat, applying inverse friction coefficients of 5.0 ps^-1 and 10.0 ps^-1 to atoms and Drude oscillators, respectively. The thermostat coupled to the relative motion of the Drude oscillators was set to 1 K for all simulations, and the thermostat on the real atoms was set to the experimentally determined phase transition temperature of the crystal in the case of ΔH_sub calculations or the experimental crystallization temperature for V_m calculations. The so-called “hard wall constraint”⁵⁴ was used in all simulations to avoid polarization catastrophe, with a Drude-atom bond length limit of 0.2 Å. ΔH_sub was calculated from the following equation:

$$\mathrm{\Delta }{H}_{\mathit{\text{sub}}}=\langle U_{\mathit{\text{gas}}}\rangle -\frac{\langle U_{\mathrm{\text{crystal}}}\rangle }{N_{\mathit{\text{mol}}}}+RT$$

where T is the absolute temperature in Kelvin, R is the gas constant, N_mol is the number of molecules in the crystal unit cell, and 〈U_crystal〉 and 〈U_gas〉 are the time-averaged potential energies in the condensed (crystal) and gas phases, respectively.

Base and χ Dihedral Refinement

Consistent with the iterative refinement protocol inherent in the Drude-2013 force field, having altered electrostatic and LJ parameters of the base atoms, it was necessary to examine and refine dihedral parameters involving the bases. Given the good agreement between the Drude-2013 energies and QM target data, this refinement, like that of the base parameters above, sought to minimally perturb the existing force field while simultaneously improving on the small defects noted. The new base parameters will alter interactions with the deoxyribofuranose sugar, and to this end a refinement of the glycosidic (χ) torsion (O4′-C1′-N9-C4 in purines, O4′-C1′-N1-C2 in pyrimidines) was necessary. One-dimensional (1-D) potential energy scans of χ were conducted for each nucleoside at 15° intervals from 0° to 345° with sugar geometries fixed at C2′-endo (BI- and BII-DNA, constraining ν₄ = 0°) or C3′-endo (A-DNA, constraining ν₀ = 0°) and backbone dihedrals fixed at canonical values of BI-, BII-, and A-DNA. The MC/SA fitting protocol was applied by targeting MP2/6-31G*//RIMP2/cc-pVTZ energies calculated previously.²⁶ In the Drude-2013 force field, the dihedral parameter phase angles were allowed to vary freely. In the present version of the force field, we restricted the fitting to allow only phase angles of 0° and 180° for simplicity and improved transferability, resulting in a complete reparametrization of the χ dihedral terms. Force constants were allowed to vary from 0 - 2.5 kcal mol^-1 rad^-2. All surfaces were offset to zero at the lowest-energy conformation, and any conformation with a QM relative energy > 12 kcal mol^-1 was excluded during fitting.

To validate and refine dihedral terms within the bases, the QM vibrational spectra of each base (calculated at the MP2/6-31G* level of theory in previous work⁴²) were used as target data. The corresponding vibrational spectra under the Drude force field were calculated using the MOLVIB module of CHARMM. Force constants of the dihedrals were adjusted empirically and phase angles were left at their original values. Multiplicities were not altered during this refinement.

3′-Terminal Hydroxyl Dihedral Refinement

Refinement of χ described above exposed an issue in the conformational energetics of the BII state, which were systematically too high relative to the QM energy surfaces (see Results). The underlying deficiency arose from the transfer of ε (C4′-C3′-O3′-P) and ε₂ (C2′-C3′-O3′-P) nucleotide parameters to the corresponding nucleoside model compound torsions (C4′-C3′-O3′-H3T and C2′-C3′-O3′-H3T). Thus, the observed errors pertain only to the nucleoside model compounds used and do not indicate any noticeable problem in simulations of full-length dsDNA. Correcting this parameter issue was required before refinement of χ could be undertaken, as fitting to the systematically shifted BII energy surfaces would prevent the identification of suitable parameters.

Refinement of the nucleoside-specific ε (C4′-C3′-O3′-H3T) and ε₂ (C2′-C3′-O3′-H3T) dihedral terms was undertaken by scanning the ε₂ torsion in adenosine from 0° to 345° in increments of 15°. The choice of nucleoside for this refinement is irrelevant as the parameters for ε and ε₂ are common to all nucleosides; to confirm the transferability of these dihedral parameters, we repeated the ε₂ potential energy scans with cytidine. Sugar pucker, β, γ, and χ were constrained to their canonical values in A, BI, and BII forms as above. Geometries were optimized at the MP2/6-31G* level of theory in Gaussian09⁵⁵ and single-point energy evaluations of the resulting structures were calculated using Q-Chem 4.0⁵⁶ using the RIMP2/cc-pVTZ model chemistry.

α and γ Backbone Dihedral Refinement

The conformational sampling of the α and γ backbone dihedrals is important for dsDNA stability, and indeed refinement of these terms was a critical improvement in additive DNA force fields.⁵⁷ Though the sampling of α and γ of the Drude-2013 DNA force field was shown to be in good agreement with A- and B-DNA crystal surveys,²⁶ transient sampling of noncanonical geometries (notably gauche+ for α) was observed in long simulations of dsDNA with Drude-2013 (data not shown). Thus, it was clear that refinement of these dihedrals was warranted. The parameters for the α and γ dihedrals were refined independently by targeting 1-D potential energy surfaces of the T3PS model compound (Figure 2) in A-, BI-, BII-, Z-, ZI-, and ZII-DNA conformations. T3PS was optimized at the MP2/6-31+G* level of theory in Gaussian03,⁵⁸ with non-target backbone dihedrals fixed in canonical values for each of the specified geometries and target dihedrals (α or γ) fixed at intervals of 15° from 0° to 345°. Sugar pseudorotation angles (pucker) were also fixed by constraining ν₀ or ν₄ dihedrals of the two sugars (ν₄ = 0° for C2′-endo or ν₀ = 0° for C3′-endo). For Z-DNA, which is characteristic of CpG steps in left-handed Z-DNA, the 5′-sugar was C2′-endo and the 3′-sugar was C3′-endo. For ZI- and ZII-DNA (GpC steps), the 5′-sugar was C3′-endo and the 3′-sugar was C2′-endo. Following optimization, single-point energies were calculated using the RIMP2/cc-pVTZ model chemistry in Q-Chem 4.0.⁵⁹ Corresponding energy minimizations and energy evaluations using the Drude force field were conducted in CHARMM.⁴⁷ QM potential energy surfaces for A-, BI-, and BII-DNA conformations of T3PS were taken from a previous study,⁶⁰ while Z-, ZI-, and ZII-DNA QM potential energy surfaces were generated in this work. In refining the α dihedral, α₂ (C5′-O5′-P-O1P/O2P) was also subjected to additional dihedral refinement.

Figure 2.

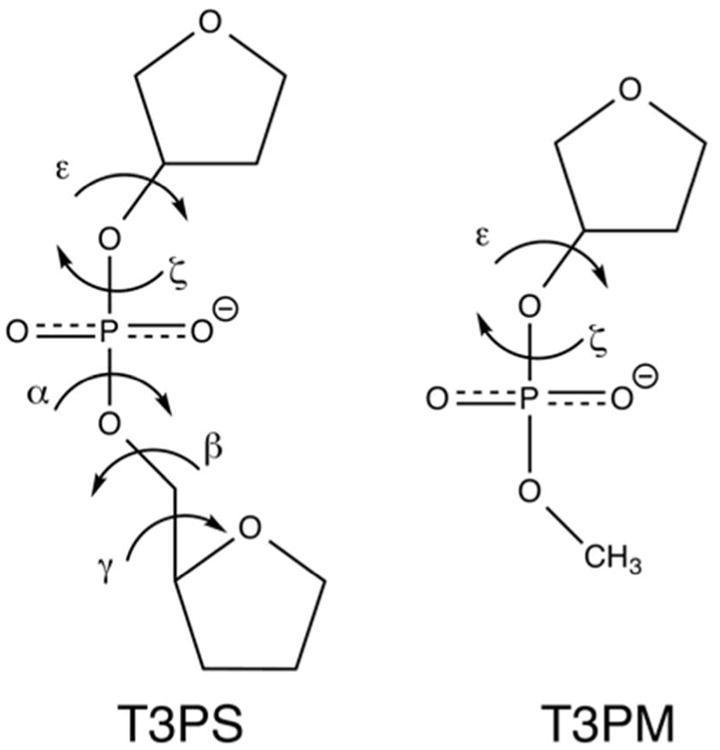
Model compounds used for α and γ (T3PS) and ε/ζ (T3PM) refinement.

ε and ζ Backbone Dihedral Refinement

The ε and ζ backbone dihedrals in dsDNA are tightly coupled, and their conformational sampling dictates the subtle balance in BI and BII sub-states in canonical B-form DNA that manifest in shifts in helicoidal parameters.^61-63 As such, in the development of the Drude-2013 DNA force field,²⁶ ε and ζ parameters were derived simultaneously by targeting a two-dimensional (2-D) ε/ζ QM potential energy surface of the T3PM model compound (Figure 2) in the range of ε and ζ values typically found in B-DNA. Doing so resulted in parameters that reasonably reproduced ε and ζ sampling in canonical B-DNA, though BII content was systematically underestimated, particularly towards the termini of oligonucleotide chains.²⁶ We expanded upon this approach to address both A- and Z-DNA conformations explicitly. Four additional 2-D ε/ζ surfaces were generated, encompassing values typically observed in crystal surveys of A-DNA (C3′-endo sugar, 150° ≤ ε ≤ 300°, 180° ≤ ζ ≤ 300°), Z-DNA (CpG steps, C2′-endo sugar, 230° ≤ ε ≤ 290°, 30° ≤ ζ ≤ 100°), ZI-DNA and ZII-DNA (GpC steps, C3′-endo sugar, 140° ≤ ε ≤ 280°, -90° ≤ ζ ≤ 90°) with sugar pucker fixed in the indicated geometries (ν₀ or ν₄ fixed at 0° for C3′-endo and C2′-endo, respectively) and α fixed at canonical values for these states. Values of ε and ζ were scanned in increments of 10° and the structures were optimized at the MP2/6-31+G* level of theory. Consistent with previous work,²⁶ the potential energy of each optimized configuration was used without subsequent single-point energy calculations to generate the 2-D target potential energy surfaces. These five T3PM ε/ζ potential energy surfaces, including 1097 conformations, were targeted simultaneously. 1-D potential energy scans of ε and ζ using the T3PS model compound (Figure 2) were used to guide additional empirical fitting. In fitting ε and ζ dihedrals, phase angles were restricted to 0° or 180° for simplicity, unlike in the previous parametrization,²⁶ during which phases were allowed to vary freely. The ε₂ (C2′-C3′-O3′-P) and ζ₂ (C3′-O3′-P-O1P/O2P) were also subjected to refinement during fitting.

Nucleoside Conformational Energetics

Changes made to base nonbonded parameters alter the interactions with the deoxyribofuranose ring of DNA nucleosides and nucleotides. While the χ refinement described above enforces ideal geometries on the sugars while χ is scanned, it is important to investigate the accessibility of noncanonical states of χ and the sugar pseudorotation angle (pucker). An examination of both the relative conformational energies of the nucleosides, as well as the values of χ relative to the QM-optimized structures allowed for refinement of other torsions in the nucleosides, particularly exocyclic torsions involving the base that are not centered on the glycosidic linkage. To this end, we carried out MP2/6-31G* optimizations of each DNA nucleoside as a function of ν₀ and ν₄ dihedrals, scanning each from -40° to 40° (for A-, BI-, and BII-DNA) and -60° ≤ ν₀ ≤ 40°, -40° ≤ ν₄ ≤ 60° for ZI- and ZII-DNA in increments of 10°. By doing so, a 2-D potential energy surface was generated for each nucleoside as a function of the sugar pucker. Backbone β, γ, and ε dihedrals were fixed at canonical values of A-, BI-, and BII-DNA. The χ dihedral was free to relax during these optimizations to enable analysis of noncanonical orientations of the base in response to variations in the sugar pucker. For syn-guanine nucleosides, the initial coordinates were constructed with χ set to 66° to generate suitable starting structures, but was allowed to relax during all geometry optimizations.

Results and Discussion

Base Stacking Interaction Energies

The nucleic acid base parameters⁴² used in the first-generation Drude-2013 DNA force field²⁶ yielded stacking interaction energies that were systematically too weak (Table 1). This observation supports the hypothesis that the instability observed in DNA systems on long time scales with that force field was a result of an inadequate description of stacking. The refined parameters in the present work dramatically reduce the error with respect to the QM interaction energies (Table 1). While the new parameters produce better agreement across the entire set of 32 configurations, particularly notable is the improvement in AA stacking. This interaction energy was too weak by 2.34 kcal mol^-1 in the original parameter set, which appears to have contributed to base opening events in A-tracts observed in the case of EcoRI with Drude-2013 (Supporting Figure S1). GC stacking was also improved by an even greater magnitude in both A-DNA and B-DNA configurations. Though we did not observe instability in GC-rich regions of DNA using the Drude-2013 force field (likely due to the large magnitude of favorable stacking energy in both parameter sets), this improvement in the new parameter set contributes to a more accurate and balanced description of the stacking in DNA. The favorable stacking interaction energies are dominated by the van der Waals dispersion term, as many stacked monomers have a net repulsive electrostatic component to their stacking interaction energies (Supporting Table S1), in agreement with HF/aug-cc-pVDZ single-point energy evaluations performed on the stacked monomers optimized at the MP2/aug-cc-pVDZ level of theory. However, the narrow windows imposed on charges, atomic polarizabilities, and Thole screening factors did not yield significant improvement in the refined Drude force field relative to Drude-2013 with respect to the electrostatic contribution to stacking as defined by the HF calculation, an outcome that was not undesirable as the previous parameters were known to produce good electronic properties.^{26, 42} However, modification of selected LJ parameters did lead to improved agreement with the QM data for the total stacking energies, as reflected by the net decrease in RMSD after the MC/SA fitting across both A- and B-DNA stacked monomers (Table 1). The new polarizable force field is an improvement over both the Drude-2013 force field and the additive CHARMM36 force field. Both polarizable force fields yield better relative energetics than CHARMM36, as reflected in the Spearman and Pearson ρ coefficients, particularly in the case of A-DNA (Table 1), suggesting that the inclusion of explicit polarization improves the representation of stacking. The absolute unsigned error (AUE) and RMSD of the new Drude force field is a significant improvement over both CHARMM36 and Drude-2013, reflecting the greater accuracy of the new force field over previously available models.

Table 1.

Total base stacking interaction energies (kcal mol^-1) in A- and B-DNA configurations.

Sequence	A-DNA				B-DNA
QMa	C36	Drude-2013	Drude-New	QM	C36	Drude-2013	Drude-New
AA	-5.03	-6.80	-4.72	-5.97	-6.78	-7.36	-4.44	-6.02
AC	-4.47	-4.33	-3.04	-4.42	-5.68	-4.81	-4.75	-5.83
AG	-7.65	-8.27	-5.73	-7.24	-8.26	-8.74	-6.53	-8.38
AT	-5.00	-5.99	-5.64	-5.93	-5.71	-6.69	-6.26	-7.15
CA	-4.17	-3.97	-2.99	-3.62	-4.60	-3.96	-2.37	-3.48
CC	-2.94	-1.78	-1.24	-1.89	-1.90	0.76	-0.67	-2.31
CG	-8.80	-5.73	-6.28	-7.40	-7.89	-6.10	-6.13	-7.59
CT	-5.53	-4.30	-4.76	-5.48	-5.66	-4.13	-4.95	-5.82
GA	-8.55	-10.52	-7.96	-9.91	-9.98	-11.59	-7.34	-9.69
GC	-12.71	-15.61	-9.87	-11.53	-12.72	-17.57	-9.09	-11.69
GG	-2.80	-2.05	-1.48	-3.60	-4.55	-1.01	-3.11	-5.81
GT	-4.23	-6.98	-3.97	-4.32	-5.77	-6.19	-4.38	-5.53
TA	-6.45	-5.99	-4.66	-5.73	-5.21	-5.40	-3.78	-5.07
TC	-3.94	-5.46	-4.11	-5.72	-3.61	-4.37	-3.55	-4.82
TG	-3.14	-2.82	-2.37	-3.23	-4.60	-3.02	-3.88	-5.21
TT	-0.69	-2.84	-2.21	-1.91	-3.44	-3.33	-3.74	-3.92
Avg. Diff.		-0.41	0.95	-0.11		0.18	1.34	-0.12
AUE		1.44	1.28	0.79		1.41	1.44	0.61
RMSD		1.67	1.45	0.95		1.34	1.21	0.75
Spearman ρ		0.80	0.94	0.92		0.93	0.91	0.92
Pearson ρ		0.88	0.93	0.94		0.95	0.93	0.96

^aQM energies were taken from McDonald et al.³⁵ at the SCS-RIMP2/aug-cc-pVTZ level of theory following MP2/aug-cc-pVDZ geometry optimization. “C36” denotes the additive CHARMM36 force field.^31-32 “Drude-2013” denotes base parameters from Baker et al.⁴² and subsequently used in the Drude-2013 DNA force field.²⁶ “Drude-New” denotes the parameters developed in the present work.

Importantly, the relative energetics between A- and B-DNA have been maintained or improved under the new force field. The relative strength of stacking interaction energies in A-and B-form DNA will contribute to the ability of DNA to convert between these two forms in response to the surrounding environment. Table 2 shows the relative interaction energies between canonical A- and B-form stacked configurations. Overall, the refined parameters lead to better agreement across the 16 stacked monomers, as indicated by the considerable reduction in the average error and improvement in the RMSD. Topologies of the nucleic acid bases and the LJ parameters for the refined base atom types are provided in the Supporting Text and Table S2.

Table 2.

Relative interaction energies (kcal mol^-1) between A- and B-DNA configurations.

Sequence	ΔE (B-A)
	QMa	C36	Drude-2013	Drude-New
AA	-1.75	-0.56	0.27	-0.05
AC	-1.21	-0.48	-1.70	-1.42
AG	-0.61	-0.47	-0.80	-1.14
AT	-0.71	-0.70	-0.62	-1.22
CA	-0.43	0.01	0.62	0.14
CC	1.04	2.54	0.57	-0.42
CG	0.91	-0.37	0.16	-0.19
CT	-0.13	0.17	-0.19	-0.33
GA	-1.43	-1.07	0.62	0.21
GC	-0.01	-1.96	0.78	-0.16
GG	-1.75	1.04	-1.63	-2.22
GT	-1.54	0.79	-0.41	-1.21
TA	1.24	0.59	0.88	0.66
TC	0.33	1.09	0.57	0.90
TG	-1.46	-0.20	-1.51	-1.98
TT	-2.75	-0.49	-1.53	-2.02
Avg. Diff.		0.64	0.40	-0.01
AUE		1.12	0.69	0.70
RMSD		1.39	0.94	0.86

^aCalculated as the difference in B-DNA and A-DNA stacked monomer interaction energies listed in Table 1.

Base Dipole Moments and Molecular Polarizabilities

To verify that the new parameters preserved good agreement with gas-phase electronic properties, we computed the dipole moments and molecular polarizabilities of each of the four DNA bases using the new parameter set. Dipole moments are listed in Table 3 and molecular polarizabilities in Table 4. The QM molecular polarizabilities are scaled by a factor of 0.85, as the absence of many-body exchange effects that are coupled with polarization requires the use of underpolarized gas-phase values.⁶⁴ It has also been argued that reduced gas-phase QM molecular polarizabilities are better target data to account for the overlap of electron clouds in the condensed phase that opposes inductive effects,^65-69 or an inhomogeneous electric field that arises from the excluded volume around the solute.⁷⁰ Evaluation of methylated bases, which were not explicitly targeted during parameter refinement (in contrast to the previous version of the base parameters⁴²), serves as an important check of the quality of the base parameters. The refined base parameters retain good agreement with the QM values for both dipole moments and the scaled molecular polarizabilities, a result that is unsurprising given the narrow windows that were imposed during MC/SA refinement. This outcome indicates that new parameters preserve the gas-phase electronic properties of the four DNA bases.

Table 3.

Total dipole moments and components (in D) of methylated and unsubstituted bases.

		Methylated		Unsubstituted
		QMa	Drude-New	QM	Drude-New
Ade	μx	-2.43	-2.67	-1.91	-1.86
	μy	1.30	1.50	1.60	1.87
	μz	0.63	-0.16	0.71	-0.01
	|μ|	2.83	3.07	2.59	2.63
Cyt	μx	-1.95	-2.54	-4.13	-4.51
	μy	5.77	4.73	5.03	4.02
	μz	0.76	0.02	0.73	0.04
	|μ|	6.14	5.37	6.55	6.05
Gua	μx	-0.45	-0.17	2.88	3.01
	μy	-7.02	-6.75	-5.90	-5.43
	μz	0.95	0.27	0.84	0.06
	|μ|	7.10	6.76	6.62	6.21
Thy	μx	-1.20	-1.85	4.48	4.32
	μy	4.71	4.34	-0.72	-1.52
	μz	0.00	0.12	-0.06	-0.26
	|μ|	4.86	4.72	4.54	4.59

^aQM values are calculated at the B3LYP/aug-cc-pVDZ level of theory following MP2/6-31G* optimization. Values are taken from Baker et al.⁴²

Table 4.

Components of molecular polarizability tensors and isotropic polarizabilities (ų) of methylated and unsubstituted bases.

		Methylated		Unsubstituted
		QM×0.85a	Drude-New	QM×0.85	Drude-New
Ade	XX	18.84	16.85	15.84	14.55
	YY	15.29	14.53	14.13	13.58
	ZZ	8.02	8.20	6.81	7.23
	Iso	14.05	13.19	12.26	11.79
Cyt	XX	16.09	15.22	13.36	13.39
	YY	11.85	14.26	10.45	11.65
	ZZ	6.99	6.61	5.74	5.76
	Iso	11.65	12.03	9.85	10.26
Gua	XX	19.85	19.29	17.72	15.93
	YY	16.59	15.34	14.36	13.82
	ZZ	8.26	8.15	7.08	6.92
	Iso	14.82	14.26	13.05	12.22
Thy	XX	16.72	15.45	11.17	11.56
	YY	12.70	12.86	14.23	14.38
	ZZ	7.56	7.03	6.32	6.15
	Iso	12.33	11.78	10.57	10.70

^aQM values are calculated at the B3LYP/aug-cc-pVDZ level of theory following MP2/6-31G* optimization and are scaled by a factor of 0.85. Values are taken from Baker et al.⁴²

Base-Water Interactions

Achieving a balance between base-base and base-water interactions is important for the stability of DNA. To this end, we assessed interactions with single water molecules and all base functional groups, an essential feature in the development of the CHARMM additive force field⁷ and the Drude-2013 polarizable force field.^{26, 42} With the refined parameters, all four methylated DNA bases retain good agreement with target QM interaction energy data calculated at the MP2/6-31G*//RIMP2/cc-pVQZ model chemistry (Table 5 and Supporting Tables S3-S6). Given that the electrostatic term dominates these interactions, the narrow window imposed during fitting for base electrostatic parameters allowed for improvements in base stacking energetics without perturbing water interactions to a significant extent. Nevertheless, two interactions in particular required specific refinement. The first was the interaction between base carbonyl groups (Thy O2 and O4, Cyt O2, and Gua O6, atom type OD2C1B) and water. The second such interaction involved atom N3 in both Ade and Gua (atom type ND2R6B). Both of these interaction types were too favorable with the new parameter set. As a result, we applied pair-specific LJ parameters (NBFIX in CHARMM, Supporting Table S7) to override the combination rule values and achieve better agreement for these interactions. The results of the base-water interaction energy analysis are summarized in Table 5, with details in Supporting Tables S3-S6, including decomposition between in-plane and out-of-plane interactions (Figure 1). In all cases, the refined parameters achieved agreement with the QM target data that was either equal to, or better than, that of the Drude-2013 force field.

Table 5.

Statistical analysis of base-water interaction energies and minimum interaction distances with Drude-2013 and the new Drude force field relative to QM MP2/6-31G*//RIMP2/cc-pVQZ data.

		Drude-2013		Drude-New
		ΔIE (kcal mol-1)a	Δr (Å)b	ΔIE (kcal mol-1)	Δr (Å)
Me-Ade	Avg. Diff.c	-0.57	-0.05	-0.43	-0.01
	AUEd	1.04	0.15	0.66	0.13
	RMSDe	1.30	0.18	0.79	0.16
Me-Cyt	Avg. Diff.	-0.40	-0.05	-0.20	0.00
	AUE	0.78	0.09	0.81	0.11
	RMSD	1.08	0.14	1.04	0.14
Me-Gua	Avg. Diff.	-0.23	-0.04	-0.15	-0.01
	AUE	0.74	0.13	0.54	0.13
	RMSD	0.85	0.17	0.63	0.17
Me-Thy	Avg. Diff.	-0.36	-0.07	-0.04	0.01
	AUE	0.80	0.10	0.81	0.08
	RMSD	1.30	0.13	1.00	0.10

^aDifference in interaction energy between QM value and the result of the calculation with the Drude force field.

^bDifference in minimum interaction distance between QM value and the result of the calculation with the Drude force field.

^cAverage difference for all interactions.

^dAbsolute unsigned error for all interactions.

^eRoot-mean-square difference for all interactions.

Base-Pair Hydrogen Bonding

The present refinement of nucleic acid base parameters led to stronger hydrogen bonding in both canonical and noncanonical base dimers relative to the previous Drude-2013 force field (Table 6). In general, the interaction energies became more favorable and the characteristic hydrogen-bonding distances are shorter than their QM counterparts. A notable improvement is in the me-Ade:me-Thy Hoogsteen base pair, which is now in considerably better agreement in terms of its interaction energy and hydrogen-bonding distance. Canonical Watson-Crick base pairs (the first three entries in Table 6) remain in relatively good agreement with the QM data and the Drude-2013 force field, though they contribute to the overall trend of greater affinity among these interactions. As will be shown below in the context of full-length DNA sequences, these shortened interactions on the in vacuo model compound level do not compromise the structural properties of DNA in solution, thus the agreement obtained here was deemed adequate, given the improvement in stacking energetics and good agreement of the water interactions.

Table 6.

Base-pair hydrogen bonded interaction energies (IE, kcal mol^-1) and minimum-energy distances (r, Å) between the indicated atoms. QM data are taken from Jurečka et al.⁴⁶

Complex	Distance	QM		Drude-2013		Drude-New
		IE	r	IE	r	IE	r
G:C WC	H1 - N3	-28.80	1.91	-28.36	1.78	-31.32	1.75
mG:mC WC	H1 - N3	-28.50	1.87	-28.45	1.80	-32.15	1.76
A:T WC	H3 - N1	-15.43	1.82	-17.02	1.69	-19.73	1.76
mA:mT H	H3 - N7	-16.27	1.75	-14.41	1.57	-16.86	1.66
A:C pl	H61 - N3	-15.90	1.89	-17.90	1.73	-20.35	1.72
G:G pl	H1 - N7	-18.40	1.85	-20.17	1.61	-20.36	1.66
G:A 1	H21 - N1	-17.50	1.82	-18.42	1.61	-19.46	1.79
G:A 1 pl	H1 - N1	-16.10	1.94	-16.58	1.80	-19.22	1.82
G:A 2	H21 - N7	-10.90	1.96	-11.04	1.64	-14.02	1.60
G:A 2 pl	H21 - N7	-10.50	1.93	-11.04	1.64	-14.02	1.60
G:A 3	N7 - H1	-16.80	1.82	-14.59	1.54	-15.92	1.68
G:A 4	N1 - H21	-12.10	1.92	-14.01	1.76	-17.15	1.70
A:A 1	N1 - H61	-13.10	1.92	-14.11	1.78	-17.97	1.71
A:A 2 pl	N1 - H62	-12.30	1.95	-11.05	1.80	-14.20	1.73
A:A 3 pl	H62 - N7	-10.90	1.98	-10.42	1.63	-13.56	1.59
			Avg. Diff.	-0.24	-0.21	-2.85	-0.19
			AUE	1.11	0.20	2.97	0.19
			RMSD	1.32	0.21	3.25	0.21

Base Step Interaction Energies

The assessment of B-DNA base steps (two stacked Watson-Crick base pairs) serves as an important validation as it reflects a balance in the hydrogen bonding and base stacking interactions. From available QM reference data applying different model chemistries,^{14, 48-49} we were able to assess the accuracy of the interaction energies for nine base steps produced by our refined Drude force field parameters (Table 7). In general, the Drude interaction energies tend to be somewhat too favorable, though the results compare well with the CCSD(T)/CBS results.^48-49 The agreement is particularly good for the rigid systems, which are directly comparable to the QM interaction energy calculations, which used fixed, planar intramolecular geometries. When allowing full intramolecular relaxation, the Drude results become more favorable due to the relaxation of base geometries and propeller twist, which are known to result in additional stabilization.^{35, 48}

Table 7.

Base step interaction energies (kcal mol^-1) for rigid and fully relaxed intramolecular geometries.

Base Step	SAPT0/jaDZa	CCSD(T)/CBSb	Drude-New (Rigid)	Drude-New (Relaxed)
AA:TT	-12.10	-13.10	-10.93	-15.52
AC:GT	-11.29	-13.40	-10.74	-16.22
AG:CT	-11.20	-13.50	-15.44	-16.96
AT:AT	-10.87	-13.30	-9.21	-15.05
CA:TG	-13.63	-15.10	-16.65	-18.18
CG:CG	-15.69	-17.30	-17.37	-18.04
GA:TC	-10.22	-12.90	-14.51	-14.97
GG:CC	-9.32	-11.50	-14.86	-17.71
TA:TA	-11.92	-12.80	-12.98	-13.26
		Avg. Diff. SAPT0	-1.82	-4.41
		AUE SAPT0	2.58	4.41
		RMSDSAPT0	3.07	4.80
		Avg. Diff. CCSD(T)	0.02	-2.56
		AUE CCSD(T)	1.96	2.56
		RMSDCCSD(T)	2.32	3.02

^aQM data from Parker et al. using a truncated Dunning-type basis set (jun-cc-VDZ).¹⁴

^bQM data from Hill and Platts⁴⁹ from a study originally performed by Sponer et al.⁴⁸

Heats of Sublimation and Crystal Volumes

One method for evaluating the quality of small-molecule parameters throughout the development of the Drude-2013 force field²¹ is to perform simulations of crystalline forms of these compounds to calculate the heat of sublimation (ΔH_sub) and molecular volumes (V_m). By doing so, it is possible to evaluate the quality of the nonbonded interactions in a complex, but well-defined environment. Baker et al. performed these calculations⁴² for the bases that were incorporated into the Drude-2013 DNA force field,²⁶ finding excellent agreement with experimental data. Such agreement suggests a good model for the nonbonded interactions, but clearly the application of these parameters during long timescale MD simulations proved inadequate. By refining these base nonbonded parameters to target A-and B-DNA geometries explicitly, we have constructed a more robust parameter set that is directly applicable to DNA structures. In doing so, the agreement with experimental ΔH_sub and V_m has decreased (Tables 8 and 9). The newly refined Drude parameters for the bases yield stronger interactions in the crystal simulations, such that V_m are systematically underestimated and ΔH_sub are too large. Based on the differences between the Drude-New and QM data presented above this overestimation is suggested to be associated with the base-pair hydrogen bonding interaction energies being too favorable (Table 6). Notably, the reduction in R_min/2 of the carbonyl oxygen atom type (OD2C1B) from 1.85 Å in Drude-2013 to 1.774 Å in the updated force field yields shortened hydrogen bonding distances that are particularly notable in the cytosine crystals, giving rise to the reduced V_m, increased ΔH_sub, and shortened WC hydrogen bonding distances (Table 6). Given that the greatest deviations are due to bifurcated N4-O2 hydrogen bonding that does not occur in canonical A- or B-DNA, the deterioration of ΔH_sub and V_m agreement relative to Drude-2013 reflects the challenge of assigning LJ parameters that yield agreement with all target data. However, given the stated goal of improving DNA stability on microsecond time scales, such a sacrifice in accuracy was deemed acceptable, given the considerable improvement in base stacking interaction energies (Table 1).

Table 8.

Heats of sublimation (ΔH_sub, kcal mol^-1). Results are the average of ten independent simulations. Experimental reference values are taken from Chickos and Acree.⁷¹

Base	Experiment	Temp (K)	Drude-2013*	% Diff	Drude-New	% Diff
Cyt	35.18	453	37.25	5.9	42.91	22.0
	38.45	298	38.27	-0.5	43.95	30.3
Thy	29.73	403	31.90	7.3	32.79	10.3
	31.60	298	31.11	-1.6	33.72	6.7
Me-Ade	29.09	428	30.74	5.7	37.88	30.2
Me-Cyt	35.64	298	35.62	-0.1	41.32	15.9
Me-Thy	29.73	398	29.26	-1.6	31.25	5.1
Avg. Diff.			0.68	2.2%	4.91	14.9%
AUE			1.01		4.91
RMSD			1.32		5.55

^*Some values obtained using the Drude-2013 differ from those reported by Baker et al.⁴² due to refinement, especially of internal terms, during the course of the development of the Drude-2013 DNA force field.^26-27

Table 9.

Molecular volumes (V_m, ų). Results are the average of ten independent simulations.

Base	Experiment	Temp (K)	Drude-2013*	% Diff	Drude-New	% Diff
Cyt	118.172	298	112.5	-4.7	111.8	-5.3
Thy	144.773	298	139.5	-3.6	137.8	-4.7
Me-Ade	164.374	126	161.7	-1.6	157.9	-3.9
Me-Cyt	143.175	298	141.3	-1.3	137.4	-4.0
Me-Thy	168.976	298	171.1	1.3	171.0	1.3
Et-Gua	218.477	298	218.8	0.2	212.0	-2.9
Ade:water	218.978	298	222.1	1.5	215.0	-1.8
Gua:water	168.579	298	173.4	2.9	174.4	3.5
Avg. Diff.			-0.56	-0.7%	-3.44	-2.2%
AUE			3.24		5.19
RMSD			3.67		5.65

^*Some values obtained using the Drude-2013 differ from those reported by Baker et al.⁴² due to refinement, especially of internal terms, during the course of the development of the Drude-2013 DNA force field.^26-27

Base and χ Dihedral Refinement

Changes to the base nonbonded parameters affect the interactions of each base with the deoxyribfuranose sugar, the phosphodiester backbone, and interactions between atoms separated by three bonds within the bases themselves. As such, it was necessary to evaluate and refine dihedrals involving base atoms. Preliminary simulations of the new base parameters revealed a tendency for out-of-plane distortion in Ade bases, which led to destabilization of dsDNA on the sub-nanosecond time scale (not shown). To correct this behavior, the force constants for dihedrals applied to the exocyclic N6 amine and the purine ring were increased (Table S8). The refined dihedrals produce agreement with QM vibrational frequencies that agree at least as well as the previous Drude-2013 force field (Table S9), indicating that the minor modification of the dihedral terms yields satisfactory behavior. With the new parameters, some of the out-of-plane motions of the exocyclic N6 amine have increased frequencies compared to both the QM target data and the Drude-2013 parameters as a result of their dihedral parameters being rigidified. The optimized geometry of adenine with a pyramidal exocyclic N6 amine is only -0.3 kcal mol^-1 lower in energy than the optimized planar N6 amine form when using the MP2/6-31G* model chemistry and -0.1 kcal mol^-1 lower with MP2/aug-cc-pVDZ. Thus, the increased rigidity of the exocyclic amine is reasonable as these two states are not significantly different in energy.

The glycosidic linkage between each base and the deoxyribfuranose sugar will dictate, in part, the conformational sampling of nucleotides in dsDNA in terms of base orientation and sugar pucker. To account for changes in base parameters, we refined the glycosidic linkage, χ (O4′-C1′-N1/9-C2/4) and χ₂ (C2′-C1′-N1/9-C2/4) by targeting 1-D potential energy surfaces of χ rotation. Figure 3 shows the potential energy surfaces for each of the four DNA nucleosides, comparing the target QM data with the Drude-2013 and new Drude parameters. Notable in the present refinement is the improved agreement with the positions of the energy minima in each scan, particularly for Cyt, which previously had a minimum shifted towards A-like structures. While Cyt does have A-like character in B-DNA,⁸⁰ preliminary simulations with the new base parameters revealed excessive sampling of North sugar puckering driven by A-like values of χ, which caused perturbed B-DNA structures, motivating the present refinement of the χ and χ₂ torsions. The magnitude and positions of the BII minima were improved for all bases, though the systematic decrease in energy relative to Drude-2013 was not solely a result of χ refinement. The better agreement is in part due to the ε₂ (C2′-C3′-O3′-H3T) reparametrization discussed below. Therefore, the improvement observed here reflects a correction to a problem on the model compound (nucleoside) level, not a defect observed in full-length DNA. The χ refinement did, however, lead to small improvements in the position of the BII minima, and the ε₂ reparametrization was necessary to properly fit the new χ and χ₂ parameters using the MC/SA approach described in the Methods.

Figure 3.

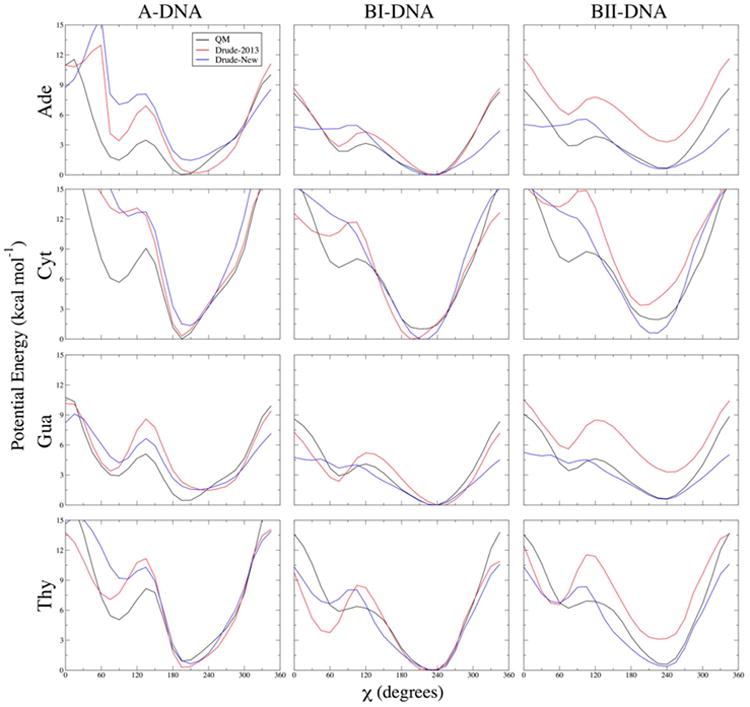
One-dimensional potential energy scans for χ dihedrals in each of the four DNA nucleosides, and each of the three indicated geometries. Backbone β, γ, and ε dihedrals and sugar pucker were constrained to canonical values in each conformational scan. QM potential energies are computed using the RIMP2/cc-pVTZ model chemistry following MP2/6-31G* optimization.

3′-Terminal Hydroxyl Dihedral Refinement

The 1-D χ potential energy surfaces in Figure 3 show a systematic upward shift in BII energies for the Drude-2013 force field. The cause of this deviation can be attributed to the Drude-2013 force field parameters for the ε₂ dihedral (C2′-C3′-O3′-H3T) in the nucleoside model compounds (note that in the nucleoside model compounds only the value of ε differentiates BI vs. BII). In the A and BI forms of the nucleosides, ε₂ is near its energy minimum in each of those forms (∼92° and ∼83°, respectively), but in the BII form, ε₂ is at ∼156°, which is near the maximum of the Drude-2013 potential energy surface for ε₂ (Figure 4). Thus, these dihedral parameters were reparametrized to obtain better agreement with QM potential energy surfaces using adenosine as a model compound. To confirm the transferability of the new dihedral parameters, the calculations were repeated by performing the same potential energy scan of ε₂ in cytidine. The new parameters achieve improved agreement for both of these nucleosides, yielding three energy minima in each profile and reproducing the energy barriers between them in near-quantitative agreement with the QM values (Figure 4). Having eliminated this source of error, the remaining parameters in the nucleoside model compounds (χ, exocyclic torsions, and sugar ring dihedrals) could be better refined without the systematic deviation arising from ε₂. This refinement should also produce a more accurate model for 3′-terminal hydroxyl sampling in full-length DNA.

Figure 4.

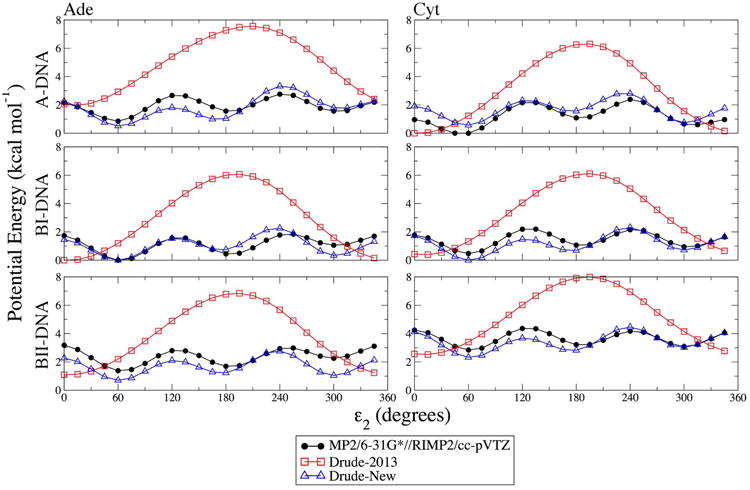
One-dimensional potential energy surfaces as a function of the ε₂ dihedral for the adenosine and cytidine model compounds. Non-target dihedrals and sugar pucker were constrained to characteristic values of the indicated geometries (see Methods). QM potential energies are computed using the RIMP2/cc-pVTZ model chemistry following MP2/6-31G* optimization.

α and γ Backbone Dihedral Refinement

Achieving a proper description of backbone energetics in DNA is a persistent challenge in force field development, and is a topic of continual refinement in many additive force fields.^5,57,81-83 Notable in these efforts is the importance of α and γ sampling; in B-DNA γ is typically gauche⁺ (g⁺) and α is gauche^- (g). In the AMBER force field by Cornell et al.,² incorrect sampling of these torsions led to unwinding of dsDNA in solution, necessitating reparametrization as part of the AMBER parmbsc0 force field.⁵⁷ As such, it is clear that ensuring that the proper α/γ sampling in g^-/g⁺ is critical for stability of B-DNA. The parametrization of the Drude-2013 DNA force field considered only A, BI, and BII geometries; in the present work we include Z-DNA configurations in the refinement as Z-DNA was unstable using the Drude-2013 force field.²⁶ Using the T3PS model compound (Figure 2), we computed 1-D potential energy surfaces as a function of all backbone dihedrals in Z-DNA (CpG steps) and ZI-/ZII-DNA (GpC steps).

By targeting the six surfaces simultaneously for each dihedral, it was possible to achieve better agreement for both α and γ. The Drude-2013 parameters had no major defects in treating these torsions, though the BII minimum in the α surface was in the g⁺ conformation; long MD simulations with this force field showed that such sampling led to transient, local distortions (data not shown) and was therefore important to fix. The new parameters for the α dihedral (Table S8) correct this problem by raising the g⁺ minimum in BII such that the g^- conformation is the lowest point on the BII surface (Figure 5). The good agreement between the Drude-2013 and QM α surfaces in A-, BI-, Z-, ZI-, and ZI-DNA was preserved with the new parameters, with small improvements obtained in both the positions of minima and the barriers between them (Figure 5).

Figure 5.

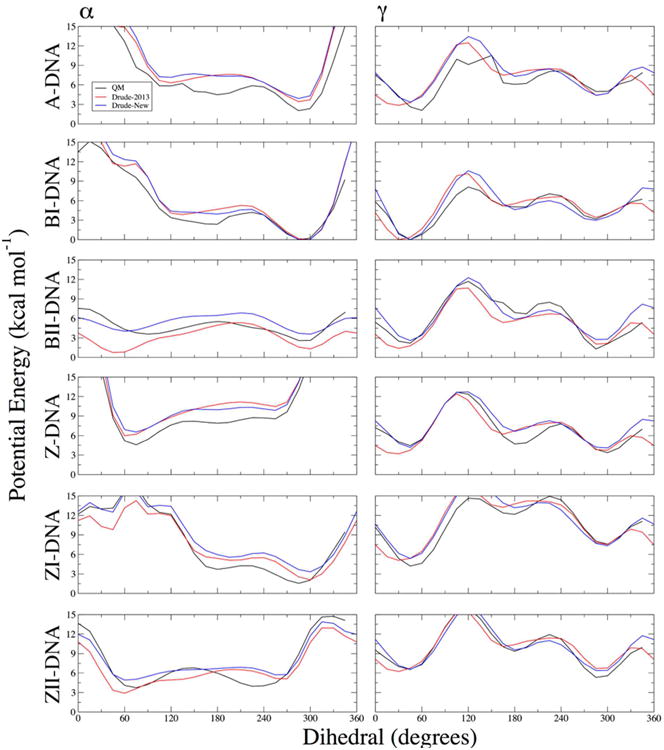
One-dimensional potential energy surfaces for the T3PS model compound for scans of α and γ dihedrals. Non-target dihedrals and sugar pucker were constrained to characteristic values of the indicated geometries (see Methods). QM potential energies are computed using the RIMP2/cc-pVTZ model chemistry following MP2/6-31+G* optimization.

A similar improvement was observed in the case of the γ torsion. No specific problem was observed in DNA simulations with the Drude-2013 force field, but in generating Z-DNA energy surfaces with T3PS (Figure 5), several small deficiencies were exposed, notably the positions of trans (t) minima, which are the dominant form in Z-DNA at CpG steps.⁸⁴ The new Drude force field parameters for γ (which involved only a refinement of force constants, with phase angles and multiplicities left alone from their Drude-2013 values) more accurately reproduce the t local minima and the positions of the g⁺ and g^- minima in all surfaces (Figure 5), suggesting that they will produce an improved description of DNA backbone conformational ensembles across A-, B-, and Z-DNA.

ε and ζ Backbone Dihedral Refinement

The highly correlated ε and ζ torsions in B-DNA give rise to two dominant sub-states, BI (ε ∼190°, ζ ∼270°) and BII (ε ∼260°, ζ ∼180°), and the equilibrium between these two states dictates aspects of the local structure of B-DNA. More generally, BI and BII can be described by subtracting the ε and ζ dihedral angles, with BI defined as ε - ζ < 0° and BII as ε - ζ > 0°. Given the tight coupling in the dynamics of these two torsions, the parametrization strategy for these dihedral angles was approached in a manner that allowed for simultaneous refinement. In the development of the Drude-2013 force field, the ε and ζ dihedrals of the T3PM model compound (Figure 2) were simultaneously scanned over values in ranges typically sampled by B-DNA, and dihedral and electrostatic terms were refined to reproduce the QM potential energy surface.^26-27 We expand upon that approach in the present work to include A-, Z-, ZI-, and ZII-DNA surfaces (Figure 6). Simulations of Z-DNA with the Drude-2013 force field were unstable, and poor ε and ζ sampling was identified as a contributing issue, motivating the present refinement.

Figure 6.

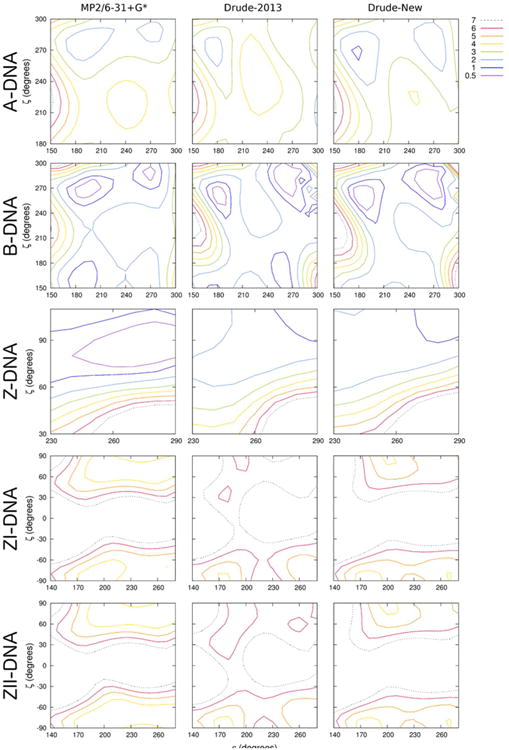
Two-dimensional potential energy surfaces (kcal mol^-1) of ζ vs. ε for the T3PM model compound. Non-target dihedrals and sugar pucker were constrained to characteristic values of the indicated geometries (see Methods). Each surface is offset to the global minimum. QM potential energies are computed using the MP2/6-31+G* model chemistry.

The new dihedral parameters for ε and ζ (Table S10) lead to better agreement with all five QM potential energy surfaces (Figure 6). Notable in the refinement is the improvement in the Z-, ZI-, and ZII-DNA surfaces. The Z-DNA surface has a broad, shallow minimum that both the Drude-2013 and the refined force field reproduce reasonably well. The Drude-2013 ZI- and ZII-DNA surfaces were in very poor agreement with the QM data, but the new force field yields the correct, broad local minima in the g^- and g⁺ conformations for ζ, which are characteristic of backbone sampling in ZI-DNA and ZII-DNA, respectively.⁸⁴ The new force field retains the quality of the T3PM potential energy surfaces for A- and B-DNA, improving the energy barriers in the A-DNA surface slightly and preserving the BI/BII energy barrier in the B-DNA surface. Together, these outcomes indicate that the updated force field is a better model of ε and ζ in all forms of DNA than the previous Drude-2013 force field.

As an additional form of validation for the ε and ζ dihedral parameters, the T3PS model compound was used to perform 1-D potential energy scans of each torsion independently (Figure 7). These surfaces were not used directly as target data for the dihedral parameter fitting, but guided the refinement by identifying energy minima to set the correct multiplicities and phase angles. Several important improvements are observed in the T3PS surfaces using the refined Drude force field. The ε surfaces generally show broad minima separated by low barriers, which the new force field parameters reproduce well. The new parameters reproduce the broad minimum around the t conformation in the ZII-DNA surface, and better model the two shallow minima in the ZI-DNA surface (Figure 7). Similar improvements are observed in the A-DNA surface and the barrier in the BI surface between minima at ∼180° and ∼270°.

Figure 7.

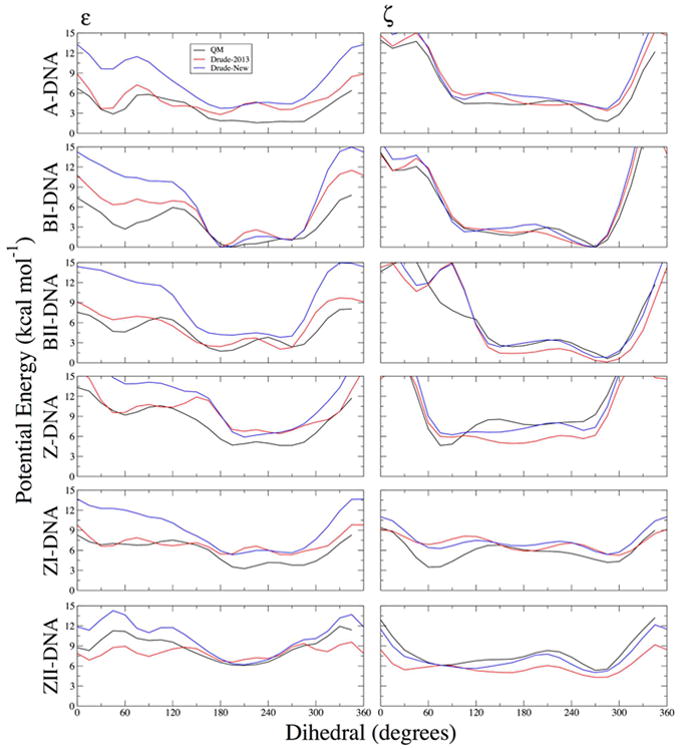
One-dimensional potential energy surfaces for the T3PS model compound for scans of ε and ζ dihedrals. Non-target dihedrals and sugar pucker were constrained to characteristic values of the indicated geometries (see Methods). QM potential energies are computed using the RIMP2/cc-pVTZ model chemistry following MP2/6-31+G* optimization.

Refinement of the ζ dihedral terms significantly improved agreement with the QM potential energy surfaces in the Z-, ZI-, and ZII-DNA conformations, notably removing aberrant minima around the t conformation (Figure 7) that gave rise to incorrect backbone conformations in the Drude-2013 force field. The updated force field parameters for ζ favor sampling in the g⁺ and g^- conformations, which are the dominant states in Z-DNA for all CpG and GpC steps.⁸⁴

Nucleoside Sugar Pucker Conformational Energetics

The conformational ensemble of sugar puckering in nucleosides and nucleotides will be strongly influenced by factors including the relative orientation of the base, as well as properties of the backbone. As such, these correlated motions require careful parametrization to accurately describe the properties of the sugar. To this end, we carried out new QM calculations on the relative conformational energetics of sugar puckering in DNA nucleosides by scanning over the ν₀ and ν4 torsions with backbone β, γ, and ε fixed in A-, BI-, and BII-DNA conformations. Additionally, syn-deoxyguanosine surfaces were generated in ZI- and ZII-DNA conformations to explicitly investigate the role of sugar puckering on the instability of Z-DNA observed with the Drude-2013 force field. Doing so allowed us to examine the conformational properties of nucleosides as a function of sugar pucker and the energy barriers that separate the North and South states. We note that in the QM optimizations and corresponding molecular mechanical calculations, the glycosidic torsion (χ) was free to relax; this is an important test of the parameters in the force field, which should not only match the energetics of each surface, but also the underlying structures. The force field parameters subject to refinement in these calculations were sugar dihedrals for ν₀ and ν₄ themselves, as well as exocyclic torsions involving base atoms, namely ν₄′ (C4′-O4′-C1′-N1/N9), ν₁′ (C3′-C2′-C1′-N1/N9), and χ₂ (C2′-C1′-N1/N9-C2/C4). In conjunction with χ (see above), these dihedrals are the ones most directly responsible for the orientation of the base relative to the sugar and the favorability of the sugar pucker itself.

Figure 8 shows the potential energy surfaces for deoxythymidine as a function of ν₀ and ν₄. The QM surfaces indicate that North (top-right) and South (bottom-left) conformations are separated by energy barriers on the order of 3-4 kcal mol^-1. The global minimum resides in the South puckering region of the BI surface, and all surfaces have local minima in the North and South regions. Similar features are observed for the other nucleosides (Figures S2-S4). The Drude-2013 force field produced reasonable energy surfaces for the nucleosides, though in the case of deoxythymidine, it over-stabilized the North state in BI-DNA, and the barrier is slightly too low relative to the QM surface. By refining select sugar and exocyclic dihedrals, we were able to better reproduce the QM potential energy surfaces, suggesting a better model of sugar puckering in full-length DNA. Additional improvements in the sugar energetics may be possible via the use of a grid-based 2D dihedral energy correction map (CMAP) that maps the energy difference between a QM target surface and the underlying empirical surface to exactly reproduce the QM (or any target surface)⁸⁵ as has been previously suggested for improving semiempirical models of nucleic acids.⁸⁶ However, as the intrinsic conformational properties of the furanose ring are sensitive to the types and chirality of its substituents, use of CMAP or related approach must be performed with care.

Figure 8.

Two-dimensional potential energy surface (kcal mol^-1) of deoxythymidine in each of the three indicated geometries. Backbone β, γ, and ε dihedrals were constrained to canonical values in each conformational scan. QM potential energies are computed using the MP2/6-31G* model chemistry.

The analysis of syn-deoxyguanosine in ZI- and ZII-DNA conformations (Figure 9) illustrated deficiencies in the Drude-2013 force field in representing these noncanonical structures. The Drude-2013 representation of ZI-DNA was uniformly too high in energy, with neither of the local minima present in the QM surface (Figure 9). Additionally, the ZII-DNA surface with Drude-2013 was shifted too far into the South pucker region. After refining the sugar and exocyclic dihedrals for deoxyguanosine, the potential energy surfaces were brought into better agreement. The new Drude force field yields ZI-DNA minima in better agreement with the target QM surface, with a similar barrier between North and South regions (3-4 kcal mol^-1). A dramatic improvement was obtained for the ZII-DNA surface, in which the energy minima are shifted toward positive values of ν₀, in much closer agreement with the QM surface. The QM has a broad region of low energy, with a small energy barrier between North and South states, less than 2 kcal mol^-1, while the Drude force field surface has a more narrowly defined minimum with a barrier that is somewhat higher, between 2-3 kcal mol^-1. A B-like minimum with C2′-endo pucker at ν₄ ∼ 0° and ν₀ ∼ -20° remains in the ZII-DNA surface with the refined Drude parameters. This minimum is present but very small in the QM surface, and the barrier between the minima in the Z-like conformations and this B-like conformation are such that any transition to a B-like form should be reversible on computationally accessible time scales. Despite these small deviations, the refined Drude force field parameters are in much better agreement with the QM puckering surface and are a considerable improvement over the previous Drude-2013 force field, which only targeted A- and B-DNA. It is therefore unsurprising that there were previously discrepancies with respect to Z-DNA, but the present parametrization efforts largely correct those problems.

Figure 9.

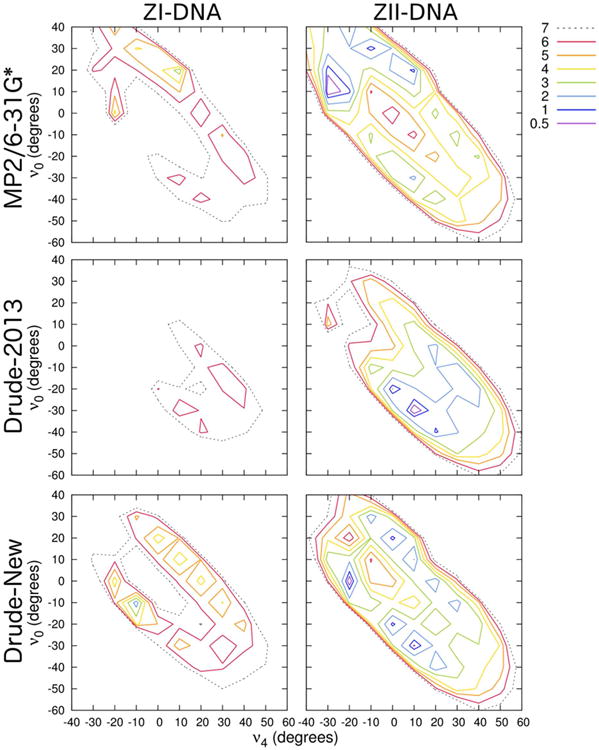
Two-dimensional potential energy surface (kcal mol^-1) of syn-deoxyguanosine in each of the two indicated Z-DNA geometries. Backbone β, γ, and ε dihedrals were constrained to canonical values in each conformational scan. QM potential energies are computed using the MP2/6-31G* model chemistry.

Conclusions

The present work describes the parametrization of a refined polarizable force field for DNA based on the classical Drude oscillator model to address deficiencies observed in the previous version of the force field, Drude-2013.²⁶ After an initial refinement of base nonbonded parameters (electrostatic and LJ) targeting high-level QM stacking energies, additional internal terms in the phosphodiester backbone and deoxyribofuranose rings were refined by targeting 1-D and 2-D QM potential energy surfaces. Notable in the present work is the explicit targeting of Z-DNA forms, including the ZI- and ZII-DNA sub-states characteristic of GpC steps in Z-DNA.

The parameter optimization strategy led to an overall improvement in backbone and sugar puckering conformational energetics with respect to the targeted QM data as well as various nonbonded interactions involving the bases. The refined force field produces significantly improved agreement with the QM base stacking interaction energies, an important advancement given the instability observed in extended simulations of duplex DNA reported recently.³⁴ In conjunction with the improved interactions between the nucleobases and water, the force field is expected to be well balanced with respect to the intermolecular forces that give rise to DNA structure and dynamics. The greater agreement in Z-DNA backbone conformational energetics and nucleoside sugar puckering is important for stable simulations of Z-DNA. An issue in the current parameter set is the overly favorable in-plane base-base interactions, which contribute to degradation in results from simulations of base crystals, which give rise to larger ΔH_sub and smaller V_m as compared to experimental values. These outcomes are largely a result of the reduced radius of the carbonyl oxygen, indicating that additional refinement may be necessary to achieve agreement across the small molecule and macromolecule levels. An extensive validation of the force field in the context of duplex DNA simulations is provided in an accompanying paper.⁸⁷