Proton Environments in Biomimetic Calcium Phosphates Formed from Mesoporous Bioactive CaO–SiO₂–P₂O₅ Glasses in Vitro: Insights from Solid-State NMR

Abstract

When exposed to body fluids, mesoporous bioactive glasses (MBGs) of the CaO–SiO₂–P₂O₅ system develop a bone-bonding surface layer that initially consists of amorphous calcium phosphate (ACP), which transforms into hydroxy-carbonate apatite (HCA) with a very similar composition as bone/dentin mineral. Information from various ¹H-based solid-state nuclear magnetic resonance (NMR) experiments was combined to elucidate the evolution of the proton speciations both at the MBG surface and within each ACP/HCA constituent of the biomimetic phosphate layer formed when each of three MBGs with distinct Ca, Si, and P contents was immersed in a simulated body fluid (SBF) for variable periods between 15 min and 30 days. Directly excited magic-angle-spinning (MAS) ¹H NMR spectra mainly reflect the MBG component, whose surface is rich in water and silanol (SiOH) moieties. Double-quantum–single-quantum correlation ¹H NMR experimentation at fast MAS revealed their interatomic proximities. The comparatively minor H species of each ACP and HCA component were probed selectively by heteronuclear ¹H–³¹P NMR experimentation. The initially prevailing ACP phase comprises H₂O and “nonapatitic” HPO₄^2–/PO₄ groups, whereas for prolonged MBG soaking over days, a well-progressed ACP → HCA transformation was evidenced by a dominating O¹H resonance from HCA. We show that ¹H-detected ¹H → ³¹P cross-polarization NMR is markedly more sensitive than utilizing powder X-ray diffraction or ³¹P NMR for detecting the onset of HCA formation, notably so for P-bearing (M)BGs. In relation to the long-standing controversy as to whether bone mineral comprises ACP and/or forms via an ACP precursor, we discuss a recently accepted structural core–shell picture of both synthetic and biological HCA, highlighting the close relationship between the disordered surface layer and ACP.

1. Introduction

Bone is a composite material consisting of platelets of Ca-deficient hydroxy-carbonate apatite (HCA) deposited on collagen-I fibrils, forming a complex hierarchical structure that underlies its extraordinary mechanical properties.^1,2 The very thin (2–10 nm) and elongated HCA platelets (30–50 nm long; 15–30 nm wide) pack themselves like a deck of cards, with the longest crystal axis aligned with the direction of the collagen fibril.¹⁻⁴ Besides minor amounts of noncollagenous proteins and glycosaminoglycans, bone comprises significant amounts of citrate (≈1 wt %) and water (≈10 wt %),^1,2,5 the latter associated with both the organic and inorganic components. While it is recognized that the H₂O content of bone is reduced on its aging, which correlates with a loss of strength and stiffness, recent research suggests that the water and citrate components may have stronger bearings on the stability and mechanical properties of bone than was previously conceived, with their role of interfacing the stacked HCA platelets by acting like a glue that enhances the tissue strength.⁵⁻⁹

The OH content of bone mineral is significantly lower than for stoichiometric calcium hydroxy-apatite (HA; Ca₅(PO₄)₃OH), which is the mother structure of biological/synthetic HCA. The deficiency of Ca²⁺, PO₄^3–, and OH^– species in biological apatite stems from various coupled ion substitutions that lead to incorporation of mainly HPO₄, CO₃^2–, and F^– anions, together with cations such as Na⁺, Mg²⁺, and Sr²⁺.^4,10 The element specificity and high signal sensitivity of magic-angle spinning (MAS) ¹H nuclear magnetic resonance (NMR) have been exploited in numerous investigations targeting the various proton (H₂O, OH, and HPO₄) species of bone mineral^6,11−14 and synthetic H(C)A,^6,15−22 as well as for unraveling the interfacing role of water between the HCA platelets.^6,8,9 Noteworthy is that the mineral-associated ¹H and ³¹P environments may be probed selectively by using cross-polarization (CP) MAS NMR experimentation utilizing interatomic ¹H–³¹P distance-dependent heteronuclear dipolar interactions:^{6,11−14,23,24} this allows for rejecting all proton resonances from the organic components of bone/dentin that otherwise dominate ¹H NMR spectra recorded directly by single pulses. CPMAS-based NMR experimentation, such as the heteronuclear correlation (HETCOR) technique,^11,25 also enables the discrimination^{8,23,24,26−28} of proton environments of amorphous calcium phosphate (ACP²⁹⁻³¹) and crystalline H(C)A. Recently, several advanced heteronuclear NMR protocols have been applied for estimating the nanometer-scale organization and the extent of (dis)ordered domains in various heterogeneous phosphate-bearing materials, encompassing bone/dentin as well as synthetic composites.^{7,8,16,17,23,24,32,33}

There are several NMR reports on the ¹H speciation in directly precipitated H(C)A¹⁸⁻²¹ and as an integrated component in various synthetic multiphase materials.^7,34 However, despite a vast literature on studies of HCA growth in vitro from biomaterials intended for bone/tooth implants, ¹H NMR studies targeting the proton environments in ACP and HCA generated biomimetically from such substrate biomaterials are very sparse.^{26−28,35,36} One class of amorphous biomaterials is melt-prepared silicate-based bioactive glasses (BGs)³⁷ and their templated mesoporous bioactive glass (MBG) counterparts with an ordered mesopore arrangement:^38,39 when subjected to simulated body fluid (SBF), biomimetic HCA forms at the (M)BG surface via an ACP precursor,^{26,27,37,40,41} as first proposed by Hench and co-workers.^37,40In vivo, this biomineral-mimicking phosphate layer interfaces strongly with bone tissue.

A detailed insight into both the fundamental ACP/HCA formation mechanisms and the similarities/differences of the phosphate and proton speciations of biomimetic HCA and biological apatite is desirable. For three series of MBGs with variable Ca, Si, and P contents and SBF-exposure intervals ranging between 15 min and 30 days, we present a comprehensive MAS NMR study unveiling the evolution of the proton environments both at the MBG surface and within each ACP and HCA component of the growing biomimetic phosphate layer. The silicate and phosphate environments of the same set of specimens were previously characterized by ²⁹Si and ³¹P MAS NMR;^42,43 those findings are summarized in Section 3. They will be contrasted with the complementary information gained herein about the H species of the heterogeneous multicomponent specimens.

We provide results from single-pulse ¹H NMR and fast-MAS ¹H–¹H double-quantum–single-quantum (2Q–1Q) correlation NMR experiments, which inform primarily about the various water and silanol (SiOH) moieties and their interatomic proximities of the dominating H reservoir at the MBG silicate surface, whereas the overall minor H populations of each ACP and HCA component of the phosphate layer were examined by heteronuclear ¹H–³¹P NMR experimentation. The present work extends our previous ¹H NMR studies, which only discussed the surface proton speciations in detail for the pristine MBGs,⁴⁴ whereas the counterparts in SBF-soaked specimens were restricted to one MBG base composition and a limited number of exposure periods,^27,35 moreover involving a much higher MBG loading in the SBF (20 g/L) than the current one (0.6 g/L).

The details of how bone mineral nucleates and to what extent this process is regulated by noncollagenous proteins and collagen remain unclear.^2,45−48 More remarkable is the long-standing controversy whether bone mineral is formed via transient precursor phases^{2,4,10,45,46,49−51} of ACP and/or octacalcium phosphate^52,53 (OCP; Ca₈(HPO₄)₂(PO₄)₄·5H₂O). Such a process is tempting, given the generally accepted feature that H(C)A forms in vitro by nucleation from an ACP phase^30,31,54—and more precisely, within it⁵⁵⁻⁵⁸—as also demonstrated in a recent study of HA crystallization in the confined space of liposomes.⁵⁹ The discussions of the biomimetic HCA formation in our present and previous reports of SBF-exposed MBGs^{27,28,42,43,60} adopt such an ACP→H(C)A conversion viewpoint. A detailed in vitro mechanism was recently inferred by Habraken et al.,⁵⁶ showing that the embryos of “ACP” constitute prenucleation clusters of Ca²⁺ and HPO₄^2– ions, which subsequently evolve into HA via OCP-like phases.

However, despite early suggestions of ACP and OCP as precursors of biological apatite,^29,31,52,53 supported by a few recent bone and enamel mineralization studies in vertebrates,⁶¹⁻⁶⁴ an unrefutable proof thereof has remained elusive,^2,45,46,50 leading to an alternative view that bone mineral crystallizes directly as tiny platelets of poorly ordered and highly ion-substituted HCA.^4,45,50,65 Nonetheless, recent insight on the structural organization of both synthetic and biological apatite involves a crystalline HCA core and a structurally disordered surface layer.^{4,8,10,16,23,24,51,59,65−67} Expanding along the lines of refs (8, 23, and 24), we argue that the latter is simply “ACP”. A potential formation mechanism via an ACP precursor is then readily rationalized, and the two seemingly disparate viewpoints may naturally be reconciled: this possibility—which generally seems to be overlooked in the literature—is commented on in Section 5.2 and will be discussed more thoroughly elsewhere (M. Edén, to be published).

2. Materials and Methods

2.1. MBG Preparation

Three MBG specimens of nominal molar compositions 10CaO–90SiO₂ (“S90”), 10CaO–85SiO₂–5P₂O₅ (“S85”), and 37CaO–58SiO₂–5P₂O₅ (“S58”) were prepared by an evaporation-induced self-assembly (EISA) procedure⁶⁸ at 40 °C, using the nonionic P123 triblock copolymer as a structure-directing agent and precursors of tetraethyl orthosilicate (TEOS), triethyl phosphate (TEP), and Ca(NO₃)₂·4H₂O to incorporate Si, P, and Ca, respectively. The detailed conditions are described in ref (69). The resulting homogeneous membranes were heated at 700 °C for 6 h to remove nitrate ions and organic molecules. The textural properties and the experimentally determined cation compositions of the pristine MBGs are listed in Table 1.

Table 1. MBG Compositions and Textural Properties^a.

sample	aCaO	bSiO2	cP2O5	stoichiometric formulab	SBET (m2g –1)c	Vp (cm3 g–1)d	dp (nm)e	mesoporous structure
S90	10.0(9.6)	90.0(90.4)	0.0(0.0)	Ca9.6Si90.4P0.0O190.4	468	0.63	5.37	p6mm
S85	10.0(10.6)	85.0(86.5)	5.0(2.9)	Ca10.3Si84.1P5.6O192.5	480	0.64	5.38	Ia3d
S58	37.0(36.6)	58.0(59.0)	5.0(4.4)	Ca35.1Si56.5P8.4O169.2	195	0.46	9.45	p6mm

^aEach MBG sample is denoted Sb, where b is the nominal oxide equivalent of SiO₂ in mol % of the composition aCaO–bSiO₂–cP₂O₅, where a + b + c = 100 mol %. Values in parentheses represent the experimentally analyzed oxide equivalents (see ref (42)).

^bCharge-balanced analyzed stoichiometric composition, with cation coefficients summing to 100.0 (mol).

^cSpecific surface area determined by the Brunauer–Emmett–Teller method.⁸⁹

^dTotal pore volume calculated from the amount of N₂ adsorbed at a relative pressure of P/P₀ = 0.98 according to Gregg et al.⁹⁰

^eAverage pore diameter obtained by the Barrett–Joyner–Halenda procedure.⁹¹ All data are reproduced from Turdean-Ionescu et al.⁴²

2.2. SBF-Exposed MBG Specimens

An SBF solution was prepared according to Kokubo et al.⁷⁰ by dissolving NaCl, KCl, NaHCO₃, K₂HPO₄·3H₂O, MgCl₂·6H₂O, CaCl₂, and Na₂SO₄ into distilled water. It was buffered at pH = 7.38 by using tris(hydroxymethyl)-aminomethane/HCl (TRIS/HCl) and then passed through 0.22 μm Millipore filters to avoid bacterial contamination. An amount of 600 mg of a fine powder (<20 μm particle diameter) of each pristine MBG was immersed in 1.000 L of SBF in a sealed polyethylene container placed in an Ecotron HT incubator at 37 °C. The solutions were stirred at 100 rpm for each of the following periods: {0.25, 1, 4, 8, 24} h and {3, 7, 15, 30} days. The solid phase was subsequently retained by filtration, soaked in acetone to quench the surface reactions, washed with water, and finally vacuum dried at 37 °C for several days. The SBF-exposed specimens are henceforth denoted S90-τ_SBF, S85-τ_SBF, and S58-τ_SBF, with the immersion period τ_SBF specified either in hours (“h”) or days (“d”). For example, S85-3d resulted by soaking the S85 MBG in SBF for 3 days (i.e., 72 h). Prior to the NMR experiments, all samples were stored under dry conditions in a desiccator.

2.3. Solid-State NMR

The solid-state NMR experimentation was performed at external magnetic fields (B₀) of 9.4 or 14.1 T, using Bruker Avance-III spectrometers operating at the respective ¹H Larmor frequencies of −400.1 and −600.1 MHz. All single-pulse (“Bloch decay”) ¹H NMR spectra were obtained at B₀ = 9.4 T with 90° radio frequency (rf) excitation pulses at a nutation frequency of v_H ≈ 70 kHz and MBG/MBG-τ_SBF powders packed in either 4 mm or 7 mm ZrO₂ rotors undergoing MAS at the rate ν_r = 7.00 kHz. The NMR acquisitions employed relaxation delays of 4.0 s and between 256 and 1024 accumulated signal transients. The NMR data of two polycrystalline HA powders (Aldrich) were recorded under similar conditions, except for using 4 mm rotors spinning at 14.00 kHz (16–64 transients).

¹H–¹H 2Q–1Q correlation NMR spectra were recorded from the S90 and S58-15d samples at B₀ = 14.1 T, using 1.3 mm ZrO₂ rotors spinning at 66.00 kHz. Double-quantum coherences (2QCs) were excited with two completed cycles of [SR2₄¹] (90°-pulse-sandwiched R2₄ R2₄^–1)⁷¹⁻⁷³ with τ_exc = τ_rec = 242.4 μs. The 2D NMR protocol shown in Figure 1c of Teymoori et al.⁷² was used, except that herein, 2QCs were generated directly from longitudinal ¹H polarization. The ¹H nutation frequency was 33.00 kHz during dipolar recoupling and 125 kHz for all strong 90°/180° pulses. Rotor-synchronization of the 2QC reconversion was accomplished by a Hahn echo lasting for two rotational periods between the excitation/reconversion events.^71,73 Both time dimensions utilized rotor-synchronized time incrementation, Δt₁ = Δt₂ = 15.15 μs, where 82(t₁) × 1024(t₂) time points were acquired with 256 and 512 transients/t₁-value for S90 and S58-15d, respectively, and using 2.0 s relaxation delays. Each 2D grid was zero-filled to 512(t₁) × 8192(t₂) points and broadened by 120 Hz (sine bell shape) and 60 Hz (Lorentzian shape) along the 2Q and 1Q dimensions, respectively.

All heteronuclear ¹H–³¹P CPMAS experiments were performed at 9.4 T, using 4 mm rotors spinning either at ν_r = 14.00 kHz (2D HETCOR) or at ν_r = 10.00 kHz when employing the ¹H-detected CPMAS protocol of Maltsev and Jäger,¹⁷ which we will refer to as “diffCP” (“difference CP”). CP was established at the modified Hartmann–Hahn condition ν_H = ν_P + ν_r, with the ³¹P nutation frequency ramped around v_P = 40 kHz by ±1.5 kHz. The 90° ¹H pulse operated at v_H = 78 kHz. The relaxation delays were 4.0 s. The contact interval (τ_CP) was 1.0 ms for the 2D HETCOR acquisition, whereas 0.2 ms or 6.0 ms was utilized for the diffCP counterparts, the latter typically averaged over 5000–24 000 transients depending on the P content of the sample and the precise {τ_CP, τ_SBF} values. The 2D HETCOR data was recorded with spectral windows of 56.0 kHz and 14.0 kHz for the direct ³¹P and indirect ¹H spectral dimensions, respectively. 400 transients/t₁-value with 40(t₁) × 400(t₂) time points were acquired and zero-filled to 256 × 2048 points.

¹H and ³¹P chemical shifts are quoted relative to neat tetramethylsilane and 85% H₃PO₄(aq), respectively. All 2D NMR acquisitions implemented the States procedure⁷⁴ to yield absorptive peaks with frequency-sign discrimination along the indirect dimension, resulting in total 2D NMR acquisition durations of 23 h (2Q–1Q; S90), 47 h (2Q–1Q; S58-15d), and 36 h (HETCOR; S85-1d). Despite using airtight rotors, the mechanical sample rotation during the NMR experimentation dehydrates the samples over extended periods of days.

3. Previous Inferences about HCA Growth from MBGs

Before discussing the ¹H NMR results of the proton environments in the three series of S90-τ_SBF, S85-τ_SBF, and S58-τ_SBF specimens, we review our main conclusions from complementary ³¹P/²⁹Si NMR investigations on these samples.^42,43 The ACP formation and its conversion into HCA were quantified independently by powder X-ray diffraction (PXRD) and ³¹P MAS NMR.⁴² The results of the two characterization techniques agreed well: no significant HCA formation was detected by either method for immersion periods τ_SBF < 24 h, except for S90, where ³¹P NMR revealed minor amounts of HCA already after 8 h. After 3 days of SBF soaking, roughly equal relative ACP:HCA fractions were observed for specimens of each S90, S85, and S58 series. Notwithstanding a net growth of ACP and HCA between 3 and 30 days, their relative fractions remained almost constant throughout, with the NMR and PXRD analyses yielding estimates of ≈50% and 60–80% of HCA, respectively, out of the total phosphate layer formed at any S90/S85/S58 MBG. It has been demonstrated that carbonate ions are present in both the crystalline and amorphous phosphate phases grown in SBF, implying that HCA forms rather than HA.²⁷

Noteworthy, the HCA formation rate is essentially independent of either the precise {Ca, Si, P} MBG composition or the textural properties⁴²—such as the surface area and pore arrangement, which differ among the S90, S85, and S58 specimens^39,42,69 (see Table 1). This feature is likely to hold for any MBG provided that its surface area is sufficiently large (≳200 m²/g); it was rationalized from the very similar silicate-reaction pathways observed for all three MBG structures, as inferred from ²⁹Si MAS NMR involving either direct excitation with single pulses or ¹H→²⁹Si CP:⁴³ after a rapid leaching of Ca²⁺, which is completed within the first 15–60 min of SBF soaking, essentially neat mesoporous silica remains that consequently degrades independently on the precise initial MBG surface area or pore arrangement.

As discussed in ref (43), the main distinction among the P-bearing S85 and S58 MBGs concerns how rapidly the structure is depleted of Ca and phosphate species, which may be rationalized from subtle distinctions in their structural roles: P is present as orthophosphate ions in amorphous calcium phosphate clusters (CaP) located in the pore walls.^35,44,75 One fraction of the Ca reservoir charge balances the PO₄^3– anions of the CaP clusters, while the remaining modifies the silicate network, whose Ca-associated silicate groups tend to accumulate near the pore-wall surface.^35,44 The latter portion only exists in Ca-rich (e.g., S58) or P-free (e.g., S90) MBGs, whereas essentially all Ca²⁺ species of the S85 structure are concentrated in the surface-associated and 1–2 nm-sized CaP clusters⁷⁵ that readily dissolve on their contact with aqueous solutions.^42,43,75 In contrast, the CaP clusters of the S58 MBG are much smaller and partly embedded within the silicate network building the pore wall,^75,76 thereby leading to a slower release of their Ca²⁺ and PO₄ constituents. The distinct CaP cluster scenarios are illustrated in Figure 2 of Turdean-Ionescu et al.⁴³

Notwithstanding the identical long-term dissolution behavior and nearly equal HCA formation rates manifested by the three S90, S85, and S58 MBGs, the net amounts of biomimetic ACP/HCA formed during SBF exposure indeed depend on the MBG composition:⁴² they grow concurrently with the P content of the pristine MBG (see Table 1). Hence, for a constant MBG mass (m_MBG) in a given SBF volume (V) and soaking period, the resulting amount of HCA increases according to S90 < S85 < S58.⁴² This stems from a larger total P reservoir available from the MBG and SBF portions during the soaking of S58 relative to that of its P-free S90 counterpart. However, the property of essentially identical in vitro response mechanisms from the three distinct MBGs only applies for SBF testing under dilute conditions (m_MBG/V ≲ 1 g/L).^42,43 Our early work employed 3–20 g/L;^{27,28,35,60,69} such high MBG concentrations perturb the HCA formation by inducing an undesirable coupling between the MBG composition and the m_MBG/V ratio, leading to markedly retarded silicate-surface reactions and an impeded ACP→HCA crystallization (notably so for Ca-rich MBGs), as discussed in refs (42, 43, and 60).

4. Results

4.1. ¹H Speciations Probed by MAS NMR

A ¹H MAS NMR spectrum reveals the quantitative proton speciation of the heterogeneous MBG-τ_SBF specimen, which may comprise up to four distinct component phases, whose relative proportions depend on the SBF-soaking interval. The first two constituents are MBG-associated: (1) The silicate-based MBG pore walls account for the largest proton reservoir, which predominantly consists of physisorbed water molecules and Si–OH moieties, regardless of the precise τ_SBF-value. (2) The MBG-associated amorphous CaP clusters comprise water and minor apatite-like OH groups.^28,44 However, this proton source is negligible and henceforth ignored, particularly because the CaP clusters readily dissolve on contact with aqueous solutions (Section 3). The remaining proton-bearing phases are the (3) ACP and (4) HCA constituents of the phosphate layer growing at the MBG surface for increasing τ_SBF. Yet, these portions of the entire proton ensemble are minor, and most of their ¹H NMR resonances are swamped by those from silanols and water; the selective probing of the phosphate-associated protons is discussed in Section 4.3.

Figure 1 displays a selection of ¹H MAS NMR spectra recorded from each series of SBF-exposed S90, S85, and S58 MBG samples, with τ_SBF increasing from top to bottom. All spectra reveal silicate surface-deriving resonances (≳2 ppm), as well some narrow signals (marked by asterisks), the most prominent ones appearing at 1.1 and 3.6 ppm and stemming from CH₃ and OCH₂ groups. They originate mainly from remnant P123 block copolymers anchored at the pore-wall surface.⁴⁴ Despite that they are minor, these resonances are emphasized by their narrow peak widths (<30 Hz). These undesirable proton species are commented on further in Section 5.1, and onward we focus on the targeted ¹H responses from the inorganic phases.

Figure 1.

¹H MAS NMR spectra recorded by single pulses (B₀ = 9.4 T; ν_r = 7.00 kHz) from the series of S90-τ_SBF (left panel), S85-τ_SBF (mid panel), and S58-τ_SBF (right panel) MBG specimens, with the SBF-exposure period (τ_SBF) increasing from top to bottom. The results for MBG-1d are representative also for those of MBG-4h and MBG-8h (not shown). The spectra are zoomed around the main centerband signals and are normalized to equal areas across this spectral region. Asterisks mark narrow resonances around {3.6, 1.3, 1.1, 0.8} ppm that stem from OCH₂ and CH₃ moieties of remnant templating molecules, whereas “#” identifies the NMR peak associated with SiOH_isol groups (only visible from the pristine MBGs). The gray boxes convey the approximate shift ranges representative for SiOH moieties experiencing weak, moderate, and strong H-bonding (in practice, their shift-spans overlaps and are not accurately known).

The precise ¹H chemical shift (δ_H) of each silicate/phosphate-associated OH/H₂O moiety is mainly dictated by its degree of hydrogen bonding to neighboring O atoms: the shift of an OH···O fragment increases when the H···O distance is decreased.^77,78 Hence, the globally lowest chemical shift (“most shielded ¹H”) is manifested by the OH resonance from HCA, δ_H ≈ 0.05 ppm, where H-bonding is absent.¹⁵ Naturally, this weak and broad peak is most pronounced in the NMR spectra from the MBG-30d specimens (Figure 1). Disregarding the HCA-associated ¹H shift and only focusing on the MBG-associated SiOH/H₂O ensemble, the lowest shift, δ_H ≈ 1.85 ppm, is observed from “isolated” SiOH groups devoid of H-bonding;^79,80 they are henceforth denoted SiOH_isol. They are present at any MBG surface (e.g., see Section 4.2) but only produce clearly discernible ¹H resonances when the physisorbed water content is low. Consequently, the narrow resonance at δ_H ≈ 1.85 ppm is readily detected from each pristine MBG but is not apparent after its exposure to the aqueous solution, owing to the substantial rehydration and thereby emphasized H-bonding network among the various SiOH and H₂O moieties. All other ¹H NMR signals in the spectral region >2 ppm are relatively ill-defined for (moderately) high surface-hydration levels, due to a continuum of H-bonding scenarios and an accompanying NMR peak broadening. Yet, three main groups of ¹H resonances may be identified in Figure 1, and their relative contributions depend on the amount of surface-bound water:⁴⁴

(i) ¹H resonances in the range of 2–4 ppm, which are signatures of a “dry” silicate surface, implying a minor water adsorption and thereby weakly H-bonded OH groups.⁷⁹⁻⁸²

(ii) A peak around 4.5–5 ppm that reflects physisorbed water and more extensively H-bonded SiOH groups.^44,80−82 This ensemble comprises two distinct portions, whose NMR signals are unresolved in the ¹H MAS NMR of Figure 1 but are distinguishable by other NMR features: the majority of the water pool is highly mobile, while the remaining (minor) portion is bound more tightly and may constitute the inner shell of the physisorbed species and/or water present as inclusions within the MBG pore walls. The sizable ¹H–¹H through-space dipolar interactions (see Section 4.2) of the immobile species give spinning sidebands (not shown) at the modest MAS rate ν_r = 7.00 kHz employed.^15,83,84 Yet, from the low sideband intensities relative to the centerband, we conclude that comparatively few H₂O molecules are immobile, whereas the dominant population does not produce sidebands but contribute to most of the centerband intensity in the spectra of Figure 1. The relative proportions of stationary and mobile water molecules depend on the precise surface hydration, but the latter portion dominates throughout (presumably ≳80%).

(iii) Weak ¹H resonances in the high-ppm region (≳8 ppm) stem from strongly H-bonded species, encompassing minute contributions from acidic protons of HPO₄^2– anions of ACP^{7,8,15−17,23,28} (see Section 4.3) but predominantly involving H-bonded SiOH ···^–OSi motifs, as observed from fragmented networks of hydrous silicate glasses comprising alkali/alkaline-earth metal ions.^83,84 Indeed, these NMR signals are only clearly discernible from the Ca-rich S58 MBG^35,44 and its S58-τ_SBF derivatives with short SBF-immersion periods up to ≈24 h; see Figure 1.

Noteworthy, the silicate-surface hydration and dehydration processes are reversible, and the precise ¹H NMR peak position observed in the 3–5 ppm range reflects the given surface water content when the NMR experiment was performed.^44,80−82 Despite that the ¹H NMR spectra presented herein were recorded on as-prepared samples stored in a desiccator prior to the NMR experiments, the quantitative proton speciations at the MBG surface are not an intrinsic sample property. Moreover, it is not possible to accurately control the amount of surface-associated water because each S90/S85/S58 specimen (and its MBG-τ_SBF counterparts) exhibits inherently distinct water affinities: the degree of water adsorption enhances concomitantly with the Ca²⁺ population at the MBG surface,⁴⁴ which increases according to S85 ≲ S90 < S58 (where the surface-associated Ca²⁺ population is slightly higher for the P-free S90 structure relative to that of S85, whose entire Ca reservoir is present in the CaP clusters).^35,43 With these caveats in mind, we only discuss the gross trends of Figure 1 concerning the evolution of the proton speciations of the various samples over the 30 days of SBF immersion, where we highlight the following:

(i) All pristine S90, S85, and S58 MBGs were heated at 700 °C (see Materials and Methods) and manifest relatively “dry” surfaces revealing ¹H NMR peak maxima at ≈4 ppm. On their SBF exposure, an enhanced surface hydration is evident for all MBG-0.25h specimens, as evidenced by the vanishing peak intensity ≈1.85 ppm from isolated silanols, accompanied by an overall resonance broadening. The elevated population of surface-adsorbed water molecules is most evident for the Ca-richest S58–0.25h specimen, which additionally manifests an NMR peak-maximum displacement from ≈3.7 ppm (pristine S58) to 5.0 ppm, the latter typical for “liquid” H₂O resonances.

(ii) For prolonged SBF exposure of S90 and S85 (τ_SBF > 24 h), the broad NMR peak gradually splits into two primary resonances that appear around 3.4–3.7 ppm and 5.0–5.4 ppm, suggesting two main “pools” of distinct proton environments that experience weak and moderately strong H-bonding, respectively (Figure 1). Overall, for a given τ_SBF value, the S90-τ_SBF and S85-τ_SBF samples exhibit very similar NMR signatures, whereas the resonance from physisorbed water (≈5 ppm) is emphasized for the S58-τ_SBF surfaces, consistent with their higher water affinity.

(iii) In good qualitative agreement with the estimated HCA contents of Turdean-Ionescu et al.⁴² (Section 3), the HCA-associated OH resonance (≈0 ppm) is clearly visible after SBF-soaking periods τ_SBF > 24 h. Its intensity grows concurrently with both the SBF-immersion period and the P content of the MBG (Table 1), i.e., along the series S90 < S85 < S58, which becomes particularly evident when comparing the peak intensity ≈0 ppm in the NMR spectra from S90-30d and S58-30d of Figure 1.

4.2. ¹H–¹H Proximities from Double-Quantum NMR

To qualitatively assess the spatial proximities among the various surface-associated proton species, we performed dipolar recoupling experimentation with the [SR2₄¹] pulse sequence⁷¹⁻⁷³ at ν_r = 66.0 kHz. These experiments utilize homonuclear through-space ¹H–¹H dipolar interactions to excite 2QCs, whose buildup rate reflects the dipolar-coupling magnitude in a pair of protons. This interaction depends on the inverse cube of the ¹H–¹H internuclear distance but is also sensitive to molecular motions and averages to zero in the presence of rapid molecular reorientations. For instance, the ¹H–¹H dipolar interaction of the CH₃/OCH₂ groups of the residual polymers are motionally averaged, the extent of which depends strongly on the precise surface hydration level (and also underlying their varying NMR peak-widths among the spectra of Figure 1).

To identify which pairs of nearest-neighboring protons exhibit “close” internuclear proximities (≲0.5 nm), 2Q–1Q 2D NMR correlation spectra were recorded from the S90 and S58–15d samples for a short 2QC excitation interval of τ_exc = 242 μs. The 2D NMR spectrum from the pristine S90 MBG is displayed in Figure 2. A close proximity between two protons—resonating at the respective shifts δ_H^A and δ_H along the horizontal “1Q dimension” of the 2D NMR spectrum—is revealed by the presence of a 2D NMR signal at the corresponding 2QC shift, δ_2Q = δ_H^A + δ_H, which appears along the vertical “2Q dimension”. A 2QC signal from two protons of the same type that feature equal chemical-shift values (δ_H) occurs at δ_2Q = 2δ_H, i.e., along the diagonal of the 2Q–1Q spectrum marked by the dotted line in Figure 2. Incidentally, such “autocorrelation” signals dominate the 2D NMR spectrum from S90.

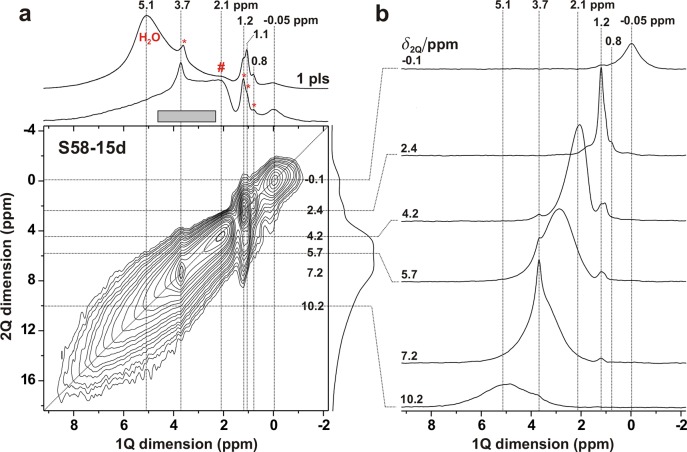
Figure 2.

(a) 2Q–1Q correlation ¹H NMR spectrum recorded from the pristine S90 MBG (B₀ = 14.1 T; ν_r = 66.00 kHz), using the [SR2₄¹] dipolar recoupling sequence with a 242 μs 2QC excitation period. The 2D NMR spectrum is shown together with projections along the horizontal 1Q (top) and vertical 2Q (right) dimension. The topmost 1D NMR spectrum (“1 pls”) was recorded directly by single pulses under otherwise identical conditions and processed using the same apodization (60 Hz Lorentzian shape) as that for the 2Q–1Q NMR spectrum. The gray box marks the approximate resonance region associated with weakly H-bonded SiOH groups, asterisks indicate signals from organic molecules, and “#” identifies the NMR peak from SiOH_isol moieties. (b) Slices extracted at the as-indicated 2Q shifts (δ_2Q).

The 2Q–1Q NMR spectrum from the S90 MBG (Figure 2) is similar to our previous result from a pristine S85 specimen:⁴⁴ besides the narrow resonances at the 2QC shifts of 7.2 ppm and across 2–4 ppm that originate from 2QCs among protons within each OCH₂ and CH₃ moiety, respectively, the primary signal represents a broad autocorrelation ridge associated with hydrogen-bonded SiOH groups. Yet, a correlation is also established among two SiOH_isol sites at the surface, as is most evident from the slice along the 1Q dimension at δ_2Q = 3.8 ppm, shown to the right of the 2D NMR spectrum. The S90 surface hydration level was lower when the 2Q–1Q experimentation was performed relative to that giving the NMR spectrum of Figure 1 (compare the directly excited spectra of Figures 1 and 2). Yet, considering that most silanols are weakly H-bonded (responsible for the overall largest NMR signal intensity ≈3.7 ppm), the shortest ¹H–¹H distance between two SiOH_isol moieties is expected to be longer than that involving an isolated silanol (δ_H = 1.8 ppm) and a H-bonded (δ_H ≈ 3.5 ppm) counterpart. Hence, the latter correlations should also be present: while they are obscured in the 2Q–1Q spectrum by the dominating autocorrelation ridge from pairs of H-bonded SiOH groups, those NMR signals appear in the slice at δ_2Q = 5.7 ppm as a broad resonance extending between 2 and 4 ppm and peaking at the shift of the SiOH_isol group (Figure 2). There is also a 2QC autocorrelation involving the resonance at δ_H = 4.8 ppm, whose origin is unknown; notwithstanding that both its chemical shift and narrow peak-width suggest physisorbed water, those mobile moieties should not permit 2QC excitation, as commented below.

The 2Q–1Q NMR spectrum obtained from S58-15d is displayed in Figure 3. It overall features the same correlations as those observed from S90 but differs primarily in two aspects. First, the SBF-exposed S58-15d specimen reveals an autocorrelation peak at 0 ppm, originating from the OH groups of HCA. Second, the S58-15d powder was rehydrated prior to the NMR experiments, as manifested by the absence of a significant spectral intensity from isolated silanols in the ¹H MAS NMR spectrum displayed in Figure 3 and by the prominent NMR peak at 5.1 ppm from mobile physisorbed water molecules. However, their motionally averaged ¹H–¹H interactions do not support 2QC excitation (see Section 4.1), as witnessed by the strong signal-intensity depletion ≳4.5 ppm in the projection of the 2Q–1Q NMR spectrum of Figure 3 relative to the Bloch-decay MAS counterpart. Noteworthy, fast-MAS experimentation at ν_r = 66 kHz (Figures 2 and 3) does not improve the NMR spectral resolution significantly relative to that at ≈10 kHz (Figure 1) because the peak widths are mainly dictated by chemical-shift dispersion rather than by homonuclear ¹H–¹H interactions.

Figure 3.

(a) 2Q–1Q correlation ¹H NMR spectrum acquired from the S58-15d sample at B₀ = 14.1 T and ν_r = 66.00 kHz. (b) Slices extracted at the as-indicated 2Q shifts (δ_2Q). See the caption of Figure 2 for further information.

Despite the higher surface hydration of S58-15d compared with S90, the 2Q–1Q NMR spectrum reveals that SiOH_isol surface groups are present (Figure 3). Yet, as expected, their associated ¹H resonances are weaker and appear to mainly involve correlations with H-bonded silanols; see the slices extracted at δ_2Q = 4.2 ppm and δ_2Q = 5.7 ppm. Moreover, the larger population of H-bonded silanols is manifested in the 2Q–1Q spectrum by the autocorrelation ridge extending over a larger shift range in both spectral dimensions (which is responsible for the “tail” toward higher shifts observed in the projection).

4.3. Phosphate-Associated Proton Environments

As follows from the hitherto discussed ¹H NMR results, only a minority of the ¹H resonances derive from the biomimetic ACP/HCA layer, most merely being associated with silanols and physisorbed water molecules at the MBG surface. Consequently, we performed ¹H→³¹P CPMAS NMR experimentation for selectively probing the protons in close spatial proximity to phosphate groups of the heterogeneous calcium phosphate layer. Figure 4 displays a ¹H–³¹P 2D HETCOR NMR spectrum recorded from the S85-1d sample. It informs which proton and phosphate species are close in space by a pairwise correlation appearing at the 2D coordinate {δ_H, δ_P}, with the chemical shifts of ¹H (δ_H) and ³¹P (δ_P) being encoded along the vertical and horizontal dimensions of the 2D NMR spectrum, respectively. Each corresponding 2D spectral projection reveals a ¹H (vertical) and ³¹P (horizontal) spectrum solely manifesting resonances that convey sufficiently strong ¹H–³¹P contacts, with a “strong” (“weak”) ¹H–³¹P contact implying a short (long) ¹H–³¹P internuclear distance and/or a higher (lower) number of protons in the vicinity of ³¹P.

Figure 4.

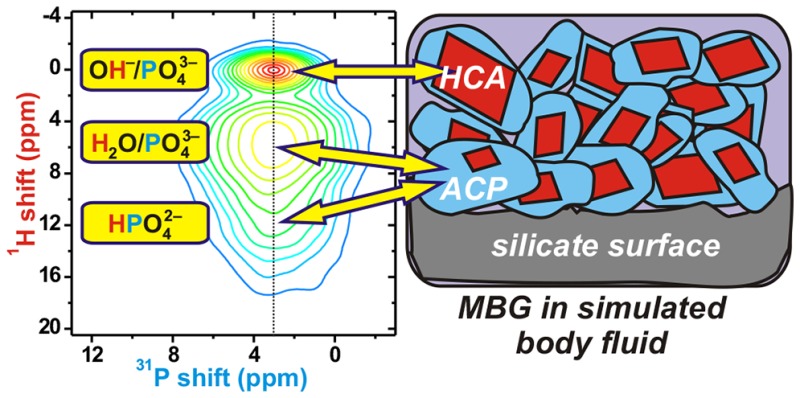
¹H–³¹P HETCOR 2D NMR spectrum (left panel) recorded from S85-1d at B₀ = 9.4 T and ν_r = 10.00 kHz (τ_CP = 1.0 ms) and shown together with its projections along the ³¹P (horizontal; top) and ¹H (vertical; right) spectral dimensions. The right panel displays slices along the ³¹P dimension, corresponding to PO₄^3–/OH correlations of HCA (δ_H = 0.0 ppm), as well as nonapatitic PO₄/H₂O (δ_H = 5.8 ppm) and HPO₄^2– (δ_H = 12.1 ppm) contacts of ACP. The ³¹P fwhm values are given at the right spectral portions of the slices. The lowest 2D contour level is at 6% of the maximum amplitude.

The ³¹P projection in Figure 4 exhibits a broad and nearly Gaussian peak at δ_P = 3.05 ppm. It comprises three main components, all centered around nearly identical ³¹P chemical shifts, as illustrated by the slices extracted at δ_H = {0.0, 5.8, 12.0} ppm from the 2D HETCOR NMR spectrum. One narrow³¹P NMR peak of full width at half-maximum (fwhm) height of 1.94 ppm (315 Hz at B₀ = 9.4 T) is correlated with the narrow OH signal appearing at δ_H = 0.0 ppm; it stems from the orthophosphate groups of HCA^27,28 that represents the well-crystalline “core” in the core–shell structural picture (see Section 5.2). All other ³¹P NMR responses are significantly broader (fwhm 5.1–5.4 ppm) and correlate with ¹H shifts δ_H > 4 ppm, all of which originate from ACP,^8,26−28,59 i.e., the “hydrated HCA surface” in the core–shell view;^16,17,65,66 the most intense NMR peak at the shift pair {δ_H, δ_P} = {5.8, 3.0} ppm is assigned to “nonapatitic” PO₄^3– groups nearby water molecules, whereas the remaining correlations with δ_H ≳ 9 ppm stem mainly from P–OH contacts in HPO₄ anions. These NMR responses account for the broad “tail” toward higher δ_H values of the 2D HETCOR spectrum. Notably, they are not visible in the directly excited NMR spectra of Figure 1, underscoring that the ACP-associated H₂O and HPO₄^2– moieties are minute components of the total¹H reservoir in any MBG-τ_SBF specimen. Yet, these strongly H-bonded species represent all protons around the phosphate groups in ACP,^{8,16,17,23,28,59} which is devoid of the OH group constituting the fingerprint of well-crystalline H(C)A.

Figure 5 displays ¹H NMR spectra obtained from each S90, S85, and S58 MBG immersed in SBF for a short (τ_SBF = 4 h) or long (τ_SBF = 30 days) period and acquired either by single pulses (“1 pls”) or by the “diffCP” protocol.¹⁷ The latter yields an ¹H NMR spectrum solely comprising the resonances from protons involved in magnetization transfers to neighboring ³¹P sites in a sole 1D NMR acquisition.¹⁷ Hence, the diffCP-derived NMR result is identical to the projection along the ¹H dimension of a ¹H–³¹P HETCOR NMR spectrum, but it circumvents the time-consuming 2D NMR acquisition. diffCP NMR is also strongly preferred over ³¹P→¹H CPMAS application,^14,85,86 which is plagued by much slower T₁ relaxation than the reverse ¹H→³¹P process. As expected, all NMR spectra of Figure 5 reveal at least one of the ¹H resonances observed in the projection of the HETCOR NMR spectrum: a narrow peak at 0 ppm from the OH groups of HCA and responses from H₂O (peaking ≈5 ppm) and HPO₄^2– anions (≈12 ppm).

Figure 5.

¹H NMR spectra of the indicated MBG-4h (top panel) or MBG-30d specimens (bottom panel); they were recorded either directly by single pulses (“1 pls”) or by the ¹H–³¹P “diffCP” protocol,¹⁷ the latter labeled by the respective contact interval (τ_CP) of 0.2 ms or 6.0 ms used for ¹H → ³¹P CPMAS. The NMR spectra are normalized to equal areas. The broad resonances, emphasized in the NMR spectra obtained with τ_CP = 0.2 ms and peaking at ≈5 ppm and ≈12 ppm stem from H₂O and HPO₄^2– moieties, respectively. The weak but sharp peak at 10 ppm (marked by an asterisk) is attributed to the HPO₄ group of brushite.^11−13,15

The ¹H–³¹P diffCP NMR experiments involved magnetization transfers activated over both short (τ_CP = 0.2 ms) and long (τ_CP = 6.0 ms) periods, thereby enabling a qualitative proximity probing over “short” (≲0.3 nm) and “longer” (≲1 nm) ¹H–³¹P distances, respectively. As discussed previously,²⁸ the overall stronger ¹H–³¹PO₄ contacts of ACP relative to HCA are mirrored in its NMR signal being maximized already at τ_CP ≈ 1.5 ms, whereas the HCA counterpart exhibits a slower but continuous growth for increasing contact periods, reaching a plateau around 6 ms. Overall, the most rapid magnetization transfers occur across the P–OH fragments of HPO₄^2– groups:¹⁶ this accounts for the generally emphasized high-ppm intensities in the diffCP-derived data of Figure 5 that utilized τ_CP = 0.2 ms, as compared with the ¹H–³¹P HETCOR counterpart of Figure 4 that employed a longer contact period of 1.0 ms and thereby favoring the H₂O/PO₄ pair.

Consequently, utilizing a short contact interval of 0.2 ms emphasizes the ¹H NMR responses from the amorphous phase(s) and enables their (near) selective probing. This is evident from Figure 5: regardless of the τ_CP value, all NMR results for the MBG-4h samples stemming from a short SBF-exposure interval reveal predominantly resonances from ACP. Yet, the very weak OH peak intensity ≈0 ppm observed for τ_CP = 6.0 ms evidences a minute HCA formation already at this short incubation period (see Section 5.4). Moreover, the nearly complete selective excitation of the ¹H NMR signals from ACP is manifested by all NMR spectra acquired with τ_CP = 0.2 ms from the MBG-30d specimens, which comprise both ACP and HCA (Figure 5). For the MBG-30d samples, all NMR data recorded by employing the longer contact period (τ_CP = 6.0 ms) reveal mainly the narrow OH signal from HCA because relaxation processes during CP damp the ACP-stemming resonances even over short contact intervals of a few milliseconds.^16,17,28

Besides the targeted ¹H→³¹P magnetization transfers from the protons of the ACP/HCA components, weak transfers also occur from those of the organic templating molecules; they are most pronounced for the MBG-4h specimens for τ_CP = 6.0 ms. We consider these signals as artifacts that might have leaked through the phase cycle, although their emphasized intensities consistently observed for the longer contact interval of 6.0 ms may indeed reflect transfers from the aliphatic surface-anchored organic moieties to the surrounding ACP phase growing at the pore surface.

5. Discussion

5.1. Origin of the ¹H Signals around 1 ppm?

The narrow resonances at 0.8, 1.1, and 1.3 ppm observed in ¹H NMR spectra from the MBG and MBG-τ_SBF samples (Figures 1–3 and 5) are doubtlessly of organic origin. Besides the results herein, we refer to Leonova et al.⁴⁴ for detailed assignments and further discussions. Concerning ¹H NMR characterizations of the already complex systems of mesoporous silica coexisting with its heterogeneous surface layer of calcium phosphates, these NMR peaks are a nuisance and may lead to assignment ambiguities—even as to the precise organic source molecules, as shown below. However, these NMR signals are worth discussing in more depth because similar (but distinct) NMR responses are frequently observed across the shift range 0.8–1.4 ppm from apatites, encompassing HA,^13−16,22 HCA,^{6,13,14,19−21} fluoro-hydroxyapatite,^15,87 as well as bone mineral.^6,13,14 These resonances are usually very weak from well-crystalline HA, as may be verified from the ¹H NMR spectra of Figure 6(a, b).

Figure 6.

¹H NMR spectra recorded at 9.4 T and 14.00 kHz MAS from two distinct HA powders, labeled (a) HA–1 and (b) HA–2; they are associated with “low” and moderately “high” surface hydration degrees, respectively, as witnessed by the broad NMR peak centered at 5.5 ppm from HA–2. Both samples manifest the HA-characteristic OH resonance ≈0 ppm. (c) The result after soaking the HA–2 powder in ethanol (red trace), as well as after repacking the powder and repeating the NMR experiment (black trace).

First focusing on the minor ¹H resonances from synthetic H(C)A, their precise shifts and intensities vary slightly among samples and studies, but (at least) two peaks are reported around 0.8–0.9 ppm and 1.2–1.4 ppm, respectively,^{6,13−16,21,22} occasionally accompanied by another resonance around 2.0 ppm.^14,21 Their narrow peak widths (≲30 Hz) and absence of magnetization transfers in ¹H–³¹P CPMAS-based experimentation suggest species that are either highly mobile and/or remote from phosphate groups.^14,16 Furthermore, the peak intensities grow concurrently with the surface area of the H(C)A crystallites and are most pronounced for nanocrystalline HA powders.¹⁶ Altogether, these characteristics point toward surface-associated species whose populations depend on the surface hydration level,²¹ but unambiguous assignments have until recently remained elusive. Similar narrow peaks are also observed from HCA with significant carbonate-for-phosphate substitutions (“B-type” HCA),^13,18−21 where they have been attributed to OH groups close to CO₃^2– ions.^6,13,18,19

The hitherto most convincing solution to the enigma of the origin of the narrow NMR responses in the 0.8–1.4 ppm range—at least for well-ordered HA—was recently provided by Ben Osman et al.,²² who applied a suite of characterization protocols to HA samples with controlled (but relatively low) surface hydration levels. All ¹H resonances appearing at {0.8, 1.1, 1.3} ppm were attributed to H₂O molecules that terminate the OH channels (which are aligned with the c axis of the crystal frame). The 1.1 ppm signal dominates for higher amounts of surface-bound water; its intensity is reduced on drying, whereupon two peaks at 0.8 and 1.3 ppm emerge, which were assigned to H₂O molecules oriented “up” and “down” relative to the OH groups in the channels, respectively.²² However, it is unlikely that the assignments of ref (22) account for the significantly more intense ¹H resonances ≈1 ppm observed from OCP, which have been tentatively attributed to mobile H₂O molecules.^9,15 Noteworthy, similar signals at {0.8, 1.1, 1.2} ppm reported by Souza et al. from biomimetic HCA (generated by exposing melt-prepared BGs to SBF) were assigned to a poorly ordered OCP-like precursor of HCA.³⁶

Yet another potential source for ¹H NMR signals ≈1.1 ppm is CH₃CH₂OH, which may arise from incompletely dried HA powders washed in ethanol.²⁰ Indeed, after soaking the “HA-2” powder in ethanol, three narrow peaks at {0.88, 1.10, 1.30} ppm are observed (Figure 6(c); red trace), incidentally at shifts indistinguishable from those we assigned to remnant templating molecules in Figure 1, as well as from those discussed by Ben Osman et al. in the context of HA.²² The sole, yet decisive, distinction to the H(C)A/OCP-associated ¹H resonances is the accompanying peak at 3.64 ppm from the OCH₂ group of ethanol [Figure 6(c)], which together with the intense signal at 1.10 ppm derives from bulk liquid ethanol. The much weaker responses at 0.88 and 1.30 ppm, on the other hand, are attributed to strongly physisorbed ethanol molecules at the HA surface: notably, the latter intensities remained almost unaffected on removal of the HA powder from the rotor, followed by its immediate repacking and subsequent NMR acquisition (black trace), whereas the intensity at 1.10 ppm diminished markedly by evaporation of the liquid. Moreover, two very weak signals at 2.04 and 1.60 ppm (with essentially unaltered intensities) are observed in both spectra of Figure 6(c). They may originate from nonvolatile impurities of the ethanol batch.

5.2. Disordered Phosphate Component: ACP or Apatite Surface Layer?

A “core–shell” structural model, involving a crystalline HCA core and a disordered surface layer rich in “nonapatitic” HPO₄^2– moieties, has been proposed and discussed in the literature.^{4,10,50,51,65−67} Recently, this structural picture of H(C)A appears to be well accepted, partially thanks to the recent and detailed NMR-derived constitution of both synthetic H(C)A and biological apatite:^8,16,23,24 besides the Ca²⁺ constituent of both core–shell components (and CO₃ in the context of HCA), the model involves an ordered H(C)A core of “apatitic” PO₄^3– and OH^– ions and a disordered surface layer comprising water and “nonapatitic” HPO₄ and PO₄^3– moieties, as illustrated in Figure 7(a).

Figure 7.

Schematic illustrations of apatite crystallization from ACP, highlighting the equivalence between the disordered surface layer of H(C)A^{4,8,10,16,65,66} and ACP. (a) Cross-section of a “HA particle” composed of a crystalline apatite core (red) and an amorphous surface layer rich in water and nonapatitic PO₄^3– and HPO₄ species (blue). (b) A distribution of such particles with variable core and shell volumes, where the “innermost” crystallites feature thinner surface layers, while the ACP-like layer is emphasized in the “outer” parts of the particle ensemble. (c) A few HA crystallites in a dominating matrix of spherical ACP particles (blue); here it appears most natural to consider the system as comprised by two separate HA and ACP phases. (d) HA particles, each coated by a surface layer, which represents the remaining of the ACP phase in (c); the domination of well-crystalline material renders the core–shell interpretation [see (a, b)] most appropriate.

Unfortunately, different nomenclatures encountered in the literature concerning the “hydrated surface layer” and “ACP” obscure their strong similarities, thereby implicitly highlighting their distinctions. Nevertheless, common to all recently reported (approximate) HCA-surface compositions^8,16,23,24 is the presence of HPO₄^2– and H₂O species, a feature also shared with both OCP^9,15 and recently deduced compositions of ACP.^56,57 Moreover, the demonstrated variable H₂O contents in both ACP and the surface layer of synthetic/biological HCA^8,65 imply an inherently nonunique chemical speciation that depends on the precise surface hydration level. The ¹H–³¹P HETCOR data of ref (8) obtained from both synthetic HCA and sheep bone are consistent with a “dry” and “wet” HCA surface reflecting a comparatively enhanced contribution from HPO₄ and PO₄^3–/H₂O species, respectively. (Analogously with the direct dependence of the ¹H speciation at the MBG silicate surface on its hydration level; see Section 4.1.) Likewise, the ¹H–³¹P HETCOR NMR spectra monitoring the transformation between disordered/HA phases in liposomes⁵⁹ are readily rationalized by ACP incarnations with variable H₂O/HPO₄ contents as the crystallization progressed (compare with the results by Wang et al.⁸). On the basis of different ¹H–³¹P CPMAS parameters, Chen et al.⁵⁹ deliberately chose the nomenclature “disordered phosphate” to highlight its distinction to “ACP” obtained directly by precipitation. Nonetheless, it may be too early to dismiss its identification with ACP, where we also note that distinct and sequential “ACP-1” and “ACP-2” precursors of HA are discussed in the literature (e.g., see refs (54 and 57)).

Furthermore, despite careful and sensible analyses,^7,8,16,23,24 the nonquantitativeness of the NMR experimentation invoked for discriminating and estimating the various proton/phosphate populations in the “core” and “surface” apatite domains implies relatively large uncertainties that merit caution in claiming precise compositions. The hurdles of precisely quantifying the relative PO₄^3–, HPO₄, and H₂O contents of “ACP” and “OCP-like” phases, coupled with the nonetheless similar compositions reported for the H(C)A surface portion,^{8,16,23,24,65} suggest that “ACP” is a good approximant. Hence, it may be premature to make too categorical statements when describing the nature of the H(C)A surface layer, as well as the “disordered calcium phosphate” phase observed in liposomes.⁵⁹ Yet, with one notable exception,⁸ the H(C)A surface layer is in general not identified explicitly as “ACP”.^{4,10,16,50,65} Moreover, adopting a looser terminology of “disordered OCP” would better bring out its structural similarity with both ACP and the H(C)A surface layer.

Concerning the issue of “separate HCA and ACP components” or an “HCA core and a disordered surface layer”, one must distinguish the aspects of (i) the core/surface parts of each individual HCA particle [Figure 7(a)] from (ii) a distribution of such particles with variable surface and core volume fractions [i.e., an ensemble of particles with varying degrees of crystallinity; see Figure 7(b)], yet noting that they are in general correlated. For instance, since the crystallization of in vitro formed HCA starts within the ACP phase,⁵⁵⁻⁵⁸ its interior will have a comparatively higher fraction of crystallites where the “HCA core” dominates over its surface (ACP) portion, while the latter prevails in the outer parts of the bulk; see Figure 7(c). This relates to the inferences of Beniash et al.,⁶² who attributed the “outer” and “inner” parts of mouse enamel to ACP and HCA, respectively. However, their interpretation did not refer specifically to the core/surface of individual HCA crystallites but merely to large collections thereof probed over a 10²–10³ nm scale. Likewise, the rat dentin model proposed by Chan and co-workers^23,24 was discussed in terms of inner (HCA) and outer (ACP) portions.

Which most naturally adopted viewpoint of an “ACP phase” or an “apatite surface layer” depends on the relative amounts of crystalline and amorphous material, where we here also comment on our interpretations in the context of the biomimetic phosphate layer of the MBG-τ_SBF specimens: In the limit of a negligible apatite core, i.e., when the volume of the HCA surface layer vastly dominates, it seems most reasonable to view the particle ensemble as an ACP phase coexisting with a low number of small apatite crystallites [Figure 7(c)]; this applies for MBGs immersed in SBF for periods τ_SBF < 24 h, where the specimen remains XRD amorphous and the HCA (“core portion”) is very minor. In contrast, for more mature nanocrystalline H(C)A/bone mineral with the surface layer accounting for ≲50% in volume^16,24—relevant for the present MBG-τ_SBF specimens with τ_SBF ⩾3 days⁴²—the core–shell picture may be most suitable [Figure 7(d)], yet with the identification of the “surface layer” as “ACP”, the latter taken to encompass a range of chemical compositions.⁸ Furthermore, the “surface layer” observed for nanocrystalline HCA particles is absent for well-ordered and micrometer-sized HA crystals prepared in vitro by precipitation followed by heat treatment;^8,16,22 see Figure 6(a) for the ¹H NMR signatures of such a specimen. This feature may be viewed as a complete ACP→HA conversion.

Worth highlighting is that once an equivalence between the HCA surface layer and ACP is accepted, the controversy of ACP being a component of (mature) bone mineral is settled, while it also becomes (even) more plausible that ACP would indeed be a precursor of biological apatite. Notably, this reconciles the viewpoints that “ACP precedes HCA formation” or “small and poorly ordered HCA particles form directly”, which are simply two sides of the same coin, with their seeming differences becoming semantic.

5.3. Proton Environments of in Vitro Grown ACP and HCA

The ¹H NMR data of Figure 5 corroborate our earlier inferences from ³¹P NMR about a dominance of ACP after 4 h of SBF exposure, whereas both ACP and HCA coexist after 30 days of MBG exposure to SBF.⁴² The ¹H–³¹P results of Figures 4 and 5 accord overall with our previous ¹H–³¹P HETCOR 2D NMR spectra^27,28 from SBF-soaked S85 specimens that featured very similar analyzed cation compositions as the present one, as well as those reported for synthetic nanocrystalline H(C)A specimens and bone/dentin.^{6,8,13,16,23,24}

However, there is one notable distinction to our earlier results: ¹H resonances from acidic protons were not observed, and structural water represented the sole proton reservoir of ACP.^27,28 The signal-to-noise ratios (S/N) of the present NMR data (notably so the ¹H–³¹P diffCP NMR spectra) are significantly higher than those of our previous ¹H–³¹P HETCOR results, suggesting that the broad resonances in the high-ppm spectral region might have escaped detection. This is, however, unlikely considering that the H₂O NMR peak was readily observed,^27,28 implying that the ¹H resonances from acidic sites should also have been detected, if present in comparable H₂O/HPO₄^2– proportions as those revealed in Figures 4 and 5. More probable is that the ACP component of our present SBF-exposed MBG specimens comprises significantly higher HPO₄ populations (except for S90-4h, see Figure 5).

The apparently distinct ACP compositions could potentially stem from the more dilute MBG loading employed in our current SBF testing relative to that of previous reports, which altered the reactions at the MBG surface and thereby also the HCA growth^42,43,60 (Section 3). However, considering that the precise ACP composition depends on the net hydration level⁸ (Section 5.2), it is more likely that the biomimetic phosphate layers of the present MBG-τ_SBF specimens were less hydrated than the previous ones (refs (27 and 28)). This readily rationalizes that the amount of acidic protons is emphasized relative to that of H₂O molecules after 30 days of SBF immersion compared with the ACP phase formed after 4 h, as follows by contrasting the ¹H–³¹P diffCP NMR results (τ_CP = 0.2 ms) of Figure 5 for the short and long SBF-soaking periods.

At a fixed τ_SBF-value of either 4 h or 30 days, the ¹H speciation of each biomimetic ACP/HCA component is almost independent of the precise {Ca, Si, P} composition and textural properties of the MBG (Table 1), thereby confirming the equal suitabilities of S90/S85/S58 for acting as a substrate for the HCA growth. The main distinction observed among the diffCP-derived ¹H NMR spectra in Figure 5 is the absence of signals from acidic protons in the S90-4h specimen. Overall, the significant shift dispersion for all H₂O/HPO₄^2– resonances from ACP reflect highly disordered ¹H environments. Yet, some ordering tendencies are evident from the ¹H NMR spectra of the MBG-30d specimens relative to their MBG-4h counterparts (τ_CP = 0.2 ms): at the longer SBF-immersion period, a well-defined NMR peak maximum ≈12 ppm is observed for the HPO₄ resonances. Incidentally, this shift agrees with that around 12–13 ppm reported for the acidic protons of OCP,^9,11,15 suggesting “disordered OCP” environments. The S85-30d sample additionally manifests a very weak and sharp peak at δ_H = 10 ppm, indicating a minute brushite (CaHPO₄·2H₂O) formation.^11−13,15 Moreover, while the biomimetic HCA phase in the MBG-30d specimens is classified as “crystalline”, a remaining structural disorder—partly stemming from incorporation of CO₃^2– and Na⁺ ions²⁷—is mirrored in the fwhm ≈ 1.0 ppm of the OH resonance (Figure 5) relative to that of ≈0.4 ppm observed from well-ordered HA crystallites (Figure 6).

5.4. Detecting the Onset of HCA Formation: ¹H versus ³¹P NMR

The reduced experimental time offered by ¹H–³¹P diffCP-MAS NMR experimentation relative to that of arranging a full 2D HETCOR or ³¹P → ¹H CPMAS NMR spectrum, suggests that diffCP is an attractive alternative for detecting the onset of HCA formation, besides the standard techniques of using infrared spectroscopy, PXRD, or electron microscopy, as well as the more recently introduced option of deconvoluting single-pulse ³¹P MAS NMR spectra.^27,88 Noteworthy, the clearly discernible HCA-associated OH resonance observed from each S90-4h, S85-4h, and S58-4h sample (Figure 5) unambiguously evidences that a minute but non-negligible HCA formation occurred already after 4 h of SBF exposure. This may be contrasted with the failure of PXRD to detect HCA from any of the present MBG specimens with τ_SBF < 24 h. The same conclusion was reached by ³¹P NMR, except that the P-free S90 MBG revealed HCA after 8 h of SBF exposure.⁴² The OH resonance intensity (Figure 5; τ_CP = 0.2 ms) grows along the series S90 < S85 < S58, in accordance with the results of Figure 1 that corroborate our previous conclusion from ³¹P NMR.⁴²

The discrepancy with ³¹P NMR—which suggested a shorter HCA induction period of 8 h from the S90 MBG relative to 24 h for S85 and S58⁴² (in contrast with the ¹H NMR data herein)—stems partially from interferences of broad ³¹P resonances from remnants of the amorphous CaP clusters of the pristine S58/S85 MBG structures: while they dissolve readily into the aqueous medium, this process is likely not completed until ≈8–24 h (and is slower for S58 relative to S85^42,43). The quantification of each biomimetic ACP and HCA component by ³¹P NMR relies on the overall peak-narrowing accompanying the ACP → HCA transformation and a deconvolution of the ³¹P NMR signal into two components, one broad from ACP and one narrow from HCA, both of which overlap and are centered around the same ³¹P chemical shift around 3 ppm;^27,42,60 see Figure 4. However, the ³¹P NMR signals from the disordered CaP clusters are essentially indistinguishable from the SBF-induced ACP component.^27,28,42 Consequently, if they are present together, the content of the (as-assumed sole) ACP phase becomes overestimated, with the CaP-stemming ³¹P resonances obscuring the detection of the narrow ³¹P counterpart from HCA: the absence of broadening of the net NMR peakshape from the CaP clusters most likely enabled the detection of HCA from the P-free S90 specimen already after 8 h in SBF, notwithstanding that larger amounts of HCA are formed from the P-bearing S85 and (particularly) S58 MBGs over longer exposure periods,⁴² as commented above. Consequently, another factor contributing to the apparently delayed HCA generation from the S85/S58 MBGs is the presence of higher amounts of ACP formed from the P-bearing MBGs, accompanied by a larger contribution of broad ³¹P resonances.

Fortunately, the undesirable CaP-stemming NMR signals are absent when exploiting ¹H NMR, although the inherently nonquantitative nature of CPMAS-based experimentation makes accurate quantifications cumbersome. Hence, once the HCA formation is significant, we recommend single-pulse ³¹P NMR for quantifying the relative ACP/HCA fractions; we guide the reader to refs (42 and 60) for discussions on the relative merits of PXRD and ³¹P MAS NMR for detecting and quantifying the relative and absolute ACP/HCA amounts. We stress that in the core–shell HCA picture (Section 5.2), the “HCA fraction” deduced from ³¹P NMR reflects the well-ordered core of the HCA particles, whereas for an essentially complete ACP → HCA conversion, the “ACP fraction” is best interpreted as the volume fraction of the disordered surface of the HCA crystallites.

6. Conclusions

We have examined the various H species present at the surfaces of three pristine MBGs, as well as in the silicate/phosphate portions of the heterogeneous MBG-τ_SBF specimens resulting after immersing each MBG in SBF for variable periods up to 30 days.

¹H NMR spectra recorded by single pulses are dominated by resonances from the MBG surface, encompassing two distinct pools of physisorbed water molecules: a main population of mobile species and a minor ensemble that is more strongly surface bound; their precise amounts are difficult to quantify and depend on the overall surface hydration level. The MBG surface is also rich in SiOH moieties that exhibit variable degrees of H-bonding, distinguished by their ¹H chemical shifts, where three coexisting proton species were identified: those of (i) “isolated silanols” devoid of H-bonding and those experiencing (ii) weak and (iii) strong H-bonding. Their relative abundances depend on the MBG-surface hydration level, where weakly H-bonded SiOH groups are most common at surfaces of the Ca-poor (pristine) S90/S85 MBGs and their MBG-τ_SBF counterparts resulting from extended SBF-soaking periods beyond 24 h. For short SBF-exposure intervals within a few hours, on the other hand, a higher surface hydration level is manifested by both the (near) absence of isolated SiOH groups and an overall resonance broadening. Protons of the strongest H-bonded motifs, such as SiOH···^–OSi, are only observed in the fragmented silicate networks of the Ca-rich—and thereby most hydrophilic—S58 MBG surface and its SBF-soaked counterparts. 2Q–1Q correlation ¹H NMR experiments revealed predominantly autocorrelations among the H-bonded SiOH/H₂O moieties, as well as between pairs of isolated silanols.

In directly excited ¹H NMR spectra, resonances from the minor ACP/HCA components are generally swamped by those from their MBG counterparts. Nevertheless, over days of SBF soaking, the HCA-characteristic OH signal (≈0 ppm) is clearly discernible. Its intensity grows concomitantly with the soaking period and the P content of the (pristine) MBG, i.e., along the series S90 < S85 < S58, thereby corroborating the HCA-formation trends deduced by ³¹P NMR from the same specimens.⁴² Yet, an accurate probing of the minor H speciations of the biomimetic ACP/HCA components of the MBG-τ_SBF specimens is best performed with heteronuclear ¹H→³¹P CPMAS-based experimentation, which revealed distinctly different ¹H reservoirs of the amorphous and crystalline phosphate portions: the latter comprises solely OH groups, whereas ACP incorporates water and acidic protons of HPO₄^2– anions. Besides the strong P–OH contacts within HPO₄ species, 2D HETCOR NMR revealed contacts between “nonapatitic” PO₄^3– ions and water molecules. Hence, in accordance with mineralization studies employing direct HCA precipitation from solution,^8,56−58 the ACP phase initially formed at the MBG surface in SBF comprises H₂O, PO₄, and HPO₄^2– species (besides Ca²⁺ and CO₃ ions²⁷). A minor ordering of ACP was observed after 30 days of MBG exposure to SBF relative to that after 4 h, as witnessed by slightly better resolved ¹H NMR signals from the H₂O and HPO₄^2– species.

Whenever the primary focus is on the ¹H environments of the biomimetic phosphate layer, we stress the advantages of using the ¹H-detected diffCP-MAS experimental protocol of ref (17) relative to either a full 2D HETCOR NMR acquisition or time-consuming ³¹P → ¹H CPMAS.^14,85,86 Surprisingly, the utility of this technique appears to be overlooked in the community. Besides that ¹H–³¹P diffCP-MAS NMR experimentation offers more rapid NMR acquisitions than single-pulse ³¹P NMR, we also demonstrated that it is a more sensitive tool for detecting the onset of HCA formation, notably so from P-bearing (M)BGs at short SBF-exposure periods, where the ³¹P resonances of the glass overlap with those from the biomimetic phases, thereby increasing the net peakwidth and obscuring the narrow but very weak NMR signal from HCA.

Author Present Address

^∥ Department of Chemistry, New York University Abu Dhabi, Abu Dhabi, United Arab Emirates.

The authors declare no competing financial interest.