Skip to main content
PMC home page
eLife logoLink to eLife
. 2017 Jun 26;6:e17331. doi: 10.7554/eLife.17331

Serial, parallel and hierarchical decision making in primates

Ariel Zylberberg 1,2,*, Jeannette AM Lorteije 1,3,*, Brian G Ouellette 1, Chris I De Zeeuw 4,5, Mariano Sigman 6, Pieter Roelfsema 1,7,8,*
Editor: Joshua I Gold9
PMCID: PMC5484613  PMID: 28648172

Abstract

The study of decision-making has mainly focused on isolated decisions where choices are associated with motor actions. However, problem-solving often involves considering a hierarchy of sub-decisions. In a recent study (Lorteije et al. 2015), we reported behavioral and neuronal evidence for hierarchical decision making in a task with a small decision tree. We observed a first phase of parallel evidence integration for multiple sub-decisions, followed by a phase in which the overall strategy formed. It has been suggested that a 'flat' competition between the ultimate motor actions might also explain these results. A reanalysis of the data does not support the critical predictions of flat models. We also examined the time-course of decision making in other, related tasks and report conditions where evidence integration for successive decisions is decoupled, which excludes flat models. We conclude that the flexibility of decision-making implies that the strategies are genuinely hierarchical.

DOI: http://dx.doi.org/10.7554/eLife.17331.001

Research Organism: Human, Rhesus macaque

eLife digest

Should you go for coffee with Jules, or go to the movie theater with Jim? Both options require you to make additional decisions, for example, which café would you go to, or what movie could you see? Many of the decisions we make in our daily lives feature a number of sub-decisions. Many of our day-to-day decisions have multiple layers of sub-decisions embedded within them that are not necessarily independent. Our opinions of the cafés in town and the movies showing at the theater may influence our decision over whom to spend the afternoon with.

In 2015, researchers at the Netherlands Institute for Neuroscience performed experiments in macaques to try to work out how the brain makes these decisions. The monkeys learned to choose between two visual stimuli (decision 1). The outcome of decision 1 determined whether the animals then had to make decision 2 or decision 3. The results suggested that the monkeys initially made all three comparisons independently and in parallel, before combining the evidence to select their overall strategy. This process is referred to as hierarchical decision-making. In the original analogy, one would compare the relative merits of Jules versus Jim, café A versus café B, and a horror movie versus a comedy at the same time before deciding what to do.

Other researchers have now reanalyzed the data from the original work using new computer simulations. This second analysis suggests that the results are more consistent with an alternative model of decision-making called a flat model, in which the brain compares all of the final options simultaneously (Jules + café A; Jules + café B; Jim + horror movie; Jim + comedy) before making a decision.

In response to these findings, Zylberberg et al. – who conducted the work reported in 2015 – reanalyzed the original data and re-ran the simulations. Zylberberg et al. argue that the flat model provides a poor fit to the original data. A new experiment with human volunteers suggests that modifying the task by adding even more decisions can lead to the different comparisons being made one after the other (in series) rather than all at the same time (in parallel), before the decision is made. This is difficult to explain with a flat model. Zylberberg et al. argue that these findings confirm the original conclusion that the monkeys use a hierarchical strategy. Moreover, the new results expose a previously unknown limit in the number of decisions that the brain can evaluate at any one time. If this limit is exceeded, decision-making becomes serial.

Future studies can build on these findings by further exploring the limits of parallel decision-making, which may help us to understand how the brain is able to make multiple decisions while keeping the future consequences in mind.

DOI: http://dx.doi.org/10.7554/eLife.17331.002

Introduction

The main aim of Lorteije et al. (2015) was to examine the neuronal correlates of hierarchical decision-making in the visual cortex. We trained monkeys to navigate through a decision tree with stochastic sensory evidence at branching points at two hierarchical levels, L1 and L2 (Figure 2 of Lorteije et al., [2015]). We measured the psychophysical kernels (Ahumada, 1996), which reflect the contribution of sensory information at different time-points to the decisions and recorded neuronal activity in visual cortical areas V1 and V4.

There are various strategies for solving this task. A decision maker could adopt a serial strategy, mentally tracing the curve from the fixation point and making a decision at each bifurcation until reaching one of the targets. Alternatively, evidence for the decisions could be integrated in parallel. In that case, the task might be represented as a ‘flat’ competition between four alternatives, or multiple decisions might first be considered independently before they are integrated to form a strategy. These models have been explored by Lorteije et al. (2015) and were reanalyzed in a companion paper by Hyafil and Moreno-Bote (H and M) (Hyafil and Moreno-Bote, 2017). The data of Lorteije et al. (2015) ruled out serial strategies, which wrongly predict that the psychophysical kernel for the L2 (level 2) decision should be protracted relative to L1 and that evidence integration for L1 (level 1) precedes evidence integration for L2.

Lorteije et al. (2015) also presented evidence against ‘flat’ models with a single accumulator per motor action, which predict that L1 difficulty should affect L2 accuracy. When the L1 decision is easy, strong evidence for L1 causes the decision variable to be close to the bound so that less evidence is required to make the L2 decision. We confirmed this intuition by fitting a simple (3-parameters) instantiation of a ‘flat’ model to the behavioral data. As in most models of sensory decision making (Smith and Ratcliff, 2004; Gold and Shadlen, 2007)—but contrary to the model by H and M—we assumed that the evidence is integrated without self-excitation (or leak) until reaching a criterion or bound. The model fits revealed that the decision-termination bound was low, which led to short integration times. This observation was supported by a model-free analysis of the psychophysical kernels, showing that the monkey’s choices were mainly influenced by the earliest luminance samples. Later samples made only a small contribution to the decision even though the monkeys had to wait at least 500 ms before they could report their decision. Unlike the monkeys, our instantiation of the flat model exhibited an influence of L1 difficulty on L2 accuracy, which led us to reject the flat model.

H and M challenge our conclusion about flat models (Hyafil and Moreno-Bote, 2017), putting forward an 8-parameter version of the leaky-competing accumulator model (LCA [Usher and McClelland, 2001; Tsetsos et al., 2012]), which at first sight captures many aspects of the monkeys’ behavior. We therefore consider this model an interesting addition to the literature on the neural mechanisms for hierarchical decision-making. In H and M’s model, the task is represented as a flat competition between the four possible motor actions. Each alternative (i) integrates evidence simultaneously from L1 and L2, (ii) is endowed with self-excitation, establishing a positive feedback loop, and (iii) is inhibited by a global process that affects all races equally.

Here, we will first examine the manner in which H and M avoided the influence of L1 difficulty on L2 accuracy and conclude that it is neither compatible with the behavioral data nor with the neurophysiological data. We then examine more general properties of flat models and conclude that they lack the flexibility to account for decision making in hierarchical tasks.

H and M’s model reduced the influence of L1 difficulty on L2 accuracy by implementing high bounds, strong recurrent excitation and sensory noise that does not scale with the strength of the evidence. Self-excitation was needed in H and M’s model to explain why the monkeys assigned high weights to the early samples in our task. Without self-excitation, models with high bounds produce flat psychophysical kernels, because they assign equal weights to many samples before committing to a choice (Brunton et al., 2013).

Unfortunately, the self-excitation in the model of H and M causes unstable activity. This can be seen in H and M’s Figure 3C where activity appears to follow an exponential time-course, which is incompatible with the findings of Lorteije et al. (2015) and other neurophysiological results (e.g. Kiani et al., 2008). One possibility to stabilize the firing rates in H and M’s model would be to use an attractor network (Wang, 2002; Wong and Wang, 2006). However, attractors act as bounds and would increase the dependency of L2 accuracy on L1 difficulty. Furthermore, in primates and rodents evidence accumulation can occur without loss of information about the later samples (Kira et al., 2015; Kiani et al., 2013; Brunton et al., 2013), which is incompatible with strong self-excitation.

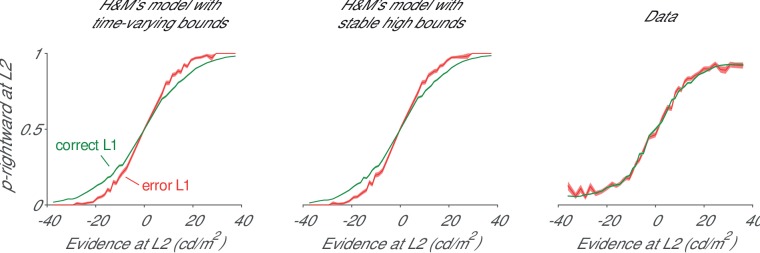
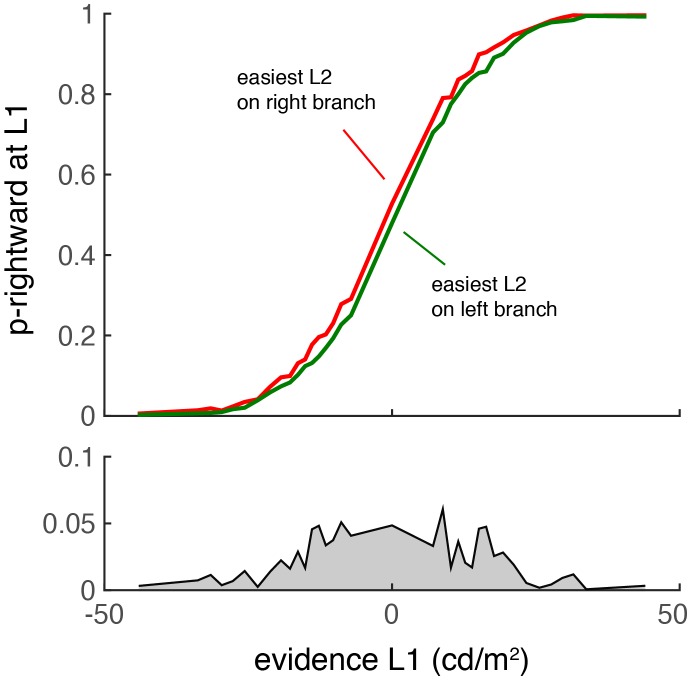
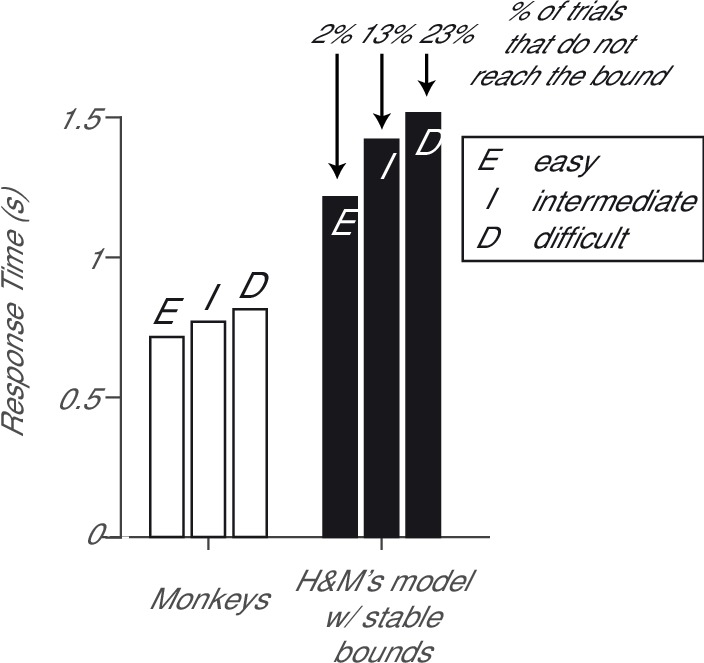
We simulated the two models proposed by H and M and observed that the high bounds combined with self-excitation did not suffice to prevent the interaction between L1 and L2. The first model had infinite bounds collapsing after 500 ms, and the second one had high constant bounds, which were not reached on a large fraction of trials (Figure 1—figure supplement 1). We investigated whether the accuracy of the L2 decision depended on the accuracy of the L1 choice. In both models, L2 decisions were less accurate if the L1 decision was correct than if it was erroneous. This decrease in accuracy is visible as a flattening of the psychometric functions (Figure 1). We reanalyzed the data of Lorteije et al. (2015) and observed much weaker interactions between the two decisions (Figure 1). Relaxing some of H and M’s assumptions (e.g. including noise that scales with the strength of the evidence [Zylberberg et al., 2016]) caused even stronger crosstalk.

Figure 1. Interaction between the accuracies at L1 and L2.

We computed the psychometric function for the L2 decision for trials with a correct (green traces) or erroneous (red) decision at L1. Left, H and M model with infinite bounds collapsing after 500 ms. Middle, H and M model with high bounds that are stable. Right, data of the monkeys in Lorteije et al. (2015). Green/red regions, s.e.m.

DOI: http://dx.doi.org/10.7554/eLife.17331.003

Figure 1.

Figure 1—figure supplement 1. Reaction times for model and data.

Figure 1—figure supplement 1.

The monkeys’ response times (white bars) exhibit a substantial increase with the difficulty of the stimulus, as expected from a decision process in which evidence is accumulated to a bound (see also Figure S1D in Lorteije et al., 2015). The model of Hyafil and Moreno-Bote with stable high bounds produces unrealistically long response times (black bars) and the decision variable does not reach the bound in a large fraction of the trials.
DOI: http://dx.doi.org/10.7554/eLife.17331.004
Open in a new tab

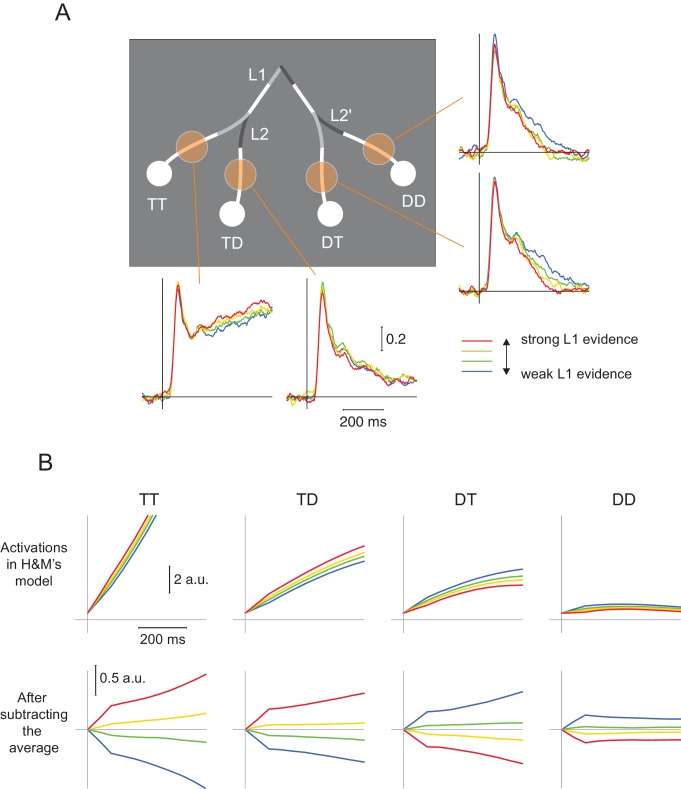
We conclude that the models of H and M fail to account for the behavioral data. We next reanalyzed our neurophysiological data to test H and M’s model more directly. Specifically, the authors stated that the model predicts that ‘selection signals at levels two are only influenced by information provided at level two branches […] and not by information provided at level 1’. To test this prediction, we grouped the trials into four categories based on the strength of evidence at L1 and examined the activity elicited by L2 branches in V4 (Figure 2A).

Figure 2. Influence of strength of evidence at L1 on V4 activity elicited by the L2 and L2’ branches in V4 and in the model of H and M.

Figure 2.

Open in a new tab

(A) In the data, high L1 signal strength increases the representation of TT, suppresses the representations of DT and DD, but has little impact on TD. This finding is incompatible with flat models that include only one source of inhibition. (B) Upper panel, Same analysis conducted for the activity in the model of H and M. Note the steep rise in activity, which is very different from the neuronal activity in area V4. High L1 signal strength increased activity elicited by both TT and TD, and suppressed DT and DD. Because of the rectification (firing rates cannot take negative values), L1 evidence has the weakest influence on the DD branch. Lower panels, same data after the average activity was subtracted. Both models by H and M yielded similar results.

DOI: http://dx.doi.org/10.7554/eLife.17331.005

Our V4 recordings revealed that trials with strong evidence at L1 boosted the representation of the TT branch, suppressed the representation of the DT and DD branches (linear regression, all Ps < 10−3), but left activity elicited by the TD branch relatively unaffected (p>0.3) (Figure 2A). These distinct effects of L1 evidence on the four L2-branches are incompatible with any model in which the interactions between decisions are governed by a single source of inhibition, including the one by H and M. Indeed, when we conducted the same analysis in H and M’s model, we observed that stronger L1 evidence decreased the activity for the DT and DD branches and increased the activity for both the TT and TD branches (Figure 2B). A possible explanation for the difference in activity elicited by the TD branch, which is suppressed in H and M’s model but not in the data, is that it was already suppressed by the selection of the TT branch. These more complex and local interactions between the L1 and L2 decisions are consistent with a genuine hierarchical decision making process and are incompatible with flat models with a single source of inhibition.

Hyafil and Moreno-Bote criticized Lorteije et al. (2015) by stating that ad-hoc assumptions need to be made to explain the interactions between local selection signals in a hierarchical model. Indeed, hierarchical models imply that there are mechanisms to enable interactions between the different decisions. For example, Lorteije et al. (2015) demonstrated that the relative difficulty of the L2 decisions biases the L1 choice, an effect that is not only visible in the animals’ behavior but also in the modulation of firing rates in visual cortex. Because H and M’s global inhibitory process is refuted by the data, it follows that another mechanism should play an equivalent role. It is conceivable, for example, that there is a process that compares the confidence in the two L2 decisions and then biases the L1 decision. Lorteije et al. (2015) implemented a simple version of this mechanism where the confidence in the two L2-decisions was evaluated to select the target that maximizes reward. Such a role of confidence is supported by previous studies demonstrating that the confidence in one decision can guide another one (Kepecs et al., 2008; van den Berg et al., 2016; Kiani and Shadlen, 2009). We believe that elucidating the interactions between local selection signals is an important topic for future research. Importantly, these interactions between local selection signals do not provide evidence in favor of or against flat models. They are equally compatible with hierarchical models.

H and M also claim that their two models are more parsimonious than the models in Lorteije et al. (2015). We disagree with this parsimony claim. The models proposed by H and M contain a large number of parameters and have the same shortcomings as the simpler flat model that was explored in Lorteije et al. (2015). We are also concerned that the results by H and M critically depend on (1) infinite bounds that collapse rapidly, which have not been observed in neurophysiology, (2) noise that does not scale with the strength of the evidence, and (3) strong self-excitation that causes a suboptimal decision making process and exponentially-increasing firing rates. More importantly, when testing the models by H and M, we found that they cannot explain the lack of an influence of L2 accuracy on L1 sensitivity, nor the absence of an influence of L1 luminance strength on the TD branch, and as such they fail to account for the behavioral and neurophysiological results in the hierarchical decision making task of Lorteije et al. (2015).

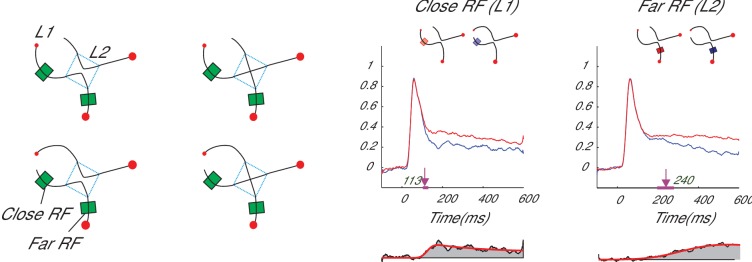
We will now turn to a more general problem that flat models incur when they are applied to hierarchical decision-making tasks. Flat models make all local decisions at the same time, because there is a single bound that governs them all. In contrast, previous curve-tracing studies presented evidence for serial decision making and we will here illustrate that shifts between parallel and serial strategies can occur. Indeed, under many conditions, curve-tracing invokes a serial operation, which is implemented in the visual cortex by the propagation of enhanced neuronal activity along a target curve (Pooresmaeili and Roelfsema, 2014). This propagation of enhanced neuronal activity has a correlate in psychology: observers gradually spread object-based attention over the relevant curve (Houtkamp et al., 2003). In one previous study (Pooresmaeili and Roelfsema, 2014) monkeys had to mentally trace a target curve that was connected to a fixation point (Figure 3). The target curve either crossed with a distractor curve or the curves did not intersect. We found that neuronal activity elicited in V1 by L1-segments of the target curve near the fixation point was enhanced before the activity elicited by the L2-segments beyond the location of the possible crossing. Thus, the enhanced V1 activity first reflects the L1-decision about the connection at the fixation point and only later reflects the L2-decision about the crossing. This result refutes flat models that implement a race between the four possible interpretations of the stimulus (i.e. one accumulator for each of the four configurations on the left of Figure 3).

Figure 3. Curve-tracing task with possible intersections.

Figure 3.

Open in a new tab

V1 activity elicited by a target curve was stronger than that elicited by a distractor curve. The latency of this enhanced activity reveals a serial decision process, as the selection signal of neurons with a receptive field near the fixation point (close RF, L1-decision) preceded the selection signal of neurons with a receptive field beyond the crossing (far RF, L2-decision). The lower panels on the right represent the selection signals (target minus distractor response). Reprinted with permission from Pooresmaeili and Roelfsema (2014)18.

DOI: http://dx.doi.org/10.7554/eLife.17331.006

Why is hierarchical decision-making parallel in some situations (Lorteije et al., 2015) and serial in others (Figure 3)? Multiple factors may be at play. The first factor is the configuration of the stimulus. The crossings in the stimulus of Figure 3 do not provide independent evidence about the target or distractor status of the L2 branches (the problem has an ‘exclusive-or’ structure), whereas in the task of Lorteije et al. (2015) local evidence at L2 permitted discarding branches as distractors before the L1 decision was taken.

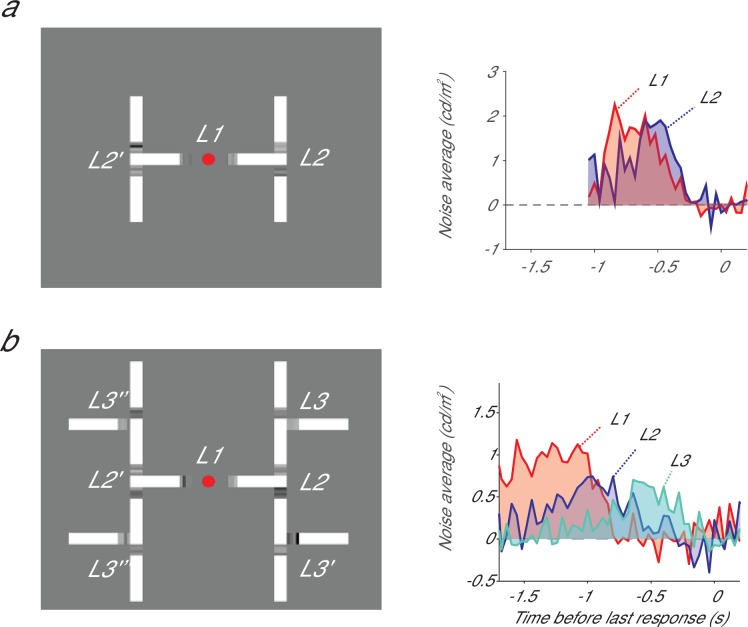
A second factor that may influence the degree of seriality is the number of decisions that have to be taken at the same time. We examined this possibility in a new experiment, which tested the capacity of parallel decision-making in human observers. We inferred the time-course of evidence accumulation by adding stochastic luminance evidence to branching points so that we could estimate the subjects’ psychophysical kernels, similarly to Lorteije et al. (2015). Figure 4a illustrates our findings with a hierarchical decision-making task with two levels. At the L1-decision, subjects had to determine which branch connected to the fixation point (left or right) had the brightest image elements and they made a second decision (highest luminance up or down) at the relevant L2 branching point. Evidence for these decisions accumulated largely in parallel, just as in Lorteije et al. (2015). However, the decision-making process switched to a more serial mode when we added a third level (L3) so that the total number of decisions increased to seven (Figure 4b). Now most of the evidence for L1 accumulated before the evidence for L2, which, in turn accumulated mostly before the evidence for L3. The implication is that there is a limited capacity for making decisions in this task. Subjects can accumulate evidence for between 3 and 7 decisions in parallel, although the exact capacity for parallel decision making remains to be determined. These results also imply that there are conditions under which evidence for L1 and L2 can accumulate independently. It is therefore parsimonious to assume that these separate accumulators also contribute to the task with only two decisions, in accordance with a genuine hierarchical decision making process. Thus, flat models can also not account for results in tasks that are intimately related to the task studied by Lorteije et al. (2015). Furthermore, flat models need to reserve a single accumulator for every configuration of successive decisions (e.g. eight accumulators for the task of Figure 4b), causing them to scale badly if decision trees become elaborate.

Figure 4. Integrating evidence in a hierarchical decision making task with two (a) and three levels (b).

Figure 4.

Open in a new tab

(a) Left, at every bifurcation, subjects had to choose the branch with the higher luminance. At L1 they chose left/right and at L2 they chose up/down. Right, the psychophysical kernel for L1 (red) and L2 (blue), which represents the influence of luminance fluctuations at different time points aligned to the second response. (b) Adding a L3 decision caused a more serial decision process and decreased the overlap between the kernels for the L1 and L2 decisions. Panel b was reproduced with permission from Zylberberg et al. (2012).

DOI: http://dx.doi.org/10.7554/eLife.17331.007

A third factor that can influence the seriality of decision making is practice. Prolonged training on a fixed set of problems is likely to result in more efficient decision making process, where multiple sources of evidence are efficiently considered and combined to form a strategy. We note, however, that the subjects of the tasks of Figures 3 and 4b performed many thousands of trials but that their decision-making process remained serial.

These results, taken together, indicate that hierarchical decision-making is a highly flexible process during which evidence can be integrated by separate accumulators, allowing subjects to adapt their strategy to the task at hand. Parallel accumulation can only occur if it is permitted by the structure of the task (i.e. if it does not have the exclusive-or structure) and if the subject’s capacity for parallel decision making is not exceeded. Flat models lack the required flexibility.

We conclude that critical predictions of the models of Hyafil and Moreno-Bote are not supported by the data and, more generally, that flat models fail to account for any situation where decision making is serial (Figure 3). Our finding in humans that adding L3 branches increases seriality at L1 and L2 (Figure 4) implies that the machinery to take independent decisions at L1 and L2 is always in place. To further elucidate the neuronal mechanisms for hierarchical decision making, future studies could record from neurons with persistent activity, in areas like LIP or FEF, using variants of the task studied by Lorteije et al. They could also focus on the neuronal mechanisms that improve the interactions between successive decisions when subjects become proficient in a task.

Materials and methods

Monkey electrophysiology

All experimental procedures complied with the National Institutes of Health Guide for Care and Use of Laboratory Animals, and were approved by the Institutional Animal Care and Use Committee of the Royal Netherlands Academy of Arts and Sciences. Detailed methods can be found in the original publication (Lorteije et al., 2015). Briefly, multi-unit activity was collected from multi-channel electrode arrays implanted in the visual cortex (area V1 and V4) of 2 monkeys, while these animals performed a hierarchical curve tracing task. For the analysis in Figure 2A, we grouped trials in quartiles of L1-evidence strength. For each trial, we averaged the luminance of the target and distractor segments at L1 over the first two samples, and then computed the difference. We then classified trials into quartiles, including only correct trials, independently for each of the three difficulty levels. Figure 2 shows the average firing rate (normalized as in Lorteije et al., 2015) within each quartile for receptive fields located at different branches. The averages are from 31 sites, and they were obtained in a total of 19 recording sessions.

Human decision-making in tasks with two- and-three level hierarchies

The three-level task displayed in Figure 4 was reproduced from Zylberberg et al. (2012). The data from the two-level hierarchical task has not been published before.

Three subjects had to trace a curve that bifurcated twice, completing between 1825 and 2534 trials each. Subjects had to make a left/right decision at L1, and an up/down decision at L2, reporting their decisions with different key-presses. As in Zylberberg et al. (2012), luminance samples were perturbed with additive Gaussian noise (σ = 10 cd/m2), the background luminance was 50 cd/m2 and the mean luminance of the target was adjusted online with a Quest procedure to keep performance at ~75% correct. The psychophysical reverse correlation analysis was conducted as explained in the Supplemental Information of Zylberberg et al. (2012).

Acknowledgements

PRR was supported by NWO (ALW grant 823-02-010) and the European Union (the Human Brain Project Grant Agreement No. 720270 and ERC Grant Agreements n. 339490 'Cortic_al_gorithms' and n. CCC).

Funding Statement

The funders had no role in study design, data collection and interpretation, or the decision to submit the work for publication.

Funding Information

This paper was supported by the following grant:

  • Nederlandse Organisatie voor Wetenschappelijk Onderzoek 823-02-010 to Pieter Roelfsema.

Additional information

Competing interests

The authors declare that no competing interests exist.

Author contributions

AZ, Conceptualization, Data curation, Software, Investigation, Visualization, Writing—original draft, Writing—review and editing.

JAML, Conceptualization, Data curation, Investigation, Writing—original draft, Writing—review and editing.

BGO, Conceptualization, Data curation, Software, Investigation.

CIDZ, Conceptualization, Supervision, Funding acquisition, Writing—review and editing.

MS, Conceptualization, Resources, Supervision, Funding acquisition, Investigation, Writing—review and editing.

PR, Conceptualization, Resources, Supervision, Funding acquisition, Investigation, Writing—original draft, Project administration, Writing—review and editing.

Ethics

Human subjects: We obtained ethical approval from the ethics committee at the University of Amsterdam and informed consent in writing from the subjects before the experiments.

Animal experimentation: All experimental procedures complied with the National Institutes of Health Guide for Care and Use of Laboratory Animals, and were approved by the Institutional Animal Care and Use Committee of the Royal Netherlands Academy of Arts and Sciences under protocol number NIN11.19 "attentional and reward modulation during multiple perceptual decision making".

References

  1. Ahumada AJ. Perceptual classification images from Vernier Acuity masked by noise. Perception. 1996;25:2–1840. doi: 10.1068/v96l0501. [DOI] [Google Scholar]
  2. Brunton BW, Botvinick MM, Brody CD. Rats and humans can optimally accumulate evidence for decision-making. Science. 2013;340:95–98. doi: 10.1126/science.1233912. [DOI] [PubMed] [Google Scholar]
  3. Gold JI, Shadlen MN. The neural basis of decision making. Annual Review of Neuroscience. 2007;30:535–574. doi: 10.1146/annurev.neuro.29.051605.113038. [DOI] [PubMed] [Google Scholar]
  4. Houtkamp R, Spekreijse H, Roelfsema PR. A gradual spread of attention during mental curve tracing. Perception & Psychophysics. 2003;65:1136–1144. doi: 10.3758/BF03194840. [DOI] [PubMed] [Google Scholar]
  5. Hyafil A, Moreno-Bote R. Breaking down hierarchies of decision-making in primates. eLife. 2017;6:16650. doi: 10.7554/eLife.16650. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Kepecs A, Uchida N, Zariwala HA, Mainen ZF. Neural correlates, computation and behavioural impact of decision confidence. Nature. 2008;455:227–231. doi: 10.1038/nature07200. [DOI] [PubMed] [Google Scholar]
  7. Kiani R, Churchland AK, Shadlen MN. Integration of direction cues is invariant to the temporal gap between them. Journal of Neuroscience. 2013;33:16483–16489. doi: 10.1523/JNEUROSCI.2094-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Kiani R, Hanks TD, Shadlen MN. Bounded integration in parietal cortex underlies decisions even when viewing duration is dictated by the environment. Journal of Neuroscience. 2008;28:3017–3029. doi: 10.1523/JNEUROSCI.4761-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Kiani R, Shadlen MN. Representation of confidence associated with a decision by neurons in the parietal cortex. Science. 2009;324:759. doi: 10.1126/science.1169405. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Kira S, Yang T, Shadlen MN. A neural implementation of Wald's sequential probability ratio test. Neuron. 2015;85:861–873. doi: 10.1016/j.neuron.2015.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  11. Lorteije JA, Zylberberg A, Ouellette BG, De Zeeuw CI, Sigman M, Roelfsema PR. The formation of hierarchical decisions in the Visual Cortex. Neuron. 2015;87:1344–1356. doi: 10.1016/j.neuron.2015.08.015. [DOI] [PubMed] [Google Scholar]
  12. Pooresmaeili A, Roelfsema PR. A growth-cone model for the spread of object-based attention during contour grouping. Current Biology. 2014;24:2869–2877. doi: 10.1016/j.cub.2014.10.007. [DOI] [PubMed] [Google Scholar]
  13. Smith PL, Ratcliff R. Psychology and neurobiology of simple decisions. Trends in Neurosciences. 2004;27:161–168. doi: 10.1016/j.tins.2004.01.006. [DOI] [PubMed] [Google Scholar]
  14. Tsetsos K, Gao J, McClelland JL, Usher M. Using Time-Varying evidence to test models of Decision Dynamics: bounded Diffusion vs. the Leaky competing Accumulator Model. Frontiers in Neuroscience. 2012;6:58. doi: 10.3389/fnins.2012.00079. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Usher M, McClelland JL. The time course of perceptual choice: the leaky, competing accumulator model. Psychological Review. 2001;108:550–592. doi: 10.1037/0033-295X.108.3.550. [DOI] [PubMed] [Google Scholar]
  16. van den Berg R, Zylberberg A, Kiani R, Shadlen MN, Wolpert DM. Confidence is the bridge between Multi-stage decisions. Current Biology. 2016;26:3157–3168. doi: 10.1016/j.cub.2016.10.021. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Wang XJ. Probabilistic decision making by slow reverberation in cortical circuits. Neuron. 2002;36:955–968. doi: 10.1016/S0896-6273(02)01092-9. [DOI] [PubMed] [Google Scholar]
  18. Wong KF, Wang XJ. A recurrent network mechanism of time integration in perceptual decisions. Journal of Neuroscience. 2006;26:1314–1328. doi: 10.1523/JNEUROSCI.3733-05.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Zylberberg A, Fetsch CR, Shadlen MN. The influence of evidence volatility on choice, reaction time and confidence in a perceptual decision. eLife. 2016;5:e17688. doi: 10.7554/eLife.17688. [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Zylberberg A, Ouellette B, Sigman M, Roelfsema PR. Decision making during the psychological refractory period. Current Biology. 2012;22:1795–1799. doi: 10.1016/j.cub.2012.07.043. [DOI] [PubMed] [Google Scholar]
eLife. 2017 Jun 26;6:e17331. doi: 10.7554/eLife.17331.009

Decision letter

Editor: Joshua I Gold1

In the interests of transparency, eLife includes the editorial decision letter and accompanying author responses. A lightly edited version of the letter sent to the authors after peer review is shown, indicating the most substantive concerns; minor comments are not usually included.

Thank you for submitting your article "Serial, parallel and hierarchical decision making in the visual cortex" for consideration by eLife. Your article has been reviewed by a Reviewing Editor and Timothy Behrens as the Senior Editor.

The reviewers have discussed the reviews with one another and the Reviewing Editor has drafted this decision to help you prepare a revised submission.

Summary:

These two papers present an enlightened and useful discussion about the interpretation of results previously published by Lorteije and colleagues. In that prior study, monkeys performed a task that required them to make a saccadic eye movement to the appropriate endpoint of a visual branching pattern with three bifurcations: one at the top, then two others under each branch, resulting in four distinct endpoints. Each bifurcation had a modulating luminance cue at each branch that determined the correct path: always choose the brighter (on average) branch. Through analyses of behavior and the activity of neurons in cortical areas V1 and V4 whose receptive fields corresponded to the locations of the luminance cues, a primary conclusion from that study was that the monkeys solved the task in a hierarchical manner, with decisions about the top- and lower-level branches first occurring in parallel, then combined for a final choice.

That landmark paper spawned several interesting discussions in the field. Hyafil and Moreno-Bote's technical comment encapsulates one of the critical lines of discussion about whether it is possible to truly distinguish a hierarchical decision-making process from a flat process based on the experimental data of Lorteije and colleagues. It is a critical and complex question. The reply by Zylerberg and colleagues adds further to the discussion, presenting several counter-arguments to the claims of Hyafil and Moreno-Bote.

All three reviewers were impressed by the tone and content of the submissions and agree that both represent worthwhile contributions to the literature. As noted by one of the reviewers, this kind of debate is "very valuable and generally underappreciated."

The above comments are included, verbatim, in our decision letters to both groups of submitting authors. We also will now make both initial submissions available to both groups, so that any potential revisions can fully take into account the claims made in the other submission. We will then allow for one more iteration: if and when we receive revised submissions and deem them appropriate, we will then again make each available to the other group for further revisions and clarifications.

Below are summaries of the discussions among the reviewers that are specific to your submission.

Essential revisions:

The reviewers agreed this paper presents several important arguments and analyses that support the idea of a hierarchical model. However, they also raised several concerns:

1) The paper may be stronger and more accessible if it was reorganized such that the rebuttals of the arguments for the flat model that were made by Hyafil and Moreno-Bote were addressed first. That is, more directly address whether the data in the original submission by Lorteije et al. exclude a flat model with inhibition.

2) It also would be useful treat more directly the claim by Hyafil and Moreno-Bote that the hierarchical model requires an "extra modulatory signal" from L2 to L1 "that must be carefully tuned." This brings up the more general point that, as the authors are well aware, sensory neural responses provide only indirect evidence for the mechanism of the decision-making process. In the absence of a clear understanding about the nature of choice-related feedback to V1 and V4 one should interpret the neural responses with caution. Making this point more explicitly would be useful.

3) Although the other data presented here are interesting, there were questions about their relevance to the main argument. For example, the authors should be more explicit about how the gradual spread of object-based attention in the "mental curve tracing" tasks relate to hierarchical decision-making. The should also clarify exactly why that result "cannot be explained by 'flat' models that implement a race between the four possible interpretations of the stimulus." Likewise, the data from the three-branch task is interesting, and under those conditions subjects likely rely on a serial and hierarchical decision-making process based on accumulation of evidence that is largely (albeit not necessarily entirely, as the authors seem to imply) independent at different levels of the decision tree. However, does this result necessarily imply that a decision tree with two branching points is complex enough to necessitate a hierarchical decision? It seems quite possible that subjects' strategy shifts from a flat process to a hierarchical process as the number of branching points increases.

4) The assertion that a flat model predicts either unrealistically long reaction times or a dependence of L2 decisions on L1 stimulus strength raised several concerns. First, the task did not have a reaction time design -- the monkey had to view the stimulus for 500ms before responding. It is unclear whether subjects curtailed their decisions after the fixation point turned off, continued to accumulate evidence toward a decision bound, or used a mixture of those strategies. The very weak dependence of RT on stimulus strength (only ~100ms RT difference between the weakest and strongest stimuli) make them particularly difficult to interpret in terms of decision models. Second, additional mechanisms, such as a collapsing decision bound (or urgency) might make a flat model compatible with the RT data. Is a quantitative match between the model and data truly impossible?

[Editors' note: further revisions were requested prior to acceptance, as described below.]

Thank you for submitting your article "Serial, parallel and hierarchical decision-making in the visual cortex" for consideration by eLife. Your article has been evaluated by a Reviewing Editor and Timothy Behrens as the Senior Editor.

We received revised manuscripts from both your group and from Hyafil and Moreno Bote. We asked them to respond to a few remaining issues, which they have done. As we indicated to them, we are now forwarding to you the newest version of their manuscript, to give you an opportunity to revise and respond accordingly. Once we hear back from you, we then will share both papers with both groups, but at that point, if any further changes are desired, they have to be essential and very well justified.

There are two points in particular that we think might benefit from further discussion/analyses in your paper. Specifically:

1) As you have indicated, the behavioral data show that stimulus difficulty at the L1 branch did not influence performance at the L2 branch. In the original Lorteije et al. paper, a flat model without lateral interactions did not reproduce this result. Hyafil and Moreno Bote then showed that it could be reproduced with a flat model with lateral interactions and rectification. You have pointed out that implementation required very high decision bounds that would have produced unrealistic RTs. Hyafil and Moreno Bote now produce a version of the model that reproduces the L1 dependence and realistic mean RTs, using a kind of "collapsing bound" that is infinite (unreachable) for the first several samples that appears to reasonably account for the task design that allowed responses only after 500 ms of stimulus viewing.

2) Both papers discuss the new analysis by Zylberberg et al. showing that the strength of evidence at L1 affects V4 activity elicited by the L2 and L2' branches. Both papers are in agreement with the finding but disagree with the interpretation. Part of the disagreement appears to stem from misunderstandings from some comments in an earlier version of the Hyafil and Moreno Bote manuscript. Specifically, as quoted by Zylberberg et al., Hyafil and Moreno Bote state in Appendix A that the flat model predicts that "selection signals at levels 2 are only influenced by information provided at level 2 branches […] and not by information provided at level 1." The new analyses by Zylberberg et al. clearly contradict this prediction. However, in their main text, Hyafil and Moreno Bote stated that "this observation is most compatible with the flat model and by itself rules out the hierarchical model that relies on complete neural segregation of integration of L1 and L2 evidence." We asked Hyafil and Moreno Bote to reconcile these statements. In the new manuscript, they provide the following comment: "At this point, an important distinction has to be made in the hierarchical model between localized activations, which indeed mix evidence from both branches, and selection signals at L2, extracted by looking at the difference between two units in the same L1 branch, and which as shown above are largely insensitive to L1 signals."

eLife. 2017 Jun 26;6:e17331. doi: 10.7554/eLife.17331.010

Author response

Essential revisions:

The reviewers agreed this paper presents several important arguments and analyses that support the idea of a hierarchical model. However, they also raised several concerns:

1) The paper may be stronger and more accessible if it was reorganized such that the rebuttals of the arguments for the flat model that were made by Hyafil and Moreno-Bote were addressed first. That is, more directly address whether the data in the original submission by Lorteije et al. exclude a flat model with inhibition.

We thank the reviewers for this suggestion and we have reorganized our manuscript accordingly.

2) It also would be useful treat more directly the claim by Hyafil and Moreno-Bote that the hierarchical model requires an "extra modulatory signal" from L2 to L1 "that must be carefully tuned." This brings up the more general point that, as the authors are well aware, sensory neural responses provide only indirect evidence for the mechanism of the decision-making process. In the absence of a clear understanding about the nature of choice-related feedback to V1 and V4 one should interpret the neural responses with caution. Making this point more explicitly would be useful.

We now discuss this point in the revised manuscript. Our results indeed demonstrate that the difficulty of the L2 decisions (or decision confidence) biases the L1 choice. However, this experimental finding is not incompatible with hierarchical decision making strategies. Previous studies have shown that monkeys (and rats) can use confidence in one decision to guide other decisions, for instance how long to wait for a reward (e.g., Kepecs et al., 2008) or whether to opt out of a difficult choice (e.g., Kiani and Shadlen, 2009). The implication is that there must be mechanisms that carry information from one decision to a later one. In these cases, interactions occurred between decisions separated in time, which is beyond the scope of “flat” accumulator models.

We believe that it would be premature to commit to a specific mechanism that mediates the interactions between local decisions, because existing data are compatible with several possibilities. The model of H and M proposes one such mechanism, where the interaction between sub-decisions is mediated by global inhibition during a ‘flat’ competition between the alternative motor actions. As we argue in our response, this mechanism cannot explain situations where decisions become serial, and it therefore lacks the required flexibility to account for the interactions between sub-decisions that are observed more generally. Furthermore, the global inhibitory process proposed by H and M is also incompatible with the re-analysis of the neural data of Lorteije et al. as presented in Figure 2 of our response.

We believe that the different possible mechanisms that might enable interactions between local decisions deserve to be tested in future modeling studies and neurophysiological work. We modeled one such alternative mechanism that can account for the influence of the relative difficulty of the two L2 decisions on the L1 decision. In a diffusion model, the state of accumulated evidence (the decision variable, D) at a particular time t is monotonically related to confidence (e.g. Kiani and Shadlen 2009). We therefore used the difference between the absolute values of the DVs of the two L2 decisions (ΔDt) as an index of the relative difficulty of the L2 decisions. We then implemented an influence of ΔDt on the L1 decision in the hierarchical model of Lorteije et al., 2015 by adding an extra term to the evidence at L1. This term equaled (ΔDt−ΔDt−1),where k is a scaling constant and t and t−1 are successive time steps. As illustrated in Author response image 1, the relative difficulties of the two L2 decisions influenced the L1 decision just as in the behavior of the monkeys. Thus, the influence of L2 difficulty on L1 choice behavior can be incorporated into our hierarchical model as an additive term (which did not require “careful tuning” other than adjusting one parameter, k). We emphasize, however, that given the large number of alternative mechanisms that could potentially mediate the interactions between local decisions, we prefer to test them in future work rather than prematurely committing to one of them.

Author response image 1. The decision at L1 is biased by the relative difficulty of the two L2 decisions.

Author response image 1.

Open in a new tab

Similar to the results of Lorteije (2015), L2 affects L1 only when the first decision is difficult.

DOI: http://dx.doi.org/10.7554/eLife.17331.008

Our revision states that the global inhibition proposed by Hyafil and Moreno-Bote is only one of a number of possible mechanisms to mediate the interactions between local decisions and we mention our preference to stay uncommitted.

The reviewers also mention that care should be taken when interpreting the role of neuronal signals in V1 and V4 for decision making. We fully agree with this point. In our original publication (Lorteije et al., 2015, page 6 paragraph 1) we reflected on the possible role of the modulation of neuronal firing rates in visual cortex and indicated that we do not have prove for a causal role of these signals in the decision making process. This is why we chose to use the neutral term ‘selection signal’ so that we could remain uncommitted about the role of these signals. Given the limited number of words of our rebuttal and because this issue was clearly addressed in our original paper, we did not repeat the discussion of the putative role of these selection signals in the decision process in our response to Hyafil and Moreno-Bote. These authors did not have concerns about the validity of measuring selection signals in visual cortex but they rather called our hierarchical decision-making model into question.

3) Although the other data presented here are interesting, there were questions about their relevance to the main argument. For example, the authors should be more explicit about how the gradual spread of object-based attention in the "mental curve tracing" tasks relate to hierarchical decision-making. The should also clarify exactly why that result "cannot be explained by 'flat' models that implement a race between the four possible interpretations of the stimulus." Likewise, the data from the three-branch task is interesting, and under those conditions subjects likely rely on a serial and hierarchical decision-making process based on accumulation of evidence that is largely (albeit not necessarily entirely, as the authors seem to imply) independent at different levels of the decision tree. However, does this result necessarily imply that a decision tree with two branching points is complex enough to necessitate a hierarchical decision? It seems quite possible that subjects' strategy shifts from a flat process to a hierarchical process as the number of branching points increases.

We thank the reviewers for pointing out that we had made it insufficiently clear why cases of more serial decision making are relevant for the issues raised by Hyafil and Moreno-Bote. We now clarify that more serial decision making strategies reveal a general insufficiency of the type of flat models proposed by Hyafil and Moreno-Bote. In a flat model, there is only one accumulator for each motor response. These models cannot account for cases where evidence for the L1 decision accumulates before evidence for the L2 decisions. One example of such a more serial decision making strategy has been illustrated in Figure 3 of our rebuttal, where information about the L1 target branch connected to the fixation point accumulates before evidence about the L2 target branch behind the possible location of an intersection.

Furthermore, the data of Figure 4 demonstrate that subjects can flexibly shift between parallel and more serial hierarchical decision making strategies in stimulus configurations equivalent to those studied by Lorteije et al., 2015. The implication is that separate accumulation processes must exist for each of the individual local decisions. Hierarchical models can shift from parallel to more serial strategies by changing the timing of the individual decisions and the later integration process.

In contrast, flat models propose a single accumulator for each of the possible interpretations of the stimulus so that all the evidence must accumulate at the same time. This machinery proposed by Hyafil and Moreno-Bote would have to be replaced by a different neuronal substrate to permit the independent integration of evidence for local decisions once the L3 decision has been added. Hence such a flat model is not parsimonious. In contrast, hierarchical models flexibly switch between parallel and more serial strategies, strengthening the claim that hierarchical models also apply to situations with fewer local decisions.

4) The assertion that a flat model predicts either unrealistically long reaction times or a dependence of L2 decisions on L1 stimulus strength raised several concerns. First, the task did not have a reaction time design -- the monkey had to view the stimulus for 500ms before responding. It is unclear whether subjects curtailed their decisions after the fixation point turned off, continued to accumulate evidence toward a decision bound, or used a mixture of those strategies. The very weak dependence of RT on stimulus strength (only ~100ms RT difference between the weakest and strongest stimuli) make them particularly difficult to interpret in terms of decision models. Second, additional mechanisms, such as a collapsing decision bound (or urgency) might make a flat model compatible with the RT data. Is a quantitative match between the model and data truly impossible?

The central question here is whether the behavioral evidence does or does not support the view of the crossing of a decision bound. The main signature of evidence integration towards a relatively stable bound (that does not quickly collapse) is a variable reaction time that depends on the difficulty of the stimulus. This is precisely what we observed. Although we did impose a minimal viewing duration of 500 ms before the monkey was allowed to make a response, additional evidence was presented until the monkey made a response (or until 1,500 ms had elapsed in which case the trial was aborted). Accordingly, the task is best viewed as a reaction-time task with a minimum viewing duration. We have added this explanation to the legend of Figure 1A.

A difference in RT of ~100ms between the easy and difficult conditions is a large effect (in the random-dot motion discrimination task, the average integration time is ~250 ms; Shadlen et al., Science 2016), because it occurred even after 500 ms of stimulus viewing. This finding is not compatible with a deadline (or quickly collapsing bound) and implies that the criterion to terminate decisions depended on the state of accumulated evidence. In support of this interpretation, in the original publication (Figure S1D, Lorteije et al., 2015), we showed that the psychophysical kernels were protracted in trials where the monkeys took longer to respond. In contrast, an external-cue or a time-based strategy predicts that response times should be independent of difficulty and that the kernels should be identical for fast and slow responses. Of course, we cannot claim that a “quantitative match between the model and data is truly impossible”. But if a solution exists it would be more complicated that the one postulated by H and M.

[Editors' note: further revisions were requested prior to acceptance, as described below.]

There are two points in particular that we think might benefit from further discussion/analyses in your paper. Specifically:

1) As you have indicated, the behavioral data show that stimulus difficulty at the L1 branch did not influence performance at the L2 branch. In the original Lorteije et al. paper, a flat model without lateral interactions did not reproduce this result. Hyafil and Moreno Bote then showed that it could be reproduced with a flat model with lateral interactions and rectification. You have pointed out that implementation required very high decision bounds that would have produced unrealistic RTs. Hyafil and Moreno Bote now produce a version of the model that reproduces the L1 dependence and realistic mean RTs, using a kind of "collapsing bound" that is infinite (unreachable) for the first several samples that appears to reasonably account for the task design that allowed responses only after 500 ms of stimulus viewing.

2) Both papers discuss the new analysis by Zylberberg et al. showing that the strength of evidence at L1 affects V4 activity elicited by the L2 and L2' branches. Both papers are in agreement with the finding but disagree with the interpretation. Part of the disagreement appears to stem from misunderstandings from some comments in an earlier version of the Hyafil and Moreno Bote manuscript. Specifically, as quoted by Zylberberg et al., Hyafil and Moreno Bote state in Appendix A that the flat model predicts that "selection signals at levels 2 are only influenced by information provided at level 2 branches […] and not by information provided at level 1." The new analyses by Zylberberg et al. clearly contradict this prediction. However, in their main text, Hyafil and Moreno Bote stated that "this observation is most compatible with the flat model and by itself rules out the hierarchical model that relies on complete neural segregation of integration of L1 and L2 evidence." We asked Hyafil and Moreno Bote to reconcile these statements. In the new manuscript, they provide the following comment: "At this point, an important distinction has to be made in the hierarchical model between localized activations, which indeed mix evidence from both branches, and selection signals at L2, extracted by looking at the difference between two units in the same L1 branch, and which as shown above are largely insensitive to L1 signals."

In our revision, we adjusted our manuscript to address the changes made by Hyafil and Moreno-Bote in their last revision. Just as the previous versions of their ‘flat’ model, their new model with collapsing decision bounds predicts a tradeoff between the accuracy at L1 and L2 that we do not observe in the data. As in our previous submission, we demonstrate that decision making can be remarkably flexible. Subjects can switch from parallel to serial strategies, which is impossible for flat models.

We have now had to address a number of versions of the commentary by H and M, which has become a moving target. We were therefore reassured with your e-mail from Nov 10th where you indicated that this is the final round of revisions. In that e-mail you also indicated that the editors may want to suggest small changes to one or both titles or abstracts for consistency. We would indeed appreciate it if the misleading title of the paper by H and M would change, because their paper did not “break down” hierarchies of decision making. In fact, we believe that these interactions bolstered the case for hierarchical decision making strategies in the primate brain.

Articles from eLife are provided here courtesy of eLife Sciences Publications, Ltd

RESOURCES