Is the Sequence of SuperAlarm Triggers more Predictive than Sequence of the Currently Utilized Patient Monitor Alarms?

Abstract

Detecting and even anticipating patient status changes using bedside monitors remains unsatisfactory as evidenced by the wide-spread alarm fatigue problem in hospitals. Our previous study has successfully predicted “code blue” events by identifying SuperAlarm patterns that are multivariate patterns hidden in the data streams of patient monitor alarms, physiological signals, and data from electronic health record systems. Benefiting from this preprocessing, in this study we demonstrate sequential patterns recognized in SuperAlarm sequences can offer better performance in predicting “code blue” events, compared with that recognized in sequences of monitor alarms. We extract monitor alarms and laboratory test results from a total of 254 adult coded patients and 2213 control patients. The training dataset is composed of subsequences that are sampled from the complete sequences and then further represented as fixed-dimensional vectors by term frequency inverse document frequency method. The information gain technique and weighted support vector machine are adopted to select the most relevant features and train classifier, respectively. Prediction performances are assessed using an independent test dataset in terms of three metrics: sensitivity of lead time (Sen^L@T), alarm frequency reduction rate (AFRR), and work-up to detection ratio (WDR). Results show that under a 12-hour sampling window, prediction of “code blue” events using SuperAlarm sequences can yield up to 93.33% sensitivity with 2-hour lead time (Sen^L@2), with 87.28% AFRR and 3.01 WDR, which outperforms that using monitor alarm sequences. The results suggest that the proposed SuperAlarm sequence classifier may assist in predicting patient deterioration and reducing alarm burden.

I. Introduction

The trajectory of a patient’s physiological state through hospitalization is dynamic, particularly for critically ill patients. Unfortunately, the ability to effectively and precisely detect and anticipate patient status changes using current patient monitors remains unsatisfactory as evidenced by the wide-spread alarm fatigue problems in hospitals [1], [2]. A straightforward approach to handle alarm fatigue is to suppress false alarms by signal processing and machine learning approaches [3]–[7]. These approaches have shown some potentials for a few types of arrhythmia and intracranial pressure alarms but additional research is needed to develop methods to remove false threshold-crossing parameter alarms [8]–[10]. In addition to false alarms, nuisance alarms are considered as a major contributor to alarm fatigue. Nuisance alarms reflect transient and sometimes minor deviations of monitored physiological variables but do not indicate major patient status changes and therefore are often not actionable. As a result, a trend in the community to address nuisance alarms is to adjust alarm limits to find optimal settings for these limits [11]. However, caution is necessary in excessively suppressing nuisance alarms because it is possible that certain patterns such as increasing frequency of these transient deviations of physiological variables may be the harbinger of some major events [12]. In our view, the number of alarms should not be the sole outcome for gauging the effectiveness of interventions for addressing alarm fatigue. Instead, a more comprehensive approach towards fulfilling the ultimate goal of patient monitoring needs to be taken.

In a recent position paper [13], the authors pointed out that future patient monitoring systems should shift focus from individual alarms to recognizing clinical patterns by integrating all patient-linked devices. This concept indeed supports our evolving approach [14], [15] to improve patient monitoring by identifying multivariate patterns hidden in data streams of patient monitor alarms, physiological signals, and data from electronic health record (EHR) systems. We refer to such a multivariate pattern as a SuperAlarm pattern. The term SuperAlarm was first introduced in our paper [14] to define a superset of patient monitor alarms that co-occur within a time window immediately preceding “code blue” events for more than a minimal percentage of coded patients but less than a maximal percentage of control patients without triggering any “code blue” calls. In our subsequent study [15], we further extended this approach by integrating laboratory test results from EHR system with monitor alarms to identify Super-Alarm patterns and demonstrated the improved performance in prediction of “code blue” events. As a consequence of this extension, a SuperAlarm pattern as referred to in the present work is a superset of co-occurring monitor alarms and laboratory test results. With a training dataset consisting of data from both coded and control patients, a set of SuperAlarm patterns can be identified. These patterns can then be deployed to monitor patients, and each detection of an emerging SuperAlarm pattern is termed a SuperAlarm trigger. A sequence of consecutive triggers is termed SuperAlarm sequence. As a next step to expand this SuperAlarm approach, we recently developed a sequence representation algorithm that uses fixed-dimensional vectors to represent SuperAlarm sequences that can have different number of triggers [16]. By exploiting a vectorization method for representing SuperAlarm sequences, there is the opportunity to use off-the-shelf machine learning approaches to recognize temporal patterns encoded by these sequences. However, it should be realized that various sequence representation methods exist and they can also be applicable to sequences of just monitor alarms directly. Therefore, an interesting question arises regarding whether it is beneficial to first identify SuperAlarm patterns and construct SuperAlarm sequence versus directly utilizing monitor alarm sequence.

The central objective of this work is to provide an answer for the above question by investigating three types of sequences: 1) sequences of raw monitor alarms; 2) sequences of modified monitor alarms where vital sign parameter alarms are preprocessed by discretizing their numerical values, e.g., systolic blood pressure alarms “systolic arterial blood pressure > 135 mmHg” and “systolic arterial blood pressure > 200 mmHg” will be treated as a different alarms if the values 135 and 200 are discretized into different bins; and 3) sequences of SuperAlarm triggers. The second sequence type is included because discretization of vital sign parameter alarms was also used as a preprocess step when identifying SuperAlarm patterns. To fairly compare these three types of sequences, we use the same sequence representation and machine learning algorithm. In particular, we use a sequence representation technique in document classification – term frequency inverse document frequency (TFIDF) [17] to convert sequences into fixed-dimensional vectors. Regarding the machine learning approach, we use the information gain (IG) technique [18] to conduct feature selection [19] and apply a modified support vector machine (SVM) called weighted SVM [20] as the classifier that incorporates different misclassification costs into the objective function to handle the imbalance training dataset.

II. Materials and Methods

A. Overview of a Classification Approach for Sequences

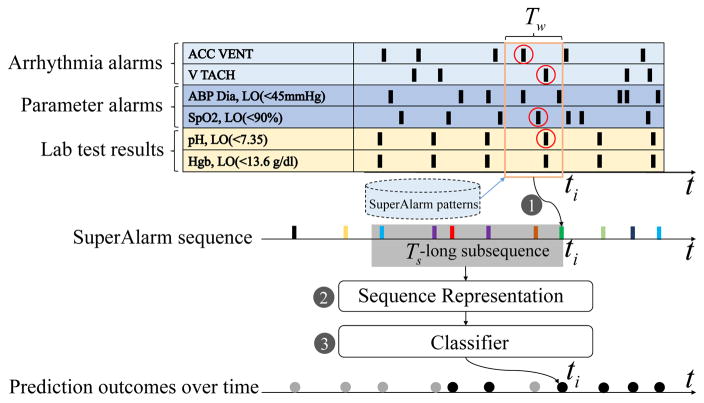
Fig. 1 illustrates the proposed algorithm to predict a clinical endpoint, e.g., “code blue” event, using a sequence of triggers. In this figure, we use SuperAlarm sequence as an example. The algorithm consists of three steps:

Fig. 1.

A graphic illustration of the proposed approach to predict “code blue” event in use of SuperAlarm sequences. This example illustrates 6 physiological variables out of the 3 groups occurring over time: arrhythmia alarms, parametric alarms, and laboratory test results. ACC VENT: accelerated ventricular; V TACH: ventricular tachycardia; ABP Dia, LO: diastole arterial blood pressure low; SpO2, LO: peripheral capillary oxygen saturation low; pH, LO: pH value low; Hgb, LO: hemoglobin low.

• Step 1, generation of SuperAlarm sequence. As shown in Fig. 1 when an alarm “ABP Dia LO < 45 mmHg” occurs at current time t_i, the algorithm first extracts all raw alarms and laboratory test results in a T_w-long time window (orange rectangle) preceding t_i. If any subset of these alarms and laboratory test results matches a SuperAlarm pattern, a SuperAlarm trigger then occurs at t_i. By repeating this process whenever a new alarm or a new laboratory test result is received, a sequence of SuperAlarm triggers will be generated and they are depicted as vertical bars in different colors in Fig. 1.

• Step 2, representation of SuperAlarm sequence. Assume at time t_i, we would assess the risk of impending “code blue” event by using all SuperAlarm triggers that are within a T_s-long window preceding t_i. A sequence representation approach is then used to convert this subsequence of SuperAlarm triggers into a fixed-dimensional vector so that it can be used as an input feature to a classifier. We use TFIDF method in this work and investigate the effect of different choices of T_s.

• Step 3, classification. In this step, the feature vector from step 2 will be subjected to a feature selection process using the IG technique and then classified by an SVM model. This process will be repeated at every single t_i where there is at least one SuperAlarm trigger. Based on SVM output, some SuperAlarm triggers will be classified as negative — i.e., not associating with the clinical endpoint (depicted as gray dots) and others will be classified as positive (black dots). This classifier essentially functions as a filter of SuperAlarm triggers.

B. Monitor Alarms, Laboratory Test Results and SuperAlarm Patterns

The present work uses the same set of SuperAlarm patterns that were identified in our previous study. Therefore, we provide a brief introduction of monitor alarms, laboratory test results, the process to identify SuperAlarm patterns as used in that study [15].

Monitor alarms were extracted from a central repository where data from patient monitors were continually archived by BedMasterEx system (Excel Medical Electronics, Inc, Jupiter, FL). A total of 100 distinct monitor alarms were used in our previous study including 14 ECG arrhythmia alarms and 86 parameter alarms that signal the deviation of vital signs outside preset upper or lower thresholds. These vital signs include heart rate, respiratory rate, pulse oximetry, systolic, diastolic, and mean arterial blood pressure, just to name a few. Crisis alarms including asystole, ventricular fibrillation (VFib) and no breath were excluded because our clinical endpoint — “code blue” is typically triggered when true crisis alarms occur. We also exclude technical alarms, e.g., “ECG LEADS FAIL” as they do not represent patient status. We further discretized the values of vital signs that triggered the corresponding parameter alarms using the algorithm described in [21]. After discretization, a total of 362 distinct types of discretized parameter alarms were obtained. Each parameter alarm can be uniquely mapped to a discretized parameter alarm.

From the EHR, we extracted laboratory test results based on a total of 62 conventional laboratory tests (e.g., arterial blood gas, complete blood count, blood chemistry). Numeric values of the laboratory test results were not utilized. Instead, we employed the abnormality flag reported for each laboratory test result by the EHR system. There are five flags available for each laboratory test indicating the deviation of the result from the reference range: HH (critically high), H (high), N (normal), L (low) and LL (critically low). In our previous work, we tested two approaches of encoding a laboratory test result as an equivalent lab “alarm”. The present work uses the delta lab approach where we encode the pair of abnormality flags of the two most recent consecutive laboratory test results, e.g., the last two potassium test results are encoded as “Potassium N → L”, which means that serum potassium level changed from normal to below normal.

A SuperAlarm pattern is identified following two steps. In the first step, we used the MAFIA frequent itemset mining algorithm [22] to identify combinations of monitor alarms and lab “alarms” that co-occurred in a T_w-hour long time window preceding a “code blue” event for more than min_sup percentage of coded patients. Those candidate patterns were then removed if they also occurred for more than FPR_max percentage of all T_w-hour windows that were consecutively selected from all control patients. Understandably, parameters including T_w, min_sup, and FPR_max control the number of final SuperAlarm patterns and the performance of the set of SuperAlarm patterns. In the present work, we use the SuperAlarm patterns that were identified based on the set of algorithm parameters that achieved highest sensitivity, which is the upper limit for the sequence classifier approach to achieve. The values for the three algorithm parameters are: T_w = 0.5, min_sup = 5%, and FPR_max = 15% and the total number of resultant SuperAlarm patterns is 428.

C. Sequence Representation

We formulate a SuperAlarm sequence as follows. Let Σ = {SA₁, SA₂, …, SA_m} be a set of m distinct SuperAlarm patterns. A SuperAlarm sequence S is denoted as S = 〈SA_t1, SA_t2, …, SA_tn〉, where SA_ti ∈ Σ is a SuperAlarm trigger occurring at time t_i. A T_s-long Super-Alarm subsequence is a segment of SuperAlarm sequence denoted as s = 〈SA_ta−Ts, SA_ta−Ts+1, …, SA_ta〉, where t₁ ≤ t_a − T_s, t_a ≤ t_n. We call SA_ta the anchor SuperAlarm trigger for the subsequence s.

Inspired by approaches developed for representing documents in the field of information retrieval [23], we treat each SuperAlarm pattern as a word in a vocabulary consisting of m distinct SuperAlarm patterns. Then each subsequence can be treated as a document written using words from this vocabulary. This analogy enables us to adopt the vector space model [24] to represent each subsequence as a vector where each component in the vector corresponds to a particular SuperAlarm pattern. In the vector space model, term frequency inverse document frequency (TFIDF) [17] is one of the well-known weighting schemes used to assign a weight to each component in the vector. TFIDF explores the importance of a given SuperAlarm pattern in a given subsequence and within the entire training dataset by evaluating the term frequency (TF) of the SuperAlarm pattern in the subsequence multiplied by its inverse document frequency (IDF) calculated over the entire training dataset [25]. As a result, a subsequence s_j represented as a numeric-valued vector using TFIDF can be written as tfidf_j = (tfidf_1j, tfidf_2j, …, tfidf_mj)^T, where m is the total number of SuperAlarm patterns in Σ. The component tfidf_ij is defined as

$${\mathit{tfidf}}_{ij}=t{f}_{ij}\times {\mathit{idf}}_i$$ (1)

where tf_ij = log(1 + n_ij), n_ij is the number of the Super-Alarm trigger SA_i occurring in the subsequence s_j, ${\mathit{idf}}_i=log\frac{N}{1+{df}_i},{df}_i={\sum }_{j=1}^N\mathbb{I}(n_{ij}>0)$ calculates the number of subsequences in the training dataset containing the Super-Alarm trigger SA_i, N is the total number of subsequences in the training dataset. Note that: 1) the logarithm transformation used for tf_ij is to reduce the effect of the SuperAlarm trigger SA_i occurring many times within the subsequence s_j; 2) the IDF favors the rare SuperAlarm triggers, which means that common SuperAlarm triggers occurring in the majority of subsequences in the training dataset will have lower IDF values than uncommon ones.

In order to eliminate the impact of length of the subsequence (i.e., the amount of SuperAlarm triggers occurring in the subsequence), the cosine normalization is applied to the TFIDF vector tfidf_j, which is defined as

$$x_{ij}=\{\begin{array}{ll}\frac{{\mathit{tfidf}}_{ij}}{{\Vert \mathbf{tfid}{\mathbf{f}}_j\Vert }_2},\hfill & \text{if}{\Vert \mathbf{tfid}{\mathbf{f}}_j\Vert }_2\ne 0\hfill \\ 0,\hfill & \text{otherwise}\hfill \end{array}$$ (2)

The vector x_j = (x_1j, x_2j, …, x_mj)^T is the final representation of subsequence s_j.

D. Feature Selection

The above normalized TFIDF representation approach will result in a high-dimensional sparse vector. For machine learning problems with high-dimensional sparse vectors, dimension reduction of features has proven to be a beneficial step [19], [26]. In this study, we adopt a feature selection method to find a subset of SuperAlarm patterns that are highly relevant to the prediction of “code blue” event.

In particular, we use information gain (IG) [18] as the feature selection method. In essence, IG measures the expected reduction in entropy of one random variable having knowledge of the other. IG generally exhibits a competitive performance in text classification in comparison with other approaches [27]. In addition to its wide use in text classification, IG has been successfully applied in bioinformatics [28] and medical diagnosis [29], which justifies its adoption in the present study.

In this study IG is used to evaluate the amount of information obtained for “code blue” event prediction by observing the presence or absence of a SuperAlarm trigger SA_i in a subsequence from the training dataset. Let c₊ be the positive class, c₋ the negative class, SA_i = 1 the presence of SuperAlarm trigger SA_i in a subsequence and SA_i = 0 the absence in the subsequence. The IG of SA_i is given by

$$\begin{array}{l}IG(S{A}_i)=-\sum _{c\in (c_{+},c_{-})}p(c,\mathbf{X})logp(c,\mathbf{X})\\ +p(S{A}_i=0,\mathbf{X})\sum _{c\in (c_{+},c_{-})}p(c,{\mathbf{X}}_{S{A}_i=0})logp(c,{\mathbf{X}}_{S{A}_i=0})\\ +p(S{A}_i=1,\mathbf{X})\sum _{c\in (c_{+},c_{-})}p(c,{\mathbf{X}}_{S{A}_i=1})logp(c,{\mathbf{X}}_{S{A}_i=1})\end{array}$$ (3)

where X is the training dataset containing all subsequences; X_SAi=0 (X_SAi=1) is the subset of X in which SA_i is absent (present); p(SA_i = 0, X) (p(SA_i = 1, X)) is the probability of subsequences in X that SA_i is absent (present); p(c, X), p(c, X_{SAi = 0)} and p(c, X_{SAi = 1})are the probabilities of subsequences in X, X_{SAi = 0} and X_{SAi = 1} that belongs to the class c, respectively. Note that p(SA_i = 0, X) + p(SA_i = 1, X) = 1, ∀SA_i ∈ Σ.

By applying (3) to each of the m distinct SuperAlarm patterns and ranking them in terms of the IG values in decreasing order, the top k SuperAlarm patterns with the highest IG values are selected for TFIDF representation.

E. Weighted Support Vector Machine

The SVM has been extensively used in numerous real-world applications as it often exhibits highly competitive performance in comparison with other classification methods [30]. Therefore, we adopt it in this study.

Due to the imbalance of the training dataset in this study (more control patients than coded patients), the conventional SVM classifier tends to simply classify positive samples into the majority class (i.e., negative class) because the learned hyperplane is too close to the positive samples [31]. A strategy to handle this issue has been proposed by assigning different penalties of misclassification costs to each of classes, which is called weighted SVM [20]. In this way, the hyperplane will be pushed away from the positive samples and towards the negative ones [31]. The weighted SVM is defined as

$$\begin{array}{l}min\frac{1}{2}{\Vert \mathbf{w}\Vert }^2+C^{+}\sum _{i\in S^{+}}{\xi }_i+C^{-}\sum _{i\in S^{-}}{\xi }_i\\ \text{subject}\text{to}\\ y_i(\mathbf{w}·\varphi ({\mathbf{x}}_i)+b)\ge 1-{\xi }_i\\ {\xi }_i\ge 0,i=1,2,\dots ,N\end{array}$$ (4)

where ξ_i is the slack variable; C⁺ and C⁻ are the penalty parameters of misclassification costs for positive samples S⁺ and negative samples S⁻ in the training set, respectively; y_i ∈ {−1, +1} is the label for x_i that indicates a positive (y_i = +1) or a negative (y_i = −1) sample; w is the normal vector to the hyperplane; ϕ(x_i) is a function to map vector x_i into a new feature space; b is the bias; N is the total number of samples in the training dataset.

An empirical method has been provided for setting the penalty ratio to the inverse of the number of samples in each class by assuming that the number of misclassified samples from each class is proportional to the number of samples in each class [32]. The penalty ratio is given by

$$\frac{C^{+}}{C^{-}}=\frac{n^{-}}{n^{+}}$$ (5)

where n⁺ and n⁻ are the amount of samples in positive class and negative class, respectively.

Let C be a parameter, ω⁺ (ω⁻) the weight of positive class (negative class). Suppose C⁺ = ω⁺C, C⁻ = ω⁻C, with (5) we have $\frac{{\omega }^{+}}{{\omega }^{-}}=\frac{n^{-}}{n^{+}}$, that is, the overall weight of each class is equal (i.e., ω⁺ · n⁺ = ω⁻ · n⁻). Let ω⁻ be fixed (e.g., ω⁻ = 1), then we have

$$C^{+}=\frac{n^{-}{\omega }^{-}C}{n^{+}}=\frac{n^{-}C}{n^{+}}$$ (6)

$$C^{-}={\omega }^{-}C=C$$ (7)

Therefore, the penalty C⁺ for positive samples in the minority class will become larger (higher weight) than the penalty C⁻ for negative samples in the majority class. Equations (6) and (7) allow leaving only one parameter (i.e., C) to be learned.

The solution to classify a new sample vector x_new using the weighted SVM classifier with optimal parameters w^* and b^* learned from objective function (4) is given by

$$f({\mathbf{x}}_{\mathit{new}})=\{\begin{array}{ll}+1,\hfill & \text{if}{\mathbf{w}}^{\ast }·\varphi ({\mathbf{x}}_{\mathit{new}})+b^{\ast }>\text{threshold}\hfill \\ -1,\hfill & \text{if}{\mathbf{w}}^{\ast }·\varphi ({\mathbf{x}}_{\mathit{new}})+b^{\ast }\le \text{threshold}\hfill \end{array}$$ (8)

where threshold is usually set equal to zero (i.e., default threshold).

In this study we will use the linear kernel (mapping function ϕ(x) = x) for the following reasons: 1) the linear kernel measures the cosine similarity between samples in the original feature space; 2) the linear kernel can achieve better performance in comparison with other types of kernel functions when the original input vector is high-dimensional and the training set is large [33]; and 3) since input vector x is a normalized TFIDF vector, the linear kernel defined by inner product of two sample vectors can approximate the Fisher kernel [34]. We use the implementation of this algorithm as found in the LIBLINEAR library [35](v1.96, http://www.csie.ntu.edu.tw/~cjlin/liblinear/).

F. Experiment and Evaluation of Results

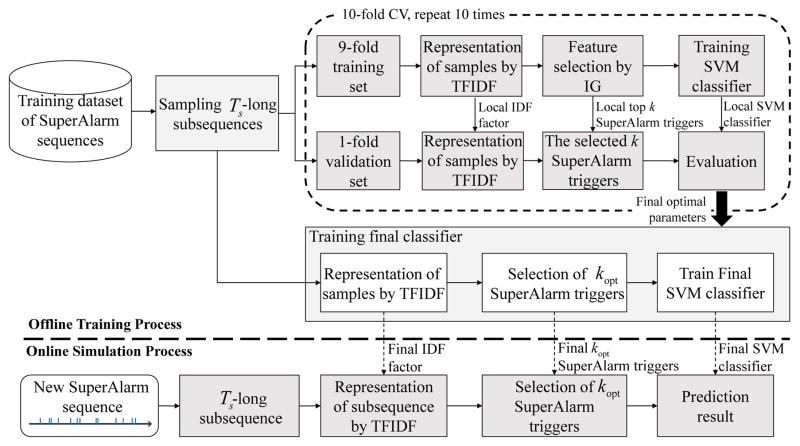
Fig. 2 provides an overview of the experiment to evaluate the proposed sequence classification approach. We use SuperAlarm sequence as an example in this figure as well as in the following description but the processes are applied to all three types of sequences. The experiment consists of two major processes: 1) offline training process, in which the SVM model with optimal parameters, the final set of relevant SuperAlarm patterns as determined by the IG method, and the IDF factor are obtained using the training dataset; and 2) online simulation process, in which evaluation of the SVM model is performed based on an independent test dataset.

Fig. 2.

The flowchart of the proposed framework of predicting code blue events using SuperAlarm sequences. k = ⌊r·m⌋, where r is feature selection ratio, m is the number of distinct SuperAlarm patterns in the dataset, ⌊r·m⌋ is referred to as the maximum integral number not greater than r·m.

1) Sampling Subsequences

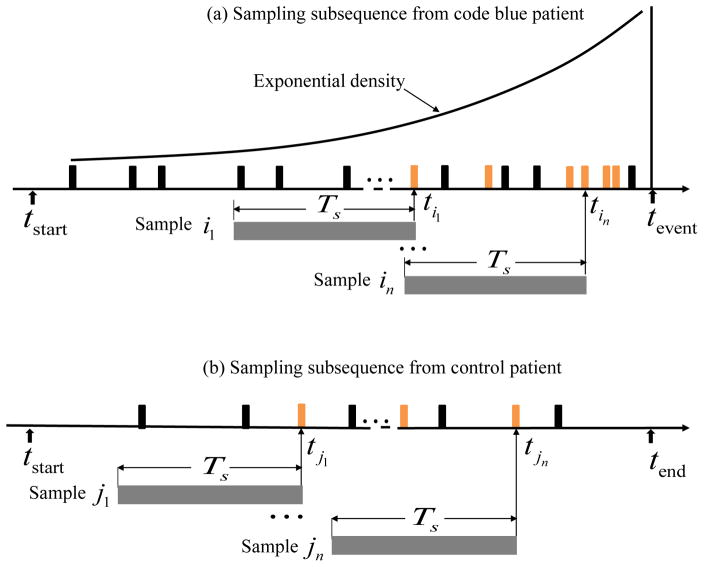
As described in Section II-C, the formulation of a SuperAlarm subsequence s is controlled by two parameters: the length of the subsequence T_s and the anchor SuperAlarm trigger SA_ta that occurs at time t_a. T_s is an algorithm parameter that will be varied to study its effect. Many anchor triggers are randomly sampled for a given patient. A conventional technique to sample these anchor triggers is window-based, which extracts samples by sliding T_s-long window along the complete sequence [36]. However, based on an intuitive heuristic that subsequences closer to “code blue” events are more predictive, we propose to have a higher probability to select anchor triggers that are closer to “code blue” events. We use an exponential probability density function to model the probability of selecting a SuperAlarm trigger as illustrated in Fig. 3(a). Subsequences that are extracted from coded patients are treated as positive samples. For control patients, we select anchor triggers following a uniform distribution as illustrated in Fig. 3(b). The orange vertical bars in Fig. 3 represent the selected SuperAlarm triggers while the black vertical bars represent the SuperAlarm triggers that are not sampled.

Fig. 3.

(a) Sampling subsequences from a coded patient, (b) sampling subsequences from a control patient.

2) Offline Training Process

The goal of the offline training process is to determine the optimal algorithm parameters for the final SVM classifier. To create the 10-fold cross-validation (CV) dataset, we randomly divide the positive samples and negative samples in the training dataset into 10 equal partitions. Samples in one partition are used for validation while the remainders for selecting features and training the classifier. This procedure is repeated 10 times and the optimal algorithm parameters can be determined by averaging a performance metric across 10 folds. In particular, we consider three algorithm parameters, including T_s, the cutoff of feature selection ratio r, and the parameter C in the SVM model. The F₁ score is used to determine the optimal parameters.

$$F_1=\frac{2·\mathit{precision}·\mathit{recall}}{\mathit{precision}+\mathit{recall}}$$ (9)

where $\mathit{precision}=\frac{TP}{TP+FP},\mathit{recall}=\frac{TP}{TP+FN}=\mathit{sensitivity}$, TP (true positive) is the number of positive samples predicted correctly by the classifier, FP (false positive) is the number of negative samples predicted incorrectly, FN (false negative) is the number of positive samples predicted incorrectly. The reasons we utilize F₁ score are: 1) the F₁ score is a harmonic mean of precision and recall and conveys a trade-off measure between them; and 2) as a composite measure, the F₁ score weights more on positive samples, making it more likely to select parameter settings that lead to more sensitive classifiers. After determining the optimal parameters, the final SVM classifier is trained using the entire training dataset obtained by coalescing the 10-fold CV dataset into a single one. It should be noted that the IDF resulting from the TFIDF weighting scheme based on the entire training dataset (termed final IDF factor as shown in Fig. 2) will be stored and used in the online simulation analysis.

3) Online Simulation Analysis

We employ an independent test dataset to simulate the application of the learned SVM classifier acting on a SuperAlarm sequence in real-time and assess the performance in predicting “code blue” event. At every single SuperAlarm trigger, a T_s-long subsequence immediately preceding this trigger will be evaluated using the learned SVM classifier. The T_s-long subsequence is first represented as a vector by the normalized TFIDF. Only those components in the vector that are retained based on IG criterion in the offline training phase will be used. To obtain a binary outcome, a threshold is specified and applied to the continuous-valued output of the learned SVM classifier. We derive an optimal threshold based on the receiver operating characteristic (ROC) analysis.

The following three metrics are employed to assess the performance of the SVM classifier based on the independent test dataset:

• Sensitivity of lead time (Sen^L@T). This metric is computed in terms of percentage of coded patients predicted correctly at least once by the SVM classifier within a 12-hour window that is T hours ahead of the “code blue” event.

• Alarm Frequency Reduction Rate (AFRR). This metric is defined as AFRR = 1−FPR, where the FPR is the false positive ratio calculated as a ratio of the hourly rate of positive predictions from the SVM model to the hourly rate of monitor alarms among the control patients.

• Work-up to detection ratio (WDR). The WDR is defined as $\text{WDR}=\frac{a+b}{a}$, where a is the number of coded patients predicted correctly at least once (i.e., true positives, TPs) by the SVM classifier within a 12-hour window preceding “code blue” events, b is the number of control patients predicted incorrectly at least once (i.e., false positives, FPs) within window of the same length. The WDR measures how many FPs can be introduced using the SVM classifier when one TP is achieved.

G. Algorithm Parameter Evaluated

We studied seven T_s values with T_s ∈ {2, 4, 6, 8, 10, 12, ∞} hours, where ∞ implies that a subsequence is sampled from the beginning of monitoring to a current anchor SuperAlarm trigger. Various values are specified for the SVM parameter C ∈ {2⁻⁵, 2⁻³, …, 2¹⁵} and feature selection ratio r ∈ {10%, 20%, …, 100%}. For each T_s, optimal values of r and C are determined by performing the 10-fold CV over a 2-D grid search in terms of F₁ score.

III. Results

A. Patient Data

The same patient cohort as described in our previous study [15] was employed in this study. This cohort has a total of 254 adult patients experiencing at least one “code blue” event during their hospitalization between March 2010 and June 2012 at the University of California, Los Angeles (UCLA) Ronald Regan Medical Center and a total of 2213 control patients. Compared with a coded patient, control patients had same APR DRG (All Patient Refined Diagnosis Related Group) or Medicare DRG, the same age (±5 years), the same gender, and stayed in the same hospital unit within the same period as coded patients. Patients’ gender was male for 54% and 68% of the coded and the control patients, respectively. Average age was 61.6 ± 18.2 years and 63.5 ± 14.6 years for the coded and control patients, respectively. The analysis of the patient data was approved by the Institutional Review Board with a waiver of patient consent. The training dataset was composed of monitor alarms and laboratory test results from randomly selected 80% of both coded and control patients. Data from the remaining 20% patients were used as the independent test dataset.

B. Characteristics of Sampled Subsequences in Training Dataset

After excluding patients without any SuperAlarm triggers, the training dataset used in this study consisted of 176 coded and 1766 control patients. The independent test dataset contained data from 30 coded and 440 control patients. This test dataset is identical to the one used in our previous study [15]. By applying the subsequence generation method described in Section II-F1 with a maximal number of sampled subsequences being 60 per each coded patient and 10 per each control patient, we obtain 7174 SuperAlarm positive samples (40.76 per each coded patient) and 12522 SuperAlarm negative samples (7.09 per each control patient) in the training dataset. We apply the same protocol as used for sampling SuperAlarm subsequences to the raw alarm sequences and discretized alarm sequences. The number of positive samples and negative samples in the training dataset are 7719 (43.86 per each coded patient) and 13709 (7.76 per each control patient) for the raw alarm sequences, and 7723 (43.88 per each coded patient) and 13709 (7.76 per each control patient) for the discretized alarm sequences, respectively.

C. Offline Training Results

For a given subsequence length T_s, each combination of the SVM parameter C and feature selection ratio r is applied to train SVM model and the average F₁ score across the 10-fold CV set is employed as a performance metric for assessing this parameter combination. In addition, we select the optimal C that corresponds to the largest average F₁ at each r. Table I reports these results for each of the three types of sequences. From Table I, we can see that for a given T_s and r, average F₁ score for SuperAlarm sequence is consistently higher than that of both discretized alarm sequence and raw alarm sequence, but no difference in F₁ score could be seen between the discretized alarm sequence and raw alarm sequence. We can also observe that as T_s increases from 2 hours to ∞, r associated with the highest average F₁ is between [30–60%] for the SuperAlarm sequence, [10–80%] for discretized alarm sequence, and [10–100%] for raw alarm sequence, respectively.

TABLE I.

F₁ scores for each of the three types of sequences based on feature selection ratio r and subsequence length T_s (hours). The bold numbers indicates the highest F₁ score for a given type of sequence based on given r and T_s

Ts	Sequence Type	F1 score (%, mean±std)
		r = 10%	r = 20%	r = 30%	r = 40%	r = 50%	r = 60%	r = 70%	r = 80%	r = 90%	r = 100%
2	SuperAlarm	61.89±8.74	67.13±11.63	70.12±10.93	68.06±10.56	68.99±9.80	67.07±9.89	65.40±9.27	63.71±8.44	60.56±10.14	61.38±10.93
	Discretized Alarm	51.72±5.94	52.85±3.55	52.56±3.16	52.11±3.14	51.60±3.78	51.43±3.72	51.48±3.96	51.48±3.96	51.48±3.96	51.48±3.96
	Raw Alarm	52.90±6.82	50.11±6.15	50.71±6.27	49.79±5.99	51.27±6.42	50.93±6.68	52.00±6.00	52.16±5.41	52.54±5.12	52.54±5.12
4	SuperAlarm	68.99±12.32	62.24±8.39	66.55±9.84	69.47±7.25	69.92±8.50	66.47±8.59	65.61±9.64	63.91±10.41	61.78±11.37	62.31±10.06
	Discretized Alarm	51.72±4.56	53.55±4.00	52.91±4.57	51.71±5.44	51.89±5.13	51.67±2.87	52.32±2.41	52.32±2.41	52.32±2.41	52.32±2.41
	Raw Alarm	55.19±10.55	51.72±7.64	50.28±7.30	51.12±8.02	51.82±8.41	51.51±8.51	50.58±8.53	50.58±7.64	52.65±7.29	52.65±7.29
6	SuperAlarm	64.96±12.61	58.72±12.85	67.19±4.95	69.67±10.41	69.63±8.45	67.78±8.68	66.20±9.89	63.62±9.55	60.59±10.42	61.81±10.69
	Discretized Alarm	50.70±4.98	51.23±5.14	51.90±3.86	51.18±3.69	51.76±3.53	51.96±3.22	51.91±2.68	52.03±2.52	52.03±2.52	52.03±2.52
	Raw Alarm	56.97±10.38	50.33±8.21	50.31±6.70	51.02±7.35	51.82±7.89	51.33±7.69	51.81±7.94	52.61±8.43	52.26±7.64	52.26±7.64
8	SuperAlarm	65.08±9.46	58.86±12.37	61.85±8.85	70.94±7.02	71.64±6.52	69.10±8.82	66.95±8.98	65.35±8.65	61.09±10.35	62.18±9.77
	Discretized Alarm	52.62±4.45	51.43±4.74	52.20±4.74	50.70±5.18	51.18±4.50	51.54±3.32	52.63±2.84	52.64±2.48	52.64±2.48	52.64±2.48
	Raw Alarm	56.57±8.75	54.49±10.14	50.61±7.77	51.70±7.83	51.33±6.56	51.54±7.55	52.17±7.00	53.13±6.59	52.01±7.99	51.84±7.84
10	SuperAlarm	66.21±11.69	61.61±12.06	66.42±8.94	71.03±7.18	72.42±7.40	70.63±7.92	67.09±9.41	65.89±8.51	62.95±10.58	62.12±7.90
	Discretized Alarm	52.59±6.34	49.45±5.51	52.04±4.75	52.85±3.55	51.33±3.75	52.44±3.80	51.53±3.45	51.75±2.54	51.75±2.54	51.75±2.54
	Raw Alarm	52.53±13.56	55.21±10.57	51.98±8.03	50.76±6.99	52.76±7.41	51.71±6.22	50.89±6.91	51.78±5.03	51.54±8.14	51.85±8.04
12	SuperAlarm	67.98±12.71	64.60±11.97	68.35±7.89	71.72±5.81	71.98±7.39	71.39±8.86	66.89±8.32	66.42±10.94	64.02±10.43	63.63±8.59
	Discretized Alarm	52.04±5.32	51.03±5.87	50.58±5.34	51.99±5.07	50.89±4.84	50.91±3.68	51.05±3.13	51.09±2.58	51.09±2.58	51.09±2.58
	Raw Alarm	51.53±13.42	52.33±10.73	52.42±9.05	51.42±8.65	51.04±7.95	51.21±6.96	52.04±5.84	51.61±7.08	51.39±7.37	51.41±8.00
∞	SuperAlarm	63.15±10.69	63.07±11.24	63.13±10.10	61.81±9.72	62.96±10.12	65.36±9.98	64.47±12.00	64.14±9.31	61.79±12.34	60.60±9.98
	Discretized Alarm	52.18±9.41	49.23±9.19	50.03±8.72	47.20±8.35	46.96±7.35	48.45±8.59	45.98±10.94	45.31±11.86	44.83±10.37	44.29±10.56
	Raw Alarm	51.44±9.26	49.40±8.42	49.43±7.62	46.89±9.74	48.68±8.79	50.20±8.73	51.11±9.59	50.09±8.96	50.68±7.47	51.78±7.09

Based on the results shown in Table I, a two-way analysis of variance (2-way ANOVA) of sampling window (T_s ∈ {2, 4, 6, 8, 10, 12, ∞}) and feature selection ratio (r ∈ {10%, 20%, …, 100%}) on average F₁ score is conducted for each of the three types of sequences. The results of the 2-way ANOVA test show that for each of the three types of sequences, the main effect of feature selection ratio on average F₁ score is not significant (p > 0.05) while significant main effect of the length of sampling window on average F₁ score exists (p < 0.05). The interaction effect between these two factors is not significant (p > 0.05).

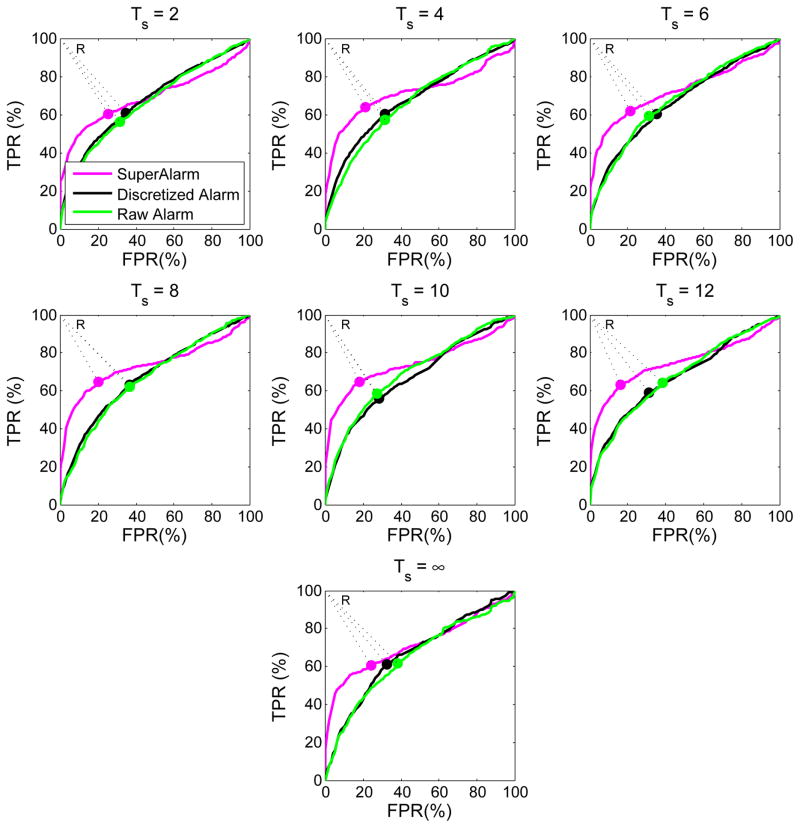
We vary the threshold to dichotomize SVM output and generate receiver operating characteristic (ROC) curves (Fig. 4) for the three types of sequences using the 10-fold CV set under their corresponding optimal algorithm parameters. We then find the optimal operating point on each ROC curve that is closest to the reference point on the upper left corner of the unit square (i.e., point R in the Fig. 4). The corresponding threshold at this optimal operating point is used as optimal SVM output threshold in the online analysis, as shown in (8).

Fig. 4.

Average ROC curves for each of the three types of sequences based on 10-fold CV set. The optimal operating point on each curve corresponds to the point closest to the reference point R.

D. Online Simulation Results

Table II lists the three performance metrics based on using optimal SVM thresholds for classification. As T_s increases from 2 hours to ∞, Sen^L@2 (sensitivity of 2-hour lead time), for instance, of the SuperAlarm sequences, discretized alarm sequences and raw alarm sequences increases by [3.33–16.67%], [6.66–16.67%] and [3.33–26.67%], respectively. Meanwhile, the AFRR decreases by [1.36–8.84%], [7.89–21.84%] and [4.23–21.75%], respectively, while the WDR increases by [0.33–1.35], [1.25–3.09] and [1.12–3.68], respectively.

TABLE II.

Results of Sen^L@T, AFRR and WDR based on SVM classifiers under optimal thresholds obtained from Fig. 4

Ts	Sequence Type	SenL @T (%)					AFRR (%, mean±std)	WDR (mean±std)
		0.5 hr	1 hr	2 hrs	6 hrs	12 hrs
2	SuperAlarm	53.33	53.33	53.33	50.00	46.67	96.20±15.84	2.32±0.19
	Discretized Alarm	93.33	90.00	90.00	83.33	80.00	57.53±23.41	11.68±0.26
	Raw Alarm	93.33	90.00	83.33	76.67	76.67	70.73±23.92	10.12±0.28
4	SuperAlarm	70.00	63.33	63.33	60.00	53.33	95.32±15.11	2.30±0.18
	Discretized Alarm	93.33	90.00	86.67	80.00	70.00	61.16±25.46	10.56±0.29
	Raw Alarm	66.67	60.00	60.00	56.67	56.67	83.80±20.16	7.88±0.38
6	SuperAlarm	76.67	70.00	70.00	70.00	63.33	95.03±16.65	2.02±0.15
	Discretized Alarm	96.67	93.33	86.67	86.67	66.67	59.55±24.39	10.74±0.27
	Raw Alarm	63.33	60.00	60.00	50.00	43.33	86.05±18.74	6.81±0.38
8	SuperAlarm	70.00	66.67	66.67	63.33	56.67	95.46±14.78	2.16±0.17
	Discretized Alarm	93.33	90.00	83.33	83.33	63.33	61.38±25.68	10.45±0.29
	Raw Alarm	60.00	56.67	56.67	50.00	43.33	86.25±18.69	6.41±0.37
10	SuperAlarm	73.33	66.67	66.67	63.33	53.33	95.80±14.72	1.94±0.15
	Discretized Alarm	93.33	90.00	86.67	83.33	66.67	68.84±26.73	8.28±0.29
	Raw Alarm	90.00	83.33	76.67	70.00	70.00	67.27±28.91	8.36±0.29
12	SuperAlarm	86.67	80.00	80.00	80.00	66.67	88.42±24.00	2.93±0.16
	Discretized Alarm	90.00	86.67	80.00	73.33	63.33	70.70±27.20	7.53±0.30
	Raw Alarm	90.00	86.67	86.67	76.67	76.67	58.97±30.54	9.11±0.28
∞	SuperAlarm	73.33	70.00	70.00	66.67	60.00	90.71±23.56	2.85±0.16
	Discretized Alarm	76.67	76.67	76.67	70.00	73.33	62.03±40.46	7.99±0.25
	Raw Alarm	90.00	86.67	86.67	86.67	86.67	51.64±41.58	8.60±0.23

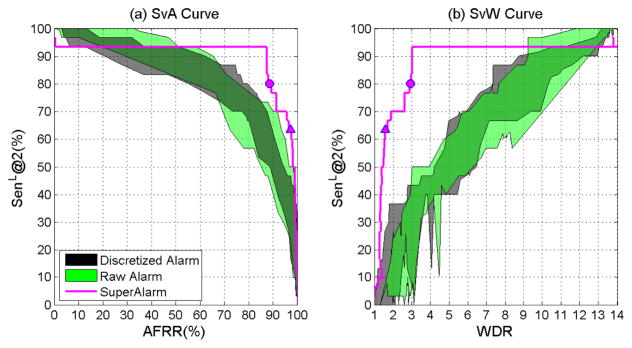
Based on results in Table II alone, it is impossible to compare the performance of the three sequences because the three performance metrics are related and yet the values of these metrics are not controlled at the same levels for comparison. To address this issue, we plot sensitivity metric against AFRR and WDR, respectively, by varying thresholds for dichotomizing SVM output. The curve thus created is termed SvA curve for sensitivity versus AFRR, and SvW curve for sensitivity versus WDR. As an examples, we create these two types of curves for Sen^L@2 for SuperAlarm sequences under the subsequence length T_s = 12 hours. Here the reason we choose the 12-hour subsequence length is because that according to Table II, given the 2-hour lead time, the SuperAlarm sequences has the highest sensitivity under the 12-hour sampling window. In addition, we plot similar curves for the raw alarm sequences and the discretized alarm sequences but under all studied sampling windows to offer a complete comparison. The results of the SvA and SvW curves are shown in Fig. 5(a) and Fig. 5(b), respectively, where the colored band corresponds to SvA and SvW curves for the raw alarm sequences and discretized alarm sequences. Comparing SvA curves, we can see that sensitivity of SuperAlarm sequence is the highest for the desirable range of high AFRR. The sensitivity of SuperAlarm sequence also remains the highest for the desirable range of low WDR. From this curve, one can see that the optimal SVM threshold could have been determined corresponding to the circle point on the SvA or SvW curve where sensitivity first reaches a plateau as AFRR decreases or WDR increases. The optimal SVM threshold as determined from the training data does not exactly match the optimal choice based on the testing data, which may not be obtainable.

Fig. 5.

(a) SvA curve: Sen^L@2 versus AFRR.(b) SvW curve: Sen^L@2 versus WDR. The ranges are displayed for discretized alarm sequences (black) and raw alarm sequences (green) under all specified subsequence lengths (from 2 hours to ∞). The curves for SuperAlarm sequences (magenta) are created based on the 12-hour subsequence length. The circle on the curve represents the pair of values obtained using the optimal SVM threshold while the triangle on the curve represents that obtained using the default SVM threshold (i.e., zero).

IV. Discussion

This study compares prediction of in hospital code blue events using sequences of SuperAlarm triggers, monitor alarms, and discretized monitor alarms. Identical sequence representation and machine learning model are used to build the classifer. Based on the results from an independent test dataset, highest sensitivity with respect to 2-hour lead time (Sen^L@2) is obtained by using the SuperAlarm sequence under a desirable range of high alarm frequency reduction rate (AFRR) or low work-up to detection ratio (WDR). Particularly, Fig. 5 shows that SuperAlarm sequence achieved 93.33% Sen^L@2 while keeping AFRR = 87.28% and WDR = 3.01. This performance is also better than what we achieved in our previous study of using individual SuperAlarm triggers to predict code blue events where Sen^L@2 was 90.0% with AFRR = 85.2% and WDR = 6.5 [15] under the same training and test datasets.

Fig. 5 clearly shows the advantage of SuperAlarm sequences to predict code blue events as compared to the raw alarm sequences and discretized alarm sequences by having a higher sensitivity under a desirable range of high AFRR or low WDR. One likely explanation for this better performance is the inherent multivariate nature of SuperAlarm patterns because each pattern is a combination of different monitor alarms and laboratory test results that can better characterize a patient’s physiological status than what a single variable can do. One could argue that sequences of raw or discretized monitor alarms also embed multivariate patterns. However, these sequences are more susceptible to false alarms. As discussed in our previous work, SuperAlarm patterns are less influenced by false alarms. For instance, a false ECG arrhythmia alarm is unlikely to have a co-occurring blood pressure alarm while clinically significant ECG arrhythmia may also compromise hemodynamic status and cause a co-occurring blood pressure alarm [37].

Comparing the triangle and circle points in Fig. 5 we can observe that adjusting SVM threshold in decision function, as shown in Equation (8), can have a significant impact on the binary prediction performance. In this study, we seek to select an optimal SVM threshold by choosing the point on the ROC curve that is closest to the ideal predictor with 100% sensitivity and 100% specificity. Nevertheless, as illustrated in Fig. 5 this optimal threshold determined from the training dataset does not exactly match the optimal choice that could have been determined using the independent test dataset. The likely contributor to this discrepancy might be due to the lack of sufficient training data that are representative of the characteristics of the testing data. Consequently, the SVM classifier with optimal threshold obtained from training data may not guarantee the same performance as that on the testing data. Determining the optimal SVM threshold in attempts to achieve the excellent prediction performance based on an imbalanced dataset remains a challenging problem. Few studies reported the adjustment of decision thresholds for machine learning algorithms based on the ROC analysis [38]–[40] and therefore further studies are needed.

All patient monitor alarms analyzed in this study were audible and contributed to the alarm fatigue problem. Since we do not include patient crisis alarms such as ventricular fibrillation (VFib) and asystole as part of SuperAlarm patterns, it would be possible to lower criticality levels of the alarms (an intervention to address alarm fatigue that has been reported) that are part of SuperAlarm patterns so that they are not audible or have fewer number of beeps on the bedside monitors but are transmitted in real-time to a backend system running SuperAlarm sequence classifier to detect patient deterioration. At a sensitivity of 93.3% of predicting “code blue” event, the alarm frequency of such a backend system would be only about 13% of the monitor alarms presumably offering a significant alleviation of alarm fatigue. Even though the current algorithm’s sensitivity is still well below 100%, it should be pointed out that the current algorithm can be easily augmented by adding back crisis alarms to offer greater sensitivity. Indeed, such a hypothetical algorithm could be adopted by the primary monitor if sensitivity is close to 100%. Another potential use case is to have this system function as a secondary patient monitor to provide additional safety net in situations where some of these non-crisis alarms may not be noticed by bedside caregivers or when their criticality levels are further lowered as an intervention to address the alarm burden.

Future work is needed to study different approaches to represent sequences, perform feature selection, and select appropriate classifier model because how these factors influence ultimate performance in detecting patient deterioration is not the focus of this work. However, the main conclusion regarding the improved performance of SuperAlarm sequence over raw and discretized monitor sequences will still hold if the improved approaches are applied in an equal fashion to these three sequences. Future studies also need to be conducted in a real-time and prospective manner to evaluate feasibility of streaming data analytics, true predictive power of the SuperAlarm approach.

V. Conclusion

We have studied the prediction of code blue events using the sequence of SuperAlarm triggers. We proposed a new method to sample subsequences from the compete sequences. We employed term frequency inverse document frequency method to represent the sequences as fixed-dimension numerical-value vectors. Information gain was used to select most relevant SuperAlarm patterns as a preprocessing step in the training phase. We applied weighted support vector machine to build the prediction model. Three metrics were assessed based on the independent test dataset in the simulation online analysis: sensitivity at different lead time choices, alarm frequency reduction rate and work up to detection ratio. Results have demonstrated that sequence of SuperAlarm triggers is more predictive than sequence of monitor alarms as it has higher sensitivity under a desirable range of high alarm frequency reduction rate or low work-up to detection ratio. Therefore, the proposed SuperAlarm sequence classifier may assist in predicting patient deterioration and reducing alarm burden.