Use of pattern recognition for unaliasing simultaneously acquired slices in Simultaneous MultiSlice Magnetic Resonance Fingerprinting

Abstract

Purpose

The purpose of this study is to accelerate a Magnetic Resonance Fingerprinting acquisition by using a simultaneous multi-slice method.

Methods

A multiband radiofrequency (RF) pulse was designed to excite two slices with different flip angles and phases. The signals of two slices were driven to be as orthogonal as possible. The mixed and undersampled MRF signal was matched to two dictionaries to retrieve T₁ and T₂ maps of each slice. Quantitative results from the proposed method were validated with the gold standard spin echo methods in a phantom. T₁ and T₂ maps of in vivo human brain from two simultaneously acquired slices were also compared to the results of MRF-FISP with a single-band RF excitation.

Results

The phantom results showed that the SMS MRF-FISP method quantified the relaxation properties accurately compared to the gold standard spin echo methods. T₁ and T₂ values of in vivo brain from the proposed method also matched the results from the normal MRF-FISP acquisition.

Conclusion

T₁ and T₂ values can be quantified at a multiband acceleration factor of two using our proposed acquisition even in a single channel receive coil. Further acceleration could be achieved by combining this method with parallel imaging or iterative reconstruction.

Introduction

Magnetic Resonance Fingerprinting (MRF) (1) is a promising method to simultaneously quantify multiple tissue properties. By pseudo-randomly varying the acquisition parameters, such as the flip angles (FA), the repetition times (TR), and the readout trajectories, the MRF framework seeks to generate spatially and temporally incoherent signal evolutions that are unique for each tissue type. A pre-calculated dictionary containing a set of expected signals is calculated based on the executed pulse sequence parameters by Bloch simulations or the extended phase graph algorithm (1–4). A pattern matching algorithm is employed to match the acquired signal to the dictionary. The tissue properties are derived from the one entry in the dictionary with the largest correlation that represents the closest signal to the acquired one. Earlier studies have shown that MRF is highly efficient in quantification of relaxation properties, and it has the potential to be extended to quantify perfusion (5,6), diffusion (7), and system parameters such as B₀ (1) and B₁+ (8). However, for a volumetric coverage where a large number of slices in a two-dimensional (2D) or a three-dimensional (3D) acquisition are needed to cover the whole region-of-interest (ROI), the total acquisition time is the acquisition time per slice multiplied by the number of slices, which could be prohibitively long for the clinical environment.

Simultaneous MultiSlice imaging (SMS) is an effective way to accelerate a volumetric acquisition by exciting and acquiring multiple slices at same time. SMS has been successfully deployed in a number of important applications including diffusion tensor imaging (DTI) (9,10) to reduce the total acquisition time, functional MRI (fMRI) (9,11) to improve the temporal resolution, as well as in cardiac and abdominal imaging (12,13) where the acquisition windows are limited by the duration of a heartbeat or a single breath-hold. Compared to conventional parallel imaging techniques (14–17) which suffer from the signal-to-noise ratio (SNR) penalty by the square-root of the acceleration rate $\sqrt{R}$, SMS acquisition does not suffer from this issue since it does not shorten the acquisition period. It actually improves SNR efficiency by $\sqrt{N}$ compared to a 2D single-slice acquisition because spins in N slices are simultaneously excited and acquired (18).

The combination of MRF and SMS would further accelerate existing MRF acquisitions. Gradient phase encoding (10,11) and radiofrequency (RF) phase encoding (12,19) are two ways to achieve slice encoding in SMS in combination with parallel imaging methods. Both methods apply a phase cycling among slices excited by a multiband RF pulse. Gradient phase encoding in SMS can be treated the same as phase encoding along the slice direction in a 3D acquisition, where the gradient imposes phase differences among slices. Similarly, the phase of each slice in SMS can also be modulated by the RF phase in a multiband RF pulse. The choice of applying either methods is dependent on the pulse sequence. Recent studies have shown the quantification of T₁ and T₂ maps from SMS-MRF at a multiband acceleration factor of two using slice-SENSE (20), and a multiband acceleration factor of three (21,22) using the combination of GROG (23) and slice-GRAPPA. Both approaches used additional gradient blips along the slice direction (G_z) in a balanced steady state free precession (bSSFP) based MRF method to create phase modulation between the simultaneously acquired slices during the acquisition. The mixed signals of multiple slices were then unaliased by the parallel imaging reconstruction. In these cases, the phase differences between the two slices generated by the G_z gradients help reduce residual signal aliasing between the slices in the parallel imaging reconstruction. A single dictionary was generated based on the acquisition parameters of the pulse sequence. Then the unmixed signal of each slice was matched to the same dictionary with different phase progressions to estimate T₁ and T₂ values.

In the bSSFP-based MRF sequence, an alternating RF phase cycle between 0 and π is required to avoid banding artifacts, which leaves the gradient phase encoding for SMS as the only option. Recently, an unbalanced gradient MRF sequence (MRF-FISP) was introduced for the quantification of relaxation properties with less sensitivity to B₀ inhomogeneities (2). Unlike the bSSFP-based MRF method, MRF-FISP has no stringent RF phase requirement, which opens the possibility to encode multiple slices through RF phase encoding.

Here we show that SMS-MRF can be further improved by varying acquisition parameters. Specifically, we show that FA and RF phases can be chosen to be different for each slice to achieve certain desired properties, such as to encode slices with the RF phase modulation and to reduce the peak RF amplitude of multiband RF pulses using different FAs. A dictionary for every slice is calculated based on the acquisition parameters specific to each slice. Compared to previous SMS-MRF methods, instead of using parallel imaging methods to unalias the signals from the simultaneously acquired slices, the proposed method employs a pattern recognition approach to distinguish the signal evolutions of each slice from the mixed signal, and quantitative T₁ and T₂ maps of each slice can be retrieved directly from the mixed signal. Therefore this method can separate the mixed signal even with a single channel receive coil, and the distance between the simultaneously acquired slices does not matter. It provides an additional dimension of flexibility on the sequence design, which could potentially improve temporal incoherence of the signals and facilitate signal separation.

In this study, this approach at a multiband acceleration factor of two was explored. T₁ and T₂ values from the proposed method were validated with the gold standard spin echo methods in a phantom study. T₁ and T₂ maps from two simultaneously acquired slices were also compared to the results of MRF-FISP with single-band RF excitation in human brain.

Methods

Pulse Sequence

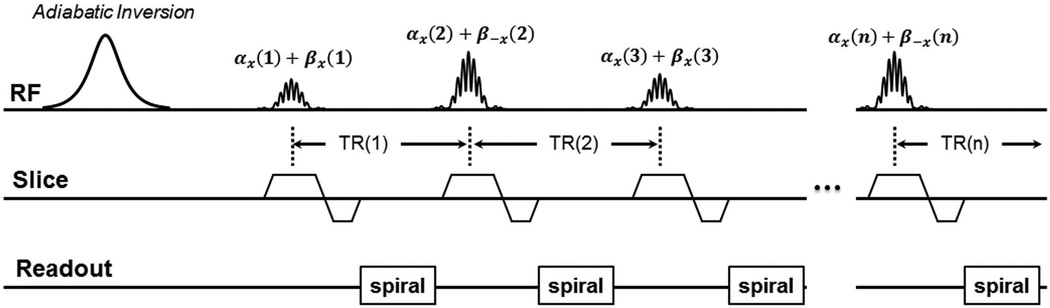
Figure 1 shows a diagram of the SMS MRF-FISP pulse sequence. The pulse sequence structure is similar to that of original MRF-FISP (2) except that an RF pulse train at a multiband factor of two was used to excite two slices simultaneously with different FAs and RF phases. The multiband pulse is a summation of two sinc waveforms with different amplitudes and phases according to

$$R{F}_{MB}(t)=a·\mathit{\text{sinc}}(t)·e^{i\mathrm{\Delta }{\omega }_{1}t+{\phi }_1}+b·\mathit{\text{sinc}}(t){·}^{i\mathrm{\Delta }{\omega }_{2}t+{\phi }_2}$$ [1]

$$\mathrm{\Delta }{\omega }_2-\mathrm{\Delta }{\omega }_1=2\pi \gamma G_{s}D$$ [2]

where a and b are the scaling factors that adjust the amplitudes of the sinc waveforms to achieve different FAs (α(n) and β(n) in Figure 1) for two slices at each time point n; Δω₁ and Δω₂ are the frequency shifts for exciting two slices at different locations; φ₁ and φ₂ are the RF phases. The difference between Δω₁ and Δω₂ needs to satisfy Eq. [2], where γ is the gyromagnetic ratio; G_s is the amplitude of the slice selection gradient; and D is the distance between the two simultaneously excited slices.

Figure 1.

A diagram of SMS MRF-FISP sequence. An RF pulse train at a multiband factor of two was used to excite two slices simultaneously with different flip angles ((α(n) and β(n)) and RF phases at each time point n.

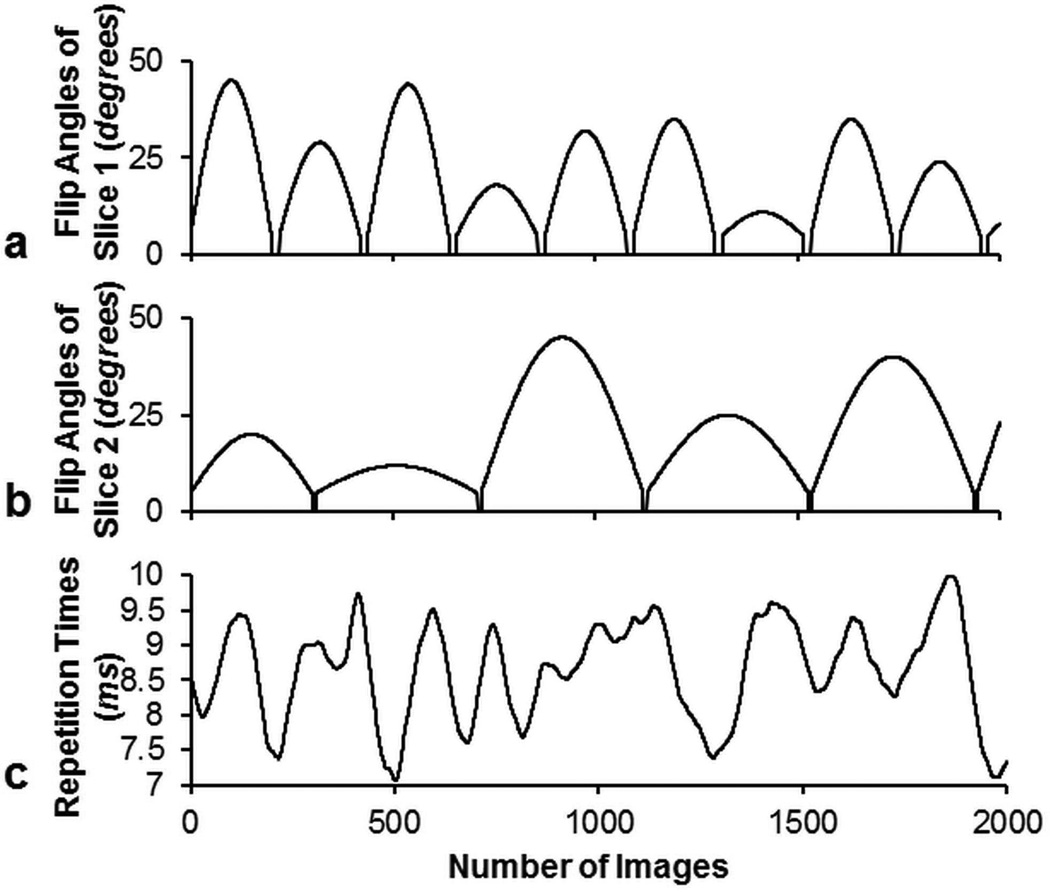
The scaling factors a and b in Eq. [1] were varied at every time point in the acquisition to achieve different FA patterns for different slices. For a multiband acceleration factor of two demonstrated in this work, one slice was excited by a FA pattern as shown in Figure 2a with the RF phase φ₁ of zero degrees, while the other slice was excited by a FA pattern as shown in Figure 2b with RF phase φ₂ alternating between 0 and π from time point to time point. In this work, a normal RF pulse and slice selection gradient were used instead of using the variable-rate selective excitation (VERSE) (24) technique. VERSE uses a time varying slice selection gradient along with a corresponding modified RF waveform to excite the same slice as would be excited with a constant gradient, as long as the spins are on resonance. In the previous studies (20–22), VERSE was used to reduce the peak B₁, since the same FA was used to excite two or three slices at each time point. In this study, different FAs for multiple slices helped reduce the peak B₁ at each time point, thus the VERSE slice selection gradient was not necessary. This should in return improve the achieved off-resonance slice profile. The repetition times were generated by a Perlin noise pattern (25) and varied between 7 and 10 ms as shown in Figure 2c. Such a Perlin noise pattern has been used since the original MRF presentation to generate smoothly varying TR patterns which can provide additional T₁ and T₂ weighting beyond what can be achieved with just the varied FAs alone. The choice of the TR pattern is dependent on the sequence design. Other studies showed that other smoothly varying TR patterns (26) or a constant TR (8,27) could also work in MRF acquisitions. An adiabatic inversion pulse with an inversion time (TI) of 20.64 ms was used at the beginning of the pulse sequence. For each time point, the echo time (TE) was fixed at 2.2 ms.

Figure 2.

Flip angles for the first slice (a), the second slice (b), and the repetition times (c) used in the SMS MRF-FISP acquisition.

In this study, the MRF-FISP sequence acquired data using a uniform density spiral trajectory with zeroth moment compensation. The spiral trajectory was designed with 48 interleaves to fully sample k-space using a freely available program (http://mrsrl.stanford.edu/~brian/vdspiral/). The spiral trajectory was designed to have a field-of-view (FOV) of 30 cm with a matrix size of 256 × 256. One spiral interleaf was used to acquire data per time point. The interleaf was rotated by 7.5° every time point to shift the aliasing artifacts into different positions along the time course. 2000 time points were acquired to achieve a higher in-plane resolution (1.2 × 1.2 mm²) in this study as compared to 2.4 × 2.4 mm² in the previous studies (20–22). The scan time was 18 seconds for both the SMS MRF-FISP and the single slice MRF-FISP, with the SMS version providing data from two slices in this time.

Dictionary and Pattern Recognition

Two dictionaries were simulated by Bloch simulations according to the acquisition parameters of each slice. The dictionaries had the same T₁ and T₂ ranges. The range, denoted as min:step:max, of T₁ was [10:10:90, 100:20:1000, 1040:40:2000, 2050:100:3000] ms, and of T₂ was [2:2:8, 10:5:100, 110:10:300, 350:50:800] ms. Dictionaries had a total of 4,141 entries that excluded the unrealistic T₂ > T₁ combinations.

A pattern matching was performed by taking a complex dot product between the measured mixed signal time course and all entries of two dictionaries. T₁ and T₂ values of each slice were derived from the entry with the largest correlation that represents the closest signal to the acquired signal time course.

Phantom Experiments

All experiments were performed on a Siemens MAGNETOM Skyra 3 Tesla (T) scanner (Siemens AG Healthcare, Erlangen, Germany).

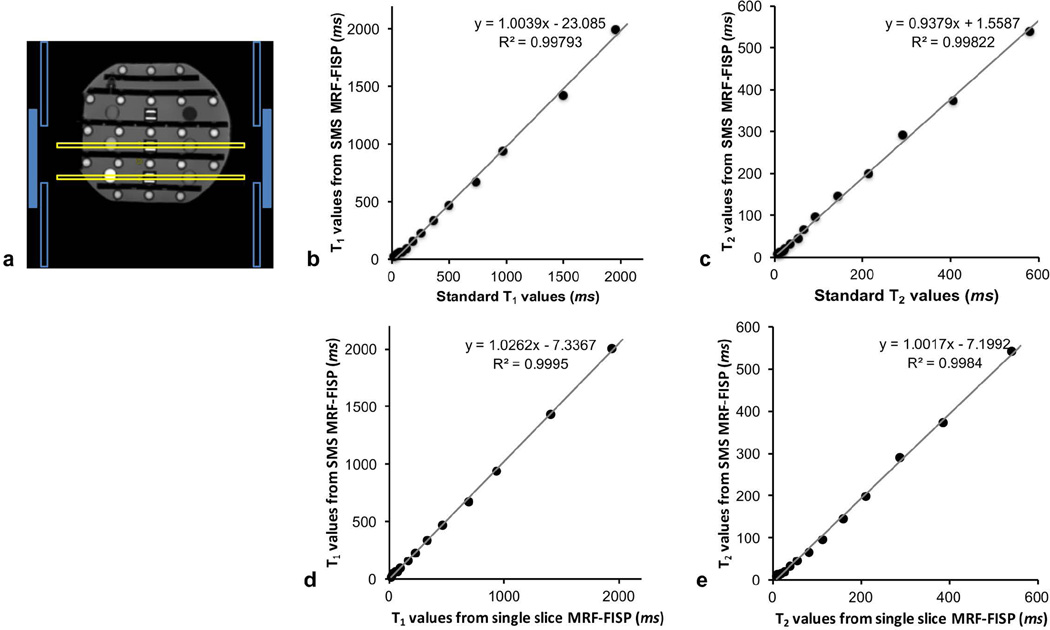
The ISMRM/NIST MRI system phantom, developed through the collaboration between the ISMRM ad-hoc committee on Standards for Quantitative Magnetic Resonance and National Institute of Standards and Technology (NIST) (28), was scanned using a 20-channel head-neck array coil. The phantom has multiple layers of sphere arrays that have a range of T₁, T₂, and proton density values. The 20-channel head-neck array coil used in the experiment has 3 rings of coils that were geometrically placed along the slice direction. Two rings with 8 channels each were the head elements, and one ring with 4 channels was the neck element. To demonstrate that the proposed method does not require the coils to be geometrically placed along the slice direction to separate the mixed signal, T₁ and T₂ arrays with a gap of 40 mm were excited simultaneously using the body coil, and one ring (eight channels) of the head elements that have the same geometrical position along the slice direction was selected to receive the signal. Figure 3a shows an illustration of the slice positions (hollow yellow rectangles) and the coil geometry (blue rectangles). The solid blue rectangles represent the channels selected to receive the signal, and the hollow blue rectangles are the channels that were not selected.

Figure 3.

a) The reference image for the coil selection in the phantom experiment. One ring of the coil arrays (solid blue rectangles) that has the same geometrical location along the slice direction was selected for receiving the signals from two slices (hollow yellow rectangles) simultaneously. The correlation plots compare T₁ values quantified by SMS MRF-FISP with those from IR-SE (b), T₂ values from SMS MRF-FISP with those from multiple single-echo spin echoes (c), T₁ values from SMS MRF-FISP with those from single slice MRF-FISP method (d) and T₂ values from SMS MRF-FISP with those from single slice MRF-FISP (e).

A series of images were reconstructed using NUFFT (29) that was provided in Fessler’s Imaging Reconstruction Toolbox (http://web.eecs.umich.edu/~fessler/irt/irt/) after noise prewhitening (30). The sensitivity map was estimated from the time-averaged image of the slice with RF phase of zero degrees. The mixed images of 2 slices from multiple coils were combined using the Walsh method (31) before applying the pattern recognition algorithm to retrieve the quantitative T₁ and T₂ maps for each slice.

To validate T₁ and T₂ values quantified by the proposed method, an inversion recovery spin echo (IR-SE) was used to scan the T₁ array with seven TIs of 21, 100, 200, 400, 800, 1600 and 3200 ms, a TR of 10 seconds, a TE of 12 ms, a 128 × 128 matrix, a FOV of 17 cm, and a slice thickness of 5 mm. A multiple single-echo spin echo method was used to scan the T₂ array with seven TEs of 12, 22, 42, 62, 102, 152 and 202 ms, a TR of 10 seconds, a matrix size of 128 × 128, a FOV of 21 cm, and a slice thickness of 5mm. The scan time was 2.5 hours for either T₁ or T₂ measurement. The magnitude of images from the IR-SE and multiple single-echo spin echo were fitted to S(TI) = a − be^−TI/T₁ to calculate T₁ values and to S(TE) = ae^−TE/T₂ to calculate T₂ values, respectively.

To compare T₁ and T₂ values from the proposed method to ones derived from the conventional single slice MRF method, T₁ and T₂ arrays in the ISMRM/ISMRM MRI system phantom were also scanned separately by a FISP-based MRF acquisition (2,32).

Circular ROIs were manually drawn on each sphere in the T₁ or T₂ map. The standard T₁ or T₂ values were averaged over 50 pixels in ROIs on the maps derived by the gold standard methods. T₁ or T₂ values from the proposed method were averaged over 75 pixels in each ROI on the maps of the SMS MRF-FISP and the single slice MRF-FISP. Higher spatial resolution in the maps of the MRF method allowed more pixels to be included in the ROI.

In vivo Experiments

All in vivo experiments were performed after written informed consent in a single volunteer. For brain imaging, the acquisition parameters were the same as the ones used for the phantom. Two slices with a gap of 40 mm were simultaneously excited by the body coil. One ring of the head array coil received the mixed signal. These two slices were also acquired by the MRF-FISP acquisition with a single-band RF pulse for comparison.

ROIs at different regions in gray matter (GM) and white matter (WM) were manually drawn in T₁ and T₂ maps to compare the results from SMS MRF-FISP to the results from the single slice MRF-FISP.

Results

T₁ values of the phantom from the proposed method were plotted against the standard values from IR-SE in Figure 3b. It displays a strong linear correlation (R² = 0.998). The linear fit has a slope of 1.004 and a y-intercept of 23.08 ms. Figure 3c shows T₂ values from SMS MRF-FISP plotted against the standard T₂ values from multiple single-echo spin echo method. The linear fit also shows a strong linear correlation (R₂ = 0.998) with a slope of 0.938 and a y-intercept of 1.56 ms.

T₁ and T₂ values estimated from SMS MRF-FISP were also plotted against the values from the single slice MRF-FISP method in Figure 3d and 3e, respectively. The linear fits for T₁ and T₂ show strong linear correlations (R² = 0.999 for T₁ and R² = 0.998 for T₂). The linear fit of T₁ values has a slope of 1.03 and a y-intercept of −7.34 ms. The linear fit of T₂ values has a slope of 1.00 and a y-intercept of −7.2 ms.

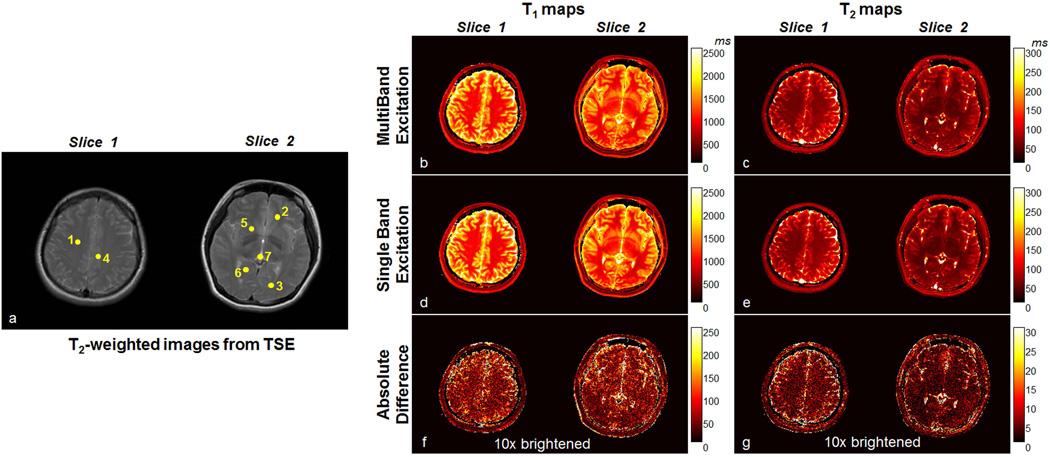
Figure 4 shows representative results from the volunteer. Figure 4a shows T₂-weighted images acquired by turbo spin echo (TSE) for indicating the positions of ROIs drawn on the maps in Table 1. Figure 4b and 4c show the T₁ and T₂ maps of two slices simultaneously acquired in the brain from the proposed SMS MRF-FISP acquisition. For comparison, the T₁ and T₂ maps of the same two slices acquired separately by the normal MRF-FISP are shown in Figure 4d and 4e. The absolute differences between the maps from SMS MRF-FISP and those from the normal MRF-FISP acquisition are shown in Figure 4f and 4g. These two images have been rescaled by a factor of 10 to amplify the difference to help visualization.

Figure 4.

a) T₂-weighted anatomical images for indicating the positions of ROIs (yellow dots) drawn on the T₁ and T₂ maps to compare the results from SMS MRF-FISP to the results of the single-band MRF-FISP method shown in Table 1. b) T₁ maps and c) T₂ maps of two slices simultaneously acquired by the proposed method, d) T₁ maps and e) T₂ maps of two slices separately measured by the single-band MRF-FISP method. The absolute difference between f) T₁ and g) T₂ maps from two methods are rescaled by a factor of 10 to amplify the difference for visualization.

Table 1.

T₁ and T₂ values derived from 2 slices that were acquired simultaneously by SMS MRF-FISP compared to those acquired separately by MRF-FISP with a single band RF pulse in regions of white matter and gray matter in one representative volunteer. The ROIs are displayed in Figure 4a.

		T1 (ms)		T2 (ms)
		SMS	Single slice	SMS	Single slice
WM	Centrum semiovale (1)	898 ± 44	902 ± 26	47 ± 4	49 ± 3
	Frontal WM (2)	846 ± 29	864 ± 26	38 ± 3	36 ± 2
	Occipital WM (3)	806 ± 22	787 ± 35	46 ± 5	46 ± 5
GM	Cingulate sulcus (4)	1534 ± 87	1597 ± 90	85 ± 11	92 ± 14
	Putamen (5)	1390 ± 28	1341 ± 55	51 ± 7	53 ± 6
	Occipital GM (6)	1645 ± 85	1688 ± 108	59 ± 8	62 ± 10

T₁ and T₂ values at different regions in GM and WM estimated from the SMS MRF-FISP method and the normal MRF-FISP are listed in Table 1, which shows that the proposed method’s T₁ and T₂ values in GM and WM are similar to those from MRF-FISP acquisition with a single-band RF pulse.

Discussion

Here we introduced a SMS MRF-FISP method using different RF pulse (FA and phase) patterns for each slice. Unlike previous methods that relied on a combination of G_z slice-encoding and the parallel imaging for slice separation, the method shown here allows one to estimate relaxation properties from simultaneously acquired slices directly through the normal MRF pattern recognition algorithm. Besides the potential improvement in reconstruction time, by changing flip angles and RF phases from time point to time point for each slice, the signals of two slices can be made to be nearly orthogonal. While only 0 and π phase modulation is used for separation of 2 slices in the current work, other phase modulations such as 0, 2/3π, and −2/3π phase modulation for 3 slices (10) or the phase modulation based on the Hadamard matrix (33,34) for more slices could also be implemented in the proposed method. In addition, the ability to modulate the FAs differently in each slice provides key opportunities to reduce the peak RF power, while still maintaining the ability to separate the individual slices. The current work achieved the excitation of two slices without having to rely on VERSE to reduce the RF peak power as used in previous studies (20–22). While we showed one empirically chosen RF FA pattern in this work, future work can further minimize the peak RF power by modulating the phase of RF pulse (35) as well the RF amplitude to achieve higher multiband acceleration factors. This study showed that a multiband acceleration factor of two can be achieved with in-plane acceleration rate of 48 in each time point without using parallel imaging reconstruction. The proposed method has the potential to be combined with the recently proposed SMS-MRF methods using parallel imaging (20–22) and iterative reconstructions (36–38) to acquire even more slices simultaneously.

The current approach also provides an alternative to accelerating the MRF acquisition that is based on the gradient spoiled sequence structure. Compared to the previously proposed bSSFP-based SMS-MRF sequence, the proposed method does not suffer from the banding artifacts that appear in bSSFP due to off-resonance. This advantage could lead to the extension of the proposed method to other applications where it is difficult to obtain a homogeneous B₀ field, such as in cardiac, abdominal, or pelvic imaging.

The phantom results showed that the relaxation properties quantified by the proposed SMS MRF-FISP have a strong correlation to the results of the traditional spin echo methods over wide ranges of T₁ and T₂ values. T₁ values in the ISMRM/NIST MRI system phantom range from 20 ms to 2000 ms. The linear fit of T₁ had the slope of 1.004. T₂ values in the phantom range from 6 ms to 580 ms. The slope of 0.938 in the T₂ trend line was mainly affected by two spheres that have T₂ values larger than 400 ms. The slope would be 0.985 if these two spheres were excluded. The in vivo brain images showed that the simultaneously acquired T₁ and T₂ values were in the range of reported values in the literature. The differences in either T₁ or T₂ between the SMS MRF-FISP and the single slice MRF-FISP in various ROIs are within the resolution of the dictionary. The most noticeable differences were located in the CSF and at the edge of the brain. This could be caused by the varied flow and pulsation in the CSF and possible head movement from the volunteer during 3 separate scans.

Conclusion

We proposed and validated a SMS-MRF approach that employs varying flip angles and phases between slices to generate mixed signals that are separable directly through the pattern recognition algorithm. The additional degrees of freedom provided by this method allows for reduction of the peak SAR and voltage through different excitation patterns in the simultaneously acquired slices. Accurate quantification of T₁ and T₂ was shown at a multiband acceleration factor of two. Further acceleration could be achieved by incorporating parallel imaging or iterative reconstruction.