Secondary phenotype analysis in ascertained family designs: application to the Leiden longevity study

Abstract

The case‐control design is often used to test associations between the case‐control status and genetic variants. In addition to this primary phenotype, a number of additional traits, known as secondary phenotypes, are routinely recorded, and typically, associations between genetic factors and these secondary traits are studied too. Analysing secondary phenotypes in case‐control studies may lead to biased genetic effect estimates, especially when the marker tested is associated with the primary phenotype and when the primary and secondary phenotypes tested are correlated. Several methods have been proposed in the literature to overcome the problem, but they are limited to case‐control studies and not directly applicable to more complex designs, such as the multiple‐cases family studies. A proper secondary phenotype analysis, in this case, is complicated by the within families correlations on top of the biased sampling design. We propose a novel approach to accommodate the ascertainment process while explicitly modelling the familial relationships. Our approach pairs existing methods for mixed‐effects models with the retrospective likelihood framework and uses a multivariate probit model to capture the association between the mixed type primary and secondary phenotypes. To examine the efficiency and bias of the estimates, we performed simulations under several scenarios for the association between the primary phenotype, secondary phenotype and genetic markers. We will illustrate the method by analysing the association between triglyceride levels and glucose (secondary phenotypes) and genetic markers from the Leiden Longevity Study, a multiple‐cases family study that investigates longevity. © 2017 The Authors. Statistics in Medicine Published by JohnWiley & Sons Ltd.

1. Introduction

In order to understand biological mechanisms underlying disease and health, epidemiological studies measure genetic markers, classical variables, and novel omics datasets and model the relationship between these variables and the phenotype of interest. Here, we consider outcome‐dependent sampling designs with binary outcome variables. In addition to studying these binary (primary) phenotypes, the classical or omics variables are typically also analysed as outcome variables (secondary phenotypes). For example, modelling of associations between these traits and genetic factors, such as single‐nucleotide polymorphisms (SNPs) or polygenic risk scores (sumscores based on SNPs) 1. However, an important complication that is often ignored is that a proper analysis of the secondary traits should correct for the sampling mechanism on the primary phenotype (Figure 1). Note that we assume that the secondary phenotype has an effect on the primary phenotype. The reverse situation will not be treated because of reverse causality challenges 2. In our motivating case study, the Leiden Longevity Study (LLS) 3 families with at least two long‐lived siblings are recruited. Obviously, these families do not represent a random sample from the population and inferences cannot be generalized to the whole population, unless the sampling mechanism is properly modelled. Several datasets are measured in the offspring of the long‐lived siblings, namely, lipidomics, glycomics, metabolomics and imaging. These offspring share a part of their genetic variation with the long‐lived parent and therefore are expected to represent a healthy subpopulation while the partners represent the population. As data example, we will model the effect of genetic factors on the secondary traits glucose and triglyceride levels in the offspring (cases) and their partners (controls). To be able to extrapolate results to the general population, we need to account for the over sampling of long‐lived subjects in the families of the LLS. There are several multiple‐case family studies. For human longevity, Genetics of Healthy Ageing 4 used the same study design as the LLS. Other examples are Genetics in Familial Thrombosis (with at least two cases with thrombosis) 5, 6 and the ongoing study from Leiden Family Lab (famlab: https://www.leidenfamilylab.nl), which recruits families with at least two cases with social anxiety disorder. The novel methods presented in this paper will also be essential for modelling secondary phenotypes in these studies.

Figure 1.

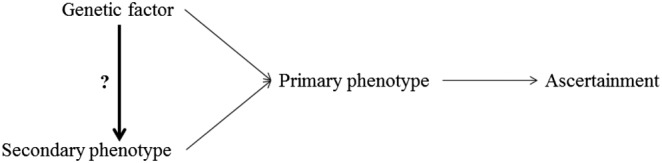
Directed acyclic graph representing the case where bias is expected when estimating the association between the genetic marker and the secondary phenotype. Arrows represent existing association between each node of the graph. A secondary phenotype analysis investigates whether there is an association between the genetic factor and the secondary phenotype.

In the context of case‐control studies, Monsees et al. 2 showed that bias can occur when estimating the SNP effect on secondary phenotypes if the primary and secondary phenotypes are associated. This is often the case because both outcomes are measured on the same subjects and secondary phenotypes are typically chosen for their potential associations with the primary phenotype. They also showed that the amount of bias is dependent on the prevalence of the primary phenotype, the strength of the association between the primary and secondary phenotypes, and the association between the tested marker and the primary trait (Figure 1).

To deal with the bias problem, investigators first used ad hoc methods, that is, using controls only, cases only, combined data of cases and controls or joint analysis of cases and controls adjusting for the case‐control status. However, several authors showed that these simple approaches can lead to false positive results 2, 7, 8. This is due to the sampling design, namely, the secondary phenotype data are not sampled according to the case‐control design as the primary phenotype. Several sophisticated methodologies have been developed to correct for the sampling mechanisms and provide unbiased genetic effect estimates: (i) inverse‐probability‐of‐sampling‐weighting approaches 2, 9, 10 that correct for the sampling mechanism by weighting appropriately individuals in case‐control studies; (ii) retrospective likelihood‐based approaches that indirectly adjust for ascertainment 8, 11; and (iii) a weighted combination of two estimates obtained with the retrospective likelihood approach in the presence or not of an interaction between SNPs and primary phenotypes 12.

Even though these approaches can successfully correct for the biased design used to collect the data, they are not directly applicable to more complex designs such as the LLS that motivates this work. In particular, inverse probability weighting approaches require knowledge of the sampling weights for each family. These weights are not available for the LLS because it is unknown what the prevalence of families with at least two nonagenarians is in the population. In addition, the correlations between the family members cannot be ignored, and therefore, it is evident that statistical methodology for proper secondary phenotypes analysis in this context is needed. To this end, under the retrospective likelihood framework, we develop a multivariate probit regression model inspired by the work of Najita et al. 13 to model jointly the distribution of the primary and secondary phenotype. This approach allows us to deal with the ascertainment issue while taking into account the individual relatedness and the genetic and environmental variations.

The paper is organized as follows: in Section 2, we present the retrospective likelihood approach to correct for the over sampling of long‐lived subjects and the multivariate probit regression model for the joint modelling of the mixed type primary and secondary phenotypes. In Section 3, we evaluate empirically the performance of the method in terms of bias and efficiency and contrast it with the naive approach that ignores the sampling mechanism. Finally, in Section 4, we illustrate the potential of our proposed method in the analysis of triglyceride levels and glucose in the LLS.

2. Methods

2.1. Retrospective likelihood approach

Let N be the total number of families in the study. For the family i(i=1…N) of size n _i, let Y _i, X _i and G _i be the n _i×1 vectors for the case‐control status, the secondary phenotype and the genotype, respectively. Motivated by the LLS, we will work under the retrospective likelihood approach to correct for the ascertainment of the families. Such an approach is attractive when modelling the ascertainment mechanism is not straightforward, as in the LLS where sampling depends on the previous generation (an example of a pedigree in LLS is shown in Figure 2). In fact the retrospective likelihood approach implicitly corrects for the ascertainment mechanism, under the assumption that the ascertainment depends only on the primary phenotype Y. In particular, for the ith family it holds

$$P\left(X_i,G_i|Y_i,Asc\right)=\frac{P\left(Asc|Y_i,G_i,X_i\right)P\left(G_i,X_i|Y_i\right)}{P\left(Asc|Y_i\right)}=P\left(X_i,G_i|Y_i\right),$$ (1)

with A s c the ascertainment process. By applying Bayes' rule, we obtain

$$P\left(X_i,G_i|Y_i\right)=\frac{P\left(X_i,Y_i|G_i\right)P\left(G_i\right)}{P\left(Y_i\right)}=\frac{P\left(X_i,Y_i|G_i\right)P\left(G_i\right)}{\sum _{g\in G}P\left(Y_i|g\right)P\left(g\right)}.$$ (2)

To fully specify (2), we need to model properly the conditional joint distribution of the primary and the secondary phenotypes given the genotype P(X _i,Y _i|G _i), the marginal probability of the primary phenotype P(Y _i|G _i) and the genotype probability of the ith family P(G _i). Each one of these elements are described in Sections 2.2 and 2.3.

Figure 2.

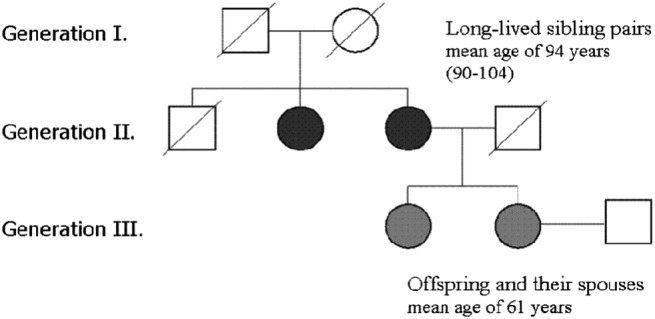
Example of a family pedigree from the Leiden Longevity Study. Squares and circles represent men and women, respectively; crossed symbols represent deceased individuals. In black are the long‐lived individuals on whom the ascertainment is based; in grey are the cases of the study (offsprings of long‐lived siblings), and in white are the controls.

2.2. Mixed‐effects models for the analysis of family data

To model the correlation of the phenotypes Y and X within families, a common choice is to use random effects. For the binary primary phenotype, we propose to use a multivariate probit model with random effects. The advantage of this model is that it involves only the integrals of the multivariate normal cumulative distribution function for which efficient algorithms have been developed. In contrast, for the more commonly used logistic regression model, the integrals have to be approximated, for example, by using Gauss–Hermite quadrature, which might be computationally intensive for large pedigrees. Let $b_i^Y={\left(b_{i1}^Y,\dots ,b_{i{n}_i}^Y\right)}^T$ be a set of family‐specific random effects designed to handle familial genetic correlation and $G_i={\left(g_{i1},\dots ,g_{i{n}_i}\right)}^T$ be the vector of genotypes for family i. For the probit model, the observed response Y is viewed as a censored observation from an underlying continuous latent variable Y ^∗ with

$$Y_{ij}=y_{ij}\iff {\gamma }_{y_{ij}}<Y_{ij}^{\ast }<{\gamma }_{y_{ij}+1},Y_{ij}\in \{0,1\},j=1,2,\dots ,n_i$$

where −∞=γ ₀<γ ₁<γ ₂=+∞ are suitable threshold parameters. For the underlying latent variable Y ^∗, we assume the mixed‐effects regression model

$$Y_i^{\ast }={\alpha }_0+{\alpha }_1{G}_i+{\sigma }_{G_Y}{b}_i^Y+\sigma {ϵ}_i^Y,$$

where ${ϵ}_i^Y\sim N_{n_i}(0,I_{n_i})$ is independent of $b_i^Y$. Here, α=(α ₀,α ₁) denotes the regression coefficient vector with α ₀ the intercept and α ₁ the parameter representing the effect of the genotype on Y. At the family level, we assume $b_i^Y\sim N_{n_i}(0,{\mathbf{R}}_i)$, with R _i the coefficient of relationships matrix with elements $r_{lm}=2^{-d_{lm}}$ with d _lm denoting the genetic distance between subjects l and m in the family. The parameter ${\sigma }_{G_Y}$ represents the residual additive genetic variation not explained by g _ij. Note that ${\sigma }_{G_Y}$ models the polygenic inheritance in a family. For identifiability reasons, restrictions are required on both the scale and location of Y ^∗, namely, we set σ ²=1 and γ ₁=0. Thus, in the mixed‐effects probit regression, the disease risk ${\pi }_{ij}=P(Y_{ij}=1|b_{ij}^Y,g_{ij})$ conditional on the random‐effects $b_{ij}^Y$ and genotypic information g _ij is modelled as follows

$$P\left(Y_{ij}=1|g_{ij},b_{ij}^Y\right)=\mathrm{\Phi }\left({\alpha }_0+{\alpha }_1{g}_{ij}+{\sigma }_{G_Y}{b}_{ij}^Y\right),$$ (3)

with Φ(z) the cumulative distribution function of the standard normal distribution. The marginal density under the probit model takes the form:

$$f\left(y_{ij}\right|g_{ij};\alpha ,{\sigma }_b)={\int }_{b_i^Y}{\int }_{{\gamma }_{y_{ij}}}^{{\gamma }_{y_{ij}}+1}f(y_{ij}^{\ast }|g_{ij},b_i^Y;\alpha ,{\sigma }_b)f\left(b_i^Y\right)d{y}_{ij}^{\ast }d{b}_i^Y.$$

To model the secondary phenotype X _i, we use a linear mixed model:

$$X_i={\beta }_0+{\beta }_1{G}_i+{\sigma }_{G_X}{b}_i^X+{\sigma }_{ϵ}{ϵ}_i^X,$$ (4)

where β=(β ₀,β ₁) denotes the regression coefficient vector with β ₀ the intercept and β ₁ the parameter representing the effect of the genotype on X, $b_i^X\sim N_{n_i}(0,{\mathbf{R}}_i)$ is the random parameter used to model the genetic correlation structure within each family for the secondary trait, and σ _ϵ is the residual standard deviation.

To model jointly X and Y using the model specifications ((3) and (4)), we introduce a shared random effect u _ij∼N(0,1) and propose the following model:

$$\begin{array}{ccc}\hfill Y_i^{\ast }& ={\alpha }_0+{\alpha }_1{G}_i+{\sigma }_{G_Y}{b}_i^Y+{\sigma }_u{u}_i+{ϵ}_i^Y,\hfill & \hfill \\ \hfill X_i& ={\beta }_0+{\beta }_1{G}_i+{\sigma }_{G_X}{b}_i^X+\delta {\sigma }_u{u}_i+{\sigma }_{ϵ}{ϵ}_i^X,\hfill \end{array}$$ (5)

where u _i is assumed to be independent of $b_i^Y,b_i^X,{ϵ}_i^Y$ and ${ϵ}_i^X$. We introduce a coefficient δ in order to have different phenotypic variances for the random effect u _i. In case of small datasets or small family sizes, it can be better to constrain δ to be equal to 1 for a simpler model. Let ${\mathrm{\Sigma }}_{X_i}$ and ${\mathrm{\Sigma }}_{Y_i^{\ast }}$ denote the corresponding variance–covariance matrices of the marginal distributions of X _i and $Y_i^{\ast }$, and let ${\mathrm{\Sigma }}_{X{Y}_i^{\ast }}$ be their covariance. The joint distribution of Y ^∗ and X is then $\left(Y_i^{\ast },X_i\right)\backsim {\mathcal{N}}_{2n_i}\left(\left[\begin{array}{c}{\alpha }_0+{\alpha }_1{G}_i\\ {\beta }_0+{\beta }_1{G}_i\end{array}\right],\left[\begin{array}{cc}{\mathrm{\Sigma }}_{Y_i^{\ast }}& {\mathrm{\Sigma }}_{X{Y}_i^{\ast }}\\ {\mathrm{\Sigma }}_{X{Y}_i^{\ast }}& {\mathrm{\Sigma }}_{X_i}\end{array}\right]\right)$. In the special case for n _i=2, the variance–covariance matrix becomes

$${\mathrm{\Sigma }}_i=\left(\begin{array}{cccc}{\sigma }_{G_Y}^2+{\sigma }_u^2+1& {\sigma }_{G_Y}^2{2}^{-d(1,2)}& {\sigma }_{G_X}{\sigma }_{G_Y}+\delta {\sigma }_u^2& {\sigma }_{G_X}{\sigma }_{G_Y}{2}^{-d(1,2)}\\ {\sigma }_{G_Y}^2{2}^{-d(1,2)}& {\sigma }_{G_Y}+{\sigma }_u^2+1& {\sigma }_{G_X}{\sigma }_{G_Y}{2}^{-d(1,2)}& {\sigma }_{G_X}{\sigma }_{G_Y}+\delta {\sigma }_u^2\\ {\sigma }_{G_X}{\sigma }_{G_Y}+\delta {\sigma }_u^2& {\sigma }_{G_X}{\sigma }_{G_Y}{2}^{-d(1,2)}& {\sigma }_{G_X}^2+{\delta }^2{\sigma }_u^2+{\sigma }_{ϵ}^2& {\sigma }_{G_X}^2{2}^{-d(1,2)}\\ {\sigma }_{G_X}{\sigma }_{G_Y}{2}^{-d(1,2)}& {\sigma }_{G_X}{\sigma }_{G_Y}+\delta {\sigma }_u^2& {\sigma }_{G_X}^2{2}^{-d(1,2)}& {\sigma }_{G_X}^2+{\delta }^2{\sigma }_u^2+{\sigma }_{ϵ}^2\end{array}\right).$$ (6)

Using the properties of the multivariate normal distribution, the joint distribution for the observed primary and secondary phenotypes takes the form

$$\begin{array}{ccc}\hfill P\left(Y_i,X_i|G_i\right)& =\int P\left(Y_i^{\ast },X_i|G_i\right)d{y}_i^{\ast }\hfill & \hfill \\ \hfill & =\int P\left(Y_i^{\ast }|X_i,G_i\right)P\left(X_i|G_i\right)d{y}_i^{\ast }\hfill \\ \hfill & =P\left(X_i|G_i\right)\int P\left(Y_i^{\ast }|X_i,G_i\right)d{y}_i^{\ast }.\hfill \end{array}$$

Thus by using the probit regression model for the primary trait, we have developed an efficient approach to model the correlation between the primary and secondary trait.

From model (5) and the variance–covariance matrix (6), several marginal correlations between and within family members can be deduced:

$$\begin{array}{ccc}\hfill cor\left(X_{ij},X_{i{j}^{\prime }}\right)& =\frac{{\sigma }_{G_X}^2{2}^{-d\left(j,j^{\prime }\right)}}{\left({\sigma }_{G_X}^2+{\delta }^2{\sigma }_u^2+{\sigma }_{ϵ}^2\right)}={\rho }_X\hfill & \hfill \\ \hfill cor\left(Y_{ij}^{\ast },Y_{i{j}^{\prime }}^{\ast }\right)& =\frac{2^{-d\left(j,j^{\prime }\right)}{\sigma }_{G_Y}^2}{\left({\sigma }_{G_Y}^2+{\sigma }_u^2+1\right)}={\rho }_Y\hfill \\ \hfill cor\left(X_{ij},Y_{ij}^{\ast }\right)& =\frac{{\sigma }_{G_X}{\sigma }_{G_Y}+\delta {\sigma }_u^2}{\sqrt{\left({\sigma }_{G_X}^2+{\delta }^2{\sigma }_u^2+{\sigma }_{ϵ}^2\right)\left({\sigma }_{G_Y}^2+{\sigma }_u^2+1\right)}}={\rho }_{XY}\hfill \\ \hfill cor\left(X_{ij},Y_{i{j}^{\prime }}^{\ast }\right)& =\frac{2^{-d\left(j,j^{\prime }\right)}{\sigma }_{G_X}{\sigma }_{G_Y}}{\sqrt{\left({\sigma }_{G_X}^2+{\delta }^2{\sigma }_u^2+{\sigma }_{ϵ}^2\right)\left({\sigma }_{G_Y}^2+{\sigma }_u^2+1\right)}}={\rho }_{XY}^{\prime },\hfill \end{array}$$

where ρ _XY represents the association between the primary and secondary phenotype. We can also derive the closed form for the heritability estimates of the secondary phenotype that quantifies the percentage of genetic variation in the total variance:

$$H^2=\frac{{\sigma }_{G_X}^2}{\left({\sigma }_{G_X}^2+\delta {\sigma }_u^2+{\sigma }_{ϵ}^2\right)}.$$ (7)

Note that when genetic factors are included in the model formula (7) gives the residual heritability.

2.3. Genotype probability

Finally, another key component in the formulation of the retrospective likelihood (2) is the computation of the genotype probability for each family i. Let G _mj and G _pj denote the genotypes of the mother and father of an individual j if this individual is a nonfounder member of family i. Under the assumption of random mating and Mendelian inheritance, the genotype probabilities can be written as presented by Duncan Thoms 14:

$$P\left(G_i\right)=\prod _{j=1}^J\left\{\begin{array}{cc}P\left(g_{ij}|G_{mj},G_{pj}\right)& \text{if}j\text{is a nonfounder}\\ P\left(g_{ij}\right)& \text{if}j\text{is a founder}\end{array}.\right.$$

The probabilities P(g _ij|G _pj,G _mj) are the transmission probabilities that can be modelled using Mendelian inheritance. Finally, P(G _pi), P(G _mi) and P(g _ij) can be modelled by assuming Hardy–Weinberg proportions (1−q)², 2q(1−q), q ² that depend on q, the minor allele frequency. Here, we propose to use external information for q or to estimate q from the control sample before maximizing the likelihood. Note that when genotypes of the parents are missing, the probability can be obtained by summing over the possible parental genotypes. In case of a more complex pedigree, a recursive algorithm known as peeling can be used 15. For the LLS where families are sibships, the probability is as follows:

$$L\left(\theta ;Y,X\right)=\prod _i\frac{\left\{P\left(X_i|G_i\right)\int P\left(Y_i^{\ast }|X_i,G_i\right)d{y}_i^{\ast }\right\}\sum _{G_p}\sum _{G_m}\prod _{j}P\left(G_{ij}|G_m,G_p\right)P\left(G_p\right)P\left(G_m\right)}{\sum _g\sum _{G_p}\sum _{G_m}\int P\left(Y_i^{\ast }|g\right)P\left(g|G_m,G_p\right)P\left(G_p\right)P\left(G_m\right)},$$ (8)

where $\theta =({\alpha }_0,{\alpha }_1,{\sigma }_{G_Y},{\beta }_0,{\beta }_1,{\sigma }_{G_X},{\sigma }_{ϵ},\delta ,{\sigma }_u)$ is the model parameters vector.

2.4. Estimation and statistical testing

To estimate the parameters of the joint model, we maximize the logarithm of the likelihood described in (8). This involves a combination of numerical optimization and integration. For the evaluation of the integral in the multivariate normal distribution, we use the deterministic algorithm Miwa described in 16. For the optimization, we use the Broyden–Fletcher–Goldfarb–Shanno algorithm implemented in the function optim(.) in R. The Broyden–Fletcher–Goldfarb–Shanno algorithm is a quasi‐Newton method, which means that the Hessian matrix does not need to be evaluated directly but is approximated by using specified gradient evaluations. To test for the presence of an effect of the SNPs on the secondary phenotype, we use the likelihood ratio test. Note that when the interest of a researcher is solely testing for genetic association, a score statistic is an alternative to the likelihood ratio statistic.

2.5. Continuous polygenic score

Our approach can also be applied in the case of modelling the association between continuous covariates and secondary phenotypes. For example, polygenic scores have been used to summarize genetic effects among an ensemble of SNPs that have been identified in large genome‐wide association studies (GWASes) 17, 18, 19. Polygenic scores are typically linear combinations of SNPs: $G={\sum }_k{\delta }_{k}SN{P}_k$, where δ _k=1 or δ _k is obtained from previous GWASes. For genetic scores, we need to integrate over the distribution of the polygenic score instead of summing over the genotypes in the denominator of (2). For the distribution of the polygenic score, we use a multivariate normal distribution $G_i\backsim {\mathcal{N}}_{n_i}\left({\mu }_g,{\sigma }_g{R}_i\right)$, with μ _g the mean value of the genetic score, σ _g the standard deviation of the genetic score and R _i the relationship matrix of family i. The likelihood contribution for family i is given by

$$\frac{P\left(Y_i,X_i|G_i\right)P\left(G_i\right)}{P\left(Y_i\right)}=\frac{P\left(Y_i,X_i|G_i\right)P\left(G_i\right)}{{\int }_{y_i^{\ast }}P\left(y_i^{\ast }\right)d{y}_i^{\ast }}=\frac{P\left(Y_i,X_i|G_i\right)P\left(G_i\right)}{{\int }_{y^{\ast }}{\int }_{g_i}P\left(y_i^{\ast }\right|g_i\left)P\right(g)d{y}_i^{\ast }d{g}_i}.$$

Computation of the integral ${\int }_{y^{\ast }}{\int }_{g}P\left(y^{\ast }\right|g\left)P\right(g)d{y}_{\ast }dg$ can be quite intensive and challenging. In order to gain efficiency, we write the marginal model of Y ^∗ (5) as $Y_i^{\ast }={\alpha }_0+b_i^{Y\ast }+u_i+{ϵ}_i^Y$, with $b_i^{Y\ast }={\sigma }_{G_Y}{b}_i^Y+{\alpha }_1{G}_i$. Now $Y_i^{\ast }$ follows the following multivariate normal distribution: $Y_i^{\ast }\backsim {\mathcal{N}}_{n_i}\left({\alpha }_0+{\alpha }_1{\mu }_g,{\mathrm{\Sigma }}_{Y_i^{\ast }}+{\alpha }_1^2{\sigma }_g^2{R}_i\right)$. Note that when a polygenic risk score is included in the model for the secondary phenotype, the parameter ${\sigma }_{G_Y}$ represents the residual polygenic inheritance.

2.6. Inclusion of covariates in the model

Often, researchers want to adjust for covariates such as age, sex, treatment and so on in the model. Let Z be such a covariate. To estimate the effect Z on the secondary phenotype, we propose to maximize the joint likelihood of X and G conditionally on the primary phenotype Y and Z. Thereby, we avoid modeling of the distribution of Z within the families. Indeed, under the assumption of independence between genotype and Z, we obtain

$$P\left(X_i,G_i|Y_i,Z_i\right)=\frac{P\left(X_i,Y_i,Z_i,G_i\right)}{P\left(Y_i,Z_i\right)}=\frac{P\left(X_i,Y_i|G_i,Z_i\right)P\left(G_i\right)P\left(Z_i\right)}{P\left(Y_i|Z_i\right)P\left(Z_i\right)}=\frac{P\left(X_i,Y_i|G_i,Z_i\right)P\left(G_i\right)}{P\left(Y_i|Z_i\right)}.$$ (9)

3. Simulation study

A simulation study was set up to evaluate the performance of our proposed method for the estimation of the association between a genetic factor and the secondary phenotype and the estimation of the heritability of the secondary phenotype. We compare the proposed method with the naive approach that is typically followed in practice, namely, analysis of the secondary trait without correcting for the sampling mechanism. In particular, in this case, we fit the standard linear mixed‐effects model for the secondary phenotype and explicitly model the familial relationships as described in ((4)). The two methods are compared in terms of bias, root mean square error (RMSE) and 95% coverage probabilities. We consider SNPs (discrete variables) and polygenic scores (continuous variables). Several settings are considered for the disease prevalence, the strength of the association between the genetic factor and the primary phenotype, the strength of the ascertainment mechanism and the number of sibships. We simulated sibships of size 5. With respect to the familial relationships, we consider only sibships such that our simulation resembles the LLS design. For the prevalence of the primary phenotype, we consider two settings, namely, a disease prevalence of 1% that corresponds to α ₀≈−2.32 and of 5% that corresponds to α ₀≈−1.64. In addition, the variance parameters have been chosen such that they correspond to a heritability of 50%. Specifically, we use ${\sigma }_{G_X}$=2, ${\sigma }_{G_Y}=\sqrt{3}$, ${\sigma }_{u_X}={\sigma }_{u_Y}=\sqrt{2}$ and ${\sigma }_{ϵ}=\sqrt{2}$. This corresponds to a correlation of 0.78 between the primary and the secondary phenotypes. To speed up computations, we assume that ${\sigma }_{u_X}={\sigma }_{u_Y}$ when fitting the models to the simulated datasets. For each scenario, 500 datasets are simulated using model (5).

3.1. Simulation results for a single‐nucleotide polymorphism

The genotypes of the SNPs are simulated assuming a minor allele frequency of 0.3 in the population. For the secondary phenotype model, the following fixed effects values are used: β ₀=3.5 and β ₁=0.2, whereas for the primary phenotype model, the effect sizes are α ₁= 0.1 or 0.5. Finally, for each of the four scenarios (rare or common disease, and weak and strong SNP effect on the primary phenotype), we consider two ascertainment mechanisms, namely, the sampled sibships of size five have at least one affected or at least two affected members.

Figure 3 presents the estimates and 95% confidence intervals for the scenario of 400 sibships. Figure 3 shows that ignoring the sampling mechanism (naive method) leads to biased estimates of the SNP effect, and the size of this bias increases with the strength of the ascertainment mechanism and the association between the SNP and the primary phenotype. Overall, we observe that the proposed method gives unbiased estimates of the SNP effect on the secondary phenotype. The coverage probabilities reach the nominal level (see section A of the Supporting Information). Regarding the prevalence of the primary phenotype, we observe that for the naive method bias increases with lower prevalence, while the proposed method remains robust to the lower amount of information because of the rare primary phenotype. In general, the proposed method leads to smaller root mean square error than the naive approach and better coverage probabilities.

Figure 3.

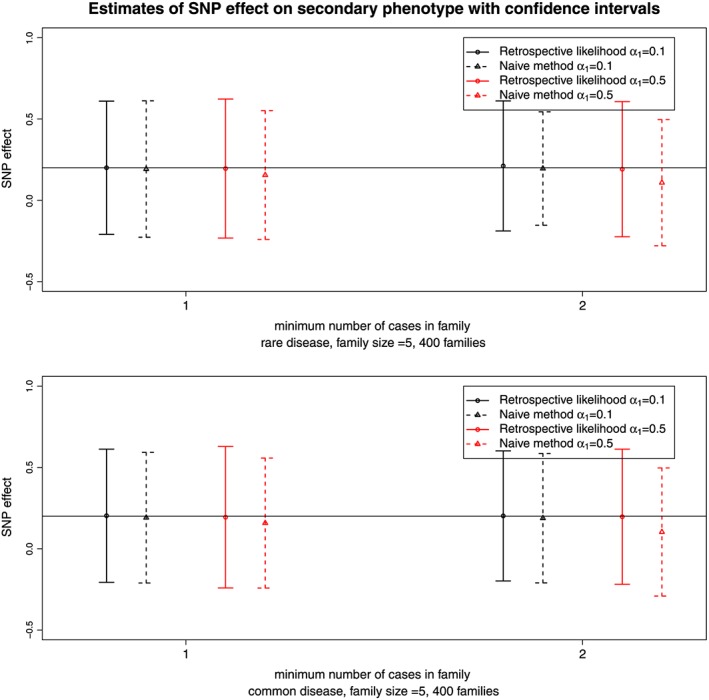
Estimates and 95% confidence intervals for the single‐nucleotide polymorphism (SNP) effect on the secondary phenotype for the retrospective likelihood approach and the naive method. Results are obtained from 500 simulated datasets of 400 sibships for two ascertainment schedules. The top and bottom panel correspond to a rare or common primary phenotype with a prevalence around 1% and 5%, respectively. In black and red are represented results for small (α ₁=0.1) and large (α ₁=0.5) effect sizes of the SNP on the primary phenotype, respectively. The horizontal line corresponds to the true SNP effect on the secondary phenotype.

In Table 1, we present the heritability estimates of the secondary phenotype for a common disease, under the various ascertainment mechanisms and the two values of α ₁. It is obvious that the heritability estimates are influenced by the ascertainment mechanisms when using the naive approach. Indeed, the naive method tends to underestimate the heritability for each mechanism and this underestimation increases as the ascertainment mechanisms become more stringent. The heritability estimates are 25–27% for sibships with at least one affected sibling and drop to 13–14% for sibships with at least two affected siblings. On the contrary, the proposed method is robust to the stringency of the ascertainment mechanism.

Table 1.

Heritability results of the simulation studies for a SNP and a polygenic score: estimates with standard deviations and root mean square error (in brackets) for the heritability of the secondary phenotype for a common disease (prevalence ≈5%), when sibships with at least one or at least two cases are sampled and for two values of α ₁, that is, SNP or polygenic score effect on primary phenotype.

		SNP model		Polygenic score model
Ascertainment	α 1	Retrospective	Naive	Retrospective	Naive
1. At least two cases
	0.10	0.48 (0.07) (0.22)	0.13 (0.07) (0.37)	0.50 (0.03) (0.13)	0.14 (0.03) (0.36)
	0.50	0.48 (0.07) (0.22)	0.14 (0.07) (0.36)	0.52 (0.03) 0.12)	0.15 (0.03) (0.34)
2. At least one case
	0.10	0.50 (0.08) (0.17)	0.25 (0.08) (0.25)	0.48 (0.04) (0.12)	0.25 (0.03) (0.24)
	0.50	0.50 (0.08) (0.17)	0.27 (0.08) (0.24)	0.50 (0.04) (0.10)	0.26 (0.04) (0.23)

The heritability value is 50% under the generating model. Datasets consist of 400 sibships of size 5. Results are based on 500 replicates. SNP, single‐nucleotide polymorphism.

Next, we study the robustness of our approach to one violation of the model assumptions, namely, we simulated under a logit link for the primary phenotype and used the probit link for modelling. Results for the SNP effect and the heritability are presented in Table 2. These results show that even though our approach gives biased estimates for the primary phenotype model, the parameters estimates for the secondary phenotype model are not affected. All the results are presented in Section A of the Supporting Information.

Table 2.

Robustness of the retrospective likelihood methods to violation of the probit model assumption for the primary phenotype: estimates of the effect size of the single‐nucleotide polymorphism on the secondary phenotype (β ₁) and heritability of the secondary phenotype are given for a common disease (prevalence ≈5%), for the two ascertainment mechanisms and two values of α ₁.

Ascertainment	α 1	β 1	Heritability
0. True value		0.200	0.500
1. At least two cases
	0.100	0.199 (0.104) (0.104) (0.948)	0.509 (0.017) (0.110)
	0.500	0.197 (0.106) (0.110) (0.945)	0.516 (0.014) (0.108)
2. At least one case
	0.100	0.200 (0.104) (0.107) (0.961)	0.510 (0.012) (0.096)
	0.500	0.199 (0.107) (0.111) (0.960)	0.513 (0.010) (0.087)

In brackets are standard deviations, root mean square error and coverage probability (for the effect size only). Datasets consist of 400 sibships of size 5. Results are based on 500 replicates.

Although we focus on parameter estimation, model fitting and heritability estimation for genetic association with a secondary phenotype, we also investigate the performance of the likelihood ratio test under the null hypothesis of no genetic association with a secondary phenotype at two levels of genetic association with the primary phenotype. In each of the four considered scenarios, we simulate 10 000 replicates. In Table 3, the empirical type I error rates are given for the rare disease scenario (i.e. prevalence 1%). We observe that while our approach preserves the type I error rate at a nominal level, the naive approach has, systematically, an inflated type I error rate. The type I error rate for the naive method increases with stronger ascertainment and larger SNP effect on the primary phenotype.

Table 3.

Empirical type I errors rates for testing for association between a genetic marker and a secondary phenotype using the likelihood ratio test for four scenarios.

	Nominal level (α)	Retrospective likelihood	Naive method
At least two cases
α 1=0.1
	0.05	0.0509	0.0580
	0.01	0.0118	0.0152
	0.001	0.0017	0.0025
α 1=0.5
	0.05	0.0505	0.0878
	0.01	0.0113	0.0222
	0.001	0.0013	0.0043
At least one case
α 1=0.1
	0.05	0.0524	0.0514
	0.01	0.0102	0.0098
	0.001	0.0018	0.0014
α 1=0.5
	0.05	0.0522	0.0558
	0.01	0.0098	0.0097
	0.001	0.0009	0.0016

Sibships with at least one or with at least two cases are considered. Two values for the association between the single‐nucleotide polymorphism and the primary phenotype, namely, α ₁ = 0.1 and α ₁ = 0.5, are used. Datasets consist of 400 sibships of size 5. Results are based on 10 000 replicates.

3.2. Simulation results for a polygenic score

To study the performance of the proposed method for polygenic score, we simulated centred and standardized scores. The parameters of the secondary phenotype model were chosen as for the SNP simulations: β ₀=3.5 and β ₁=0.2, whereas for the primary phenotype model, effect sizes of α ₁= 0.1 or 0.5 were used. Figure 4 presents the estimates and confidence intervals for datasets with 400 sibships. Our approach provides unbiased estimates of the effect of the polygenic score on the secondary phenotype. In contrast, the naive approach provides biased estimates and the bias increases when the ascertainment process is more stringent or when α ₁ is larger.

Figure 4.

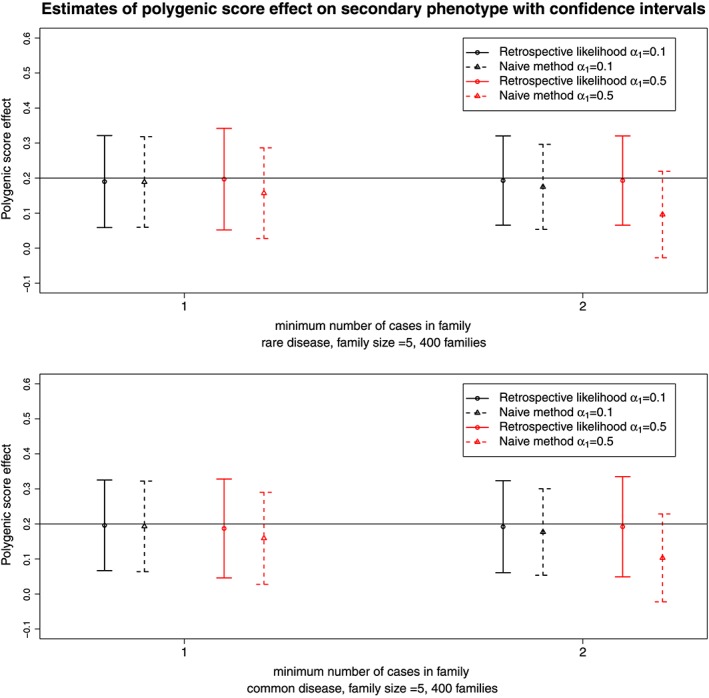
Estimates and 95% confidence intervals for the polygenic score effect on the secondary phenotype for the retrospective likelihood approach and the naive method. Results are obtained from 500 simulated datasets of 400 sibships for two ascertainment schedules. The top and bottom panel correspond to a rare or common primary phenotype with a prevalence around 1% and 5%, respectively. In black and red are represented results for small (α ₁=0.1) and large (α ₁=0.5) effect sizes of the polygenic score on the primary phenotype, respectively. The horizontal line corresponds to the true polygenic score effect on the secondary phenotype.

The results of the residual heritability estimates after adjustment for polygenic scores agree with the results obtained when a SNP is included in the model (Table 1). The naive approach did not perform well: estimates between 25–26% and 14–15% for an ascertainment process of at least one affected sibling and at least two affected siblings, respectively, instead of 50%.

4. Application: analysis of the Leiden Longevity Study

In this Section, we will exemplify our proposed method in the analysis of the LLS briefly introduced in Section 1. The LLS is a family‐based study set up to identify mechanisms that contribute to healthy ageing and longevity. The inclusion criteria of the study are sibships with at least two nonagenarian siblings, that is, the selection takes place at Generation II (Figure 2). Several secondary phenotypes and GWAS data have been measured for the offspring of these siblings (Generation III in Figure 2) and their partners. Because the offspring have at least one nonagenarian parent, they are also likely to become long‐lived. Therefore, the set of offspring and their partners corresponds to a case‐control design with related subjects where the offspring in Generation III are considered as cases and their partners as controls. Overall, 421 families with 1671 offspring (cases) and 744 partners (controls) have been included in the study. Because the families are relatively small, we use the model that assumes an equal variance for the shared effect for the two traits.

Here, we model the association between genetic factors and the secondary phenotypes triglyceride and glucose levels. For both traits, there is evidence of an association with human longevity and both traits are normally distributed. For the sake of comparison in addition to our proposed method, we will present results using the naive approach, that is, standard linear mixed model. Analyses using the linear mixed model that conditions also on the case‐control status will not be presented because the parameters do not have a comparable interpretation between the two approaches. The p‐values presented subsequently are obtained using the likelihood ratio test.

4.1. Triglyceride levels analysis

Triglyceride levels have been found to be associated with the primary trait longevity ( p‐value = 0.0005 for women and p‐value = 0.04 for men), and the size of association is sex dependent. Therefore, a sex‐stratified analysis has been considered further. For the purposes of our illustration, we restricted our analysis to seven genes on chromosome 11 that are known to be associated with triglyceride levels. These genes are APOA1, APOA4, APOA5, APOC3, ZNF259, BUD13 and DSCAML1. The selection of the genes was performed using the NHGRI‐EBI GWAS catalog 20. For these genes, we have genotypes of 41 SNPs that have no missing values in our datasets. Triglyceride levels were standardized, and we included age as a covariate in the analysis.

We ran the analysis with the constrained approach, that is, δ=1. We observe that none of the SNPs analysed is significantly associated with triglyceride levels either in men or in women; hence, for most SNPs, the estimates of the effect sizes agree between the two approaches. The SNPs showing the largest differences are, in men, SNP 22: ${\beta }_1^{RA}=0.047$ for our Retrospective Approach (RA) and ${\beta }_1^{NA}=0.052$ for the Naive Approach (NA) and SNP 26: ${\beta }_1^{RA}=0.088$ and ${\beta }_1^{NA}=0.092$. For women, more SNPs give different estimates between the two approaches, that is, SNP 1 ( ${\beta }_1^{RA}=0.024$, ${\beta }_1^{NA}=0.020$), SNP 2 ( ${\beta }_1^{RA}$ = 7.2e‐06 ${\beta }_1^{NA}=0.006$), SNP 13 ( ${\beta }_1^{RA}=-0.013$, ${\beta }_1^{NA}=-0.009$) and SNP 19 ( ${\beta }_1^{RA}=0.011$, ${\beta }_1^{NA}=0.007$) showed the biggest differences. Results for the SNPs are presented in Section B of the Supporting Information.

We verified whether the assumption of equal variances for the primary and secondary phenotype for the shared effects is justified. We fitted also the model with non‐constrained δ. We noticed that for some of the SNPs, the model parameters are hard to estimate and the estimates of the variances of the shared and residual random effects in the model for the second phenotype are swapped. Overall, the estimates of the effect of the SNP on the secondary phenotype are very similar to the model that assumes equal variances. Results of these analyses are presented in Section B of the Supporting Information.

4.2. Glucose levels analysis

In previous analysis of glucose levels in the offspring and partners of the LSS, Mooijart 21 studied the association between glucose and a polygenic score. The genetic score was defined as the total number of risk alleles across 15 SNPs that are known to be associated with Type II diabetes. The generalized estimating equation method was applied to take into account the familial relationships. The paper showed that a higher number of Type II diabetes risk alleles is associated with a higher serum concentration of glucose ( p‐value = 0.016). A statistically significant association was found between the glucose level and case‐control status ( p‐value < 0.001). However, the sampling process was not taken into account in the analysis and thus the results might be biased. We applied the proposed method to estimate the heritability of glucose levels and to test for the presence of an association between the glucose levels and the polygenic score. In addition, we applied the naive approach that did not correct for case‐control status. We did not stratify according to sex in these analyses.

For this analysis, the polygenic score was standardized. Using the RA, the association between the genetic score and the glucose level is estimated by ${\beta }_1^{RA}=0.630$ with a standard error of s t E=0.023(p‐value =0.015). The naive approach also yields a significant association between the genetic score and glucose levels ( ${\beta }_1^{NA}=0.622$, s t E=0.026, p−v a l u e=0.020). By using the NA, we obtained for the glucose levels a genetic variance of ${\sigma }_{G_X}^2=0.302$ and a total variance of ${\sigma }_T^2=1.322$, which corresponds to a residual heritability of $h_{NA}^2=0.228$. Our RA yields a genetic variance of ${\sigma }_{G_X}^2=0.384$ and a total variance of ${\sigma }_T^2=1.457$ that corresponds to a residual heritability of $h_{RA}^2=0.263$.

5. Discussion

In this paper, we developed a new method for the proper analysis of secondary traits for multiple‐cases family designs. A key component in our proposed method is the joint modelling of the primary and secondary phenotypes. We developed a multivariate probit model that can also capture the within families dependencies. A retrospective likelihood approach has been followed to correct for the ascertainment process. Thereby unbiased estimates of the association between genetic factors and secondary traits can be obtained. Simulation results showed that our approach preserves the type I error at nominal level and provides accurate estimates irrespective of the disease prevalence, the strength of the association between the genetic variants and the primary phenotype, and the ascertainment mechanism. Another important empirical finding is that the heritability estimates for the secondary traits can be severely underestimated unless the sampling mechanism is taken into account. With respect to the analysis of the motivating case study, for the SNPs, the differences between the effect sizes obtained by our proposed method and the naive approach were small. The small differences obtained between the naive and the retrospective approach are mainly because of the small effect sizes of the genetic markers selected on the primary phenotype. Indeed, the three main factors influencing the magnitude of the bias when using the naive approach are the correlation between the secondary phenotype and the primary phenotype, the strength of the ascertainment, and the strength of the association between the genetic marker and the primary phenotype.

Heritability is one of the properties that a trait needs to possess to be declared an endophenotype for a specific disease. The other criteria are the trait is associated with the disease status in the population, the trait manifests whether illness is active or in remission (state independent) and the trait and the disease status co‐segregate within a family 22. The Leiden Family Lab (https://www.leidenfamilylab.nl) aims to identify endophenotypes for social anxiety disorder. The study comprises families with at least two cases with social anxiety. The methods presented in this paper will be used for the analyses of this study to identify endophenotypes and are relevant for other family studies, as well.

In this paper, we proposed to include additional covariates in the model by using the likelihood conditional on these covariates. Alternatively, the joint likelihood of the secondary phenotype, genotype and covariate conditionally on the primary phenotype can be used. This alternative approach might be more efficient 23. However, this likelihood requires distributional assumptions for the covariates within families, which can be complex for related individuals. Moreover, maximization of the likelihood might become time consuming. Ghosh et al. 24 propose a pseudo‐likelihood and a profile approach to include covariates in a secondary phenotype analysis for case‐control data. This work needs to be extended to family data. A Monte Carlo approach might be considered to compute the integrals (Tsonaka et al. 25).

Typically, there are missing genotypes. In unrelated individuals, genotypes can be imputed based on the haplotype structure obtained from a reference panel. For family data, the imputation should also take into account the genotypes of other family members. Software exists that can perform such analysis, for example, the Genotype Imputation Given Inheritance program 26. However, for the computation of the denominator in Equation (2), these imputed genotype probabilities have to be taken into account.

Because of the computational intensity of the proposed method, it is not yet possible to run full GWAs analyses of secondary phenotypes. However, the proposed method can be used on a set of pre‐selected variants, for example, after an initial screening with the naive approach to the primary and secondary phenotypes or when investigating pleiotropic effects. To reduce the computation time of the multivariate integrals in the numerator and the denominator, a faster algorithm can be used than the one used in this paper. The randomized quasi‐Monte Carlo procedure, developed by Genz 27, is less accurate but faster especially for large pedigrees. Development of less computational intensive methods is one of the topics for future research.

With regard to pleiotropic effects, a criticism of probit random‐effects models is that in the presence of high dimensional random effects we cannot move from the subject‐specific interpretation for the fixed effects parameters to the population‐level interpretation as in the random‐intercepts case. When the outcome is binary and families are relatively small, estimation of the intercept and variances terms can be difficult, and consequently, coverage probabilities can be poor. Tsonaka et al. 6 showed efficiency gains by using information on disease prevalence. Their methods need to be adapted to our setting of the analysis of two phenotypes. When the parameters of the primary phenotype model are not of interest and this model is only used to correct for the ascertainment mechanism that is driven by the primary phenotype, we showed that secondary phenotype analyses with the proposed method are robust to using the probit instead of the logit link function.

Future directions in the LSS and Leiden Family Lab Study will address the pending availability of multiple omics and functional MRI data, respectively, and joint modelling of several glycans or voxels is of interest. Extending our approach, in this case, is algebraically straightforward, but practical implementation may be challenging because of computational intensity especially with a large number of secondary phenotypes. The use of composite likelihood approaches might be a solution and is our current research topic.

Finally, an attractive alternative approach to properly analyse secondary traits is to apply inverse probability weighting. However, it is crucial to correctly specify the weights. Currently, we do not have sufficient information to be able to estimate these weights for our studies. However, with access to electronic records for research, such as information from general practitioners to estimate the weights, it is likely that inverse probability weighting approaches can be developed.

Supporting information

Table S1: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a rare disease (prevalence around 1%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S2: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a rare disease (prevalence around 1%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S3: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a rare disease (prevalence around 1%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S4: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a rare disease (prevalence around 1%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S5: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a common disease (prevalence around 5%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S6: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a common disease (prevalence around 5%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S7: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a common disease (prevalence around 5%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S8: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a common disease (prevalence around 5%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S9: Estimates with standard deviations and RMSE of the heritability of the secondary phenotype are given for a common disease (prevalence ≈ 5%), for the four ascertainment mechanisms and two values of α₁.

Table S10: Estimates with standard deviations and RMSE of the heritability of the secondary phenotype are given for a rare disease (prevalence ≈ 1%), for the four ascertainment mechanisms and two values of α₁.

Figure S1: Estimates and 95% confidence intervals for the SNP effect on the secondary phenotype for the retrospective likelihood approach and the naive method. Results are obtained from 500 simulated datasets of 100 families for 2 ascertainment schedules. The top and bottom panel correspond to a rare or common primary phenotype with a prevalence around 1% and 5% respectively. In black and red are represented results for small (α₁=0.5) and large (α₁=1) effect sizes of the SNP on the primary phenotype respectively. The horizontal line corresponds to the true SNP effect on the secondary phenotype.

Table S11: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a rare disease (prevalence around 1%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S12: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a rare disease (prevalence around 1%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S13: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a rare disease (prevalence around 1%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S14: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a rare disease (prevalence around 1%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S15: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a common disease (prevalence around 5%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S16: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a common disease (prevalence around 5%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S17: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a common disease (prevalence around 5%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S18: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a common disease (prevalence around 5%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S19: Estimates with standard deviations and RMSE of the heritability of the secondary phenotype are given for a common disease (prevalence ≈ 5%), for the four ascertainment mechanisms and two values of α₁.

Table S20: Estimates with standard deviations and RMSE of the heritability of the secondary phenotype are given for a rare disease (prevalence ≈ 1%), for the four ascertainment mechanisms and two values of α₁.

Table S21: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a rare disease (prevalence around 1%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S22: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a rare disease (prevalence around 1%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S23: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a rare disease (prevalence around 1%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S24: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a rare disease (prevalence around 1%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S25: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a common disease (prevalence around 5%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S26: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 2 cases of a common disease (prevalence around 5%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S27: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a common disease (prevalence around 5%) and α₁=0.1. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S28: Simulations results obtained on 500 datasets with 400 families of size 5 with at least 1 case of a common disease (prevalence around 5%) and α₁=0.5. Into brackets are respectively standard deviations, root mean square errors and the coverage probabilities.

Table S29: Estimates with standard deviations and RMSE of the heritability of the secondary phenotype are given for a rare disease (prevalence ≈ 1%), for the four ascertainment mechanisms and two values of α₁.

Figure S2: Estimates for the association of 41 SNPs with triglyceride in the LLS. In the top and bottom are the estimates of the 41 SNPs for women and for men respectively. The black line represents no SNP effect on triglyceride.

Table S30: Leiden Longevity Study: Estimates of the association between the 41 selected SNPS and triglyceride levels for womend and for three different approaches. The retrospective likelihood approach with same variance assumed for the shared random effect, with different variances, and the naive approach. Are also presented the absolute difference between the estimates of the two last approaches with the first one. Into brackets are the standard errors.

Table S31: Leiden Longevity Study: Estimates of the association between the 41 selected SNPS and triglyceride levels for men and for three different approaches. The retrospective likelihood approach with same variance assumed for the shared random effect, with different variances, and the naive approach. Are also presented the absolute difference between the estimates of the two last approaches with the first one. Into brackets are the standard errors.

Tissier, R. , Tsonaka, R. , Mooijaart, S. P. , Slagboom, E. , and Houwing‐Duistermaat, J. J. (2017) Secondary phenotype analysis in ascertained family designs: application to the Leiden longevity study. Statist. Med., 36: 2288–2301. doi: 10.1002/sim.7281.