Polarizable Force Field for DNA Based on the Classical Drude Oscillator: II. Microsecond Molecular Dynamics Simulations of Duplex DNA

Abstract

The structure and dynamics of DNA are governed by a sensitive balance between base stacking and pairing, hydration, and interactions with ions. Force field models that include explicit representations of electronic polarization are capable of more accurately modeling the subtle details of these interactions versus commonly used additive force fields. In this work, we validate our recently refined polarizable force field for DNA based on the classical Drude oscillator model, in which electronic degrees of freedom are represented as negatively charged particles attached to their parent atoms via harmonic springs. The previous version of the force field, called Drude-2013, produced stable A- and B-DNA trajectories on the order of hundreds of nanoseconds, but deficiencies were identified that included weak base stacking ultimately leading to distortion of B-DNA duplexes and unstable Z-DNA. As a result of extensive refinement of base nonbonded terms and bonded parameters in the deoxyribofuranose sugar and phosphodiester backbone, we demonstrate that the new version of the Drude DNA force field is capable of simulating A- and B-forms of DNA on the microsecond time scale and the resulting conformational ensembles agree well with a broad set of experimental properties, including solution X-ray scattering profiles. In addition, simulations of Z-form duplex DNA in its crystal environment are stable on the order of 100 ns. The revised force field is to be called Drude-2017.

Graphical abstract

Introduction

DNA is central to the maintenance and inheritance of genetic information. Its structure must be sufficiently stable to preserve genomic integrity, but flexible enough to locally unwind to carry out replication and transcription. In the process of regulating gene expression, DNA is packaged in chromatin, in which it undergoes million-fold compaction to wrap tightly around histone proteins in nucleosomes. This compaction arises from local flexibility intrinsic to the DNA and attractive electrostatic forces between the DNA and histone proteins that overcome energetic penalties to deformation.^1-3 While DNA is predominantly found in right-handed, B-form double helices in aqueous solution, it can also populate A-helices and left-handed, Z-form structures depending upon nucleotide sequence and solution conditions such as water activity and salt concentration.^4-5

The stability of the DNA structure depends on a balance of electrostatic and van der Waals forces that give rise to intra-strand base stacking and inter-strand hydrogen bonding. The ability of an atomistic force field to capture these forces is essential for carrying out accurate molecular dynamics (MD) simulations. To this end, numerous fixed-charge (additive) force fields such as AMBER,^6-7 CHARMM,^8-10 GROMOS,¹¹ and BMS¹² have been developed to simulate DNA. The AMBER and CHARMM nucleic acid force fields are the most widely used, though recent quantum mechanical (QM) calculations have shown that their descriptions of base stacking,^13-15 hydrogen bonding,¹⁵ and interactions with ions¹⁶ are lacking in the treatment of electrostatic effects. This is not to say that the force fields are poorly parametrized, rather there is an intrinsic deficiency in the additive functional form that limits the accuracy of such empirical models. Thus, pursuing the development of polarizable force fields is an attractive approach to achieve a better description of structural properties and complex interactions in biomolecular systems.

The constituent moieties comprising DNA experience a range of environments of different electric field strengths, from the polar surrounding solvent to the relatively hydrophobic interior of the double helix. Moreover, given the high charge density of DNA, its interactions with aqueous solvent and ions are dominated by electrostatic interactions.¹⁷ In this regard, additive force fields, while computationally efficient, lack the ability to adequately respond to variations in the local electric field. Recently, a polarizable force field for DNA based on the classical Drude oscillator,¹⁸ termed Drude-2013, was introduced.^{17, 19-20} This model represents electronic polarization by attaching negatively charged particles (Drude oscillators) to the non-hydrogen atoms of the system via a harmonic spring. Partial charges are assigned to each Drude oscillator, q_D, and its parent atom, q_A, according to the atomic polarizability, α, given a total charge on the Drude-atom pair, q_tot:

$$\alpha =\frac{q_D^2}{K_D}$$ (1)

$$q_A=q_{\mathit{\text{tot}}}-q_D$$ (2)

where k_D is the force constant on the Drude-atom bond. The present version of the force field supports Thole screening of neighboring (i.e. 1-2 and 1-3 atom pairs) atomic dipoles²¹ to achieve a correct description of molecular polarizability and anisotropic polarization in conjunction with virtual sites representing lone pairs to improve hydrogen bonding and ion interactions.²² Interactions with water and ions have also been tuned using pair-specific Lennard-Jones (NBFIX) and through-space Thole screening (NBTHOLE) to better represent intermolecular interactions in heterogeneous environments.^23-25

The Drude-2013 DNA force field¹⁹ has recently been applied in studies of DNA conformational dynamics and interactions with ions. It has been found that the polarizable model predicts that the DNA conformational ensemble is sensitive to the identity of cations in solution, whereas the additive force fields like AMBER parmbsc0²⁶ and CHARMM36^{8, 10, 27} do not show this ion-specific response, nor do they represent DNA conformational ensembles in solution as well as Drude-2013.^28-29 Moreover, it was also shown using the Drude-2013 DNA force field that monovalent ions can modulate the DNA minor groove width in a size-dependent manner.³⁰ Taken together, these results suggest that a polarizable model is particularly important for modeling ion-DNA interactions, in which electrostatics dominate, and for which the additive approximation may ultimately be insufficiently accurate. As a final example, it was also shown that the Drude-2013 DNA force field could quantitatively reproduce base opening equilibrium constants from NMR.³¹ Whereas the CHARMM36 additive model significantly underestimated the equilibrium associated between the base-open and base-closed flipped states, the Drude force field more accurately modeled the equilibrium as a result of mutual polarization between bases and water molecules in the first solvation shell. Thus, it is clear that explicit polarization is an important consideration in studies of DNA conformational dynamics. However, in carrying out additional simulations of DNA with Drude-2013, it was found that B-DNA sequences could become unstable after several hundred nanoseconds (see below), consistent with a recently published study,³² and that Z-DNA was not stable. The causes of these phenomena were described in an accompanying paper.³³

In the present work, we carry out extensive condensed phase simulations of A-, B-, and Z-DNA using the refined parameter set, called Drude-2017, to demonstrate that this force field allows for microsecond MD simulations of A-, B- and Z-form DNA duplexes in the condensed phase.

Methods

Force Field Refinement

In the previous validation of the Drude-2013 DNA force field,¹⁹ simulations of canonical B-form helices were shown to be stable on the order of 200 ns. However, extension of these simulations on the order of ∼300 ns revealed that some structures could become unstable (Supporting Figure S1). The instability manifested itself most prominently in A-tracts (sequences of four or more consecutive adenine-containing base pairs), and the underlying problem was suspected to be inadequate base stacking energies, which include van der Waals, electrostatic, and Drude self-polarization terms. These observations motivated refinement of the Drude-2013 DNA force field. The complete details of the refinement are described in the accompanying paper,³³ and included refinement of the nucleobase nonbonded parameters (electrostatic and Lennard-Jones, LJ) and several important dihedrals in the deoxyribofuranose sugar and phosphodiester backbone. This refinement explicitly included the conformational energetics of Z-DNA backbone dihedral rotation and sugar puckering for the first time. All results in the present manuscript are based on the final set of refined parameters.

Z-DNA Crystal Survey

Following the method of Zgarbová et al.,³⁴ we assembled crystallographic distributions of Z-DNA backbone and glycosidic dihedrals and sugar pucker. This Z-DNA crystal survey was the basis for comparing the outcomes of the Z-DNA crystal simulations described below. We included 17 structures in the survey, all with resolution ≤ 1.0 Å and only GC base pairing, which is characteristic of Z-DNA. The PDB codes of these structures were 131D,³⁵ 1D48,³⁶ 1DCG,³⁷ 1DJ6,³⁸ 1I0T,³⁹ 1ICK,⁴⁰ 292D,⁴¹ 293D,⁴² 2DCG,⁴³ 2ELG,⁴⁴ 336D,⁴⁵ 3P4J,⁴⁶ 3WBO,⁴⁷ 4HIF,⁴⁸ 4HIG,⁴⁸ 4OCB,⁴⁹ and 4R15.⁵⁰ Structural analysis was carried out in CHARMM.⁵¹

Simulations of Duplex DNA

To assess the quality of the newly derived parameters in full-length, double-stranded DNA (dsDNA), several systems were studied, covering both canonical and noncanonical structures (Table 1). Initial coordinates for all available systems were obtained from the Protein Databank (PDB), to which any missing hydrogen atoms were added within CHARMM. Each DNA was then centered within a cubic simulation cell with a minimum distance between the solute and the box edge of 10 Å. For canonical B-DNA structures EcoRI (PDB 1BNA),⁵² 1S2R,⁵³ and 2L8Q,⁵⁴ the unit cells were filled initially with TIP3P water^55-57 and ∼100 mM NaCl, including additional neutralizing Na⁺ counterions. These structures were subsequently equilibrated using the CHARMM36 force field^{9, 27} for 5 ns with restraints applied to DNA non-hydrogen atoms. The final coordinates and topology of each system were converted to the Drude force field using CHARMM,⁵¹ which also converted TIP3P to SWM4-NDP water,⁵⁸ after which another energy minimization was performed.

Table 1.

List of DNA systems used for validation of the updated Drude DNA FF.

Sequence	Method	PDB ID	Size (bp)	Reference/Notes	Simulation time
d(CGCGAATTCGCG)	X-ray	1BNA	12	Dickerson-Drew dodecamer (EcoRI)52a	> 1.0 μs
d(CGCATGCTACG)	NMR	2L8Q	11	B-DNA	1.0 μs
d(CGCA3T3GCG)	X-ray	1S2R	12	B-DNA with A-tract	1.0 μs
d(CCGCTAGCGG)	X-ray	1DCV	10	B-DNA	1.0 μs
d(GAAGAGAAGC)	NMR	1AXP	10	B-DNA with purine-rich strand	1.0 μs
d(CCGGGCCCGG)	X-ray	1ZF1	10	A- to B-DNA conversion	1.0 μs
d(TGCGCA)	X-ray	1LJX	6	Z-DNA crystal with 2 Mg2+	100 ns
d(CGCGCG)	X-ray	1ICK	6	Z-DNA crystal with 1 Mg2+	100 ns
d(CGCGCG)	X-ray	292D	6	Z-DNA crystal with 3 Mg2+, Na+	100 ns

^aThe EcoRI sequence was used in initial screening of intermediate parameter sets and may be considered a training system for evaluating the force field parameters. All other DNA sequences are considered an unbiased evaluation of the new force field. Z-DNA simulations were all performed in the crystal environment.

To test the robustness of the refined Drude DNA force field, an additional simulation of EcoRI was performed. The 180-ns simulation from previous work²⁸ was extended using the Drude-2013 DNA force field,¹⁹ and the B-form DNA structure distorted by ∼320 ns, driven by base opening in the central A-tract (Supporting Figure S1), a behavior that motivated the present work. Using the new force field developed here, another simulation was initiated from the coordinates and velocities of the snapshot at 180 ns, well before any instability was observed. By doing so, the new parameters were assessed in terms of their ability to maintain stability based on maintenance of the B-DNA conformation.

To assess the sensitivity of DNA conformation to solvent water activity, as was done in the development of the CHARMM27 nucleic acid force field^{8, 10} and the first-generation Drude-2013 DNA force field,¹⁹ we simulated an A-DNA structure (PDB code 1ZF1⁵⁹) in a solution of 75% ethanol/25% water (v:v, with ∼120 mM NaCl) and an aqueous solution of ∼120 mM NaCl. Pre-equilibrated coordinates for these systems were taken from previous work.^{8, 10, 19}

Simulations were carried out using the extended Lagrangian method⁶⁰ for integrating the equations of motion. The short-range van der Waals potential was switched to zero from 10 - 12 Å. Electrostatic interactions were calculated using particle mesh Ewald,^61-62 with a real-space cutoff of 12 Å. Neighbor lists were updated within 16 Å. Bonds involving hydrogen atoms were constrained using SHAKE⁶³ and the hard wall constraint⁶⁴ at 0.2 Å was employed to prevent polarization catastrophe, allowing an integration time step of 1 fs. Each system was equilibrated for 1 ns under an NPT ensemble with restraints (k = 5.0 kcal mol^-1 Å^-2) on all non-hydrogen atoms in NAMD.⁶⁵ Following equilibration, restraints were removed and simulations were carried out in OpenMM⁶⁶ for 1 μs or more. Production simulations were carried out using an NPT ensemble, with temperature maintained using dual Nosé-Hoover thermostats (298 K for real atoms with τ = 0.1 ps and 1 K for the relative Drude thermostat with τ = 0.005 ps) and pressure maintained at 1 atm using the Monte Carlo barostat with pressure changes attempted every 25 steps.

We also performed crystal simulations of left-handed Z-DNA structures 1ICK,⁴⁰ 292D,⁴¹ and 1LJX,⁶⁷ retaining crystallographic waters and monoatomic ions (Mg²⁺ and Na⁺), employing our recently developed parameters for Mg²⁺ interactions with water and nucleic acid moieties.⁶⁸ Co-solutes such as polyamines were removed. Orthorhombic crystals (P2₁2₁2₁ space group) were constructed by applying the prescribed symmetry operations using the CRYSTAL BUILD facility in CHARMM.⁵¹ Simulations were then performed in CHARMM, using the extended Lagrangian velocity Verlet method⁶⁰ to integrate the equations of motion. Temperature was maintained using a dual Langevin thermostat (293 K for real atoms and 1 K for Drude oscillators) using friction coefficients of 5.0 ps^-1 and 10.0 ps^-1 for real atoms and Drude oscillators, respectively. Simulations were carried out under an NPT ensemble for 100 ns, allowing full anisotropic flexibility of the crystal unit cell. Pressure was maintained at 1 atm using a modified Andersen-Hoover barostat⁶⁹ with a relaxation time of 0.5 ps.

Solution X-Ray Scattering

To characterize the conformational ensemble of the EcoRI and 1DCV structures in solution, we used CRYSOL⁷⁰ to compute the solution X-ray scattering profiles of 1000 snapshots extracted at 1-ns intervals from each trajectory. Solution X-ray scattering, including both small- and wide-angle X-ray scattering (SAXS and WAXS, respectively) reports on interatomic distances over different length scales, making it a powerful method of assessing the agreement of the structures produced by the force field over the course of the MD trajectory with the solution conformational ensemble obtained experimentally. Comparisons of MD results to static crystal structures are hindered by the fact that such experimental structures may not reflect the conformational ensemble in aqueous solution due to crystal packing effects.^71-74 Even NMR studies of nucleic acid structure may suffer from limitations associated with the underlying mathematical models used during refinement.⁷⁵ Solution X-ray scattering profiles inform on the conformational ensemble in solution, allowing a direct comparison between the simulation outcomes and experimentally observed structures.

Peak positions in the scattering profiles are important indicators of the conformational ensembles, but identifying peaks can be challenging given the noise in experimental data. We undertook the comparison between computed and experimental solution scattering profiles in the following way. Putative peaks were identified using zero-crossing points of the first derivative of the scattering profiles. Crossing points that fell within ± 0.1 Å of experimentally assigned peaks were considered for analysis (see Results and Discussion) and the crossing point with the local maximum I(q) value in this range was assigned as the peak. The first derivative analysis was also applied to computed scattering profiles from the MD trajectories, but given the smoothness of the resulting profiles, peaks were identified unambiguously.

DNA Structural Analysis

To describe the details of DNA conformational ensembles, we analyzed dihedral and sugar puckering time series from the MD trajectories. We adopt a two-state model to describe BI/BII equilibrium as well as North-South sugar puckering. The BI and BII sub-states of B-DNA are characterized by the values of the ε and ζ dihedrals, with BI corresponding to ε ∼190° and ζ ∼270°, while BII is defined as ε ∼260° and ζ ∼180°. For the purposes of assigning BI and BII states from the trajectories, we adopt a more general definition in which BI is assigned to a given base step when ε - ζ < 0° and BII is assigned when ε - ζ > 0°. This simple counting method differs from interpolation analysis from ³¹P NMR, which converts chemical shift data into an average value of the ε - ζ difference, which is then interpolated between 0% BI (ε - ζ = 90°) and 100% BI (ε - ζ = -90°).⁷⁶

Similarly, we adopted a two-state approximation for describing sugar puckering between South (S, or C2′-endo) and North (N, or C3′-endo) states, by calculating the pseudorotation angle, P, of the ring according to Cremer and Pople.⁷⁷ From the MD time series, we assigned North pucker for -90° ≤ P ≤ 90°. All other values were considered South pucker. The North fraction of each nucleotide was then computed as the fraction of snapshots fitting the North pucker definition divided by the total number of snapshots saved in the simulation.

Helicoidal parameters (rise, roll, twist, buckle, etc.) and characteristics such as groove width and axis bending for B-DNA were computed with the Curves+ program.⁷⁸ Distributions from the MD simulations were compared to a survey of B-DNA structures with resolution ≤ 2.5 Å used previously in the development of the additive CHARMM36⁹ and polarizable Drude-2013¹⁹ force fields.

Results and Discussion

dsDNA Simulations

Having significantly improved conformational energetics at the model compound level as well as improving base stacking and water interactions, we conducted validation simulations on A-, B-, and Z-forms of DNA. Condensed phase A- and B-DNA simulations were performed for a minimum of 1 μs each, representing the longest and most stringent test of a polarizable DNA force field to date. Given the more restricted conformational space of Z-DNA crystals, these simulations were carried out for 100 ns, as was done during the validation of the additive CHARMM36 force field.⁹ Convergence was tested by splitting each trajectory in two halves; results were not substantially different when considering the whole trajectory or either half. The EcoRI system was extended for an additional 300 ns to 1.3 μs to further demonstrate its stability (Figure 1). For consistency, we present results from the first 1 μs trajectory for all systems.

Figure 1.

RMSD time series for non-terminal heavy atoms of each of the five B-DNA sequences with respect to the experimentally determined B-form structures.

Time series of non-terminal heavy atom RMSD for each of the five B-DNA sequences (EcoRI, 2L8Q, 1DCV, 1AXP, and 1S2R) are shown in Figure 1. The RMSD values are stable with no systematic deviations, indicating that there were no major structural changes in any of these systems over the course of 1 μs. EcoRI, which was previously unstable with Drude-2013 after 300 ns (Supporting Figure S1), had an RMSD of 1.5 ± 0.3 Å using the refined force field, indicating that the instability has been corrected. 1AXP and GC-rich 1DCV were similarly stable, with RMSD values of 1.6 ± 0.2 Å and 1.7 ± 0.3 Å, respectively. The 1S2R sequence, containing a six-nucleotide A-tract, had an average RMSD of 1.8 ± 0.4 Å but did show a brief RMSD spike (Figure 1) due to a transient kink in the middle of the A-tract, lasting for ∼80 ns. Given that A-tracts are flexible (discussed below), this reversible kinking is reasonable and not indicative of a problem in the force field. The 2L8Q sequence deviated the most from its initial structure, with an average RMSD of 2.4 ± 0.5 Å, but as will be shown below all its conformational sampling is in line with expectations for B-DNA and this comparatively large RMSD is still indicative of reasonable behavior.

Dihedral Sampling in B-DNA

As an indicator of the correctness of the refined Drude DNA force field, we examined the dihedral sampling in B-DNA structures simulated in aqueous solution. As reference data, we use the dihedral distributions from a crystal survey of B-DNA structures with resolution ≤ 2.5 Å. It is important to note that exact agreement with the crystal survey is not expected and deviations are not necessarily suggestive of incorrect behavior, as a crystal environment is very different from aqueous solution, in which the DNA sequences are more flexible. We use the crystal survey only as a guide for reasonable sampling of backbone torsions.

Figure 2 shows the outcomes of the dihedral analysis. All five B-DNA sequences sampled dihedrals in regions that align well with the survey data. The α, β, and γ distributions are in near-exact agreement with the survey data. The ε and ζ distributions show an under-sampling of the BII sub-state (ε ∼260°, ζ ∼180°), a defect that persists from the Drude-2013 force field despite having completely reparametrized the dihedral parameters for these two torsions in the present study. The χ and sugar pucker distributions indicate somewhat greater sampling of A-like states (χ ∼ 200°, North/C3′-endo pucker) than the survey data suggest should be present. The reasons for this behavior will be explored in subsequent sections.

Figure 2.

Dihedral distributions from 1-μs simulations of five B-DNA structures compared to a crystal survey consisting of all B-DNA structures with resolution ≤ 2.5 Å, excluding any structures containing modified nucleotides, protein, RNA, or ligands. (A) Backbone and glycosidic torsions. (B) Sugar pucker. Each distribution from the MD simulations is based on snapshots at 10-ps intervals for a total of 100,000 samples per system. Histograms were constructed using a bin size of 5°.

Sugar Puckering in B-DNA

While the results of the five B-DNA simulations clearly indicate that South pucker is the dominant form in these sequences (Figure 2), it is useful to consider the agreement of the Drude results with additional experimental data. Sugar pucker populations (North and South) can be calculated on a per-nucleotide basis using NMR, and data for the EcoRI sequence exist from residual dipolar coupling (RDC)⁷⁹ and J-coupling.⁸⁰ Figure 3 shows the calculated populations of North pucker compared to the available experimental data. In general, the fraction of North pucker is reproduced well, particularly through the AATT motif. A notable deviation occurs in guanine nucleotides, which show North populations that are somewhat too high. The Thy8 position also shows elevated North pucker, an outcome that was also observed in the Drude-2013 force field.¹⁹ This over-sampling of North pucker is unlikely to be a problem directly related to thymine, as the relative energetics of North and South states, and the barrier between them, was improved by the present refinement relative to Drude-2013 in a manner that should disfavor North pucker to a greater extent than the previous version of the force field.³³ Thus, additional factors, perhaps the over-sampling of North pucker in guanine nucleotides sampling local A-like geometries, may give rise to this behavior.

Figure 3.

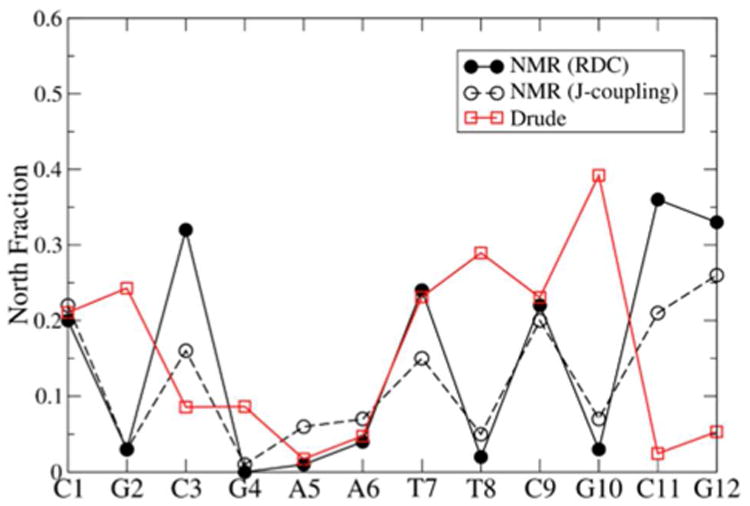
Fraction of North pucker content per nucleotide in the EcoRI dodecamer. Data were averaged over symmetric positions in the palindromic sequence. RDC data were taken from Wu et al.⁷⁹ and J-coupling data from Bax and Lerner.⁸⁰

Sequence-Specific BII Sampling in EcoRI

Additional insight into backbone torsional sampling can be obtained by calculating the BII content at each base step in a DNA sequence. Distinguishing between the BI and BII sub-states provides details into ε and ζ sampling, which give rise to local variations in the DNA backbone and properties of the major and minor grooves. Experimental data for the EcoRI sequence has been obtained using NMR, including refinement against SAXS ensembles.^81-82 Thus, it is possible to compare the backbone properties of the simulated EcoRI sequence with this important experimental observable. Figure 4 shows the fraction of BII as a function of the EcoRI sequence. Under-sampling of the BII sub-state was observed with the Drude-2013 force field, and this outcome persists using the reparametrized ε and ζ dihedrals, despite good agreement between the 1-D and 2-D QM and Drude potential energy surfaces.³³ The BII content through the central AATT motif of EcoRI is accurately represented, but BII content is very low towards the termini of the oligonucleotide chains.

Figure 4.

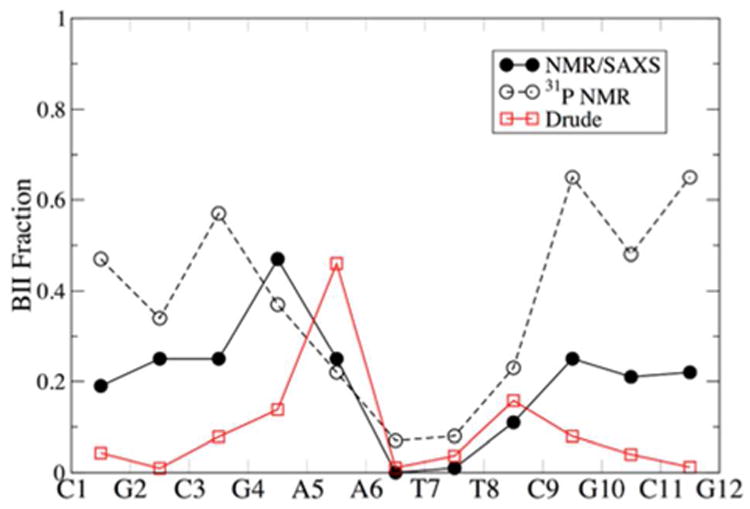
Fraction of BII content as a function of base step in the EcoRI dodecamer. Data were averaged over symmetric positions in the palindromic sequence. The NMR/SAXS data were taken from Schwieters and Clore,⁸¹ who used NOE, RDC, J-coupling, and chemical shift anisotropy data in concert with SAXS spectra for refinement, using the results of the optimal N_e = 4 model. The ³¹P NMR data were taken from Tian et al.⁸²

Sugar puckering is tightly coupled with χ sampling, which in turn modulates local DNA backbone geometry. Though the χ surfaces for all nucleoside model compounds indicate that the BII state (∼270°) is accessible,³³ it is rarely sampled across all B-DNA sequences examined here (Figure 2), with values instead shifted slightly downward towards A-like values (∼200°). The slight overrepresentation of A-like states is coupled to North sugar puckering, which is over-sampled in guanine nucleotides (Figure 3). Thus, it appears that the dominant BI sub-state of DNA is in equilibrium with A-like structures rather than the BII sub-state. Additional revision of sugar puckering dihedral terms may be required to rectify this sampling, but as will be shown below, agreement in puckering of A-DNA and Z-DNA structures presents an additional challenge in achieving such an agreement.

Helicoidal Parameters in B-DNA

The orientation of DNA bases relative to the helical axis can be quantified by a number of translational and rotational descriptors known as helicoidal parameters. These observables are a collective result of dihedral sampling and the strength of intermolecular forces between the bases, and as such are a stringent test of the quality of the force field model. Figure 5 shows the distributions of the twelve rotational and translational degrees of freedom from the MD simulations of B-DNA sequences, overlaid with the distributions from a crystal survey of B-DNA structures. In general, the helicoidal parameters obtained from the simulations align well with the crystal data, suggesting a reasonable representation of base orientations within the DNA structures. The refined parameters improve on the Drude-2013 results in terms of rise, which is the distance between consecutive bases along the helix axis. With the previous force field, rise was slightly overestimated,¹⁹ a reflection of the weaker stacking interactions between the bases.³³ As a result of the improved base stacking energetics, the values of rise fall in better agreement with the crystal survey (Figure 5). Propeller twist is slightly underestimated in the MD simulations, which is likely a result of the A-like sampling of some χ dihedrals (Figure 2), largely arising from cytosine and guanine nucleotides. Additional refinement of χ and exocyclic dihedrals may be required to obtain better agreement with propeller twisting across multiple B-DNA sequences.

Figure 5.

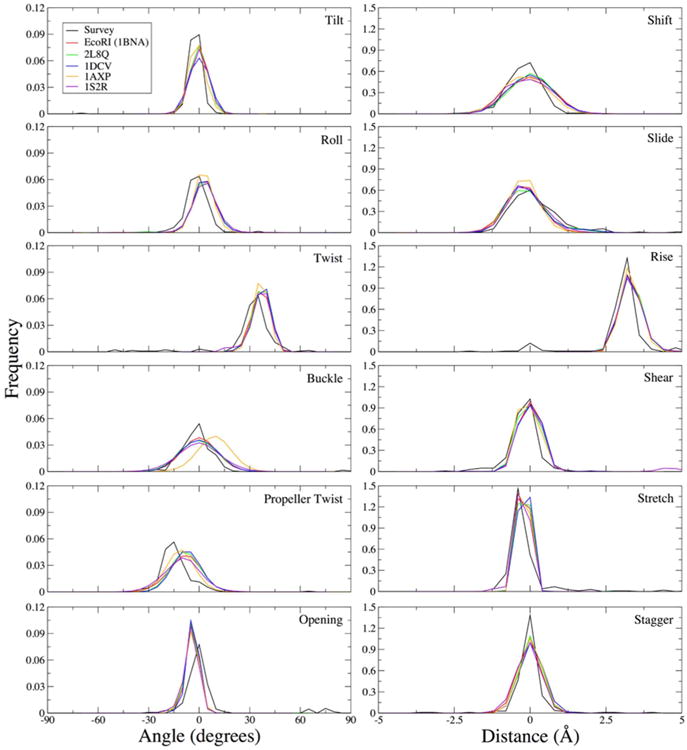
Helicoidal parameter distributions from 1-μs simulations of five B-DNA structures compared to a crystal survey consisting of all B-DNA structures with resolution ≤ 2.5 Å, excluding any structures containing modified nucleotides, protein, RNA, or ligands. Each distribution from the MD simulations is based on snapshots at 10-ps intervals for a total of 100,000 samples per system. Histograms were constructed using a bin size of 5° for angles and 0.4 Å for distances.

Base opening distributions are slightly shifted towards negative values, indicating opening of Watson-Crick hydrogen bonding in the minor groove. This outcome was observed in the Drude-2013 force field, as well, suggesting that additional refinement is necessary, as the current parameter refinement has not completely addressed this issue. Balancing water interactions with minor groove atoms required pair-specific LJ terms to resolve two overly favorable interactions (see above), but it is possible that additional corrections are required. Base pairing is described by the stretch parameter, which is the displacement along the local y-axis (along the hydrogen-bonding vector between paired bases). These distributions are in good agreement with the crystal survey (Figure 5). Distributions of N1…N3 distances in all five B-DNA sequences show similarly good agreement with the crystal survey (Figure S2). Together, these results indicate that the somewhat overly favorable in vacuo base-pair hydrogen bonding³³ does not distort DNA structures in solution.

Properties of A-tracts in B-DNA

DNA sequences containing four or more consecutive base pairs involving adenine are known as A-tracts. These sequences introduce curvature in the DNA along the helical axis^83-85 and are important for modulating DNA compaction in nucleosomes⁸³ and transcriptional activity.^{84, 86-88} Two of the sequences simulated in the present work contain A-tracts. 1S2R contains a six-base pair stretch of AAATTT and EcoRI has a four-base pair stretch of AATT. A-tracts are typically characterized by having narrower minor groove widths than GC-rich sequences and manifest more prominent propeller twisting,⁸³ as an A-T base pair forms only two hydrogen bonds, compared to the three formed in a C-G base pair, which favor a greater degree of co-planarity. Analysis of the sequence-dependent groove properties and propeller twisting in EcoRI is shown in Figure 6.

Figure 6.

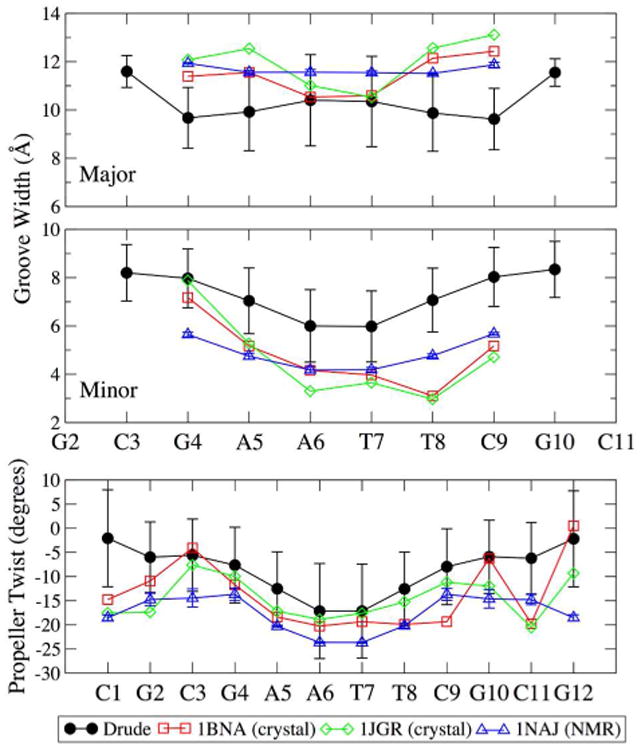
Groove widths and propeller twisting of EcoRI as a function of nucleotide position, calculated by Curves+.⁷⁸ Simulation data are the average for each equivalent nucleotide position in both strands over all frames, and error bars are the RMS fluctuations. Crystal structure properties were computed from PDB entries 1BNA⁵² and 1JGR⁸⁹ and average and standard deviations are shown for the five structures in the 1NAJ⁷⁹ NMR ensemble.

As expected, the minor groove narrowed through the EcoRI A-tract (Figure 6); this phenomenon was more pronounced in 1S2R (∼5.4 Å at the central AT step, Figure S3B) than it was in EcoRI (∼6 Å at the central AT step, Figure 6) since the A-tract in 1S2R is longer by two base pairs. The EcoRI minor groove widths as a function of the position in the A-tract (Figure 6) are slightly larger than those observed in crystal structures^{52, 89} and in crystals of similar A-tract sequences,⁸⁴ which have values on the order of ∼4 Å. The slight expansion of the minor groove relative to the crystal structures is likely due to hydration and the greater conformational flexibility of the structures in solution, but the narrowing as a function of sequence is in good agreement with the expected behavior. The minor groove widths are in better agreement with the NMR ensemble taken from PDB 1NAJ,⁷⁹ though the NMR experiments were performed in a lower ionic strength solution (∼40 mM NaCl), which may account for some differences in the structural properties.

Similarly, we observe the expected tendencies in propeller twisting as a function of the nucleotide sequence (Figures 5 and S3C). Propeller twisting is more exaggerated in the A-tracts than the terminal GC-rich regions, and again 1S2R manifests a more prominent degree of propeller twisting than EcoRI (Figure S3C). Although the overall tendency for propeller twisting across the five B-DNA sequences simulated in the present work is somewhat underestimated relative to the crystal survey populations (Figure 5), the sequence dependence of this property in simulations carried out in solution is well represented and agrees with expectations. Moreover, propeller twisting on the order of 15 - 20°, as manifested here in the EcoRI and 1S2R sequences, allows for the transient formation of bifurcated hydrogen bonds, believed to be a stabilizing factor in A-tract DNA sequences.⁸³ Propeller twisting towards the ends of the EcoRI nucleotide strands is slightly underestimated relative to crystal and NMR structures, but the behavior of the A-tract is consistent with experimental structures (Figure 6).

These A-tract properties give rise to an overall helix bending angle of 20° for EcoRI, in good agreement with the experimental value of 17.4 ± 0.3° calculated from the 1NAJ NMR ensemble.⁷⁹ The largest single-nucleotide contribution to bending (2.5 ± 1.7°) came from the central AT base pair, comparing well with the NMR value of 2.25 ± 0.02°. A-tracts bend towards the minor groove (negative roll), while non-A-tract DNA bends towards the major groove (positive roll).⁸⁵ Our simulation of EcoRI produced a roll value of -4.4 ± 12.4° at the central AT base pair, in reasonably good agreement with the NMR value of -2.9 ± 0.6°.

B-DNA Solution Conformational Ensembles

Solution X-ray scattering is a powerful experimental technique that provides a quantitative description of biomolecular size and shape in solution, as well as interactions across a range of length scales, thus informing our understanding of conformational ensembles. With respect to duplex DNA, the peak positions resolved in the scattering profiles provide information regarding backbone and sugar conformations (0.2 ≤ q ≤ 1.7 Å^-1) and base stacking (1.7 ≤ q ≤ 2.1 Å^-1), where the momentum transfer, q = (47πsinθ)/λ, λ is the X-ray wavelength, and 2θ is the scattering angle. The features of DNA X-ray scattering profiles are the summation of these different contributions,^90-91 and can be utilized as a stringent test of force field quality.⁹¹ We computed scattering profiles for the EcoRI and 1DCV sequences from snapshots at 1-ns intervals over the 1-μs simulations. For EcoRI, the whole sequence was considered, while the central 8 base pairs of the 10-base pair 1DCV were analyzed, as this region of the sequence was analyzed experimentally.⁹⁰ Figure 7 shows the computed and experimental X-ray scattering profiles for these two sequences, and peak positions are listed in Table 2.

Figure 7.

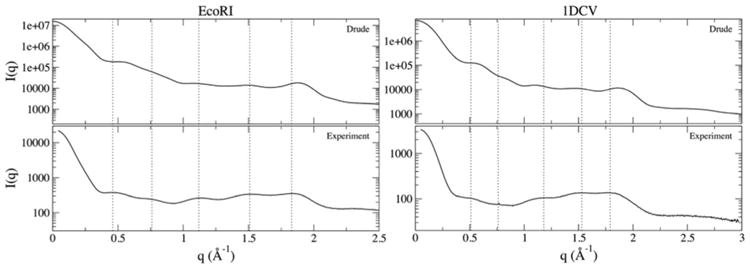
Solution X-ray scattering profiles for EcoRI and 1DCV from experiments⁹⁰ and from MD simulations using the Drude force field developed in this work. The computed simulation trajectories are the average of 1,000 snapshots extracted at 1-ns intervals over the course of the 1-μs trajectories. Simulation scattering profiles were calculated with CRYSOL.⁷⁰

Table 2.

Peak positions (Å^-1) from experimental and computed solution X-ray scattering profiles.

	Experiment		MD Simulation
	Assignmenta	First Derivativeb	Drude-2013c	Drude-New
EcoRI (12 bp)
P1	0.48	0.46	0.51	0.49
P2d	-	0.76	0.79	0.76
P3	1.14	1.12	1.12	1.07
P4	1.54	1.51	1.49	1.50
P5	1.87	1.83	1.80	1.88
1DCV (8 bp)
P1		0.51	0.52	0.52
P2d		0.76	0.82	0.81
P3		1.18	1.11	1.09
P4		1.53	1.50	1.47
P5		1.79	1.80	1.86

^aAssigned peak positions for EcoRI are from work by Zuo and Tiede,⁹⁰ as reported by Schwieters and Clore.⁸¹

^bComputed from zero-crossing points in the first derivative of the scattering profiles.

^cDrude-2013 results are taken from a previous study by Savelyev and MacKerell.²⁸

^dPlateau position estimated from first-derivative plots.

Peaks in the scattering profiles were calculated from zero-crossing points of the first derivative of the numerical data. In some cases, the calculated peaks differed from those reported experimentally (Table 2 and Figure S4). Peak positions for the EcoRI profile from Zuo and Tiede⁹⁰ were reported by Schwieters and Clore as part of their X-ray scattering refinement of the NMR ensemble.⁸¹ Discrepancies may arise from the noise in the experimental profiles near the peaks or smoothing functions that may have been applied after data collection. Peaks from the scattering profiles calculated from the MD snapshots could be identified unambiguously. For consistency, we rely solely on the first-derivative method for identifying peaks in the computed profiles, though we also interpret our results in terms of the experimental assignments for EcoRI.

Overall, the peak positions from the simulation ensembles for both EcoRI and 1DCV agree well with those obtained experimentally. The P1 and P2 positions in EcoRI are slightly improved with the refined Drude parameter set relative to those obtained using the Drude-2013 force field (Table 2).²⁸ The P1 peak is of particular importance as it describes the backbone structure and minor groove width; the good agreement between the simulation results and the experimental peak suggests that the refined Drude force field produces a reasonable model of backbone and minor groove properties. As noted above, the minor groove widths produced in our simulations of EcoRI were slightly larger than those observed in crystal and NMR structures, but the P1 peak position in the scattering profile suggests it is being modeled correctly. The P3-P5 positions remain in comparable agreement, though P5 merits additional discussion. The shift of P5 towards a larger q value (1.88 Å^-1) with the present force field is in better agreement with the experimental peak position (1.87 Å^-1) but is in slightly worse agreement with the peak position computed from the first-derivative analysis (1.83 Å^-1) than with Drude-2013. The P5 peak reports on base rise, with larger values of rise causing a downshift in the P5 position.⁹⁰ The distributions of rise obtained from all of our B-DNA simulations agreed well with expectations from the crystal survey (Figure 5), but the upshift in P5 position suggests that some values of rise were too small, perhaps reflecting contributions from GC steps that sampled A-like values of χ and sugar pucker, as described above. The agreement of the P5 position with the experimental assignment (1.87 Å^-1) suggests that any deviations from experimental structures may be small, especially given the fairly broad shape of the peak (Figure 7) and the greater uncertainty of peak positions in the WAXS region (q > 1.5 Å^-1) arising from limited theoretical and experimental resolution.⁹² Similar observations were made for the 1DCV sequence (Table 2), but overall the level of agreement between the experimental data and Drude simulation ensemble remains strong, suggesting that the properties of this GC-rich DNA sequence are modeled well.

A-DNA Response to Water Activity

DNA structure is sensitive to the polarity of the surrounding solution. In low water-activity media, the A-form helix dominates, while in more polar solvents (including water), the B-form dominates. To test the sensitivity of the refined Drude DNA force field to these effects, we carried out simulations of the 1ZF1 sequence⁵⁹ in 75%:25% (v:v) ethanol/water and in aqueous solution. In the low-polarity ethanol solution, the A-DNA form was largely maintained over the course of a 1-μs simulation (Figure 8A,B). The RMSD of non-terminal heavy atoms relative to the crystal (A-DNA) structure is 2.78 ± 0.1 Å, while using a modeled, ideal B-DNA form as reference, the RMSD is 3.66 ± 0.51 Å, indicating that the structure remains A-like. The RMSD relative to the A-form is slightly higher than that obtained with the Drude-2013 force field,¹⁹ but the structure retains characteristic A-DNA features, including a wide and broad minor groove, and displacement of the bases away from the helical axis (Figure 8B). The slightly elevated RMSD reflects greater flexibility of the structure relative to the previous version of the force field. Importantly, the refined force field retains the sensitivity to water observed previously. When simulated in aqueous solution with 120 mM NaCl, the 1ZF1 structure rapidly (< 25 ns) converted to a B-form helix that has a more compact structure along the helix axis (Figure 8C). The RMSD relative to the A-form is 3.30 ± 0.55 Å, while using an ideal B-form as reference yielded an RMSD of 2.24 ± 0.46 Å, similar to the results obtained with the Drude-2013 force field.¹⁹ Thus, the reparametrization carried out in the present work reasonably models A-form DNA as well as B-DNA, including the response to low-and high-polarity solvents.

Figure 8.

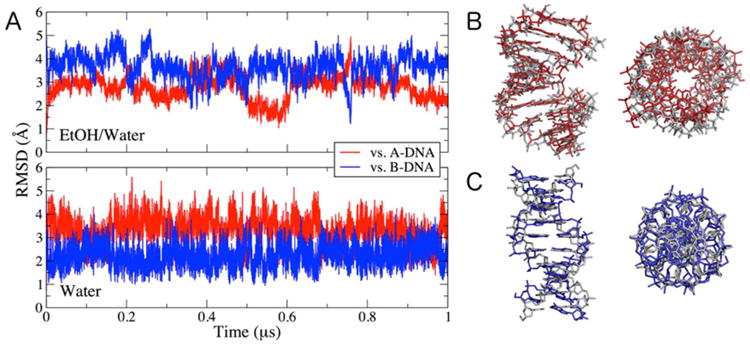
Stability of A-DNA sequence 1ZF1 in 75%:25% ethanol/water and water. (A) RMSD time series of non-terminal heavy atoms using the 1ZF1 A-DNA crystal structure and ideal B-DNA form as reference structures. (B) The final snapshot of the simulation in ethanol/water (red) overlaid with the crystal structure (gray) shown from the side and along the DNA helix axis. (C) The final snapshot of the simulation in water (blue) overlaid with the modeled, ideal B-DNA form (gray) shown from the side and along the DNA helix axis.

Z-DNA Crystals

In the development of the Drude-2013 DNA force field, it was observed that left-handed, Z-DNA structures were unstable on the time scale of a few ns in simulations in the crystal environment.¹⁹ Whereas Drude-2013 force field development focused on A- and B-DNA conformational energetics, the present refinement additionally targeted Z-DNA explicitly to correct this problem. A contributing defect in the Drude-2013 parameters that led to Z-DNA unwinding was inadequate backbone dihedral terms, particularly ε and ζ. One-dimensional conformational energy scans of the T3PS model compound revealed minima that did not coincide with QM potential energy surfaces or crystal survey populations.³³ Following the refinement described in the present work, we assessed the stability of three Z-DNA structures in their crystal environments. Given that the stability of Z-DNA is highly sensitive to its environment, this evaluation is a useful and important test of the quality of the new parameters.

Over the course of 100-ns simulations, the three Z-DNA structures (1ICK, 292D, and 1LJX) remain stable, with heavy atom RMSD values generally below 1.5 Å (Figure 9A). Distributions of sugar pucker (Figure 9B) indicate both North and South puckers are observed, with North pucker arising solely due to guanine nucleotides, as expected. However, the fraction of North pucker in guanine is somewhat underestimated (Figure 9B). Despite having achieved better agreement with the QM target data in the puckering potential energy surfaces of syn-deoxyguanosine with the updated Drude force field,³³ the presence of accessible C2′-endo minima appear to influence conformational sampling, though the errors are less pronounced than with the Drude-2013 force field, with which minimum energy positions deviated considerably from those of the QM surfaces. Efforts to increase the North-South energy barrier or to eliminate the C2′-endo minimum in the syn-deoxyguanosine sugar puckering surfaces led to undesirable distortion in B-DNA and were not pursued further. However, despite being somewhat under-sampled relative to the crystal survey data, it is clear that North pucker is more frequently sampled in these Z-DNA simulations than in the case of B-DNA, as expected. The present force field yields stable structures, but subtle details like sugar pucker equilibrium may require further attention and refinement. Achieving broad agreement in sugar puckering across different forms of DNA has been a persistent challenge in empirical force field development, and may be difficult to solve in light of issues such as anomeric effects around the glycosidic linkage.⁷ This outcome is manifested in the results shown above regarding B-DNA, which slightly over-sampled North pucker at guanine nucleotides (Figure 3).

Figure 9.

Structural properties of Z-DNA crystals. (A) Heavy atom RMSD of non-terminal nucleotides, (B) sugar puckering distributions, and (C) backbone and glycosidic dihedral distributions. For panels (B) and (C), the crystal survey includes the 17 structures listed in Methods.

Distributions of backbone and χ dihedrals (Figure 9C) indicate that the dihedral sampling of Z-DNA is in good agreement with the crystal survey data. An important consideration in evaluating these results is the fact that nearly all of the Z-DNA structures in the crystal survey were in complex with polyamines or multivalent ions, or were obtained at temperatures significantly below room temperature. While Mg²⁺ ions were retained in the structures simulated here, our simulations were carried out in the absence of any additional stabilizing co-solutes such as polyamines, which are present in both the 1ICK and 292D structures. Simulations were carried out at 293 K, which is the temperature at which the 1ICK and 1LJX crystals were grown; diffraction data were collected at 160 and 293 K, respectively. No temperature information was reported for 292D.⁴¹ Structural properties of 1LJX at 120 K were also reported,⁶⁷ though there were no major differences from those at 293 K, suggesting that the temperature chosen for the simulation is appropriate and unlikely to produce distorted structures. Additionally, since the 1LJX structure has B-factors reported at 293 K, a direct comparison can be made between these values and those computed from the MD simulation. The results of these calculations are shown in Supporting Figure S5. The pattern of the relative values of the B-factors is in good agreement between the simulation and the experimental crystal structure. The systematically higher experimental values are likely due to lattice disorder or other imperfections in the crystal, as previously discussed.^93-95 Thus, in light of the many experimental factors that enhance Z-DNA stability, the outcomes of our simulations indicate that the refined DNA force field yields stable Z-DNA structures in crystal environments, a significant improvement over the Drude-2013 force field, with which Z-DNA was unstable.

Conclusions

The present work has reported the development and validation of a refined polarizable force field for DNA based on the classical Drude oscillator model. The previous version of the force field, named Drude-2013,¹⁹ was stable on the scale of 100-200 ns, but subsequent simulations revealed that an inadequate description of base stacking led to destabilization during long simulations. Refinement of base nonbonded parameters (electrostatic and LJ) targeting high-level QM stacking energies, and bonded terms in the phosphodiester backbone and deoxyribofuranose sugar led to an overall improvement in backbone and sugar puckering conformational energetics.³³ Together, these efforts produced a refined polarizable force field capable of simulating DNA on the microsecond scale. B-DNA sequences, including those with A-tracts, were stable in 1-μs simulations and produced expected distributions of backbone dihedral angles. The computed solution X-ray scattering profiles of EcoRI and 1DCV were in good agreement with the experimental profiles, suggesting that the solution conformational ensemble produced in the simulation reflects many of the characteristics of these sequences that are observed experimentally. However, analysis of sequence-dependent behavior of local geometric terms such as sugar pucker and sampling of BII conformations indicate that there is room for improvement in the force field. The 1ZF1 A-DNA sequence retained its sensitivity to solvent polarity, reflecting the quality in the relative A-DNA and B-DNA stacking energetics. Z-DNA structures in their crystal environments were stable on the order of 100 ns, a considerable improvement from the Drude-2013 results, which showed Z-DNA unfolded to a ladder-like structure within 5 ns.

As we have previously shown the importance of explicit polarization in DNA dynamics, including base flipping thermodynamics³¹ and response to ions,^28-30 the stability of DNA during long MD simulations is critical towards the goal of studying biologically relevant phenomena in detail. The present version of the force field achieves such stability. Future refinement will be necessary to correct guanine sugar puckering, as the North form is somewhat overestimated in B-DNA, yet underestimated in Z-DNA, suggesting that refinement of the barrier between North and South states requires additional attention. The BII state is under-sampled in EcoRI, though comparable agreement is achieved with respect to the Drude-2013 results. Given that the ε and ζ dihedral terms had to be completely reparametrized to yield stable Z-DNA, this outcome is acceptable, and may be due in greater part to a deficiency in sugar puckering rather than the dihedral terms describing these torsions, as North pucker is sterically incompatible with the BII backbone sub-state.

The refined Drude DNA force field, to be referred to as Drude-2017, will be made available on the MacKerell lab website (http://mackerell.umaryland.edu/) and will be incorporated in the CHARMM-GUI⁹⁶ Drude Prepper module (http://www.charmm-gui.org).