Abstract
The unbinding dynamics of complexes involving cell-adhesion molecules depends on the specific ligands. Atomic force microscopy measurements have shown that for the specific P-selectin–P-selectin glycoprotein ligand (sPSGL-1) the average bond lifetime 〈t〉 initially increases (catch bonds) at low (≤10 pN) constant force, f, and decreases when f > 10 pN (slip bonds). In contrast, for the complex with G1 anti-P-selectin monoclonal antibody 〈t〉 monotonically decreases with f. To quantitatively map the energy landscape of such complexes we use a model that considers the possibility of redistribution of population from one force-free state to another force-stabilized bound state. The excellent agreement between theory and experiments allows us to extract energy landscape parameters by fitting the calculated curves to the lifetime measurements for both sPSGL-1 and G1. Surprisingly, the unbinding transition state for P-selectin–G1 complex is close (0.32 nm) to the bound state, implying that the interaction is brittle, i.e., once deformed, the complex fractures. In contrast, the unbinding transition state of the P-selectin–sPSGL-1 complex is far (≈ 1.5 nm) from the bound state, indicative of a compliant structure. Constant f energy landscape parameters are used to compute the distributions of unbinding times and unbinding forces as a function of the loading rate, rf. For a given rf, unbinding of sPSGL-1 occurs over a broader range of f with the most probable f being an order of magnitude less than for G1. The theory for cell adhesion complexes can be used to predict the outcomes of unbinding of other protein–protein complexes.
Formation and breakage of noncovalent protein–protein interactions are crucial in the functions of cell-adhesion complexes. Adhesive interactions between leukocytes and blood vessel walls involve a dynamic competition between bond formation and breakage (1). Under physiological conditions of blood circulation, the hydrodynamic force of the flow is applied to the linkage between leukocytes and endothelium. Rolling of cells requires transient tethering of the cell to the substrate and subsequent dissociation at high shear rates that are generated by the hydrodynamic flow field. Because of the requirement of adhesive interaction and the breakage of such bonds to facilitate rolling, only a certain class of molecules is involved in the recognition process. The remarkable rolling function is mediated by Ca2+-dependent specific bonds between the family of L-, E-, and P-selectin receptors and their specific ligands such as ESL-1, podocalyxin, and PSGL-1 (2–6). Specific interactions of P-selectins, expressed in endothelial cells or platelets, with PSGL-1 (P-selectin glycoprotein ligand 1) enable leukocytes to roll on vascular surfaces during the inflammatory response by transient interruption of cell transport (tethering) in blood flow under constant wall shear stress. These interactions have been used extensively to probe tethering and rolling of leukocytes on vascular surfaces in flow channel experiments (2–15). Experiments show that the dissociation rates (also referred to as off-rates), which govern cell unbinding kinetics, increase with increasing shear stress or equivalently the applied force.
It is generally believed that the applied force lowers the free-energy barrier to bond rupture and, thus, shortens bond lifetimes (16). In contrast, Dembo et al. (17, 18) hypothesized that force could also prolong bond lifetimes by deforming the adhesion complexes into an alternative locked or bound state. These two distinct dynamic responses to external force are referred to as slip and catch bonds (17, 18). Whereas the dynamics of slip bonds has been extensively studied (5, 6, 13, 19–22), up until recently, evidence for catch bonds has been lacking. Using atomic force microscopy (AFM), Marshall et al. (1) measured the force dependence of lifetimes of P-selectin with two forms of PSGL-1, namely, the monomeric and dimeric ligands sPSGL-1 and PSGL-1, which form, respectively, a single and double bond with P-selectin, and with G1, a blocking anti-P-selectin monoclonal antibody. The bond lifetimes were measured at values of forces that are lower than the level of their fluctuations by averaging over a large number of single lifetime-force trajectories (1). The average bond lifetime of the highly specific P-selectin interaction with PSGL-1 initially increased with force, indicating catch bonds (1). Beyond a critical force, the average lifetime decreased with force, as expected for slip bonds (1). In contrast to the behavior for specific P-selectin–PSGL-1 complexes, P-selectin–G1 bond lifetimes decreased exponentially with force in accordance with the predictions of the Bell model (16). Marshal et al. (1) also found that both P-selectin–PSGL-1 and P-selectin–G1 bond lifetimes measured at a fixed force appeared to follow a Poissonian distribution.
The complex dynamical response of the P-selectin–PSGL-1 complex to force can be used to map the energy landscape of interaction between the macromolecules (23). For complexes, whose force-dependent behavior can be described by the Bell model, the unbinding involves escape from a single bound state. The observed behavior in P-selectin–PSGL-1 complex requires an energy landscape model with at least two bound states, one of which is preferentially stabilized by force. Such a model has already been proposed for a complex involving GTPase Ran, a small protein that regulates transport of macromolecules between the cell nucleus and cytoplasm, and the nuclear import receptor importin β1 (24). Unbinding studies by AFM reveals that this complex fluctuates between two conformational states at different values of the force. The purpose of the present work is to show that the observed catch–slip behavior in specific protein–protein complexes in general and P-selectin–PSGL-1 in particular can be captured by using an energy landscape that allows for just two bound states. The lifetime associated with bound states of the complex are assumed to be given by the Bell model (16). Although the Bell model is only approximate (25), it describes well the dissociation of single L-selectin bonds over a broad range of loading rates (26). Using the two-state model, we show that the experimental results for P-selectin–PSGL-1 complex can be quantitatively explained by using parameters that characterize the energy landscape. In accord with experiments, we also find that the application of the same model to the unbinding of the ligand from P-selectin–G1 complex shows the absence of the second bound state. Thus, a unified description of specific and nonspecific protein–protein interaction emerges by comparing theory with experiments.
Theory and Methods
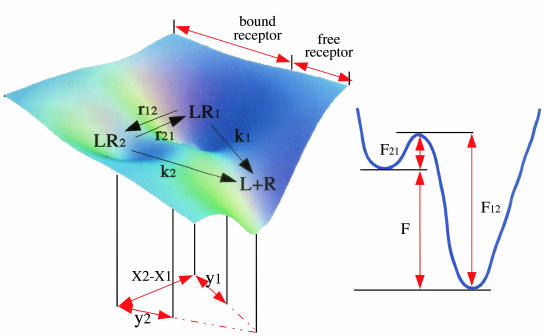
The Model. We use a two-state model (Fig. 1) for the energy landscape governing P-selectin–ligand interaction, in which a single P-selectin receptor (R) forms an adhesion complex (LR) with a ligand (L). The complex LR undergoes conformational fluctuations between states LR1 and LR2 with rates r12 = r10exp[–F12/kBT] and r21 = r20exp[–F21/kBT] for transitions LR1 → LR2 and LR2 → LR1 with barrier height F12 and F21, respectively. The attempt frequencies r10 and r20 depend on the shape of the free-energy landscape characterizing LR1 ⇄ LR2 transitions. In the absence of force, f, the equilibrium constant, Keq, between LR1 and LR2 is given by Keq ≡ r12/r21 = (r10/r20) e–F/kBT, where F is the free energy of stability of LR1 with respect to LR2 (Fig. 1). In the presence of f, Keq becomes 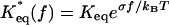 , where σ = x2 – x1, the conformational compliance, is the distance between the minima. Force alters the free-energy landscape of P-selectin–ligand unbinding (Fig. 1) and, thus, alters the bond breakage rates k1(f) and k2(f), which, according to the Bell model, are given by k1 = k10 ey1f/kBT and k2 = k20ey2f/kBT (16). The prefactors k10 and k20 are the force-free bond-breakage rates, and y1, y2 are the minimal adhesion bond lengths at which the complex becomes unstable [distances between energy minima of states LR1 and LR2 and their respective transition states (Fig. 1)]. We assume that in the presence of f, the probability of rebinding is small. The dynamics of the adhesion complex in free-energy landscape, which is set by the parameters σ, y1, and y2, can be inferred by using lifetime measurements of P-selectin–ligand bonds subject to a pulling force. We consider an experimental setup in which the applied force is either constant or ramped up with a constant loading rate rf = κv0, where κ is a cantilever spring constant and v0 is the pulling speed.
, where σ = x2 – x1, the conformational compliance, is the distance between the minima. Force alters the free-energy landscape of P-selectin–ligand unbinding (Fig. 1) and, thus, alters the bond breakage rates k1(f) and k2(f), which, according to the Bell model, are given by k1 = k10 ey1f/kBT and k2 = k20ey2f/kBT (16). The prefactors k10 and k20 are the force-free bond-breakage rates, and y1, y2 are the minimal adhesion bond lengths at which the complex becomes unstable [distances between energy minima of states LR1 and LR2 and their respective transition states (Fig. 1)]. We assume that in the presence of f, the probability of rebinding is small. The dynamics of the adhesion complex in free-energy landscape, which is set by the parameters σ, y1, and y2, can be inferred by using lifetime measurements of P-selectin–ligand bonds subject to a pulling force. We consider an experimental setup in which the applied force is either constant or ramped up with a constant loading rate rf = κv0, where κ is a cantilever spring constant and v0 is the pulling speed.
Fig. 1.
Schematic of the energy landscape for protein–protein interaction in general and complexes involving cell adhesion molecules in particular (Left). The 1D-profile on the right shows the conformational free energy and the parameters that characterize the binding landscape. External force shifts the force-free equilibrium, resulting in redistribution of population from LR1 to LR2. Force-induced alteration in the free-energy landscape is dynamically coupled to forced unbinding.
Distributions of Bond Lifetime at Constant Force. When f is constant, the populations P1(t) and P2(t) of states LR1 and LR2 can be calculated by solving the system of equations
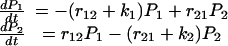 |
[1] |
subject to initial conditions P1(0) = 1/(Keq + 1) and P2(0) = Keq/(Keq + 1). In the AFM experiments, f fluctuates slightly around a constant value. The smoothness of the dependence of the lifetimes on f suggests that these fluctuations are not significant. The solution to Eq. 1 is
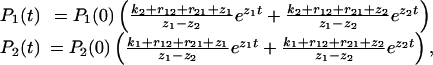 |
[2] |
where 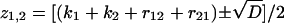 and D = (k1 + k2 + r12 + r21)2 – 4(k1k2 + k1r21 + k2r12). The ensemble average nth moment of the bond lifetime is
and D = (k1 + k2 + r12 + r21)2 – 4(k1k2 + k1r21 + k2r12). The ensemble average nth moment of the bond lifetime is
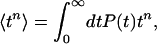 |
[3] |
where the distribution of lifetimes, P(t) = P1(t) + P2(t), is given by the sum of contribution from states LR1 and LR2. In the limit of slow conformational fluctuations (i.e., when r12, r21 ≪ k1, k2), P(t) = P1(0)exp[–k1t] + P2(0)exp[–k2t], whereas P(t) = exp[–(k1 + k2)t] in the opposite case.
Distributions of Unbinding Times and Forces for Time-Dependent Force. When the pulling force is ramped up with the loading rate, i.e., f(t) = rft, the rate constants k1 k2, r12 and r21 become time-dependent and P1(t) and P2(t) are computed by numerically solving Eq. 1. The distribution of unbinding times, pt(t), is pt(t) ≡ k1(t)P1(t) + k2(t)P2(t) and the distribution of unbinding forces, pf(f), can be computed by rescaling (t, pt(t)) → (rft, pf(f)), where pf = (1/rf)[k1(f)P1(f/rf) + k2(f)P2(f/rf)]. The typical rupture force vs. loading rate, f*(rf), is obtained from pf(f) by finding extremum, (d/dt)pf|f=f* = 0 (5, 6).
Results
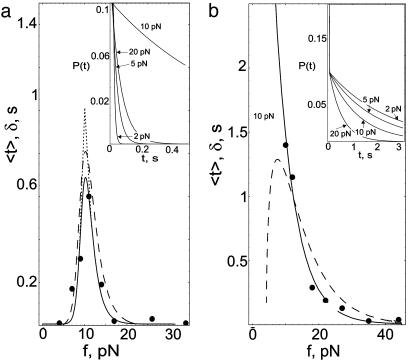
Unbinding Under Constant Force. We calculated the distribution of bond lifetimes, P(t), average lifetime-force characteristics, 〈t(f)〉, and lifetime fluctuations, 〈t2〉 – 〈t〉2. The model parameters of the energy landscape were obtained by fitting the theoretical curves of 〈t〉 vs. f to the experimental data (1) for P-selectin adhesion complexes with monomeric form sPSGL-1 and antibody G1 (see Fig. 3 in ref. 1). The lifetime-force data were adjusted to exclude experimental noise. The results displayed in Fig. 2 were obtained by using the model parameters given in Table 1 (all calculations were performed at room temperature). Since Keq ≪ 1 for sPSGL-1, in the absence of force, binding of P-selectins with sPSGL-1 stabilizes LR1 of the P-selectin. For the antibody G1, Keq = 1(k10 = k20 and y1 = y2), indicating that both states are equally stable, leading to a landscape with one minimum. P-selectins form a stronger adhesion complex with G1 compared to sPSGL-1: k10 for G1 is smaller than k10 for sPSGL-1, and y1 is smaller than y1 or y2 for sPSGL-1. This finding implies that adhesion complexes with G1 are less sensitive to the applied force.
Fig. 2.
Computed average lifetime 〈t(f)〉 (solid line) and standard deviation δ(f) (dashed line) vs. pulling force for P-selectin complex with sPSGL-1 (a) and G1 (b). Filled circles are experimental data points from figure 3 in ref. (1). 〈t〉 decays monotonically for G1. Sharp growth of 〈t〉 for sPSGL-1 at f < fc ≈ 10 pN, followed by decay to zero at f > fc marks the transition from catch to slip regime of unbinding. Average catch and slip bond lifetimes computed from the corresponding distributions kcatche–kcatcht and kslipe–kslipt are denoted by ascending and descending dotted lines, respectively. The distributions of bond lifetimes, P(t), for f = 2, 5, 10, and 20 pN are shown in the Inset. Note the redistribution of P(t) at longer unbinding times for sPSGL-1 as f is increased to fc followed by narrowing at shorter times for f > fc. In contrast, P(t) for G1 narrows as f is increased in the range 2–20 pN.
Table 1.
Model parameters for specific ligand sPSGL-1 and antibody G1 unbinding kinetics obtained by fitting the average lifetime-force characteristics, 〈t(f)〉, for P-selectin adhesion complexes reported in ref. 1 with the theoretical results (see Eq. 3)
| Ligand | r10, 1/s | r20, 1/s | σ, nm | k10, 1/s | k20, 1/s | y1, nm | y2, nm |
|---|---|---|---|---|---|---|---|
| sPSGL-1 | 5.0 | 40.0 | 5.5 | 100 | 0.05 | 1.5 | 1.1 |
| G1 | 10.0 | 10.0 | 6.0 | 0.35 | 0.35 | 0.32 | 0.32 |
Let us discuss the kinetic mechanism of transition from catch to slip bonds for unbinding of sPSGL-1. At forces below ≈3pN, r12 ≈ r10, r21 ≈ r20, and k1 ≈ k10, k2 ≈ k20. In this regime, unbinding occurs from state LR1 (P*1(0) ≫ P*2(0)). In the intermediate force regime, 3 < f ≤ 10 – 12pN, k1 ≫ k2, r12 ≫ r21, and, hence, P*1(0) ≪ P*2(0) (k1 ≪ r12 due to y1 ≪ σ, see Table 1). In this limit, the unbinding dynamics is dominated by decay from state LR2 with the smallest eigenvalue z1 (corresponding to the longest time scale 1/z1), which is 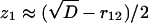 , where
, where 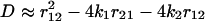 . Expanding
. Expanding 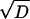 in power of
in power of 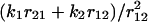 and retaining only the first order term, we see that the distribution of bond lifetimes is determined by the unbinding rate
and retaining only the first order term, we see that the distribution of bond lifetimes is determined by the unbinding rate
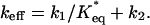 |
[4] |
At low forces, keff is dominated by the first term in Eq. 4 so that keff is given by the catch rate constant, keff = kcatch ≈ k1/K*eq, decreasing with f due to the increase in K*eq. For f greater than a critical force fc ≈ 10 pN, unbinding occurs from state LR2 with rate keff = kslip ≈ k2, which increases with f. As a result, the dual behavior is observed in the average lifetime, 〈t〉, which grows sharply at low f reaching a maximum at (fc, 〈t*〉) ≈ (10 pN, 0.7s). For f > fc, 〈t〉 decays to zero, indicating the transition from catch to slip bonds (Fig. 2a). In contrast, 〈t〉 for a complex with G1 starts off at ≈5 s for f ≈ 5 pN (data not shown) and decays to zero at higher values of f (Fig. 2b). There is also qualitative difference in the lifetime fluctuations for sPSGL-1 and G1. For sPSGL-1, 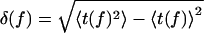 has a peak at (fc, 〈t*〉). However, for G1, δ(f) is peaked at lower f and undergoes a slower decay at large f compared with sPSGL-1 (Fig. 2).
has a peak at (fc, 〈t*〉). However, for G1, δ(f) is peaked at lower f and undergoes a slower decay at large f compared with sPSGL-1 (Fig. 2).
For binding to sPSGL-1, increase of f to ≈10 pN, results in the redistribution of P(t) around longer lifetimes (compare curves for f = 2, 5, and 10 pN in Fig. 2a). When f exceeds 10 pN, P(t) shifts back toward shorter lifetimes. In contrast, P(t) for complexes with G1 is Poissonian, ≈e–tk1(f) and the growth of k1 with f favors shorter bond lifetimes as f is increased. Stretching of complexes with sPSGL-1 couples conformational relaxation and unbinding in the range 0–10 pN and leads to unbinding only when f > 10 pN. Thus, force plays two competing roles: It facilitates unbinding and funnels the P-selectin population into a force-stabilized bound state, LR2. At low forces redistribution of initial (force-free) population of bound states [P1 = 1/(Keq + 1) > P2 = Keq/(Keq + 1)] into force-dependent population 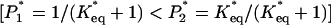 competes with unbinding. When f exceeds a critical force ≈10 pN, the dynamics of unbinding is determined by the bond breakage from maximally populated state LR2. In this force regime, the distribution of lifetimes becomes again Poissonian,
competes with unbinding. When f exceeds a critical force ≈10 pN, the dynamics of unbinding is determined by the bond breakage from maximally populated state LR2. In this force regime, the distribution of lifetimes becomes again Poissonian, 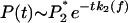 , and narrows at shorter lifetimes for large f (Fig. 2).
, and narrows at shorter lifetimes for large f (Fig. 2).
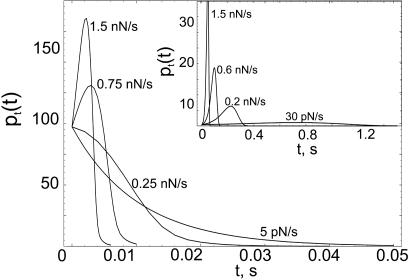
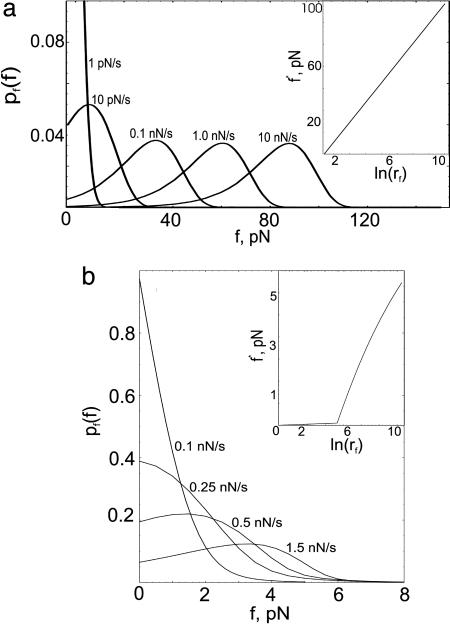
Pulling Speed Dependence of Unbinding Times and Forces. The excellent agreement between theory and experiment, which allows us to extract the parameters that characterize the energy landscape (Fig. 1) of the adhesion complexes, validates the model. By fixing these parameters, we have obtained predictions for pt(t), pf(f), and f* as a function of rf for sPSGL-1 and G1 unbinding from P-selectins. Because G1 possesses a higher affinity to P-selectins (compare k10, k20, and y1, y2 in Table 1), pt(t) computed for G1 exhibits an order of magnitude slower decay compared with pt(t) for sPSGL-1. For a given rf, pt for G1 has a peak that is smeared somewhat out at smaller rf, whereas pt for sPSGL-1 starts to develop a peak only at rf > 0.3 nN/s (Fig. 3). The peak position of pt approaches zero and the width decreases as rf is increased implying faster unbinding for both ligands. In contrast to pt(0), pf(0) decreases and f* increases as rf is increased for both G1 and sPSGL-1 (see Fig. 4). This finding implies that in contrast to unbinding times, increasing rf favors unbinding events occurring at larger forces (5, 6). Comparison of pt(t) and pf(f) for G1 and sPSGL-1 at a given rf shows that, although P-selectin forms a tighter adhesion complex with G1, a linear increase of the applied force affects the stability of the complex with G1 more profoundly compared with sPSGL-1. The presence of force-stabilized bound state LR2 for sPSGL-1 facilitates a dynamical mechanism for alleviating the applied mechanical stress with higher efficiency, compared with single-state Michaelis–Menten kinetics, L + R ⇋ LR for G1. This is illustrated in the Insets of Fig. 4, where we compared f* as a function of log(rf) for sPSGL-1 and G1. f* is a straight line for G1. Due to dynamic disorder (27, 28), f*(rf) for sPSGL-1 is convex up with initial and final slopes signifying two distinct mechanisms of P-selectin–sPSGL-1 bond rupture.
Fig. 3.
The distribution of unbinding times, pt(t), for sPSGL-1 computed for loading rates rf = 5pN/s, and 0.25, 0.75, and 1.5 nN/s. Same distribution for G1 is given in the Inset for rf = 30 pN/s, and 0.2, 0.6, and 1.5 nN/s. For both sPSGL-1 and G1, pt(t) starts off at a fixed probability and decays to zero at longer unbinding times for G1. For both ligands, the peak position of pt approaches zero and the width decreases as rf is increased.
Fig. 4.
The distribution of unbinding forces, pf(f), for G1 computed for loading rates rf = 1.0 pN/s, 10 pN/s, and 0.1, 1.0, 10 nN/s(a) and for sPSGL-1 (rf = 0.1, 0.25, 0.5, and 1.5 nN/s; b). For G1, pf(f) is broad, varying in the range 0 < f < 120 pN for 0.1 nN/s < rf < 1.5 nN/s. Variation in f is greatly reduced to 0–10 pN for sPSGL-1. For both ligands, the width of pf(f) does not vary with rf. Semilogarithmic plots of typical rupture force f* vs. rf (in unites of pN/s) given in the Insets show that f* is nonvanishing already at rf ∼ 10 pN/s and grows to 60 pN in the range 0 < rf < 1.2 nN/s for G1, while f* = 0 until rf ∼ 150 pN/s and barely reaches 3 pN in the same range of rf for sPSGL-1.
Discussion and Conclusions
To account for the transition between catch and slip bonds of P-selectin–PSGL-1 complex in the forced unbinding dynamics, we have considered a minimal kinetic model that assumes that P-selectins may undergo conformational fluctuations between the two states. Both fluctuations and P-selectin–ligand bond breaking are modulated by the applied force that not only enhances the unbinding rates but also alters the thermodynamic stability of the two states (Fig. 1). Using four parameters, namely, the rates r12, r21 of conformational fluctuations and k1, k2 of unbinding and the Bell model, we computed the distribution of bond lifetimes, the ensemble average bond lifetime, and lifetime fluctuations. The calculations are in excellent agreement with the experimental data on the unbinding of cell-adhesion complexes at constant force (1). The parameters, extracted by fitting the theoretical curves to experiment, allow us to obtain quantitatively the energy landscape characteristics. The fitted parameters show that the dual catch–slip character of the P-selectin–sPSGL-1 complex can only be explained in terms of two bound states. In the force-free regime, P-selectin–sPSGL-1 exists predominantly in one conformational state with higher thermodynamic stability (Keq ≪ 1). The release of sPSGL-1 is much faster compared with the unstable state (k10 ≫ k20). In contrast, using the same model, we found that G1 forms a tighter adhesion complex with P-selectin compared with sPSGL-1. The two states are equally stable when P-selectins bind to form a tighter complex (compared with binding with sPSGL-1) with antibody G1 (Keq = 1). For G1, these states are kinetically indistinguishable both in the force-free regime (k10 = k20) and when the force is applied (y1 ≈ y2), implying a single bound state.
The conformational compliance, σ, which leads to a decrease, σ f, of the free-energy barrier separating the two free-energy minima, are similar for sPSGL-1 and G1. Bound and unbound P-selectin states are more separated in the free-energy landscape when bound to sPSGL-1. For sPSGL-1, the LR1 and LR2 bond starts to break when the bond length exceeds 1.5 nm (y1) and 1.1 nm (y2), respectively. For G1 the distance from the only bound state to the transition state is only 0.32 nm, implying that the transition state is close to the bound state. The free-energy difference F between states LR1 and LR2 of P-selectin–sPSGL-1, which is obtained by equating r12 and r21 for sPSGL-1, is of the order of 2kBT. From the assumption that when P1 ≪ P2 the free-energy barrier for transition LR1 → LR2 disappears, we found that the barrier height is F21 ≈ 5 – 6kBT (see Fig. 1). Because of the presence of a more thermodynamically stable conformational state at higher values of f (for sPSGL-1), the average P-selectin–sPSGL-1 complex lifetime exhibits an initial increase at 0 ≤ f ≤ 10 pN (catch bond). After the force exceeds a critical force fc ∼ 10 pN, the bond breakage rate of the force-stabilized state becomes nonnegligible and the bond lifetime decreases (slip bond). In both catch and slip regimes, the dynamics of unbinding can be characterized by the catch and slip bond rates kcatch and kslip, respectively. The transition from catch to slip regime allows P-selectins to dynamically regulate their activity toward specific ligands such as sPSGL-1 by means of extending the bond lifetime within a physiologically relevant range of mechanical stress and differentiate them from other biological molecules such as antibody G1 with k1 ≈ k2. Because of this, force profiles of bond lifetime for unbinding of G1 and sPSGL-1 are both qualitatively and quantitatively different. The microscopic mechanisms for dissipating external perturbation induced by mechanical stress or hydrodynamic flow are distinctly different for sPSGL-1 and G1. In the case of G1, a mechanical stress breaks the P-selectin–G1 bond. However, in the case of sPSGL-1, at low values of force the mechanical stress is dissipated by P-selectin conformational relaxation rapidly attaining a new equilibrium (P1 > P2) → (P*1 < P*2) as force is increased. When f = fc ≈ 10 pN, the population of the locked state reaches a maximum (P*2 ≈ 1), and only at higher forces, f > fc, does unbinding occur.
We have used our model to obtain testable experimental predictions for the distributions of unbinding times, pt(t), unbinding forces, pf(f), and typical rupture force, f*, at finite pulling speeds. These quantities can be directly accessed through experiment in which a pulling force is ramped up following a linear dependence on time, i.e., f = rft. These calculations further confirm that P-selectin forms a tighter adhesion complex with antibody G1 that lives (on average) 10–20 times longer compared with a complex with sSPGL-1. In contrast to pt(t) for which the average lifetime is inversely proportional to rf for both ligands, the peak position of pf(f) increases with pulling speed. This tendency is slower for a complex with sPSGL-1; a 10-fold increase of rf from 0.1 nN/s to 1.0 nN/s shifts pf by 30 pN for G1 and only by 3 pN for sPSGL-1. We directly compared the most probable rupture force f* vs. rf for G1 and sPSGL-1 in the range 0 < rf < 1.2 nN/s and observed an increase of f* from 0 to 80 pN in the case of G1 and only a marginal change from 0 to 3.5 pN in the case of sPSGL-1 (Fig. 4). Our findings demonstrate that a two-state P-selectin system with an increasingly more stable (at large forces) slow ligand releasing locked state may serve as an effective molecular device that can relieve mechanical stress with a surprisingly high efficiency. The resulting dual response to stretching provides a simple mechanokinetic mechanism for regulating cell adhesion under physiological conditions of varying shear force. The theory described here can also be used to analyze force-induced unfolding of protein–protein complexes. More generally, the model in conjunction with mechanical unfolding experiments can be used to map the characteristics of the energy landscape of complexes involving biological macromolecules.
Acknowledgments
This work was supported by the National Science Foundation.
Author contributions: V.B. and D.T. designed research; V.B. performed research; V.B. analyzed data; and V.B. and D.T. wrote the paper
This paper was submitted directly (Track II) to the PNAS office.
Note Added in Proof. After this article was accepted, we became aware of a related article (29).
References
- 1.Marshall, B. T., Long, M., Piper, J. W., Yago, T., McEver, R. P. & Zhu, C. (2003) Nature 423, 190–193. [DOI] [PubMed] [Google Scholar]
- 2.Lawrence, M. B. & Springer, T. A. (1991) Cell 65, 859–873. [DOI] [PubMed] [Google Scholar]
- 3.Springer, T. A. (1994) Cell 76, 301–314. [DOI] [PubMed] [Google Scholar]
- 4.Springer, T. A. (1990) Nature 346, 425–434. [DOI] [PubMed] [Google Scholar]
- 5.Evans, E., Leung, A., Hammer, D. & Simon, S. (2001) Proc. Natl. Acad. Sci. USA 98, 3784–3789. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Evans, E. & Ritchi, K. (1997) Biophys. J. 72, 1541–1555. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Westweber, D. & Blanks, J. E. (1999) Physiol. Rev. 79, 181–213. [DOI] [PubMed] [Google Scholar]
- 8.McEver, R. P. & Cummings, R. D. (1997) J. Clin. Invest. 100, 485–491. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Sako, D., Comess, K. M., Barone, K. M., Camphausen, R. T., Cummings, D. A. & Shaw, G. D. (1995) Cell 83, 323–331. [DOI] [PubMed] [Google Scholar]
- 10.Alon, R., Chen, S., Puri, K. D., Finger, E. B. & Springer, T. A. (1997) J. Cell Biol. 138, 1169–1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Lawrence, M. B., Kansas, G. S., Kunkel, E. J. & Ley, K. (1997) J. Cell Biol. 136, 717–727. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Finger, E. B., Purl, K. D., Alon, R., Lawrence, M. B., von Andrian, U. H. & Springer, T. A. (1996) Nature 379, 266–269. [DOI] [PubMed] [Google Scholar]
- 13.Alon, R., Hammer, D. A. & Springer, T. A. (1995) Nature 374, 539–542. [DOI] [PubMed] [Google Scholar]
- 14.Kaplanski, G., Farnarier, C., Tissot, O., Pierres, A., Benoliel, A.-M., Alessi, M.-C., Kaplanski, S. & Bongrand, P. (1993) Biophys. J. 64, 1922–1933. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Brunk, D. K., Goetz, D. J. & Hammer, D. A. (1996) Biophys. J. 71, 2902–2907. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Bell, G. L. (1978) Science 200, 618–627. [DOI] [PubMed] [Google Scholar]
- 17.Dembo, M., Tourney, D. C., Saxman, K. & Hammer, D. (1988) Proc. R. Soc. London 234, 55–83. [DOI] [PubMed] [Google Scholar]
- 18.Dembo, M. (1994) Lectures on Mathematics in the Life Sciences: Some Mathematical Problems in Biology (Am. Mathematical Soc., Providence, RI), pp. 51–77.
- 19.Pierres, A., Banoliel, A. M., Bongrand, P. & van der Merwe, P. A. (1996) Proc. Natl. Acad. Sci. USA 93, 15114–15118. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Smith, M. J., Berg, E. L. & Lawrence, M. B. (1999) Biophys. J. 77, 3371–3383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ramachandran, V., Yago, T., Epperson, T. K., Kobzdej, M. M. A., Nollert, M. U., Cummings, R. D., Zhu, C. & McEver, R. P. (2001) Proc. Natl. Acad. Sci. USA 98, 10166–10171. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Merkel, R., Nassoy, P., Leung, A., Ritchi, R. & Evans, E. (1999) Nature 397, 50–53. [DOI] [PubMed] [Google Scholar]
- 23.Hyeon, C. & Thirumalai, D. (2003) Proc. Natl. Acad. Sci. USA 100, 10249–10253. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nevo, R., Stroh, C., Kienberger, F., Kaftan, D., Brumfeld, V., Elbaum, M., Reich, Z. & Hinterdorfer, P. (2003) Nat. Struct. Biol. 10, 553–557. [DOI] [PubMed] [Google Scholar]
- 25.Hummer, G. & Szabo, A. (2003) Biophys. J. 85, 5–15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Chen, S. & Springer, T. A. (2001) Proc. Natl. Acad. Sci. USA 98, 950–955. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Barsegov, V., Shapir, Y. & Mukamel, S. (2003) Phys. Rev. E 68, 011101–011114. [DOI] [PubMed] [Google Scholar]
- 28.Barsegov, V. & Mukamel, S. (2002) J. Chem. Phys. 117, 9465–9477. [Google Scholar]
- 29.Evans, E., Leung, A., Heinrich, V. & Zhu, C. (2004) Proc. Natl. Acad. Sci. USA 101, 11281–11286. [DOI] [PMC free article] [PubMed] [Google Scholar]